Abstract
One critical step in tumor metastasis is tumor cell adhesion to the endothelium forming the microvessel wall. Understanding this step may lead to new therapeutic concepts for tumor metastasis. Vascular endothelium forming the microvessel wall and the glycocalyx layer at its surface are the principal barriers to, and regulators of the material exchange between circulating blood and body tissues. The cleft between adjacent ECs (interendothelial cleft) is the principal pathway for water and solutes transport through the microvessel wall in health. It is also suggested to be the pathway for high molecular weight plasma proteins, leukocytes and tumor cells across microvessel walls in disease. Thus the first part of the review introduced the mathematical models for water and solutes transport through the interendothelial cleft. These models, combined with the experimental results from in vivo animal studies and electron microscopic observations, are used to evaluate the role of the endothelial surface glycocalyx, the junction strand geometry in the interendothelial cleft, and the surrounding extracellular matrix and tissue cells, as the determinants of microvascular transport. The second part of the review demonstrated how the microvascular permeability, hydrodynamic factors, microvascular geometry and cell adhesion molecules affect tumor cell adhesion in the microcirculation.
Keywords: Inter-endothelial cleft, Permeability measurement, Transport models, Endothelial surface glycocalyx, Integrins, Adhesive dynamic models, Microvessel curvature, Shear/shear gradient
INTRODUCTION
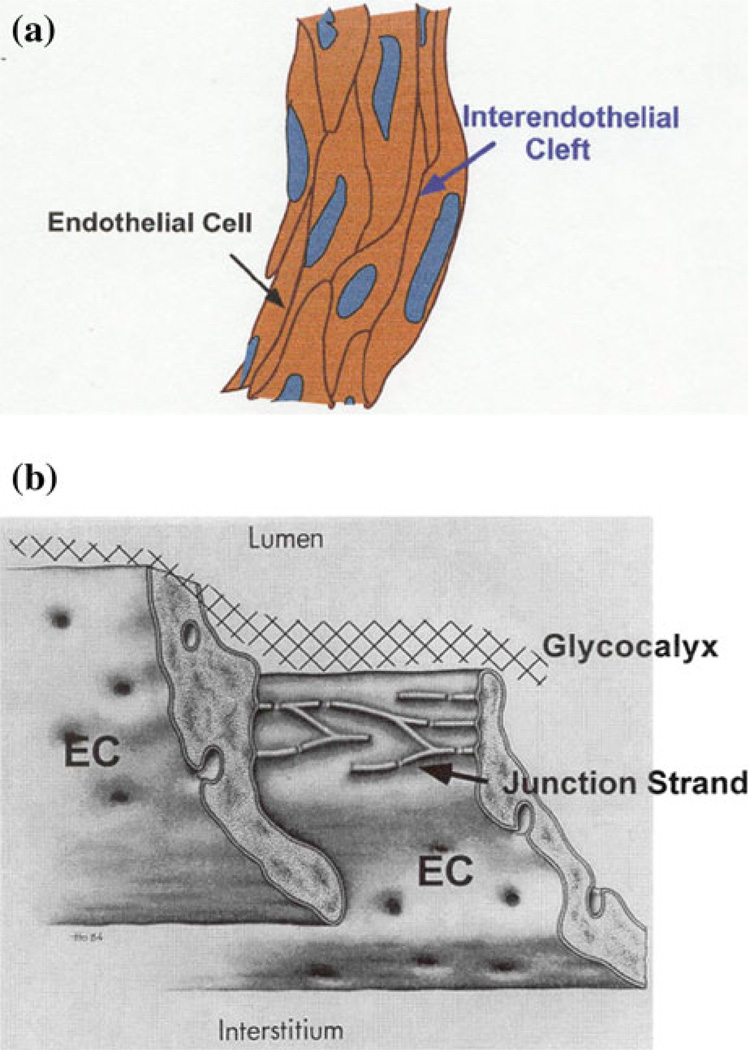
Microvascular bed is the primary location where water and nutrients are exchanged between circulating blood and body tissues. Microvessel walls consist mainly of endothelial cells (ECs) (Fig. 1a). Under normal conditions, the cleft between ECs (interendothelial cleft) is widely believed to be the principal pathway for water and hydrophilic solutes (such as glucose, amino acids, vitamins, hormones) transport across the capillary wall.61 Direct and indirect evidence indicates that there are junctional strands with discontinuous leakages14 and fiber matrix components61,77 at the endothelial surface (Fig. 1b). The transport of proteins or other macromolecules was thought to be through vesicle shuttle mechanisms.61 In disease, large gaps are formed in the microvessel endothelium to allow the passage of plasma proteins and cells such as blood cells and tumor cells. Microvascular permeability is a quantitative measure of how permeable the microvessel wall is to all kinds of substances including water and solutes with a variety of sizes. Under healthy conditions, the microvessel wall maintains a normal permeability to water and small solutes for the material exchange during our body’s metabolic processes. While in disease, the integrity of the vessel wall structure can be destroyed and much larger particles such as proteins, leukocytes and tumor cells can transfer through the wall. It is the transvascular pathways at the vessel wall and their structural barriers that determine and regulate the microvascular permeability. Therefore, we first introduce the basic information about transport across microvessels.
FIGURE 1.
(a) A typical mesenteric post-capillary venule of diameter 30 µm, whose wall consists of ECs. The gap between adjacent ECs is called inter-endothelial cleft. (b) Ultrastructural organization of junction strands in the inter-endothelial cleft and the ESG. Revised from Bundgaard.14
MICROVASCULAR INTERGRITY AND TRANSPORT ACROSS CONTINUOUS MICROVESSELS
The ECs lining microvessel walls provide the rate-limiting barrier to extravasation of plasma components of all sizes from electrolytes to proteins. So far, there are three primary pathways observed in the wall of a continuous microvessel by using electron microscopy: intercellular clefts, transcellular pores, and vesicles. Microvessels of different types and in different tissues may have different primary transvascular pathways. Under different physiological and pathological conditions, the primary pathway can be changed for the same microvessel.61
Interendothelial (Intercellular) Cleft
The cleft between adjacent ECs is widely believed to be the principal pathway for water and hydrophilic solute transport through the microvessel wall under normal physiological conditions. The interendothelial cleft is also suggested to be the pathway for the transport of high molecular weight plasma proteins, leukocytes and tumor cells across microvessel walls in disease. Direct and indirect evidence (summarized in Michel and Curry61) indicates that there are tight junction strands with discontinuous leakages and fiber matrix components (glycocalyx layer)22 at the endothelial surface. These structural components of the microvessel wall form the barrier between the blood stream and body tissues, which maintains the normal microvessel permeability to water and solutes. Changes in permeability are caused by the changes in these structural components.
The molecular basis for the passage of molecules at the level of the breaks in tight junctions is more likely to be the localized absence of cell–cell contacts with corresponding loss of a closely regulated molecular sieve as suggested by Weinbaum et al.,88 Fu et al.,31 and Michel and Curry.61 Thus the junction break-surface matrix model suggests independent mechanisms to regulate the permeability properties of the microvessel wall. The junction break size and frequency is likely to involve regulation of cell–cell attachment via occludin and other junction proteins including the cadherins associated junctions.25 On the other hand, the regulation of glycocalyx density and organization is likely to involve interaction of the molecules forming the cell surface with the cytoskeleton, and with circulating plasma proteins. Some of the cellular mechanisms underlying these interactions are reviewed in Drenckhahn and Ness25 and Michel and Curry.61 Under physiological and pathological conditions, microvessel permeability can be regulated acutely and chronically by mechanisms that are underway to being understood.
Serial section electron microscopy study on frog and rat mesenteric capillaries by Adamson et al.1 demonstrated that the junction strand was interrupted by infrequent breaks that, on average, were 150 nm long, spaced 2–4 µm apart along the strand, and accounted for up to 10% of the length of the strand under control conditions. At these breaks, the space between adjacent ECs (average ~20 nm) was as wide as that in regions of the cleft between adjacent cells with no strands. The luminal surfaces of ECs lining vasculature are coated with a glycocalyx of membrane-bound macromolecules comprised of sulfated proteoglycans, hyaluronic acid, sialic acids, glycoproteins and plasma proteins that adhere to this surface matrix.69,83 The thickness of this endothelial surface glycocalyx (ESG) was observed from <100 nm to 1 µm on the microvessels in different tissues and species by using different preparation and observing methods.21,37,56,59,61,77,84,86,92 Although the ESG thickness varies, its density and organization was reported to be the same among different tissues and species. The glycocalyx fiber radius is ~6 nm and gap spacing between fibers ~8 nm.5,77
Vesicles
Cytoplasmic vesicular exchange, which behaves like a shuttle bus, is presumed to be the major pathway for transport of plasma proteins and large molecules under normal physiological conditions.61
Transcellular Pores
In response to local tissue injury or inflammation, additional transport pathways for large molecules may be opened (transcellular pores) and existing pathways made less restrictive. The response is complex, and varies among different animals, organs, and tissues.61
Transport Coefficients
Aforementioned ultrastructural study using electron microscopy and other methods shows that the microvessel wall behaves as a passive membrane for water and hydrophilic solute transport. The membrane transport properties are often described by Kedem–Katchalsky equations derived from the theory of irreversible thermodynamics,
| (1) |
| (2) |
where Js and Jv are the solute and total volumetric fluxes; ΔC and Δp are the concentration and pressure difference across the membrane. Lp, the hydraulic conductivity, describes the membrane permeability to water. P, the diffusive permeability, describes the permeability to solutes. σf is the solvent drag or ultrafiltration coefficient that describes the retardation of solutes due to membrane restriction, and σd, the reflection coefficient, describes the selectivity of membrane to solutes. In many transport processes, σf is equal to σd61 and thus we often use σ, the reflection coefficient, to represent both of them. R is the universal gas constant and T is the absolute temperature.
Permeability Measurement
All of the permeability measurements have been interpreted in terms of Lp, P and σ, which are measured experimentally on intact whole organisms (including human subjects), on perfused tissues and organs, on single perfused microvessels, and on monolayers of cultured microvascular ECs. Different experimental preparations have their advantages and disadvantages. Although measurements made on the intact regional circulation of an animal subject (usually using radioactive isotope labeled tracers) suffer from uncertainties surrounding the exchange surface area of the microvessel wall and the values of the transvascular differences in pressure and concentration, they usually involve minimal interference with the microvessels themselves. These studies can provide valuable information concerning microvascular exchange under basal conditions. At the other end are measurements on single perfused vessels. The Landis technique has been used to measure the hydraulic conductivity Lp and reflection coefficient σ. Quantitative fluorescence microscope photometry is used to measure solute diffusive permeability P. Both of these techniques are described in detail in Michel and Curry.61 The surface area of the microvessel can be measured directly, as also can the difference in pressure and concentration across the vessel walls. The disadvantages of the single vessel preparation are (1) that they have direct interference with the vessels involved, and (2) that they are usually restricted to a small number of convenient vessel types (e.g., mesenteric vessels on a two dimensional translucent tissue). Direct interference with a vessel whether it is exposure to light or micromanipulation might be expected to increase permeability. However, this concern was allayed when it was shown that Lp and P to potassium ions in single muscle capillaries were similar to values based on indirect measurements on the intact muscle microcirculation.61
Although the rapid growth of EC biology is largely a result of experiments on cultured ECs in vitro (in dishes), there are limitations to the use of monolayers of cultured ECs for gaining direct information about vascular permeability. In general, the in vitro permeability to albumin is 2–10 times larger than that from the in vivo (in live animals) measurement. Although the monolayers of cultured ECs do not completely reflect the permeability characteristics of microvascular endothelium in vivo, they are the most accessible and convenient models for studying the molecular mechanisms by which the microvascular permeability is regulated. The techniques for measuring endothelial monolayer permeability to water and solutes were described in Antonetti et al.,4 Cancel et al.,15 and Li et al.53
TRANSPORT MODELS
1-D Models
Prior to the late 1980s, there were two major one-dimensional theories: the pore-slit and the fiber matrix theory, which attempted to correlate cleft structure with the large amount of experimental data for Lp, P and σ. In microvessels with continuous endothelium, the principal pathway for water and solutes lies between the ECs through the interendothelial cleft. 1-D pore-slit models were developed in terms of the ultrastructure of the cleft.
In the pore-slit theory, the permeability properties of the microvessel wall can be described in terms of flow through water-filled cylindrical pores or rectangular slits through the vessel wall. The characteristic Reynolds number for the flow is in the order of 10−8. A Poiseuille type viscous flow was assumed in the pore/slit to describe the resistance to water flow. The resistance to solute diffusion was described in terms of the additional drag on a spherical molecule moving within the pore relative to movement in free solution, and the selectivity of the membrane in terms of steric exclusion at the pore entrance.61
In the fiber matrix theory, the principal hypothesis to describe the molecular filter of the transvascular pathway is the fiber matrix theory due to the presence of a glycocalyx layer at the EC surface. Using the stochastic theory of Ogston et al.,66 Curry and Michel61 described the solute partition coefficient and the restricted solute diffusion coefficient in terms of the fraction of the matrix volume occupied by fibers and the fiber radius. The partition coefficient is defined as the space available to a solute of radius a relative to the space available to water with a = 0. In fact, their expressions for the effective diffusivity of a solute only consider the steric exclusion of solutes by the fiber array; they do not include the hydrodynamic interactions between the fibers and the diffusing solute, which are important when the solute size is comparable to the gap spacing between fibers. Using two approaches, Philips et al.68 calculated the effects of hydrodynamic interactions on the hindered transport of solid spherical macromolecules in ordered or disordered fibrous media. One approach was a rigorous “Stokesian-dynamics” method or generalized Taylor dispersion theory,11 which can calculate local hydrodynamic coefficients at any position in a fibrous bed.12 But detailed information about the fiber configuration needs to be given.61 Another approach was an effective medium theory based on Brinkman’s equation. Comparing the calculating results with the experimental data for several proteins transport in hyaluronic acid solutions, they found that the use of Brinkman’s equation was in good agreement with the more rigorous methods for a homogeneous fiber matrix.61
By using a simplified model of the ESG, in which the core proteins in the ESG were assumed to have a circular cylindrical shape and to be aligned in parallel to form a hexagonal arrangement, which was based on recent detailed structural analyses of the ESG,77 Sugihara-Seki et al.80,81 analyzed the motion of solute and solvent to estimate the filtration reflection coefficient as well as the diffusive permeability of the ESG. Later, Zhang et al.95 studied osmotic flow through the ESG using a method developed by Anderson and Malone3 for osmotic flow in porous membranes. Instead of a rigorous treatment of the hexagonal geometry of the cylinders, they adopted an approximation in which the geometry is replaced by an equivalent fluid annulus around each cylinder and estimated the osmotic reflection coefficient of the ESG. Further, Akinaga et al.2 examined the charge effect on the osmotic flow for membranes with circular cylindrical pores by extending the formulation of osmotic flow developed by Anderson and Malone.3
3-D Models
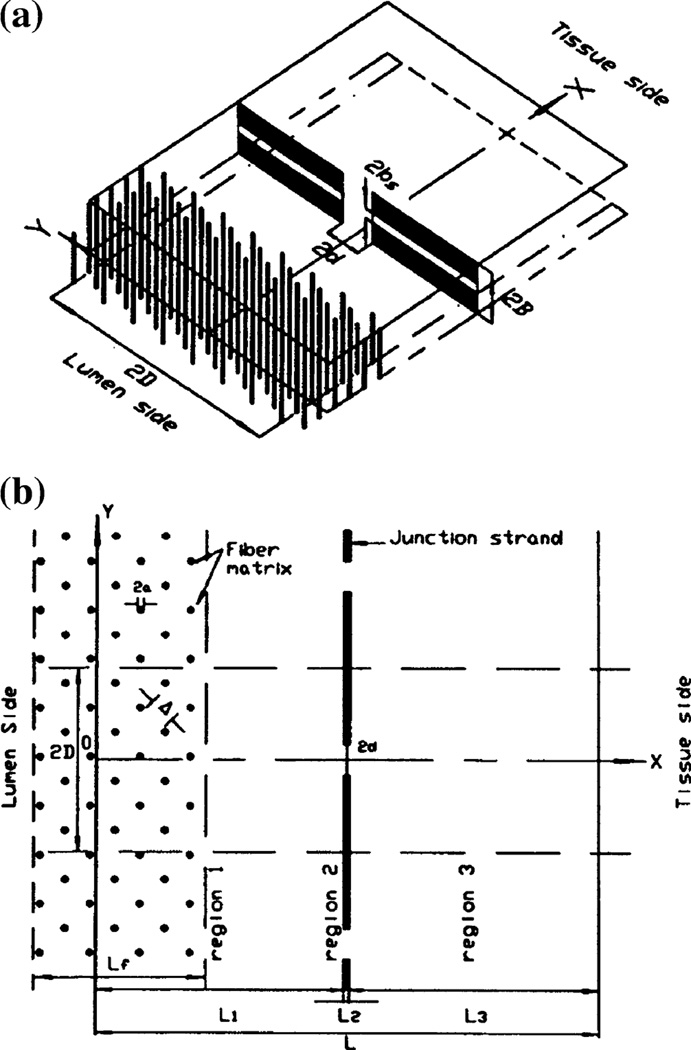
Previous 1-D models are based on the random section electron microscopy until 1984. Bundgaard14 was the first to attempt to reconstruct the 3-D junction strand ultrastructure using serial section electron microscopy. Later, Ward et al. examined the 3-D features of the junction strands of rat cardiac capillaries by using a goniometric tilting technique. Based on the study of Bundgaard14 and Ward et al., Tsay et al., and Weinbaum et al.61 proposed a basic 3-D model for the interendothelial cleft. Their 3-D models showed that 1-D models are a poor description of a cleft with infrequent large breaks since the solute will be confined to small wake-like regions on the downstream side of the junction strand discontinuities and thus not fill the wide part of the cleft. The prediction in Weinbaum et al.61 as to the likely geometry of the large pores in the junction strand was confirmed by the serial section electron microscopic study on frog mesenteric capillaries in Adamson and Michel.61 According to these new experimental results, a modified combined junction-orifice-fiber entrance layer model (Fig. 2), which included a large orifice-like junctional break, a finite region of fiber matrix components at the entrance of the cleft and very small pores or slits in the continuous part of the junction strand, was developed by Fu et al.36 This combined junction-orifice-fiber entrance layer model predicted that in order to provide an excellent fit for the hydraulic conductivity and the diffusive permeability data for solutes of size ranging from potassium to albumin for frog mesenteric capillaries, there should be a significant fiber layer at the luminal side of the endothelium, and large infrequent breaks of ~150 nm and a continuous small slit of several nm in the junction strand in the inter-endothelial cleft. Due to the similarity in morphological wall structure of microvessels in different tissues,61 this 3-D model can be easily adapted to explain the permeability data in other types of microvessels.52,54,94 Fu et al.32 in another work described a new approach to explore junction strand structure. The time dependent diffusion wake model in Fu et al.32 provided a new interpretation of labeled tracer studies to define the permeability pathways for low molecular weight tracers which depend on the time dependent filling of the extravascular space.
FIGURE 2.
(a) 3-dimensional sketch of the junction-orifice-matrix entrance layer model for the interendothelial cleft. 2B is the width of the cleft. Large junction breaks observed in Adamson et al.1 are 2d × 2B, while the small continuous slit in the junction strand is 2bs. (b) plane view of the model. Junction strand with periodic openings lies parallel to the luminal front of the cleft. L2, depth of pores in junction strand. L1 and L3, depths between junction strand and luminal and abluminal fronts of the cleft, respectively. 2D, distance between adjacent large junction breaks. At the entrance of the cleft on luminal side, cross-bridging structures are represented by a periodic square array of cylindrical fibers. a, radius of these fibers, Δ, gap spacing between fibers, and Lf, thickness of entrance fiber layer (from Fu et al.30–32,36). The fiber matrix (surface glycocalyx) carries negative charge due to its molecular composition.69,83 The charge density of the surface glycocalyx is in the range of 20–30 mEq/L for mesenteric and brain microvessels.30,52
In Fu et al.31 a time dependent convective-diffusion wake model for high molecular weight tracers was proposed to design experiments that can test for the location of the molecular filter. Combined with the experimental results, this model confirmed the role of the ESG as the primary molecular filter to large molecules and particles. Hu and Weinbaum61 also showed that coupling of water flow to albumin flux on the tissue side of the ESG could give rise to a nonuniform distribution of albumin concentration and a corresponding nonuniform distribution of effective osmotic pressure. Similar model for oncotic pressures opposing filtration across rat microvessels1 further conforms the hypothesis that colloid osmotic forces opposing filtration across non-fenestrated continuous capillaries are developed across the ESG and that the oncotic pressure of interstitial fluid does not directly determine fluid balance across microvascular endothelium.
Effects of Charge Carried by the Endothelial Surface Glycocalyx
Due to the composition of the ESG, it carries negative charge61,93 and would affect the permeability and selectivity of the microvessel wall to water and solutes.71,72 Previously, a simple 1-D Donnan-type model was proposed to describe the charge effect on microvessel permeability.61 It was based on a Donnan equilibrium distribution of ions, which exists as a result of retention of negative charges on the capillary membrane. Later, an electrochemical model was proposed by Damiano and Stace23 for the transport of charged molecules through the capillary glycocalyx without considering transport through the cleft region. To investigate the charge selectivity on microvessel permeability, Fu et al.30 extended the 3-D junction-orifice-fiber matrix model developed by Fu et al.36 for the interendothelial cleft to include a negatively charged glycocalyx layer at the entrance of the inter-endothelial cleft. Both electrostatic and steric exclusions on charged solutes are considered at the interfaces of the glycocalyx layer between the vessel lumen and between the endothelial cleft. The effect of electrostatic interactions between charged solutes and the matrix on solute transport is also described within the glycocalyx layer. Their model can successfully explain the observations in Michel and Curry.61 Recently, an electrodiffusion-filtration model was developed to describe the transport of negatively charged macromolecules, bovine serum albumin, across venular microvessels in frog mesentery.19 A very interesting prediction is that the convective component of albumin transport is greatly diminished by the presence of a negatively charged glycocalyx. Most recently, Li et al.52 has developed a model for the charge effect of the ESG and the basement membrane between the endothelium and astrocyte foot processes on the transport across the blood–brain barrier.
Bhalla and Deen9 studied the effects of charge on osmotic reflection coefficients of macromolecules in porous membranes. Sugihara-Seki et al.82 proposed an electrostatic model to predict the effects of surface charge on the osmotic reflection coefficient of charged spherical solute across the ESG, based on the combination of low-Reynolds-number hydrodynamics and a continuum description of the electric double layers. The ESG was assumed to consist of identical circular cylinders with a fixed surface charge, aligned parallel to each other so as to form an ordered hexagonal arrangement. Their model predicts that the charge of the ESG contributes significantly to the microvessel reflection coefficient to albumin, which was reported in Michel and Curry.61
MICROVASCULAR HYPERPERMEABILITY AND TUMOR METASTASIS
The danger of cancer is organ failure caused by metastatic tumors that are derived from the primary tumor.78 One critical step in tumor metastasis is adhesion of primary tumor cells to the endothelium forming the microvascular wall in distant organs. Understanding this step may lead to new therapeutic concepts for tumor metastasis targeting tumor cell arrest and adhesion in the microcirculation. Microvascular hyperpermeability due to compromised microvessel wall integrity by inflammatory agents and cytokines is one factor that increases tumor cell adhesion to the microvessel endothelium.
VEGF Effect on Microvascular Integrity
Vascular endothelial growth factors (VEGFs) are a family of cytokines that act to increase the delivery of nutrients to tissue by three distinct mechanisms: (a) EC growth, migration, and new blood vessel formation (angiogenesis)26; (b) increased blood flow (by vasodilatation)7; and (c) increased vascular permeability to water and solutes.6,26,33,34,45,70,89 Combining in vivo permeability measurement and a mathematical model for the inter-endothelial transport, Fu et al.33 predicted that acute effects of VEGF on microvascular integrity are widened gap opening of the inter-endothelial cleft and partial degradation of the ESG. Longer term effects of VEGF include formation of gaps between adjacent ECs in venular microvessels,60 vesiculovascuolar organelle pathways,29 transcellular pores,29,62 and fenestra.29,70 Fu et al.35 also found that the VEGF-induced microvascular hyperpermeability can be abolished by enhancing intra-cellular levels of adenosine 3′,5′-cyclic monophosphate (cAMP), which strengthens the microvessel integrity by increasing the number of junction strands in the cleft between ECs forming the microvessel wall.
VEGF Effect on Tumor Cell Adhesion
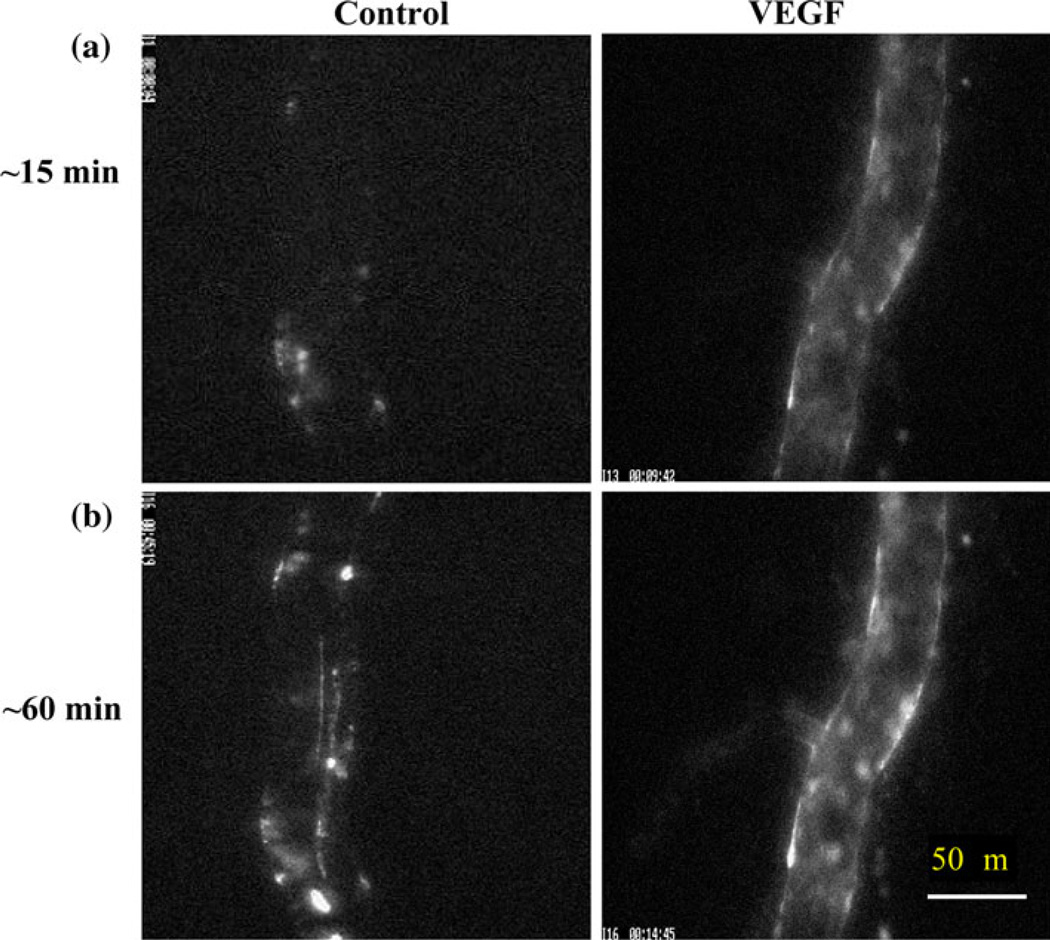
Previous studies have found that many cancer cells express VEGF to a high degree,51 while the microvascular endothelium has abundant VEGF receptors including VEGFR2 (KDR/Flk-1).65 VEGFR2 has been implicated in normal and pathological vascular EC biology.67 Recently, it has been shown that ectopic administration of VEGF, enhances the adhesion and transmigration of human breast cancer MDA-MB-231 cells across a monolayer of human brain microvascular ECs under a static condition in vitro.51 In addition, VEGF enhances the adhesion of malignant MDA-MB-435 cells and ErbB2-transformed mouse mammary carcinomas to intact rat mesenteric microvessels under flow in vivo75 (Fig. 3).
FIGURE 3.
Photomicrographs showing in vivo MDA-MB-435s tumor cell adhesion to a single perfused microvessel under control with 1% BSA Ringer perfusate and under treatment with 1 nM VEGF perfusate after (a) ~15 min and (b) ~60 min perfusion. The perfusion velocity is ~1000 µm/s, which is the mean normal flow velocity in post-capillary venules. Bright spots indicate adherent tumor cells labeled with fluorescence. From Shen et al.75
Integrin Signaling, Cell Adhesion Molecules and Tumor Metastasis
Although the non-specific trapping due to the friction between the tumor cells and the narrow part of microvasculature is found to be responsible for the initial tumor cell arrest,38,41,47,64 the cell adhesion molecules are required for the adhesion in larger microvessels and transmigration.13,28,38–40,46,51,55,73,75,76,78 The integrins are a family of signaling and cell adhesion receptors, which attach cells to the extracellular matrix (ECM) and in some cases to other cells, and cooperate with growth factor and cytokine receptors to regulate cell behavior. Signals elicited by integrins enable tumor cells to survive, proliferate, migrate independently of positional constrains,42,46 and adhere.28 The α6β4 integrin is a laminin-5 receptor and was originally described as a “tumor-specific” protein, because of its apparent upregulation in multiple metastatic tumor types.39 The β4 integrin is unique among integrins, because the cytoplasmic portion of the β4 subunit is 1017 amino-acid-long and possesses distinctive adhesive and signaling functions.39 Upon binding of the ectodomain of β4 to the basement membrane protein laminin-5, the cytoplasmic portion of β4 interacts with the keratin cytoskeleton to promote the assembly of hemidesmosomal adhesions.57 In addition, β4 activates intracellular signaling autonomously as well as by associating with multiple receptor tyrosine kinases (RTKs), including the EGFR, ErbB2, Met, and Ron.42,63 Deletion of the β4 signaling domain delayed mammary tumor onset and inhibited primary tumor growth. The tumors arising in mutant mice were significantly more differentiated histologically as compared to control tumors. In addition, primary tumor cells expressing signaling-defective β4 displayed a reduced proliferative rate and invasive ability and underwent apoptosis when deprived of matrix adhesion. Finally, upon injection in the tail vein of nude mice, the mammary tumor cells expressing mutant β4 exhibited reduced ability to metastasize to the lung.43
Most recently, Fan et al.28 examined the adhesion of ErbB2-transformed mammary tumor cells to mouse brain microvascular endothelial monolayer. They found that integrin β4 signaling does not exert a direct effect on adhesion to the endothelium or the underlying basement membrane. Rather, it enhances ErbB2-dependent expression of VEGF by tumor cells. VEGF in turn partially disrupts the tight and adherens junctions that maintain the adhesion between ECs, enabling tumor cells to intercalate between ECs and extend projections reaching the underlying exposed basement membrane, and enabling the adhesion between cell adhesion molecules (e.g., integrins) and ECM proteins (e.g., laminins).
TUMOR CELL ADHESION IN THE MICROCIRCULATION
In vitro static adhesion assays have been utilized to investigate tumor cell adhesion to ECs27,51 and to ECM proteins.43 Tumor cell adhesion has also been investigated using flow chambers20,40,76 or artificial blood vessels13 to address flow effects. Direct injection of tumor cells into the circulation has enabled the observation of tumor cell metastasis in target organs after sacrificing the animals,73 while intravital microscopy has been used to observe the interactions between circulating tumor cells and the microvasculature both in vivo and ex vivo.38,41,47,64,75,79
Tumor Cell Adhesion Under Flow
Tumor cell extravasation is a dynamic process in which tumor cell adhesion to the vascular endothelium and transendothelial migration occurs under flow conditions. Therefore, the geometry of microvasculature and the local hydrodynamic factors, along with the cell adhesion molecules at the tumor cell and EC should play a crucial role in tumor cell adhesion and extravasation. Tumor cells are exposed to flow while (a) circulating from the primary tumor, (b) arresting on downstream vascular endothelium, and (c) transmigrating into the secondary target organ. Investigations of the role of shear flow in tumor cell adhesion and extravasation will contribute to the understanding of the complex process of tumor metastasis. Tumor cell extravasation would normally occur in the microvasculature where shear forces are relatively low (like in post-capillary venules) although of sufficient magnitudes to activate cell surface receptors and alter vascular cell function. During tumor cell extravasation there are significant changes in the structure and function of both tumor and ECs. For example a significant rearrangement of the cell cytoskeleton is required in both the tumor cells during migration50 and in the ECs as the barrier function is altered.85 The extravasation of tumor cells also induces EC remodeling.47
In an in vitro flow chamber study, Slattery et al.76 found that the shear rate, rather than the shear stress, plays a more significant role in PMN (polymorpho-nuclear neutrophils)-facilitated melanoma adhesion and extravasation. β2 integrins/ICAM-1 adhesion mechanisms were examined and the results indicate LFA (lymphocyte function-associated)-1 and Mac-1 (CD11b/CD18) cooperate to mediate the PMN-EC (endothelial cell)-melanoma interactions under shear conditions. In addition, endogenously produced IL-8 contributes to PMN-facilitated melanoma arrest on the EC through the CXC chemokine receptors 1 and 2 (CXCR1 and CXCR2) on PMN.55,76
To investigate tumor cell adhesion in a well-controlled in vivo system, Shen et al.75 and Yan et al.90 used intravital video microscopy to measure the adhesion rate of malignant MDA-MB-435 and 231 cells in straight and curved post-capillary venules on rat mesentery. A straight or curved microvessel was cannulated and perfused with tumor cells by a glass micropipette at a velocity of ~1 mm/s, which is the mean normal blood flow velocity in this type of vessels. At <10 min after perfusion, there was a significant difference in cell adhesion to the straight and curved vessel walls. In 60 min, the averaged adhesion rate in the curved vessels was ~1.5-fold of that in the straight vessels. In 51 curved segments, 45% of cell adhesion was initiated at the inner side, 25% at outer side, and 30% at both sides of the curved vessels. To investigate the mechanical mechanism by which tumor cells prefer adhering at curved sites, Yan et al.90 performed a computational study, in which the fluid dynamics was carried out by the lattice Boltzmann method (LBM), and the tumor cell dynamics was governed by the Newton’s law of translation and rotation. The details of this multi-scale modeling are summarized below.
Mathematical Models for Tumor Cell Adhesion in the Microcirculation
General Cell Adhesion Models
The extensive studies on biophysical experiments of cell adhesion have led to the development of a number of mathematical models. The construction and application of these models have demonstrated that it is possible to analyze cellular and molecular processes by highly quantitative approaches.96 Hammer and Apte44 proposed a mathematical model to simulate the interaction of a single cell with a ligand-coated surface under flow. This model can simulate the effect of many parameters on adhesion, such as the number of receptors on microvilli tips, the density of ligands, the rates of reaction between receptors and ligands, the stiffness of the resulting receptor–ligand springs, the response of springs to strains, and the magnitude of the bulk hydrodynamic stresses. The model can successfully recreate the entire range of expected and observed adhesive phenomena, from completely unencumbered motion, to rolling, to transient attachment, and to firm adhesion. Moreover, this model can generate meaningful statistical measures of adhesion, including the mean and variance in velocity, rate constants for cell attachment and detachment, and the frequency of adhesion. King and Hammer48 used the completed double-layer boundary integral equation method to study the adhesive interactions between multiple rigid particles and a planar boundary in a viscous fluid. The simulation results revealed a mechanism for the capture of free-stream cells when an initial cell has adhered to provide a nucleation site. Wang et al.87 developed a population balance model for cell aggregation and adhesion process in a non-uniform shear flow, and they carried out Monte Carlo simulation based on the model for the heterotypic cell–cell collision and adhesion to a substrate under dynamic shear forces. Shao and Xu74 numerically studied the adhesion between a microvillus-bearing cell and a ligand-coated substrate by using Monte Carlo method. They found that most of the adhesion was mediated by a single bond if the total adhesion frequency was <20%.
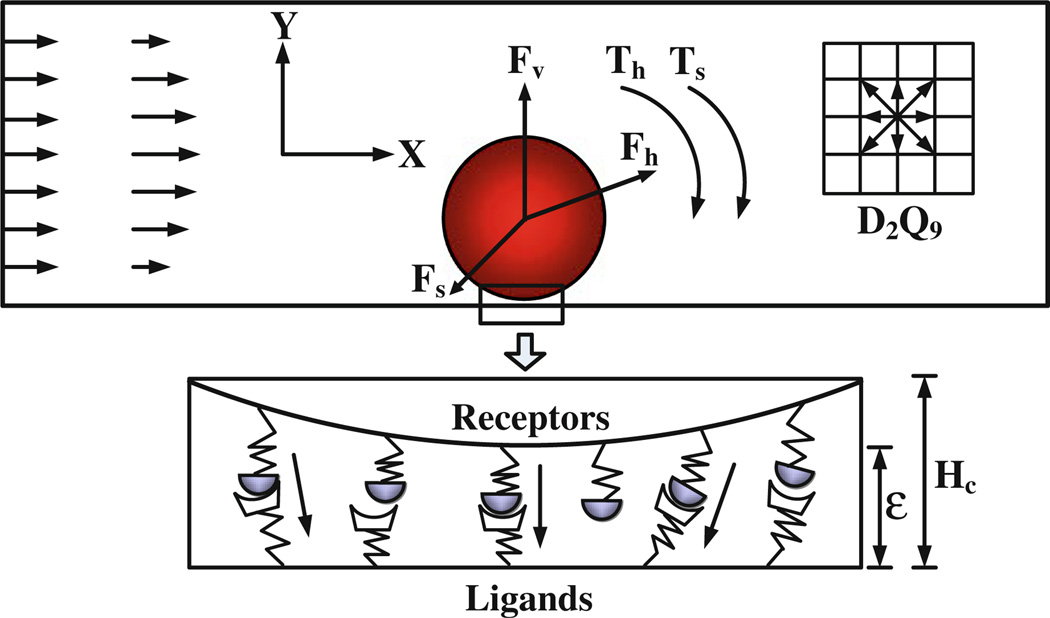
Mathematical models of cell adhesion relate the forward and reverse reaction rates for receptor–ligand bonds. These reaction rates laws for cell adhesion have been defined as ‘adhesive dynamics models’, which can be used to couple the effect of receptor–ligand bonds on cell adhesion. Figure 4 shows the schematic view of adhesive dynamics model for the cell. In this model, the cell adhesion molecules on the surface of circulating cell are defined as receptors, and these on the surface of ECs are defined as ligands. Once the distance between receptor and ligand is smaller than the critical length Hc, it has the chance to form receptor– ligand bonds. Interactions between receptors and ligands are realized by the ideal adhesive springs, and the spring forces are calculated via the compression or expansion of these springs. This dynamic process relates the bond association and dissociation rate of adhesive dynamics models. The following are the two typical cell dynamic models.
FIGURE 4.
Schematic diagram of the adhesive dynamics model. is the hydrodynamic force which can be calculated by momentum exchange method,49 is the repulsive van der Waals force which can be derived by the Derjaguin approximation,10 is the total spring force that contributed by the adhesive receptor–ligand bonds, and Th and Ts are the torques induced by the hydrodynamic force and spring force, respectively. ε is the bond length. From Yan et al.90,91
Bell’s Model
This model8 was validated to be a good approximation for different states of cell adhesion in the straight microvessels, such as no adhesion, rolling, landing, and firm adhesion.16 In this model, the association rate of the bond is 84 s−1, which is a reasonable value that extensive simulations have shown can properly recreate experimental values for velocity and dynamics of rolling in the straight microvessels. As to the dissociation rate of the bond, Bell8 adapted the kinetic theory of the strength of solids and proposed a constitutive relation between dissociation rate and force. Therefore, the bond association rate kf and bond dissociation rate kr are,
| (3) |
| (4) |
where kb is the Boltzmann constant, T the absolute temperature, the unstressed dissociation rate, and γ the reactive compliance that describes the degree to which force facilitates bond breakage. Both and γ are the functional properties of adhesion molecules. f is the spring force of each bond which can be obtained according to the Hooke’s law:
| (5) |
where σ is the spring constant, χ is the distance between the end points of receptor and ligand, and λ is the equilibrium bond length.
Dembo et al.’s Model
Dembo et al.24 modeled a piece of membrane with immobile discrete bonds and allowed the membrane to detach. They did this by letting the applied tension exceed the bond stress. This model can be used to predict the critical membrane tension required for detachment, and the resulting peeling velocities of the membrane. The main contribution of this model is the expression for the rate constants as a function of distance between the membranes. Dembo et al.24 demonstrated the reasonable, thermodynamically consistent rate expressions relating the bond association rate kf and bond dissociation rate kr to χ as,
| (6) |
| (7) |
where and are the reaction rate constants when the spring is at its equilibrium length, and σ and σts is the spring constant and “transition state” spring constant, respectively.
Once the forward association rate and the reverse dissociation rate of the bond are known, the appropriate expressions for the probability of formation and breakage of the bond tethers in a time step dt can be obtained by Chang and Hammer,17
| (8) |
| (9) |
where Pf is the probability of forming a bond, and Pr is the probability of breaking a bond in a time interval dt. Recently, these adhesive dynamic models were adapted to describe tumor cell adhesion in the microcirculation on the basis of experimental observations. The major results are presented below.
Model Predictions for Tumor Cell Adhesion in the Microcirculation
Effect of Curvature
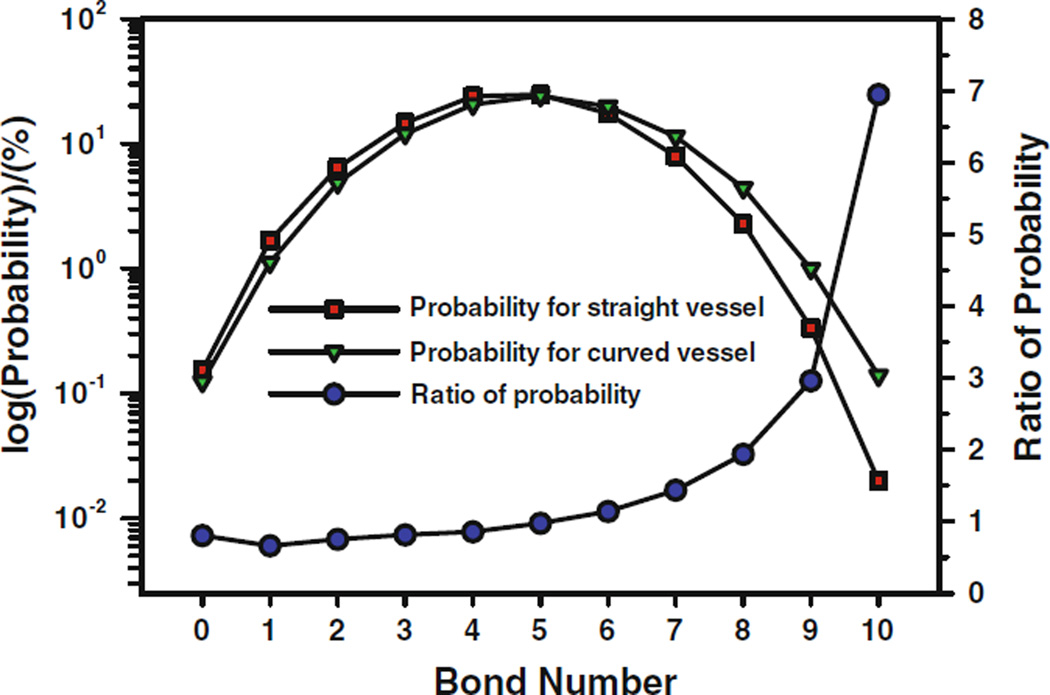
It has been found that both the circulating blood cells and tumor cells prefer to adhere to the curved microvessels than the straight ones.58,90 To study the effect of vessel curvature on tumor cell adhesion, Yan et al.91 carried out numerical simulation using the scheme proposed by Hammer and Apte,44 which was based on Dembo et al.’s model24. They compared the variation of cell velocity and rotational velocity, calculated the force acting on the cell, and computed the bonds formed during the cell migration process between straight and curved microvessels. The higher number of bonds means there is a higher opportunity for a cell to adhere to the vessel wall. For a single cell in a straight vessel, after off and on interactions between the circulating cell and ECs forming the vessel wall, the steady bonds are formed throughout the journey; for a single cell in a curved vessel, the cell adhesion only takes place at the positive curvature wall, once leaving the positive curvature wall, the cell moves as a free cell, and there is no cell adhesion in the negative curvature wall at all. To compare the probability of cell adhesion between the straight and curved microvessels, they calculated the statistics of bonds number, the probability of each bond number occurring, and the ratio of these two probabilities as shown in Fig. 5. It can be found that, for the smaller bonds number, the probability in the straight vessel is larger than that in the curved vessel, and the turning point is at bonds number being 5 with the probability of 25.5%. For the larger bonds number, i.e., the bonds number larger than 5, the probability in the curved vessel is obviously higher than that in the straight vessel, and the larger the bonds number, the higher the probability in the curved vessel. It is understandable that the final cell adhesion depends on the number of bonds, the more the simultaneous bonds form, the higher probability the cell adheres to the vessel wall. Therefore the vessel curvature has a significant influence on the cell adhesion.
FIGURE 5.
Comparison of bond formation probabilities and the ratio of the probabilities between the straight and curved microvessels for a single cell in the vessel 1. From Yan et al.90
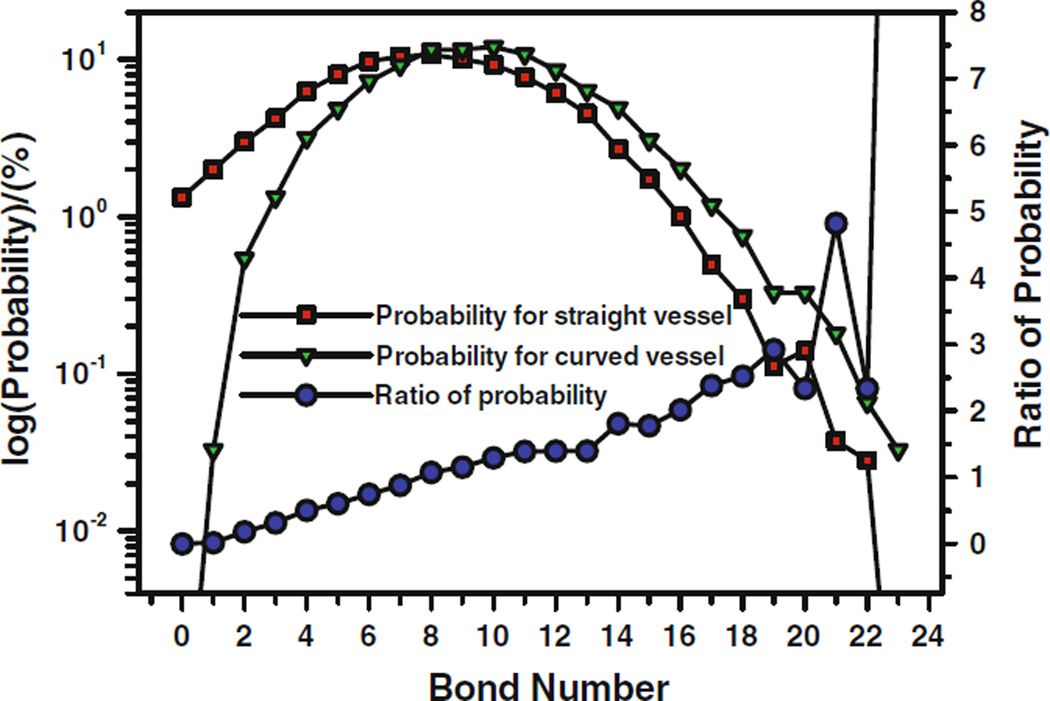
The blood flow always involves multiple cells, and the interaction of the cells would affect the cell adhesion and migration. For two cells in a straight vessel, due to the interaction between cells, the number of bonds is more than twice that in the single cell case; for two cells in a curved vessel, the number of bonds increases significantly as well, the number of bonds changes dramatically during the whole process, and similar to the single cell, the bonds form in the negative curvature wall. From the statistical comparison of bonds number as shown in Fig. 6, similar to the single cell case, at lower bond numbers, the straight vessel has higher probability to form the bonds. The turning point is at the bonds number of 8. When the bond number is larger than 8, the curved vessel has more chances to form bonds between cell and the ECs at the vessel wall. At higher bonds number, e.g., bonds number of 21 or more, the bond forming probability of the curved vessel can be five times that of the straight vessel. The final cell adhesion is actually dependent on the simultaneous bond forming. The higher the bonds number, the more likely cell adhesion occurs. Therefore, the cell, particularly under the interaction of other cells, has higher probability to adhere to the ECs in the curved vessel than in the straight vessel.
FIGURE 6.
Comparison of bond formation probabilities and the ratio of the probabilities between the straight and curved microvessels for two cells in the vessel. From Yan et al.90
Effect of Wall Shear Stress
At the curved sites, there are rather complicated distributions of wall shear stress, and the wall shear stress or its variation may activate receptor–ligand bond forming, which appears to render these sites to be prone to catch cells. Based on the experimental observation, Yan et al.90 revised the Bell’s model by integrating the effect of wall shear stress and its gradient, respectively. The models are:
Case 1
The bond association/dissociation rates are related to shear stress:
Case 2
The bond association/dissociation rates are related to shear stress gradients:
where τ and τ0 are the wall shear stress along the curved vessel and along the straight vessel, respectively, and dτ/dl is the wall shear stress gradient along the curved vessel. k1, k2 and k3, k4 are coefficients that represent the sensitivity of wall shear stress and its gradient to bond association/dissociation rates, respectively.
Case 3
Use the same model as case 2. Only the jumps or drops in the wall shear stress gradient can trigger the change of bond association/dissociation rates. Once triggered, the association/dissociation rates will keep the maximum/minimum value until the next wall shear stress gradient jump or drop occurs.
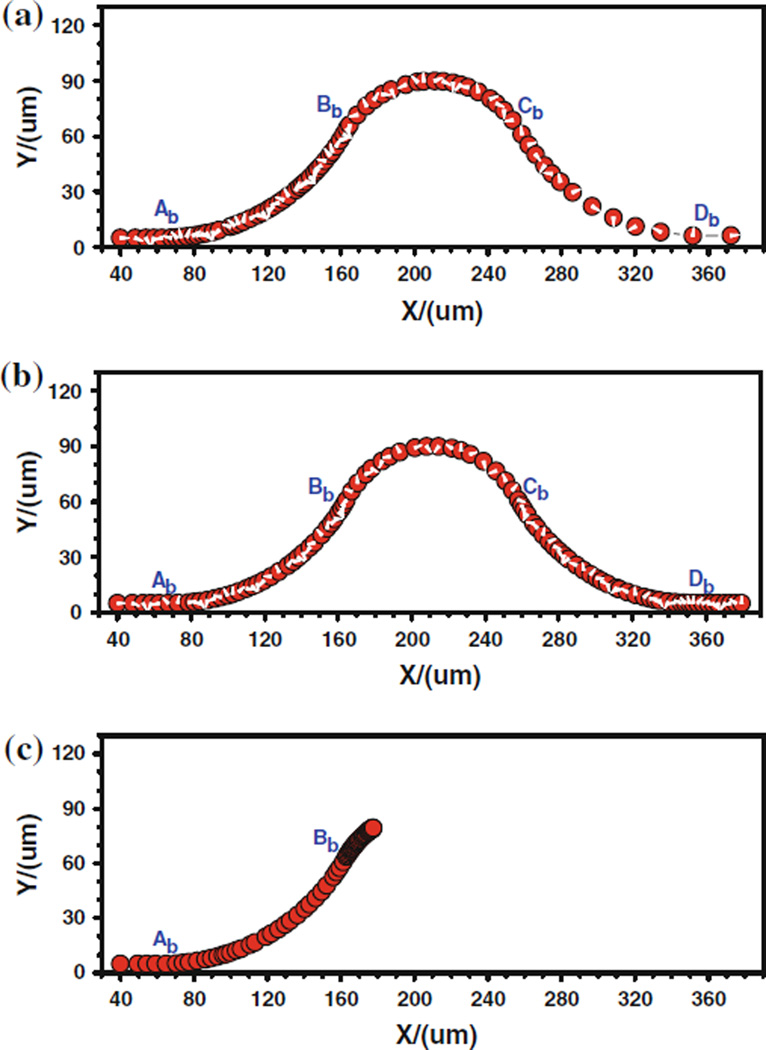
Figure 7 shows the cell trajectory for these three cases where the denser trajectory indicates a slower motion and the coarse trajectory a faster motion. For case 1, The denser trajectory occurs between Ab and Bb due to the centrifugal effect; and the coarser trajectory happens between Cb and Db, indicating a faster cell motion due to the decrease in kf and increase in kr, both of which result from the drop of wall shear stress. For case 2, the denser trajectory occurs near the conjunction Bb, indicating a slower cell motion there due to the stronger adhesive effect caused by the large jump in the wall shear stress gradient at Bb. Another denser trajectory happens near the conjunction Cb where the shear stress gradient has a sudden drop. This slower cell motion is not due to the adhesive effect but due to the centrifugal effect. The coarser trajectory exists in the positive curvature vessel (between Bb and Cb), indicating a faster cell motion due to the centrifugal effect. For case 3, when the cell approaches the conjunction Bb, the cell moves slower and slower, which is represented by a black band in the cell trajectory. Generally, the positive wall shear stress/gradient jump would enhance tumor cell adhesion while the negative wall shear stress/gradient jump would weaken tumor cell adhesion. The wall shear stress/gradient, over a threshold, had a significant contribution to tumor cell adhesion by activating or inactivating cell adhesion molecules. These results explain why the tumor cell adhesion prefers to occur at the positive curvature of curved microvessels with very low Reynolds number (in the order of 10−2) laminar flow.
FIGURE 7.
The history of the trajectory of the tumor cell along the inner wall of a curved vessel, (a) case 1, (b) case 2, and (c) case 3. From Yan et al.90
In general, the revised Bell’s models are capable of simulating the tumor cell adhesion phenomenon in the curved microvessel. From a physiological point of view, it can be deemed that the binding affinity of cell adhesion molecules would be enhanced or weakened by the variation of wall shear stress. The data in the literature have shown that the initial arrest of tumor cells in normal organs is resulted from the non-specific friction between tumor cells and microvessel wall38,41,47,64 in narrow microvessels but the tumor–EC adhesion in larger microvessels needs specific molecules.13,28,38–40,46,51,55,73,75,76,78 The data from Yan et al.90,91 support the idea that the tumor cell adhesion requires a critical wall shear stress/gradient in the curved microvessel, once the wall shear stress/gradient is superior to the critical value, it would trigger the bond association/dissociation rates to change.
SUMMARY AND FUTURE STUDY
Although transport across endothelium is a classical problem that has been investigated for more than several decades, the fundamental questions related to the structure-transport function of the microvessel wall and the interaction between the circulating cells and the cells forming the wall still remain unclear. With the help from mathematical models for more accurate interpretations and predictions, new techniques involving transgenic animals with fluorescent proteins expressed ECs and circulating blood and tumor cells, new fluorescent dyes for labeling the structural components of transvascular pathways, intravital and electron microscopy, and new developments in molecular biology and biochemistry will lead to more fascinating discoveries in this field.
One problem that has not been investigated thoroughly is the selectivity of the microvessel wall to solutes with various sizes, shapes, and charges, especially in the glycocalyx layer. New models are expected to elucidate the interactions between solutes and the fiber matrix as well as between solutes when the solute size is very close to the gap spacing between fibers and when the solution is no longer dilute. Another problem is the development of models for dynamic water and solute transport through multi-transvascular pathways including intercellular, transcellular, fenestrae and vesicle routes. They are important for predicting the malfunction in the transvascular process in disease. The third problem is to create transvascular models for cells such as leukocytes and cancer cells. The current multi-scale cell adhesion model can be revised to include the mechanical properties and morphological changes of adherent and ECs in developing the cell transmigration models. The cell transport is crucial in many physiological and pathological processes including inflammatory response and tumor metastasis.
Acknowledgments
We thank the support from the NSF CBET 0754158 and NIH CA153325-01 and CA137788-01, and Hong Kong Research Grants Council of the Government of the HKSAR PolyU 5238/08E.
REFERENCES
- 1.Adamson RH, Lenz JF, Zhang X, Adamson GN, Weinbaum S, Curry FE. Oncotic pressures opposing filtration across non-fenestrated rat microvessels. J. Physiol. 2004;557:889–907. doi: 10.1113/jphysiol.2003.058255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Akinaga T, Sugihara-Seki M, Itano T. Electrical charge effect on osmotic flow through pores. J. Phys. Soc. Jpn. 2008;77:053401. [Google Scholar]
- 3.Anderson JL, Malone DM. Mechanism of osmotic flow in porous membranes. Biophys. J. 1974;14:957–982. doi: 10.1016/S0006-3495(74)85962-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Antonetti DA, Wolpert EB, DeMaio L, Harhaj NS, Scaduto RC., Jr Hydrocortisone decreases retinal endothelial cell water and solute flux coincident with increased content and decreased phosphorylation of occludin. J. Neurochem. 2002;80:667–677. doi: 10.1046/j.0022-3042.2001.00740.x. [DOI] [PubMed] [Google Scholar]
- 5.Arkill KP, Knupp C, Michel CC, Neal CR, Qvortrup K, Rostgaard J, Squire JM. Similar endothelial glycocalyx structures in microvessels from a range of mammalian tissues: evidence for a common filtering mechanism? Biophys. J. 2011;101:1046–1056. doi: 10.1016/j.bpj.2011.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bates DO, Curry FE. Vascular endothelial growth factor increases hydraulic conductivity of isolated perfused microvessels. Am. J. Physiol. 1996;271(40):H2520–H2528. doi: 10.1152/ajpheart.1996.271.6.H2520. [DOI] [PubMed] [Google Scholar]
- 7.Bates DO, Heald RI, Curry FE, Williams B. Vascular endothelial growth factor increases Rana vascular permeability and compliance by different signalling pathways. J. Physiol. 2001;533(Pt. 1):263–272. doi: 10.1111/j.1469-7793.2001.0263b.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 9.Bhalla G, Deen WM. Effects of charge on osmotic reflection coefficients of macromolecules in porous membranes. J. Colloid Interface Sci. 2009;333:363–372. doi: 10.1016/j.jcis.2009.01.019. [DOI] [PubMed] [Google Scholar]
- 10.Bongrand P, Bell GI. Cell–cell adhesion: parameters and possible mechanisms. In: Perelson A, DeLisi C, Wiegel FW, editors. Cell Surface Dynamics: Concepts and Models. New York: Marcel Dekker; 1984. [Google Scholar]
- 11.Brandy JF, Bossis G. Stokesian dynamics. Annu. Rev. Fluid Mech. 1988;20:111. [Google Scholar]
- 12.Brenner H, Adler PM. Dispersion resulting from flow through spatially periodic media: II. Surface and intraparticle transport. Philos. Trans. R. Soc. Lond. A. 1982;307:149–200. [Google Scholar]
- 13.Brenner W, Langer P, Oesch F, Edgell CJ, Wieser RJ. Tumor cell-endothelium adhesion in an artificial venule. Anal. Biochem. 1995;225:213–219. doi: 10.1006/abio.1995.1146. [DOI] [PubMed] [Google Scholar]
- 14.Bundgaard M. The three-dimensional organization of tight junctions in a capillary endothelium revealed by serial-section electron microscopy. J. Ultrastruct. Res. 1984;88:1–17. doi: 10.1016/s0022-5320(84)90177-1. [DOI] [PubMed] [Google Scholar]
- 15.Cancel LM, Fitting A, Tarbell JM. In vitro study of LDL transport under pressurized (convective) conditions. Am. J. Physiol. 2007;293:H126–H132. doi: 10.1152/ajpheart.01188.2006. [DOI] [PubMed] [Google Scholar]
- 16.Caputo KE, Hammer DA. Effect of microvillus deformability on leukocyte adhesion explored using adhesive dynamics simulations. Biophys. J. 2005;89:187–200. doi: 10.1529/biophysj.104.054171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chang KC, Hammer DA. Influence of direction and type of applied force on the detachment of macromolecularly-bound particles from surfaces. Langmuir. 1996;12:2271–2282. [Google Scholar]
- 18.Chang KC, Tees DFJ, Hammer DA. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. PNAS. 2000;12:2271–2282. doi: 10.1073/pnas.200240897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen B, Fu BM. An electrodiffusion-filtration model for effects of surface glycocalyx on microvessel permeability to macromolecules. ASME J. Biomech. Eng. 2004;126:614–624. doi: 10.1115/1.1800571. [DOI] [PubMed] [Google Scholar]
- 20.Chotard-Ghodsnia R, Haddad O, Leyrat A, Drochon A, Verdier C, Duperray A. Morphological analysis of tumor cell/endothelial cell interactions under shear flow. J. Biomech. 2007;40:335–344. doi: 10.1016/j.jbiomech.2006.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Constantinescu A, Spaan JA, Arkenbout EK, Vink H, Vanteeffelen JW. Degradation of the endothelial glycocalyx is associated with chylomicron leakage in mouse cremaster muscle microcirculation. Thromb. Haemost. 2011;105(5):790–801. doi: 10.1160/TH10-08-0560. [DOI] [PubMed] [Google Scholar]
- 22.Curry FE, Adamson RH. Endothelial glycocalyx: permeability barrier and mechanosensor. Ann. Biomed. Eng. 2012;40(4):828–839. doi: 10.1007/s10439-011-0429-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Damiano ER, Stace TM. A mechano-electrochemical model of radial deformation of the capillary glycocalyx. Biophys. J. 2002;82:1153–1175. doi: 10.1016/S0006-3495(02)75474-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dembo M, Torney DC, Saxman K, Hammer DA. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 25.Drenckhahn D, Ness W. The endothelial contractile cytoskeleton. In: Born GVR, Schwartz CJ, editors. Vascular Endothelium: Physiology, Pathology and Therapeutic Opportunities. Stuttgart: Schattauer; 1997. pp. 1–15. [Google Scholar]
- 26.Dvorak HF, Brown LF, Detmar M, Dvorak AM. Vascular permeability factor/vascular endothelial growth factor, microvascular hyperpermeability, and angiogenesis. Am. J. Pathol. 1995;146:1029–1039. [PMC free article] [PubMed] [Google Scholar]
- 27.Earley S, Plopper GE. Disruption of focal adhesion kinase slows transendothelial migration of AU-565 breast cancer cells. Biochem. Biophys. Res. Commun. 2006;350:405–412. doi: 10.1016/j.bbrc.2006.09.056. [DOI] [PubMed] [Google Scholar]
- 28.Fan J, Cai B, Zeng M, Hao Y, Giancotti FG, Fu BM. Integrin β4 signaling promotes mammary tumor cell adhesion to brain microvascular endothelium by inducing ErbB2-medicated secretion of VEGF. Ann. Bio-med. Eng. 2011;39(8):2223–2241. doi: 10.1007/s10439-011-0321-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Feng D, Nagy JA, Payne K, Hammel I, Dvorak HF, Dvorak AM. Pathways of macromolecular extravasation across microvascular endothelium in response to VPF/VEGF and other vasoactive mediators. Microcirculation. 1999;6(1):23–44. [PubMed] [Google Scholar]
- 30.Fu BM, Chen B, Chen W. An electrodiffusion model for effects of surface glycocalyx layer on microvessel solute permeability. Am. J. Physiol. 2003;284:H1240–H1250. doi: 10.1152/ajpheart.00467.2002. [DOI] [PubMed] [Google Scholar]
- 31.Fu B, Curry FE, Adamson RH, Weinbaum S. A model for interpreting the tracer labeling of interendothelial clefts. Ann. Biomed. Eng. 1997;25:375–397. doi: 10.1007/BF02648050. [DOI] [PubMed] [Google Scholar]
- 32.Fu BM, Curry FE, Weinbaum S. A diffusion wake model for tracer ultrastructure-permeability studies in microvessels. Am. J. Physiol. 1995;269(38):H2124–H2140. doi: 10.1152/ajpheart.1995.269.6.H2124. [DOI] [PubMed] [Google Scholar]
- 33.Fu BM, Shen S. Structural mechanisms of vascular endothelial growth factor (VEGF) on microvessel permeability. Am. J. Physiol. 2003;284(6):H2124–H2135. doi: 10.1152/ajpheart.00894.2002. [DOI] [PubMed] [Google Scholar]
- 34.Fu BM, Shen S. Acute VEGF effect on solution permeability of mammalian microvessels in vivo. Microvasc. Res. 2004;68(1):51–62. doi: 10.1016/j.mvr.2004.03.004. [DOI] [PubMed] [Google Scholar]
- 35.Fu BM, Shen S, Chen B. Structural mechanisms in the abolishment of VEGF-induced microvascular hyperpermeability by cAMP. ASME J. Biomech. Eng. 2006;128(3):313–328. doi: 10.1115/1.2187047. [DOI] [PubMed] [Google Scholar]
- 36.Fu BM, Weinbaum S, Tsay RY, Curry FE. A junction-orifice-fiber entrance layer model for capillary permeability: application to frog mesenteric capillaries. ASME J. Biomech. Eng. 1994;116:502–513. doi: 10.1115/1.2895802. [DOI] [PubMed] [Google Scholar]
- 37.Gao L, Lipowsky HH. Composition of the endothelial glycocalyx and its relation to its thickness and diffusion of small solutes. Microvasc. Res. 2010;80:394–401. doi: 10.1016/j.mvr.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gassmann P, Kang ML, Mees ST, Haier J. In vivo tumor cell adhesion in the pulmonary microvasculature is exclusively mediated by tumor cell-endothelial cell interaction. BMC Cancer. 2010;10:177. doi: 10.1186/1471-2407-10-177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Giancotti FG. Targeting integrin beta4 for cancer and anti-angiogenic therapy. Trends Pharmacol. Sci. 2007;28:506–511. doi: 10.1016/j.tips.2007.08.004. [DOI] [PubMed] [Google Scholar]
- 40.Giavazzi R, Foppolo M, Dossi R, Remuzzi A. Rolling and adhesion of human tumor cells on vascular endothelium under physiological flow conditions. J. Clin. Invest. 1993;92:3038–3044. doi: 10.1172/JCI116928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Glinskii OV, Huxley VH, Glinsky GV, Pienta KJ, Raz A, Glinsky VV. Mechanical entrapment is insufficient and intercellular adhesion is essential for metastatic cell arrest in distant organs. Neoplasia. 2005;7(5):522–527. doi: 10.1593/neo.04646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Guo W, Giancotti FG. Integrin signalling during tumour progression. Nat. Rev. Mol. Cell Biol. 2004;5:816–826. doi: 10.1038/nrm1490. [DOI] [PubMed] [Google Scholar]
- 43.Guo W, Pylayeva Y, Pepe A, Yoshioka T, Muller WJ, Inghirami G, Giancotti FG. Beta 4 integrin amplifies ErbB2 signaling to promote mammary tumorigenesis. Cell. 2006;126:489–502. doi: 10.1016/j.cell.2006.05.047. [DOI] [PubMed] [Google Scholar]
- 44.Hammer DA, Apte SM. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 1992;63:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hippenstiel S, Krull M, Ikemann A, Risau W, Clauss M, Suttorp N. VEGF induces hyperpermeability by a direct action on endothelialcells. Am. J. Physiol. 1998;18:L678–L684. doi: 10.1152/ajplung.1998.274.5.L678. [DOI] [PubMed] [Google Scholar]
- 46.Hood JD, Cheresh DA. Role of integrins in cell invasion and migration. Nat. Rev. Cancer. 2002;2:91–100. doi: 10.1038/nrc727. [DOI] [PubMed] [Google Scholar]
- 47.Kienast Y, von Baumgarten L, Fuhrmann M, Klinkert WE, Goldbrunner R, Herms J, Winkle F. Real-time imaging reveals the single steps of brain metastasis formation. Nat. Med. 2010;16(1):116–122. doi: 10.1038/nm.2072. [DOI] [PubMed] [Google Scholar]
- 48.King MR, Hammer DA. Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. PNAS. 2001;98:14919–14924. doi: 10.1073/pnas.261272498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ladd CAJ. Numerical simulation of particulate suspensions via a discretized Boltzmann equation. J. Fluid Mech. 1994;271:285–309. [Google Scholar]
- 50.Lauffenburger DA, Horwitz AF. Cell migration: a physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
- 51.Lee TH, Avraham HK, Jiang S, Avraham S. Vascular endothelial growth factor modulates the transendothelial migration of MDA-MB-231 breast cancer cells through regulation of brain microvascular endothelial cell permeability. J. Biol. Chem. 2003;278:5277–5284. doi: 10.1074/jbc.M210063200. [DOI] [PubMed] [Google Scholar]
- 52.Li G, Fu BM. An electro-diffusion model for the blood-brain barrier permeability to charged molecules. ASME J. Biomech. Eng. 2011;133(2):0210. doi: 10.1115/1.4003309. [DOI] [PubMed] [Google Scholar]
- 53.Li G, Simon M, Shi Z, Cancel L, Tarbell JM, Morrison B, Fu BM. Permeability of endothelial and astrocyte cocultures: in vitro blood-brain barrier models for drug delivery. Ann. Biomed. Eng. 2010;38(8):2499–2511. doi: 10.1007/s10439-010-0023-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Li G, Yuan W, Fu BM. A model for water and solute transport across the blood-brain barrier. J. Biomech. 2010;43(11):2133–2140. doi: 10.1016/j.jbiomech.2010.03.047. [DOI] [PubMed] [Google Scholar]
- 55.Liang S, Slattery MJ, Dong C. Shear stress and shear rate differentially affect the multi-step process of leukocyte-facilitated melanoma adhesion. Exp. Cell Res. 2005;310(2):282–292. doi: 10.1016/j.yexcr.2005.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lipowsky HH. The endothelial glycocalyx as a barrier to leukocyte adhesion and its mediation by extracellular proteases. Ann. Biomed. Eng. 2012;40(4):840–848. doi: 10.1007/s10439-011-0427-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Litjens SH, de Pereda JM, Sonnenberg A. Current insights into the formation and breakdown of hemidesmosomes. Trends Cell Biol. 2006;16:376–383. doi: 10.1016/j.tcb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 58.Liu Q, Mirc D, Fu BM. Mechanical mechanisms of thrombosis in intact bent microvessels of rat mesentery. J. Biomech. 2008;41:2726–2734. doi: 10.1016/j.jbiomech.2008.06.013. [DOI] [PubMed] [Google Scholar]
- 59.Long DS, Smith ML, Pries AR, Ley K, Damiano ER. Microviscometry reveals reduced blood viscosity and altered shear rate and shear stress profiles in microvessels after hemodilution. Proc. Natl Acad. Sci. USA. 2004;101:10060–10065. doi: 10.1073/pnas.0402937101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.McDonald DM, Thurston G, Baluk P. Endothelial gaps as sites for plasma leakage in inflammation. Microcirculation. 1999;6(1):7–22. [PubMed] [Google Scholar]
- 61.Michel CC, Curry FE. Microvascular permeability. Physiol. Rev. 1999;79(3):703–761. doi: 10.1152/physrev.1999.79.3.703. [DOI] [PubMed] [Google Scholar]
- 62.Michel CC, Neal CR. Openings through endothelial cells associated with increased microvascular permeability. Microcirculation. 1999;6(1):45–62. [PubMed] [Google Scholar]
- 63.Moasser MM, Basso A, Averbuch SD, Rosen N. The tyrosine kinase inhibitor ZD1839 (“Iressa”) inhibits HER2-driven signaling and suppresses the growth of HER2-overexpressing tumor cells. Cancer Res. 2001;61:7184–7188. [PubMed] [Google Scholar]
- 64.Mook ORF, Marle J, Vreeling-Sindelarova H, Jongens R, Frederiks WM, Noorden CJK. Visualisation of early events in tumor formation of eGFP-transfected rat colon cancer cells in liver. Hepatology. 2003;38:295–304. doi: 10.1053/jhep.2003.50297. [DOI] [PubMed] [Google Scholar]
- 65.Mukhopadhyay D, Nagy JA, Manseau EJ, Dvorak HF. Vascular permeability factor/vascular endothelial growth factor-mediated signaling in mouse mesentery vascular endothelium. Cancer Res. 1998;58(6):1278–1284. [PubMed] [Google Scholar]
- 66.Ogston AG, Preston BN, Wells JD. On the transport of compact particles through solutions of chain-polymers. Proc. R. Soc. Lond. A. 1973;333:297–316. [Google Scholar]
- 67.Olsson AK, Dimberg A, Kreuger J, Claesson-Welsh L. VEGF receptor signalling—in control of vascular function. Nat. Rev. Mol. Cell Biol. 2006;7(5):359–371. doi: 10.1038/nrm1911. [DOI] [PubMed] [Google Scholar]
- 68.Phillips RJ, Deen WM, Brady JF. Hindered transport in fibrous membranes and gels: effect of solute size and fiber configuration. J. Colloid Interface Sci. 1990;139(2):363–373. [Google Scholar]
- 69.Reitsma S, Slaaf DW, Vink H, van Zandvoort MA, oude Egbrink MG. The endothelial glycocalyx: composition, functions, and visualization. Pflugers Arch. 2007;454:345–359. doi: 10.1007/s00424-007-0212-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Roberts WG, Palade GE. Increased microvascular permeability and endothelial fenestration induced by vascular endothelial growth factor. J. Cell Sci. 1995;108:2369–2379. doi: 10.1242/jcs.108.6.2369. [DOI] [PubMed] [Google Scholar]
- 71.Salmon AH, Neal CR, Sage LM, Glass CA, Harper SJ, Bates DO. Angiopoietin-1 alters microvascular permeability coefficients in vivo via modification of endothelial glycocalyx. Cardiovasc. Res. 2009;83(1):24–33. doi: 10.1093/cvr/cvp093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Salmon AH, Satchell SC. Endothelial glycocalyx dysfunction in disease: albuminuria and increased microvascular permeability. J. Pathol. 2012;226(4):562–574. doi: 10.1002/path.3964. [DOI] [PubMed] [Google Scholar]
- 73.Schluter K, Gassmann P, Enns A, Korb T, Hemping-Bovenkerk A, Holzen J, Haier J. Organ-specific metastatic tumor cell adhesion and extravasation of colon carcinoma cells with different metastatic potential. Am. J. Pathol. 2006;169:1064–1073. doi: 10.2353/ajpath.2006.050566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Shao JY, Xu G. The adhesion between a microvillus-bearing cell and a ligand- coated substrate: a Monte Carlo study. Ann. Biomed. Eng. 2007;35:397–407. doi: 10.1007/s10439-006-9221-6. [DOI] [PubMed] [Google Scholar]
- 75.Shen S, Fan J, Cai B, Lv Y, Zeng M, Hao Y, Giancotti FG, Fu BM. Vascular endothelial growth factor enhances mammary cancer cell adhesion to endothelium in vivo. J. Exp. Physiol. 2010;95:369–379. doi: 10.1113/expphysiol.2009.050260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Slattery MJ, Liang S, Dong C. Distinct role of hydrodynamic shear in leukocyte-facilitated tumor cell extravasation. Am. J. Physiol. 2005;288:C831–C839. doi: 10.1152/ajpcell.00439.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Squire JM, Chew M, Nneji G, Neal C, Barry J, Michel CC. Quasi-periodic substructure in the microvessel endothelial glycocalyx: a possible explanation for molecular filtering? J. Struct. Biol. 2001;136:239–255. doi: 10.1006/jsbi.2002.4441. [DOI] [PubMed] [Google Scholar]
- 78.Steeg PS, Theodorescu D. Metastasis: a therapeutic target for cancer. Nat. Clin. Pract. Oncol. 2008;5(4):206–219. doi: 10.1038/ncponc1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Steinbauer M, Guba M, Cernaianu G, Köhl G, Cetto M, Kunz-Schugart LA, Gcissler EK, Falk W, Jauch KW. GFP-transfected tumor cells are useful in examining early metastasis in vivo, but immune reaction precludes long-term development studies in immunocompetent mice. Clin. Exp. Metastasis. 2003;20:135–141. doi: 10.1023/a:1022618909921. [DOI] [PubMed] [Google Scholar]
- 80.Sugihara-Seki M. Transport of spheres suspended in the fluid flowing between hexagonally arranged cylinders. J. Fluid Mech. 2006;551:309–321. [Google Scholar]
- 81.Sugihara-Seki M, Akinaga T, Itano T. Flow across microvessel walls through the endothelial surface glycocalyx and the interendothelial cleft. J. Fluid Mech. 2008;601:229–252. [Google Scholar]
- 82.Sugihara-Seki M, Akinaga T, Itano T. Effects of electric charge on osmotic flow across periodically arranged circular cylinders. J. Fluid Mech. 2010;664:174–192. [Google Scholar]
- 83.Tarbell JM, Pahakis MY. Mechanotransduction and the glycocalyx. J. Intern. Med. 2006;259:339–350. doi: 10.1111/j.1365-2796.2006.01620.x. [DOI] [PubMed] [Google Scholar]
- 84.van den Berg BM, Vink H, Spaan JA. The endothelial glycocalyx protects against myocardial edema. Circ. Res. 2003;92:592–594. doi: 10.1161/01.RES.0000065917.53950.75. [DOI] [PubMed] [Google Scholar]
- 85.van Hinsbergh VW, Nieuw Amerongen GP. Intracellular signalling involved in modulating human endothelial barrier function. J. Anat. 2002;200:549–560. doi: 10.1046/j.1469-7580.2002.00060.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Vink H, Duling BR. Identification of distinct luminal domains for macromolecules, erythrocytes, and leukocytes within mammalian capillaries. Circ. Res. 1996;79:581–589. doi: 10.1161/01.res.79.3.581. [DOI] [PubMed] [Google Scholar]
- 87.Wang JK, Slattery MJ, Hoskins MH, Liang SL, Dong C, Du Q. Monte Carlo simulation of heterotypic cell aggregation in nonlinear shear flow. Math. Biosci. Eng. 2006;3:683–696. doi: 10.3934/mbe.2006.3.683. [DOI] [PubMed] [Google Scholar]
- 88.Weinbaum S, Tarbell JM, Damiano ER. The structure and function of the endothelial glycocalyx layer. Annu. Rev. Biomed. Eng. 2007;9:121–167. doi: 10.1146/annurev.bioeng.9.060906.151959. [DOI] [PubMed] [Google Scholar]
- 89.Wu HM, Huang Q, Yuan Y, Grange HJ. VEGF induces NO dependent hyperpermeability in coronary venules. Am. J. Physiol. 1996;40:H2735–H2739. doi: 10.1152/ajpheart.1996.271.6.H2735. [DOI] [PubMed] [Google Scholar]
- 90.Yan WW, Cai B, Liu Y, Fu BM. Effects of wall shear stress and its gradient on tumor cell adhesion in curved microvessels. Biomech. Model. Mechanobiol. 2012 doi: 10.1007/s10237-011-0339-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Yan WW, Liu Y, Fu BM. Effects of curvature and cell–cell interaction on cell adhesion in microvessels. Biomech. Model. Mechanobiol. 2010;9:629–640. doi: 10.1007/s10237-010-0202-1. [DOI] [PubMed] [Google Scholar]
- 92.Yen WY, Cai B, Zeng M, Tarbell JM, Fu BM. Quantification of the endothelial surface glycocalyx on rat and mouse blood vessels. Microvas. Res. 2012 doi: 10.1016/j.mvr.2012.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Yuan W, Li G, Zeng M, Fu BM. Modulation of the blood–brain barrier permeability by plasma glycoprotein orosomucoid. Microvasc. Res. 2010;80(1):148–157. doi: 10.1016/j.mvr.2010.03.011. [DOI] [PubMed] [Google Scholar]
- 94.Yuan W, Lv Y, Zeng M, Fu BM. Non-invasive method for the measurement of solute permeability of rat pial microvessels. Microvasc. Res. 2009;77:166–173. doi: 10.1016/j.mvr.2008.08.004. [DOI] [PubMed] [Google Scholar]
- 95.Zhang X, Curry FE, Weinbaum S. Mechanism of osmotic flow in a periodic fiber array. Am. J. Physiol. 2006;290:H844–H852. doi: 10.1152/ajpheart.00695.2005. [DOI] [PubMed] [Google Scholar]
- 96.Zhu C. Kinetics and mechanics of cell adhesion. J. Biomech. 2000;33:23–33. doi: 10.1016/s0021-9290(99)00163-3. [DOI] [PubMed] [Google Scholar]