Energetic cost of brain functional connectivity

Abstract

The brain's functional connectivity is complex, has high energetic cost, and requires efficient use of glucose, the brain's main energy source. It has been proposed that regions with a high degree of functional connectivity are energy efficient and can minimize consumption of glucose. However, the relationship between functional connectivity and energy consumption in the brain is poorly understood. To address this neglect, here we propose a simple model for the energy demands of brain functional connectivity, which we tested with positron emission tomography and MRI in 54 healthy volunteers at rest. Higher glucose metabolism was associated with proportionally larger MRI signal amplitudes, and a higher degree of connectivity was associated with nonlinear increases in metabolism, supporting our hypothesis for the energy efficiency of the connectivity hubs. Basal metabolism (in the absence of connectivity) accounted for 30% of brain glucose utilization, which suggests that the spontaneous brain activity accounts for 70% of the energy consumed by the brain. The energy efficiency of the connectivity hubs was higher for ventral precuneus, cerebellum, and subcortical hubs than for cortical hubs. The higher energy demands of brain communication that hinges upon higher connectivity could render brain hubs more vulnerable to deficits in energy delivery or utilization and help explain their sensitivity to neurodegenerative conditions, such as Alzheimer’s disease.

The high energetic cost of human brain function, which is 10 times higher than what would be expected from its weight alone (1, 2), can only be maintained through a combination of strategies for efficient energy use (3–5). Neural communication accounts for a significant fraction of the energy consumed by the brain (6), most of which was termed “dark energy” because it reflects intrinsic activity of uncertain functional origin (7).

Under normal physiological conditions, the brain derives most of its energy requirements from the metabolism of glucose and energy reserve glucose equivalents (8, 9). In vivo PET imaging studies with [¹⁸F]fluorodeoxyglucose (FDG), a radiotracer used for measuring glucose metabolism, have demonstrated high baseline glucose metabolic rates in ventral posterior regions of the brain (10). The brain uses a large fraction of this energy to support synaptic transmission, which is associated with the hemodynamic responses (11, 12) that are captured during stimulation studies with functional magnetic resonance imaging (fMRI) and the spontaneous oscillations captured during resting-state fMRI (R-fMRI), and also to sustain the resting potentials in neurons and glia (13, 14). Thus, the high degree of connectivity of the ventral posterior regions of the brain with other brain regions (15) suggests an association between energy consumption and R-fMRI (16). However, the energy budget of the spontaneous R-fMRI signals remains largely unknown, and a better understanding of the relationship between energy consumption and functional connectivity could be valuable for R-fMRI studies on neuropsychiatric disorders of metabolic origin.

Here, we present a model for the in vivo energy demands of functional connectivity. We tested this model in humans at rest by mapping the cerebral metabolic rate of glucose (CMRGlu) with FDG and PET, and the amplitudes of the blood oxygen level-dependent (BOLD) signals and the degree of functional connectivity with MRI. Specifically, we hypothesized that CMRGlu would show a linear association with the amplitude of the R-fMRI signal fluctuations. We also hypothesized that CMRGlu scales with the degree of the functional connectivity, the number of connections of the network nodes, which support functional integration (global degree) and functional segregation (local degree) in the brain. In addition, we propose an alternative approach to study the energy cost of the functional connectivity based on the degree-to-metabolism ratio. Specifically, this voxelwise measure of energy efficiency evaluates the degree of connectivity of the brain regions relative to their glucose consumption and reflects the energy demands of neural communication.

Model

To model the brain’s in vivo energy demands that support functional connectivity, we assumed that the energy consumed by a cluster of neurons (and supporting glial cells) in a brain image element (voxel) is proportional to its glucose metabolism, Q, and to the amplitude of the hemodynamic signal fluctuations, A,

used in the detection of functional connectivity (17, 18).

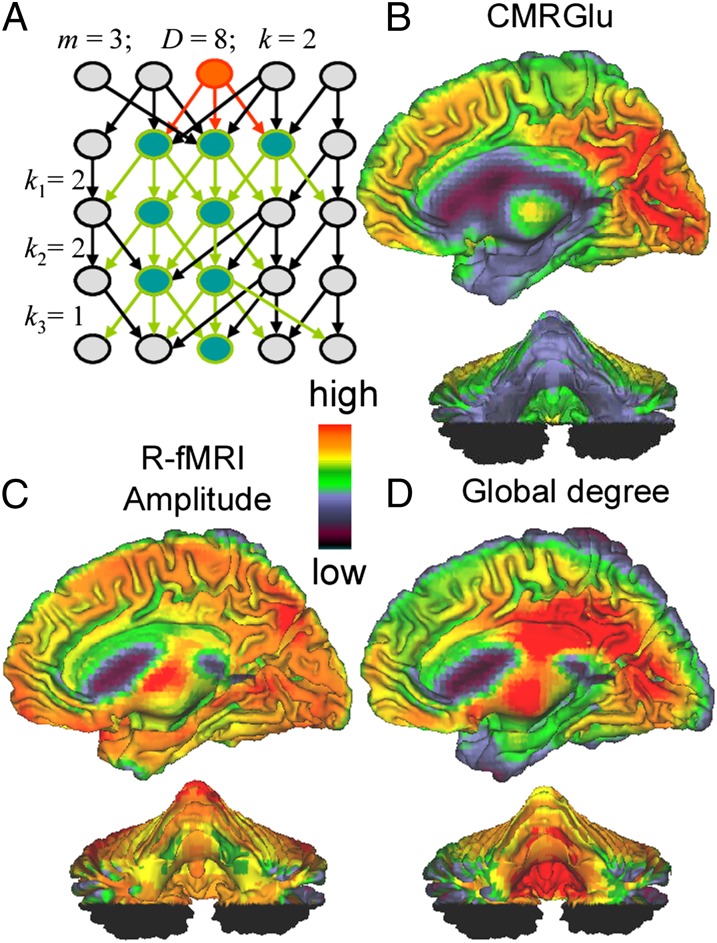
Let us further assume as in Hopfield neural networks (19) that the metabolic cost of neuronal signaling in a voxel x₀ is proportional to k, the average number of direct functional connections to other voxels in the brain. These stimulated voxels can in turn stimulate other voxels in a sequence of connectivity cascades (Fig. 1A). If k >> 1, the total number of stimulated voxels (or functionally connected voxels with x₀; i.e., degree), D, can be approximated as D ∝ k^m ∼ Q^m in terms of Q and the number of cascades, m, in the network of voxels stimulated by x₀.

Fig. 1.

(A) Schematic representation. Neuronal firing in the voxel x₀ (red) stimulates secondary voxels (green) trough a sequence of m = 3 sequential stimulation cascades (primary red and secondary green arrows) with k = 2 stimulated voxels per cascade in average, and a total number of D = k^m stimulated voxels (degree of x₀). (B) Absolute maps of CMRGlu computed from PET scans collected in resting conditions (eyes open) in 54 healthy subjects. Subjects were injected with 4–6 mCi of FDG i.v. and were asked to refrain from moving or speaking during the 30-min uptake period. Absolute CMRGlu maps were computed from 20-min emission scans that were acquired using standard PET procedures. (C) The amplitude of the low-frequency MRI signal fluctuations were computed for all 54 subjects from R-fMRI time series (40). (D) Global and local degree, graph theory measures of the number of functional connections per voxel, were mapped at 3-mm isotropic resolution from R-fMRI time series (21), to quantify the degree of the functional connectivity in the brain.

Based on these considerations and the fact that power laws involving metabolic budget are common in biology, we predict that glucose metabolism and the degree of the functional connectivity would have power scaling across voxels:

where the scaling factor, 0 ≤ b = m⁻¹ ≤ 1, reflects in part the communication speed of the network because shorter path lengths communicate information faster than longer path lengths. Note that m is analogous to the maximum of the shortest path lengths, d_max, between x₀ and all other voxels in the subnetwork defined by voxels functionally connected to x₀, which can be computed independently from R-fMRI data alone. The goal of this study was to assess the energy cost of R-fMRI in various networks because prior studies have reported differences in aerobic glycolysis across brain regions (20). We hypothesized that differences in aerobic glycolysis would cause differences in power scaling in the brain. For this purpose, we used PET-FDG and R-fMRI to test Eqs. 1 and 2, and the extent of the similarity between m and d_max in the healthy human brain.

Results

CMRGlu.

In the cerebral cortex, glucose metabolism was maximal in medial occipital [Brodmann areas (BAs) 17–19], parietal (BAs 7, 39, and 40), frontal (BAs 9, 11, 44, 46, and 47), and temporal (BA 22) regions and in anterior cingulum (BA 32) (70 > CMRGlu > 50 μmol⋅100 g⁻¹⋅min⁻¹; Fig. 1B). Outside of the cerebral cortex glucose metabolism was also high in the superior posterior cerebellar lobe (55 > CMRGlu > 45 μmol⋅100 g⁻¹⋅min⁻¹) and in the putamen (60 > CMRGlu > 50 μmol⋅100 g⁻¹⋅min⁻¹).

R-fMRI Signal Amplitude.

The amplitude of the R-fMRI signal fluctuations in the thalamus, auditory and visual areas, cuneus, precuneus, posterior parietal and frontal cortices, and posterior cerebellum was higher than the whole-brain average (Fig. 1C).

Degree.

The most prominent global degree hubs (two times or higher degree than the whole-brain average) were located in posterior cingulate/ventral precuneus (BAs 7 and 23), visual cortex (BAs 17–19 and 37), left angular gyrus (BA 39), insula, supplementary motor area (BA 6), cerebellum (posterior lobe and vermis), thalamus, and globus pallidus (Fig. 1D). The most prominent local degree hubs were located in posterior cingulate/ventral precuneus (BAs 7 and 23), left parietal (BA 39), occipital (BAs 17 and 19), left frontal (BAs 4, 44, and 45), and cingulate (BA 24) cortices, as well as cerebellum (posterior lobe and vermis) and thalamus. These findings are consistent with the previously reported locations of hubs in the human brain (21).

CMRGlu vs. R-fMRI Signal Amplitude.

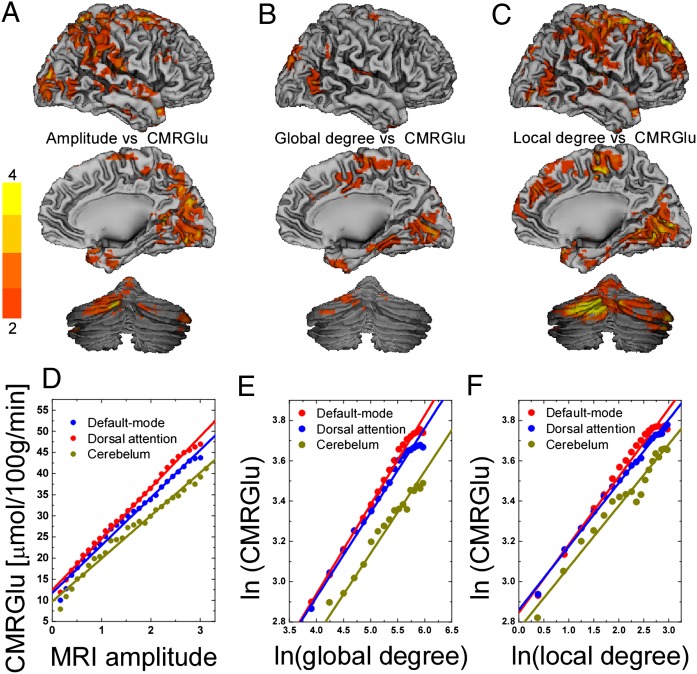
Voxelwise correlations across subjects between CMRGlu and the amplitude of the R-fMRI signal in the brain (P_FWE < 0.05; Table 1 and Fig. 2A), revealed that higher metabolism was associated with higher R-fMRI signal amplitudes in cerebellum, occipital (BAs 17 and 18) and parietal (BA 47) cortices.

Table 1.

Correlations with R-fMRI signal amplitude

Region	BA/lobe	MNI coordinates, mm			CMRGlu,μmol⋅100 g−1⋅min−1	A	D	CMRGlu vs. D	CMRGlu vs. A		η
		x	y	z			[k]	[T]	[T]	[k]
Cerebellum	Crus	−12	−90	−24	43.0 ± 1.3	2.5 ± 0.1	367 ± 32	2.4	4.1	282	1.1 ± 0.1
Calcarine	17	3	−87	−6	63.7 ± 1.5	3.2 ± 0.1	446 ± 45	3.0	3.6		0.9 ± 0.1
Lingual	17	−3	−93	−18	42.5 ± 1.6	2.3 ± 0.1	309 ± 33	1.9	3.6		0.9 ± 0.1
Cuneus	18	−3	−75	30	60.9 ± 1.3	3.1 ± 0.1	544 ± 63	NS	3.9	335	1.1 ± 0.1
Precuneus	7	−3	−66	57	48.0 ± 1.2	2.7 ± 0.1	341 ± 36	NS	3.9		0.9 ± 0.1
Precuneus	7	0	−69	39	60.6 ± 1.4	3.2 ± 0.1	455 ± 40	NS	3.6		1.0 ± 0.1

Metabolism (CMRGlu), R-fMRI signal amplitude (A), global degree centrality (D), and efficiency (η) for brain regions showing significant correlations (P_FWE < 0.05) between CMRGlu and A across 54 healthy subjects. A correlation threshold level R = 0.6 was used to compute D.

Fig. 2.

Statistical maps of the voxelwise correlations between CMRGlu and R-fMRI signal amplitude (A) and between CMRGlu global (B) and local (C) degree across 54 healthy subjects, superimposed on surface views of the cerebral cortex (medial and lateral) and the posterior cerebellum. The color bars indicate t-score values. Scatter plots exemplifying the linear association between CMRGlu and R-fMRI signal amplitudes (D) and the power scaling of CMRGlu and degree (E and F) across 54 healthy subjects for three different networks. The color lines are reduced-major axis regression fits to the data (0.96 < R² < 0.99).

Average metabolism and R-fMRI signal amplitudes were also linearly associated across voxels, independently for default-mode (DMN), dorsal attention (DAN), and cerebellar networks (Fig. 2D). Differences in the linear relationships for the networks might reflect the overall higher metabolism in the cortex than the cerebellum. The linear relationship between CMRGlu and the amplitude of the R-fMRI signals also emerged for each individual (SI Methods). Across subjects, the differences in linear scaling between metabolism and R-fMRI amplitude among these networks was highly significant, both for the slope (P < 0.001; paired t test) and the intercept (P < 0.004; Table 2). Note that the adjustable parameters of the model (γ, the slope, and β, the intercept) of the metabolic increases with increased R-fMRI signal amplitudes were robust across subjects (t score > 18, SE < 6%; Table 2) for all networks. On average across regions, γ = 8.1 ± 0.8 μmol⋅100 g⁻¹⋅min⁻¹, and β = 17.3 ± 1.4 μmol⋅100 g⁻¹⋅min⁻¹, were not different for DMN, DAN, and cerebellum (P > 0.01; Table 2). The correlation between whole-brain average values of CMRGlu and R-fMRI signal amplitude did not reach statistical significance (P > 0.08).

Table 2.

Average parameters of the model

Region	a (T)		b (T)		γ (T)	β (T)
	Global degree	Local degree	Global degree	Local degree	R-fMRI amplitude
Cerebellum	8.7 ± 0.9 (9.9)	19.0 ± 0.9 (21.7)	0.30 ± 0.02 (17.3)	0.26 ± 0.02 (15.3)	7.3 ± 0.3 (22.2)	15.8 ± 0.9 (18.0)
DMN	12.3 ± 1.2 (10.8)	19.4 ± 0.6 (32.5)	0.25 ± 0.02 (14.5)	0.29 ± 0.01 (27.0)	8.0 ± 0.3 (31.5)	17.8 ± 0.6 (31.2)
DAN	12.8 ± 1.2 (10.7)	19.2 ± 0.6 (33.5)	0.25 ± 0.02 (14.6)	0.32 ± 0.01 (30.0)	8.9 ± 0.3 (35.9)	18.4 ± 0.5 (36.0)

Parameters for the power scaling model, Q = a Db, that optimally fit CMRGlu (Q) and degree centrality (D), and for the linear model, Q = γ A+ β that optimally fit Q and the R-fMRI signal amplitude (A) in the default mode (DMN) and dorsal attention (DAN) networks, and in the cerebellum. The average and SEs of the parameters were computed across 54 subjects. T: t-score values (values in parentheses). Units of measures: [a], [β], and [γ] = μmol⋅100 g⁻¹⋅min⁻¹.

CMRGlu vs. Degree.

Whole-brain average values of CMRGlu and local degree were significantly correlated across subjects (R = 0.42; P < 0.006). However, the correlation between whole-brain average values of CMRGlu and global degree did not reach statistical significance (P > 0.11).

Voxelwise degree–CMRGlu correlations across subjects revealed that higher metabolism was associated with higher global degree in occipital (BAs 17 and 37), frontal (BA 6), temporal (BAs 21 and 22), and parietal (BA 40) cortices and cerebellum (P_FWE < 0.05; Table 3 and Fig. 2B). Similar correlations with CMRGlu across subjects were observed for the local degree (Fig. 2C).

Table 3.

Correlations with degree

Region	BA/lobe	MNI coordinates, mm			CMRGlu, μmol⋅100 g−1⋅min−1	Amplitude	D	CMRGlu vs. A	CMRGlu vs. D		η
		x	y	z			[k]	[T]	[T]	[k]
Inferior parietal	40	−51	−42	57	32.0 ± 0.8	1.5 ± 0.3	206 ± 21	NS	3.5	1,752	0.8 ± 0.1
Superior temporal	22	−66	−48	21	32.0 ± 0.7	1.5 ± 0.4	228 ± 27	NS	3.5		0.9 ± 0.1
Cerebellum	Post	−42	−84	−30	19.0 ± 0.7	1.1 ± 0.4	141 ± 12	1.8	3.8	1,877	1.0 ± 0.1
Middle temporal	37	45	−66	3	40.9 ± 1.0	2.2 ± 0.7	479 ± 77	2.4	3.4		1.3 ± 0.2
Lingual	17	3	−78	3	65.7 ± 1.5	3.1 ± 0.9	488 ± 53	2.5	3.4		1.0 ± 0.1
Superior frontal	6	−18	−3	54	34.4 ± 1.0	1.9 ± 0.6	644 ± 92	1.9	3.6	1,951	1.9 ± 0.2
Rolandic operculum	6	−48	3	9	42.2 ± 0.8	2.2 ± 0.6	522 ± 66	NS	3.5		1.4 ± 0.1
Middle temporal	21	−48	6	−24	33.8 ± 0.7	2.8 ± 0.7	297 ± 37	NS	3.5		1.1 ± 0.1

Metabolism (CMRGlu), R-fMRI signal amplitude (A), global degree centrality (D), and efficiency (η) for brain regions showing significant correlations (P_FWE < 0.05) between CMRGlu and the D across 54 healthy subjects. A correlation threshold level R = 0.6 was used to compute D.

The power scaling model robustly fitted the voxel values of CMRGlu with those of global degree (Fig. 2E) and local degree (Fig. 2F), averaged across subjects independently for DMN, DAN, and cerebellar networks. The power scaling between CMRGlu and degree (local and global) also emerged for each individual (SI Methods). Even though the adjustable parameters of the model (a and b) showed significant interindividual variability (SI Methods), they were highly significant across subjects (t score > 9.9, SE ∼10%; Table 2) for all networks. The basal glucose metabolism (metabolism in absence of global degree) averaged a = 11 ± 2 μmol⋅100 g⁻¹⋅min⁻¹ (mean ± SD) across networks. Across subjects, the basal metabolism was significantly lower for the cerebellum than for DMN and DAN (P < 0.005; paired t test). In average across regions, the power scaling factor of the metabolic cost of global degree, b = 0.27 ± 0.03, was similar to that of local degree, b = 0.29 ± 0.03, and for DMN, DAN, and cerebellum (P > 0.01; Table 2).

Glucose Efficiency.

We computed the glucose efficiency (η) index using the ratio between the strength of global degree and CMRGlu at each voxel, which was rescaled to a whole-brain mean of 1. These relative efficiency maps reflect the metabolic cost of global degree (η > 1: lower CMRGlu per functional connection than that of the whole-brain mean) for each subject. Across subjects, η was highly significant in most brain voxels (P_FWE < 0.05). In posterior cingulum (BA 23), parahippocampal (BAs 37 and 20), fusiform and inferior occipital (BA 19) gyri, motor and premotor cortex (BAs 4 and 6), middle cingulum/corpus callosum, cerebellum (vermis and tonsil), anterior thalamus and substantia nigra η was two times or higher than its average brain value (Fig. 3). Rolandic operculum (BA 6), angular (BA 39), superior frontal (BA 10), anterior cingulate (BA 24), medial orbitofrontal cortex (BA 11), caudate also exhibited high η.

Fig. 3.

Average distribution of glucose efficiency (η) across subjects superimposed on the surface views of the Colin human brain.

Path Length.

In average across voxels and subjects, the maximum of the shortest path lengths in the local functional connectivity clusters was d_max = 2.7 ± 0.5 for DMN and DAN and d_max = 2.9 ± 0.5 for the cerebellum. The number of functional cascades within the local clusters, m = b⁻¹ = 3.5 ± 0.5, and d_max were not significantly different (P > 0.2).

Discussion

Energy-efficient synaptic neurotransmission may dominate the brain energy budget (4). We found that CMRGlu and functional connectivity measures (R-fMRI amplitude, and local and global degree) were significantly correlated across subjects, and that the correlation of whole-brain values of CMRGlu and local degree accounted for 18% of the variability in global CMRGlu. This indicates that the differences in whole-brain CMRGlu (range, ±5 mmol⋅100 g⁻¹⋅min⁻¹) between subjects partially reflect differences in their degree of local functional connectivity. The metabolic demands associated with neurotransmission in response to external stimuli are believed to cause dynamic changes in blood supply (12). Thus, R-fMRI signals likely reflect the energy demands associated with synaptic currents and action potentials (13, 14). Previous MRI studies that evaluated the BOLD/perfusion ratio at varying metabolic demands during rest and task conditions have suggested that resting-state activity reflects metabolic processes (16). These findings, however, could have partially reflected the similar vascular origins of the BOLD and perfusion MRI signals. Here, using a PET-MRI multimodal approach, we demonstrate a linear association between baseline measures of absolute glucose metabolism, a direct marker of neuronal activity, and the amplitude of the low-frequency MRI signal fluctuations of the brain regions at rest. Thus, signal fluctuations with larger amplitudes were localized in brain regions characterized by higher metabolism. This robust linear relationship across brain regions was demonstrated for every subject and supports our model hypothesis about the proportionality between R-fMRI amplitudes and glucose metabolism (Eq. 1).

Increases in local and global degree were associated with power law increases in CMRGlu across voxels. Digital electronic circuits show similar power scaling (Rent's rule) between the number of processing elements and the number of external connections or “pins” (22). Similarly, the amount of gray matter (containing the central processing part of the neuron or “soma”) and white matter (containing the axons, the physical connections between distant neurons) shows power scaling across a wide range of mammalian species (23). Previous studies have revealed that glucose metabolism (24) and the number of synapses per neuron (25) increase allometrically with brain volume across species. Thus, our findings suggest an association between increased CMRGlu and increased synaptic density across brain regions. The voxelwise correlations between metabolism and degree across subjects are consistent with the assumption that neural networks rely on a well-established “small-world” topology to accomplish maximal communication speed with minimal energy consumption (26–30). Overall, our results are robust and support the power scaling of glucose metabolism with degree (Eq. 2).

It is worth noting that the metabolic demands of local and global degree were greater for the cerebral cortex than for the cerebellum. This finding is consistent with different levels of aerobic glycolysis (glucose metabolism that exceeds its metabolism through oxidative phosphorylation despite sufficient oxygen availability) between the cerebellum and the cortex (20), and with the highest energy efficiency of the cerebellar granule cells and thalamocortical relay neurons (14). More specifically, the more negative scaling for the cerebellum than for the DMN and DAN could reflect the lower level of aerobic glycolysis for the cerebellum than for the cortex (20) and thus explain its apparent higher efficiency.

The basal metabolism (in absence of connectivity) that emerged from the nonlinear metabolic demands of global degree was 30% of the whole-brain CMRGlu and could reflect the average energy required for vital functions of neurons such as maintenance of resting potentials and action potentials (31). This suggests that the spontaneous brain activity accounts for 70% of the energy consumed by the brain, which is consistent with the high energy demands (80% of the brain energy) of active signal processing (2, 32, 33) and cortical computation (34). Our estimation of the energy cost of spontaneous brain activity is also consistent with the energy demands of synaptic neurotransmission (64% of the energy budget for gray matter) (14).

The power scaling factor, 0 ≤ b = m⁻¹ ≤ 1, reflects in part the communication speed of the network. Energy-efficient networks can support fast communication at low energy cost because of their short path length. In such networks, most voxels do not connect to one another but can be reached from every other voxels by a short path length. Our power-scaling model estimates that the average number of functional cascades (i.e., the path length) in the local functional connectivity clusters is m ∼3.5 ± 0.5. This is consistent with our independent estimation of the average maximum shortest path length, d_max ∼2.8 ± 0.5, computed directly from the R-fMRI data.

The glucose efficiency of global degree (assessed with degree-to-CMRGlu ratio index) in association areas (BAs 4, 6, 19, 20, 23, and 37), cerebellum (vermis and tonsil), and anterior thalamus was two or more times higher than that of the whole-brain average (Fig. 3). These regions show strong connectivity with other brain regions (15), which is consistent with the energy efficiency of the cerebellar granule cells and thalamocortical relay neurons (14). Because the capacity of the human brain hinges on energy-efficient cortical networks (26–30) and glucose metabolism supports the energy requirements of neuronal activity (8, 9), our findings suggest that higher glucose metabolism in those functional hubs serves to supports their higher communication rate. However, and in another example of the “robust yet fragile” nature of complex systems endowed with highly optimized tolerance (35), these functional hubs may be highly vulnerable to conditions that endanger their energy supply (3) and become primary targets of normal processes, like aging (36) or neurodegenerative diseases, like Alzheimer’s (37).

Methods

Subjects.

Fifty-four healthy right-handed participants (age, 36 ± 12 y; mean ± SD; 26 females) signed a written consent approved by the Institutional Review Board at Brookhaven National Laboratory before the study. These participants were screened carefully with a detailed medical history, physical and neurological examination (SI Methods).

PET Acquisition.

PET images were acquired in resting conditions (eyes open) with a Siemens/CTI ECAT HR+ using standard procedures (38). Arterialization was achieved by warming the hand to 44 °C and automated arterial sampling every 2.5 s for the first 2 min and then every minute from 2 to 5 min and then at 10, 15, 20, 30, 45, and 60 min. Subjects were injected with 4–6 mCi of FDG and were asked to refrain from moving or speaking during the 30-min uptake period. The 20-min emission scan (3D mode) was started 35 min after radiotracer injection. The PET scans were transformed into metabolic images as previously described (38), and the CMRGlu was computed using an extension of Sokoloff's model (39).

MRI Acquisition.

Subsequently, subjects underwent BOLD fMRI in a 4-tesla Varian/Siemens MRI scanner. A T2*-weighted single-shot gradient-echo planar imaging sequence (echo time/repetition time, 20/1,600 ms; 4-mm slice thickness; 1-mm gap; 33 coronal slices; 3.1 × 3.1 mm in-plane resolution) was used to sample the spontaneous signal fluctuations in the brain. The participants were instructed to remain silent, motionless, and awake with their eyes open during the 5-min resting-state scan.

The CMRGlu images were normalized to the standard stereotactic space of the Montreal Neurological Institute (MNI) with 3-mm isotropic voxels, and the R-fMRI time series were realigned and normalized to the MNI space with 3-mm isotropic voxels. Global signal intensity was normalized across time points, voxels with poor signal-to-noise were eliminated, and bandpass temporal filtering (0.01–0.10 Hz) was used to remove magnetic field drifts of the scanner and minimize physiologic noise of high-frequency components (15).

R-fMRI Signal Amplitude.

The fast Fourier transform of the preprocessed R-fMRI time series was used to compute the amplitude of the low-frequency fluctuations in the whole brain as the average of the power spectrum's square root in the low-frequency bandwidth (0.01–0.06 Hz) (40). R-fMRI signal amplitude maps were rescaled to a mean of 1 across brain voxels and subjects.

Global Degree.

R-fMRI time points that were severely contaminated with motion were removed using a “scrubbing” method (41) and the remaining motion effects on R-fMRI were controlled using motion covariates (15). The Pearson correlation was used to assess the strength of the functional connectivity, C_ij, between voxels i and j in the brain, and a correlation threshold 0.6 was used to compute the binary undirected connectivity coefficients, a_ij = 1 (if C_ij > 0.6) or 0 (if C_ij ≤ 0.6).

This correlation threshold ensures significant correlations between time-varying signal fluctuations at P_FWE < 0.05, minimizes false-positive rate and central processing unit time, and maximizes sensitivity and dynamic range (15). The global functional connectivity density, also called “degree” (42, 43), was calculated from the N × (N − 1)/2 binary matrices (n = 57,713 voxels) as k_i = ∑a_ij, using a C-algorithm and parallel computing (21).

Local Degree.

The local functional connectivity density (“local degree”) reflects the number of connections in the local functional connectivity cluster (k_i = ∑a_ij)_local, and was computed as the number of elements in the local functional connectivity cluster using “growing” algorithm (15).

Shortest Path Length.

The maximum of the shortest path lengths, d_max, between a voxel, x_i and all other j voxels in the local functional connectivity cluster of x_i was computed as the largest element in the i row of the shortest path length matrix (42),

where the coefficients a_uv ∈ g _{i↔ j} were defined by the shortest geodesic distance, g, between nodes i and j. The adjacency matrix used to calculate d_ij was computed from the corresponding correlation matrix of the local network cluster, C_ij, using a correlation threshold R = 0.9.

Energy Scaling.

Image voxels were sorted by their degree of connectivity and averaged into bins of Δk = 20 (global degree) or Δk = 1 (local degree), independently for cerebellum, DMN, and DAN. To assess the power scaling between metabolism and degree across voxels, a linear model, ln(Q) = ln(a) + b ln(D), was fitted to the average values of CMRGlu (Q_i) and degree (D_i) from each bin, independently for each network, and for each subject using reduced-major axis regression, which takes into account the error variance in both variables [ln(Q) and ln(D)] and is ideal for testing the power scaling. Similarly, image voxels were sorted by their R-fMRI signal amplitude and averaged independently for cerebellum, DMN, and DAN, and a standard linear regression model, Q = γ A + β, was fitted to the average values of CMRGlu (Q_i) and R-fMRI signal amplitude (A_i), independently for each network, and for each subject to assess the relationship between CMRGlu and R-fMRI signal amplitude across voxels. The coefficient of determination R² was used to assess the goodness of the regressions. A rigorous R² > 0.95 was used to evaluate the agreement between the power-scaling model and the data.

Glucose Efficiency Index.

Relative maps of the glucose efficiency index, η, were computed for each subject as the ratio between the strengths of global degree and CMRGlu at each voxel, and rescaled to a whole-brain mean of 1. These relative efficiency maps reflect the metabolic cost of the global hubs (η > 1 reflect lower CMRGlu per functional connection than that of the whole-brain mean).

Statistical Methods.

The brain maps (CMRGlu, amplitude, local degree, global degree, η) were spatially smoothed (8-mm isotropic FWHM) in SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK), and one-sample t test was used to assess their statistical significance. The Biological Parametric Mapping (44) was used to access the linear association of absolute glucose metabolism (CMRGlu) with R-fMRI signal amplitude, and with local and global degree across subjects. Statistical significance for group analyses was set by cluster-level P_FWE < 0.05, corrected for multiple comparisons with the random field theory and a familywise error.