Abstract
The stability of RNA tertiary structures depends heavily on Mg2+. The Mg2+-RNA interaction free energy that stabilizes an RNA structure can be computed experimentally through fluorescence-based assays that measure Γ2+, the number of excess Mg2+ associated with an RNA molecule. Previous explicit-solvent simulations predict that the majority of excess Mg2+ ions interact closely and strongly with the RNA, unlike monovalent ions such as K+, suggesting that an explicit treatment of Mg2+ is important for capturing RNA dynamics. Here we present a reduced model that accurately reproduces the thermodynamics of Mg2+-RNA interactions. This model is able to characterize long-timescale RNA dynamics coupled to Mg2+ through the explicit representation of Mg2+ ions. KCl is described by Debye-Hückel screening and a Manning condensation parameter, which represents condensed K+ and models its competition with condensed Mg2+. The model contains one fitted parameter, the number of condensed K+ ions in the absence of Mg2+. Values of Γ2+ computed from molecular dynamics simulations using the model show excellent agreement with both experimental data on the adenine riboswitch and previous explicit-solvent simulations of the SAM-I riboswitch. This agreement confirms the thermodynamic accuracy of the model via the direct relation of Γ2+ to the Mg2+-RNA interaction free energy, and provides further support for the predictions from explicit-solvent calculations. This reduced model will be useful for future studies of the interplay between Mg2+ and RNA dynamics.
Introduction
The thermodynamics and kinetics of biological macromolecules like RNA and proteins can be described by energy-landscape theory. In an energy-landscape description, each highly populated configuration of the system corresponds to a basin of attraction on the energy landscape. Various features of the landscape explain different processes. Macromolecular folding requires a native energetic bias to guide the search for the native basin to overcome Levinthal’s paradox and fold on biological timescales (1–3). This native bias implies that the free energy of a structure is determined largely by its similarity to the native structure. Such a landscape is well described by the principle of minimal frustration: native contacts are energetically stabilizing, and other contacts are less energetically significant (3).
Function occurs on the same landscape as folding, but frequently there are multiple basins of attraction within, and occasionally outside, the broader folded basin. To capture this functional frustration (4), inclusion of contacts and other information from these multiple basins is required (5). In some cases, the roughness of the landscape due to nonnative interactions is an important perturbation to the native-biased landscape (6,7). Nonspecific interactions, including electrostatics, are a source of frustration, because they stabilize interactions between both native and nonnative contacts. In proteins, electrostatic interactions can modulate the unfolded ensemble (8) and explain differences in thermodynamics and kinetics between homologous sequences (9). Although a minimally frustrated landscape is an apt baseline approximation for RNA with a native structure (10), frustration likely plays an even more important role in RNA than in proteins (11,12), including frustration and trapping that arise from electrostatic interactions (13,14). Indeed, the RNA energy landscape is quite electrostatically sensitive to the ionic environment (15,16), as the species and concentrations of ions in the ionic environment modulate the stability of competing structures. Modeling the ionic dependence of the RNA energy landscape is the focus of this work.
RNA is sensitive to the ionic environment because it is strongly negatively charged. For RNAs, such as riboswitches and ribosomal RNAs, to form compact structures that carry out biological function, counterbalancing RNA charge with cations such as Mg2+, K+, and Na+ is essential. Mg2+ is especially effective in competing with other ions to balance RNA charge, because it is divalent and small. Although monovalent ions are generally present in much greater concentrations, only half as many Mg2+ ions as monovalent ions need to be localized to the region surrounding the RNA, which leads to a comparable entropic cost for localization. The small size of Mg2+ allows it to outcompete and displace larger divalent ions by approaching the RNA more closely (17–19).
Mg2+ plays a ubiquitous role in RNA stability and dynamics, and it exhibits many complex behaviors in the vicinity of RNA. A description of the ionic dependence of the landscape should encompass these features. Mg2+ is particularly effective at stabilizing compact RNA structures by inducing effective attraction between otherwise repulsive phosphates (13,19), and as a result, it plays a dramatic role in energetically stabilizing RNA tertiary structure (15). In turn, higher concentrations of Mg2+ tend to slow RNA kinetics by stabilizing compact structures (14,20). Explicit-solvent studies have suggested that Mg2+ fluctuations couple with RNA dynamics (21). This study also found that most Mg2+ associated with RNA is in the outer-sphere regime, separated from the RNA by one hydration layer (21). Ion-ion correlations in the dense outer-sphere regime are important for obtaining accurate free energies (22). Recent experimental studies of the SAM-I riboswitch have revealed a complex interplay between Mg2+ and S-adenosyl methionine (SAM) in stabilizing the SAM-I riboswitch (23). Modeling these features requires a more detailed representation of Mg2+ than of other ions. In this article, we focus on extending a minimally frustrated description of the landscape to include electrostatic frustration and ionic effects with an explicit representation of Mg2+. The resulting model is able to accurately reproduce the thermodynamics of Mg2+-RNA interaction.
A structure-based model (SBM) is an ideal way to represent a minimally frustrated landscape. In the simplest form, only native contacts are stabilized energetically, resulting in a smooth, native-biased landscape. The usefulness of this approximation is shown by the ability of such models to capture many aspects of protein (5,24–27) and RNA (28–33) folding and function. SBMs are also attractive from a modeling perspective due to their simplicity and rapid sampling. Smoother landscapes, together with underdamping (34), result in enhanced sampling approximately 104 times faster than explicit-solvent simulations (35,36). The simplicity of the SBM means that the effects of energetic perturbations like electrostatics on the overall native bias can be modeled and understood. In a pure SBM, electrostatic interactions and ions are only represented implicitly by their contribution to effective interactions of native contacts, and there is no ionic concentration dependence. To model the effects of ionic concentration dependence and of Mg2+ behavior in investigations of long-time dynamics of RNA, we design an SBM with explicit Mg2+ ions and an effective potential that implicitly represents KCl.
The energetic stabilization by Mg2+ is quantified by the Mg2+-RNA interaction free energy, ΔGMg2+. Theoretical calculations have shown that in the presence of excess KCl, ΔGMg2+ is related to the excess Mg2+ (Γ2+) according to
| (1) |
where both ΔGMg2+ and Γ2+ are functions of the Mg2+ concentration (C2+) (37). The excess ions of an ionic species i per RNA molecule is a thermodynamic quantity called the preferential interaction coefficient, Γi (37), and varies with ionic concentration. Ionic subscripts i of 2+, +, and − refer to Mg2+, K+, and Cl−, respectively. The charge of excess cations and depleted anions associated with the RNA must balance the RNA charge. Differences in ΔGMg2+ between conformational ensembles (ΔΔGMg2+) reveal preferential structural stabilization by Mg2+ that can be modulated by Mg2+ concentration.
Experimental curves for Γ2+ have been obtained for several systems using the fluorescent dye 8-hydroxyquinoline-5-sulfonic acid (HQS) (37). With these measurements, one can measure ΔΔGMg2+ between conformational ensembles (38,39) or characterize chelated Mg2+ binding in a specific site (40). Γ2+ has also been computed from microsecond-timescale explicit-solvent molecular dynamics simulations (21). Because the excess Mg2+ can be measured both experimentally and computationally, Γ2+ presents a powerful metric for uniting theory and experiment to build models of Mg2+-RNA interactions. Furthermore, because of the relation between Γ2+ and ΔGMg2+, such models will be well parameterized thermodynamically.
In this study, we focus on two well characterized riboswitches to calibrate the model. Riboswitches are attractive systems for the study of Mg2+-RNA interactions, because they are small and relatively simple but still possess many of the rich Mg2+-sensitive tertiary interactions seen in larger systems (Fig. 1, B and D). Riboswitches are responsible for regulating a wide range of metabolic pathways in bacteria. These noncoding RNAs reside in the 5′ untranslated region and often control transcription of their mRNA by binding metabolites directly related to their protein product. Riboswitches have proved to be excellent systems to investigate RNA structure, function, and dynamics using a wide range of experimental (23,41–43) and computational techniques (21,30,44–48). The adenine riboswitch (Fig. 1, A and B) has been extensively studied experimentally (39,49–51), and Γ2+ data obtained by HQS titrations are available for Mg2+ concentrations ranging from 1 μM to 1 mM (39). The SAM-I riboswitch (Fig. 1, C and D) binds the SAM metabolite, and has been extensively studied experimentally (23,52,53) and computationally (21,30,54). Γ2+ for the SAM-I riboswitch has been computed in explicit-solvent studies (21).
Figure 1.
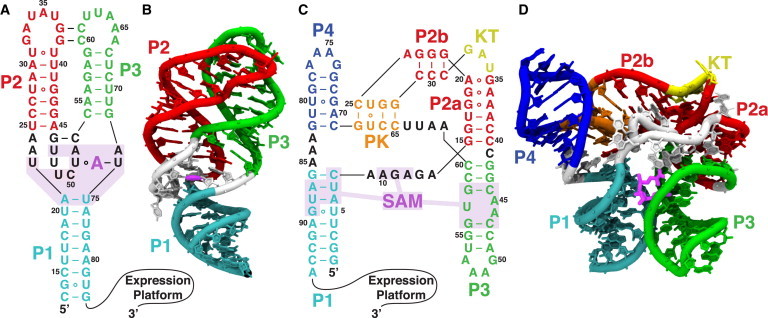
Secondary and tertiary structures of the two riboswitches used in this study. Mg2+ further stabilizes tertiary interactions induced by the metabolites. Metabolites are shown in magenta, and binding pockets are shaded. (A and B) Secondary (A) and tertiary (B) structures of the adenine riboswitch aptamer. The adenine metabolite stabilizes the tertiary interaction between the P2 and P3 helices. (C and D) Secondary (C) and tertiary (D) structures of the SAM-I riboswitch aptamer. The SAM metabolite stabilizes the tertiary interaction between the P3 helix and the nonlocal P1 helix, stabilizing the P1 helix and preventing strand invasion by the competing antiterminator helix in the expression platform. To see this figure in color, go online.
Using thermodynamic data from these previous studies as a guide, we develop a model that incorporates ionic effects into SBMs. The model includes explicit Mg2+ ions that interact with the RNA through a Debye-Hückel potential, whereas KCl is represented implicitly through the screening length and a Mg2+-dependent Manning condensation factor that scales RNA charge. We calibrate the model to accurately reproduce the preferential interaction coefficient Γ2+ and the related Mg2+ interaction free energy, ΔGMg2+, in the native basin of these two riboswitches. The predictions for Γ2+ are consistent with experimental HQS measurements of the adenine riboswitch (39) and simulation results of the SAM-I riboswitch (21). With this hybrid structure-based model in hand, we are poised to address more sophisticated questions about the interplay of Mg2+, ligands, and RNA during folding and function.
Model and Methods
Structure-based models
SBMs have been used extensively in studies of proteins (24,25,55), and in several studies of RNA (28,30,31,48). Previous studies have included electrostatic effects in the SBM of RNA. The simplest models utilize a repulsive Debye-Hückel interaction between phosphates (28,29). In these models, all ions are implicit. We utilize Debye-Hückel interactions and include explicit Mg2+ ions, because explicit counterions are required for Debye-Hückel interactions to produce the attractive effective phosphate-phosphate interactions that Mg2+ induces.
Although they still lack explicit counterions, more recent SBMs with electrostatics have added a scaling of RNA charge to Debye-Hückel interactions to account for Manning condensed ions (56). Manning counterion condensation is a useful theoretical tool for understanding the behavior of polyelectrolyte chains like RNA in solution (57,58). Manning counterion condensation theory was originally conceived as the low-concentration limiting behavior of an infinite line of charge in solution. If the linear charge spacing, b, is shorter than the Bjerrum length, , the length scale where the electrostatic and thermal energy scales cross (see Eq. 10), ions will condense out of solution onto the RNA and effectively rescale the charge. Although Manning condensation was assumed to be constant in previous SBMs (56), we have developed a model of Manning condensation that can vary with ionic concentration and allow separation of the condensed populations of Mg2+ and K+. This separation is critical for capturing Mg2+ concentration effects, since condensed Mg2+ replaces condensed K+, and hence the effective rescaling of RNA charge induced by K+ diminishes as Mg2+ concentration increases.
The competition between condensed Mg2+ and KCl provides the interface between discrete and continuum treatments, and if it is modeled well, treating Mg2+ as discrete ions and KCl as a continuum inducing an effective potential is a reasonable approximation. Continuum models can capture KCl behavior well, but cannot capture Mg2+ behavior because ion-ion correlations become important (59). Continuum approaches break down when the electrostatic coupling parameter (60) approaches unity (see Section S3 in the Supporting Material). The electrostatic coupling parameter varies like the surface charge density and the ion valency squared. Thus, the coupling parameter is four times higher for Mg2+ than for K+. Although the surface charge density of RNA is hard to estimate, the success of continuum models with KCl and their failure with Mg2+ suggests that RNA is in the intermediate regime where the electrostatic coupling parameter of Mg2+ is greater than one, whereas for K+ it is less than one. This is the regime to which a discrete Mg2+ and continuum KCl model is best suited.
We modify an all-atom SBM (30,55), which explicitly includes all heavy atoms, to include explicit Mg2+ ions and electrostatic interactions. Explicit Mg2+ ions are included to properly represent Mg2+-induced phosphate attraction, Mg2+-Mg2+ correlation, and the dense outer-sphere Mg2+ population. KCl screening is represented by a Debye-Hückel potential with a Mg2+-dependent KCl Manning condensation factor. The functional form of the potential is
| (2) |
where VSBM is the all-atom SBM potential containing the minimally frustrated native bias, VMg-Size controls the size of the explicit Mg2+ ions, and VES contains the effective electrostatic interactions. Simulation input files can be obtained at http://smog-server.org/forcefields. VSBM is given by
| (3) |
where
| (4) |
Geometric parameters (, , , , and ) are set by their values in a crystal structure, so that the crystal structure is the global minimum in energy. Energetic parameters have been calibrated (30,55) and are listed in Section S1 in the Supporting Material. The shadow method (61) was used to obtain the contact map for the sum over contacts. The final term controls the excluded volume and enforces steric constraints. Excluded-volume parameters are given by σNC = 1.7 Å and ϵNC = ϵR, where ϵR = 1.5 kBT is the reduced energy unit (see Section S1 in the Supporting Material), and T is the simulation temperature of 300 K.
The excluded volume of the Mg2+ ions is controlled by VMg-Size, which is given by
| (5) |
Parameters are calibrated in the first subsection under Results. For ϵMgRNA = ϵMgMg = ϵR, it is determined that σMgRNA = 3.4 Å and σMgMg = 5.6 Å.
The electrostatic potential is given by
| (6) |
where the dielectric constant mimics water, is the permittivity of free space, is the Debye length (excluding Mg2+ screening), and α is the Manning condensation prefactor that rescales the charges q due to the presence of implicit condensed K+. Note that the sum includes only Mg2+-RNA and Mg2+-Mg2+ interactions. Since the SBM already implicitly includes native RNA-RNA interactions in VSBM, such as hydrogen bonding and base-pairing interactions, RNA-RNA electrostatic interactions were excluded to avoid double counting. Since RNA-RNA electrostatic interactions are excluded, the model can only capture the indirect effect of KCl upon the Mg2+ dependence of the RNA energy landscape. This model is most appropriate at intermediate KCl concentrations where the native basin is stabilized by KCl. A different model of RNA-RNA electrostatic interactions that can overcome the native bias of VSBM would be required to capture the full KCl dependence of the energy landscape, such as unfolding under low salt conditions.
Previous studies have shown that the Mg2+ distribution is controlled by many negatively charged atoms on the RNA, as opposed to only the phosphates (21,62). Since hydrogens are not represented in the SBM, united atom charges were placed on every heavy atom to reproduce the electrostatic potential and resultant Mg2+ distribution. United atom charges were obtained from Amber 99 (63) by adding all hydrogen charges to the nearest heavy atom. This approximation does not alter the charge of any atoms that interact strongly with Mg2+, with the possible exception of OH2′, which interacts moderately (21).
The Debye length in VES is given by
| (7) |
where and are the number density and charge of ionic species i, and is the Boltzmann constant. To compute for VES, Mg2+ is excluded from the sum over ionic species i, because Mg2+ is accounted for explicitly. The Manning condensation prefactor is given by
| (8) |
θ+ is the number of Manning condensed K+ per phosphate, which is explained in the second subsection under Results. Thus, α rescales the RNA charge due to the presence of implicit condensed K+, leaving the Mg2+ charge unchanged. Since SBMs use reduced units, VES is multiplied by the conversion factor in Eq. S3 to convert from kJ/mol to reduced energy units. The conversion factor was determined by noting that a temperature of 80 in simulation units corresponded to 300 K and then equating thermal energy scales. This conversion resulted in an ionic distribution appropriate to 300 K within our simulations. See Section S1 in the Supporting Material for more details.
Molecular dynamics simulations
Simulations were run using the Gromacs-4.6.1 molecular dynamics package (64). Langevin dynamics in the underdamped limit were used as a thermostat (see Section S1 in the Supporting Material for details). Implicit KCl concentrations of 50 mM (adenine riboswitch) and 100 mM (SAM-I riboswitch) were chosen for direct comparison with previous experiments (39) and simulations (21) on these systems. Simulations were run at varying concentrations of explicit Mg2+. Cubic boxes were chosen such that the box was at least 500 Å on a side, but also such that there was a minimum of 200 bulk Mg2+ ions in the box, in addition to the Γ2+ Mg2+ ions associated with the RNA. For the most dilute simulations (10−6 M Mg2+), this resulted in boxes 7000 Å on a side. Such low Mg2+ concentrations are completely inaccessible with explicit-solvent simulations, but have little effect on the computational expense of this model. Production simulations at each Mg2+ concentration were run for 2.5 × 108 time steps.
Nonlinear Poisson-Boltzmann calculations
Two theoretical models have been used extensively in studies of RNA: nonlinear Poisson-Boltzmann (NLPB) theory (65,66) and Manning counterion condensation theory (57,67). Poisson-Boltzmann methods have played a critical role in shedding light on RNA electrostatics. These methods have been advanced by the seminal contribution of Baker and co-workers, whose methods have enabled rapid calculation of electrostatic potentials for very large molecules (68–70). NLPB treats ions in a mean-field manner, which neglects ion-ion correlations (22,71) and ion size effects (59,72,73). NLPB has been successfully applied to many systems (66,74) and predicts ΔΔGMg2+ within computational uncertainty (75,76). Although NLPB accurately predicts ΔΔGMg2+, values for Γ2+ and ΔGMg2+ are systematically low by ∼25%. We choose not to use NLPB directly in our SBM, partly because removing the double counting of RNA-RNA electrostatic interactions implicitly represented in the contact terms is not straightforward with NLPB and partly because of the systematically low values of Γ2+ and ΔGMg2+ given by NLPB calculations. NLPB calculations are used to corroborate the model and parameters obtained for Manning condensed K+ in the second subsection under Results. NLPB calculations were performed using the adaptive Poisson-Boltzmann solver (APBS) (68), with parameters listed in Section S2 in the Supporting Material.
The NLPB equation determines the potential by assuming that the mean ionic density fields are governed by the Boltzmann distribution. The linearized Poisson-Boltzmann (LPB) equation is obtained by linearizing the Boltzmann distribution around zero potential. The Debye-Hückel (DH) approximation is further obtained by neglecting the solute’s dielectric constant and ionic accessibility. Both LPB and DH are described by homogenous differential equations, and thus the solution may be multiplied by a coefficient α. By Gauss’ law, , where is the valence and is the Manning condensed fraction per phosphate of the ionic species i. This implies that the excess ions, Γi, may be split into a population that screens and a population that condenses.
The total condensed charge, , may be obtained by fitting either LBP or DH to NLPB far from the RNA, where the potential is small and the linearized Boltzmann distribution is valid. In this case, fitting was performed at a set of points within a 240 Å box but outside a 120 Å box centered on the RNA. The condensed ions obtained by LPB and DH fits are identical at low concentrations but begin to differ near the 50 mM concentrations used in this study. Fitting to Debye-Hückel is used because that is more appropriate to the form of the potential used in Eq. 6, but for completeness, fits to both are shown in Fig. S1 in the Supporting Material.
To partition the Manning condensed ions by species, ion densities were computed from the full NLPB and scaled DH potentials. The difference in ion densities integrated over all space gives the condensed ions for that species. At high ionic concentrations, this also results in a nonzero condensation of Cl−. This occurs because the linearized potential predicts a nonphysical negative density in regions of strong potential, but NLPB gives approximately zero density.
Results
Calibration of Mg2+ ion size
Previous studies have shown that the affinity between an ion and RNA is strongly dependent on ion size (17–19,77). Given , the effective size of Mg2+ is controlled by and in the excluded-volume term. Because the ionic affinity for RNA is sensitive to ion size, these parameters must be carefully calibrated to accurately predict Γ2+.
Explicit-solvent simulations have shown that most excess Mg2+ resides in the outer-sphere peak between 3.5 and 5 Å from the RNA, separated by a single hydration layer (21). In this model, the position of this peak is controlled by the values of in the excluded volume term (Eq. 5) and by the electrostatic potential (Eq. 6). To deconvolute the calibration of the Mg2+ excluded volume from the calibration of implicit Manning condensed KCl, excluded volume calibrations were performed in the high Mg2+ concentration regime (10 mM Mg2+ vs. 100 mM K+) where negligible KCl is condensed, and therefore . Within trial simulations, two metrics for the position of the peak were used: the position of the maximum of the peak and the the weighted average position between 3 and 5 Å. For ϵMgRNA = ϵR, both metrics suggest that σMgRNA = 3.4 Å yields a distribution most consistent with the outer-sphere peak observed in explicit-solvent simulations (Fig. 2).
Figure 2.
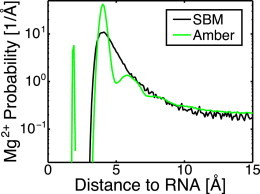
Comparison of the Mg2+ distribution about the SAM-I riboswitch in SBM and explicit-solvent Amber simulations. Distances to the closest RNA heavy atom were computed and binned. SBM captures well the general shape of the distribution, but misses the more subtle hydration features. The chelated ion at 2 Å could have been included in the SBM, but was omitted for simplicity. These curves were used to calibrate the excluded volume between Mg2+ and RNA atoms. The position of the maximum of the peak as well as the weighted average position between 3 and 5 Å both suggest that σMgRNA = 3.4 Å. To see this figure in color, go online.
To calibrate the Mg2+-Mg2+ excluded volume, the Mg2+-Mg2+ radial distribution function was used (Fig. S2). The radial distribution function rises sharply between 5 and 7 Å, and plateaus beyond this. σMgMg = 5.6 Å was found to most closely reproduce the midpoint of this rise.
Competition between Manning condensed Mg2+ and K+ modulates the effective electrostatic potential
The Debye-Hückel potential assumes a linearized dependence of the Boltzmann distribution of ions on the electrostatic potential. Such an assumption is good far from the RNA, but breaks down near the RNA where the potential is large. Equation 6 uses Manning counterion condensation to account for the nonlinear effects in this region, so that the far-field potential is correct. The additional ions near the RNA deviating from linearity may be regarded as the Manning condensed counterions. Thus, the excess ions Γ may be split into a diffuse screening population and a condensed population close to the RNA.
Manning counterion condensation theory was originally derived for an infinite line of charge under limiting law conditions: as the salt concentration approaches zero while taking the thermodynamic limit. If the linear charge spacing (b) is shorter than the Bjerrum length ( – the length scale where the electrostatic and thermal energy scales cross), ions will condense out of solution onto the RNA. For an infinite line of charge, the number of ions per phosphate (θ) that condense is given by
| (9) |
where Z is the valency of the counterion, , and
| (10) |
Grouping phosphate and condensed counterion charges together results in an effective rescaling of phosphate charges by .
If explicit ions are used, bare RNA charges should be used, because condensation is captured by the ions. However, if ions are only represented implicitly through an effective potential, effective RNA charges that are rescaled by α must be used to account for Manning condensation. Because Mg2+ in the model is explicit and KCl is implicit, the condensed K+ per phosphate (θ+) and condensed Mg2+ per phosphate (θ2+) must be separated so that θ+ can be included in the effective potential, VES. θ2+ and θ+ can be separated by solving the system of equations
| (11) |
| (12) |
describing competition between condensed Mg2+ and K+ (78), where e is Euler's number. Equation 11 balances the entropic cost of localizing one Mg2+ ion with the cost of localizing two K+ ions. V is the effective volume into which a condensed ion is localized, and together with the K+ and Mg2+ concentrations, C+ and C2+, determines the entropic cost of localization. Equation 12 balances the entropic cost of localizing a condensed ion with the energy benefit. is the free energy per phosphate to assemble the phosphate charges from infinity to the native geometry, originally approximated as an infinite line, and thus depends on screening length and RNA geometry. Computing F for an infinite line of charge (Eq. S11) and taking the appropriate limits in Eqs. 11 and 12 returns Eq. 9. The condensation is constant over a wide range of concentrations because both the entropic cost and F go like .
Manning counterion condensation may be applied to finite systems with the caveat that whereas the entropic cost of condensation goes like , F does not. Thus, as the concentration goes to zero, so does the condensation, and the condensation is not constant over a wide range of concentrations as it is for an infinite line of charge (Fig. 3 A). Equation 12 can be reexpressed as
| (13) |
where θ0 is the number of condensed K+ per phosphate in the absence of Mg2+ and A is . θ0 and A in principle depend on RNA geometry, , and through their dependence on F. Note that in the region where K+ and Mg2+ compete, . Thus, for constant , is also approximately constant. Since our simulations remain in the native basin, RNA geometry is also constant, and θ0 and A are constant as varies at a fixed KCl concentration.
Figure 3.
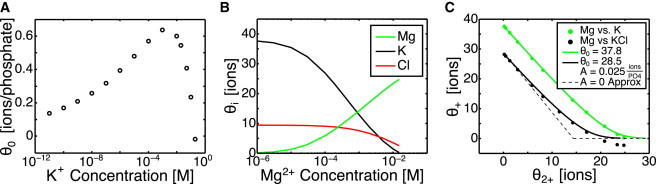
NLPB calculations of Manning condensation for the adenine riboswitch. (A) The Manning condensed ions obtained from NLPB in the absence of Mg2+ over a wide range of KCl concentrations. The Manning condensed fraction is not constant with concentration, as predicted by Manning theory for an infinite line of charge. (B) The Manning condensed ions partitioned into the three ionic species. The Debye length is held constant at the value for 50 mM KCl, whereas the Mg2+ level is increased. θ2+ increases with increasing Mg2+ concentration. (C) Competition between condensed Mg2+ and condensed K+. Manning condensed ions from NLPB calculations are plotted along with fits to Eq. 13. Cl− is a nonnegligible portion of the condensed fraction. The fit to Eq. 13 is better if Cl− is ignored (green), but subtracting it from θ+ (black) is more appropriate, so that the effect of condensed Cl− will be included in the effective electrostatic potential. A schematic of the A = 0 assumption (Eq. 14) is plotted as a dashed line. To see this figure in color, go online.
Due to the difficulty of computing F, θ0 and A are treated as fitting parameters, leaving only θ+ and free to vary with . NLPB calculations at fixed corroborate the form of Eq. 13, but there is also a nonnegligible population of condensed Cl− (Fig. 3, B and C). This occurs because Debye-Hückel predicts a nonphysical negative concentration of Cl− near the RNA. To account for their effect on electrostatic interactions, these condensed Cl− must be subtracted from θ+ in Eq. 6. Even if these condensed Cl− ions () are subtracted from θ+, the fit with Eq. 13 is still quite good. A can be estimated by fits to NLPB calculations (Fig. 3 C), but for this work, is assumed for simplicity. Equation 13 then has the intuitive meaning that each additional condensed Mg2+ displaces two condensed K+. The effect of this assumption is most pronounced between medium and high , near .
To compute θ+ in Eq. 6, an estimate of is required. For nearly all the Mg2+ and K+ concentrations considered, . Thus, the screening is almost exclusively due to K+ and Cl−. Since the excess Mg2+ can be divided into a screening population, which is approximately zero, and a condensed population, any excess Mg2+ is condensed. This means is approximately equal to (when both are expressed in units of ions per phosphate), and
| (14) |
The approximate equality of and is evidenced by the large population of Mg2+ in the outer-sphere regime and the near absence of diffuse Mg2+ observed in previous studies, even with a relatively high Mg2+ concentration (21).
To determine θ+ for a particular Mg2+ concentration, an iterative, self-consistent approach is used. A value for θ0 is chosen. After an initial guess for and subsequent calculation of θ+ with Eq. 14, the simulation is run and is computed from the Mg2+ distribution and updated. The process is repeated until converges. The single remaining adjustable parameter, θ0, was used to fit the experimental data for the adenine riboswitch and was estimated from NLPB methods for the SAM-I riboswitch.
SBMs capture excess Mg2+ and Mg2+-RNA interaction free energy
With the Mg2+ excluded volume calibrated, and with a method for including Manning condensed KCl, we can compute preferential interaction coefficients and interaction free energies from simulation. The agreement with previous experimental data (39) and explicit-solvent data (21) is quite close (see Fig. 5), and suggests the model is well parameterized thermodynamically.
Figure 5.
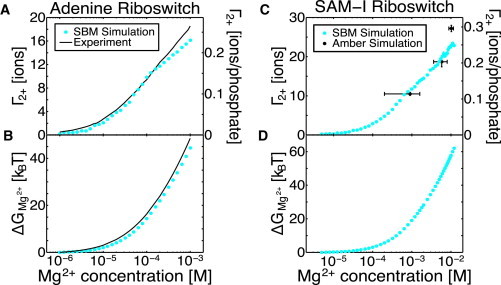
Excess Mg2+ (Γ2+) and Mg2+-RNA interaction free energy (ΔGMg2+) in the hybrid SBM with explicit Mg2+ agree with previous experimental and computational findings. Uncertainties from bootstrap analysis are plotted as error bars, but are too small to see in most cases. (A) Comparison between Γ2+ for the adenine riboswitch obtained in this study with SBM and a previous experimental fluorescence study (39). The 71 base RNA has a net charge of −70. KCl is present at 50 mM. Even at comparatively low concentrations, Mg2+ is able to effectively compete with K+ and Cl−. (B) The Mg2+ interaction free energy (ΔGMg2+) obtained from Eq. 1 by integrating Γ2+. Agreement between the two curves suggests that SBMs with explicit Mg2+ are capable of capturing the energetic stabilization due to Mg2+. (C) Comparison between Γ2+ for the SAM-I riboswitch obtained in this study with SBM and a previous Amber 99 molecular dynamics study (21). The 94 base RNA has a net charge of −92. KCl is present at 100 mM. Since θ0 is 18 ions, all values of Γ2+ above 9 ions are unaffected by K+ condensation. (D) Predicted ΔGMg2+ obtained by integrating Γ2+ of SAM-I. No data exist for comparison. To see this figure in color, go online.
For the adenine riboswitch, Leipply and Draper performed fluorescence measurements down to very low Mg2+ concentrations (39), where Mg2+ competition with K+ condensation is important. If condensed K+ is neglected in our model, the fit to experimental data is good for high Mg2+ concentration where , but poor for low Mg2+ concentration (Fig. 4). NLPB calculations estimate ions for the adenine riboswitch in 50 mM KCl. We find that ions (0.29 ions per phosphate) produces a much closer fit (Fig. 4). With this fitted K+ condensation, it can be seen that the Mg2+-RNA interaction free energy is within 8% at 1 mM Mg2+, compared to the 25% typically observed with NLPB theory (75,76).
Figure 4.
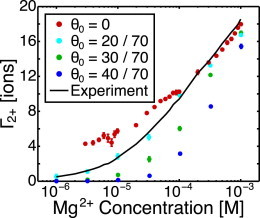
Comparison of preferential interaction coefficients of the adenine riboswitch at 50 mM KCl obtained for several choices of θ0 to experimental data. Although NLPB estimates suggest that θ0 = 28.4 ions, θ0 = 20 ions provides a closer fit to the experimental data. Manning condensed K+ cannot be neglected, as seen by the data for θ0 = 0. To see this figure in color, go online.
It is unclear whether the NLPB estimation and experimental fit of θ0 disagree because the approximations or parameters of NLPB break down or because the fit of θ0 is compensating for other neglected effects, such as hydration or nonuniform K+ displacement. In either case, these discrepancies likely exist in the SAM-I system as well. Therefore, as an initial approximation, the NLPB estimate of θ0 for the SAM-I riboswitch (25.7 ions) was scaled by the same ratio of 70% as observed for the adenine riboswitch to obtain ions (0.20 ions per phosphate).
An estimate of θ0 was required for the SAM-I riboswitch because previous explicit solvent simulations could only be performed in a high Mg2+ concentration range (1–10 mM) where Mg2+ completely outcompetes K+ condensation (i.e., ). Since for all three simulations, θ0 cannot be constrained by a fit or adjusted to improve the fit. The agreement with previous explicit-solvent results for for these high Mg2+ concentrations is quite close. The KCl condensation and choice of θ0 is of importance for low Mg2+ concentrations and for the computation of the free energy. Although no data exist for comparison, it would be useful to devise new experiments to test predictions and constrain θ0. It should be noted that there is a chelated ion in SAM-I that was neglected in this study. This ion would likely raise near Mg2+ concentrations of M, and would raise by a few .
Discussion
Model captures outer-sphere Mg2+ and can be extended for chelated Mg2+
Although the outer-sphere population accounts for the majority of excess Mg2+ (21), Mg2+ chelation sites can have an effect on and . A chelated Mg2+ ion raises by nearly one ion at low Mg2+ concentrations, due to the typically high affinity of chelation sites. At higher Mg2+ concentrations, an absent chelated ion is largely replaced by less tightly associated ions, and is independent of the presence of the chelated ion. A chelated ion affects over all concentrations, because the integral over includes the lower concentrations, but the effect is generally small. For example, in one study, a chelation site became occupied near 2 μM and was shown to contribute several to (40). This contribution was only a small fraction of . Since most of is due to outer-sphere Mg2+, accurately representing outer-sphere Mg2+ is essential for a model of Mg2+-RNA interactions. Although sometimes important, especially for , energetic contributions from chelated ions are a perturbation in comparison.
This model focuses on modeling outer sphere and diffuse Mg2+. Previous work has demonstrated that for the SAM-I riboswitch, and likely for other RNAs of similar size, the outer-sphere population is dominant (21). That result is underscored here by the ability of this model to capture and without chelated ions. For larger systems (62) or highly compact systems with buried phosphates (79), chelated ions are more important. Chelated ions have been included with harmonic restraints in the SBM without electrostatics (31). These techniques can be easily extended to this charged model by adding charge to the Mg2+ ion, and are quite adequate for native basin fluctuations. Further extensions to allow unbinding will be required for fluctuations outside the native basin or for computation of in systems where chelated Mg2+ is important.
Mg2+-RNA interactions are sensitive to Manning condensed KCl
Manning theory, as formulated for an infinite line of charge, suggests that condensation is constant over a wide range of concentrations. Although this is correct for infinite lines of charge, the riboswitch systems considered in this work show substantial variation of the Manning condensed ions over the small range of physiologically relevant KCl concentrations (Fig. 3 A). As a result, θ0 varies with KCl concentration and RNA geometry. The excess Mg2+, and hence , are sensitive to θ0 (Fig. 4). Thus, accurate methods for estimating θ0 for the structures and concentrations of interest are critical for the accuracy of the hybrid SBM. Two methods were used to estimate θ0: a fitting of the experimental HQS data and NLPB calculations. These methods disagree by eight ions, which is about 10% of the RNA charge. As mentioned in the third subsection under Results, the reasons for this disagreement are unclear but likely stem from either approximations or parameter choices in the NLPB calculation or from the θ0 fit compensating for other effects neglected by the SBM.
It could be that NLPB does not capture θ0 well because of the parameters used in the calculations, specifically the K+ radius. Previous studies (75,76) have shown that standard NLPB parameters underestimate , and from our experimental fit, the parameters also seem to overestimate θ0. This suggests that RNA affinity for K+ may be too high with these NLPB parameters. The K+ affinity can be lowered by increasing the radius of K+. Indeed, in NLPB theory, the ion radius is sometimes used as a fitting parameter (80). In the parameterization presented in this study, Mg2+ and K+ have the same radius of 2.0 Å. For Mg2+, this captures the hexahydrated size of Mg2+ well, but for K+ this is larger than the bare radius, and smaller than the hydrated radius. Other standard NLPB parameters use a larger K+ radius that corresponds to hydrated K+, and argue against using a smaller radius because NLPB cannot capture several effects relevant to dehydrated ions (81). Simulations have shown that some K+ dehydrates to associate with RNA (80), but this may be a force-field artifact, since NMR experiments suggest that K+ does not dehydrate in the presence of RNA (82). As a result, it is unclear what K+ radius is appropriate for NLPB calculations, but a larger radius may improve agreement with the fitted value for θ0.
It is also possible that NLPB estimates of θ0 differ from the experimental fit because the θ0 fit compensates for other effects neglected by the hybrid SBM. θ0 weakens Mg2+-RNA interactions at low Mg2+ concentrations. Thus, if the hybrid SBM underpredicts Mg2+-RNA affinity, especially at low Mg2+ concentrations, it will also underpredict θ0 to compensate. Hydration is one possible neglected effect. In Fig. 2, the outer-sphere peak at 4 Å is higher for the explicit-solvent simulation (which includes hydration effects), than for the SBM. Although the area under the curves is nearly equal due to compensation by the width and height of the peak, the SBM slightly underpredicts Mg2+-RNA affinity at high concentrations, as seen in Fig. 5, A and C). If this trend continues to low concentrations, the model will underpredict θ0 to compensate. Another possible neglected effect is the nonuniform displacement of K+. In the proposed SBM, condensed Mg2+ displaces K+ uniformly by lowering θ+, whereas in reality the K+ is instead likely displaced from the immediate neighborhood of a Mg2+ ion, which could allow stronger interactions with the nearby phosphates.
The transferability of the model to other RNAs, other KCl concentrations, or other ionic species is of great interest. The form of the model is transferable, but results are sensitive to the specific value of the parameter θ0. Transfer to other ionic species may be as simple as adjusting θ0 for monovalent ions and and for divalent ions (see Section S7 in the Supporting Material). A systematic way of predicting θ0 is required to generalize the model to other KCl concentrations or other RNA systems where no experimental data exist for fitting. In this study, θ0 could not be directly fit to experimental data for the SAM-I riboswitch. Since the experimental fit value for the adenine riboswitch was 70% of the NLPB estimate, the NLPB estimate of θ0 was scaled by 70% in the SAM-I riboswitch as well. Explicit solvent simulations could not confirm or refute the choice of θ0 because the low Mg2+ concentrations involved are inaccessible. Thus, SBM simulations of several systems must be compared with HQS fluorescence measurements to learn how to predict θ0. NLPB estimates may turn out to be the best method for estimating θ0. NLPB estimates might be improved by adjusting the NLPB K+ radius, or else the KCl concentration dependence NLPB estimate scaling factor, 70% here, could be probed. The tightly bound ion model (22) may give better results than NLPB. Alternatively, developing methods to compute the free energy, F, in Eq. 12 rather than fitting it may be fruitful. Models of θ0 should be tested against fluorescent HQS titrations at several KCl concentrations. Such data already exist for an rRNA 58-mer (76), but new HQS titrations of other systems are of great interest.
Generalizing and applying the model
With the model of Mg2+-RNA interactions presented here corroborated by previous experimental and computational studies, one can investigate the effects of Mg2+ upon the RNA energy landscape. Such models can explore the relative stability of various basins on the energy landscape as a function of ionic concentration, from the intermediates of riboswitch folding to functional transitions in the ribosome. In this study, we have computed as a first step toward computing the differential Mg2+-RNA interaction free energy between two ensembles, . is the relevant biological quantity because it determines the Mg2+-dependent free-energy difference between the two ensembles and thus the thermodynamic change in occupation probability as the ionic concentration changes. Several previous studies (75,76) have sought to compute with NLPB, but the precision of these calculations is limited by large uncertainties in the partially unfolded ensemble, which was represented by a few static structural models. With the SBM approach, one can more fully sample the partially unfolded ensemble and probe how the ensemble changes with Mg2+ concentration, removing a large source of uncertainty in the NLPB approach.
As we move toward probing between interconverting ensembles, care must be taken to ensure that the K+ condensation, θ+, does not radically change between ensembles. Since we only examine ensembles close to the crystal structure, this investigation is only able to check the θ+ dependence on Mg2+ concentration. However, as expressed in Eq. 13, θ+ can also depend on Mg2+ condensation for which concentration is a proxy, and on geometry and screening length, , through the parameters A and θ0. Fortunately, changes in θ0 and due to structural changes will have opposite effects on θ+ and may largely cancel. If it turns out that K+ condensation depends radically on structure, θ+ can be made a time-dependent function of structural order parameters, likely through calculation of F in Eq. 12. Although this is undesirable from a modeling perspective, it is valid, since the relaxation time of the K+ condensation is much faster than the Mg2+ dynamics.
The hybrid SBM will be a useful tool for addressing questions beyond . Cooperativity in Mg2+-induced transitions can be quantified, and changes to transition states can be identified. Mg2+ is known to have a strong effect on RNA kinetics. This is due at least in part to higher barriers between states, but may also result from changes in diffusion due to coupling between Mg2+ and RNA dynamics. Extensive sampling of an SBM can partition the effect of Mg2+ on RNA kinetics into changing barrier height and diffusion. These effects will be quite interesting to examine in future investigations.
Conclusion
Structure-based models provide a baseline representation of the minimally frustrated landscape predicted by energy-landscape theory. Roughness, frustration, and nonspecific interactions such as electrostatics may be added to this baseline to determine their effects on RNA folding and function. To account for the ionic sensitivity and highly charged nature of RNA, we have extended an all-atom structure-based model to include electrostatic interactions with explicit Mg2+ and implicit KCl.
The excess Mg2+ is a powerful metric, which allows coupling of the SBM with fluorescence measurements and explicit-solvent simulations. The model was extensively parameterized and tested against previous explicit-solvent simulations and HQS fluorescence measurements of excess Mg2+. Because of the close connection between excess Mg2+ and the Mg2+-RNA interaction free energy, the agreement of the model with experiment suggests that the model is well parameterized to capture Mg2+-RNA interaction free energies. The success of the hybrid SBM model, which is designed to capture the dynamics of the outer-sphere Mg2+ population, further corroborates the dominance of this population suggested by explicit-solvent simulations.
NLPB calculations suggest that for compact RNA structures, Manning condensed ions are not constant over a wide range of ionic concentrations as they are for lone RNA helices approximated by infinite lines of charge. Manning counterion condensation and competition between condensed populations is seen to be a critical correction to the Debye-Hückel approximation implemented here. A model of Mg2+-RNA interactions must account for the effect of Manning condensed KCl.
The hybrid SBM opens up concentration regimes and timescales inaccessible to explicit-solvent simulation. With these models, one can explore the relative stability of basins of the energy landscape as a function of ion concentration. The effects of ions on kinetics through barrier height, transition states, and diffusion can also be investigated. SBMs are now poised to address complex questions about the interplay of Mg2+, ligands, and RNA in folding and function.
Acknowledgments
We are grateful for the support of the Los Alamos National Laboratory (LANL) Institutional Computing for computing resources.
This work was supported by the Center for Theoretical Biological Physics sponsored by the National Science Foundation (Grant PHY-1308264), by the NSF (Grant MCB-1214457), and by LANL Laboratory Research and Development. U.M. is a John Simon Guggenheim Memorial Foundation fellow. J.N.O. is a CPRIT Scholar in Cancer Research sponsored by the Cancer Prevention and Research Institute of Texas.
Contributor Information
Karissa Y. Sanbonmatsu, Email: kys@lanl.gov.
José N. Onuchic, Email: jonuchic@rice.edu.
Supporting Material
References
- 1.Bryngelson J.D., Wolynes P.G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zwanzig R., Szabo A., Bagchi B. Levinthal’s paradox. Proc. Natl. Acad. Sci. USA. 1992;89:20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Onuchic J.N., Luthey-Schulten Z., Wolynes P.G. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 4.Ferreiro D.U., Hegler J.A., Wolynes P.G. On the role of frustration in the energy landscapes of allosteric proteins. Proc. Natl. Acad. Sci. USA. 2011;108:3499–3503. doi: 10.1073/pnas.1018980108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Whitford P.C., Miyashita O., Onuchic J.N. Conformational transitions of adenylate kinase: switching by cracking. J. Mol. Biol. 2007;366:1661–1671. doi: 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Clementi C., Plotkin S.S. The effects of nonnative interactions on protein folding rates: theory and simulation. Protein Sci. 2004;13:1750–1766. doi: 10.1110/ps.03580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Oliveira R.J., Whitford P.C., Leite V.B.P. The origin of nonmonotonic complex behavior and the effects of nonnative interactions on the diffusive properties of protein folding. Biophys. J. 2010;99:600–608. doi: 10.1016/j.bpj.2010.04.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Weinkam P., Pletneva E.V., Wolynes P.G. Electrostatic effects on funneled landscapes and structural diversity in denatured protein ensembles. Proc. Natl. Acad. Sci. USA. 2009;106:1796–1801. doi: 10.1073/pnas.0813120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Azia A., Levy Y. Nonnative electrostatic interactions can modulate protein folding: molecular dynamics with a grain of salt. J. Mol. Biol. 2009;393:527–542. doi: 10.1016/j.jmb.2009.08.010. [DOI] [PubMed] [Google Scholar]
- 10.Behrouzi R., Roh J.H., Woodson S.A. Cooperative tertiary interaction network guides RNA folding. Cell. 2012;149:348–357. doi: 10.1016/j.cell.2012.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rangan P., Masquida B., Woodson S.A. Architecture and folding mechanism of the Azoarcus Group I Pre-tRNA. J. Mol. Biol. 2004;339:41–51. doi: 10.1016/j.jmb.2004.03.059. [DOI] [PubMed] [Google Scholar]
- 12.Marek M.S., Johnson-Buck A., Walter N.G. The shape-shifting quasispecies of RNA: one sequence, many functional folds. Phys. Chem. Chem. Phys. 2011;13:11524–11537. doi: 10.1039/c1cp20576e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thirumalai D., Hyeon C. Springer; Berlin/Heidelberg: 2009. Chapter 2: Theory of RNA Folding: From Hairpins to Ribozymes. [Google Scholar]
- 14.Hyeon C., Lee J., Thirumalai D. Hidden complexity in the isomerization dynamics of Holliday junctions. Nat. Chem. 2012;4:907–914. doi: 10.1038/nchem.1463. [DOI] [PubMed] [Google Scholar]
- 15.Draper D.E. A guide to ions and RNA structure. RNA. 2004;10:335–343. doi: 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Draper D.E., Grilley D., Soto A.M. Ions and RNA folding. Annu. Rev. Biophys. Biomol. Struct. 2005;34:221–243. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 17.Lambert D., Leipply D., Draper D.E. The influence of monovalent cation size on the stability of RNA tertiary structures. J. Mol. Biol. 2009;390:791–804. doi: 10.1016/j.jmb.2009.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koculi E., Hyeon C., Woodson S.A. Charge density of divalent metal cations determines RNA stability. J. Am. Chem. Soc. 2007;129:2676–2682. doi: 10.1021/ja068027r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Heilman-Miller S.L., Thirumalai D., Woodson S.A. Role of counterion condensation in folding of the Tetrahymena ribozyme. I. Equilibrium stabilization by cations. J. Mol. Biol. 2001;306:1157–1166. doi: 10.1006/jmbi.2001.4437. [DOI] [PubMed] [Google Scholar]
- 20.Heilman-Miller S.L., Pan J., Woodson S.A. Role of counterion condensation in folding of the Tetrahymena ribozyme. II. Counterion-dependence of folding kinetics. J. Mol. Biol. 2001;309:57–68. doi: 10.1006/jmbi.2001.4660. [DOI] [PubMed] [Google Scholar]
- 21.Hayes R.L., Noel J.K., Sanbonmatsu K.Y. Magnesium fluctuations modulate RNA dynamics in the SAM-I riboswitch. J. Am. Chem. Soc. 2012;134:12043–12053. doi: 10.1021/ja301454u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen G., Tan Z.J., Chen S.-J. Salt-dependent folding energy landscape of RNA three-way junction. Biophys. J. 2010;98:111–120. doi: 10.1016/j.bpj.2009.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hennelly S.P., Novikova I.V., Sanbonmatsu K.Y. The expression platform and the aptamer: cooperativity between Mg2+ and ligand in the SAM-I riboswitch. Nucleic Acids Res. 2013;41:1922–1935. doi: 10.1093/nar/gks978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Whitford P.C., Noel J.K., Onuchic J.N. An all-atom structure-based potential for proteins: bridging minimal models with all-atom empirical forcefields. Proteins. 2009;75:430–441. doi: 10.1002/prot.22253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clementi C., Nymeyer H., Onuchic J.N. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000;298:937–953. doi: 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
- 26.Hyeon C., Onuchic J.N. Mechanical control of the directional stepping dynamics of the kinesin motor. Proc. Natl. Acad. Sci. USA. 2007;104:17382–17387. doi: 10.1073/pnas.0708828104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sułkowska J.I., Noel J.K., Onuchic J.N. Energy landscape of knotted protein folding. Proc. Natl. Acad. Sci. USA. 2012;109:17783–17788. doi: 10.1073/pnas.1201804109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hyeon C., Thirumalai D. Mechanical unfolding of RNA hairpins. Proc. Natl. Acad. Sci. USA. 2005;102:6789–6794. doi: 10.1073/pnas.0408314102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cho S.S., Pincus D.L., Thirumalai D. Assembly mechanisms of RNA pseudoknots are determined by the stabilities of constituent secondary structures. Proc. Natl. Acad. Sci. USA. 2009;106:17349–17354. doi: 10.1073/pnas.0906625106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Whitford P.C., Schug A., Sanbonmatsu K.Y. Nonlocal helix formation is key to understanding S-adenosylmethionine-1 riboswitch function. Biophys. J. 2009;96:L7–L9. doi: 10.1016/j.bpj.2008.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Whitford P.C., Geggier P., Sanbonmatsu K.Y. Accommodation of aminoacyl-tRNA into the ribosome involves reversible excursions along multiple pathways. RNA. 2010;16:1196–1204. doi: 10.1261/rna.2035410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ratje A.H., Loerke J., Spahn C.M.T. Head swivel on the ribosome facilitates translocation by means of intra-subunit tRNA hybrid sites. Nature. 2010;468:713–716. doi: 10.1038/nature09547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Whitford P.C., Ahmed A., Sanbonmatsu K.Y. Excited states of ribosome translocation revealed through integrative molecular modeling. Proc. Natl. Acad. Sci. USA. 2011;108:18943–18948. doi: 10.1073/pnas.1108363108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hamelberg D., Shen T., McCammon J.A. Insight into the role of hydration on protein dynamics. J. Chem. Phys. 2006;125:094905. doi: 10.1063/1.2232131. [DOI] [PubMed] [Google Scholar]
- 35.Zwanzig R. Diffusion in a rough potential. Proc. Natl. Acad. Sci. USA. 1988;85:2029–2030. doi: 10.1073/pnas.85.7.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kouza M., Li M.S., Thirumalai D. Effect of finite size on cooperativity and rates of protein folding. J. Phys. Chem. A. 2006;110:671–676. doi: 10.1021/jp053770b. [DOI] [PubMed] [Google Scholar]
- 37.Grilley D., Soto A.M., Draper D.E. Mg2+-RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc. Natl. Acad. Sci. USA. 2006;103:14003–14008. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Leipply D., Draper D.E. Dependence of RNA tertiary structural stability on Mg2+ concentration: interpretation of the Hill equation and coefficient. Biochemistry. 2010;49:1843–1853. doi: 10.1021/bi902036j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Leipply D., Draper D.E. Effects of Mg2+ on the free energy landscape for folding a purine riboswitch RNA. Biochemistry. 2011;50:2790–2799. doi: 10.1021/bi101948k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Leipply D., Draper D.E. Evidence for a thermodynamically distinct Mg2+ ion associated with formation of an RNA tertiary structure. J. Am. Chem. Soc. 2011;133:13397–13405. doi: 10.1021/ja2020923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chen B., Zuo X., Dayie T.K. Multiple conformations of SAM-II riboswitch detected with SAXS and NMR spectroscopy. Nucleic Acids Res. 2012;40:3117–3130. doi: 10.1093/nar/gkr1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Haller A., Rieder U., Micura R. Conformational capture of the SAM-II riboswitch. Nat. Chem. Biol. 2011;7:393–400. doi: 10.1038/nchembio.562. [DOI] [PubMed] [Google Scholar]
- 43.Bastet L., Dubé A., Lafontaine D.A. New insights into riboswitch regulation mechanisms. Mol. Microbiol. 2011;80:1148–1154. doi: 10.1111/j.1365-2958.2011.07654.x. [DOI] [PubMed] [Google Scholar]
- 44.Priyakumar U.D., MacKerell A.D., Jr. Role of the adenine ligand on the stabilization of the secondary and tertiary interactions in the adenine riboswitch. J. Mol. Biol. 2010;396:1422–1438. doi: 10.1016/j.jmb.2009.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Banás P., Walter N.G., Otyepka M. Protonation states of the key active site residues and structural dynamics of the glmS riboswitch as revealed by molecular dynamics. J. Phys. Chem. B. 2010;114:8701–8712. doi: 10.1021/jp9109699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Doshi U., Kelley J.M., Hamelberg D. Atomic-level insights into metabolite recognition and specificity of the SAM-II riboswitch. RNA. 2012;18:300–307. doi: 10.1261/rna.028779.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Huang W., Kim J., Aboul-ela F. The impact of a ligand binding on strand migration in the SAM-I riboswitch. PLOS Comput. Biol. 2013;9:e1003069. doi: 10.1371/journal.pcbi.1003069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lin J.-C., Thirumalai D. Relative stability of helices determines the folding landscape of adenine riboswitch aptamers. J. Am. Chem. Soc. 2008;130:14080–14081. doi: 10.1021/ja8063638. [DOI] [PubMed] [Google Scholar]
- 49.Serganov A., Yuan Y.-R., Patel D.J. Structural basis for discriminative regulation of gene expression by adenine- and guanine-sensing mRNAs. Chem. Biol. 2004;11:1729–1741. doi: 10.1016/j.chembiol.2004.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lemay J.-F., Penedo J.C., Lafontaine D.A. Folding of the adenine riboswitch. Chem. Biol. 2006;13:857–868. doi: 10.1016/j.chembiol.2006.06.010. [DOI] [PubMed] [Google Scholar]
- 51.Noeske J., Schwalbe H., Wöhnert J. Metal-ion binding and metal-ion induced folding of the adenine-sensing riboswitch aptamer domain. Nucleic Acids Res. 2007;35:5262–5273. doi: 10.1093/nar/gkm565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Montange R.K., Batey R.T. Structure of the S-adenosylmethionine riboswitch regulatory mRNA element. Nature. 2006;441:1172–1175. doi: 10.1038/nature04819. [DOI] [PubMed] [Google Scholar]
- 53.Stoddard C.D., Montange R.K., Batey R.T. Free state conformational sampling of the SAM-I riboswitch aptamer domain. Structure. 2010;18:787–797. doi: 10.1016/j.str.2010.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang W., Kim J., Aboul-ela F. A mechanism for S-adenosyl methionine assisted formation of a riboswitch conformation: a small molecule with a strong arm. Nucleic Acids Res. 2009;37:6528–6539. doi: 10.1093/nar/gkp664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Noel J.K., Whitford P.C., Onuchic J.N. SMOG@ctbp: simplified deployment of structure-based models in GROMACS. Nucleic Acids Res. 2010;38(Web Server issue):W657–W661. doi: 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Denesyuk N.A., Thirumalai D. Coarse-grained model for predicting RNA folding thermodynamics. J. Phys. Chem. B. 2013;117:4901–4911. doi: 10.1021/jp401087x. [DOI] [PubMed] [Google Scholar]
- 57.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 58.Manning G.S. Electrostatic free energy of the DNA double helix in counterion condensation theory. Biophys. Chem. 2002;101-102:461–473. doi: 10.1016/s0301-4622(02)00162-x. [DOI] [PubMed] [Google Scholar]
- 59.Chu V.B., Bai Y., Doniach S. Evaluation of ion binding to DNA duplexes using a size-modified Poisson-Boltzmann theory. Biophys. J. 2007;93:3202–3209. doi: 10.1529/biophysj.106.099168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Moreira A.G., Netz R.R. Strong-coupling theory for counter-ion distributions. Europhys. Lett. 2000;52:705–711. [Google Scholar]
- 61.Noel J.K., Whitford P.C., Onuchic J.N. The shadow map: a general contact definition for capturing the dynamics of biomolecular folding and function. J. Phys. Chem. B. 2012;116:8692–8702. doi: 10.1021/jp300852d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Klein D.J., Moore P.B., Steitz T.A. The contribution of metal ions to the structural stability of the large ribosomal subunit. RNA. 2004;10:1366–1379. doi: 10.1261/rna.7390804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang J., Cieplak P., Kollman P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 64.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 65.Honig B., Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 66.Chen S.W., Honig B. Monovalent and divalent salt effects on electrostatic free energies defined by the nonlinear Poisson-Boltzmann equation: application to DNA binding reactions. J. Phys. Chem. B. 1997;101:9113–9118. [Google Scholar]
- 67.Manning G.S., Mohanty U. Counterion condensation on ionic oligomers. Physica A. 1997;247:196–204. [Google Scholar]
- 68.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Baker N.A. Improving implicit solvent simulations: a Poisson-centric view. Curr. Opin. Struct. Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 70.Baker N.A. Poisson-Boltzmann methods for biomolecular electrostatics. Methods Enzymol. 2004;383:94–118. doi: 10.1016/S0076-6879(04)83005-2. [DOI] [PubMed] [Google Scholar]
- 71.He Z., Chen S.-J. Predicting ion-nucleic acid interactions by energy landscape-guided sampling. J. Chem. Theory Comput. 2012;8:2095–2101. doi: 10.1021/ct300227a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Boschitsch A.H., Danilov P.V. Formulation of a new and simple nonuniform size-modified Poisson-Boltzmann description. J. Comput. Chem. 2012;33:1152–1164. doi: 10.1002/jcc.22946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Borukhov I., Andelman D. Steric effects in electrolytes: a modified Poisson-Boltzmann equation. Phys. Rev. Lett. 1997;79:435–438. [Google Scholar]
- 74.Misra V.K., Draper D.E. A thermodynamic framework for Mg2+ binding to RNA. Proc. Natl. Acad. Sci. USA. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Soto A.M., Misra V., Draper D.E. Tertiary structure of an RNA pseudoknot is stabilized by “diffuse” Mg2+ ions. Biochemistry. 2007;46:2973–2983. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 76.Grilley D., Misra V., Draper D.E. Importance of partially unfolded conformations for Mg2+-induced folding of RNA tertiary structure: structural models and free energies of Mg2+ interactions. Biochemistry. 2007;46:10266–10278. doi: 10.1021/bi062284r. [DOI] [PubMed] [Google Scholar]
- 77.Savelyev A., Papoian G.A. Polyionic charge density plays a key role in differential recognition of mobile ions by biopolymers. J. Phys. Chem. B. 2008;112:9135–9145. doi: 10.1021/jp801448s. [DOI] [PubMed] [Google Scholar]
- 78.Wilson R.W., Rau D.C., Bloomfield V.A. Comparison of polyelectrolyte theories of the binding of cations to DNA. Biophys. J. 1980;30:317–325. doi: 10.1016/S0006-3495(80)85097-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Draper D.E. Folding of RNA tertiary structure: Linkages between backbone phosphates, ions, and water. Biopolymers. 2013;99:1105–1113. doi: 10.1002/bip.22249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kirmizialtin S., Silalahi A.R., Fenley M.O. The ionic atmosphere around A-RNA: Poisson-Boltzmann and molecular dynamics simulations. Biophys. J. 2012;102:829–838. doi: 10.1016/j.bpj.2011.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Chen A.A., Marucho M., Pappu R.V. Simulations of RNA interactions with monovalent ions. Methods Enzymol. 2009;469:411–432. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 82.Braunlin W.H. NMR studies of cation-binding environments on nucleic acids. Adv. Phys. Chem. 1995;5:89–139. [Google Scholar]
- 83.Tsai J., Taylor R., Gerstein M. The packing density in proteins: standard radii and volumes. J. Mol. Biol. 1999;290:253–266. doi: 10.1006/jmbi.1999.2829. [DOI] [PubMed] [Google Scholar]
- 84.Perel V., Shklovskii B. Screening of a macroion by multivalent ions: a new boundary condition for the Poisson-Boltzmann equation and charge inversion. Physica A. 1999;274:446–453. [Google Scholar]
- 85.Eisenhaber F., Lijnzaad P., Scharf M. The double cubic lattice method: efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 1995;16:273–284. [Google Scholar]
- 86.Auffinger P., Grover N., Westhof E. Metal ion binding to RNA. Met. Ions Life Sci. 2011;9:1–35. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


