Multiscale modeling of diffusion in a crowded environment

Abstract

We present a multiscale approach to model diffusion in a crowded environment and its effect on the reaction rates. Diffusion in biological systems is often modeled by a discrete space jump process in order to capture the inherent noise of biological systems, which becomes important in the low copy number regime. To model diffusion in the crowded cell environment efficiently, we compute the jump rates in this mesoscopic model from local first exit times, which account for the microscopic positions of the crowding molecules, while the diffusing molecules jump on a coarser Cartesian grid. We then extract a macroscopic description from the resulting jump rates, where the excluded volume effect is modeled by a diffusion equation with space dependent diffusion coefficient. The crowding molecules can be of arbitrary shape and size and numerical experiments demonstrate that those factors together with the size of the diffusing molecule play a crucial role on the magnitude of the decrease in diffusive motion. When correcting the reaction rates for the altered diffusion we can show that molecular crowding either enhances or inhibits chemical reactions depending on local fluctuations of the obstacle density.

1 Introduction

Living cells are spatially organized, e.g. eukaryotic cells have a confined nucleus containing the DNA and reaction complexes are often bound to the cell membrane. To simulate reaction networks accurately it is therefore important to incorporate the molecules’ movement into the models and account for the time it takes for a signal to transmit e.g. from the nucleus to the membrane.

Molecules move by diffusion through biological media such as the cytoplasm, which is a non-solute medium, where an estimated 40% [50, 71] of the available space is occupied by macromolecules, such as proteins, ribosomes, RNA and the cytoskeleton. The environment is called crowded, meaning that the space is densely packed by molecules but individual species are only present at very low concentrations. Macromolecular crowding is especially important on the cell membrane [30], where attaching actin filaments [55] create barriers, that hinder the displacement of membrane bound molecules [44, 46]. In mitochondria more than 60% of the matrix can be occupied by enzymes and proteins [80]. Moreover, the extracellular space between e.g. brain cells [41] is also considered crowded.

The steric repulsions between molecules in a crowded environment force diffusing molecules to move around obstacles, or “crowders”, this slows down diffusion. New techniques such as fluorescence-fluctuation analysis [12] have shown that diffusion is not simply slowed down but that crowding can lead to anomalous diffusion, where the mean square displacement (MSD) of the molecule is no longer linear, but sublinear in time. As the crowder density increases, space is divided into subdomains and becomes inhomogeneous. For this fractal space, the dimension decreases to a non integer and the MSD no longer follows the linear law applicable in integer dimensions [5, 37].

The change of the diffusion rate in a crowded environment is a hydrodynamic effect. The excluded volume effect on the reaction rates is a thermodynamic consequence [34] and can be both impeding and promoting. While diffusion limited reaction rates are decreased due to the slower diffusion, transition state limited reactions and dimerizations are accelerated [17] since intermediate products reside longer in the vicinity of reaction complexes and dimers occupy less volume than two monomers. Hindered diffusion also leads to localized reactions and a heterogeneous distribution of products, which increases intrinsic noise [35].

Scaled particle theory (SPT) has been used to describe the thermodynamic effect on the reaction rates in a crowded environment [31, 34, 69]. Another approach is to perform Brownian dynamics (BD) simulations and fit the reaction rates to the microscopic results, [48, 74]. In [6], Michaelis-Menten reaction dynamics are best fitted by fractal kinetics and the results are verified by microscopic cellular automata (CA) simulations. The fractal kinetics are modified in [71] to a Zipf-Mandelbrot distribution of the reaction rates.

To better understand the effects of excluded volume on both diffusion and reactions, accurate reaction-diffusion simulations in the crowded cell environment are needed. The microscopic approaches mentioned above are computationally very expensive due to the high number of collisions in such a medium. In this paper we present a novel multiscale approach to simulate diffusion of a spherical particle surrounded by inert and inactive crowders of any size and shape. We resolve the microscopic positions and shapes of the crowders initially to precompute jump rates for the moving molecules. The molecule follows a random walk on a coarse Cartesian grid that no longer resolves the multiple crowders for computationally more efficient simulations. With our approach we can connect a given distribution of obstacles to a space dependent diffusion map which can be used to compute space dependent reaction rates representing reactions in the crowded environment. The method can easily be extended to moving crowders and an advantage over other techniques such as SPT is the versatility in the shape of the crowders. The upscaling to a coarse grid makes the stochastic simulations computationally much more efficient than BD and CA simulations.

In the next section we present existing models of spatial simulations in systems biology and how they incorporate crowding effects. We then present how the microscopic motion of a molecule can be used to calculate its first exit time (FET) from domains, which provides the jump rates in a coarse grained discrete jump process on the mesoscopic level. We continue by extending the FET approach to include macromolecular crowders. In Section 3.2, we use the jump coefficients and compute a space dependent diffusion map for the macroscopic level and show in Section 3.3 how that affects the reaction rates in the crowded environment. We conclude with numerical experiments in the final section.

Vectors and matrices are written in boldface. A vector u has the components u_i and the elements of a matrix A are A_ij. The derivative of a variable u with respect to time t is written u_t.

2 Spatial modeling in systems biology

In this section we first present existing models of diffusion simulations in systems biology and then describe how they can be adapted to include macromolecular crowding.

2.1 Models of diffusion in dilute media

Molecules undergoing diffusion and reactions inside living cells are often modeled by the reaction-diffusion equations. These are continuous, deterministic partial differential equations (PDEs) describing the time evolution of the concentrations of molecules. For a diffusing molecule the concentration u(x, t) is described by the diffusion equation

$$u_t(\mathbf{x},t)={\gamma }_0\mathrm{\Delta }u(\mathbf{x},t),\mathbf{x}\in \mathrm{\Omega }$$ (2.1)

with diffusion coefficient γ₀ and suitable boundary conditions on ∂Ω. To include reactions corresponding terms are added. This macroscopic description is accurate in the limit of large molecule numbers, when stochastic fluctuations are small and the mean value is the quantity of interest. Important molecules such as DNA or transcription factors are, however, only present at very low copy numbers inside living cells. It has been observed in experiments [18, 53, 59, 61, 67, 75] and shown theoretically [26, 54] that stochastic fluctuations play an important role and a discrete stochastic description is more accurate than the deterministic equations.

We distinguish two levels of accuracy of stochastic models. In the mesoscopic model the domain Ω is partitioned into N non-overlapping voxels 𝒱_i with nodes x_i at the center. The state vector y(t) contains the number of molecules y_i(t) in each voxel 𝒱_i at time t. The voxels are small enough that the molecules can be considered well mixed inside so that reactions can occur between molecules residing in the same voxel. An individual molecule can jump from a voxel 𝒱_i to a neighboring voxel 𝒱_j to model diffusion. The diffusion master equation (DME) describes the time evolution of the probability to be in state y of a system with only diffusion

$$\frac{\partial p(\mathbf{y},t)}{\partial t}=\sum _{i=1}^N\sum _{j=1}^N{\lambda }_{ij}(\mathbf{y}-{\mathit{\mu }}_{ij})p(\mathbf{y}-{\mathit{\mu }}_{ij},t)-{\lambda }_{ii}(\mathbf{y})p(\mathbf{y},t),$$ (2.2)

where λ_ij is the jump propensity from 𝒱_i to 𝒱_j and ${\lambda }_{ii}={\sum }_{j=1}^N{\lambda }_{ij}$ is the total propensity to leave voxel 𝒱_i. The transition vector μ_ij is zero except for μ_ij,i = −1 and μ_ij,j = 1. Let θ_ij be the splitting probability, that a jump from 𝒱_i goes to 𝒱_j, then

$${\lambda }_{ij}={\theta }_{ij}{\lambda }_{ii}.$$ (2.3)

By including reaction terms in a similar manner, the DME can be extended to the reaction-diffusion master equation (RDME). In the presence of bimolecular reactions there exists no analytical solution and a numerical solution is impossible due to the high dimension of y. Instead, one samples trajectories of the system with the stochastic simulation algorithm (SSA), first presented by Gillespie [28] for only reactions and improved in [9, 27]. The algorithm was extended to space dependent problems with a Cartesian partitioning of the domain in [15] implemented in [36]. The propensities λ_ii are here used to generate random numbers for the time until the next jump. To represent the complicated geometries present in cells the algorithm was extended to curved boundaries in [43] and adapted for unstructured meshes in [19] with software in [14, 40].

In the more accurate microscopic model the molecules are tracked along their Brownian trajectories in a continuous space, continuous time Markov process. Brownian dynamics (BD) simulations discretize time and sample the positions of a particle at these discrete time points from a normal distribution. Versions of this method are for example implemented in the software packages Smoldyn [1], ReaDDy [72] and MCell [45]. Another approach is called Green’s function reaction dynamics (GFRD) [79, 81], where protective domains are constructed around individual molecules in which they cannot interact with other molecules. This is an event driven algorithm with an asynchronous time step that is chosen such that the probability to exit the protective domain is small. In [77] the algorithm is improved to eGFRD using the exact first exit times from [13, 64] to make it exact and more efficient. The exit times and exit positions from these domains are sampled to propagate the system until molecules are close enough to interact without sampling all the intermediate jumps.

2.2 Include macromolecular crowding

The macroscopic, mesoscopic and microscopic models presented above are designed to simulate diffusion in a dilute medium. The microscopic model automatically incorporates crowding effects since the molecules are modeled as hard spheres with a given volume, but it becomes computationally very expensive in a densely packed space of inactive crowders, because the protective domains around molecules will be small and many short jumps will be simulated before meeting a potential reaction partner.

Cellular automata (CA) have been used in [6, 10, 71, 76] to simulate diffusion in a crowded environment. This is a lattice, or voxel, based microscopic approach, where each site can hold one molecule and crowders are represented as already occupied lattice points. The jump length is here the size of a molecule which also leads to expensive simulations with many short jumps and the shape of the molecules corresponds to the shape of the chosen lattice. The choice of the lattice, moreover, influences the excluded volume effect [32, 57].

In [70] a mesoscopic approach is used where each voxel can hold more than one molecule. After distributing immobile crowders it is decided which voxels are accessible and which are full. The crowders can move in [21, 78] and the jump propensity to an adjacent node is scaled by the number of available spaces in the target voxel. Macroscopic nonlinear PDEs are then derived in [21] to model diffusion in the crowded cell environment and the results are validated by physical experiments in [22]. This approach is extended in [65] to derive nonlinear diffusion equations modeling more complicated interactions than steric repulsion between the molecules. Similarly, the averaged occupied volume in the whole domain is used in [47] to rescale the jump propensities. These approaches at most take the averaged occupied volume in the target voxel into account and neglect the microscopic positions, the shape of the molecules and the surrounding medium. Hence only an averaged behavior is observed and the MSD is linear like for normal diffusion but with a reduced diffusion constant [66]:

$$\langle {\mathbf{x}}^2(t)\rangle =(1-\varphi ){\gamma }_{0}t,$$ (2.4)

where ϕ is the occupied volume fraction.

In this paper we present a novel multiscale approach to simulate molecular crowding. We will use the microscopic information of the crowders’ positions to recalculate the jump propensities on an overlying mesoscopic mesh. Instead of simulating diffusion in the detailed environment, as in BD, we will have to solve many PDEs on small subdomains resolving the microscopic positions of the crowders. This is similar to homogenization techniques used e.g. for flow simulations in porous media, [8, 51]. The crowding molecules can have any shape and this approach is especially useful when the crowded environment is stationary or evolves on a much slower time scale than the diffusing molecule, so that the jump coefficients can be precomputed and used for a long simulation time. This is reasonable since the macromolecules responsible for the majority of occupied volume are ribosomes, microtubules and actin filaments [17], which are large and hence diffuse on a slower time scale than for example transcription factors. Moreover, it was shown in [12] that anomalous behavior is most likely to happen in a stationary environment, since otherwise averaging effects simply reduce the coefficient of normal diffusion. But, it is important to mention that by computing statistics our method can be made efficient also for moving crowders.

3 Upscaling of the crowding effects

We will now present a method of upscaling the detailed information about diffusion in a crowded environment on the microscopic level to the mesoscopic simulation framework and further to the macroscopic description. Moreover, we describe a way of accounting for crowding effects in the reaction dynamics on the mesoscopic and macroscopic levels.

3.1 Microscopic to mesoscopic: first exit times

In this section we will use the methods developed for microscopic simulations of Brownian motion with protective domains [64], to derive the jump propensities λ_ii and splitting probabilities θ_ij for the mesoscopic model. For simplicity the illustrations are given in dimension d = 2 but the method can be extended to d = 3 without modification.

3.1.1 First exit times

Let c(x, t) be the probability distribution that a molecule in Brownian motion is at x at time t and has not yet exited a domain ω. If x₀ is the starting position of the molecule diffusing with γ₀, then c(x, t) fulfills

$$\begin{array}{ll}{c}_t(\mathbf{x},t)={\gamma }_0\mathrm{\Delta }c(\mathbf{x},t)\hfill & \mathbf{x}\in \omega ,\hfill \\ c(\mathbf{x},t)=0,\hfill & \mathbf{x}\in \partial \omega ,\hfill \\ c(\mathbf{x},0)={\delta }_{{\mathbf{x}}_0}.\hfill & \hfill \end{array}$$ (3.1)

The homogeneous Dirichlet boundary condition here models that the particle is removed once it hits the boundary. The survival probability of the particle inside ω until time t is then

$$S(t)={\int }_{\omega }c(\mathbf{x},t)d\omega .$$ (3.2)

By Gauss’ formula the probability density p_ω(t) that the particle leaves ω at t is

$$p_{\omega }(t)=-\frac{\partial S(t)}{\partial t}=-{\gamma }_0{\int }_{\partial \omega }\mathbf{n}·\nabla c(\mathbf{x},t)ds,$$ (3.3)

where n is the outward normal. The expected time E for the molecule to leave ω for the first time is given by

$$E={\int }_0^{\infty }t{p}_{\omega }(t)dt={\int }_0^{\infty }S(t)dt.$$ (3.4)

We now use this FET approach to compute the jump propensities λ_ii in the space discrete mesoscopic model. We use a Cartesian grid with space discretization h and N nodes x_i in the domain Ω. The voxels 𝒱_i are here defined by the dual mesh, see Fig. 3.1(b). Since the molecules are considered well mixed inside the voxels, the domain ω that diffusing particles have to leave to be well mixed in the next voxel has to include the centers of the neighboring voxels. On a Cartesian grid we showed in [49] that solving (3.1) on the circle ω_i with center x_i and radius h (similarly a line of length 2h in 1D or a sphere with radius h in 3D) and choosing x₀ = x_i gives the correct exit time from node i, see Fig. 3.1(b). Observe that ω_i ⊋ 𝒱_i and ω_i ∩ ω_j ≠ ∅ for neighboring nodes i and j. Using (3.2) and (3.4) the expected exit time E_i from 𝒱_i is

Fig. 3.1.

(a)Excluded volume (grey and red) for the center of mass of the diffusing molecule (blue). (b) Cartesian mesh and protective domain ω_i without crowding. (c) Solution of (3.9) with the effect of molecular crowding.

$$E_i=\frac{h^2}{2d{\gamma }_0},$$ (3.5)

see [25]. Since the jump propensity is the inverse of the exit time this agrees with the mesoscopic rate on Cartesian grids

$${\lambda }_{ii}=\frac{2d{\gamma }_0}{h^2}=E_i^{-1}.$$ (3.6)

The probability to leave ω_i through a given part of the boundary ∂ω_ij at time t is given by the proportion of fluxes

$${\theta }_{ij}(t)=\frac{{\int }_{\partial {\omega }_{ij}}\mathbf{n}·\nabla c(\mathbf{x},t)ds}{{\int }_{\partial {\omega }_i}\mathbf{n}·\nabla c(\mathbf{x},t)ds},$$ (3.7)

and we can compute the expected probability to jump to a certain neighboring voxel by

$${\theta }_{ij}={\int }_0^{\infty }{\theta }_{ij}(t)p_{{\omega }_i}(t)dt=-{\gamma }_0{\int }_0^t{\int }_{\partial {\omega }_{ij}}\mathbf{n}·\nabla c(\mathbf{x},t)\mathit{dsdt}.$$ (3.8)

Choosing ∂ω_ij to be the quarter segment of the boundary closest to x_j, see the blue line in Fig. 3.1(b), yields the splitting probability θ_ij = 0.25 as expected on a Cartesian grid. The method has been extended to a rectangular grid and possible jumps to the diagonal neighbors in [58].

By conditioning on the first step, these time dependent equations can be converted to equations describing directly the expected quantities [68]. The expected exit time for a molecule starting to diffuse in x from the domain ω_i fulfills the Poisson’s equation

$$\begin{array}{lll}\hfill {\gamma }_0\mathrm{\Delta }E(\mathbf{x})& \hfill =-1,\hfill & \mathbf{x}\in {\omega }_i,\hfill \\ \hfill E(\mathbf{x})& \hfill =0,\hfill & \mathbf{x}\in \partial {\omega }_i.\hfill \end{array}$$ (3.9)

Equivalently, the expected splitting probability for this molecule to exit through the boundary ∂ω_ij can be computed by the harmonic measure [63, Ch. 7], and fulfills the Laplace equation

$$\begin{array}{lll}\hfill \mathrm{\Delta }{\theta }_{ij}(\mathbf{x})& =0,\hfill & \mathbf{x}\in \omega ,\hfill \\ \hfill {\theta }_{ij}(\mathbf{x})& =1,\hfill & \mathbf{x}\in \partial {\omega }_{ij},\hfill \\ \hfill {\theta }_{ij}(\mathbf{x})& =0,\hfill & \mathbf{x}\in \partial {\omega }_i\backslash \partial {\omega }_{ij}.\hfill \end{array}$$ (3.10)

We solve equations (3.9) and (3.10) and evaluate them at x_i instead of solving the time-dependent equations and the integrals above. It is sufficient to solve (3.10) three times for each node since ${\sum }_{j=1}^4{\theta }_{ij}=1$.

In the following, we will not simply use the circle ω_i to compute the mesoscopic rates, but we will prohibit the molecule from diffusing where the crowders are located.

3.1.2 Include crowding molecules

The crowding molecules are represented as obstacles or holes in the domain ω_i with reflecting boundary conditions. Equations (3.1),(3.9) and (3.10) describe the diffusion of point particles. To account for the volume of the diffusing molecule its radius is added to the excluded volume for the center of mass, see Fig 3.1(a). We depict the crowder as a circle with radius R, but it is important to mention that any shape is possible for the crowding molecules, see Fig. 3.1(c). The shape of the small (as compared to crowders) diffusing molecule is, however, restricted to circles or spheres with radius r.

Solving (3.9) and (3.10) numerically on the perforated domain ω_i means that the crowding molecules have to be resolved by a fine mesh. But, we have divided the global problem into N smaller local subproblems (one protective domain ω_i around each node i). For each subproblem we have to solve 4 PDE’s ((3.9) and three equations of type (3.10)). These equations have to be solved only once in a precomputing step which is straight forward parallelizable. This is similar to the approach in [8] where deterministic local equations are solved on media with porous microstructures. The costly stochastic simulations of the spatial SSA are then performed on the coarse mesh with N nodes, that do no longer resolve the individual obstacles. The boundary conditions on the global domain Ω (reflective or absorbing) are implemented by posing these conditions on the secants of the half or quarter circles, which are the protective domains for boundary nodes, see Fig. 3.2(a). In Fig. 3.2(b) we briefly illustrate how the first exit time approach can be further used to compute the jump rates for a Cartesian grid, discretizing a domain Ω with a curved boundary. Here the part of ∂ω_i originating from the circle is imposed with the boundary conditions in (3.9) and (3.10) and the part originating from ∂Ω with the boundary condition valid on Ω, which is usually reflecting or (partially) absorbing. The circle is then divided in the same way as before to compute the splitting probabilities to the neighboring nodes remaining inside Ω.

Fig. 3.2.

(a) Boundary treatment. (b) Using the first exit time approach to compute Cartesian jump rates on the boundary of a curved domain Ω. (c) Model error when interpreting molecules as well mixed and jumping between nodes simultaneously.

The simultaneous interpretation of the moving molecules being well-mixed inside the voxels 𝒱_i and jumping from node x_i to x_j leads to problems when including crowders. Consider the case where just the center x_i is blocked, but voxel 𝒱_i is sufficiently empty to be traversed, see Fig. 3.2(c). In this case the jump into voxel 𝒱_i, is possible (λ_ji > 0), but the expected time to leave 𝒱_i is infinity and hence the molecules get trapped inside 𝒱_i. This does not agree with the microscopic situation, where molecules diffuse around x_i. To avoid this unrealistic trapping, all jump propensities λ_ji to voxels whose vertex is isolated are set to zero. In the case when a node x_i is covered by the excluded volume (not pictured) equations (3.9) and (3.10) cannot be evaluated. Setting all λ_ji to zero in this scenario would over estimate the crowding effect considerably, so we constrain the crowder distribution such that x_i remains inside ω_i.

By using the expected first exit time from ω_i around x_i to calculate the jump coefficients in a crowded environment it is the crowder distribution inside the whole circle ω_i that affects the coefficients λ_ii and θ_ij. This differs from other approaches to simulate diffusion in a crowded environment with a discrete space jump process. In [47, 70, 78] it is only the percentage of occupied volume in the target voxel 𝒱_j and in [33] the difference in occupancy between 𝒱_j and the origin 𝒱_i that affect the jump rate λ_ij = θ_ijλ_ii. In our approach the microscopic positions of all crowding molecules inside ω_i are resolved and influence the jump coefficients. In the case of non-spherical crowding molecules also the orientation is taken into account and long thin molecules with small volume can have a significant effect on λ_ij and θ_ij, see Fig. 3.3. Note that in contrast to normal diffusion the jump propensities are no longer symmetric, i.e. in general λ_ij ≠ λ_ji and λ_ij ≠ λ_im for j ≠ m.

Fig. 3.3.

Not only the occupancy ϕ, but also the microscopic positions and orientations of the crowding molecules affect the jump propensities λ_ij = θ_ijλ_ii. (a) θ_ij = 0. (b) θ_ij > 0.25.

3.1.3 Statistics on the mesoscopic level

Solving N local problems where complicated geometries have to be resolved, see Fig. 3.1(c) is computationally expensive and will be inefficient if the crowding molecules move and the coefficients λ_ii and θ_ij have to be recomputed frequently. Since the crowders’ exact location is generally unknown we can compute statistics on a reference domain ω_i for given a percentage of occupied volume, a given shape and size of the molecules and h. Instead of solving N PDEs of type (3.9) and 3N of type (3.10) at each time step, we can then sample the coefficients λ_ii and θ_ij from these precomputed distributions. This will be especially applicable for moving crowders, where new coefficients can be drawn from the distributions on the time scale of their diffusion.

3.2 Mesoscopic to macroscopic: a space dependent diffusion map

In this section we derive a macroscopic diffusion equation with a space dependent diffusion coefficient γ(x), representing the effect of macromolecular crowding. We approximate the mesosocpic jump process by Fickian diffusion with a constant diffusion coefficient γ_i inside each voxel 𝒱_i. The mesoscopic expected exit time E_i from a node x_i or voxel 𝒱_i is connected via (3.5) to this diffusion coefficient γ_i. So we obtain a modified version of the macroscopic deterministic diffusion equation (2.1)

$$u_t(\mathbf{x},t)=\nabla ·(\gamma (\mathbf{x})\nabla u(\mathbf{x},t)),\mathbf{x}\in \mathrm{\Omega },$$ (3.11)

where

$$\gamma {(\mathbf{x})\mid }_{{\mathcal{V}}_i}={\gamma }_i=\frac{h^2}{2d{E}_i}.$$ (3.12)

For transferring the mesoscopic jump rate to the less detailed macroscopic level we only use λ_ii and the random walk becomes symmetric in each voxel, i.e. θ_ij = θ_im = 0.25 for j ≠ m, but the asymmetry between back and forth jumps is preserved, i.e. λ_ij ≠ λ_ji. Alternatively γ(x) can be defined on the edges ∂𝒱_ij (see Fig. 3.1(b)) of voxel 𝒱_j by γ_ij = h²/2(λ_ij + λ_ji). This corresponds to a mesoscopic jump process with symmetry in λ_ij = λ_ji and non-symmetric jumps out of a box λ_ij ≠ λ_im for j ≠ m.

The anomalous diffusion is here modeled by a space dependent diffusion coefficient. A different description of anomalous diffusion on the macroscopic level are fractional PDE’s (FPDE’s), which are used to derive a mesoscopic description in [7], where molecules change their internal state, i.e. their diffusion constant, spontaneously in time. This correlates to our model when the crowding macromolecules are moving and the diffusion constant hence also becomes time-dependent: γ(x, t), in [20] we connect statistics from our mesoscopic description to the internal states model in [7] and hence to a FPDE description on the macroscopic level.

In the next section we will use the diffusion map γ(x) to derive space dependent reaction rates.

3.3 Reactions

Approaches to correct the reaction rates for crowding effects use either time dependent reaction rates k(t) [6, 71] or static modifications [17, 31, 33]. Similarly to the latter we will use the space dependent diffusion coefficient γ(x) from the previous section to compute mesoscopic reaction rates k_i inside each voxel 𝒱_i. This static rate becomes time-dependent k_i(t) if we model moving crowders. According to [39] the dilute mesoscopic rate k₀ for bimolecular reactions in a three dimensional cube of volume h³ is linked to the effective rate k_CK by Collins and Kimball [11] by

$$k_0=k_{CK}/h^3,k_{CK}=\frac{4\pi \sigma {\gamma }_0{k}_r}{4\pi \sigma {\gamma }_0+k_r},$$ (3.13)

where k_r is the intrinsic reaction rate and σ the sum of the two reaction radii. In 2D there is no equivalent formula but approximations are derived in [23, 38].

Assuming constant Fickian diffusion inside each voxel as in Sec. 3.2, we can now compute mesoscopic reaction rates k_i for each voxel by inserting the γ_i from (3.12) into (3.13)

$$k(\mathbf{x})=\frac{1}{h^3}\frac{4\pi \sigma \gamma (\mathbf{x})k_r}{4\pi \sigma \gamma (\mathbf{x})+k_r}\text{and}k{(\mathbf{x})\mid }_{{\mathcal{V}}_i}=k_i.$$ (3.14)

We can now add a space dependent reaction term to the PDE (3.11) using these space dependent reaction rates k_i. To model reactions under excluded volume effects on the mesoscopic level the reactions inside each voxel 𝒱_i have their specific reaction rate k_i.

In this model only bimolecular associations are affected by macromolecular crowding, since the hindered diffusion changes the hitting time for the reaction partners. In the internal states model [7] also birth-death processes and isomerizations become anomalous. It is, however, questionable if it is meaningful to talk about birth-death processes, when considering excluded volume effects, since all reactants and products also occupy space. With scaled particle theory [30] also dissociation events are affected by the excluded volume which is due to two spherical molecules having a different activity coefficient than one molecule with the same total area. In our model, dissociation is not affected either.

In Section 4.4, we perform numerical experiments to examine for which parameters crowding molecules enhance or decrease the rate of bimolecular reactions.

4 Numerical Experiments

In the following experiments we solve (3.9) and (3.10) in 2D with COMSOL Multiphysics on ω_i, i = 1 …N. To be able to evaluate the solutions at x_i the crowders are randomly distributed such that the nodes x_i remain inside the perforated domain ω_i and are not cut out by the excluded volume.

4.1 Effect of crowding on jump propensities

We first investigate how the jump propensity λ_ii changes in different crowding situations. We therefore compute λ_ii on a reference domain ω_i with h = 1 and different crowders and sizes of the moving molecule r and compare it to the jump rate λ_0,ii in dilute medium. In Fig. 4.1, we compare the mean value of the jump propensities 𝔼[λ_ii] for different distributions of crowders and an increasing percentage of occupied volume ϕ with the jump propensities when no crowders are present, where 𝔼[λ_0,ii] = λ_0,ii = 4. We test two different sizes of crowding molecules for both rectangles and spheres. The reference line is the linear scaling where λ_ii = (1 − ϕ)λ_0,ii as in [47, 66].

Fig. 4.1.

The mean value of the mesoscopic jump coefficients in the crowded environment 𝔼[λ_ii] compared to 𝔼[λ_0,ii] = 4 in dilute media and its dependence on the occupancy ϕ. Averages are taken over M = 100 different crowder distributions. The obstacles are either spheres (blue and red) with radius R or rectangles (orange and green) with ratio of width to length equal to 20. The dashed reference line corresponds to equation (2.4) when only the averaged occupied volume in the target voxel is taken into account. The spherical moving molecule has radius r. In (e) we compare the mesoscopic coefficients with the results from a Brownian dynamics simulation, where we generate 10⁴ trajectories for 10 different crowder distributions with the software Smoldyn.

We observe that small obstacles (blue and orange in Fig. 4.1) hinder diffusion more than big crowders for the same percentage of occupied volume, since they have more reflecting surfaces than larger crowders. The same holds for elongated rectangular crowders (green and orange in Fig. 4.1), as they create long barriers without occupying a lot of volume. In three space dimensions the crowding effect is weaker and higher occupation fractions ϕ would be necessary for a similar slow down. Since multiple small spheres or a cylinder of the same size as a large sphere also have larger surface areas in three dimensions, the same relative effects of crowders of different shapes are expected. An increasing size r of the diffusing molecule leads to an increase in the crowding effect, which is intuitive, since a bigger molecule finds less holes through which to escape. These results agree with the findings in [62] and [16]. We see that the averaged linear reduction of the jump propensity can be a good model when the diffusing molecule is about a tenth of the size of the crowders, but over- or underestimates the effect of occupied volume when the diffusing species is smaller or bigger, respectively. Since an average protein has a radius of ca. 2nm [66] and the biggest macromolecules in the cell, the ribosomes, have a radius of up to 15nm the linear correction is a good approximation for many scenarios. The reduction in jump propensity, however, starts to behave exponentially, as in [33], for large diffusing molecules. The case r = 0 corresponds to a point particle which is irrelevant when simulating excluded volume effects, but we include it to show the limit for very small particles. To confirm these mesoscopic jump rates we compare them to the inverse of the expected exit time computed by a Brownian dynamics simulation. We simulate 10⁴ trajectories with the open source software Smoldyn [1, 2] for 10 different crowder distributions and equally sized crowding and moving molecules with R = r = 0.1 and see in Fig. 4.1(e) that the computationally expensive microscopic results agree well with the mesoscopic coefficients. In our previous work [57] we have compared the computational time for detailed Brownian dynamics simulations on the full domain Ω with microscopic grid based methods and measured a 42-fold speedup. Coarser mesoscopic simulations on Ω will be even faster than the CA simulations and our method hence promises a great safe in computational time compared to detailed BD simulations.

In Fig. 4.2, the standard deviation σ(λ_ii/λ_0,ii) initially increases as more and more crowders are added but converges towards zero when the system approaches the state where no escape to the boundary is possible.

Fig. 4.2.

Standard deviation σ(λ_ii/λ_0,ii) around the mean value of the change in jump coefficients in (a) and (d) in Fig. 4.1.

Simply rescaling the jump propensity λ_ii for each node i by a constant factor will lead to normal diffusion at reduced rate. To observe anomalous diffusion in the crowded environment it is helpful to investigate the mean square displacement (MSD).

4.2 The mean square displacement

As mentioned in Section 2.2 the MSD is linear in time for normal diffusion

$$\langle {\mathbf{x}}^2(t)\rangle =2d{\gamma }_{0}t,$$ (4.1)

but for anomalous diffusion the relation is no longer linear

$$\langle {\mathbf{x}}^2(t)\rangle =2d{\gamma }_0{t}^{\alpha },$$ (4.2)

where α < 1 for subdiffusion. In [12, 24, 60] it was shown that diffusion in a crowded environment can be modeled by a temporal change of the diffusion constant. First the molecule diffuses normally with rate γ₀ for very short time-scales, before it undergoes a transient anomalous phase with a changing diffusion coefficient γ and finally stagnates into normal diffusion at a lower diffusion rate γ_∞. The initial normal diffusion represents the time the molecule diffuses in the solution before it encounters the first adjacent macromolecule and is slowed down by collisions. On a large time scale the molecule appears to diffuse in a denser medium instead of around obstacles, hence the reduced diffusion rate γ_∞, see Fig. 4.3. If the crowding macromolecules are distributed evenly the MSD decays monotonically between γ₀ and γ_∞ (pale line), but due to stochastic variations in the medium it fluctuates before converging to γ_∞ (dark line). In Fig. 4.3(a) we only depict collisions with the macromolecules responsible for excluded volume effects, but note that there are many collisions with the much smaller solvent molecules responsible for the Brownian motion.

Fig. 4.3.

(a) Diffusion in the crowded cell environment: Initial free diffusion with γ₀ (green). After colliding with the first macromolecules the observed diffusion is slowed down and the molecule’s diffusion coefficient decays (orange) to the long time behavior of slower diffusion with constant γ_∞ in a dense medium (red). (b) MSD curve for diffusion in a crowded medium (solid line) and as reference normal diffusion (dashed line). The pale line corresponds to an ideal well mixed medium and the dark line to a realistic medium with stochastic fluctuations in the positions of the crowders.

Since we choose h > R a jump in the mesoscopic model spans a number of macromolecules and the initial free diffusion phase is not resolved and we start to observe diffusion after the first jump of length h, that occurs after a critical time t_c which can be approximated by

$$t_c~\frac{h^2}{2d{\gamma }_0}.$$ (4.3)

In the following we will plot the 〈x²〉/2dγ₀t in log-log-scale for different crowding situations to examine when anomalous behavior occurs. Let p(t) ∈ ℝ^N be the probability vector for a diffusing molecule, such that p_i(t) is the probability that the molecule is in voxel 𝒱_i at time t. As described in Section 2, p(t) evolves by the master equation

$${\mathbf{p}}_t=\mathbf{Dp}(t),\mathbf{p}(0)={\mathbf{p}}_0,$$ (4.4)

where D_ij = λ_ji for i ≠ j and D_ii = −λ_ii. The initial probability distribution p₀ is (0, …, 1, …, 0)^T with one at the starting node x₀. We choose the discretization such that D is small enough to solve (4.4) numerically and compute the mean square displacement by

$$\langle {(\mathbf{x}(t)-{\mathbf{x}}_0)}^2\rangle =\sum _{i=1}^N{p}_i(t){({\mathbf{x}}_i-{\mathbf{x}}_0)}^2.$$ (4.5)

In the following experiments we discretize the square [0, 1] × [0, 1] into N = n² voxels with space discretization h = 1/(n − 1). If not mentioned otherwise we release the molecules in [0.5, 0.5] at time t = 0 and choose n = 41. To avoid boundary effects we set homogeneous Dirichlet boundary conditions on ∂Ω and show the solutions as long as more than 99% of the mass is preserved, i.e. ${\sum }_{i=1}^N{p}_i(t)>0.99$.

4.2.1 The effect of γ₀ and ϕ

In Fig. 4.4(a) we plot MSD/(4γ₀t) in the crowded environment for different distributions of crowders. Lines in the same color show diffusion in the same environment with starting positions [0.5, 0.5] (solid) and [0.5 ± h, 0.5 ± h] (dashed). We clearly observe the anomalous behavior since MSD/(4γ₀t) is not constant in time and the fluctuations due to the variations of the local environment around the starting position, but for longer times they converge towards the same long time behavior, before the boundary effects become apparent.

Fig. 4.4.

The MSD on a mesoscopic grid with h = 0.025 for different distributions of spherical crowders with R = 5 × 10⁻³ and a moving molecule with r = 5 × 10⁻⁴. (a) Two different crowder distributions (red and blue), where we vary the starting position of diffusion from the center [0.5, 0.5] (solid line) to one voxel to the right/left and up/down [0.5 ± h, 0.5 ± h] (dashed lines) to show the sensibility of the MSD plot to the local environment. The crowding coefficient is ϕ = 0.4 and the diffusion constant is γ₀ = 1. (b) By varying the diffusion coefficient γ₀ for the two extreme distributions highlighted in grey in (a) we see that the diffusion coefficient only affects when the molecules undergo anomalous diffusion. (c) Changing the crowding percentage ϕ for γ₀ = 1 for the same two distributions as in (b) affects both the long time reduced diffusion and the duration of the anomalous phase. (d) Varying the space discretization h for the red distribution in (a) for all 5 starting positions. We see that a finer discretization better resolves the transient regime.

We choose the distributions and starting positions of the curves highlighted in grey to examine the effect of γ₀ and ϕ on the MSD. In Fig. 4.4(b) we observe that the diffusion constant γ₀ only affects when the molecule undergoes anomalous diffusion but the length of the anomalous phase and the long time behavior are independent of γ₀. The percentage of occupied volume ϕ on the other hand changes both, the average diffusion constant in the long time behavior and the duration of the transient regime of anomalous diffusion, Fig 4.4(c).

4.2.2 Dependence on the space discretization h

The mesoscopic model is designed for a voxel size h considerably larger than the molecular radius in order to save computational effort compared to a microscopic simulation. For h → 0 the dilute and well-mixed assumptions in each voxel do no longer hold and the mesoscopic model is known to break down for the simulation of bimolecular reactions [42]. Different corrections to the reaction rates have been suggested [29] and the references therein, but a minimal h_min > R remains and space cannot be resolved any finer in the mesoscopic model. For a finer resolution one has to switch to microscopic models, such as BD or CA and we examine the effect of h only for h ≫ R. A larger h shifts the critical time t_c after which we start to observe the molecule’s motion to the right in Fig. 4.3(b), so for very large h we will only see the long time behavior. In Fig. 4.4(d) we see that the initial faster diffusion with γ ~ γ₀ is less resolved for large h where the trajectories start at a much later time. Furthermore the boundary effects become apparent earlier for a larger h, but all discretizations are expected to converge towards the same long time behavior.

4.3 Comparison of mesoscopic and macroscopic simulations

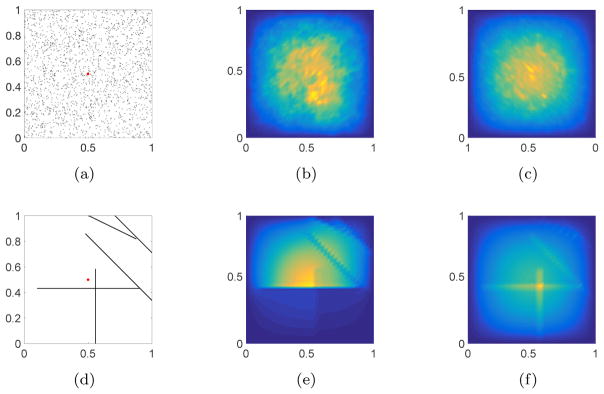
The MSD is only one quantity of interest to examine, but since it is a mean not all features are captured and we will now compare the distributions of molecules resulting from either a mesoscopic or macroscopic simulation. Again, we discretize the square [0, 1] × [0, 1] with homogeneous Dirichlet boundary conditions into 41 nodes in each direction and let molecules start diffusing in (0.5, 0.5) in an environment with rectangular crowders of different sizes. We solve (4.4) once with the mesoscopic D and once with D̃, where the off-diagonal elements are all equal to λ_ii/4, corresponding to a finite difference approximation of the macroscopic equation with the space dependent diffusion constant γ(x) derived from the λ_ii’s. In Fig. 4.5 the macroscopic model agrees with the mesoscopic results for small and evenly distributed crowding molecules, whereas for long barriers only the mesoscopic approach simulates the expected behavior. This is due to the symmetrization of D̃, so that only D can capture the asymmetric diffusion close to the barriers. The diagonal barriers are not completely impermeable in the mesoscopic model since a small part of the boundary ∂ω_ij remains.

Fig. 4.5.

Mesoscopic and macroscopic simulations with crowders of different sizes and a moving molecule with radius r = 10⁻³ starting in the center of the domain (red dot). The heat maps show the probability distribution p(0.5) of the location of the diffusing molecule at t = 0.5, which is the solution to equation (4.4) with homogeneous Dirichlet boundary conditions. (a) Rectangles of size 0.0005 × 0.01 and ϕ = 0.01. (b) & (c) The mesoscopic (D) and symmetrized macroscopic (D̃) simulation results with the distribution in (a), respectively. (d) 5 rectangles of size 0.004 × 0.8. (e) & (f) The mesoscopic (D) and symmetrized macroscopic (D̃) simulation results with the distribution in (d), respectively.

4.4 Reaction rates

Due to the reduction of diffusion in a crowded environment and (3.14) the overall reaction rate is decreased. It has, however, been shown [30, 71], that protein associations can also be enhanced. We examine the mean time ${\mathbb{E}}_j^r$ until the bimolecular reaction

$$A+B\stackrel{k_r}{\to }C$$ (4.6)

happens, where reactant A is confined to voxel 𝒱_i, and molecule B starts diffusing in voxel 𝒱_j at time t = 0, see Fig. 4.6(a). Due to molecular crowding we assume a simplified space dependent diffusion map with γ_i < γ₀ inside 𝒱_i and γ < γ₀ in the rest of the domain. With k_i given by (3.14) and λ_ii by (3.6) we can use conditioning on the first step to compute the expected time until the reaction happens:

$${\mathbb{E}}_i^r=\frac{k_i}{k_i+{\lambda }_{ii}}\frac{1}{k_i+{\lambda }_{ii}}+\frac{{\lambda }_{ii}}{k_i+{\lambda }_{ii}}\left[\frac{1}{k_i+{\lambda }_{ii}}+\sum _m{\theta }_{im}E({\mathbf{x}}_m)+{\mathbb{E}}_i^r\right]$$ (4.7)

$${\mathbb{E}}_j^r=E({\mathbf{x}}_j)+\frac{h^2+4{\gamma }_i{\sum }_m{\theta }_{im}E({\mathbf{x}}_m)}{h^2{k}_i},$$ (4.8)

where E(x_m) is the expected time it takes a molecule located in the neighboring voxel 𝒱_m to jump into voxel 𝒱_i and can be computed by solving

Fig. 4.6.

(a) Two-dimensional projection of the three-dimensional experimental setting where a B molecule (blue) starts diffusing in x_j = (0.7, 0.5, 0.5) and reacts with A (red) that is confined to voxel 𝒱_i with x_i = (0.5, 0.5, 0.5) (red shaded region). Due to an uneven distribution of crowders we assume that the diffusion rate is γ_i inside 𝒱_i and γ (vertical dashed lines in (b) and (c)) in the rest of the domain. In (b) and (c) we compare the time it takes to react in this crowded environment ${\mathbb{E}}_j^r$ to the time it takes in an uncrowded environment ${\mathbb{E}}_{j,0}^r$ with γ₀ = 1 for different intrinsic reaction rates k_r. (b) γ = 0.7. (c) γ = 0.9.

$${\mathbf{p}}_t(t)=(\mathbf{D}-{\mathbf{K}}_i)\mathbf{p}(t),\mathbf{p}(0)={\mathbf{p}}_0,$$ (4.9)

$$E({\mathbf{x}}_m)={\int }_0^{\infty }\sum _{k=1}^N\mid {\mathcal{V}}_k\mid p_k(t)dt,$$ (4.10)

where K_i models a sink at node x_i and is the zero matrix except for a suitably large K_ii, (e.g. K_i,i = 10⁹) and p₀ is the zero vector except for p_0,m = 1/h³, see [56] for a derivation. We solve these equations numerically in 3D for a cube with length L = 1 and a uniform discretization with h = 0.1 in space and reflecting boundary conditions. The voxel 𝒱_i, where the reaction happens is chosen to be the center voxel, such that E(x_m) are equal for all 6 neighbors. The diffusing molecule B starts in x_j = (0.7, 0.5, 0.5). In Fig. 4.6 we compare the mean binding time in the crowded ${\mathbf{E}}_j^r$ environment with different γ_i and γ to the time ${\mathbf{E}}_{j,0}^r$ it takes to react in a dilute solution where γ(x) = γ₀ = 1. The data points with scaled error bars ( $\pm (\frac{\sigma }{\sqrt{M}{\mathbb{E}}_j^r}+\frac{{\sigma }_0}{\sqrt{M}{\mathbb{E}}_{j,0}^r})$) are from a SSA simulation of the reaction-diffusion process with M = 200 trajectories for k_r = 10⁻⁴ and k_r = 10⁻³ and M = 500 for k_r = 5 × 10⁻³ and k_r = 10⁻².

An overall slower diffusion rate γ < γ₀ as a result of obstacles reduces the rate of bimolecular reactions (3.14) in each voxel. But, due to an uneven distribution of crowding agents compartmentalization with locally differing diffusion rates can occur inside the cells. In this case Fig. 4.6 shows that our model of reaction-diffusion dynamics in a crowded environment can model the increase of reaction rates due to crowders. For certain intrinsic reaction parameters the overall reaction rate increases for a compartmentalization where γ_i is smaller than γ, despite the locally slower reaction. The intuitive explanation for this is that once the diffusing molecule enters voxel 𝒱_i it escapes slower and hence gets trapped close to its reaction partner, which increases the chance of collisions. Like this, cells can boost their efficiency by locating important reaction complexes in areas of slower diffusion, which will be especially productive for reaction cascades where intermediate products are already produced inside the compartment and have a low chance of escaping before being processed further. The fact that macromolecular crowding and locally slower diffusion rates can change the qualitative behavior of a multistep reaction have also been shown by microscopic simulations [77] and experimentally [3]. In the limit when γ_i → 0 the binding time goes towards infinity, since then both reactants are immobile inside 𝒱_i and never collide. For the case γ_i = 1 the reaction dynamics inside voxel i behave as in the dilute case with γ₀ = 1 and the time until reaction is hence only governed by the expected time to reach voxel i, which is inversely proportional to the diffusion rates γ and independent of k_r.

5 Conclusion

We have presented a multiscale framework to model diffusion and reactions in a crowded environment, which is an important feature for realistic simulations inside living cells and on their membranes. First, we homogenize the system by solving a set of PDEs on local domains resolving the microscopic positions and shapes of the crowding molecules. This precomputing step is perfectly parallelizable and yields local first exit times, which can be transformed into the jump rates on an overlying Cartesian grid at the mesoscopic level. We then use these local first exit times to compute a space dependent diffusion coefficient for the macroscopic diffusion equation, which corresponds to space dependent reaction rates according to the formula by Collins and Kimball.

Our approach is general in the sense that the crowding molecules can have arbitrary shapes and can be located anywhere inside the domain. We indicate how to adapt our method to moving crowders by computing statistics which is presented in more detail in [20]. As the jump process is simulated on a coarse Cartesian mesh, no longer resolving the numerous crowders, the stochastic simulation is computationally much more efficient than a microscopic simulation capturing all the collisions.

In numerical experiments we foremost observe that shape and size considerably affect how strongly diffusion is impeded: small crowders have more reflective surface and hence hinder diffusion more severely than bigger obstacles, so do elongated crowders, which create long barriers. The effect is also stronger for larger diffusing molecules than for smaller ones, since the former need bigger gaps to pass through. This gives some new insight into how non-idealized (non-spherical) macromolecules affect the diffusion, since most existing models either assume that all particles are spheres or only consider the percentage of occupied volume.

Comparing the mesoscopic and macroscopic models for diffusion in the crowded environment we note that the former captures the asymmetries created by long barriers better and that they both behave similarly for small crowding molecules compared to the grid size.

The space dependent diffusion rate can be interpreted as a compartmentalization effect, which has been observed in cells. In a simplified example we see that reactions located inside a compartment with high crowding/low diffusivity can be enhanced since the reaction partners reside longer in the vicinity of each other. Hence, the concentration of reaction complexes in an area with slow diffusion as compared to the rest of the cytoplasm or cell membrane can increase the reaction turn-over, an effect that has been capitalized by cells through colocalization of reaction complexes and scaffolding. Otherwise, reactions between initially distant molecules are impeded by excluded volume since it takes longer time for the reactants to find each other.

Hard sphere reflections on obstacles are not the sole cause of anomalous diffusion [69], but there are other interactions between macromolecules, such as transient binding or electrostatic repulsion, which have been modeled by a continuous time random walk [4, 73] and fractional or multifractional Brownian motion [52]. We can include these types of interactions, by modifying boundary conditions on the crowders from reflecting to partially absorbing or adding potential barriers.