Learning to make external sensory stimulus predictions using internal correlations in populations of neurons

Significance

To produce appropriate behavioral responses, such as catching fast-moving prey, the visual system copes with significant sensory processing delays. Spiking activity in the retina captures some of the most predictive aspects of the visual information, but this information must be accessible to downstream circuits. We tested how efficiently predictive information could be read out in downstream neurons and how difficult it is to learn to read out this information, using biologically plausible rules applied only to local inputs. Very simple learning rules could find near-optimal readouts of predictive information without any external instructive signal. This suggests that bottom-up prediction may play an important role in sensory processing.

Abstract

To compensate for sensory processing delays, the visual system must make predictions to ensure timely and appropriate behaviors. Recent work has found predictive information about the stimulus in neural populations early in vision processing, starting in the retina. However, to utilize this information, cells downstream must be able to read out the predictive information from the spiking activity of retinal ganglion cells. Here we investigate whether a downstream cell could learn efficient encoding of predictive information in its inputs from the correlations in the inputs themselves, in the absence of other instructive signals. We simulate learning driven by spiking activity recorded in salamander retina. We model a downstream cell as a binary neuron receiving a small group of weighted inputs and quantify the predictive information between activity in the binary neuron and future input. Input weights change according to spike timing–dependent learning rules during a training period. We characterize the readouts learned under spike timing–dependent synaptic update rules, finding that although the fixed points of learning dynamics are not associated with absolute optimal readouts they convey nearly all of the information conveyed by the optimal readout. Moreover, we find that learned perceptrons transmit position and velocity information of a moving-bar stimulus nearly as efficiently as optimal perceptrons. We conclude that predictive information is, in principle, readable from the perspective of downstream neurons in the absence of other inputs. This suggests an important role for feedforward prediction in sensory encoding.

To respond efficiently to changing sensory inputs the brain must predict the future state of the world from past sensory information. For instance, in the salamander visual system at the minimum such predictions need to compensate for the 50- to 80-ms processing time of the retina (1) as well as the time for a motor response to be generated. Making these predictions requires leveraging the spatiotemporal structure of the natural world, a computation that is performed efficiently at the first stage of visual processing, in populations of retinal ganglion cells (RGCs) (2). Neurons downstream of the retina likely infer predictions about object motion, but to do so these downstream cells must learn to read out predictive information from retinal inputs.

The retina has been used as a model to evaluate the theory of predictive coding (3–6), in which deviations from an expected signal are encoded to maximize information transmission efficiency (7–10). Predictive information (11–13) in the retina, in contrast, is a bottom-up encoding of the predictive aspects of spatiotemporal structure in sensory stimuli (2, 14). Depending on context and timescales, it could be advantageous for neural circuits to use the predictability of stimuli in different ways (6, 15–23). In the retina, internal temporal correlation in population activity over tens to hundreds of milliseconds can be leveraged to make predictions about the future state of the external world (2). Thus, for early visual processing the efficient computation of predictive information may be a principal function of retinal circuits and their downstream readouts.

Here we explore how this predictive information encoded in retinal population firing can be read out and learned by downstream circuits. One possible readout mechanism is the perceptron (24), that is, a linear weighting of inputs, followed by a threshold nonlinearity. Such a readout has the advantage of being a biologically feasible, single-step computation, and previous work has shown that perceptrons can efficiently read out predictive information in small sets of cells (2). We show that optimal perceptron readouts of predictive information are learnable, via spike-timing–dependent plasticity (STDP) rules, in the absence of other instructive signals about the stimulus. We find that each readout’s internal word–word predictive information, the information it has about the future input activity, is also related to that readout’s external word–stimulus predictive information, the information it has about the future of the stimulus. Moreover, optimal readouts of one are likely to be near-optimal readouts of the other. This remarkable fact allows for the efficient encoding of external, stimulus-predictive information by efficient downstream readout of retinal input correlations. These results are most relevant to early visual processing stages.

Results

Fundamentally what matters to the survival of an organism is not the optimal readout of spiking activity from a particular stimulus for which information can be explicitly calculated, but instead the optimal readout of predictive information from stimuli it encounters in the natural environment. We investigated whether efficient readouts of predictive information during a natural-movie stimulus can be learned. Supposing this readout function had access to information calculations to determine readout efficiency, the number of possible readout functions for sets of four cells exceeds 32,000 (i.e., $2^{2^4-1}$). For sets of five cells there are more than two billion possible readout functions. This sampling problem is simplified by restricting to readouts to perceptrons, but then the question remains of how the brain finds the optimal perceptron. A possible solution lies in taking advantage of the internal word–word predictive information of RGC population spiking activity and learning an optimal readout based on these correlated inputs.

We analyzed optimal readouts of predictive information in a population of larval tiger salamander RGCs (n = 53) previously recorded using a multielectrode array (2). The retina was stimulated using a moving-bar stimulus as well as a video approximating the natural habitat of the larval tiger salamander. Evoked spike patterns were expressed as a binary word across a set of cells, with a 0 for silence and a 1 for spiking activity (one or more spikes) in each 16.7-ms time bin. Throughout the paper we will discuss stimulus information (quantifiable only for activity recorded during the moving-bar stimulus) and internal wordword information (quantifiable for both stimulus types).

Reading Out Stimulus Predictive Information in a Sensory Population.

We compared stimulus information and internal predictive information for spiking activity driven by a moving bar with position and velocity determined by second-order damped harmonic motion (phase plot, Fig. 1A, Top) driven by random velocity perturbations (Fig. 1A, Bottom). While such dynamics are simple, they capture some features that are common in the physics of everyday motion and known to be effective drivers of retinal activity (15, 25, 26), such as periods of constant velocity and reversals of direction. Random velocity kicks can trigger a long excursion from the origin, during which the current position and velocity of the bar are highly predictive of its future position and velocity. While we did not directly estimate bar position and velocity from RGC spiking activity, others have done so with high accuracy (27) using linear decoding (28).

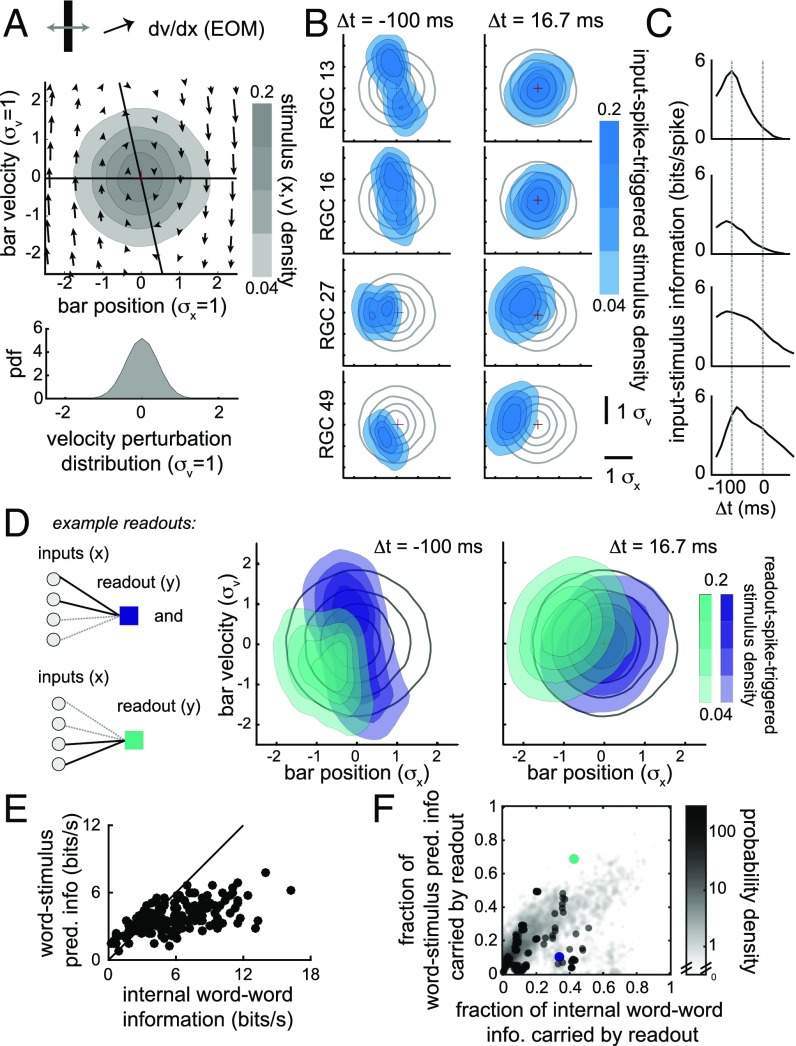
Fig. 1.

Spikes in sets of RGCs are informative of both past and future position and velocity of a moving-bar stimulus. (A) A population of RGCs was stimulated using a moving-bar stimulus, with dynamics of the stochastic overdamped harmonic oscillator. (Top) Phase plot of the dynamics with overlaid shading showing the distribution of bar position and velocity over the duration of the recording. (Bottom) Distribution of stochastic “kicks” to velocity. (B) Cross-section of the distribution of position and velocity of the bar stimulus relative to spiking in each of four RGCs, taken at two time points, $\mathrm{\Delta }t=-100\hspace{0.17em}\text{ms}$ (Left, past) and $\mathrm{\Delta }t=+16.7\hspace{0.17em}\text{ms}$ (Right, future). Prior distribution of position and velocity is shown as gray contours in background to illustrate how spiking in an RGC constrains expected values of bar position and velocity. (C) Stimulus information quantified for each of the four RGCs in B as a function of perispike time, from 150 ms before the RGC spike to 100 ms after. RGC 27 and 49 have large amounts of stimulus-predictive information ($\mathrm{\Delta }t>0$). (D) Two example readouts (Left: solid black lines indicate strong connections and dashed gray lines weak ones). The readout-spike-triggered distribution of position and velocity was computed at perispike time $\mathrm{\Delta }t=-100\hspace{0.17em}\text{ms}$ and $\mathrm{\Delta }t=+16.7\hspace{0.17em}\text{ms}$. Both readouts have high (5.1 and 5.4 bits per s) past information ($\mathrm{\Delta }t=-100\hspace{0.17em}\text{ms}$), but only the green readout has high stimulus-predictive information (4.2 bits per s). (E) Word–word internal predictive information is correlated with word–stimulus predictive information across sets of four cells. (F) The fraction of word–stimulus information carried by a readout is correlated with the fraction of internal word–word information carried by that readout. Grayscale shows density of readouts across the sets in E; superimposed dots show all perceptron readouts for this particular set of four cells. Purple and green dots are the example readouts from D. Error bars for information estimates are smaller than the marker size (<0.2 bits per s in E; <0.02 in F). EOM, equation of motion; info, information; pdf, probability density function; pred, predictive.

As an example of how position and velocity encoding in RGCs generated predictive information we show four cells, all with sensitivity to particular position and velocity features occurring 100 ms in the past (Fig. 1B), which is consistent with the 50- to 100-ms delay incurred by retinal circuitry (1). Spikes in two of the RGCs (RGC 13 and 16) indicated, with high probability, that the bar passed through the center of the image with high speed 100 ms before the spike, whereas spikes in RGC 27 and 49 indicated the bar had low velocity and position far from the center. All four of these cells were informative of past features of the moving-bar stimulus, while two of these RGCs (RGC 27 and 49) were also predictive of future stimulus features (Fig. 1B). This can be interpreted in the phase plot of the bar dynamics (Fig. 1A). RGC 27 and 49 spiked when the bar was in a region of phase space where the deterministic forces on the bar were strong and the deterministic trajectory traveled far from the fixed point at (0,0), so trajectories were predictable for longer periods of time.

Graphically, the information spiking activity carries about the bar stimulus features (position and velocity) is the difference between entropies of the prior distribution (gray contours, Fig. 1B, replotting the data from Fig. 1A) and the spike-triggered distribution (Fig. 1B, blue). This is quantified as the mutual information (Fig. 1C) between spiking activity at time t and the stimulus position and velocity at $t+dt$. Following our qualitative observations above, each of these cells was highly informative about past features, but only RGC 27 and 49 conveyed much predictive stimulus information, defined here and throughout the rest of the paper as the mutual information $I\left({\mathit{x}}_t;\left\{p_{t+dt},v_{t+dt}\right\}\right)$ of spiking activity and stimulus position/velocity at relative time dt (=1 bin, or +16.7 ms).

Activity across these four cells was informative of future stimulus, but highly redundant. By reading out only the most predictive spike patterns nearly all of the predictive information of a cell group can be compressed to a single bit (2). Exhaustively sampling a full set of binary readouts for more than four cells is computationally intractable. Restricting readouts to perceptrons ameliorates this sampling problem (see Fig. S1 for an estimate of the impact of this restriction). For this set of four RGCs we show two illustrative examples of perceptron readouts. Both readouts are highly informative of past stimulus features (Fig. 1D), but only one readout carried predictive information (green, Fig. 1D). More generally, a large majority (mean: 78%, SE: 16% across n = 240 sets) of linear readouts will have predictive information less than 1 bit per s. For this particular example with known stimulus feature selectivity a readout with high predictive information (5.1 bits per s, or 65% of total word–stimulus information) was found by pooling the most predictive cells with similar feature selectivity. However, downstream circuits in the brain must find an effective readout without direct access to labeled stimulus features.

The generalized correlation between present and future spiking activity, or internal predictive information, is $I\left({\mathit{x}}_t;{\mathit{x}}_{t+dt}\right)$, where the “word” ${\mathit{x}}_t$ is the binary pattern of spikes (1) and silence (0) at time t. Across sets of four cells, the stimulus predictive information is highly correlated with the internal word–word predictive information (Fig. 1E, r = 0.65, n = 240 sets). Moreover, readouts that carried a large fraction of the word–stimulus predictive information tended to also carry a large fraction of the internal word–word predictive information (Fig. 1F). Thus, by finding effective readouts of internal predictive information the strong relationship between internal and stimulus prediction enables downstream neurons to read out stimulus predictive information without having direct access to the stimulus.

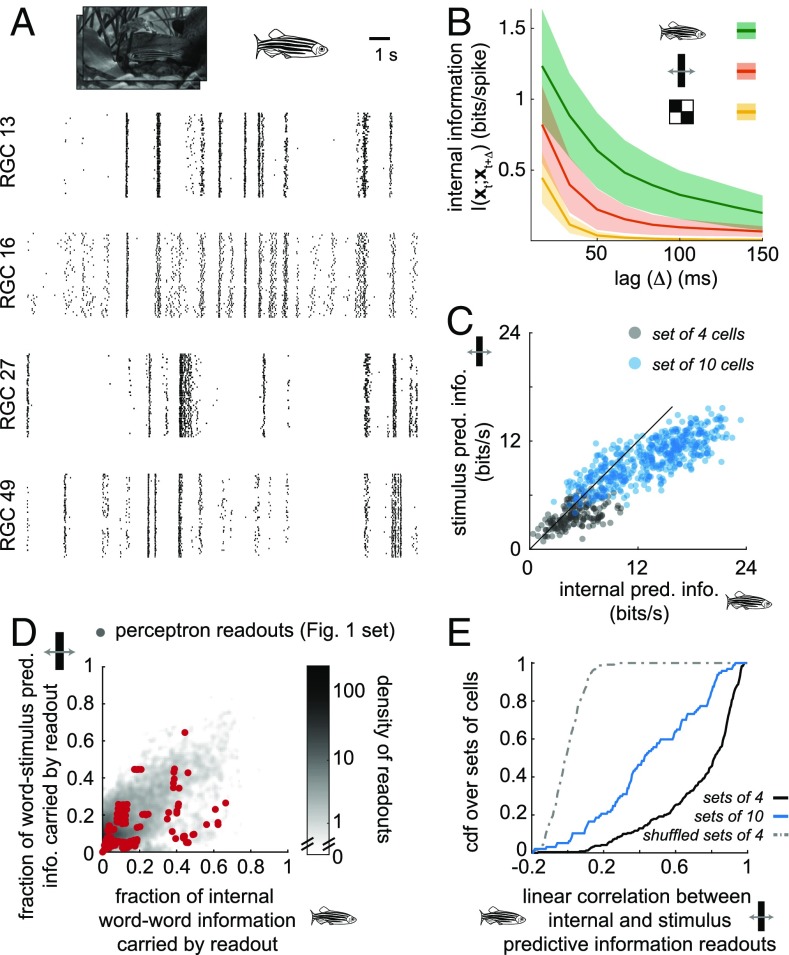
This relationship between internal and stimulus prediction was established for data recorded during the moving-bar stimulus. To determine whether this is more general and extends to spiking activity under different types of visual stimuli for which stimulus prediction may not be possible to quantify we evaluated the internal predictive information of spiking activity driven by a natural video, a clip of a swimming fish at the 10-cm viewing distance of a typical salamander eye (Fig. 2A), as well as during a checkerboard stimulus, which is not predictable. To perform these calculations, we took up to 1,000 random samples of 4- and 10-cell groups of cells from the salamander retina recording and computed their internal as well as their stimulus predictive information. Internal predictability reflects the timescale of correlation in the stimulus (Fig. 2B), with the longest timescale for natural movies and the shortest for a random, flickered checkerboard stimulus (Materials and Methods). However, the specific values of stimulus predictive information during the moving-bar stimulus and the internal predictive information during natural-movie stimulation were highly correlated across randomly drawn groups of cells (Fig. 2C; r = 0.65 for sets of 4 cells and 0.80 for sets of 10 cells; P < 1e-7). Moreover, the efficiency of individual readouts for each group of cells was highly correlated between the stimulus types (Fig. 2 D and E). An efficient readout under one set of stimulus conditions (natural-movie responses) was likely to be a good readout under other conditions (moving-bar responses). However, of all possible readouts only a small minority were efficient readouts of predictive information. We therefore turned to the question of whether efficient readouts of predictive information could be learned using simple, biologically plausible learning rules based on STDP.

Fig. 2.

Internal predictive information can guide stimulus prediction without explicit reference to stimulus parameters. (A) Raster plot of spikes from a set of four RGCs (same cells as in Fig. 1) to a 19.2-s clip of a natural movie (frame, Top), with 51 (of 102 total) repetitions of the clip shown. A fish icon in later plots denotes calculations based on responses to the natural-movie stimulus. (B) Internal information reflects the spatial and temporal correlations in the stimulus. Average internal information of four-cell sets during the natural movie (green, longest timescale), moving bar (red), and checkerboard (yellow, shortest timescale). Shaded region represents $\pm 1$ SE across cell sets. (C) Stimulus-predictive information during the moving-bar movie is correlated with internal predictive information during the natural movie. Error bars smaller than marker size. (D) The fraction of word–stimulus information carried by a readout during the moving-bar stimulus is correlated with the fraction of internal word–word information carried by that readout during the natural movie. Shading represents average density of readouts across all randomly sampled sets of four cells (n = 240), with the readouts of one set of four cells (red; same set in Fig. 1 and A) overlaid. Most readouts have low predictive information. Error bars are <0.02, smaller than the point size. (E) For sets of 4 and of 10 cells, linear correlations between the readout-word internal predictive information and the readout-stimulus predictive information are high. The distribution of correlations in which readout identity was shuffled is shown for sets of four cells. pred. info., predictive information.

Learning the Optimal Readouts of Internal Word–Word Predictive Information.

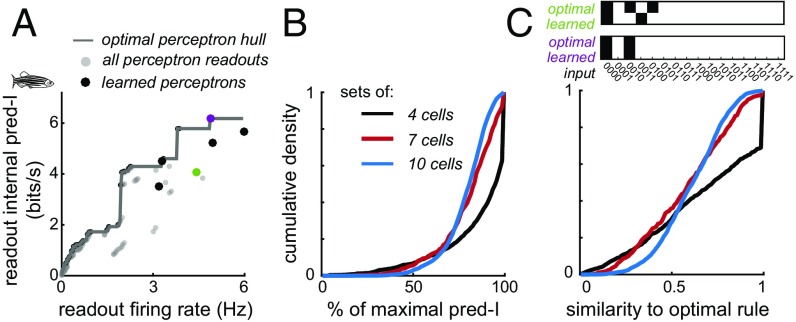
By finding efficient readouts with high predictive information we identified a subset of words at time t that were predictive of activity at time $t+\mathrm{\Delta }t$. We next asked whether efficient readouts could be found in an unsupervised fashion using local learning rules, depending only on the activity of the inputs and the output, and absent any teaching signal. The success of a given learning rule is strongly dependent on the structure of predictive patterns in the data, and in general the complex word–word temporal structure may make it impossible for a single rule to find effective weights for all groups of cells. Random weightings of inputs do not maintain a large fraction of the internal or stimulus predictive information (Figs. 1F and 2D). Using the RGC data as inputs, we quantify the predictive capacity of readouts learned under simple spike-timing–dependent rules. We simulated a classical form of an STDP rule (29), which strengthens synapses to inputs that evoke an output spike and weakens synapses to inputs that follow an output spike. Results for variants of this basic rule, including triplet-spike STDP (30) and homeostatic mechanisms, are shown in Fig. S3. In other contexts, such temporal asymmetry in learning dynamics has been linked to prediction of neural sequences in populations (31), and we hypothesized that this could also be useful for identifying the most predictive patterns. For each set of cells we generated a random set of initial patterns of input weights and ran a simulation driven by the spiking data recorded during the natural-movie stimulus. The natural-movie clip (19.2 s) was repeated 102 times in the experiment, and we drew the training set from half of these clips (Materials and Methods). Predictive information was computed on the left-out movie clips. Depending on initial connectivity, one of several final configurations of readout weights was learned, so each set has multiple learned readouts (Fig. 3A and Fig. S3). We quantified efficiency of learned readouts using a firing-rate-adjusted metric that compared the predictive information of learned readouts to the highest predictive information of any readout at or below the firing rate of the learned readout (Fig. 3A). This was done to normalize across readouts and to ameliorate biases resulting from those that produce more output spikes; with a wider dynamic range, more input information can be represented, but we wish to restrict the output cell to a biologically plausible firing rate.

Fig. 3.

Near-optimal readouts are learned under STDP rules. (A) Learned readouts (dots) are close to the optimal perceptron hull (gray line); the highest internal predictive information of any readout at or a below a given firing rate. (B) Learned readouts for sets of 4 (black), 7 (red), and 10 (blue) cells capture a large percent of maximal predictive information, defined as the learned readout predictive information divided by the optimal perceptron hull value at that firing rate. Cumulative distributions are across cell sets and initial conditions. (C, Top) Two learned readouts, with their corresponding optimal readout. Each input word either evokes a readout spike (white box) or not (black box). (C, Bottom) Cumulative distribution of the similarity to the optimal rule of learned readouts. Similarity is the fraction of time bins with one or more input spikes for which the learned and optimal rule produced the same output (Materials and Methods). For sets of four cells, a large fraction (39%) of initial conditions led to learned readouts that were optimal. pred-I, predictive information.

For small input groups (four cells), learned readouts conveyed near-optimal predictive information (Fig. 3B). The average percent of the optimal predictive information learned was 86% (14% SE, n = 240 sets). Learned readouts did not saturate the maximum firing rate and were distributed across the range of readout firing rates, with an average firing rate (mean: 2.3 Hz, SE: 0.9 Hz, n = 240 sets) that was 68% of the maximum firing rate. We quantified the similarity of learned readout rules to the optimal readout rule (Fig. 3A, gray line) based on how frequently the rules produced the same output for a given input, weighted by the frequency of the input. Learned readout rules were similar, but not identical, to optimal readout rules (Fig. 3C; mean: 0.71, SE: 0.20, n = 240 sets; black line). Although they did not precisely match the optimal readout rules, readouts learned under the STDP rule were efficient at representing predictive information.

Learning Efficient Readouts of Up to 10 Cells.

Estimating the statistics of anatomical convergence from RGCs, via thalamus, to cortical neurons is difficult knowing only the convergence rates from retina to lateral geniculate nucleus (LGN) (estimated at 10–30, refs. 32–34) and LGN to cortex (estimated at 30, ref. 35), and without knowing how these rates are correlated. Still, it is useful to know if efficient readouts can be found for modest-sized input groups. We therefore simulated learning under the pair STDP rule for sets of 7 and 10 cells. Exhaustive sampling is not possible for these larger groups. We estimate that our subsampling of readouts of sets of 7 and 10 cells underestimates the optimal bound by less than 5%, based on comparison with an optimized probabilistic rule (Fig. S1). However, the optimized probabilistic readout is not a single-step, biologically tractable function, so we continue to compare learned readouts to the most informative sampled readouts.

Compared with the optimal sampled readouts we observe a small decrease in readout efficiency (Fig. 3B), from 87% on average for groups of 4, to 82% (SE over groups, 10%, n = 244) for groups of 7 (red) and 80% (SE over groups, 8%, n = 244) for groups of 10 (blue). Learned readouts for these larger groups are less similar to the optimal readout than for groups of four inputs (0.63 and 0.62 for groups of 7 and 10, respectively; Fig. 3C). While there is some correlation between similarity to the optimal rule and readout efficiency, many readouts have a high degree of predictive information efficiency with low structural similarity to the optimal rule (Fig. S3). Thus, for sets of 4–10 cells, efficient readouts of predictive information can be learned without finding the exact structure of the optimal readout.

Stimulus Information of Learned Readouts.

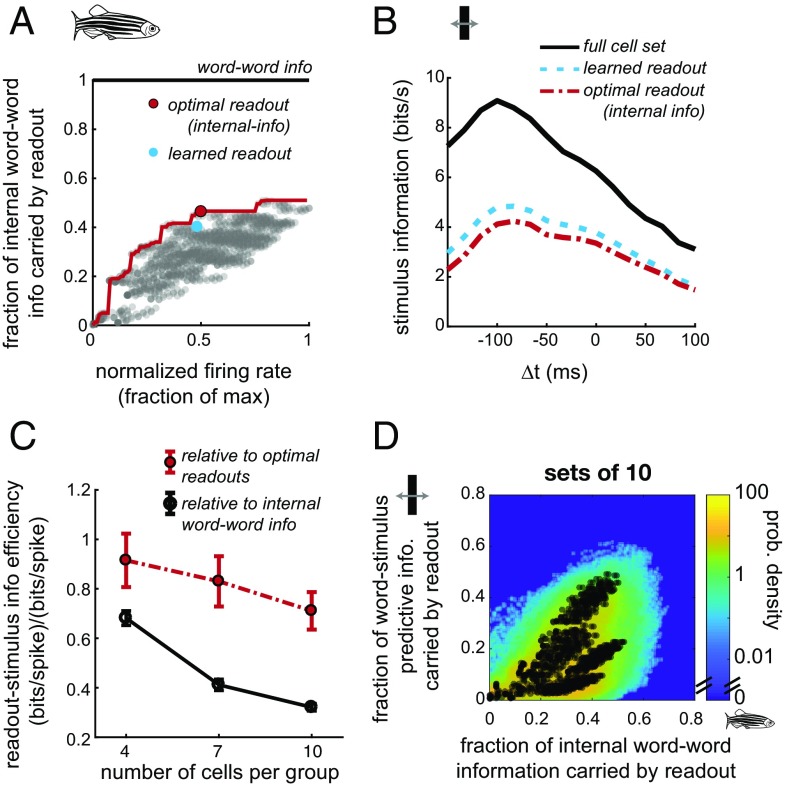
For sets of 4–10 cells, learned readouts capture most of the optimal readout predictive information, measured as a percent of the optimal readout internal predictive information (measured for responses to natural-movie stimuli). How efficient are learned readouts at representing stimulus information? To address this, we compare the stimulus information of the learned readouts to that of the full set of cells and to the optimal readouts. For each group of cells we identified the learned (blue) and corresponding optimal (red) internal-information readouts in our simulations (Fig. 4A) and computed information about stimulus position and velocity for those pairs of readouts (Fig. 4B). Because the optimality criterion is based on the efficiency of the readout of internal predictive information, it is possible that the readout-stimulus information is higher for other readouts, as we observed with this pair of learned and optimal readouts (Fig. 4B). The learned readout-stimulus information is compared with the word–stimulus information (solid black line, Fig. 4 B and C) and the optimal readout-stimulus information (dashed red line, Fig. 4 B and C). Because the firing rates of learned and corresponding optimal readouts may change depending on the stimulus type, we compared information efficiency in bits per spike by normalizing by the respective firing rates. The results were qualitatively unchanged without this normalization. Relative to the word–stimulus information, learned readouts are much more efficient for groups of 4 cells than for groups of 10 cells. Across sampled initial conditions the median (based on internal information) learned readout of a set of four cells is 67% (SEM: 4%, taken across sets) as efficient for stimulus information as the full cell set. For readouts of the sets of 10 cells the efficiency is only 32% (2%, SEM) of the full set (Fig. 4C, solid line). However, compared with the optimal linear readouts, typical learned readouts remained relatively efficient, with an average of 91% (8%, SEM) of the information retained for the sets of 4 cells and 71% (8%, SEM) for the sets of 10 cells. Moreover, a highly efficient readout (defined as >95% efficiency relative to the optimal linear readout) is learned for at least one of the simulated initial conditions in the vast majority of sampled sets of cells (223/240 sets of 4, 231/244 sets of 7, and 225/244 sets of 10). In general, for 10-cell groups, a saturating amount of stimulus predictive information is recovered as internal information grows (Fig. 4D), possibly because higher-order correlations in the inputs begin to have a larger effect and cannot be captured by a single-layer perceptron readout.

Fig. 4.

Stimulus information of learned readouts is near-optimal. (A) Identification of a learned readout (blue) and its respective optimal readout (red) from a set of input 10 cells, with sampled readouts (gray) and the optimal perceptron hull (red line; see Fig. S1). Readout-word information is normalized by word–word information during the natural movie. (B) The full word (black line) captures the most stimulus information, but the learned (dashed blue line) and optimal (dotted-dashed red line) readouts have comparable stimulus information. Stimulus information is predictive over the $\mathrm{\Delta }t>0$ portion of the curves. (C) Efficiency of typical readouts of stimulus predictive information relative to the full cell set (black) and relative to the optimal readout under natural-movie stimulation (red). As set size increases, efficiency remains high relative to the optimal readouts and decreases relative to the full word. Error bars represent SEM across sampled sets of cells. (D) For sets of 10 input cells the fraction of internal word–word information carried by a readout during the natural movie tends to be higher than the fraction of word–stimulus information carried by that readout during the moving-bar stimulus. A single cell set example is plotted as dots overlaid on the density, averaged across all sampled sets of 10 cells. info, information; prob, probability.

Discussion

Producing successful behavior in an ever-changing environment using sensory information, acquired in the recent past, necessitates prediction at least at one stage of neural processing. Such predictions are enabled by long-range spatiotemporal correlations present in natural stimuli. For example, in recordings of populations of RGCs of salamander retina driven by a simple stimulus with partially predictable dynamics, joint activity patterns transmit information that is predictive of future stimuli (2). However, for the organism to make use of this information, downstream networks need to read it out. In early sensory processing stages this learning likely occurs without independent instructive signals providing stimulus information.

We examined whether the temporal correlations within populations of RGCs can be used to guide the search for readouts of predictive information. Sets of cells were drawn agnostic to the cell types of constituent cells, although RGC populations are made up of diverse anatomical cell types (36, 37) and whether anatomical or functional cell types of cells in a set explain the variability in predictive information across sets and its efficient readout is an interesting question for future work. We showed that groups of cells with high external, stimulus-predictive information also had high internal predictive information on two classes of stimuli, a moving bar with stochastically driven damped oscillator dynamics and a natural movie. While there is not a perfect correlation between the two, efficient readouts of one type of information were likely to be efficient readouts of the other. The generalization of internal predictability across stimulus classes partially reflects the ability of the retina to adapt to the statistics of stimuli (4, 38), as well as the qualitative features of damped harmonic motion—inertial motion, reversals, and starts and stops—that also appear in the natural movie. The relationship between stimulus-predictive information and internal correlation potentially arises because firing in the retina is maintained by short-term plasticity mechanisms and other network nonlinearities when stimuli are predictable. The implication of the generalization across stimulus classes and between internal and stimulus prediction is that reading out predictive information in one context remains relevant in other settings.

We simulated a set of biologically plausible learning rules based on STDP using as “training data” the spiking activity recorded from a set of RGCs driven by a natural movie. This training condition is challenging but intended to approach a realistic scenario: A downstream neuron reading out bottom-up predictive information does not have independent access to the stimulus or to an error signal to guide its selection of readout weights. While the learning dynamics did not lead to the absolute optimal readout weight structure for all initial conditions, the readouts that were found had high information efficiency: Relative to the optimal readout of internal predictive information, learned readouts conveyed >80% of the predictive information available to perceptron readouts. Thus, a very simple learning rule found synaptic weights that effectively read out most of the available predictive information. Recent work in machine learning has demonstrated that STDP combined with recurrent units can be used to implement gradient descent (39) and could be used to extend the prediction of external stimulus features further into the future.

Finally, we extended our simulations to larger groups of cells. We found that while the efficiency of the learned readouts relative to optimal single-bit readouts remained high the efficiency relative to the full input group decreased, such that readouts of groups of 10 cells typically preserved 30% of the total predictive information. This suggests a limit to the compressibility of predictive information, and thus an estimate of how many inputs a downstream cell can efficiently read out. In other words, reading out from groups of four cells can be accomplished with high absolute efficiency. Perhaps the best way to combine more than four cells is to break down the readout into indivisible units of four cells, which are later recombined in subsequent processing. Alternatively, it could be that restricting our readout to a simple perceptron is overly limiting, and if we knew how to fully sample the $2^{2^N}$ readouts for a group of N cells we could retain much more of the input predictive information. We do not expect this is the case, however, based on the picture painted by the exhaustive sampling of readouts of sets of four cells and our analysis of the estimated readout bound for larger groups (Fig. S1).

We emphasized convergence: reading out a single bit from pools of inputs, which would happen downstream from the retina. This particular dataset was taken from the larval salamander, and in the visual system of amphibians retinal projections terminate in the optic tectum and thalamus (40). Classic work in the optic tectum of amphibians showed that feeding behavior can be evoked directly from electrical stimulation of parts of the optic tectum (41). Perhaps utilizing predictive information is primarily useful for making fast, subconscious predictions of the future of sensory stimuli and thus limited to automatic, reflex-like behaviors. However, salamander RGCs are not unique in encoding predictive information: Predictive information is also encoded by rat RGCs.* In the mammalian visual system there are both convergence and divergence as visual information passes from the limited number of channels of the optic nerve to LGN and on to cortex. This pattern may be required to chain together combinations of single-bit readouts that are predictive over larger spatial and temporal regions. In future work it will be interesting to see if it is possible to build such predictions out of an ensemble of single-bit readouts of many small groups of cells.

Materials and Methods

Multielectrode Recordings During Movie Stimulation of Dissected Retina.

The dataset used in this study was previously published (2), and complete experimental details can be found in ref. 42. Briefly, a multielectrode array (252 electrodes, 30-µm spacing) was used to record from a larval tiger salamander retina as images were projected onto the photoreceptor layer. Voltages from the electrodes were recorded at 10 kHz over the course of the multihour experiment and spikes were sorted, yielding 53 simultaneously recorded single units. The movies, referred to as either the naturalistic movie or moving bar, were presented using a 360- by 600-pixel display at 60 frames per second with 8 bits of grayscale. The naturalistic movie was a 19-s clip of fish swimming in a tank with plants in the background and was repeated 102 times. The moving bar was an 11-pixel-wide black bar against a gray background, with dynamics for its position and velocity following the equations for a stochastic damped harmonic oscillator in the overdamped regime (SI Materials and Methods). The naturalistic movie responses were used for the training dataset and for predictive information calculations (Figs. 2–4), except where specifically noted otherwise. The moving-bar responses were used for calculating the information about past and future bar position and velocity (Figs. 1, 2, and 4). The checkerboard stimulus (Fig. 2) consisted of a checkerboard pattern which updated randomly every 33.33 ms.

Binary Neuron Model.

Sorted spikes were binned into time bins of width $\mathrm{\Delta }t=1/60\hspace{0.5em}\text{s}$. Activity of a set of m cells at time $t=n\mathrm{\Delta }\text{t}$ is described by the m-bit binary word ${\mathit{x}}_t$. The readout $y_t$ of this set of cells is a binary function on the set of $2^m$ possible binary words. In the case of a perceptron readout (24), this function is $y_t=0if\mathit{w}\cdot {\mathit{x}}_t\le b$ and otherwise $1$, where w is the length-m synaptic weight vector and $b=1$. We require weights to be excitatory ($w_i\ge 0$).

Information Calculations.

Word–word internal predictive information is the mutual information between the binary word ${\mathit{x}}_t$ at time $t$ and time $t\prime =t+dt$ for some temporal offset dt (43–45): $I\left({\mathit{X}}_t;{\mathit{X}}_{t\prime }\right)={\displaystyle \sum _x{P}_X\left({\mathit{x}}_t\right)P_X\left({\mathit{x}}_{t\prime }|{\mathit{x}}_t\right)}{\log }_2\frac{P_X\left({\mathit{x}}_{t\prime }|{\mathit{x}}_t\right)}{P_X\left({\mathit{x}}_{t\text{'}}\right)}$. Readout predictive information is the mutual information of the perceptron activity $y_t$ at time $t$ and the word ${\mathit{x}}_{t+dt}$ at time $t\prime =t+dt$. Details of information calculation methods are in SI Materials and Methods. Distributions were generally well-sampled, so uncertainty in information estimates were less than 0.06 bits per s for readout information quantities and 0.18 bits per s for word–word information quantities (SI Materials and Methods).

Drawing Cell Sets and Sampling Readout Functions.

Cell sets were drawn from the population of 53 total recorded cells (SI Materials and Methods and Fig. S5). To estimate the predictive information bound as a function of firing rate, we sampled all positive-weight perceptrons for sets of 4 cells and up to 1,500 perceptrons for the sets of 7–10 cells for which learning simulations were carried out. The efficiency of this sampling method is analyzed in Fig. S1.

STDP.

The learning rule is a simplified STDP rule (29, 46) adapted for binary neurons and depends on the timing of a single presynaptic and a single postsynaptic spike: $\mathrm{\Delta }{\mathit{w}}_t=\epsilon \left(y_t{\mathit{x}}_t-{\alpha }_{LTD}{y}_{t-1}{\mathit{x}}_t\right)$. This rule generates potentiation of a weight $w_t^{\left(i\right)}$ if the input spike triggered an output spike at time t and depression if an output spike preceded an input spike. We use hard bounds on $\mathit{w}$, $0<w_i<w_{max}$ and set $\epsilon =0.01$. Practically, because firing is sparse, the maximum weight was chosen to be superthreshold (1.1), which ensured nonzero firing rates of learned readouts. Results from variations of this learning rule are shown in Fig. S2.

Similarity to the Optimal Rule.

The similarity to the optimal readout is the fraction of time bins with one or more input spikes for which the learned and optimal rule produced the same output. See Fig. S3 for details. MATLAB code used for the analysis is available from the authors at github.com/ajsederberg/learning-predictive-info-readouts.