Cell-type–specific neuromodulation guides synaptic credit assignment in a spiking neural network

Significance

Synaptic connectivity provides the foundation for our present understanding of neuronal network function, but static connectivity cannot explain learning and memory. We propose a computational role for the diversity of cortical neuronal types and their associated cell-type–specific neuromodulators in improving the efficiency of synaptic weight adjustments for task learning in neuronal networks.

Abstract

Brains learn tasks via experience-driven differential adjustment of their myriad individual synaptic connections, but the mechanisms that target appropriate adjustment to particular connections remain deeply enigmatic. While Hebbian synaptic plasticity, synaptic eligibility traces, and top-down feedback signals surely contribute to solving this synaptic credit-assignment problem, alone, they appear to be insufficient. Inspired by new genetic perspectives on neuronal signaling architectures, here, we present a normative theory for synaptic learning, where we predict that neurons communicate their contribution to the learning outcome to nearby neurons via cell-type–specific local neuromodulation. Computational tests suggest that neuron-type diversity and neuron-type–specific local neuromodulation may be critical pieces of the biological credit-assignment puzzle. They also suggest algorithms for improved artificial neural network learning efficiency.

Mathematical “gradient backpropagation” algorithms (1, 2) now solve the problem of credit assignment for artificial neural networks effectively enough to have ushered in an era of shockingly powerful artificial intelligence. Nevertheless, their exact implementation on advanced tasks can be extremely costly in terms of computation, storage, and circuit interconnects (3), driving a search for more efficient credit-assignment algorithms, such as approximate gradient methods (4–7), which, e.g., limit temporal contributions to learning (8) or exploit neuromorphic methods to improve energy efficiency (9, 10). Neuroscientists meanwhile recognize that exact gradient backpropagation demands precise, but nonlocal, communication that is implausible in the biological brain and instead propose approximate learning rules that sidestep the demands. These have shown impressive performance, largely in feedforward networks (11–20), with recent extensions to the more enigmatic case of recurrently connected networks (21, 22). This said, biological neural networks feature a spectacular array of dynamical and signaling mechanisms, whose potential contributions to credit assignment have not yet been considered. Taken together, this creates a remarkable need and opportunity for bio-inspired network-learning algorithms to advance both neuroscience and computer science research. Here, we follow this path and present evidence for a previously unrecognized temporal credit-assignment mechanism inspired by recent advances in brain genetics.

Prior efforts to address the biology of synaptic credit assignment have focused on Hebbian spike-timing-dependent synaptic plasticity and “top-down” (TD) signaling by dopamine (13, 23–25), a monoamine neuromodulator released from axons that ramify extensively throughout the brain from small midbrain nuclei. All cellular actions of dopamine are exerted by activation of G protein-coupled receptors (GPCRs), which can strongly modulate the timing dependence of Hebbian synaptic plasticity (25–27). While such actions clearly contribute to synaptic credit assignment, and recent evidence suggests spatiotemporal sculpting of the dopaminergic signal (28, 29), biologically plausible models based on these principles significantly underperform gradient backpropagation algorithms, let alone the brain, and many gaps in our understanding remain (12, 13).

Transcriptomic studies have now revealed that genes encoding hundreds of other modulatory GPCRs, including those selective for serotonin, norepinephrine, acetylcholine, amino acids, and the many neuropeptides (NPs), are expressed throughout the brain. Downstream actions of these other GPCRs on nerve membranes and synapses are similar to those of dopamine receptors, suggesting that they, too, could participate in credit assignment. Single-cell RNA-sequencing studies now show also, however, that expression of this diverse array of GPCR genes is highly neuron-type–specific (30). Furthermore, virtually every neuron expresses one or more GPCR-targeting NP ligands, again, in highly neuron-type–specific patterns. These new single-cell transcriptomic data thus suggest the prospect of an interplay between synaptic and local peptidergic modulatory networks that could help to guide credit assignment.

The new genetic results have led us to formulate a theory of network learning that casts neuronal networks in terms of interacting synaptic and modulatory connections, with discrete neuron types as common nodes. To explore this normative theory, we have instantiated the simplified computational model schematized by Figs. 1 and 2. The model comprises both dopamine-like TD and NP-like local modulatory signaling, shown with a network of arrow-spray glyphs connecting populations of cells, in addition to synaptic transmission via discrete spikes, shown with a network of lines connecting individual cells (Fig. 1A). Our model has multiple neuron types distinguished by both their synaptic connectivity and differential expression of modulatory ligand–receptor pairs that regulate Hebbian synaptic plasticity (Fig. 1 B and C). Our proof-of-concept implementation shows significant improvements over previous literature. The key development is that neurons utilize modulatory networks to actively broadcast their own contribution to the network performance to nearby neurons via cell-type–specific local neuromodulation (Figs. 1D and 2C)—specifically, each cell broadcasts its own direct contribution to the overall task “error” signal. This is a major departure from more global roles for modulators previously proposed, such as carrying error or reward signals. From a neuroscience perspective, our study proposes a model of cortical learning shaped by the interplay of local modulatory signaling carrying credit-assignment information and synaptic transmission and potentially brings us closer to understanding biological intelligence. From a computer science perspective, our method offers a significantly smaller number of interconnects for on-chip neuro-inspired artificial intelligence.

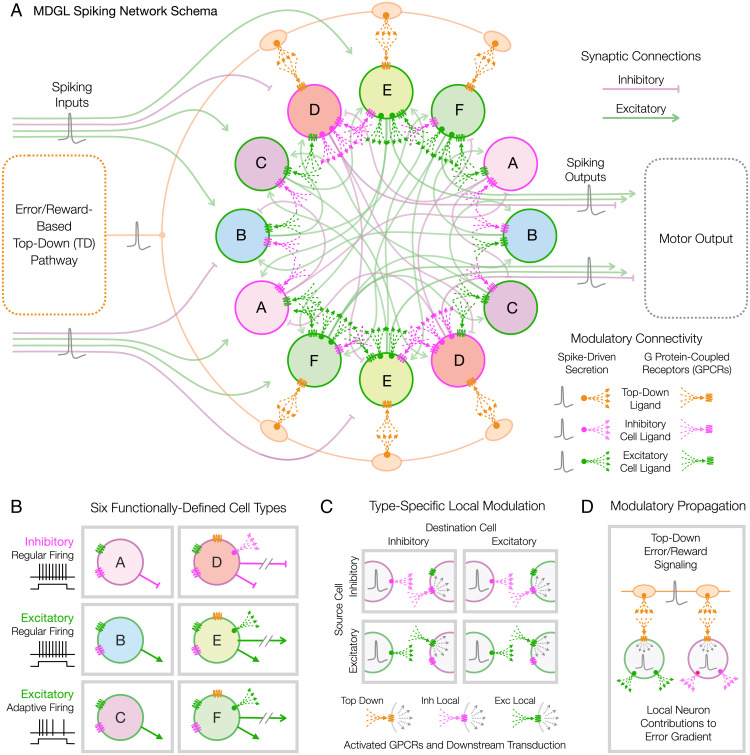
Fig. 1.

MDGL network schema. (A) Six diametrically paired circles (labeled A–F) represent six types of spiking neurons, each defining a population of units on the basis of differential synaptic and modulatory connection and affinity statistics. Inhibitory and excitatory synaptic connections are cartooned here by faint curving lines, while both TD and local modulatory connections are indicated by arrow-spray glyphs representing secretion of TD and local modulatory ligands and activation of modulatory GPCRs, all differentially color coded as captioned. Learning tasks are defined by temporal patterns of the indicated spike inputs and outputs, as described in Fig. 3. (B) Six cell types based on excitatory vs. inhibitory synaptic actions, regular vs. adaptive spiking, and internal-only vs. output connectivity. Excitatory and inhibitory cells are further distinguished by which NP-like modulators they secrete, while only output cells are directly responsive to the dopamine-like TD modulator. (C) Cell-type–specific channels of local modulatory signaling established by activity-dependent secretion of two different modulatory ligands and two differentially selective receptors. (D) An error/reward-encoding TD signal impacts target neurons and synapses both 1) directly via activity-dependent secretion of TD ligand and 2) indirectly via activity-dependent secretion of local modulatory ligands.

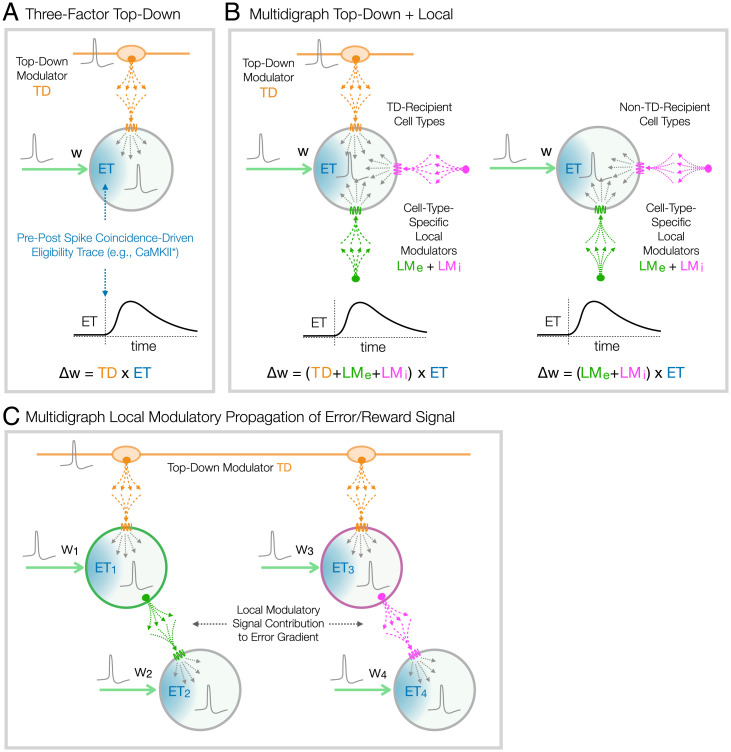
Fig. 2.

Modulator-based neo-Hebbian local learning rules. (A) A conventional three-factor local learning rule models action of a “third,” TD GPCR-activating ligand (e.g., dopamine) that governs synapse reweighting ($\mathrm{\Delta }w$) in proportion to temporal coincidence of the two Hebbian factors (presynaptic and postsynaptic activity). Such models generally require a lingering ET to sustain information about Hebbian coincidence until arrival of the TD signal. (B) Embracing new genetic evidence for local GPCR-based modulatory machinery, the MDGL theory introduces additional factors that allow spike-dependent secretion of NP-like local modulators (${\text{LM} }_{\text{e}}$ from excitatory neurons and ${\text{LM}}_{\text{i}}$ from inhibitory neurons) to participate in governing synapse reweighting ($\mathrm{\Delta }w$) (35). As indicated here and in Fig. 1, the present MDGL model comprises both directly TD-recipient cells (types D–F; B, Left) and non–TD-recipient cells (types A–C; B, Right). Synapse reweighting requires combined GPCR activation with a persistent ET for all cell types, but GPCRs are activated on non–TD-recipient cells only by the local modulatory ligands. (C) Propagation of TD error/reward signal via spike-dependent secretion of local modulators from both excitatory and inhibitory cell types to cells lacking direct access to TD modulatory signal. For simplicity, this schema represents only the four subscripted synapses/weights, while the full model represents many more synaptic inputs per cell.

Results

Overview of Multidigraph Learning in Recurrent Spiking Neural Networks.

Gradient descent on the task error (or negative reward) E can iteratively adjust synaptic weights to learn the task. However, computing the error gradient in a recurrent network requires unwrapping the dynamics over time because weights influence future activity in synaptically far-away neurons. The Backpropagation Through Time (BPTT) and Real-Time Recurrent Learning (RTRL) algorithms calculate this error gradient by allowing cell-specific, nonlocal communication among synapses in adjusting their weights; for example, in Fig. 1A, the synapse between the uppermost cells labeled C and E would receive information about the many synaptic weights and cell activities downstream of that cell E. They also require either noncausal dependencies (BPTT) or infeasible memory scalability (RTRL) (detailed in Methods, Eqs. 2–17 and see Fig. 6). Faced with this, a key step in state-of-the-art rate-based (21) and spike-based (ref. 22; “e-prop”) biologically plausible learning algorithms is to drop the nonlocal terms so that the activities of only the presynaptic and postsynaptic neurons would be needed to update the weight of the synapse between them. As illustrated in Fig. 2A, the resulting three-factor local learning rules represent this presynaptic and postsynaptic information as a time-dependent eligibility trace (ET) and combine it with TD signals to update the weight $\mathrm{\Delta }w$ of each synapse (31–34) (detailed further in Methods; see Figs. 5B and 6 D, ii; see also ref. 7).

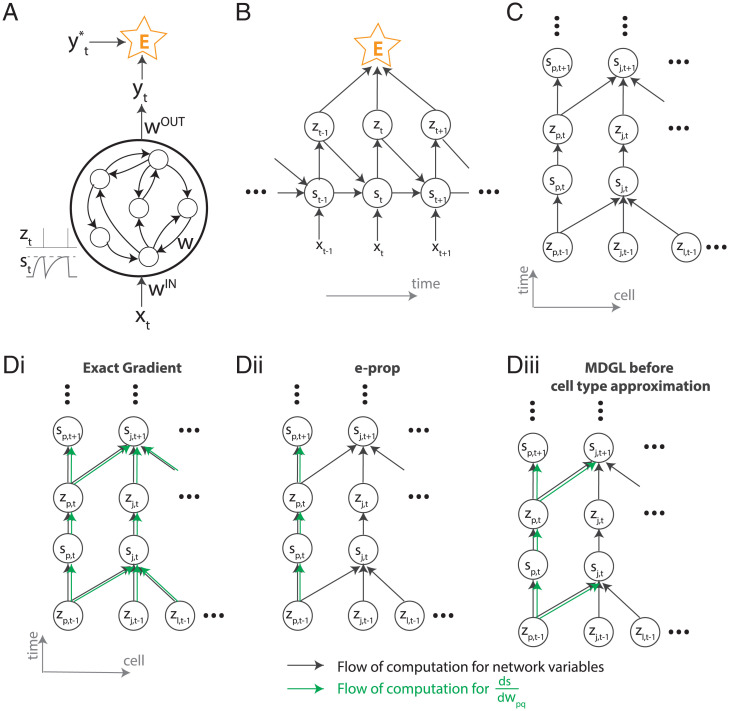
Fig. 6.

Computational graph and gradient propagation. (A) Schematic illustration of the recurrent neural network used in this study. (B) The mathematical dependencies of input x, state s, neuron spikes z, and loss function E unwrapped across time. (C) The dependencies of state s and neuron spikes z unwrapped across time and cells. (D) The computational flow of $\text{d}s/\text{d}{w}_{pq}$ is illustrated for exact gradients computed using exact calculation (Eq. 17) (i), e-prop (ii), and our truncation in Eq. 18, where dependency within one connection step has been captured (iii). Black arrows denote the computational flow of network states, output, and the loss; for instance, the forward arrows from z_t and s_t going to $s_{t+1}$ are due to the neuronal dynamics equation in Eq. 2. Green arrows denote the computational flow of $\text{d}s/\text{d}{w}_{pq}$ for various learning rules.

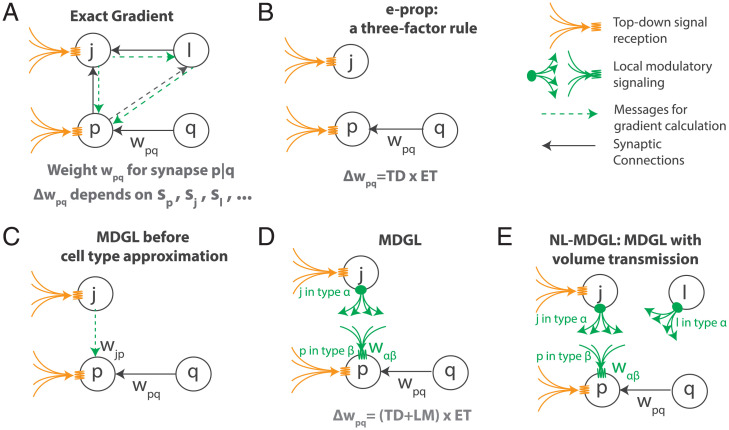
Fig. 5.

Cartoon summary of learning rules explored in this work. (A) The exact gradient: Updating weight w_pq, the synaptic connection strength from presynaptic neuron q to postsynaptic neuron p, involves nonlocal information inaccessible to neural circuits, i.e., the knowledge of activity (e.g., voltage s) for all distant neurons j and l in the network. This is because w_pq affects the activities of many other cells through indirect connections, which will then affect the network output at subsequent time steps (Eq. 17 in Methods). (B) E-prop, a state-of-the-art biologically plausible learning rule, restricts the weight update to depend only on presynaptic and postsynaptic activity and TD learning signal, as in a three-factor learning rule (Fig. 2A). (C) We allow the weight update to capture dependencies within one connection step, which are omitted in e-prop. The activity of neuron j could be delivered to p through local modulatory signaling. (D) For the signaling in C to be cell-type–specific, as consistent with experimental observation in ref. 42 and biologically plausible mechanisms, we approximate the cell-specific gain with cell-type–specific gain (Eq. 23), which leads to our MDGL. Effect of this cell-type approximation is explored in SI Appendix, Fig. S9. (E) NL-MDGL, where modulatory signal diffuses to all cells in the network without attenuation (Fig. 4).

We propose a role for cell-type-based modulatory signals in recovering a key part of the error-gradient information that is lost by dropping nonlocal terms in such conventional three-factor rules. We describe this in terms of the update $\mathrm{\Delta }w$ to a synapse $p|q$ from neuron q to neuron p with strength w. To begin, we consider the contributions to the error gradient of those neurons that are one synapse away from the postsynaptic site (i.e., neurons j such that synapse $j|p$ exists) (illustrated in Methods; see Fig. 5C). We find that this set of contributions can be realized by activity-dependent signals emitted by neurons j and the ET for the synapse $p|q$ (Eq. 19). Intriguingly, this signal is precisely neuron j’s contribution to the task error, thereby taking into account the indirect contribution of the synapse $p|q$ to the network performance via neurons j for more accurate synaptic credit assignment.

This initial form, however, still requires the knowledge of cell-specific signals from cells j not participating in the synapse of interest. We further make the key observation that when just the contributions from cells up to two synapses away are considered, those terms only appear under a sum: The mechanism updating the synapse $p|q$ does not need to know the contributions from individual “indirect” neurons j, as their sum suffices. This observation is critical in elucidating a role for diffusive neuromodulatory signaling in carrying this summed, indirect signal and thus serving as an additional factor in synaptic plasticity.

To fully remove cell-specific dependencies in the indirect signal, we further approximate the cell-specific weights w_jp that it contains with the cell-type–specific terms $w_{\alpha \beta }={\langle w_{jp}\rangle }_{j\in \alpha ,p\in \beta }$ when postsynaptic cell j belongs to type α and presynaptic cell p belongs to type β. We postulate that w_αβ represents the affinity of GPCRs expressed by cells of type β to peptides secreted by cells of type α (Fig. 1C and Methods, Eq. 20; see Fig. 5D), and this cell-type–specific variable is genetically determined. The local diffusion assumption (35) suggests a further idealization, where this type of signaling is registered only by local synaptic partners and therefore preserves the connectivity structure of w_jp (Eq. 23). It is also worth noting that the rich set of ligand and receptor types with different downstream actions (30) can support that w_αβ is a signed term.

Bringing these together, we have the learning rule illustrated in Fig. 2B. The weight update is given as

$$\begin{array}{l}\mathrm{\Delta }{w}_{pq}\propto \left({\text{TD}}_p+{\displaystyle \sum _{\alpha \in C}{\text{LM}}_{\alpha \beta }}\right)\times {\text{ET}}_{pq}\\ {\text{LM}}_{\alpha \beta }=(\text{affinity} w_{\alpha \beta })\times {\displaystyle \sum _{j\in \alpha ,p\to j}\underset{\text{modulatory} \text{signal} j}{\underbrace{{\text{TD}}_j\hspace{0.17em}\times \hspace{0.17em}(\text{activity} j)}}},\end{array}$$ [1]

where neuron j is of type α and neuron p is of type β, $p\to j$ denotes that synapse $j|p$ exists, C denotes the set of neuronal cell types, ${\text{TD}}_p$ denotes the TD signal received by p, ${\text{ET}}_{pq}$ denotes the ET for $p|q$, affinity w_αβ denotes the effect of ligands secreted by class α neurons on class β receptors, and ${\text{LM}}_{\alpha \beta }$ denotes the contribution of local modulation to synaptic plasticity that has been ignored so far. Thus, our update rule suggests a set of modulatory terms that combine with the ET in order to more accurately assign credit across a network when updating its synapses. Neurons that receive TD feedback regarding their role on the circuit goals propagate this information to nearby synaptic partners via cell-type–specific local modulatory signals (Fig. 2C; see also Eq. 24 for details). Specifically, the modulatory signal j in Eq. 1 is precisely the contribution of cell j to the task error, as measured by the (partial) derivative of the error with respect to cell j’s membrane potential. Moreover, this framework proposes that cell-type–specific GPCR affinities allow these local signals to be informative without the need to know precise synaptic weights. The ability to assess the indirect impact of neurons on the overall loss via such communication is critical to accurate synaptic reweighting and improved performance over existing biologically plausible rules, as we demonstrate next (Fig. 3 and SI Appendix, Fig. S2).

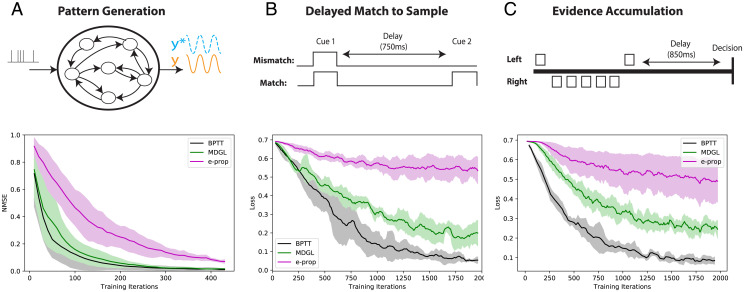
Fig. 3.

Cell-type–specific neuromodulation guides learning across multiple tasks. (A) Learning to produce a time-resolved target output pattern. (B) A delayed match to sample task, where two cue alternatives are represented by the presence/absence of input spikes. (C) An evidence-accumulation task (29, 36). (Lower) Addition of cell-type–specific modulatory signals improves learning outcomes across tasks. In line with these results, SI Appendix, Fig. S2 shows that gradients approximated by MDGL are more similar to the exact gradients than those approximated by e-prop. Solid lines/shaded regions: mean/SD of loss curves across runs (Methods).

In summary, we have proposed a rule for updating a synapse w_pq, which we refer to as the multidigraph learning rule, or MDGL, where the Hebbian ET is compounded not only with TD learning signals—as in modern biologically plausible learning rules (31, 32)—but also with cell-type–specific, diffuse modulatory signals.

Simulation Framework for Testing Multidigraph Learning in Recurrent Spiking Neural Networks.

To test the MDGL formulation, we study its performance in recurrent spiking neural networks (RSNNs) learning well-known tasks involving temporal processing: pattern generation, delayed match to sample, and evidence accumulation. We use two main cell classes, inhibitory (I) and excitatory (E) cells, and obey experimentally observed constraints (e.g., refractoriness, synaptic delay, and connection sparsity). We further endow a fraction of the E cells with threshold adaptation (37). This mimics the hierarchical structure of cell types (38) through the simple example of two main cell types, one of which has two subtypes (E cells with and without threshold adaptation). The existence/lack of synaptic connections to output neurons further divides each population into two, thus bringing the cell type tally to six in our conceptual model (Fig. 1). Our implementation does not involve rapid and random formation of new synapses after each experience (39), further increasing its biological plausibility.

We compare the learning performance of MDGL (Fig. 2B) with the state-of-the-art biologically plausible learning rule [e-prop (22)] (Fig. 2A and SI Appendix, Fig. S1). As a three-factor rule, e-prop does not involve local cell-type–specific signaling and restricts the update to depend only on presynaptic and postsynaptic activity, as well as a TD instructive signal. To provide a lower bound on task error, we also compare performance with BPTT (see Fig. 5A), which uses exact error gradients to update weights. These learning rules are further illustrated in Methods; see Fig. 5 A, B, and D.

Multidigraph Learning Guides Temporal Credit Assignment in Benchmark Tasks.

We first study pattern generation with RSNNs, where the aim is to produce a one-dimensional target output, generated from the sum of five sinusoids, given a fixed Poisson input realization (40). We change the target output and the Poisson input along with the initial weights for different training runs (SI Appendix, Fig. S3A) and illustrate the learning curve in Fig. 3A and SI Appendix, Fig. S4A across five such runs. We observe that MDGL performs significantly better than e-prop.

Next, to study how RSNNs can learn to process discrete cues that impact delayed rewards, we consider a delayed match to sample task (41). Here, two cue alternatives are encoded by the presence/absence of input spikes. The RSNN is trained to remember the first cue and learn to compare it with the second cue delivered at a later time (SI Appendix, Fig. S3B). Fig. 3B and SI Appendix, Figs. S4B and S5 display the learning curve for novel inputs. We observe that the same general conclusions as for the pattern-generation task hold; introducing cell-type–specific neuromodulation significantly improves learning outcomes.

Finally, we study an evidence-accumulation task (29), which involves integration of several cues to produce the desired output at a later time: A simulated agent moves along a path while encountering a series of sensory cues presented either on the right or left side of a track (Fig. 3C and SI Appendix, Figs. S3C and S4C). When it reaches a T-junction, it decides if more cues were received on the left or right. We test our learning rule to see if the addition of diffuse modulatory signals can indeed bring the learning curve closer to BPTT, without relying on rapid and random rewiring (39). Fig. 3C demonstrates that the performance trends of the previous two experiments continue to hold. SI Appendix, Fig. S6 illustrates that without threshold adaptation and recurrent connectivity, the network cannot significantly decrease loss and thus is unable to learn this task. In line with these experiments, gradients approximated by MDGL are more similar to the exact gradients (SI Appendix, Fig. S2), shedding light on its superior performance. We also observe that MDGL’s performance depends only weakly on the hypothesized link (Eq. 23) between abstract cell-type-based connectivities and modulatory receptor affinities (SI Appendix, Fig. S7), enabling flexible implementations in vivo and in silico.

We conducted further studies to better quantify how a model’s network architectures impact the performance of MDGL relative to other learning rules. First, as depicted in Figs. 1 and 2, recall that only output-projecting neurons receive TD signals, which is a consequence of gradient-based learning (22), and only these neurons secrete local neuromodulators (i.e., nonzero LM in Eq. 1). Consistent with this, we found that MDGL is most advantageous relative to e-prop in cases where relatively small fractions of recurrently connected neurons are output projecting, as we may expect in many biological networks (SI Appendix, Fig. S8). In these “sparse-output” cases, while many neurons do not receive learning signals in the e-prop formulation, MDGL still allows these neurons to receive such signals via local modulation. The result is more accurate approximation of gradients and more efficient learning. Next, SI Appendix, Fig. S9 demonstrates the effectiveness of using the cell-type–specific, rather than more precise cell-specific, weights of the modulatory signals within the MGDL framework. We find that the cell-type-based approximation does degrade performance, but that this effect is relatively minor.

Finally, we note that while our proof-of-concept implementation assumes symmetric feedback weights for the output connections (i.e., the same output projection weight is used during the computation of TD feedback signal), the random feedback-alignment approach (14) or approximating the feedback weights using the same cell-type-based calculations in Eq. 23 both offer improved biological plausibility for this single-layer feedforward problem.

Spatiotemporal Extent of Multidigraph Learning.

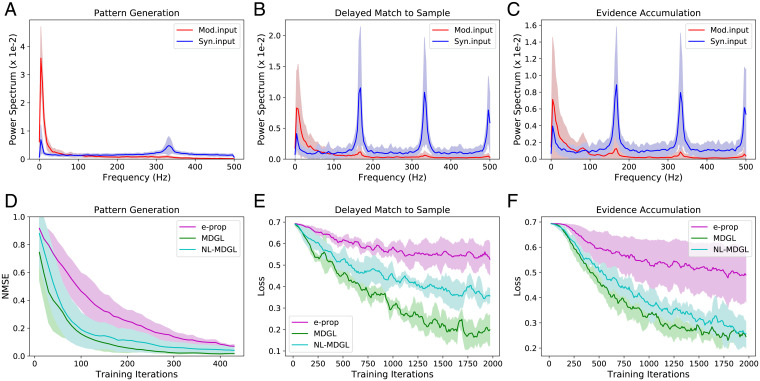
Owing both to extracellular ligand-diffusion biophysics and the complex metabolic nature of GPCR-based signal transduction, neuromodulation time scales are generally much longer than those of conventional synaptic transmission (42). Since our model does not explicitly limit the communication bandwidths of either channel, comparing the frequency content offers an important check for biological plausibility. It also provides a test of our approximation that the summation over cells in Eq. 19 acts as a smoothing operation. Fig. 4 A–C and SI Appendix, Fig. S10 demonstrate that the modulatory input indeed has significantly lower frequency content than the synaptic input for all three tasks.

Fig. 4.

Spatiotemporal characteristics of local neuromodulation. (A–C) Power spectra of modulatory (Mod.input; total cell-type–specific modulatory signal detected by each cell—Eq. 21) and synaptic inputs (Syn.input; total input received through synaptic connections by each cell—Eq. 22) are compared after learning for all tasks. Solid lines denote the average, and shaded regions show the SD of power spectrum across recurrent cells. Raw input traces are included in SI Appendix, Fig. S10. (D–F) Performance degrades when neighborhood specificity of modulatory signaling (NL-MDGL) is removed so that cell-type–specific modulatory signals diffuse to all cells in the network without attenuation. Learning with spatially nonspecific modulation still outperforms that without modulatory signaling (e-prop).

The distance ranges of diffusive modulatory signals remain uncertain (43). For most of the simulations described here (those according to Eq. 23), modulatory signaling was limited to synaptically coupled pairs (a token of anatomic proximity), representing an idealization of the short-range signaling case. We also examined the opposite extreme case, where modulatory signals extend to all cells (independent of any anatomic proximity), referring to this nonlocal form of MDGL as NL-MDGL. This would make w_αβ a worse approximation to w_jp, presumably degrading the quality of the gradient estimate. Indeed, removing the locality of modulatory signals degrades performance while remaining superior to that in the absence of modulatory signaling (Fig. 4 D–F)—suggesting that the biophysics of diffusive modulatory signaling may condition the efficiency of synaptic learning.

Discussion

Here, we have presented a multidigraph theory and instantiated simple models based on this theory that explicitly represent diverse neuron types classified by their synaptic and neuromodulatory connections. Simulations based on these simple models show that diverse signaling modes can facilitate credit assignment and enhance learning. A wealth of new genetic data provide strong support for the biological plausibility of this array of signaling modes and furthermore argue strongly that most or all modern eumetazoans (all multicellular animals except sponges) comprise numbers of cell types and modulatory signals far in excess of those represented in our simulations (43). We believe therefore that conceiving of neuronal networks as multidigraphs, involving multiple modulatory and synaptic signals, integrated by discrete cell-type nodes, may offer fruitful paths toward the understanding of synaptic credit assignment in biological neuronal networks. This multidigraph theory may also lead to more computationally efficient local learning rules for neural-network-based artificial intelligence.

In addition to established elements of Hebbian plasticity, ETs, and reward feedback signals, our normative theory posits important roles for neuronal cell-type diversity and local neuromodulatory communication in enabling efficient synaptic credit assignment. In particular, our findings predict that neurons secrete information about TD feedback signals they receive to nearby neurons in an activity-dependent and cell-type–specific manner using local modulation. As a consequence, levels of local modulatory signals may reflect the learning process. Indeed, our computational experiments imply that the level of modulatory input decreases over training and sharply rises in response to changes in task condition (SI Appendix, Fig. S11). It is also interesting to note that phylogenomic studies now suggest that peptidergic neuromodulation may evolutionarily predate dopamine signaling (43) and thus may have actually provided the foundation upon which dopaminergic TD signaling evolved.

The nature of “intermediate” cells (38), whose phenotypes appear to be a mixture of “pure” cell types, is a key problem in cell-types research. Our findings may explain the existence of such phenotypes from a connectivity perspective: While average connectivities between types remain relatively constant during training, connectivities of individual cells can deviate significantly from those averages (SI Appendix, Fig. S12). We hypothesize a link between abstract cell-type-based connectivities and modulatory receptor affinities, where the average synaptic connection weights between types are taken to be the cell-type–specific modulatory receptor affinities (Eq. 23). How tightly the individual synaptic weights and cell-type–specific receptor affinities should be coupled may be explored in future work. SI Appendix, Fig. S2 indicates that even with imprecise GPCR affinities, MDGL can still improve gradient approximation, while SI Appendix, Fig. S7 suggests that the effect of imprecise GPCR affinities on the performance is task-dependent.

Learning rules often explicitly minimize a loss function, and the error gradient, if available, tells exactly how much each network parameter should be adjusted to reduce this loss function. Rules that follow this gradient, RTRL and BPTT, are well established, but are not biologically plausible and have unmanageably vast memory storage demands. However, a growing body of studies have demonstrated that learning rules that only partially follow the gradient, while alleviating some of these problems of the exact rules, can still lead to desirable outcomes (44, 45). An example is the seminal concept of feedback alignment (14), which rivals backpropagation on a variety of tasks, even using random feedback weights for credit assignment. In addition, approximations to RTRL have been proposed (4–9, 21) for efficient online learning in recurrent neural networks. Our learning rule has $O(N^2)$ complexity, where N is the number of neurons, which is less expensive than SnAp-2 that has a storage cost of $O(N^3)$ (8) (for simplicity, connection sparsity factor is neglected here). It also outperforms biological learning rules with similar complexity scale (21, 22). Thus, our model further advances approximated gradient-based learning methods and continues the line of research in energy-efficient, on-chip learning through spike-based communications (10, 46). Such efficient approximations of the gradient computation can be especially important as artificial networks become ever larger and are used to tackle ever more complex tasks under both time and energy-efficiency constraints.

Examination of the learning capability of MDGL under a broader range of tasks and conditions represents a valuable future avenue. For instance, our preliminary simulations on modulating the delay period in the match to sample task (SI Appendix, Fig. S13) suggests that such studies can help reveal the reasons underpinning the observed animal behavior (47), as well as limitations of MDGL. In addition, brain cells are extremely diverse (38, 48) with a matching diversity in the expression of peptidergic genes (30). Further studies can also investigate the interplay of task complexity and cell diversity. A starting point for that could be further dividing inhibitory cells into subtypes with and without threshold adaptation.

Our work suggests that multiple cell-type–specific, diffuse, and relatively slow modulatory signals should be considered as possible bases for credit-assignment computations. Though inspiration for the present work came primarily from new transcriptomic data on local NP signaling in neocortex (30, 42), it is quite possible that other cell-type–specific neuromodulators could likewise contribute to credit assignment. Many of these alternative agents act, as do NPs, via GPCRs (e.g., the monoamines, amino acids, acetylcholine, and endocannabinoids), but our multidigraph template might even apply to other neuronally secreted neuromodulators, such as the neurotrophins and cytokines, that act via different classes of receptors (49, 50). While experimental tests of such hypotheses have not seemed feasible up until now, emerging methods for genetically addressed measurement of various neuromodulatory signals in specific cell types (30, 51) are now bringing the necessary critical tests within reach (e.g., ref. 52).

Methods

Visual Summary of Learning Rules.

An overview of our network model and the mathematical basis of the learning rules used in this work is given in the beginning of Results. Here, we first present an additional, more detailed visual illustration of these learning rules in Fig. 5, beginning with the exact gradient update (Fig. 5A), as for BPTT, and leading from its dramatic truncation in the e-prop rule (Fig. 5B), to MGDL (Fig. 5 C–E), which partially recovers gradient information lost in this truncation.

Spiking neuron model.

We consider a discrete-time implementation of RSNNs. The model, as shown in Fig. 6A, denotes the observable states, i.e., spikes, as z_t at time t, and the corresponding hidden states as s_t. For leaky integrate-and-fire (LIF) cells, the state s_t corresponds to membrane potential, and the dynamics of those states are governed by

$$\begin{array}{l}{z}_{j,t}=H(s_{j,t}-v_{\text{th}})\\ s_{j,t+1}=\eta \hspace{0.17em}{s}_{j,t}+(1-\eta )\left({\displaystyle \sum _{l\ne j}{w}_{jl}}\hspace{0.17em}{z}_{l,t}+{\displaystyle \sum _m{w}_{jm}^{\text{IN}}}\hspace{0.17em}{x}_{m,t+1}\right)-z_{j,t}\hspace{0.17em}{v}_{\text{th}},\end{array}$$ [2]

where $s_{j,t}$ denotes the membrane potential for neuron j at time t, $v_{\text{th}}$ denotes the spiking threshold potential, $\eta =e^{-dt/{\tau }_m}$ denotes the leak factor for simulation time step dt and membrane time constant τ_m, w_lj denotes the weight of the synaptic connection from neuron j to l, $w_{jm}^{\text{IN}}$ denotes the strength of the connection between the input neuron m and neuron j, x_t denotes the external input spike at time t, and H denotes the Heaviside step function.

Following ref. 22, which implemented adaptive threshold LIF (ALIF) units (37) and observed that this neuron model improves computing capabilities of RSNNs relative to networks with LIF neurons only, we also include ALIF cells in our model. In addition to the membrane potential, ALIF cells have a second hidden variable, b_t, governing the adaptive threshold. The spiking dynamics of both LIF and ALIF cells can be characterized by the following set of equations:

$$s_{j,t+1}=\eta \hspace{0.17em}{s}_{j,t}+(1-\eta )({\displaystyle \sum _{l\ne j}{w}_{jl}}\hspace{0.17em}{z}_{l,t}+{\displaystyle \sum _p{w}_{jm}^{\text{IN}}}\hspace{0.17em}{x}_{m,t+1})-z_{j,t}\hspace{0.17em}{v}_{\text{th}},$$ [3]

$$z_{j,t}=H(s_{j,t}-A_{j,t}),$$ [4]

$$A_{j,t}=v_{\text{th}}+\beta b_{j,t},$$ [5]

$$b_{j,t}=\rho b_{j,t-1}+(1-\rho )z_{j,t-1},$$ [6]

where the voltage dynamics in Eq. 3 is the same as Eq. 2. A spike is generated when the voltage $s_{j,t}$ exceeds the dynamic threshold $A_{j,t}$. Parameter β controls how much adaptation affects the threshold, and state $b_{j,t}$ denotes the variable component of the dynamic threshold. The decay factor ρ is given by $e^{-dt/{\tau }_b}$ for simulation time step dt and adaptation time constant τ_b, which is typically chosen on the behavioral task time scale. For regular LIF neurons without adaptive threshold, one can simply set β = 0.

Network output and loss function.

Dynamics of leaky, graded readout neurons is implemented as

$$y_{k,t}=\kappa \hspace{0.17em}{y}_{k,t-1}+(1-\kappa ){\displaystyle \sum _j{w}_{kj}^{\text{OUT}}}{z}_{j,t}+b_k^{\text{OUT}},$$ [7]

where $w_{kj}^{\text{OUT}}$ denotes the strength of the connection from neuron j to output neuron k, $b_k^{\text{OUT}}$ denotes the bias of the k-th output neuron, $\kappa \in (0,1)$ defines the leak, and $\kappa =e^{-dt/{\tau }_{\mathit{OUT}}}$ for output membrane time constant τ_OUT.

We quantify how well the network output matches the desired target using error function E:

$$E=\{\begin{array}{l}\frac{1}{2}{\displaystyle \sum _{k,t}{(y_{k,t}^{*}-y_{k,t})}^2},\text{for} \text{regression} \text{tasks}\hfill \\ -{\displaystyle \sum _{k,t}{\pi }_{k,t}^{*}}log{\pi }_{k,t},\text{for} \text{classification} \text{tasks}\hfill \end{array}\text{},$$ [8]

where $y_{k,t}^{*}$ is the time-dependent target, ${\pi }_{k,t}^{*}$ is the one-hot encoded target, and ${\pi }_{k,t}={\text{softmax}}_k(y_{1,t},\dots ,y_{N_{\mathit{OUT}},t})=\exp (y_{k,t})/{\displaystyle {\sum }_{k\prime }\exp }(y_{k\prime ,t})$ is the predicted category probability. We provide all simulation and training parameters in SI Appendix, Note 3.

While the tasks involving time-delayed rewards studied in this manuscript can be labeled as regression and classification tasks due to the nature of the objective function, we note that the theoretical development is general and applies to all loss functions whose partial derivative with respect to spiking activity can be expressed as

$$\frac{\partial E}{\partial z_{j,t}}={\displaystyle \sum _{t\prime \ge t}{\kappa }^{t\prime -t}}{\varphi }_{j,t\prime }.$$ [9]

As an important example, our derivation is immediately applicable to the actor–critic reinforcement learning framework (22). For the regression task,

$${\varphi }_{j,t\prime }=(1-\kappa ){\displaystyle \sum _k(y_{k,t\prime }-y_{k,t\prime }^{*})}{w}_{kj}^{\text{OUT}},$$ [10]

and for the classification task,

$${\varphi }_{j,t\prime }=(1-\kappa ){\displaystyle \sum _k{\pi }_{k,t\prime }^{*}}{\pi }_{k,t\prime }{\displaystyle \sum _{k\prime }(w_{k\prime j}^{\text{OUT}}-w_{kj}^{\text{OUT}})\exp (y_{k\prime ,t\prime }-y_{k,t\prime })}.$$ [11]

One can see that when the leak κ is not zero, the error derivative will depend on future errors, which seemingly poses an obstacle to online learning. We provide the online implementation for this readout convention in SI Appendix, Note 1. In addition to accuracy optimization described above, we added a firing-rate regularization term $E_{\mathit{reg}}=\frac{1}{2}{c}_{\text{reg}}{\displaystyle {\sum }_j{(f_j^{\text{av}}-f_j^{\text{target}})}^2}$ to the loss function to ensure sparse firing (22). Here, $f_j^{\text{target}}$ and $f_j^{\text{av}}=\frac{1}{T}{\displaystyle {\sum }_t{z}_{j,t}}$ are the desired and actual average firing rate for cell j, respectively, and $c_{\text{reg}}$ is a positive coefficient that controls the strength of the regularization.

Notation for derivatives.

There are two types of computational dependencies in RSNNs: direct and indirect dependencies. For example, variable w_pq can impact state $s_{p,t}$ directly through Eq. 2, as well as indirectly via its influence through other cells in the network. We distinguish direct dependencies vs. all dependencies (including indirect ones) using partial derivatives ($\partial$) vs. total derivatives (d).

Gradient descent learning in RSNNs.

We study iterative adjustment of all synaptic weights (input weights w^IN, recurrent weights w, and output weights w^OUT) using gradient descent on loss E:

$$\begin{array}{l}{w}_{pq,\text{new}}=w_{pq,\text{old}}-\lambda \mathrm{\Delta }{w}_{pq},\\ \mathrm{\Delta }{w}_{pq}=\frac{\text{d}E}{\text{d}{w}_{pq,\text{old}}},\end{array}$$ [12]

where λ denotes the learning rate, and the gradient of the error with respect to the synaptic weights must be calculated. This error gradient can be calculated with classical machine-learning algorithms, BPTT and RTRL, by unwrapping the RSNN dynamics over time (Fig. 6B). While these two algorithms yield equivalent results, their bookkeeping for chain rule differs. Gradient calculations in BPTT depend on future activity, which poses an obstacle for online learning and biological plausibility. Our learning-rule derivation follows the RTRL factorization because it is causal. Therefore, we focus our analysis on RTRL and factor the error gradient across time and space as

$$\frac{\text{d}E}{\text{d}{w}_{pq}}={\displaystyle \sum _{j,t}\frac{\partial E}{\partial z_{j,t}}}\frac{\text{d}{z}_{j,t}}{\text{d}{w}_{pq}},$$ [13]

$$\frac{\text{d}{z}_{j,t}}{\text{d}{w}_{pq}}=\frac{\partial z_{j,t}}{\partial s_{j,t}}\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}},$$ [14]

following the derivative notation explained above. The factor $\frac{\partial E}{\partial z_{j,t}}$ in Eq. 13 is related to the TD learning signal $L_{j,t}≔{\displaystyle {\sum }_k{w}_{kj}^{\mathit{OUT}}}(y_{k,t}-y_{k,t}^{*})$ (22). SI Appendix, Notes 1 and 2 show that the leak term of the output neurons makes these two terms different and derives an online implementation that uses $L_{j,t}$. We thus take TD learning signals to be cell-specific rather than global, which is justified in part by recent reports that dopamine signals (28, 29) and error-related neural firing (53) can be specific to a population of neurons (22). Moreover, approximating the sum in $L_{j,t}$ as in our main derivation below, following the argument on cognate receptors, or using the random feedback alignment theory (14) (on only the outgoing connections between spiking neurons and output units) suggest further biologically plausible implementations.

We now discuss the second factor in Eq. 13, i.e., $\frac{\text{d}{z}_{j,t}}{\text{d}{w}_{pq}}$. This is expanded into two factors in Eq. 14. The first factor, $h_{j,t}≔\frac{\partial z_{j,t}}{\partial s_{j,t}}$ is problematic to compute for spiking neurons due to the discontinuous step function H in Eq. 3, whose derivative is not defined at zero and is zero everywhere else. We overcome this issue by approximating the decay of the derivative using a piece-wise linear function (10, 22, 46, 54). Here, the pseudoderivative $h_{j,t}$ is defined as follows:

$$h_{j,t}=\frac{\text{d}{z}_{j,t}}{\text{d}{s}_{j,t}},$$ [15]

$$\approx \gamma \max \left(0,1-\mid \frac{s_{j,t}-A_{j,t}}{v_{\text{th}}}\mid \right).$$ [16]

The dampening factor γ (typically set to 0.3) dampens the increase of backpropagated errors in order to improve the stability of training very deep (unrolled) RSNNs (22). Throughout this study, neuronal firing displays refractoriness, where $h_{j,t}$ and $z_{j,t}$ are fixed at zero after each spike of neuron j (SI Appendix, Note 3).

Key problems that RTRL poses to biological plausibility and computational cost reside in the factor $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ that arises during the factorization of the gradient (Eqs. 13 and 14). The factor $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ keeps track of all direct and indirect dependencies of neuron state j on weight w_pq. In other words, this factor accounts for both the spatial and temporal dependencies in RSNNs: State dependencies across time t, as explained above, result from unwrapping the temporal dependencies illustrated in Fig. 6B; state dependencies across space, however, are due to the indirect dependencies (of all z_t on w and all $z_{t\prime }$ [$t\prime <t$]) arising from recurrent connections (Fig. 6C). These recurrent dependencies are all accounted for in the $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ factor, which can be obtained recursively as follows:

$$\begin{array}{l}\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}=\frac{\partial s_{j,t}}{\partial w_{pq}}+{\displaystyle \sum _l\frac{\partial s_{j,t}}{\partial s_{l,t-1}}}\frac{\text{d}{s}_{l,t-1}}{\text{d}{w}_{pq}}\\ =\frac{\partial s_{j,t}}{\partial w_{pq}}+\frac{\partial s_{j,t}}{\partial s_{j,t-1}}\frac{\text{d}{s}_{j,t-1}}{\text{d}{w}_{pq}}+\underset{\text{depends} \text{on} \text{all} \text{weights} w_{jl}}{\underbrace{{\displaystyle \sum _{l\ne j}{w}_{jl}}\frac{\partial z_{l,t-1}}{\partial s_{l,t-1}}\frac{\text{d}{s}_{l,t-1}}{\text{d}{w}_{pq}}}}.\end{array}$$ [17]

Thus, the factor $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ is a memory trace of all intercellular dependencies (Fig. 6 D, i) and requires $O(N^3)$ memory and $O(N^4)$ computations. This makes RTRL expensive to implement for large networks. Moreover, this last factor poses a serious problem for biological plausibility: It involves nonlocal terms, so that knowledge of all other weights in the network is required in order to update the weight w_pq.

To address this, Murray (21) and Bellec et al. (22) (e-prop) dropped the nonlocal terms so that the updates to weight w_pq would only depend on presynaptic and postsynaptic activity (Figs. 5B and 6 D, ii) and applied this truncation to train rate-based and spiking neural networks, respectively. While both works succeed in improving over previous biologically plausible learning rules, a significant performance gap with respect to the full BPTT/RTRL algorithms remains.

Derivation of multidigraph learning in RSNNs.

We continue from the previous section in giving a detailed derivation of our learning rule. To reveal a potential role for cell-type-based modulatory signals in synaptic plasticity as well as improve upon the aforementioned biologically plausible gradient descent approximations, we begin by partially restoring nonlocal dependencies between cells—those within one connection step. This is the “truncated” RTRL framework (Figs. 5D and 6 D, iii), and the memory trace term $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ becomes

$$\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}\approx \{\begin{array}{ll}\frac{\partial s_{j,t}}{\partial z_{p,t-1}}\frac{\partial z_{p,t-1}}{\partial s_{p,t-1}}\frac{\text{d}{s}_{p,t-1}}{\text{d}{w}_{pq}}=w_{jp}\frac{\partial z_{p,t-1}}{\partial s_{p,t-1}}\frac{\text{d}{s}_{p,t-1}}{\text{d}{w}_{pq}},\hfill & p\ne j\hfill \\ \frac{\partial s_{j,t}}{\partial w_{jq}}+\frac{\partial s_{j,t}}{\partial s_{j,t-1}}\frac{\text{d}{s}_{j,t-1}}{\text{d}{w}_{jq}},\hfill & p=j\hfill \end{array}.$$ [18]

Thus, when j = p, our truncation implements $\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}}\approx \frac{\partial s_{j,t}}{\partial w_{jq}}+\frac{\partial s_{j,t}}{\partial s_{j,t-1}}\frac{\text{d}{s}_{j,t-1}}{\text{d}{w}_{jq}}$, which coincides with e-prop. Eq. 18 adds the case when $p\ne j$, for which $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ was simply set to zero in e-prop. We note that the truncation in Eq. 18 resembles the n-step RTRL approximation recently proposed in ref. 8, known as SnAP-n, which stores $\frac{\text{d}{s}_{j,t}}{\text{d}{w}_{pq}}$ only for j such that parameter w_pq influences the activity of unit j within n time steps. The computations of SnAp-n converge to those of RTRL as n increases, resonating with our improved performance when more terms of the exact gradient are included. Our truncation in Eq. 18 is similar to SnAp-n with n = 2 with two differences: 1) We apply it to spiking neural networks, and 2) we drop the previous time step’s Jacobian term $\frac{\text{d}{s}_{j,t-1}}{\text{d}{w}_{pq}}$, which would necessitate the maintenance of a rank-three (“3-d”) tensor with costly storage demands ($O(N^3)$) and for which no known biological mechanisms exist. Thus, the truncation in Eq. 18 requires the maintenance of only a rank-two (“2-d”) tensor specific to synapse $p|q$, which can be realized via an ET, as we explain next.

By substituting Eq. 18 into Eqs. 13 and 14, we approximate the overall gradient as

$$\begin{array}{l}\widehat{\frac{\text{d}E}{\text{d}{w}_{pq}}}={\displaystyle \sum _t\left[\frac{\partial E}{\partial z_{p,t}}\frac{\partial z_{p,t}}{\partial s_{p,t}}\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}}+{\displaystyle \sum _{j\ne p}\frac{\partial E}{\partial z_{j,t}}}\frac{\partial z_{j,t}}{\partial s_{j,t}}{w}_{jp}\frac{\partial z_{p,t-1}}{\partial s_{p,t-1}}\frac{\text{d}{s}_{p,t-1}}{\text{d}{w}_{pq}}\right]}\\ ={\displaystyle \sum _t{L}_{p,t}}{e}_{pq,t}+\underset{≔\widehat{{\mathrm{\Gamma }}_{pq,t}}}{\underbrace{{\displaystyle \sum _j{a}_{j,t}}{w}_{jp}{e}_{pq,t-1}}},\end{array}$$ [19]

where $L_{p,t}≔\frac{\partial E}{\partial z_{p,t}}$ is the TD learning signal to cell p, $a_{j,t}$ (Eq. 24) denotes the activity-dependent modulatory signal emitted by neuron j at time t, and $e_{pq,t}$ (Eq. 25) is the ET maintained by postsynaptic cell p to keep a memory of the preceding activity of presynaptic cell q and postsynaptic cell p. In Eq. 19, the first term $L_{p,t}{e}_{pq,t}$ alone gives exactly the e-prop synaptic update rule. The second term, which we define as $\widehat{{\mathrm{\Gamma }}_{pq,t}}$, is a synaptically nonlocal term due to contributions from local modulatory signals. As seen in Eq. 19, our truncation requires maintaining a {p, q}-dependent double tensor (for $e_{pq,t}$) instead of a triple one, thereby reducing the memory cost of RTRL from $O(N^3)$ to $O(N^2)$.

Importantly, we observe that, for the update to synapse w_pq in Eq. 19, the terms that depend on cells j only appear under a sum. Therefore, the mechanism updating the synapse $p|q$ does not need to know the individual terms indexed by j. Rather, only their sum suffices.

While it is tempting to consider the first factors in $\widehat{{\mathrm{\Gamma }}_{pq,t}},\hspace{0.17em}{a}_{j,t}{w}_{jp}$, as the modulatory signal emitted by neuron j, the involvement of the synapse from neuron p via w_jp and a lack of known mechanisms in calculating this neuron-specific composite signal suggest that this is unlikely to be a biological solution. Instead, inspired by the cell-type–specific (rather than neuron-specific) affinities for peptidergic neuromodulation (30, 42), we propose to approximate the signaling gain w_jp in Eq. 19 by the average value w_αβ across its presynaptic and postsynaptic cell types. More specifically, when postsynaptic cell j belongs to type α and presynaptic cell p belongs to type β, we approximate neuron-specific weight w_jp with cell-type–specific gain $w_{\alpha \beta }=<w_{jp}{>}_{j\in \alpha ,p\in \beta }$. We hypothesize that w_αβ represents the affinity of the GPCRs expressed by cells of type β to the modulators secreted by cells of type α (Cell-type–specific receptor affinities).

Thus, the gradient estimate at time t due to our learning rule involves compounding ET with both TD and local modulatory signals, thereby recovering the general form introduced in Eq. 1:

$$\begin{array}{l}{\frac{\text{d}E}{\text{d}{w}_{pq}}\mid }_{t,\text{MDGL}}\approx L_{p,t}{e}_{pq,t}+{\mathrm{\Gamma }}_{pq,t},\\ {\mathrm{\Gamma }}_{pq,t}=\left({\displaystyle \sum _{\alpha \in C}{w}_{\alpha \beta }}{\displaystyle \sum _{j\in \alpha ,p\to j}{a}_{j,t}}\right)e_{pq,t-1},\end{array}$$ [20]

where neuron p is of type β, C denotes the set of neuronal cell types, $p\to j$ denotes that there is a synaptic connection from neuron p to j, and ${\mathrm{\Gamma }}_{pq,t}$ approximates the second term in Eq. 19 with cell-type–specific weight averages.

In summary, cell p receives local modulatory input $\mathit{Mod}.\mathit{inpu}{t}_p$ that gets combined with the ET (as per Eq. 20) in addition to synaptic input $\mathit{Syn}.\mathit{inpu}{t}_p$ (as per Eq. 2):

$$\mathit{Mod}.\mathit{inpu}{t}_p≔{\displaystyle \sum _{\alpha \in C}{w}_{\alpha \beta }}{\displaystyle \sum _{j\in \alpha ,p\to j}{a}_{j,t}},$$ [21]

$$\mathit{Syn}.\mathit{inpu}{t}_p≔{\displaystyle \sum _{l\ne p}{w}_{pl}}\hspace{0.17em}{z}_{l,t}+{\displaystyle \sum _p{w}_{pm}^{\text{IN}}}\hspace{0.17em}{x}_{m,t+1}.$$ [22]

It may be instructive to note the dichotomy in the functions of these two different inputs: The cell uses $\mathit{Mod}.\mathit{inpu}{t}_p$ to regulate its synaptic plasticity, but not to change its internal state, and it uses $\mathit{Syn}.\mathit{inpu}{t}_p$ to change its internal state, but not to regulate synaptic plasticity.

Hence, our update rule suggests an additive term to compute the plasticity update at synapse $p|q$ at time t, ${\mathrm{\Gamma }}_{pq,t}$, which calculates multiplicative contributions of the modulatory signal $a_{j,t}$ secreted by neuron j, the affinity of receptors of cell type β to ligands of type α, w_αβ, and the ET at the synapse $p|q,\hspace{0.17em}{e}_{pq,t}$. The following two sections explain how two main components of Γ, cell-type–specific signals and ET, can be implemented.

Cell-type–specific receptor affinities.

We explain cell-type–specific signaling implementation, notably, how type–specific receptor affinity w_αβ is defined. As introduced in our learning rule derivation, w_αβ is an approximation of gain w_jp (Eqs. 19 and 20), and we proposed to define w_αβ as the weight average across its presynaptic and postsynaptic cell types:

$$w_{jp}\approx \{\begin{array}{ll}{w}_{\alpha \beta },\hfill & p\to j\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array},$$ [23]

where $p\to j$ denotes that there is a synaptic connection from neuron p to j, motivated by the local diffusion assumption discussed in ref. 35, in which this type of signaling is registered only by local synaptic partners and therefore preserves the connectivity structure of w_jp. One obvious variant of this receptor-affinity definition is one with a different spatial extent, for which we examine the opposite extreme in Fig. 4 D–F, where modulatory signals diffuse to all cells in the network. More specifically, the signaling gain w_αβ is replaced by $w_{\alpha \beta }^{NL}=<w_{jp}{>}_{j\in \alpha ,p\in \beta }$, even for w_jp = 0 so that modulatory signals diffuse to all cells with the same strength in the network.

For a proof of concept, we implemented MDGL with modulatory types mapped to the two main cell classes; i.e., cell-type–specific signaling gain, $w_{\alpha \beta }=<w_{jp}{>}_{j\in \alpha ,p\in \beta }$ with $\alpha ,\beta \in \{E,I\}$. We demonstrate the effectiveness of this cell-type discretization by comparing its learning performance to the case without cell-type discretization ($w_{\alpha \beta }=w_{jp}$, i.e., each cell is its own type) and observed little difference in performance (SI Appendix, Fig. S9). On the other hand, increasing the number of modulatory types involved in the cell-type discretization could be key to realizing the potential of MDGL in more complicated tasks, suggesting an explanation for the observed diversity of cell types in the brain.

We implemented receptor affinities as weight averages across types, but how tightly coupled those modulatory gains and synaptic weights are is a subject for future investigation. SI Appendix, Fig. S7 explores the sensitivity of the learning performance to imprecise receptor affinities.

Activity-dependent modulatory emission implementation.

As introduced in Eq. 20, activity-dependent modulatory signal emitted by neuron j at time t, an important component of MDGL, is defined as

$$a_{j,t}=\frac{\partial E}{\partial z_{j,t}}\frac{\partial z_{j,t}}{\partial s_{j,t}}.$$ [24]

As defined, $a_{j,t}$ is a package of two components: $\frac{\partial E}{\partial z_{j,t}}$, which is referred to as the TD signal (22), and $h_{j,t}=\partial z_{j,t}/\partial s_{j,t}$, which is the pseudoderivative of spiking activity as a function of cell j’s membrane potential explained above. While Eq. 20 suggests an “online” implementation with the update at t, the factor $a_{j,t}$ cannot be calculated causally unless the output is not leaky. SI Appendix, Note 1 derives an online update for the more general case, which has the same form as Eq. 20.

ET implementation.

As introduced in Eq. 20, ET, another important component of MDGL, is defined as

$$e_{pq,t}≔\frac{\partial z_{p,t}}{\partial s_{p,t}}\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}},$$ [25]

$$\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}}=\frac{\partial s_{p,t}}{\partial w_{pq}}+\frac{\partial s_{p,t}}{\partial s_{p,t-1}}\frac{\text{d}{s}_{p,t-1}}{\text{d}{w}_{pq}},$$ [26]

where Eq. 26 follows directly from Eq. 18. $\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}}$ can be obtained recursively and is referred to as the eligibility vector (22). $e_{pq,t}$ keeps a fading memory of activity pertaining to presynaptic cell q and postsynaptic cell p. A discussion on interpreting ETs as derivatives can be found in ref. 22. Here, we briefly explain its implementation by expanding the factors in Eqs. 25 and 26 for both LIF and ALIF cells.

For LIF cells, there is no adaptive threshold, so the hidden state consists only of the membrane potential. Thus, we have factors $\frac{\partial z_{p,t}}{\partial s_{p,t}}=h_{p,t}$ with pseudoderivative $h_{p,t}$ defined in Eq. 15, $\frac{\partial s_{p,t}}{\partial w_{pq}}=z_{q,t-1}$ and $\frac{\partial s_{p,t+1}}{\partial s_{p,t}}=\eta -v_{\text{th}}{h}_{p,t}$ following Eq. 2.

For ALIF cells, there are two hidden variables, so the eligibility vector is now a two-dimensional vector $\frac{\text{d}{s}_{p,t}}{\text{d}{w}_{pq}}=[\frac{\text{d}{s}_{p,t}^v}{\text{d}{w}_{pq}},\frac{\text{d}{s}_{p,t}^b}{\text{d}{w}_{pq}}]\in {\mathrm{R}}^{2x1}$ pertaining to membrane potential $v_{p,t}$ and adaptive threshold state $b_{p,t}$. Following Eq. 3, one can obtain factors $\frac{\partial z_{p,t}}{\partial s_{p,t}}=[\frac{\partial z_{p,t}}{\partial v_{p,t}},\frac{\partial z_{p,t}}{\partial b_{p,t}}]$ $=[h_{p,t},-\beta h_{p,t}]\in {\mathrm{R}}^{1x2},\hspace{0.17em}\frac{\partial s_{p,t}}{\partial w_{pq}}=[z_{q,t-1},0]\in {\mathrm{R}}^{2x1}$, and $\frac{\partial s_{p,t}}{\partial s_{p,t-1}}$ is now a 2-by-2 matrix:

$$\begin{array}{l}\frac{\partial s_{p,t}}{\partial s_{p,t-1}}=\left[\begin{array}{cc}\frac{\partial v_{p,t}}{\partial v_{p,t-1}}& \frac{\partial v_{p,t}}{\partial b_{p,t-1}}\\ \frac{\partial b_{p,t}}{\partial v_{p,t-1}}& \frac{\partial b_{p,t}}{\partial b_{p,t-1}}\end{array}\right]\\ =\left[\begin{array}{cc}\eta -v_{\text{th}}{h}_{p,t}& v_{\text{th}}\beta h_{p,t}\\ (1-\rho )h_{p,t}& \rho -(1-\rho )\beta h_{p,t}\end{array}\right]\in {\mathrm{R}}^{2x2}.\end{array}$$ [27]

Thus, the ET $e_{pq,t}$ is scalar valued, regardless of the dimension of the eligibility vector.

Data Availability

Code for data generation and analysis is available in GitHub at https://github.com/Helena-Yuhan-Liu/MDGL-main.