Abstract.
Purpose
The coronary arteries are embedded in a layer of fat known as epicardial adipose tissue (EAT). The EAT influences the development of coronary artery disease (CAD), and increased EAT volume can be indicative of the presence and type of CAD. Identification of EAT using echocardiography is challenging and only sometimes feasible on the free wall of the right ventricle. We investigated the use of spectral analysis of the ultrasound radiofrequency (RF) backscatter for its potential to provide a more complete characterization of the EAT.
Approach
Autoregressive (AR) models facilitated analysis of the short-time signals and allowed tuning of the optimal order of the spectral estimation process. The spectra were normalized using a reference phantom and spectral features were computed from both normalized and non-normalized data. The features were used to train random forests for classification of EAT, myocardium, and blood.
Results
Using an AR order of 15 with the normalized data, a Monte Carlo cross validation yielded accuracies of 87.9% for EAT, 84.8% for myocardium, and 93.3% for blood in a database of 805 regions-of-interest. Youden’s index, the sum of sensitivity, and specificity minus 1 were 0.799, 0.755, and 0.933, respectively.
Conclusions
We demonstrated that spectral analysis of the raw RF signals may facilitate identification of the EAT when it may not otherwise be visible in traditional B-mode images.
Keywords: epicardial adipose tissue, spectral analysis, tissue characterization, radiofrequency signals, ultrasound
1. Introduction
Obesity is a major public health crisis and various studies have predicted an increase in obesity to over 85% of adults in the United States by 2030.1 Obesity is characterized by the accumulation of excess adipose tissue, which is often categorized into two main types: subcutaneous adipose tissue (SAT) and visceral adipose tissue (VAT). The SAT is the tissue accumulated immediately beneath the skin, whereas VAT is the adipose tissue around the internal organs. Studies have identified the relationship between VAT and the development of metabolic syndromes, such as insulin resistance, hypertension, diabetes, and dyslipidemia.2,3 The epicardial adipose tissue (EAT), a specific type of the VAT deposited around the heart, has been linked to the development of cardiovascular disease (CVD), coronary artery disease, increase in left ventricular (LV) mass, enlarged right ventricular cavity size, diabetes, insulin resistance, LV hypertrophy, and obstructive sleep apnea.4–11 EAT also interacts directly with the coronary arteries and the myocardium and affects cardiac function by secreting and diffusing adipokines into the walls of the heart and the arteries.12,13 Hence, the measurement of EAT deposition is paramount in understanding cardiovascular risk.
Cardiac computed tomography (CT) has proven useful in quantifying EAT4,14–19 but is associated with the delivery of radiation to patients. Magnetic resonance imaging (MRI) has also emerged as an effective imaging modality for identifying whole body fat and ectopic fat depots.20 Cardiac-specific cine-scan MRI protocols have also evolved and facilitated precise EAT assessment as a means to measure EAT volume at different phases of the cardiac cycle. However, MRI is expensive, and the analysis is time-consuming and cumbersome. Efforts to automate the analysis have helped reduce the burden and have improved the ability to measure EAT volume via MRI,21,22 but studies using MRI for assessment of EAT volume are limited to large research facilities or hospitals. Echocardiography has also been used to quantify EAT. The nominal method is to make a single user-defined linear thickness measurement on the free wall of the right ventricle (RV).23 The RV is typically chosen as the location for the thickness measurement because the EAT is sometimes visible in traditional parasternal short and long axis views.2,3,23,24 The linear thickness measurements can be indicative of cardiac function and risk,2,3,24–26 but provide no information on the overall volume, the change in volume over time, or the distribution of the fat across the myocardial surface. In addition, the layer of fat is often difficult to identify and visualize in traditional B-mode ultrasound images.26
However, radiofrequency (RF) backscatter data have been shown to relate to tissue microstructural properties, such as scatterer size and concentration.27,28 Studies have investigated the potential of the spectral analysis of RF signals in tissue characterization in a wide range of other applications. It has been shown to reduce the subjectivity associated with diagnosing fatty liver disease.29 In previous work in our lab, spectral analysis aided in identifying tissue types in the intercostal space.30,31 It has also been used in several different cardiovascular applications, including coronary plaque characterization,32–35 carotid plaque characterization,36 and differentiating myocardial viability.37,38 Traditionally, these studies use Fourier-based techniques to compute the power spectral density (PSD) of the ultrasound backscatter data.27,28,34,35 However, the Fourier-based techniques are subject to the limitations of the Fourier transform in its use for spectral estimation, including a lack of resolution and spectral leakage. These weaknesses make Fourier-based techniques ill-equipped for spectral estimation with short-time stochastic data. Autoregressive (AR) models are known to provide a better estimate of the PSD for short-time data,30–32,39 making them potentially well-suited to identifying the thin layer of EAT that is often challenging to locate in the traditional B-mode images. In addition, the order of the AR models used can be tuned for the application. This process is known as regularization and helps to ensure stability of the system by increasing the signal-to-noise ratio.32 An order too large for the process being modeled will result in too much noise included in the estimate, but an order too small will result in an inadequate representation of the frequency content of the process. The intent of this study was to investigate the feasibility of using AR-based spectral analysis of the raw RF signals to differentiate EAT, myocardium, and blood.
This preliminary study was conducted to investigate whether the spectral content would have the potential to provide information beyond the gray-scale B-mode image data for segmentation of the images, including the endocardial contour outlining the left ventricle, the epicardial contour on the outside of the left myocardium, a contour outlining the right myocardium, and the fat. Our goal is to leverage the spectral analysis to locate fat around the surface of the heart when it is not obviously visible in the standard B-mode image. Differentiating fat from muscle using the classification scheme presented would allow the identification of the presence and thickness of the fat around the outside surface of the heart. In addition, the differentiation of the blood and muscle can be used to assist the segmentation of the left myocardium and left ventricle. In this manner, a successful classification scheme can be used as a foundation to build more automated analysis algorithms to characterize EAT volume and distribution. Using echocardiography alone would be a more cost-effective and portable solution than traditional volumetric imaging modalities.
2. Materials and Methods
2.1. Ultrasound Data Acquisition
The study involved 26 physically inactive but healthy volunteer female subjects, all between the ages of 18 and 40 with body mass index ranging from 30 to . The study was approved by the Institutional Review Board at Southern Illinois University Edwardsville (SIUE). The participants were required to provide informed consent and have no known metabolic and/or CVDs. This initial pilot study targeted females specifically because previous studies have found that women tend to have larger EAT depots than men.40,41
The echocardiography data were acquired using a Mindray Zonare ZS3 machine (Mindray Zonare North America, Mountain View, California), enabled for RF signal acquisition, and a P4-1c phased array transducer. Each participant was imaged using six different views of the heart, including a parasternal long-axis view, parasternal short-axis (PSAX) views of the mitral valve, papillary muscles, and near the apex, a subcostal view, and an apical view. Each view of the heart was imaged twice resulting in 12 B-mode image loops per participant. The RF data required for the calculation of the spectral parameters were simultaneously obtained from the machine during B-mode imaging. It was acquired for all six different views for each participant. The data were acquired with the transducer operating at 3.5 MHz using harmonic image acquisition and default transmit and receive characteristics. The mechanical index (MI) was 1.5 and the thermal index for soft tissue (TIs) was 0.5. Gain and TGC curves were adjusted for optimal image review but were not reflected in the recorded raw RF data. For parasternal long and short axis views, image data were acquired at a depth of 16 and 10 cm. For apical views and the subcostal view, image data were acquired with a depth of 20 cm. The raw data for this study, post-beam-formation, were stored onto a separate acquisition system during the imaging sessions. The acquisition system operated a Linux terminal that issues the acquisition commands to the Zonare ultrasound system, and the data were later retrieved for processing.
2.2. Region-of-Interest Selection
Custom Python software was written to reconstruct the gray-scale B-mode images from the raw data acquired for each view for each subject. The gray-scale images contained 201 A-lines whereas the number of samples depended on the depth of each image. From the reconstructed images, regions-of-interest (ROIs) that target EAT, myocardium, and blood were manually selected in the software. A screen shot of the custom Python-based software for ROI selection is shown in Fig. 1. The importance of identifying the reference labels for training the machine learning algorithm necessitated the application of user-expertise to the process of ROI selection. In addition, the motion associated with playing the video-loops recorded on the Zonare system make the relevant tissue types much more identifiable. Therefore, the recorded loops were always used as reference when selecting the small ROIs.
Fig. 1.
A screen capture of custom Python-based program for ROI selection and review is shown. Seven example ROIs are illustrated in both the rectangular format image created from the raw signals (left) and the scan-converted image (right). Red is used for ROIs labeled as fat, blue is used for muscle, and green is used for blood. The dashed line represents the location of the A-line shown in Fig. 2.
The raw data were processed on a line-by-line basis, including envelope detection, log compression, master gain and time-gain-compensation, and dynamic range clipping. The image frames in the recorded loop were presented in both native rectangular format and in their traditional B-mode scan-converted format (see Fig. 1). While using the recorded video-loop on the Zonare system as reference, the user reviewed the reconstructed images in the user interface. Each image loop contained 80 reconstructed images. The user identified image frames from the loop where small homogeneous regions could be located with high confidence. The specific ROIs for fat, muscle, or blood where then selected by clicking the top-left and bottom-right corners of an ROI in the rectangular, non-scan-converted image. A total of 805 ROIs were identified, including 271 ROIs for EAT, 332 ROIs for myocardium, and 202 ROIs for blood. The ROIs were selected only in areas on the images with a known tissue type with high confidence and therefore the sizes depended on the thickness of that tissue type. The segments of the A-lines corresponding to the ROIs were extracted from the raw data for further processing. In each of the rectangular ROIs, the columns correspond to the A-lines of the transducer, whereas the rows represent the sample depth in the ROI. In the raw data, the ROIs are therefore rectangular, but in the geometry of the scan-converted B-mode images, the ROIs have a sector shape dependent on the size of the ROI selected. An example A-line, corresponding to the location marked by the dashed line in Fig. 1, is shown in Fig. 2.
Fig. 2.
An example RF signal is shown, with color-coded vertical lines indicating the starting and stopping sample for three of the example ROIs shown in Fig. 1. The location of this A-line in the B-mode image in Fig. 1 is indicated with the white dashed line.
2.3. Spectral Analysis
The scan lines extracted from the ROIs were analyzed using custom MATLAB® software. An example A-line that traverses through three identified ROIs, one of each tissue type, is shown in Fig. 2. Its location is shown in both the rectangular image and the scan converted image in the screen shot in Fig. 1. The example ROI locations in that specific A-line are also noted, with color-coded vertical lines indicating the start and stop samples of the ROI in the RF signal.
The spectral features were computed from the frequency spectrum of the short signal-segments extracted from the ROIs. An AR model of a random process is shown as
| (1) |
where is the AR order, are the AR coefficients, and is a white noise random process. The present value is represented as a weighted sum of past values, where the weights are the AR coefficients. The input is modeled as white noise () that has variance . The PSD of the all-pole AR model can be estimated as shown
| (2) |
where PSD is the power spectral density as a function of frequency (), is the variance of the white noise, and are AR coefficients, and is the AR order of the model.
2.4. AR Order Estimation
When using the AR-based approach, the variance of the noise is equal to the modeling error in the spectral estimate, given as
| (3) |
where is the AR order, is the mean squared error (MSE) as a function of order, is the number of samples used for analysis, are the data samples, and are the samples predicted by the model. For ultrasound applications where there is diffuse scattering from heterogeneous tissue, some of the noise introduced by the increasing order of the AR model may provide information to the tissue characterization.42–44 The noise in this case refers to the component of the echo from the randomly unresolvable scatterers which may still provide information on the tissue microstructure. An optimal range of AR orders may exist that allows some of this “noise” to be included in the tissue characterization but not so much that the noise dominates.43
Several methods exist to estimate the appropriate order, including Akaike’s information criterion (AIC), final prediction error (FPE), and the minimum description length (MDL).30,32,45 Each is a function of the MSE but includes a mechanism for penalizing increasing order. They are shown in Eqs. (4)–(6):
| (4) |
| (5) |
| (6) |
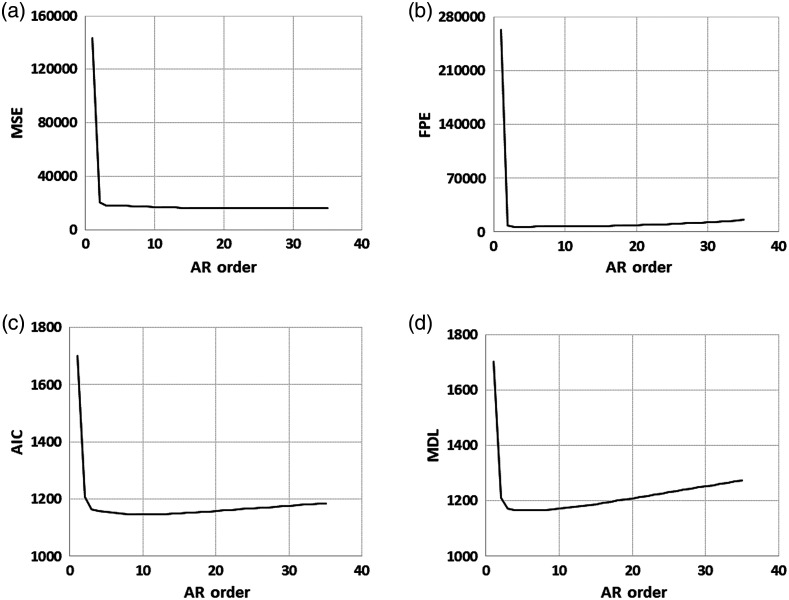
where is the AR order, is the error as a function of order, and is the number of samples used for analysis. This approach was used to determine a range of AR orders to evaluate. The mean of the cost functions across each set of ROIs versus AR order is shown in Fig. 3, with MSE in Fig. 3(a), AIC in Fig. 3(b), FPE in Fig. 3(c), and MDL in Fig. 3(d). The smallest ROI had 36 samples, and since the order cannot be larger than the number of samples, the maximum order investigated was chosen to be 35. As shown in Fig. 3, the order penalty associated with FPE, AIC, and MDL appear to only modestly increase after the initial drop in MSE. The smallest ROI has 36 samples, and the AR-model can only be computed with an order up to one less than the number of samples. Therefore, a range of orders that accommodated the initial drop in MSE and did not accrue significant order penalty was chosen and orders 5 to 35 (in increments of 5) were investigated. A previous preliminary study demonstrated early feasibility with features derived from the unnormalized power spectrum and used them to classify three cardiac tissue types: fat, muscle, and blood.46 The study presented here included an investigation of optimal AR order and significantly expanded the number of ROIs available for analysis. In addition, this study also included collection of reference data from a tissue-mimicking phantom (Model 040GSE, CIRS, Inc., Norfolk, Virginia, -MHz side), which was used to compensate for attenuation, diffraction, and the transmit and receive characteristics of the system. The depth and size of each ROI was used to obtain an ROI of the same depth and size from the data collected using the calibrated phantom. The spectra were calculated and averaged in the same way as with the tissue ROI data, resulting in one average PSD per ROI. The normalized PSD for each ROI was calculated by subtracting the reference phantom PSD of the same depth and size.
Fig. 3.
Plots of the AR order range assessment. (a) MSE. (b) AIC. (c) FPE. (d) MDL. The MSE is significantly reduced by order 3 and the penalty associated with order in AIC, FPE, and MDL only modestly increases to order 35, the upper limit based on the smallest ROI. Based on this data, an order range of 5 to 35 was chosen for assessment.
2.5. Classification Experiments
A regression line was fit to the normalized PSD and several spectral parameters were computed based on both the regression line and the normalized PSD. They included: (1) maximum power (dB), (2) frequency of maximum power (MHz), (3) mean power (dB), (4) slope in dB/MHz of the regression line, (5) -intercept of the regression line (dB), (6) mid-band power (dB) (based on 20-dB bandwidth of unnormalized PSD), (7) mid-band frequency (MHz), (8) the depth of the ROI (cm), and (9) integrated backscatter (dB). These normalized spectral features have been used in previous studies to characterize tissue types47 and were selected here as the primary set of features.
The preliminary feasibility study suggested that using the 20-dB bandwidth had the most promise.46 Therefore, the 20-dB bandwidth was used for computation of the spectral features in the current study. Example PSDs and their corresponding lines used for the slope and -intercept spectral feature calculation are shown in Fig. 4.
Fig. 4.
Diagram illustrating normalized and unnormalized spectra with spectral parameters indicated where possible. The unnormalized spectra is shown in gray, phantom spectra in dashed-gray, and normalized spectra in black. The line fit to the PSD data and used for calculation of the slope and -intercept is also shown, as indicated in the legend. Example spectral parameters are indicated where possible: (1) maximum power (dB), (2) frequency of maximum power (MHz), (3) mean power (dB), (4) slope in dB/MHz, (5) -intercept (dB), (6) mid-band power (dB), (7) mid-band frequency (MHz), (8) the depth of the ROI (cm) (not shown), and (9) integrated backscatter (dB) (not shown).
Previous studies have indicated that random forests have worked well for applications in ultrasound tissue characterization.30–32,46,47 In addition, the use of random forests facilitates insights into the predictive power of individual features and were therefore chosen for this study. The forests are built using classification trees, a process where data are partitioned repeatedly until a sample is identified as belonging to a particular class. Each tree starts with a subset of the features, typically the square root of the number of total features. In this study, nine spectral features were used for the normalized data so three randomly selected features were used at each node of each classification tree in the random forest. The data are evaluated for possible partitions at each node based on the split resulting in the largest decrease of Gini impurity.48 The branch nodes are repeatedly split into left and right children nodes using the chosen split criterion until no further splits are possible. The last node is known as the leaf node and indicates the class. An unknown sample would be evaluated for each split criterion and navigated through the branch nodes until it reached a leaf node that indicated the class of the sample. The final prediction of a random forest is the majority vote of all the trees in the forest.49
In the training process for a random forest, a subset of random samples is chosen to create one of the classification trees. The samples that are not chosen for the subsample are called the “out-of-bag” (OOB) samples. The error in prediction for these OOB samples is called the OOB error and can be used to optimize parameters to be used for the classification. In this study, the OOB error was computed for an increasing number of trees used in the random forest. More trees will begin to minimize error, but a plateau will be reached. Beyond the plateau, additional trees included in the random forest only increase computational cost and do not decrease error. An example plot of the OOB error versus the number of trees for one of the random forests is shown in Fig. 5. Based on the beginning of the plateau in the plot, 30 classification trees were chosen as the nominal value for each random forest built. The OOB error was also used to compare the predictive importance of the spectral parameters. In a classification tree, if a feature is not important, permuting the values of that feature within the data will not impact the prediction accuracy. The OOB error is calculated before and after permuting the data for each feature and the difference between OOB errors is averaged across all trees in the forest. This results in a relative predictive importance for each feature. Assessment of classification techniques or machine learning algorithms typically involves the random separation of the data into training and test sets. However, rather than using a single randomized split into training and test data, a more robust validation approach called Monte Carlo cross-validation (MCCV) strategy was adopted. It involves repeated randomizations into training and test sets containing 75% and 25% of the data, respectively. A new random forest is built using each set of training data and tested with the corresponding test data for that randomization. For each of those random forests, accuracy (), sensitivity (), and specificity () were calculated as follows:
| (7) |
| (8) |
| (9) |
Youden’s index (), a metric that takes both sensitivity and specificity into account, was also calculated for each MCCV randomized sample.
Fig. 5.
Example plot of OOB error versus number of trees. The beginning of the plateau is reached by classification trees in the random forest. Therefore, 30 trees were used in the random forests presented in this study.
An additional question associated with this study was whether the ability to differentiate tissue types would be robust to the size of the ROIs available. Using an AR model for PSD estimation is better for short-time data compared with more traditional Fourier-based methods that assume infinite periodic signals. The layer of cardiac fat and the associated ROIs can be thin with only short snippets of the A-lines included. To understand whether AR-based PSD estimation improved the results for this application with short-time data, comparisons were made between classification results using PSDs computed with the Fourier transform, Welch’s periodogram, and the proposed AR-model.
3. Results
The accuracy for each order is shown in Fig. 6(a) and YI for each order is shown in Fig. 6(b). The mean accuracy and YI values are plotted with error bars indicating the standard deviation from the 1000-run MCCV. The classification for blood had mean accuracies above 0.929 with standard deviations all below 0.022. Fat and muscle could also be distinguished with accuracy above 0.871 for fat and 0.839 for muscle. Standard deviations from the MCCV for fat and muscle were below 0.088 and 0.024, respectively.
Fig. 6.
Plots of mean () accuracy and Youden’s Index (YI) versus AR order. YI is shown in (a) and accuracy is shown in (b). The accuracy and YI suggest an AR order of 15-20 may be most appropriate for this application and an order of 15 was chosen.
YI is a combined metric that incorporates both sensitivity and specificity, making it more stringent than accuracy alone. The mean YI values for blood were above 0.824 with standard deviations below 0.061. Fat and muscle mean YI values were all above 0.716 and 0.663 with standard deviations below 0.088 and 0.061, respectively. The plots of accuracy and YI versus AR order also provide insights into the best order to use for the PSD estimation in this application. There is a small increase in accuracy with an order of 20, but the increase in YI at the order of 15 is more pronounced. The standard deviations are larger in the YI data, but given that the increase is larger and YI is a more stringent metric than accuracy alone, an order of 15 was chosen for the comparisons between AR-based PSD estimation and Fourier-based PSD estimation using the FFT and Welch’s periodogram (with 50% overlap).
The database of all 805 ROIs was rerun using the three PSD estimation techniques: a fast-Fourier-transform-based (FFT-based) PSD estimation (magnitude of FFT squared), Welch’s periodogram, and an AR model using order 15. The accuracy and YI from each are shown in Fig. 7.
Fig. 7.
Plots of accuracy and YI for the FFT-based approach, Welch’s periodogram, and the AR model with order 15. The AR model had better accuracy and YI in (a) fat, (b) blood, and (c) muscle classification.
To provide insight into which tissue types may be misclassified as which other tissue types, an example confusion matrix is shown in Table 1. The rows are the known ROI tissue types of the test data, and the columns are the classification results.
Table 1.
Confusion matrices (representative for 20-dB bandwidth and order of 15) for classification of test data based on spectral parameters.
| Tissue type | Fat | Muscle | Blood |
|---|---|---|---|
| Fat | 58 | 6 | 7 |
| Muscle | 14 | 62 | 9 |
| Blood | 2 | 1 | 43 |
4. Discussion
The random forest classifiers implemented in this study demonstrate the feasibility of using spectral analysis of the raw ultrasound signals from echocardiography to differentiate tissue types, including the EAT. Figure 6 shows that the accuracies for EAT, myocardium, and blood ranged from 0.839 to 0.933, highlighting the general ability of this approach based on spectra computed via autoregressive (AR) models, normalized using a tissue-mimicking phantom, and classified via random forests to predict the correct tissue type from a small ROI.
4.1. AR Order Determination
In addition to general feasibility using ROIs of limited size, one additional objective of this study was the identification of an optimal order for the AR-based spectral analysis. To assess the effect of AR order on the classification, both the accuracy and the YI were calculated and compared. Accuracy is a standard metric regarding the number of correct predictions but can be misleading when there is an imbalance between classes.50 Sensitivity and specificity, both encompassed by YI, are also reported to supplement the comparison. Accuracy and YI were computed from the ROI data set, but random training-test splits of the data produce different accuracies and YI. To estimate the true accuracy and YI in the data set for the different tissue types, the MCCV approach, also known as repeated random subsampling validation, was adopted. Compared to -fold validation, MCCV explores many more possible training-test splits and has less variance, at the cost of more possible bias in the estimate. The random 75%/25% training-test split was repeated 1000 times and accuracy and YI were computed and recorded for each. These values were chosen to balance the bias/variance tradeoff.51,52 The results shown in Fig. 6, with mean () accuracy and YI plotted versus AR order, suggest that an order of to 20 is best for incorporating enough information from the random scattering process to provide accurate classification without the noise becoming dominant or using an unnecessarily high order. The YI values shown in Fig. 6(a) had larger standard deviations, but the improved classification at order 15 was more apparent and was therefore chosen for the comparison with FFT-based approaches.
4.2. Small Regions-of-Interest
The ROIs used in this study were short-time, with an average of only 104.1 RF samples. These short-time data were not expected to be well-suited for traditional Fourier-based spectral techniques, but a direct comparison was made in this study between three PSD estimation techniques, including the magnitude of the Fourier transform squared (basic periodogram), Welch’s periodogram with 50% overlap, and an AR model with order 15. The results shown in Fig. 7 demonstrate that the AR model was superior to the Fourier-based approaches for both accuracy and YI in all three tissue types. In addition, the accuracy for fat, muscle, and blood using the AR model were 0.913, 0.818, and 0.814, respectively, suggesting that the three tissue types can be differentiated accurately even with very short signals from thin regions of tissue. Investigating the feasibility of using spectral parameters to help differentiate fat from muscle was a major goal in this study. The layer of fat along the myocardium can be thin and is not often visible in traditional B-mode images. The accuracy in differentiating fat from muscle with very small ROIs, as shown by the data, suggests that spectral features can be used to help find fat when it is not obviously visible in the regular images.
4.3. Predictor Importance
One advantage of the random forest algorithm is that predictive power of the feature set can be explicitly investigated. Figure 8 shows a comparison of relative predictive importance for an example random forest built using spectral parameters based on a normalized PSD using an AR order of 15. The relative comparison of the Y-intercept and the slope parameter with the power-based parameters confirms that the frequency content is relevant and supports the idea that there is more to distinguishing these tissues than simply the reflected intensity. More specifically, as shown in Fig. 8, the quantitative importance assessment yielded a value of 0.163 for the maximum power parameter and a value of 0.127 and 0.043 for the -intercept and slope parameters, respectively. While not equivalent to the predictive power of the most important power-based parameter, the -intercept and slope register values that are 77.9% (0.127/0.163) and 26.4% (0.043/0.163) of that of the maximum power, suggesting that spectral analysis can play a relevant role in differentiating the tissue types. These results are another example outcome that confirms the early theoretical framework of ultrasound tissue characterization relating specific spectral parameters to specific characteristics of the tissue microstructure, including the size and density of scatterers.27,28,53,54 Much effort in the use of machine learning goes into “feature engineering,” which, in this case, may correspond to the idea that the features that have the most predictive power are those connected to the physical tissue microstructure. Leveraging the spectral analysis, combined with a random forest, is particularly important in this application because the EAT is often difficult to visualize in traditional B-mode echocardiographic images created only utilizing the reflected intensity, even when it can be visualized and quantified with cardiac MRI. Figure 9 shows an example image comparison of a PSAX echocardiogram [Fig. 9(a)] and the corresponding cardiac MRI image [Fig. 9(b)] from approximately the same location from the same volunteer subject. The yellow arrow indicates the location of fat on the free wall of the right ventricle, which is typically visible in the ultrasound. However, the orange arrow indicates the location of fat that is common in the interventricular sulci. Fat in this area is visible in the MRI but is not distinguishable in the ultrasound. Leveraging the underlying spectral parameters may be a viable method for locating and quantifying the EAT in the ultrasound when it is not otherwise visible.
Fig. 8.
Relative predictive importance for one example random forest using the 20-dB bandwidth and spectral parameters from the normalized PSD. The difference between OOB error before and after permuting the individual feature is used to compute the relative importance, providing indication of the relative value of the specific parameter in the classification.
Fig. 9.

(a) Example short axis cardiac magnetic resonance image and (b) corresponding parasternal short axis echocardiogram. The images are from the same volunteer subject and have been cropped and rotated for approximate alignment. The yellow arrow shows fat on the free wall of the right ventricle, which can often be seen in the ultrasound. The orange arrow shows fat in the interventricular sulci, which is generally not distinguishable.
4.4. Limitations
Several limitations of the study are noteworthy and can be improved upon. The ROIs were chosen based solely on visual inspection, and the success of the tissue type identification is based on the initial confidence of the user-defined ROIs. The intent of the current preliminary study was to prove feasibility while relying on manual ROI selection, but future work will pursue leveraging the corresponding cardiac MRI as a systematic reference for the location of EAT. In addition, there was no distinction among ROIs with respect to which view they were selected from. It is therefore not known how the different echocardiographic views may affect the tissue characterization. No attempt was made at assessing the different cardiac adipose tissue types either. The cardiac fat is generally split into two classes based on its location with respect to the pericardium—that on the inside of the visceral pericardium is generally referred to as epicardial adipose tissue and that between the visceral and parietal pericardium is generally referred to as paracardial adipose tissue. While MRI and CT can sometimes differentiate them, it is substantially more challenging with ultrasound. Therefore, the two potentially distinct cardiac adipose tissue types were treated as one in this study and referred to as a more general EAT. While the results from this study convey the ability of spectral analysis to differentiate the general EAT, no investigation of generating tissue maps was presented. The use of the spectral analysis algorithm in producing more general segmentation strategies for the EAT targeted at generating tissue maps will be a major focus of our work moving forward.
4.5. Conclusions
Data were presented suggesting that spectral parameters derived from the frequency content of raw ultrasound signals can adequately differentiate three cardiac tissue types, including EAT, myocardium, and blood. The use of AR models allowed proper accommodation of very short-time signals. Random forests built with the spectral parameters based on normalized PSDs yielded classification of the tissue types with accuracy ranging from 83.9% to 94.1% and YI ranging from 0.663 to 0.875. Results from this study suggest that spectral analysis of the underlying raw ultrasound signals may make identification of EAT feasible more often and across more of the surface of the heart than would otherwise be possible in traditional B-mode images.
Acknowledgments
This study was supported by an American Heart Association Institutional Research Enhancement Award (17AIREA33670361).
Biographies
Jon D. Klingensmith is an associate professor in the Department of Electrical and Computer Engineering at Southern Illinois University Edwardsville. He received his PhD in biomedical engineering from Case Western Reserve University in 2003. He was project staff at the Cleveland Clinic Foundation from 2003 to 2004 and held various positions in R&D at Volcano Corporation from 2004 to 2012. His current research interests include cardiovascular imaging, 3D medical image analysis, and ultrasonic tissue characterization.
Akhila Karlapalem is a radio frequency software integration and test engineer at Qualcomm Inc. She received her master’s degree in electrical and computer engineering from Southern Illinois University Edwardsville in 2018.
Michaela M. Kulasekara is an engineer at Leonardo DRS, but finished her MS degree in the Department of Electrical and Computer Engineering at Southern Illinois University Edwardsville in 2021. Her current research interests include machine learning with biomedical imaging applications.
Maria Fernandez-del-Valle is an assistant professor in the Faculty of Health Sciences at Universidad Isabel I in Spain. She received her PhD in clinical exercise physiology from the Universidad Europea de Madrid in 2012. She developed her independent research while at Texas Tech University and Southern Illinois University Edwardsville from 2012 to 2021. Her research interests include exercise prescription in chronic pathologies with a focus on understanding the effects of interventions on biomarkers and physical and mental health.
Disclosures
The authors have no conflicts of interest relating to this article.
Contributor Information
Jon D. Klingensmith, Email: jokling@siue.edu.
Akhila Karlapalem, Email: karlapalemakhila@gmail.com.
Michaela M. Kulasekara, Email: mkulase@siue.edu.
Maria Fernandez-del-Valle, Email: marfern@siue.edu.
References
- 1.Hruby A., Hu F. B., “The epidemiology of obesity: a big picture,” Pharmacoeconomics 33(7), 673–689 (2015). 10.1007/s40273-014-0243-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Iacobellis G., et al. , “Epicardial fat from echocardiography: a new method for visceral adipose tissue prediction,” Obes. Res. 11(2), 304–310 (2003). 10.1038/oby.2003.45 [DOI] [PubMed] [Google Scholar]
- 3.Iacobellis G., Corradi D., Sharma A. M., “Epicardial adipose tissue: anatomic, biomolecular and clinical relationships with the heart,” Nat. Clin. Pract. Cardiovasc. Med. 2(10), 536–543 (2005). 10.1038/ncpcardio0319 [DOI] [PubMed] [Google Scholar]
- 4.Alexopoulos N., et al. , “Epicardial adipose tissue and coronary artery plaque characteristics,” Atherosclerosis 210(1), 150–154 (2010). 10.1016/j.atherosclerosis.2009.11.020 [DOI] [PubMed] [Google Scholar]
- 5.Brinkley T. E., et al. , “Pericardial fat is associated with carotid stiffness in the Multi-Ethnic Study of Atherosclerosis,” Nutr. Metab. Cardiovasc. Dis. 21(5), 332–338 (2011). 10.1016/j.numecd.2009.10.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Iacobellis G., “Epicardial fat: a new cardiovascular therapeutic target,” Curr. Opin. Pharmacol. 27, 13–18 (2016). 10.1016/j.coph.2016.01.004 [DOI] [PubMed] [Google Scholar]
- 7.Iacobellis G., “Relation of epicardial fat thickness to right ventricular cavity size in obese subjects,” Am. J. Cardiol. 104(11), 1601–1602 (2009). 10.1016/j.amjcard.2009.07.032 [DOI] [PubMed] [Google Scholar]
- 8.Iacobellis G., et al. , “Relation between epicardial adipose tissue and left ventricular mass,” Am. J. Cardiol. 94(8), 1084–1087 (2004). 10.1016/j.amjcard.2004.06.075 [DOI] [PubMed] [Google Scholar]
- 9.Iacobellis G., et al. , “Threshold values of high-risk echocardiographic epicardial fat thickness,” Obesity 16(4), 887–892 (2008). 10.1038/oby.2008.6 [DOI] [PubMed] [Google Scholar]
- 10.Lim S., Meigs J. B., “Ectopic fat and cardiometabolic and vascular risk,” Int. J. Cardiol. 169(3), 166–176 (2013). 10.1016/j.ijcard.2013.08.077 [DOI] [PubMed] [Google Scholar]
- 11.Parisi V., et al. , “Sleep-disordered breathing and epicardial adipose tissue in patients with heart failure,” Nutr. Metab. Cardiovasc. Dis. 28(2), 126–132 (2018). 10.1016/j.numecd.2017.09.012 [DOI] [PubMed] [Google Scholar]
- 12.Iacobellis G., Bianco A. C., “Epicardial adipose tissue: emerging physiological, pathophysiological and clinical features,” Trends Endocrinol. Metab. 22(11), 450–457 (2011). 10.1016/j.tem.2011.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ouchi N., et al. , “Adipokines in inflammation and metabolic disease,” Nat. Rev. Immunol. 11(2), 85–97 (2011). 10.1038/nri2921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cullu N., et al. , “Does epicardial adipose tissue volume provide information about the presence and localization of coronary artery disease?” Anatol. J. Cardiol. 15(5), 355–359 (2015). 10.5152/akd.2014.5431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mihl C., et al. , “Automated quantification of epicardial adipose tissue (EAT) in coronary CT angiography: comparison with manual assessment and correlation with coronary artery disease,” J. Cardiovasc. Comput. Tomogr. 8(3), 215–221 (2014). 10.1016/j.jcct.2014.04.003 [DOI] [PubMed] [Google Scholar]
- 16.Nakazato R., et al. , “Interscan reproducibility of computer-aided epicardial and thoracic fat measurement from noncontrast cardiac CT,” J. Cardiovasc. Comput. Tomogr. 5(3), 172–179 (2011). 10.1016/j.jcct.2011.03.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nikolaou K., et al. , “Advances in cardiac CT imaging: 64-slice scanner,” Int. J. Cardiovasc. Imaging 20(6), 535–540 (2004). 10.1007/s10554-004-7015-1 [DOI] [PubMed] [Google Scholar]
- 18.Rodrigues E. O., et al. , “Towards the automated segmentation of epicardial and mediastinal fats: a multi-manufacturer approach using intersubject registration and random forest,” in IEEE Int. Conf. Ind. Technol. (ICIT), pp. 1779–1785 (2015). 10.1109/ICIT.2015.7125355 [DOI] [Google Scholar]
- 19.Spearman J. V., et al. , “Automated quantification of epicardial adipose tissue using CT angiography: evaluation of a prototype software,” Eur. Radiol. 24(2), 519–526 (2014). 10.1007/s00330-013-3052-2 [DOI] [PubMed] [Google Scholar]
- 20.Thomas E. L., et al. , “Whole body fat: content and distribution,” Prog. Nucl. Magn. Reson. Spectrosc. 73, 56–80 (2013). 10.1016/j.pnmrs.2013.04.001 [DOI] [PubMed] [Google Scholar]
- 21.Cristobal-Huerta A., et al. , “Automated quantification of epicardial adipose tissue in cardiac magnetic resonance imaging,” in Int. Conf. IEEE Eng. Med. and Biol. Soc. (EMBC), pp, 7308–7311 (2015). 10.1109/EMBC.2015.7320079 [DOI] [PubMed] [Google Scholar]
- 22.Homsi R., et al. , “3D-Dixon MRI based volumetry of peri- and epicardial fat,” Int. J. Cardiovasc. Imaging 32(2), 291–299 (2016). 10.1007/s10554-015-0778-8 [DOI] [PubMed] [Google Scholar]
- 23.Iacobellis G., et al. , “Echocardiographic epicardial adipose tissue is related to anthropometric and clinical parameters of metabolic syndrome: a new indicator of cardiovascular risk,” J. Clin. Endocrinol. Metab. 88(11), 5163–5168 (2003). 10.1210/jc.2003-030698 [DOI] [PubMed] [Google Scholar]
- 24.Silaghi A., et al. , “Epicardial adipose tissue extent: relationship with age, body fat distribution, and coronaropathy,” Obesity 16(11), 2424–2430 (2008). 10.1038/oby.2008.379 [DOI] [PubMed] [Google Scholar]
- 25.Cetin M., et al. , “Effect of epicardial adipose tissue on diastolic functions and left atrial dimension in untreated hypertensive patients with normal systolic function,” J. Cardiol. 61(5), 359–364 (2013). [DOI] [PubMed] [Google Scholar]
- 26.Eroglu S., “How do we measure epicardial adipose tissue thickness by transthoracic echocardiography?” Anatol. J. Cardiol. 15(5), 416–419 (2015). 10.5152/akd.2015.5991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lizzi F. L., et al. , “Theoretical framework for spectrum analysis in ultrasonic tissue characterization,” J. Acoust. Soc. Am. 73(4), 1366–1373 (1983). 10.1121/1.389241 [DOI] [PubMed] [Google Scholar]
- 28.Lizzi F. L., et al. , “Relationship of ultrasonic spectral parameters to features of tissue microstructure,” IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 34(3), 319–329 (1987). 10.1109/T-UFFC.1987.26950 [DOI] [PubMed] [Google Scholar]
- 29.Acharya U. R., et al. , “Ultrasound-based tissue characterization and classification of fatty liver disease: a screening and diagnostic paradigm,” Knowl.-Based Syst. 75, 66–77 (2015). 10.1016/j.knosys.2014.11.021 [DOI] [Google Scholar]
- 30.Klingensmith J. D., et al. , “Spectral analysis of ultrasound radiofrequency backscatter for the detection of intercostal blood vessels,” Ultrasound Med. Biol. 44(7), 1411–1422 (2018). 10.1016/j.ultrasmedbio.2018.03.007 [DOI] [PubMed] [Google Scholar]
- 31.Klingensmith J. D., et al. , “Tissue classification in intercostal and paravertebral ultrasound using spectral analysis of radiofrequency backscatter,” J. Med. Imaging 6(4), 047001 (2019). 10.1117/1.JMI.6.4.047001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nair A., Calvetti D., Vince D. G., “Regularized autoregressive analysis of intravascular ultrasound backscatter: improvement in spatial accuracy of tissue maps,” IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 51(4), 420–431 (2004). 10.1109/TUFFC.2004.1295427 [DOI] [PubMed] [Google Scholar]
- 33.Nair A., et al. , “Coronary plaque classification with intravascular ultrasound radiofrequency data analysis,” Circulation 106(17), 2200–2206 (2002). 10.1161/01.CIR.0000035654.18341.5E [DOI] [PubMed] [Google Scholar]
- 34.Moore M. P., et al. , “Characterisation of coronary atherosclerotic morphology by spectral analysis of radiofrequency signal: in vitro intravascular ultrasound study with histological and radiological validation,” Heart 79(5), 459–467 (1998). 10.1136/hrt.79.5.459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Watson R. J., et al. , “Classification of arterial plaque by spectral analysis of in vitro radio frequency intravascular ultrasound data,” Ultrasound Med. Biol. 26(1), 73–80 (2000). 10.1016/S0301-5629(99)00112-X [DOI] [PubMed] [Google Scholar]
- 36.Bando M., et al. , “Noninvasive quantitative tissue characterization of carotid plaques using color-coded mapping based on ultrasound integrated backscatter,” JACC Cardiovasc. Imaging 9(5), 625–627 (2016). 10.1016/j.jcmg.2015.02.017 [DOI] [PubMed] [Google Scholar]
- 37.Kumon R. E., et al. , “Spectral analysis of ultrasound backscatter for characterization of HIFU lesions in cardiac tissue high-frequency imaging,” in IEEE Int. Ultrasonics Symp., IEEE, pp. 244–247 (2009). 10.1109/ULTSYM.2009.5441628 [DOI] [Google Scholar]
- 38.Pérez J. E., et al. , “Applicability of ultrasonic tissue characterization for longitudinal assessment and differentiation of calcification and fibrosis in cardiomyopathy,” J. Am. Coll. Cardiol. 4(1), 88–95 (1984). 10.1016/S0735-1097(84)80323-X [DOI] [PubMed] [Google Scholar]
- 39.Wear K. A., Wagner R. F., Garra B. S., “A comparison of autoregressive spectral estimation algorithms and order determination methods in ultrasonic tissue characterization,” IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 42(4), 709–716 (1995). 10.1109/58.393113 [DOI] [Google Scholar]
- 40.Akilli H., et al. , “Gender-related changes of the epicardial fat thickness and leptin in obstructive sleep Apnea,” Echocardiography 31(4), 411–419 (2014). 10.1111/echo.12392 [DOI] [PubMed] [Google Scholar]
- 41.Hu F. B., “Overweight and obesity in women: health risks and consequences,” J. Womens Health 12(2), 163–172 (2003). 10.1089/154099903321576565 [DOI] [PubMed] [Google Scholar]
- 42.Kay S. M., Marple S. L., “Spectrum analysis: a modern perspective,” Proc. IEEE 69(11), 1380–1419 (1981). 10.1109/PROC.1981.12184 [DOI] [Google Scholar]
- 43.Georgiou G., Cohen F. S., “Tissue characterization using the continuous wavelet transform. I. Decomposition method,” IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 48(2), 355–363 (2001). 10.1109/58.911718 [DOI] [PubMed] [Google Scholar]
- 44.Georgiou G., et al. , “Tissue characterization using the continuous wavelet transform. Part II: Application on breast RF data,” IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 48(2), 364–373 (2001). 10.1109/58.911719 [DOI] [PubMed] [Google Scholar]
- 45.Wear K. A., Wagner R. F., Garra B. S., “High resolution ultrasonic backscatter coefficient estimation based on autoregressive spectral estimation using Burg’s algorithm,” IEEE Trans. Med. Imaging 13(3), 500–507 (1994). 10.1109/42.310881 [DOI] [PubMed] [Google Scholar]
- 46.Karlapalem A., et al. , “Classification of cardiac adipose tissue using spectral analysis of ultrasound radiofrequency backscatter,” Proc. SPIE 10955, 109550F (2019). 10.1117/12.2512972 [DOI] [Google Scholar]
- 47.Nair A., et al. , “Assessing spectral algorithms to predict atherosclerotic plaque composition with normalized and raw intravascular ultrasound data,” Ultrasound Med. Biol. 27(10), 1319–1331 (2001). 10.1016/S0301-5629(01)00436-7 [DOI] [PubMed] [Google Scholar]
- 48.Raileanu L. E., Stoffel K., “Theoretical comparison between the gini index and information gain criteria,” Ann. Math. Artif. Intel. 41(1), 77–93 (2004). 10.1023/B:AMAI.0000018580.96245.c6 [DOI] [Google Scholar]
- 49.Breiman L., “Random forests,” Mach. Learn. 45(1), 5–32 (2001). 10.1023/A:1010933404324 [DOI] [Google Scholar]
- 50.Canbek G., et al. , “Binary classification performance measures/metrics: a comprehensive visualized roadmap to gain new insights,” in Int. Conf. Comput. Sci. and Eng., pp. 821–826 (2017). [Google Scholar]
- 51.Burman P., “A comparative study of ordinary cross-validation, v-fold cross-validation and the repeated learning-testing methods,” Biometrika 76(3), 503–514 (1989). 10.1093/biomet/76.3.503 [DOI] [Google Scholar]
- 52.Zhang P., “Model selection via multifold cross validation,” Ann. Stat. 21(1), 299–313 (1993). 10.1214/aos/1176349027 [DOI] [Google Scholar]
- 53.Nair A., Vince D. G., Calvetti D., “‘Blind’ data calibration of intravascular ultrasound data for automated tissue characterization,” IEEE Ultrasonics Symp. 2, 1126–1129 (2004). [Google Scholar]
- 54.Insana M. F., et al. , “Describing small-scale structure in random media using pulse-echo ultrasound,” J. Acoust. Soc. Am. 87(1), 179–192 (1990). 10.1121/1.399283 [DOI] [PMC free article] [PubMed] [Google Scholar]