Electronic, redox, and optical property prediction of organic π-conjugated molecules through a hierarchy of machine learning approaches

Abstract

Accelerating the development of π-conjugated molecules for applications such as energy generation and storage, catalysis, sensing, pharmaceuticals, and (semi)conducting technologies requires rapid and accurate evaluation of the electronic, redox, or optical properties. While high-throughput computational screening has proven to be a tremendous aid in this regard, machine learning (ML) and other data-driven methods can further enable orders of magnitude reduction in time while at the same time providing dramatic increases in the chemical space that is explored. However, the lack of benchmark datasets containing the electronic, redox, and optical properties that characterize the diverse, known chemical space of organic π-conjugated molecules limits ML model development. Here, we present a curated dataset containing 25k molecules with density functional theory (DFT) and time-dependent DFT (TDDFT) evaluated properties that include frontier molecular orbitals, ionization energies, relaxation energies, and low-lying optical excitation energies. Using the dataset, we train a hierarchy of ML models, ranging from classical models such as ridge regression to sophisticated graph neural networks, with molecular SMILES representation as input. We observe that graph neural networks augmented with contextual information allow for significantly better predictions across a wide array of properties. Our best-performing models also provide an uncertainty quantification for the predictions. To democratize access to the data and trained models, an interactive web platform has been developed and deployed.

A hierarchical series of machine learning models are developed to provide robust predictions of the electronic, redox, and optical properties of π-conjugated molecules.

Introduction

Organic, π-conjugated molecules, whether discovered as natural products or synthesized in the laboratory, have been essential drivers in the development of chemistry as a science over the past century-plus. π-conjugated molecules present tremendous chemical diversity, and offer immense capacity to the synthetic chemist to tailor molecular electronic, redox, and optical properties. Furthermore, physicochemical (noncovalent) interactions of π-conjugated molecules with the environment (e.g., solution solubility, solid-state packing arrangements, binding to biological agents) can be altered, leading to a growing application space that includes dyes, pharmaceuticals, (semi) conductors, energy generation and storage, and catalysis, to name but a few.^1–13

This vast chemical diversity, including what we formally understand as well as knowledge we do not currently possess, prevents easy and rapid assessment of a proposed molecule's suitability for a given application. Hence, influential discoveries often happen through slow, and with great resource and human costs, synthetic trial-and-error approaches. With rapid computer hardware and software developments, high-performance computing has become a powerful and more accessible tool to aid molecular design and discovery. These computational advances have resulted in high-throughput virtual screening procedures that reduce the time for determining molecular properties from several months/weeks/days of synthesis and purification to several hours or even minutes and seconds.^14–21 These computational screening procedures often use quantum chemical calculations to evaluate properties, including the ionization (both oxidation and reduction) energies, relaxation energies, and low-lying excited state energies, to name but a few, to filter promising molecules for synthesis follow-up.

The computational time and resources required to evaluate molecular descriptors can further be reduced by using machine learning (ML) techniques. With ever-growing, curated high-throughput computational and experimental datasets, ML models are now being trained to predict expansive sets of molecular properties.^22–31 A widely used benchmark dataset for training ML models to predict molecular properties is the quantum-chemically derived QM9 dataset, a subset of the GDB-17 database.^32,33 The QM9 dataset is limited to molecules that contain only select atoms, including C, H, O, N, and F, and fewer than nine heavy atoms. Hence, molecular property predictions by models trained with QM9 are typically not generalizable for larger organic π-conjugated molecules or molecules that contain atoms such as S or Cl. To overcome this challenge, several datasets are being created and expanded for large organic π-conjugated molecules.^{14,18,34–40} These datasets generally sample a niche chemical space with a strict value range for the electronic structure and optical property descriptors or are limited in the properties evaluated quantum mechanically. Furthermore, the trained ML models are usually not readily available to synthetic chemists to validate their chemical intuition before synthesis.

Here, we present a curated dataset of 25 251 organic, π-conjugated molecules to serve as a benchmark dataset for training ML models. The dataset contains electronic, redox, and optical property descriptors such as frontier molecular orbital energies, vertical and adiabatic ionization potentials and electron affinities, relaxation energies and corresponding reorganization energies (often used in understanding charge and energy transfer), and singlet and triplet excitation energies, all computed via density functional theory (DFT) and time-dependent DFT (TDDFT). We then train a hierarchy of ML models – from simple classical ML models such as ridge regression to sophisticated models like graph neural network (GNN) – to predict these properties in seconds using the molecular SMILES representation⁴¹ as the input. Our systematic approach allows us to gain insights into the effects of model complexity and the featurization of the SMILES input on prediction accuracy. Furthermore, we provide an uncertainty estimate for our best-performing models, which is critical for inferring the trustworthiness of ML predictions. An interactive web interface (https://oscar.as.uky.edu/ocelotml_2d) has been developed and deployed to democratize access to and use of the ML models. The best trained models are accessible through the web interface and can be downloaded programmatically, as demonstrated in the GitHub repository (see the Data availability statement for the link).

Methods

The curated dataset used in this study is derived from the OCELOT (Organic Crystals in Electronic and Light-Oriented Technologies) database of DFT computed properties for organic, π-conjugated molecules and crystal structures.⁴² A detailed description of the methods to generate the high-throughput data is provided elsewhere.⁴² In brief, the π-conjugated molecules were obtained from the crystal structures in the OCELOT database using the OCELOT API.⁴² Each molecule is fragmented to obtain the largest, contiguous π-conjugated fragment that is then used for the subsequent DFT calculations (see Fig. S1 in the ESI†). The DFT structure optimizations, single-point energies, and TDDFT evaluations for the low-lying excited states are performed with (ionization potential) IP-tuned LC-ωHPBE functionals, derived for each distinct molecule, and the Def2SVP basis set.^43–45 Entries that do not contain all the DFT/TDDFT values or have erroneous values are removed. All calculations were performed with the Gaussian 16 Rev. A.03 software suite.⁴⁶

Full details of the DFT and TDDFT calculations and ML model training are provided in the ESI;† here, for the sake of brevity, we provide salient features of the ML model development pipeline. ML model training was performed in PyTorch version 1.10 and used Cuda 11.4 for GPU acceleration.^47,48 A five-fold cross-validation method was implemented instead of a fixed train-test data split for training the models as the dataset is small. Moreover, this method provides insights into the trained models' generalizability over the dataset's diversely sampled chemical space. All models, except models with evidential deep learning, were subject to five-fold cross-validation. The performance metrics reported here are the averaged results of five-fold cross-validation and the respective standard deviations. The hyperparameters for each model were tuned with Optuna version 2.10, where the metric R² is maximized.⁴⁹ The hyperparameters for all models were obtained using only one random 80 : 20 split of the dataset. The mean squared error (MSE) loss function was used for training all models except the evidential deep learning models. The two-dimensional molecular descriptors and extended connectivity fingerprints of radius 2 (ECFP2) that were used as the input features to some models were generated with RDKit 2021.3.5.^50,51 The two-dimensional descriptors were normalized by first dividing each feature by its maximum absolute value and then fitting each feature to the normal distribution. The ESI† provides a complete list of descriptors and a detailed discussion on hyperparameter tuning.

First-generation models were trained with scikit-learn version 0.24.2 with training accelerated by scikit-learn-intelex version 2021.2.⁵² Two model sets were generated – one with only molecular descriptors as input features and the other with molecular descriptors and ECFP2, where the length of the bit-vector of ECFP2 was tuned along with the other hyperparameters of the model. Similar to the first-generation models, second-generation models using feed-forward networks (FFN) made use of two model sets, one with only the molecular descriptors as input and one that used both molecular descriptors and ECFP2 bit-vectors with their lengths tuned.

Third-generation models were created with message-passing neural networks (MPNN) for quantum chemistry.⁵³ The MPNN utilized a graph-based representation of molecules where nodes represent atoms and edges represent bonds. The nodes and edges were associated with features like the type of atom and the type of bond on which the MPNN operated to provide a learned representation of the molecule. The learning process for MPNN involved T message-passing steps. During each step t < T, the features h_v^t associated with a node v were updated using an update function U_t. The information m_t to update the feature was gathered by the message function M_t from features h_w^t of atoms w in the neighborhood of v and associated bonds e_vw as described by:

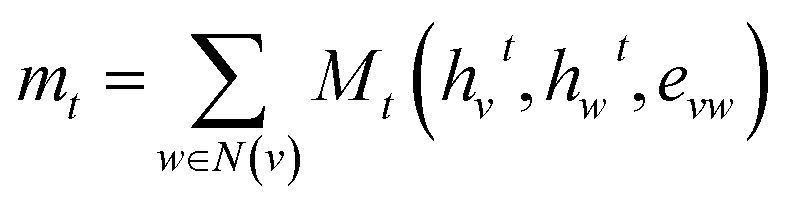1

h_v^t+1 = U_t(h_v^t,m_v^t+1) 2

To fetch the learned representation after T message-passing steps, the set2set model as described by Gilmer et al. was used.⁵³ The representation from the MPNN was then passed to a 2-layer FFN for molecular property prediction. The molecular graphs for MPNNs were created from SMILES and embedded with atom and bond features using the deep graph library 0.7.2 (DGL) and DGL-Lifesci v0.2.8 Python packages.^54,55 The atom and bond features used for generating the MPNN input are listed in Table 1 and Table 2, respectively.

Atom features used for the MPNN input generation. The features use the Canonical AtomFeaturizer in the DGL-Lifesci package⁵⁵.

Atom feature	Size
One-hot encoding of atom type	43
One-hot encoding of atom degree	11
One-hot encoding of the number of implicit hydrogens on the atom	7
The formal charge on the atom	1
Number of radical electrons	1
One-hot encoding of atom hybridization	5
Whether the atom is aromatic	1
One-hot encoding of total hydrogens in the atom	5

Bond features used for the MPNN input generation. The features use the Canonical BondFeaturizer in the DGL-Lifesci package⁵⁵.

Bond feature	Size
One-hot encoding of the bond type	4
Whether the bond is conjugated	1
Whether the bond is in a ring	1
One-hot encoding of the stereo configuration of a bond	6

The fourth-generation models used the same MPNN network as the third generation. However, the output features from MPNN were concatenated with molecular or DFT descriptors before being passed to the FFN. The hyperparameter tuning process was the same as that of the third-generation models.

Evidential uncertainties for the fourth-generation models were evaluated by factoring the code to include an evidential deep learning layer.⁵⁶ Evidential deep learning assumes that the prediction (y) of a model arises from a Gaussian distribution (N) with unknown mean and variance (μ, σ²). Accordingly, the mean and variance are represented as –

μ ∼ N(γ, σ²ν⁻¹) 3

σ² ∼ Γ⁻¹(α, β) 4

where, Γ is the gamma function, and γ, ν, α, β are parameters. The posterior distribution follows a normal inverse gamma distribution from which the prediction ( [μ]) and epistemic uncertainty (Var[μ]) are computed from the following equations:

[μ] = γ 5

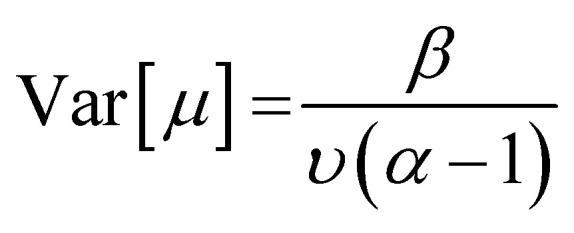6

The loss function L(x) for training the evidential deep learning model includes a negative likelihood loss L^NLL(x) that is responsible for maximizing the model prediction and an evidential loss L^EL(x) which minimizes the evidence of errors.

L^EL(x) = |y − γ|·(2ν + α) 7

L(x) = L^NLL(x) + λL^EL(x) 8

The hyperparameter λ in the loss function was set to 0.2 for training the models with uncertainty quantification.⁵⁶ The errors were recalibrated with a python-based uncertainty toolbox package by minimizing the miscalibration area.⁵⁷ The recalibration of uncertainty used a black-box optimizer to find a standard deviation scalar factor that produced the best recalibration. The hyperparameters of the model MPNN and FFN were the same as those without the uncertainty quantification. The chemical space visualizations were created with ChemPlot 1.2.0 with SMILES as input.⁵⁸

Results and discussion

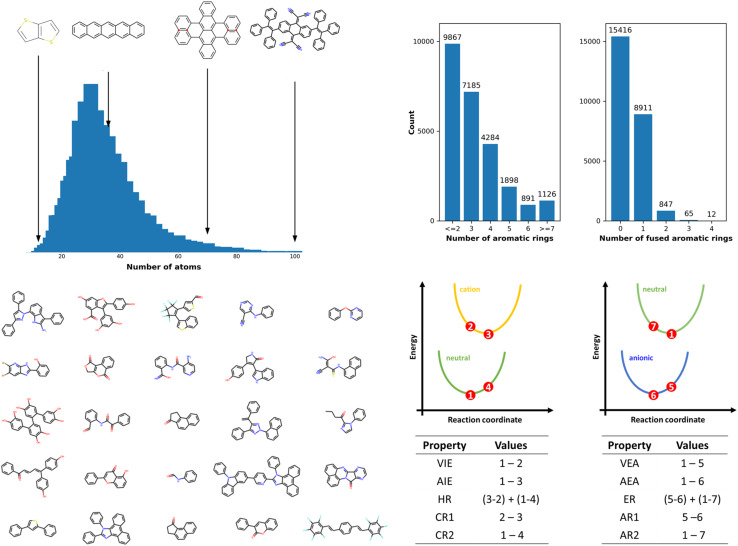
The OCELOT chromophore v1 dataset contains 25 251 organic π-conjugated molecules and their electronic, redox, and optical properties computed with the high accuracy DFT/TDDFT calculations. The molecules in the dataset are fragments of experimentally synthesized organic compounds. The dataset contains elements C, N, O, F, S, Cl, Br, Se, P, Si, B, As, Te, I, and H with up to 100 atoms per molecule, as shown in Fig. 1. The dataset is chemically diverse, with the number of π-conjugated rings ranging from one for benzene derivatives to 28 for large π-conjugated systems, including fullerene derivatives. Over 15k molecules (ex., biphenyl) do not have fused-aromatic rings, and 8k molecules (ex., naphthalene) have one fused-aromatic ring. The dataset has 33 molecules in common with the QM9 dataset (see Fig. S2†). Details concerning DFT/TDDFT data generation and dataset curation are presented in the Methods section and in the ESI†. The DFT and TDDFT properties available in the dataset are vertical (VIE) and adiabatic (AIE) ionization energies, vertical (VEA) and adiabatic (AEA) electron affinities, cation (CR) and anion (AR) relaxation energies, HOMO energies (HOMO), LUMO energies (LUMO), HOMO–LUMO energy gaps (H–L), electron (ER) and hole (HR) reorganization energies, and lowest-lying singlet (S0S1) and triplet (S0T1) excitation energies. Select derived properties are depicted in Fig. 1, and statistics for each property are provided in Table S1 (see ESI†). Dataset generation required over 5 M core hours of computing time on high-performance computing resources. While this dataset contains over 25k entries and 200k energy entries, it is still small compared to ML training datasets in other fields.^32,59 The dataset is available on the OCELOT website, and can be downloaded programmatically.⁶⁰

Fig. 1. (Top left) Atom count distributions in the OCELOT chromophore v1 dataset. (Top right) Bar plots show the dataset's distribution of aromatic rings and fused aromatic rings. (Bottom left) Random selection of 25 molecules from the dataset. (Bottom right) Schematic representation of the potential energy surfaces of molecular neutral (green), radical-cation (yellow), and radical-anion (blue) states. The numbers 1–7 represent points at which DFT energies are evaluated. The tables at the bottom show the computation involved in obtaining some properties described in the dataset.

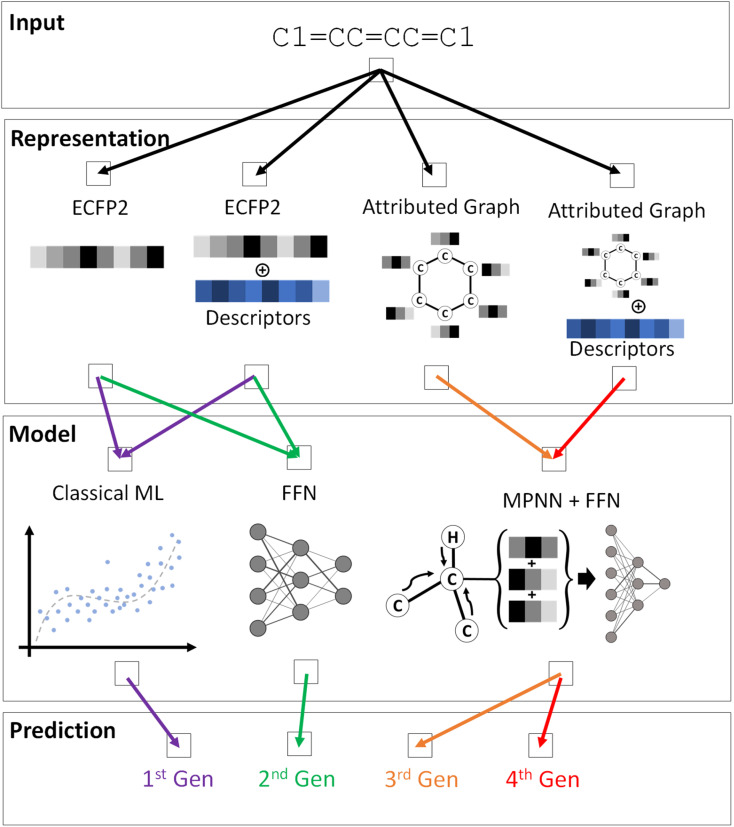
A variety of ML models were trained to predict the DFT or TDDFT computed properties at reduced computational cost, following a systematic hierarchical approach. While molecular electronic, redox, and optical properties depend on the conformation, the generation of accurate 3D conformations from 2D molecular representations is challenging and an active area of research.^61–63 Hence, as a baseline, we used the 2D SMILES representation of a molecule as input to train the ML pipeline and predict DFT/TDDFT-level computed properties. Four generations of ML models, each with increasing complexity from the predecessor, were created to investigate the prediction accuracy for different ML architectures, as schematically depicted in Fig. 2 and S3.† In our preliminary ML model training, we compared a model's performance to predict single and multiple properties. The results shown in Table S2† indicate that training an ML model to predict a single property generally yields better performance. Hence, each ML model is trained to predict one property from the dataset; the best-trained ML models for every property from each generation are publicly available.

Fig. 2. Schematic representation of the ML pipeline explored in this work. The input is a SMILES representation of a molecule, in this case benzene, from which the molecular representations are generated. The input representation for an ML model and the model architecture for the four generations is indicated by the color-coded arrows.

In the first-generation ML models, three classical ML algorithms were employed: ridge regression (RR), support vector machine (SVM), and kernel ridge regression (KRR). We focused on these models as previous reports have shown that SVM and KRR perform well in predicting molecular properties.^64,65 RR was used as the baseline instead of linear regression (LR) as preliminary LR results provided large coefficients that led to significant prediction outliers. To train the models, we generated a set of 266 molecular descriptors that included the number of rotatable bonds, the molecular weight, and the number of rings as the input features for the model from the 2D SMILES molecular representation. R² and mean absolute error (MAE) were used to evaluate the model performance, with results in Table S3 (see ESI†). The first-generation ML models perform well on a few properties, namely AIE, AEA, VIE, and VEA, with R² values in the range of 0.70 to 0.79. The models overfit training data for other target properties, which could be due to the low number of input features, 266, used as input to the models. Before trying more sophisticated models, we enriched the input feature by concatenating the ECFP2, which provides more local information about a molecule than the molecular descriptors. While the molecular descriptor vector length was fixed to 266, the length of the ECFP2 bit-vector was optimized for each property during hyperparameter tuning. A performance improvement was observed for the models with both molecular descriptors and ECFP2 used (Table 3). For the SVM, the R² for AIE, AEA, and VIE exceeds 0.80, and the MAE is reduced by about 30 meV with the inclusion of ECFP2. The predictions for S0S1 and S0T1 also improved. Though these models are not as complex as those discussed below, they effectively predict some electronic properties at a low computational cost. Of the three algorithms, SVM outperformed KRR and LR for most properties, while KRR has better performance than RR for all properties, which corroborates with previous reports.³⁵

Performance metrics for the first-generation ML models. MAE is reported in eV for all models. The best R² and MAE for each property are in bold. The values are averaged over five-fold cross-validation models. The input features for these models are the molecular descriptors and ECFP2.

Property	RR		SVM		KRR
	R 2	MAE	R 2	MAE	R 2	MAE
HOMO	0.53 ± 0.015	0.345 ± 0.005	0.58 ± 0.007	0.317 ± 0.003	0.54 ± 0.011	0.337 ± 0.003
LUMO	0.60 ± 0.012	0.340 ± 0.006	0.73 ± 0.011	0.277 ± 0.005	0.67 ± 0.012	0.306 ± 0.002
H–L	0.42 ± 0.006	0.580 ± 0.005	0.44 ± 0.012	0.604 ± 0.006	0.45 ± 0.004	0.561 ± 0.004
VIE	0.76 ± 0.006	0.231 ± 0.004	0.81 ± 0.007	0.204 ± 0.002	0.74 ± 0.008	0.241 ± 0.004
AIE	0.77 ± 0.010	0.222 ± 0.002	0.82 ± 0.004	0.193 ± 0.002	0.77 ± 0.008	0.222 ± 0.004
CR1	0.29 ± 0.015	0.058 ± 0.001	0.32 ± 0.008	0.059 ± 0.001	0.33 ± 0.009	0.057 ± 0.001
CR2	0.34 ± 0.008	0.059 ± 0.001	0.36 ± 0.010	0.061 ± 0.001	0.38 ± 0.009	0.056 ± 0.001
HR	0.35 ± 0.012	0.112 ± 0.001	0.37 ± 0.011	0.114 ± 0.001	0.33 ± 0.016	0.113 ± 0.001
VEA	0.82 ± 0.004	0.218 ± 0.004	0.88 ± 0.004	0.172 ± 0.002	0.79 ± 0.006	0.231 ± 0.004
AEA	0.82 ± 0.005	0.210 ± 0.001	0.85 ± 0.005	0.182 ± 0.002	0.81 ± 0.004	0.219 ± 0.002
AR1	0.36 ± 0.009	0.057 ± 0.001	0.44 ± 0.013	0.053 ± 0.001	0.37 ± 0.013	0.057 ± 0.001
AR2	0.36 ± 0.013	0.052 ± 0.001	0.39 ± 0.010	0.051 ± 0.001	0.34 ± 0.009	0.053 ± 0.000
ER	0.40 ± 0.019	0.104 ± 0.02	0.43 ± 0.011	0.099 ± 0.002	0.38 ± 0.012	0.105 ± 0.002
S0S1	0.60 ± 0.009	0.307 ± 0.006	0.67 ± 0.009	0.275 ± 0.004	0.60 ± 0.004	0.307 ± 0.002
S0T1	0.68 ± 0.008	0.230 ± 0.003	0.76 ± 0.007	0.183 ± 0.003	0.67 ± 0.008	0.235 ± 0.004

Though adding the ECFP2 to the input features improved the performance of the first-generation ML models, the relaxation energies (ARs and CRs) suffered from low prediction accuracy. We hypothesize that this inadequate accuracy could be due to the models' limited ability to find the complex functions mapping the input features to the DFT-derived values. Hence, for the second-generation ML models, we implemented a feed-forward network (FFN) architecture known to represent arbitrarily complex functions, given sufficient data.⁶⁶ For the second-generation ML models, we used the same input features as the first-generation models. Second-generation model performance is tabulated in Table 4. The models with molecular descriptors and ECFP2 again outperform models with only molecular descriptors as input features for all properties except for the CR1, AR1, and HOMO energies. Interestingly, the predictions from the first-generation SVM models are as good as the second-generation models with corresponding input features. There is no significant increase in performance on properties such as the relaxation energies (ARs and CRs) and reorganization energies (ER and HR) over the first-generation models. This observation indicates that prediction accuracy relies less on the complexity of the models and that a more robust input feature may be needed to improve the predictions.

Performance metrics computed for the second-generation ML models. MAE is reported in eV for all models. The best R² and MAE for each property are in bold. The values are averaged over five-fold cross-validation models. The second-generation ML model results with and without ECFP2 are included.

Property	2nd gen without ECFP2		2nd gen with ECFP2
	R 2	MAE	R 2	MAE
HOMO	0.51 ± 0.011	0.351 ± 0.011	0.49 ± 0.009	0.354 ± 0.012
LUMO	064 ± 0.011	0.323 ± 0.007	0.69 ± 0.011	0.297 ± 0.004
H–L	0.39 ± 0.008	0.589 ± 0.015	0.42 ± 0.009	0.578 ± 0.011
VIE	0.75 ± 0.010	0.238 ± 0.006	0.78 ± 0.003	0.219 ± 0.001
AIE	0.76 ± 0.012	0.230 ± 0.003	0.80 ± 0.008	0.207 ± 0.003
CR1	0.26 ± 0.009	0.060 ± 0.001	0.17 ± 0.017	0.063 ± 0.001
CR2	0.29 ± 0.008	0.062 ± 0.001	0.34 ± 0.013	0.059 ± 0.001
HR	0.30 ± 0.013	0.118 ± 0.002	0.35 ± 0.012	0.110 ± 0.002
VEA	0.79 ± 0.012	0.233 ± 0.004	0.86 ± 0.003	0.186 ± 0.002
AEA	0.80 ± 0.003	0.224 ± 0.002	0.86 ± 0.001	0.176 ± 0.002
AR1	0.32 ± 0.007	0.059 ± 0.001	0.27 ± 0.037	0.062 ± 0.002
AR2	0.33 ± 0.023	0.053 ± 0.000	0.37 ± 0.015	0.051 ± 0.001
ER	0.38 ± 0.008	0.106 ± 0.001	0.41 ± 0.007	0.101 ± 0.002
S0S1	0.59 ± 0.016	0.313 ± 0.004	0.65 ± 0.010	0.282 ± 0.003
S0T1	0.62 ± 0.018	0.254 ± 0.005	0.75 ± 0.003	0.194 ± 0.003

With learned molecular representations from message-passing neural networks (MPNN), FFN is able to provide more accurate predictions of molecular properties.^67,68 Thus, the third-generation ML models use an MPNN architecture to generate a robust input feature for FFN. The MPNN uses a graph representation of a molecule as input where the nodes represent the atoms, and bonds are represented by the edges between the nodes. Node attributes included atom type and hybridization, while edge attributes included bond type and whether a bond is π-conjugated (part of the sp² hybridized system), which the MPNN used to generate learned molecule representations. The output representation from the MPNN acted as the input feature for an FFN, which was used to predict the molecular property.

The MPNN models show improved performance over the previous ML model generations (see Table 5). VIE and S0T1, along with AIE, AIE, and VEA, have R² values greater than 0.85. The MAE is also reduced on average by 40 meV for these properties compared to the second-generation ML models. The relaxation energies (CR and AR), reorganization energies (HR and ER), and HOMO–LUMO energy gaps (HL) have significantly improved R² values compared to previous generations; however, the MAE reduction is small. The R² values that remain smaller than 0.6 for these properties indicate that the learned representation alone is insufficient and that more global molecular features, including the number of rotatable bonds, number of aromatic rings, etc., are required. It has previously been shown that concatenating the features from MPNN with handcrafted features can improve prediction accuracy.⁶⁹

Performance metrics computed for the third and fourth-generation ML models. MAE is reported in eV for all models. The best R² and MAE for each property are in bold. The values are averaged over five-fold cross-validation models. The fourth-generation ML models include molecular descriptors concatenated to the MPNN output.

Property	3rd gen		4th gen
	R 2	MAE	R 2	MAE
HOMO	0.60 ± 0.01	0.796 ± 0.446	0.61 ± 0.01	0.330 ± 0.028
LUMO	0.76 ± 0.01	0.291 ± 0.044	0.76 ± 0.01	0.289 ± 0.028
H–L	0.47 ± 0.02	1.264 ± 0.696	0.50 ± 0.01	0.548 ± 0.029
VIE	0.86 ± 0.01	0.202 ± 0.043	0.86 ± 0.00	0.191 ± 0.024
AIE	0.87 ± 0.01	0.176 ± 0.015	0.87 ± 0.01	0.173 ± 0.006
CR1	0.37 ± 0.01	0.054 ± 0.001	0.38 ± 0.02	0.055 ± 0.002
CR2	0.40 ± 0.01	0.061 ± 0.001	0.44 ± 0.01	0.053 ± 0.001
HR	0.38 ± 0.02	0.126 ± 0.022	0.43 ± 0.02	0.133 ± 0.019
VEA	0.92 ± 0.01	0.193 ± 0.052	0.93 ± 0.00	0.157 ± 0.018
AEA	0.93 ± 0.01	0.160 ± 0.027	0.94 ± 0.01	0.154 ± 0.027
AR1	0.46 ± 0.02	0.057 ± 0.002	0.47 ± 0.02	0.051 ± 0.001
AR2	0.45 ± 0.01	0.048 ± 0.002	0.43 ± 0.02	0.052 ± 0.001
ER	0.50 ± 0.01	0.093 ± 0.002	0.50 ± 0.01	0.098 ± 0.006
S0S1	0.76 ± 0.01	0.252 ± 0.017	0.76 ± 0.01	0.249 ± 0.013
S0T1	0.87 ± 0.00	0.148 ± 0.012	0.87 ± 0.00	0.150 ± 0.028

With this insight, we concatenated molecular descriptors in the fourth-generation ML models to a learned representation derived from an MPNN. The fourth-generation ML models have the lowest MAE for most properties in the dataset (see Table 5). The improvement in R² value over the third generation is marginal for some properties, including molecular descriptors into the input for FFN. HR and HL show the most significant improvement in R² (≈0.05), though the R² values remain close to 0.5. It is worth noting that the values of the relaxation energies (CR and AR) are of the same magnitude as the MAEs of properties like AIE, VIE, AEA, and AIE. Thus, the difficulty in predicting the relaxation energies could be due to the lack of descriptors that accurately describe the different diabatic potential energies involved (see Fig. 1). Moreover, the models were not provided with any 3D geometry information.

To further improve the performance of the fourth-generation ML models, DFT values for AIE, AIE, VEA, and VIE were used as concatenated features to the learned representation rather than the molecular descriptors. Using this feature set, we only trained the models for the properties with R² below 0.8; CR1 and AR1 were omitted as these properties are obtained by subtracting two of the given DFT values. The corresponding models show a significant improvement in the R² values from less than 0.5 to over 0.69 for AR2 and CR2 and above 0.90 for ER, HR, and S0S1 (see Table 6). The MAEs are reduced to 45 meV for ER and 39 meV for HR. However, importantly, the models require DFT values to achieve this accuracy. Using the predicted values of AIE, AEA, VIE, and VEA from the fourth-generation model with molecular descriptors instead of the DFT computed values did not yield a significant improvement in the accuracy of CR2, ER, AR2, and HR when compared to the fourth-generation model with molecular descriptors (see Tables 5 and 6). However, R² for LUMO, HOMO, and HL improved by 0.04. This observation suggests that only highly accurate descriptors are necessary to improve the performance on properties like relaxation energy and reorganization energy. Including 3D geometry information in the input features could further enhance the accuracy of predictions. We are actively working in this direction.

Performance metrics computed for the fourth-generation ML models with DFT and ML predicted DFT (ML-DFT) properties for AIE, AEA, VIE, and VEA concatenated to the MPNN representation. For ML-DFT, the required input DFT values were predicted from the fourth-generation ML model with molecular descriptors (see Table 5 for the performance of the model). MAE is reported in eV for all models. The values are averaged over five-fold cross-validation models.

Property	DFT		ML-DFT
	R 2	MAE	R 2	MAE
HOMO	0.81 ± 0.01	0.327 ± 0.140	0.68 ± 0.01	1.105 ± 1.661
LUMO	0.93 ± 0.00	0.132 ± 0.009	0.82 ± 0.01	0.235 ± 0.020
H–L	0.84 ± 0.01	0.415 ± 0.169	0.59 ± 0.01	0.872 ± 0.291
CR2	0.69 ± 0.01	0.036 ± 0.003	0.44 ± 0.00	0.057 ± 0.006
HR	0.92 ± 0.01	0.039 ± 0.011	0.44 ± 0.01	0.107 ± 0.005
AR2	0.77 ± 0.01	0.034 ± 0.008	0.47 ± 0.02	0.057 ± 0.009
ER	0.94 ± 0.01	0.045 ± 0.014	0.52 ± 0.02	0.117 ± 0.032
S0S1	0.90 ± 0.01	0.396 ± 0.041	0.80 ± 0.01	0.322 ± 0.042

Predictions from ML models are not always accurate, as inherent uncertainty is associated with each prediction.⁷⁰ Though not all of the models we trained are accurate over the entire chemical space, an estimation of prediction confidence is beneficial. Uncertainty quantification of ML models is rapidly evolving.^71,72 Here, we employed an evidential deep learning algorithm, due to its ease of implementation, to estimate the uncertainty⁵⁶ of the best-performing models, i.e., the fourth-generation ML models (see Fig. S5†).

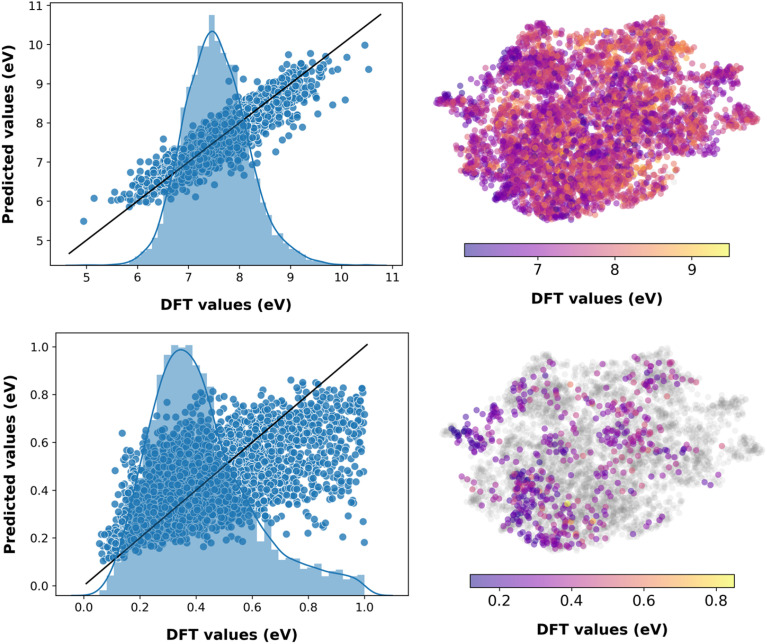
The trained evidential deep learning model provides uncertainty estimates that are overconfident, underconfident, or well-calibrated,⁷³ as shown in Fig. S6.† Hence, we recalibrated the uncertainties and used miscalibration area, sharpness, and negative log-likelihood (NLL) as metrics to quantify uncertainty (see Table S4†).^56,74,75 After recalibration, the miscalibration area and NLL decrease, indicating improved uncertainty estimates. The sharpness, which is analogous to the average variance of the uncertainty estimates, decreases for underconfident models and increases for overconfident ones corroborating with improvement in the estimates. The performance of these models is marginally lower compared to the fourth-generation ML models with molecular descriptors (see Table S5†). This is expected as there is a trade-off between predicting the property and estimating the uncertainty.⁵⁶ As shown in Fig. 3 and S6,† predicting VIE, VEA, AEA, AIE, and S0T1 have low uncertainty associated with the chemical space of the test dataset, while CR2, CR1, AR1, AR2, ER, and HR have relatively high prediction uncertainty, as expected from the corresponding model accuracy metrics. Analogous to machine predictions, the trained evidential uncertainty estimations are not accurate on data points that lie towards the lower or higher end of the distributions. For instance, the prediction of S0T1 for pentacene with uncertainty is 1.225 ± 6.029 eV, while the DFT computed value is 0.859 eV. Nevertheless, the predictions and uncertainty estimates are reasonable for the region of well-distributed data points.

Fig. 3. Predictions from the fourth generation ML model with evidential learning and molecular descriptors as the concatenated feature on the test dataset for properties VIE (top) and HR (bottom). The histograms on the left plot represent the distribution of the corresponding DFT evaluated property in the test dataset. Scatter plots on the right represent the chemical space of the test dataset. The data points where the uncertainty is greater than 10% of the DFT values are in gray.

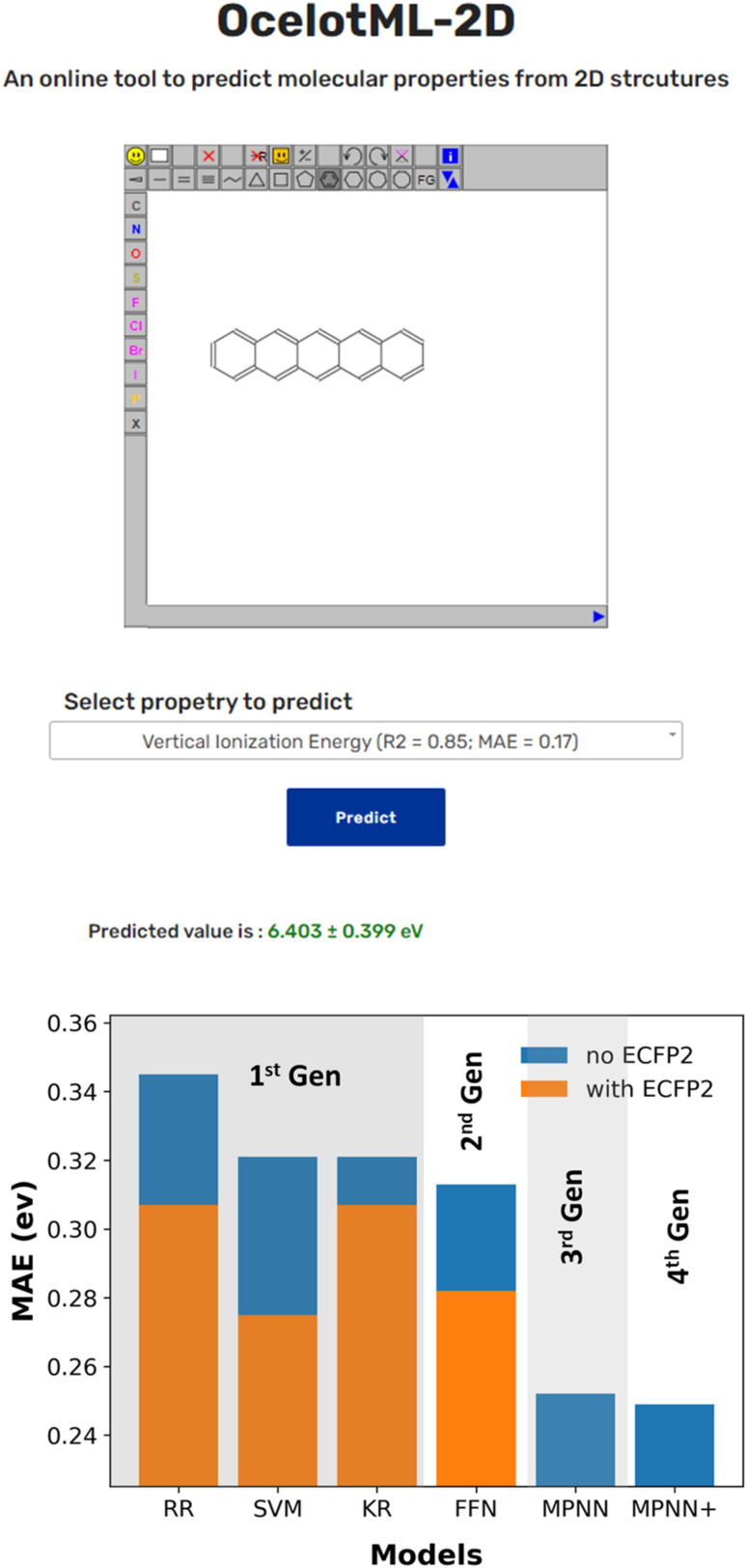
While several reported ML pipelines exist that predict the molecular properties, their accessibility to those with no little-to-no expertise in ML or computer programming is limited. To overcome this barrier and democratize ML access and use, we created the OCELOT ML (https://oscar.as.uky.edu/ocelotml) architecture, where ML pipelines for the organic, π-conjugated molecules can be deployed for easy access to the predictions. OCELOT ML provides a dashboard with performance metrics from various ML models on the dataset. We also deployed an interactive web interface on the OCELOT ML architecture, allowing users to draw a two-dimensional representation of the molecule and obtain property prediction using the ML models (Fig. 4). The fourth-generation ML models from this article with uncertainty predictions are available on the OCELOT ML platform.

Fig. 4. (Top) Snapshot of the publicly available interface deployed at the OCELOT website (https://oscar.as.uky.edu/ocelotml_2d) for predicting the properties using the trained models discussed in this article. The prediction is made in seconds when a 2D structure of a molecule is submitted. (Bottom) Representative bar plot indicating the improvement in ML model performance over the four generations for the property S0S1.

Conclusion

Here, we present a curated dataset of 25k molecules from the OCELOT database that contains computed a suite of electronic, redox, and optical properties for organic, π-conjugated molecules to serve as a benchmark for training ML models for property prediction. This dataset can be downloaded both interactively and programmatically from the OCELOT website.

We trained a hierarchy of ML models with varying complexity to predict the electronic, redox, and optical properties of π-conjugated molecules. Interestingly, we observe no significant improvement in performance on switching from classical ML algorithms like SVM to FFN, as shown in Fig. 4. Moreover, the results indicate that the input features are critical in achieving better prediction accuracy. The MAE for properties like AIE, AIE, VIE, VEA, and S0T1 decrease when learned representations from MPNN are used in conjunction with handcrafted molecular descriptors. However, the relaxation and reorganization energy predictions improved only on concatenating DFT computed AIE, AIE, VEA, and VIE values to the learned representation from MPNN. Nevertheless, the incorporated uncertainty quantifications provide a confidence to accept or ignore the ML models' predictions. The best ML models for the prediction of ionization energies and electron affinities presented here have low average errors of less than 10% in predicting the DFT computed properties from only a SMILES representation of a molecule over a vast chemical space. These models reduce the computational time to estimate properties to a few seconds compared to DFT methods which can take a few hours. We also present OCELOT ML, a web-based platform for hosting ML models to allow easy access to ML predictions.

Data availability

The code used for training and testing is available on GitHub at https://github.com/caer200/ocelotml_2d. The OCELOT chromophore v1 dataset is available on the OCELOT website at https://oscar.as.uky.edu/datasets.

Author contributions

V. B.: conceptualization, data curation, investigation, methodology, writing – original draft, writing – review & editing. P. S.: data curation, investigation, methodology, writing – original draft, writing – review & editing. B. S. S. P.: conceptualization, methodology, writing – review & editing. R. D.: resources, writing – review & editing. B. G.: supervision, writing – review & editing. C. R: supervision, funding acquisition, writing – review & editing.

Conflicts of interest

The authors declare no competing financial interest.