The flattening of spacetime hierarchy of the N,N-dimethyltryptamine brain state is characterized by harmonic decomposition of spacetime (HADES) framework

ABSTRACT

The human brain is a complex system, whose activity exhibits flexible and continuous reorganization across space and time. The decomposition of whole-brain recordings into harmonic modes has revealed a repertoire of gradient-like activity patterns associated with distinct brain functions. However, the way these activity patterns are expressed over time with their changes in various brain states remains unclear. Here, we investigate healthy participants taking the serotonergic psychedelic N,N-dimethyltryptamine (DMT) with the Harmonic Decomposition of Spacetime (HADES) framework that can characterize how different harmonic modes defined in space are expressed over time. HADES demonstrates significant decreases in contributions across most low-frequency harmonic modes in the DMT-induced brain state. When normalizing the contributions by condition (DMT and non-DMT), we detect a decrease specifically in the second functional harmonic, which represents the uni- to transmodal functional hierarchy of the brain, supporting the leading hypothesis that functional hierarchy is changed in psychedelics. Moreover, HADES’ dynamic spacetime measures of fractional occupancy, life time and latent space provide a precise description of the significant changes of the spacetime hierarchical organization of brain activity in the psychedelic state.

To understand the effects of the classical serotonergic psychedelic N,N-Dimethyltryptamine (DMT), researchers have employed the novel HADES framework revealing changes to functional spacetime hierarchy under DMT.

INTRODUCTION

The brain is endowed with complex dynamics and can be perceived along spatial and temporal dimensions [1]. Traditionally, neuroscience has focused on delineating and studying localized cortical regions to map brain function in a temporarily static fashion [2]. However, recent developments in neuroscience have started to indicate more spatially continuous representations of functional topography [3,4], and at the same time to stress the importance of temporally varying brain dynamics [5]. Indeed, the notion of brain spacetime has been described as a ‘common currency’ between the neuronal and mental brain features [6,7], and has been used to delineate various altered states of consciousness [8]. Despite such progress, it remains unknown what underlying mechanisms drive, on one hand, the gradient-like organization of cortical topography, and on the other, the waning and waxing of the brain's spatiotemporal patterns of activity.

Here we investigate one of the most potent psychedelic (i.e. ‘mind-manifesting’) experiences induced by the N,N-dimethyltryptamine (DMT)—a naturally occurring serotonergic psychedelic [9]. Unlike psilocybin and lysergic acid diethylamide, its expression is marked by a short duration of the psychedelic experience. It is often associated with alterations in visual and somatic effects. At high doses, a complete dissociation from the external environment precedes an immersion into mental worlds or dimensions described as ‘other’ but not less ‘real’ than the one inhabited in normal waking consciousness. Such experiences correlate with subjective rating items such as ‘I experienced a different reality or dimension’, ‘I saw geometric patterns’ and ‘I felt unusual bodily sensations’ [10,11]. It is these qualities of one's conscious experience that motivate a renewed interest in DMT drawing parallels with phenomena such as the near-death experience (NDE) and dreaming [12].

Furthermore, like other psychedelics, DMT may have clinical relevance and is currently being trialled for the treatment of depressive symptoms [13,14]. Studies with Ayahuasca, containing DMT itself as well as monoamine oxidase inhibitors (MAOIs), have shown promising results in patients with depression [15]. However, further investigations exploring the neural and plasticity dynamics of DMT experiences are necessary to provide mechanistic accounts for the relevance of DMT and related psychedelics for the treatment of mental health disorders [16–18].

In the brain, psychedelics enhance the richness of spatiotemporal dynamics along both the temporal and spatial dimensions. This has been corroborated by repertoire broadening of functional states and increases in temporal complexity as well as shifting of the brain to a more integrated state with the subversion of functional systems [19–22]. Consistently, neuroimaging DMT has revealed an increase in global functional connectivity—featuring a functional network disintegration and desegregation that is a reliable feature of the psychedelic state, and a collapse of the unimodal to transmodal functional gradient [11]. Taken together, the current findings and subjective reports are in line with the entropic [23,24] and anarchic brain [25] models, where an increase in entropy of spontaneous brain activity parallels the undermining of hierarchically organized brain function [23–25].

Here, we studied DMT with the Harmonic Decomposition of Spacetime (HADES) framework, which can describe the brain's hierarchical processing across both spatial and temporal dimensions. Historically, Brodmann's interactive atlas of cellular morphology and organization has given rise to the view of functional specialization of individual brain areas [26,27]. Spatially, this suggests a sharp delineation between cortical areas in terms of their anatomy and function. However, supported by evolutionary and developmental neuroscience [28,29], cortical gradients have challenged this view by suggesting gradually varying boundaries between and within brain regions, both in terms of function and anatomy [3,4,30]. Functionally, gradient-like organization proposes an intrinsic coordinate system of human brain organization continuously varying from unimodal to transmodal cortical areas [3,31]. Similarly, topographical maps of retinotopy, somatotopy and tonotopy have shown smooth variation of anatomy and function within brain areas [32–35].

Along the temporal dimension, studies of dynamic functional connectivity in functional magnetic resonance imaging (fMRI) have revealed the importance of characterizing the temporal features of brain activity as opposed to the static picture described by known resting-state networks [5,36]. Such approaches describe temporal functional connectivity in terms of sliding-window analysis [37], by considering the most salient events in the timeseries [38,39] constrained by structural connectivity [40,41], as a temporal process of hidden states [42,43] or as a temporal trajectory in a landscape of attractors [44,45]. Broadly, these approaches share the description of complex brain dynamics in terms of spatial patterns expressed in time and therefore can be represented in terms of the patterns’ fractional occupancy, lifetimes or probability of transitions. Uniquely, in this paper, HADES brings this dynamic perspective to the functional gradients and their temporal expression.

Importantly, HADES characterizes the brain's spatiotemporal activity in an atlas-free manner in terms of functional gradients (functional harmonics) defined in space and expressed over time. To that end, we derived functional harmonics (FHs) [4] and their temporal expression by decomposing fMRI data into FHs via harmonic decomposition [46]. The motivation for HADES is to reproduce the spatially distributed multiscale nature of functional gradients while accounting for their temporal evolution, and therefore focus the analysis on the functional gradients over time. In practice, HADES, as the decomposition of space and time, can be extended to any modality to obtain the spatial configuration of the modes over time. In this paper, the analysis of FHs renders HADES a unimodal application, which distinguishes it from other methods that estimate harmonic modes from the structural information (either from the anatomical connectome [47] or surface mesh [48]).

We analysed the fMRI data of the DMT-induced brain state with HADES. This allowed us to test the anarchic brain or ‘Relaxed Beliefs Under Psychedelics’ (REBUS) model, as well as findings of enhanced signatures of criticality under these compounds [21,46,49]. We hypothesized that the DMT state is associated with a flatter spacetime hierarchy of cortical functional organization with enhanced integrative properties across the cortex.

RESULTS

HADES describes the spatiotemporal dynamics in terms of spatial bases (defined from the brain's communication structure) and the spatial bases functional contributions to the fMRI recording evolving in time. To do so, we first constructed dense functional connectome from the Human Connectome Project (HCP) S1200 release of 812 subjects (Fig. 1B). The dense functional connectome was represented as a sparse, symmetric, and binary adjacency matrix (Fig. 1C) and decomposed into the functional harmonics (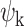(x)) using the eigen-decomposition of the graph Laplacian applied to the dense functional connectome (Fig. 1D). Consistent with [4], we focused our analysis on the first 11 lowest functional harmonics together with the 0th global harmonic. We analysed functional significance of the functional harmonics by comparing them to the Yeo seven and 17th functional networks (Fig. S1). To obtain the temporal signature, we further projected the individual harmonics on the fMRI timeseries (in surface representation), using functional harmonic decomposition, and thus calculated the FHs temporal weights (Fig. 1E). We reconstructed the timeseries with a few harmonics to motivate the similarity to the empirical data (Fig. S2). Then, using a collection of spatiotemporal and dynamic measures (Fig. 1F and G) and latent space representation (Fig. 1H), we applied HADES to study the DMT state and its functional reorganization in terms of flattening of functional hierarchies and integrative properties across the cortex.

Figure 1.

Overview of HArmonic DEcomposition of Spacetime (HADES) framework. (A) Here we used HADES to analyse data from DMT-induced resting-state fMRI in healthy participants and show the design for this experiment. (B) HADES uses the dense functional connectome constructed from the HCP S1200 release of 812 subjects to (C) construct a graph representation as a sparse, symmetric, and binary adjacency matrix of the dense functional connectome. (D) First, functional harmonics (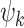(x)) are obtained from the Laplacian decomposition of the sparse adjacency matrix. (E) Functional harmonic decomposition is computed by projecting individual harmonics on the fMRI timeseries (surface representation) and calculating their contributions. (F) From this decomposition, HADES can be used to compute spatiotemporal measures for the first 11 FHs and 0th global FH—absolute contribution and condition normalized absolute contribution on any neuroimaging dataset. (G) Importantly, HADES can also be used to construct dynamic measures for the first 11 FHs and 0th global FH—fractional occupancy, life times and transition matrix. (H) These measures can be used as latent space representation in terms of temporal trajectory embedded in the functional harmonic space.

Absolute contribution across functional harmonics

To quantify contributions of individual harmonics in the different conditions, we computed the absolute and condition-normalized absolute contributions of each harmonic (Fig. 2A). The absolute contribution results show a decrease in the DMT-induced state (compared to DMT before injection and placebo-induced states) across most of the 11 FHs except of the 0th global FH. This is contrasted by the condition-normalized absolute contribution results demonstrating an increase in the global FH and a decrease in FH 2 after DMT injection versus before injection and the placebo data (Fig. 2B). Spider plots in Fig. 2A and B represent a visual redistribution of FHs across different conditions for the two measures.

Figure 2.

Spatiotemporal analysis of DMT and placebo neuroimaging data. The harmonic spatiotemporal analysis of the neuroimaging data shows that the contribution of functional harmonic 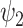(FH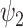) is very significantly reduced (P < 0.05, Bonferroni corrected) when participants were given DMT, both in terms of absolute and normalized contribution. (A) Specifically, the absolute contribution across the first 11 FHs and the 0th global FH is shown both visually, on a spider plot, and statistically for individual FH across the four DMT-based conditions. The results show a decrease in the DMT-induced state (compared to DMT before injection and the placebo state) across many of the 11 FHs except the global FH 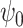(green star: P < 0.05, Bonferroni corrected paired t-test; red star: P < 0.05, not Bonferroni corrected paired t-test). (B) Equally, we show the normalized absolute contribution across the first 11 FHs and the 0th global FH represented both visually, on a spider plot, and statistically for individual FHs across the four DMT-based conditions. Again, the results demonstrate an increase in the global FH 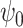but specifically a decrease in FH 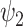compared to DMT before injection and the placebo state (green star: P < 0.05, Bonferroni corrected paired t-test; red star: P < 0.05 not, Bonferroni corrected paired t-test).

Dynamic measures of HADES

To assess the temporal evolution of FH weights, we apply a winner-takes-all approach whereby we select the most prominent FH at every time point and compute fractional occupancy (FO) and lifetimes (LT) of each FH. In Fig. 3A and B, we show results when choosing the 11 FHs. We excluded the 0th FH in this analysis to focus on the dynamical properties of functionally resolved FHs. As before, strongest statistical significance for FO and LT is observed in 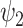(Fig. 3C). Furthermore, we computed the first order Markov process in terms of the Transition Probability Matrix (TPM) (Fig. S3A). We report statistics for the two DMT conditions (P-value < 0.05, uncorrected paired t-test).

Figure 3.

Dynamic analysis for the 11 FHs. Extending the spatial analysis into the spatiotemporal domain shows that functional harmonic 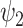(FH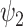) is significantly reduced in the DMT condition. (A) Specifically, fractional occupancy was found to be statistically different in the 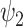. (B) Lifetimes were found statistically different in the 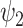(green star: P-value < 0.05 (# of 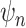), where n = 11, paired t-test; red star: P-value < 0.05, uncorrected paired t-test). (C) The full spatial extent of FH 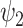is shown along with the significant results for fractional occupancy and lifetimes.

Latent space

Functional harmonics were used as the basis of a latent space representation in which the temporal trajectory of the brain dynamics was embedded in the latent space representation of the 11 FHs and the 0th global FH (Fig. 4A, here visualized for the first three FHs with colour shading representing the temporal trajectory). To further analyse how the temporal embedding in this latent space changes, we defined the expansion/contraction of the trajectory in terms of the latent dimension spread. The DMT-induced state contracts the contribution of the FHs across the board. Latent dimension spread was computed for all 11 FHs and the 0th global FH i.e. 12th dimensional space for the four conditions. We also report its statistics (green star P-value <0.05 Bonferroni corrected paired t-test). The temporal trajectory significantly contracts in the DMT-induced state.

Figure 4.

Latent space representation using the 11 FHs and the 0th global FH. Importantly, HADES can be used to create a latent space representation of the DMT neuroimaging data that immediately brings out important spacetime differences. (A) Here we show the figures with latent space representation using the first three FHs for visualization of the neuroimaging data. The green colour shading represents the temporal trajectory embedded in the three latent spatial dimensions of the FHs of DMT pre, PCB pre and PCB post. As can be immediately seen for the DMT-induced state (DMT post), there is a clear contraction of the contribution of the FHs across board (shown in red colour shading). (B) This can be directly quantified in terms of the latent dimension spread computed for all the 11 FHs and the 0th global FH i.e. 12th dimensional space for the four conditions. As can be seen, DMT post is significantly different from DMT pre and PCB post (green star: P < 0.05, Bonferroni corrected paired t-test).

DISCUSSION

In this study, we analysed spacetime hierarchy of the DMT-induced brain state in healthy participants using the HADES framework. We found a significant change of brain spacetime hierarchy in line with the theoretical predictions of the REBUS theory [25] and the anarchic brain hypothesis, integrating Friston's free-energy principle [50] with Carhart-Harris’ entropic brain hypothesis [23,24].

Consistent with previous literature, we have demonstrated the functional relevance of functional harmonics [4]. Moreover, we have demonstrated that an empirical fMRI signal can be accurately reconstructed with a subset of functional harmonics. Applying HADES to the DMT-induced state has shown decreases in absolute contribution across most FHs, while the global FH has remained unchanged. However, when looking at condition-normalized absolute contribution in individual subjects, a decrease in FH 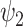was mirrored by an increase in the global harmonic. These results motivate a non-trivial reconfiguration whereby the DMT-induced state decreases in overall magnitude with a relative increase towards the global substate and a decrease of FH 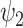representative of the functional hierarchies of the brain. This was further reinforced by the analysis of functional harmonic dynamics with decreases both in fractional occupancy and lifetimes of FH 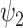demonstrating further dynamic collapse of this harmonic. Last, when the temporal trajectories were embedded in the latent space of the functional harmonic, the DMT-induced state showed significant contraction of its temporal trajectory spread.

Remarkably, FH 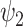resembles the so-called ‘principal gradient’—i.e. a unimodal to transmodal gradient previously found to explain the greatest proportion of variance in a principal components analysis of cortical functional connectivity [3]. This gradient has been proposed to reflect a hierarchy of brain function from low- to high-order cognitive networks. This is in line with several theories of brain organization; namely REBUS and the anarchic brain where functional hierarchies are undermined under psychedelics [34,38,50], Temporo-spatial Theory of Consciousness where temporo-spatial nestedness becomes abnormal resulting in loss of spatial topographic organization [51], and the Operational Spacetime Theory where operational spacetime is hypothesized to be altered reflecting disruptions in the phenomenal spacetime [52]. Furthermore, the relative increase in global FH speaks to a less functionally defined and more integrated global substate under the influence of DMT. Indeed, at the RSN level, psychedelic-induced states have been shown to subvert within-functional network connectivity, especially in higher-order frontoparietal and default mode networks [11,22,53,54], while enhancing between-network connectivity and overall global and integrative tendencies [11,19].

Traditionally, neuroscience has focused on delineating and studying localized cortical regions to map the brain's function. Such an approach has been of importance albeit with fragmented insights as to how multiscale brain organization gives rise to complex spatiotemporal dynamics and ultimately behaviour. A recent development in system neuroscience has been that of cortical gradients [3]. This proposes an intrinsic coordinate system of human brain organization continuously varying from unimodal to transmodal cortical areas [31]. Gradient-type organization has been demonstrated in terms of myelination [55], anatomical structure [30], white matter tract length [56], evolutionary expansion [57], ontogenetic expansion [58], temporal processing [59], semantic processing [60] and physiologically coupled travelling waves [61]. The framework of multidimensional harmonic representation and decomposition [4,46,47] adds to this list by decomposing brain activity maps into frequency-specific communication channels that unveil contributions of connectivity gradients and cortical parcellations to brain function. HADES extends these frameworks by considering the dynamic aspects of these frequency-specific channels of functional communication.

The brain as a complex system has been hypothesized to manifest hierarchies across time and space. Indeed, such a nested organization was suggested both in terms of the structural architecture of the brain as well as its temporal frequencies [62,63]. Functional harmonics are by construction intrinsically ordered according to their spatial frequencies and as such provide a multiscale representation of brain activity across cortical space. Intuitively, spatial frequencies relate to temporal frequencies of oscillations where global spatial frequencies of harmonics reflect slow oscillations and local spatial frequencies of harmonics reflect fast oscillations. Drawing a closer relationship between the spatial and temporal scales is an important further step (possibly explore with M/EEG modalities) as the relevance of intrinsic neuronal timescales (INT) have been proposed for input sharing [64] with a hierarchical organization closely relating to the spatial organization of FH 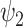[57]. This hierarchical organization is important for temporal integration and segregation of input stimuli [65], with Default Mode Network possibly sitting at the apex integrating information over long timescales [66]. Indeed, recent work has shown how this temporal hierarchy changes in rest and task MEG data [67]. Yet how the changes in spatial distribution of the INT maps on the temporal frequencies of the functional harmonics remains to be seen. This could in part be due to the conceptual difference between the approaches whereby functional harmonics associate temporal frequency to individual harmonics, while INT mostly pertains to individual nodes.

Previously, connectome harmonics have been used to decompose the brain's spatiotemporal activity into a combination of time-varying contributions [46]. Using long-range and local connectivity as an underlying structure has been relevant in exploring the structure-function relationship of large-scale brain organization [47]. However, it seems that structural connectivity alone cannot explain the emergence of rich and spontaneous activity of the human brain [68,69]. First, neocortex is endowed with remarkable heterogeneity in cytoarchitecture. This will result in various computational differentiations across the cortex, for example in terms of temporal processing [59]. Second, the neuromodulatory system is known to alter the electrical composition of neurons and thus exercise non-linear effects on the emergent activity of various microcircuits across the brain [70,71]. The hypothesis here is that the communication structure of dense FC has implicitly embedded within it information on anatomical structure, cortical computational heterogeneity as well as neuromodulatory expression and as such serves as a prominent candidate to be used for the derivation of fundamental functional building blocks of spatiotemporal activity [4]. This in turn is expanded upon in the HADES framework with dynamic measures and latent space embeddings, whereby the emphasis is on the importance of the temporal dimension along which these spatiotemporal blocks building unfold.

Latent space representation has become an important research topic in neuroscience due to its ability to retrieve meaningful features contained in large and complex datasets [72]. It is possible to identify patterns and relationships in a lower-dimensional space between regions and between cognitive processes as the underlying computations giving rise to cognitive functions are likely to be integrated [1]. There are many techniques that serve this purpose from more traditional linear approaches such as singular value decomposition or principal component analysis [73], to popular techniques based on independent component analysis [74]. More recent works use autoencoders as an elegant way of compressing the fMRI signal while accounting for non-linearity in the data [75]. Here, we chose functional harmonics as they preserve nonlinear relationship between regions and have multiscale and interpretable representation of its latent dimensions [4,76]. However, it is to be noted that the idea of HADES as a framework goes beyond the actual representation of the dimension of the latent space (here in terms of functional harmonics) as it attempts to combine the spatial and temporal representation of complex brain dynamics. Moreover, in theory, other techniques could be applied in a similar way as to account for the complex spatiotemporal activity of the human brain.

A limitation of the current approach for describing functional harmonics propagating in time is that it might be too reductionist. ‘Winner-takes-all’ is a powerful technique summarizing the brain's dynamics in terms of fractional occupancy and lifetimes of the functional harmonics. However, it considers only one FH to be active at a given timepoint and as such might neglect other potential important information included in other FHs. Future work should implement weighted contributions of individual FHs at given timepoints and as such more completely describe the multidimensional representation of spatiotemporal dynamics. Another aspect for repeatability and robustness of the functional harmonics is the choice of the binarization of the adjacency matrix. Future work should for example investigate how the nearest-neighbours approach compares to distance-dependent binarizations [77] or data-driven topological approach [78].

CONCLUSION

Taken all together, in this study we have examined the spatiotemporal dynamics of the brain under DMT with the sensitive and robust new HADES framework, which uses FHs derived from the brain's communication structure to model dynamics as weighted contributions of FHs evolving in time. Overall, we corroborate the REBUS and anarchic brain model of psychedelic action by demonstrating dynamic changes to brain's functional spacetime hierarchies.

METHODS

Detailed methods and materials are given in the online supplementary data.

CODE AVAILABILITY

Codes to apply the HADES framework and to follow the DMT analysis can be found publicly available at https://github.com/jvohryzek/HADES

FUNDING

Jakub Vohryzek is supported by EU H2020 FET Proactive project Neurotwin (101017716). Morten L. Kringelbach is supported by the European Research Council Consolidator Grant: CAREGIVING (615539), Pettit Foundation, Carlsberg Foundation, Center for Music in the Brain, and the Danish National Research Foundation (DNRF117). Joana Cabral is supported by ‘la Caixa’ Foundation, Spain (LCF/BQ/PR22/11920014) and the Portuguese Foundation for Science and Technology, Portugal (UIDB/50026/2020 and UIDP/50026/2020). Gustavo Deco is supported by the Spanish Research Project (PSI2016-75688-P, Agencia Estatal de Investigación/Fondo Europeo de Desarrollo Regional, European Union), the European Union's Horizon 2020 Research and Innovation Programme (720270 (Human Brain Project [HBP] SGA1) and 785907 (HBP SGA2)), and the Catalan Agency for Management of University and Research Grants (2017 SGR 1545).

AUTHOR CONTRIBUTIONS

J.V., G.D. and M.L.K. conceived and designed the analysis. J.V., S.A. and J.C. contributed with analysis tools. C.T., L.R., D.N. and R.C.H. contributed with the dataset. L.R. preprocessed the data. J.V. analysed the data. M.L.K., G.D., D.N. and R.C.H. supervised the analysis. J.V. wrote the original draft and the Supplementary Information. All authors reviewed and edited the final paper and the Supplementary Information.

Conflict of interest statement. Robin Carhart-Harris is a scientific advisor to Usona Institute, Journey Colab, Osmind, Maya Health, Beckley Psytech, Anuma, MindState and Entheos Labs.