Abstract
BACKGROUND:
Single nucleotide polymorphism–based heritability is a fundamental quantity in the genetic analysis of complex traits. For case-control phenotypes, for which the continuous distribution of risk in the population is unobserved, observed-scale heritability estimates must be transformed to the more interpretable liability scale. This article describes how the field standard approach incorrectly performs the liability correction in that it does not appropriately account for variation in the proportion of cases across the cohorts comprising the meta-analysis. We propose a simple solution that incorporates cohort-specific ascertainment using the summation of effective sample sizes across cohorts. This solution is applied at the stage of single nucleotide polymorphism–based heritability estimation and does not require generating updated meta-analytic genome-wide association study summary statistics.
METHODS:
We began by performing a series of simulations to examine the ability of the standard approach and our proposed approach to recapture liability-scale heritability in the population. We went on to examine the differences in estimates obtained from these 2 approaches for real data for 12 major case-control genome-wide association studies of psychiatric and neurologic traits.
RESULTS:
We found that the field standard approach for performing the liability conversion can downwardly bias estimates by as much as approximately 50% in simulation and approximately 30% in real data.
CONCLUSIONS:
Prior estimates of liability-scale heritability for genome-wide association study meta-analysis may be drastically underestimated. To this end, we strongly recommend using our proposed approach of using the sum of effective sample sizes across contributing cohorts to obtain unbiased estimates.
Single nucleotide polymorphism (SNP)–based heritability quantifies the proportion of total variance in a phenotype within a population that is attributable to the additive effect of tagged genetic variants. For continuously measured quantitative traits, in which phenotypic variation is directly observed, estimates produced from standard methods such as linkage disequilibrium (LD) score regression (LDSC) (1) are directly interpretable. However, when the measured phenotypes are binary (e.g., for case-control psychiatric traits) conventional estimates of are not easily interpreted for 2 reasons. The first is because of the binarized scale of the data in which is most interpretable when taking into account the continuous distribution of risk in the population. The second relates to the fact that genome-wide association studies (GWASs) of disease traits are often performed on ascertained samples, in which affected individuals are overrepresented so as to increase statistical power for rare disorders. The standard transformation for binary traits then uses a liability threshold model to convert observed-scale SNP-based heritability to liability-scale SNP-based heritability to produce an estimate that both accounts for the continuous distribution of risk in the population and is not biased by ascertainment. In practice, is commonly estimated with summary-based methods such as LDSC using results from GWAS meta-analysis across many different samples, varying in their levels of ascertainment.
Here, we highlight a critical error in the standard practice for calculating from GWAS meta-analysis that can cause substantial downward bias due to variation in cohort-specific ascertainment, and we formally derive a simple procedure for obtaining unbiased estimates. We report results from simulations that illustrate the extent of the downward bias across a variety of conditions and showcase the unbiased nature of the proposed procedure within these same conditions. We go on to quantify the extent of this bias in 12 recent GWAS meta-analyses of case-control psychiatric and neurologic traits. It appears that the biased approach has been used for estimates for nearly all meta-analytic GWAS of binary traits.
Observed-scale heritability is estimated within univariate LDSC as
| (1) |
where N is the sample size, is the observed-scale heritability, is the total LD score for SNP j, M is the total number of SNPs used to calculate the LD scores, and a is a term representing unmeasured sources of confounding such as population stratification (1).
When summary data are derived from a single case-control GWAS (either of a single sample or of raw data that have been combined across multiple samples prior to GWAS), the observed-scale heritability can be converted to the liability scale as follows:
| (2) |
where v is the sample prevalence, P is the population prevalence, and is the height of the standard normal probability density function at the threshold corresponding to P (2–4). Combining equations 1 and 2 produces the reduced form LDSC equation for binary traits:
| (3) |
In Supplement 1, we show that when GWAS summary data are derived from meta-analysis of summary statistics from multiple, individual case-control GWASs, the appropriate reduced form equation for estimating is
| (4) |
which resembles equation 3 for summary statistics derived from a single GWAS, with the key difference being that is replaced by .
Importantly, currently available software does not allow for direct entry of , and the standard practice in LDSC analysis of meta-analytic GWAS summary data has been to compute a single meta-analytic v as the total sample prevalence (i.e., aggregate number of cases across all samples divided by the aggregate sample size and enter this quantity into equation 3). When samples are differentially ascertained, as is nearly always the case in empirical settings, such an approach is not equivalent to the correct approach given by equation 4. Indeed, the 2 calculations can produce very different results in the presence of varying levels of ascertainment across contributing cohorts, with corresponding effects on estimates of . For example, consider 2 case-control cohorts each comprising 10,000 participants but with disparate levels of ascertainment wherein the first cohort has 10% cases (i.e., ) and the second cohort has 50% cases (correct value given by . In this example, , whereas the correct value given by .
Put more formally, we can express the inequivalence of the 2 approaches as follows:
| (5) |
We refer to the quantity on the left of the inequality as the summation of cohort-specific ascertainments and the quantities on the right of the inequality as the total sample ascertainment.
In Supplement 1, we describe a simple procedure in which the correct estimate of (as would be obtained via equation 4) can be obtained for meta-analytic summary statistics using standard software (i.e., implementing equation 2) [e.g., LDSC (1), genomic structural equation modeling (Genomic SEM) (5), MTAG (6), LDAK (7)]. First, the effective sample size, is computed for each study, k, as
| (6) |
where represents the sample size for an equivalently powered GWAS within a balanced sample (i.e., 50% cases, 50% controls)1. Because the values are directly comparable across GWAS samples they can be summed. The sum of across all contributing GWASs is then entered for N along with the , so as to represent the balanced nature of the design. Relatedly, we note that multiplying the quantity by 4 when calculating effective sample counterbalances the fact that entering results in the quantity 0.5 (1–0.5) (i.e., ). This proposed solution of using the is applied at the point of estimating the SNP-based heritability and does not require redoing the GWAS meta-analysis. The population prevalence from collateral epidemiological data is entered for P as usual. As with the quantities described in equation 5, the effective sample size calculated using total sample prevalence is not equal to the sum of effective sample sizes calculated using cohort-specific sample prevalence. This inequality can be expressed as
| (7) |
In addition to being pragmatically appealing, given current available software, this approach has 3 additional advantages. First, a number of statistical pipelines adopted by major, genomic research consortia default to outputting in the GWAS summary statistics output. In recognition of the fact that the RICOPILI (Rapid Imputation and Computational Pipeline for GWAS) pipeline implemented by the Psychiatric Genomics Consortium (1) defaults to outputting . We have updated the GenomicSEM software to automatically double this column (typically labeled as Neff_half) and use it as input for subsequent heritability calculations (of course, for other software, the researcher can easily double this quantity prior to running analyses). Second, this allows the researcher to account for both cohort-specific and SNP-specific information. That is, when participant sample size varies by SNP, as is often the case given different genotyping platforms used by cohorts, it is preferrable to use this SNP-specific information. Third, when cohort-level information is not available to compute , the sum of effective sample sizes can be approximated directly from GWAS summary statistics (see Section S6 of Supplement 1) (8,9). Annotated code and examples for applying this proposed procedure can be found in a new section on how to calculate sample size on the GenomicSEM GitHub (https://github.com/GenomicSEM/GenomicSEM/wiki/2.1-Calculating-Sum-of-Effective-SampleSize-and-Preparing-GWAS-Summary-Statistics ). Note that we also describe in Section S5 of Supplement 1 how to extend this approach to produce unbiased, SNP-based heritability estimates for meta-analyses that combine binary and continuous measures of the same trait.
METHODS AND MATERIALS
Simulation and Recovery of SNP Heritability for Binary Traits
Simulation of Summary Statistics.
Each simulation began by generating genome-wide summary statistics for binary traits for 10 individual cohorts. We began with a series of simulations that specified a population prevalence of 1%, a liability-scale heritability of 15% in the population, cross-trait intercepts of 0 to reflect no sample overlap across the 10 cohorts, and a univariate intercept of 1.0 to reflect no uncontrolled for population stratification. Each cohort was specified to have a sample prevalence of either 10% (low ascertainment) or 50% (high ascertainment), with the balance of cohorts with low and high ascertainment varying across 11 simulation conditions (see Table 1 for details on each condition). Note that when liability-scale heritability is equal, but sample prevalence differs across cohorts, observed-scale heritability will differ across cohorts.
Table 1.
Simulation Results Across Conditions
| Proposed Approach: |
Field Standard Approach: |
|||||||
|---|---|---|---|---|---|---|---|---|
| Condition | 50% Cases/50% Controls | 10% Cases/90% Controls | Mean (SD) | Range | Mean % Bias (SD) | Mean (SD) | Range | Mean % Bias (SD) |
| Condition 1 | 0 | 10 | 15.06 (0.56) | 13.51–16.42 | 0.39% (3.70%) | 15.06 (0.56) | 13.51–16.42 | 0.39% (3.70%) |
|
| ||||||||
| Condition 2 | 1 | 9 | 14.98 (0.50) | 13.51–16.14 | −0.12% (3.34%) | 13.19 (0.44) | 11.89–14.22 | −12.07% (2.94%) |
|
| ||||||||
| Condition 3 | 2 | 8 | 14.99 (0.48) | 13.67–16.23 | −0.11% (3.18%) | 12.39 (0.39) | 11.30–13.41 | −17.43% (2.63%) |
|
| ||||||||
| Condition 4 | 3 | 7 | 15.02 (0.37) | 14.13–15.93 | 0.15% (2.48%) | 12.08 (0.30) | 11.37–12.81 | −19.46% (1.99%) |
|
| ||||||||
| Condition 5 | 4 | 6 | 14.97 (0.35) | 14.33–15.62 | −0.21% (2.35%) | 11.98 (0.28) | 11.47–12.50 | −20.13% (1.88%) |
|
| ||||||||
| Condition 6 | 5 | 5 | 15.02 (0.32) | 14.01–15.75 | 0.12% (2.10%) | 12.15 (0.26) | 11.34–12.75 | −18.95% (1.70%) |
|
| ||||||||
| Condition 7 | 6 | 4 | 15.07 (0.28) | 13.83–15.63 | 0.48% (1.87%) | 12.49 (0.23) | 11.47–12.95 | −16.72% (1.55%) |
|
| ||||||||
| Condition 8 | 7 | 3 | 14.99 (0.26) | 14.37–15.73 | −0.04% (1.70%) | 12.86 (0.22) | 12.32–13.49 | −14.29% (1.46%) |
|
| ||||||||
| Condition 9 | 8 | 2 | 15.03 (0.26) | 14.39–15.63 | 0.24% (1.75%) | 13.46 (0.24) | 12.88–13.99 | −10.30% (1.57%) |
|
| ||||||||
| Condition 10 | 9 | 1 | 15.01 (0.25) | 14.37–15.67 | 0.08% (1.68%) | 14.14 (0.24) | 13.53–14.76 | 25.72% (1.58%) |
|
| ||||||||
| Condition 11 | 10 | 0 | 15.03 (0.22) | 14.36–15.57 | 0.22% (1.50%) | 15.03 (0.22) | 14.36–15.57 | 0.22% (1.50%) |
The 50% cases/50% controls and 10% cases/90% controls columns denote the total number of cohorts with this case-control split for each condition. The Proposed Approach columns denote the simulation results when using ; reflecting the sum of effective sample sizes across cohorts, and for the liability correction. The Field Standard Approach columns report simulation results when using , which denotes using the total sample prevalence calculated using the aggregate number of cases and controls across cohorts and the total sample size for the liability correction.
, SNP-based heritability estimate; SNP, single nucleotide polymorphism.
We went on to perform a second set of simulations that aimed to systematically characterize the effect of different population generating parameters on liability-scale heritability estimates. For all conditions in this second set of simulations, the 10 cohorts consisted of 5 cohorts with 10% sample prevalence and 5 cohorts with 50% sample prevalence. The same population generating parameters from the first set of simulations were used (population prevalence = 1%; liability-scale heritability = 15%; cohort-level sample size = 5000; univariate LDSC intercept = 1) with the exception that one of these values was changed within each condition. This second set of simulations then consisted of 12 distinct conditions that examined the downstream consequences of changing the cohort-level sample size (1000, 10,000, 20,000, or 25,000), the liability-scale heritability (5%, 10%, 20%, or 25%), the population prevalence (1%, 5%, 10%, or 15%), or the LDSC univariate intercept (1.04) (see Table S1 in Supplement 2).
Data Generating Model.
For all simulations, data were simulated using European population LD scores provided by the original LDSC developers (10) for 1,184,461 HapMap3 SNPs, excluding the major histocompatibility complex region and sex chromosomes, according to simulation procedures first described in de la Fuente et al. (11). More specifically, summary statistics were simulated following the multivariate LDSC equation:
| (8) |
where
| (9) |
and reflects the Z statistics for the 10 GWAS cohorts (expressed in condensed form, not depicting cohorts 3 to 9 from the current simulations for display reasons), M is the number of SNPs from the LD file (1,184,461), is the number of overlapping individuals, N is the sample size of the individual GWAS, is the LD score of SNP j, and reflects the univariate LDSC intercept that picks up on unmeasured confounds, such as population stratification. The bivariate LDSC intercept, expressed as for cohorts 1 and 2, was 0 owing to setting the sample overlap () to 0 for all simulations. GWAS z statistics were simulated following the equation above and using the mvrnorm R function from the MASS package for each SNP. For each condition, 100 sets of summary statistics were simulated (i.e., 1000 cohort-level summary statistics per condition for a total of 11,000 simulated cohorts across the 11 conditions).
From the simulated cohort-level GWAS z statistics, we computed logistic betas as follows:
| (10) |
where and reflects the cohort-specific sample prevalence and sample size, respectively, and reflects the variance of a given SNP j calculated as , where MAF is the minor allele frequency. The logistic standard errors for a given SNP j and cohort k were then calculated as
| (11) |
These logistic betas and standard errors were used to calculate the inverse-variance weighted meta-analytic beta across the 10 contributing cohorts as described in Supplement 1. This procedure then produced a single summary statistics file reflecting the meta-analyzed output across the 10 simulated cohorts. This summary statistics file was finally analyzed in LDSC in 1 of 2 ways, as described in the section below.
Analysis of Simulated Summary Statistics.
We compared the ability to recover the population liability-scale heritability for 2 approaches: the standard procedure of inputting the total sample prevalence and the total sample size , versus our proposed approach of inputting the sum of effective sample sizes and a sample prevalence (v) of 0.5 to reflect the fact that the effective sample size equation already accounts for cohort-specific sample ascertainment. For each simulation condition and liability correction approach, we report the mean liability-scaled heritability estimate, standard deviation across the 100 simulations, the range of parameter estimates, and the mean proportional bias relative to the population generating parameter, calculated as
| (12) |
where is the parameter estimate for a given run, r, and was the population generating value of 15%.
Simulating Ascertainment Variability
The key error in the field standard approach is that it does not account for variation in ascertainment across cohorts. As such, the expectation for the degree of bias in liability-scale heritability for the field standard approach can be indexed using the ratio of the sum of effective sample sizes (our proposed approach) over the effective sample size calculated using the total number of cases and controls (statistically equivalent to the field standard approach). In other words,
| (13) |
Note that equation 13 makes it explicit that bias with respect to the heritability estimate is an inverse function of bias with respect to the computation of .
We went on then to perform a series of simulations that relied on this property by generating a wide variety of cohort-specific sample sizes and analytically computing bias in the heritability estimate, rather than generating GWAS summary statistics and estimating heritability. We began by performing a set of simulations that mirrored the simulating conditions when GWAS summary statistics were generated (i.e., mixtures of cohorts consisting of 50%/50% and 10%/90% cases/control ratios) to confirm the equivalence of the 2 approaches. We then expanded the range of simulating conditions to consider the full scope of potential bias within a plausible range. This involved running 1000 simulations that all consisted of generating 10 cohorts of 1000 participants, with each cohort set to randomly contain a proportion of cases between 5% and 95%.
Analysis of Real Data
We examined liability-scale heritability estimates for publicly available, European only summary statistics for 12 major disorders: attention-deficit/hyperactivity disorder (12), alcohol dependence (13), Alzheimer’s disease (ALZ) (14), anorexia nervosa (15), autism spectrum disorder (16), bipolar disorder (17), cannabis use disorder (18), major depressive disorder (19), obsessive-compulsive disorder (20), posttraumatic stress disorder (21), schizophrenia (22), and Tourette syndrome (23). For each set of summary statistics, we followed the standard quality control procedure of filtering out SNPs with an imputation quality (INFO) score < 0.9 and minor allele frequency <1% and filtering to SNPs present in the HapMap3 file excluding the major histocompatibility complex region and sex chromosomes. In line with prior work for ALZ, we also removed the APOE region prior to calculating heritability. In addition, for ALZ we confirmed that the GERAD (Genetic and Environmental Risk in Alzheimer’s Disease) consortium was analyzed as a single cohort while the remaining contributing consortia (ADGC [Alzheimer’s Disease Genetics Consortium], CHARGE [Cohorts for Heart and Aging Research in Genomic Epidemiology], and EADI [European Alzheimer’s Disease Initiative]) reflected meta-analyzed summary statistics obtained from individual cohorts. Thus, a single was calculated for GERAD while was calculated for each of the contributing cohorts for the other consortia prior to summing them all together to produce a single for ALZ. For all traits, the liability-scale heritability was then calculated using either our proposed approach of inputting or the field standard approach of using . For , the SNP-specific sum of effective sample sizes was used when available. Similarly, when using , the SNP-specific total sample size was used when this information was available. Bias was calculated here as the proportion of the estimate captured by :
| (15) |
RESULTS
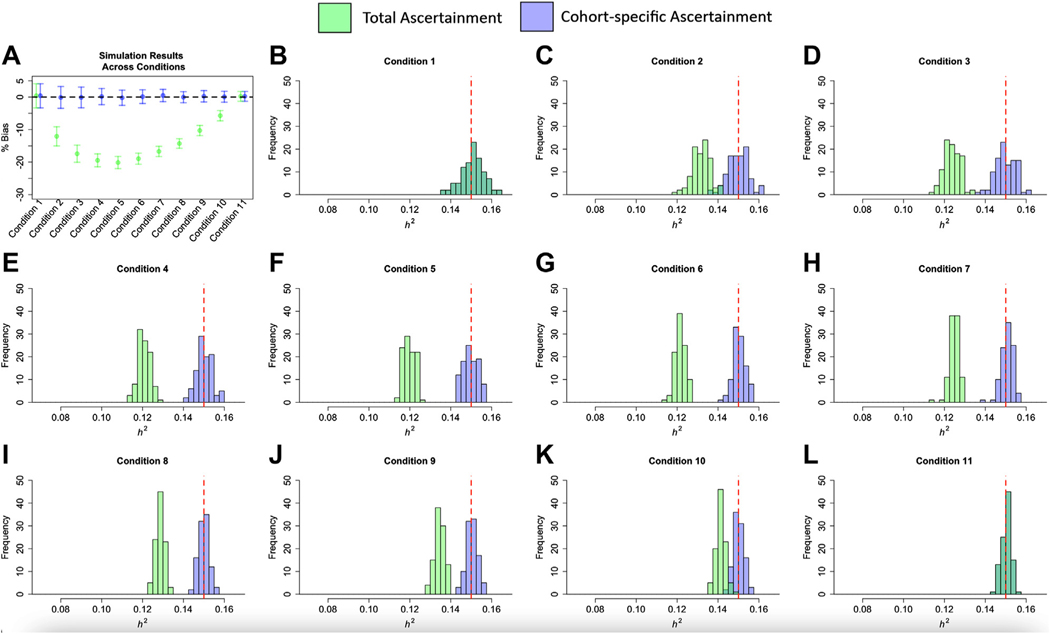
Simulation results using GWAS summary statistics are presented in Figure 1, Table 1, and Table S1 in Supplement 2. Simulation results that directly simulated ascertainment variability are presented in Figure S1 in Supplement 1. These results reveal 3 primary findings. First, the field standard approach of using can produce substantial, downward bias for liability-scale heritability estimates, with bias increasing as a function of the degree of variability in ascertainment across contributing cohorts (Figure 1A; Figure S1 in Supplement 1). Thus, bias was greatest for those conditions when the ascertainment variability was highest across cohorts. Indeed, holding ascertainment variability constant resulted in the same level of bias for different population SNP-based heritability estimates, cohort sample sizes, population prevalence, and levels of unaccounted for population stratification (Table S1 in Supplement 2). For simulations using GWAS summary statistics within a relatively narrow range of conditions and those directly simulating ascertainment variability across a wider range of conditions, the downward bias was as much as approximately 20% and approximately 50%, respectively (Table 1; Figure S1 in Supplement 1). Second, both the field standard and our proposed approaches produce the same estimates when ascertainment is equivalent across all cohorts (Figure 1B, L). Importantly, the standard procedure of using total sample prevalence () is not biased as a function of the overall degree of ascertainment. Rather, the bias is attributable to the level of ascertainment variability across cohorts. Third, our proposed procedure of using removes this bias, producing accurate estimates of the population-level, liability-scale heritability (Table 1 and Figure 1) across a range of population generating conditions (Table S1 in Supplement 2). Having established that using P EffNk produces an accurate estimate of , we went on to examine the difference across using and in real data.
Figure 1.
Simulation results across conditions. Panel (A) depicts the mean percentage bias on the y-axis across the 11 simulation conditions on the x-axis. Error bars depict ±1 SD. Panels (B–L) depict the individual point estimates from the 100 simulations per condition across the 11 conditions. The red dashed line indicates the liability-scale of 15% in the population. All panels depict the results from using to account for cohort-specific ascertainment in green and the results from using for the liability correction in blue, which denotes using the total sample prevalence calculated using the aggregate number of cases and controls across cohorts. Because and produced equivalent solutions for panels (B) and (L), the blue and green distributions are entirely overlapping.
We compared the field standard procedure of using versus our proposed approach of using for 12 major, binary traits for which sufficient cohort-level information was available: We used the same population prevalences from the original GWAS publications from which the summary statistics were derived. We quantified bias here as the proportional difference across and (i.e., ). Consistent with simulation findings, real data results revealed that in all cases using produced a deflated estimate of liability-scale heritability relative to . This bias ranged from as little as 1.3% for autism spectrum disorder to as much as 28.1% for alcohol use disorder and 31.8% for bipolar disorder (17) (Table 2). In all but one instance, the heritability estimates reported in the corresponding manuscripts most closely matched those produced from using (Table S2 in Supplement 2). The exception was the most recent release (Freeze 3) of the Psychiatric Genomics Consortium bipolar summary statistics (17), which reports a liability-scale heritability consistent with using .
Table 2.
LDSC Heritability Estimates Using Total or Cohort-Specific Ascertainment
| Trait | Reference | Population Prevalence | Cases | Controls | Field Standard Approach | Proposed Approach | % Bias |
|---|---|---|---|---|---|---|---|
| ADHD | Demontis et al., 2019 (12) | 5.0% | 19,099 | 34,194 | 22.1% (1.4) | 23.7% (1.6) | −6.7% |
| ALCH | Walters et al., 2018 (13) | 15.9% | 10,206 | 28,480 | 10.0% (1.8) | 13.9% (2.5) | −28.1% |
| ALZ | Kunkle et al., 2019 (14) | 4.3% | 21,982 | 41,944 | 5.8% (0.9) | 7.0% (1.1) | −20.7% |
| AN | Watson et al., 2019 (15) | 0.9% | 16,992 | 55,525 | 13.8% (0.9) | 15.5% (1.0) | −10.8% |
| ASD | Grove et al., 2019 (16) | 1.2% | 18,381 | 27,969 | 11.7% (1.0) | 11.9% (1.0) | −1.3% |
| BIP | Mullins et al., 2021 (17) | 2.0% | 41,917 | 371,549 | 12.8% (0.5) | 18.7% (0.8) | −31.8% |
| CUD | Johnson et al., 2020 (18) | 1.0% | 14,080 | 343,726 | 6.7% (0.6) | 7.5% (0.7) | −11.5% |
| MDD | Wray et al., 2018 (19) | 15.0% | 59,851 | 113,154 | 10.2% (0.6) | 11.5% (0.7) | −11.8% |
| OCD | Arnold et al., 2018 (20) | 2.5% | 2688 | 7037 | 28.5% (4.4) | 29.9% (4.6) | −4.7% |
| PTSD | Nievergelt et al., 2019 (21) | 30.0% | 23,212 | 151,447 | 5.3% (0.9) | 6.1% (1.1) | −12.9% |
| SCZ | Trubetskoy et al., 2022 (22) | 1.0% | 53,386 | 77,258 | 20.7% (0.7) | 22.3% (0.8) | −6.9% |
| TS | Yu et al., 2019 (23) | 0.8% | 4819 | 9488 | 21.5% (2.5) | 22.4% (2.6) | −4.0% |
The field standard approach column report liability-scale heritability results when using and the total sample size for ascertainment correction. The proposed approach column reports results when using and for ascertainment correction. Liability-scale heritability estimates were calculated using the SNP-specific total sample sizes, or the SNP-specific , when possible. Table S1 in Supplement 2 reports the original heritability estimates from the corresponding publication along with heritability estimates calculated using both the SNP-specific or total sample sizes for reference. Population prevalence was chosen based on the prevalence reported in the original publication for that trait for comparability purposes. % Bias was calculated as the proportional attenuation in heritability estimates when using total over cohort-specific ascertainment to perform the liability correction; this was calculated using the direct output from LDSC and therefore will not exactly match the numbers obtained from using the liability reported in the table owing to rounding. Results are reported for GWAS data that are strictly publicly available (e.g., 23andMe data are not included for MDD or ADHD).
ADHD, attention-deficit/hyperactivity disorder; ALCH, alcohol use disorder; ALZ, Alzheimer’s disease; AN, anorexia nervosa; ASD, autism spectrum disorder; BIP, bipolar disorder; CUD, cannabis use disorder; , LDSC liability-scale heritability estimate; LDSC, linkage disequilibrium score regression; MDD, major depressive disorder; OCD, obsessive-compulsive disorder; PTSD, posttraumatic stress disorder; SCZ, schizophrenia; SNP, single nucleotide polymorphism; TS, Tourette syndrome.
DISCUSSION
SNP-based heritability is a fundamental quantity in complex trait genetics. As such, SNP-based heritability estimates from GWAS summary statistics are standard results to report in any major GWAS meta-analysis effort. For binary traits, such as case-control disease traits, SNP-based heritability estimates must be converted to the liability scale to be meaningfully interpreted. We demonstrate here that the field standard approach for estimating liability-scale heritability from meta-analytic GWAS summary data can downwardly bias liability-scale heritability estimates by as much as approximately 50% in simulations and approximately 30% in real data. We have therefore proposed a simple procedure for obtaining unbiased estimates of liability-scale SNP-based heritability in these contexts.
Downwardly biased estimates of SNP-based heritability will propagate to produce downwardly biased estimates of genetic covariance, which may in turn bias methods that rely on these estimates [e.g., MTAG (6), GenomicSEM (5)]. Importantly, genetic correlations are expected to be unaffected by this bias because they standardize genetic covariance estimates relative to heritability estimates, thereby canceling out the bias. Another issue that merits further investigation is the presence of ascertainment differences that stratify by meaningful covariates across cohorts. For example, it is currently unknown how estimates may be biased when ascertainment varies across GWAS cohorts more for one sex than the other. In addition, it will be important to examine the effect of ascertainment differences when cohorts systematically vary with respect to the severity of cases, as may be observed for meta-analyses of inpatient and community samples.
Genomic-relatedness matrix restricted maximum likelihood (2,24) is a major alternative to LDSC that estimates heritability using raw genotypes among unrelated individuals. While LDSC has the advantage of requiring only summary-level data, and is thus especially applicable to GWAS meta-analysis results, genomic-relatedness matrix restricted maximum likelihood is often considered preferable when raw data are available (25,26) because it is typically found to produce larger SNP-based heritability estimates than those obtained from LDSC (27). One potential explanation for this discrepancy includes the possibility that, because LDSC is typically applied to meta-analytic GWAS data, it will only detect the portion of heritable signal that is consistent across contributing GWAS datasets. A second potential explanation for this discrepancy is that LDSC may produce attenuated heritability estimates because of discrepancies between LD structure in the reference data used to construct the LD scores and the samples from which the GWAS estimates were derived. In addition to these issues, the present findings highlight another, easily correctable, source of discrepancy across LDSC and genomic-relatedness matrix restricted maximum likelihood for binary traits.
In summary, the field standard approach to estimating SNP-based for GWAS meta-analysis of binary traits results in a downward bias because it fails to account for variation in the proportion of cases (i.e., variable levels of ascertainment) across contributing cohorts. Our proposed solution of using corrects for this bias and is applied at the stage of SNP-based estimation such that it does not require rerunning the GWAS meta-analysis. For most psychiatric traits, is already available in the GWAS summary statistics or can be straightforwardly computed from information provided in the original publication reporting the GWAS meta-analysis. In addition, we have shown that when cannot be obtained, it can be straightforwardly approximated from the GWAS summary data. Thus, the use of can be widely applied for the liability correction going forward so as to produce more accurate estimates of SNP-based heritability.
Supplementary Material
ACKNOWLEDGMENTS AND DISCLOSURES
ADG and EMT-D were supported by National Institutes of Health (NIH) (Grants Nos. R01MH120219 and RF1AG073593). MGN was supported by ZonMw (Grants Nos. 849200011 and 531003014) from The Netherlands Organization for Health Research and Development, a Veni grant awarded by NWO (Grant No. VI Veni.191G.030), NIH (Grants No. R01MH120219) and is a Jacobs Foundation Fellow. EMT-D and JdlF are members of the Population Research Center (PRC) and Center on Aging and Population Sciences (CAPS) at The University of Texas at Austin, which are supported by NIH (Grant Nos. P2CHD042849 and P30AG066614, respectively).
Footnotes
A previous version of this article was published as a preprint on medRxiv: https://doi.org/10.1101/2021.09.22.21263909.
The authors report no biomedical financial interests or potential conflicts of interest.
Supplementary material cited in this article is available online at https://doi.org/10.1016/j.biopsych.2022.05.029.
We note that we have observed different, statistically equivalent versions of calculating effective sample size in the literature, any of which may be used as long as they are calculated at the cohort-level prior to summation. At the cohort-specific level, these equivalent versions can be expressed as either .
REFERENCES
- 1.Bulik-Sullivan BK, Loh PR, Finucane HK, Ripke S, Yang J, Schizophrenia Working Group of the Psychiatric Genomics Consortium, et al. (2015): LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet 47:291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee SH, Wray NR, Goddard ME, Visscher PM (2011): Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet 88:294–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dempster ER, Lerner IM (1950): Heritability of threshold characters. Genetics 35:212–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Peyrot WJ, Boomsma DI, Penninx BWJH, Wray NR (2016): Disease and polygenic architecture: Avoid trio design and appropriately account for unscreened control subjects for common disease. Am J Hum Genet 98:382–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Grotzinger AD, Rhemtulla M, de Vlaming R, Ritchie SJ, Mallard TT, Hill WD, et al. (2019): Genomic structural equation modelling provides insights into the multivariate genetic architecture of complex traits. Nat Hum Behav 3:513–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Turley P, Walters RK, Maghzian O, Okbay A, Lee JJ, Fontana MA, et al. (2018): Multi-trait analysis of genome-wide association summary statistics using MTAG [published correction appears in Nat Genet 2019; 51:1190 and Nat Genet 2019; 51:1295]. Nat Genet 50:229–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Speed D, Cai N, UCLEB Consortium, Johnson MR, Nejentsev S, Balding DJ (2017): Reevaluation of SNP heritability in complex human traits. Nat Genet 49:986–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Privé F, Arbel J, Aschard H, Vilhjálmsson BJ (2022): Identifying and correcting for misspecifications in GWAS summary statistics and polygenic scores. HGG Adv 3(4):100136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mallard TT, Linnér RK, Grotzinger AD, Sanchez-Roige S, Seidlitz J, Okbay A, et al. (2022): Multivariate GWAS of psychiatric disorders and their cardinal symptoms reveal two dimensions of cross-cutting genetic liabilities. Cell Genom 2:100140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bulik-Sullivan B, Finucane HK, Anttila V, Gusev A, Day FR, Loh PR, et al. (2015): An atlas of genetic correlations across human diseases and traits. Nat Genet 47:1236–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.de la Fuente J, Grotzinger AD, Marioni RE, Nivard MG, Tucker-Drob EM (2021): Multivariate modeling of direct and proxy GWAS indicates substantial common variant heritability of Alzheimer’s disease. medRxiv. 10.1101/2021.05.06.21256747. [DOI]
- 12.Demontis D, Walters RK, Martin J, Mattheisen M, Als TD, Agerbo E, et al. (2019): Discovery of the first genome-wide significant risk loci for attention deficit/hyperactivity disorder. Nat Genet 51:63–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Walters RK, Polimanti R, Johnson EC, McClintick JN, Adams MJ, Adkins AE, et al. (2018): Transancestral GWAS of alcohol dependence reveals common genetic underpinnings with psychiatric disorders. Nat Neurosci 21:1656–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kunkle BW, Grenier-Boley B, Sims R, Bis JC, Damotte V, Naj AC, et al. (2019): Genetic meta-analysis of diagnosed Alzheimer’s disease identifies new risk loci and implicates Ab, tau, immunity and lipid processing [published correction appears in Nat Genet 2019; 51: 1423–1424]. Nat Genet 51:414–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Watson HJ, Yilmaz Z, Thornton LM, Hübel C, Coleman JRI, Gaspar HA, et al. (2019): Genome-wide association study identifies eight risk loci and implicates metabo-psychiatric origins for anorexia nervosa. Nat Genet 51:1207–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grove J, Ripke S, Als TD, Mattheisen M, Walters RK, Won H, et al. (2019): Identification of common genetic risk variants for autism spectrum disorder. Nat Genet 51:431–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mullins N, Forstner AJ, O’Connell KS, Coombes B, Coleman JRI, Qiao Z, et al. (2021): Genome-wide association study of more than 40,000 bipolar disorder cases provides new insights into the underlying biology. Nat Genet 53:817–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Johnson EC, Demontis D, Thorgeirsson TE, Walters RK, Polimanti R, Hatoum AS, et al. (2020): A large-scale genome-wide association study meta-analysis of cannabis use disorder [published correction appears in Lancet Psychiatry 2022; 9:e12]. Lancet Psychiatry 7:1032–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wray NR, Ripke S, Mattheisen M, Trzaskowski M, Byrne EM, Abdellaoui A, et al. (2018): Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression. Nat Genet 50:668–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Arnold PD, Askland KD, Barlassina C, Bellodi L, Bienvenu OJ, Black D (2018): Revealing the complex genetic architecture of obsessive–compulsive disorder using meta-analysis. Mol Psychiatry 23:1181–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nievergelt CM, Maihofer AX, Klengel T, Atkinson EG, Chen CY, Choi KW, et al. (2019): International meta-analysis of PTSD genome-wide association studies identifies sex-and ancestry-specific genetic risk loci. Nat Commun 10:4558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Trubetskoy V, Pardiñas AF, Qi T, Panagiotaropoulou G, Awasthi S, Bigdeli TB, et al. (2022): Mapping genomic loci implicates genes and synaptic biology in schizophrenia. Nature 604:502–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yu D, Sul JH, Tsetsos F, Nawaz MS, Huang AY, Zelaya I, et al. (2019): Interrogating the genetic determinants of Tourette’s syndrome and other tic disorders through genome-wide association studies. Am J Psychiatry 176:217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang J, Lee SH, Goddard ME, Visscher PM (2011): GCTA: A tool for genome-wide complex trait analysis. Am J Hum Genet 88: 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maier RM, Visscher PM, Robinson MR, Wray NR (2018): Embracing polygenicity: A review of methods and tools for psychiatric genetics research. Psychol Med 48:1055–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Akingbuwa WA, Hammerschlag AR, Bartels M, Middeldorp CM (2022): Systematic review: Molecular studies of common genetic variation in child and adolescent psychiatric disorders [published correction appears in J Am Acad Child Adolesc Psychiatry 2022; 61:837]. J Am Acad Child Adolesc Psychiatry 61:227–242. [DOI] [PubMed] [Google Scholar]
- 27.Yang J, Bakshi A, Zhu Z, Hemani G, Vinkhuyzen AA, Nolte IM, et al. (2015): Genome-wide genetic homogeneity between sexes and populations for human height and body mass index. Hum Mol Genet 24:7445–7449. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.