Approximating Scaffold Printability Utilizing Computational Methods

Abstract

Bioprinting facilitates the generation of complex, three-dimensional (3D), cell-based constructs for various applications. Although multiple bioprinting technologies have been developed, extrusion-based systems have become the dominant technology due to the diversity of materials (bioinks) that can be utilized, either individually or in combination. However, each bioink has unique material properties and extrusion characteristics that affect bioprinting utility, accuracy, and precision. Here, we have extended our previous work to achieve high precision (i.e., repeatability) and printability across samples by optimizing bioink-specific printing parameters. Specifically, we hypothesized that a Fuzzy Inference System (FIS) could be used as a computational method to address the imprecision in 3D bioprinting test data and uncover the optimal printing parameters for a specific bioink that result in high accuracy and precision. To test this hypothesis, we have implemented a FIS model consisting of four inputs (bioink concentration, printing flowrate, speed, and temperature) and two outputs to quantify the precision (scaffold bioprinted linewidth variance) and printability. We validate our use of the bioprinting precision index (BPI) with both standard and normalized printability factors. Finally, we utilize optimized printing parameters to bioprint scaffolds containing up to 30 × 10⁶ cells/mL with high printability and precision. In total, our results indicate that computational methods are a cost-efficient measure to improve the precision and robustness of extrusion 3D bioprinting with gelatin-based bioinks.

1. Introduction:

1.1. Bioprinting

Additive manufacturing is a process by which three-dimensional objects are generated by depositing material in sequential layers [1–3]. Bioprinting is an emerging field of additive manufacturing, in which bioactive scaffolds can be quickly generated by depositing layers of cell-laden biocompatible materials, such as collagen or other hydrogels [4]. After slicing a computational three-dimensional (3D) model of a desired scaffold, the appropriate extrusion path and required printing parameters can be used to direct the fabrication of the construct in a layer-by-layer fashion. Indeed, the ability to place cells in biologically relevant scaffold materials with a high spatial resolution has made bioprinting a popular fabrication method for tissue engineering [4–6].

However, the parameters used to perform the bioprinting procedure will have significant effects on the final properties of the scaffold [7]. Therefore, it is essential to fully characterize and optimize the bioprinting parameters (e.g., print speed or bioink viscosity) necessary to reach the desired outputs, such as architectural matching of the defect shape, high cell viability, appropriate cell function, and mechanical properties [8]. For example, increasing the nozzle size on the bioprinter decreases the shear stress placed on the biomaterial during extrusion, resulting in increased cell viability but reduced print resolution [9]. Therefore, determining the optimal print parameters is imperative for success in bioprinting. As a result, several studies have been performed in the field of bioprinting optimization, such as the optimization of a computational model for 3D bioprinting, bioink optimization, and bioprinting parameter selection [10,11].

Hydrogels provide three-dimensional (3D) support for cellular growth and tissue formation similar to native extracellular matrix (ECM) and are widely utilized to study cellular proliferation, migration, differentiation, and interaction [12–14]. In general, hydrogels are crosslinked networks of hydrophilic polymers that swell in water [13,15,16]. One of the most common natural hydrogels in biomedical applications and bioprinting is gelatin, which is derived through collagen hydrolysis. Although there are several ways to hydrolyze the collagen, we have used Type A (acid-derived) gelatin in this experiment. Gelatin is particularly useful for drug release and tissue engineering due to its biocompatibility [17], rapid biodegradability, constituent purity, high cell attachments due to arginine-glycine-aspartic acid (RGD) sequences [18], and tunable physical properties [16]. The composition, crosslinking method, and level of crosslinking of gelatin-based materials affect its physical and biochemical properties. Crosslinking gelatin bioink can be done by photo crosslinking [7,19], enzymatic crosslinking [20], thermal crosslinking [21], or chemical crosslinking [22]. As a result, our study is directly applicable to a variety of other gelatin-based bioinks, such as gelatin methacryloyl (GelMA) [13,23].

1.2. Approximation and Prediction

There is a significant degree of imprecision and uncertainty inherent in bioprinting optimization. A potential approach to handling this issue, which arises from normal biological variation, is implementing approximation systems based on computational methods [24]. In recent years, systems biology has become a critical multidisciplinary research area between computer science and biology. Studies in this field aim to develop computational models of biological processes, requiring both a robust dynamic model and a large dataset of experimental results [25,26].

Developing a dynamic model is challenging and requires well-characterized control parameters to approximate laboratory experiments’ outcomes. Nonetheless, recent studies have observed that machine learning algorithms can effectively predict output parameters using either a deterministic or stochastic biological model. A partial list of the approaches employed to this end includes meta-heuristic, evolutionary, global optimization, genetic programming, simulated annealing, simplex, ant-colony, fuzzy genetic hybrid system, and multi-objective optimization [25,27]. In-silico models have significantly helped reproducibility and quality in the in-vitro experiments in tissue engineering fields [28–30].

1.3. Fuzzy Inference System (FIS)

Fuzzy Logic (FL) is an extension of standard logic, in which values can only be completely false or completely true. In contrast to the standard logic set with a crisp boundary, values in the Fuzzy set can have a degree of truth between 0 (completely false) and 1 (completely true) [31]. Moving from discrete to continuous values provided a computational approach to approximate the model output with the inherited uncertainty and imprecision. As a result, this status offers a computational model to move from discrete to continuous values. A system based on FL is called a Fuzzy Inference System (FIS). A FIS is a framework consisting of Fuzzification, Inference Engine, and Defuzzification. A complete discussion of the Fuzzy Set theory and implementation can be found in the Supplement.

As a potential solution for overcoming potential uncertainty, we have developed a quantitative model of a biomanufacturing process using the FIS approach. Previous studies have shown that the accuracy of a fuzzy system approach is the same as the deterministic mathematical approach (ordinary differential equations) for the same kinetic dataset [32]. Moreover, fuzzy systems can be utilized to find a qualitative system response when a quantitative dataset is unavailable [31,33]. In decision-making systems, theoretical fuzzy models have been used to approximate biomechanical properties such as the stress/strain of a bone structure in a biological process [34–36]. The mathematical model of the FIS has been provided in the Supplement.

1.4. Approximation in 3D printed Scaffold

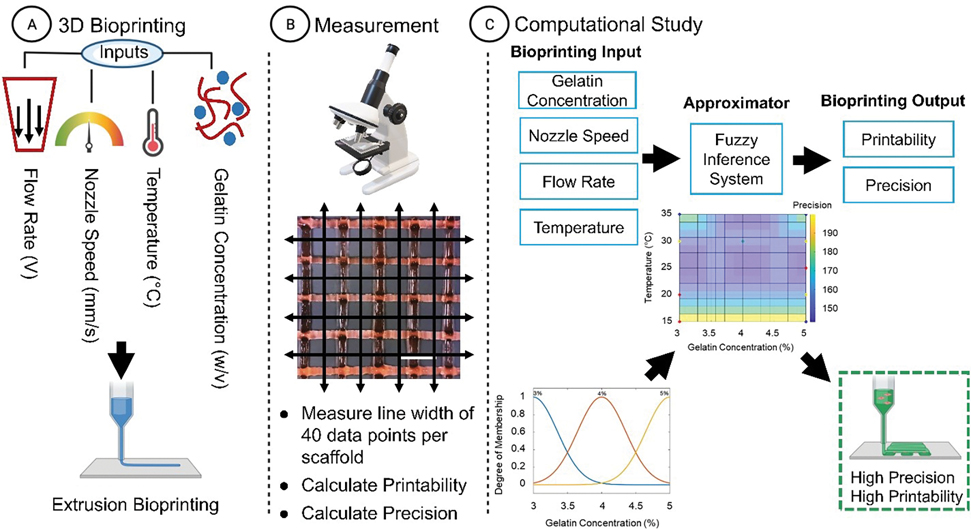
Bioprinting outputs can be predicted using classic physics formulation or computational and machine learning methods. We recently demonstrated that computational methods are precise in the output approximation, which can be measured and optimized based on the bioprinting inputs of speed, pressure, and dilution percentage [34]. Here, we propose to implement an approximation model using a 3D scaffold with greater complexity of inputs. To do so, we implemented a fuzzy system and measured the approximation error on the dataset. Ultimately, we optimized and approximated the bioprinting output for extrusion parameters in four different precision and printability indexes and measured the validation error. Fig. 1 shows the general workflow of the process.

Figure 1. General workflow of the study.

(A) First, the 3D model was designed with four different input parameters, and the sample was printed by an extrusion-based bioprinter. (B) Next, the data was acquired using brightfield microscopy. (C) The data were normalized, processed, and interpolated by a Gaussian function. Then the dataset was used as the FIS rules for implementing the FIS model; the final model was generated to approximate and optimize the BPI for the parameter set.

2. Methods

2.1. Bioprinting parameters and study design

Gelatin was chosen as a bioink for acellular 3D printing and bioprinting due to its ability to form hydrogel constructs of similar stiffness to soft tissue as well as permit adequate cellular proliferation and differentiation [14,37]. Here, we refer to both acellular and cellular gelatin as bioink. Importantly, gelatin is a highly temperature-dependent material whose viscosity generally decreases as a function of temperature and concentration [38]. Therefore, optimization of gelatin concentrations and bioink temperature is critical for achieving high-precision bioprinting. Furthermore, the extrusion flow rate (corollary to the input voltage to the extrusion motor) and travel speed of the nozzle strongly affects printing precision. To investigate the effect of these four factors (gelatin concentration, bioink temperature, flow rate, and nozzle speed) on the precision and printability of gelatin, a full factorial design (all possible combinations) is the most reliable experimental design. However, this method is not practical in terms of time and cost due to the large number of experiments required. Therefore, we utilized a common experimental design to identify the minimum number of experiments required, known as response surface methodology (RSM) [39]. Specifically, we used a central composite design (CCD) in which the center points have enough replication to allow for a test of the model’s lack of fit. Here, our input parameters were designed to span the range of optimal values as follows: the input voltage of the extrusion motor (0.9, 1.1, and 1.3 V), travel speed of the nozzle (4, 8, and 12 mm/s), bioink temperature (15, 25, and 35 °C), and bioink concentration (3, 4, and 5% w/v). Since each parameter had three discrete values, the number of experiments required to provide FIS input data was 31 prints including 7 center points (Table 1). Each print condition was performed in triplicate.

Table 1.

Experimental Design and FIS Input Data

Order	Gelatin bioink Conc. (W/V%)	Printing Speed (mm/s)	Flow Rate (V)	Bioink Temperature (°C)	Experimental (Input) Data (Output)				FIS Approximation (Output)
					Printability	Categorized	Precision	Categorized	Printability	Categorized	Precision	Categorized
1	4	8	1.1	15	0.4	L	292	L	0.3248	L	199	H
2	4	8	0.9	25	1	H	135	H	0.8717	H	142	H
3	4	8	1.1	25	1	H	128	H	0.8717	H	142	H
4	4	8	1.1	25	1	H	241	H	0.8717	H	142	H
5	4	8	1.1	25	0.8	L	145	H	0.8717	H	142	H
6	4	8	1.1	25	1	H	240	H	0.8717	H	142	H
7	4	8	1.1	25	1	H	207	H	0.8717	H	142	H
8	4	8	1.1	25	1	H	161	H	0.8717	H	142	H
9	4	8	1.1	25	0.84	H	182	H	0.8717	H	142	H
10	4	8	1.3	25	0.95	H	144	H	0.8717	H	142	H
11	4	12	1.1	25	1	H	101	H	0.8716	H	142	H
12	4	4	1.1	25	0.9	H	152	H	0.8716	H	142	H
13	4	8	1.1	35	0.82	H	199	H	0.8717	H	142	H
14	3	4	1.3	15	1	H	350	L	0.8716	H	255	L
15	3	12	1.3	15	0.13	L	305	L	0.3284	L	255	L
16	3	4	0.9	15	0.31	L	149	H	0.3284	L	202	H
17	3	12	0.9	15	0.05	L	258	L	0.3284	L	250	L
18	3	8	1.1	25	1	H	160	H	0.8717	H	142	H
19	3	12	0.9	35	0.4	L	216	H	0.3284	L	140	H
20	3	12	1.3	35	0.17	L	456	L	0.3284	L	255	L
21	3	4	0.9	35	0.45	L	234	H	0.3284	L	140	H
22	3	4	1.3	35	0.12	L	437	L	0.3284	L	255	L
23	5	4	0.9	15	0.18	L	263	L	0.3284	L	250	L
24	5	12	1.3	15	0.12	L	249	H	0.3284	L	140	H
25	5	4	1.3	15	0.67	L	496	L	0.6	L	255	L
26	5	12	0.9	15				Not printed
27	5	8	1.1	25	1	H	225	H	0.8717	H	142	H
28	5	12	0.9	35	0.6	L	188	H	0.6	L	140	H
29	5	4	1.3	35	0.66	L	385	L	0.6	L	255	L
30	5	4	0.9	35	0.22	L	171	H	0.328	L	140	H
31	5	12	1.3	35	0.35	L	396	L	0.3284	L	255	L

2.2. Acellular 3D bioprinting

Three different concentrations of ink (3%, 4%, and 5% w/v) were prepared and stored in 50 mL centrifuge tubes. Type A gelatin from porcine skin (gel strength 300, G2500-500G, Sigma-Aldrich) was measured and gradually added to warmed Dulbecco’s phosphate-buffered saline (DPBS) (Gibco 14190136). For better contrast during the imaging, 100 μL of red food dye was added to each solution. Next, 2.5 mL of each gelatin ink concentration was pipetted into a 3 mL syringe. The syringe was capped with a 25-gauge 0.25 mm internal diameter tapered plastic tip nozzle (8001279, Fisnar), and the syringe was loaded into a custom-built extrusion bioprinter with a temperature control system. The extrusion of the biomaterial was controlled via voltage delivered to a 6V 30:1 micromotor with a threaded shaft (Pololu). The print layout was a 30 mm × 30 mm grid square with a 500 μm layer height. Infill distances were 5 mm. Three replicates of each printing parameter set were performed (n=3). Each freshly loaded ink syringe was maintained for ten minutes in a water bath inside a 4 °C fridge. Then, the syringe was put in the preheated bioprinter extruder and kept at the printing temperature for at least 10 minutes before printing. Room humidity was maintained at less than 40% with a room temperature range of 22–24 °C. Constructs were imaged using a stereo microscope (LAXCOTM) at 0.67X zoom and analyzed in FIJI [21].

2.3. Gaussian (nominal) Distribution Analysis

To determine and quantify the actual bioprinted construct line width, we measured each side of the 16 squares (40 data points per sample). In order to implement the FIS with our measured data series for each printed scaffold, we used a nominal distribution to find the variance for the linewidth data for each printing parameter. Here, low variance indicates a more uniform line width data in a printed scaffold. Therefore, our approximator used the variance as a precision measurement (the first output). The Gaussian distribution is a two-parameter family of curves, which is a continuous probability distribution for a real-valued random variable. The general form of the normal probability density function (pdf) is:

$$y=f(x\mid \mu ,\delta )=\frac{1}{\delta \sqrt{2\pi }}{e}^{\frac{-(x-\mu {)}^2}{2{\delta }^2}}$$

Where $\mu$ is the mean and $\delta$ is the variance.

2.4. Printability Factor

Printability is a factor that quantifies shape fidelity with a referenced formula for multiple shapes. For a square shape, the bioink printability ($pr$) uses the following function:

$$pr=\frac{L^2}{16A}$$

Where $L$ is the perimeter and $A$ is the area of the enclosed area. For an ideal gelation condition or perfect printability status, the interconnected channels of the constructs would demonstrate a square shape, and the $pr$ value is 1. $pr$ indicates the degree of gelatin bioink to maintain the construct shape fidelity [40]. Although a shape can have the $pr$ value equivalent to 1, this metric does not represent the overall 3D construct shape fidelity. Therefore, we introduced a new ${pr}_{normalized}$ metric generated by multiplying by the normalization coefficient. We use the following normalization coefficient to normalize the $pr$ value:

$${pr}_{normalized}=\frac{closedloopprintedsquares}{totalnumberoftheexpectedsquares}\times pr$$

Here, we expected 16 squares in each printed scaffold. In this approximation model, $p{r}_{normalized}$ is the second system output.

2.5. Fuzzy Inference System

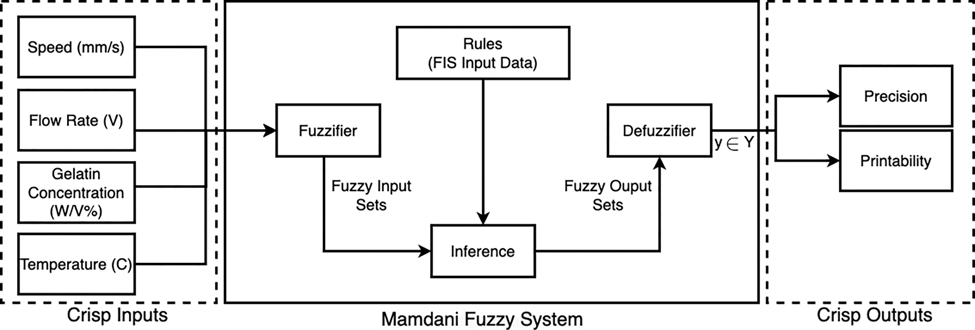
The FIS structure is programmed utilizing the MATLAB FIS editor toolbox to implement the model and approximate the precision and printability. The Sugeno-based fuzzy inference system and the Gaussian membership functions are used to fuzzify the datasets and map the relationship between the process inputs and the outputs. In the first step, we designed FIS membership functions with four inputs (gelatin concentration (% w/v), bioink temperature (°C), flowrate (V), speed (mm/s)), and two outputs (precision and printability) (Supplemental Figure 1). The detailed implemented FIS also includes the inputs, fuzzifier, rules, inference engine, defuzzifier, and outputs (Fig. 2). The implemented fuzzy rules are detailed in the Supplemental Methods. Next, we measured the Root Mean Square Error (RMSE) and accuracy between the experimented output (precision and printability) and the approximated outputs.

Figure 2. Type-1 Fuzzy Logic Algorithm and Study Design.

General overview and different features of the Type-1 Fuzzy system including fuzzification, rules, inference engine, and defuzzification. Schematic of our study design, including three inputs (speed, flow rate, temperature, and gelatin concentration) and two outputs (precision and printability).

The approximation RMSE is calculated based on the error between the actual (printed) precision for a printing set and the approximated for each print set as follows:

$$RMSE(ApproximationError)=\sqrt{\sum _{i=1}^n \frac{{\left(Approximated-{Actual}_i\right)}^2}{n}}$$

Where $n$ is the number of observations (printed scaffolds Table 1–2). The accuracy of the FIS on given datasets is derived as follows:

$$Acccuracy=\frac{NumberofCorectPredictions}{TotalNumberofPredictions}$$

Table 2.

FIS Validation

Order	Gelatin bioink Conc. (W/V%)	Printing Speed (mm/s)	Flow Rate (V)	Bioink Temperature (C)	Validation Data FIS Approximation				Validation Data Experimental Result
					Printability	Categorized	Precision	Categorized	CP	Printability	Categorized	Precision	Categorized
Group A) High Printability, High Precision
V 7	4	6	0.9	30	0.82	H	150	H	9.3	0.7	L	155	H
V 14	3	8	1	30	0.82	H	150	H	12.8	0.93	H	178	H
V 8	4	6	1	30	0.82	H	150	H	4	0.85	H	164	H
V 5	5	8	1	30	0.82	H	150	H	12.8	0.85	H	170	H
Group B) Low Printability, High Precision
V 1	5	12	1.2	15	0.37	L	150	H	43	0.12	L	231	H
V 16	3	6	0.9	35	0.37	L	150	H	13.2	0.7	L	238	H
V 6	5	6	0.9	35	0.37	L	150	H	13	0.87	H	201	H
V 15	3	12	1	30	0.37	L	150	H	44	0.8	L	220	H
Group C) High printability, Low Precision
V 9	3	4	1.2	15	0.85	H	255	L	61	0.95	H	434	L
V 10	3	6	1.3	15	0.85	H	255	L	45	0.66	H	421	L
V 12	3	4	1.3	20	0.85	H	255	L	45.7	0.96	H	192	H
V 3	5	8	1.3	25	0.85	H	255	L	72.6	1	H	245	H
Group D) Low Printability, Low Precision
V 2	3	10	1.3	30	0.37	L	255	L	116	0.95	H	548	L
V 13	5	6	0.9	20	0.37	L	255	L	88.4	0.3	L	292	L
V 11	3	12	1	15	0.37	L	255	L	58	0.36	L	300	L
V 4	5	12	1.2	30	0.37	L	255	L	116	0.85	H	293	L

2.6. Bioprinting Precision Index

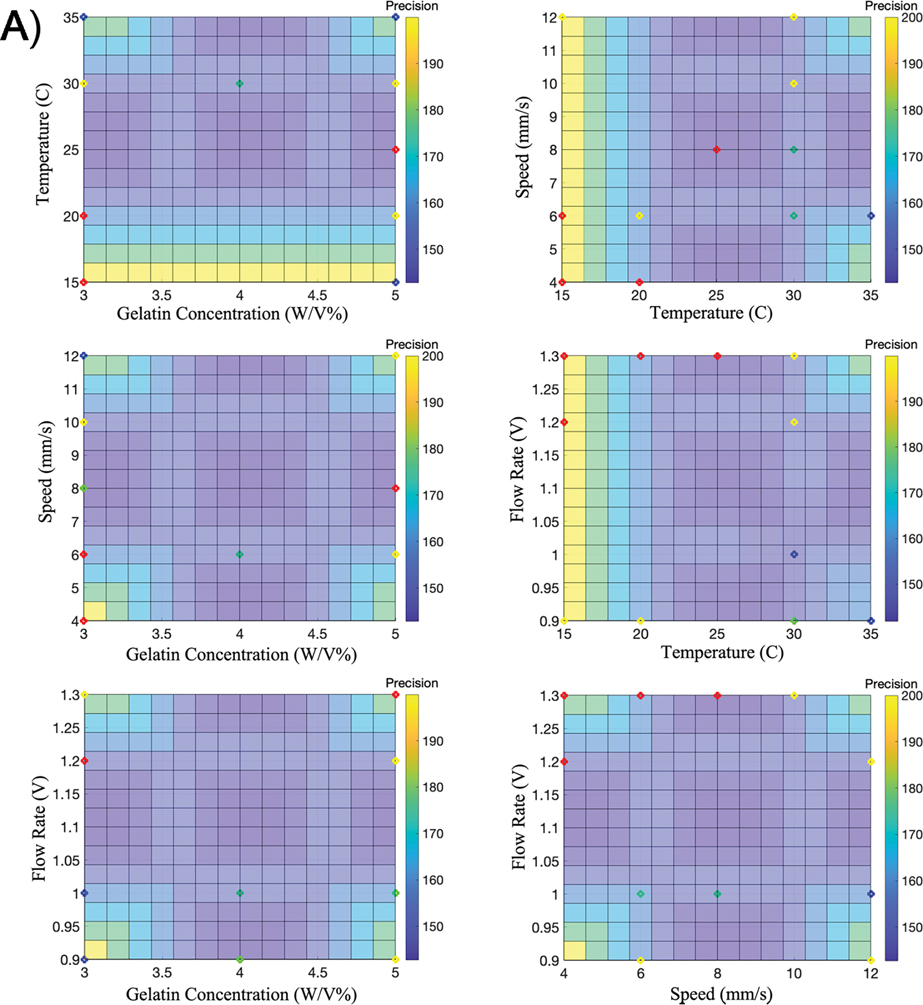
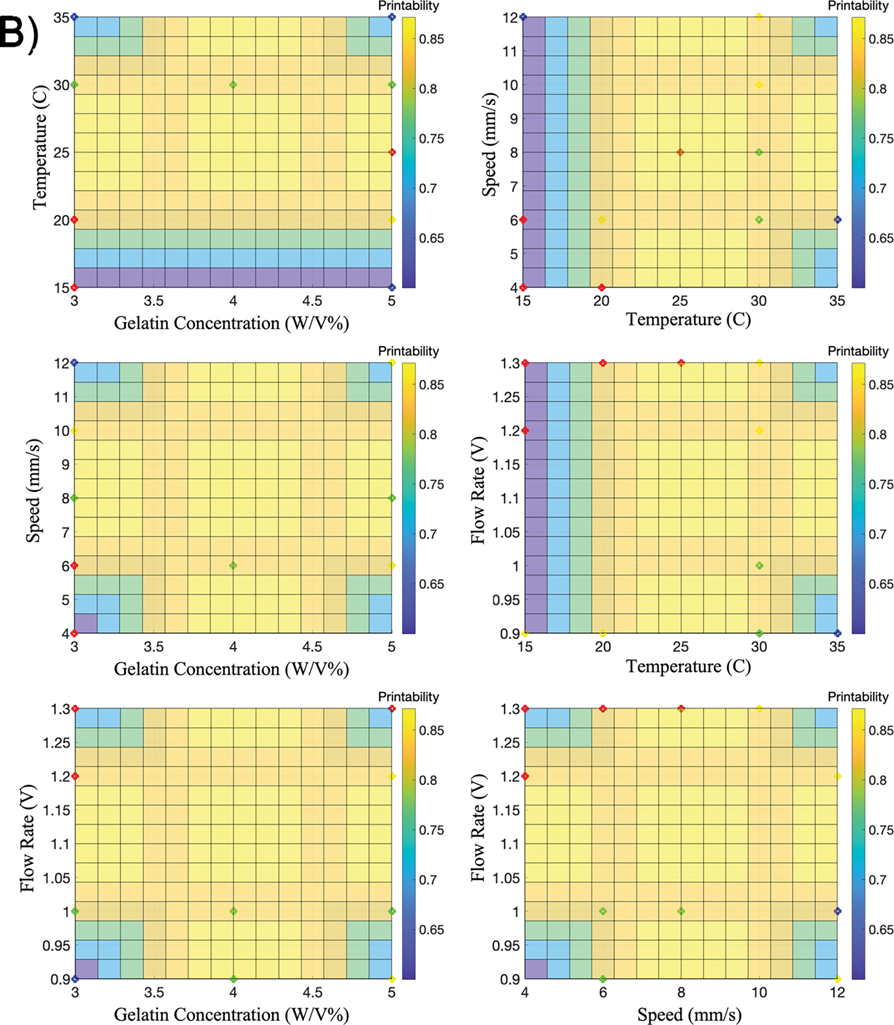
In recent work, we introduced the Bioink Precision Index (BPI) as a new metric for evaluating bioink precision [34]. BPI is a metric derived from a fuzzy surface gradient value (e.g. Fig. 4); therefore, this metric is dimensionless to measure precision and system robustness. Furthermore, this technique can be applied to the printing of any 2D or 3D shape. In contrast to our previous work, we applied this method to a 3D shape (scaffold) to approximate the printability and precision to optimize and achieve the BPI.

Figure 4. Fuzzy Surface Gradients.

Six 3D graphs are used to illustrate FIS surfaces (BPI) using A) precision as the output or B) printability as the output. The colored points represent the parameter sets used for validation – Group A (green), Group B (blue), Group C (red), and Group D (yellow).

The standard calculation for a gradient of a 3D surface with four inputs:

$$\begin{array}{l}f(x,y,z,k)\approx f\left(x_0,y_0,z_0,k_0\right)+(\nabla f{)}_x\left(x_0,y_0,z_0,k_0\right)\left(x-x_0\right)+(\nabla f{)}_y\left(x_0,y_0,z_0,k_0\right)\left(y-y_0\right)\\ & +(\nabla f{)}_z\left(x_0,y_0,z_0,k_0\right)\left(z-z_0\right)+(\nabla f{)}_k\left(x_0,y_0,z_0,k_0\right)\left(k-k_0\right)\end{array}$$

Thus, BPI is calculated from the sum of the squared error of the above equation:

$$\begin{array}{l}BPI\\ =\sqrt{(\nabla f{)}_x{\left(x_0,y_0,z_0,k_0\right)}^2+(\nabla f{)}_y{\left(x_0,y_0,z_0,k_0\right)}^2+(\nabla f{)}_z{\left(x_0,y_0,z_0,k_0\right)}^2+(\nabla f{)}_k{\left(x_0,y_0,z_0,k_0\right)}^2}\end{array}$$

Where $x_0$, $y_0$, $z_0$, and $k_0$ are the inputs in our system (gelatin concentration, flowrate, speed, and temperature).

2.7. Cell Culture

C2C12 immortalized mouse myoblasts (CRL-1772TM, ATCC) were cultured in T75 and T175 flasks with proliferation medium: Dulbecco’s Modified Eagle Medium, high glucose, pyruvate (Gibco, 11995-081); qualified, heat-inactivated fetal bovine serum (Gibco, 16140-071) at 10% (v/v); and penicillin-streptomycin (Gibco, 15070-063) at 1% (v/v). When the cells reached above 80% confluency, they were suspended using a 0.05% of Trypsin-EDTA solution (Gibco, 15400054), diluted in DPBS, and reseeded into a new flask at an appropriate seeding density to enable cell expansion. Once an adequate number of cells were generated, the cells were again suspended, counted, and encapsulated in the gelatin bioink warmed to 37 °C at concentrations of 1, 10, and 30×10⁶ cells/mL for rheological and cell printing tests.

2.8. Bioink rheological testing

The viscosities of the 4% (w/v) gelatin bioinks at concentrations of 1, 10, and 30×10⁶ cells/mL were evaluated using a Discovery Hybrid Rheometer-3 (TA Instruments). The system was controlled using TRIOS software. Each of the bioinks at varying cell concentrations was tested by pipetting 1.9 mL of the bioink onto the testing surface and a 60 mm flat parallel plate testing geometry (511600.905, TA Instruments) was lowered to a testing gap of 600 μm. The top bowl of the parallel plate geometry was filled with distilled water and enclosed with a solvent trap to prevent evaporation of the hydrogel. The sample was heated to 37 °C and preshear was performed at a rate of 100 1/s for 60 s. The material was allowed to stabilize by cooling the sample to 4 °C and then warming the sample to 30 °C for 10 min. The viscosity was measured by flow sweep with a shear rate range of 1–333 1/s collecting 10 points per decade.

2.9. Cellular 3D bioprinting

Bioinks consisting of cellular concentrations of 1, 10, and 30 × 10⁶ cells/mL in 4% (w/v) gelatin were loaded into 3 mL syringes and bioprinted as described using the same printing geometry. However, no food dye was added to these bioinks. The printing parameter set was predicted by the model to exhibit high printability and high precision: a temperature of 30 °C, extrusion voltage of 0.9, and speed of 6 mm/s. The macroscopic scaffold was again captured using a stereo microscope. Magnified phase-contrast images to display the varying cell densities were captured on an Axio Observer 7 microscope (Zeiss).

3. Results

3.1. FIS Approximator Performance

First, the series of parameter sets designed to function as the FIS input data (Table 1) were used for bioprinting and the resultant constructs were imaged. Next, printing precision and printability were quantified for each parameter set. Printability values over 0.8 and precision values lower than 250 were categorized as “high”. Conversely, printability factors equal and less than 0.8 and precision over 250 were categorized as “low”. As a result, the parameter sets could be divided into four groups: A) high precision, high printability; B) high precision, low printability; C) low precision, high printability; and D) low precision, low printability (Fig. 3). Overall, we observed that the FIS approximated the experimental input data with 95% accuracy and low relative RMSE for both precision (92.9) and printability (0.12) outputs (Table 3).

Figure 3. Acellular printing used for FIS input data.

Representative images of acellular gelatin prints of various input settings used to implement the model are grouped by high or low printability and precision. Scale bars are 5 mm.

Table 3.

FIS Performance

	Printability		Precision
	RMSE	Accuracy	RMSE	Accuracy
FIS Input Dataset	0.12	95%	92.9	95%
Validation Dataset	0.28	75%	105.3	87%

3.2. FIS Validation

Next, we used six BPI surfaces to visualize the results of the multi-dimensional FIS approximation, considering either precision as an output (Fig. 4a) or printability as an output (Fig. 4b). To validate this model for approximating and optimizing precision and printability, we randomly chose three printing parameter sets to represent each of the four groups characterized previously (Table 2). Importantly, these validation parameter sets were not included in the parameter sets used to generate the FIS input data. Each validation parameter set was used to generate three individual constructs using the same conditions as the FIS input data (Fig. 5). Here, the printability and precision validation accuracy was 75% and 87%, respectively. Furthermore, the RMSE value for printability and precision with the validation dataset was 0.28 and 105.3 (Table 3).

Figure 5. Acellular validation prints.

Representative images of acellular gelatin prints from predicted inputs expected to result in either high or low printability or precision. Scale bars are 5 mm.

In general, the printed constructs were consistent with our model approximations (Fig. 5). In particular, the mean precision (166 ± 9.7) and printability (0.8 ± 0.09) in Group A were both categorized as high, and resulted in continuous, uniform fibers with little bleeding of the deposited filament. Similarly, the results from Group B were as predicted, with mean printability categorized as low (0.6 ± 0.3) and mean precision categorized as high (222.5 ± 16.13). Here, the resultant printed constructs had relatively uniform fibers with discontinuous filaments or non-sharp corners. In Group C, the results were consistent with the approximated data and categorized as high mean printability (0.89 ± 0.15) and low mean precision (323 ± 122). Group C printed constructs exhibited relatively continuous fibers with good intersections in most groups, but the prints were often over-gelated with inconsistent fibers, jagged edges, discontinuities, and various diameters. Finally, the results from Group D were categorized as low mean printability (0.6 ± 0.3) and low mean precision (358 ± 126), consistent with model predictions. Thus, Group D constructs had highly variable diameters and discontinuous fibers that were too fluid and bled into each other.

3.3. Cell-laden bioink

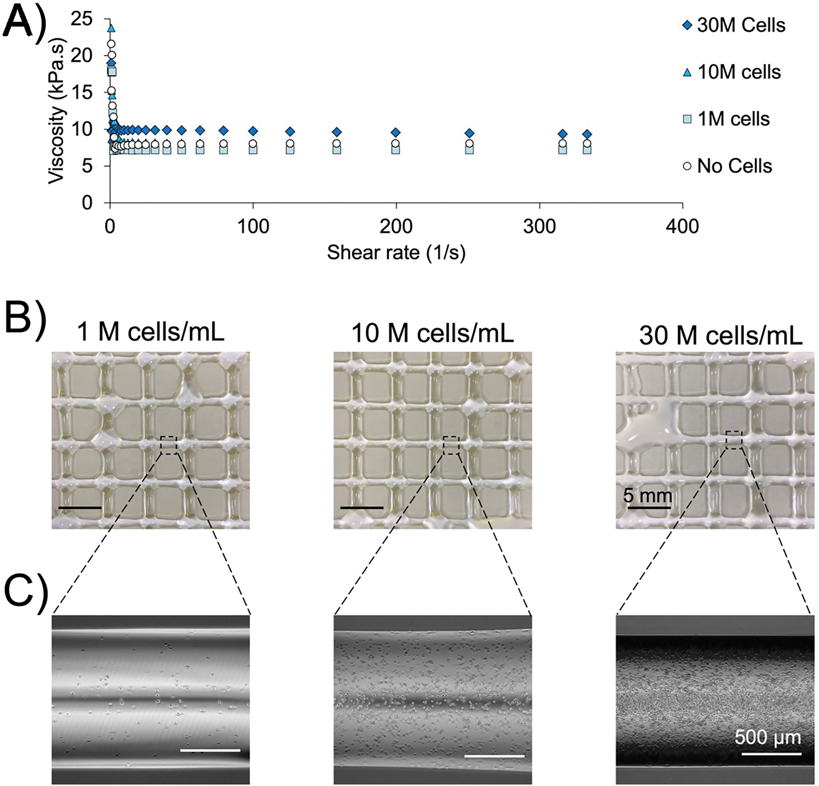
Finally, we analyzed bioink viscosity following the inclusion of cells of varying concentration into a 4% (w/v) gelatin bioink (Fig. 6A). The viscosity of the bioink at 30 °C was similar across cellular concentrations from 0, 1, 10, and 30 × 10⁶ cells/mL. During the constant portion of the viscosity curve, the bioink containing 30 × 10⁶ cells/mL did exhibit a modest increase in viscosity that is unlikely to affect bioprinting outcomes. Next, cell-laden gelatin bioinks were bioprinted using parameter sets predicted to have high precision and printability: 4% (w/v), 30 °C, 0.9 V, and 6 mm/s (Fig. 6B). Here, we observed results from all cell concentrations were similar to the acellular prints. The varying cell densities of the bioprinted fibers were confirmed using phase contrast microscopy (Fig. 6C).

Figure 6. Validation using cell-laden bioink.

A) Changes in viscosity across shear rate for 4% gelatin bioinks with cellular concentration from 0 to 30 × 10⁶ cells/mL. B) Bioinks containing 1, 10, or 30 × 10⁶ cells/mL were bioprinted in 4% gelatin bioink using optimized printing parameters. C) Phase contrast micrographs demonstrate the varying cellular densities across the bioprinted groups.

4. Discussion

In this study, we introduced a novel approach to approximate the Bioink Precision Index (BPI) by utilizing a fuzzy inference system (FIS) in a 3D bioprinting process with multiple inputs and outputs. In this model, inputs included gelatin bioink concentration, bioprinting flowrate, printing speed, and bioink temperature along with two outputs (precision and printability). Next, the BPI surface was generated using the experimental design data. We then tested four new printing parameter sets that had not been in the FIS input dataset. As expected, the precision and printability of the constructs varied widely based on the parameter set. Importantly, the experimental results were consistent with the approximation model that accurately predicted parameter sets with both high and low precision. Finally, we utilized the optimal printing parameters to generate high-precision constructs with cell-laden bioink. In total, our study demonstrates that computational methods are a cost-effective way to significantly improve precision in 3D bioprinting.

The difference between fuzzy systems and machine learning methods, such as neural networks, is that fuzzy systems can utilize raw and ambiguous data whereas neural networks rely on training data to learn and improve system accuracy over time. Moreover, fuzzy systems have transparency in data inferencing and approximation, whereas the inference model used with machine learning methods cannot be precisely extracted. Therefore, we used an FIS model to robustly approximate precision and printability in gelatin-based bioprinting. Nonetheless, we note that this system can be adapted to essentially any bioink or bioprinting environment. In contrast, conventional physics-based formulations cannot be utilized for optimization since they are not reversible in the multi-parameter domain. Also, the non-convex solution space and discrete values in the traditional formulation of the process decrease the probability of obtaining optimized bioprinting parameter sets.

One of the limitations of this study is the lack of experiments using alternative nozzle sizes. Furthermore, since the BPI is specifically a measure of output precision, utilizing a parameter set with optimal BPI may not result in high accuracy. As a result, choosing a parameter set for bioprinting may result in a necessary tradeoff between accuracy and precision. Furthermore, future work could extend this approach to other parameters that bioprinting experimental outcomes, such as cell viability or biocompatibility. Nonetheless, we note that BPI is independent of input dimensions/units and will remain a valuable metric as bioprinting needs and technology evolves.

To ensure that our optimization of printing parameters extended to cell-laden bioink, we bioprinted gelatin containing C2C12 myoblasts in a range of common cell densities. Indeed, previous work identified 30 × 10⁶ cells/mL to be the most effective concentration of cells for direct implantation and differentiation of skeletal muscle cells [41]. Importantly, the inclusion of cells did not dramatically change the viscosity of the bioink across any of the tested cell concentrations. While a 1–2 kPa.s increase in viscosity was noticed for the 30 M cells/mL, we do not expect that this modest effect would have any impact on bioprinting. Indeed, previous studies demonstrated that cell concentrations under a 40% volume fraction do not induce changes in viscosity that affect bioprinting; 30 × 10⁶ cells/mL is well under a 40% volume fraction [42,43]. Furthermore, we found that optimized parameter sets resulted in similar bioprinted constructs utilizing bioink with or without cells. In total, experimental validation of our optimization method using cell-laden bioink increases the impact of this work by demonstrating that optimization of bioprinting parameters can be performed without cells and their associated costs.

5. Conclusion

Obtaining high precision in bioprinting is a necessary step toward the mass production of bioprinted 3D constructs for use in research and medicine. Here, we have demonstrated that the Fuzzy Inference System (FIS) approach can be used to approximate output precision and printability with a set of bioprinting parameters, including printing speed, flowrate, gelatin bioink concentration, and bioink temperature, as well as determine bioprinting parameter sets that maximize precision in 3D constructs. Furthermore, we have applied the previously defined Bioink Precision Index (BPI) that can be used to quickly compare the ease of reproducibility regardless of the number of inputs, and environment.