Polymer folding through active processes recreates features of genome organization

Significance

The regulation of gene transcription is vital for controlling cell state and involves active, energy-consuming processes. However, it is largely unknown how these active processes affect chromatin structure and dynamics. We develop an exactly solvable model that links patterns of activity in sequence space implied by dynamical measurements with the folded genome shape observed in structural data. We find that correlated active forces can mediate an effective attraction between distal polymer segments, offering a nonequilibrium mechanism for the formation of genomic compartments. Similarly, changing the magnitude of active forces can reproduce the segregation of active euchromatin and inactive heterochromatin. Our work thus motivates future experiments to disentangle active and passive mechanisms of genome organization.

Abstract

From proteins to chromosomes, polymers fold into specific conformations that control their biological function. Polymer folding has long been studied with equilibrium thermodynamics, yet intracellular organization and regulation involve energy-consuming, active processes. Signatures of activity have been measured in the context of chromatin motion, which shows spatial correlations and enhanced subdiffusion only in the presence of adenosine triphosphate. Moreover, chromatin motion varies with genomic coordinate, pointing toward a heterogeneous pattern of active processes along the sequence. How do such patterns of activity affect the conformation of a polymer such as chromatin? We address this question by combining analytical theory and simulations to study a polymer subjected to sequence-dependent correlated active forces. Our analysis shows that a local increase in activity (larger active forces) can cause the polymer backbone to bend and expand, while less active segments straighten out and condense. Our simulations further predict that modest activity differences can drive compartmentalization of the polymer consistent with the patterns observed in chromosome conformation capture experiments. Moreover, segments of the polymer that show correlated active (sub)diffusion attract each other through effective long-ranged harmonic interactions, whereas anticorrelations lead to effective repulsions. Thus, our theory offers nonequilibrium mechanisms for forming genomic compartments, which cannot be distinguished from affinity-based folding using structural data alone. As a first step toward exploring whether active mechanisms contribute to shaping genome conformations, we discuss a data-driven approach.

The folding of various biopolymers into specific conformations is vital for cellular function. Decades of research on equilibrium polymer theory have revealed basic principles of sequence-controlled folding (1–6). Specifically, polymers composed of sequences of chemically distinct monomers can, via affinity-based monomer–monomer and monomer–solvent interactions, fold into particular shapes despite the dramatic loss of conformational entropy. These ideas range from simple hydrophobic effects that explain the positioning of residues within globular proteins (7–9), to complex free energy landscapes that precisely predict protein structure (1, 5). More recently, analogous concepts have been applied to the folding of interphase chromatin—a complex heteropolymer consisting of genomic DNA and associated proteins (10).

Advances in imaging and sequencing technology have revealed that transcriptionally active euchromatin, which typically resides in the nuclear interior, spatially segregates from transcriptionally silent heterochromatin at the nuclear periphery (11). Chromosome conformation capture (3C) experiments measure this segregation via an enrichment of contact frequencies within euchromatic (A) and heterochromatic (B) regions and depletion of contacts between them (12). These “A/B-compartments” are thought to form because of pairwise attraction between chromatin segments with similar histone modifications, which leads to equilibrium microphase separation (13). Borrowing thermodynamic ideas from protein folding, increasingly sophisticated equilibrium models have designed interaction landscapes to simulate genomic structures that recapitulate 3C data (14–22). This success is remarkable, yet also raises the question if additional mechanisms could be at play in the far-from-equilibrium intracellular environment.

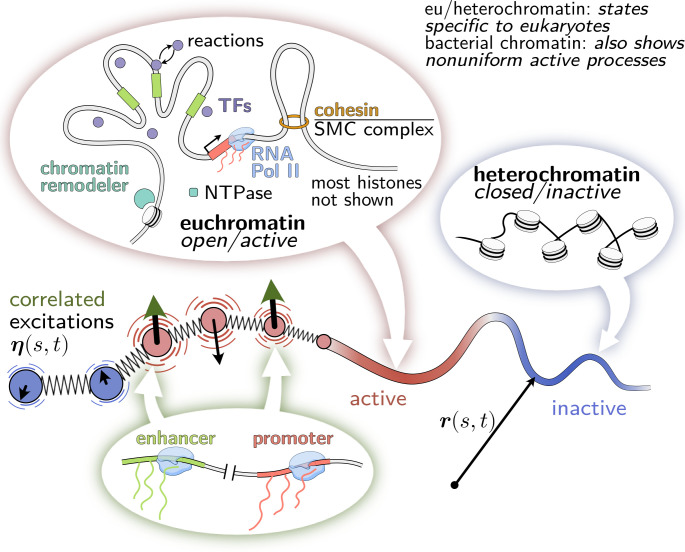
Many chromatin-associated proteins are enzymes (23–25) that break detailed balance by turning over chemical energy (26), such as adenosine triphosphate (ATP) or metabolites, to perform nonequilibrium reactions and/or exert mechanical forces (27), cf. Fig. 1. Such active processes characteristically lead to faster motion that cannot be explained by thermal fluctuations alone (31). Indeed, the subdiffusion of chromosomal loci slows down in the absence of ATP in both bacteria and eukaryotes (32).

Fig. 1.

Model of the genome as an active heteropolymer. The genome acts as a scaffold for a myriad of active processes. Motor proteins, such as RNA polymerase II and loop extruding factors, consume chemical energy to exert forces on DNA (24). These nucleoside triphosphatases (NTPases) hydrolyze nucleoside triphosphates (NTP) such as ATP, thereby switching to an NDP-bound state, and restore their NTP-bound conformation by nucleotide exchange (28). For example, specialized proteins actively modify DNA-bound histones and transcription factors via nonequilibrium reactions (23, 29, 30). In the context of eukaryotes, active processes are enriched in transcriptionally active euchromatin compared to inactive heterochromatin. (For visual clarity in the figure, histones in euchromatin and active processes in heterochromatin are omitted.) In our coarse-grained model, we describe active processes by random forces that have larger magnitude and thus drive faster diffusion in active regions than in inactive regions. We also stipulate that the active forces at different loci are not necessarily independent. We hypothesize that correlated excitations could arise, for example, from the coordinated activation of an enhancer and its cognate promoter. Alternatively, correlated excitations could also arise from fluctuating concentration gradients of molecules that show sequence-specific interactions with chromatin.

In addition, nucleus-wide tracking of fluorescently labeled histones has unveiled micron-scale regions of correlated chromatin motion, which disappear after ATP depletion or ATPase inhibition (33, 34). Moreover, the distribution of active processes varies along the genome, which is consistent with heterogeneous chromatin motion (35). The apparent diffusion coefficient of individual loci depends on their location in sequence space (36) and on transcriptional state (37), although the precise effect of transcription is debated (38, 39). Similarly, histone tracking experiments have measured faster motion in active euchromatin in the nuclear interior than in heterochromatin at the nuclear periphery (39, 40). These observations point toward the presence of sequence-controlled active forces that affect the polymeric genome’s mobility. To study how such active processes may contribute to shaping genome structure, we need a theory that can link active polymer dynamics to folding patterns (41).

By modeling activity via persistent monomer motion, past work has predicted nonequilibrium phenomena such as coherent motion and polymer collapse or swelling (42–52). However, these studies consider uniform activity along the polymer and thus cannot explain heterogeneous folding patterns. More recent models have incorporated nonuniform activity via active forces that vary in magnitude along the chain (53–59), akin to a local effective temperature (60). Simulations have shown that large (30-fold) activity differences can drive phase separation between different polymer regions (53), analogous to mixtures of active and passive particles (61, 62), although smaller activity differences are sufficient in polymeric mixtures (63, 64). Finer grained models have incorporated motor activity via force dipoles (65–67) that align tangentially with the chain (68–71), or through explicit simulation of translocating proteins (72). However, an analytic framework that explains why and how nonuniform activity can fold polymers is still lacking. Moreover, prior work has assumed that active processes at distinct genomic loci are statistically independent. In the context of chromatin, however, we hypothesize that correlations could arise from the coordinated transcriptional activation of different regions, such as enhancers and corresponding promoters (73, 74) or coregulation of genes by common transcription factors (75–77).

To address these open issues, we study a model of a polymer that is driven by correlated active forces with nonuniform magnitude. Our continuum theory shows that active (A) regions of the polymer expand and bend, when averaged over an ensemble, whereas inactive (B) regions contract and straighten out. Therefore, increased activity within euchromatin could help preserve its expanded state and increase its accessibility to active proteins. Using polymer simulations, we find that even modest activity ratios (two- to ten-fold) can recapitulate the degree of A/B compartmentalization observed in Hi-C data. Moreover, we find that distinct loci experiencing correlated active forces will effectively attract, while anticorrelations lead to repulsion. Our results provide a nonequilibrium mechanism that links activity-driven correlated motion to the folding patterns observed in 3C data. Finally, we derive an analytical mapping from our active polymer model to an effective equilibrium model where folding is determined by pairwise affinities. These two models are indistinguishable based on structural data alone, raising the need for future dynamic measurements. For example, our model assumptions could be tested via measurements of pairwise velocity correlations of specific loci. Furthermore, given ensemble-averaged conformational data of a polymer, our analytical theory enables us to propose an activity profile that could reproduce the observed steady state. By comparing the inferred activity profile to DNA-binding patterns of chromatin-associating proteins, one could determine whether active processes contribute significantly to certain folding patterns. Taken together, our results provide an avenue for analyzing and interpreting data on chromosomes, and have broad implications for active polymer systems.

Model

To study the folding of an active polymer, we combine analytical calculations (of a linear, continuous model) and Brownian dynamics simulations (of a discrete chain). For our theoretical analysis, we idealize the polymer as a space curve r(s, t), where s is a continuous, dimensionless material coordinate along the polymer backbone. We approximate the large-scale dynamics of the polymer by the Rouse model, an extensible chain of material points that interact through Hookean springs κ (42, 78–80),

$$\begin{array}{c}\hfill {\partial }_t\mathit{r}(s,t)={\xi }^{-1}{\partial }_s[\kappa {\partial }_s\mathit{r}(s,t)]+\mathit{\eta }(s,t),\end{array}$$ [1]

where ξ is the drag friction with the surrounding solution and η(s, t) is a zero-mean Gaussian random displacement velocity field which we refer to as “excitations.” In general, the covariance of the excitations at different material points is given by

$$\begin{array}{c}\hfill 〈\mathit{\eta }(s,t)·\mathit{\eta }(s^{\prime },t^{\prime })〉:=\mathcal{C}(s,s^{\prime })\delta (t-t^{\prime }),\end{array}$$ [2]

on timescales longer than the decorrelation time. For a passive polymer that reaches thermal equilibrium, the excitations are determined by the heat bath, 𝒞(s, s′) = 6k_BTξ⁻¹ δ(s − s′), which follows from the fluctuation-dissipation theorem. However, sequence-specific active processes that stir the polymer through random forces will drive the system away from thermal equilibrium. These “athermal excitations” may vary in magnitude along the polymer and exhibit sequence-specific correlations,

$$\begin{array}{c}\hfill \mathcal{C}(s,s^{\prime })={\xi }^{-1}\sqrt{A(s)A(s^{\prime })}\mathbb{C}(s,s^{\prime }),\end{array}$$ [3]

where A(s)=A₀ [1 + ϵ(s)] is the activity at locus s (in units of energy), and ℂ(s, s′) is the “normalized” correlation function. Thermal noise can be interpreted as a baseline activity A₀, which introduces a homogeneous diagonal contribution to the correlation function. Fig. 1 depicts possible molecular drivers of these athermal excitations in the context of the genome. Note that (3) is directly proportional to the pairwise velocity correlation function (SI Appendix, 1 C). Thus, by describing the polymer response to these excitations, our model links patterns of correlated motion with patterns of folding.

Brownian Dynamics Simulations of a Discrete Chain.

To numerically test our theoretical analysis, we developed Brownian dynamics simulations of a discretized Rouse chain, (1), where each of the n ∈ [1, N] monomers represents a Kuhn segment with characteristic length b. In our simulations, we use the Kuhn length b and the average diffusion coefficient D₀ of a free monomer, which is related to the average activity A₀ = ∑_nA_n/N via D₀ = A₀/(6ξ), to define the stiffness of the springs connecting neighboring monomers, κ/ξ = 3D₀/b². Having discretized all fields of our continuum theory, the covariance matrix between the athermal excitations of different beads is then given by

$$\begin{array}{c}\hfill {\mathcal{C}}_{\mathit{nm}}={\xi }^{-1}\sqrt{A_n{A}_m}{\mathbb{C}}_{\mathit{nm}},\end{array}$$ [4]

where we have defined the Pearson correlation matrix ℂ_nm ∈ [ − 1, 1]. To implement more realistic polymer simulations, including self-avoidance and a hard confinement, we adapt the “polychrom” software package (81) as described in Methods. These simulations allow us to test the continued validity of results from our theory in a strongly nonlinear setting that is inaccessible to analytical calculations.

Steady-State Polymer Conformation.

We analytically solve the linearized active polymer model (1) via a Rouse mode decomposition (82), where $\mathit{r}(s,t)\to {\tilde{\mathit{r}}}_q(t)$ and $\mathit{\eta }(s,t)\to {\tilde{\mathit{\eta }}}_q(t)$ indicate Fourier transforms. For a compact notation, we concatenate all Rouse modes row-wise into a matrix R(t) with rows $R_{q,\cdots }(t):={\tilde{\mathit{r}}}_q(t)$. Analogously, we define the random velocity mode matrix H(t) with rows $H_{q,\cdots }(t):={\tilde{\mathit{\eta }}}_q(t)$, which has zero mean and covariance ⟨H(t)⋅H^†(t′)⟩:=C δ(t − t′). In the resulting Rouse mode dynamics,

$$\begin{array}{c}\hfill {\partial }_t\mathit{R}(t)=-\mathit{J}·\mathit{R}(t)+\mathit{H}(t),\end{array}$$ [5]

the response matrix J encodes all material properties (Methods) and is diagonal for a homogeneous Rouse polymer (1), J_qk = ξ⁻¹κ q² δ_qk. In contrast, athermal excitations that break translational invariance are characterized by off-diagonal entries in their covariance matrix 𝒞(s, s′) → C_qk. Although this coupling precludes an isolated analysis of individual Rouse modes, one can derive an exact expression for the long time limit of the second Rouse moment (Methods) as

$$\begin{array}{c}\underset{t\to \infty }{\lim }\langle R(t)·R^{†}(t)\rangle =\underset{\infty }{\overset{0}{\int }}d\tau e^{-J\tau }·C·e^{-J^{†}\tau }.\end{array}$$ [6]

Note, however, that the above equation describes polymer conformations on average, which are liquid-like in the sense that ⟨R(t)⋅R^†(t)⟩ ≫ ⟨R(t)⟩ ⋅ ⟨R^†(t)⟩. The resulting “folding” is thus distinct from most proteins, which form globules with a well-defined conformation, ⟨R(t)⟩ ⋅ ⟨R^†(t)⟩ ∼ ⟨R(t)⋅R^†(t)⟩. Nevertheless, our analysis reveals how inhomogeneous excitations alone can effectively give rise to patterned polymer conformations by coupling different mechanical modes. To quantify these patterns, we transform (6) back into real space, which yields the spatial correlation between pairs of material points. Subsequently, we determine their pairwise mean squared separation and the alignment of different contour vectors, ∂_sr(s) for a continuum polymer or r_i + 1 − r_i for a discrete chain.

Results

Local Activity Modulations Induce Long-Range Correlations Akin to Bending.

To elucidate how active processes affect a polymer’s conformation, we first study a minimal scenario with inhomogeneous activity A(s) represented by statistically independent excitations 𝒞(s, s′) = ξ⁻¹ A(s) δ(s − s′). Simulations have shown that less active monomers localize closer to the boundary of a hard confinement than their more active counterparts (53, 54). This positioning trend reverses if the volume packing fraction is small or if the confinement is soft (54), and can be forcibly inverted by introducing selective monomer–boundary interactions (53), or self-attraction between inactive monomers (58). Thus, past theoretical work has shown that activity differences can reproduce nuclear positioning of (active) euchromatin and (inactive) heterochromatin. However, it is not yet clear how and why active processes affect polymer shape, a question that we now address.

Eq. 6 predicts the preferred polymer conformation in response to any predetermined profile of activity (SI Appendix, 2 A.3 for Green’s function kernels). As an example, we focus on sinusoidal activity modulations A(s)=A₀ [1 + ϵcos(s/λ)] around an average value A₀, with amplitude ϵA₀ and characteristic length λ. These excitations elicit a spatial correlation (SI Appendix, 2 A.3) between pairs of material points, which we use to calculate the pairwise mean squared separation in terms of the Kuhn length $b:=\sqrt{A_0/(2\kappa )}$ (above the diagonal in Fig. 2B):

$$\begin{array}{cc}\hfill 〈{[\mathit{r}(s,t)-\mathit{r}(s^{\prime },t)]}^2〉& =b^2\lambda \{\frac{|s-s^{\prime }|}{\lambda }\hfill \\ \hfill & +2ϵcos(\frac{s+s^{\prime }}{2\lambda })[cos(\frac{s-s^{\prime }}{2\lambda })-e^{-\frac{|s-s^{\prime }|}{2\lambda }}]\}.\hfill \end{array}$$ [7]

Fig. 2.

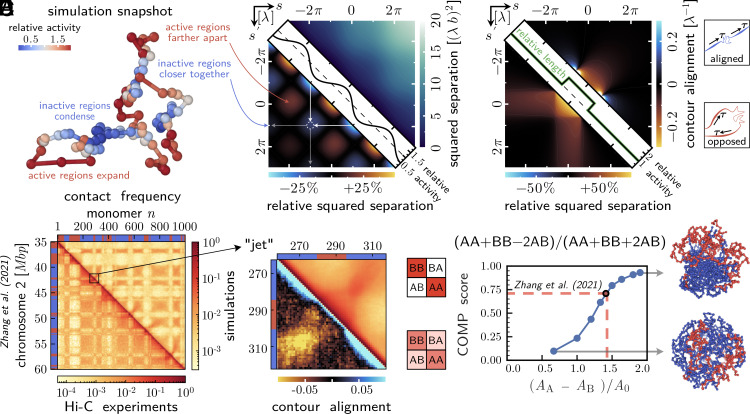
Activity modulations induce polymer folding. (A) Simulation snapshot of a Rouse chain composed of 100 monomers, driven by statistically independent athermal excitations that vary in magnitude, with local activity A(s)=A₀ [1 + ϵcos(s/λ)] and ϵ = 0.5. We plot the same activity profile normalized by its average value, A(s)/A₀, along the diagonal of panel B. (B) Above the diagonal: Mean squared separation between pairs of material points with coordinates s and s′ along the polymer backbone. Below the diagonal: Change in mean squared separation relative to a Rouse polymer with homogeneous activity A₀. Active regions locally expand while inactive regions locally condense. Distant active polymer segments get farther apart while inactive polymer segments come closer together (dashed circle). (C) Response of the polymer to a localized increase in activity. Above the diagonal: A local increase in activity induces effective polymer bending [antialignment of contour vectors ∂_sr(s)] when averaged over a large ensemble. Analogously, a local decrease in activity (sign change) leads to polymer straightening (alignment of contour vectors). Below the diagonal: A local increase in activity leads to a larger spatial separation between the active region and the remainder of the polymer, which maintains the homogeneous activity A₀. Analogously, a local decrease in activity (sign change) leads to a smaller spatial separation between the less active region and the remainder of the polymer. Local expansion and contraction of the polymer backbone are reflected in the relative contour length (plotted on the diagonal), which is proportional to the relative level of activity. (D) Below the diagonal: Hi-C data from ref. (83) showing the contact frequencies between pairs of genomic coordinates within a section of chromosome 2 in murine erythroblast cells. Above the diagonal: Simulated contact probability between pairs of monomers of a 1000-mer self-avoiding chain in a hard spherical confinement. The activity difference between active (A, red) and inactive (B, blue) monomers is chosen to match the degree of compartmentalization observed in the Hi-C data. (E) Above the diagonal: Simulated contact map shows antidiagonal contacts (“jets”) between B regions that flank a small A region. Below the diagonal: Jets are associated with antialignment of contour vectors, suggesting that the A region loops out and zips together neighboring B regions. (F) Simulated contact frequency maps show increasing compartmentalization (COMP score) as a function of the normalized activity difference between A and B regions. Dashed lines illustrate the activity difference (A_A/A_B ≈ 6) required to reproduce the COMP score observed in the Hi-C data of ref. (83). Representative simulation snapshots show phase separation within the polymer.

In comparison to a reference polymer with uniform activity (ϵ = 0), we observe that active polymer segments locally expand while inactive segments locally condense (below the diagonal in Fig. 2B), resembling the morphology of euchromatin and heterochromatin (84, 85). Thus, our theory suggests that active processes like transcription could lead to chromatin decondensation, which might form a positive feedback loop by further increasing genome accessibility to the transcription machinery (86). Indeed, it was shown experimentally that euchromatin requires ATP and thus dissipation of energy to preserve its expanded state (33).

Consistent with prior work (53, 55, 57, 58), we find that pairs of active segments move farther apart while inactive segments come closer together (below the diagonal in Fig. 2B). To explain this observation, we investigate the response of the polymer to a localized change in activity (below the diagonal in Fig. 2C). We find a long-ranged (logarithmic in sequence space) increase in spatial separation between more active regions and the remainder of the polymer. Conversely, regions with decreased activity move closer to the remainder of the polymer, and more complicated excitation patterns can be analyzed based on the superposition principle.

To investigate the shape changes associated with this spatial separation, we measure the pairwise alignment of contour vectors, τ(s, t):=∂_sr(s, t), at different material points for an arbitrary activity profile A(s)=A₀ [1 + ϵ(s)],

$$\begin{array}{cc}\hfill 〈\mathit{\tau }(s,t)·\mathit{\tau }(s^{\prime },t)〉& =\left[1+ϵ(s)\right]\delta (s-s^{\prime })\hfill \\ \hfill & +\int dxϵ(x)G^{\tau }(s-x,s^{\prime }-x).\hfill \end{array}$$ [8]

The Green’s kernel has the most convenient representation in polar coordinates G^τ(αcosϕ, αsinϕ)=sin(2ϕ)/(πα²). The last term demonstrates that local activity modulations induce correlations (effective pairwise couplings) between distant material points, scaling with the distance in sequence space as a power law with exponent −2. Note that the quantitative value of this term will also depend on the local length of the polymer backbone (Fig. 2C, on the diagonal), whereas the sign qualitatively distinguishes alignment from antialignment. However, abolishing changes in contour length by enforcing inextensibility on an ensemble-averaged level does not change the result (SI Appendix, 2 A.4).

Fig. 2C shows above the diagonal that increased activity within a segment of size λ effectively induces bending (pairwise antialignment of contour vectors), while decreased activity leads to straightening (pairwise alignment of contour vectors). Heuristically, active monomers “run away” from their inactive neighbors and effectively bring these neighbors together into a loop-like conformation. This explanation is supported by ref. (61), which studied the dynamics of two particles with different activities that interact through some pair potential. It was shown that, on average, the particle experiencing smaller excitations will move along the applied force whereas the more active particle will move opposite to the applied force. While ref. (61) considered steric repulsion where the active particle “pushes” around the passive one, here, we are dealing with attractive Hookean springs where instead active particles pull on their inactive neighbors. Thus, in our model, segmented activity variations lead to the emergence of spontaneous curvature.

The first term in Eq. 8 describes local compaction (or expansion) of the polymer backbone from reduced (or increased) activity (59). Similar changes in the local contour length could be induced by variations in tension, i.e., the spring constant κ(s). Therefore, it is natural to inquire if conformational changes due to activity variations can be equivalently achieved in a system in thermal equilibrium through variations in the local mechanical properties of the polymer. However, as shown in SI Appendix, 2 A.2, modulations in tension fail to produce any long-ranged contour correlations akin to polymer bending. Changes in the spring stiffness only affect the distance between material points (bond length) and have no effect on the bond angles. Similarly, variations of the drag friction coefficient ξ(s), for example, due to differences in monomer size, do not change the polymer conformation (SI Appendix, 2 A.1). This is because in equilibrium with a thermal heat bath, polymer conformations sample a Boltzmann distribution determined by a free energy, independent of dynamic effects such as friction. Thus, in the absence of long-ranged interactions, activity differences, which can act globally, are required to fold a Rouse polymer into specific conformations.

Activity Differences Recapitulate A/B-Compartments in Simulated Contact Maps.

We next apply our model to study the formation of A/B-compartments, a cornerstone of eukaryotic genome organization (12). To make a meaningful comparison to Hi-C data, we model a region of Chromosome 2 in murine erythroblast cells (83) as an active, self-avoiding polymer that occupies a volume fraction of 11.7% in a nuclear confinement (Methods), where each monomer corresponds to 25 kbp. We ask whether the compartmentalization observed in ref. (83) (Fig. 2D, below the diagonal) can be reproduced purely by differences in the magnitude of athermal excitations in active (A) and inactive (B) regions. To that end, we derive the identities of A and B monomers from the data in ref. (83), as discussed in Methods. The simulated contact frequencies between pairs of monomers display a checkerboard pattern featuring strong B–B contacts, despite the lack of explicit attractive interactions between monomers (Fig. 2D, above the diagonal). While A–A contacts in our simulations are weaker than in the data of ref. (83), more balanced A/B compartments emerge for larger volume fractions (SI Appendix, Fig. S8 B and D) or, as discussed in the next section, if A monomers experience correlated excitations.

The strong B compartments in our model are reminiscent of previous work on equilibrium copolymers with short-ranged B–B attractions and little to no A–A attraction (13). Since this model successfully reproduced microscopy and Hi-C data (13), we compared it to our active polymer simulations (SI Appendix, 4). While both models show A/B compartments (SI Appendix, Fig. S8A), the compartment boundaries are more blurred in the active model due to the presence of antidiagonal features, “jets” (87), which extend from A regions into neighboring B compartments (Fig. 2E and SI Appendix, Fig. S8C). Consistent with the linear theory (Fig. 2C), on average, A regions loop out and zip together the flanking B regions (contour alignment in Fig. 2E). In contrast, the equilibrium model lacks any structure in contour alignment (SI Appendix, Fig. S8C, below the diagonal) and, surprisingly, also predicts faster folding kinetics than the active model (SI Appendix, 4 B). The cell likely leverages both active and passive mechanisms of compartmentalization, and thus hybrid models will invariably fit the data better (58). Nonetheless, the existence of A/B-compartments in the purely active model demonstrates that activity differences are capable of contributing to genome organization.

To explore how the degree of compartmentalization varies with the activity difference between A and B regions, we extract a scalar order parameter (“compartment score,” COMP) from both simulated and experimental contact maps (Methods). This compartment score, defined in ref. (88), measures the contrast in the checkerboard pattern as the normalized contact frequency difference between same-type and different-type chromatin, namely COMP = (AA + BB − 2AB)/(AA + BB + 2AB). We find that the compartment score increases in a sigmoidal fashion with the activity difference between A and B regions (Fig. 2F), indicating a typical scale for onset of compartmentalization in our simulations. This activity difference scale depends on many parameters, including the A and B block sizes (63) and the capture radius used to construct the contact frequency map. For this particular A/B pattern, we find nontrivial compartmentalization for activity differences as small as the average level of activity, A_A − A_B = A₀ = (A_A + A_B)/2. Note that in our analytic theory, which describes a phantom chain without volume exclusion, compartmentalization, as detected in the mean squared separation, is simply a linear response to the activity difference, Eq. 7.

Finally, the compartment score curve in Fig. 2F can be used to read off the activity difference required to reproduce A/B compartmentalization in a given Hi-C dataset. While the degree of chromatin compartmentalization will vary by cell type, a whole-genome analysis of the murine erythroblast data of ref. (83) (Fig. 2F) suggests a score of COMP ∼ 0.71, which corresponds to an activity ratio of A_A/A_B ≈ 6. We used this inferred activity ratio in the polymer simulations depicted above the diagonal in Fig. 2D.

While the activity ratio cannot be measured directly, one can use the monomer mean squared displacement, MSD(t)=Γ t^α, as a proxy. On sufficiently short time scales in a phantom Rouse chain, the ratio of anomalous diffusion coefficients in active and inactive regions is identically the activity ratio, Γ_A/Γ_B = A_A/A_B. However, the value of Γ and α in active and inactive regions will depend on the observation time window and the microscopic properties of the chain, as shown in our nonlinear simulations (SI Appendix, 3 C). Thus, our predicted activity ratio serves as an upper bound for the ratio of MSDs in A and B regions, which can be extracted from measurements of euchromatic and heterochromatic motion (39).

Correlated Active Processes Create Compartments.

Experiments that track the movement of GFP-tagged histones have demonstrated spatial correlations in chromatin motion that depend on RNA polymerase II activity and on ATP (33, 34). While these experiments cannot relate spatial and genomic proximity, ref. (89) has observed pairwise correlated movement of specific loci. Motivated by these experiments, we hypothesize that correlated movement could be driven by correlated active forces, which produce athermal excitations with a nondiagonal covariance 𝒞(s, s′). This hypothesis is plausible if the active processes at distinct genomic locations are not completely independent.

To model sequence correlations, we define a heteropolymer with three types of monomers (+, −, and neutral). We then introduce a stochastic process that has opposing effects on + and − monomers, but does not affect neutral monomers. The choice of + and − as labels for the monomer type evokes the analogy of a charged heteropolymer (for example, a polyelectrolyte or polyampholyte) in a fluctuating electric field. In this example, the random electrical forces at a given time will point in the same direction for monomers of the same charge, but in opposite directions for monomers of opposing charge. More generally, correlated excitations could be achieved by a fluctuating, large-scale concentration gradient of proteins that show sequence-specific interactions with the polymer backbone (Fig. 3A).

Fig. 3.

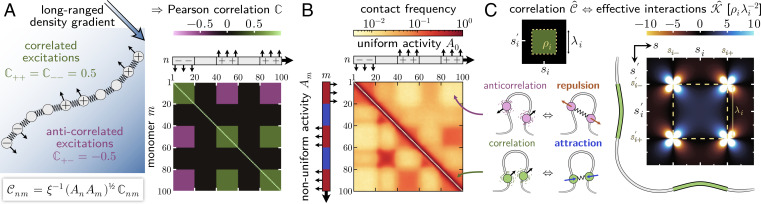
Correlated activity leads to compartments via an effective attraction. (A) Pearson correlation matrix that relates the directions of the random forces acting on different monomers. We construct this matrix by assigning each monomer a chemical identity (+, −, or neutral) whereby monomers of the same chemical species experience correlated excitations, while monomers of different species experience anticorrelated excitations. In the schematic above the matrix, up arrows indicate + monomers and down arrows indicate − monomers. (B) Simulated contact frequencies between pairs of monomers of a 100-mer self-avoiding chain in a spherical confinement. The polymer is driven by athermal excitations with the Pearson correlation matrix shown in panel A. Above the diagonal: When activity is uniform, contacts between monomers that experience correlated excitations are enhanced, while anticorrelated excitations lead to a depletion of contacts. Below the diagonal: We introduce activity modulations where + and − monomers have activity 1.9A₀ (red), and neutral monomers have activity 0.1A₀ (blue). As in Fig. 2, inactive regions form compartments, without disrupting the folding pattern caused by correlated excitations. (C) Correlated excitations fold an active polymer analogously to effective harmonic interactions in a passive polymer, cf. (9). To illustrate these couplings, we consider two polymer segments of equal length λ_i located at coordinates s_i and s_i′, which experience excitations with correlation coefficient ρ_i (green box). Positive correlations (ρ_i > 0) lead to an effective attraction (blue) between these segments through weak, long-ranged harmonic interactions. Conversely, anticorrelated excitations (ρ_i < 0) lead to an effective repulsion (orange) between these segments. If the coordinates s_i and s′_i coincide (that is, if we consider correlated excitations within a contiguous segment), then the correlation coefficient is positive and the segment condenses.

Based on these ideas, we construct a sample Pearson correlation matrix for the excitations of a polymer with an alternating pattern of +, −, and neutral monomers (Fig. 3A). Using this Pearson correlation matrix as input and assuming a homogeneous level of activity, cf. (4), we then perform Brownian dynamics simulations featuring self-avoidance and a spherical confinement. Fig. 3B shows, above the diagonal, that contacts between loci driven by correlated excitations are enhanced, whereas contacts between anticorrelated loci are depleted. These folding patterns are accompanied by long-range correlations between the contour vectors at distant material points, as shown in our theoretical calculations (SI Appendix, 2 A.6). In addition to the pattern of correlations, we superimpose activity modulations, A_n, such that charged (±) monomers are active and neutral monomers are inactive. We find an enhancement of contacts between inactive regions, leading to a full checkerboard pattern (Fig. 3B, below the diagonal). Thus, correlated active forces and activity differences offer complementary, nonequilibrium mechanisms for the formation of genomic compartments.

The Effects of Correlated, Nonequilibrium Excitations on Polymer Shape can be Recapitulated by an Equilibrium Model with Intersegment Interactions.

The linear active polymer, driven by athermal Gaussian excitations with covariance $\mathcal{C}(s,s\prime )={\xi }^{-1}{A}_0[\delta (s-s\prime )+\widehat{\mathcal{C}}(s,s\prime )]$, maintains a Gaussian steady-state distribution of conformations. This Gaussian steady state is, up to translational invariance, fully characterized by its two-point correlation function ⟨r(s, t)⋅r(s′,t)⟩, which can be computed in terms of the prescribed entries of 𝒞(s, s′). To illuminate the characteristics of active polymer folding, we note that any Gaussian steady state can be regarded as the thermal equilibrium weight of a phantom polymer with additional Hookean springs, $\widehat{\mathcal{K}}(s,s\prime )$, which harmonically couple pairs of material points (18). After setting a temperature scale by A₀ = 6k_BT, one can obtain the harmonic couplings by inverting the two-point correlation function ⟨r(s, t)⋅r(s′,t)⟩, as shown in Methods:

$$\begin{array}{cc}\hfill \widehat{\mathcal{K}}(s,s^{\prime })& =-\left[{\partial }_s^2+{\partial }_{s^{\prime }}^2\right]\widehat{\mathcal{C}}(s,s^{\prime })\hfill \\ \hfill & +\int \int dxd{x}^{\prime }\widehat{\mathcal{C}}(x,x^{\prime })G^K(s-x,s^{\prime }-x^{\prime }).\hfill \end{array}$$ [9]

The Green’s kernel has the most convenient representation in polar coordinates G^K(αcosϕ, αsinϕ)= − 6cos(4ϕ)/(πα⁴). Eq. 9 establishes a mapping between active and passive polymers whose conformations, in steady state, are sampled from the same distribution (i.e., identical mean squared separation and contour alignment). While the active polymer folds due to constraints on the excitations (i.e., correlations; the special case of activity modulations is discussed in SI Appendix, 2 B.3), in the corresponding passive polymer constraints are introduced in the form of springs. These harmonic couplings can be positive or negative, mediating pairwise attraction or repulsion between distant material points. The first term of Eq. 9 indicates that pairs of polymer segments experiencing maximally correlated excitations will show effective pairwise attraction, while maximally anticorrelated excitations lead to repulsion. By using a box-shaped correlation function to study the second term of Eq. 9, we confirm that correlated excitations in general induce pairwise attraction (Fig. 3C), whereas anticorrelated excitations lead to repulsion.

These results can be heuristically understood via the dynamics of the end-to-end distance vector of, say, a trimer (N = 3). For such a trimer, fluctuations of the end-to-end distance Δ are driven by a noise term with variance ⟨[η_Δ(t)]²⟩=⟨[η₁(t)−η₃(t)]²⟩=⟨[η₁(t)]²⟩+⟨[η₃(t)]²⟩−2⟨η₁(t)⋅η₃(t)⟩. When the excitations are independent and equal in magnitude, one has ⟨[η_Δ(t)]²⟩=2 ⟨[η₁(t)]²⟩. In comparison, anticorrelated excitations (⟨η₁(t)⋅η₃(t)⟩ < 0) increase the variance of the end-to-end separation, whereas correlated excitations (⟨η₁(t)⋅η₃(t)⟩ > 0) cause the end points to come closer together. While these effects are diminished for longer polymers, they provide basic insights into the effective harmonic interactions that lead to the contact frequency map shown in Fig. 3B.

The existence of an analytical mapping between active and passive mechanisms of polymer folding suggests that many equivalent models could explain structural data on chromosomes. In this context, our passive linear model can be regarded as a harmonic approximation to a contact energy landscape, which has been exploited by past theoretical work on genome organization (14–17, 19–21). Our results shed further light on the success of these equilibrium models in reproducing Hi-C data despite the undeniable presence of active processes (90). As such, how can one experimentally disentangle equilibrium and nonequilibrium mechanisms of compartment formation? Based on static snapshots, our theory can be used to propose a candidate pattern of active processes that drive chromatin toward its observed steady-state conformation. Then, one can test whether the inferred activity profile matches orthogonal experimental measurements, such as the DNA-binding patterns of active enzymes, or if passive folding mechanisms are more plausible.

Inferring an Activity Profile from Ensemble-Averaged Polymer Conformations.

In the following, we infer a candidate map of athermal excitations that could fold a polymer into a desired (target) conformation. To that end, we use our linear theory to predict the activity of each monomer given the mean squared separation between all pairs of monomers (cf. workflow depicted in Fig. 4A). We test our approach on artificial target conformations, which we generate via simulations of (nonlinear) polymers driven by activity modulations, with profiles corresponding to Fig. 2D–F.

Fig. 4.

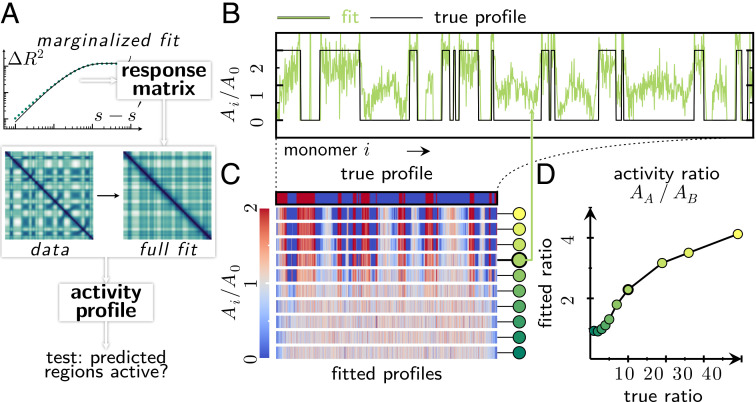
Inferring an activity profile based on structural data. (A) Data analysis workflow, which takes as input a heatmap with the pairwise mean squared separation between all monomers. First, we infer the mechanical properties of the homogeneous polymer on top of which activity differences will be imposed. We then propose a profile of activity that minimizes the mean squared error between the predicted mean squared separation map and the data. This workflow can be used to identify candidate active regions of the polymer, which could then be tested against alternative measurements. (B) We applied the workflow shown in A to simulated data on self-avoiding polymers driven by activity modulations in a spherical confinement (cf. Fig. 2F). We find, in general, good agreement between the inferred activity profile and the true profile used in the simulations. (C) The fitted activity profiles correctly identify the boundaries between active and inactive regions in the true activity profile. Color-coded circles next to the activity profiles correspond to the plot points (fitted activity ratios) in panel D; highlighted circle indicates activity profile in panel B. (D) The fitted activity ratio between active (A) and inactive (B) regions correlates with the activity ratios of the athermal excitations used in our simulations. In our linear model, a systematically lower activity ratio is sufficient to reproduce the folding patterns observed in the nonlinear simulations.

As it is not clear how nonlinear constraints such as self-avoidance or a hard confinement translate into our linearized theory, we invoke no prior knowledge of the mechanical properties of the polymer. Instead, we adopt a data-driven approach and first determine an effective response matrix J that approximates the mechanical properties of the simulated polymer (SI Appendix, 5 A and B; (130)). Next, we set up a numerical optimization scheme whereby we seek the activity profile (Fig. 4B) that minimizes the squared deviation between the mean squared separation map predicted by our theory and our artificial data (SI Appendix, 5 C; (130)). Inference from the linear theory captures the overall block-like structure of the mean squared separation map, but does not account for some of the finer qualitative features observed in the nonlinear simulations (SI Appendix, 5 C). We hypothesize that these fitting results could be improved in future studies by introducing constraints on the analytical theory, or by considering excitations that have an effective correlation length in addition to activity modulations.

Correspondingly, the linear model successfully infers the structure of the activity profile used in our nonlinear simulations (Fig. 4 B and C). The inferred and original activity profiles visually appear similar and have comparable amplitudes A_A − A_B (Fig. 4B). However, the inferred ratio of activity A_A/A_B is systematically lower than in our simulations (Fig. 4D). These results suggest that the lack of constraints in the linearized model makes it easier to create folding patterns than in our simulations. Despite these quantitative differences, this approach successfully identifies active and inactive polymer segments in all simulations that show pronounced folding patterns (Fig. 4C).

In closing, we propose an approach to infer a distribution of active processes along chromatin from of experimental data. As a first test for plausibility, one could compare inferred activity profiles against orthogonal experimental measurements such as ChIP-Seq for ATPases or histone marks associated with active chromatin.

Discussion

Using our nonequilibrium polymer theory, we have demonstrated that differences in activity and correlations between athermal excitations at different loci can fold a polymer into specific shapes. These liquid-like conformations have a large variability and are therefore only realized as a population average. Our model could thus be applicable to chromatin, which shows a much larger cell-to-cell variability than stable protein structures (91, 92). In this context, we zoom out to large length scales, where molecular drivers of active processes (Fig. 1) produce effective athermal excitations. Although it neglects many details of chromatin structure, including nucleosome packaging and solvent effects, the Rouse model can still provide valuable insights into the configurations of real polymers. Indeed, our simulations of self-avoiding, confined polymers show very similar results to the linear theory. Moreover, Rouse models have been used to recapitulate the dynamics and response of chromosomal loci to an applied force (93–95). Our model then makes several testable predictions that could be further investigated with experiments and theory.

We predict that a local increase in activity should lead to chromatin decondensation (Fig. 2 A and B). Indeed, it was shown that recruiting a transcriptional activator, and hence RNA polymerase II, to mouse chromocenters caused these heterochromatic regions to decollapse (96). The resulting increase in chromatin accessibility could further increase transcriptional activity (86), forming a nonlinear positive feedback loop. Such a feedback loop would, over time, stabilize an open chromatin structure in active regions. Furthermore, our model shows that a local decrease of activity leads to straightening of the polymer backbone, whereas a local increase in activity induces bending (Fig. 2C). These results could explain an observation in recent simulations, which demonstrated that forces exerted by bound molecular motors can bend polymers into hairpins (72). Such zipped structures also arise in Hi-C maps (87, 97, 98) and in our simulated contact maps as jet-like, antidiagonal features originating from small A regions and extending into the neighboring B compartment (Fig. 2 D and E). Experiments suggest that these structures could be formed by active loop extrusion (87), which is not explicitly accounted for in our model. Nevertheless, it is interesting that the spontaneous loops induced by a local hot spot of activity could still create jet-like features. These predictions could be directly tested by measuring mean squared distances and average contour alignment in chromatin tracing data (99–101).

In addition to locally deforming the polymer backbone, activity differences lead to a “checkerboard” pattern indicative of compartmentalization. We show that the degree of A/B compartmentalization observed in experimental contact maps can be recapitulated in our simulations with activity ratios in the two-fold to ten-fold range (Fig. 2F). These ratios are much smaller than the 20- to 30-fold activity differences reported in prior numerical studies which focused on the spatial positioning of active and inactive regions within a confinement (53, 54). Instead, our results are more similar to the activity differences required for phase separation in mixtures of active and inactive homogenous polymers (63, 64).

To test whether these activity ratios are plausible, one could measure the ratio of the anomalous diffusion coefficients of euchromatic (A) and heterochromatic (B) regions, as has been done in histone tracking experiments (39). Since euchromatin has a higher level of transcriptional activity, we may expect that it will exhibit faster (sub)diffusion than heterochromatin (39, 40). However, the effect of transcription on the subdiffusion of individual loci is controversial (37, 38). One way to explain these conflicting results is to note that diffusion is not only proportional to activity, which increases during transcription, but is also inversely proportional to friction, which increases when the transcriptional machinery binds to the promoter. Concomitant with this idea, it was observed that during transcription inhibition, the subdiffusion of DNA-bound histones increases after RNA polymerase II disassociates (39, 40), but decreases if RNA polymerase II remains bound (39). Future work could elucidate how the polymer conformation responds to simultaneous changes in friction and activity.

Another test of activity-induced compartmentalization would be to perform Hi-C experiments after knocking out active processes. However, global ATP depletion runs the risk of glassifying the intracellular environment (102). In addition, ATPase inhibition may also modify the effective pairwise chemical affinities between loci. Nonetheless, existing experiments with transcription inhibition show that A/B-compartments remain, but the contrast in the checkerboard pattern decreases (83, 103). It therefore seems plausible that transcription plays some role in compartmentalization, which must be clarified in future studies (104). We hypothesize that activity differences may complement known mechanisms of eu/heterochromatin segregation, including phase separation mediated by linker histone H1 and heterochromatin protein HP1-α, as well as association of heterochromatic domains to the nuclear lamina (10).

In addition, whole-nucleus histone tracking has shown that transcription and ATP-dependent processes are required for coherent motion of chromatin (33, 34). The mechanistic origin of correlated motion is under active research (58, 65, 66, 69, 70, 105, 106) and its consequences for chromatin folding are still unknown. Our theory predicts that regions exhibiting correlated motion will, when driven by sequence-specific athermal excitations, form compartments. This raises the question of whether coordinated transcription of enhancers and promoters could lead to contacts, or “microcompartments,” as has been observed in increasingly high-resolution contact maps (107–109). However, further research is needed to investigate the relationship between coordinated transcriptional programs and correlated motion. To directly test our model assumptions, one could measure pairwise velocity correlations between specific loci, as a function of transcriptional state and sequence coordinate (89). For example, one could measure whether cis regulatory elements show correlated movement, and then test whether transcription inhibition at one locus decorrelates this movement and the associated contacts. A similar procedure could be used to test whether the colocalization of coregulated genes is a consequence of correlated active processes (75, 76, 110, 111). For example, coordinated transcription factor–binding events can initiate processes that break detailed balance (112, 113).

Overall, dynamic measurements will play a major role in disentangling active and passive mechanisms of chromatin folding, which we have demonstrated to be indistinguishable based on Hi-C data alone. For example, our predictions regarding the kinetics of compartment formation (SI Appendix, 4 B) could be compared to Hi-C data at multiple points in the cell cycle of synchronized cells (83, 114, 115). In future work, we hope to also identify dynamic signatures of activity (116) that can be extracted from trajectories of genomic loci (117) in order to examine the role of active processes in chromatin folding. As a complementary technique, we have here presented a proof of concept that an activity profile can be inferred from structural data on a polymer. In future work, we propose to extend this method to chromatin tracing data (99, 100), which measures the pairwise mean squared separation of genetic loci along with other attributes such as transcriptional (100) and epigenetic state (118, 119).

In closing, we note that our theory also has broad implications beyond chromatin folding. We hypothesize that one could, for example, use electromagnetically driven colloidal (Janus) particles to engineer active polymers that fold into desired conformations (120), by applying targeted excitations through dynamic light patterns. Furthermore, on large length scales, our model shares its mathematical structure with mechanical models of membranes. Interestingly, it was recently shown that Min proteins can deform giant unilamellar vesicles by binding to the membrane (121). While it was hypothesized that Min proteins induce spontaneous curvature (122) and that this could even affect their binding kinetics (123), the underlying mechanism remains unknown. Our theory could provide some hints as to how reactions themselves could effectively induce spontaneous curvature in membranes. Overall, our analysis motivates future research into the role that active processes play in determining the mechanical conformation of a variety of pattern-forming systems.

Materials and Methods

Derivation of the Steady-State Polymer Conformation.

We now outline a brief derivation of the steady-state polymer conformation, starting from Eq. 5; a more elaborate calculation is provided in SI Appendix, 1 B, while corresponding Mathematica and Julia code is provided in ref ([insert Zenodo ref here]) and in the Github repository: https://github.com/Driy/Active-Polymer-Conformation. Given an unknown matrix-valued function H(t), which encodes a possible trajectory of the excitations, Eq. 5 is formally solved by

$$\begin{array}{c}\hfill \mathit{R}(t)=e^{-\mathit{J}(t-t_0)}·\mathit{R}(t_0)+{\int }_{t_0}^{t}d\tau e^{-\mathit{J}(t-\tau )}·\mathit{H}(\tau ),\end{array}$$ [10]

where the first term vanishes in the limit t − t₀ → ∞. We use the formal solution for a single trajectory of the Rouse matrix, Eq. 10, to determine the second Rouse moment, ⟨R(t)⋅R^†(t)⟩, in response to athermal excitations with covariance ⟨H(t)⋅H^†(t′)⟩:=C δ(t − t′). To that end, we multiply Eq. 10 with its conjugate transpose and average over many trajectories. Both in the limit of late times (t → ∞ for arbitrary t₀), or equivalently early reference times (t₀ → −∞ for arbitrary t), one then finds

$$\begin{array}{c}\underset{t-t_0\to \infty }{\lim }R(t)·R^{†}(t)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}d\tau e^{-J\tau }·C·e^{-J^{†}\tau }.\end{array}$$ [6]

Here and henceforth, we consider reference times that lie infinitely far in the past (t₀ → −∞), and therefore omit the time limit (lim_{t − t0 → ∞}…) for brevity of notation. For polymers whose material properties such as line tension and friction are homogeneous, the response matrix is diagonal (J_qk ≡ J_qq δ_qk) and Eq. 6 evaluates to:

$$\begin{array}{c}\hfill 〈{\tilde{\mathit{r}}}_q(t)·{\tilde{\mathit{r}}}_k^{\ast }(t)〉=\frac{C_{\mathit{qk}}}{J_{\mathit{qq}}+J_{\mathit{kk}}}.\end{array}$$ [11]

For a Rouse polymer (J_qk = ξ⁻¹κ q² δ_qk) that, as discussed in the main text, is driven by correlated athermal excitations with mode covariance $C_{\mathit{qk}}={\xi }^{-1}{A}_0[L{\delta }_{\mathit{qk}}+{\widehat{C}}_{\mathit{qk}}]$, one has:

$$\begin{array}{c}\hfill 〈{\tilde{\mathit{r}}}_q(t)·{\tilde{\mathit{r}}}_k^{\ast }(t)〉=b^2\left[\frac{L{\delta }_{\mathit{qk}}}{q^2}+\frac{2{\widehat{C}}_{\mathit{qk}}}{q^2+k^2}\right],\end{array}$$ [12]

where the characteristic length is given by $b:=\sqrt{A_0/(2\kappa )}$. In general, however, the response matrix will be nondiagonal and we need to use a perturbation approach (SI Appendix, 1 E) to approximate the matrix exponentials in Eq. 6.

Steady-State Conformation of a Passive Polymer.

We now consider the steady-state conformation of a polymer of length L, which is in thermal equilibrium with a heat bath of temperature T. The passive polymer is governed by reciprocal interactions and therefore has a Hermitian response matrix, J = J^†. In thermal equilibrium, the excitations are statistically independent and homogeneous, with covariance 𝒞(s, s′) = ξ⁻¹A₀ δ(s − s′) and activity A₀ = 6k_BT. Because different excitation modes are now independent, C_qk = ξ⁻¹A₀ Lδ_qk, Eq. 6 evaluates to

$$\begin{array}{c}\hfill 〈\mathit{R}(t)·{\mathit{R}}^{†}(t)〉=\frac{1}{2}{\xi }^{-1}{A}_{0}L{\mathit{J}}^{-1},\end{array}$$ [13]

so that polymer folding can only be induced by nondiagonal elements in the response matrix J. We herein assume that the response matrix is dominated by topological connectivity of neighboring material points and by homogeneous mechanical features of the polymer backbone. Therefore, we decompose the response matrix into a dominant diagonal contribution ${\overline{J}}_{\mathit{qk}}:=J_{\mathit{qq}}{\delta }_{\mathit{qk}}$ and a weak off-diagonal contribution $\delta \mathit{J}:=\mathit{J}-\overline{\mathit{J}}$, so that

$$\begin{array}{c}\hfill 〈\mathit{R}(t)·{\mathit{R}}^{†}(t)〉\approx \frac{1}{2}{\xi }^{-1}{A}_{0}L\left({\overline{\mathit{J}}}^{-1}-{\overline{\mathit{J}}}^{-1}·\delta \mathit{J}·{\overline{\mathit{J}}}^{-1}\right).\end{array}$$ [14]

To enforce polymer folding in our equilibrium model, we introduce additional Hookean springs to Eq. 1,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\partial }_t\mathit{r}(s,t)& =\mathit{\eta }(s,t)\hfill \\ \hfill & +\frac{\kappa }{\xi }\{{\partial }_s^2\mathit{r}(s,t)+\int d{s}^{\prime }\widehat{\mathcal{K}}(s,s^{\prime })\left[\mathit{r}(s^{\prime },t)-\mathit{r}(s,t)\right]\}.\hfill \end{array}\end{array}$$ [15]

With ${\widehat{K}}_q^k:=\iint dsds\prime e^{-iqs}\widehat{\mathcal{K}}(s,s\prime )e^{iks\prime }$ as convention for Fourier transforms, the diagonal and off-diagonal components of the response matrix are given by ${\overline{J}}_q^k={\xi }^{-1}\kappa q^2{\delta }_q^k$ and $\delta J_q^k=-{\xi }^{-1}\kappa L^{-1}({\widehat{K}}_q^k-{\widehat{K}}_{q-k,0})$, respectively. Thus, Eq. 14 evaluates to:

$$\begin{array}{c}\hfill 〈{\tilde{\mathit{r}}}_q(t)·{\tilde{\mathit{r}}}_k^{\ast }(t)〉=b^2\left[\frac{L{\delta }_q^k}{q^2}+\frac{{\widehat{K}}_q^k-{\widehat{K}}_q^{-k},0}{q^2{k}^2}\right],\end{array}$$ [16]

where the characteristic length is given by $b:=\sqrt{A_0/(2\kappa )}$, as before. Note that the homogeneous Fourier modes of the harmonic interaction map, q = 0 and k = 0, cancel out in the polymer’s Langevin equation [15], and thus also in the steady-state conformation, 16. Therefore, in the following we assume ${\widehat{K}}_{q0}=0\forall q$. Equating Eqs. 12 and 16, and transforming back into real space, one obtains Eq. 9.

Rouse Polymer Simulation Details.

To test the approximations in our analytical theory and visualize individual polymer conformations, we perform Brownian dynamics of a discretized Rouse chain without self-avoidance or confinement: https://github.com/kannandeepti/active-polymers. Since the average monomer diffusion coefficient D₀ only rescales time and has no effect on the steady state conformation, we arbitrarily set D₀ = 1 and the Kuhn length b = 1, such that all simulated length scales are now in units of Kuhn lengths. We integrate the discrete version of Eq. 1 using a first-order Stochastic Runge Kutta scheme detailed in ref. (124) with time step h = 0.01 chosen to be an order of magnitude smaller than the time to diffuse a Kuhn length, b²/6D. We then run the simulation for a Rouse time to allow the polymer to reach steady state. The snapshot in Fig. 2A was visualized with OVITO (125) and taken from a simulation with monomer diffusion coefficient D_n = D₀[1 + ϵcos(2πn/λ)], where λ = 25 Kuhn lengths and the total chain is 100 Kuhn lengths.

Self-Avoiding, Confined Polymer Simulation Details.

We also develop more realistic polymer simulations by adapting the “polychrom” software package (81), a thin wrapper around OpenMM (126): https://github.com/open2c/polychrom. The deterministic forces applied to the polymer are given by the following potential energy functions detailed in the polychrom.forces module: 1) Polymer connectivity via harmonic bonds with energy 0.5κ(r_ij − 1)², where r_ij is the distance between the centers of adjacent monomers with diameter d = 1, and κ is chosen such that the average extension of the bond is 0.1 when the harmonic energy is k_BT. 2) Spherical confinement with radius r_C of the form f_C[((r_n − r_C)² + δ²)^1/2 − δ] if r_n > r_C and 0 if not, where r_n is the distance of the n^th monomer to the origin, f_C = 5k_BT/d is the confining force, and δ = 0.1 is some small number inserted to prevent rounding errors. The confinement energy is thus a smooth version of the function f_C|r − r_c|, where the radius r_C is chosen such that the total volume fraction of all monomers within the confinement is 0.117. 3) Repulsive short-ranged interactions via a Lennard-Jones like potential:

$$\begin{array}{c}\hfill U(r_{\mathit{ij}})=U_0\left\{1+{\left({\tilde{r}}_{\mathit{ij}}\right)}^{12}\left[{\left({\tilde{r}}_{\mathit{ij}}\right)}^2-1\right]\right\},{\tilde{r}}_{\mathit{ij}}:=\frac{r_{\mathit{ij}}}{d}\sqrt{\frac{6}{7}},\end{array}$$ [17]

where U₀ = 3k_BT represents a finite energy barrier to allow chain passing when r_ij < 0.6d. The stochastic forces are implemented according to Eq. 4 using custom Brownian integrators, as detailed in the contrib/integrators module of the GitHub repository: https://github.com/kannandeepti/polychrom_analysis.

Random initial configurations were generated by growing the polymer on a cubic lattice in a cubic box of size r_C. Steady state was determined by running the simulation until the monomer mean squared displacement plateaus at the squared radius of confinement, i.e., until each monomer has had enough time to explore its volume (10⁷ time steps). We then ran each simulation for twice this equilibration time and sampled 10 steady-state conformations from each run. For each set of parameters, we repeated this procedure over 200 independent simulation runs and thus computed average contact maps from an ensemble of 2,000 snapshots. We define a contact as an intermonomer separation that is less than two monomer diameters. Simulation snapshots in Fig. 2F were generated with nglview (127).

Hi-C Data Processing and Compartment Identification.

To make a meaningful comparison to Hi-C data, we model a region (35 Mbp to 60 Mbp) of Chromosome 2 in murine erythroblasts, a model eukaryotic cell line (83). We then derive the identities of active (A) and inactive (B) monomers in our simulated chain from the data in the following way (130). First, we iteratively correct the experimental contact map at 100-kbp resolution such that the rows and columns sum to one, a process that removes experimental biases and ensures equal visibility of all loci (128). We then divide each diagonal of the experimental contact frequency map by its mean in order to produce an “observed over expected” map, which measures structure in the data beyond the average decay of contacts with genomic separation. Subtracting the mean from this “observed over expected” map yields a matrix where positive entries indicate enrichment of contacts above the mean and negative entries denote depletion of contacts below the mean. The first eigenvector (E1) of the resulting map captures the checkerboard pattern characteristic of A/B compartmentalization, and can thus be used to binarize the genome into active (A) and inactive (B) segments. Since the A/B identities are determined up to a sign of the entries of E1, we “align” the E1 track to a binned profile of GC content, such that positive entries correlate with active chromatin and negative entries with inactive chromatin (128). Since compartments are typically measured at the 100-kbp resolution, it is sufficient to assign 4 monomers to each Hi-C bin, i.e., one monomer per 25 kbp. Note that this resolution is well beyond the persistence length of chromatin, which is on the order of 1 kbp (129), justifying the omission of bending rigidity in our simulations.

Compartment Scores.

To quantify the degree of compartmentalization observed in both experimental and simulated contact maps, we compute an order parameter—the compartment score (130). Specifically, we use the definition of the “COMP score 2” introduced in ref. (88). We first process the simulated contact maps in the same way as the experimental data, i.e., via iterative correction and computation of E1 (see previous section). The rows and columns of the observed over expected map are sorted and binned by quantiles of the E1 track, such that the top left quadrant shows B–B contacts, the bottom right quadrant shows A–A contacts, and the off-diagonal quadrants show contacts between A and B regions. The COMP score is defined by averaging over the top 25% of contacts in each of the 4 quadrants and computing (AA + BB − 2AB)/(AA + BB + 2AB). The resulting score is 0.0 if there is no difference between the contact frequencies of same-type and different-type chromatin, and 1.0 if A and B regions are perfectly demixed.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Source code used for simulations and numerical analysis, as well as simulation scripts containing parameters used. Data have been deposited in Zenodo (10.5281/zenodo.7274942) (130).