Abstract
Despite numerous innovative designs having been published for phase I drug-combination dose finding trials, their use in real applications is rather limited. As a working group under the American Statistical Association Biopharmaceutical Section, our goal is to identify the unique challenges associated with drug combination, share industry’s experiences with combination trials, and investigate the pros and cons of the existing designs. Toward this goal, we review seven existing designs and distinguish them based on the criterion of whether their primary objectives are to find a single maximum tolerated dose (MTD) or the MTD contour (i.e., multiple MTDs). Numerical studies, based on either industry-specified fixed scenarios or randomly generated scenarios, are performed to assess their relative accuracy, safety, and ease of implementation. We show that the algorithm-based 3+3 design has poor performance and often fails to find the MTD. The performance of model-based combination trial designs is mixed: some demonstrate high accuracy of finding the MTD but poor safety, while others are safe but with compromised identification accuracy. In comparison, the model-assisted designs, such as BOIN and waterfall designs, have competitive and balanced performance in the accuracy of MTD identification and patient safety, and are also simple to implement, thus offering an attractive approach to designing phase I drug-combination trials. By taking into consideration the design’s operating characteristics, ease of implementation and regulation, the need for advanced infrastructures, as well as the risk of regulatory acceptance, our paper offers practical guidance on the selection of a suitable dose-finding approach for designing future combination trials.
Keywords: Clinical trial, Drug combination, Dose finding, Maximum tolerated dose, Toxicity
Introduction
In the era of precision medicine, drug combinations have been widely used to enhance treatment efficacy and overcome the resistance of monotherapy1,2, especially in oncology. Notable drug-combination trials include the combination of trastuzumab with chemotherapy for HER2-positive metastatic breast cancer3, BRAF plus MEK inhibitors for melanoma with BRAF V600 mutations4, and the combination of neratinib and temsirolimus for multiple solid tumors5, among others. In the past decades, the rapid development of immuno-oncology leads to immunotherapy becoming a backbone option for combination in many cancer treatments and in the year of 2019 alone, there are 592 active combination dose-finding studies registered in clinicaltrials.gov. Due to drug–drug interaction, the combination of multiple drugs often demonstrates different toxicity profiles from that of each individual drug. Phase I trial is critically important to assess and ensure the safety of drug combinations. The primary objective of phase I combination trials is to identify the maximum tolerated dose (MTD) or MTDs, defined as the dose combination with the joint dose-limiting toxicity (DLT) probability that is closest to a pre-specified target level, from a range of possible dose combinations of the considered agents6.
Because of unknown drug–drug interaction effects, dose-finding trials for combined drugs should be conducted with more caution and care than monotherapy6–8. In contrast to single-agent phase I trials, which usually assume a monotone dose-toxicity relationship and only perform one-dimensional searching, drug-combination trials typically need to test multiple doses of each of the combined drugs to establish the MTD9, leading to a multi-dimensional dose-searching space. As a result, the number of dose combinations to be explored in a combination trial is much larger than that of a single-agent trial. In addition, due to unknown drug–drug interactions, the toxicity order among dose combinations is only partially known (see the left panel of Figure S1 of Supplementary Materials), making the determination of dose escalation/de-escalation complicated8. For example, to escalate the dose, there are three options, including increasing the dose of one drug while fixing the dose of the other drug, increasing the dose of one drug while decreasing the dose of the other drug, or simultaneously increasing the dose of each drug, and we must determine which option is the most appropriate. Another important aspect of combination trials is the existence of the MTD contour (i.e., multiple MTDs) in the two-dimensional dose-searching space, as shown in the right panel of Figure S1 of Supplementary Materials. Thus, unlike single-agent trials, the objective of combination trials can be to find a single MTD or to find the MTD contour. Identification of the MTD contour is more challenging than identification of a single MTD as the former requires a more thorough exploration and learning of the whole dose combination space, thus demanding additional design considerations.
Industry’s experiences with combination trial designs
Our working group consists of biostatisticians from pharmaceutical companies, ranging from large international companies to small regional startups, regulatory agencies, and academia. Although experiences with combination trial designs have varied across different pharmaceutical companies, the consensus of the working group is that, (i) compared to single-agent trials, biostatistical and clinical teams are substantially less familiar with designing combination trials that have desirable properties (for example, modeling entire dose-DLT relationship in multiple dimensions followed by appropriately guided dose decisions), and (ii) the lack of clear guidance on the pros and cons of existing combination designs further limits research team’s ability to choose a proper design for combination trials. As a result, pharmaceutical companies often rely on an oversimplified approach, which involves only varying the dose levels of one drug while fixing the other drug’s dose. When the latter is a marketed drug, its dose is often fixed at the dose recommended on the label, or the MTD identified from a previous monotherapy study, or one dose level lower. Therefore, the combination trial reduces to a one-dimensional dose escalation study. This approach is simple and allows the use of the conventional single-agent dose-finding methods (e.g., the 3+3 design) to find an MTD, but it restricts the dose finding to a small subset of possible combinations, thus increasing the chance of missing the MTD and failing to establish a clinically meaningful recommended phase II dose (RP2D). In addition, the approach of fixing the dose of one drug also largely limits the ability to estimate the potential synergistic effect between drugs. Another commonly used approach is to pre-select a subset of combinations, where the doses of both drugs vary, and makes strong assumptions that they follow a specific known toxicity order. This approach also allows the use of single-agent trial designs, but suffers from the same drawback. In addition, it is often challenging, if possible, to pre-specify the toxicity order of different combinations due to unknown drug–drug interactions. The members of the working group are aware of the limitation of these oversimplified approaches and the availability of novel designs that are capable of finding the MTD without restricting to a subset of combinations10–35, but few pharmaceutical companies have consistently applied these novel designs in their trials due to lack of guidance on the operating characteristics of these designs. Some of our working group members had experiences in some designs, such as the extension of the model-based Bayesian logistic regression method (BLRM)32,36, an ad hoc design based on the two-dimensional pool-adjacent-violators algorithm37, and Bayesian optimal interval (BOIN) drug-combination design25,38. While some designs (e.g., BLRM) have some clear advantages that the model can readily be extended for multiple (two or more) drug combinations and the mathematical construct allows formal incorporation of historical and emerging data (from single agent studies as well as combination studies), it is also recognized that the use of these methods in real trials is rather limited to only a few organizations due to the unawareness of benefits of such designs over simple-to-use designs, in addition to lack of experience in delineating model parameters.
The objective of this paper is to remove these barriers and provide practical guidance for choosing appropriate designs for drug-combination dose-finding trials where more than one dose level for each single drug is planned. We review seven existing drug-combination designs and conduct a comprehensive Monte Carlo study (i.e., simulations) to compare these designs’ relative performance in accuracy and safety. In the literature, there are some existing studies on comparisons of drug-combination designs, however, most are based on limited fixed scenarios and only consider designs for finding a single MTD39,40. Different from these publications, we cover algorithm-based, model-based, and model-assisted methods, and further distinguish them to methods finding a single MTD and methods finding multiple MTDs. To ensure the practical applicability and generality of our results, we compare the designs under both a set of representative scenarios and a large number of randomly generated scenarios. The set of representative scenarios is elicited from working group members who have extensive practical experience in the pharmaceutical industry to represent what may occur in practice. To avoid scenario selection bias, the working group members who conduct the simulation are excluded and “blinded” from the scenario elicitation. The operating characteristics of the designs are assessed and compared using a comprehensive set of performance metrics, including accuracy and safety. To confirm the generality of our finding, we further perform simulation studies using a large number of scenarios randomly generated based on a novel random scenario generator. All the simulation studies conducted in this paper are independently validated by the group members. To the best of our knowledge, this is the first drug-combination comparable study that uses random scenarios, and separates scenario elicitation from simulation comparison, and validates the results using random scenarios. To promote the use of innovative designs in real trials, we summarize available software applications for implementing the drug-combination designs.
Review of existing combination designs
Because of the existence of the MTD contour, when designing a drug-combination trial, the first important question requiring careful consideration is
Are we interested in finding a single MTD or multiple MTDs?
The answer to this question determines the choice of different design strategies for combination trials (see Figure 1). This important question, unfortunately, is largely ignored by many designs. Deciding whether to find one or multiple MTDs requires close collaboration between statisticians and clinical investigators so that the need for current study and prospective of future studies can be accurately reflected. In general, if the investigators are interested in only one potential dose combination for subsequent phase II trials, it is reasonable to find a single MTD. On the other hand, if the investigators are interested in identifying the most promising combination with the highest synergistic effect, among the MTDs, as the RP2D, then finding multiple MTDs is more suitable. In contrast to finding a single MTD, where the trial can be stopped as long as only one MTD is identified, finding multiple MTDS requires a larger sample size to perform a complete search of the entire dose space to ensure that no MTD will be missed. Thus, setting the objective as finding one or multiple MTDs also needs to take the trial budget and duration into consideration. In this paper, we review study designs for finding one MTD, followed by the designs for finding multiple MTDs.
Figure 1.
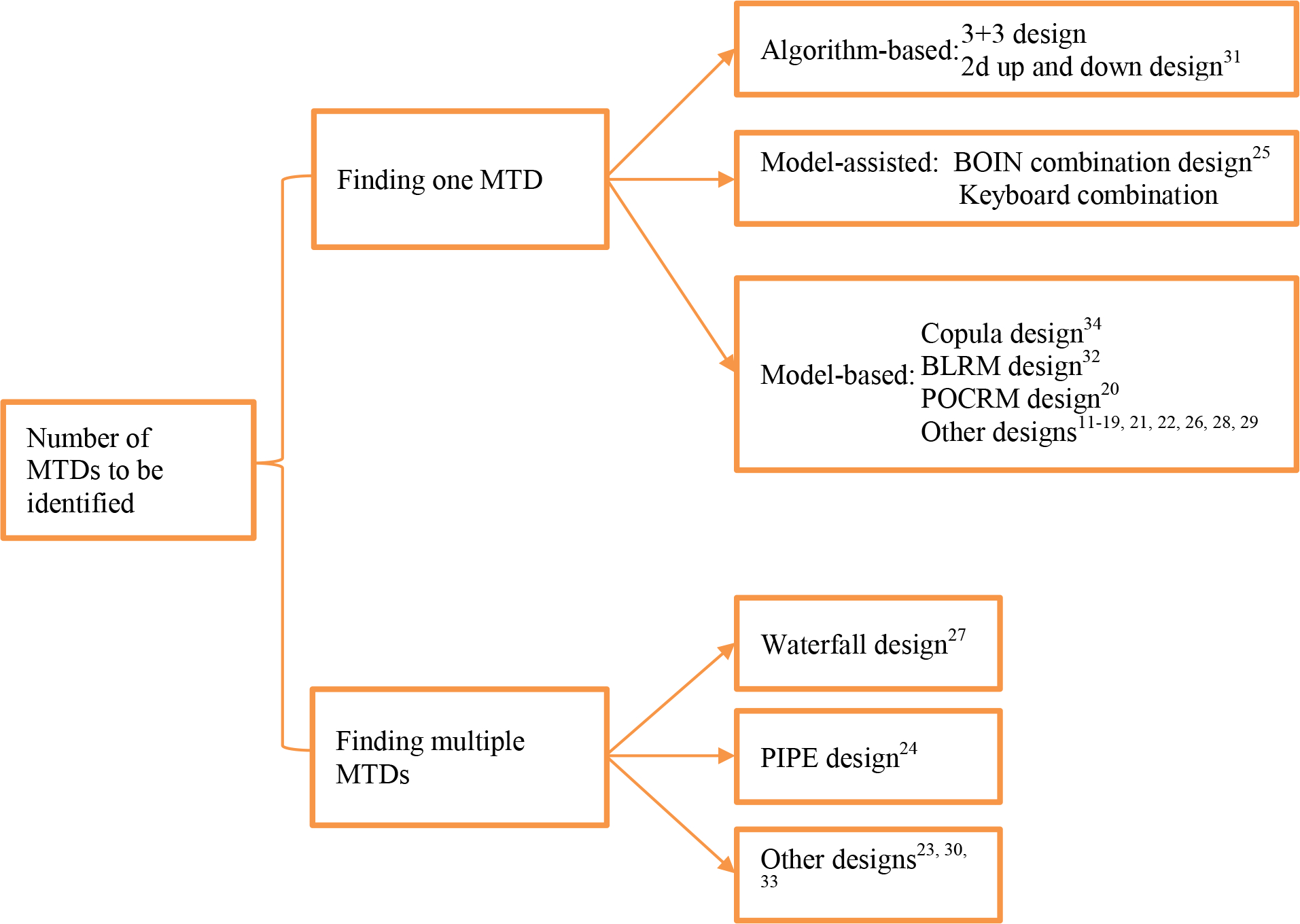
A collection of existing drug-combination designs classified based on the number of MTDs to be identified.
Finding one MTD
Over the last decade, numerous designs have been proposed for finding one MTD in phase I combination trials. Similar to the single-agent designs41, drug-combination designs also can be generally classified into three categories: algorithm-based, model-based, and model-assisted designs. In this section, we will review some key features of each type of design and introduce some representative examples, while delegating the technical details of each design to Supplementary Materials.
(1). Algorithm-based designs
Algorithm-based designs use simple, prespecified rules to guide the dose escalation/de-escalation process. Typical examples include the 3+3 and the two-dimensional up and down designs31. To implement the 3+3 design in combination trials, a subset of doses should first be selected from the two-dimensional dose-searching space, and then the standard 3+3 rule is applied to the selected dose subset. The algorithm-based designs are generally easy to understand and simple to implement. However, they adopt ad hoc and not well statistically justified rules for dose finding, usually leading to inferior MTD identification accuracy and poor patient allocation.
(2). Model-based designs
The model-based designs employ statistically sound models to quantify the dose-toxicity relationship, and they use all available data for model estimation and dose recommendation at each decision point. Most of the model-based drug-combination designs are extensions of some well-known single-agent designs, such as the continual reassessment method (CRM)42, in the sense that the drug-combination designs reduce to their monotherapy counterparts when only one drug is considered marginally. Albeit different in modeling, the following dose-finding strategy is usually adopted for model-based combination trial designs:
Posit a parametric/non-parametric probability model to quantify the dose-toxicity relationship.
Based on the observed data accumulated from the treated patients, continuously update the model estimate using either a Bayesian or frequentist approach, and assign the incoming new patients to the dose combination according to some predetermined criteria, such as the dose combination for which the estimated DLT rate is closest to the target, or the combination that maximizes the probability in a target interval while employing the escalation with overdose control principle.
Upon the end of the trial, identify the MTD based on the estimated toxicity probabilities of the dose combinations.
Most of the existing designs for combination trials are model-based (see Figure 1). In our paper, we particularly focus on three representative model-based designs that are widely cited in the combination design literature, including the copula method34, the partial ordering CRM (POCRM)20, and the two-dimensional Bayesian logistic regression method (BLRM)32. The copula method models the joint toxicity probability of the combined drug by linking the marginal toxicity probabilities of each individual drug based on the copula regression model; the POCRM prespecifies several complete toxicity orders (or models) for all the dose combinations, using the observed data to select the best one and making the corresponding dose-assignment decisions based on the single-agent CRM; the BLRM first uses logistic regression models to quantify the marginal toxicity probabilities of each drug, and then links these two marginal models based on an association parameter. Both Copula and BLRM characterize drug-drug interaction effects by a model parameter, therefore prior information on drug-drug interaction can be explicitly incorporated. The statistical details of the three designs are provided in Supplementary Materials. Model-based designs often require a rule-based start-up phase to collect more data to ensure reliable and stable dose assignment at the beginning of the trial when data are very sparse. We implement the same start-up phase for the three considered model-based designs by randomly escalating one dose level of one drug for cases of no DLT. The model-based drug-combination designs are more statistically justified, and thus generally offer more favorable performance than the algorithm-based methods. When both drugs are previously marketed, each drug has been thoroughly studied when administered alone prior to the combination trial, which provides valuable prior information on the marginal toxicity rates. Many model-based designs can naturally incorporate the prior information in the model, which is an important advantage. On the other hand, the model-based designs need complex statistical modelling and computationally intensive model re-estimation at each decision making, and are often viewed as “black-box” by clinicians. In addition, to obtain appropriate operating characteristics, these methods for drug-combination trials require extensive model and prior calibration, which can be challenging even for biostatisticians. Of note, for single-agent model-based designs, simulation-free methods to check the operating characteristics have been developed43. However, as far as we are aware, there are no simulation-free approaches for drug-combination designs.
(3). Model-assisted designs
Recently, a novel class of trial designs, known as model-assisted designs, is getting more and more attention in practice due to their simplicity and desirable performance41,44,45. Model-assisted designs can be considered as a middle ground between model-based and algorithm-based designs. Similar to the model-based designs, model-assisted designs use simple probability models for efficient decision making. Before trial initiation, the dose escalation/de-escalation rules of model-assisted designs can be pretabulated in a similar fashion as the algorithm-based designs. For single-agent dose finding, examples of model-assisted designs include the Bayesian optimal interval (BOIN) design38 and the keyboard design46, among others44. Extensive simulation studies have shown that single-agent model-assisted designs yield performance comparable to model-based designs, but they are simpler to implement and free of possible irrational decision issues caused by model misspecification41,44.
Both the BOIN and keyboard designs have been extended to drug-combination trials25,35. In this paper, we only consider the BOIN combination design25, because the performance of the keyboard combination design is similar to that of BOIN. Since BOIN makes decisions based on the data observed from the current dose only, the escalation/de-escalation rule of single-agent BOIN can be directly used for combination trials. To decide the next dose combination, suppose that the current dose is and when escalation/de-escalation is needed, the BOIN combination design chooses the next dose from an admissible escalation set (or an admissible de-escalation set ), whichever has the highest posterior probability that the true DLT rate is located within the “stay” interval of BOIN. A prominent feature of the BOIN combination design is that its dose-assignment rule, based on the Bayesian posterior probabilities, can be equivalently translated into a rule based on a so-called desirability score. Technically speaking, given specific DLT data, the desirability score is defined as the rank of that outcome among all possible DLT outcomes in terms of the posterior probability that the true DLT rate is located within the stay interval. Thus, choosing a combination with the highest desirability score is equivalent to choosing a combination with the highest posterior probability of stay. In other words, the phase I combination trials based on BOIN can be conducted solely based on a dose escalation/de-escalation decision table and a desirability score table (see an example in Table S1 of Supplementary Materials), which makes the implementation much simpler, as compared to model-based designs in the setting of combination trials.
Finding multiple MTDs
Due to the existence of the MTD contour and the fact that the drug–drug interactions may cause varying efficacy effects among the multiple MTDs, it is also of interest to find multiple MTDs for many combination trials. In this case, the efficacy of the multiple MTDs can be further evaluated in cohort expansion studies to determine a good RP2D. Although some of the model-based designs for finding a single MTD are capable of estimating the combination space, they tend to have a high misidentification rate of the MTD contour. This is because the designs for finding a single MTD tend to yield restricted exploration within the neighborhood of a certain MTD, thus fewer patients would be allocated to other areas and the estimation of the true dose-toxicity surface suffers from high variability due to the sparse data.
To avoid missing MTDs, it is desirable to explore the entire dose matrix in a trial with limited sample size. Finding multiple MTDs is substantially more challenging than finding a single MTD. Research on finding multiple MTDs is particularly limited. To the best of our knowledge, we can only identify five relevant designs24,27,28,30,33 from the literature (see Figure 1). We choose the product of independent beta probabilities escalation (PIPE) design24 and the waterfall design27 in our study. The PIPE design is a curve-free approach, where a Bayesian independent beta model is devised for each dose combination. At each decision time, a product of independent beta tail probabilities is calculated to choose the next dose combination amongst the admissible doses. Developed from another perspective, the waterfall design implements a divide- and-conquer strategy for finding multiple MTDs. Specifically, the waterfall design first partitions the two-dimensional dose-finding study into a series of simpler one-dimensional dose-finding subtrials so that the single-agent BOIN design can be applied to each subtrial. The starting dose level of each subtrial is informed by its preceding subtrial. At the end of the trial, the waterfall design collects all observed data from dose combinations that have been tested to estimate the MTD contour.
Incorporating Historical Data
Before conducting a drug-combination trial, each individual drug under investigation has been extensively studied, leading to rich historical information. Both the model-based and model-assisted designs can incorporate such prior data into the trial. In general, there are two main approaches to borrowing historical information. The first approach is to directly integrate the marginal information for each individual drug, which is the proposal of the BLRM and copula designs. This is because these two designs model the joint toxicity probabilities by linking the marginal toxicity probabilities of individual drugs. On the other hand, an indirect approach is to first use some joint modeling approaches to obtain joint prior probabilities based on the marginal data and then indirectly integrate the derived prior distributions for the joint toxicity probabilities into the designs. This approach can be used in the POCRM, BOIN, PIPE, and waterfall designs. For fair comparisons, we only consider the situation where no prior information from historical trials is incorporated, and we will investigate the performance of different designs (combined with different information borrowing approaches) in another paper.
Software to Implement the Combination Trial Designs
Several software applications have been developed to implement the aforementioned drug-combination trial designs. A glimpse of these available applications can be found in Table 1. Most of the software applications are freely available. For example, R packages have been developed for some designs such as BLRM, POCRM, and BOIN. Implementation of these R packages, however, requires prior R programming skills. User-friendly software applications with graphical interfaces, such as web-based R shiny and desktop applications for BOIN, POCRM, and waterfall designs, are also available to facilitate and simplify the design implementation among non-statisticians or non-R users, see Figures S2 (for BOIN) and S3 (for POCRM) in Supplementary Materials for more details. Some designs, such as BLRM and PIPE, are also included in the commercial software “EAST” developed by Cytel. Additionally, some applications also can generate design protocol templates (e.g., the BOIN web and desktop applications), which provides further convenience in design preparation and regulatory review.
Table 1.
Available software applications to implement the existing phase I drug-combination trial designs.
| Designs | Software | Next dose recommendation* | Protocol template included | Ease of implementation |
|---|---|---|---|---|
| 3+3 | No | |||
| Copula | Executable | No | No | Easy |
| POCRM | R package | Yes | No | Need R skills |
| Web app | No | Yes | Easy | |
| BLRM | R package | Yes | No | Need R skills |
| EAST appa | Yes | No | Easy | |
| BOIN | R package | Yes | No | Need R skills |
| Web app | Yes | Yes | Easy | |
| Desktop app | Yes | Yes | Easy | |
| Waterfall | R package | Yes | No | Need R skills |
| Web app | Yes | Yes | Easy | |
| Desktop app | Yes | Yes | Easy | |
| PIPE | R package | Yes | No | Need R skills |
| EAST appa | Yes | No | Easy |
Note:
The function to obtain the dose assignment for the next new patient when conducting the trial.
A commercial software developed by Cytel, other applications are freely available. All the listed software applications can obtain the design operating characteristics via simulations. Website URLs for the software applications are provided in Table S2 of Supplementary Materials.
Monte Carlo experiment
Simulation setting
We conducted a Monte Carlo experiment to compare the operating characteristics of the 3+3, Copula, POCRM, BLRM, and BOIN designs for finding a single MTD, and another study to compare the PIPE and waterfall designs for finding multiple MTDs, based on the target DLT probability of 25%. The performance of each design was evaluated using either fixed or random scenarios for trials combing two drugs. For fixed-scenario simulation, nine different dose-toxicity scenarios with 2 × 3 and 2 × 4 dose combinations were considered, as shown in Figure 2. These fixed scenarios were specified by experienced biostatisticians among us, and they reflected many practical dose-toxicity situations that might be encountered in real combination trials. To avoid cherry-picked scenarios that may incur selection bias, we also performed the simulation study by randomly generating 3000 scenarios for each of the 2 × 4, 3 × 5 and 4 × 4 dose spaces, respectively. The details of the random-scenario generating algorithm can be found in the Supplementary Materials. We uniformly assumed one, two, or three MTDs (only for the 3 × 5 and 4 × 4 space) may exist in each scenario. The maximum sample size for fixed scenarios was 36, while that for random scenarios varied from 27 to 48. All designs started at the lowest dose combination, and made dose-assignment decisions after each cohort of three patients had been treated. Each trial would not stop until exhaustion of the sample size, unless early termination due to excessive toxicity at the lowest dose combination was needed. The parameters of each design were well-calibrated with the details given in the Supplementary Materials. To ensure a fair comparison, no historical data were incorporated into the model-based and model-assisted designs. For the model-based designs, the prior distributions were specified such that the prior toxicity probabilities of each dose combination are comparable, i.e., similar. More details about the prior calibration process can be found in Section F of Supplementary Materials. For the 3+3 design, the selected dose levels are displayed in Figure 2, and cohort expansion was conducted at the estimated MTD to match the sample size of other designs. The results of all designs were computed using R. To ensure unbiased comparison, the simulation study was initially performed by XY (fixed scenarios) and HZ (random scenarios), and then the results were further validated by RL.
Figure 2.
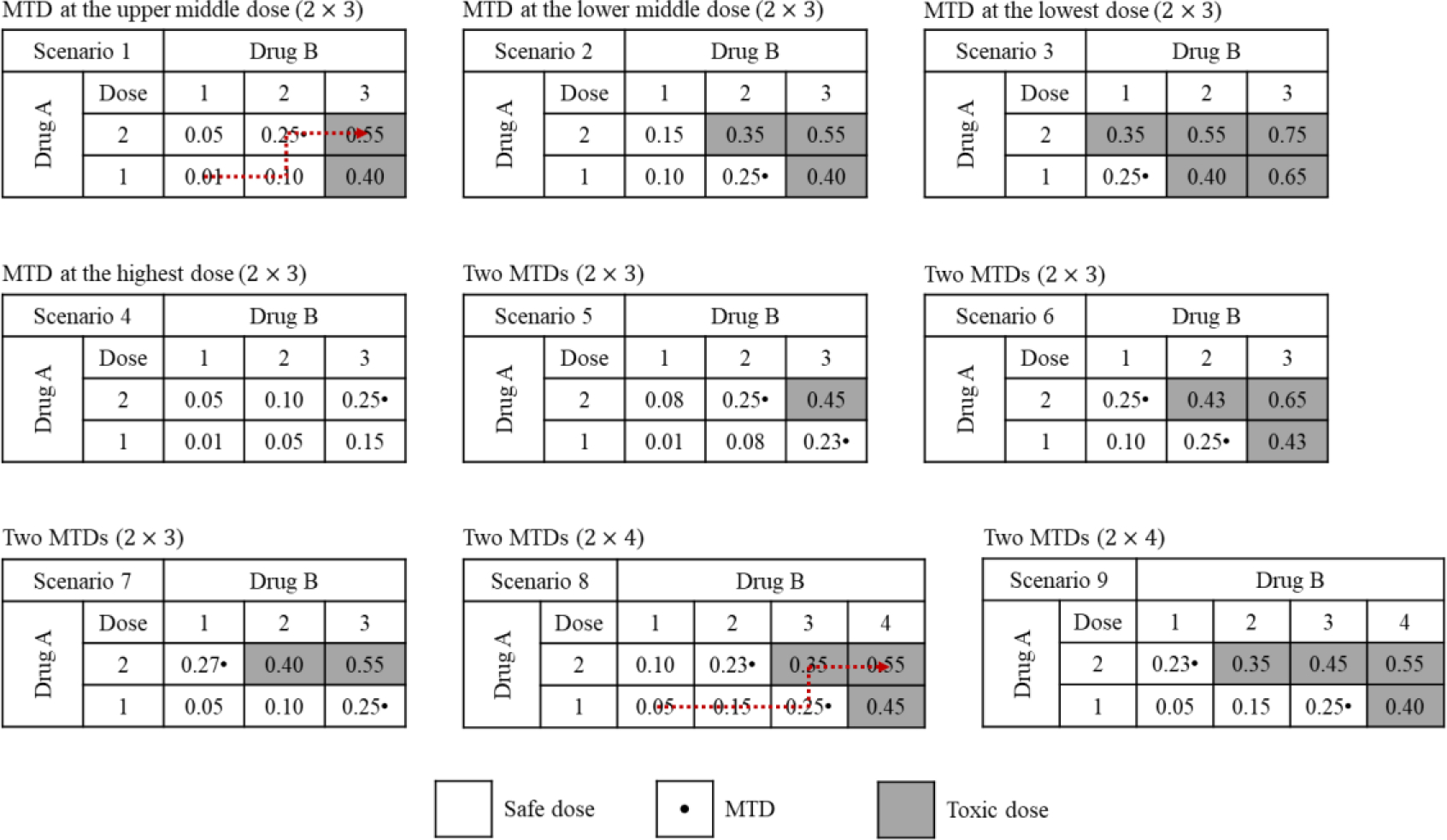
Nine fixed dose-toxicity scenarios considered in the simulation study. The selected dose combinations for the 3+3 design are highlighted by the dotted arrow line.
Performance metrics
To fully characterize the operating characteristics of each design, the following metrics were computed based on 5000 simulated trials under each fixed scenario, respectively, and 500 simulated trials under each random scenario.
(A). Accuracy
A1. To evaluate the designs aimed at finding one MTD, we report the percentage of correct selection, which is defined as the percentage of simulated trials in which one of the target doses is correctly selected as the MTD. For designs aimed at finding multiple MTDs, we report the percentage of trials selecting at least one MTD, as well as the percentage of trials selecting all correct MTDs (i.e., the selected dose combinations are identical to the true MTDs). When all the dose levels are above the MTD (i.e., the DLT probability of the lowest dose ≥ 33%), the correct selection percentage is defined as the percentage of early terminated trials.
A2. The percentage of patients treated at the MTDs across the simulated trials. When all the dose levels are above the MTD (i.e., the DLT probability of the lowest dose ≥ 33%), we use the percentage of remaining patients who are not enrolled in the trial for this metric.
(B). Safety
B1. The percentage of simulated trials in which a toxic dose with the true DLT probability ≥ 33% is selected as the MTD.
B2. The percentage of patients treated at the toxic doses with true DLT probabilities ≥ 33%.
(C). Computation time
D1. The average time needed for simulating 2000 trials.
Results
The simulation results based on fixed scenarios of the designs finding one MTD and multiple MTDs are displayed in Figures 3 and 4, respectively. In terms of random scenarios, we considered four settings: (i) the combination space with 27 patients; (ii) the combination space with 36 patients; (iii) the combination space with 48 patients; and (iv) the combination space with 48 patients. The operating characteristics for each design under random scenarios were summarized in boxplots, see Figure 5 for the designs finding one MTD, and Figure 6 for the designs finding multiple MTDs. The detailed simulation results stratified by the number of MTDs presenting in the dose space are reported in Supplementary Materials.
Figure 3.
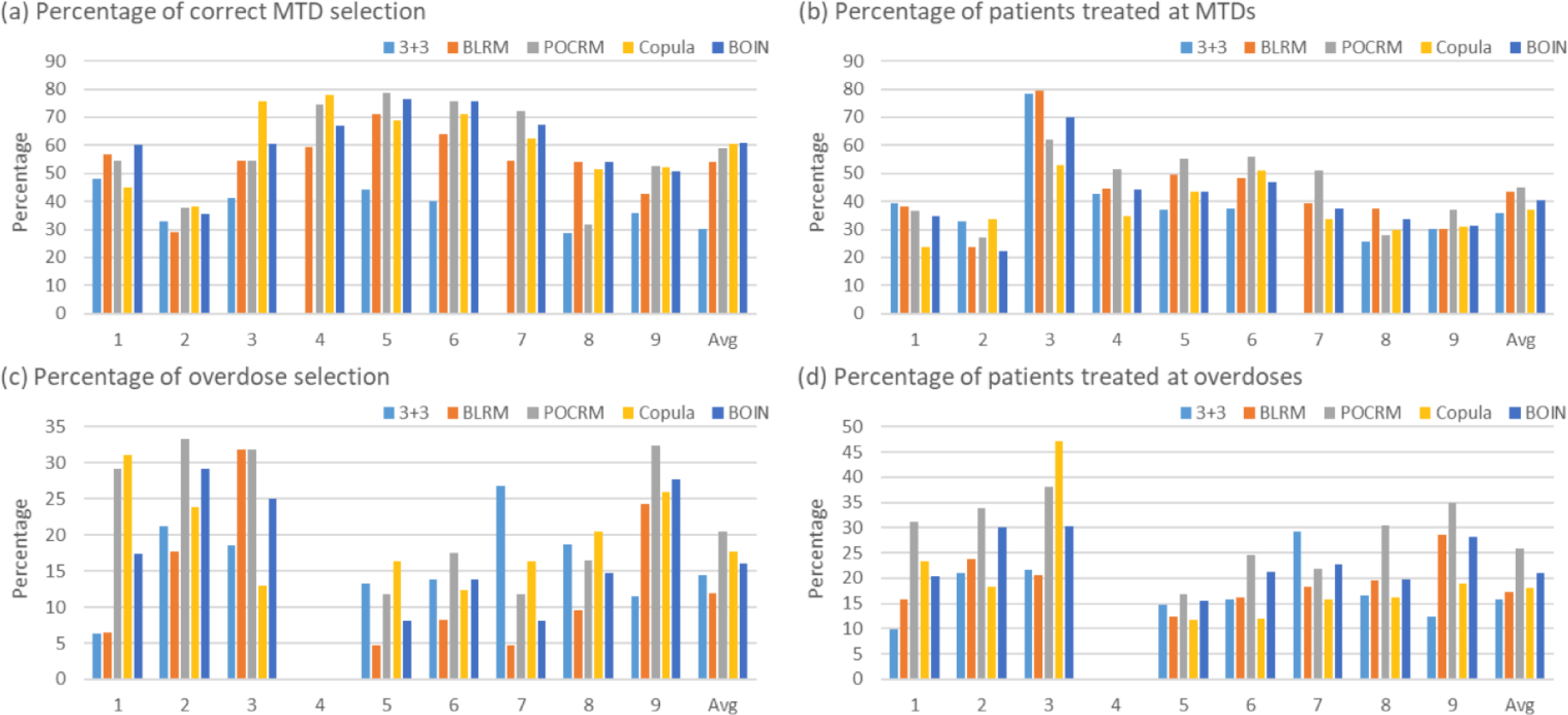
Simulation results summarized based on 5000 simulated trials under 9 fixed scenarios for each combination trial designs for finding one MTD, including the 3+3 design, the two-dimensional Bayesian logistic regression method (BLRM)32, the partial ordering continual reassessment method (POCRM)20, the copula regression method34, and the Bayesian optimal interval (BOIN) combination design25. Four performance metrics are reported: (a) percentage of correct MTD selection; (b) percentage of patients allocated to MTDs; (c) percentage of overdose selection; and (d) percentage of patients allocated to overdoses, where the overdose is defined as the dose combination that has a DLT probability greater than 33%.
Figure 4.
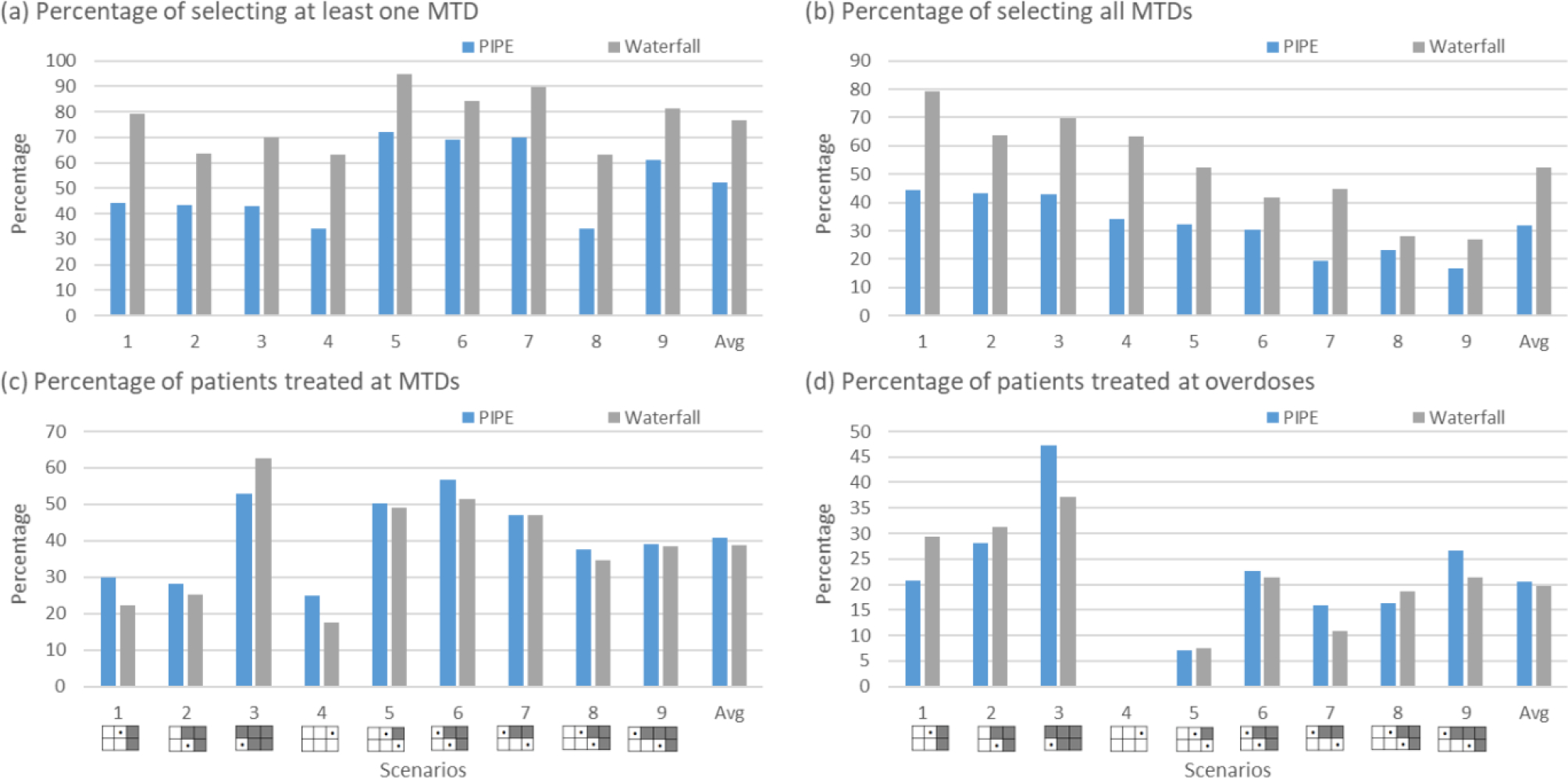
Simulation results summarized based on 5000 simulated trials under 9 fixed scenarios for each combination designs for finding multiple MTDs, including the product of independent beta probabilities escalation (PIPE) design24 and the waterfall design27. Four performance metrics are reported: (a) percentage of trials selecting at least one MTD; (b) percentage of trials selecting all MTDs; (c) percentage of patients allocated to the MTD; and (d) percentage of patients allocated to overdoses, where the overdose is defined as the dose combination that has a DLT probability greater than 33%. The percentage of selecting at least one overdose is provided in Figure S10 of Supplementary Materials.
Figure 5.
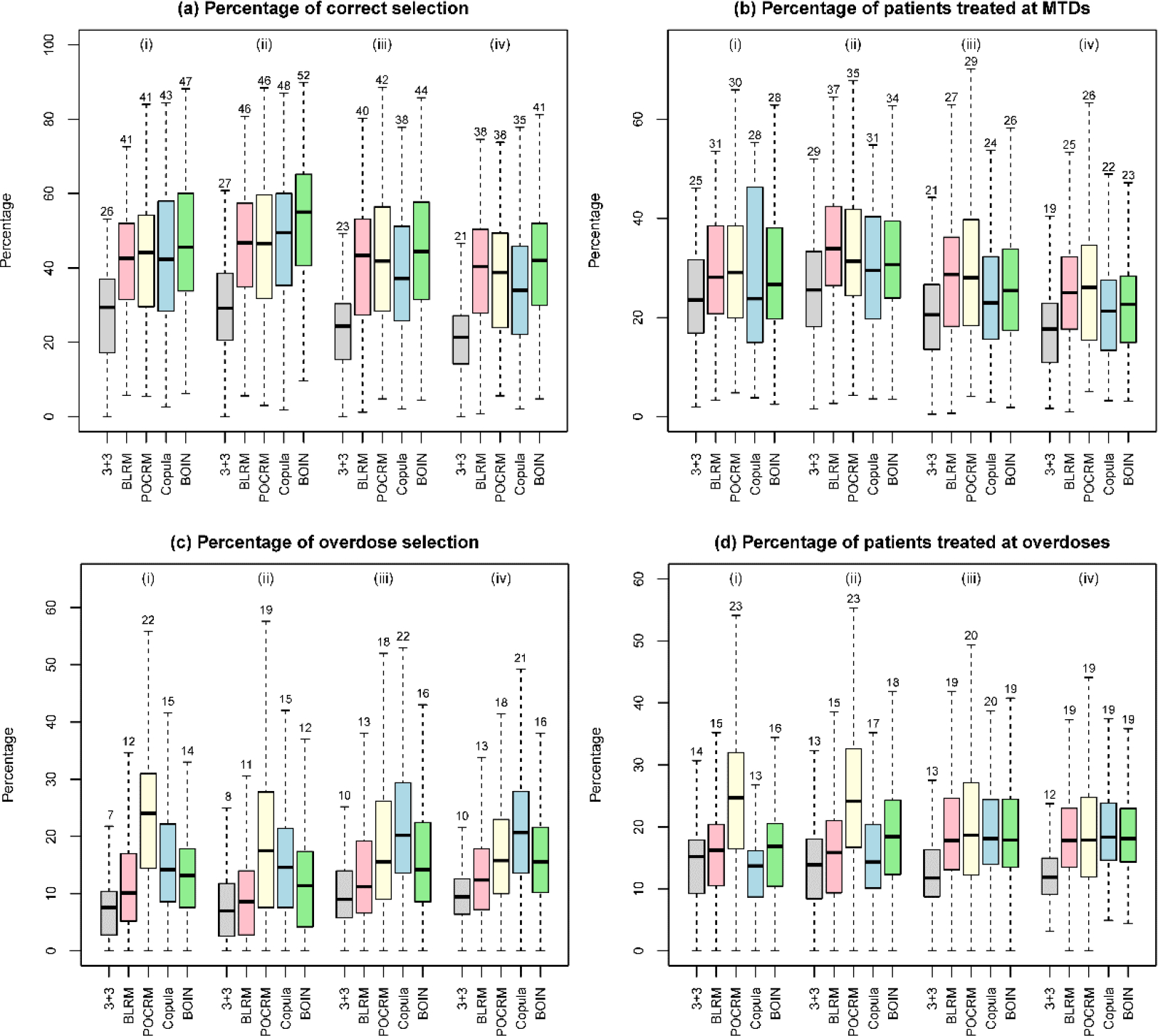
Simulation results of designs for finding one MTD, based on 3000 random scenarios of the (i) 2 × 4 combination trial with 27 patients; (ii) 2 × 4 combination trial with 36 patients; (iii) 3 × 5 combination trial with 48 patients; and (iv) 4 × 4 combination trial with 48 patients. Five designs were included: the 3+3 design, the two-dimensional Bayesian logistic regression method (BLRM)32, the partial ordering continual reassessment method (POCRM)20, the copula regression method34, and the Bayesian optimal interval (BOIN) combination design25. The target DLT rate was 0.25, and the overdoses were defined as the dose combinations with DLT rates greater than 0.33. The boxplot displays the minimum, the maximum, the sample median, and the 1st and 3rd quartiles. The number indicates the sample mean.
Figure 6.
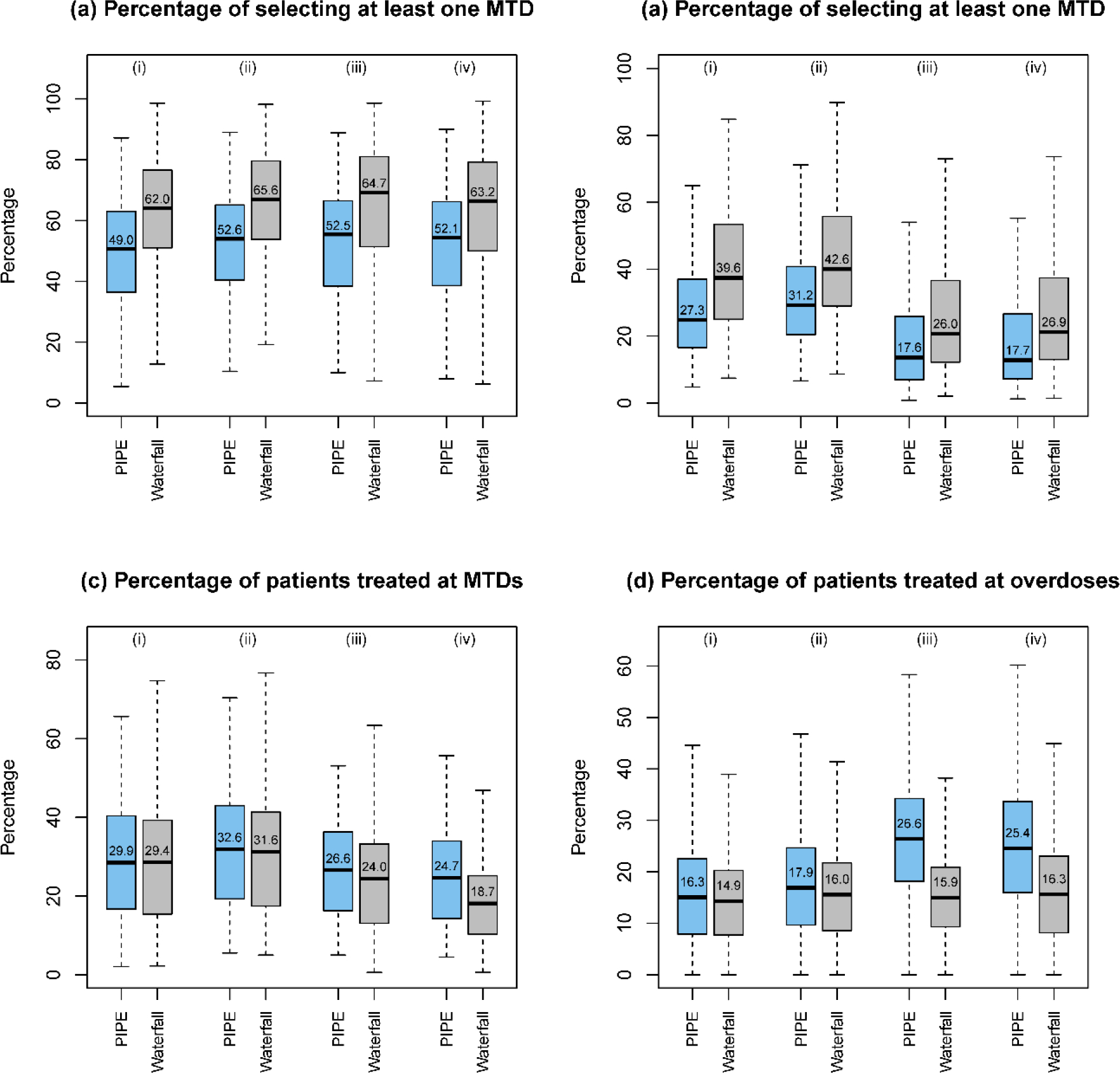
Simulation results of designs for finding multiple MTDs, based on 3000 random scenarios of the (i) 2 × 4 combination trial with 27 patients; (ii) 2 × 4 combination trial with 36 patients; (iii) 3 × 5 combination trial with 48 patients; and (iv) 4 × 4 combination trial with 48 patients. Two designs were included: the product of independent beta probabilities escalation (PIPE) design24 and the waterfall design27. The target DLT rate was 0.25, and the overdoses were defined as the dose combinations with DLT rates greater than 0.33. The boxplot displays the minimum, the maximum, the sample median, and the 1st and 3rd quartiles. The number indicates the sample mean.
Finding one MTD
(A). Accuracy
Figure 3 panels (a) and (b) show that, under the nine fixed scenarios, the widely-used 3+3 design is outperformed by the other four designs in terms of the accuracy of correctly identifying the MTD. The performance of the 3+3 design heavily relies on the subset of selected doses: when the subset does not contain any MTD (e.g., scenario 7), the MTD selection percentage of the 3+3 design is 0. The performance of the model-based designs such as BLRM and POCRM is sensitive to the scenarios, and they may achieve low selection percentages in some specific situations such as in scenarios 2 and 8.
In addition to fixed scenarios, random scenarios contain more objective, yet still reasonable situations. Figure 5 panels (a) and (b) as well as Figure S5 of Supplementary Materials demonstrate that the accuracy of designs increases with the number of MTDs presenting in the combination space and the sample size. Overall, BOIN stands out as possessing the highest MTD identification accuracy among the considered designs. In terms of patient assignment, the BLRM and POCRM designs allocate slightly more patients to the MTDs than BOIN and Copula.
(B). Safety
Panels (c) and (d) in Figures 3 and 5 show that the 3+3 design is least likely to select dose combinations with the toxicity probabilities ≥ 33% as the MTD, while also allocating much fewer patients to overdoses. However, such a safety benefit comes at a price of inferior MTD identification accuracy. Among the model-based and model-assisted designs, BLRM is relatively safer in terms of overdose selection and patient allocation, POCRM is the most aggressive design, and BOIN is in between.
Early termination
In Supplementary Materials, we present an additional simulation study, for the designs aimed at one MTD, by allowing for early termination if 15 patients have been treated in the 2 combination trial and more than six patients have been assigned to a certain dose. According to Figure S9 of Supplementary Materials, BOIN achieves the highest correct selection percentage with comparably small sample size. The trial efficiency index, defined as the ratio of the correct MTD selection percentage divided by the average sample size, shows that both the BLRM and BOIN are more efficient than the other designs in MTD identification.
Finding multiple MTDs
To evaluate the performance of the designs for finding multiple MTDs, we considered five metrics including the percentage of trials selecting one MTD, the percentage of trials selecting all MTDs, the percentage of patients at MTD, the percentage of patients at overdoses, and the percentage of trials selecting at least one overdose. As shown in Figure 4, where nine fixed scenarios are considered, the waterfall design outperforms the PIPE design in terms of MTD selection accuracy. The waterfall design treats slightly more patients at the MTDs (as well as the overdoses) than the PIPE design. Furthermore, according to Figure S10 in the Supplementary Materials, the two designs have similar percentages of selecting overdoses as the MTDs. The results based on the random scenarios reveal similar patterns for these two designs in terms of accuracy, as displayed in Figure 6. A partial reason why the waterfall design performs better than PIPE is that the divide-and-conquer strategy employed by the waterfall design leads to more thorough exploration of the drug-combination space, and thus increases the MTD identification accuracy. In terms of safety, the waterfall design treats fewer patients at overdoses, however, it has a higher percentage of trials selecting overly toxic doses as the MTDs than the PIPE design. This is because the waterfall design tends to select more doses (i.e., for each row in the drug-combination space) than the PIPE design. Such a property is a double-edged sword: on one hand, it yields a higher percentage of selecting all correct MTDs; on the other hand, when some rows only have overly toxic doses, the waterfall design sometimes would select a lower, but still toxic dose as the row-specific MTD for each of those rows.
Computation time
We reported the average time needed to simulate 2000 trials for each design in Table 2. It shows that the algorithm-based 3+3 design, and the model-assisted BOIN and waterfall designs only needed a few seconds for running 2000 simulated trials, which indicates that they can save more time in the simulation for trial preparation. On the other hand, the model-based designs needed repeated model fitting at each decision-making time. For example, it took on average more than two hours for the BLRM and Copula designs to generate the operating characteristics based on 36 patients with 11 interim analyses for a total of 12 cohorts of patients. Hence, these designs took much more time and effort for simulating trials.
Table 2.
Average computation time needed for each design to simulate 2000 trials.
| Design | 3+3 | BLRM | POCRN | Copula | BOIN | PIPE | Waterfall |
|---|---|---|---|---|---|---|---|
| 2 × 4 combination trials with 27 patients | |||||||
| Time (min) | 0.01 | 131.4 | 8.1 | 92.7 | 0.05 | 1.9 | 0.9 |
| 2 × 4 combination trials with 36 patients | |||||||
| Time (min) | 0.01 | 192.7 | 12.2 | 140.0 | 0.06 | 2.4 | 0.9 |
| 3 × 5 combination trials with 48 patients | |||||||
| Time (min) | 0.02 | 456.7 | 16.2 | 302.0 | 0.07 | 9.5 | 0.9 |
| 4 × 4 combination trials with 48 patients | |||||||
| Time (min) | 0.02 | 498.6 | 16.9 | 352.1 | 0.08 | 11.8 | 1.0 |
Note: Dose-assignment decisions for each design were updated after three patients have been treated. The average computation time is recorded using 2000 different jobs (i.e., scenarios) based on Red Hat Enterprise Linux high-throughput computing cluster with the processor speed ranging from 2.00 GHz to 2.67 GHz. Each job requires one node, one processor core, and one gigabyte memory per node.
Discussion
In terms of finding one MTD, our simulation results show that the 3+3 design is excessively conservative and has poor accuracy in identifying the MTD and patient allocation at the MTD. On the other hand, the performance of the model-based design is mixed: The POCRM design has high MTD identification accuracy, but is more likely to overdose the patients. The BLRM and Copula methods have good safety profiles, but perform relatively poorly in the accuracy of finding the MTD. For POCRM, BLRM and Copula methods, their respective safety or accuracy issues can be avoided by further tunning the corresponding parameters, however, might at the price of deterioration of other design properties, as there is always a tradeoff between accuracy, efficiency, and safety. We have replicated the same simulation studies based on other noninformative priors for the model-based designs, and found that the results are nearly unchanged given that the prior distributions are non-informative, comparable between designs, and carefully calibrated. The model-assisted BOIN design generally yields well-balanced operating characteristics in terms of accuracy and safety.
For finding multiple MTDs, the waterfall design on average performs better than PIPE in finding the multiple MTDs and is relatively safer in terms of patient allocation. However, it also generally yields a higher chance of selecting an overly toxic dose. In terms of implementation, the model-assisted BOIN and waterfall designs are simple, virtually calibration-free, and require minimal computational effort and infrastructure to implement. In contrast, the model-based designs are more complicated and require highly specialized statistical skills and extensive, computation-intensive simulation to choose and calibrate the model structure and prior.
There are several limitations of our present paper. First of all, for the purpose of ensuring a fair comparison, we do not consider informative priors for the model-based and model-assisted designs. Therefore, our conclusions in terms of the accuracy and safety of the designs only apply to the situation where no prior data are limited or are not incorporated into the combination trial. We intend to investigate the design performance under informative priors in a separate paper. However, our conclusions in terms of the robustness and easiness of implementation of the considered designs will be still valid in these situations. Another limitation of the paper is that we only consider trials combing two drugs. Some designs, such as the BLRM and BOIN designs, are also applicable to trials combining more than two drugs. Based on our extensive experience, our findings in this paper still hold for trials investigating more than two drugs.
Our simulation study assumes that the DLT outcomes can be quickly observed before decision making for the new cohort. There are some occasions, such as radiation therapy or immunotherapy trials, that need prolonged time to observe the DLT outcomes, causing delayed toxicities. Furthermore, our simulation focuses on the combination of two drugs. In some indications, there may be a need to combine more than two drugs. Although it is not common for pharmaceutical companies to vary dose levels of more than two drugs due to resource limitations and other practical considerations, most methods evaluated in this paper can be extended to this. Investigation of the performance of the combination trial designs under the aforementioned settings can be a direction of future study. These dose-escalation methods presented in this manuscript consider toxicity data only. In some situations, such as trials with CAR-T therapy, it will be beneficial to jointly incorporate toxicity and efficacy data to determine the acceptable dose level. Several methods have been developed for monotherapy with model-based designs47–49 as well as model-assisted designs50,51. Extension of these methods to combination trials will be of future interest.
Conclusions
In this paper, we have conducted a comprehensive comparison study of several well-known designs for dose finding in drug-combination trials, and studied their unique features. For each of the designs reviewed, the extensive simulation studies based on various scenarios provide a detailed overview of its operating characteristics and robustness; and the software applications and computation times we summarized shed light on the efficiency and ease of implementation. Due to the limited sample size in early-phase trials, dose finding for drug combinations is vital, and the design of drug-combination trials needs a more intensive infrastructural effort as well as a closer collaboration between statisticians and trialists. We have shown that the choice of a combination design critically depends on whether the trial’s primary objective is to identify one MTD or multiple MTDs.
The pros and cons of methods are discussed throughout the paper. In general, the 3+3 rule is not recommended due to its poor performance and a high failure rate to find the MTD. The model-based designs provide a nice way to incorporate historical data via model prior specification, and can be considered when data is available on marginal toxicity of each drug or when potential drug-drug interaction effects are known. The model-based designs enjoy reasonably good performance, but its implementation requires careful model specification and calibration upfront. Based on noninformative priors, the model-assisted designs provide competitive and balanced performance in terms of MTD identification accuracy and patient safety, and they are simple to implement, thus offering an attractive approach to designing phase I drug-combination trials. However, this paper does not investigate whether the performance of model-assisted designs is still competitive, compared to the model-based designs, when prior information is available.
By taking into consideration the design’s operating characteristics, ease of implementation and regulation, the need for advanced infrastructures, as well as the risk of regulatory acceptance, our paper offers practical guidance on the selection of a suitable dose-finding approach for designing future combination trials. In real trials, there are many more practical or logistical details that are not considered by our paper. Therefore, clinical investigators and biostatisticians must thoroughly discuss the purpose and challenges of the dose-finding trial for combination therapies, and carefully choose suitable design strategies. Biostatisticians also have to evaluate the design operating characteristics by realistic simulations for the upcoming study before recommending the design for practical use. Therefore, closer collaborations between clinical investigators and biostatisticians are required.
Supplementary Material
Acknowledgement
We would like to thank the Editor, the Associate Editor, and the two reviewers for their valuable comments and suggestions, with special thanks to the reviewer whose dedicated and meticulous effort has led to a much-improved version of our paper.
Footnotes
Disclaimers
Dr. Yuan served as a consultant to Boehringer Ingelheim Pharmaceuticals, Abbvie Pharmaceuticals, Amgen Pharmaceuticals, and Midas Medical Technologies. Dr. Lin served as a consultant to Monte Rosa Therapeutics. No conflicts of interest to report for other authors.
The study has not been presented elsewhere.
Supplementary Materials
The Supplementary Materials include details of the drug-combination designs, simulation configurations, additional simulation results, and the algorithm and R code of the random scenario generator.
References
- 1.Foucquier J, Guedj M: Analysis of drug combinations: current methodological landscape. Pharmacology Research & Perspectives 3, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Liu S, Nikanjam M, Kurzrock R: Dosing de novo combinations of two targeted drugs: Towards a customized precision medicine approach to advanced cancers. Oncotarget 7:11310–11320, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Slamon DJ, Leyland-Jones B, Shak S, et al. : Use of chemotherapy plus a monoclonal antibody against HER2 for metastatic breast cancer that overexpresses HER2. New England Journal of Medicine 344:783–792, 2001 [DOI] [PubMed] [Google Scholar]
- 4.Flaherty KT, Infante JR, Daud A, et al. : Combined BRAF and MEK Inhibition in Melanoma with BRAF V600 Mutations. New England Journal of Medicine 367:1694–1703, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gandhi L, Bahleda R, Tolaney SM, et al. : Phase I Study of Neratinib in Combination With Temsirolimus in Patients With Human Epidermal Growth Factor Receptor 2-Dependent and Other Solid Tumors. Journal of Clinical Oncology 32:68–+, 2014 [DOI] [PubMed] [Google Scholar]
- 6.Harrington JA, Wheeler GM, Sweeting MJ, et al. : Adaptive designs for dual-agent phase I dose-escalation studies. Nature Reviews Clinical Oncology 10:277–288, 2013 [DOI] [PubMed] [Google Scholar]
- 7.Mandrekar SJ: Dose-Finding Trial Designs for Combination Therapies in Oncology. Journal of Clinical Oncology 32:65–+, 2014 [DOI] [PubMed] [Google Scholar]
- 8.Yuan Y, Lin R: Novel designs for early phase drug combination trials. Bayesian Applications in Pharmaceutical Development, edited by Lakshminarayanan M and Natanegara F, Chapman and Hall/CRC, 2019 [Google Scholar]
- 9.FDA: Guidance for industry: Codevelopment of two or more new investigational drugs for use in combination. . 2013 [Google Scholar]
- 10.Thall PF, Millikan RE, Mueller P, et al. : Dose-finding with two agents in Phase I oncology trials. Biometrics 59:487–96, 2003 [DOI] [PubMed] [Google Scholar]
- 11.Wang K, Ivanova A: Two-dimensional dose finding in discrete dose space. Biometrics 61:217–22, 2005 [DOI] [PubMed] [Google Scholar]
- 12.Conaway MR, Dunbar S, Peddada SD: Designs for single- or multiple-agent phase I trials. Biometrics 60:661–9, 2004 [DOI] [PubMed] [Google Scholar]
- 13.Mandrekar SJ, Cui Y, Sargent DJ: An adaptive phase I design for identifying a biologically optimal dose for dual agent drug combinations. Stat Med 26:2317–30, 2007 [DOI] [PubMed] [Google Scholar]
- 14.Yuan Y, Yin G: Sequential continual reassessment method for two-dimensional dose finding. Stat Med 27:5664–78, 2008 [DOI] [PubMed] [Google Scholar]
- 15.Yin G, Yuan Y: A latent contingency table approach to dose finding for combinations of two agents. Biometrics 65:866–75, 2009 [DOI] [PubMed] [Google Scholar]
- 16.Braun TM, Wang S: A hierarchical Bayesian design for phase I trials of novel combinations of cancer therapeutic agents. Biometrics 66:805–12, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shi Y, Yin G: Escalation with overdose control for phase I drug-combination trials. Stat Med 32:4400–12, 2013 [DOI] [PubMed] [Google Scholar]
- 18.Braun TM, Jia N: A Generalized Continual Reassessment Method for Two-Agent Phase I Trials. Stat Biopharm Res 5:105–115, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hirakawa A, Hamada C, Matsui S : A dose-finding approach based on shrunken predictive probability for combinations of two agents in phase I trials. Stat Med 32:4515–25, 2013 [DOI] [PubMed] [Google Scholar]
- 20.Wages NA, Conaway MR, O’Quigley J: Dose-finding design for multi-drug combinations. Clin Trials 8:380–9, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cai C, Yuan Y, Ji Y: A Bayesian Dose-finding Design for Oncology Clinical Trials of Combinational Biological Agents. J R Stat Soc Ser C Appl Stat 63:159–173, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Riviere MK, Yuan Y, Dubois F, et al. : A Bayesian dose-finding design for drug combination clinical trials based on the logistic model. Pharm Stat 13:247–57, 2014 [DOI] [PubMed] [Google Scholar]
- 23.Tighiouart M, Piantadosi S, Rogatko A: Dose finding with drug combinations in cancer phase I clinical trials using conditional escalation with overdose control. Statistics in medicine 33:3815–3829, 2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mander AP, Sweeting MJ: A product of independent beta probabilities dose escalation design for dual-agent phase I trials. Stat Med 34:1261–76, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lin R, Yin G: Bayesian optimal interval design for dose finding in drug-combination trials. Stat Methods Med Res 26:2155–2167, 2017 [DOI] [PubMed] [Google Scholar]
- 26.Lin R, Yin G: Bootstrap Aggregating Continual Reassessment Method for Dose Finding in Drug-Combination Trials. Annals of Applied Statistics 10:2349–2376, 2016 [Google Scholar]
- 27.Zhang L, Yuan Y: A practical Bayesian design to identify the maximum tolerated dose contour for drug combination trials. Stat Med 35:4924–4936, 2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tighiouart M, Li Q, Rogatko A: A Bayesian adaptive design for estimating the maximum tolerated dose curve using drug combinations in cancer phase I clinical trials. Statistics in medicine 36:280–290, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mozgunov P, Jaki T, Paoletti X: Randomized dose-escalation designs for drug combination cancer trials with immunotherapy. J Biopharm Stat 29:359–377, 2019 [DOI] [PubMed] [Google Scholar]
- 30.Lam CK, Lin R, Yin G: Non‐parametric overdose control for dose finding in drug combination trials. Journal of the Royal Statistical Society: Series C (Applied Statistics) 68:1111–1130, 2019 [Google Scholar]
- 31.Ivanova A: A new dose-finding design for bivariate outcomes. Biometrics 59:1001–7, 2003 [DOI] [PubMed] [Google Scholar]
- 32.Neuenschwander B, Matano A, Tang Z, et al. : Bayesian industry approach to phase I combination trials in oncology. Statistical methods in drug combination studies 2015:95–135, 2015 [Google Scholar]
- 33.Wages NA: Identifying a maximum tolerated contour in two-dimensional dose finding. Statistics in Medicine 36:242–253, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yin GS, Yuan Y: Bayesian dose finding in oncology for drug combinations by copula regression. Journal of the Royal Statistical Society Series C-Applied Statistics 58:211–224, 2009 [Google Scholar]
- 35.Pan H, Lin R, Zhou Y, et al. : Keyboard design for phase I drug-combination trials. Contemporary Clinical Trials:105972, 2020. [DOI] [PubMed] [Google Scholar]
- 36.Neuenschwander B, Branson M, Gsponer T: Critical aspects of the Bayesian approach to phase I cancer trials. Stat Med 27:2420–39, 2008 [DOI] [PubMed] [Google Scholar]
- 37.Dykstra RL, Robertson T: An algorithm for isotonic regression for two or more independent variables. The Annals of Statistics:708–716, 1982 [Google Scholar]
- 38.Liu SY, Yuan Y: Bayesian optimal interval designs for phase I clinical trials. Journal of the Royal Statistical Society Series C-Applied Statistics 64:507–523, 2015 [Google Scholar]
- 39.Riviere MK, Dubois F, Zohar S: Competing designs for drug combination in phase I dose-finding clinical trials. Stat Med 34:1–12, 2015 [DOI] [PubMed] [Google Scholar]
- 40.Hirakawa A, Wages NA, Sato H, et al. : A comparative study of adaptive dose-finding designs for phase I oncology trials of combination therapies. Stat Med 34:3194–213, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhou H, Yuan Y, Nie L: Accuracy, Safety, and Reliability of Novel Phase I Trial Designs. Clin Cancer Res 24:4357–4364, 2018 [DOI] [PubMed] [Google Scholar]
- 42.O’Quigley J, Pepe M, Fisher L: Continual reassessment method: a practical design for phase 1 clinical trials in cancer. Biometrics 46:33–48, 1990 [PubMed] [Google Scholar]
- 43.Braun TM: A simulation-free approach to assessing the performance of the continual reassessment method. Statistics in Medicine 39:4651–4666, 2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhou H, Murray TA, Pan H, et al. : Comparative review of novel model-assisted designs for phase I clinical trials. Stat Med 37:2208–2222, 2018 [DOI] [PubMed] [Google Scholar]
- 45.Yuan Y, Lee JJ, Hilsenbeck SG: Model-Assisted Designs for Early-Phase Clinical Trials: Simplicity Meets Superiority. JCO Precision Oncology 3:1–12, 2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yan F, Mandrekar SJ, Yuan Y: Keyboard: A Novel Bayesian Toxicity Probability Interval Design for Phase I Clinical Trials. Clin Cancer Res 23:3994–4003, 2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Thall PF, Cook JD: Dose-finding based on efficacy-toxicity trade-offs. Biometrics 60:684–693, 2004 [DOI] [PubMed] [Google Scholar]
- 48.Yin GS, Li YS, Ji Y: Bayesian dose-finding in phase I/II clinical trials using toxicity and efficacy odds ratios. Biometrics 62:777–784, 2006 [DOI] [PubMed] [Google Scholar]
- 49.Quintana M, Li DH, Albertson TM, et al. : A Bayesian adaptive phase 1 design to determine the optimal dose and schedule of an adoptive T-cell therapy in a mixed patient population. Contemp Clin Trials 48:153–65, 2016 [DOI] [PubMed] [Google Scholar]
- 50.Lin R, Yin G: STEIN: A simple toxicity and efficacy interval design for seamless phase I/II clinical trials. Stat Med 36:4106–4120, 2017 [DOI] [PubMed] [Google Scholar]
- 51.Takeda K, Taguri M, Morita S: BOIN-ET: Bayesian optimal interval design for dose finding based on both efficacy and toxicity outcomes. Pharm Stat 17:383–395, 2018 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


