Abstract
Tissues derive ATP from two pathways—glycolysis and the tricarboxylic acid (TCA) cycle coupled to the electron transport chain. Most energy in mammals is produced via TCA metabolism1. In tumours, however, the absolute rates of these pathways remain unclear. Here we optimize tracer infusion approaches to measure the rates of glycolysis and the TCA cycle in healthy mouse tissues, Kras-mutant solid tumours, metastases and leukaemia. Then, given the rates of these two pathways, we calculate total ATP synthesis rates. We find that TCA cycle flux is suppressed in all five primary solid tumour models examined and is increased in lung metastases of breast cancer relative to primary orthotopic tumours. As expected, glycolysis flux is increased in tumours compared with healthy tissues (the Warburg effect2,3), but this increase is insufficient to compensate for low TCA flux in terms of ATP production. Thus, instead of being hypermetabolic, as commonly assumed, solid tumours generally produce ATP at a slower than normal rate. In mouse pancreatic cancer, this is accommodated by the downregulation of protein synthesis, one of this tissue’s major energy costs. We propose that, as solid tumours develop, cancer cells shed energetically expensive tissue-specific functions, enabling uncontrolled growth despite a limited ability to produce ATP.
Cells use ATP asa main energy currency, powering functions including muscle contraction, ion pumping and protein synthesis. In animals, ATP can be produced either by glycolysis or by mitochondrial oxidative metabolism. In the latter pathway, the tricarboxylic acid (TCA) cycle oxidizes fat and carbohydrates to generate the high-energy electron donors NADH and FADH2, which then drive ATP production by the electron transport chain. Catabolism of a glucose molecule in glycolysis yields 2 ATP molecules, whereas the coupled TCA cycle and electron-transport chain make around 14.5 ATP molecules per TCA turn while consuming one half of a glucose molecule (or, equivalently, one lactate) or one fatty acid two-carbon unit. Accordingly, in the body as a whole, ATP production by oxidative metabolism exceeds glycolytic ATP generation by at least 14.5-fold.
Tumours display metabolic alterations relative to healthy tissues, probably due both to dysregulated signalling and to the metabolic demands of proliferation4,5. Pioneering studies by Warburg and others in the 1920s demonstrated that, even in the presence of oxygen, tumours rapidly convert glucose into lactate (aerobic glycolysis)2,3,6,7. Indeed, high glucose uptake by tumours is the basis for cancer detection by fluorodeoxyglucose positron emission tomography8 (FDG-PET).
One potential trigger of glycolysis is impaired oxidative ATP production, as cells must fulfil ATP demand and, in response to ATP deficiency, activate glycolysis. Warburg hypothesized that tumours are intrinsically respiration deficient. Initial experimental evidence was conflicting on whether tumour TCA flux is higher or lower compared with other tissues2,3,6,7. Nevertheless, the concept that tumours have defective mitochondria persisted until recent studies, which have shown that the TCA cycle and the electron transport chain are important for tumour cell growth and survival, with human tumours exhibiting active selection against certain mitochondrial DNA mutations9–14.
Isotope tracing has previously been used to map fuel sources of tumour TCA metabolism. Although tumours often select similar substrates to their tissue of origin15, human lung cancer showed increased glucose contribution to the TCA cycle16. However, comparable assessment of TCA turning rate (flux) in tumours has been lacking. TCA flux is distinct from carbon substrate selection, as in the distinction between how fast a furnace burns fuel versus which type of fuel it takes. Whereas the latter can be measured by steady-state isotope tracing, measuring flux requires kinetic isotope labelling measurements, as have been performed in culture for cancer cells and using nuclear magnetic resonance in vivo for selected organs17–20.
Here we developed and validated a strategy to measure TCA cycle flux in tissues and tumours in mice, using isotope tracer infusion, mass spectrometry (MS) and quantitative modelling of the resulting metabolite labelling data. We also quantified glucose use flux using 2-deoxyglucose infusion. Together, these methods show that healthy mouse tissues generate at least 90% of their ATP using the TCA cycle and oxidative phosphorylation. Notably, primary solid tumours show markedly suppressed TCA turning, but still make a majority of their ATP oxidatively, with implied total ATP production rates in solid tumours substantially lower than in healthy organs.
In vivo TCA flux measurement
We set out to generate a systems-level map of mouse tissue energy metabolism. Conceptually, TCA flux (like any metabolic flux) is the product of the initial rate at which labeled fraction rises when labeled substrate is introduced and the pool size of the pathway metabolites21. Across tissue types, lactate is a major fuel feeding the TCA cycle15 and it enters tissues quickly (Extended Data Fig. 1a,b). Thus, by intravenously infusing [U-13C]lactate (fully carbon-13 labelled at three positions) in mice and measuring tissues at different timepoints, the speed of TCA metabolite labelling can reveal TCA flux.
We developed a primed [U-13C]lactate infusion paradigm that achieves steady-state blood lactate labelling within 90 s with only modest perturbations to endogenous metabolism (no mean metabolite concentration change greater than 1.5-fold; Extended Data Fig. 1c,d). We next sampled TCA labelling at multiple timepoints in different mice (Fig. 1a–e and Extended Data Fig. 1e) using euthanasia by cervical dislocation, snap-freezing the tissues within 5 min, grinding tissues and extracting metabolites, and measuring metabolite concentrations and labelling using liquid chromatography coupled with MS (LC–MS). During the less than 5 min between euthanasia and tissue freezing, TCA metabolite concentrations and their labelling from [U-13C]lactate infusion change minimally (Extended Data Fig. 2a–e). The data were then fit to a differential equation model encompassing all major TCA cycle reactions, including entry of lactate-derived carbon through both pyruvate carboxylase and pyruvate dehydrogenase (Extended Data Fig. 3a, Supplementary Note and Supplementary Tables 1–7). The model calculates TCA flux from several data inputs: the kinetic carbon-13 labelling of tissue TCA metabolites (including M+1 forms resulting from repeated TCA turning), the absolute TCA metabolite concentrations in that tissue, and the blood labelling enrichment of the tracer metabolite18–20,22,23 (Fig. 1a–e and Extended Data Fig. 3a–f). Note that tissue lactate labelling, in contrast to TCA metabolite labelling, is not stable during tissue collection, so tissue lactate data were not included as a model input (Extended Data Fig. 2a,b). In this way, we measured TCA fluxes for 15 normal mouse tissues (Fig. 1f).
Fig. 1 |. In vivo measurement of TCA flux by kinetic [U-13C]lactate infusion.
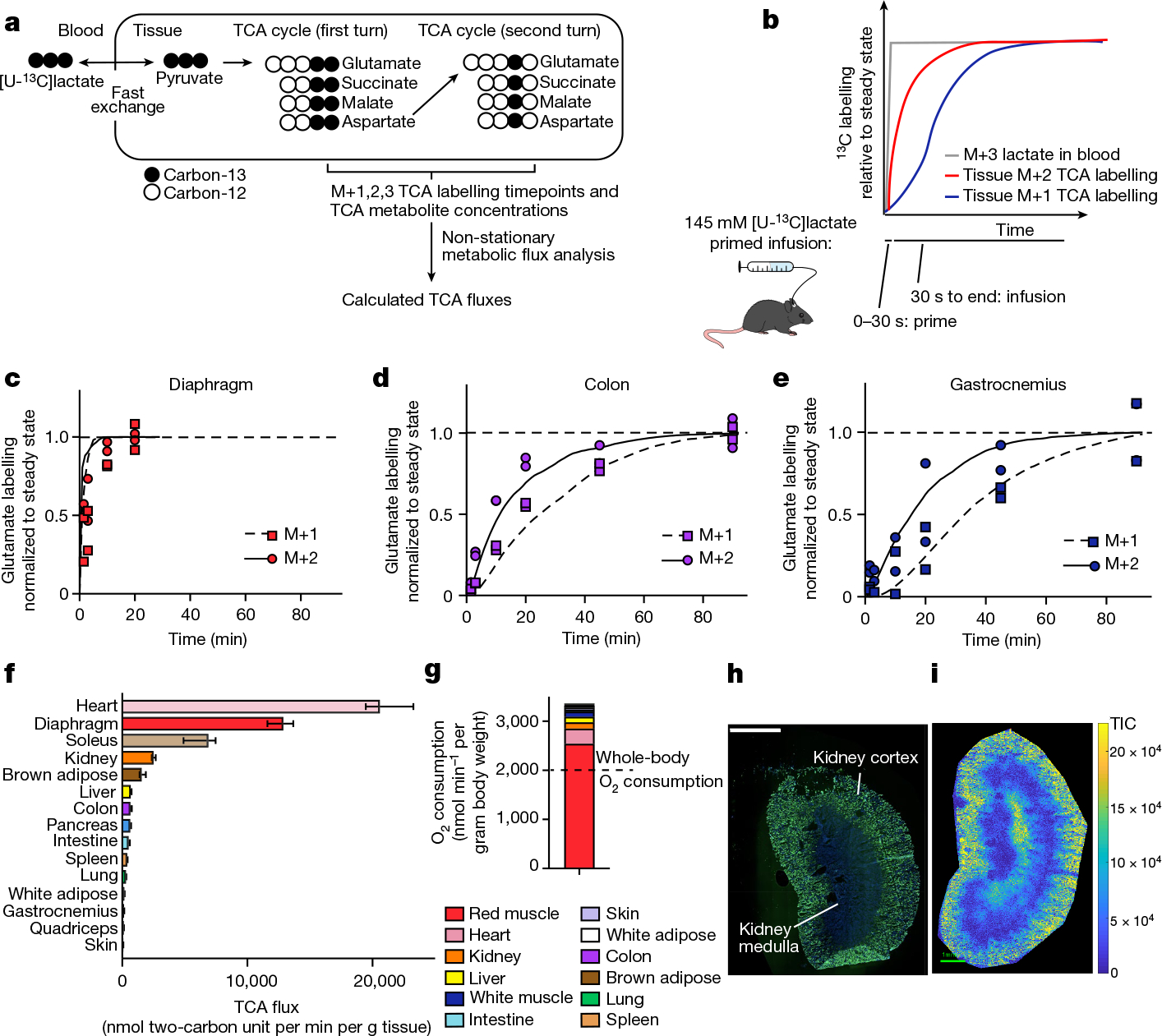
a, Schematic of carbon labelling of TCA metabolites resulting from a [U-13C] lactate infusion. b, Schematic of the kinetics of blood lactate and tissue TCA metabolite labelling from a [U-13C]lactate primed infusion. c, Labelling of diaphragm glutamate M+2 and M+1 using a [U-13C]lactate-primed infusion, normalized to steady-state labelling. d, Labelling of colon glutamate M+2 and M+1 using a [U-13C]lactate primed infusion, normalized to steady-state labelling (that is, final timepoint measured). e, Labelling of gastrocnemius muscle glutamate M+2 and M+1 using a [U-13C]lactate-primed infusion, normalized to steady-state labelling. For c–e, n = 12 mice in each panel, two mice per timepoint, 6 timepoints. f, Tissue TCA fluxes. Data are best estimate of flux from computational modeling ± s.d. of the model fits. Fluxes were calculated for the primed infusion timepoints in n = 12 mice per tissue (except n = 19 for brown adipose and intestine, and n = 17 for soleus) and tissue metabolite concentrations measured in n = 4 mice for each tissue (except n = 3 for diaphragm). g, Oxygen consumption by each tissue calculated from tissue mass and TCA flux. The dotted line is the whole-body oxygen consumption measured using a metabolic cage. h, Immunofluorescence staining of the kidney proximal tubule using lotus tetragonolobus lectin. Scale bar, 2 mm. i, IMS analysis of glutamate M+2 labelling after 90 s [U-13C]lactate-primed infusion. Scale bar, 1 mm; labeling intensity in TIC, total ion counts. The experiments in h and i were performed on serial tissue slices; data are representative of n = 2 mice.
Healthy tissues displayed a wide range of TCA fluxes. The heart and the working muscles diaphragm and soleus displayed the highest TCA fluxes per gram of tissue, consistent with muscle contraction being among the most ATP-costly physiological activities. The measured TCA fluxes of tissues correlated well with historic oxygen consumption measurements of ex vivo tissue slices and perfused organs (Extended Data Fig. 4a), as well as with values determined using a simpler TCA flux calculation method based on single exponential fitting, using only the total TCA pool size and M+2 TCA labelling as inputs (Extended Data Fig. 4b). TCA fluxes calculated based on [U-13C]lactate primed infusion were similar to those measured using [U-13C]glutamine , validating that our measurements reflect TCA turning, not substrate preference (Extended Data Fig. 4c).
We next examined which tissues might account for the greatest share of whole-body oxygen consumption. Oxygen consumption is tightly linked to TCA flux, as the majority of cellular NADH/FADH2 is produced in the TCA cycle or through associated reactions, such as pyruvate dehydrogenase and fatty acid dehydrogenases. NADH/FADH2 in turn power the electron transport chain to consume oxygen at an approximate rate of 3 O2 per TCA turn (that is, per two-carbon unit from glucose, lactate or fat consumed as acetyl-CoA). Owing to the little direct use of lactate by the brain TCA cycle15, we did not measure the brain’s TCA flux, but the brain is expected to account for only around 2% of whole-body oxygen consumption in mice24. The TCA flux of each tissue, multiplied by its mass (Extended Data Fig. 4d), implied a whole-body oxygen consumption of around 3,200 nmol min−1 per gram mouse mass, somewhat greater than direct measurements using a metabolic cage (Fig. 1g). Heterogeneity in muscle TCA metabolism is a probable cause of the discrepancy, with our data showing considerably higher TCA activity in red muscle (soleus) than in white muscle (quadriceps and gastrocnemius). Overall, red muscle (fibre type I and IIa) accounted for a majority of whole-body TCA turning, and thus a majority of inferred oxygen consumption and calorie expenditure.
Spatial analysis of TCA flux
The experiments above used homogenized whole tissues to measure TCA flux; however, tissues consist of a mixture of cell types with distinct biological roles and metabolic needs. One example of spatial heterogeneity in metabolism is the kidney, of which the cortex and medulla constitute two different tissue types with distinct biological roles1. Combining a 90 s primed [U-13C]lactate infusion with imaging MS (IMS) enabled us to visualize TCA flux across the kidney. Specifically, as glutamate is the most abundant TCA-associated metabolite (Extended Data Fig. 3b), the M+2 glutamate intensity measured in the initial pre-steady-state phase of carbon-13 label accumulation approximates TCA turning flux. The kidney cortex displayed a higher M+2 glutamate intensity than the medulla (Fig. 1h,i and Extended Data Fig. 4e), consistent with the literature showing that ATP use is faster in the cortex due to the demands of ion pumping to reabsorb kidney filtrate1.
In vivo glucose use flux
Glycolysis is the other pathway that yields substantial cellular ATP; thus, to quantify energy metabolism in tissues, we optimized a method to measure tissue glycolysis flux. We infused [1-13C]2-deoxyglucose, a glucose analogue that is taken up by glucose transporters and phosphorylated in tissues, but cannot be further metabolized25 (the benefit of the 13C label is avoiding background signal from an isomeric compound at the same mass as unlabelled 2-deoxyglucose phosphate in tissues; Extended Data Fig. 5a). Measuring 2-deoxyglucose timepoints in arterial blood as well as 2-deoxyglucose phosphate timepoints in tissues enabled us to calculate glucose use flux (Fig. 2a–d, Extended Data Fig. 5b–f and Supplementary Tables 8–12) according to the following equation:
| (1) |
where is the rate of glucose uptake and phosphorylation, is glucose concentration in the blood, is 2-deoxyglucose phosphate concentration in the tissue, and the integral of with respect to time is the integrated concentration of the blood 2-deoxyglucose concentration up to that timepoint25. Glucose use flux measured in this way approximates glycolysis: although glucose 6-phosphate can also undergo transformation to ribose phosphate through the pentose phosphate pathway or glycogen synthesis, in fasted mice, glycolysis is by far the greatest flux1,26,27. This strategy for measuring glucose use flux is similar to FDG-PET28 (Fig. 2e) but, by using MS rather than imaging as a readout, we were able to measure even small tissues while also avoiding the use of radioactivity and obtaining reliable absolute flux quantification.
Fig. 2 |. Kinetic 2-deoxyglucose infusion quantifies glucose use flux in vivo.
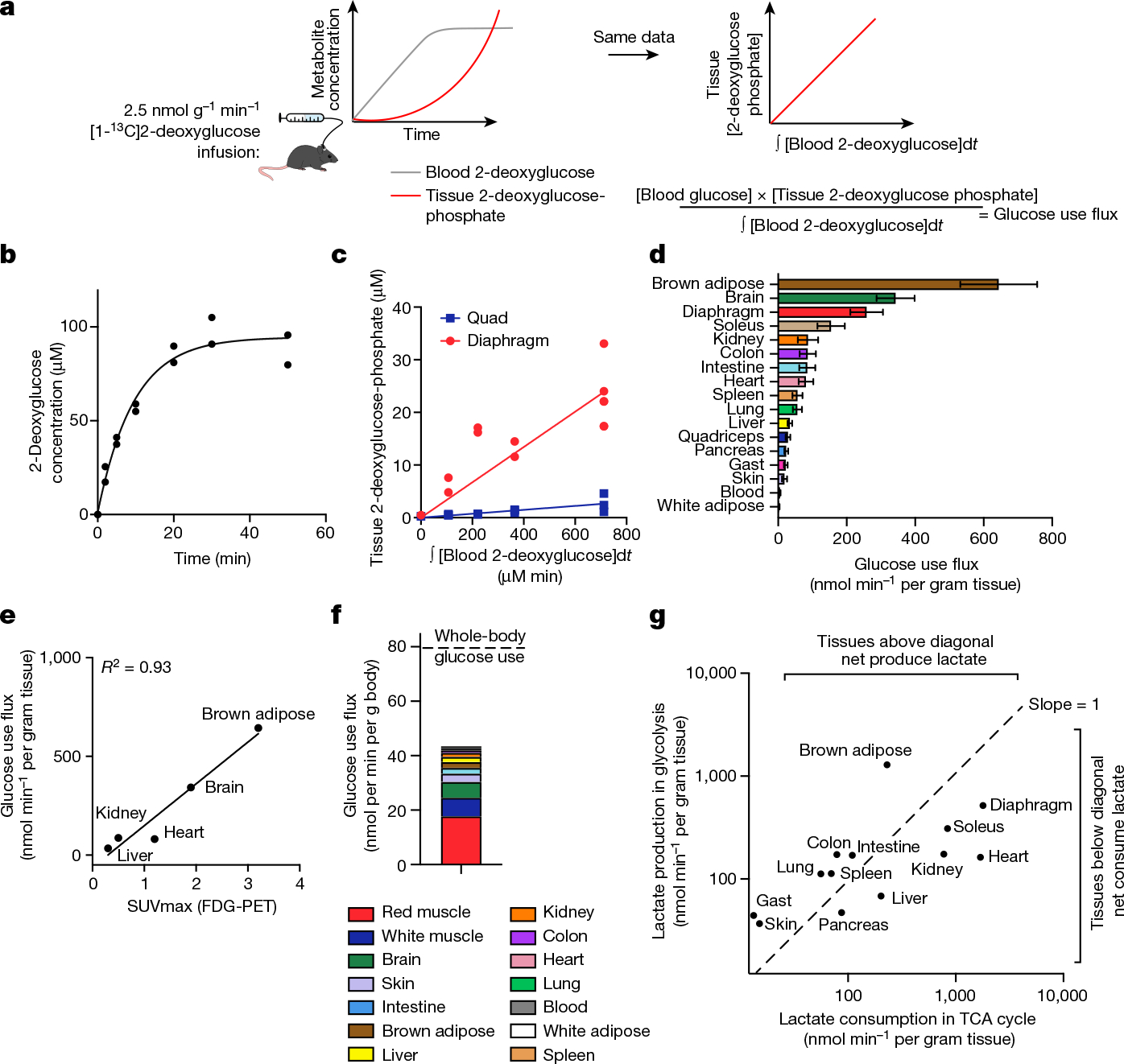
a, Schematic of [1-13C]2-deoxyglucose infusion. b, The concentration of [1-13C]2-deoxyglucose in arterial blood during infusion. n = 2 mice, 7 timepoints each. c, The concentration of diaphragm and quadriceps muscle [1-13C]2-deoxyglucose phosphate versus the integral of blood [1-13C]2-deoxglucose with respect to time during [1-13C]2-deoxyglucose infusion. n = 12 mice (quadriceps) and n = 13 (diaphragm). d, Tissue glucose use flux. n = 4 mice (colon and blood), n = 9 (gastrocnemius (gast), intestine, lung, pancreas, skin, spleen, white adipose), n = 12 (kidney, liver, quadriceps) and n = 13 (brain, brown adipose, diaphragm, heart, soleus). Data are values determined by linear fit ± s.d. e, The correlation between absolute glucose use measured by [1-13C]2-deoxyglucose infusion and relative glucose use measured using FDG-PET28. f, The calculated glucose use by each tissue at the whole-body level. The dotted line shows the whole-body glucose turnover rate measured by [U-13C]glucose infusion. g, The production and consumption of lactate by tissues, calculated from glucose use flux and from TCA flux multiplied by lactate contribution to TCA cycle, respectively.
Among healthy mouse tissues, brown adipose and the brain had the highest glucose use flux per gram (Fig. 2d). The high glucose use of brown adipose was probably driven by the mice being at room temperature (around 24 °C) rather than at thermoneutrality28. The working muscles diaphragm, which is required for breathing, and soleus, which is required forstanding or walking, also consumed glucose quickly.
We next investigated which tissues might account for the greatest share of whole-body glucose use. We reasoned that the glucose use of all healthy tissues should sum to the whole-body circulating glucose turnover rate (Ra or Fcirc15,29), as measured using infused [U-13C]glucose tracer. Tissue glucose use fluxes multiplied by tissue masses yielded a total glucose use rate of 43.5 nmol min−1 per gram body mass–54% of whole-body circulating glucose flux (Fig. 2f). Uncertainty regarding glucose flux in different muscle types may contribute to the undermeasurement of total body flux, as different muscles showed high variation in glucose use, with red muscle (exemplified by soleus) accounting for the greatest share of glucose use–around 44% of the measured total.
Combining our measurements of TCA flux and glucose use enabled us to identify which tissues produce or consume net lactate. Lactate is a product of glycolysis, a major substrate for the TCA cycle, and is metabolized rapidly at the whole-body level15,30. However, to date, methods to determine whether there is net lactate consumption by tissues or merely exchange with the blood have been limited to arteriovenous sampling. We estimated lactate production by each tissue as two lactate molecules produced per glucose used, and calculated lactate consumption in the TCA cycle as the product of TCA flux and the fraction of the TCA cycle contributed by lactate (Extended Data Fig. 6a). This approach identified the kidneys, liver, heart, soleus and diaphragm as net lactate consumers (Fig. 2g). These findings are robust to the whole-body lactate production rate being underestimated by twofold (Extended Data Fig. 6b–d). The kidneys, liver and heart had been previously identified to consume lactate31–33 on the basis of arteriovenous sampling, but such sampling is not currently feasible for the diaphragm or soleus owing to their lack of a dedicated major draining vein. Collectively, our data highlight the central role in whole-body metabolism of red working muscle, which acts as a major glucose user, calorie consumer and lactate burner.
Tumours have slow TCA flux
The energy metabolism of tumours has long been a subject of study. Otto Warburg first observed that tumours perform avid glycolysis in the presence of oxygen, and hypothesized that this might be due to a defect in the oxidative machinery of cancer cells2,3. However, the absolute TCA flux of tumours in vivo has not been systematically measured.
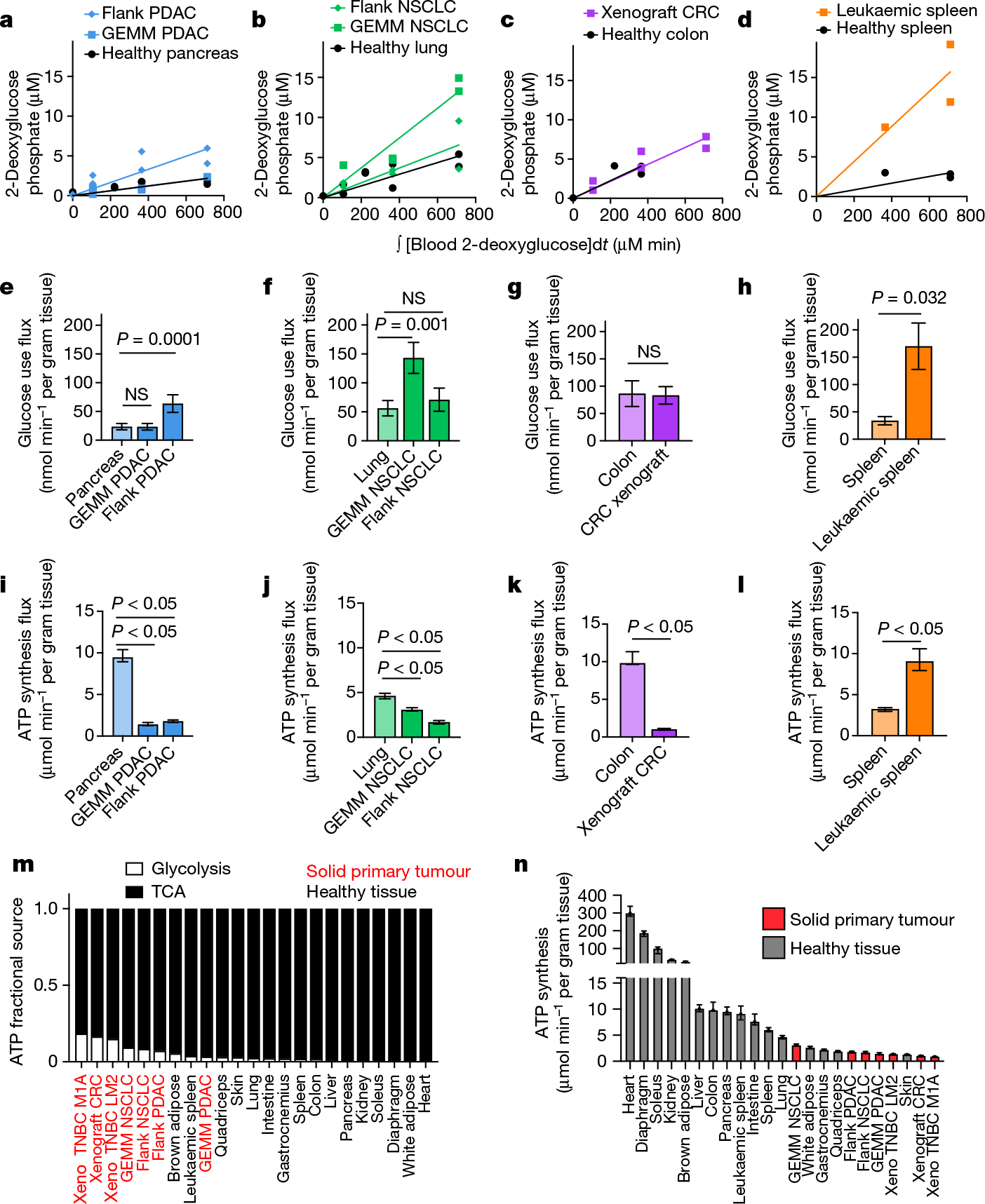
We applied our TCA flux measurement method to several models of cancer in mice. Across five primary solid tumour models, TCA fluxes measured by [U-13C]lactate primed infusion were lower than those of almost all healthy tissues, including the relevant tissues of origin (Fig. 3 and Extended Data Fig. 7a–g). Note that all healthy tissues were measured in non-tumour-bearing mice. Two models of Kras-mutant and Trp53-deficient pancreatic tumours, either genetically engineered to develop in the mouse pancreas or subcutaneously implanted, displayed sixfold slower TCA flux compared with the healthy pancreas (Fig. 3a,b and Extended Data Fig. 7a–e). Slow TCA flux was also measured in both pancreatic tumour models using [U-13C]glutamine primed infusion (Extended Data Fig. 7g). Similar mouse tumours that developed in the lungs (also with LKB1 loss) or that were derived from lung tumours and subcutaneously implanted both displayed lower TCA flux than healthy lung (Fig. 3c,d and Extended Data Fig. 8a,b). Finally, a human colon-cancer-derived xenograft displayed lower TCA flux compared with healthy mouse colon (Fig. 3e,f and Extended Data Fig. 8c). Low TCA flux was not caused by tumour necrosis, because tumours were viable throughout (Extended Data Figs. 7b and 8b). Lactate entry into tumours was faster than TCA labelling appearance, suggesting that lactate entry was not limiting (Extended Data Fig. 7c,d). In contrast to the low TCA fluxes in solid tumours, a transplantable mouse model of NOTCH1-driven T cell acute lymphocytic leukaemia displayed around threefold higher TCA flux compared with healthy mouse spleen (Fig. 3g,h and Extended Data Fig. 8d). Thus, mouse primary solid tumours, but not leukaemia, have lower TCA flux compared with healthy tissues. The solid tumour data are consistent with Warburg’s hypothesis, but are not obvious in light of extensive recent data demonstrating active and functionally important TCA metabolism in tumours9–14.
Fig. 3 |. Tumours have lower TCA flux compared with healthy tissues.
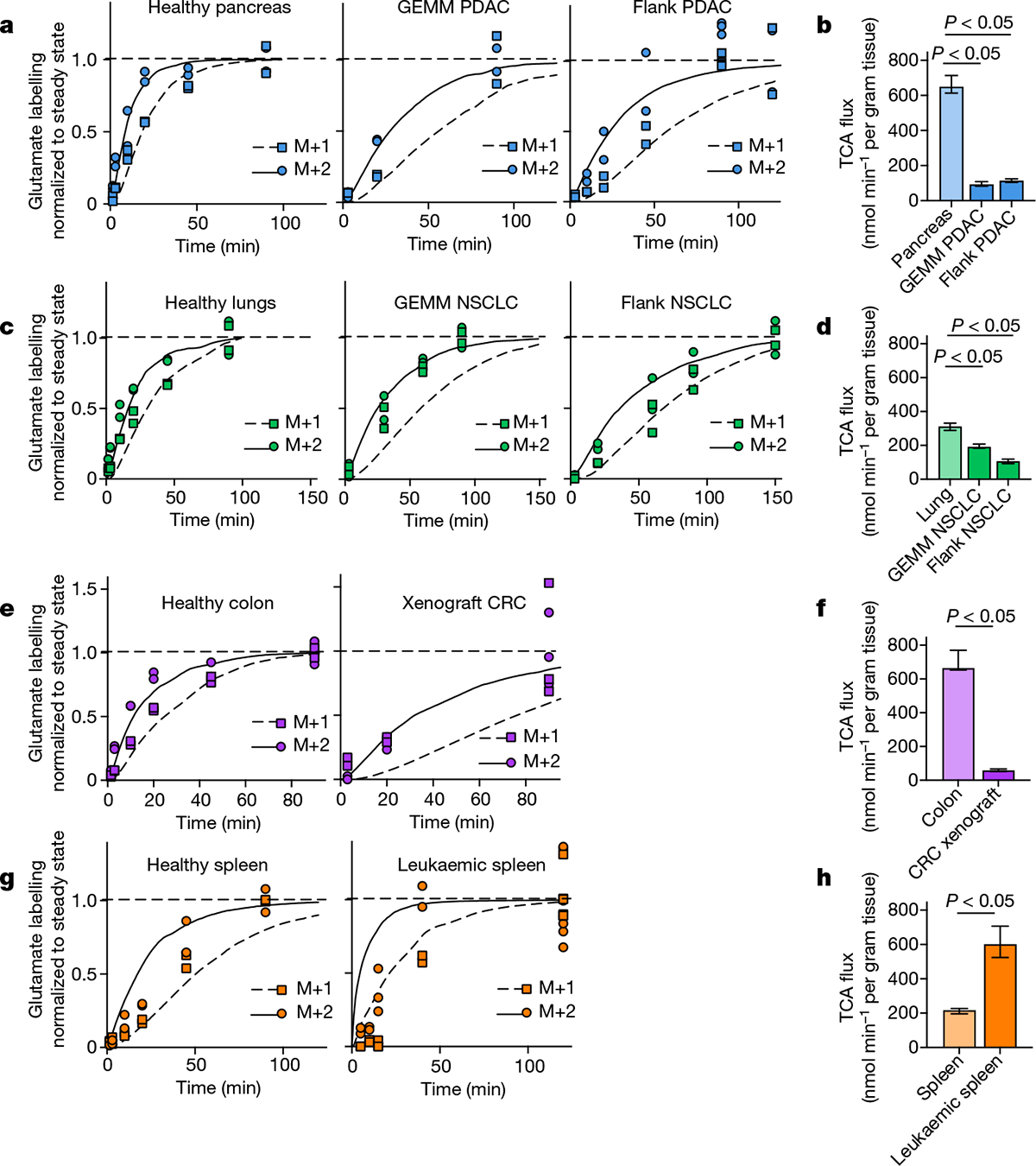
a, Glutamate M+2 and M+1 labellingusing a [U-13C]lactate primed infusion in healthy pancreas, in a genetically engineered mouse model of pancreatic adenocarcinoma (Pdx1-cre;LSL-KrasG12D/+Trp53−/− (GEMM PDAC)) and in a flank-implanted model of pancreatic adenocarcinoma (implanted tumour fragments were Pdx1-cre;LSL-KrasG12D/+Trp53R172H/+ (flank PDAC)), normalized to steady-state labelling (labelling at the latest timepoint measured). b, TCA fluxes of pancreas and pancreatic tumour models. Primed infusion timepoints in n = 12 mice (pancreas), n = 6 (GEMM PDAC), n = 13 (flank PDAC); tissue metabolite concentrations in n = 4 mice per tissue or tumour. c,d, Glutamate labelling (c) and TCA fluxes (d) for healthy lung, a genetically engineered mouse model of non-small cell lung cancer (adenovirus-cre LSL-KrasG12D/+; Stk11−/−;Trp53−/− (GEMM NSCLC)) and a flank-implanted model of non-small cell lung cancer (implanted cell line derived from tumour that was adenovirus-cre LSL-KrasG12D/+;Trp53−/− (flank NSCLC)). Primed infusion timepoints in n = 12 mice (lung), n = 9 (GEMM NSCLC), n = 10 (flank NSCLC); tissue metabolite concentrations in n = 4 mice per tissue. e,f, Glutamate labelling (e) and TCA fluxes (f) for healthy colon and a xenograft of the human colorectal cancer cell line HCT116 (xenograft CRC). Primed infusion timepoints in n = 12 mice (colon) and n = 7 mice (xenograft CRC); tissue metabolite concentrations in n = 4 mice per tissue. g,h, Glutamate labelling (g) and TCA fluxes (h) for healthy spleen and spleen from mice with transplanted NOTCH1-constitutively-active mouse T acute lymphocytic leukaemia (leukaemic spleen). Primed infusion timepoints in n = 12 mice (healthy spleen) and n = 15 mice (leukaemic spleen); tissue metabolite concentrations in n = 3 mice (healthy spleen) and n = 4 mice (leukaemic spleen). All measured healthy tissues were from non-tumour-bearing mice. For b, d, f and h, data are best estimates of flux from computational fitting of experimental data ± s.d. For b, d, f and h, P values were calculated using two-tailed t-tests.
Metastases increase TCA flux
Tumour metastasis requires cancer cells to migrate out of tissues, survive in the blood or lymph, and establish themselves in a new tissue niche; evidence is accumulating that these challenges correlate with altered metabolism. Metastatic cells display increased levels of reactive oxygen species, probably produced by the electron-transport chain34,35. There is also indirect evidence that metastatic cells may increase TCA flux and electron-transport chain activity–investigators have noted higher expression of oxidative phosphorylation genes in melanoma brain metastases compared with in primary tumours36 and higher oxygen consumption of metastasis-prone cell lines in vitro37. However, measurement of the TCA flux of metastasis in vivo is lacking.
We investigated two orthotopic breast cancer xenograft models that metastasize to the lungs. Human triple-negative breast cancer cells (MDA-MB-231-LM2 or Sum159-M1A) were implanted into the mammary fat pad of female mice, and the primary tumours spontaneously seeded lung metastases (Fig. 4a and Extended Data Fig. 9a–c). These models therefore enabled us to measure the metabolism of advanced solid tumours and metastases in the same mouse. In both models, metastasis-colonized lungs had a higher TCA flux (but indistinguishable glucose use) compared with the primary tumours (Fig. 4b,c and Extended Data Fig. 9d–g).
Fig. 4 |. Lung metastases have higher TCA flux than the primary tumours.
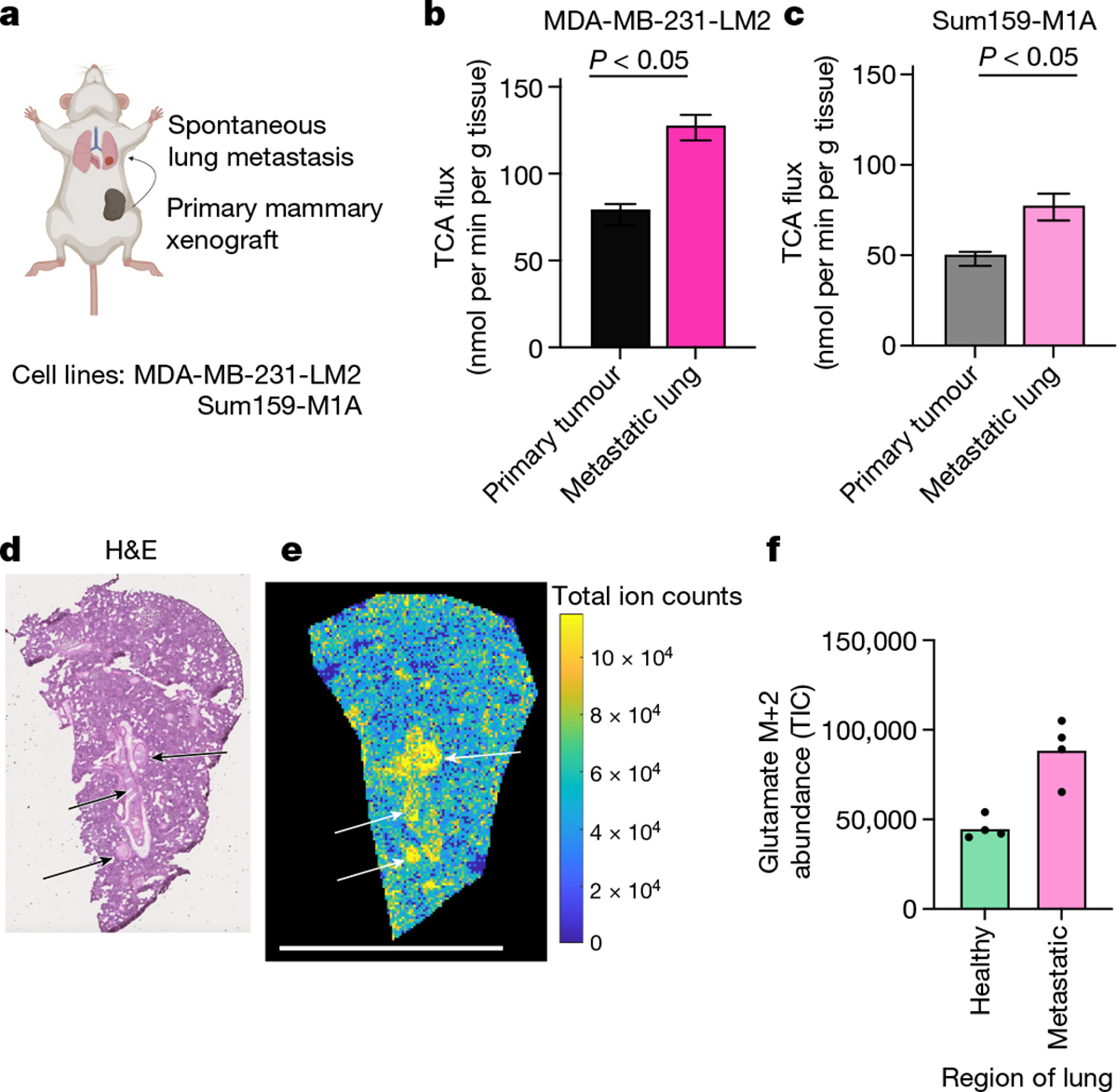
a, Schematic of mammary-fat-pad-implanted breast cancer xenograft tumours, which lead to spontaneous lung metastases. b, The TCA flux of primary mammary fat pad tumour and of whole lung containing metastases from mice bearing MDA-MB-231-LM2 xenograft tumours. n = 6 mice per tissue type for lactate infusion and n = 4 mice per tissue type for tissue metabolite concentrations. c, The TCA flux of primary mammary fat pad tumour and whole lung containing metastases from mice bearing Sum159-M1A xenograft tumours. n = 8 mice per tissue type for lactate infusion and n = 4 mice per tissue type for tissue metabolite concentrations. d, Haematoxylin and eosin (H&E) staining of the lungs of a mouse bearing a Sum159-M1A mammary fat pad tumour. The arrows indicate metastatic regions. e, IMS analysis of glutamate M+2 labelling intensity in the lung of a mouse bearing Sum159-M1A mammary fat pad tumour after 10 min [U-13C]lactate primed infusion. Scale bar, 5 mm. For d and e, experiments were performed on the same tissue slice; the arrows indicate metastatic regions identified from d. f, Quantification of glutamate M+2 intensity (in units of total ion counts, TIC) from metastatic and non-metastatic regions of the lungs from d and e. n = 1 mouse. Each point represents a different region of the image in e. For b and c, data are best estimates of flux from computational fitting of experimental data ± s.d. For b and c, P values were calculated using two-tailed t-tests. The schematic in a was created using BioRender.
As TCA flux measured in the whole metastatic lung included both healthy lung and cancer cells, we used IMS to distinguish between the TCA flux of metastatic nodules and the healthy lung regions. We used haematoxylin and eosin staining to identify metastatic nodules in the lungs of mice with primary MDA-MB-231-LM2 tumours (Extended Data Fig. 9h) or Sum159-M1A tumours (Fig. 4d) by looking for dense regions lacking air sacs. We then used IMS to visualize the relative TCA flux in healthy and metastatic regions of the lung, on the basis of the M+2 glutamate intensity after a 10 min [U-13C]lactate-primed infusion. Metastatic nodules had higher TCA flux compared with the surrounding healthy lung regions (Fig. 4e,f and Extended Data Fig. 9i–j). Despite the higher TCA flux, compared with the primary tumours, the metastases did not have higher levels of mitochondrial oxidative phosphorylation proteins (Extended Data Fig. 9k). In summary, breast cancer metastases have higher TCA flux compared with both primary tumours and healthy lungs.
Tumours make energy slowly
We next set out to determine the total ATP synthesis rates of tumours. Although TCA flux in solid tumours was lower than in healthy tissues, in principle, they could compensate through high glycolysis flux. We used our [1-13C]2-deoxglucose method to measure glucose use flux in tumours and found that solid tumours and leukaemia displayed similar or higher glycolytic flux compared with the corresponding healthy tissues (Fig. 5a–h). This finding is consistent with the Warburg effect and FDG-PET positivity of cancer2,8,38.
Fig. 5 |. Tumours generate ATP slower than healthy tissues.
a–h, Quantification of tumour glucose use flux. Tissue [1-13C]2-deoxyglucose phosphate concentration versus the integral of blood [1-13C]2-deoxyglucose concentration with respect to time in healthy pancreas, GEMM PDAC and flank PDAC (n = 9, 5 and 6 mice, respectively) (a), in healthy lung, GEMM NSCLC and flank NSCLC (n = 9, 5 and 6 mice, respectively) (b), in healthy colon and xenograft CRC (n = 4 and 6 mice, respectively) (c) and in healthy spleen and leukaemic spleen (n = 3 mice each) (d). e–h, The glucose use flux in healthy tissues and cancer models calculated from a–d (pancreas (e), lung (f), colon (g) and spleen (h)). n values are shown. Data are value determined by linear fit ± s.d. i–l, The calculated total ATP production flux in healthy tissues and cancer models (pancreas (i), lung (j), colon (k) and spleen (l)), calculated from the glucose use fluxes shown in e–h and TCA fluxes shown in Fig. 3b–h. Glucose use fluxes: n = 9 mice (pancreas), n = 5 (GEMM PDAC), n = 6 (flank PDAC), n = 9 (lung), n = 5 (GEMM NSCLC), n = 6 (flank NSCLC), n = 4 (colon), n = 6 (xenograft CRC), n = 3 (spleen), n = 3 (leukaemic spleen); lactate infusion timepoints: n = 12 mice (pancreas), n = 6 (GEMM PDAC), n = 13 (flank PDAC), n = 12 (lungs), n = 9 (GEMM NSCLC), n = 10 (flank NSCLC), n = 12 (colon), n = 7 (xenograft CRC), n = 12 (spleen), n = 15 (leukaemic spleen); tissue metabolite concentrations: n = 4 mice for all except n = 3 for healthy spleen. Data are best estimates of flux from computational fitting of experimental data ± s.d. m, The fraction of total ATP derived from glycolysis or the TCA cycle in tumours and healthy tissues. n, The calculated total ATP production flux in healthy tissues and cancer models. Data are best estimates of flux from computational fitting of experimental data ± s.d. All healthy tissues in this figure were from non-tumour-bearing mice. For e–l, P values were calculated using two-tailed t-tests; NS, not significant. Tumour name abbreviations are the same as in Fig. 3, with the addition of MDA-MB-231-LM2 triple-negative breast cancer xenograft tumour (xeno TNBC LM2) and Sum159-M1A triple-negative breast cancer xenograft tumour (xeno TNBC M1A).
We then calculated total ATP synthesis rates using the glucose use and TCA fluxes measured above. In glycolysis, 2 moles of ATP are generated per mole of glucose consumed, whereas approximately 14.5 moles of ATP are generated per mole of two-carbon unit (acetyl-CoA) consumed in the TCA cycle. This assumes that mitochondria are well-coupled, so that NADH from the TCA cycle efficiently drives ATP production (which does not apply in brown adipose, in which mitochondrial uncoupling is used to generate body heat39, but is probably a decent approximation in other tissues40,41).
We found that primary solid tumours in mice produced ATP more slowly compared with the corresponding healthy tissues, including two pancreatic tumour models, two lung tumour models and a colon tumour model (Fig. 5i–k), although a leukaemia model had higher TCA flux (Fig. 5l). We further found that tumours derived a higher fraction of their ATP from glycolysis compared with healthy tissues but, nevertheless, most ATP was made oxidatively in every tissue and tumour type (Fig. 5m). Overall, primary solid tumour models fell towards the bottom end of the ATP synthesis range compared with the healthy tissues measured in this study (Fig. 5n). Note that this approach cannot distinguish whether tumours make ATP slowly due to low metabolic demand or due to low ATP production ability, for example, due to limited nutrient availability. Thus, solid tumours in mice make and use ATP more slowly than most healthy tissues, arguing against the perception that tumours are generically hypermetabolic42.
Tumours suppress ATP-costly activities
We next examined how tumours might proliferate while making and therefore using less ATP compared with healthy tissues. As the ATP pools of tissues and tumours are close to steady state over time, slow ATP production implies slow consumption. Healthy tissues use energy to perform their physiological functions–the kidney pumps ions, the pancreas synthesizes and secretes digestive enzymes, and so forth. We hypothesized that tumours might downregulate such physiological tasks, thereby conserving energy. To investigate this possibility, we measured protein synthesis flux in both the pancreas and in pancreatic cancer. Protein synthesis to support digestive enzyme secretion is the major physiological task of the pancreas43,44 (Extended Data Fig. 10a), which synthesizes protein at the fastest rate per gram of tissue of any organ in mice45. We measured the protein synthesis rate in healthy tissues and two pancreatic cancer models by infusing [U-13C]valine and quantifying its accumulation in total protein (Fig. 6a). As expected, healthy pancreas synthesized protein quickly compared with other healthy tissues (Fig. 6b). However, pancreatic tumours carried out around fourfold less protein synthesis compared with the healthy pancreas (Fig. 6c). Thus, at least in pancreatic tumours, downregulation of ATP production occurs in concert with the loss of the native tissue’s hallmark ATP-consuming process.
Fig. 6 |. Tumours downregulate ATP-costly tissue activities.
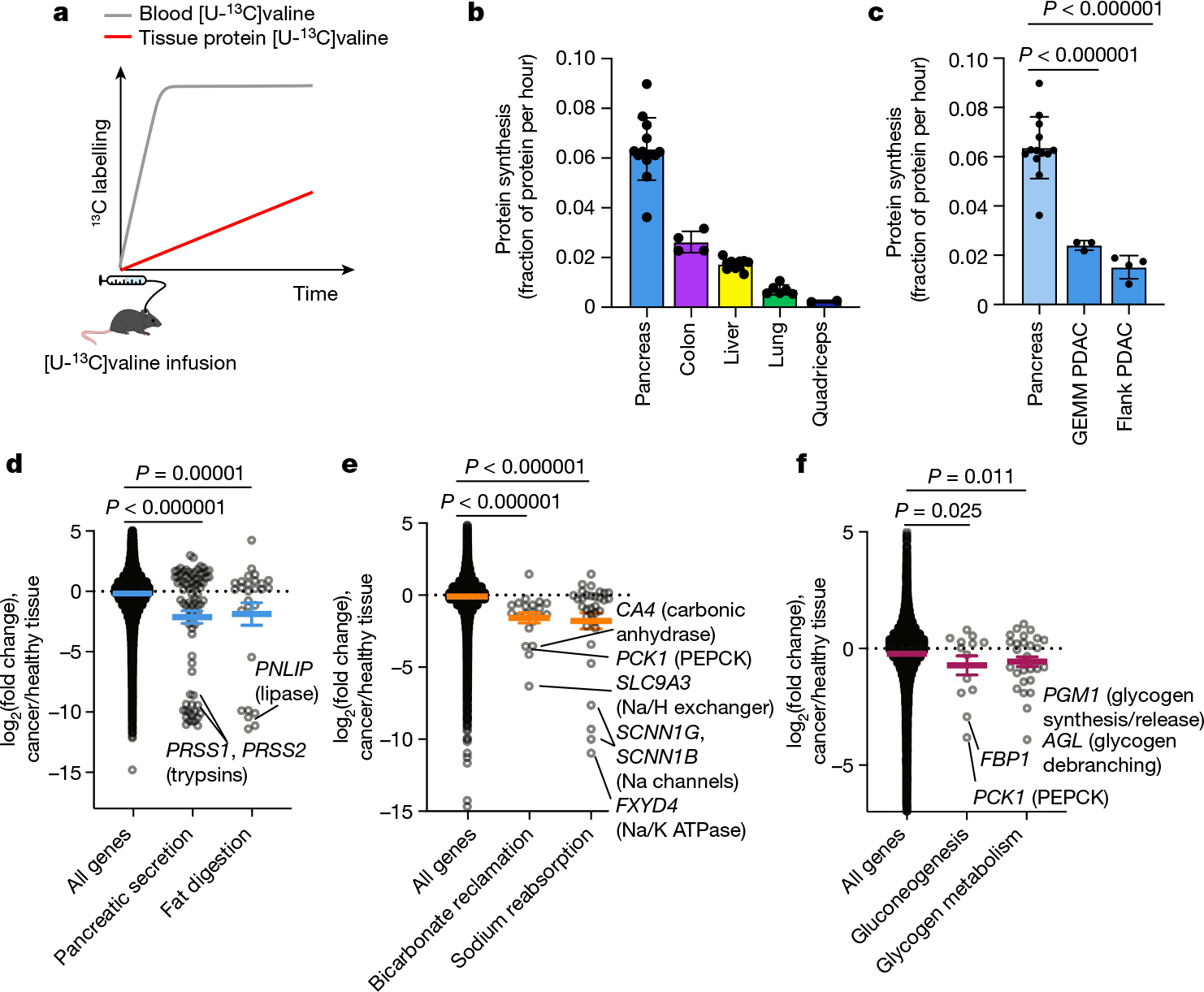
a, Schematic of [U-13C]valine infusion to measure tissue protein synthesis. b,c, Healthy tissue (b) and GEMM PDAC and flank PDAC (c) protein synthesis was measured using [U-13C]valine infusion. Data are mean ± s.d. Healthy pancreas data are the same in b and c. n = 13 mice (pancreas), n = 4 (colon), n = 12 (liver), n = 6 (lungs), n = 2 (quadriceps), n = 3 (GEMM PDAC), n = 4 (flank PDAC). d–f, Gene expression changes between human tumours and their tissues of origin (pancreatic cancer versus healthy pancreas (d); kidney cancer versus healthy kidney (e); and liver cancer versus healthy liver (f)); each point represents the log2(fold change) of one gene between cancer and corresponding healthy tissue. Genes are drawn from the indicated KEGG pathways; bicarbonate reclamation represents proximal tubule bicarbonate reclamation and sodium reabsorption represents aldosterone-regulated sodium reabsorption. Human tissue and tumour gene expression data are from the Xena database (https://xenabrowser.net/; n = 167 patients (healthy pancreas), n = 178 (pancreatic adenocarcinoma), n = 140 (healthy kidneys), n = 884 (kidney tumours, including n = 530 clear cell carcinoma and n = 354 papillary cell carcinoma), n = 50 (healthy liver) and n = 360 (hepatocellular carcinoma)). Colored lines show mean ± s.e.m. For c–f, P values were calculated using two-tailed t-tests.
To examine whether tumours may generally downregulate ATP-costly functions specific to the tissue of origin’s organismal role, we examined gene expression changes between human tumours and the corresponding healthy organs in the Xena database. First, we selected KEGG pathways for each organ that represented known major ATP-costly functions of those organs: enzyme secretion and fat digestion in the pancreas43,44, bicarbonate and sodium recovery from blood filtrate in the kidney1,46, and gluconeogenesis and glycogen metabolism in the liver1,47. Gene expression for each of these pathways was significantly downregulated in tumours compared with healthy tissue (Fig. 6d–f and Extended Data Fig. 10b). In the cases of the liver and kidneys, lower expression of these genes presumably results in less ATP expenditure by the encoded enzymes and ion pumps, whereas in the pancreas, the ATP savings occur through reducing the synthesis of the exocrine enzymes themselves. Collectively, these data suggest that solid tumours downregulate ATP-expensive functions that are characteristic of the tissue of origin, sparing ATP to support proliferation.
Discussion
Our kinetic [U-13C]lactate tracing method revealed that five solid primary Kras-mutant tumour models have suppressed TCA cycle fluxes compared with healthy tissues. By contrast, both breast cancer metastases and a leukaemia model exhibited higher TCA fluxes. Although we used lactate as a tracer, our fundamental results concern overall TCA turning, as we confirmed by similar flux values measured using kinetic glutamine tracing. TCA turning can be traced by lactate because ubiquitous expression of MCT transporters and lactate dehydrogenase results in lactate being a nearly universal and rapidly assimilated TCA substrate.
TCA turning and glucose use measurements can be combined to infer rates of ATP production. Accelerated glucose catabolism is the longest-standing metabolic hallmark of tumours2,4,5, and is driven in part by oncogenes4. We used [1-13C]2-deoxyglucose to quantify glucose use fluxes in tissues and tumours. At the whole-body level, these measurements fell short of accounting for all glucose consumption by about twofold, perhaps reflecting intrinsic differences in glucose and 2-deoxyglucose as substrates25, or higher glucose use in unsampled muscle types. Nevertheless, our measurements confirmed increased glucose flux in tumours. However, the associated ATP production was far insufficient to compensate for the suppressed respiration. Moreover, the examined tumours generated the majority of ATP oxidatively.
Thus, upregulated glycolysis does not imply a general hypermetabolic energy metabolism program in mouse solid primary tumours. Although quiescent lymphocytes broadly upregulate their metabolism to proliferate in response to an infection48, our data argue for tumours engaging in a different metabolic strategy. The tissues of origin of most solid tumours are not metabolically dormant like quiescent lymphocytes; rather, they include some of the most metabolic cells in the body, such as the renal tubular epithelium. As such, tumour cells do not need to broadly ramp up all aspects of metabolism to proliferate. Instead, as they undergo oncogene-driven dedifferentiation (or emerge in a relatively dedifferentiated state from stem cells49), they lack the energetically demanding tissue-specific functions such as digestive enzyme synthesis in the exocrine pancreas or ion pumping in the kidney50,51. This enables cancer cells to proliferate with decreased, rather than elevated, ATP production flux. The nefarious ability of cancer to proliferate with suppressed TCA turning and low ATP consumption positions them unfortunately well to succeed in the face of metabolic challenges.
Our results raise the question of whether low ATP synthesis by tumours is caused by a low supply or demand. For example, it could arise from slow ATP production due to limited nutrient availability or, alternatively, from slow ATP consumption due to downregulation of ATP-expensive tissue functions. As ATP levels are strictly maintained by all cells to ensure homeostasis, ATP consumption and production are matched, and our data do not distinguish between these possibilities.
Data on mitochondrial membrane potential in tumours are consistent with limited ATP consumption (that is, low ATP demand) sometimes gating TCA turning. Specifically, some lung cancers show elevated mitochondrial membrane potential38. A logical cause of such elevation is bottlenecking of ATP synthase activity due to limited ATP consumption, leading to proton accumulation in the mitochondrial intermembrane space. Thus, rather than tumours having defective mitochondria as Warburg hypothesized, they may sometimes have supercharged mitochondria with nowhere to put the available energy.
That said, cancer cells often face a hostile metabolic microenvironment in which oxygen and nutrients are scarce, and competition with other cell types is fierce52,53. The supply of oxygen, probably the most limiting substrate in the blood, could restrain TCA flux, while the availability of glucose might cap compensatory glycolysis upregulation (which can be caused directly by oncogenes or by compensation for low TCA flux).
These constraints may differ between primary and metastatic niches, enabling higher respiration in metastasis. An interesting possibility is that metastasis requires enhanced metabolic flexibility to enable both redox and ATP homeostasis across environments. Consistent with this, melanoma metastasis is promoted by increased expression of MCT transporters, which can facilitate both glycolytic ATP generation (through enabling lactate export) and respiratory ATP generation (through enabling lactate import)54. In our study, TCA and electron-transport-chain proteins were not upregulated in metastasis, supporting the concept that metabolic differences between primary and metastatic tumours substantially reflect the environmental milieu.
Our observations suggest several directions for future study. One is to determine the energy demands of different cell types within tumours, such as macrophages, lymphocytes, fibroblasts and endothelial cells. A recent study suggests that macrophages in tumours may be major glucose users55, but little is known about the TCA flux or ATP synthesis rates of different cell populations in tumours. Moreover, clinical studies are needed to determine whether energy production is also low in primary human tumours and higher in metastases; and the extent to which such changes reflect enzyme expression or, as our data in mouse metastases suggest, microenvironmental metabolic conditions. One potential approach to clinical TCA flux measurement is hyperpolarized MRI studies56 tracking pyruvate conversion to glutamate in tumours. Finally, as ATP synthesis flux is low in tumours, it would be informative to test whether ATP may be limiting for tumour proliferation; for example, using genetic strategies to increase tumour ATPase activity could test whether targeting ATP levels is a viable strategy to slow tumour growth.
Online content
Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41586-022-05661-6.
Methods
Mouse strains
All of the animal studies were approved either by the Princeton Institutional Animal Care and Use Committee (majority of experiments), the Rutgers Institutional Animal Care and Use Committee (all T acute lymphocytic leukaemia experiments, all GEMM NSCLC experiments and some GEMM PDAC experiments) or the MIT Institutional Animal Care and Use Committee (some GEMM PDAC experiments). Experiments in non-cancer-bearing mice were performed in C57Bl/6N mice (aged 9–14 weeks) from Charles River Laboratory. Mice were fed a standard rodent diet (PicoLab Rodent 5053 Laboratory Diet).
GEMM PDAC tumours
For experiments with spontaneous pancreatic adenocarcinoma, Pdx1-cre;LSL-KrasG12D/+;Trp53fl/fl (GEMM PDAC) mice were used at 5–8 weeks of age, and tumours were typically much larger and more fibrous than healthy pancreas at this timepoint.
GEMM NSCLC tumours
For experiments with spontaneous lung adenocarcinoma, LSL-KrasG12D/+;Trp53fl/fl;Stk11fl/fl (GEMM NSCLC) mice were inoculated intranasally with 4 × 107 particles of Cre-expressing adenovirus; experiments were performed at 13–16 weeks of age, around 8 weeks after adenovirus inoculation (see Extended Data Fig. 8a for GEMM NSCLC lung tumour mass).
Xenograft CRC (HCT116) tumours
HCT116 colon-cancer-derived cells were grown in DMEM with 10% fetal bovine serum. For tumour implantation, cells were grown to confluency, then trypsinized and resuspended at 50 × 106 cells per ml in medium. Cells were mixed with Matrigel (Corning, 354234) at a 1:1 (v/v) ratio, and 200 μl of this mixture was injected subcutaneously into the flank of CD1 nude mice (Charles River Laboratory, strain 086) using a 26-gauge needle. Tumour growth was monitored by measuring the tumour dimensions (length, width and height) twice per week using callipers. Infusions were carried out 20–30 days after tumour implantation (see Extended Data Fig. 8c for tumour size). The maximum tumour volume permitted by Princeton IACUC for this tumour type is 2,000 mm3 and no mice in this study reached this tumour size (Extended Data Fig. 8c).
Flank NSCLC tumours
Cell line was established as described in ref. 57. from LSL-KrasG12D/+; Trp53fl/fl mice inoculated intranasally with Cre-expressing adenovirus. Cells were grown in DMEM with 10% fetal bovine serum. For tumour implantation, cells were grown to 70% confluency, then trypsinized and resuspended at 2 × 106 cells per ml in PBS, and 100 μl was injected subcutaneously into the flank of C57/Bl6 mice. Tumour growth was measured as described above. Infusions were carried out 25–35 days after tumour implantation. The maximum tumour volume permitted by Princeton IACUC for this tumour type is 2,000 mm3 and no mice in this study reached this tumour size.
Flank PDAC tumours
Syngeneic pancreatic adenocarcinoma allograft tumours were established by collecting tumours from Pdx1-cre;LSL-KrasG12D/+;LSL-Trp53R172H/+ mice, mincing the tissue into small particles, suspending in DMEM medium, mixing with Matrigel (Corning 354234) at a 1:1 (v/v) ratio and injecting 200 μl subcutaneously into flank of C57Bl/6 recipient mice. Allograft tumours were passaged up to two times in C57Bl/6 syngeneic recipient mice before implantation for use in experiments. Tumour growth was measured as described above. Infusions were carried out 10–18 days after tumour implantation. The maximum tumour volume permitted by Princeton IACUC for this tumour type is 2,000 mm3 and no mice in this study reached this tumour size (Extended Data Fig. 7a).
T cell acute lymphocytic leukaemia model
Generation of NOTCH1-induced mouse primary T cell acute lymphocytic leukaemia and secondary transplantation into sublethally irradiated recipients was performed as previously described58. Leukaemia cells (1 × 106) were transplanted from primary recipients into sublethally irradiated (4.5 Gy) 9-week-old C57BL/6 secondary recipients that were precatheterized by Charles River Laboratories in the right jugular vein. The animals were monitored for signs of distress or motor function daily. Tracer infusions were carried out 9–10 days after leukaemia transplantation. In these experiments, metabolite concentrations were remeasured in the spleen of the control mice in parallel with leukaemia, and these concentration measurements were used specifically for the TCA flux determination for comparison with leukemic spleen. (Fig. 3g–h and Supplementary Tables 1, 2, 3, 4, 8 and 12 (‘controlSpleen_forLeukemia’)). Similarly, we measured [1-13C]2-deoxyglucose in the spleens of control mice in the same experiments to calculate glucose use flux for comparison with leukemic spleen (Fig. 5h).
MDA-MB-231-LM2 breast cancer xenograft model
MDA-MB-231-LM2 cells, which express luciferase, were derived from MDA-MB-231 cells as previously described59,60. Cells (5 × 104) were injected in 10 μl of PBS per side using a Hamilton syringe (Model 701, Hamilton, 80330) near the fourth pair of mammary glands in female NSG mice (Jackson Labs, 005557). Tumour growth was monitored by measuring the tumour dimensions once per week using callipers. Mice were catheterized, and nutrient infusions were performed to assess tumour and metastatic lung metabolism at 52 days after tumour cell implantation. The maximum tumour volume permitted by Princeton IACUC for this tumour type is 4,000 mm3 and no mice in this study reached this tumour size (tumour volumes and metastatic lung weights are shown in Extended Data Fig. 9a,b).
Sum159-M1A breast cancer xenograft model
Sum159-M1A cells, which express luciferase, were derived from Sum159 cells61. Cells (5 × 104) were injected in 10 μl of PBS per side using a Hamilton syringe (Model 701, Hamilton, 80330) near the fourth pair of mammary glands in female NSG mice (Jackson Labs, 005557). Tumour growth was monitored by measuring the tumour dimensions once per week using callipers. Mice were catheterized, and nutrient infusions were performed to assess tumour and metastatic lung metabolism at 36–37 days after tumour cell implantation. The maximum tumour volume permitted by Princeton IACUC for this tumour type is 4,000 mm3 and no mice in this study reached this tumour size (tumour volumes and metastatic lung weights are shown in Extended Data Fig. 9a,b).
Bioluminescence imaging of breast cancer xenograft models
Bioluminescence imaging of the lungs of mice bearing one of the two breast cancer xenograft models was performed by retroorbital injection of luciferin (Goldbio, LUCK-10G) followed by euthanasia, dissection and imaging using the Xenogen IVIS-200 System (Perkin Elmer).
Jugular vein catheterization
Aseptic surgical techniques were used to place a catheter (Instech, C20PV-MJV1301, 2 French, 10 cm) in the right jugular vein and to connect the catheter to a vascular access button (Instech, VABM1B/25, 25 gauge, one-channel button) implanted under the back skin of the mouse. Mice were allowed to recover from surgery for at least 5 days before tracer infusion. For leukaemia experiments only, mice were purchased with jugular vein catheters implanted by Charles River Laboratories.
Lactate primed infusion to measure TCA flux
[U-13C]l-Lactate tracer (98% 13C, 20 w/w% solution, CLM-1579, Cambridge Isotope Laboratories) was diluted to 1.67% (12-fold) in sterile water (not saline) to match the osmolarity of blood. This tracer was stored at 4 °C until the day of the experiment. Jugular-vein-catheterized mice were fasted by switching to a fresh cage with no food at 09:00. Around 13:00, the mice were connected to the infusion line with a swivel and tether (Instech, swivel, SMCLA; line, KVABM1T/25) and infusion pump (SyringePump, NE-1000), with the infusate advanced through the tubing to the point of connection with the mouse. Before attaching the line, each mouse was confirmed to have blood backflow through the jugular vein catheter, indicating that infused tracer would enter directly into the mouse bloodstream, and the mice were weighed to calculate the tracer infusion rate. Each mouse was left in a cage connected to a line for 1–2 h to acclimatize. Note that minimizing stress in the experiment is key to reproducing results; the animals should be in a quiet room for the infusion and should not be handled between line attachment and euthanasia, especially including no tail blood sampling. Around 14:30–15:30, infusion was initiated: a prime dose of 13 μl (to clear the mouse catheter up to jugular vein—this volume may vary depending on the surgeon, so it is best to measure after surgery if possible) + 0.48 μl per gram mouse weight was provided over 30 s, and then the infusion rate was slowed to 0.3 μl min−1 per gram mouse weight. At the desired timepoint, the mice were euthanized quickly by cervical dislocation, and the tissues were collected as quickly as possible (in 5 min or less) and freeze-clamped using a liquid-nitrogen-cooled Wollenberger clamp. Tissues were stored at −80 °C until processed.
Tissue sampling to measure metabolite concentrations
Mice were fasted by switching to a fresh cage with no food at 09:00. Between 15:00 and 17:00, each mouse was quickly euthanized by cervical dislocation, and tissues were sampled in 3 min or less (no more than 8 tissues were sampled per mouse) and freeze-clamped using a liquid nitrogen-cooled Wollenberger clamp. Tissues were stored at −80 °C until processed. In one quality-control experiment, tissues were collected after waiting 5 min after euthanasia to take the first tissue (Extended Data Fig. 2). Note that ‘quadriceps’ in figures represents collection of vastus medialis muscle.
Glutamine primed infusion to measure TCA flux
[U-13C]Glutamine (99% purity, CLM-1822, Cambridge Isotope Laboratories) was diluted to 100 mM in sterile saline. This tracer was made fresh for every experiment due to potential tracer instability. Infusion and tissue collection was performed as described above for [U-13C] lactate infusion, with the following modifications: a priming dose of 13 μl + 1.6 μl per gram mouse weight was provided in 60 s, and then the infusion rate was slowed to 0.1 μl min−1 per gram mouse weight.
[1-13C]2-Deoxyglucose-primed infusion to measure the glucose use flux
[1-13C]2-Deoxyglucose (99% purity, CLM-1824, Cambridge Isotope Laboratories) was diluted to 8.3 mM in sterile saline. This tracer was stored at 4 °C until the day of the experiment. Infusion was performed as described above, with the following modifications: a priming dose of 13 μl (to clear mouse catheter up to jugular vein) was provided in 30 s, and then the infusion rate was slowed to 0.3 μl min−1 per gram mouse weight. At the desired timepoint, the mice were euthanized quickly by cervical dislocation, and tissues were collected as quickly as possible (in 5 min or less) and freeze-clamped using a liquid-nitrogen-cooled Wollenberger clamp. Tissues were stored at −80 °C until processing. In one quality-control experiment, tissues were collected after waiting 10 min after euthanasia to take the first tissue (Extended Data Fig. 5d).
In the colon, there is a peak at the m/z of [1-13C]2-deoxyglucose phosphate in uninfused tissues, precluding measurement of glucose use using this tracer (Extended Data Fig. 5e). Instead, for the colon, [U-13C]2-deoxyglucose (Omicron Biochemicals, GLC-107) was infused instead (also at 8.3 mM in sterile saline, 13 μl priming dose for 30 s, then 0.3 μl min−1 per gram mouse weight, as for [1-13C]2-deoxyglucose).
[U-13C]Valine infusion to measure protein synthesis flux
[U-13C]Valine (99% purity, CLM-2249, Cambridge Isotope Laboratories) was diluted to 20 mM in sterile saline. This tracer was stored at 4 °C until the day of the experiment. Infusion and tissue collection was performed as described above, with the following modifications: an infusion of 0.1 μl min−1 per gram mouse weight for 2, 3 or 4 h (no priming dose).
Blood enrichment sampling in double catheterized mice
Arterial blood sampling in double-catheterized mice allows measurement of blood without touching the mice at the time of sampling, minimizing stress and consequent changes in metabolite levels and tracer enrichments. Therefore, we measured blood enrichment of lactate from [U-13C]lactate primed infusion, and concentrations of [1-13C]2-deoxyglucose from infusions of that metabolite, in double-catheterized mice (in separate experiments from tissue measurements). This allowed us to establish a primed infusion for lactate that achieved steady-state labelling quickly without overshooting or markedly perturbing metabolite levels, and we used circulating lactate labeling measured in this manner for all modeling and TCA flux determination. Infusions were performed as described above, but in mice purchased from Charles River Laboratory with both carotid artery and jugular vein catheters. In that case, the infusion line used was for double-catheterized mice with two access sites (Instech, swivel, SMCLA; line, KVABM1T/25; second line and double-channel button, VABM2T/25GCY; 25G tubing, VAHBPU-T25; pinport for sampling from arterial catheter, PNP3F25R).
Blood was sampled from the arterial catheter at timepoints after the start of infusion using a capillary blood collection tube (Sarstedt, 16.440.100) and a pinport-to-tube connector (Instech, PNP3MS). Before and after sampling, the arterial catheter line was flushed using a syringe and syringe-to-pinport connector (Instech PNP3M) with heparin-saline (1:50 heparin solution made with heparin SAI HGS-10). Blood was placed on ice, then centrifuged after all of the samples were collected at 4 °C, 14,000g for 10 min. Serum was moved to another tube and stored at −80 °C.
For measuring blood glucose concentration, the same fasting and sampling procedure was performed in double-catheterized mice but without any infusion.
[U-13C]Glucose infusion to measure whole-body glucose use
[U-13C]Glucose (99% purity, CLM-1396, Cambridge Isotope Laboratories) was diluted to 200 mM in sterile saline. This tracer was stored at 4 °C until the day of experiment. Infusion was performed using double-catheterized mice as described above, with the following modifications: infusion of 0.1 μl min−1 per gram mouse weight for 2.5 h (no priming dose).
Blood and tissue processing and extraction
Throughout processing until extraction, tissues were kept buried in dry ice, or in metal racks surrounded by dry ice. Tissues were ground into powder using the Retsch CryoMill, in 2-ml locking microcentrifuge tubes with grinding balls such as Fisher Scientific NC1419150. Tissue powder was weighed (5–20 mg in dry-ice-precooled microcentrifuge tubes), and tissues were extracted by vortexing in 40× volumes precooled acetonitrile/methanol/water (40%/40%/20%, v/v/v), then left on water ice over dry ice for 10 min. Then the solution was centrifuged at 4 °C, 14,000g for 25 min, moved to a new tube, and then centrifuged again at 4 °C, 14,000g for 25 min, to remove any particulates. Then extract was moved to MS vials (Thermo Fisher Scientific, 200046; caps, Thermo Fisher Scientific, 501313) for measurement.
For blood samples, blood was kept on ice for up to 60 min after sampling, then centrifuged at 4 °C, 14,000g for 10 min. The serum fraction was transferred to another tube and stored at −80 °C. For MS, 2–3 μl of serum was extracted in 50 volumes methanol, then centrifuged at 4 °C, 14,000g for 20 min, and then transferred to a MS vial for measurement.
To prepare serum samples to measure [1-13C]2-deoxyglucose concentration, the samples were phosphorylated using purified hexokinase (Sigma-Aldrich, H4502) according to the protocol described in ref. 62. [U-13C]2-deoxyglucose (Omicron Biochemicals, GLC-107) was phosphorylated using the same approach, added at 300 μM to the reaction mixture. Serum and standard (fivefold diluted to 60 μM) were mixed and extracted in methanol (3 μl serum + 3 μl standard + 144 μl methanol).
To prepare tissues to measure [1-13C]2-deoxyglucose phosphate concentration, a known concentration of [U-13C]2-deoxyglucose (Omicron Biochemicals, GLC-107) was phosphorylated using the protocol described in ref. 62. This reaction mixture was then stored at −20C and used as an internal standard for absolute quantification when extracting tissues: thawed standard was mixed into extraction buffer at a concentration of 0.25 μM (that is, corresponding to 10 μM tissue 2-deoxyglucose phosphate, as tissues were extracted in 40× volume extraction buffer). To measure glucose use in the colon, as we infused [U-13C]2-deoxyglucose due to colon tissue background as described above, we performed MS analysis of [U-13C]2-deoxyglucose infused colon samples along with other tissues which were extracted with [U-13C]2-deoxyglucose phosphate standard, and used those as an external standard to quantify the concentration in colon.
To measure glucose use rate in the blood cells, tail blood was sampled from mice infused with [1-13C]2-deoxyglucose. Blood was extracted at a 1:40 dilution in extraction buffer including 0.25 μM [U-13C]2-deoxyglucose phosphate standard, similarly to approach used to measure tissue glucose use.
To measure tissue metabolite concentrations, standards were made by resuspending 13C- or 15N-labelled metabolites (Cambridge Isotope Laboratories, [U-15N]glutamate and [U-15N]aspartate from algal amino acid mix NLM-2161; [U-13C]α-ketoglutarate, CLM-4442; [U-13C]citrate, CLM-9021; [U-13C]malate, CLM-8065; [U-13C]succinate, CLM-1571) in water (at concentrations of 3,040 μM glutamate, 1,980 μM aspartate, 515 μM α-ketoglutarate, 2,693 μM citrate, 483 μM malate, 1,365 μM succinate). Standards were mixed into 40:40:20 (acetonitrile:methanol:water) extraction buffer at 1:100 concentration, and tissue powder samples were extracted in 100× volume extraction buffer on dry ice over water ice, and then processed as described above.
To measure the glucose concentration in arterial blood, standards were made by resuspending 13C-labelled glucose (Cambridge Isotope Laboratories, CLM-1396) in water at a known concentration and mixing standard into methanol extraction buffer, and the blood serum samples were extracted in extraction buffer on water ice over dry ice, then processed as described above.
To measure protein enrichment from [U-13C]valine infusion, tissues were ground using the Retsch CryoMill, and 5 mg of tissue powder was weighed into Eppendorf tubes. Free tissue amino acids were removed using methanol–chloroform extraction as follows: 400 μl methanol, 200 μl chloroform and 300 μl water were added to each Eppendorf tube, vortexing after each addition. The tubes were centrifuged at 4 °C and 14,000g for 10 min, and the top layer was discarded. The remaining sample was washed twice with 500 μl methanol, centrifuging at 4 °C and 14,000g for 10 min between each wash. Finally, the supernatant was removed and the pellet was air dried. Then, 250 μl 6 M hydrochloric acid was added and the tubes were incubated overnight at 98 °C. A total of 10 μl was moved to a new tube, then dried under nitrogen gas, resuspended in 500 μl methanol and measured using MS. Each [U-13C] valine-infused tissue sample was also measured without methanol–chloroform extraction using the conventional sample-preparation method to measure free valine enrichment in the tissue.
MS analysis
Water-soluble metabolite measurements were obtained by running samples on the Q Exactive Plus hybrid quadrupole-orbitrap mass spectrometer (Thermo Fisher Scientific) coupled with hydrophilic interaction chromatography (HILIC). An XBridge BEH Amide column (150 mm × 2.1 mm, 2.5 μM particle size, Waters) was used. The gradient using solvent A (95%:5% H2O:acetonitrile with 20 mM ammonium acetate, 20 mM ammonium hydroxide, pH 9.4) and solvent B (100% acetonitrile) was as follows: 0 min, 90% B; 2 min, 90% B; 3 min, 75% B; 7 min, 75% B; 8 min, 70% B, 9 min, 70% B; 10 min, 50% B; 12 min, 50% B; 13 min, 25% B; 14 min, 25% B; 16 min, 0% B, 20.5 min, 0% B; 21 min, 90% B; 25 min, 90% B. The flow rate was 150 μl min−1 with an injection volume of 10 μl and a column temperature of 25 °C. The MS scans were in negative-ion mode with a resolution of 140,000 at m/z 200. The automatic gain control target was 5 × 106 and the scan range was m/z 75–1,000. Xcalibur (v.4.3; Thermo Fisher Scientific) was used to collect raw data.
To measure [1-13C] or [U-13C]2-deoxyglucose phosphate, the method above was supplemented with the following SIM scan to boost the signal-to-noise ratio for these analytes: during minutes 11–15 of the method, a 240–255 m/z range SIM scan was performed.
MALDI–IMS
Primed infusion of [U-13C]lactate was performed as described above for the length of time indicated in the figure. Tissues were quickly dissected and snap-frozen on dry ice, then stored intact at −80 °C until matrix-assisted laser desorption/ionization (MALDI)–IMS analysis. Tissues were transferred to a cryostat (Leica, CM3050S) at −20 °C and left to thermally equilibrate for 45–60 min, after which approximately 10-μm-thick sections were collected, thaw-mounted on indium tin oxide (ITO)-coated glass slides (Bruker Daltonics), and desiccated under vacuum for 10–15 min. Alternating serial sections for immunohistochemistry and immunofluorescence were collected on standard glass slides.
Desiccated tissue sections mounted on ITO glass slides were sprayed using an HTX TM-Sprayer (HTX Technologies) with 10 mg ml−1 N-(1-naphthyl)ethylenediamine dihydrochloride (NEDC, Sigma-Aldrich, 222488) dissolved in 70%:30% methanol:water. The sprayer temperature was set to 70 °C, with a flow rate of 0.1 ml min−1, velocity of 1,200 mm min−1, track spacing of 2 mm, pressure of 10 psi and a gas flow rate of 3 l min−1. Ten passes of the matrix were applied to slides with 10 s of drying time between each pass.
For MALDI–Fourier-transform ion cyclotron resonance (FTICR) measurements, the matrix-coated slides were immediately loaded into a slide adapter (Bruker Daltonics) and then into a solariX XR FTICR mass spectrometer equipped with a 9.4 T magnet (Bruker Daltonics) operated at a resolving power of 91,000 at m/z 400 and a transient length of 0.5592 s. Mass accuracy was calibrated within 1 ppm by using 1 mg ml−1 arginine solution before starting the run. Lock masses of m/z 124.0068 (taurine), m/z 133.0136 (malate) and m/z 145.0611 (glutamate) were used during the negative-ion mode run because of their high abundance in the analysed tissues. The laser focus was set either to ‘small’ or ‘minimum’, which were operated at x–y raster widths of 50 μm and 20 μm, respectively, using Smartbeam-II laser optics. A spectrum was accumulated from 200 laser shots at 1,200 Hz in the range 70 ≤ m/z ≤ 800, and the ions were accumulated using the ‘cumulative accumulation of selected ions mode’ (CASI) within an m/z range of 70–250 before being transferred to the ICR cell for a single scan.
Analysis of images was performed in IsoScope, a program written in MATLAB63; the code is available for non-commercial use at GitHub (https://github.com/xxing9703/Isoscope). This software allows region of interest selection and intensity determination of different labelled isotopomers of detected metabolites.
Haematoxylin and eosin staining after MALDI–IMS
Staining was performed on same section as MALDI–IMS after the scan. Matrix was washed off by submerging the slide in ice-cold methanol, then fixed with fresh methanol for 5 min. The slide was washed with PBS three times and water, then submerged in Meyer and Briggs haematoxylin (Sigma-Aldrich, MHS32) for 15 min. The slide was then transferred to a 15 min warm water soak, then dehydrated in 95% ethanol for 30 s, incubated with eosin (Sigma-Aldrich, HT110332) for 1 min, then dehydrated again stepwise with 95% and 100% ethanol. After a 2 min xylene wash, slides were mounted using Cytoseal 60 mounting medium (Thermo Fisher Scientific, 8310–4) and imaged using a Hamamatsu Nanozoomer with the NDP.view2 (Hamamatsu) software.
Immunofluorescence analysis
At the time of collection, tumour samples were snap-frozen on dry ice for 30 min and stored at −80 °C until sectioning. Tumour sections (10 μm thickness) were collected on a cryomicrotome (Leica, CM3050S) and mounted onto slides. The slides were brought to room temperature and fixed with 4% paraformaldehyde, then washed with PBS and then PBS + 0.1%Triton X-100. The slides were stained using Lotus Tetragonolobus Lectin-fluorescein (Vector Laboratories, FL-1321) in combination with the M.O.M. Immunodetection Kit (Vector Laboratories, BMK-2202) according to the manufacturer’s protocol. The slides were counterstained with DAPI and mounted using Fluoromount-F (Thermo Fisher Scientific, 00–4958-02), and then imaged using the Cytation 5 microscope.
Proteomics
Mice were euthanized quickly by cervical dislocation, and tissues were collected as quickly as possible (in 5 min or less) and freeze-clamped using a liquid-nitrogen-cooled Wollenberger clamp. Tissues were stored at −80 °C until processed. Tissues were ground to powder using a Retsch Cryomill, and then 5 mg of tissue powder per sample was collected in 100 mM HEPES pH 7.2 and 2% SDS64. To reduce disulfides, dithiothreitol (DTT) (500 mM in water) was added to a final concentration of 5 mM (20 min, 60 °C). The samples were cooled to room temperature and cysteines were alkylated by the addition of N-ethyl maleimide (NEM, 1 M in acetonitrile) to a final concentration of 20 mM followed by incubation for 20 min at room temperature. Then, 10 mM DTT (500 mM stock, water) was added at room temperature for 10 min to quench any remaining NEM. A paramagnetic bead-based protein protocol was performed for protein clean-up65. Hydrophilic and hydrophobic Speed-Bead Magnetic Carboxylate (Cytiva) bead mixture was washed twice with HPLC-grade water. After the last wash, the beads were resuspended in water to final concentration of 50 μg l−1. The cell lysate was combined with the bead slurry to a bead to protein ratio of 15 μg:1 μg and ethanol was added to 50% ethanol concentration. The samples were then incubated on a thermomixer at 1,400 rpm, for 1 h at 24 °C. The supernatant was next removed using a magnetic rack. The mixture was washed three times with 200 μl of 80% ethanol. The samples were then diluted to a final volume of 100 μl with 2 M guanidine chloride in 200 mM EPPS pH 8.5 for overnight digestion with 20 ng μl−1 Lys-C (Wako) at room temperature. Subsequently, the samples were diluted to 0.5 M guanidine chloride in 200 mM EPPS pH 8.5 for overnight digestion with an additional 20 ng μl−1 Lys-C and 10 ng μl−1 trypsin (Promega) at 37 °C overnight. The digested samples were dried using a vacuum evaporator at room temperature and taken up in 200 mM EPPS pH 8.0. Then, 15 μg of the total peptides from each condition was labelled with 75 μg of TMTpro for 2 h at room temperature. Labelled samples were quenched with 0.5% hydroxylamine solution. Samples from all of the conditions were combined into one tube, acidified to a pH of <2 with phosphoric acid (HPLC grade, Sigma-Aldrich) and cleared by centrifugation at 20,000g at room temperature for 10 min. The supernatants were dried using a vacuum evaporator at room temperature. Dry samples were taken up in HPLC-grade water and stage-tipped66 and resuspended in 1% formic acid to 1 μg μl−1 for MS analysis. Approximately 3 μg of the sample was analysed using LC–MS. LC–MS experiments were performed using the nLC-1200 HPLC (Thermo Fisher Scientific) system coupled to an Orbitrap Fusion Lumos (Thermo Fisher Scientific). Peptides were separated on an Aurora Series emitter column (25 cm × 75 μm inner diameter, 1.6 μm C18) (IonOpticks), held at 60 °C during separation by a custom built column oven. Separation was achieved by applying a 12–35% acetonitrile gradient in 0.125% formic acid and 2% DMSO over 180 min at 350 nl min−1. Electrospray ionization was enabled by applying a voltage of 2.6 kV through a MicroTee at the inlet of the microcapillary column. The samples were measured using the Orbitrap Fusion Lumos using the TMTpro-SPS-MS3 method67.
MS data analysis
All metabolomics LC–MS data were analysed using El-Maven (v.0.6.1). For infusion experiments involving 13C labelling, outputs were corrected for natural 13C abundance using the accucor package in R68 (v.0.3.0).
For measuring metabolite concentrations in tissues, we used a mixture of 13C- and 15N-labelled standards. We developed a software package in MATLAB to perform and visualize natural isotope correction for MS data labelled with a mixture of 13C and 15N (https://github.com/xxing9703/MIDview_isocorrCN). This package requires that the instrumental resolution is high enough to fully resolve all the detectable 13C- and 15N-labelled peaks of a given compound, with a total number of possible peaks :
| (2) |
where and represent the number of carbon atoms and of nitrogen atoms in the compound respectively. In brief, a correction matrix of size is constructed to relate the measured isotope labelling pattern before correction to the isotope labelling pattern after correction :
| (3) |
Each matrix element represents the jth labelled fraction contributing to the ith measured mass fraction. The impurity matrix is constructed to take into account impurities in 13C and 15N tracers (a value reported by the tracer manufacturer: typically, 99% purity is used). Finally, we solve for by non-negative least-squares fitting using the lsqnonneg solver in MATLAB.
Non-stationary metabolic flux analysis to calculate TCA fluxes
TCA fluxes were determined by fitting a predicted labelling distribution from a reduced isotopomer model describing the dynamic labelling propagation23 (a full description is provided in the Supplementary Note, input and output files are provided in Supplementary Tables 1–7, the code is available at GitHub (https://github.com/weilandtd/tca_fluxes) or at Zenodo (https://zenodo.org/record/7328216#.Y3vnROzMKEs)). The reduced isotopomer model is constructed from a minimal reaction network of the TCA cycle, pyruvate carboxylase, malic enzyme, phosphoenolpyruvate carboxykinase, aspartate and glutamate transaminase around 8 mass balances: lactate/pyruvate pool (pyr), acetyl-CoA (accoa), citrate/isocitrate (cit), α-ketoglutarate (akg), glutamate (glu), succinate (succ), malate (mal), oxaloacetate (oaa) and aspartate (asp) (Extended Data Fig. 3a). From the reaction network and the atom mapping of the individual reactions, we compute all of the possible isotopomers that can be produced from a specified input tracer (that is, [U-13C]lactate or [U-13C]glutamine). Assuming that condensation reactions between two labelled molecules is very unlikely, we construct a reduced network that describes the interconversion of the most likely isotopomers (this simplification does not significantly alter calculated TCA fluxes; Extended Data Fig. 3d). The isotopomer interconversion network is then used to derive a set of ordinary differential equations describing the time evolution of the enrichment of the individual isotopomers for the case that the system is in a concentration (but not isotopic) steady state. We then find the fluxes that best explain the observed labelling dynamics by minimizing least-squares residuals between the measured and simulated time-dependent isotope enrichments for a fixed set of metabolite concentrations. To solve the optimization problem, we use the Levenberg–Marquardt algorithm69,70. The experimental data used to fit the model parameters were the M+1,2,3 isotope forms of tissue glutamate, malate, aspartate and succinate resulting from tissue sampling at different timepoints after primed tracer infusion, blood labelling of tracer metabolite (that is, lactate or glutamine), and tissue concentrations of glutamate, malate, aspartate, succinate, α-ketoglutarate and citrate/isocitrate. To determine the error of the flux estimate we solve the optimization problem with different initial guesses and tissue concentrations drawn from a normal distribution. Subsequently, we estimate the median flux and its 95% confidence interval by bootstrapping: we randomly resample the best 20 fits from 2,000 parameter estimates 100 times.
For certain tissues, later timepoints were excluded from the model because they exhibited a slow secondary increase after reaching an early plateau. For brown adipose, diaphragm and kidneys, timepoints over 30 min were excluded; for the intestine and white adipose, timepoints over 50 min were excluded. Exclusion of these datapoints consistently decreased the Bayesian information criterion by increasing the likelihood, suggesting that these points overconstrain the model (Extended Data Fig. 3f).
For all tissues and tumours, at least 6 and typically 12 different mice were used for timepoints of labelling after tracer infusion (n values for each experiment are shown in Extended Data Fig. 10c and the figure legends), while each metabolite concentration was measured in at least 3 and typically 4 replicates.
TCA flux calculation using simple M+2 labelling and total TCA pool approach
Note that this approach was used only in Extended Data Fig. 4b. For [U-13C]lactate infusion, the M+2-labelled fractions of glutamate, malate and succinate were averaged for each sample. The first-order labelling rate constant k was calculated using nonlinear fitting of a single exponential-decay function using the R nls() function. To calculate the TCA pool size, concentrations of glutamate, malate, succinate, aspartate, α-ketoglutarate and citrate (calculated by internal standard as described above) were summed for each organ. TCA flux was calculated as the product of the labelling constant k and the TCA pool size. Note that TCA flux in the brain could not be measured using [U-13C]lactate, as glucose is the main brain TCA feedstock71.
This flux quantification approach assumes that TCA metabolites in a tissue are well-mixed and not compartmentalized and precursors to TCA (for example, serum lactate and tissue lactate) label much faster than TCA metabolites. If this last assumption is not met, the observed labelling will be slowed by the rate of precursor labelling, leading to flux underestimation.
Calculation of tissue oxygen consumption flux
To calculate oxygen consumption from TCA flux, we used
| (4) |
where is rate of oxygen consumption and is rate of TCA cycle. When lactate is oxidized, it yields 5 NADH (from lactate dehydrogenase, pyruvate dehydrogenase, isocitrate dehydrogenase, α-ketoglutarate dehydrogenase and malate dehydrogenase) and 1 FADH2 (from succinate dehydrogenase). When a two-carbon unit of fatty acid is oxidized, it yields 4 NADH (from fatty acid oxidation, isocitrate dehydrogenase, α-ketoglutarate dehydrogenase and malate dehydrogenase) and 2 FADH2 (from fatty acid oxidation and succinate dehydrogenase). Thus, each molecule of nutrient contributes six reducing equivalents per TCA turn (that is, per acetyl-CoA consumed). Each reducing equivalent results in consumption of 1/2 O2 molecule in the electron-transport chain, so each TCA turn leads to around 3 O2 molecules consumed.
Glucose use calculation
To calculate glucose use flux, the [1-13C]2-deoxyglucose phosphate concentration in tissues was measured at timepoints from 0 to 15 min of [1-13C]2-deoxyglucose intravenous infusion. The approach assumes that [1-13C]2-deoxyglucose is infused in trace amounts that do not inhibit endogenous glucose metabolism and, indeed, the peak 2-deoxyglucose concentration measured in the blood was around 90 μM, or around 86-fold lower than the blood glucose concentration (Fig. 2b and Extended Data Fig. 5b). Each healthy tissue was measured from at least n = 2 mice at 5, 7.5, 10, 15 min of [1-13C]2-deoxyglucose infusion (with at least one zero timepoint); tumours were measured from at least n = 2 mice at 5, 10 and 15 min (for GEMM NSCLC, one of the 5 min samples was missing). As brown adipose demonstrated saturation of 2-deoxyglucose phosphate after 10 min, the 15 min timepoint was omitted for this tissue only (Extended Data Fig. 5c). In the colon, [1-13C]2-deoxyglucose phosphate displayed a poor signal-to-noise ratio (Extended Data Fig. 5e) so, instead, [U-13C]2-deoxyglucose infusion timepoints were used to calculate glucose use.
The [1-13C]2-deoxyglucose concentration in arterial blood was measured using double-catheterized mice, and the integrated concentration over time was calculated. The slope of the [1-13C]2-deoxyglucose phosphate tissue concentration versus the integral of blood [1-13C]2-deoxyglucose concentration with respect to time was calculated using linear fitting in R (equation (1)). The glucose use flux for each tissue was calculated as the slope of this line multiplied by the blood glucose concentration (7.7 mM in mice fasted from 09:00 to 15:30; Extended Data Fig. 5b,f).
Note that glucose use flux measured by 2-deoxyglucose infusion is similar to glycolysis flux, but strictly measures the flux of circulating glucose into the glycolysis, oxidative pentose phosphate, glycogen synthesis and protein glycosylation pathways. Glucose flux to protein glycosylation and the pentose phosphate pathway are small relative to glycolysis26,72, while in the fasting non-exercising state, glycogen synthesis is likely to be low73.
Whole-body metabolism calculations
To calculate the contribution of each tissue to whole-body TCA flux or glucose flux, the measured flux was multiplied by the fraction of body mass made up of each tissue, using tissue fractional masses from previous studies74–77. We estimated that total body muscle consisted of 70% white muscle fibres (similar to quadriceps/vastus lateralis and gastrocnemius, majority type IIB/IID/IIX fibres) and 30% red muscle fibres (similar to soleus, majority type I and IIA fibres)76,77. Red muscle TCA and glucose use flux were estimated as soleus fluxes. White muscle TCA and glucose use flux were estimated using the means of quadriceps and gastrocnemius fluxes.
Lactate consumption/production calculation
To estimate whether a tissue consumed or released net lactate, we estimated net lactate production as two times the glucose use flux. We calculated net lactate consumption in the TCA cycle as the TCA flux multiplied by the fractional contribution of lactate to the TCA cycle, which is the pseudo-steady-state labelling of TCA metabolites from [U-13C]lactate infusion (Extended Data Fig. 6a) divided by the blood lactate labelling from [U-13C]lactate infusion (Extended Data Fig. 3c).
ATP production rate calculation
ATP production from glycolysis was calculated as 2 ATP per glucose consumed (we did not consider ATP derived from the NADH from the GAPDH reaction as, in aerobic glycolysis, this is consumed by the lactate dehydrogenase reaction). ATP production from the TCA cycle was calculated as follows: for lactate, 1 ATP equivalent (succinyl CoA synthetase reaction), 5 NADH (lactate dehydrogenase, pyruvate dehydrogenase, isocitrate dehydrogenase, α-ketoglutarate dehydrogenase and malate dehydrogenase) and 1 FADH2 (succinate dehydrogenase). From one two-carbon unit of fatty acid, 1 ATP equivalent (succinyl CoA synthetase), 4 NADH (fatty acid oxidation, isocitrate dehydrogenase, α-ketoglutarate dehydrogenase and malate dehydrogenase) and two FADH2 (fatty acid oxidation and succinate dehydrogenase). One NADH generates approximately 2.5 ATP in the electron-transport chain, while one FADH2 generates approximately 1.5 ATP. Thus, for the two most dominant TCA substrates71, one TCA cycle turn generates either 14 or 15 ATP, so we estimated 14.5 ATP per TCA turn.
Protein synthesis rate calculation
To calculate protein synthesis rate, fractional enrichment of valine in protein was normalized to fractional enrichment of free valine in tissue from [U-13C]valine infusion. This fractional protein synthesis during the time of the infusion, which was 2–4 h depending on the experiment, was divided by the length of that infusion to yield fractional protein synthesis per hour.
Calculation of ATP cost of protein synthesis
To estimate the ATP cost of pancreas’s or pancreatic tumour’s measured protein synthesis rate, we used the following equation:
| (5) |
where is the rate of ATP use to synthesize protein (in units of micromoles ATP per minute per gram tissue), is the fractional synthesis rate of protein calculated from [U-13C]valine infusion (in units of min−1), is the fraction of tissue wet mass that consists of protein (0.15 for pancreas78), while (1/112) is the ratio of moles of amino acid used to make a gram of protein, as the mean amino acid molar mass is 112, and 4 is the number of ATP equivalents (including GTP) used to add one amino acid to a growing peptide chain.
Human tumour and healthy tissue gene expression analysis
RNA-seq data were downloaded from the Xena database (https://xenabrowser.net/)79 TCGA Target GTEX study (https://ucsc-xena.gitbook.io/project/how-do-i/tumour-vs-normal). The tissue type of interest was selected, then differential expression analysis was performed to generate a file of log2-transformed fold changes between tumour and healthy tissues. Then, the log2-transformed fold change in gene expression of a subset of genes belonging to a KEGG pathway representing a major ATP-using tissue function was examined (https://www.genome.jp/kegg/pathway.html)80 or, alternatively, the top two most significantly downregulated KEGG pathways in tumours were identified using Enrichr (https://maayanlab.cloud/Enrichr/)81.
Proteomics data analysis
MS peptide identification was performed essentially as previously described67,82,83. The MS data in the Thermo RAW format were analysed using the Gygi Lab software platform (GFY Core, v.3.8) licensed through Harvard University. For protein references, we used a fasta file with contaminants followed by human (Uniprot ID: UP000005640) followed by mouse (Uniprot ID: UP000000589). Only peptides that matched uniquely to one human (and not any mouse) protein were used, as the samples came from mice bearing human-derived xenograft tumours.
To identify mitochondrial-localized proteins that are involved in oxidative phosphorylation, we used the human MitoCarta3.0 list (https://www.broadinstitute.org/mitocarta/mitocarta30-inventory-mammal ian-mitochondrial-proteins-and-pathways).
Experimental sample sizes
A list of the number of independent mouse samples for each experiment is provided in Extended Data Fig. 10c. Each sample is an independent biological replicate.
Statistics
All t-tests used were two-tailed; the number of mice in every experiment is recorded in Extended Data Fig. 10c as well as each figure legend.
To compute two-sided t-tests for differences in glucose use fluxes, the s.d. of the slope of the tissue 2-deoxyglucose phosphate concentration versus the integrated serum [1-13C]2-deoxyglucose concentration with respect to time was calculated using the lm() function in R. The s.d. of the glucose use flux (the product of the slope and the blood glucose concentration) was computed as the sum of the per cent s.d.: the s.d. of the slope divided by the slope, plus the s.d. of serum glucose concentration divided by the mean serum glucose, all multiplied by the flux. The P value of a two-sided t-test comparing two glucose use fluxes was then computed using a Welch’s two-tailed t-test using the Welch–Satterthwaite equation (not assuming equal variances).
To compute two-sided t-tests for differences in ATP production fluxes, the s.d. was computed as the square root of the sum of squared s.d. of 2 × glucose use flux and 14.5 × TCA flux. The P value of a two-sided t-test comparing two ATP production fluxes was then computed using a Welch’s two-tailed t-test using the Welch–Satterthwaite equation (not assuming equal variances).
All values of linear correlation were computed using linear regression.
Figure construction
Graphs were created in Prism (v.9) and assembled into figures in Adobe Illustrator 2022. The mouse schematic in Fig. 4a was created using BioRender.
Extended Data
Extended Data Fig. 1 |. Kinetic primed [U-13C] lactate infusion.
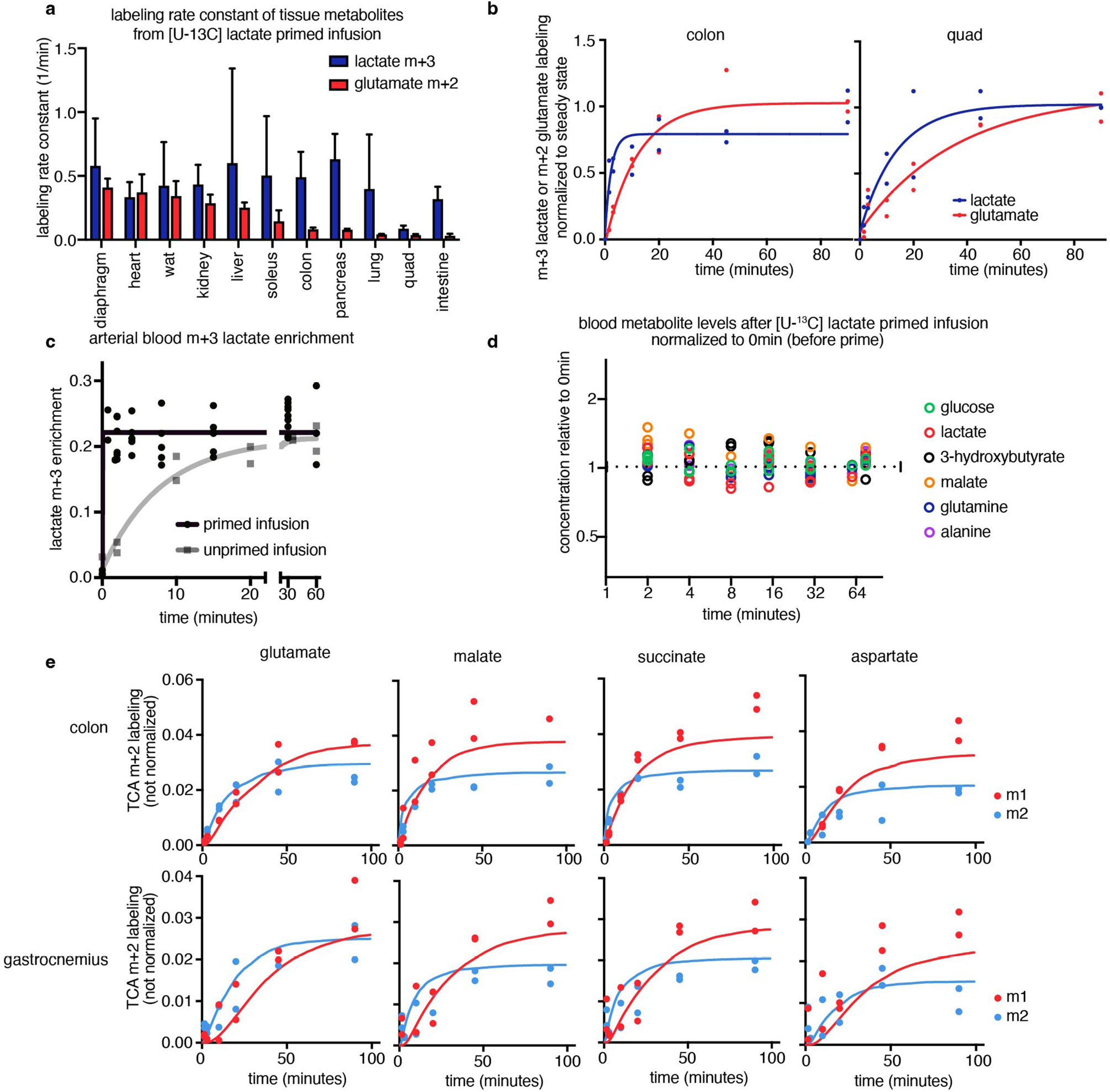
(a) Rate constant of m+3 tissue lactate or m+2 tissue glutamate labelling from [U-13C] lactate primed infusion, calculated by fitting an exponential curve, bars show mean +/− standard deviation. For accurate TCA flux measurement, tissue lactate labelling (blue bars) must be faster than TCA labelling (red bars), lactate primed infusion timepoints in n = 12 mice per tissue (except n = 19 for intestine and n = 17 for soleus). (b) M+3 tissue lactate and m+2 tissue glutamate labelling in U-13C] lactate primed infusion, n = 12 mice each. (c) Arterial blood m+3 lactate enrichment in primed [U-13C] lactate infusion reaches steady state in around 90 s, while blood m+3 lactate enrichment in [U-13C] lactate infusion without a priming bolus takes around 20 min to reach steady state (primed: n = 8 mice, 4,4,5,5,6,6,6,and 6 blood timepoints each; unprimed: n = 2 mice, 6 blood timepoints each). (d) [U-13C] lactate primed infusion does not alter any arterial blood metabolite levels more than 1.5x, n = 3 mice (7,7, and 6 timepoints measured per mouse respectively). (e) M+2 and m+1 labelling of glutamate, malate, succinate, and aspartate from [U-13C] lactate primed infusion in colon and gastrocnemius muscle (not normalized). Curves are model fits, n = 12 timepoints for each tissue, each timepoint for one tissue type represents a tissue from a different mouse.
Extended Data Fig. 2 |. Five-minute tissue harvesting delay after primed [U-13C] lactate infusion does not greatly alter TCA metabolite labelling or concentration.
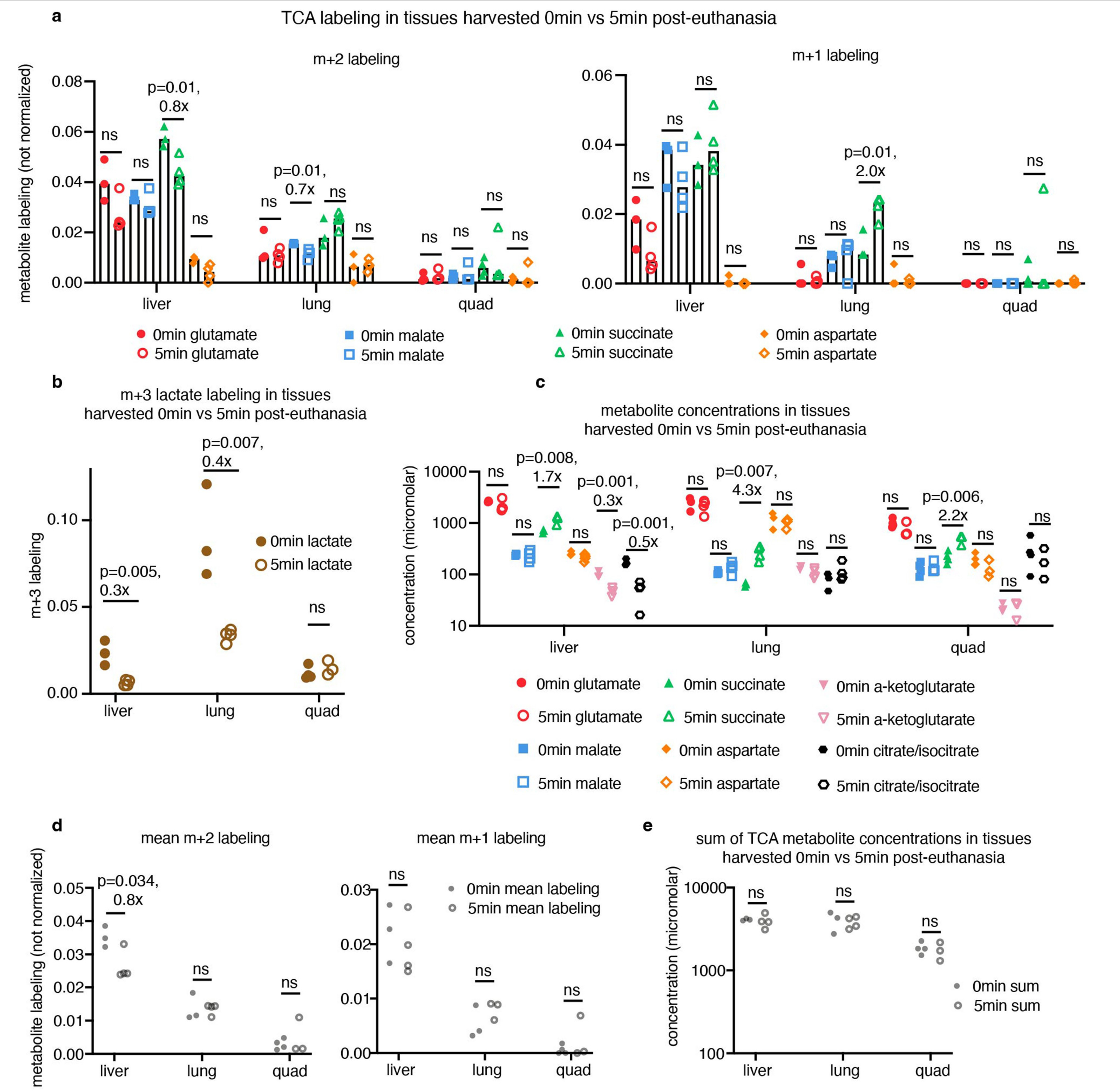
(a) TCA metabolite m+2 and m+1 labelling from primed [U-13C] lactate infusion in tissues harvested 0 or 5 min after euthanasia. (b) Tissue lactate m+3 labelling from same experiment as in (a). (c) Tissue TCA metabolite concentrations from the experiment in (a). (d) The mean m+2 and m+1 labelling of four TCA metabolites (glutamate, malate, succinate, aspartate) from the experiment in (a), each point represents the mean m+2 or m+1 labelling of four metabolites for one tissue from one mous e. (e) The sum of glutamate, malate, succinate, aspartate, citrate/isocitrate, and α-ketoglutarate concentrations from the experiment in (a), each point represents the sum of metabolite concentrations for one tissue from one mouse. All bar graphs show mean values, all t-tests are unpaired two-tailed t-tests; in all graphs, n = 3 mice for 0 min liver, 0 min lung, and 5 min quad; n = 4 for 0 min quad, 5 min liver, 5 min lung.
Extended Data Fig. 3 |. Non-stationary metabolic flux analysis (NMFA) model calculates in vivo tissue TCA fluxes.
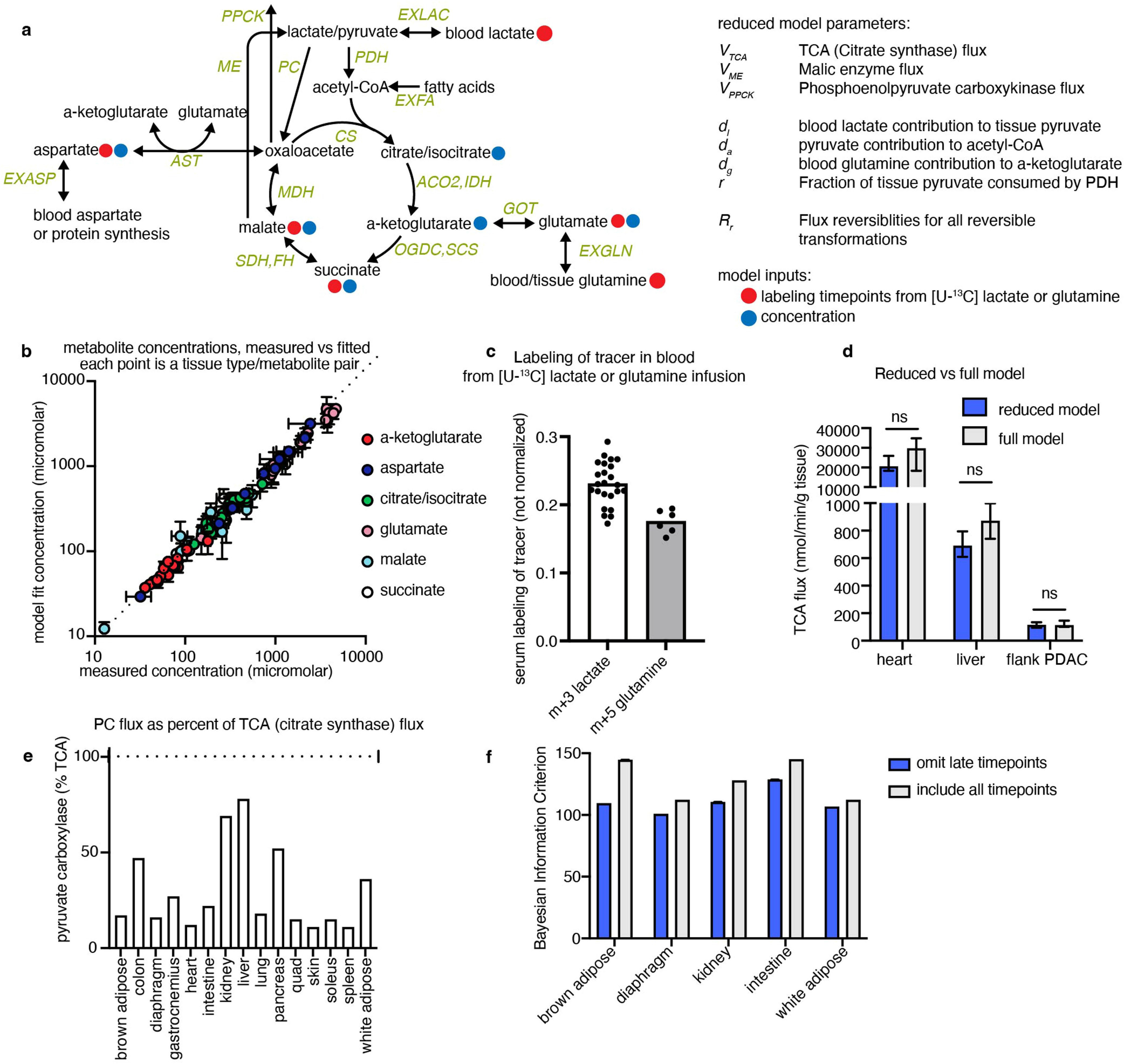
(a) Schematic of model structure for calculating TCA flux, indicating the concentrations and labelling timepoints used as input data. (b) Tissue TCA metabolite concentrations fitted by NMFA model vs. measured experimentally, n = 4 mice per measurement except n = 3 for diaphragm, each point is one metabolite from one healthy tissue. (c) Labelling of m+3 lactate or m+5 glutamine in arterial blood during [U-13C] lactate or glutamine primed infusions respectively, used as input data for TCA flux model, n = 3 mice with 8 blood timepoints each for lactate, n = 2 mice with 6 timepoints each for glutamine. (d) Including collisions of multiple labelled metabolites in the model (‘full model’) does not alter calculated TCA fluxes compared to model without including such collisions (‘reduced model’) (see Methods and Supplementary Note for description of models). (e) Calculated pyruvate carboxylase flux as a fraction of total TCA flux (citrate synthase flux). (f) Omitting some late [U-13C] lactate timepoints lowers (i.e. improves) Bayesian information criterion for certain tissues. Error bars show mean +/− standard deviation, p-values from two-tailed t tests.
Extended Data Fig. 4 |. Healthy tissue TCA fluxes.
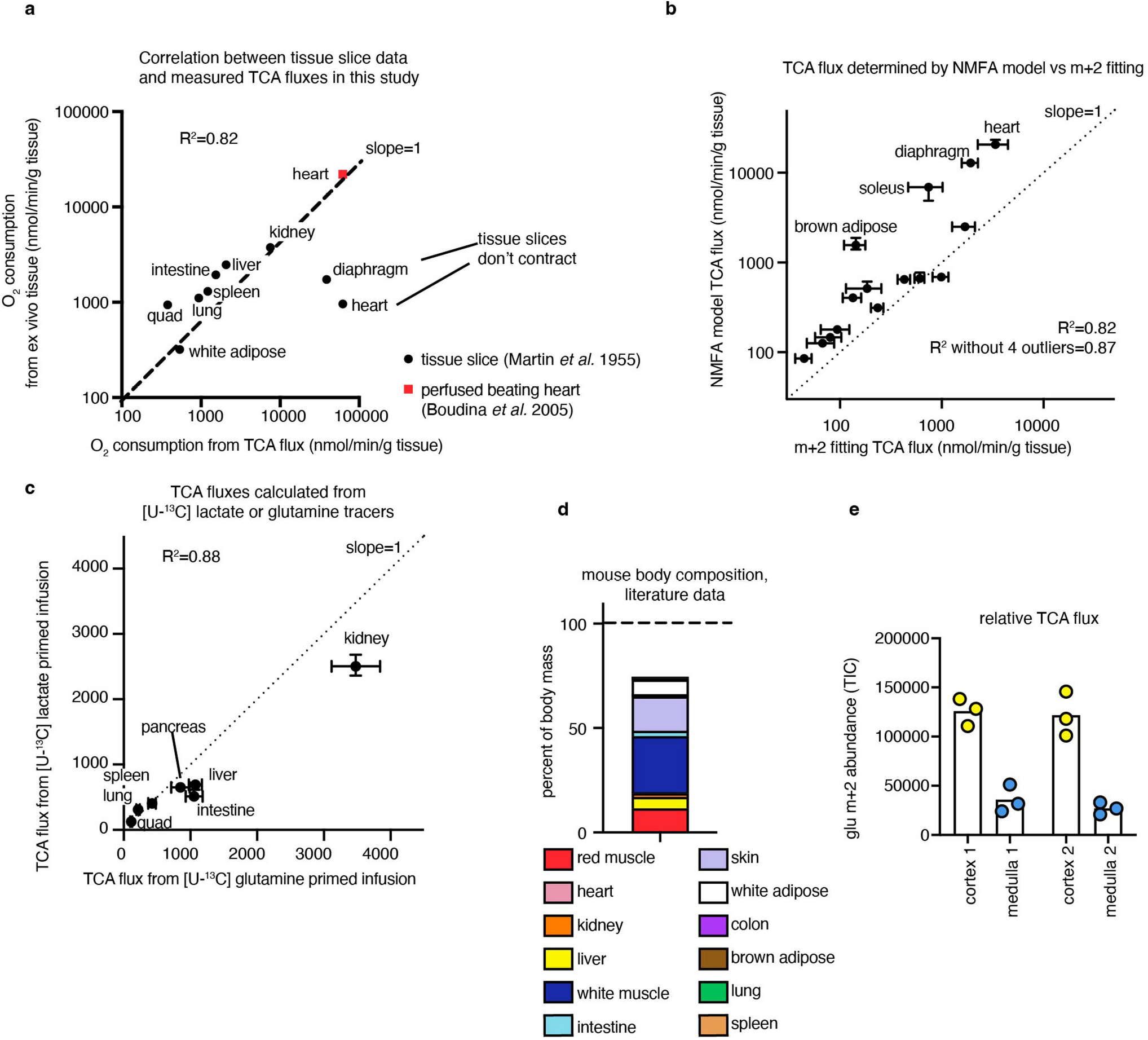
(a) Oxygen consumption calculated from TCA fluxes measured in this study correlates well to literature tissue slice oxygen consumption data (Martin & Fuhrmann, Phys Zool 1955), except for diaphragm and heart; heart correlates better to ex vivo beating heart oxygen consumption data from Boudina et al., Circulation 2005 (n = 12 mice per tissue for [U-13C] lactate infusion timepoints except n = 19 for brown adipose, n = 19 for intestine, n = 17 for soleus; n = 4 mice to measure tissue metabolite concentrations except n = 3 for diaphragm). (b) TCA fluxes calculated by non-stationary metabolic flux analysis (NMFA) model versus multiplying m+2 TCA metabolite labelling speed with summed TCA metabolite concentration are similar, except for heart, soleus, diaphragm, and brown adipose (n = 12 mice per tissue for [U-13C] lactate infusion timepoints except n = 19 for brown adipose, n = 19 for intestine, n = 17 for soleus; n = 4 mice to measure tissue metabolite concentrations except n = 3 for diaphragm). (c) TCA fluxes calculated using NMFA model from [U-13C] lactate infusion data or [U-13C] glutamine infusion data are similar (n = 12 mice per tissue for lactate primed infusion timepoints, n = 10 mice per tissue for glutamine primed infusion timepoints, n = 4 mice per tissue to measure tissue metabolite concentrations). (d) Mouse tissues as a percent of body mass (Brown et al., Toxicol Ind Health 1997). (e) Relative TCA flux in kidney cortex and medulla, measured using glutamate m+2 abundance after 1.5 min [U-13C] lactate primed infusion using imaging mass spectrometry, n = 2 mice, each point is a measurement in a distinct region in one of the images (showing 3 points per image per region). Error bars show median +/− standard deviation.
Extended Data Fig. 5 |. Kinetic 2-deoxyglucose infusion.
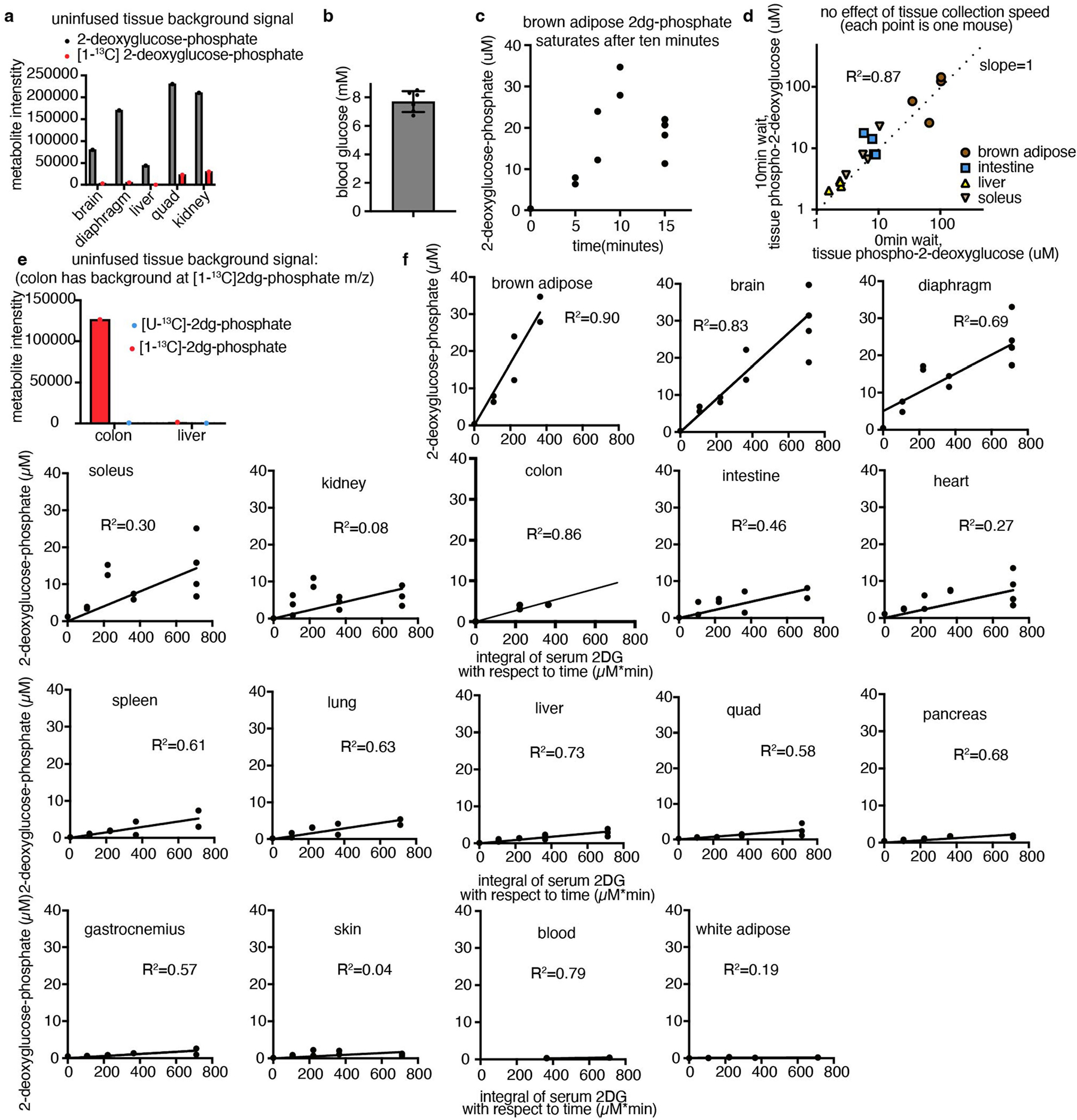
(a) The m/z of [1-13C] 2-deoxyglucose-phosphate has lower background signal in uninfused tissues compared to the m/z of unlabelled carbon-12 2-deoxyglucose-phosphate, n = 1 mouse shown, representative of n = 4 mice. (b) Arterial blood glucose concentration, n = 6 mice, error bar shows mean +/− standard deviation. (c) Brown adipose [1-13C] 2-deoxyglucose-phosphate concentration saturates after 10 min of [1-13C] 2-deoxyglucose infusion; therefore later timepoints were discarded in calculating glucose usage flux, n = 13 mice. (d) Waiting ten minutes after euthanasia to harvest tissues does not alter 2-deoxyglucose-phosphate concentrations after 10 min [1-13C] 2-deoxyglucose infusion, n = 4 mice per tissue per collection time, each point represents a pair of tissues from a single mouse (x and y axis values). (e) Colon and not liver (or other tissues) has a substantial background peak at the m/z of [1-13C] 2-deoxyglucose-phosphate (n = 1 mouse shown, representative of n = 13 mice); to measure glucose usage in this tissue, [U-13C] 2-deoxyglucose infusion was used. (f) [1-13C] or [U-13C] 2-deoxyglucose-phosphate concentrations in tissues at different timepoints after start of infusion (all infused with [1-13C] 2-deoxyglucose, except [U-13C] 2-deoxyglucose for colon); slope of line is the glucose usage flux, calculated from the datapoints, requiring a y-intercept of 0 (n = 4 mice for colon and blood; n = 9 mice for gastrocnemius, intestine, lung, pancreas, skin, spleen, white adipose; n = 12 mice for kidney, liver, quad; n = 13 for brain, brown adipose, diaphragm, heart, soleus).
Extended Data Fig. 6 |. Calculated tissue lactate consumption and production.
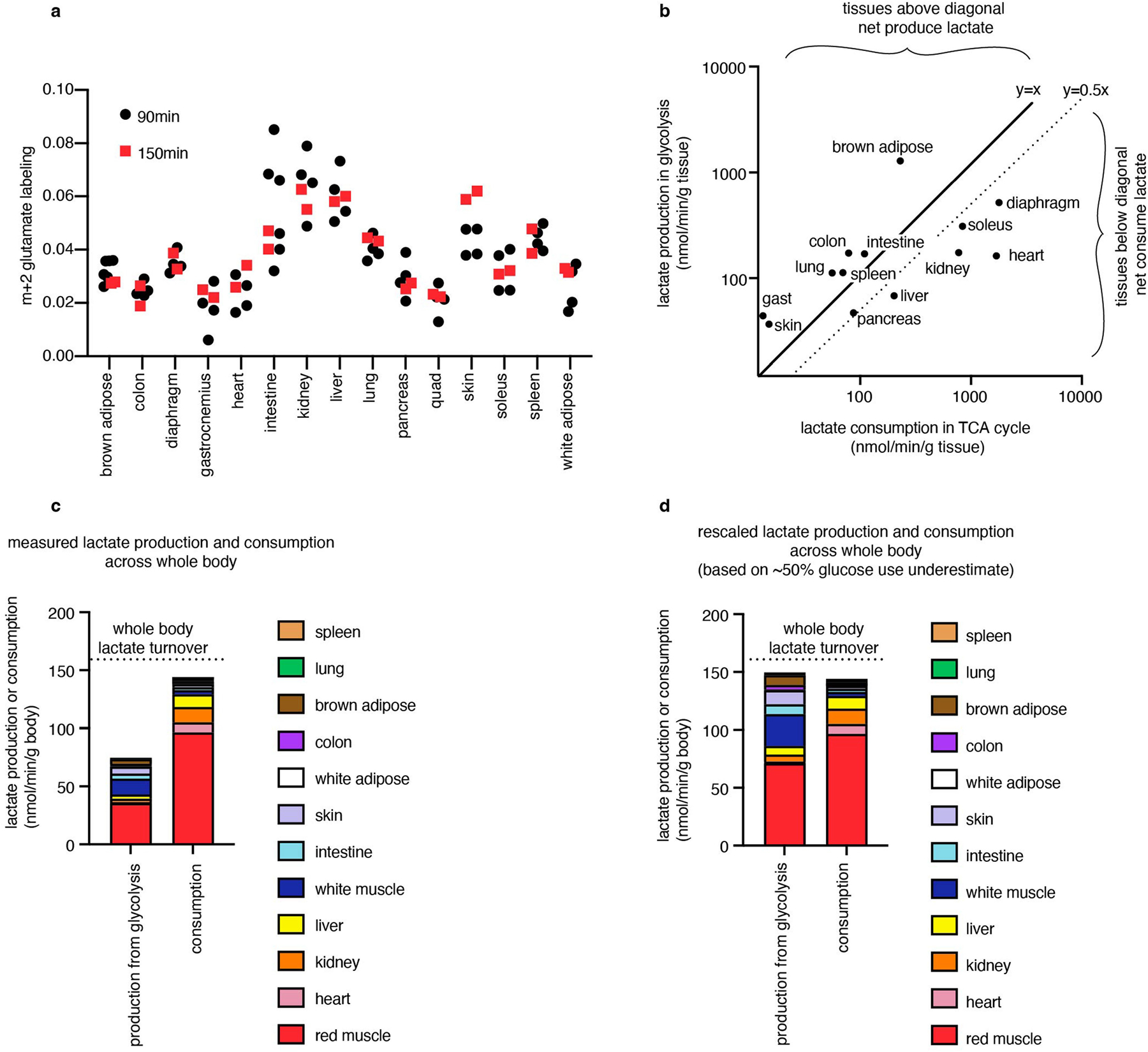
(a) Non-normalized labelling of m+2 glutamate from primed [U-13C] lactate infusion after 90 min (n = 4 mice for each tissue except n = 6 for brown adipose and intestine) or 150 min (n = 2 mice for each tissue). Mean labelling from 90 min was used as pseudo-steady state to normalize labelling in figures, and to calculate tissue lactate consumption from TCA flux values. (b) Production and consumption of lactate by tissues, calculated from glucose usage flux and from TCA flux multiplied by lactate contribution to TCA cycle respectively, showing both y = x line (equal measured lactate production and consumption) and y = 0.5x line (equal production and consumption of lactate if glucose use rate is truly twice as high as we measured). (c) Tissues producing and consuming lactate in the whole body, considering mass of each mouse tissue as a fraction of the whole body. (d) Tissues producing and consuming lactate calculated as in (c) but if true glucose usage is twice as high as we measured. For (b–d), glucose usage fluxes were measured with n = 4–13 mice, TCA fluxes were measured with n = 12 mice to measure kinetic infusion timepoints and n = 4 mice to measure TCA metabolite concentrations (except n = 3 for diaphragm).
Extended Data Fig. 7 |. TCA flux measurement in tumours by kinetic [U-13C] lactate infusion.
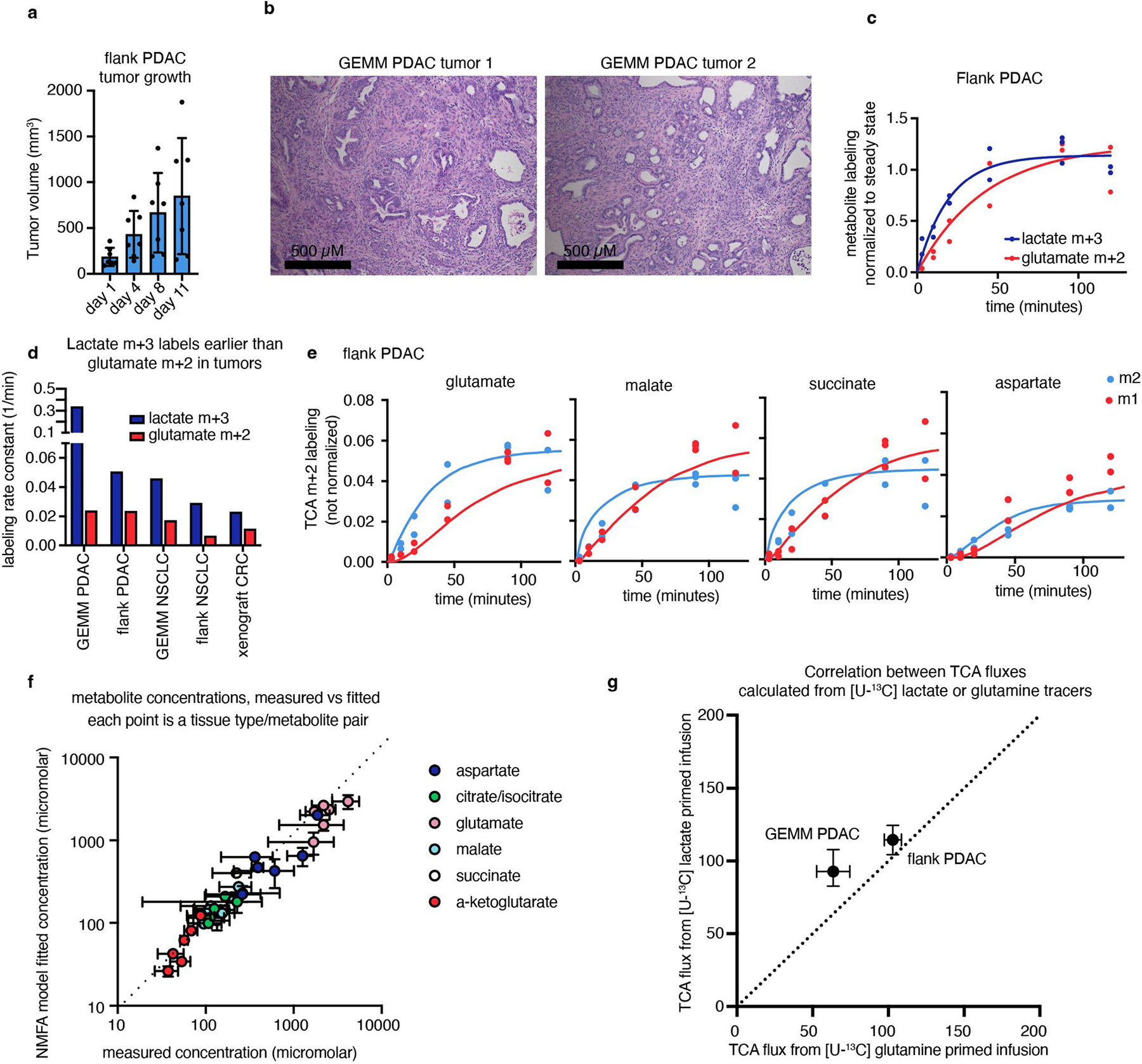
(a) Growth of flank PDAC tumours, n = 7 mice per timepoint, error bars show mean +/− standard deviation. (b) Hematoxylin and eosin staining of GEMM PDAC tumours showing tumours are viable and not necrotic, showing n = 2 mice, representative of n = 5 mice. (c) Timepoints of m+3 lactate and m+2 glutamate labelling in flank PDAC from primed [U-13C] lactate infusion, n = 13 mice. (d) Rate constant of glutamate m+2 labelling compared to lactate m+3 labelling in tumours from [U-13C] lactate primed infusion suggests that lactate entry does not gate TCA turning (n = 6 mice for GEMM PDAC, 13 for flank PDAC, 9 for GEMM NSCLC, 10 for flank NSCLC, 7 for xenograft CRC). (e) M+2 and m+1 labelling of TCA metabolites from [U-13C] lactate primed infusion (points) and model fits (lines) in flank PDAC tumours, n = 13 mice. (f) Model fit versus measured metabolite concentrations in tumours, each point is a metabolite from one tumour type, measured in n = 4 mice. (g) TCA fluxes of pancreatic tumour models calculated from [U-13C] lactate or [U-13C] glutamine primed infusion are similar (for lactate primed infusion, n = 6 mice for GEMM PDAC, n = 13 mice for flank PDAC; for glutamine primed infusion, n = 7 mice for GEMM PDAC, n = 10 mice for flank PDAC, n = 4 mice per tumour type to measure tumour metabolite concentrations). Error bars show medians+/− standard deviation.
Extended Data Fig. 8 |. Tumour models used for TCA and glucose usage flux measurement.
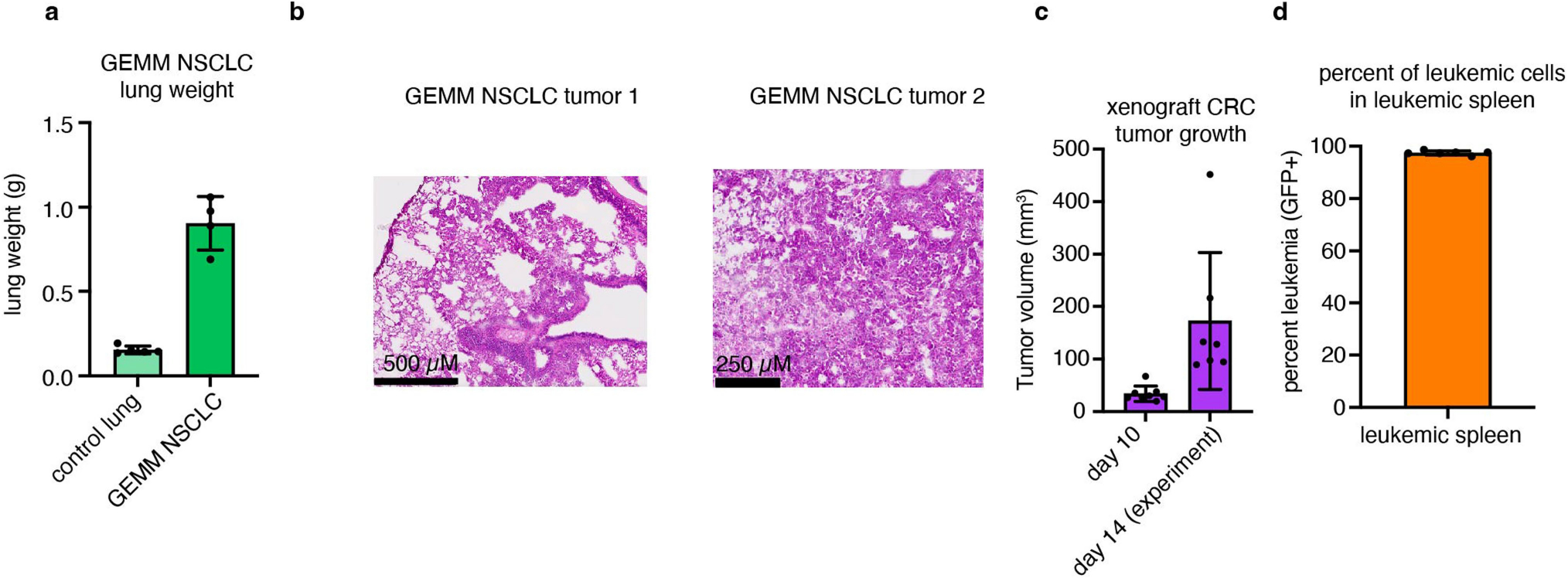
(a) Weights of lungs from GEMM NSCLC mice compared to littermate controls, n = 5 mice for control lung and n = 4 mice for GEMM NSCLC. (b) Hematoxylin and eosin staining from GEMM NSCLC tumours showing tumours are viable and not necrotic, n = 2 mice. (c) Volume of xenograft CRC tumours, n = 8 mice at day 10 and n = 7 mice at day 14. (d) Percent of leukaemic cells in leukaemic spleens after red blood cell lysis, n = 6 mice. All error bars show mean +/− standard deviation.
Extended Data Fig. 9 |. TCA and glucose use flux measurement in primary breast cancer xenograft tumours and their spontaneous lung metastases.
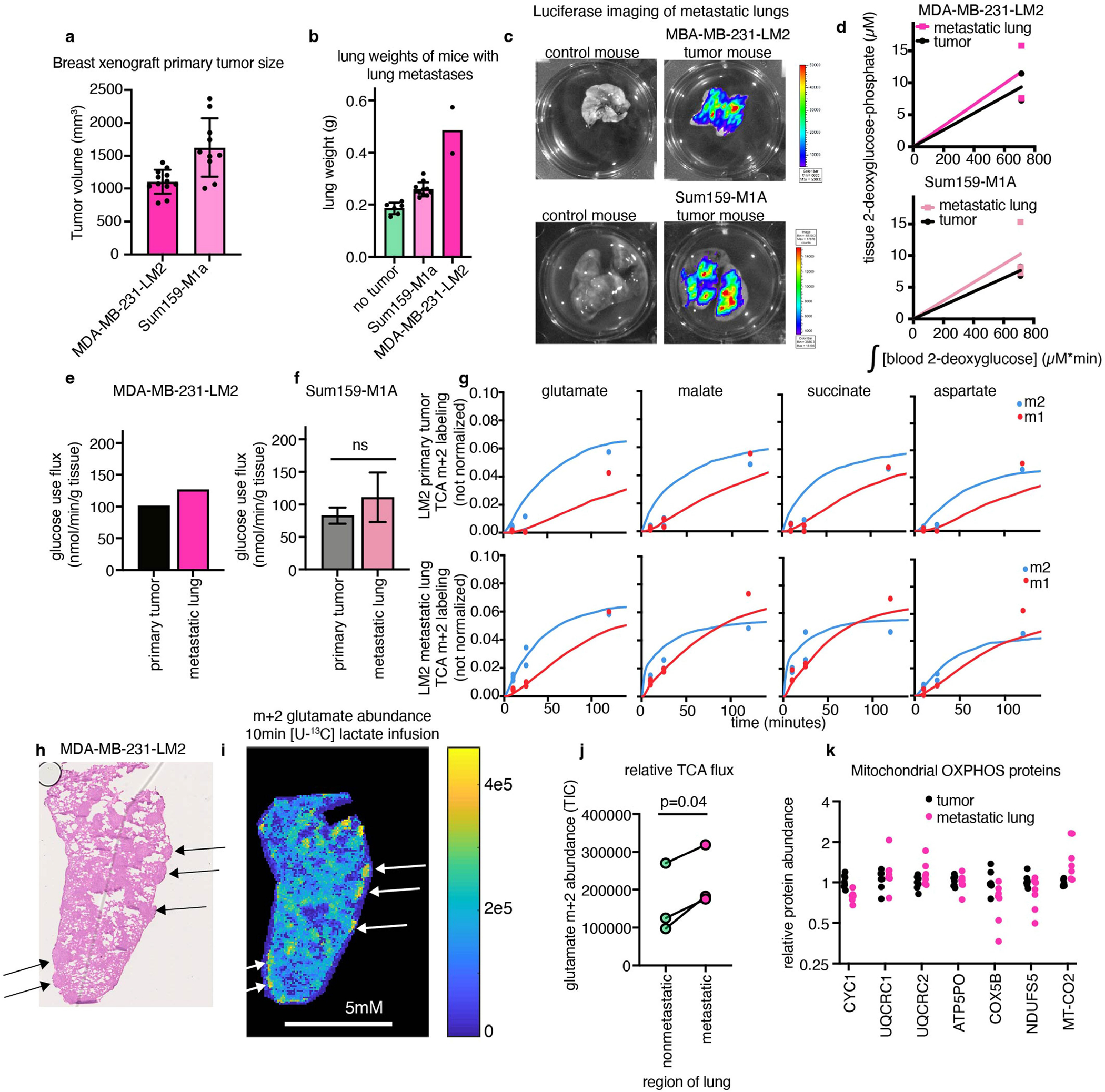
(a) Volume of breast cancer xenograft primary tumours (n = 12 mice MDA-MB-231-LM2, n = 10 mice Sum159-M1a). (b) Weight of mouse lungs, either in non-tumour-bearing mice or mice with metastases seeded from primary breast cancer xenograft tumours (n = 6 mice no tumour, n = 11 mice Sum159-M1a, n = 2 mice MDA-MB-231-LM2). (c) Luciferase imaging showing metastases in lungs of mice with primary breast cancer xenograft tumours, n = 1 mouse per tumour type shown. (d) [1-13C] 2-deoxyglucose-phosphate concentration after 15 min [1-13C] 2-deoxyglucose infusion in primary breast xenograft tumours, and lungs with metastases from the same mice (n = 2 mice for MDA-MB-231-LM2 tumour and lung, n = 3 for Sum159-M1a tumour and lung). (e) Glucose use fluxes of primary tumour and lung from mice with MD-MBA-231-LM2 breast xenograft tumours, n = 2 mice per tissue. (f) Glucose use fluxes of primary tumour and lung from mice with Sum159-M1A breast xenograft tumours, n = 3 mice per tissue, p-value from two-tailed t test. (g) TCA metabolite m+2 and m+1 labelling from [U-13C] lactate primed infusion (points) and model fits (lines) in primary tumours and lungs of mice with MDA-MB-231-LM2 tumours, n = 6 mice per tissue. (h) Hematoxylin and eosin staining of lung from mouse with MDA-MB-231-LM2 primary tumour; arrows indicate metastatic nodules. (i) Glutamate m+2 labelling intensity after 10 min [U-13C] lactate primed infusion, same lung as in (h), arrows indicate metastatic nodules. (j) Glutamate m+2 labelling intensity from healthy and metastatic regions of lungs with MDA-MB-LM2 metastases, n = 3 mice, paired t-test. (k) Protein abundance of detected human mitochondrial oxidative-phosphorylation proteins in MDA-MB-231-LM2 primary tumours and lungs bearing metastases from the same mice, all values normalized to the median value of that protein in the primary tumour, n = 7 per sample type. All error bars show mean +/− standard deviation.
Extended Data Fig. 10 |. ATP usage in tumours versus healthy tissues, and experimental sample sizes.
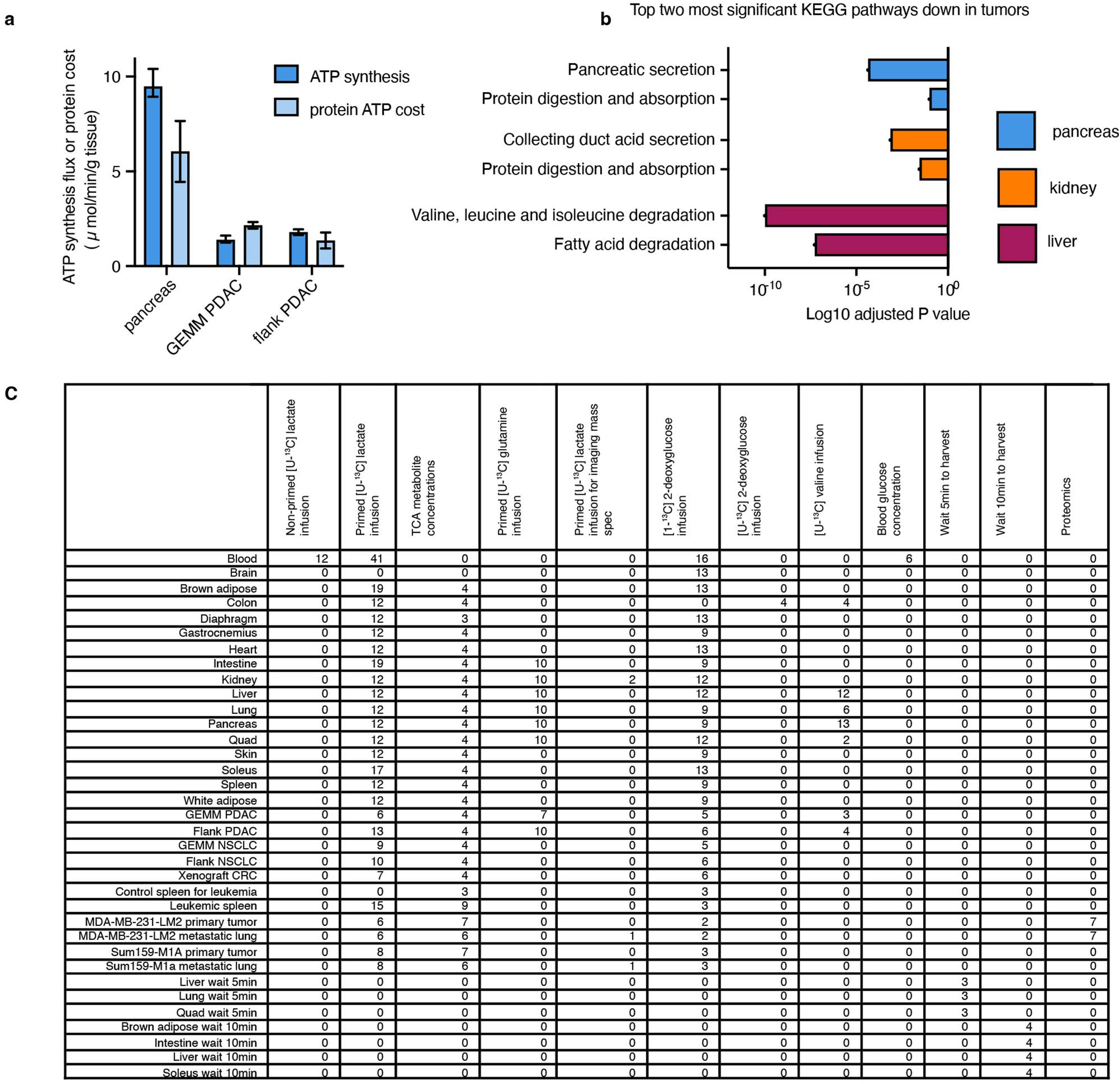
(a) Total ATP synthesis flux calculated from glucose use flux and TCA flux is similar to the predicted cost of protein ATP synthesis calculated from protein synthesis rates measured using [U-13C] valine infusion in pancreas and pancreatic tumours; n = 13 mice for pancreas, n = 3 for GEMM PDAC, n = 4 for flank PDAC; bars shown mean +/− standard deviation. (b) Adjusted p values of two most significantly enriched KEGG pathways for the genes downregulated in human tumours compared to the corresponding healthy tissue; n = 167 patients for healthy pancreas, n = 178 pancreatic tumour, n = 140 for healthy kidney, n = 884 for kidney tumour, n = 50 for healthy liver, n = 360 for liver tumour; data from UCSC Xena database. (c) Experimental replicates for all experiments shown in this study. Each replicate is a separate mouse tissue. All healthy tissues are from non-tumour bearing mice.
Supplementary Material
Acknowledgements
This work was funded by NIH R01CA163591 to J.D.R.; NIH DP1DK113643 to J.D.R.; Ludwig Cancer Research funding to J.D.R. and Y.K.; Stand Up to Cancer SU2CAACR-DT-20-16 to J.D.R.; American Cancer Society funding to Y.K.; NIH grants 35GM128813 and P30CA072720 to M.W.; NIH CA237347-01A1 and American Cancer Society 134036-RSG-19-165-01-TBG to J.Y.G.; NIH R01CA236936 and Leukemia and Lymphoma Society Scholar Award Scholar Award 1386-23 to D.H.; NIH R50CA211437 to W.L.; R35CA242379 to M.G.V.H.; Allen Foundation and Stand Up to Cancer funding to S.D.; Damon Runyon Foundation/Mark Foundation Postdoctoral Fellowship and K99CA273517 to C.R.B.; New Jersey Commission on Cancer Research grant COCR22PDF002 to V.d.S.-D.; the Charles H. Revson Senior Fellowship in Biomedical Science to Y.H.; NIH F32DK127843 to W.D.L.; New Jersey Commission on Cancer Research postdoctoral fellowship to A.R.; and T32GM007388 to C.S.R.J.
Footnotes
Competing interests J.D.R. is an advisor and stockholder in Colorado Research Partners, L.E.A.F. Pharmaceuticals, Bantam Pharmaceuticals, Barer Institute and Rafael Pharmaceuticals; a paid consultant of Pfizer and Third Rock Ventures; a founder, director and stockholder of Farber Partners, Serien Therapeutics and Sofro Pharmaceuticals; a founder and stockholder in Empress Therapeutics; and a director of the Princeton University–PKU Shenzhen collaboration. M.G.V.H. is a scientific advisor for Agios Pharmaceuticals, iTeos Therapeutics, Sage Therapeutics, Drioa Ventures and Auron Therapeutics. Y.K. is a co-founder and chair of scientific advisory board of Firebrand Therapeutics and KayoThera.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Code availability
Code to calculate tissue TCA cycle fluxes is available at GitHub (https://github.com/weilandtd/tca_fluxes) and Zenodo (https://zenodo.org/record/7328216#.Y3VQsezMI6B).
Additional information
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41586-022-05661-6.
Peer review information Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Reprints and permissions information is available at http://www.nature.com/reprints.
Data availability
All analysed data (including MS carbon-13-labelling timepoints and metabolite concentrations) used in this study are available in Supplementary Tables 1–12 and the source data. Source data are provided with this paper.
References
- 1.Frayn KN & Evans R Human Metabolism: A Regulatory Perspective (John Wiley & Sons, 2019). [Google Scholar]
- 2.Warburg O The metabolism of carcinoma cells. J. Cancer Res. 9, 148–163 (1925). [Google Scholar]
- 3.Warburg O The metabolism of tumors in the body. J. Gen. Physiol. 8, 519–530 (1927). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vander Heiden MG, Cantley LC & Thompson CB Understanding the Warburg effect: the metabolic requirements of cell proliferation. Science 324, 1029–1033 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liberti MV & Locasale JW The Warburg effect: how does it benefit cancer cells? Trends Biochem. Sci. 41, 211–218 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cori CF & Cori GT The carbohydrate metabolism of tumors: III. The rate of glycolysis of tumor tissue in the living animal. J. Cancer Res. 12, 301–313 (1928). [Google Scholar]
- 7.Crabtree HG Observations on the carbohydrate metabolism of tumours. Biochem. J. 23, 536–545 (1929). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fletcher JW et al. Recommendations on the use of 18F-FDG PET in oncology. J. Nucl. Med. 49, 480–508 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Birsoy K et al. An essential role of the mitochondrial electron transport chain in cell proliferation is to enable aspartate synthesis. Cell 162, 540–551 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ju YS et al. Origins and functional consequences of somatic mitochondrial DNA mutations in human cancer. eLife 3, e02935 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weinberg F et al. Mitochondrial metabolism and ROS generation are essential for Kras-mediated tumorigenicity. Proc. Natl Acad. Sci. USA 107, 8788–8793 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sullivan LB et al. Supporting aspartate biosynthesis is an essential function of respiration in proliferating. Cell 162, 552–563 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Viale A et al. Oncogene ablation-resistant pancreatic cancer cells depend on mitochondrial function. Nature 514, 628–632 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gorelick AN et al. Respiratory complex and tissue lineage drive recurrent mutations in tumour mtDNA. Nat Metab. 3, 558–570 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hui S et al. Glucose feeds the TCA cycle via circulating lactate. Nature 551, 115–118 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hensley CT et al. Metabolic heterogeneity in human lung tumors. Cell 164, 681–694 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mason GF et al. Simultaneous determination of the rates of the TCA cycle, glucose utilization, α-ketoglutarate/glutamate exchange, and glutamine synthesis in human brain by NMR. J. Cereb. Blood Flow Metab. 15, 12–25 (1995). [DOI] [PubMed] [Google Scholar]
- 18.Jucker BM, Lee JY & Shulman RG In vivo 13C NMR measurements of hepatocellular tricarboxylic acid cycle flux. J. Biol. Chem. 273, 12187–12194 (1998). [DOI] [PubMed] [Google Scholar]
- 19.Petersen KF et al. Mitochondrial dysfunction in the elderly: possible role in insulin resistance. Science 300, 1140–1142 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wijnen JP et al. In vivo 13C magnetic resonance spectroscopy of a human brain tumor after application of 13C-1-enriched glucose. Magn. Reson. Imaging 28, 690–697 (2010). [DOI] [PubMed] [Google Scholar]
- 21.Yuan J, Bennett BD & Rabinowitz JD Kinetic flux profiling for quantitation of cellular metabolic fluxes. Nat. Protoc. 3, 1328–1340 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Befroy DE et al. Direct assessment of hepatic mitochondrial oxidative and anaplerotic fluxes in humans using dynamic 13 C magnetic resonance spectroscopy. Nat. Med. 20, 98–102 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nöh K, Wahl A & Wiechert W Computational tools for isotopically instationary 13C labeling experiments under metabolic steady state conditions. Metab. Eng. 8, 554–577 (2006). [DOI] [PubMed] [Google Scholar]
- 24.Martin AW & Fuhrman FA The relationship between summated tissue respiration and metabolic rate in the mouse and dog. Physiol. Zool. 28, 18–34 (1955). [Google Scholar]
- 25.Sokoloff L et al. The [14c]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino Rat. J. Neurochem. 28, 897–916 (1977). [DOI] [PubMed] [Google Scholar]
- 26.Hostetler KY & Landau BR Estimation of the pentose cycle contribution to glucose metabolism in tissue in vivo. Biochemistry 6, 2961–2964 (1967). [DOI] [PubMed] [Google Scholar]
- 27.Munger J et al. Systems-level metabolic flux profiling identifies fatty acid synthesis as a target for antiviral therapy. Nat. Biotechnol. 26, 1179–1186 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fueger BJ et al. Impact of animal handling on the results of 18F-FDG PET studies in mice. J. Nucl. Med. 47, 999–1006 (2006). [PubMed] [Google Scholar]
- 29.Wolfe RR Tracers in Metabolic Research: Radioisotope and Stable Isotope/Mass Spectometry Methods (A.R. Liss, 1984). [PubMed] [Google Scholar]
- 30.Donovan CM & Brooks GA Endurance training affects lactate clearance, not lactate production. Am. J. Physiol. Endocrinol. Metab. 244, E83–E92 (1983). [DOI] [PubMed] [Google Scholar]
- 31.Levy MN Uptake of lactate and pyruvate by intact kidney of the dog. Am. J. Physiol. 202, 302–308 (1962). [DOI] [PubMed] [Google Scholar]
- 32.Murashige D et al. Comprehensive quantification of fuel use by the failing and nonfailing human heart. Science 370, 364–368 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jang C et al. Metabolite exchange between mammalian organs quantified in pigs. Cell Metab. 30, 594–606 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Piskounova E et al. Oxidative stress inhibits distant metastasis by human melanoma cells. Nature 527, 186–191 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ubellacker JM et al. Lymph protects metastasizing melanoma cells from ferroptosis. Nature 585, 113–118 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fischer GM et al. Molecular profiling reveals unique immune and metabolic features of melanoma brain metastases. Cancer Discov. 9, 628–645 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rodrigues MF et al. Enhanced OXPHOS, glutaminolysis and β-oxidation constitute the metastatic phenotype of melanoma cells. Biochem. J. 473, 703–715 (2016). [DOI] [PubMed] [Google Scholar]
- 38.Momcilovic M et al. In vivo imaging of mitochondrial membrane potential in non-small-cell lung cancer. Nature 575, 380–384 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Nicholls DG & Locke RM Thermogenic mechanisms in brown fat. Physiol. Rev. 64, 1–64 (1984). [DOI] [PubMed] [Google Scholar]
- 40.Divakaruni AS & Brand MD The regulation and physiology of mitochondrial proton leak. Physiology 26, 192–205 (2011). [DOI] [PubMed] [Google Scholar]
- 41.Brown GC Control of respiration and ATP synthesis in mammalian mitochondria and cells. Biochem. J. 284, 1–13 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pavlova NN & Thompson CB The emerging hallmarks of cancer metabolism. Cell Metab. 23, 27–47 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bauduin H, Colin M & Dumont JE Energy sources for protein synthesis and enzymatic secretion in rat pancreas in vitro. Biochim. Biophy. Acta 174, 722–733 (1969). [DOI] [PubMed] [Google Scholar]
- 44.Campagne RN & Gruber M Amino acid and energy requirements of protein synthesis in rat pancreatic tissue in vitro. Biochim. Biophys. Acta 55, 353–360 (1962). [Google Scholar]
- 45.Neinast MD et al. Quantitative analysis of the whole-body metabolic fate of branched-chain amino acids. Cell Metab. 29, 417–429 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lassen NA, Munck O & Thaysen JH Oxygen consumption and sodium reabsorption in the kidney. Acta Physiol. Scand. 51, 371–384 (1961). [DOI] [PubMed] [Google Scholar]
- 47.Müller MJ Hepatic fuel selection. Proc. Nutr. Soc. 54, 139–150 (1995). [DOI] [PubMed] [Google Scholar]
- 48.Frauwirth KA et al. The CD28 signaling pathway regulates glucose metabolism. Immunity 16, 769–777 (2002). [DOI] [PubMed] [Google Scholar]
- 49.Lapidot T et al. A cell initiating human acute myeloid leukaemia after transplantation into SCID mice. Nature 367, 645–648 (1994). [DOI] [PubMed] [Google Scholar]
- 50.Storz P Acinar cell plasticity and development of pancreatic ductal adenocarcinoma. Nat. Rev. Gastroenterol. Hepatol. 14, 296–304 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rajasekaran SA et al. Reduced expression of beta-subunit of na,k-atpase in human clear-cell renal cell carcinoma. J. Urol. 162, 574–580 (1999). [PubMed] [Google Scholar]
- 52.Chang C-H et al. Metabolic competition in the tumor microenvironment is a driver of cancer progression. Cell 162, 1229–1241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kamphorst JJ et al. Human pancreatic cancer tumors are nutrient poor and tumor cells actively scavenge extracellular protein. Cancer Res. 75, 544–553 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tasdogan A et al. Metabolic heterogeneity confers differences in melanoma metastatic potential. Nature 577, 115–120 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Reinfeld BI et al. Cell-programmed nutrient partitioning in the tumour microenvironment. Nature 593, 282–288 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brindle KM Imaging metabolism with hyperpolarized 13C-labeled cell substrates. J. Am. Chem. Soc. 137, 6418–6427 (2015). [DOI] [PubMed] [Google Scholar]
- 57.Davidson SM et al. Environment impacts the metabolic dependencies of Ras-driven non-small cell lung cancer. Cell Metab. 23, 517–528 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Herranz D et al. Metabolic reprogramming induces resistance to anti-NOTCH1 therapies in T cell acute lymphoblastic leukemia. Nat. Med. 21, 1182–1189 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kang Y et al. A multigenic program mediating breast cancer metastasis to bone. Cancer Cell 3, 537–549 (2003). [DOI] [PubMed] [Google Scholar]
- 60.Minn AJ et al. Genes that mediate breast cancer metastasis to lung. Nature 436, 518–524 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Esposito M et al. TGF-β-induced DACT1 biomolecular condensates repress Wnt signalling to promote bone metastasis. Nat. Cell Biol. 23, 257–267 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Chiles E et al. Fast LC-MS quantitation of glucose and glycerol via enzymatic derivatization. Anal. Biochem. 575, 40–43 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang L et al. Spatially resolved isotope tracing reveals tissue metabolic activity. Nat. Methods 19, 223–230 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gupta M, Sonnett M, Ryazanova L, Presler M & Wühr M Quantitative proteomics of Xenopus embryos I, sample preparation. Methods Mol. Biol. 1865, 175–194 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hughes CS et al. Single-pot, solid-phase-enhanced sample preparation for proteomics experiments. Nat. Protoc. 14, 68–85 (2019). [DOI] [PubMed] [Google Scholar]
- 66.Rappsilber J, Mann M & Ishihama Y Protocol for micro-purification, enrichment, pre-fractionation and storage of peptides for proteomics using StageTips. Nat. Protoc. 2, 1896–1906 (2007). [DOI] [PubMed] [Google Scholar]
- 67.Li J et al. TMTpro-18plex: The expanded and complete set of TMTpro reagents for sample multiplexing. J. Proteome Res. 20, 2964–2972 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Su X, Lu W & Rabinowitz JD Metabolite spectral accuracy on orbitraps. Anal. Chem. 89, 5940–5948 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Levenberg K A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 2, 164–168 (1944). [Google Scholar]
- 70.Marquardt DW An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 11, 431–441 (1963). [Google Scholar]
- 71.Hui S et al. Quantitative fluxomics of circulating metabolites. Cell Metab. 32, 676–688 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Ghergurovich JM et al. Local production of lactate, ribose phosphate, and amino acids by human triple-negative breast cancer. Med 2, 736–754 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Petersen MC, Vatner DF & Shulman GI Regulation of hepatic glucose metabolism in health and disease. Nat. Rev. Endocrinol. 13, 572–587 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Brown RP, Delp MD, Lindstedt SL, Rhomberg LR & Beliles RP Physiological parameter values for physiologically based pharmacokinetic models. Toxicol. Ind. Health 13, 407–484 (1997). [DOI] [PubMed] [Google Scholar]
- 75.West DB, Boozer CN, Moody DL & Atkinson RL Dietary obesity in nine inbred mouse strains. Am. J. Physiol. 262, R1025–R1032 (1992). [DOI] [PubMed] [Google Scholar]
- 76.Burkholder TJ, Fingado B, Baron S & Lieber RL Relationship between muscle fiber types and sizes and muscle architectural properties in the mouse hindlimb. J. Morphol. 221, 177–190 (1994). [DOI] [PubMed] [Google Scholar]
- 77.Mathewson MA, Chapman MA, Hentzen ER, Fridén J & Lieber RL Anatomical, architectural, and biochemical diversity of the murine forelimb muscles. J. Anat. 221, 443–451 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Kim YS Human tissues: chemical composition and photon dosimetry data. Radiat. Res. 57, 38–45 (1974). [PubMed] [Google Scholar]
- 79.Goldman MJ et al. Visualizing and interpreting cancer genomics data via the Xena platform. Nat. Biotechnol. 38, 675–678 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kanehisa M & Goto S KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 28, 27–30 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Chen EY et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinform. 14, 128 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Sonnett M, Gupta M, Nguyen T & Wühr M Quantitative proteomics for Xenopus embryos II, data analysis. Methods Mol. Biol. 1865, 195–215 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Sonnett M, Yeung E & Wühr M Accurate, sensitive, and precise multiplexed proteomics using the complement reporter ion cluster. Anal. Chem. 90, 5032–5039 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All analysed data (including MS carbon-13-labelling timepoints and metabolite concentrations) used in this study are available in Supplementary Tables 1–12 and the source data. Source data are provided with this paper.


