Bayesian negative binomial regression model with unobserved covariates for predicting the frequency of north atlantic tropical storms

Abstract

Predicting the annual frequency of tropical storms is of interest because it can provide basic information towards improved preparation against these storms. Sea surface temperatures (SSTs) averaged over the hurricane season can predict annual tropical cyclone activity well. But predictions need to be made before the hurricane season when the predictors are not yet observed. Several climate models issue forecasts of the SSTs, which can be used instead. Such models use the forecasts of SSTs as surrogates for the true SSTs. We develop a Bayesian negative binomial regression model, which makes a distinction between the true SSTs and their forecasts, both of which are included in the model. For prediction, the true SSTs may be regarded as unobserved predictors and sampled from their posterior predictive distribution. We also have a small fraction of missing data for the SST forecasts from the climate models. Thus, we propose a model that can simultaneously handle missing predictors and variable selection uncertainty. If the main goal is prediction, an interesting question is should we include predictors in the model that are missing at the time of prediction? We attempt to answer this question and demonstrate that our model can provide gains in prediction.

1. Introduction

Prediction of tropical cyclone (TC) activity for the North Atlantic region started in the early 1980s [5,6], while the very first attempt for prediction of TC activity around the world was taken by Neville Nicholls in the late 1970s [13]. Since then, the prediction of North Atlantic tropical storms has received more and more attention and previous studies have built forecast systems which give retrospective forecasts for the hurricane season that reaches its peak during August to October [2,6,24]. Although it is difficult to give accurate forecasts of TC activity 9–10 months prior to a particular season [18], considerable progress has been made for shorter lead times [2,17,19,22].

In this paper, we focus on developing models for the annual frequency of tropical storms, which is one of the measures of the severity of a hurricane season. Knowing in advance, whether it will be an active season or not can help in improved preparedness. The existing literature [20,23] has shown that SSTs averaged over the peak hurricane season are good predictors of tropical storm activity (aggregated over the hurricane season for a given year). For example, warmer temperature in the tropical Atlantic Ocean during August–October is expected to be favorable for the formation of tropical storms. However, observed SSTs are available after the hurricane season and, thus, cannot be directly used for prediction. Instead, forecasts of SSTs are available from multiple climate models, also known as general circulation models (GCMs). We focus on forecasts of Atlantic sea surface temperatures ( $SS{T}_{Atl}$) and tropical mean sea surface temperatures ( $SS{T}_{Trop}$) by five GCMs (GFDLB01, GFDLA06, GFDL, NASA, CMC2) from the North American Multi-Model Ensemble Project (NMME; Kirtman et al. [7]). The NMME [7] represents a multi-agency supported effort for intraseasonal to interannual prediction experiment. A number of research groups in North America have been providing outputs from their hindcasts and real-time forecasts since 2011. The GCMs we use provide a set of monthly forecasts from 1982 to the present. Predictions are available with a lead time from 9 to 12 months; multiple members are available for each GCM, and here we consider their ensemble average as representative of a given model.

The response variable is the total number of tropical storms that occur during August to October of each year, and the predictors are SSTs (true or forecasts) averaged over the same period (August to October of that year). To be clear, we have data aggregated for each year and not for each month. The predictors (SSTs) are time varying and capture the dependency across years; thus, time series models are typically not used in the climate science literature for this setting. Based on exploratory data analysis, we found the residuals satisfy the independence assumption reasonably well, so we do not consider time series models in this work. Some plots for model diagnostics are included in the Supplemental Material. Each of the five climate models issues a new forecast of SSTs every month, so our predictors change every month, and in this paper, we focus on monthly forecasts issued in June, July, and August. The SST forecasts change every month; however, they are all forecasts of the same quantity: the average true SST during August to October of a given year.

Because the structure of the data is somewhat complicated, we provide a schematic representation in Table 1. In Table 1, Year, TS, and SST denote the calendar year, the count of tropical storms in the year during August to October, and the average true SST during August to October of the year, respectively. The averages are obtained from monthly SST data. The SST forecasts from five climate models are denoted by SST ${}_{F1}$, $\dots$, SST ${}_{F4}$, SST ${}_{F5}$, and in this work, we focus on the forecasts issued in June, July, and August. During the period 1958–1981, only TS and SST (true) are available and denoted with a checkmark (✓). The climate models did not issue forecasts during that period and are unavailable and denoted with a cross-mark (✗). During the period 1982–2018, TS and SST (true) are available as before, and most of the SST forecasts are available. However, a few SST forecasts are missing in that period because some climate models did not issue forecasts in all years, which are denoted by cross-marks. In reality, there are two kinds of SSTs that are used as predictors (Atl and Trop), but we did not show that information in Table 1 for simplicity.

Table 1.

Schematic presentation of the data.

	True		Forecasts Issued in June				Forecasts Issued in July				Forecasts Issued in August
Year	TS	SST	SST ${}_{F1}$	···	SST ${}_{F4}$	SST ${}_{F5}$	SST ${}_{F1}$	···	SST ${}_{F4}$	SST ${}_{F5}$	SST ${}_{F1}$	···	SST ${}_{F4}$	SST ${}_{F5}$
1958	✓	✓	✗	···	✗	✗	✗	···	✗	✗	✗	···	✗	✗
1959	✓	✓	✗	···	✗	✗	✗	···	✗	✗	✗	···	✗	✗
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
1981	✓	✓	✗	···	✗	✗	✗	···	✗	✗	✗	···	✗	✗
1982	✓	✓	✓	···	✓	✓	✓	···	✓	✓	✓	···	✓	✓
1983	✓	✓	✓	···	✓	✓	✓	···	✓	✓	✓	···	✓	✓
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
2011	✓	✓	✓	···	✓	✗	✓	···	✓	✗	✓	···	✓	✗
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
2014	✓	✓	✓	···	✗	✓	✓	···	✓	✓	✓	···	✓	✓
···	···	···	···	···	···	···	···	···	···	···	···	···	···	···
2018	✓	✓	✓	···	✓	✓	✓	···	✓	✓	✓	···	✓	✓

To accommodate the missing data, we propose a two-level Bayesian regression model. The top level models the frequency of tropical storms as the response variable with the predicted and observed SSTs as covariates. The second level models the covariates via a sequence of regression models. Of the two levels, the top level which relates the response variable to the covariates is of more interest because our focus is on prediction of the frequency of tropical storms. Previous studies (e.g. Villarini et al. [21]) have shown that all climate models do not have equally good predictive power. This motivates us to use a variable selection prior in the top level of the model, that can automatically discriminate covariates, and retain covariates that are supported more strongly by the data. Mitra and Dunson [11] have developed such a model for linear and binary regression models. In this work, we extend their approach to a negative binomial regression model for count data. It is possible to use variable selection priors in both the top and lower level regression models, but based on the results in Mitra and Dunson [11], the gain from such an approach appears to be small compared to the increased computational burden. Thus, we specify variable selection priors only for the top level. Based on simulations and the North Atlantic TC data, we illustrate that this model can provide improved predictive performance compared to some existing models in the literature.

The organization of this paper is as follows. In Section 2, we provide a brief review of variable selection in a Bayesian framework. In Section 3, we provide a detailed description of the model development, prior specification, and posterior computation. In Section 4, we conduct two simulation studies. The simulation studies examine the predictive performance of our Bayesian model in comparison to a hierarchical model [21] under different scenarios. Through these simulation studies, we also try to answer the following important question: if a predictor is unavailable/missing for prediction, should we use a fully Bayesian procedure that includes that predictor or should we use a reduced Bayesian model that discards this predictor? In Section 5, we present results from applying the different methods to data from North Atlantic tropical storms. In Section 6, we discuss some directions for future work.

2. Review of Bayesian approach to variable selection

In this section, we provide a brief introduction to Bayesian model selection and Bayesian model averaging. For a more detailed review, see Clyde and George [1]. In a Bayesian framework, models are treated as additional unknown parameters and they are assigned a prior probability distribution.

In the context of variable selection in regression models, different models represent different subsets of variables (covariates). Suppose there are p variables. Let $\mathit{\gamma }=({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_p{)}^{\prime }$ represent a particular subset of these p variables, where ${\gamma }_j=1$ if the variable is included in the model and 0 otherwise. For example, a choice of $\mathit{\gamma }=(1,0,\dots ,0{)}^{\prime }$ would represent a model with the first covariate only. Each model is encoded by $\mathit{\gamma }$, and let the probability distribution for the observables $\mathit{W}$ be $p(\mathit{W}\mid {\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma })$ where ${\mathit{\kappa }}_{\mathit{\gamma }}$ is a model specific parameter.

In the Bayesian approach, we assign a prior distribution $p({\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma })$ to the parameters for each model and a prior probability, $p(\mathit{\gamma })$ to each model. This prior formulation leads to the following joint distribution:

$$p(\mathit{W},{\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma })=p(\mathit{W}\mid {\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma })p({\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma })p(\mathit{\gamma }).$$ (1)

Suppose our goal is to predict a new observation ${\mathit{W}}_f$, which is assumed to be generated from the same process that generated the observed data $\mathit{W}$. Then the posterior predictive distribution of ${\mathit{W}}_f$ under model $\mathit{\gamma }$ is obtained as

$$\begin{array}{rl}p({\mathit{W}}_f\mid \mathit{\gamma },\mathit{W})& =\int p({\mathit{W}}_f,{\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma },\mathit{W})\mathrm{d}{\mathit{\kappa }}_{\mathit{\gamma }}=\int p({\mathit{W}}_f\mid {\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma },\mathit{W})p({\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma },\mathit{W})\mathrm{d}{\mathit{\kappa }}_{\mathit{\gamma }}\\ & =\int p({\mathit{W}}_f\mid {\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma })p({\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma },\mathit{W})\mathrm{d}{\mathit{\kappa }}_{\mathit{\gamma }}.\end{array}$$ (2)

The last equality in (2) holds because of the assumption of independence between $\mathit{W}$ and ${\mathit{W}}_f$, given the model and model specific parameters.

After marginalizing out parameters ${\mathit{\kappa }}_{\mathit{\gamma }}$, conditional on the observed data $\mathit{W}$, we have the posterior probability for model $\mathit{\gamma }$ as

$$p(\mathit{\gamma }\mid \mathit{W})=\frac{p(\mathit{W}\mid \mathit{\gamma })p(\mathit{\gamma })}{\sum _{\mathit{\gamma }}p(\mathit{W}\mid \mathit{\gamma })\mathrm{d}(\mathit{\gamma })},$$ (3)

where

$$p(\mathit{W}\mid \mathit{\gamma })=\int p(\mathit{W}\mid {\mathit{\kappa }}_{\mathit{\gamma }},\mathit{\gamma })p({\mathit{\kappa }}_{\mathit{\gamma }}\mid \mathit{\gamma })\mathrm{d}{\mathit{\kappa }}_{\mathit{\gamma }}$$ (4)

is called the marginal likelihood of model $\mathit{\gamma }$. To measure the importance of a covariate based on all models, the posterior marginal inclusion probability for the jth covariate is defined as follows:

$$p({\mathit{\gamma }}_j=1\mid \mathit{W})=\sum _{\mathit{\gamma }\in \mathrm{\Gamma }:{\mathit{\gamma }}_j=1}p(\mathit{\gamma }\mid \mathit{W}).$$ (5)

Under Bayesian model averaging, the posterior predictive distribution of ${\mathit{W}}_f$ is given by

$$p({\mathit{W}}_f\mid \mathit{W})=\sum _{\mathit{\gamma }\in \mathrm{\Gamma }}p({\mathit{W}}_f\mid \mathit{\gamma },\mathit{W})p(\mathit{\gamma }\mid \mathit{W}),$$ (6)

which is a mixture of the conditional predictive distributions under each model, with mixture weights given by the posterior probabilities of models.

The marginal likelihood in (4) is typically not available in closed form, except for a small class of models with certain prior structures, like linear regression models with conjugate priors. When it is available in closed form, posterior computation is greatly simplified. In most cases, including our negative binomial regression model, the posterior distribution is not available in closed form and these quantities cannot be computed analytically. However, we can use a Markov chain Monte Carlo (MCMC) algorithm to sample approximately from the posterior predictive distribution and estimate quantities of interest such as the posterior inclusion probability of a covariate.

3. Bayesian negative binomial regression model with missing covariates

We first introduce some notation. Let $\mathit{Y}$ denote the n dimensional vector containing the count of the tropical storms from the the National Oceanic and Atmospheric Administration's (NOAA) National Hurricane Center's best-track database (HURDAT2) [8]. Let $\mathit{X}=({\mathit{x}}_0,{\mathit{x}}_1,\dots ,{\mathit{x}}_p)$ denote the $n\times (p+1)$ design matrix, whose first column is a column of ones, corresponding to the intercept term. The remaining columns correspond to $SS{T}_{Atl}$ and $SS{T}_{Trop}$ from the climate models, as well as the true $SS{T}_{Atl}$ and $SS{T}_{Trop}$ from the Met Office Hadley Centre [15].

Let $\mathit{M}=({\mathit{m}}_1,\dots ,{\mathit{m}}_p)$ be the $n\times p$ matrix of indicators for the p covariates [9] denoting whether it is available or missing. Here $m_{ij}=1$ denotes that $x_{ij}$ is observed and $m_{ij}=0$ denotes that $x_{ij}$ is missing. Let the observed predictor values be denoted by ${\mathit{X}}_{\mathit{o}\mathit{b}\mathit{s}}=\{x_{ij},i=1,\dots ,n,j=1,\dots ,p:m_{ij}=1\}$ and the missing predictor values by ${\mathit{X}}_{\mathit{m}\mathit{i}\mathit{s}}=\{x_{ij},i=1,\dots ,n,j=1,\dots ,p:m_{ij}=0\}$. Here we assume that the covariates have been standardized using the observed values to have mean 0 and standard deviation 1 for the observed part of each covariate. Such standardization converts covariates to the same scale and leads to ease in prior specification for the regression coefficients.

3.1. Negative binomial regression model

The top level regression model relates the frequency of tropical storms to SSTs as predictors. Commonly used distributions for modeling count data are Poisson or negative binomial distributions, both of which have support over the set of non negative integers $\{0,1,2,\dots \}$. While using a Poisson model could be a reasonable approach for our data, we choose the negative binomial distribution because Bayesian posterior computation is much more amenable for a negative binomial regression model with variable selection priors, using the Pólya Gamma data augmentation approach [14]. Zhou et al. [25] have developed algorithms for overdispersed count data based on Pólya Gamma data augmentation. Neelon [12] has extended the model of Pillow and Scott [14] to the zero-inflated case for spatial and time series data. However, instead of overdispersion our focus in this work is mainly on Bayesian model averaging via variable selection priors in the presence of missing covariates. Note that even though we use a negative binomial model for our data, we put a prior on the dispersion parameter. So if the data does not exhibit overdispersion, as in our case, the results are very similar to that under a Poisson regression model. As suggested by one reviewer, we have included results for an approximate Poisson regression model for the tropical storm data set in the Supplemental Materials.

Let ${\mathit{X}}_i$ denote the $(p+1)\times 1$ vector of predictors for the ith observation, and let the corresponding response variable be $Y_i$. Let $\mathit{\beta }$ be a $(p+1)$ dimensional vector of regression coefficients. Then the top level negative binomial regression model is given as follows:

$$p(Y_i\mid {\mathit{X}}_i,\mathit{\beta },\eta )=\frac{\mathrm{\Gamma }(Y_i+\eta )}{\mathrm{\Gamma }(\eta )Y_i!}{(1-{\pi }_i)}^{\eta }{{\pi }_i}^{Y_i},i=1,2,\dots n,$$ (7)

where ${\pi }_i=e^{{\mu }_i}/(1+e^{{\mu }_i})$, ${\mu }_i={\mathit{X}}_i^T\mathit{\beta }$, and $\eta >0$ is the dispersion parameter.

We assume a Gaussian prior for the intercept ${\beta }_0$ and a spike and slab prior [3] for all other regression coefficients:

$$\begin{array}{rl}{\beta }_0& \sim N(0,{\lambda }_0)\\ {\beta }_j& \sim (1-\rho ){\delta }_0+\rho N(0,{\lambda }_j),j=1,2,\dots ,p,\end{array}$$ (8)

where ${\delta }_0$ is a degenerate distribution at zero. This implies that the prior for ${\beta }_j$ is a mixed distribution. With probability ρ, ${\beta }_j$ comes from a Gaussian distribution, and with probability $(1-\rho )$, ${\beta }_j$ is exactly 0. Setting ${\beta }_j=0$, allows the corresponding covariate ${\mathit{x}}_j$ to be dropped from the model and lead to variable selection. If we let ${\gamma }_j$ be an indicator variable for including the $j^{th}$ predictor ${\mathit{x}}_j$, such that ${\gamma }_j=1$ if ${\mathit{x}}_j$ is included in the model, and 0 otherwise, then $\{{\gamma }_j=0\}\equiv \{{\beta }_j=0\}$. We set ${\lambda }_0=100$ to have a reasonably diffuse prior for the intercept term. We standardize the covariates and set ${\lambda }_j=1$, as large values of ${\lambda }_j$ in a variable selection prior can lead to favoring the null model, without any covariates. We choose $\rho =0.5$ which leads to a discrete uniform prior on the space of models $\mathit{\gamma }$, giving each model a prior probability of $1/2^p$. The dispersion parameter η controls the deviation of the negative binomial distribution from the Poisson distribution, where smaller values of η lead to larger variance compared to the Poisson distribution. If the mean remains fixed and $\eta \to \mathrm{\infty }$, the negative binomial distribution converges to the Poisson distribution. We assume that η has a uniform prior on the interval $(0,1000)$.

3.2. Sequence of linear regression models for covariates

Since the covariates may not be fully observed, we specify a joint distribution for the predictors in the second level of the model. We adopt the method developed by Mitra and Dunson [11], where a joint distribution is specified using a series of univariate models:

$$p\left({\mathit{X}}_i\right)=p\left(x_{i1}\right)\prod _{j=2}^{p}p(x_{ij}\mid x_{i1},\dots ,x_{i(j-1)}).$$ (9)

Specifically, we assume, for $i=1,2,\dots ,n,$

$$\begin{array}{rl}{x}_{i1}& \sim N({\theta }_{10},\frac{1}{{\psi }_1}),\\ x_{i2}\mid x_{i1}& \sim N({\theta }_{20}+x_{i1}{\theta }_{21},\frac{1}{{\psi }_2}),\\ & ⋮\\ x_{ip}\mid x_{i1},\dots ,x_{i(p-1)}& \sim N({\theta }_{p0}+x_{i1}{\theta }_{p1}+\dots ,+x_{i(p-1)}{\theta }_{p(p-1)},\frac{1}{{\psi }_p}).\end{array}$$ (10)

We put conjugate prior distributions on all regression coefficients and intercepts, i.e.

$$\begin{array}{rl}{\theta }_{j0}& \sim N(0,\frac{{\lambda }_{j0}}{{\psi }_j})\\ {\theta }_{jk}& \sim N(0,\frac{{\lambda }_{jk}}{{\psi }_j}),j=1,\dots ,p,k=1,\dots ,j-1.\end{array}$$ (11)

We set ${\lambda }_{j0}=100$ for the intercept terms. We set ${\lambda }_{jk}=1$ for other regression coefficients to have the same prior variance on the standardized scale. For the residual precision parameters we specify the following prior:

$${\psi }_j\sim Gamma(c,d),j=1,\dots ,p,$$ (12)

where we set the shape and rate parameters as c = 1 and $d=\frac{1}{5}$, respectively. This choice of hyperparameters offers reasonably diffuse priors, when the covariates are standardized.

3.3. Posterior computation

For the aforementioned model and prior specification, the posterior distribution does not have a closed form. In such cases, a natural option is to use MCMC sampling, where a Markov chain is constructed so that its stationary distribution is the posterior distribution. Gibbs sampling, when possible, makes computation relatively straightforward as tuning is not needed. Gibbs sampling is not immediately applicable to the above posterior distribution, as the full conditional distributions are not available in closed form for a negative binomial regression model.

The Pólya Gamma data augmentation approach of Pillow and Scott [14] greatly simplifies posterior computation for the negative binomial model with a Gaussian prior on the regression coefficients. We extend their approach to spike and slab priors for regression coefficients, where spike refers to the degenerate distribution at 0, and slab refers to a normal distribution. We give a brief description of this data augmentation method to show why it simplifies posterior computation.

Following Pillow and Scott [14], the conditional posterior distribution of $\mathit{\beta }$ can be expressed as

$$\begin{array}{rl}p(\mathit{\beta }\mid \eta ,\mathit{X},\mathit{Y})& \propto p\left(\mathit{\beta }\right)\prod _{i=1}^n\frac{{\left(e^{{\mu }_i}\right)}^{Y_i}}{{(1+e^{{\mu }_i})}^{\eta +Y_i}}\end{array}$$ (13)

$$\begin{array}{rl}& \propto p\left(\mathit{\beta }\right)\prod _{i=1}^n{e}^{\frac{(Y_i-\eta ){\mu }_i}{2}}{\int }_0^{\mathrm{\infty }}{e}^{-\frac{w_i{\mu }_i^2}{2}}p(w_i\mid \eta +Y_i,0)\mathrm{d}{w}_i,\end{array}$$ (14)

where the last line follows from an integral identity via which the terms in the negative binomial likelihood can be expressed as an integral with respect to the density of a Pólya Gamma random variable $w_i\sim PG(\eta +Y_i,0)$. Thus conditional on $w_i$, the contribution from the likelihood terms starts to resemble a likelihood for linear regression with normal errors. With some more algebra, Pillow and Scott [14] have shown that the conditional posterior distribution of $\mathit{\beta }$ simplifies to a normal distribution, under a normal prior. Exploiting this data augmentation framework, we derive full conditional distributions for spike and slab priors, in closed form.

For our two-level Bayesian model, the posterior distribution of interest is $p(\eta ,\mathit{w},\mathit{\beta },{\mathit{X}}_{\mathit{m}\mathit{i}\mathit{s}},\mathit{\theta },\mathit{\psi }\mid \mathit{Y},{\mathit{X}}_{\mathit{o}\mathit{b}\mathit{s}})$. Full conditionals are available for all components except η. Thus samples can be drawn from the above posterior distribution approximately, using a Gibbs sampler with a Metropolis Hastings (MH) step for drawing η [16]. For the MH step we use a normal proposal for η centered at the current value, with support over $(0,1000)$. We outline the full conditionals for the remaining components in Appendix 1.

4. Simulation study

We perform a simulation study to investigate the performance of the Bayesian model in comparison to the existing hierarchical model of Villarini et al. [21]. We first review the different methods that were considered in that paper.

4.1. Review of Villarini et al. [21]

Villarini et al. [21] noted that not all climate models (GCMs) have similar predictive power. They considered various kinds of weighting schemes to combine the forecasts of SSTs from different climate models. They first used a Poisson regression to model the count of tropical storms based on the true/observed Atlantic sea surface temperatures ( $SS{T}_{Atl}$) and the tropical mean sea surface temperatures ( $SS{T}_{Trop}$), respectively. Maximum likelihood estimation was used and suppose the MLE of the $3\times 1$ vector $\mathit{\beta }$ is denoted as ${\hat{\mathit{\beta }}}_O$, where O in the suffix denotes that this regression coefficient was estimated based on the ‘observed’ SSTs.

In terms of forecasts, the true SSTs during the upcoming tropical storm season are not available, because they depend on a future event. But forecasts of these two covariates are available from six climate models. The simplest method is to take an average over the forecasts by the six climate models, and plug those averaged predictors in a Poisson regression model with regression parameter ${\hat{\mathit{\beta }}}_O$. There is a weighted average version of this Poisson regression model which weights the forecasts from different climate models, based on how well they predict the real SSTs.

The final model considered by Villarini et al. [21] is a mixture of six Poisson regression models, with mixture components corresponding to the six climate models. The weight for each climate model is taken as 1/RMSE, where RMSE is the root mean squared error in predicting the response variable for that climate model. Weights are normalized over the six climate models to sum to 1. For prediction, the Poisson mean parameter of each climate model is taken as $\exp ({\mathit{X}}_{GCM}^T{\hat{\mathit{\beta }}}_O)$, where ${\mathit{X}}_{GCM}$ is the GCM specific forecast of SSTs. Among the different weighting schemes, no method was always the best, but this mixture model, called the hierarchical model, seemed to have the best performance overall.

The hierarchical model has a similar flavor to Bayesian model averaging, since predictions are made using a mixture of models and model probabilities are related to accuracy in prediction. Since the mixture weights and parameters are known, sampling from this model can be done by independent Monte Carlo sampling. However, it has two main drawbacks. It uses the observed SSTs for estimation ( ${\hat{\mathit{\beta }}}_O$) but uses the forecasts of these SSTs for prediction. The Poisson mean parameter $\exp ({\mathit{X}}_{GCM}^T{\hat{\mathit{\beta }}}_O)$ used for each mixture component can lead to a mismatch and affect predictions, if the forecasts of SSTs are not good predictors of the real SSTs. The second drawback is that the predictive distribution for the hierarchical model assumes that the true value of $\mathit{\beta }$ is known and equal to the MLE, ${\hat{\mathit{\beta }}}_O$. This can underestimate uncertainty. Since the hierarchical model ignores the uncertainty in the estimation of parameters, the predictive distribution under it boils down to a mixture of Poisson regression models, with completely known mixture weights and known mixture specific parameters (Poisson means). As a result, independent Monte Carlo sampling can be used to draw samples from the predictive distribution and prediction sets can be formed based on those samples.

4.2. Data generation

For the North Atlantic tropical storms, we have data on the frequency of storms (response variable) and observed SSTs from 1958–2018, from the HURDAT2 database [8]. However, the forecasts of SSTs from six GCMs from the North American Multi Model Ensemble [7], are available from 1982-2018. This means the hierarchical model which uses the observed SSTs can use roughly twice the number of observations compared to the Bayesian models developed in this work. Thus, we design a simulation study which maintains a similar structure, to enable a fair comparison of different procedures.

We generate data sets of 150 observations. For each of the simulated data sets, we generate the covariates from a multivariate normal distribution with mean vector $\mathit{\mu }$ and covariance matrix $\mathbf{\Sigma }$:

$$\mathit{X}\sim MVN(\mathit{\mu }=\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\\ \dots \\ {\mu }_p\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ \dots \\ 0\end{array}\right),\mathbf{\Sigma }=\left(\begin{array}{cccc}{\sigma }_1^2& {\sigma }_{12}& \dots & {\sigma }_{1p}\\ {\sigma }_{12}& {\sigma }_2^2& & ⋮\\ ⋮& & \ddots & {\sigma }_{(p-1)p}\\ {\sigma }_{1p}& \dots & {\sigma }_{(p-1)p}& {\sigma }_p^2\end{array}\right)),$$

where p = 12, ${{\sigma }_i}^2=1,\mathrm{for}i=1,\dots ,12$, and the off-diagonal elements of $\mathbf{\Sigma }$ are set as ${\sigma }_{12}=0.7$, ${\sigma }_{13}=0.9$, ${\sigma }_{14}=0.7$, ${\sigma }_{23}=0.6$, ${\sigma }_{24}=0.7$, ${\sigma }_{34}=0.7$, and ${\sigma }_{ij}=0.5$ elsewhere.

This structure tries to mimic the real data to a certain extent, but in a somewhat more simplified setting. The real data in Section 5 also has p = 12 covariates, which includes SST forecasts from 5 GCMs and the true SSTs. Since one of the six GCMs is known to have consistently poor predictive performance [21], we focus on the 5 remaining GCMs in this work. Here the first two covariates are assumed to play the role of the real/observed SSTs, ( $SS{T}_{Atl}$ and $SS{T}_{Trop}$), and the next two covariates resemble the forecasts of the same quantities from the strongest climate model in the real data.

In our application, there is no overdispersion so a Poisson regression model seems most reasonable for generating the counts in the simulation study. We developed a negative binomial regression model mainly for computational convenience. But the added flexibility to account for overdispersion could be useful in other applications.

We generate an outcome, $Y_i$, using a Poisson regression model with mean $\exp ({\mathit{X}}_i^T\mathit{\beta })$, and consider the following two scenarios:

1. Scenario 1: $\mathit{\beta }=(1.8,0.4,-0.2,0.35,-0.25,0,\dots ,0)$

2. Scenario 2: $\mathit{\beta }=(1.8,0.5,-0.2,0,\dots ,0)$

Scenario 1 assumes that the response variable is generated using the pair of true SSTs and a pair of strong SST forecasts. Scenario 2 assumes that the response variable is generated solely by the true SSTs. While Scenario 2 seems more plausible, Scenario 1 is closer to what we find in the real data. One possible explanation is that while it is known that a difference in SSTs in the tropical Atlantic and global tropics is a driving force for formation of storms, there are many other factors that are not accounted for by the model in Scenario 2. The GCM forecasts themselves come from climate models that try to model the physical processes that affect SSTs. So it is possible that the forecasts are systematically capturing other factors that are also related to the formation of storms.

For each simulated data set, we have 150 observations. We assume that the first two predictors ${\mathit{x}}_1$ and ${\mathit{x}}_2$ that represent the real SSTs, are only accessible to the hierarchical model for the first 50 observations. The other predictors ${\mathit{x}}_3-{\mathit{x}}_{12}$ are not accessible to any method, for these first 50 observations, to indicate the fact that the climate models did not issue forecasts for the initial period in our real data set. We split the next 100 observations into two equal halves. The middle 50 observations of the entire 150, are accessible to all methods (Bayesian and hierarchical) and used for estimation. The final 50 observations are used for prediction to compare methods. For prediction, we treat ${\mathit{x}}_1$ and ${\mathit{x}}_2$ as missing, to represent that the true SSTs will not be available when making forecasts. We use the same prior hyperparameters that were described in the preceding section. We conduct the Bayesian analysis using the package R2jags in R.

4.3. Missing covariates for prediction

If our main goal is prediction and some of the covariates are missing/unobserved at the time of prediction, one can envision using two approaches for dealing with the missing covariates in a Bayesian framework:

1. Method 1: Retain all covariates in the model; sample the unobserved covariates from their predictive distribution; and marginalize over them using Monte Carlo integration.

2. Method 2: Drop all covariates that are unavailable for prediction and consider posterior computation with a reduced model.

We generate 100 data sets under Scenarios 1 and 2. Each data set is analyzed using the (i) hierarchical model, (ii) a Bayesian model without missing covariates (best case scenario), (iii) Method 1, and (iv) Method 2. For the Bayesian methods, we run the MCMC algorithm for five million iterations and discard the first 20,000 samples as burn in. Samples are drawn from the hierarchical model using independent Monte Carlo sampling, with same sample size of five million.

4.4. Results and analysis

The results under Scenarios 1 and 2, averaged over 100 data sets, are presented in Tables 2 and 3. All results in these Tables are related to the predictive distribution of the response variable. Because the posterior distribution can be skewed, the median of the predictive distribution is used as a robust estimate for point estimation. Its accuracy in predicting the response variable is evaluated using correlation coefficients (between the true response variable and its point estimate), RMSE, and mean absolute error (MAE). For assessing uncertainty, we construct two kinds of prediction sets. Prediction sets with approximately $90\mathrm{\%}$ posterior probability are constructed with end points as 5th and 95th percentiles of the predictive distribution. These are referred to as Equal-tailed sets. We also construct prediction sets using HPD (highest posterior density) regions, which could give smaller sets. Since smaller sets with good coverage are desirable, we look at the cardinality of the $90\mathrm{\%}$ prediction sets for the different methods, and denote it as size in Tables 2 and 3. For this particular application, frequentist coverage is of interest, so we also assess that.

Table 2.

Simulation Scenario 1: Results related to the predictive distribution of the response variable, under Scenario 1, when the first 4 covariates (representing real and GCM SSTs) are included in the true Poisson regression model. Method 1 retains all covariates; Method 2 discards the covariates with missing values. Results are averaged over 100 simulated data sets.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.52	0.49	3.76	2.81	0.95	0.94	17.33	14.64
No missing	0.74	0.70	3.00	2.27	0.93	0.91	10.27	9.65
Method 1	0.69	0.66	3.24	2.44	0.94	0.92	11.18	10.42
Method 2	0.70	0.67	3.18	2.40	0.91	0.90	10.22	9.48

Table 3.

Simulation Scenario 2: Results related to the predictive distribution of the response variable, under Scenario 2, when only the first 2 covariates (representing real SSTs) are included in the true Poisson regression model. Method 1 retains all covariates; Method 2 discards the covariates with missing values. Results are averaged over 100 simulated data sets.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.31	0.29	3.46	2.66	0.94	0.93	14.00	12.65
No missing	0.66	0.61	2.74	2.11	0.94	0.92	9.88	9.28
Method 1	0.56	0.52	3.04	2.33	0.93	0.91	10.83	10.11
Method 2	0.56	0.53	3.03	2.33	0.92	0.89	9.92	9.31

Based on the results reported in Tables 2 and 3, the RMSE and MAE of the Bayesian methods tend to be less than that of the hierarchical method. The Bayesian methods also have reasonably good frequentist coverage with smaller size than the hierarchical method. The difference between Methods 1 and 2 is negligible in terms of point estimates, with very similar RMSE and MAE. Method 1 which retains all variables tends to produce larger sets than Method 2, which discards predictors with missing values during prediction. All methods have frequentist coverage close to $90\mathrm{\%}$.

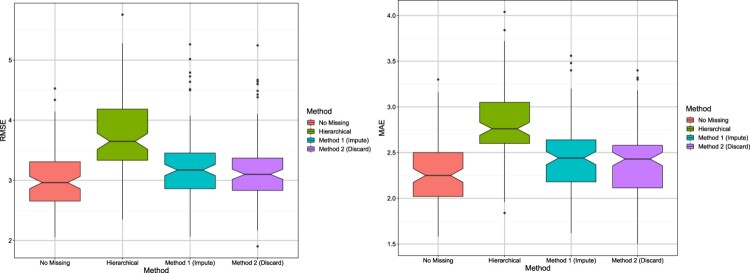
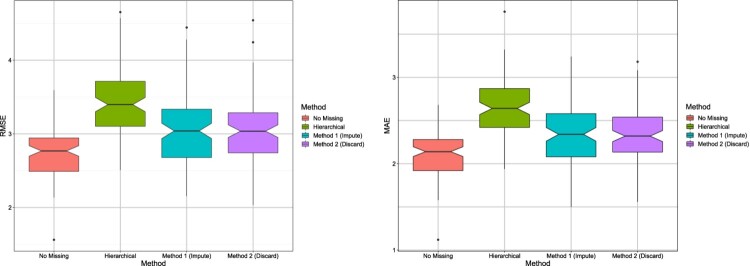
To get an idea of the variability of the results across different data sets, notched box plots [10] are shown in Figures 1 and 2. These are similar to traditional box plots with additional information provided by the notches around the medians, for each box. The notches provide an informal way to test whether the true (population) medians are equal or not. If the notches of two box plots do not overlap, it indicates the true medians are different. The notches for the hierarchical model do not overlap with notches of any of the Bayesian methods, suggesting that the Bayesian methods have substantially improved RMSE and MAE under both scenarios. As expected, the Bayesian method without missing data has the smallest RMSE and MAE.

Figure 1.

Scenario 1: Notched box plots showing RMSE/MAE of each method; results are shown for 100 data sets.

Figure 2.

Scenario 2: Notched box plots showing RMSE/MAE of each method; results are shown for 100 data sets.

To have a better understanding of Methods 1 and 2, we examine their estimates of posterior inclusion probabilities and regression coefficients, under Scenarios 1 and 2, reported in Tables 4–5 and Tables 6–7, respectively. The posterior inclusion probabilities are the same under Method 1 and the case with no missing observations, because they have identical posteriors. In Scenario 1, covariates 1–4 are included in the true model. Method 2 discards covariates 1–2, and thus covariates 3–4, especially 3 seems to be doing double duty to compensate for missing covariate 1, as evident from Tables 4–5. The regression coefficient for covariate 3 seems to compensate for both 1 and 3. A similar phenomenon can be seen in Tables 6–7 under Scenario 2. In Scenario 2 covariates 1–2 are included in the true model. Here covariate 3 (strongly positively correlated with covariate 1) seems to compensate for missing covariate 1. This partly explains why discarding covariates with missing values during prediction, tends to do equally well as retaining those covariates.

Table 4.

Scenario 1: Estimates of posterior inclusion probabilities of 12 covariates; covariates 1–4 were included in the true model; values $>0.75$ are highlighted.

Predictors	Method 1	Method 2	No Missing
1	0.67		0.67
2	0.52		0.52
3	0.70	1.00	0.70
4	0.67	0.84	0.67
5	0.10	0.12	0.10
6	0.10	0.11	0.10
7	0.10	0.11	0.10
8	0.10	0.10	0.10
9	0.09	0.10	0.09
10	0.12	0.13	0.12
11	0.12	0.12	0.12
12	0.12	0.11	0.12

Table 5.

Scenario 1: True and estimated values of regression coefficients $\mathit{\beta }$.

		Method 1 (Retains covariates 1 and 2)	Method 2 (Discards covariates 1 and 2)
Predictors	True value	Mean	Mean
Intercept	1.80	1.80	1.81
1	0.40	0.32	–
2	−0.20	−0.14	–
3	0.35	0.32	0.57
4	−0.25	−0.20	−0.25
5	0.00	0.00	0.00
6	0.00	0.00	0.00
7	0.00	0.00	−0.01
8	0.00	0.00	0.00
9	0.00	0.00	0.00
10	0.00	0.00	0.00
11	0.00	0.00	0.00
12	0.00	0.00	−0.04

Table 6.

Scenario 2: Estimates of posterior inclusion probabilities of 12 covariates; covariates 1 and 2 were included in the true model; values $>0.75$ are highlighted.

Predictors	Method 1	Method 2	No Missing
1	0.89		0.89
2	0.48		0.48
3	0.27	0.97	0.27
4	0.14	0.15	0.14
5	0.09	0.10	0.09
6	0.10	0.13	0.10
7	0.11	0.11	0.11
8	0.11	0.13	0.11
9	0.10	0.11	0.10
10	0.12	0.13	0.12
11	0.11	0.12	0.11
12	0.12	0.14	0.12

Table 7.

Scenario 2: True and estimated values of regression coefficients $\mathit{\beta }$.

		Method 1 (Retains covariates 1 and 2)	Method 2 (Discards covariates 1 and 2)
Predictors	True value	Mean	Mean
Intercept	1.80	1.80	1.82
1	0.50	0.39	–
2	−0.25	−0.12	–
3	0.00	0.03	0.32
4	0.00	0.00	−0.01
5	0.00	0.00	0.01
6	0.00	0.00	0.00
7	0.00	0.00	0.01
8	0.00	0.00	0.00
9	0.00	0.00	0.01
10	0.00	0.00	0.00
11	0.00	0.00	0.00
12	0.00	0.00	0.00

A natural question is how sensitive the results are to the choice of prior hyperparameters. Thus, in addition to the priors specified in 3.1 and 3.2, we consider the choice of ${\lambda }_j=100$, ${\lambda }_{jk}=100$, and a gamma prior with shape parameter 2 and inverse scale (rate) parameter 1/10 on ${\psi }_j$. The results are given in Appendix 2. As summarized in Tables A1 and A2, there is a negligible difference in the point estimates; however there is some difference in the prediction sets which tend to get larger, due to the priors being more diffuse in the present setting. Overall, the posterior does not seem very sensitive to these choices.

5. Illustration of the methods with the north atlantic tropical storms data set

We have data on the frequency of tropical storms, tropical Atlantic and tropical mean SSTs, for the period 1958–2018. TC activity occurs during August to October and SSTs are averaged over this period to serve as predictors in our model. We consider forecasts of SSTs for 1982–2018, from five climate prediction systems which are part of the NMME. The Bayesian models use data from 1982–2018, for all variables, as the climate model forecasts do not exist prior to 1982. The non Bayesian hierarchical model, is set up in such a way, that it uses data from 1958–2018 for estimating regression coefficients.

Data from 1982–2010 were used as a testbed when the climate prediction systems were developed. Thus, we focus on the later period 2011–2018 for prediction. Forecasts of SSTs are issued every month, from 9 to 2 months before the hurricane season. Here we focus on June, July, and August as initialization months, as the forecasts of SSTs before June can be rather inaccurate. Given that the size of the data set is not large, we use leave-one-out predictions for each of the years during 2011–2018. During the period 2011–2018, there are two years with missing forecasts for two (NASA and CMC2) of the five climate models used in the analyses. We choose the ordering of covariates, in our second level sequence of regression models, such that the normality and independence assumptions of errors are reasonable. The names of the response variables and covariates used in the analyses are provided in Appendix 3.

For the Bayesian methods, the MCMC sampling algorithm is run for five million iterations after discarding the first 20,000 samples as burn in. The hierarchical model is run for five million iterations. The same prior hyperparameters used in the simulation studies are applied to this data set. Analysis is done for each month separately. Note that the covariates (GCM SSTs) change across months because forecasts of true SSTs are issued every month by the climate prediction systems. However, the true SSTs and the count of tropical storms during a hurricane season, for a given year, do not change across months. In other words, in each monthly analysis, the same response variable (annual count of tropical storms during a hurricane season) is being predicted, but a new set of covariates (GCM SSTs) is used for each month. Thus, if a covariate is deemed to be important in a given month, say July, it is retained in the Bayesian model for the next month, August, because important covariates from earlier months may improve predictions.

Table 8 shows the marginal posterior inclusion probability for each covariate, by month, which can be used to determine whether a covariate is important or not. Under a discrete uniform prior for the model space, the prior inclusion probability of each covariate is 0.5. For testing ${\gamma }_j=1$ (jth covariate is included) versus ${\gamma }_j=0$ (jth covariate is excluded), the Bayes factor $\frac{p({\gamma }_j=1\mid \mathit{Y},{\mathit{X}}_{obs})/p({\gamma }_j=0\mid \mathit{Y},{\mathit{X}}_{obs})}{p({\gamma }_j=1)/p({\gamma }_j=0)}$ can be used. A value of the Bayes factor greater than 3 provides positive evidence against ${\gamma }_j=0$. The Bayes factor is larger than 3 if the corresponding marginal posterior inclusion probability is larger than 0.75. Thus we use 0.75 as the threshold for retaining a covariate in the model for the next month.

Table 8.

Estimates of marginal posterior inclusion probabilities of 12 covariates for June and July and 13 covariates for August. Values $>0.75$ are highlighted.

Predictor	June	July	August
$GFDLA{06}_{Atl}$	0.64	0.85	0.28
$GFDLA{06}_{Trop}$	0.16	0.20	0.20
$GFD{L}_{Atl}$	0.12	0.10	0.12
$GFD{L}_{Trop}$	0.14	0.16	0.26
$GFDLB{01}_{Atl}$	0.34	0.35	0.33
$GFDLB{01}_{Trop}$	0.17	0.19	0.21
$NAS{A}_{Atl}$	0.27	0.16	0.16
$NAS{A}_{Trop}$	0.27	0.17	0.20
$CMC{2}_{Atl}$	0.09	0.09	0.11
$CMC{2}_{Trop}$	0.19	0.13	0.19
$OB{S}_{Atl}$	0.24	0.16	0.16
$OB{S}_{Trop}$	0.50	0.69	0.66
$GFDLA{06}_{At{l}_{July}}$	–	–	0.79

It is well known that under high collinearity among covariates, marginal inclusion probabilities of correlated covariates can sometimes be misleadingly low, even though the covariates are strongly associated with the response variable [4]. So, there is a danger of concluding the covariates are not needed, when in fact they are all associated with the response variable. Ghosh and Ghattas [4] noted that such an erroneous conclusion can usually be avoided by also considering the Bayes factor BF(H ${}_{\mathrm{A}}$:H ${}_0$), where H ${}_0$ corresponds to the model which only contains the intercept and H ${}_{\mathrm{A}}$ is the complement of H ${}_0$. All covariates are correlated in our data, and the marginal posterior inclusion probabilities for most of the variables are lower than 0.75, so we also calculate the Bayes factor BF(H ${}_{\mathrm{A}}$:H ${}_0$) for each month. The Bayes factors are 30.403 for June, 60.806 for July, and 40.537 for August. Since the Bayes factor for July is substantially larger than June and August, it seems reasonable to not add any variables from June to July, but add important variables from July to August. We add the GFDLA06 ${}_{Atl}$ from July to August as it has a marginal posterior inclusion probability of 0.85. With this added variable, the Bayes factor BF(H ${}_{\mathrm{A}}$:H ${}_0$) for August increases to 60.798. The results with this additional covariate for August are denoted by ‘(added)’ in Table 11.

Table 11.

Results for August.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.65	0.68	2.92	2.50	1.00	1.00	12.00	11.38
Method 1	0.87	0.93	1.77	1.38	1.00	1.00	15.25	13.88
Method 1 (added)	0.85	0.97	1.50	1.25	1.00	1.00	15.00	13.88
Method 2	0.63	0.69	2.29	1.75	1.00	1.00	15.13	13.75
Method 2 (added)	0.78	0.73	1.80	1.25	1.00	1.00	14.75	13.50

For comparison, both approaches for handling missing covariates are presented: Method 1 retains all covariates and Method 2 discards covariates with missing/unobserved values in the year of prediction. The results summarized in Tables 9–11 show that, overall, the Bayesian methods (1 and 2) give improved predictive performance compared to the hierarchical model [21]. Adding the GFDLA06 ${}_{atl}$ covariate from July to the model in August (‘(added)’ in Table 11) leads to some improvement in RMSE and MAE. The (average) size of the prediction set tends to be larger than the hierarchical method.

Table 10.

Results for July.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.69	0.72	2.98	2.38	1.00	1.00	12.50	12.13
Method 1	0.76	0.82	1.87	1.25	1.00	1.00	14.13	13.38
Method 2	0.71	0.70	2.00	1.50	1.00	1.00	13.50	13.13

Table 9.

Results for June.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.44	0.40	3.14	2.38	0.88	0.88	12.50	12.00
Method 1	0.45	0.34	2.78	2.00	1.00	1.00	13.75	13.13
Method 2	0.37	0.27	2.92	2.25	1.00	1.00	13.50	13.13

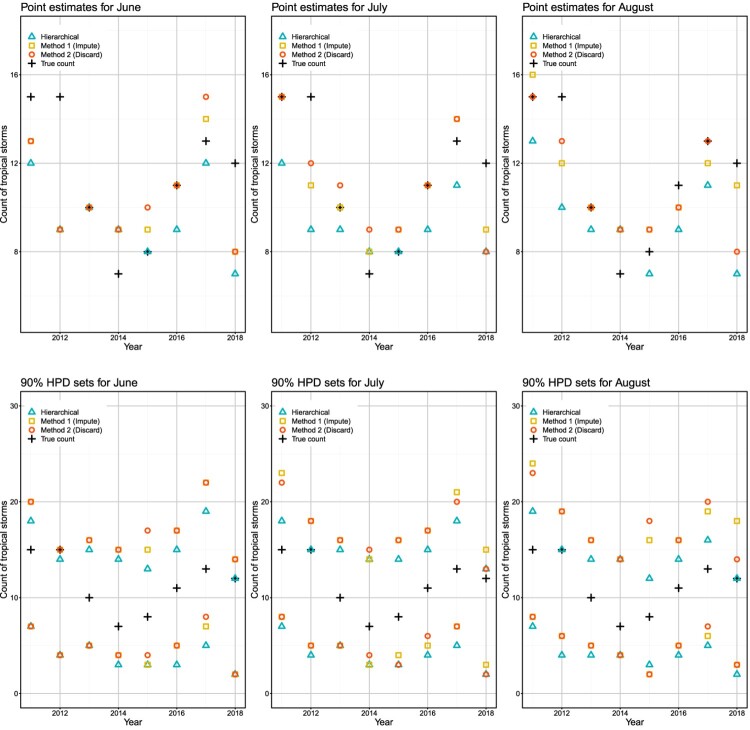
A visual representation of these results is provided in Figure 3. Based on Figure 3, all methods have the largest prediction errors in the years 2012 and 2018. In these two years, the point estimates corresponding to the Bayesian methods with the ‘added’ variable approach, improve from June to July and retain the improvement in August. The hierarchical model tends to underestimate the uncertainty compared to the Bayesian methods. For example, in 2012, the upper limit of the 90 $\mathrm{\%}$ prediction set for the hierarchical model, is lower than the true count of tropical storm in June, and it coincides with the true count in July and August.

Figure 3.

Top panel: Plots showing the observed and predicted (based on medians) counts of tropical storms over 2011–2018. Bottom panel: Plots showing the observed counts of tropical storms over 2011–2018, and endpoints of associated 90 $\mathrm{\%}$ prediction (HPD) sets.

6. Discussion and future work

In this paper, we have proposed a Bayesian negative binomial regression model that can incorporate missing covariates and variable selection uncertainty. This model was primarily developed to propose a fully Bayesian alternative to the hierarchical model of Villarini et al. [21]. Based on simulations and the North Atlantic tropical storm data set, we have shown that the Bayesian model can lead to better predictive performance.

We also made an attempt to answer an interesting question, whether we should retain or discard predictors which are missing at the time of prediction. In the set up of our model, we found both methods (retaining or discarding) perform similarly in terms of prediction using point estimates. However, the method that retained all predictors had larger prediction sets with somewhat higher frequentist coverage. Based on our results, predictions with a reduced model can work fairly well and is somewhat less computationally demanding. For example, the approximate running times needed to fit the model and predict for a single year for the real data, are 2.6 hours, 1.6 hours, and 1 second, for Methods 1 and 2, and the hierarchical model, respectively, on the ARGON cluster at The University of Iowa.

In this work, we have implicitly assumed that the missing data are missing at random (MAR), that is the distribution of the missing data mechanism does not depend on the values of the missing data. We think this is a reasonable assumption about the missing pattern in our data. We have also assumed that the parameters governing the distribution of the missing data mechanism are independent of the parameters in the observed data likelihood. This leads to an ignorable missing data mechanism for Bayesian inference and inference can be done based on the observed data likelihood and prior distributions.

Although the Bayesian methods are more time consuming, running an algorithm for 2–3 hours, once per month (when forecasts of SSTs are issued) does not seem daunting. Nevertheless, in the future, we will explore alternative methods that are faster, and try to strike a balance between the hierarchical model and the Bayesian methods in terms of speed and accuracy. In this paper, our focus has been on predicting the count of tropical storms, but several other response variables are also available, such as the number of hurricanes, and variables that measure the duration and intensity of the storms [21]. One direction of future research is to model the response variables in a multivariate regression model framework, that also incorporates variable selection uncertainty and missing covariates.

Appendices.

Appendix 1. Full Conditionals

$$\begin{array}{rl}p(w_i\mid -)& =PG(w_i;Y_i+\eta ,{\mathit{X}}_i^T\mathit{\beta })\end{array}$$ (A1)

$$\begin{array}{rl}p({\beta }_j\mid -)& =(1-{\rho }_j){\delta }_0+{\rho }_{j}N({\beta }_j;E_j,V_j)\end{array}$$ (A2)

$$\begin{array}{rl}{\rho }_j& =1-\frac{1-\rho }{1-\rho +\rho \frac{\varphi \left(0\right)}{\sqrt{\frac{{\lambda }_j}{V_j}}\varphi \left(E_j{V}_j^{-\frac{1}{2}}\right)}}\\ z_i& =\frac{Y_i-\eta }{2w_i}\\ E_j& =V_j\sum _{i=1}^n{x}_{ij}{w}_i(z_i-{\beta }_0-\sum _{h=1,h\ne j}^p{\beta }_h{x}_{ih})\\ V_j& ={(\sum _{i=1}^n{w}_i{x}_{ij}^2+\frac{1}{{\lambda }_j})}^{-1}\\ p(x_{ij}\mid -)& =N(x_{ij};{\mu }_{ij},{\widetilde{{\psi }_{ij}}}^{-1})\end{array}$$ (A3)

$$\begin{array}{rl}& \mathrm{if}{\mathit{x}}_j\text{ is included in the model}\\ {\mu }_{ij}& ={\widetilde{{\psi }_{ij}}}^{-1}(w_i(z_i-{\beta }_0-\sum _{h=1,h\ne j}^p{x}_{ih}{\beta }_h){\beta }_j+{\psi }_j({\theta }_{j0}+\sum _{h=1}^{j-1}{x}_{ih}{\theta }_{jh}))\\ & +{\widetilde{{\psi }_{ij}}}^{-1}\left(\sum _{m=j+1}^p{\psi }_m(x_{im}-{\theta }_{m0}-\sum _{h=1,h\ne j}^{m-1}{x}_{ih}{\theta }_{mh}){\theta }_{mj}\right)\\ \widetilde{{\psi }_{ij}}& =w_i{\beta }_j^2+{\psi }_j+\sum _{m=j+1}^p{\theta }_{mj}^2{\psi }_m\\ z_i& =\frac{Y_i-\eta }{2w_i}\\ & \mathrm{if}{\mathit{x}}_j\text{ is not included in the model}\\ {\mu }_{ij}& ={\widetilde{{\psi }_{ij}}}^{-1}({\psi }_j({\theta }_{j0}+\sum _{h=1}^{j-1}{x}_{ih}{\theta }_{jh})+\sum _{m=j+1}^p{\psi }_m(x_{im}-{\theta }_{m0}-\sum _{h=1,h\ne j}^{m-1}{x}_{ih}{\theta }_{mh}){\theta }_{mj})\\ \widetilde{{\psi }_{ij}}& ={\psi }_j+\sum _{m=j+1}^p{\theta }_{mj}^2{\psi }_m\\ z_i& =\frac{Y_i-\eta }{2w_i}\\ p({\theta }_{jk}\mid -)& =N({\theta }_{jk};E_{jk},V_{jk})\end{array}$$ (A4)

$$\begin{array}{rl}{E}_{jk}& =V_{jk}\sum _{i=1}^n(x_{ij}-{\theta }_{j0}-\sum _{h=1,h\ne k}^{j-1}{x}_{ih}{\theta }_{jh})x_{ik}{\psi }_j\\ V_{jk}& ={\left({\psi }_j(\sum _{i=1}^n{x}_{ik}^2+\frac{1}{{\lambda }_{jk}})\right)}^{-1}\\ p({\psi }_j\mid -)& =Gamma({\psi }_j;\frac{n+j}{2}+c,\frac{1}{2}(\sum _{i=1}^n{(x_{ij}-{\theta }_{j0}-\sum _{h=1}^{j-1}{x}_{ih}{\theta }_{jh})}^2\\ & +\sum _{k=0}^{j-1}\frac{{\theta }_{jk}^2}{{\lambda }_{jk}}+2d))\end{array}$$ (A5)

Table A1.

Simulation Scenario 1 Under ${\lambda }_j=100$, ${\lambda }_{jk}=100$, and a Gamma (2, 1/10) prior for ${\psi }_j$: Results related to the predictive distribution of the response variable, under Scenario 1, when the first 4 covariates (representing real and GCM SSTs) are included in the true Poisson regression model. Method 1 retains all covariates; Method 2 discards the covariates with missing values. Results are averaged over 100 simulated data sets.

					Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.52	0.49	3.76	2.81	0.95	0.94	17.33	14.63
No missing	0.73	0.69	3.03	2.29	0.93	0.91	10.38	9.78
Method 1	0.69	0.65	3.21	2.40	0.94	0.92	11.36	10.66
Method 2	0.71	0.68	3.11	2.33	0.92	0.91	10.35	9.68

Table A2.

Simulation Scenario 2 Under ${\lambda }_j=100$, ${\lambda }_{jk}=100$, and a Gamma (2, 1/10) prior for ${\psi }_j$: Results related to the predictive distribution of the response variable, under Scenario 2, when the first 2 covariates (representing real SSTs) are included in the true Poisson regression model. Method 1 retains all covariates; Method 2 discards the covariates with missing values. Results are averaged over 100 simulated data sets.

Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Coverage		Size
Method	Cor.Pearson	Cor.Spearman	RMSE	MAE	Equal-tailed	HPD	Equal-tailed	HPD
Hierarchical	0.31	0.29	3.46	2.66	0.94	0.93	14.00	12.65
No missing	0.65	0.60	2.78	2.14	0.94	0.93	10.11	9.78
Method 1	0.56	0.52	3.04	2.33	0.93	0.91	10.98	10.38
Method 2	0.55	0.52	3.02	2.32	0.92	0.89	10.13	9.82

Appendix 3. The Models Used in the Tropical Storm Example

In this section, we provide the list of models used in the analysis of the tropical storm data set. The covariates for the second level linear regression models were chosen after careful examination of the residual plots, to check the assumptions of normality and independence of residual errors. The conditional regression models for the response variable and each missing predictor, for Method 1, are summarized in Tables A3–A5, for June, July, and August. The same models were also used for Method 2, except in June, when the model for $CM{C}_{Atl}$ had the predictors $GFDL{A}_{Trop}$ and $GFD{L}_{Trop}$.

Table A3.

Models for June.

Response
TS	$OB{S}_{Atl}$	$OB{S}_{Trop}$	$NAS{A}_{Atl}$	$NAS{A}_{Trop}$	$CM{C}_{Atl}$	$CM{C}_{Trop}$
intercept	intercept	intercept	intercept	intercept	intercept	intercept
$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$		$GFDL{A}_{Atl}$		$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$
$GFDL{B}_{Atl}$			$GFDL{B}_{Atl}$		$GFDL{B}_{Atl}$	$GFDL{B}_{Atl}$
$GFD{L}_{Atl}$			$GFD{L}_{Atl}$	$GFD{L}_{Atl}$	$GFD{L}_{Atl}$	$GFD{L}_{Atl}$
$GFDL{A}_{Trop}$			$GFDL{A}_{Trop}$		$GFDL{A}_{Trop}$	$GFDL{A}_{Trop}$
$GFDL{B}_{Trop}$			$GFDL{B}_{Trop}$		$GFDL{B}_{Trop}$	$GFDL{B}_{Trop}$
$GFD{L}_{Trop}$		$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$
$OB{S}_{Atl}$		$OB{S}_{Atl}$	$OB{S}_{Atl}$	$OB{S}_{Atl}$	$OB{S}_{Atl}$	$OB{S}_{Atl}$
$OB{S}_{Trop}$			$OB{S}_{Trop}$	$OB{S}_{Trop}$	$OB{S}_{Trop}$	$OB{S}_{Trop}$
$NAS{A}_{Atl}$				$NAS{A}_{Atl}$	$NAS{A}_{Atl}$	$NAS{A}_{Atl}$
$NAS{A}_{Trop}$					$NAS{A}_{Trop}$	$NAS{A}_{Trop}$
$CMC{2}_{Atl}$						$CMC{2}_{Atl}$
$CMC{2}_{Trop}$

Table A4.

Models for July.

Response
TS	$OB{S}_{Atl}$	$OB{S}_{Trop}$	$CMC{2}_{Atl}$	$CMC{2}_{Trop}$
intercept	intercept	intercept	intercept	intercept
$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$		$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$
$GFDL{B}_{Atl}$	$GFDL{B}_{Atl}$		$GFDL{B}_{Atl}$	$GFDL{B}_{Atl}$
$GFD{L}_{Atl}$	$GFD{L}_{Atl}$		$GFD{L}_{Atl}$	$GFD{L}_{Atl}$
$NAS{A}_{Atl}$	$NAS{A}_{Atl}$		$NAS{A}_{Atl}$	$NAS{A}_{Atl}$
$GFDL{A}_{Trop}$	$GFDL{A}_{Trop}$		$GFDL{A}_{Trop}$	$GFDL{A}_{Trop}$
$GFDL{B}_{Trop}$	$GFDL{B}_{Trop}$		$GFDL{B}_{Trop}$	$GFDL{B}_{Trop}$
$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$
$NAS{A}_{Trop}$	$NAS{A}_{Trop}$		$NAS{A}_{Trop}$	$NAS{A}_{Trop}$
$OB{S}_{Atl}$		$OB{S}_{Atl}$	$OB{S}_{Atl}$
$OB{S}_{Trop}$			$OB{S}_{Trop}$	$OB{S}_{Trop}$
$CMC{2}_{Atl}$				$CMC{2}_{Atl}$
$CMC{2}_{Trop}$

Table A5.

Models for August.

Response
TS	$OB{S}_{Atl}$	$OB{S}_{Trop}$	$CMC{2}_{Atl}$	$CMC{2}_{Trop}$
intercept	intercept	intercept	intercept	intercept
$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$		$GFDL{A}_{Atl}$	$GFDL{A}_{Atl}$
$GFDL{B}_{Atl}$	$GFDL{B}_{Atl}$		$GFDL{B}_{Atl}$	$GFDL{B}_{Atl}$
$GFD{L}_{Atl}$	$GFD{L}_{Atl}$		$GFD{L}_{Atl}$	$GFD{L}_{Atl}$
$NAS{A}_{Atl}$	$NAS{A}_{Atl}$	$NAS{A}_{Atl}$	$NAS{A}_{Atl}$	$NAS{A}_{Atl}$
$GFDL{A}_{Trop}$	$GFDL{A}_{Trop}$		$GFDL{A}_{Trop}$	$NAS{A}_{Atl}$
$GFDL{B}_{Trop}$	$GFDL{B}_{Trop}$		$GFDL{B}_{Trop}$	$GFDL{B}_{Trop}$
$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$	$GFD{L}_{Trop}$
$NAS{A}_{Trop}$	$NAS{A}_{Trop}$		$NAS{A}_{Trop}$	$NAS{A}_{Trop}$
$OB{S}_{Atl}$		$OB{S}_{Atl}$	$OB{S}_{Atl}$	$OB{S}_{Atl}$
$OB{S}_{Trop}$			$OB{S}_{Trop}$	$OB{S}_{Trop}$
$CMC{2}_{Atl}$				$CMC{2}_{Atl}$
$CMC{2}_{Trop}$

Funding Statement

Joyee Ghosh's research was supported by NSF Grant DMS-1612763. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author and do not necessarily reflect the views of the National Science Foundation.

Disclosure statement

No potential conflict of interest was reported by the author(s).