ACES: Optimized Alchemically Enhanced Sampling

Abstract

We present an alchemical enhanced sampling (ACES) method implemented in the GPU-accelerated AMBER free energy MD engine. The methods hinges on the creation of an “enhanced sampling state” by reducing or eliminating selected potential energy terms and interactions that lead to kinetic traps and conformational barriers while maintaining those terms that curtail the need to otherwise sample large volumes of phase space. For example, the enhanced sampling state might involve transforming regions of a ligand and/or protein side chain into a non-interacting “dummy state” with internal electrostatics and torsion angle terms turned off. The enhanced sampling state is connected to a real-state endpoint through a Hamiltonian replica exchange (HREMD) framework that is facilitated by newly developed alchemical transformation pathways and smoothstep softcore potentials. This creates a counter-diffusion of real and enhanced-sampling states along the HREMD network. The effect of differential response of the environment to the real and enhanced-sampling states is minimized by leveraging the dual topology framework in AMBER to construct a counter-balancing HREMD network in the opposite alchemical direction with the same (or similar) real and enhanced sampling states at inverted endpoints. The method has been demonstrated in a series of test cases of increasing complexity where traditional MD, and in several cases alternative REST2-like enhanced sampling methods, are shown to fail. The hydration free energy for acetic acid was shown to be independent of starting conformation, and the values for four additional edge case molecules from the FreeSolv database were shown to have significantly closer agreement with experiment using ACES. The method was further able to handle different rotamer states in a Cdk2 ligand identified as fractionally occupied in crystal structures. Finally, ACES was applied to T4-lysozyme and demonstrated that the side chain distribution of V111χ₁ could be reliably reproduced for the apo state, bound to p-xylene, and in p-xylene→benzene transformations. In these cases, the ACES method is shown to be highly robust, and superior to a REST2-like enhanced sampling implementation alone.

Graphical Abstract

1. Introduction

So-called “alchemical” free energy (AFE) simulations^1–4 are routinely applied in drug discovery in the prediction (ranking) of binding affinities of ligands to protein targets in order to facilitate optimization of potency and selectivity.^5–11 A critical barrier to progress in the field is the ability to accurately and robustly sample the relevant configurational space such that reliable AFE estimates can be made with high precision. Recent advances in AFE software that leverage performance advantages of graphical processing units (GPUs) has significantly extended the accessible timescales that can be routinely achieved in molecular dynamics (MD) simulations.^12–17 However, for most drug discovery applications, the use of GPU-accelerated AFE simulations alone is necessary but not sufficient to achieve the sampling required to obtain robust and reliable statistical free energy predictions.^{7,9,10,18–24} Hence, it is of considerable importance to develop improved enhanced sampling methods for AFE prediction, and implement them into high-performance simulation software. In the present work we report the development of an alchemically enhanced sampling (ACES) method for AFE simulations and its implementation into AMBER’s GPU-accelerated MD engine.

AFE simulations involve the transformation between real physical states along a non-physical “alchemical” pathway. In the case of a relative binding free energy (RBFE) calculation between two ligands “A” and “B”, ligand A is transformed into ligand B along the alchemical pathway, alternately in an aqueous solution environment and in a complex with the protein target. The transformation is parameterized by the alchemical “λ” coordinate such that values of λ=0 and λ=1 represent the “real-state endpoints” for ligands A and B, respectively, and values of 0 < λ < 1 are intermediate alchemical states along the transformation pathway. In the process of this transformation, certain atoms may be “annihilated” by transforming them into so-called “dummy” atoms^25–29 that are decoupled from the environment. In theory, the transformation pathway between the ligands is arbitrary, owing to the fact that the free energy is a state function, and as such, changes in free energy are path-independent. In practice, however, the choice of the transformation pathway is crucial, and has been discussed in detail elsewhere,^30–38 including a comparison of several long-standing and recently developed methods.³⁹ The statistical precision of the free energy estimates is highly sensitive to the phase space overlap of states along the pathway (and particularly at the real-state endpoints),^36,37 such that simulations must be conducted in a series of small steps or else continuously as in λ-dynamics.⁴⁰ This often requires extensive sampling even for fairly modest alchemical transformations.

Enhanced sampling methods for free energy simulations have been discussed extensively in the literature.^{7,9,21,24,41–46} Examples of these methods include Replica Exchange (RE)^47,48 and multiple-replica strategies that use adaptive biasing forces,⁴⁹ umbrella sampling (US),^50,51 parallel or simulated tempering,^47,52–54 metadynamics,⁵⁵ replica-exchange with solute tempering (REST⁵⁶ or REST2⁵⁷), multi-canonical algorithm (MUCA),^58–60 orthogonal space random walk (OSRW),⁶¹ enveloping distribution sampling (EDS/λ-EDS),^37,62,63 thermodynamic integration with enhanced sampling (TIES) and others.^{45,59,64–68}

Of particular background relevance to the current work are “Generalized Ensemble Monte Carlo” methods^45,64,69,70 that use Boltzmann sampling involving exchanges between discrete states that differ either in state variables (e.g., temperature, pH or ionic strength) or Hamiltonian, the latter for which can include completely artificial states designed to “tunnel through” barriers between conformational free energy basins.^71–74 A widely used set of generalized ensemble methods in drug discovery are REST/REST2^57,75 approaches and later variants.^76–79 In these methods, a local selected part of the system is assigned a set of variable “effective temperatures” (created through scaling certain energy terms) each of which are simulated in a separate “window” (simulation) that are connected through a replica-exchange framework. These approaches have two main requirements to achieve enhanced sampling: 1) a mechanism to lower the energy barriers, e.g., through raising the effective temperature^57,75 or modifying/scaling the intramolecular and intermolecular energy terms⁷² such as with softcore potentials;^71,73,74 and 2) Boltzmann exchange of conformational information between windows so that different basins can be explored and sampled. These general ideas have been around for many years,⁵⁰ but their fruition into robust practical methods for prediction of protein-ligand binding affinities has been met with challenges and remains a very active area of research and software development. It is in the details of how these requirements are achieved that distinguishes many of the different methods reported in the literature to date.^80–82

A practical challenge for these methods in AFE simulations is mitigating the often contradictory requirements of the enhanced sampling state and replica exchange framework that otherwise can produce adverse side-effects. Creation of an enhanced sampling state through scaling of interactions between the target sampling region and the environment will inevitably affect the structural integrity of the latter. For example, scaling of the interactions between a ligand and the protein to which it is bound so as to enable enhanced sampling of the ligand can also lead to re-arrangement of the protein binding pocket and/or infiltration of solvent that impairs replica exchange efficiency or can sometimes even corrupt the ensemble of the real-state endpoint. This type of behavior is a known complication for the original REST/REST2 methods^57,75 that originates from large temperature gaps between the “hot” enhanced sampling region and the “cold” surroundings. Progress has been made to reduce these “hot-spot” problems with the generalized REST (gREST) approach.^79,83

We report here an alchemical enhanced sampling method (ACES) implemented into the AMBER free energy tool set^6,16,84–86 that integrates the following features: 1) Creation of localized enhanced sampling states through tuning of intra- and intermolecular energy terms for selected groups of atoms, 2) Design of robust alchemical transformation pathways³⁹ to connect real and enhanced sampling states using new smoothstep softcore potentials, non-linear Hamiltonian mixing and flexible λ-scheduling capabilities, 3) Construction of efficient replica-exchange networks to facilitate Boltzmann sampling of the real-state endpoints and maintain equilibrium between discrete windows along the alchemical transformation pathway(s).

The paper is organized as follows. The Theory section outlines the theoretical development of the method, including introduction of terminology and definitions required to provide precise implementation-level details. The Computational Details are described next, followed by the Results and Discussion. The latter section starts from a simple illustrative example (absolute hydration free energy of acetic acid), followed by examination of outlier cases from the FreeSolv database^87,88 and more complex protein-ligand binding examples in Cdk2 that involve ring flips and T4-lysozyme that involve concerted ligand and protein side-chain conformational changes.

2. Theory

We begin by briefly introducing key terminology and notation that will facilitate later discussion and enable implementation-level details of the ACES approach to be described. Full details can be found in Supporting Information and other work that will be referenced in context.^39,85

2.1. Thermodynamic integration formulation

The free energy is a state function, and thus the free energy difference between thermodynamic states is independent of the path that connects them and can be evaluated by the thermodynamic integration formalism.^89,90 Consider the transformation of a system of N particles in an initial state “0” characterized by potential energy function U₀(r^N), where r^N = r₁, r₂ · · · r_N represents the degrees of freedom of the system (e.g., Cartesian positions of each particle along with any system state variables), to a final state “1” characterized by potential energy function U₁(r^N) having the same degrees of freedom. A thermodynamic parameter λ can be defined to smoothly connect these states through a λ-dependent potential U(r^N; λ) such that U(r^N; 0) = U₀(r^N) and U(r^N; 1) = U₁(r^N). In this case, the change in free energy ΔA_0→1 = A₁ − A₀ can be determined through the thermodynamic integration formula

$$\Delta A_{0\to 1}={\int }_0^{1}d\lambda \cdot \left(\frac{dA}{d\lambda }\right)={\int }_0^{1}d\lambda \cdot {\langle \frac{\partial U\left({\mathbf{r}}^N;\lambda \right)}{\partial \lambda }\rangle }_{\lambda }\approx \sum _{k=1}^M{w}_k\cdot {\langle \frac{\partial U\left({\mathbf{r}}^N;\lambda \right)}{\partial \lambda }\rangle }_{{\lambda }_k}$$ (1)

where the second sum indicates numerical integration over M quadrature points (λ_k, for k = 1, · · · , M) with associated weights w_k. While the free energy is a state function, and formally is invariant to the pathway connecting states, the statistical convergence, and thus the resulting values in finite simulations are very sensitive to the pathway although there are different pathways that could surmount the problems. Similar issues arise for FEP methods with traditional BAR,^50,91 MBAR^92,93 and formally equivalent unbinned weighted histogram analysis methods (UWHAM),⁹⁴ as well as their recent extensions that enable large-scale network-wide analysis using a constrained variational approach (BARnet and MBARnet).⁸⁶

Our goal here is to construct a flexible form of the λ-dependent total potential energy U(r^N; λ) that enables both stable alchemical transformations as well as robust enhanced sampling. We begin the construction of U(r^N; λ) by first considering a decomposition of the potential energy for the real-state endpoints U₀(r^N) and U₀(r^N) without initially considering an explicit λ dependence. These can be expressed in terms of their energy term components (indexed by t) as

$$U_0\left({\mathbf{r}}^N\right)=\sum _t{U}_{0,t}\left({\mathbf{r}}^N\right)$$ (2)

and similarly for U₁(r^N; λ). The energy term components of relevance to the present work are bond stretch, bond angle, torsion, Lennard-Jones, 1–4 Lennard-Jones, PME direct/real space, 1–4 Electrostatic, and PME reciprocal space, and are denoted as U_bond, U_ang, U_tor, U_LJ, U_1−4LJ, U_dir, U_1−4Ele, and U_rec, respectively (also see Table S1 in Supporting Information).

To set the stage for alchemical transformations described below, the energy terms can be further decomposed into interacting sets of atoms divided into three non-overlapping regions as described in details elsewhere³⁹ (see additional details in Table S2 of the Supporting Information): I (immutable - not transforming), CC (transforming constrained coordinate/common core) and SC (transforming separable coordinate/softcore). In previous work⁸⁵ we used the the abbreviations TC and TS for the common core and softcore regions, respectively, but feel that SC and CC are more straight forward. In the context of the alchemical transformation, the I region has the same atomic coordinates, parameters and internal potential energy for both states 0 and 1. The CC region can have different parameters between states 0 and 1, but the coordinates of mapped atoms are constrained to be the same. The SC region also can have different parameters between states 0 and 1, but unlike the CC region each state has its own separable set of atomic coordinates. Within the hybrid single/dual-topology approach in AMBER, the immutable region is represented by a single “topology” and set of coordinates. The transforming region of the system is represented by a formal dual topology with separate sets of coordinates for each state. The CC region has corresponding atoms in each topology constrained to have the same positions in order to facilitate phase space overlap between states during the alchemical transformation. The SC region, on the other hand, has separable independent coordinates for each topology corresponding to states 0 and 1 that can adopt different conformations and do not directly interact with one another. While a detailed illustration of the CC/SC concept can be found elsewhere,³⁹ Figure 1 compares the CC/SC region definitions in the Cdk2 ligand 1h1q and 1h1r example, using the commonly-used Maximum Common Structure (MCS) approach and using the ACES approach when a specific torsion angle is targeted to be enhanced sampled.

Figure 1:

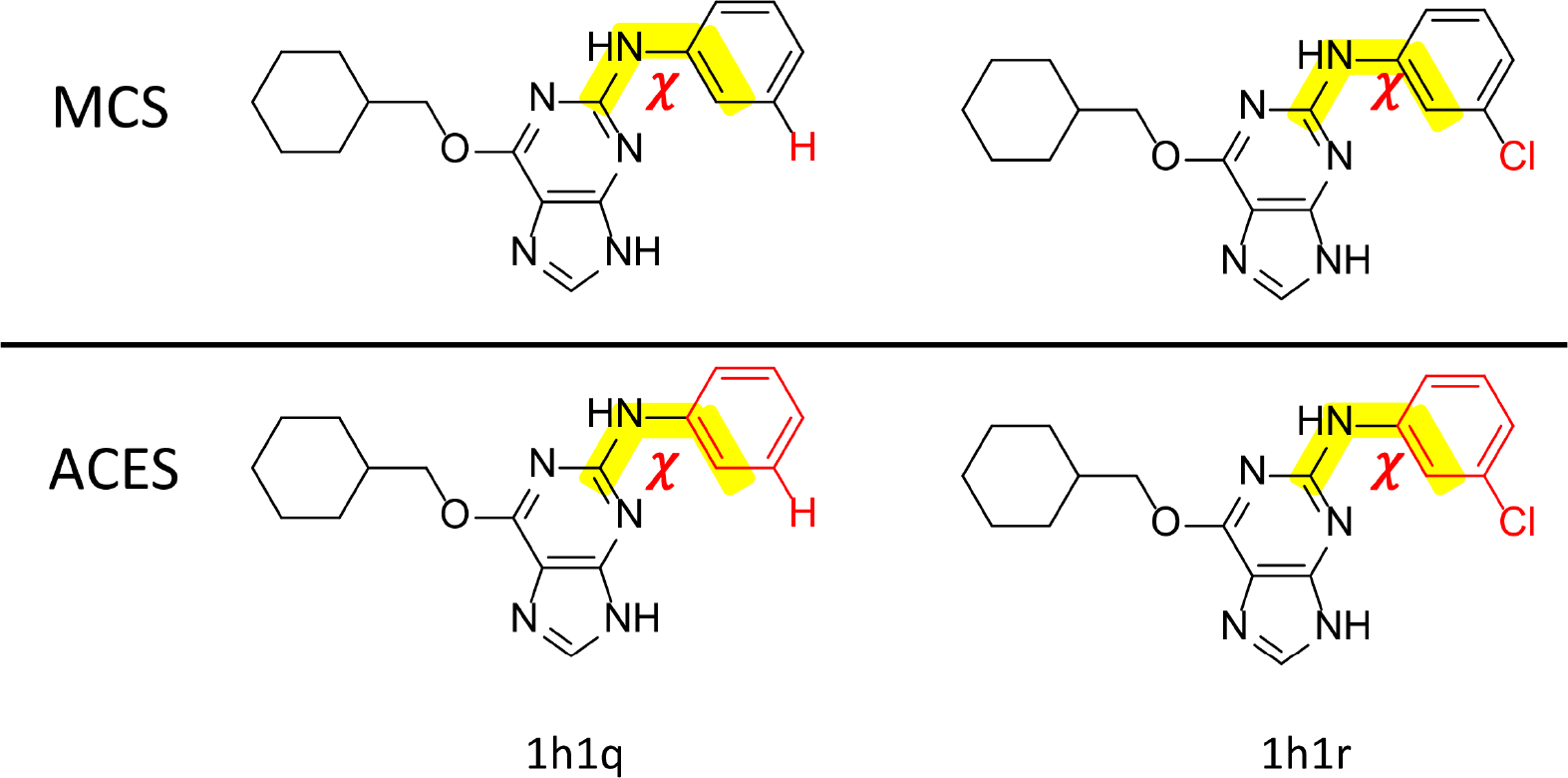
Illustration of the CC/SC regions and torsion angle of the phenyl ring of the 1h1r/1h1q ligands. Upper panel: Maximum Common Structure (MCS) atom-mapping approach⁹⁵ used to define the SC region (shown in red). Lower panel: Using ACES, with the χ angle is the enhanced sampling target and hence the entire phenyl ring is defined as the SC region. The rest of the ligand, i.e., the non-SC part, is defined as the CC region while the environment, solvent or protein, is defined as the immutable (I) region.

Based on the above definitions of regions, we introduce superscripts of the energy term components to indicate the energy decomposition (also see Table S2 in Supporting Information):

• U^SC: Internal energy of softcore (SC) region.

• U^CC: Internal energy of common core (CC) region.

• U^I: Internal energy of immutable (I) region.

• U^(CC+I): Internal energy of the combined CC and I regions.

• U^SC/(CC+I): Interaction energy between SC and (CC+I) regions; U^SC/(CC+I) = U^SC/CC+ U^SC/I.

• U^(SC+CC+I): Total internal of the system; U = U^(SC+CC+I).

The general expanded form of the λ-independent potential energy U₀(r^N) can be written as

$$U_0\left({\mathbf{r}}^N\right)=U_{0,rec}^{SC+CC+I}\left({\mathbf{r}}^N\right)+\sum _{t\ne rec}{U}_{0,t}^{SC}\left({\mathbf{r}}^N\right)+U_{0,t}^{SC/(CC+I)}\left({\mathbf{r}}^N\right)+U_{0,t}^{(CC+I)}\left({\mathbf{r}}^N\right)$$ (3)

and similarly for U₁(r^N). With the exception of the PME reciprocal space energy that is not convenient (cost effective) to decompose, each energy term is divided into three interacting atomic sets: 1) internal energy of the SC region, 2) the internal energy of the (CC+I) region, and 3) the interaction between the SC and (CC+I) regions. Here, the SC/(CC+I) interaction is defined if for any 1, 2, 3 or 4-body potential energy term contains at least one atom in the SC region and one atom in the (CC+I) region.

The decomposition in eq 3 is important as it enables a flexible framework for introducing the required λ dependence into the the total potential energy U(r^N; λ) to enables a robust and stable alchemical transformation pathway. This λ dependence will be integrated in two different ways: 1) λ-dependent softcore potentials to “soften” interactions so as to stabilize transformations involving creation and/or annihilation of atoms or functional groups, and 2) λ-dependent weight functions that alternatively switch off the energy terms of state 0 while turning on those of state 1. Herein we will utilize the recently developed 2nd-generation smoothstep softcore potentials for non-bonded interactions and optimized non-linear weight functions for alchemical transformation pathways that have been described in detail elsewhere.³⁹ The new form, with modified Coulomb and Lennard-Jones exponents in the softcore potentials to achieve consistent power scaling of Coulomb and Lennard-Jones interactions, and with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions, has been shown to be superior to the traditional methods in terms of numerical stability and minimal variance of the free energy estimates.³⁹ The new form has been shown to be superior to the traditional methods in terms of numerical stability and minimal variance of the free energy estimates.³⁹ Here we now extend this framework to create a new alchemical enhanced sampling method.

The general expanded form of the λ-dependent total potential energy U(r^N; λ) can be written as

$$\begin{gathered} U\left({\mathbf{r}}^N;\lambda \right)=W_{0,rec}(\lambda )\cdot U_{0,rec}^{SC+C+I}\left({\mathbf{r}}^N;\lambda \right)+W_{1,rec}(\lambda )\cdot U_{1,rec}^{SC+CC+I}\left({\mathbf{r}}^N;\lambda \right) \\ +\sum _{t\ne rec}{W}_{0,t}^{SC}(\lambda )\cdot U_{0,t}^{SC}\left({\mathbf{r}}^N;\lambda \right)+W_{1,t}^{SC}(\lambda )\cdot U_{1,t}^{SC}\left({\mathbf{r}}^N;\lambda \right) \\ +\sum _{t\ne rec}{W}_{0,t}^{SC/(CC+I)}(\lambda )\cdot U_{0,t}^{SC/(CC+I)}\left({\mathbf{r}}^N;\lambda \right)+W_{1,t}^{SC/(CC+I)}(\lambda )\cdot U_{1,t}^{SC/(CC+I)}\left({\mathbf{r}}^N;\lambda \right) \\ +\sum _{t\ne rec}{W}_{0,t}^{(CC+I)}(\lambda )\cdot U_{0,t}^{(CC+I)}\left({\mathbf{r}}^N;\lambda \right)+W_{1,t}^{(CC+I)}(\lambda )\cdot U_{1,t}^{(CC+I)}\left({\mathbf{r}}^N;\lambda \right) \end{gathered}$$ (4)

The above equation builds off of the decomposition in eq 3 by introducing λ-dependence through the softcore potential, indicated by the addition of the explicit λ parameter argument in the individual energy terms for each state, and the weight functions W(λ) that control the scaling (switching off/on) of state 0 and 1 energy term as λ is varied continuously from 0 to 1. It is in the details of which specific energy terms are scaled by λ and precisely how they are scaled that enables a robust alchemical enhanced sampling approach.

Form of the λ-dependent weight functions W(λ) used to combine/mix energy terms in alchemical transformations

Here we describe a flexible scheme for the scaling behavior of the weight functions W(λ) for different energetic terms and interacting atomic sets that have been implemented in AMBER22.^36,96 The form of the weight functions are chosen from the family of so-called smoothstep functions of different orders P, S_P (λ). These functions and their use in alchemical transformations have been described recently.³⁹ Briefly, these functions have the properties that they are monotonically increasing functions in the interval [0,1] that have endpoint/boundary properties

$$S_P(0)\le 0\text{and}{S}_P(1)\ge 1\forall \text{P}$$ (5)

endpoint derivative properties

$${\left[\frac{d^k{S}_P(x)}{d{x}^k}\right]}_{x=0}={\left[\frac{d^k{S}_P(x)}{d{x}^k}\right]}_{x=1}=0\forall k\in \mathbb{N},0<k\le \text{P}$$ (6)

and symmetry conditions

$$S_P\left(1-x\right)=1-S_P\left(x\right)$$ (7)

The zeroth-order (P = 0) smoothstep function is simply a linear function, S₀(x) = x, 0 ≤ x ≤ 1, and is the only order that does not have derivatives that vanish at the boundaries x = 0, 1. AMBER22 allows flexible selection of the order of the smoothstep function used to define the weight functions, in addition to more advanced λ-scheduling features described in other work.³⁹ Here we use the form of the λ-dependent weight functions validated previously³⁹ that are based on the 2nd-order smoothstep functions using a symmetric norm-preserving constraints, i.e.,

$$\begin{gathered} W_{0,t}(\lambda )=1-S_2(\lambda )=S_2(1-\lambda ) \\ {W}_{1,t}(\lambda )=S_2(\lambda )=1-W_{0,t}(\lambda )=W_{0,t}(1-\lambda ) \end{gathered}$$ (8)

2.2. Flexible control of the λ-scaling in the SC region

In the previous section, the form of the λ-dependent weight functions for scaling energy terms was presented. This section discusses the mechanism to control which specific energy terms involving the SC region should be scaled and which should be retained is discussed. Recall that when an alchemical transformation involves annihilation of particles, these particles do not truly disappear, but rather are transformed into so-called “dummy” atoms.²⁹ Dummy atoms are placeholders that are designed to interact with the real atoms of the physical system only through select bonded interactions such that they do not alter the relative free energy (i.e., they do not introduce a net potential of mean force on any of the real atoms).^25–29,97 Nonetheless, as the dummy atoms still contribute to the potential energy through the internal potential energies between dummy atoms even at the endpoint dummy state, thus they will contribute to the free energy corresponding to a given alchemical transformation. This contribution will amount to an additive constant if simulations are properly sampled and the interactions between dummy atoms and real atoms are treated adequately.²⁹ Under such conditions, the free energy contribution from dummy atoms is independent of the environment such that it will be canceled if the same alchemical transformation is made in a different environment as is usually the case for solvation and binding free energy simulations, although theoretically it requires careful considerations in certain cases. Transformation of real atoms into dummy atoms requires use of a softcore potential,^{30,31,34,39,98,99} and can be especially challenging if there is poor phase space overlap of neighboring states along the transformation coordinate.^29,100–103 Hence, while the specific choice of the internal energy of the region containing the dummy atoms is theoretically somewhat arbitrary, the ability efficiently sample the necessary configurational space to satisfy theoretical constraint conditions is highly sensitive to this choice. In the present context, real atoms that will be transformed into dummy atoms are contained in the SC region. As will be described in more detail below, we will exploit the flexibility in defining the internal energy of the SC region to create a tunable and focused (local) enhanced sampling state that forms a key element in the ACES approach.

When performing an alchemical transformation, we will refer to the specific energy terms that are being switched off/on by the weight functions in eq 4 as being “scaled by λ” or simply “scaled” (S), whereas those terms that are not are not scaled with λ and are therefore present in the dummy state are referred to as “not scaled” or simply “present” (P) in the dummy state. Alternatively stated, the energy terms that are “scaled” will have weight functions that are λ-dependent controlled by the functional form described above, and the energy terms that are “unscaled” (present in the dummy state) will have weight functions that are constant (unity):

$$W_{\{0/1\},t}^{SC}(\lambda )=\{\begin{array}{ll}{W}_{\{0/1\},t}(\lambda ),\hfill & \text{if}\text{scaled}\text{with}\lambda (“\text{S}”\text{in}\text{Table}1),\hfill \\ 1,\hfill & \text{if}\text{not}\text{scaled}\text{with}\lambda (“\mathrm{P}”\text{in}\text{Table}1);\hfill \end{array}$$ (9)

Recall, ALL interactions between the SC and (CC+I) regions, with the possibly exception of select bonded terms that connect the SC region with the CC region and obey dummy-atom constrain conditions,^25–29,97 are scaled and therefore switched off/on in the alchemical transformation. It is only the terms that affect the internal energy of the SC region (and possibly the select bonded terms across the SC/CC boundary) that we can chose to be unscaled and thus present in the dummy state. AMBER22 enables flexible selection of the scaled and unscaled (present) internal energy terms of the SC region. These options are controlled by the gti_add_sc flag and are summarized in Table 1.

Table 1:

The scaling behavior/λ-dependence of the weight functions in eq. 4, controlled by the gti_add_sc flag, for different energy terms and regions/interactions in AMBER22^a.

Weight Symbol	Energy Term Abbreviation	Region / Interaction	gti_add_sc flag
			1	2	3	4	5	6
$W_{\{0/1\},bond}^{SC}$	bond	SC	P	P	P	P	P	P
$W_{\{0/1\},ang}^{SC}$	ang	SC	P	P	P	P	P	P
$W_{\{0/1\},tor}^{SC}$	tor	SC	P	P	P	S	S	S
$W_{\{0/1\},dir}^{SC}$	dir	SC	P	S	S	P	S	S
$W_{\{0/1\},1-4Ele}^{SC}$	1–4 Ele	SC	P	S	S	S	S	S
$W_{\{0/1\},LJ}^{SC}$	LJ	SC	P	P	S	P	P	S
$W_{\{0/1\},1-4LJ}^{SC}$	1–4 LJ	SC	P	P	S	S	S	S
$W_{\{0/1\},bond}^{SC/(CC+I)}$	bond	SC/(CC+I)	Special treatmentb
$W_{\{0/1\},ang}^{SC/(CC+I)}$	ang	SC/(CC+I)	Special treatmentb
$W_{\{0/1\},tor}^{SC/(CC+I)}$	tor	SC/(CC+I)	Special treatmentb
$W_{\{0/1\},dir}^{SC/(CC+I)}$	dir	SC/(CC+I)	S	S	S	S	S	S
$W_{\{0/1\},1-4Ele}^{SC/(CC+I)}$	1–4 Ele	SC/(CC+I)	S	S	S	S	S	S
$W_{\{0/1\},LJ}^{SC/(CC+I)}$	LJ	SC/(CC+I)	S	S	S	S	S	S
$W_{\{0/1\},1-4LJ}^{SC/(CC+I)}$	1–4 LJ	SC/(CC+I)	S	S	S	S	S	S
$W_{\{0/1\}}^{CC+I}$	all	CC+I	S	S	S	S	S	S
W {0/1},rec	rec	all	S	S	S	S	S	S

^aEnergy terms and interacting regions are defined in the text (and also Tables S1 and S2 of the Supporting Information).

Flags:

S: Scaled (S) with λ (weight in eq 9 set to the λ-dependent weight function) and the corresponding energy term is NOT present in the dummy state.

P: Not scaled with λ (weight in eq 9 set to 1) and corresponding energy term is present (P) in the dummy state.

^bBonded terms between the SC and (CC+I) regions require special treatment such that they obey certain conditions in order that the ensembles generated in the state that contains “dummy atoms” reproduce the same potential of mean force on the real atoms as the real system without the dummy atoms. A discussion of the energy term requirements that satisfy these conditions has been made by Boresch and Karplus^26,27 and Roux and co-workers,^25,28 and recently discussed in depth in the context of alchemical transformations.²⁹

2.3. AlChemically Enhanced Sampling (ACES) method

We have now set the stage for development of the ACES method that can be used as a stand-alone enhanced sampling method or one used in the context of alchemical free energy simulations. As mentioned earlier, there are a number of existing enhanced sampling methods that have been reported,^80–82 an perhaps the most widely cited in the field of drug discovery being the REST/REST2/gREST family of methods.^{56,57,75–78} Our initial strategy was to implement and test some of these methods from their description in the published literature, and in doing so, we confirmed some of the limitations that other studies have recently reported.^{46,79,104–107} In working to overcome these limitations, we arrived at the current ACES method. It should be emphasized that many of the existing enhanced sampling methods share similar conceptual strategies, but it is in the details of how these strategies are actually achieved through choice of enhanced sampling states and their coupling with the environment, functional forms of the pathways connecting states, and approaches to efficient exchange within the generalized ensemble that distinguishes many of the different methods and ultimately makes them into useful practical tools.

The current ACES method brings together three fundamental elements:

• Creation of localized (focused) enhanced sampling states through tuning of intra- and intermolecular energy terms for selected groups of atoms in the SC region

• Design of a robust alchemical transformation pathways to connect real and enhanced sampling end-states using new smoothstep softcore potentials, λ-dependent weight functions and flexible λ-scheduling capabilities

• Construction of efficient Hamiltonian replica-exchange (HREMD) networks to facilitate Boltzmann sampling of the real-state endpoints and maintain equilibrium between windows along the alchemical transformation pathway(s)

The first element creates a fictitious “enhanced sampling” state with barrier-reducing potential energy, whereas the second and third elements work together provide a mechanism to rigorously and efficiently connect the conformational ensembles of the real state and enhanced sampling state endpoints using a Hamiltonian replica exchange framework. To achieve this, the following are needed:

Creation of localized (focused) enhanced sampling state.

The creation of a focused enhanced sampling state has two requirements: 1) selection of the atoms to be targeted for enhanced sampling (i.e., selection of atoms that define the SC region), and 2) selection of the internal SC potential energy terms to be scaled (Table 1). The selection of the atoms to be targeted for enhanced sampling is problem specific and somewhat subjective. As a general guideline, the minimal number of atoms required to distinguish and represent the different important conformational states should be selected. Choosing an excessively large SC region increases the amount of conformational space required in the enhanced sampling state, and as will be discussed below, may also lead to less efficient replica exchange. As a series of examples that will be illustrated in the Results and Discussion, selection could involve: 1) atoms within a single functional group such as a carboxylic acid so as to enhance the sampling of hydrogen bond orientations, 2) atoms of an aromatic ring substituent in a drug compound so as to enhance sampling of orientations that involve high-barrier ring flipping, and 3) atoms within a protein amino acid side chain so as to enhance sampling of coupled ligand-binding/side chain rotamer transitions.

The selection of the internal SC potential energy terms to be scaled should balance the enhanced sampling of relevant conformations by eliminating kinetic traps and conformational barriers, and reduction of phase space volume by excluding non-relevant structures and conformations. We explored the use of all the gti_add_sc options listed in Table 1, and found the single most significant sampling obstacle in the SC region in the enhanced sampling “dummy” state are internal electrostatic interactions. Recall, that both electrostatic and Lennard-Jones interactions between the SC region and the environment (CC+I region) are switched off (not present) in the enhanced sampling dummy state. Whereas the SC internal electrostatic interactions can produce kinetic traps, for example through internal hydrogen bonding, the SC internal LJ terms are weak interactions that can be helpful to maintain as they eliminate phase space associated with conformations that have high-energy atomic overlap. The second most significant sampling obstacle are the torsion angle energy terms. The remainder of the energy terms we not found to significantly enhance sampling and were chosen to remain unscaled so as to benefit from the resulting reduction of phase space volume. For these reasons, moving forward we chose to eliminate both SC internal electrostatic and torsion angle energy terms (gti_add_sc=5 in Table 1) for the ACES method, and for comparison purposes, also ran simulations eliminating only electrostatic interactions (gti_add_sc=2).

Design of a robust alchemical transformation pathways.

The goal is to develop a stable pathway that connects the real state and enhanced sampling state endpoints using the dual topology framework in AMBER and leveraging very recently developed new alchemical free energy transformation methods and infrastructure.³⁹ This form of the softcore potential and weight functions has the following key features:

• use of smoothstep functions to stabilize behavior near the transformation endpoints

• consistent power scaling of Coulomb and Lennard-Jones interactions with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions

• pairwise form based on the LJ contact radius for the effective interaction distance with separation-shifted scaling

• rigorous smoothing of the potential at the non-bonded cut-off boundary

A critically important feature of the new smoothstep softcore potential and alchemical transformation is that path-dependent thermodynamic derivatives are well-behaved and rigorously vanish at the λ=0, 1 end states eliminating commonly encountered instabilities that arise along the transformation pathway but often are most prominent at the endpoints, even when the simulations at the endpoints are stable. These instabilities arise from poor phase space overlap^29,100–103 between neighboring λ windows leading to large variances that in turn directly affect the HREMD acceptance ratio and efficiency. The latest official AMBER22 release offers a rich set of options for customizing alchemical transformation pathways that are not exhaustively explored here. Rather we use the latest tested and validated set of recommended functional forms and control parameters reported in concurrent work.³⁹

Construction of efficient Hamiltonian replica-exchange (HREMD) networks.

Hamiltonian replica exchange has been used in wide variety of contexts for enhanced sampling. In the context of free energy simulations, HREMD also facilitates ensemble equilibrium between different λ windows so as to reduce variance in the free energy estimates. A common issue that can create an obstacle for HREMD sampling is when different Hamiltonians along the λ dimension produce large changes in conformational ensembles and energy differences that create poor phase space overlap.

Consider an enhanced sampling problem involving a single ligand that is bound to a protein target. One strategy that has been used, for example in REST/REST2, is to create a HREMD network whereby the ligand is “annihilated” through transformation into a non-interacting enhanced sampling dummy state in much the same way an absolute binding free energy calculation might be conducted (bearing in mind that certain restraints would be required to maintain the dummy state in the binding pocket²⁹). In the present work, this approach would imply a transformation where the U₀ terms in eq 4 correspond to the ligand annihilation and the U₁ terms would be set to zero such that U(r^N; 0) and U(r^N; 1) would correspond to the ligand real state and enhanced sampling dummy state, respectively. As the U₁ terms are not present, this transformation can be carried out using a single topology. However, at the λ=1 state, the ligand would not be interacting with the protein, potentially causing unwanted or irrelevant re-arrangement of the protein binding pocket and/or infiltration of solvent. Under such circumstances, obtaining efficient exchanges might require a very large number of replicas and/or extensive sampling time.

In order to circumvent this problem in the context of a stand-alone enhanced sampling application, we introduce a real and enhanced sampling state counter-diffusion approach. Rather than creating a HREMD network that has one real-state endpoint at λ=0 and one enhanced sampling state endpoint at λ=1 modeled within a single topology, we introduce a dual topology where both U₀ and U₁ terms in eq 4 correspond to the same ligand but represented by two distinct topologies and coordinate sets (and as above, restraints are used for each topology to maintain the dummy state in the binding pocket²⁹). At λ=0, the U₀ potential would represent the real state of the ligand, but the U₁ potential would be in a pure non-interacting enhanced sampling dummy state. At λ=1, these roles would be reversed. The HREMD network would couple the real and enhanced sampling states for both topologies at the same time, but at both λ=0 and 1 endpoints, the real-state ligand would be fully represented. Similarly, along the entire set of HREMD windows, as the U₀ ligand representation is being annihilated, the U₁ ligand representation is being created such that there is minimal re-arrangement of the protein and solvent environment. In this way the HREMD network facilitates a counter-diffusion of real and enhanced sampling states such that both real-state endpoints achieve enhanced sampling with minimal perturbation along the λ coordinate.

In the context of an alchemical free energy simulation, the ACES method can be applied to any of the real-state endpoints to achieve enhanced sampling. However, in the context of a relative binding free energy calculation that involves the transformation between two somewhat similar ligands, the ACES method can be seamlessly integrated into the free energy simulation itself. The counter-diffusion of real and enhanced sampling states works in the same was as described previously, with the only difference that is a net free energy involved with the transformation that can be easily computed at the same time as the ACES simulations are being conducted.

2.4. Distinguishing features and advantages of ACES

As mentioned previously, there exists a number of methods that utilize conceptually similar alchemical strategies to achieve enhanced sampling that have been discussed in recent reviews.^80,82 It is the details of how these strategies are implemented that distinguish them as practical tools. Meaningful cross-comparison between different methods is made challenging as no one software package has a consistent implementation of all of the methods with the same set of features. Due to the popularity of the REST2 method⁵⁷ for drug discovery applications, we implemented a REST2/gREST¹⁰⁸ like method into the AMBER22 package (see Supporting Information) in order to directly compare with ACES. While the simulation results are reported in Section 4.2, here we provide a brief theoretical comparison of the ACES method developed here with the REST2 method.

The central REST2 equation is given by (U is used for potential energy, instead of E in the original work⁵⁷)

$$U_m^{\text{REST}2}\left({\mathbf{r}}^N\right)=\sqrt{\frac{{\beta }_m}{{\beta }_0}}{U}^{Re/Env}\left({\mathbf{r}}^N\right)+\frac{{\beta }_m}{{\beta }_0}{U}^{Re/Re}\left({\mathbf{r}}^N\right)+U^{Env/Env}\left({\mathbf{r}}^N\right),$$ (10)

where U^Re/Env, U^Re/Re, and U^Env/Env represent the REST–environment, REST–REST, and environment–environment interaction energies, respectively, REST is the region to be enhanced sampled, r^N represents the configuration of the whole system, m is the index of different temperatures with β_m ≡ 1/(k_BT_m), and T₀ is the temperature of interest. This equation illustrates that the REST2 equation is conceptually similar to eq 4 if one relates the REST region with the SC region of the present work, where $\sqrt{\frac{{\beta }_m}{{\beta }_0}}$ is related to the weight functions for interactions between the REST region and the environment, while $\frac{{\beta }_m}{{\beta }_0}$ is related to the weight functions of interactions within the REST region. Typically the weight functions $\sqrt{\frac{{\beta }_m}{{\beta }_0}}$ are only used for non-bonded and torsion terms, and are set to 1 (i.e., “not scaled”) for bond stretch and bond angle terms.⁵⁷ One key difference between eq 4 of the current work and eq 10 of the REST2 approach is that the latter does not discriminate the scaling of different types of energy terms and interactions as in the current method and implementation in AMBER22. This universal treatment of the weight functions in the original REST2 might be not optimal. A follow up improvement, the gREST¹⁰⁸ approach allows different weight functions for different types of interactions that greatly increases the transition probability in REMD and hence reduces the number of replicas needed.

Many of the existing enhanced sampling methods are formulated as an additional layer of HREMD simulations, for example as a set of “boost” replicas connecting to the real-state endpoints as in FEP/λ-REMD⁶⁹ and FEP/REST^109,110 approaches, or in 2D networks as in the FEP/HREMD,^111,112 or condensed 1D variations such as HREST-BP.¹¹³ These added simulations increase the computational requirements of the calculations. In the context of an AFE calculation, the ACES approach makes use of the same discretized alchemical pathway (set of λ windows) used for free energy estimation to enhance sampling without the increase in computational cost of additional simulations. This is achieved through the dual-topology approach used by ACES that has unique advantages also recognized in other work.⁷² The counter-diffusion of real and enhanced sampling states enables tunneling through physical barriers and produces minimal rearrangement of the environment along the λ path. This allows ACES to more easily overcome the local “hot-spot” problems sometimes encountered in REST/REST2 approaches,⁷⁹ and facilitates seamless integration with free energy simulations as will be illustrated in the examples below. The implementation of ACES within AMBER22 further leverages the newly developed optimized alchemical transformation pathways (with flexible λ scheduling) and smoothstep softcore potentials,³⁹ along with custom selection of internal energy terms that enhance sampling by eliminating kinetic traps and conformational barriers while otherwise minimizing the required volume of phase space to be sampled. Combined with the high performance of the GPU-accelerated MD and free energy simulation engine in AMBER, ACES provides a powerful new tool for free energy drug discovery applications.

3. Computational Methods

We describe the relevant molecular system setup and simulation protocols as follows. All simulations in the present work were performed with the pmemd.cuda module of AMBER Drug Discovery Boost package (AMBER DD Boost)⁸⁵ as a modified software patch to AMBER20 that now has been fully implemented and is available in AMBER22.⁹⁶

Absolute hydration free energy simulations:

The hydration free free energy simulations for acetic acid and the selected FreeSolv entries reported in the next section were modeled using the GAFF force field^16,114 and solvated with TIP3P¹¹⁵ waters extending to 12 Å from the ligand. All the initial structures for gaseous simulations were prepared by stripping water from those equilibrated structures in the aqueous phase with a periodic box. One-step concerted softcore potential were used with 11 alchemical states: λ = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. Four independent trials of each simulation were run using different random number seeds to adjust the initial conditions. Each simulation was run in the isothermal-isobaric ensemble for 2.5 ns using a 1 fs timestep. The Berendsen barostat¹¹⁶ and Langevin thermostat¹¹⁷ were used to maintain a temperature of 298 K and 1 atm pressure. The long-range electrostatics were evaluated with the particle mesh Ewald method using a 1 ų grid spacing.^118,119

PMF profile of acetic acid:

The PMF calculations of acetic acid were done with ff14SB¹²⁰ and GAFF force field^16,114 with TIP3P¹¹⁵ waters. There are a total of 61 umbrella simulations involving equally-spaced displacements along the O=C-O-H torsion angle coordinate between 0 and 180 degrees. Each window is minimized and followed by 5 ps equilibration. Each simulation is performed for 2.7 ns (the first 200 ps was discarded and the remaining 2.5 ns was used for data for analysis), and restrained harmonically using a force constant of 200 kcal/mol/rad².

REST2-like enhanced sampling implementation:

To compare the established REST2 and gREST enhanced sampling methods, we implemented a REST2-like enhanced sampling approach in the AMBER DD Boost package. While the details are described in the Supporting Information, the implemented REST2-like enhanced sampling approach provides flexible mechanisms to control interactions withing the enhanced sampling region and the interactions between the enhanced sampling region and its environment and can replicate REST2 and gREST approaches. This REST2-like enhanced sampling implementation also can be utilized together with alchemical transformation simulations to enhance sample the λ = 0 and λ = 1 real states. Three additional windows for REST2-like enhanced sampling are added (resulting in total 14 windows) with effective REST2 temperatures of 367.90K, 465.63K, and 608.16K.

Relative binding free energy simulation preparation:

Cdk2 with 1h1r to 1h1q mutation setup: For the ligands in the protein complex, the crystal structure of the chain A of PDBID:1H1R (Structure of human Thr160-phospho Cdk2/cyclin A complexed with the inhibitor NU6086) is selected as the starting point. Hydrogen atoms were added by the tLeap module. Water molecules were added to have at least 12 Å buffer. Total 40 Na⁺ and 43 Cl⁻ ions were added to counter balance the protein charge and reach the physiological concentration of 0.15 M. The initial positions of ligand 1h1q atoms were simply taken from 1h1r and modified. For the ligands in aqueous solution, the initial structures of ligands were taken from the protein complex, followed by adding water molecules to have at least 15 Å buffer. T4 – lysozyme with xylene to benzene mutation setup: For the ligands in the protein complex, the crystal structure of the chain A of PDBID:3GUM (T4 lysozyme M102E/L99A mutant with buried charge in apolar cavity p-xylene binding) is selected as the starting point. The Cys-Cys bridge bond between Residue 21 and Residue 142 was manually added. Hydrogen atoms were added by the tLeap module. Water molecules were added to have at least 15 Å buffer. Total 34 Na⁺ and 40 Cl⁻ ions were added to counter balance the protein charge and reach the physiological concentration of 0.15 M. The initial positions of benzene atoms were simply taken from xylene and removed the extra atoms. For the ligands in aqueous solution, the initial structures of ligands were taken from the protein complex, followed by adding water molecules to have at least 15 Å buffer.

PMF along the T4-lysozyme V111 χ₁ angle:

Umbrella sampling simulations for PMF along the T4-lysozyme V111 χ₁ angle were performed with 25 windows starting from −180° to 180° with a 15° spacing. A harmonic force constant of 70 kcal/rad² is used to keep the V111 χ₁ angle near the desired range and the simulation of each window is 1 ns. The resulting angle distributions were analyzed using the vFEP program^121,122 to produce the PMF results.

Relative binding free energy simulation protocols:

The protein and the ligand were modeled using the AMBER ff14SB and the GAFF2 force fields,¹²³ respectively, and the condensed phase environment was explicitly modeled with TIP4P Ewald¹²⁴ waters. The whole ligands are defined as the transforming regions (CC+SC) while the phenyl ring is defined as the SC region in the Cdk2 1h1r to 1h1q transformation. The transformations were performed in the modified SSC(2) softcore potentials with (m=n=2, α=0.5; unitless β = 1)³⁹ and with one-step concerted softcore protocol using 21 alchemical evenly-spaced states between λ = 0.0 and λ = 1.0 with spacing of 0.05. SHAKE¹²⁵ with Hydrogen Mass Repartition are applied to both the protein and the ligand.¹²⁶ Each simulation was performed in the isothermal-isobaric ensemble for 25 ns using a 2 fs time step. The Monte Carlo barostat¹²⁷ and Langevin thermostat¹¹⁷ were used to maintain a temperature of 298 K and 1 atm pressure. The long-range electrostatics were evaluated with the particle mesh Ewald method using a 1 ų grid spacing.^118,119 The HREMD exchange interval is 20 time steps.

4. Results and Discussion

In the sections that follow, we compare the effectiveness of different methods to the ACES approach. In order to facilitate these comparisons, we introduce an abbreviated notation that is used in the figures, tables and discussion. We will use the notation “SC1”, “SC2”, ... “SC5” to indicated the integer value of the gti_add_sc flag (1, 2, ... 5) that controlled the energy terms that are scaled by λ in the dummy state indicated in Table 1. When comparisons are being made with and without the use of replica exchange, we use the notation SCX/R and SCX/N to indicate the gti_add_sc=”X” model using HREMD (SCX/R) and not using HREMD (SCX/N). In this notation, the ACES approach is equivalent to SC5/R, but for clarity we will endeavor to consistently refer to this as simply “ACES”. In some instances, we also perform comparison with a REST2/gREST-like enhanced sampling method that has been implemented in the AMBER Drug Discovery Boost package (see details in Supporting Information). This is an endpoint enhanced sampling method that can be used independently or in conjunction with HREMD along the alchemical dimension and also the ACES approach. We indicate the use of the REST2/gREST-like approach applied to the real states with an additional “/E” designation, e.g., SC2/R/E indicates the use of SC2 with HREMD in the alchemical dimension (R) plus REST/gREST enhanced endpoint sampling (E). The notation “ACES/E” indicates the ACES approach with REST/gREST enhanced endpoint sampling (E). it is noteworthy to mention that the addition of HREMD along the λ dimension (“/R”) does not considerably increase the computational cost, as HREMD typically requires a fairly small overhead (~20%) with respect to running independent simulations without HREMD. On the other hand, the addition of REST/gREST enhanced sampling (“/E”) is a significant added computational cost as is adds a new set of replica exchange simulations to those already being performed along the alchemical dimension with “/R”. Finally, in some instances we perform exhaustive umbrella sampling (many independent simulations for a given real or dummy endpoint state) along a selected torsion angle coordinate to generate reference distributions and free energy profiles for comparison, in which case we do not use the “/N”, “/R” or “/E” notation.

4.1. Simple illustrative example: acetic acid

4.1.1. Free energy barriers of acetic acid along the O=C-O-H torsion

It is well known that acetic acid has different favorable conformations of the acid hydrogen in gas phase and in aqueous phase that are also related to the molecular dipole moment. The energy barriers between the syn and anti conformations (about the O=C-O-H torsion) are ~11.0 and ~6.5 kcal/mol in gas phase and in aqueous phase, respectively.¹²⁸ These high energy barriers lead to challenges for accurate calculation of the absolute hydration free energy of acetic acid. One might naively think that simply using a starting structure that had the proton in the correct conformation, should that conformation be known a priori, would solve the problem. In fact, this is not the case in general. Conformational barriers may persist even in the dummy state, depending on how the dummy state is defined. Recall, for an absolute hydration free energy, the dummy state arising from the gas phase and aqueous phase edges are formally identical. However, if there is a large energy barrier between conformations in the dummy state itself, the transformation from the gas phase (syn) will remain trapped in the syn conformation in the dummy state, whereas the transformation from the aqueous phase (anti) will remain trapped in the anti conformation in the dummy state, leading to inconsistent results. In order to remedy this potential problem, one must define the energy terms in the dummy state such that transitions can readily occur between syn and anti, and an enhanced sampling equilibrium can be achieved. This also ensures, that the conformers in the real state will be sampled with the correct occupations. As discussed previously and illustrated below, this can be achieved by inclusion of only the bond, angle and van der Waals terms contribution to the internal SC potential energy in the dummy state (SC5: no electrostatics, torsion angle or 1–4 terms).

In order to establish an independent benchmark for the conformational free energy profile (PMF) for acetic acid, we first performed umbrella sampling simulations scanning the relevant O=C-O-H torsion angle. Figure 2 shows the PMF’s of the O=C-O-H torsion angle of acetic acid in different conditions: in aqueous or gas phases, in real (the acetic acid molecule has full interactions with its environment) or dummy (the acetic acid molecule has no interactions with its environment) states, and with different gti_add_sc flags which control the internal interactions of acetic acid. With SC1, all internal interactions within the SC region (defined as the whole acetic acid molecule) are not scaled and hence present in the dummy states, and the dummy states of the acetic acid both in gas phase and in aqueous phase are exactly the same as the real state in gas phase. This is confirmed and illustrated in the leftmost panel of Figure 2. The forward and reverse barriers of the dummy state with SC1 are 10.9 and 6.5 kcal/mol, respectively. With SC2, the internal electrostatic interactions within the SC region are scaled to zero in the dummy states, and this leads to a dummy state that prefers the anti conformation and energy barriers are similar in magnitude but the order is reversed (forward and reverse barriers are 7 and 11, respectively), shown in the middle panel of Figure 2. With SC5, when only the internal LJ interactions (excluding 1–4 LJ), bond length and bond angles terms are kept in the dummy state (Table 1), the PMFs become essentially flat in the dummy states (forward and reverse barriers less than 0.1 kcal/mol, shown in the rightmost panel of Figure 2). As a result, simulations of latter dummy state will not be kinetically trapped by artificial high energy barriers between the syn and anti conformations, enabling enhanced conformational sampling and free energy convergence using ACES.

Figure 2:

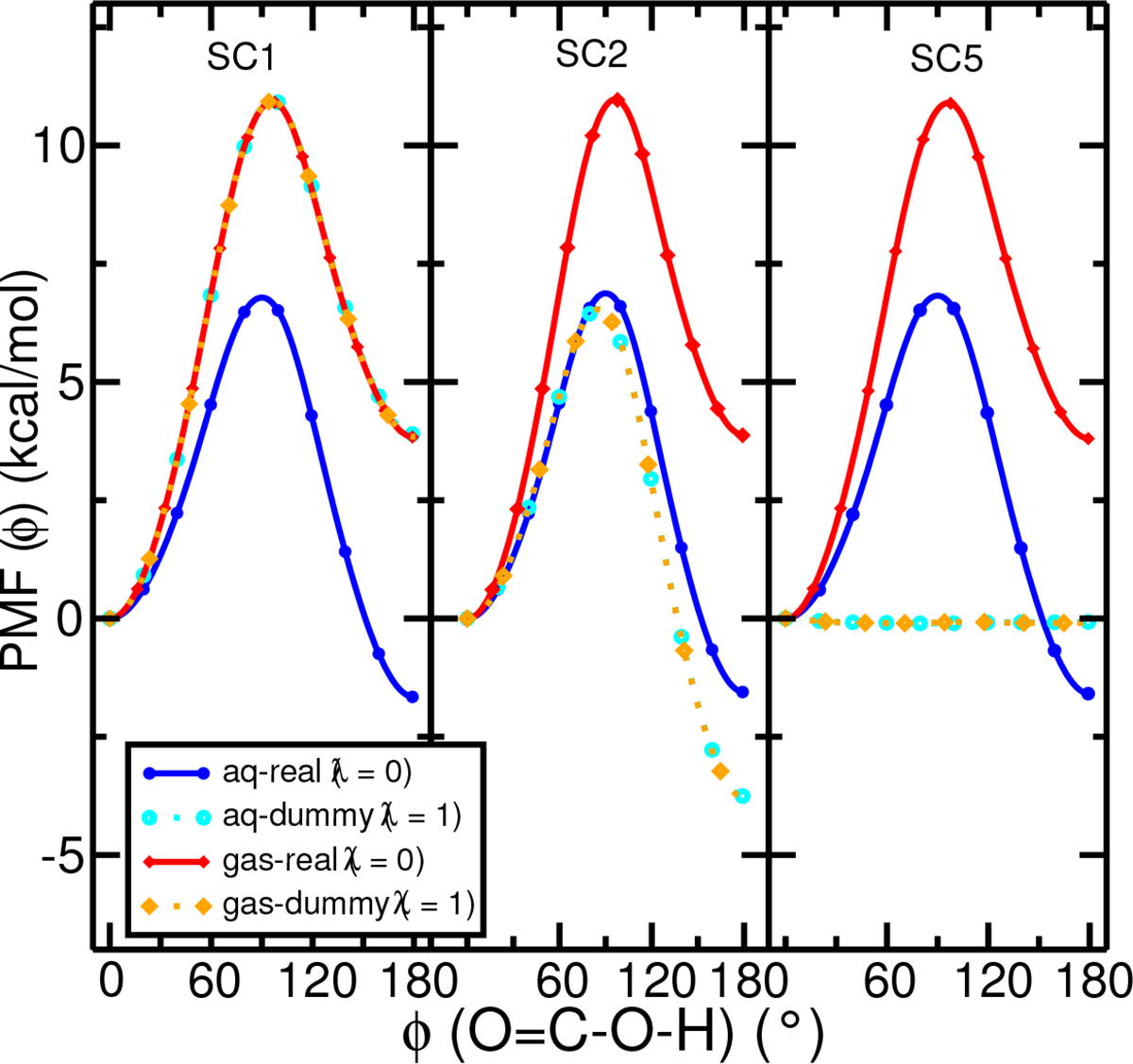
The PMF profiles along the O=C-O-H torsion angle of acetic acid in the aqueous and gas phases, created through umbrella sampling with 61 windows for the real state (λ=0, the acetic acid has full interactions with the environment) and the dummy state (λ = 1, the acetic acid is fully decoupled from the environment) and with three gti_add_sc switches (see Table 1). In the gas phase, the preferred orientation is syn whereas in the aqueous phase, the preferred orientation is anti.

4.1.2. Hydration free energy of acetic acid

In order to achieve the ACES requirement of conformation propagation between different λ-windows, the HREMD framework of AMBER20 is utilized. Herein, we performed the absolute free energy calculation of acetic acid with SC5 but with different starting conformations (Table 2). Since the HREMD framework propagates the conformational ensembles through the different λ states, the real-state endpoint can sample conformations originating from the enhanced sampling dummy state, and will do so in the correct Boltzmann populations. As a result, the computed absolute hydration free energies without the HREMD are 5.33 ± 0.23 kcal/mol and 6.83 ± 0.28 kcal/mol started from syn and anti, respectively. The free energy differences derived from different conformational starting points here reflects the degree to which sampling of the conformations is incomplete (larger differences result from less complete sampling). With ACES (SC5/R), the absolute hydration free energies are 6.06 ± 0.08 kcal and 5.95 ± 0.10 kcal/mol from syn and anti starting conformations, respectively, which are not statistically distinguishable. A previous study of absolute hydration free energy of acetic acid employing multiple real and dummy state conformations connected with rigorous umbrella sampling PMFs⁸⁴ produced 5.96 ± 0.10 kcal/mol, the same as the ACES result here. The agreement suggests that ACES successfully overcomes the conformational challenges in calculating the absolute free hydration free energy of acetic acid.

Table 2:

The forward and reverse energy barriers for acetic acid and the absolute hydration free energy with different gti_add_sc flags.

Method	Phase	ΔG (syn/anti)	SC1	SC2	SC5
PMF profile (dummy state)	aq	ΔG‡ (forward)	10.95	6.54	−0.10
		ΔG‡ (reverse)	7.05	10.29	−0.03
		ΔG	3.90	−3.75	−0.07
	gas	ΔG‡ (forward)	10.94	6.54	−0.10
		ΔG‡ (reverse)	7.10	10.32	−0.01
		ΔG	3.84	−3.78	−0.09
Method	ΔG hyd		SC1/R	SC2/R	ACES
TI with HREMD	starting in syn		4.57	4.41	6.06*
	starting in anti		9.60	9.64	5.95*
	differenc†		5.03 †	5.23 †	0.11 †

All free energy values are in kcal/mol. The data for ΔG (syn/anti) is derived from the PMF profiles for acetic acid in the dummy state (λ=1) as defined by different gti_add_sc flags as follows.

gti_add_sc=1 (SC1): U^SC = U_bond + U_ang + U_LJ + U_tor + U_1–4LJ + U_dir + U_1–4Ele;

gti_add_sc=2 (SC2): U^SC = U_bond + U_ang + U_LJ + U_tor + U_1–4LJ.

gti_add_sc=5 (SC5): U^SC = U_bond + U_ang + U_LJ.

The data for the ΔG_hyd is the hydration free energy as defined by ΔG_hyd=ΔG_aq−ΔG_gas, where the ΔG_gas and ΔG_aq values are obtained from alchemical free energy simulations in the gas phase and in aqueous solution, respectively.

^†The ideal result (in the sampling limit) result should be zero, i.e., ΔG_hyd should not depend on the starting conformation.

4.2. Absolute hydration free energy example: edges cases from the FreeSolv database

The FreeSolv database^87,88 provides an excellent source of calculated and experimental solvation free energies of a wide range of small molecules. In the current latest version (v0.51) of the FreeSolv database, the deviations between the calculated AMBER/GAFF and experimental solvation free energies are generally smaller than 2 kcal/mol. Nevertheless, there are still 34 entries (out of a total of 643) having deviations larger than 3 kcal/mol when comparing the results of experiment and those calculated with a older version of AMBER prior to the methods developed in the current work. We selected 5 FreeSolv database entries (Table 3) with among the largest deviations and that exhibited different accessible conformations in the gas phase and in the aqueous solution, similar to the acetic acid case, in order that they form a set for which calculated hydration free energies would be particularly sensitive to sampling.

Table 3:

The calculated absolute hydration free energy for selected FreeSolv entries with different simulation protocols, along with the experimental values and the errors with respect to experiment^a.

FreeSolv ID	compound name	ΔΔGhyd
		FreeSolv	SC2/N	SC2/R	SC2/R/E	SC5/N	ACES	ACES/E	Expt
2099370	ketoprofen	−17.24(06)	−17.35(09)	−17.48(15)	−14.43(37)	−14.98(38)	−13.09(19)	−13.00(17)	−10.78
1527293	flurbiprofen	−13.95(05)	−5.79(14)	−6.26(15)	−7.17(59)	−9.76(15)	−9.67(17)	−9.51(17)	−8.42
2078467	ibuprofen	−10.86(05)	−10.72(29)	−11.05(16)	−8.13(31)	−8.93(16)	−7.52(15)	−7.60(15)	−7.00
7758918	propionic acid	−9.09(03)	−1.95(09)	−2.09(12)	−2.64(21)	−5.94(17)	−5.72(10)	−5.75(10)	−6.46
3034976	acetic acid	−7.28(02)	−9.63(06)	−9.96(13)	−6.47(22)	−6.62(23)	−5.96(10)	−5.97(09)	−6.69
MAE		3.81	4.07	4.11	2.01	1.61	1.11	1.07
RMSE		4.35	4.31	4.38	2.48	2.16	1.28	1.22

^aAll free energy values are in kcal/mol. The data for the ΔΔG_hyd is the hydration free energy as defined by ΔΔG_hyd=ΔG_aq−ΔG_gas, where the ΔG_gas and ΔG_aq values are obtained from alchemical free energy simulations in the gas phase and in aqueous solution, respectively. As defined in the text, SC2 refers to gti_add_sc=2, SC5 to gti_add_sc=5, R to HREMD, and E to REST2/gREST-like enhanced sampling. The entries under the heading “FreeSolv” are those reported in the FreeSolv database^87,88 for version 0.51 (latest version at this time).

Table 3 shows the hydration free energies of the five selected FreeSolv entries calculated with different enhanced sampling protocols: SC2/R, SC2/R/E, ACES and ACES/E, where as mentioned previously, the “R” indicated HREMD along the λ dimension, and “/E” indicates additional REST2/gREST-like enhanced sampling applied to the real states (i.e., λ = 0). The mean absolute error (MAE) and RMS error (RMSE) with respect to experimental values reported for by FreeSolv (using a different protocol described in published work^87,88) are 3.8 and 4.4 kcal/mol, respectively. The results for SC2/R show similar MAE and RMSE (4.1 and 4.4 kcal/mol, respectively), although individual errors values differ. Upon additional REST2/REST-like real-state sampling (SC2/R/E), the MAE and RMSE are significantly reduced to 2.0 and 2.5 kcal/mol, respectively. The ACES values, on the other hand, are considerably improved (MAE/RMSE 1.1/1.2 kcal/mol) that is relatively insensitive to additional enhanced sampling with ACES/E (MAE/RMSE 1.1/1.2 kcal/mol). The origin of these differences involve the inability of SC2 to overcome barriers in the dummy state that creates kinetic traps and hinders enhanced sampling all along the λ dimension. While application of additional REST2/gREST-like sampling to the SC2/R (i.e., SC2/R/E) results in reducing errors by roughly 1/2. The SC2/R/E is expected to improve the sampling of the real state itself, but not the dummy state and not necessarily more non-locally along the λ dimension. The relative invariance of ACES with respect to additional REST2/gREST sampling (ACES/E) suggests that the ACES method alone is able to accomplish the required enhanced sampling.

This simple examples highlight a few key points. First, HREMD is needed along the λ dimension. Second, for HREMD to be effective as an enhanced sampling mechanism, the real-state endpoint must be connected with an enhanced sampling dummy state (this can be achieved through the dual topology ACES approach at minimal cost, or partially through REST2/gREST-like approach). Third, use of REST2/gREST alone on the real-state endpoint does not guarantee the required enhanced sampling along the full λ dimension (and particularly to avoid traps latent in the dummy state endpoint) needed to improve the free energy estimates. In the remainder of the manuscript, we examine two successively more complex examples that involve protein-ligand binding and correlated side-chain conformational transitions. For these examples, we focus on demonstrating that the ACES approach is robust and can overcome the limitations of other selected methods, but in doing so we select the most relevant illustrative methods and do not exhaustively compare to all the combinations enumerated and analyzed in this section.

4.3. Protein-ligand binding example: 1h1r → 1h1q transformation in Cdk2

In this section we apply the ACES approach on a well-known protein-ligand binding problem: the 1h1r/1h1q ligands bound to Cdk2.^12,129,130 The torsion angle of the phenyl ring (Fig. 1) of the 1h1r ligand has two distinguished states, syn (torsion angle = −8.81 ° ) and anti (torsion angle = 150.75 °), in the crystal structure (PDBID: 1H1R¹²⁹). A binding free energy study using the REST2 enhanced sampling approach¹¹⁰ has demonstrated that simulations without enhanced sampling cannot access both syn and anti conformational states and utilizing the REST2 approach will at least in part overcome the problem.

We applied ACES on this system with different starting conformational states and studied the distributions of both syn and anti conformational states in the Cdk2–1h1r to Cdk2–1h1q alchemical relative binding simulations (details of the simulation set up and protocol are described in the Computational Methods section). Figure 3 shows the time series and distributions of the relevant torsion of the real state of 1h1r (λ = 0) with and without ACES. ACES is clearly able to to sample both states, leading to the same population ration (80:170 for anti:syn) regardless of the starting conformation. This ability is particularly important when the relative occupations of syn and anti conformational states changes during a transformation from one ligand into another.

Figure 3:

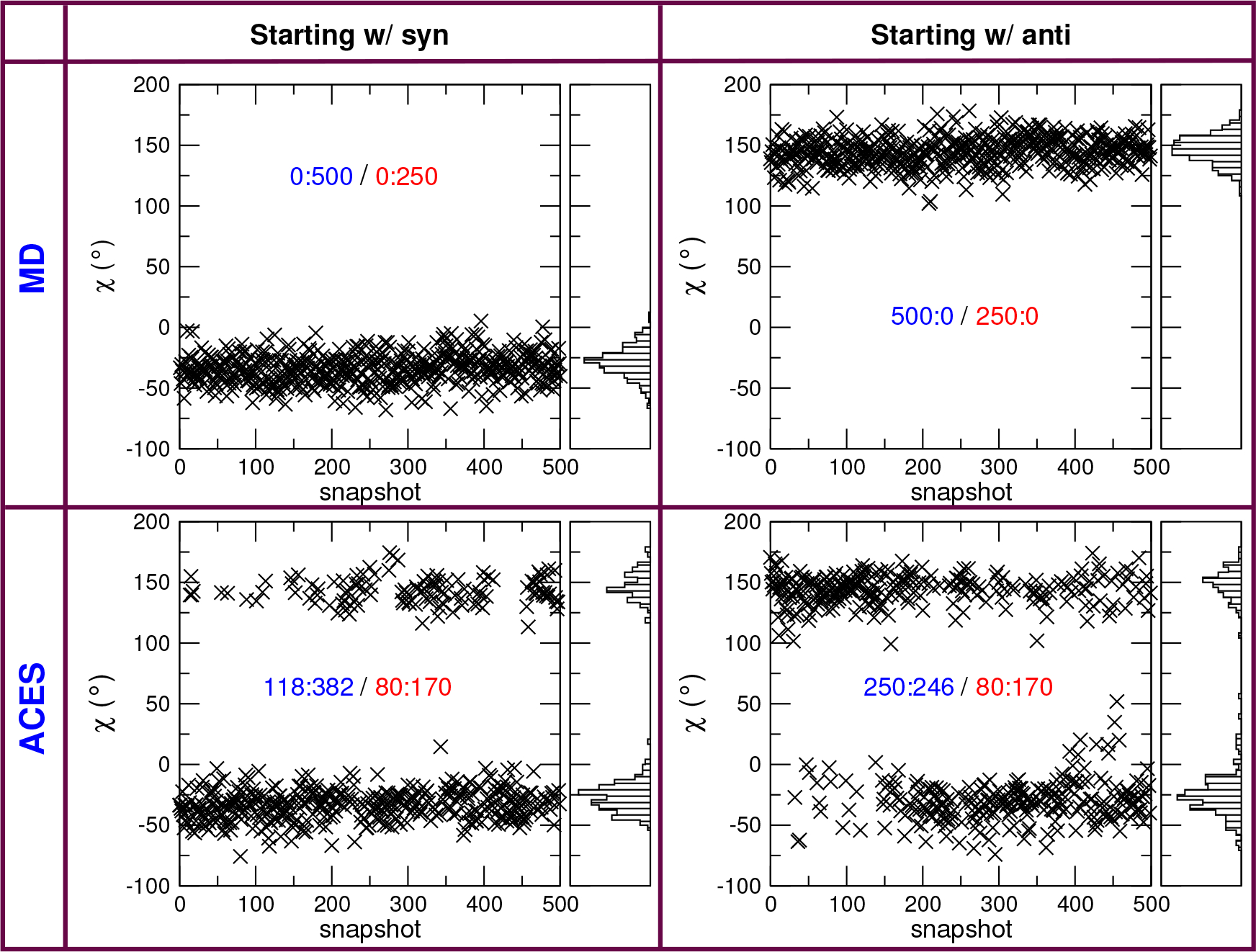
Time series (5 ns) of the relevant torsion angle with and without ACES from Cdk2–1h1r to Cdk2–1h1q alchemical relative binding simulations. The distributions are for the the real state of 1h1r (λ = 0). Without ACES, the ligand torsion will stay trapped in the initial conformation (syn or anti) for the duration of the simulations. With ACES, the ligand torsion will jump between syn and anti regardless of the initial conformation. The distribution figures are created for the last 2.5 ns data and show that ACES delivers similar distributions for simulations starting from different initial conformations. The number pairs are the counts of (anti:syn) and the blue colored pairs are for all 500 snapshots collected while the red pairs are for the last 250 snapshots (i.e., the last 2.5 ns).

In the present example, the occupations do not change significantly, and both syn and anti states are thermally accessible (as supported by the fact that both states are observed in the crystal structures with partial occupancy¹²⁹). Table 4 lists the calculated relative binding free energies (ΔΔG values) of Cdk2–1h1r to Cdk2–1h1q alchemical simulations using different procedures. Without ACES using SC2/N, SC5/N and SC2/R methods, the calculated ΔΔG values starting from syn and from anti conformations give about a 0.2 kcal/mol difference, although as illustrated previously these methods produce different anti/syn distributions. As these states are similar in energy and populated in both the 1h1r and 1h1q states, we do no expect a significant resulting free energy result (although in other work using a different force field, a difference between FEP/MD and FEP/REST2 of 1.43 kcal/mol has been reported¹²). With ACES, the calculated ΔΔG values starting from syn and from anti conformations in Table 4 give statistically identical results (0.02 kcal/mol difference, which is below the statistical error estimates).

Table 4:

The calculated relative binding free energies (ΔΔG) of Cdk2–1h1r to Cdk2–1h1q alchemical simulations under various conditions. The bold entries are for ACES (SC5 and REMD enabled) while others are without ACES. The results are calculated from 20 ns trajectories with the last 15 ns for analysis.

	Starting w/ syn	Starting w/ anti
SC2/N	0.41(27)	0.63(28)
SC5/N	0.46(32)	0.55(22)
SC2/R	0.33(20)	0.50(13)
ACES	0.50(16)	0.48(12)

SC2/N: Simulation with SC2 and without HREMD.

SC5/N: Simulation with SC5 and without HREMD.

SC2/R: Simulation with SC2 and with HREMD.

ACES: Simulation with SC5 and with HREMD.

4.4. Coupled ligand-binding/side chain rotamer transition example: T4-lysozyme V111 χ₁ angle

The L99A mutant of the T4 lysozyme (T4L) is a classic example of conformational changes upon the binding of various aromatic molecules to the nonpolar cavity of the protein and hence a good illustration case for enhanced sampling methods.^131–134 Specifically, for the bound complexes with small ligands, e.g., benzene, the side chain torsion of Valine 111, the V111 χ₁ angle, has a dominant trans (180°) population with a smaller population of gauche+ (~ +60°), while with larger ligands such as p-xylene, the V111 χ₁ angle still has a dominate trans population but the second largest population is now gauche-(~ −60°). The energy barriers around the V111 χ₁ angle are sufficient (~ 5–10 kcal/mol) to prevent the side chain from rotating and visiting different conformation states effectively on the time scale of typical practical MD and free energy simulations; hence simulations started from the different rotation states of V111 will likely deliver different resulting conformational distributions. It has been further suggested that larger scale conformation changes involving multiple residues need be considered in order to get accurate estimations of the binding free energy,⁶⁹ which is beyond the scope of the current work. Here, we focus only on one key aspect of the problem: the V111 χ₁ distributions in different environments and using different sampling procedures.

We performed various simulations on T4L complexed with benzene and p-xylene, and analyzed the V111 χ₁ distributions using umbrella sampling and different methods and transformations between (B) and p-xylene (X) (see Computational Details):

• Umbrella sampling (US) simulations on T4L-p-xylene complex, T4L-benzene complex, and T4L apo state, to obtain the relevant baseline PMF curves along the V111 χ₁ angle.

• alchemical simulations of p-xylene to benzene transformation in T4L complex, where the V111 side chains are defined as part of the SC region in both end states. The two non-ring carbon atoms and their connected hydrogens of p-xylene, and the corresponding hydrogens of benzene are included in the SC regions as well. We denote this alchemical simulation as XB.

• alchemical simulations of p-xylene to dummy state transformation in T4L complex, where the V111 side chains are defined as part of the SC region in both end states. We denote this alchemical simulation as X0.

• alchemical simulations of p-xylene to p-xylene transformation in T4L complex, where the V111 side chains as well as the entire p-xylene molecules are defined as part of the SC region in both end states. We denote this alchemical simulations as XX.

Figure 4 shows the baseline PMF results (the left y-axis in kcal/mol) from US simulations (shown on the leftmost column), the predicted V111 χ₁ distributions based on the PMF results (gray curves in all sub-figures), and the histogram distributions from simulations using SC2/N, SC2/R and ACES (from 2500 snapshots and with 45 bins between −180° and 180°, the right y-axis is the histogram count). The upper, middle, and the bottom rows correspond to the p-xylene-bound, benzene-bound, and apo states. respectively. While the PMF results are qualitatively similar to previously reported,^69,111,135 the calculated energy barriers here differ by about 1–2 kcal/mol. In the XB simulations, the p-xylene-bound state is the λ = 0 real state and the distribution of the first copy of V111 in the dual topology (V111₁) is shown; while the benzene-bound state is the λ = 1 real state and the distribution of the second copy of V111 in the dual topology (V111₂) is shown. In the X0 simulations, the apo state is the λ = 1 real state and the distribution of the second copy of V111 in the dual topology (V111₂) is shown.

Figure 4:

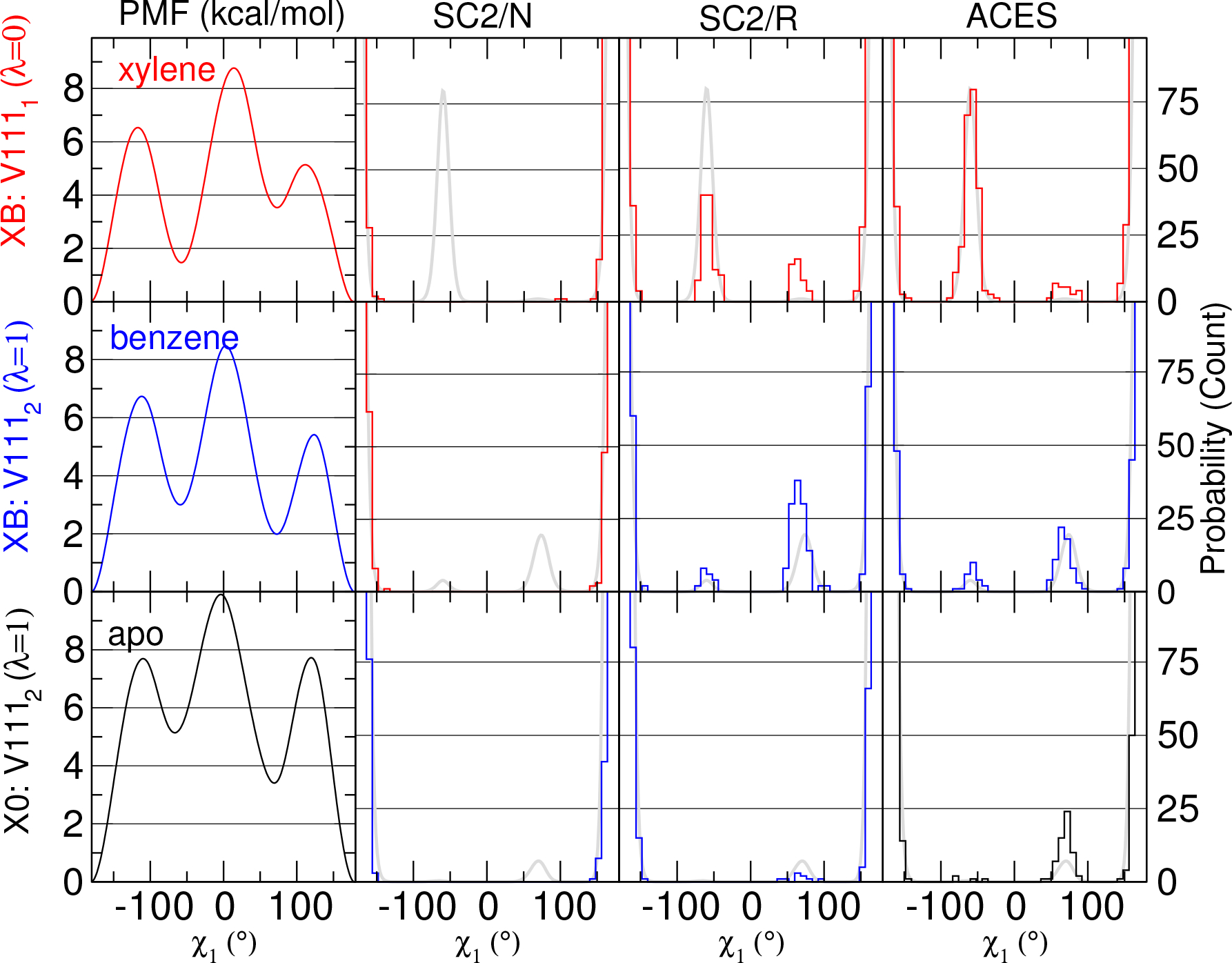
Comparison of the PMF results, and their resulting predicted V111 χ₁ histogram distributions (from 2500 snapshots and with 45 bins between −180° and 180°, the y-axis is the histogram count) along with histogram distributions of real states of alchemical simulations with different protocols. In all cases, V111 is contained in the enhanced sampling SC region for both end states and are contained in both copies of the dual topology. V111₁ and V111₂ indicate the first or second copy of the side chain within the dual topology. Hence for xylene→benzene (XB), at λ=0 the system is represented as xylene in the first copy of the topology that contains V111₁, whereas at λ=1 the system is represented as benzene in the second copy of the topology that contains V111₂. For xylene→0 (X0), at λ=1 the system is in the enhanced sampling “dummy” state such that the apo enzyme is represented by the second copy of the topology that contains V111₂.

The ACES results of all three binding states (the rightmost column in Figure 4) are consistent with the PMF reference results (shown as gray curves), suggesting that ACES naturally produces the correct distributions without explicitly sampling along a predefined torsion coordinate. Contrarily, the SC2/N results of all three binding states (the second column from left in Figure 4) produce trans only distribution, suggesting the simulations were trapped in the local trans basins. Nevertheless, the SC2/R results of all three binding states (the second column from right in Figure 4) suggest that the reduction of energy of the dummy states with SC2, although can escape the local energy traps to certain degree, is not quite enough to produce the desired distributions, demonstrated by the overpopulated gauche+ (~60°) distributions of the p-xylene and benzene bound states and underpopulated gauche+ distributions of the apo states.

To further understand the underlining reasons leading to the incorrect distributions from the (SC2 /R) simulations, we examine the corresponding distributions of the dummy states. Figure 5 shows the V111 χ₁ histogram distributions from SC2/N, SC2/R and ACES simulations. The upper, middle, and the bottom rows are referred to the same simulations as shown in Figure 4 but the distributions are for the dummy copy V111s, instead of the real copy V111s.

Figure 5:

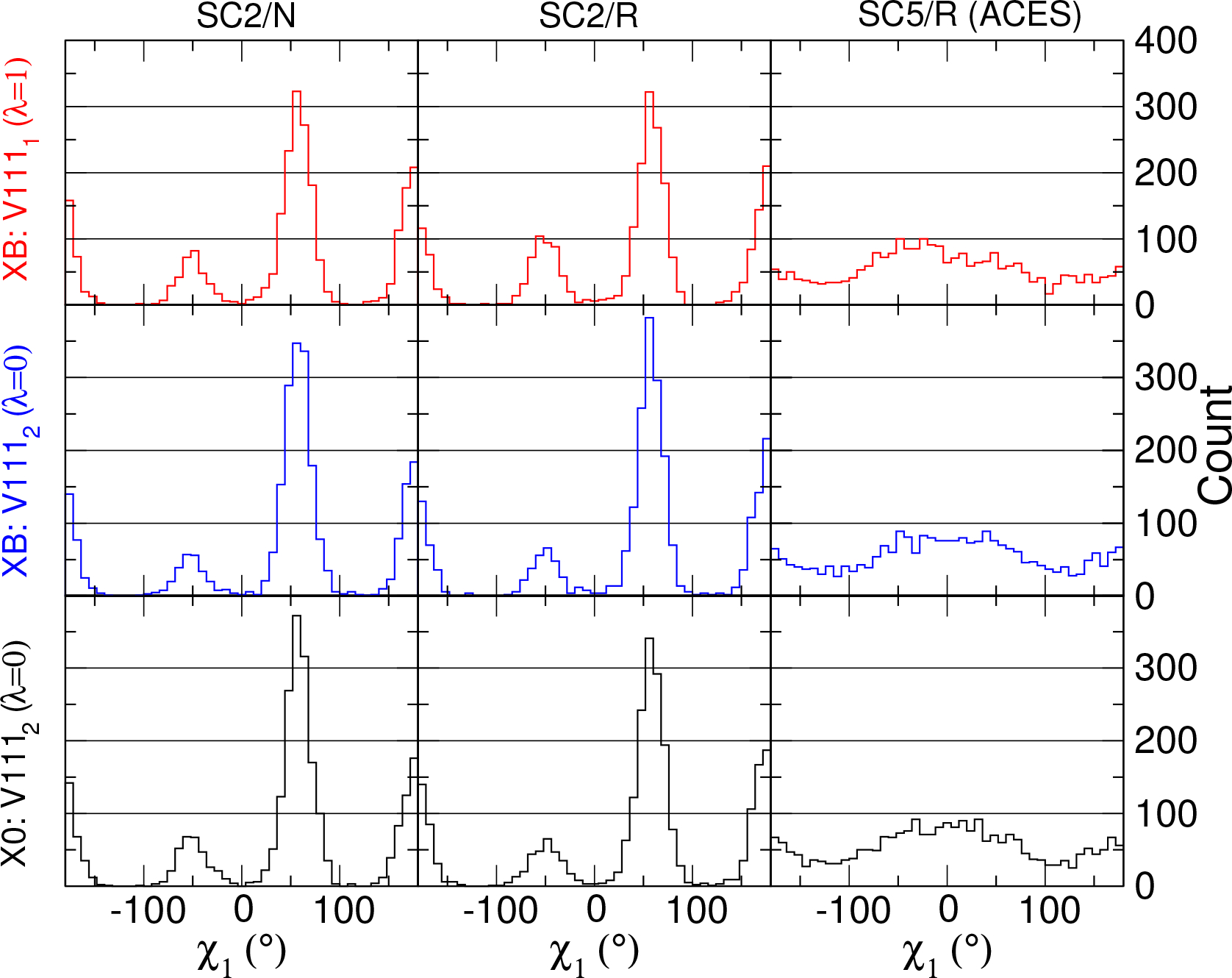
The V111 χ₁ histogram distributions (from 2500 snapshots and with 45 bins between −180° and 180°, the y-axis is the histogram count) of dummy states from different alchemical simulations protocols.

The SC5/R results of all three binding states (the rightmost column in Figure 5) show that the V111 χ₁ can almost freely rotate in its dummy state with SC5; while the rotation is still hindered with SC=2 (the left and the middle column, regardless of the usage of replica exchange). The results shown in Figure 4 and Figure 5 reconfirm what has been observed from the acetic acid case: to produce the correct distribution, or to effectively escape the local energy traps, a simulation must have an enhanced sampling dummy state that is able to overcome relevant conformational barriers and provide and effective replica exchange mechanism to transmit that information along the λ dimension and to the real state.

To further explore different ways that ACES can be applied, we examine the V111 χ₁ distributions from alchemical transformations with different SC region definitions. Figure 6 shows the V111 χ₁ histogram distributions of V111 of the p-xylene-bound states from different alchemical transformation simulations. The upper sub-figure shows the result of the second copy of V111 at λ = 1 in the XX simulation. The middle sub-figure shows the result of the first copy of V111 at λ = 0 in the XX simulation. The bottom sub-figure shows the result of the first copy of V111 at λ = 0 in the XB simulation. The results show that SC5/R (ACES) give virtually the same results from the p-xylene real state of the XB simulations and from the both copies of p-xylene in the XX simulations.

Figure 6:

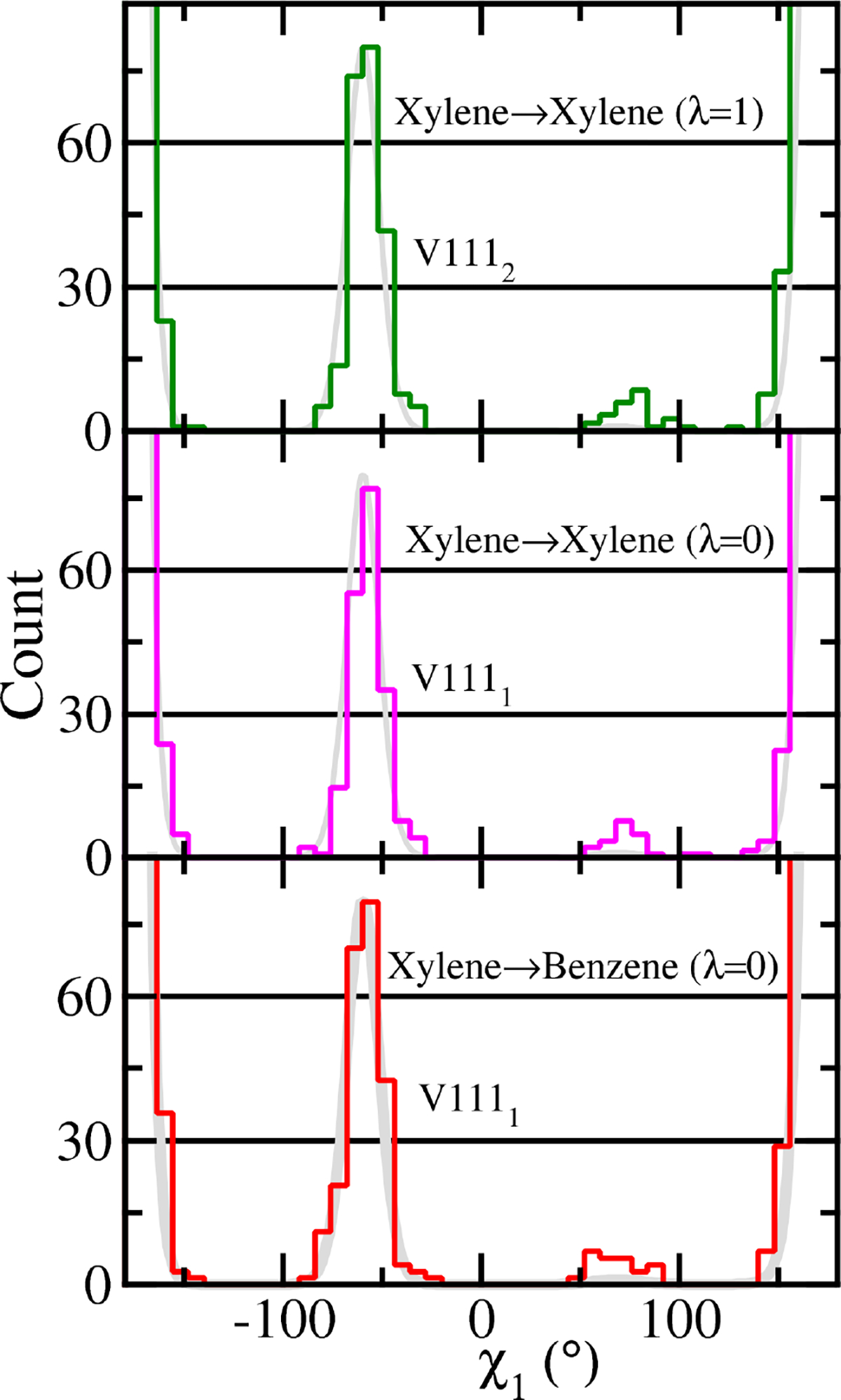
The V111 χ₁ histogram distributions (from 2500 snapshots and with 45 bins between −180° and 180°, the y-axis is the histogram count) real states from XX and XB ACES simulations.

Noticeable is that the XX simulations, where two copies of p-xylene and two copies of V111 side chains are defined with each copy corresponding to one end state, are not formally “alchemical transformation” simulations, since the two end states are exactly the same. In such ACES scenarios there is no net contribution to the free energy that arises in the transformation, but the greatest enhanced sampling is realized. As the enhanced sampling dummy states do not interact with the environment, they are analogous to an infinite REST2 effective temperature. In the XX simulations, there are two identical copies of the xylene and V111 that are defined in the SC region and contained within the dual topology framework. Each copy achieves enhanced sampling as the real-state endpoints are connected to the enhanced sampling dummy state through HREMD. However, as the first copy is being turned “off” by being transformed into the dummy state, the second copy is being “turned on” in the compensating transformation such that the net effect on the environment is minimal. This counter-diffusion of real and enhanced sampling states prevents large scale rearrangements of parts of the system that were not selected in the SC region and targeted for enhanced sampling. In this way, ACES avoids “hot-spot” problems and exchange bottlenecks that can occur with REST2-like approaches^46,104–106 and an effective “infinite” temperature (for interactions with the environment) can be utilized to accelerate the sampling in the dummy states.

5. Conclusion

We present a new alchemical enhanced sampling method (ACES) that combines: 1) creation of localized (focused) enhanced sampling states through flexible selection of the atoms to be targeted for enhanced sampling and tuning of the internal potential energy terms of the atoms in the enhanced sampling region; 2) design of a robust alchemical transformation pathways that connects the real state and enhanced sampling state endpoints using very recently developed new smoothstep alchemical free energy transformation methods and infrastructure; and 3) construction of efficient Hamiltonian replica-exchange networks using a real and enhanced sampling state counter-diffusion approach to reduce or eliminate exchange bottlenecks caused by re-arrangement of the environment. The ACES approach has unique advantages due to its dual-topology nature that enables the counter-diffusion of real and enhanced sampling states to overcome local “hot-spot” problems sometimes encountered in REST/REST2 approaches and enables seamless integration with free energy simulations. The method is demonstrated with a tiered set of examples of increasing complexity: the absolute hydration free energies of acetic acid and several edge cases from the FreeSolv database, protein-ligand binding in the 1h1r→1h1q transformation in Cdk2, and coupled ligand-binding/side chain (V111 χ₁ angle) rotamer transition in T4-lysozyme. In all cases, the ACES method was shown to be superior to the other methods compared, and able to circumvent kinetic traps and robustly sample complex conformational states and produce reliable free energy estimates. In this way ACES can be used as a stand-alone enhanced sampling method, or as an importance sampling method integrated with alchemical free energy simulations.