Summary
Randomized trials are an established method to evaluate the causal effects of interventions. Despite concerted efforts to retain all trial participants, some missing outcome data are often inevitable. It is unclear how best to account for missing outcome data in sample size calculations. A standard approach is to inflate the sample size by the inverse of one minus the anticipated dropout probability. However, the performance of this approach in the presence of informative outcome missingness has not been well-studied. We investigate sample size calculation when outcome data are missing at random given the randomized intervention group and fully observed baseline covariates under an inverse probability of response weighted (IPRW) estimating equations approach. Using M-estimation theory, we derive sample size formulas for both individually randomized and cluster randomized trials (CRTs). We illustrate the proposed method by calculating a sample size for a CRT designed to detect a difference in HIV testing strategies under an IPRW approach. We additionally develop an R shiny app to facilitate implementation of the sample size formulas.
Keywords: cluster randomized trials, inverse probability weighting, missing data, missing at random, M-estimation, randomized clinical trials
1 |. INTRODUCTION
Randomized trials are established as the gold standard for evaluating the causal effect of an intervention because the allocation of intervention versus control is independent of participants’ characteristics due to randomization, so that the difference in outcome can be attributed to the intervention1,2. Despite concerted efforts in trial design and conduct to retain all trial participants, some missing data on the primary contrast of interest are often inevitable. There have been several review articles describing the potential biases and efficiency loss introduced by missing outcome data in randomized trials, as well as analysis techniques that address such missingness1,3,2,4. In 2010, the US National Research Council issued a panel report on ‘The Prevention and Treatment of Missing Data in Clinical Trials’5 followed by a New England Journal of Medicine article summarizing their findings2. The report and article highlight that how to account for missing outcome data in sample size calculation is an important and neglected design issue, and therefore an area for research.
A standard approach to handle potential missing outcome data in sample size calculation is to inflate the randomized trial sample size by the inverse of one minus the anticipated dropout probability2,6. For example, if it is expected that 20% of trial participants will dropout, the number of participants recruited will be inflated by 1/(1–0.2). The performance of this approach in the presence of informative missingness has not been well-studied and motivates the work in this paper.
When outcome data are missing at random (MAR), i.e., the propensity of missingness depends on observed data7, multiple imputation (MI) and weighted estimating equations are commonly used methods to estimate the marginal intervention effect. MI methods impute missing outcome data several times based on an imputation model, and average the estimates of the marginal intervention effect over the imputations8. Weighted estimating equations account for MAR outcome data by weighting participants with a response by the inverse probability of being observed given their covariates and randomized intervention group9.
For MI methods, variance estimation is often based on Rubin’s rules that combine the within-imputation and between-imputation variability. Zha and Harel10 have described power calculation based on Rubin’s rules for a difference in means. For an inverse probability of response weighted (IPRW) estimator, variance inflation or reduction has previously been studied in the context of survey sampling when weighting by a categorical variable11, and asymptotic equivalence between an IPRW and MI approach has been shown in special settings when weighting by a categorical variable9. Power and sample size for observational studies in the context of weighting for potential confounders by inverse probability of treatment weights (IPTWs) has also been studied12, but, to date, sample size calculation in the context of IPRWs has not been evaluated.
Other previous literature on sample size calculation in the context of missing outcome data for individually randomized trials (IRTs) has either been based on a missing not at random assumption7 with principled sensitivity analyses for a binary outcome13, or has incorporated repeated measures of the outcome variable. For repeated outcome measures under the generalized estimating equation (GEE) framework, methods tend to assume outcome data are missing completely at random (MCAR) 14,15. Otherwise, a hierarchical statistical model is usually assumed with outcome data MAR given observed outcomes and the randomized intervention group16,17,18.
For cluster randomized trials (CRTs) it is well known sample size needs to be inflated compared to IRTs by a design effect to account for the correlation of outcomes in the same cluster19. A standard further inflation of sample size for missing outcome data in CRTs is less well established. Taljaard et al20 reports simple approaches that inflate the sample size by the inverse of one minus the anticipated dropout probability or use the anticipated average cluster size, tend to respectively over-estimate or under-estimate the required sample size. To the best of our knowledge, variance inflation factors in the design of CRTs when employing IPRWs have not been studied.
In this paper, we aim to present sample size calculation methods for IRTs and CRTs with missing data for a single outcome measure when the analysis technique will be based on IPRWs that incorporate fully observed baseline covariates and the randomized intervention group. We focus on uncensored outcomes that are continuous or binary. By stacking estimating equations for the parameters needed for the primary contrast of interest with those for the IPRWs, we use an M-estimation framework21 to derive large sample variance formulas that take into account the fact the weights are estimated from the data. We describe a simplification when the paradoxical efficiency gain from estimating the IPRWs from the data22,23 is ignored, as well as an approximation that separates the variance of the outcome from the weights. We provide simplified formulas when weighting by a single categorical or continuous covariate and a description of how pilot data with several weighting variables can be used in sample size calculation under the IPRW framework.
The paper is structured as follows: Section 2.1 reviews standard sample size calculation methods for IRTs, including a description of the standard inflation to account for missing outcome data. Section 2.2 introduces sample size calculation for an IPRW estimator of the primary contrast of interest when outcome data are MAR, and describes the simplification and approximation to the method when the IPRWs are considered known. Section 2.3 reviews standard sample size calculation methods for CRTs and Section 2.4 describes sample size calculation for an IPRW estimator in the context of CRTs. Further details when weighting by a single categorical or continuous covariate are provided in Sections 2.5 and 2.6 respectively. This is followed by a description of utilizing pilot data for sample size calculation based on an IPRW estimator in Section 2.7. Simulation studies are described in Section 3. Section 4 provides two examples. The first is a tutorial on performing sample size calculation based on an IPRW estimator for a confirmatory CRT, and the second example is a case study of an IRT that illustrates how different missingness patterns can influence sample size under an IPRW estimator. We conclude with a Discussion (Section 5).
2 |. METHODS
2.1 |. Review of Standard Sample Size Calculation
In a randomized trial we typically quantify an intervention effect of primary interest by a contrast , where is a function of the population mean outcome under intervention and is a function of the population mean outcome under control. When is the identity function the contrast of primary interest is the mean difference for a continuous outcome and the risk difference for a binary outcome. For a binary outcome, the marginal log odds ratio is often of interest, where is the logit function. To calculate the required sample size, a value for this contrast of primary interest is hypothesized, and the number of participants needed to be observed to detect such a difference at the specified significance level and power is found. The number of participants needed to be observed, , to detect a difference via the Wald test can be obtained by (Web Appendix A, Chow et al24 Sections 3.2, 4.2 and 4.6):
| (1) |
where is the power, is the significance level and represents the ath quantile of the standard normal distribution. Letting the random variable represent a continuous or binary outcome for each participant , be 1 if participant is randomized to the intervention group and 0 if participant is randomized to the control group, and be the probability a participant is randomized to the intervention group, then,
For a continuous outcome we have assumed that the variability of the outcome is the same under intervention and control, i.e. . When half the participants are randomized to each intervention group, so that , for a continuous outcome has the familiar form25.
Furthermore, let indicate that participant has an observed outcome and indicate a missing outcome for participant . Then, if is the anticipated probability participant has an observed outcome, the number of participants recruited into the randomized trial is standardly calculated by inflating the the number needed to be observed by (Web Appendix A, Little el al2, Donner6):
| (2) |
This formula can be justified by considering the complete-case analysis, that is, estimating the difference between the randomized intervention groups , as follows,
| (3) |
and assuming outcome data are MCAR7, i.e., both that the probability of the outcome being observed is the same in the intervention and control group and the outcome is independent of missingness .
2.2 |. Sample Size Calculation Weighted for Response
Now suppose that represents a vector of fully observed baseline covariates and that we will use an IPRW estimator of the primary contrast of interest based on weighting by the fully observed baseline covariates and the randomized intervention group. Then, we can estimate the difference between intervention groups as:
| (4) |
where is the estimated probability of being observed in the intervention group and is the estimated probability of being observed in the control group. Assuming outcome data are MAR, that is 7, we can model the probability of being observed in each intervention group, as follows,
For notational convenience the same set of covariates is used for each randomized intervention group, where the coefficients of those covariates that do not appear in the model are zero. Defining , where and , an M-estimator is obtained by solving the following estimating equations for
By M-estimation theory (Web Appendix A, Stefanski and Boos21) we have,
| (5) |
where
The variance formula in Equation 5 leads to the following sample size formula accounting for IPRWs,
| (6) |
where
When compared to Equation 2, this formula provides a relative efficiency due to weighting for response of . The terms and in Equation 5 represent the reduction in the variance achieved through incorporation of estimating equations for the IPRWs. This paradoxical efficiency gain through estimation of the IPRWs from the data has been highlighted in previous literature22,23. In the trial planning stage, hypothesizing values for and may be a difficult task, so a conservative approach to sample size calculation could consider the following upper bound for ,
| (7) |
Equation 7 leads to the following sample size formula assuming the weights are known,
| (8) |
where
The upper bound of the variance formula provided in Equation 7 can be written as,
where and . By the Cauchy-Schwarz inequality, we know
Therefore, a strategy similar to the one taken by Shook-Sa and Hudgens12 in the context of confounding adjustment by weighting ignores and and approximates as:
| (9) |
So, by ignoring the correlation between the IPRWs and the squared deviation of the outcome from its mean, the approximate number of participants needed to be recruited under IPRW is,
where
We later explore, in Sections 2.5, 2.6 and 3, the number of participants calculated by this approximate formula compared to the other approaches.
2.3 |. Review of Sample Size Calculation for CRTs
Suppose instead of randomizing individual participants to the intervention or control group, the trial is designed to randomize clusters of individuals. Assuming there are clusters where the probability that a cluster is randomized to the intervention group is , and that each cluster contains individuals, then a common approach for sample size calculation in CRTs inflates the number of participants required in an IRT by a design effect that accounts for the correlation of outcomes from individuals within each clusters, as follows (Web Appendix A, Rutterford et al19):
| (10) |
where and is the intercluster correlation under the usual assumption of an exchangeable correlation structure and is defined as the correlation of the outcomes for two different individuals and in cluster . An approach for CRTs based on the complete-case estimator and assuming that outcome data are MCAR, i.e. for and , and there is no clustering of missingness, for and , results in the following sample size formula (Web Appendix A):
| (11) |
where .
2.4 |. Sample Size Calculation for CRTs Weighted for Response
Now considering a weighted analysis, which weights response by fully observed baseline covariates and the randomized intervention group, then the equivalent to Equation 5 for CRTs, which assumes and for , is (Web Appendix A):
| (12) |
where
This leads to the following sample size formula accounting for IPRWs in CRTs,
| (13) |
where
Since the component of that depends on the correlation between outcomes in the same cluster is a separate additional term, a similar approach to that taken in Section 2.2 for IRTs would approximate by or for CRTs (see Web Appendix A).
2.5 |. Weighting for a Single Baseline Categorical Variable
Studying each sample size formula for IRTs in the context of weighting by a single fully observed categorical variable provides some intuition. Suppose consists of a single baseline covariate with categories, then based on Equation 5 can be written in closed-form (Web Appendix B), as follows:
| (14) |
where , , , , and . Due to the randomization, . Using the variance in Equation 14 in sample size calculation, results in recruiting the following number of participants:
| (15) |
where
It can be noted that by the law of total variance, we can write and , therefore Equation 2 could be re-written as,
where
This helps to see that when performing a sample size calculation based on the weighted estimator, the inflation comes from weighting the within-category variance of the outcome by the probability of being observed in that category. Whereas, when performing a sample size based on the complete-case estimator we weight the overall variance by the marginal probability of the outcome being observed, i.e. .
It is also instructive to calculate the variance when weighting for a single baseline categorical variable using the formula in Equation 7 that ignores the efficiency gained from estimating the weights from the data. This results is the following expression:
| (16) |
If the upper bound for the variance is used in sample size calculation, we would calculate that we would need to recruit the following number of participants:
| (17) |
where
In this case the inflation comes from weighting both the within-category and between-category variance in each intervention group by the probability of being observed in each category. If the probability of being observed is the same in all categories of for each intervention group this sample size calculation reduces to that of Equation 2
Finally, consider the scenario in Equation 9 where a component of the correlation between the weights and the outcome is ignored in each intervention group. This would result in (Web Appendix B),
| (18) |
where
In this case the inflation comes from weighting the overall variance of the outcome in each intervention group by the probability of being observed in each category. Again, if the probability of being observed is the same in all categories of for each intervention group, this sample size calculation reduces to that of Equation 2. This approach ignores the heterogeneity of within-category variances.
As a demonstration, Figure 1 displays the sample size calculated using each of the techniques when is binary and is the identity function for a trial where half the participants are randomized to the intervention group and responses are weighted by a baseline binary variable with half the participants in each category in each intervention group. By the formula the sample size peaks when the within-category variance components are largest. As expected, the sample size calculated by is always higher than that from as the efficiency gain from estimating the IPRWs from the data is ignored22,23. The sample size from does not curve as the within-category probability of the outcome changes, as the expression for divides both the within-category and between-category variance by the probability of being observed in each category. and are both independent of the within-category probability of the outcome, and can result in an over-estimation or under-estimation of the sample size when compared to .
FIGURE 1.
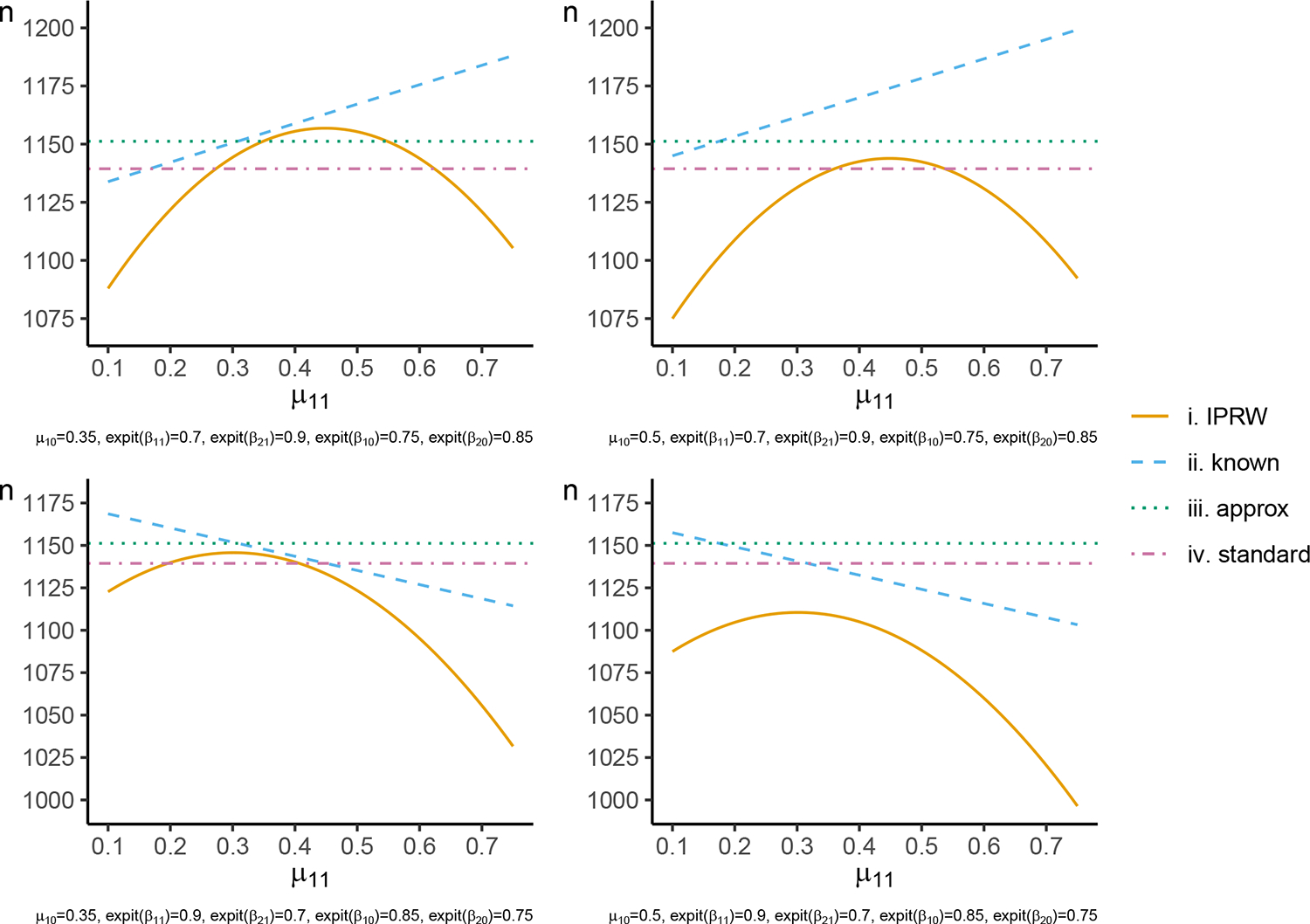
Sample size calculated to detect a risk difference of with 90% power at a two-sided 5% significance level using the , , and formulas. The within-category prevalence of the outcome in the intervention group ( and ) is varied on the x-axis, and within-category prevalence of the outcome in the control group is held fixed at the displayed values of and . The probability of the outcome being observed in each category and intervention group is as displayed for , , and .
2.6 |. Weighting for a Single Baseline Normally Distributed Variable
A similar exercise was performed for IRTs when and have a bivariate normal distribution. In this case, a closed-form expression for based on Equation 5 is not available as it requires integration over the expit function. Expressions for an approximation to under Equation 5 using Gauss-Hermite quadrature are available in Web Appendix B. Using Equation 7 a conservative expression for is obtained as:
| (19) |
where , , , , and . Due to the randomization, . Using the variance in Equation 19 in sample size calculation, results in recruiting the following number of participants:
| (20) |
The variance of the outcome is inflated by the weight at the mean of attenuated by a variance factor dependent upon the strength of the association between and the outcome being observed in each intervention group, plus a factor that depends on the correlation between and .
If the variance approximation in Equation 9 was used instead, we would have the following expression for ,
The corresponding sample size calculation is (Web Appendix B):
| (21) |
where
In this approximation the variance of the outcome is inflated by the weight at the mean of attenuated by a variance factor dependent upon the strength of the association between and the outcome being observed in each intervention group. The correlation between and is ignored and assumed to be zero.
As a demonstration, Figure 2 displays the sample size calculated using each of the techniques when and have a bivariate normal distribution and is the identity function for a trial where half the participants are randomized to the intervention group . As expected, for and the sample sizes calculated coincide at , and when , is larger than . Additionally, as before, the sample size calculated by is larger than . has a concave shape in the left panel of Figure 2 and is inbetween and , whereas has a convex shape in the right panel and is below both and . can either over-estimate or under-estimate the sample size as displayed in the right panel of Figure 2.
FIGURE 2.
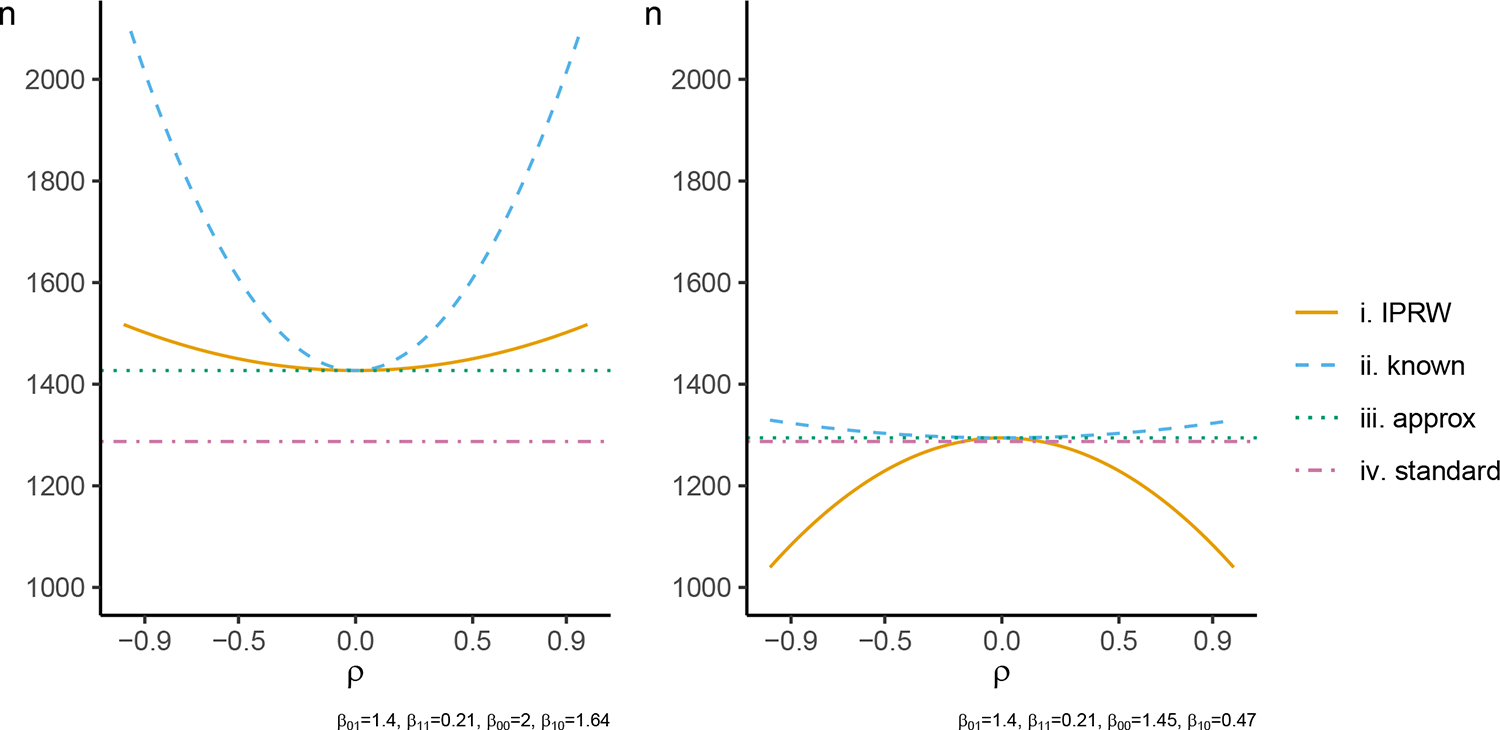
Sample size calculated to detect a mean difference of with 90% power at a two-sided 5% significance level using the , , and formulas. The correlation between the weighting variable and the outcome is varied on the x-axis. The probability of the outcome being observed at each value and intervention group is as displayed for and . is approximated by Gauss-Hermite quadrature with 100 quadrature points.
Sample size formulas in Section 2.5 and 2.6 would also apply to CRTs if the term is added to the component.
2.7 |. Utilizing Pilot Data with Several Weighting Variables
Although it is instructive to understand how weighting for response based on a single categorical or continuous variable may affect the calculated sample size, in practice several variables may be included in the model to estimate the response probability in each intervention group. Here, we describe how sample size can be calculated by utilizing pilot data. In IRTs, the variance of the primary contrast of interest weighted for response can be estimated from pilot data containing individuals with approximately on intervention using the empirical sandwich variance estimator, as follows:
| (22) |
where and are defined in Web Appendix B. This results in the following sample size formula:
For CRTs, the variance of the primary contrast of interest weighted for response can be estimated from pilot data containing clusters each with approximately individuals and approximately of the clusters on intervention, as follows:
| (23) |
where and are defined in Web Appendix B. This results in the following sample size formula:
3 |. SIMULATION STUDIES
Simulation studies were conducted firstly to verify that the and formulas resulted in sample sizes with the correct statistical power to detect an intervention effect using the IPRW estimator under outcome missingness that depended on a single baseline covariate as well as the randomized intervention group. Secondly, we compared the power obtained when the standard approach ( and ) or the approaches that consider the IPRWs to be known (, , and ) were used. Lastly, we assessed the impact of estimating parameters needed for the component of the sample size formulas from pilot trial data.
3.1 |. Dataset Generation
For each scenario specified in Table 1(a) and Table 2(a), 10000 datasets were simulated corresponding to the number of participants calculated by the standard, IPRW, known and approx approaches to have 90% power to detect an intervention effect at the two-sided 5% significance level. For IRTs, half the participants were assigned to the intervention group . The baseline binary variable and the randomized intervention group determined outcome missingness. The baseline binary variable, , was generated by random draws from a Bernoulli distribution. The probability of the outcome being observed, given the covariate and the randomized intervention group , was generated from a Bernoulli distribution such that , , and . Some scenarios considered to be a continuous outcome; in which case was generated by random draws from a normal distribution such that and , where , , and are given in Table 1 a) for . Other scenarios considered to be a binary outcome; in which case was generated by random draws from a Bernoulli distribution such that and for . The scenarios simulated covered heterogeneity (scenarios 1 and 2) and homogeneity (scenarios 3 and 4) of intervention effect over values of . The simulated scenarios for CRTs are in Table 2(a) and the process used to simulate CRT datasets is described in Web Appendix C.
TABLE 1.
Datasets generated and simulations results for individually randomized trials (IRTs) with missing outcome data based on a single fully observed baseline binary covariate
| (a) Datasets generated | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| continuous, identity | binary, identity | binary, logit | |||||||
|
| |||||||||
| Scenario | 1 | 2 | 3 | 4 | 1 | 2 | 1 | 2 | |
|
| |||||||||
| Parameters | 0.5 | 0.5 | 0.7 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | |
| 0.9 | 0.62 | 0.2 | 0.2 | 0.9 | 0.62 | 0.9 | 0.62 | ||
| 0.3 | 0.95 | 0.3 | 0.3 | 0.3 | 0.95 | 0.3 | 0.95 | ||
| 0.15 | 0.63 | 0.1 | 0.1 | 0.15 | 0.63 | 0.15 | 0.63 | ||
| 0.85 | 0.74 | 0.2 | 0.2 | 0.85 | 0.74 | 0.85 | 0.74 | ||
| 0.026 | 0.41955 | 0.01 | 0.01 | 0.09 | 0.2356 | 0.09 | 0.2356 | ||
| 0.294 | 0.026 | 0.3 | 0.3 | 0.21 | 0.0475 | 0.21 | 0.0475 | ||
| 0.026 | 0.46795 | 0.01 | 0.01 | 0.1275 | 0.2331 | 0.1275 | 0.2331 | ||
| 0.229 | 0.026 | 0.3 | 0.3 | 0.1275 | 0.1924 | 0.1275 | 0.1924 | ||
| 0.7 | 0.7 | 0.64 | 1 | 0.7 | 0.7 | 0.7 | 0.7 | ||
| 0.9 | 0.9 | 1 | 0.64 | 0.9 | 0.9 | 0.9 | 0.9 | ||
| 0.75 | 0.75 | 0.64 | 1 | 0.75 | 0.75 | 0.75 | 0.75 | ||
| 0.85 | 0.85 | 1 | 0.64 | 0.85 | 0.85 | 0.85 | 0.85 | ||
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.41 | 0.52 | ||
|
| |||||||||
| Sample size | 1314 | 1314 | 558 | 468 | 1288 | 1012 | 1306 | 1034 | |
| 1150 | 1412 | 434 | 630 | 1164 | 1038 | 1180 | 1068 | ||
| 1266 | 1430 | 436 | 634 | 1280 | 1056 | 1298 | 1088 | ||
| 1328 | 1328 | 582 | 488 | 1300 | 1020 | 1318 | 1044 | ||
|
| |||||||||
| For all scenarios: , | |||||||||
| (b) Simulation results | |||||||||
| continuous, identity | binary, identity | binary, logit | |||||||
|
| |||||||||
| Scenario | 1 | 2 | 3 | 4 | 1 | 2 | 1 | 2 | |
|
| |||||||||
| Sample size | 1314 | 1314 | 558 | 468 | 1288 | 1012 | 1306 | 1034 | |
| IPRW estimator | power | 93 [0.10] | 87 [0.10] | 96 [0.10] | 80 [0.10] | 93 [0.10] | 89 [0.10] | 93 [0.41] | 90 [0.52] |
|
| |||||||||
| Sample size | 1150 | 1412 | 434 | 630 | 1164 | 1038 | 1180 | 1068 | |
| IPRW estimator | power | 90 [0.10] | 90 [0.10] | 90 [0.10] | 90 [0.10] | 90 [0.10] | 89 [0.10] | 90 [0.41] | 90 [0.52] |
|
| |||||||||
| Sample size | 1266 | 1430 | 436 | 634 | 1280 | 1056 | 1298 | 1088 | |
| IPRW estimator | power | 92 [0.10] | 91 [0.10] | 90 [0.10] | 90 [0.10] | 93 [0.10] | 91 [0.10] | 92 [0.41] | 91 [0.52] |
|
| |||||||||
| Sample size | 1328 | 1328 | 582 | 488 | 1300 | 1020 | 1318 | 1044 | |
| IPRW estimator | power | 93 [0.10] | 88 [0.10] | 96 [0.10] | 81 [0.10] | 92 [0.10] | 89 [0.10] | 93 [0.40] | 90 [0.52] |
displays the average estimated intervention effect across the 10 000 simulations
TABLE 2.
Datasets generated and simulations results for cluster randomized trials (CRTs) with missing outcome data based on a single fully observed baseline binary covariate
| (a) Datasets generated | |||||||
|---|---|---|---|---|---|---|---|
| continuous, identity | binary, identity | binary, logit | |||||
|
| |||||||
| Scenario | 1 | 2 | 1 | 2 | 1 | 2 | |
|
| |||||||
| Parameters | 0.9 | 0.62 | 0.9 | 0.62 | 0.9 | 0.62 | |
| 0.3 | 0.95 | 0.3 | 0.95 | 0.3 | 0.95 | ||
| 0.15 | 0.63 | 0.15 | 0.63 | 0.15 | 0.63 | ||
| 0.85 | 0.74 | 0.85 | 0.74 | 0.85 | 0.74 | ||
| 0.026 | 0.41955 | 0.09 | 0.2356 | 0.09 | 0.2356 | ||
| 0.294 | 0.026 | 0.21 | 0.0475 | 0.21 | 0.0475 | ||
| 0.026 | 0.46795 | 0.1275 | 0.2331 | 0.1275 | 0.2331 | ||
| 0.229 | 0.026 | 0.1275 | 0.1924 | 0.1275 | 0.1924 | ||
| 0.1 | 0.1 | 0.1 | 0.1 | 0.41 | 0.52 | ||
|
| |||||||
| Sample size | 1524 | 1524 | 1494 | 1172 | 1514 | 1200 | |
| 1360 | 1622 | 1370 | 1200 | 1388 | 1232 | ||
| 1476 | 1640 | 1486 | 1216 | 1506 | 1254 | ||
| 1538 | 1538 | 1506 | 1182 | 1528 | 1210 | ||
| 306 | 306 | 320 | 236 | 304 | 240 | ||
| 272 | 326 | 274 | 240 | 278 | 248 | ||
| 296 | 328 | 298 | 244 | 302 | 252 | ||
| 308 | 308 | 302 | 238 | 306 | 242 | ||
|
| |||||||
| For all scenarios: , | |||||||
| (b) Simulation results | |||||||
| continuous, identity | binary, identity | binary, logit | |||||
|
| |||||||
| Scenario | 1 | 2 | 1 | 2 | 1 | 2 | |
|
| |||||||
| Sample size | 1524 | 1524 | 1494 | 1172 | 1514 | 1200 | |
| IPRW estimator | power | 93 [0.10] | 89 [0.10] | 94 [0.10] | 91 [0.10] | 94 [0.41] | 91 [0.52] |
|
| |||||||
| Sample size | 1360 | 1622 | 1370 | 1200 | 1388 | 1232 | |
| IPRW estimator | power | 90 [0.10] | 90 [0.10] | 91 [0.10] | 90 [0.10] | 92 [0.41] | 91 [0.52] |
|
| |||||||
| Sample size | 1476 | 1640 | 1486 | 1216 | 1506 | 1254 | |
| IPRW estimator | power | 92 [0.10] | 90 [0.10] | 94 [0.10] | 91 [0.10] | 94 [0.41] | 91 [0.52] |
|
| |||||||
| Sample size | 1538 | 1538 | 1506 | 1182 | 1528 | 1210 | |
| IPRW estimator | power | 93 [0.10] | 88 [0.10] | 94 [0.10] | 90 [0.10] | 94 [0.40] | 91 [0.52] |
displays the average estimated intervention effect across the 10 000 simulations
Six of the scenarios in Table 1(a), labeled as scenario 1 and 2 for each combination of outcome type and function , were altered to observe simulation results when the amount of missingness was varied. Specifically, the probability of the outcome being observed, , was varied from 80% to be between 20% and 90%. This was done by specifying , , and as varied. Additionally, in Web Appendix C other parameters were varied for these simulation scenarios to observe results when missingness per intervention group, the association between the covariate and the probability of missingness, the proportion randomized to the intervention group and the sample size were varied. Furthermore, simulations exploring missingness dependent on a single baseline continuous covariate are described in Web Appendix C.
Finally, the impact of estimating the parameters needed for the sample size calculation from a pilot trial of size ranging from 50 to 500 was assessed. For each simulation iteration, pilot trial data were generated using the underlying true distributions and then used to estimate the component for each sample size formula for the four approaches: standard, IPRW, known and approx. The full trial datasets were then simulated with the calculated number of participants based on the pilot data estimates, and analyzed by the IPRW estimator.
3.2 |. Analysis Approaches
For all simulation scenarios the IPRW estimator (Equation 4 for IRTs) was used in the analysis. As a consequence, unbiased estimation of the primary contrast of interest by the IPRW estimator was also verified when outcome data are MAR. A Wald test for the primary contrast of interest was constructed using a large sample variance estimator (given in Web Appendix C), and the empirical power was calculated as the proportion of times the null hypothesis of no intervention effect was rejected.
3.3 |. Results
The results for IRTs with missingness dependent upon a single fully observed baseline binary covariate are in Table 1(b). The sample averages of the intervention effect estimates obtained using the IPRW estimator were virtually identical to their corresponding true values. A sample size of coupled with the IPRW estimator resulted in 90% empirical power. For scenario 1 for each combination of outcome type and function , the empirical power based on , or and the IPRW estimator was slightly above the target of 90%; ranging from 92 to 93%. Whereas, for scenario 2 for each combination of outcome type and function , the empirical power based on or and the IPRW estimator was at or slightly below the target of 90%; ranging from 87 to 90%. For scenario 3, the empirical power based on or was above the target at 96%. For scenario 4, the empirical power based on or was below the target at 80% and 81%, respectively. Results for the six scenarios simulated for CRTs were similar (Table 2(b)).
Figure 3 displays the results when the amount of missingness was varied for IRTs. Figure 3 (a) displays the six scenarios with the sample size calculated by each method as was varied on the x-axis. Figure 3 (b) displays the empirical power for each sample size when the IPRW estimator was used in the analysis. For scenario 1 for each combination of outcome type and function , was lower than the sample size calculated by each of the other three approaches, with a larger difference when there were more missing outcome data. The empirical power for the IPRW estimator when the sample size was calculated by the IPRW formula was very close to the target of 90%, whereas the empirical power for the other three approaches was greater than 90% with higher power as the amount of missing data increased. For scenario 2 for each combination of outcome type and function , was lower than the sample size calculated by and higher than the sample size calculated by and , with larger differences when there were more missing outcome data. The empirical power for the IPRW estimator when the sample size was calculated by the IPRW formula was very close to the target of 90%, whereas the power for was greater than 90% and for and was lower than 90% with lower power as the amount of missing data increased.
FIGURE 3.
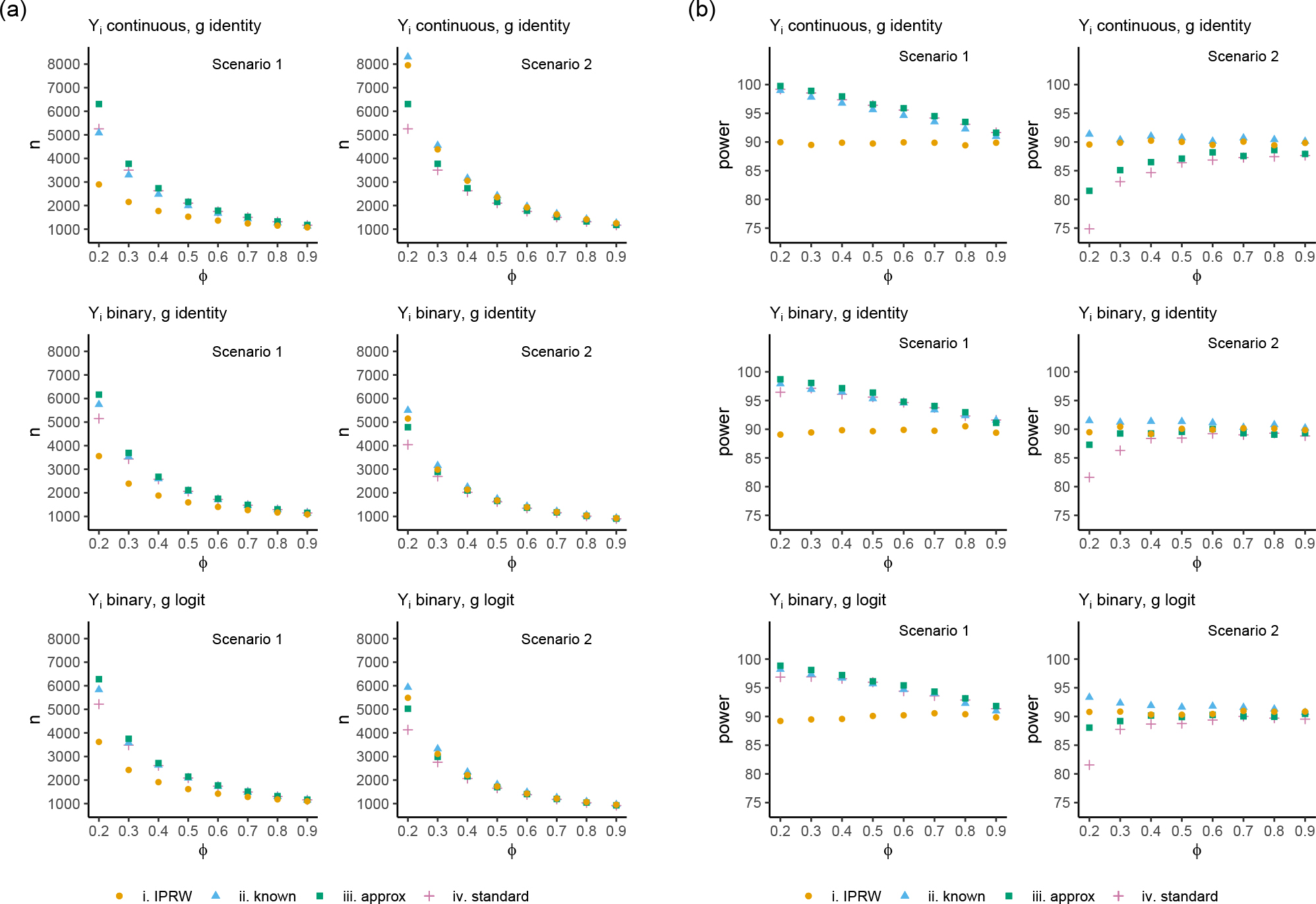
(a) Datasets generated with the sample size calculated to have 90% power at a two-sided 5% significance level using the , , and formulas when weighting by a baseline binary covariate in an IRT, where the probability of the outcome being observed is varied on the x-axis. (b) Simulation results displaying the empirical power for each sample size with the IPRW estimator.
Figure 4 displays the results when parameters for the component of the sample size formulas were estimated from a pilot trial. Figure 4(a) displays six scenarios with the mean sample size calculated as the size of the pilot trial was varied on the x-axis. Figure 4(b) displays the empirical power for each sample size calculation approach when the IPRW estimator was used in the analysis. The empirical power using the IPRW sample size formula gets close to the target of 90% when for all scenarios. For the two continuous outcome scenarios and scenario 2 for the binary outcome with an identity link function (g), the empirical power for the IPRW sample size formula is ~85% (lower than the target of 90%) when . For the other scenarios the empirical power is closer to the 90% target when . Furthermore, for scenario 1 when the sample size is calculated by the and approaches using pilot trial data estimates, the empirical power is at or above 90%, and for scenario 2 the empirical power is at or below 90%. As expected, the formula results in higher empirical power than all other sample size calculation approaches.
FIGURE 4.
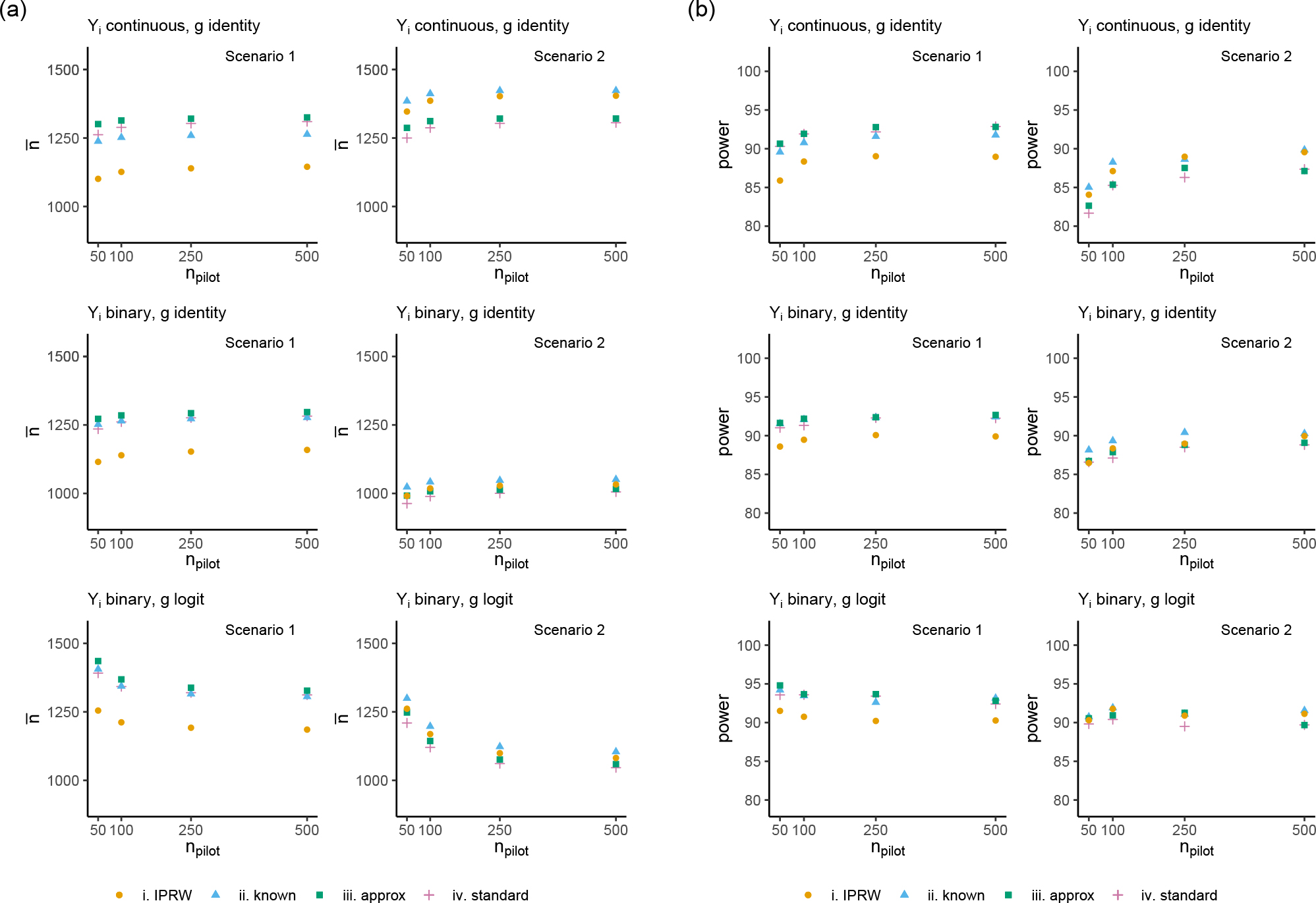
(a) Mean sample size of datasets generated with calculation from pilot trial estimates to have 90% power at a two-sided 5% significance level using the , , and formulas when weighting by a baseline binary covariate in an IRT, where the size of the pilot trial is varied on the x-axis. (b) Simulation results displaying the empirical power for each sample size calculation method with the IPRW estimator.
The differences in sample size calculated by each formula can be explored on an R shiny app we developed at https://lindajaneharrison.shinyapps.io/SampleSizeMissing/. Output from the R shiny app for scenario 3 and 4 in Table 1 is displayed in Web Figure 14.
4 |. EXAMPLES
4.1 |. Tutorial on sample size calculation based on an IPRW estimator for a confirmatory CRT
The sample size calculation formulas derived in this paper require several parameters. To aid researchers to implement these formulas, this tutorial walks through the process of obtaining the parameters needed for the sample size calculation from a published CRT that evaluated HIV testing strategies among sex workers26. The published trial, which for the purpose of this tutorial we will consider as a pilot study, randomized about 50 peer educators (the clusters) to direct delivery of HIV self-tests to sex workers and 50 peer educators to refer sex workers to standard HIV testing. Each peer educator recruited 6 sex workers (i.e. ), and the primary outcome was a binary outcome of whether or not a sex worker reported having a HIV test.
We illustrate our methods by proposing a design for a confirmatory CRT to detect a difference in HIV testing proportions between the direct delivery and standard testing groups based on the observed difference in the ‘pilot’ published study where the planned primary analysis for the confirmatory study will be by IPRW estimating equations. The baseline binary variable ‘Where do you get healthcare?’ with answer choices of a ‘community clinic’ or ‘elsewhere’ that was fully observed in the pilot study will be used in the logistic regression model for the probability of observing an outcome response in each randomized intervention group.
We firstly need an estimate from the pilot trial of the proportion of sex workers who got healthcare at a community clinic. This was 67% (, see Table 3 for the estimator and estimate from the pilot data). The remaining 33% of sex workers got healthcare elsewhere ( in Table 3). Secondly, we need an estimate of the chance of observing the outcome in both intervention groups for sex workers receiving healthcare in both settings. In the direct delivery group, the probability that the outcome was observed for sex workers who got healthcare at the community clinic was 61% [ in Table 3], whereas for sex workers receiving healthcare elsewhere it was 96% [ in Table 3]. In the standard testing group, the probability that the outcome was observed for sex workers who got healthcare at the community clinic was 57% [ in Table 3, whereas for sex workers who received healthcare elsewhere it was 97% [ in Table 3]. Thirdly, we need an estimate of the outcome prevalence in each of the four groups determined by intervention and healthcare. As the outcome is assumed to be MAR given the intervention and healthcare group, we can obtain these estimates from the unweighted observed data. Eighty-five percent of sex workers had a HIV test among those receiving healthcare at a community clinic in the standard testing group ( in Table 3), whereas in the other three groups the proportion of sex workers who had a HIV test was ≥ 94% (, and in Table 3). Fourthly, we need an estimate of the outcome prevalence in each intervention group. This is obtained from the pilot data using the IPRW estimator weighting for where sex workers got their healthcare in each intervention group ( and in Table 3). For completeness, an IPRW estimate of the intercluster correlation of 0.36 was obtained from the pilot data ( in Table 3). The rationale for the IPRW estimator used to obtain the intercluster correlation is explained in more detail in Web Appendix D.
TABLE 3.
Design of a confirmatory cluster randomized trial (CRT) accounting for missing outcome data based on a single fully observed baseline binary variable
| Estimation of parameters from the pilot CRT data | ||
|
| ||
|
| ||
| 1 community | 0.67 | |
| 2 elsewhere | 0.33 | |
|
| ||
| , , | ||
|
| ||
| 1 observed, 1 community, 1 direct delivery | 0.61 | |
| 1 observed, 2 elsewhere, 1 direct delivery | 0.96 | |
| 1 observed, 1 community, 0 standard testing | 0.57 | |
| 1 observed, 2 elsewhere, 0 standard testing | 0.97 | |
|
| ||
| , , | ||
|
| ||
| 1 HIV test, 1 community, 1 direct delivery | 0.94 | |
| 1 HIV test, 2 elsewhere, 1 direct delivery | 0.98 | |
| 1 HIV test, 1 community, 0 standard testing | 0.85 | |
| 1 HIV test, 2 elsewhere, 0 standard testing | 0.94 | |
|
| ||
| , | ||
|
| ||
| 1 HIV test, 1 direct delivery | 0.95 | |
| 1 HIV test, 0 standard testing | 0.88 | |
|
| ||
|
| ||
| intercluster correlation | 0.36 | |
|
| ||
| Sample size calculation for a confirmatory CRT | ||
|
| ||
| IPRW design component | 214.6 | |
| number of individuals | 2150 | |
| number of clusters | 360 | |
|
| ||
|
is the indictor function. is the covariate ‘Where do you get your healthcare?’ with answer choices 1 ‘community clinic’ or 2 ‘elsewhere’. is the intervention group: 1 direct delivery of HIV self-tests to sex workers or 0 refer sex workers to standard HIV testing. is the observed indicator: 1 sex worker’s HIV testing status is observed or 0 sex worker’s HIV testing status is missing. is the outcome: 1 sex worker had a HIV test and 0 sex worker did not have a HIV test. | ||
Based on parameter estimates obtained from the pilot data, we can calculate . It follows that a confirmatory CRT would require 2150 sex workers across the two randomized groups to detect the difference observed in the pilot trial on the log odds ratio scale at a two-sided 5% significance level with 90% power. Therefore, about 360 peer educators would need to be recruited with about half the peer educators randomized to each intervention group. R code to estimate the parameters for this tutorial can be found at https://github.com/lindajaneharrison/missing/releases/tag/v3.0 and output from the R shiny app (https://lindajaneharrison.shinyapps.io/SampleSizeMissing/) displaying this calculation is in Web Figure 15. Sensitivity analysis varying any of the parameters can easily be performed using this app.
As a note, the primary outcome was actually observed for 93% of sex workers in the published trial rather than 71% in the above example. We modified the published trial data to have a higher proportion of sex workers with missing outcomes in the group getting healthcare at a community clinic for illustration. Furthermore, the calculations conducted are based on weighting by a single binary variable. If further variables from the pilot data were considered, the technique for pilot data with several weighting variables in Section 2.7 could be utilized.
4.2 |. Case study of an IRT
In Web Appendix D we provide an additional illustration of how different patterns of missing outcome data can influence the required sample size under an IPRW estimator compared to the standard approach for an IRT. Briefly, the example highlights that the relative efficiency of the IPRW versus the standard approach is dependent upon the association between the weighting variable and the probability of the outcome being observed, as well as the variability of within-category variances of the chosen outcome measure when weighting by a categorical variable.
5 |. DISCUSSION
When designing a randomized trial, the number of participants to recruit is an important consideration. If outcome data are expected to be MAR and the primary analysis will employ corresponding methods to account for this missingness, it would be desirable to use sample size calculation techniques that match the analysis method. In this paper, we investigate sample size calculation when a single outcome variable is MAR given the randomized intervention group and fully observed baseline variables. Our approach uses weighted estimating equations to weight participants with observed outcomes by the inverse probability of being observed. A weighting technique that employs weight stabilization could alternatively be used in the analysis phase. Stabilization adjusts the weights by a constant that minimizes the large sample variance27, so in this case our sample size technique is likely to be conservative.
The variance formula for the intervention effect estimator under single imputation/simple g-computation can be derived (Web Appendix E). When single imputation is based on a categorical covariate the variance formula is the same as when employing unstabilized IPRWs. Weight augmentation incorporates both an outcome model and a missingness model to form a doubly robust estimator of the primary contrast of interest, which will be consistent if either the outcome or missingness model is correctly specified. If both models are correct, the augmentation approach can be more efficient that unstabilized weights or single imputation4,27. For MI, previous power calculation work has focused on a difference in means10. While a closed-form formula is available when outcome data are MCAR and the outcome and covariates are normally distributed28, derivation of a formula when outcome data are MAR is challenging. Extensions to non-linear link function and categorical covariate settings would require further derivation and would be an interesting area of research.
In randomized trials it is common to adjust for baseline covariates in the outcome model. If outcome data are MAR given baseline covariates and the randomized intervention group, an outcome model to estimate the difference between the intervention and control groups based on the complete cases adjusted for baseline covariates is a valid approach for a continuous outcome under a linear model when the intervention effect is homogeneous across values of the baseline covariates29. Indeed, sample size calculation formulas based on analysis of covariance30 could be further adapted for MAR data settings. However, for a binary outcome analyzed with a logit model, due to ‘non-collapsibility’ of the odds ratio, adjustment for baseline covariates leads to a different intervention effect estimand. If the intervention effect is heterogeneous over values of the baseline covariates, subgroup analysis may be of interest. Where resources are available, trials can be designed with enough power to detect intervention effects in certain subgroups31. Nonetheless, the marginal causal effect of the intervention is often estimated from clinical trial data and is usually of public health importance. Since adjustment for baseline covariates as precision variables in randomized trials can also be performed via IPTWs32, and combining IPTWs and IPRWs has been proposed33, an additional avenue for research could evaluate weighting for both precision variables and for missing outcome data in randomized trials.
Our method could easily be adapted to consider a mean or risk ratio, where would be the log function. Another extension of our work could consider weighted estimating equations with repeated measures of the outcome. Under a monotone missingness assumption and known IPRWs, Sun34 derived expressions for sample size calculation in this context. We extended our sample size formulas to CRTs with a single outcome measure under a weighted GEE approach. In our derivation, we assumed no clustering of missingness of the outcome. A further adaptation could allow for clustering of missingness within the weighted GEE approach by including a missingness indicator correlation parameter in the estimating equations, as in Chen et al35.
While this paper provides a way forward to calculate sample size in the study design phase when a weighted analysis to account for MAR outcome data is planned, it is unlikely that all parameters needed for the calculation will be known at the design phase. In the absence of pilot data, a method that weights for a single baseline categorical or normally distributed variable could be considered along with sensitivity analysis conducted using our R shiny app. In this simplified scenario, the same parameters are required for the IPRW approach and the approach that considers the weights as known. Therefore, it would be better to use the IPRW approach with the approach considering the weights as known as a conservative alternative. The further approximation we explored that separates information needed on the IPRWs from the variability of the outcome measure allows an outcome invariant relative efficiency for weighting for continuous outcomes as previously described in the context of IPTWs12. Unfortunately, since a component of the correlation between the weights and the outcome is ignored, the approximation can be inaccurate when both the association of the covariates with the outcome and with the probability of the outcome being observed is strong. Therefore, we would not recommend this approach. The standard approach could be used for simplicity if it gave a very similar sample size to the IPRW approach and the approach that considers the weights as known when utilizing our R shiny app. When pilot data are available, an approach to estimate parameters needed for the sample size calculation is described in Section 2.7. The accuracy of this approach for various pilot trial sizes was explored in our simulation studies. Pilot trials with 100 or more participants resulted in empirical power close to the target in the settings evaluated. A similar observation has been made by Julious et al36 and Fay at al37 for the standard sample size calculation approach for a continuous outcome in the context of accounting for the uncertainty in variance estimation from pilot data.
Lastly, we have assumed outcome data are MAR. Cook and Zea13 explored power for a binary outcome based on a missing not at random assumption with principled sensitivity analyses. They reported dramatic losses of power for certain sensitivity analyses. Future research could aim to identify scenarios where power is dramatically reduced for other outcome measures under a missing not at random assumption and when covariates are incorporated. As sensitivity analyses are recommended to assess the robustness of inferences about intervention effects to various missing data assumptions2, this would be important to additionally consider in the trial design stage.
Supplementary Material
Funding Information
This research was supported by the National Institute of Allergy and Infectious Diseases: T32 AI007358, UM1 AI068634 and R01 AI136947
Footnotes
Conflict of interest
The authors declare no potential conflict of interests.
SUPPORTING INFORMATION
Web appendices can be found online in the Supporting Information section at the end of the article. An R shiny app for sample size calculation using formulas displayed in this paper can be found at https://lindajaneharrison.shinyapps.io/SampleSizeMissing/. R code for the simulations and examples is available at https://github.com/lindajaneharrison/missing/releases/tag/v3.0.
DATA AVAILABILITY STATEMENT
Data for the CRT tutorial example is available in Harvard Dataverse at https://doi.org/10.7910/DVN/OCWCF5 Data for the IRT illustrative example is available on request from sdac.data@sdac.harvard.edu.
References
- 1.Carpenter JR, Kenward MG. Missing data in randomised controlled trials: a practical guide. https://researchonline.lshtm.ac.uk/id/eprint/4018500/1/rm04_jh17_mk.pdf; 2007. [Google Scholar]
- 2.Little RJ, D’Agostino R, Cohen ML, et al. The prevention and treatment of missing data in clinical trials. New England Journal of Medicine 2012; 367(14): 1355–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.White IR, Horton NJ, Carpenter J, Pocock SJ. Strategy for intention to treat analysis in randomised trials with missing outcome data. BMJ 2011; 342: d40. doi: 10.1136/bmj.d40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Prague M, Wang R, Stephens A, Tchetgen Tchetgen E, DeGruttola V. Accounting for interactions and complex inter-subject dependency in estimating treatment effect in cluster-randomized trials with missing outcomes. Biometrics 2016; 72(4): 1066–1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Panel on the Handling of Missing Data in Clinical Trials. The prevention and treatment of missing data in clinical trials. https://www.ncbi.nlm.nih.gov/books/NBK209904/pdf/Bookshelf_NBK209904.pdf; 2010. [Google Scholar]
- 6.Donner A Approaches to sample size estimation in the design of clinical trials—a review. Statistics in Medicine 1984; 3(3): 199–214. [DOI] [PubMed] [Google Scholar]
- 7.Little RJ, Rubin DB. Statistical analysis with missing data. John Wiley & Sons. second ed. 2002. [Google Scholar]
- 8.Rubin DB. Multiple imputation for nonresponse in surveys. John Wiley & Sons. 1987. [Google Scholar]
- 9.Seaman SR, White IR. Review of inverse probability weighting for dealing with missing data. Statistical Methods in Medical Research 2013; 22(3): 278–295. [DOI] [PubMed] [Google Scholar]
- 10.Zha R, Harel O. Power calculation in multiply imputed data. Statistical Papers 2021; 62(1): 533–599. [Google Scholar]
- 11.Little RJ, Vartivarian S. Does weighting for nonresponse increase the variance of survey means?. Survey Methodology 2005; 31(2): 161. [Google Scholar]
- 12.Shook-Sa BE, Hudgens MG. Power and sample size for observational studies of point exposure effects. Biometrics 2020: doi: 10.1111/biom.13405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cook T, Zea R. Missing data and sensitivity analysis for binary data with implications for sample size and power of randomized clinical trials. Statistics in Medicine 2019; 39(2): 192–204. doi: 10.1002/sim.8428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rochon J Application of GEE procedures for sample size calculations in repeated measures experiments. Statistics in Medicine 1998; 17(14): 1643–1658. [DOI] [PubMed] [Google Scholar]
- 15.Ahn C, Jung SH. Effect of dropouts on sample size estimates for test on trends across repeated measurements. Journal of Biopharmaceutical Statistics 2004; 15(1): 33–41. [DOI] [PubMed] [Google Scholar]
- 16.Wu MC. Sample size for comparison of changes in the presence of right censoring caused by death, withdrawal, and staggered entry. Controlled Clinical Trials 1988; 9(1): 32–46. [DOI] [PubMed] [Google Scholar]
- 17.Hedeker D, Gibbons RD, Waternaux C. Sample size estimation for longitudinal designs with attrition: comparing time-related contrasts between two groups. Journal of Educational and Behavioral Statistics 1999; 24(1): 70–93. [Google Scholar]
- 18.Roy A, Bhaumik DK, Aryal S, Gibbons RD. Sample size determination for hierarchical longitudinal designs with differential attrition rates. Biometrics 2007; 63(3): 699–707. [DOI] [PubMed] [Google Scholar]
- 19.Rutterford C, Copas A, Eldridge S. Methods for sample size determination in cluster randomized trials. International Journal of Epidemiology 2015; 44(3): 1051–1067. doi: 10.1093/ije/dyv113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Taljaard M, Donner A, Klar N. Accounting for expected attrition in the planning of community intervention trials. Statistics in Medicine 2007; 26(13): 2615–2628. [DOI] [PubMed] [Google Scholar]
- 21.Stefanski LA, Boos DD. The calculus of M-estimation. The American Statistician 2002; 56(1): 29–38. [Google Scholar]
- 22.Henmi M, Eguchi S. A paradox concerning nuisance parameters and projected estimating functions. Biometrika 2004; 91(4): 929–941. [Google Scholar]
- 23.Tsiatis A Semiparametric theory and missing data. Springer Science & Business Media. 2006. [Google Scholar]
- 24.Chow SC, Shao J, Wang H, Lokhnygina Y. Sample size calculations in clinical research. CRC Press. second ed. 2008. [Google Scholar]
- 25.Lachin JM. Introduction to sample size determination and power analysis for clinical trials. Controlled Clinical Trials 1981; 2(2): 93–113. [DOI] [PubMed] [Google Scholar]
- 26.Chanda MM, Ortblad KF, Mwale M, et al. HIV self-testing among female sex workers in Zambia: a cluster randomized controlled trial. PLoS Medicine 2017; 14(11): e1002442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine 2004; 23(19): 2937–2960. doi: 10.1002/sim.1903 [DOI] [PubMed] [Google Scholar]
- 28.Zha R Advances in the Analysis of Incomplete Data Using Multiple Imputations. PhD Dissertation, University of Connecticut. 2018. [Google Scholar]
- 29.Little RJ. Regression with missing X’s: a review. Journal of the American Statistical Association 1992; 87(420): 1227–1237. [Google Scholar]
- 30.Borm GF, Fransen J, Lemmens WA. A simple sample size formula for analysis of covariance in randomized clinical trials. Journal of Clinical Epidemiology 2007; 60(12): 1234–1238. [DOI] [PubMed] [Google Scholar]
- 31.Wang R, Lagakos SW, Ware JH, Hunter DJ, Drazen JM. Statistics in Medicine — Reporting of Subgroup Analyses in Clinical Trials. New England Journal of Medicine 2007; 357(21): 2189–2194. doi: 10.1056/NEJMsr077003 [DOI] [PubMed] [Google Scholar]
- 32.Williamson EJ, Forbes A, White IR. Variance reduction in randomised trials by inverse probability weighting using the propensity score. Statistics in Medicine 2014; 33(5): 721–737. doi: 10.1002/sim.5991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Williamson EJ, Forbes A, Wolfe R. Doubly robust estimators of causal exposure effects with missing data in the outcome, exposure or a confounder. Statistics in Medicine 2012; 31(30): 4382–4400. [DOI] [PubMed] [Google Scholar]
- 34.Sun A Applying Weighted GEE for Missing Data Analysis and Sample Size Estimation in Repeated Measurement Studies with Dropout. PhD Dissertation, University of Maryland. 2013. [Google Scholar]
- 35.Chen T, Tchetgen Tchetgen EJ, Wang R. A stochastic second-order generalized estimating equations approach for estimating association parameters. Journal of Computational and Graphical Statistics 2020; 29(3): 547–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Julious SA, Owen RJ. Sample size calculations for clinical studies allowing for uncertainty about the variance.. Pharm Stat 2006; 5(1): 29–37. doi: 10.1002/pst.197 [DOI] [PubMed] [Google Scholar]
- 37.Fay MP, Halloran ME, Follmann DA. Accounting for variability in sample size estimation with applications to nonadherence and estimation of variance and effect size.. Biometrics 2007; 63(2): 465–474. doi: 10.1111/j.1541-0420.2006.00703.x [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data for the CRT tutorial example is available in Harvard Dataverse at https://doi.org/10.7910/DVN/OCWCF5 Data for the IRT illustrative example is available on request from sdac.data@sdac.harvard.edu.


