Abstract
The relationship between chromatin architecture and function defines a central problem in biology and medicine. Many computational chromatin models with atomic, coarse-grained, mesoscale, and polymer resolution have been used to shed light onto the mechanisms that dictate genome folding and regulation of gene expression. The associated simulation techniques range from Monte Carlo to molecular, Brownian, and Langevin dynamics. Here, we present an efficient Compute Unified Device Architecture (CUDA) implementation of Brownian dynamics (BD) to simulate chromatin fibers at the nucleosome resolution with our chromatin mesoscale model. With the CUDA implementation for computer architectures with graphic processing units (GPUs), we significantly accelerate compute-intensive hydrodynamic tensor calculations in the BD simulations by massive parallelization, boosting the performance a hundred-fold compared with central processing unit calculations. We validate our BD simulation approach by reproducing experimental trends on fiber diffusion and structure as a function of salt, linker histone binding, and histone-tail composition, as well as Monte Carlo equilibrium sampling results. Our approach proves to be physically accurate with performance that makes feasible the study of chromatin fibers in the range of kb or hundreds of nucleosomes (small gene). Such simulations are essential to advance the study of biological processes such as gene regulation and aberrant genome-structure related diseases.
Significance
Brownian dynamics simulations of chromatin fibers can provide valuable insight into genome-related processes such as chromatin folding and epigenetic regulation. By using a Compute Unified Device Architecture programming platform on graphics processing units, we accelerate the expensive Brownian dynamics force calculations including hydrodynamic interactions. Such an implementation opens the possibility to study kb- to Mb-range chromatin fibers containing explicit histone tails and linker histones at nucleosome resolution.
Introduction
Chromatin, a complex of DNA and histone proteins, has an essential role in gene expression (1). Yet, its three-dimensional (3D) structure and folding mechanisms to condense meters of eukaryotic DNA into a micrometer nucleus remain obscure (2). The regulation of these mechanisms by posttranslational modifications, binding of linker histone (LH) or other proteins, or the wrapping/unwrapping of nucleosomes is essential to control chromatin architecture and hence DNA accessibility and genome integrity (3).
With state-of-the-art experimental techniques, such as chromosome conformation capture, superresolution microscopy, and high-throughput sequencing, as well as computational modeling, we have changed our view of the 3D genome organization from a regular ordered folding to a heterogeneous ensemble of folds (4). Experiments have shown that chromosomes are hierarchically organized, and the genome is segregated into transcriptionally active and inactive compartments. Inside these compartments, chromatin establishes self-interactions, creating substructures called topological-associated domains, which often arise from the formation of loops mediated by the CTCF-cohesin complex.
Computational efforts have similarly contributed to our understanding of chromatin architecture and its relationship to function (5,6,7,8,9). These studies have provided valuable information on chromatin’s ionic dependence, the role of histone tails and LH, DNA electrostatics and sequence dependence, the effect of LH and nucleosome depletion or posttranslational modifications, gene silencing and folding mechanisms, loop formation, and regulation of topological-associated domains, among others.
The approaches used in chromatin modeling span a huge range, from all-atom simulations of single nucleosomes to coarse-grained and mesoscale simulations of oligonucleosome fibers and gene systems and polymer models of whole chromosomes, with decreasing resolution as system size increases (see recent reviews in (7,10,11,12,13,14,15,16,17)). While all-atom, coarse-grained, and mesoscale models are constructed based on the atomic structures of chromatin components, such as nucleosomes and LHs, some polymer models are data driven and use experimental information, usually from chromosome conformation capture, to describe chromatin architecture (6,14).
These multiscale modeling approaches for chromatin rely on various simulation techniques for conformational sampling like molecular dynamics (MD) (e.g., (18,19,20)), Monte Carlo (MC) (e.g., (21,22)), Brownian dynamics (BD) (e.g., (23) (24)), and Langevin dynamics (e.g., (25) (26)). In particular, BD is suitable for simulating physical systems containing large particles where diffusive forces are significant compared with internal forces. The bottleneck in BD is the frequent calculation of the hydrodynamic interactions between BD particles, a matrix D, which has an complexity with system size n (n particles). Moreover, to calculate the Brownian random force, whose properties depend on D, a Cholesky factorization of the dense matrix D is required, and this task has an complexity. This limits BD system size (27).
With the emerging Compute Unified Device Architecture (CUDA) for simulations on graphics processing units (GPUs), the calculation of D can be parallelized on as many threads (basic computing elements) as the number of interactions between BD particles, reducing the time complexity to . The corresponding Cholesky factorization can be parallelized to reduce its time complexity to . As has been proven for other molecular modeling applications, such as MD simulations (28) and quantum chemistry (29), the use of GPUs allows significant speed ups and, hence, simulation of larger system sizes over longer simulation times (30,31).
In our early chromatin modeling studies, Beard and Schlick developed and applied BD to investigate the structure and dynamics of small oligonucleosome fibers that did not include LH and flexible histone tails (32). When we incorporated flexible histone tails into the mesoscale model to investigate their role in chromatin folding (33), MC simulations became more efficient for equilibrium sampling of large systems (34,35,36,37,38).
While MC has allowed us to study numerous important structural features of chromatin fibers and gene systems (e.g., (39,40,41,42,43,44)), BD introduces an exciting dynamic component to study the evolution of chromatin structure, transitions, and rearrangements. Here, we present the implementation of BD simulations of our mesoscale chromatin model with CUDA for calculation on GPUs and examine its performance using different metrics. We then validate the strategy by reproducing experimentally determined properties of different oligonucleosome systems, as well as previous MC results.
Overall, our implementation of BD to simulate mesoscale chromatin fibers reproduces experimental trends as MC and demonstrates exceptional computational performance, opening the possibility to study chromatin fibers of several hundred nucleosomes in a reasonable computer time. Such studies, in turn, could help reveal the mechanisms by which chromatin is compacted inside the cell nucleus and the impact of protein regulators on its folding.
Materials and methods
Chromatin mesoscale model
Our mesoscale model of chromatin has evolved for over 20 years, with the current model considering flexible histone tails (45) and their acetylation (46,47), two LH variants (H1E and H1C) with several binding modes (on versus off dyad) (48,49), and nonuniform linker DNA lengths (36), among other features (7).
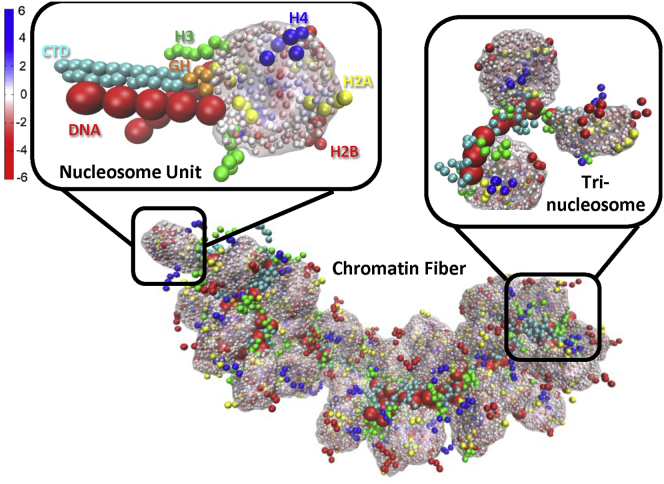
The chromatin elements are coarse grained at different levels of resolution. The nucleosome cores are treated as charged disks according to the atomistic core particle, whereas linker DNA, histone tails, and LHs are treated as beads (Fig. 1).
Figure 1.
Chromatin mesoscale model. 50-nucleosome chromatin fiber with the enlarged basic unit (chromatosome) showing each element and the enlarged tri-nucleosome showing the connection between nucleosomes by linker DNA. Linker DNA is shown as red beads; histone tails as green (H3), yellow (H2A), red (H2B), and blue (H4) beads; LHs are shown as orange (globular head) and cyan (C-terminal domain) beads; and nucleosome cores are shown with their distributed charge beads. To see this figure in color, go online.
The nucleosome core with 300 point charges distributed on its irregular surface calculated by the DiSCO algorithm is designed to reasonably approximate the electric field of the atomistic core particle by a Debye-Hückel (screened electrostatics) approximation (50). An optimization is performed once the charges are distributed to determine the approximation error. DiSCO assigns charges as follows: 1) a distance vector is defined from each atom to the center of the molecule, and its associated surface area is defined as a surface element; 2) multiple rounds of smoothing are performed; 3) surface points are distributed evenly at a density of 4.0 per Å2; and 4) the overall surface points are divided into 300 groups with representative surface charges assigned. The number 300 was determined to be a good balance between computational cost and electric field approximation. Linker DNAs are treated with a combined worm-like chain and bead model (51) based on the charged colloidal cylinder approach derived by Stigter (52). Histone tails (53) and LHs (48,49) are coarse grained as five residues per bead with the Levitt-Warshel united-atom protein model.
The water solvent surrounding the chromatin fibers is modeled with a continuum of dielectric constant of 80. The screening effect of monovalent salt on electrostatic interactions within the chromatin fiber is treated by the Debye-Hückel electrostatic potential. Thus, electrostatic interactions between all charged beads are screened depending on the salt concentration.
The chromatin model can be considered as a ball/spring system. In particular, linker DNAs connect nucleosome cores, and histone tails and LHs are attached to the nucleosome cores. Each bead can move freely during the simulation, except for the 300 charge beads within each nucleosome core, one fixed tail bead per histone tail, and the six LH globular head beads, which move together with the nucleosome core. Hence, the mesoscale chromatin model has flexible linker DNA, histone tails, LHs, and rigid nucleosome cores.
The total potential energy function of the model includes stretching, bending, and twisting terms for the linker DNA (, , ), stretching and bending terms for histone tails (, ) and LHs (, ), and excluded volume () and electrostatic () terms for all beads as
| (1) |
where r is the collective position vector.
The forces (F) on the system are defined as the negative gradient of the potential energy as
| (2) |
The torques (τ) due to the forces (F) are calculated by the equation
| (3) |
The supporting material provides further details on parameters and connections between elements, energy terms, and force calculations.
Simulation
A commonly used BD algorithm was first proposed in 1978 (54) based on the Langevin equation and then was improved in 1989 (55) with a second-order algorithm based on the Runge-Kutta method. The latter overcomes an issue associated with the first-order approximation: when the time step is small, the procedure can be inefficient and, when large, unstable. In 2001, Beard and Schlick (32) further modified the second-order BD algorithm to include rotational motions and to evaluate the dense matrix D less frequently. The derived second-order translational and rotational equations are given by
| (4a) and (4b) |
| (5a) and (5b) |
where r is the position vector, is the time step, is the Boltzmann’s constant, T is the absolute temperature, D is the diffusion tensor, F is the force, τ is the torque, is the rotational friction coefficient, and R and are the stochastic terms (32,54), which are Gaussian-distributed random vectors with means of 0 and variance-covariance of
| (6a) and (6b) |
The Cholesky approach is used to calculate the vector R from the relationship in Eq. 6a. The Cholesky decomposition of the diffusion tensor D is determined by , where L is a lower triangular matrix and each element in L is given by
| (7) |
The terms D, F, and R are derived from three types of forces. D is derived from the friction force, F is a systematic force that includes the interaction between Brownian particles and any external force, and R is derived from a random force and determined by the Cholesky decomposition of the diffusion tensor D.
Following the first-order estimate of the translation and rotation from Eq. 4a at time , namely and , we calculate the forces and torques at the end of the time step and use them to construct an explicit second-order update as shown in Eq. 4b.
The calculation of forces and torques are described in the supporting material. Below, we show the calculation of the diffusion tensor.
Diffusion tensor
There are two types of diffusion tensors introduced in (54), the Oseen and Rotne-Prager tensors. Our approach uses the Rotne-Prager tensor because in the BD simulation, the diffusion tensor needs to be a positive definite matrix to apply the Cholesky decomposition. The Oseen tensor becomes a nonpositive definite when the separation between the particles is small. The Rotne-Prager tensor is given by
| (8) |
where η is the solvent viscosity and a is the sphere radius of the particles.
Eq. 8 is for the two nonoverlapping particles, . For overlapping particles, we use
| (9) |
Here, , which has been proven for (56) and has been proposed for (53,57).
CUDA application
To efficiently run BD simulations, we first incorporated the message-passing interface (MPI) procedure, which can compute the forces on 24 processors in parallel. However, the calculation of H requires significant memory as the system size increases. Thus, we calculated it on one processor, and as a result, only small systems could be simulated with proper time consumption.
With the increasing availability of GPU computing, CUDA implementation becomes feasible and preferable in our application. Because the time complexity to calculate forces and H is , and the Cholesky decomposition , with parallelizable algorithms, the use of GPUs has the potential to accelerate computations significantly.
Instead of nested “for” loops through all the interactions in the original MPI code, we assign many threads (basic computing elements) in CUDA and use “if” statements to accomplish the job. Namely, the calculations are performed in parallel instead of one by one. Thus, we assign an individual thread with index to calculate the interaction between beads i and j. This means that, for example, for a 100-nucleosome system, 519 million threads are assigned to calculate the interactions between all pairs of beads. Compared with the 24 processors used in computer processing unit (CPU) parallel computation, this is a huge speed up.
In the GPU architecture, the threads are grouped into blocks, which are grouped onto a 3D grid. Each block might contain up to 1,024 threads, and the 3D grid contains up to 2,147,483,647, 65,535, and 65,535 blocks in the x, y, and z dimensions. Thus, the maximum number of threads in a single GPU is ∼2 billion, which is more than enough to assign one thread for each interaction in a 100-nucleosome system. While the threads inside the same block can communicate with each other, those in different blocks can only communicate through the global memory, which increases noncalculation latencies due to the launching of extra kernel invocations (parallel function executions) and transferring of data to the global memory. Namely, in the CUDA code, each calculation is performed by a separate kernel (i.e., kernel A calculates forces, and kernel B calculates translation), and each kernel uses all needed threads; only after kernel A’s calculations are done are the data saved to the global memory, and kernel B calculations begin.
Implementation
To convert the MPI to a CUDA application, we create as an N × N matrix where each element is a three-component row vector corresponding to the force between beads i and j as
Thus, we calculate all energies and forces as described in the supporting material and store them in . Then, we reduce the matrix by adding the collection of rows in into one row () to obtain the array of the forces F applied to each bead and feed it into Eqs. 4a and 4b.
Similarly, we create as an N × N matrix where each element is a 3 × 3 matrix that stores the diffusion tensor coming from the hydrodynamic interactions between beads i and j as
As shown in Eqs. 8 and 9, each component can be calculated individually. Thus, it is straightforward to assign 3N × 3N threads, one for each calculation, to obtain the dense matrix with a time complexity of only and use it directly as D in Eqs. 4a and 4b.
For the Cholesky decomposition of the linear system, we implement the library provided by the vendor cuSolver and use the function “cusolverDnDpotrf,” which computes the Cholesky factorization of a real double-precision Hermitian positive-definite matrix, suitable for the diffusion tensor matrix. In theory, positive definiteness is guaranteed by the diffusion tensor construction (56), but in practice, round-off error can make the matrix nonpositive definite. When this happens (infrequently), we use the diffusion tensor from the previous BD step.
The parallelization of the Cholesky decomposition is not straightforward, since the calculation of each element ij depends on information from the previous elements 1 to i − 1 and 1 to j − 1. In practice, this is calculated column by column rather than element by element. By looping through the columns, the results of each columni can be achieved by calling three parallelized CUDA kernels: square root kernel (calculates the diagonal element ij), normalization kernel (updates all the elements below the current diagonal element ij), and submatrix update kernel (updates the submatrix ranging from i + 1, i + 1 to ). In this way, the time complexity of the Cholesky decomposition is reduced from to .
Since we do not need D and F directly, just their product (Eqs. 4a and 4b), besides the calculation of the large matrices and and the Cholesky decomposition, we calculate the translation and rotation inside the CUDA kernel. The efficient way to do so is to assign N threads for each bead i and let each thread i only calculate one translation and rotation for bead i with the corresponding data from D and F based on Eqs. 4a and 4b and Eqs. 5a and 5b.
Because GPUs cannot read and write data, after calculations are complete, we transfer the results of the locations and orientations of all the beads back from GPU to CPU to generate the desired files (i.e., trajectory, energy, checkpoint files).
Results and discussion
Performance
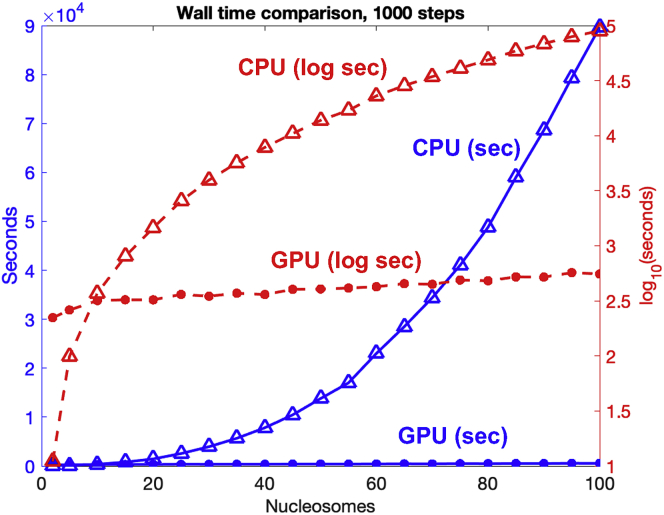
To assess performance, we run on both CPU and GPU simulations of chromatin fibers ranging from 2- to 100-nucleosome cores with nucleosome repeat length (NRL) = 191 bp, histone tails, and one LH per nucleosome. The timestep is 1 ps. The CPU used is an Intel Xeon Platinum 8268 24C 205W 2.9 GHz processor, and the GPU is an Nvidia Tesla v.100 16 GB processor. We recorded times for 1,000 simulation steps using the MPI code run on the CPU and the CUDA code run on the GPU. We display the wall time in Fig. 2, and its breakdown by task in Fig. 3. The wall time measures the actual time taken by the program to complete a task, including calculations, writing/reading, and communication.
Figure 2.
CPU versus GPU architecture for chromatin fibers of 2–100 nucleosomes. Wall time needed to complete 1,000 steps with a time step of 1 ps when running on CPU (triangle) versus GPU (circle) as a function of system size. Blue: plot in seconds. Red: plot in logarithmic scale. To see this figure in color, go online.
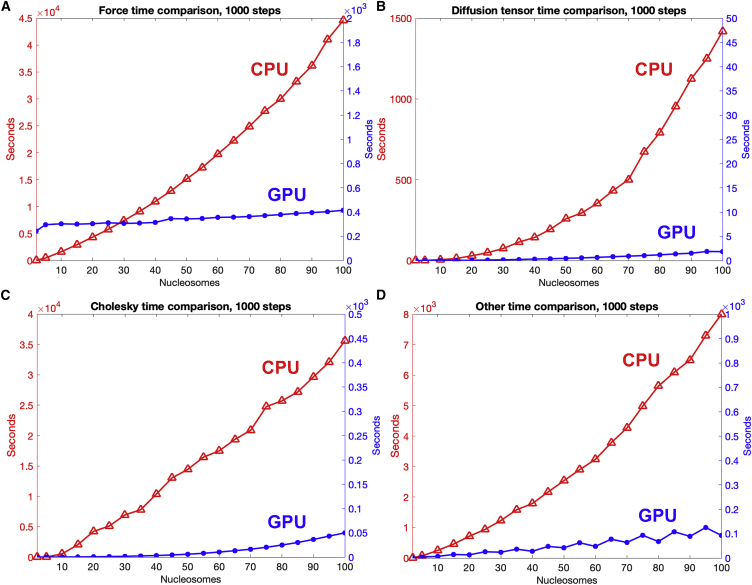
Figure 3.
Computation time breakdown on CPU and GPU for chromatin systems of 2–100 nucleosomes. (A–D) Force (A), diffusion tensor (B), Cholesky decomposition (C), and other calculations (D). Note different timescales for each plot. The force includes all forces and energy calculations mentioned in the supporting material, such as stretching, bending, twisting, nonbonded electrostatics, and excluded volume. Other calculations include reading and writing from/to files; translation and rotation of the beads; Euler angle calculations; and math functions such as random, exp., log, sin, cos, tan, cross product, norm, etc. To see this figure in color, go online.
The CPU wall time increases with the system size steeply (Fig. 2, blue triangles). On the other hand, no increase in wall time is observed on GPUs (Fig. 2, blue circles). For example, for a 100-nucleosome system, a calculation of 1,000 steps on CPUs takes 25 h, versus less than 10 min on GPUs. As observed in the plot with log scale (Fig. 2, red curves), the CPU calculation (red triangles) is advantageous compared with the GPU (red circles) for very small systems (1–9 nucleosomes) due to the “noncalculation latencies” associated with data transfer, kernel launch, and synchronization. As mentioned above, we must transfer data, such as locations and orientations of all beads, as well as random numbers between GPUs and CPUs. The kernel launch overhead reflects the time required for the GPU to execute a launched kernel. Because we cannot limit usage to a single GPU block, we must launch additional kernels, and this increases the time needed in each step of the simulation. During the simulation, each thread either belonging to the same block or different blocks needs to be synchronized to ensure that data are ready for the calculations in the next step. While synchronization of threads belonging to the same block is fast due to the use of shared memory, synchronization of threads belonging to different blocks requires the use of the global memory, which is more time consuming.
Fig. 3 shows the profiling breakdown for wall times by the MPI code for the CPU and the CUDA code for the GPU. The wall time includes the calculation time and the noncalculation latencies. When the system size increases, the time consumption of noncalculation latency increases as . For the MPI code, all calculations show exponential trends, and for CUDA, the calculations show linear and exponential trends (which are constant and linear trends when ignoring the noncalculation latency).
Fig. 3A shows that in the MPI code, the force calculations range from 0 to ∼45,000 s for systems containing 2–100 nucleosomes, which is due to the complexity with system size. Meanwhile, the time is ∼400 s for all the systems on CUDA because this calculation is performed in parallel on many threads. In addition (see implementation), each thread handles one interaction between one pair of Brownian particles, and since the nucleosome core is treated as one particle, the calculation for 300 charged beads is assigned to one thread. For calculations between two nucleosome cores, 300 × 300 = 90,000 calculations are done on one thread, explaining the force calculation time of 400 s. Although this approach might increase the force calculation time compared with treating each nucleosome charge individually, it reduces the force matrix size and thus the memory usage, allowing us to simulate larger systems.
The calculations for the diffusion tensor and Cholesky decomposition are performed every 20 steps. Fig. 3 B shows that the time used for the diffusion tensor calculation is smaller than the time used for the force calculation due to our treatment of the nucleosome core as one hydrodynamic particle instead of 300 charged beads as in the force calculation. The calculation on the MPI code takes as much as 1,400 s for the 100-nucleosome system, while on the CUDA code, it takes less than 1 s for all the systems.
Fig. 3C shows that the most time-consuming computation is the Cholesky decomposition. Even though the Cholesky decomposition is calculated every 20 steps, it requires 36,000 s in the MPI code due to its complexity. In comparison, in the CUDA code, the Cholesky decomposition only increases from 0 to ∼50 s ().
Fig. 3D shows the time for other calculations (such as reading and writing from and to files; translation and rotation of the beads; Euler angles; math functions such as random, exp., log, sin, cos, tan, cross product, norm, etc.) is also reduced from the CPU to the GPU due to the parallel implementations. The GPU time shows a linear trend due to remaining serial computations that increase with system size, such as random number generation at each step. Note that the “zigzag” pattern results from system sizes not being divisible by the kernel’s block size, in which case larger matrices filled with zeros need to be allocated in the GPU memory before transferring the data and launching the kernel, increasing the allocation time. Still, the time consumed for these calculations remains very small.
Validation
For our chromatin BD simulations, we set the temperature to 293.15 K and the time step to ps. We saved coordinates every 100 steps and simulated at least five independent replicas started from different random seeds for each trajectory. Full details of parameters are provided in the supporting material.
Translational diffusion coefficient of nucleosomes
The velocity of the Brownian motion is defined by the translational diffusion coefficient (D), which depends on the size of the particle, the surface structure, and the ionic concentration and viscosity of the medium.
Here, we calculate D from the Einstein relation for 3D space as
| (10) |
where t is the simulation time, is the initial time, and is an average over the simulation time.
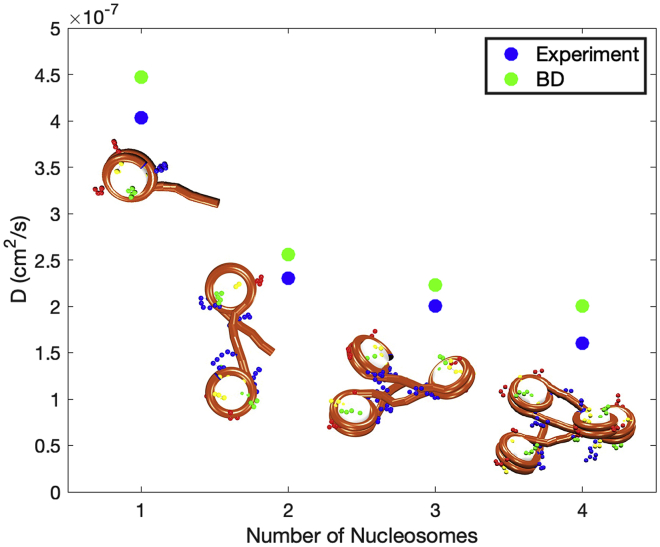
We calculate D for nucleosome arrays containing 1 to 4 nucleosomes with NRL = 209 bp at salt of 150 mM NaCl. We perform 10 independent trajectories started from different random seeds for 700 ns and compare the average (D) values with experimental data (Fig. 4) by (8,58,59,60) of 1- to 4-nucleosome systems obtained by fluorescence correlation spectroscopy experiments that measure fluorescence intensity fluctuations due to particle diffusion. These in vitro experiments are comparable with our BD simulations because major relevant parameters can be matched. Nonetheless, in vivo nucleosome diffusion experiments in the context of interphase chromatin report values on the order of to cm2/s (61,62), close to predicted values here.
Figure 4.
Diffusion coefficients for 1- to 4-nucleosome systems obtained from BD simulations (green) compared with experimental results (blue) from (8,58,59,60). To see this figure in color, go online.
As shown in Fig. 4, the trend for diffusivity as a function of system size is reproduced by our BD simulations, and the values are close to experimental data.
Salt-dependent chromatin folding
The effect of salt concentration on chromatin folding is well known. Here, we study the folding of 12-nucleosome chromatin arrays at different monovalent salt concentrations and compare our results with two sets of experimental values obtained by Hansen et al. (63) and Howe et al. (64). In particular, we study 1) arrays with NRLs = 173, 191, and 209 bp, without LHs, and with 20, 50, 100, 150, and 200 mM NaCl, and 2) arrays with an NRL of 209 bp, with and without LH, and with 25, 50, 75, and 100 mM NaCl.
Fibers are simulated for 700 ns with a time step of ps. For the systems without LHs, we start the simulations from an ideal zigzag extended geometry, whereas for the systems with LHs, which have 336 more particles, we start them from the equilibrated structures obtained with MC simulations to reduce the simulation time needed to reach equilibrium conformations. We run 10 independent trajectories starting with different random seeds. Results are obtained from the last 10 ns of each simulation and averaged over the 10 trajectories.
We calculate the sedimentation coefficient at each salt concentration as follows:
| (11) |
where and are the sedimentation coefficients of a mononucleosome without LHs ( S) (65) and with LHs ( S) (66), respectively, ρ is the LH density on the fiber, is the radius of a nucleosome ( 5.5 nm), is the number of nucleosomes in the chromatin fiber, and is the distance between the nucleosomes i and j.
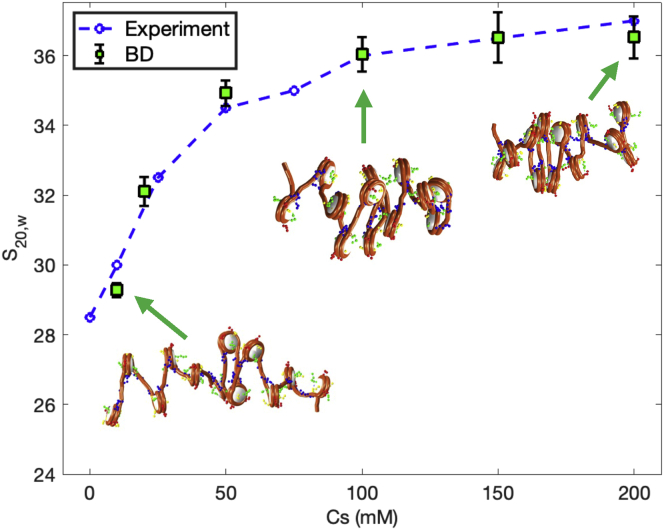
BD simulations accurately reproduce the fiber compaction as a function of salt concentration observed experimentally. The sedimentation coefficient increases with the salt concentration, with a plateau reached at around 100 mM NaCl (Fig. 5). This difference in compaction is also clearly seen in the fiber configurations. Fibers at low salt appear unfolded, whereas fibers in physiological conditions are compact. Similar results are seen for the other two fibers with NRLs = 173 and 191 bp (see Table 1). Moreover, in agreement with the observations of Hansen et al. in (63), the increase of fiber compaction with salt concentration does not depend on the NRL.
Figure 5.
Salt-dependent folding of 12-nucleosome chromatin fibers. Sedimentation coefficients for 12-nucleosome fibers with NRL = 209 bp, without LHs, and with 10, 20, 50, 100, 150, and 200 mM NaCl. Blue dashed line represents experimental data taken from (63). Green squares with error bars show the average and standard deviation obtained from our BD simulations. Chromatin fiber configurations at increasing salt concentrations, from 10 to 200 mM. Linker DNA is shown in orange, and histone tails beads are shown in green (H3), yellow (H2A), red (H2B), and blue (H4). To see this figure in color, go online.
Table 1.
Chromatin compaction assessment by sedimentation coefficients of 12-nucleosome fibers with NRLs = 173, 191, and 209 bp and with 20, 50, 100, 150, and 200 mM NaCl
| NRL (bp) | Monovalent salt (mM) | Computed (S) |
|---|---|---|
| 173 | 20 | 35.4 0.4 |
| 50 | 41.5 0.8 | |
| 100 | 47.5 0.9 | |
| 150 | 49.8 1.7 | |
| 200 | 51.9 2.0 | |
| 191 | 20 | 32.7 0.5 |
| 50 | 37.0 1.1 | |
| 100 | 40.0 1.4 | |
| 150 | 41.0 1.1 | |
| 200 | 42.0 1.3 | |
| 209 | 20 | 32.1 0.4 |
| 50 | 34.9 0.4 | |
| 100 | 36.0 0.5 | |
| 150 | 36.5 0.7 | |
| 200 | 36.5 0.6 |
See Fig. 5 for plots with NRL = 209 bp.
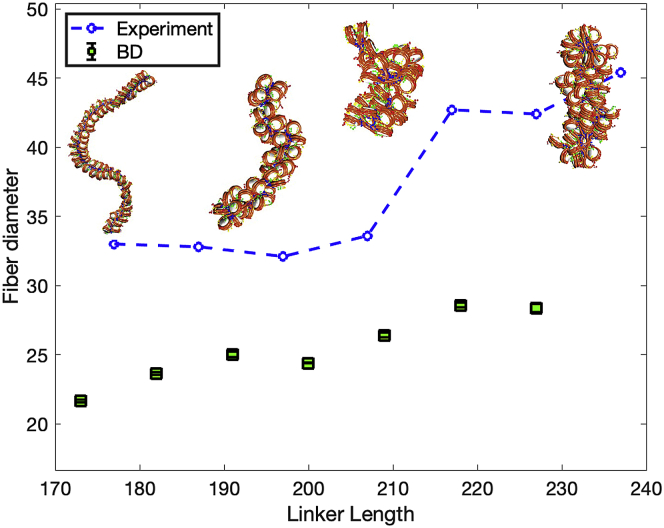
At a single salt concentration, an increase in NRL produces an increase in fiber diameter, and two distinct chromatin structural classes emerge, as previously shown by Rhodes and coworkers by cryo-electron microscopy (67). As we show in Fig. 6, although absolute values are smaller, BD simulations reproduce the experimental trend for fiber diameters, showing a first structural class, composed of fibers with NRLs = 177 to 207 bp, and a second class, composed of fibers with NRLs = 217 to 237 bp. Additionally, the fiber structures resemble those seen by Rhodes et al. (67). These simulations of 20 ns were started from equilibrated structures obtained from MC simulations. Five independent trajectories were run for each system starting from different random seeds, and the last 10 ns of each replica’s trajectory were used for analysis.
Figure 6.
Fiber diameters for NRL-dependent folding of chromatin fibers. Fiber systems of 72, 52, 52, 61, 47, 55, 66, and 56 nucleosomes, with NRLs = 173, 182, 191, 200, 209, 218, 227, and 237 bp, respectively, without LHs, and with 120 mM NaCl. Blue dashed line represents experimental data taken from (67). Green squares with error bars show the average and standard deviation obtained from our BD simulations. Representative chromatin fiber configurations at NRLs = 173, 191, 209, and 237 bp are shown with linker DNA in orange and histone tails beads in green (H3), yellow (H2A), red (H2B), and blue (H4). To see this figure in color, go online.
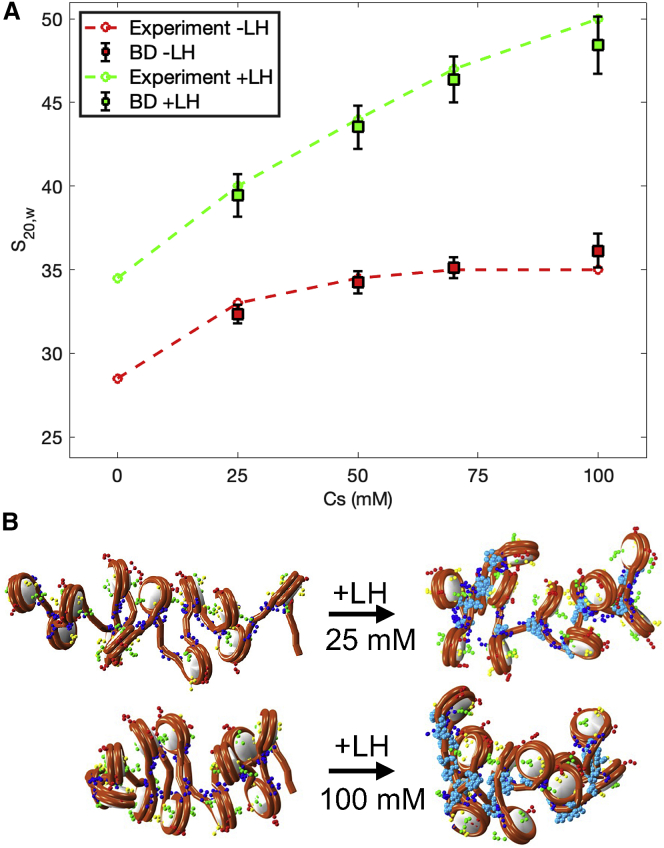
As shown in Fig. 7 A, BD simulations can also accurately reproduce the experimental fiber compaction for arrays with NRL = 209 bp with and without LHs. As before, the sedimentation coefficient increases with salt concentration, and LH further increases compaction compared with fibers without LHs. Fiber configurations (Fig. 7 B) clearly show the impact of salt and LHs on compaction.
Figure 7.
Salt- and LH-dependent folding of 12-nucleosome chromatin fibers. (A) Sedimentation coefficients of chromatin fibers with NRL = 209 bp, with and without LHs, and with 25, 50, 75, and 100 mM NaCl. Green (with LHs) and red (without LHs). Dashed lines represent experimental data taken from (64), and squares with error bars show average and standard deviation obtained from BD. (B) Fiber configurations with and without LHs at 25 and 100 mM NaCl. To see this figure in color, go online.
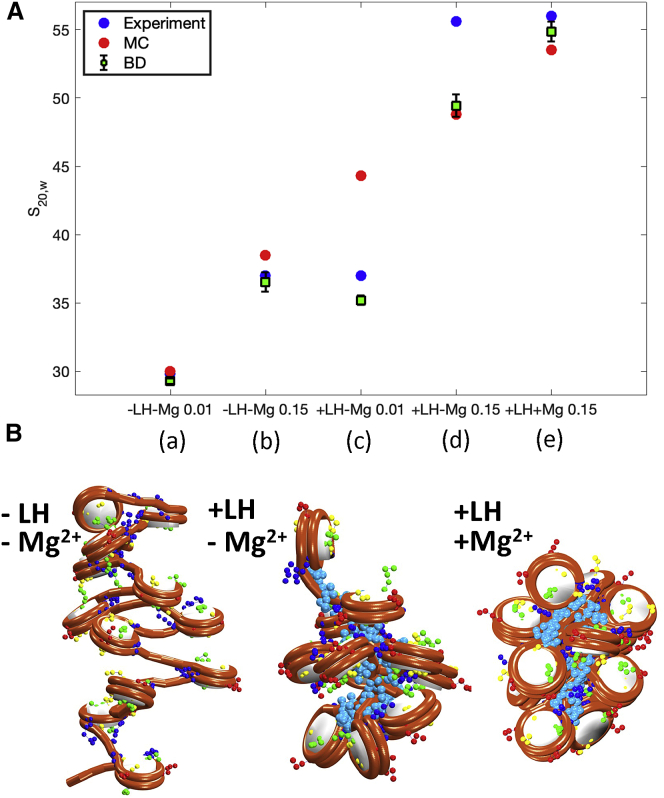
Salt, Mg2+, and LH roles in chromatin compaction
In a previous study, we combined our MC simulations of chromatin fibers with electron microscopy nucleosome interaction capture experiments to study the internal organization of chromatin fibers (68).
There, we assessed chromatin compaction at different monovalent salt concentrations and with/without Mg2+ and LHs. We showed that physiological salt concentrations and LHs produce a zigzag topology with dominant k ± 2 internucleosome contacts. Addition of Mg2+ further compacts the fibers and increases the bending of the linker DNA, promoting k ± 1 contacts.
Here, we reproduce these results by simulating 12-nucleosome chromatin arrays with NRL = 209 bp in the following conditions: 1) 10 and 150 mM NaCl, 2) 10 and 150 mM NaCl plus 1 LH per nucleosome, and 3) 150 mM NaCl plus 1 LH per nucleosome and 1 mM Mg2+. BD simulations are run for 100 ns starting from MC-equilibrated configurations in the case of fibers with LHs and from ideal zigzag structures in the case of fibers without LHs. Note that although similar results are expected from MC and BD, MC samples the equilibrium conformational ensemble, while BD samples thermal fluctuations around representative conformations.
The Mg2+ effect is modeled using our phenomenological approach developed in (68). That is, we reproduce the effect of 1 mM Mg2+ on fiber compaction by reducing the DNA persistence length from 50 to 30 nm, according to published data (69), and by increasing the inverse Debye length in the electrostatic term from 1.48 to 2.52 nm-1 to reflect altered electrostatic repulsion between linker DNAs.
BD simulations reproduce the experimental trends, as well as the MC results (Fig. 8 A). Fibers without LHs show the same compaction as the experimental and MC values. Such compaction increases with the addition of LHs and further with the addition of Mg2+ (Fig. 8 B). For low salt with LHs, BD conformations are slightly more open than experimental measurements suggest, while MC configurations are much more compact. For physiological salt with LHs, both BD and MC fibers are less compact than the experiment suggests. This is likely due to our fixed (rather than dynamic) LH treatment.
Figure 8.
Effect of salt, Mg2+, and LHs on chromatin compaction of 12-nucleosome chromatin fibers. (A) Sedimentation coefficient as a function of simulation condition for five fiber conditions (left to right): (a) 0.01 mM NaCl, no LH; (b) 0.15 mM NaCl, no LH; (c) 0.01 mM NaCl, with LH, no Mg2+; (d) 0.15 mM NaCl, with LH, no Mg2+; and (e) 0.15 mM NaCl, with LH, with Mg2+. Blue circles represent experimental data and red circles MC results, both taken from (68). Green squares with error bars show averages and standard deviations obtained from our BD simulations. (B) Fiber configurations from (b), (d), and (e), respectively. To see this figure in color, go online.
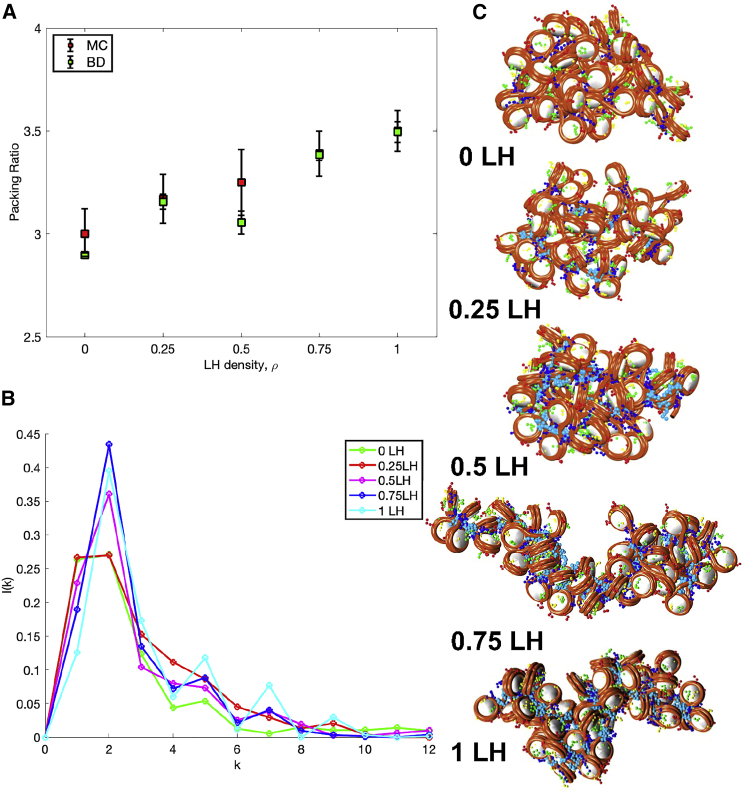
Role of LH in chromatin transitions
The role of LH in compacting chromatin is well known (70). Recently, we further studied how LH density, ρ, regulates chromatin architecture in relationship with the development of lymphoma (43). There, we showed that ρ triggers a transition from a flexible and globular to a rigid and straight configuration that could be related to the overexpression of genes that drive lymphoma when LHs are mutated or deficient.
Here, we reproduce this transition by studying the same chromatin fibers for different ρ values. In particular, we study 50-nucleosome arrays with an irregular DNA linker length distribution found in mammalian cells (71), and 0, 0.25, 0.5, and 0.75 and 1 LH per nucleosome, with LHs randomly distributed along with the fiber. Simulations of 100 ns are started from equilibrated structures obtained from MC simulations. Five independent trajectories are run for each system starting from different random seeds, and the last 10 ns of each replica’s trajectory are used for analysis.
To characterize the transition, we measure the fiber packing ratio as the number of nucleosomes contained in 11 nm of fiber length as
| (12) |
where is the total number of nucleosomes, and the fiber length is calculated by defining the fiber axis with a cubic smoothing spline interpolation to the nucleosomes x, y, and z coordinates (see (72)).
We also measure the internucleosome interaction patterns. That is, we determine the tail-mediated interactions between each pair of cores in the chromatin fiber, constructing an interaction intensity matrix that describes the fraction of configurations that nucleosome pairs interact with one another. An interaction is defined when any nucleosome tail i is less than 2 nm apart from any charged bead or tail of nucleosome j. The internucleosome matrix is further decomposed into a normalized 1D plot that represents the relative intensity of interactions between nucleosomes separated by k neighbors as
| (13) |
As we see from Fig. 9 A, BD simulations accurately reproduce the compaction trends obtained by MC simulations. As expected, fiber compaction increases with ρ. The internucleosome interaction plots (Fig. 9 B) show that lower ρ produces high k ± 1 contacts due to higher linker DNA bending and a more globular and disordered structure, whereas higher ρ increases the k ± 2 interactions, which indicates a strong zigzag topology. Fiber configurations (Fig. 9 C) reveal this structural transition from a globular and loose fiber to a straight and compact fiber as ρ increases.
Figure 9.
The effect of ρ on compaction of a 50-nucleosome fiber. (A) Packing ratio as a function of ρ (LH density) as obtained from BD simulations (green) and MC simulations (red). (B) Internucleosome interactions for each ρ from BD. (C) Representative fiber configurations from BD at each ρ. To see this figure in color, go online.
Role of histone tails in chromatin folding
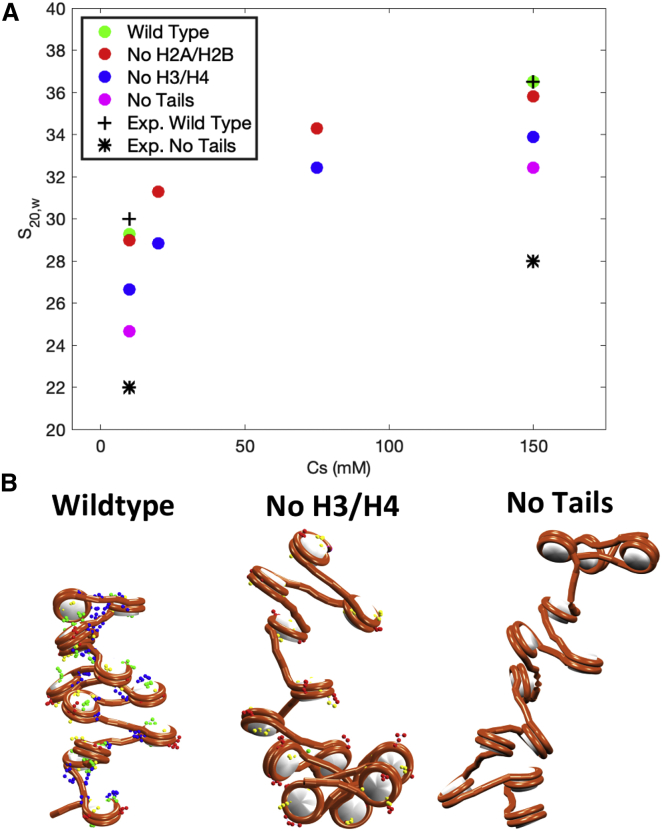
Many experimental studies have shown how truncation of all tails or specific tails, such as H3 and H4, affect chromatin compaction (73,74,75). As we have shown (45), histone tails mediate chromatin compaction and higher-order folding through internucleosome interactions, which are regulated by salt conditions and the presence of LHs.
To further validate our BD approach, we reproduce sedimentation coefficient values obtained in (73) on the effect of histone tails in chromatin folding. In particular, we study 12-nucleosome fibers with NRL = 207 bp and without LHs in the following conditions: 1) all tails wild-type at 10 and 150 mM NaCl; 2) H2A and H2B tails truncated at 10, 20, 75, and 150 mM NaCl; 3) H3 and H4 tails truncated at 10, 20, 75, and 150 mM NaCl; and 4) all tails truncated at 10 and 150 mM NaCl. To truncate any tails, we set selected tail beads charges to zero.
Each system is run for 700 ns with ps starting from ideal zigzag structures. Data are collected over the last 10 ns of five independent replicas started from different random seeds.
As is evident by the sedimentation coefficient values (Fig. 10 A) and chromatin fiber configurations (Fig. 10B), truncation of all tails produces a dramatic opening of the chromatin fibers. Similar results are obtained when H3/H4 tails are truncated, but the extent of the effect is smaller. In the case of H2A/H2B truncation, fibers look similar to the wild-type fibers, with almost the same sedimentation coefficients. These results are in agreement with our previous findings demonstrating the importance of histone tails in chromatin folding and, particularly, that H3 and H4 tails have a major role by mediating internucleosome interactions through cross fiber contacts that enhance long-range interactions (45).
Figure 10.
Effect of histone tails on chromatin folding at different monovalent salt concentrations for 12-nucleosome fibers. (A) Sedimentation coefficients as a function of salt concentration and wild-type/truncated tails. Green: all tails wild-type at 10 and 150 mM NaCl. Red: truncated H2A/H2B tails at 10, 20, 75, and 150 mM NaCl. Blue: truncated H3/H4 tails at 10, 20, 75, and 150 mM NaCl. Magenta: all tails truncated at 10 and 150 mM NaCl. (B) Fiber configurations obtained at 150 mM NaCl with all tails wild-type, H3/H4 tails truncated, and all tails truncated. To see this figure in color, go online.
Moreover, as shown in Table 2, our trends on sedimentation coefficients reproduce the experimental trends of (73) reasonably. Our BD computed values generally reflect slightly more compact fibers.
Table 2.
Chromatin compaction assessment by sedimentation coefficients of 12-nucleosome fibers with different tails
| Array type | NaCl (mM) | Computed (S) | Experimental (S) |
|---|---|---|---|
| All tails wild-type | 10 | 29.3 0.2 | 30 |
| 150 | 36.5 0.7 | 36.5 | |
| Truncated H2A/H2B | 10 | 29.0 0.1 | 29.5 |
| 20 | 31.3 0.6 | 31 | |
| 75 | 34.3 0.8 | 32 | |
| 150 | 35.8 1.7 | 34 | |
| Truncated H3/H4 | 10 | 26.6 0.6 | 26 |
| 20 | 28.8 0.6 | 27.5 | |
| 75 | 32.4 1.0 | 28.5 | |
| 150 | 33.9 1.0 | 31 | |
| All tails truncated | 10 | 24.6 0.1 | 22 |
| 150 | 32.4 0.4 | 28 |
See Fig. 10.
Summary and outlook
We have developed an efficient BD simulation protocol for GPU computing architectures to simulate chromatin fibers using our mesoscale model at nucleosome resolution. With the CUDA implementation, our BD is faster compared with a CPU implementation by two orders of magnitude, which allows us to study kb-range chromatin fibers with hundreds of nucleosomes in a few days.
Our mesoscale model for chromatin fibers has proven valuable for many applications including metaphase chromatin folding (38), compartmentalization (76), mouse cell differentiation (40), lymphoma-associated genome folding (43), yeast cell genome silencing mechanism (77), and gene folding (39,41). Although we originally started our chromatin modeling using BD (32), we moved to MC as our model increased in complexity with the introduction of flexible histone tails and LH variants with different orientations, as MC was more efficient for large systems. Here, we demonstrate that, with the advance of GPU computing, BD simulations of large nucleosome fibers are feasible with our nucleosome-resolution chromatin mesoscale model. We show the agreement of our BD results with experimental measurements such as diffusion coefficients and chromatin sedimentation on different systems, including nucleosomes at different salt concentrations and with/without LHs, ions, and tails, as well as the effect of different LH densities. With BD, dynamic chromatin problems at the nucleosome level can be studied, including chromatin flexibility, effect of binding proteins on chromatin mobility, and dynamics of gene loops.
Although BD is not likely efficient for folding fibers from ideal zigzag structures into equilibrium structures, it is suitable to study the dynamics of systems around equilibrium. Moreover, BD can be used to generate and simulate efficiently fiber topologies based on Hi-C maps. Our CUDA code ideas could also be applied to MC sampling to quickly and efficiently fold fibers into equilibrated structures in parallel. Together, MC and BD implementations for GPU architectures will allow the study of Mb-range chromatin fibers, a size not reached until now for nucleosome resolution chromatin models with explicit histone tails and LHs.
Author contributions
Z.L. designed the research, developed the BD simulation C++ code with MPI and CUDA implementation, performed data analysis, prepared figures, and wrote the manuscript. S.P.-L. performed results analysis, wrote the manuscript, prepared figures, and performed some MC simulations. T.S. designed the research, reviewed the data and results analysis, wrote the manuscript, and obtained funding.
Acknowledgments
This work was supported by the National Institutes of Health, National Institutes of General Medical Sciences Award R35-GM122562, the National Science Foundation RAPID Award (2030377) from the Divisions of Mathematical Sciences and Chemistry, and National Science Foundation Award 2151777 from the Division of Mathematical Sciences, and Philip-Morris International to T.S. The NYU IT High Performance Computing resources, services, and staff expertise are gratefully acknowledged.
Declaration of interests
The authors declare no competing interests.
Editor: Alberto Perez.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.09.013.
Supporting material
Data availability
The working BD code has been deposited in GitHub under the Schlick lab group: https://github.com/Schlicklab/Brownian_Dynamics_CUDA.
References
- 1.Szerlong H.J., Hansen J.C. Nucleosome distribution and linker DNA: connecting nuclear function to dynamic chromatin structure. Biochem. Cell. Biol. 2011;89:24–34. doi: 10.1139/O10-139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fussner E., Ching R.W., Bazett-Jones D.P. Living without 30nm chromatin fibers. Trends Biochem. Sci. 2011;36:1–6. doi: 10.1016/j.tibs.2010.09.002. [DOI] [PubMed] [Google Scholar]
- 3.Klemm S.L., Shipony Z., Greenleaf W.J. Chromatin accessibility and the regulatory epigenome. Nat. Rev. Genet. 2019;20:207–220. doi: 10.1038/s41576-018-0089-8. [DOI] [PubMed] [Google Scholar]
- 4.Rowley M.J., Corces V.G. Organizational principles of 3D genome architecture. Nat. Rev. Genet. 2018;19:789–800. doi: 10.1038/s41576-018-0060-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bendandi A., Dante S., Rocchia W., et al. Chromatin compaction multiscale modeling: a complex synergy between theory, simulation, and experiment. Front. Mol. Biosci. 2020;7:15. doi: 10.3389/fmolb.2020.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dans P.D., Walther J., Orozco M., et al. Multiscale simulation of DNA. Curr. Opin. Struct. Biol. 2016;37:29–45. doi: 10.1016/j.sbi.2015.11.011. [DOI] [PubMed] [Google Scholar]
- 7.Portillo-Ledesma S., Schlick T. Bridging chromatin structure and function over a range of experimental spatial and temporal scales by molecular modeling. WIREs Comput. Mol. Sci. 2020;10:1434. doi: 10.1002/wcms.1434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jimenez-Useche I., Nurse N.P., Yuan C., et al. DNA methylation effects on tetra-nucleosome compaction and aggregation. Biophys. J. 2014;107:1629–1636. doi: 10.1016/j.bpj.2014.05.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yildirim A., Boninsegna L., Alber F., et al. Uncovering the principles of genome folding by 3D chromatin modeling. Cold Spring Harbor Perspect. Biol. 2021;14:a039693. doi: 10.1101/cshperspect.a039693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ozer G., Luque A., Schlick T. The chromatin fiber: multiscale problems and approaches. Curr. Opin. Struct. Biol. 2015;31:124–139. doi: 10.1016/j.sbi.2015.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bascom G.D., Schlick T. In: Lavelle C., Victor J.-M., editors. volume 2. Academic Press; 2017. Mesoscale modeling of chromatin fibers; pp. 123–147. (Nuclear Architecture and Dynamics). [Google Scholar]
- 12.Huertas J., Woods E.J., Collepardo-Guevara R. Multiscale modelling of chromatin organisation: resolving nucleosomes at near-atomistic resolution inside genes. Curr. Opin. Cell Biol. 2022;75:102067. doi: 10.1016/j.ceb.2022.02.001. [DOI] [PubMed] [Google Scholar]
- 13.Brackey C.A., Marenduzzo D., Gilbert N. Mechanistic modeling of chromatin folding to understand function. Nat. Methods. 2020;17:767–775. doi: 10.1038/s41592-020-0852-6. [DOI] [PubMed] [Google Scholar]
- 14.Moller J., de Pablo J.J. Bottom-up meets top-down: the crossroads of multiscale chromatin modeling. Biophys. J. 2020;118:2057–2065. doi: 10.1016/j.bpj.2020.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lin X., Qi Y., Zhang B., et al. Multiscale modeling of genome organization with maximum entropy optimization. J. Chem. Phys. 2021;155:010901. doi: 10.1063/5.0044150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chiang M., Brackley C.A., Gilbert N., et al. Predicting genome organisation and function with mechanistic modelling. Trends Genet. 2022;38:364–378. doi: 10.1016/j.tig.2021.11.001. [DOI] [PubMed] [Google Scholar]
- 17.Portillo-Ledesma S., Li Z., Schlick T. Genome modeling: from chromatin fibers to genes. Curr. Opin. Struct. 2022 doi: 10.1016/j.sbi.2022.102506. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Annunziatella C., Chiariello A.M., Nicodemi M., et al. Molecular dynamics simulations of the strings and binders switch model of chromatin. Methods. 2018;142:81–88. doi: 10.1016/j.ymeth.2018.02.024. [DOI] [PubMed] [Google Scholar]
- 19.Woods D.C., Rodríguez-Ropero F., Wereszczynski J. The dynamic influence of linker histone saturation within the poly-nucleosome array. J. Mol. Biol. 2021;433:166902. doi: 10.1016/j.jmb.2021.166902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tan C., Jung J., Sugita Y., et al. Implementation of residue-level coarsegrained models in GENESIS for large-scale molecular dynamics simulations. PLoS Comput. Biol. 2022;18:e1009578. doi: 10.1371/journal.pcbi.1009578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Aumann F., Lankas F., Langowski J., et al. Monte Carlo simulation of chromatin stretching. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:041927. doi: 10.1103/PhysRevE.73.041927. [DOI] [PubMed] [Google Scholar]
- 22.Arya G., Schlick T. Efficient global biopolymer sampling with end-transfer configurational bias Monte Carlo. J. Chem. Phys. 2007;126:044107. doi: 10.1063/1.2428305. [DOI] [PubMed] [Google Scholar]
- 23.Lequieu J., Córdoba A., de Pablo J.J., et al. 1CPN: a coarse-grained multi-scale model of chromatin. J. Chem. Phys. 2019;150:215102. doi: 10.1063/1.5092976. [DOI] [PubMed] [Google Scholar]
- 24.Ehrlich L., Münkel C., Langowski J., et al. A brownian dynamics model for the chromatin fiber. Comput. Appl. Biosci. 1997;13:271–279. doi: 10.1093/bioinformatics/13.3.271. [DOI] [PubMed] [Google Scholar]
- 25.Di Pierro M., Zhang B., Onuchic J.N., et al. Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. USA. 2016;113:12168–12173. doi: 10.1073/pnas.1613607113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shi G., Liu L., Thirumalai D., et al. Interphase human chromosome exhibits out of equilibrium glassy dynamics. Nat. Commun. 2018;9:3161. doi: 10.1038/s41467-018-05606-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu X., Chow E. 2014 IEEE 28th Int. Parallel Distrib. Process. Symp. IEEE; 2014. Large-scale hydrodynamic brownian simulations on multicore and manycore architectures; pp. 563–572. [Google Scholar]
- 28.Lee T.-S., Cerutti D.S., York D.M., et al. GPU-accelerated molecular dynamics and free energy methods in Amber18: performance enhancements and new features. J. Chem. Inf. Model. 2018;58:2043–2050. doi: 10.1021/acs.jcim.8b00462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ufimtsev I.S., Martínez T.J. Quantum chemistry on graphical processing units. 1. Strategies for two-electron integral evaluation. J. Chem. Theor. Comput. 2008;4:222–231. doi: 10.1021/ct700268q. [DOI] [PubMed] [Google Scholar]
- 30.Schlick T., Portillo-Ledesma S. Biomolecular modeling thrives in the age of technology. Nat. Comput. Sci. 2021;1:321–331. doi: 10.1038/s43588-021-00060-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schlick T., Portillo-Ledesma S., Xue E., et al. Biomolecular modeling and simulation: a prospering multidisciplinary field. Annu. Rev. Biophys. 2021;50:267–301. doi: 10.1146/annurev-biophys-091720-102019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beard D.A., Schlick T. Computational modeling predicts the structure and dynamics of chromatin fiber. Structure. 2001;9:105–114. doi: 10.1016/s0969-2126(01)00572-x. [DOI] [PubMed] [Google Scholar]
- 33.Arya G., Schlick T. Role of histone tails in chromatin folding revealed by a mesoscopic oligonucleosome model. Proc. Natl. Acad. Sci. USA. 2006;103:16236–16241. doi: 10.1073/pnas.0604817103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schlick T., Perisić O. Mesoscale simulations of two nucleosome-repeat length oligonucleosomes. Phys. Chem. Chem. Phys. 2009;11:10729–10737. doi: 10.1039/b918629h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Collepardo-Guevara R., Schlick T. Crucial role of dynamic linker histone binding and divalent ions for DNA accessibility and gene regulation revealed by mesoscale modeling of oligonucleosomes. Nucleic Acids Res. 2012;40:8803–8817. doi: 10.1093/nar/gks600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Collepardo-Guevara R., Schlick T. Chromatin fiber polymorphism triggered by variations of DNA linker lengths. Proc. Natl. Acad. Sci. USA. 2014;111:8061–8066. doi: 10.1073/pnas.1315872111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bascom G.D., Kim T., Schlick T. Kilobase pair chromatin fiber contacts promoted by living-system-like DNA linker length distributions and nucleosome depletion. J. Phys. Chem. B. 2017;121:3882–3894. doi: 10.1021/acs.jpcb.7b00998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Grigoryev S.A., Bascom G., Schlick T., et al. Hierarchical looping of zigzag nucleosome chains in metaphase chromosomes. Proc. Natl. Acad. Sci. USA. 2016;113:1238–1243. doi: 10.1073/pnas.1518280113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bascom G.D., Sanbonmatsu K.Y., Schlick T. Mesoscale modeling reveals hierarchical looping of chromatin fibers near gene regulatory elements. J. Phys. Chem. B. 2016;120:8642–8653. doi: 10.1021/acs.jpcb.6b03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gómez-García P.A., Portillo-Ledesma S., Lakadamyali M., et al. Mesoscale modeling and single-nucleosome tracking reveal remodeling of clutch folding and dynamics in stem cell differentiation. Cell Rep. 2021;34:108614. doi: 10.1016/j.celrep.2020.108614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bascom G.D., Myers C.G., Schlick T. Mesoscale modeling reveals formation of an epigenetically driven HOXC gene hub. Proc. Natl. Acad. Sci. USA. 2019;116:4955–4962. doi: 10.1073/pnas.1816424116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Portillo-Ledesma S., Tsao L.H., Schlick T., et al. Nucleosome clutches are regulated by chromatin internal parameters. J. Mol. Biol. 2021;433:166701. doi: 10.1016/j.jmb.2020.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yusufova N., Kloetgen A., Melnick A.M., et al. Histone H1 loss drives lymphoma by disrupting 3D chromatin architecture. Nature. 2021;589:299–305. doi: 10.1038/s41586-020-3017-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Myers C.G., Olins D.E., Schlick T., et al. Mesoscale modeling of nucleosome-binding antibody PL2-6: mono- versus bivalent chromatin complexes. Biophys. J. 2020;118:2066–2076. doi: 10.1016/j.bpj.2019.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Arya G., Schlick T. A tale of tails: how histone tails mediate chromatin compaction in different salt and linker histone environments. J. Phys. Chem. A. 2009;113:4045–4059. doi: 10.1021/jp810375d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Collepardo-Guevara R., Portella G., Orozco M., et al. Chromatin unfolding by epigenetic modifications explained by dramatic impairment of internucleosome interactions: a multiscale computational study. J. Am. Chem. Soc. 2015;137:10205–10215. doi: 10.1021/jacs.5b04086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bascom G.D., Schlick T. Chromatin fiber folding directed by cooperative histone tail acetylation and linker histone binding. Biophys. J. 2018;114:2376–2385. doi: 10.1016/j.bpj.2018.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Luque A., Collepardo-Guevara R., Schlick T., et al. Dynamic condensation of linker histone C-terminal domain regulates chromatin structure. Nucleic Acids Res. 2014;42:7553–7560. doi: 10.1093/nar/gku491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Perišić O., Portillo-Ledesma S., Schlick T. Sensitive effect of linker histone binding mode and subtype on chromatin condensation. Nucleic Acids Res. 2019;47:4948–4957. doi: 10.1093/nar/gkz234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang Q., Beard D.A., Schlick T. Constructing irregular surfaces to enclose macromolecular complexes for mesoscale modeling using the discrete surface charge optimization (DiSCO) algorithm. J. Comput. Chem. 2003;24:2063–2074. doi: 10.1002/jcc.10337. [DOI] [PubMed] [Google Scholar]
- 51.Jian H., Vologodskii A.V., Schlick T. A combined wormlike-chain and bead model for dynamic simulations of long linear DNA. J. Comput. Phys. 1997;136:168–179. doi: 10.1006/jcph.1997.5765. [DOI] [Google Scholar]
- 52.Stigter D. Interactions of highly charged colloidal cylinders with applications to double-stranded DNA. Biopolymers. 1977;16:1435–1448. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- 53.Arya G., Zhang Q., Schlick T. Flexible histone tails in a new mesoscopic oligonucleosome model. Biophys. J. 2006;91:133–150. doi: 10.1529/biophysj.106.083006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ermak D.L., McCammon J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978;69:1352–1360. doi: 10.1063/1.436761. [DOI] [Google Scholar]
- 55.Iniesta A., García de la Torre J. A second-order algorithm for the simulation of the Brownian dynamics of macromolecular models. J. Chem. Phys. 1990;92:2015–2018. doi: 10.1063/1.458034. [DOI] [Google Scholar]
- 56.Rotne J., Prager S. Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 1969;50:4831–4837. doi: 10.1063/1.1670977. [DOI] [Google Scholar]
- 57.Carrasco B., García de la Torre J., Zipper P. Calculation of hydrodynamic properties of macromolecular bead models with overlapping spheres. Eur. Biophys. J. 1999;28:510–515. doi: 10.1007/s002490050233. [DOI] [PubMed] [Google Scholar]
- 58.Yao J., Lowary P.T., Widom J. Direct detection of linker DNA bending in defined-length oligomers of chromatin. Proc. Natl. Acad. Sci. USA. 1990;87:7603–7607. doi: 10.1073/pnas.87.19.7603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yao J., Lowary P.T., Yao J., et al. Linker DNA bending induced by the core histones of chromatin. Biochemistry. 1991;30:8408–8414. doi: 10.1021/bi00098a019. [DOI] [PubMed] [Google Scholar]
- 60.Bednar J., Horowitz R.A., Woodcock C.L., et al. Chromatin conformation and salt-induced compaction: three-dimensional structural information from cryoelectron microscopy. J. Cell Biol. 1995;131:1365–1376. doi: 10.1083/jcb.131.6.1365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Nozaki T., Kaizu K., et al. Maeshima K. 2013. Flexible and Dynamic Nucleosome Fiber in Living Mammalian Cells. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hihara S., Pack C.-G., Maeshima K., et al. Local nucleosome dynamics facilitate chromatin accessibility in living mammalian cells. Cell Rep. 2012;2:1645–1656. doi: 10.1016/j.celrep.2012.11.008. [DOI] [PubMed] [Google Scholar]
- 63.Hansen J.C., Ausio J., Van Holde K.E., et al. Homogeneous reconstituted oligonucleosomes, evidence for salt-dependent folding in the absence of histone H1. Biochemistry. 1989;28:9129–9136. doi: 10.1021/bi00449a026. [DOI] [PubMed] [Google Scholar]
- 64.Howe L., Iskandar M., Ausió J. Folding of chromatin in the presence of heterogeneous histone H1 binding to nucleosomes. J. Biol. Chem. 1998;273:11625–11629. doi: 10.1074/jbc.273.19.11625. [DOI] [PubMed] [Google Scholar]
- 65.Garcia-Ramirez M., Dong F., Ausio J. Role of the histone “tails” in the folding of oligonucleosomes depleted of histone H1. J. Biol. Chem. 1992;267:19587–19595. doi: 10.1016/S0021-9258(18)41815-7. [DOI] [PubMed] [Google Scholar]
- 66.Butler P.J., Thomas J.O. Dinucleosomes show compaction by ionic strength, consistent with bending of linker DNA. J. Mol. Biol. 1998;281:401–407. doi: 10.1006/jmbi.1998.1954. [DOI] [PubMed] [Google Scholar]
- 67.Robinson P.J.J., Fairall L., Rhodes D., et al. EM measurements define the dimensions of the “30-nm” chromatin fiber: evidence for a compact, interdigitated structure. Proc. Natl. Acad. Sci. USA. 2006;103:6506–6511. doi: 10.1073/pnas.0601212103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Grigoryev S.A., Arya G., Schlick T., et al. Evidence for heteromorphic chromatin fibers from analysis of nucleosome interactions. Proc. Natl. Acad. Sci. USA. 2009;106:13317–13322. doi: 10.1073/pnas.0903280106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Baumann C.G., Smith S.B., Bustamante C., et al. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Happel N., Doenecke D. Histone H1 and its isoforms: contribution to chromatin structure and function. Gene. 2009;431:1–12. doi: 10.1016/j.gene.2008.11.003. [DOI] [PubMed] [Google Scholar]
- 71.Voong L.N., Xi L., Wang X., et al. Insights into nucleosome organization in mouse embryonic stem cells through chemical mapping. Cell. 2016;167:1555–1570.e15. doi: 10.1016/j.cell.2016.10.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Perišić O., Collepardo-Guevara R., Schlick T. Modeling studies of chromatin fiber structure as a function of DNA linker length. J. Mol. Biol. 2010;403:777–802. doi: 10.1016/j.jmb.2010.07.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Moore S.C., Ausió J. Major role of the histones H3-H4 in the folding of the chromatin fiber. Biochem. Biophys. Res. Commun. 1997;230:136–139. doi: 10.1006/bbrc.1996.5903. [DOI] [PubMed] [Google Scholar]
- 74.Hansen J.C., Tse C., Wolffe A.P. Structure and function of the core histone N-termini: more than meets the eye. Biochemistry. 1998;37:17637–17641. doi: 10.1021/bi982409v. [DOI] [PubMed] [Google Scholar]
- 75.Dorigo B., Schalch T., Richmond T.J., et al. Chromatin fiber folding: requirement for the histone H4 N-terminal tail. J. Mol. Biol. 2003;327:85–96. doi: 10.1016/s0022-2836(03)00025-1. [DOI] [PubMed] [Google Scholar]
- 76.Rao S.S.P., Huang S.-C., Aiden E.L., et al. Cohesin loss eliminates all loop domains. Cell. 2017;171:305–320.e24. doi: 10.1016/j.cell.2017.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Swygert S.G., Lin D., Tsukiyama T., et al. Local chromatin fiber folding represses transcription and loop extrusion in quiescent cells. Elife. 2021;10:e72062. doi: 10.7554/eLife.72062. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The working BD code has been deposited in GitHub under the Schlick lab group: https://github.com/Schlicklab/Brownian_Dynamics_CUDA.