Adaptive metrics for an evolving pandemic: A dynamic approach to area-level COVID-19 risk designations

Significance

In the rapidly evolving COVID-19 pandemic, public health risk metrics have often become less relevant over time. Risk metrics are designed to predict future severe disease and mortality based on currently available surveillance data, such as cases and hospitalizations. However, the relationship between cases, hospitalizations, and mortality has varied considerably over the course of the pandemic, in the context of new variants and shifts in vaccine- and infection-induced immunity. We propose an adaptive method for risk designations that is regularly updated to reflect the evolving relationship between surveillance data inputs and future outcomes of policy interest. Our method captures changing pandemic dynamics, requires only hospitalization input data, and outperforms static methods, providing more reliable and actionable risk designations.

Abstract

Throughout the COVID-19 pandemic, policymakers have proposed risk metrics, such as the CDC Community Levels, to guide local and state decision-making. However, risk metrics have not reliably predicted key outcomes and have often lacked transparency in terms of prioritization of false-positive versus false-negative signals. They have also struggled to maintain relevance over time due to slow and infrequent updates addressing new variants and shifts in vaccine- and infection-induced immunity. We make two contributions to address these weaknesses. We first present a framework to evaluate predictive accuracy based on policy targets related to severe disease and mortality, allowing for explicit preferences toward false-negative versus false-positive signals. This approach allows policymakers to optimize metrics for specific preferences and interventions. Second, we propose a method to update risk thresholds in real time. We show that this adaptive approach to designating areas as “high risk” improves performance over static metrics in predicting 3-wk-ahead mortality and intensive care usage at both state and county levels. We also demonstrate that with our approach, using only new hospital admissions to predict 3-wk-ahead mortality and intensive care usage has performed consistently as well as metrics that also include cases and inpatient bed usage. Our results highlight that a key challenge for COVID-19 risk prediction is the changing relationship between indicators and outcomes of policy interest. Adaptive metrics therefore have a unique advantage in a rapidly evolving pandemic context.

Understanding the evolution of infectious disease risk is critical for individuals making decisions about personal precautions, policymakers recommending mitigation measures, and health care institutions planning for future surges. Throughout the COVID-19 pandemic, indicators such as reported cases and percent of PCR tests positive for SARS-CoV-2 have been used to guide pandemic response (1–4). Currently, the Centers for Disease Control and Prevention (CDC)’s Community Levels designate areas as low, medium, or high risk based on reported cases, new COVID-19 hospital admissions, and the percentage of inpatient beds occupied by COVID-19 patients (2).

However, COVID-19 risk metrics have several weaknesses. First, policymakers have struggled to identify leading indicators of key health outcomes. For example, PCR test positivity was abandoned as a trigger for school closures because it did not reliably predict in-school transmission (5). Similarly, Community Transmission metrics developed by the CDC based on cases and test positivity were deemphasized due to poor prediction of future severe outcomes (2). Other community metrics have focused on predicting severe disease and mortality (2, 6). For example, the indicators used in CDC Community Levels were selected because they correlated with ICU rates and mortality 3 wk in the future (2). However, the thresholds for low, medium, and high were not selected to correspond to specific future mortality rates (7), thus complicating the understanding of a high-risk designation.

Second, many metrics fail to distinguish different error types. Falsely classifying an area as high risk may prompt unnecessary or harmful interventions, while a false negative may fail to activate needed public health measures (8). Individuals and policymakers may vary in their preferences for avoiding these two types of errors, but current methods fail even to make these preferences explicit (9).

Finally, changes in available data, COVID-19 variants, and levels of immunity can render metrics obsolete as the pandemic evolves (10). For instance, with the omicron variant, cases and hospital admissions have corresponded to lower levels of mortality than in earlier waves. Shifts from PCR to at-home testing and changes in case reporting have also made case data less reliable and available over time (11, 12). Ad hoc updates to risk designations are insufficient to ensure that the metrics remain relevant. Moreover, transparency in the process is key to alleviating concerns about “moving the goalposts” (13).

This paper makes two contributions to address these weaknesses in the context of COVID-19 community risk metrics. First, we propose a framework for predictive accuracy that incorporates preferences over false negatives versus false positives, using weights to optimize metrics for specific policy objectives. Second, we present a method to update risk thresholds over time and show that this adaptive approach outperforms static metrics. With our approach, we demonstrate that metrics using only new hospital admissions often perform as well in prediction as metrics that also include cases and inpatient bed usage.

Materials and Methods

The CDC used indicators available nationwide (cases, hospitalizations, and occupancy of staffed inpatient beds) to develop Community Levels (2). In this research, we used the same indicators to define alternative state and county metrics, then compared metrics based on their ability to predict future health outcomes.

Outcomes.

The primary evaluation criterion was predictive power for high mortality. We defined “high mortality” as > 1 death per 100,000 per week and “very high mortality” as > 2 deaths per 100,000 per week. The lower threshold was defined in reference to peak mortality of other respiratory viruses (influenza and respiratory syncytial virus) during a severe season (7, 14). Let T ∈ 1, 2 denote these mortality thresholds. The true outcome was a binary variable equal to 1 if mortality three weeks from the current week (i.e., at time w + 3) in location i exceeded the threshold; formally, Y_{i, w + 3} = 𝕀(mortality at w + 3 >  T)∈0, 1. In secondary analyses of health care strain, we evaluated predictive power for 3-wk-ahead ICU admissions, defining “high” as > 2 ICU hospitalizations per 100,000 population per week, and as > 10% for 3-wk-ahead COVID-19 inpatient bed occupancy (the lowest threshold meeting the CDC classification of “high inpatient bed usage”) (2).

We used a 3-wk prediction window because previous CDC analyses indicated that this maximized the correlation between indicators and severe outcomes (2). This also reflects the necessary lead-time for interventions to begin to have an impact on severe outcomes; a metric that predicts severe mortality tomorrow will come too late for effective action. We used discrete outcomes to mirror CDC risk categories and to reflect the common practice of adopting pandemic interventions in response to threshold crossing.

Indicators.

Indicators are the observed quantities that enter our prediction models. We used the same three indicators as the CDC’s Community Levels: new COVID-19 cases per 100,000 (weekly total), new COVID-19 hospital admissions per 100,000 (weekly total), and the occupancy of staffed inpatient hospital beds by COVID-19 patients (7-d average). Let X_{C, i, w}, X_{H, i, w}, and X_{O, i, w} denote the levels of these three indicators respectively, in location i during week w.

Data.

We obtained data on indicators and outcomes at both state and county levels and conducted separate analyses for each geographic level. For cases and deaths, we used aggregated counts compiled by state and local health agencies (15). For new COVID-19 admissions and bed occupancy, we used data reported to the US Department of Health and Human Services Unified Hospital Data Surveillance System (16, 17). Consistent with CDC Community Level calculations, we calculated county-level hospitalizations at the Health Service Area (HSA)-level to account for care-seeking across counties and computed measures at the midpoint of each week (2). HSAs are defined by the National Center for Health Statistics to be one or more contiguous counties with self-contained hospital care (18). In sensitivity analyses, we also present analyses with all inputs and outcomes calculated at the HSA-level.

Metrics.

Metrics take indicators as inputs and produce a binary risk classification for a geographic area as output. Our metrics used data available at week w to predict outcomes above the prespecified threshold, T, 3 wk in the future, classifying a locality as high risk, ${\widehat{Y}}_{w+3}=1$, or not high-risk, ${\widehat{Y}}_{w+3}=0$. (For readability, we omit location subscripts i when referring to a single observation in this section.)

Objective.

We used weighted classification accuracy to compare metrics on their ability to predict future outcomes, where weights reflected preferences for avoiding different types of errors.

We assumed a simple underlying decision-analytic framework: a decision maker receives a prediction of, for example, mortality 3 wk hence, ${\widehat{Y}}_{w+3}$, and takes action in response to that prediction. If the metric predicts high mortality (${\widehat{Y}}_{w+3}=1$), she will take one action; if the model does not predict high mortality (${\widehat{Y}}_{w+3}=0$), she will take a different action. Each action has benefits and costs that depend on the true outcome. For example, avoiding unnecessary interventions under a true negative conserves public health resources, while inaction due to a false negative may lead hospitals to become overburdened. By contrast, a false positive may have costs such as wasted resources and harming public trust due to unnecessary interventions.

We consider costs in terms of disease burden and public health resources. We anchor costs at 0 in the scenario in which the model correctly predicts low mortality (${\widehat{Y}}_{w+3}=Y_{w+3}=0$). If the model incorrectly predicts high mortality (${\widehat{Y}}_{w+3}=1$, Y_w + 3 = 0), we denote public health resources spent and social costs as S₀. By contrast, if a model incorrectly predicts low mortality (${\widehat{Y}}_{w+3}=0$, Y_w + 3 = 1), policymakers incur disease costs of D. Last, if a model correctly predicts high mortality (${\widehat{Y}}_{w+3}=Y_{w+3}=1$), we assume policymakers implement an intervention that reduces disease by a factor of α, but pay resource costs, for a total cost of (1 − α)D + S₁.

The total cost associated with a particular metric, M (omitting subscripts for parsimony) is:

$$\begin{array}{cc}\hfill C(M)=& Pr(\widehat{Y}=1,Y=0)S_0+Pr(\widehat{Y}=0,Y=1)D\hfill \\ \hfill & +Pr(\widehat{Y}=1,Y=1)\left((1-\alpha )D+S_1\right)\hfill \\ \hfill =& Pr(\widehat{Y}=1,Y=0)S_0\hfill \\ \hfill & +Pr(\widehat{Y}=0,Y=1)(\alpha D-S_1)\hfill \\ \hfill & +Pr(Y=1)((1-\alpha )D+S_1).\hfill \end{array}$$

Because the last term is constant across all metrics (which cannot affect prevalence of high outcomes), this cost is proportional to the weighted misclassification rate:

$$\begin{array}{cc}\hfill C(M)& \propto p_{\mathit{FP}}{S}_0+p_{\mathit{FN}}(\alpha D-S_1)\hfill \\ \hfill & \propto p_{\mathit{FP}}+p_{\mathit{FN}}wt.\hfill \end{array}$$

We can therefore rank metrics based only on performance (i.e., their probabilities of making each error type) and the decision maker’s relative preference for false positives compared to false negatives (wt). As the above expression indicates, we can conceptualize weight wt as the ratio of the net benefit from taking action on a true positive (αD − S₁) to costs incurred by unnecessary action in the case of a false positive (S₀).

We considered three values of this weight. “Neutral” weighted false negatives and false positives equally (wt = 1, equivalent to unweighted accuracy), “don’t cry wolf” down-weighted false negatives as half the cost of false positives (wt = 0.5), and “better safe than sorry” down-weighted false positives as half the cost of false negatives (wt = 2).

We estimated weighted accuracy for each metric as 1 minus the weighted misclassification rate:

$$\begin{array}{cc}\hfill {\delta }_{\mathit{wt}}(M)& =1-p_{\mathit{FP}}{w}_P-p_{\mathit{FN}}{w}_N.\hfill \end{array}$$

While any w_N and w_P such that $\frac{w_P}{w_N}=wt$ would produce the same ranking of metrics, the absolute value of δ_wt depends on w_N and w_P. We set w_N and w_P such that both error weights are shifted equally in magnitude to achieve the desired ratio, with an increase in one and corresponding decrease in the other. That is, we set w_N and w_P using the value a such that w_N = (1 − a), w_P = (1 + a), and w_N/w_P = (1 − a)/(1 + a)=wt. With neutral weighting, w_N = w_P = 1.

We used weighted accuracy as our primary measure of performance, with higher weighted accuracy indicating better performance. We further weighted δ_wt by population to reflect the total proportion of individuals living in a location with an accurate classification (SI Appendix, Text A).

Static metrics.

We considered two types of metrics, static and adaptive. Static metrics used the same threshold each week to classify a locality as high risk. They differed in input indicators, which could include 1) new cases only (C), 2) new hospital admissions only (H), 3) cases and hospital admissions (CH), 4) hospital admissions and bed occupancy (HO) or 5) all three indicators (CHO)). We varied the threshold on cases from 50 to 300 per 100,000 (in increments of 50), on new hospitalizations from 5 to 25 per 100,000 (in increments of 5), and on occupancy from 5 to 20% (in increments of 5). We designated an area as high risk if all the indicators in a given indicator set were above their specified thresholds.

We also replicated the CDC’s Community Levels, designating an area as highrisk if

$$\begin{array}{cc}& \left[X_{C,i,w}<200\text{AND}(X_{H,i,w}\ge 20\text{OR}{X}_{O,i,w}\ge 15\%)\right]\text{OR}\hfill \\ \hfill & \left[X_{C,i,w}\ge 200\text{AND}(X_{H,i,w}\ge 10\text{OR}{X}_{O,i,w}\ge 10\%)\right].\hfill \end{array}$$

Last, we considered a metric (Z) that designated an area as high risk if the outcome was above the threshold of interest at the time of prediction, i.e., ${\widehat{Y}}_{i,w+3}=\mathbb{I}\left(Y_{i,w}=1\right)$, predicting ${\widehat{Y}}_{i,w+3}=1$ at time w + 3 only if Y_{i, w} was equal to 1, indicating the area was currently observing the high designation.

Adaptive metrics.

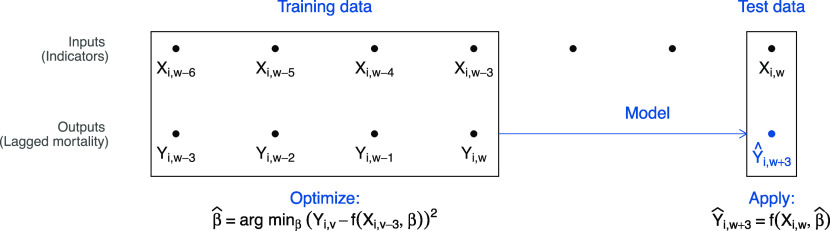
Adaptive metrics changed thresholds over time based on their ability to predict mortality during the recent past (Fig. 1). At time w, we used the most recent weeks of past indicator data with complete 3-wk-ahead outcomes as training data. To these training data, we fit logistic regression models with outcomes on the Left-hand side and indicators from previous weeks on the Right-hand side. For example, in the model corresponding to the CHO indicator set, we fit

$$\begin{array}{c}\hfill \text{logit}(Pr(Y_{i,v}=1))={\beta }_0+{\beta }_1{X}_{C,i,v-3}+{\beta }_2{X}_{H,i,v-3}+{\beta }_3{X}_{O,i,v-3}.\end{array}$$ [1]

Fig. 1.

Adaptive metrics. The diagram shows the model-fitting process using 4 wk of training data. We trained a model using the 4 most recent weeks with complete outcome data, including inputs from w − 6 to w − 3 and outputs from w − 3 to w. We then used this model, with input data from w, to estimate the probability of “high” or “very high” future mortality at w + 3 and specified a binary prediction based on whether this probability exceeded the user’s cutoff. (When a single indicator is used as the only input, this process is equivalent to identifying the optimal threshold for the indicator over the training period, accounting for user preferences.)

for v ∈ [w − 3, w]. From this model, we obtained ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$, and ${\widehat{\beta }}_3$, which we then used to produce fitted probabilities for each locality’s mortality 3 wk ahead using:

$$\begin{array}{cc}\hfill \widehat{\mathit{Pr}}(Y_{i,w+3}=1)=& {\text{logit}}^{-1}\left({\widehat{\beta }}_0+{\widehat{\beta }}_1{X}_{C,i,w}+{\widehat{\beta }}_2{X}_{H,i,w}\right.\hfill \\ \hfill & +{\widehat{\beta }}_3{X}_{O,i,w}).\hfill \end{array}$$ [2]

Logistic regression smoothed over noise in the small training data and reduced the dimension of multiple indicators by converting to a probability scale.

With predictions on a probability scale, we specified a probability cutoff above which we classified a location as high risk. We selected this cutoff based on the relative weighting of different error types (wt). We classified a locality as high risk whenever the probability was above 1/(1 + wt) (SI Appendix, Text B for optimal cutoff derivation). For our three weights (neutral, don’t cry wolf, and better safe than sorry), the cutoff values were $\frac{1}{2}$, $\frac{2}{3}$, and $\frac{1}{3}$, respectively. With a single predictor, this process would be equivalent to identifying the optimal threshold for the indicator over the training period, accounting for user preferences.

To assess sensitivity to different functional forms, we specified analogous models based on CHOZ and HZ indicator sets and an additional model (CHOD) that included all indicators as well as the change in each indicator from the prior week. We also included a simplified version that was updated less frequently, only refitting to the training data each quarter, rather than each week. We varied the number of training weeks from 4 to 12 (i.e., fitting Eq. 1 to training datasets as large as v ∈ [w − 11, w]).

Head-to-Head Comparison.

We compared the performance of the metrics during training and out-of-sample test periods. To define the training period, we began with the window the CDC used to fit Community Levels (March 1, 2021, through January 24, 2022). We further allowed the month of March for model fitting including 3 wk of past mortality data. Thus, our training inputs spanned April 1, 2021 through December 31, 2021, 2021 Q3 and Q4, with outcomes extending through January 21, 2022.

We compared performance across metrics separately for each outcome (e.g., >1 or >2 deaths/100k/wk), preference weight (wt = 0.5, 1, or 2), and geographic area (state or county). Within each combination of these, we chose the best-performing static metric during the training period from among the 6, 5, 30, 20, or 120 possibilities within the C, H, CH, HO, and CHO indicator sets. The CDC Community Levels and current outcome (Z) metrics were fixed, so there was no selection within this metric type. For adaptive metrics, we used the training period to optimize the number of training weeks.

Performance evaluation.

We present weighted accuracy of each selected metric in the training quarters (during which the best performer of each type was selected) and a test period of January 1, 2022, through September 30, 2022 (i.e., 2022 Q1–Q3). As a sensitivity analysis, we used December 15, 2021 through February 15, 2022, as a training period, to only include training data from the omicron period when the infection-fatality rate fell sharply. We then used data from February 16 through September 30, 2022, as the test period.

In addition to presenting overall weighted accuracy, we summarize variation in performance across quarters with maximum quarterly regret, the difference between a metric’s predictive accuracy and the best performing metric (19). We calculated regret for each selected metric in each quarter and took the maximum across quarters:

$$\begin{array}{c}M{R}_M=\underset{q\in \mathcal{Q}}{\max }\left(\underset{m\in \mathcal{M}}{\max }{\delta }_{wt,q}(m)\right)-{\delta }_{wt,q}(M),\end{array}$$

where M is a metric of interest, 𝒬 is a set of quarters, ℳ is a set of metrics, and δ_{wt, q} is weighted accuracy during quarter q.

Last, to decompose variation between metrics into differences in predictive power and differences in error preferences, we computed sensitivity ($Pr({\widehat{Y}}_{i,w+3}=1|Y_{i,w+3}=1)$) and specificity ($Pr({\widehat{Y}}_{i,w+3}=0|Y_{i,w+3}=0)$) across different wt values for adaptive metrics and compared these to sensitivity and specificity for static metrics.

Simulations.

To generalize our approach beyond the specific pandemic periods considered, we developed simple simulations, varying the relationship between indicators and outcomes over time as well as the prevalence of high maturity outcomes (SI Appendix, Text C). We considered several functional forms for the relationship between inputs and synthetic outputs, including a scenario with a true constant optimal cutoff above which to classify ${\widehat{Y}}_{w+3}$ as 1 and scenarios with time-varying optimal cutoffs (linear, logistic, and nonmonotonic). We also varied prevalence of high mortality outcomes, including a constant case, a case based on empirical hospitalization waves, and a case in which waves designed to be much sharper than true waves. We then estimated predictive accuracy across different scenarios.

Results

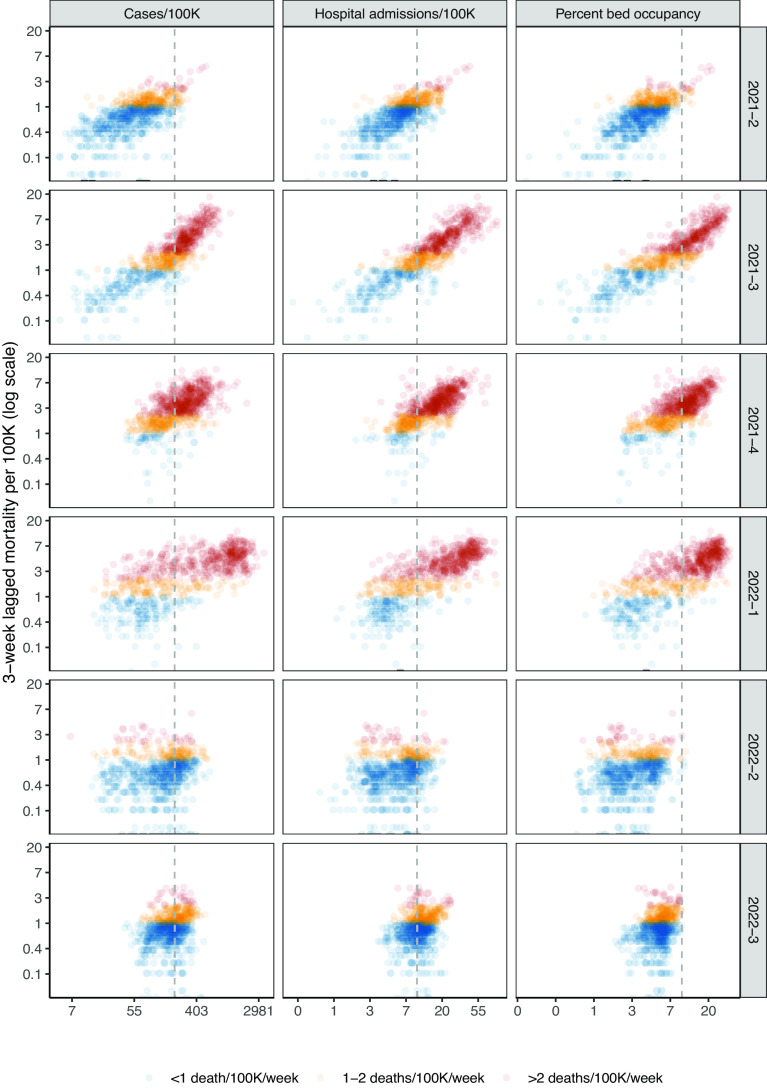
Indicator levels and mortality varied substantially over the study period (Fig. 2), which included two major waves of illness (delta and omicron BA.1) and a smaller wave in summer 2022 (omicron BA.5) (SI Appendix, Figs. S2 and S3 for detailed dynamics of indicators and outcomes over the study period.) The percentage of population-weighted state-weeks with high future mortality ranged from a peak of 94% during Q4 2021 to a low of 17% during Q2 2021. For very high mortality, this ranged from 61% (Q1 2022) to 3% (Q2 2022). We observed similar variation in counties, with less extreme swings (e.g., from 74% to 25% for high mortality). The relationship between indicators and outcomes shifted substantially over the period studied. In particular, in the third quarter of 2022, cases, hospitalizations, and bed occupancy all increased, but mortality remained lower than in previous waves (Fig. 2).

Fig. 2.

State-level lagged mortality vs. indicator levels by quarter. Columns indicate different indicators (weekly cases per 100,000 population, new hospital admissions per 100,000 population, and percentage of inpatient beds occupied by COVID-19 patients), and rows indicate quarters. The x-axis displays indicator values on a log scale, and the y-axis displays 3-week-ahead mortality per 100,000 population on a log scale. Each point on the scatterplot is a state-week. Colors show the mortality outcome level. The vertical gray dotted lines indicate thresholds from CDC Community Levels for each indicator (≥200 cases/100K/wk and ≥10 new admissions/100K/wk or ≥10% COVID-19 bed occupancy). See SI Appendix, Fig. S1 for a county-level plot.

Static Metrics.

In Fig. 3, we present the performance of the best-performing static metrics from different health care indicator sets (C, H, CH, HO, and CHO) during the training and test periods. Recall that the static metrics designated an area as high-risk if all included indicators exceeded their respective optimal thresholds from the training period. For the high mortality outcome (>1 death/100k/wk) at the state level with neutral weighting, the chosen thresholds for static metrics were 50 cases/100k (C); 5 hospitalizations/100k (H); 50 cases/100k, 5 hospitalizations/100k (CH); 5 hospitalizations/100k, 5% bed occupancy (HO); and 50 cases/100k, 5 hospitalizations/100k, 5% bed occupancy (CHO). The thresholds for the remaining outcomes and geographic levels are given in SI Appendix, Table S1.

Fig. 3.

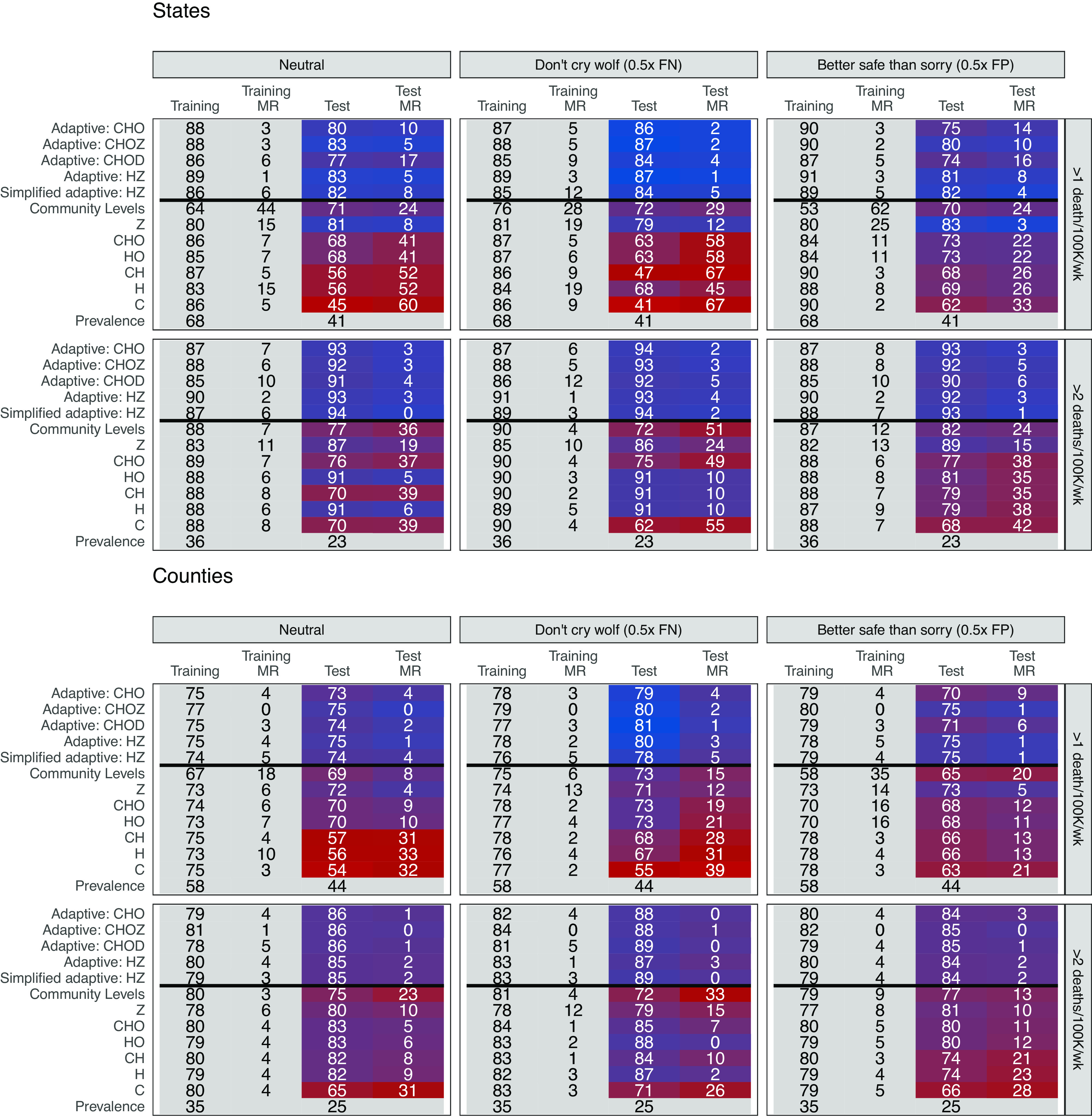
Head-to-head comparison results. The top plots display results from state-level analyses and the bottom plots display results from county-level analyses, both weighted for population. Metrics are displayed on the Left, with training data from Q2–Q4 2021 and test data from Q1–Q3 2022. Cells report weighted accuracy and maximum regret (MR) over training and test periods. Rows vary outcomes, and columns vary preferences for false positives versus false negatives, with “neutral” corresponding to unweighted accuracy. Prevalence indicates the proportion of high location-weeks in a given time period. A version including HSA-level analyses can be found in SI Appendix, Fig. S4. Secondary outcomes are presented in SI Appendix, Fig. S5, and weighted accuracy by quarter is presented in SI Appendix, Figs. S6–S8. For adaptive metrics, models vary functional form to include: 1) CHO (cases, hospitalizations, inpatient bed occupancy); 2) CHOZ (cases, hospitalizations, inpatient bed occupancy, current risk designation); 3) CHOD (cases, hospitalizations, inpatient bed occupancy, weekly changes in each indicator); 4) HZ (hospitalizations, current risk designation); 5) Simplified HZ (hospitalizations, current risk designation—updated quarterly). (For additional adaptive functional forms, SI Appendix, Fig. S9.)

During the training period, there were only minor differences in training accuracy between static metrics that used different health care indicator sets (e.g., 83 to 87% in predicting high mortality for states with neutral weighting, 73 to 75% for counties). However, for nearly all static metrics and outcomes, test accuracy was lower and more variable than training accuracy (e.g., 45 to 68% and 54 to 70% for high mortality in states and counties, respectively).

Some of this variation was due to the shifting relationship between indicators and lagged outcomes over time. We illustrate this in Fig. 4, where gray lines show the performance of metrics based on different hospitalization cutoffs with neutral weighting. No single cutoff dominated during the full study period. For example, the cutoff of 5 per 100,000 performed best for high mortality during 3 quarters of the study period, with accuracy above 90% in states and 75% in counties, but was the worst performing in Q2–Q3 2022, with less than 50% accuracy. The accuracy of the single best-performing metric also varied across quarters (e.g., from 61 to 80% for high mortality and 72 to 90% for very high mortality in counties).

Fig. 4.

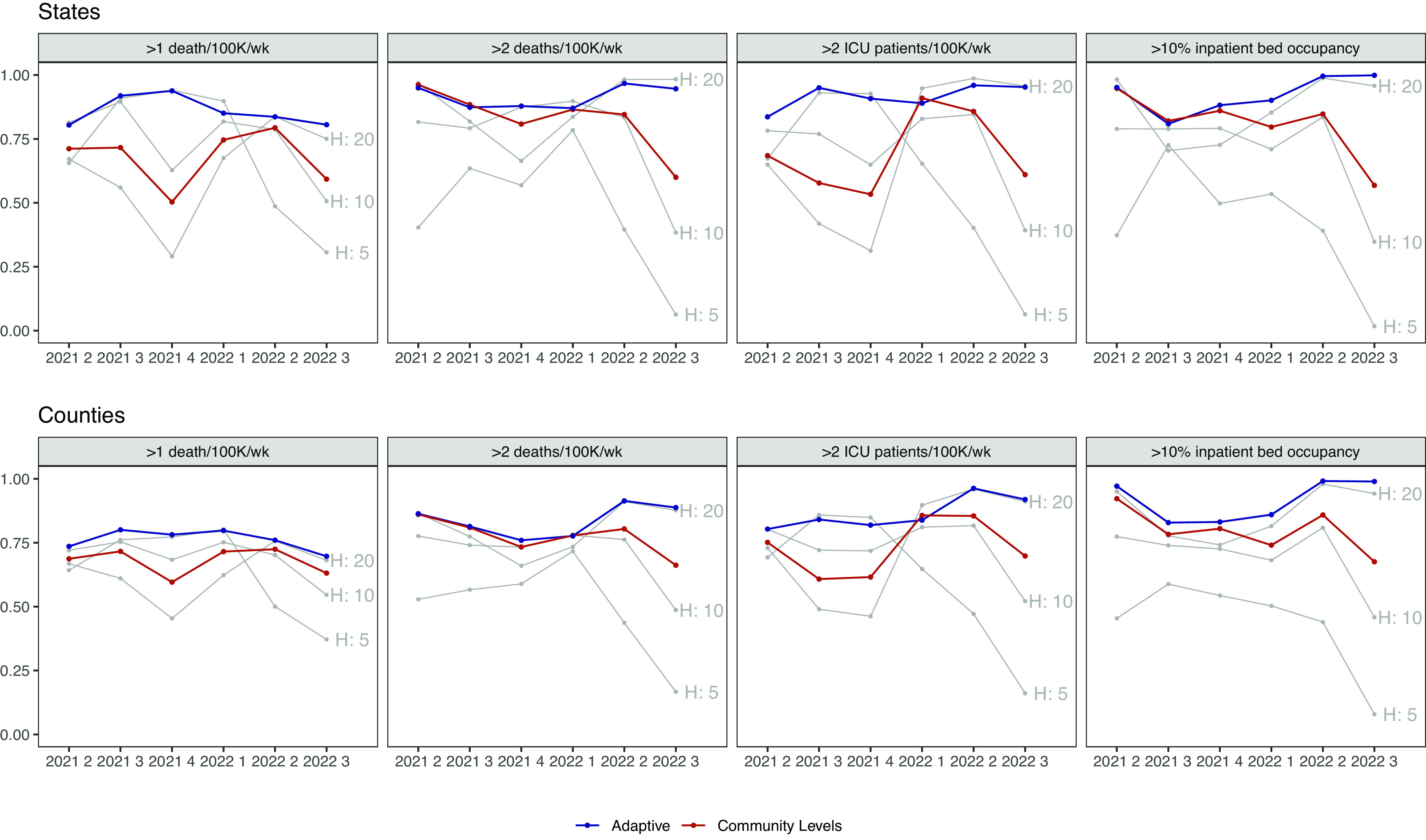
Weighted accuracy by metric. The top plot displays states, and the bottom plot displays counties. Columns indicate different outcomes. The x-axis indicates quarter, and the y-axis predictive accuracy with neutral weighting. Gray lines depict metrics based on new hospital admissions exceeding the labeled threshold. The red line indicates CDC Community Levels and the blue line the best-performing adaptive metric in the training period of those listed in Fig. 3. A version with HSA-level results can be found in SI Appendix, Fig. S10.

Other static metrics similarly reflected the evolving relationship between indicators and mortality. For example, while prediction based on current risk designation (Z) was the second-worst performing static indicator during the training period for high mortality (after Community Levels) in states, it performed best during the test period, when waves of infection were less extreme and variable. CDC Community Levels performed relatively worse compared to other static metrics at predicting high mortality during the training period, but similar or better during the test period; the converse was true for predicting very high mortality (Fig. 3). Overall, static metrics that used hospitalizations and bed occupancy (HO) performed most consistently across training and test periods, but we would have been unable to discern this with only training data. Across static metrics, training accuracy was an unreliable signal of test accuracy.

Adaptive Metrics.

Adaptive metrics consistently outperformed static metrics for both primary outcomes in training and test periods (Fig. 3). For example, when predicting high mortality in states with neutral weighting, adaptive metrics had an overall accuracy of 86 to 89% in the training period and 77 to 83% in the test period; for very high mortality, this was 85 to 90% and 91 to 94% respectively. While all adaptive functional forms performed well, metrics corresponding to CHOZ and HZ (88 to 89% training, 83% test for high mortality) slightly outperformed CHO and the simplified HZ version with less frequent updating. They also performed better than metrics that included week-on-week indicator changes (CHOD). Importantly, while adaptive metrics performed similarly to static metrics during some quarters, they rarely underperformed by a substantial margin and often achieved substantial gains (Fig. 4). This was reflected in regret, which was better controlled by adaptive metrics than static metrics in nearly all cases at both state and county levels. Adaptive metrics also weakly dominated static indicator-based metrics and Community Levels in the sense that HZ could achieve at least equal (and often higher) sensitivity and specificity for at least one value of wt at both geographic levels (SI Appendix, Fig. S11).

Alternative Preferences, Secondary Outcomes, and Sensitivity Analyses.

Adaptive metrics similarly outperformed static metrics across preference weights (Fig. 3) and for secondary outcomes of future ICU hospitalizations over 2 per 100,000 and future COVID-19 inpatient bed occupancy >10% (Fig. 4 and SI Appendix, Fig. S5). Across outcomes, we only observed substantial improvement in predictive performance from adding weekly changes for the inpatient bed occupancy outcome; for this outcome, adaptive metrics without weekly changes had smaller improvements over static metrics (SI Appendix, Figs. S6–S8). The gain in weighted accuracy for adaptive metrics was higher when estimated at the HSA level rather than at the county level (about 2 percentage points for both mortality outcomes with neutral weighting) (SI Appendix, Fig. S4). Running the training period from December 15 to February 15 to capture the omicron variant did not substantially alter the relative benefit of adaptive metrics, with a 14 percentage point increase in weighted accuracy in states for high mortality compared to Community Levels with a neutral weighting (compared to 12% in the base case) and 7% in counties (compared to 6%) (SI Appendix, Fig. S12).

Simulations.

In simulations, adaptive metrics outperformed static metrics when the relationship between indicators and outcomes was changing over time, across different input/output functional forms and regardless of whether prevalence was constant or followed waves generated from empirical hospitalization data (SI Appendix, Fig. S14). There was no gain when the relationship between indicators and outcomes was constant; adaptive metrics performed worse than static metrics when waves were extremely sharp, and there could be insufficient training data near the threshold to estimate the optimal cutoff.

Discussion

We proposed an adaptive approach to estimating local risk which continually updates metrics to ensure they predict outcomes of policy interest. We showed that this would have outperformed static approaches, including CDC Community Levels over the past year. Our metrics have a unique advantage in a rapidly evolving pandemic context. They quickly pick up new information as the relationship between indicators and future mortality shifts, allowing us to refine the threshold for “high risk” and improve discrimination.

Previous papers have proposed adaptive policies for COVID-19 management, in which policymakers shift responses depending on observed indicators like cases and deaths (20–22). We extend this work by allowing the trigger thresholds for indicators to also vary over time. Such an approach could be particularly advantageous for maintaining public trust when the relationship between indicators and outcomes is not yet well-understood or is changing quickly (23).

Our approach draws on ideas that have been applied in the online calibration literature and in forecasting, but have not yet been widely applied to population risk metrics (6, 24–26). Nevertheless, some previous authors have noted that accounting for the evolving pandemic conditions is important for effective decision-making, suggesting policies that are adjusted for the changing costs of mitigation over the course of a pandemic or the number of people vaccinated over time (27, 28). We particularly emphasize parsimony for policy metrics, demonstrating that policymakers can obtain equal predictive performance with fewer inputs potentially reducing the burden of data collection on state and local public health departments. Similar to other authors, we find hospitalizations to be the most powerful predictor of future mortality (6). We further emphasize that it is valuable to collect real-time data on outcomes of policy interest, like mortality. In the case of COVID-19, while state mortality is still collected and reported weekly, many counties have reduced reporting frequency (15).

Our method can also reflect a policymaker’s preferences for the trade-off between avoiding false negatives and false positives, filling a previously identified gap between models and decision theory (29). In practice, different indicators could be used to guide different policies. For the most burdensome interventions (e.g., business closures), policymakers might prefer a low risk of false negatives, while for less burdensome interventions, (e.g., distribution of rapid tests), they might have a higher tolerance for false positives. Future work could formally expand adaptive metrics to include multiple levels of risk designations (e.g., low/medium/high) based on different outcomes of interest, prediction of multiple levels of a single outcome, or different preferences for false negatives versus false positives. Metrics could also be modified to reflect different outcomes for different users, such as employers and workplaces, and to map designations to institution-specific risk tolerances.

There are several additional limitations and potential extensions to this study. First, we model only outcomes related to severe disease and death from COVID-19, as national policymakers have designated these priority outcomes. Nevertheless, metrics to track illness are also important for understanding the full burden of disease, which can include disruptions from illness and Long COVID, and work is also needed to predict surges with longer lead time (26, 30). In addition, no adaptive framework can automatically incorporate all possible variations. Manual tuning may be needed, for example, if the frequency of reporting of hospitalization changes over time. Furthermore, in high-danger situations, such as if an unusually lethal new variant were identified in one country, it may be preferable to implement preventative measures even prior to observing a changing relationship between indicators and severe outcomes. Mortality is a lagging indicator, following rises in cases and hospitalizations, and changes in transmission dynamics are influenced by other factors (e.g., seasonality, new variants) that have proven difficult to predict (31). As a result, metrics based on mortality should not be construed as leading indicators of future surges, but rather a ‘fire alarm’ once a surge has begun. However, metrics could be refined to upweight performance during critical periods such as the start of a surge. Finally, future work could also expand these methods to other contexts, such as prediction of combined respiratory disease outcomes (including influenza and RSV). Overall, adaptive metrics may be a powerful tool for designing trustworthy, transparent metrics to guide infectious disease policy.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Anonymized cleaned data and code have been deposited in GitHub (https://github.com/abilinski/AdaptiveRiskMetrics). Previously published data were used for this work (public data, URLs in text and on GitHub (32)).