Stress-dependent activation entropy in thermally activated cross-slip of dislocations

Significance

A quantitative understanding of the strength and plasticity of crystalline solids requires the ability to predict the rate of thermally activated processes such as dislocation cross-slip. However, current transition-state theory predictions for the rate of dislocation cross-slip are orders of magnitude lower than what is observed in molecular dynamics simulations. This long-standing discrepancy has been challenging to resolve. Here, we show that the discrepancy is caused by the anharmonic effects of thermal expansion and thermal softening, which have been previously neglected. Our findings demonstrate the importance of including these anharmonic effects in the rate predictions of all stress-driven, thermally activated processes in solids.

Abstract

Cross-slip of screw dislocations in crystalline solids is a stress-driven thermally activated process essential to many phenomena during plastic deformation, including dislocation pattern formation, strain hardening, and dynamic recovery. Molecular dynamics (MD) simulation has played an important role in determining the microscopic mechanisms of cross-slip. However, due to its limited timescale, MD can only predict cross-slip rates in high-stress or high-temperature conditions. The transition state theory can predict the cross-slip rate over a broad range of stress and temperature conditions, but its predictions have been found to be several orders of magnitude too low in comparison to MD results. This discrepancy can be expressed as an anomalously large activation entropy whose physical origin remains unclear. Here, we resolve this discrepancy by showing that the large activation entropy results from anharmonic effects, including thermal softening, thermal expansion, and soft vibrational modes of the dislocation. We expect these anharmonic effects to be significant in a wide range of stress-driven thermally activated processes in solids.

Dislocation slip is the primary source of plastic deformation in crystalline solids. Cross-slip occurs when a screw dislocation changes its slip plane (Fig. 1A). This stress-driven, thermally activated process is critical in creating dislocation patterns (1) and bypassing obstacles (2, 3), which leads to strain hardening and dynamic recovery (4–6) during plastic deformation. It has long been challenging to accurately predict the cross-slip rate as a function of stress and temperature. Many experimental (7, 8) and theoretical (9, 10) analyses have been performed to determine the activation parameters for cross-slip based on the continuum theory of dislocations. However, the applicability of the continuum theory is questionable (11) since the changes in dislocation core structure during cross-slip can be confined to only a few lattice spacings. Fully atomistic models are needed to uncover the fundamental physical mechanisms of cross-slip. Unfortunately, direct molecular dynamics (MD) simulation has a limited timescale (typically less than 100 ns), so it is applicable only when cross-slip occurs at a high rate, i.e., under a high-stress or high-temperature condition (12, 13).

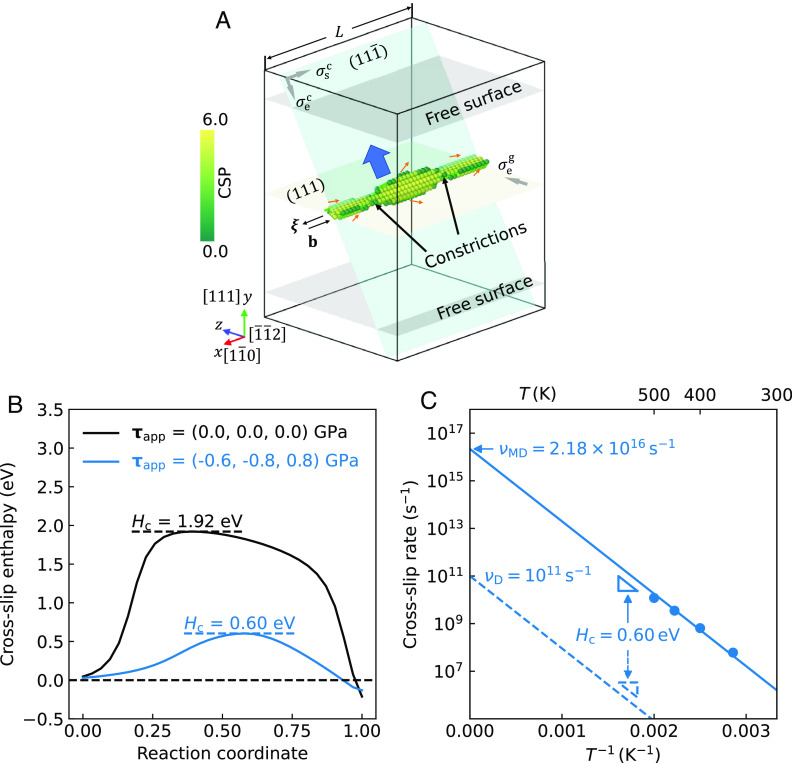
Fig. 1.

Discrepancy between MD rates and TST predictions. (A) Simulation cell ($20[1\overline{1}0]\times 20[111]\times 10[\overline{1}\overline{1}2]$) with a screw dislocation along the $x$-direction, visualized by OVITO (26). Atoms are colored according to their centrosymmetric parameter (CSP), given an fcc crystal structure (12 neighbors). The atoms with $\text{CSP}>1$ are extracted to visualize the dislocation core structure. The screw dislocation changes the slip plane from $(111)$ to $(11\overline{1})$ following the Freidel–Escaig mechanism (27). The three Escaig–Schmid stresses components ${\mathit{\tau }}_{\text{app}}=({\sigma }_{\mathrm{e}}^{\mathrm{g}},{\sigma }_{\mathrm{s}}^{\mathrm{c}},{\sigma }_{\mathrm{e}}^{\mathrm{c}})$ controlling the cross-slip process are applied on the two slip planes. The cross-slipped dislocation moves along the cross-slip plane (blue arrow) if ${\sigma }_{\mathrm{s}}^{\mathrm{c}}$ is applied and finally annihilates at the free surface. (B) Converged minimum-energy paths of cross-slip, calculated at zero stress ${\mathit{\tau }}_{\text{app}}=0$ and fixed applied stress ${\mathit{\tau }}_{\text{app}}=(-0.6,-0.8,0.8)\text{GPa}$. The positive directions of the shear stresses are marked as arrows in A. (C) Cross-slip rates at different temperatures obtained by MD simulations (solid line) and predicted by TST Eq. 1 (dashed line) under fixed applied stress ${\mathit{\tau }}_{\text{app}}$.

The transition state theory (TST), combined with minimum energy paths (MEP) calculations, provides a theoretical framework to predict the rate of thermally activated processes in solids over a wide range of stress and temperature conditions (14–16). For a screw dislocation segment of length $L$, the cross-slip rate as a function of temperature $T$ under applied stress tensor ${\mathit{\tau }}_{\text{app}}$ (Fig. 1B) can be written as

$$\begin{array}{c}\hfill r(T,{\mathit{\tau }}_{\text{app}},L)=\nu (L)exp\left[-\frac{H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})}{k_{\mathrm{B}}T}\right],\end{array}$$ [1]

where $H_{\mathrm{c}}$ is the activation enthalpy obtained from MEP calculations, and $k_{\mathrm{B}}$ is the Boltzmann constant. The rate prefactor $\nu (L)$ is proportional to the dislocation length $L$ and can be written as $\nu (L)={\nu }_{\mathrm{e}}L/b$, where ${\nu }_{\mathrm{e}}$ is an effective attempt frequency, and $b$ is the magnitude of the dislocation Burgers vector and hence the smallest repeat distance along the dislocation. In cross-slip models used in discrete dislocation dynamics (DDD) simulations, the rate prefactor is linked to the vibrational frequency of the dislocation line and is commonly expressed as $\nu (L)={\nu }_{\mathrm{D}}L/L_0$, where ${\nu }_{\mathrm{D}}\sim {10}^{13}{\mathrm{s}}^{-1}$ is the Debye frequency, and $L_0=1\mathrm{\mu }\mathrm{m}$ is a reference length (17, 18). Given that the reported activation enthalpy $H_{\mathrm{c}}$ for the cross-slip in Cu is in the range of 0.5–3 eV (7–9, 19), together with the rate prefactor estimates above, cross-slip is not expected to occur in direct MD simulations except at very high temperatures or stresses.

However, previous studies (10, 12, 13) have shown that cross-slip occurs in direct MD simulations at a much higher rate than expected (Fig. 1C). This discrepancy has led to the suggestion that the previous estimates of the rate prefactor are incorrect and need to be multiplied by a factor of $exp\left[S_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})/k_{\mathrm{B}}\right]$, where $S_{\mathrm{c}}$ is a stress-dependent activation entropy whose physical origin has remained elusive for dislocation cross-slip. It has been estimated either through an empirical estimate based on the Meyer–Neldel rule (13) or simplified line tension models (20) but not from fully atomistic models due to numerical difficulties (10). The anomalous activation entropy has also been reported in atomistic simulations of dislocation nucleation (21, 22) and dislocation motion (23, 24). The unknown origin of the activation entropy has even raised doubts about whether TST is applicable in certain thermally activated dislocation processes (23, 25).

This work provides a systematic and fully atomistic approach to resolve the discrepancy in the cross-slip rates and uncover the physical origin of the anomalously large activation entropy. We carry out high-throughput minimum-energy paths (MEP) calculations to map out the stress dependence of the activation enthalpy $H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})$. The rate prefactor is determined from the harmonic transition state theory (HTST), with essential corrections applied to soft vibrational modes of the dislocation. Our approach reveals that in order to resolve the rate discrepancy between MD and TST predictions, anharmonic effects of thermal softening and thermal expansion must be appropriately considered. These effects cause the solid to experience more significant shear and volumetric deformations when temperature increases at constant applied stress and cause a pronounced drop in the cross-slip activation barrier, giving rise to the activation entropy $S_{\mathrm{c}}$. We find that $S_{\mathrm{c}}$ is more pronounced at higher stress, contrary to previous estimates (13) based on the Meyer–Neldel rule (28). This work demonstrates the applicability of HTST (after corrections) to dislocation cross-slip and provides a quantitative approach to predict its rate and activation entropy. The significant activation entropy is expected to influence the rate of a wide range of stress-driven thermally activated processes in solids, such as phase transformation and twin boundary migration.

Results

We use face-centered cubic (FCC) nickel as an example to investigate dislocation cross-slip behaviors. The interatomic force field is modeled by the embedded-atom model (EAM) “vnih” (29) because its stacking fault energy is in good agreement with both experimental measurements and first-principle calculations (11, 30). The simulation cell is large enough ($N=$78,400 atoms) to avoid boundary effects on dislocation cross-slip rates. A screw dislocation along the $x$-direction passes through the center of the simulation cell. The cell is periodic in $x$- and $z$- directions and has free surfaces on the $y$-direction. Shear stresses ${\mathit{\tau }}_{\text{app}}=({\sigma }_{\mathrm{e}}^{\mathrm{g}},{\sigma }_{\mathrm{s}}^{\mathrm{c}},{\sigma }_{\mathrm{e}}^{\mathrm{c}})$ are applied to provide driving forces for cross-slip. As shown in Fig. 1A, the applied stress contains Escaig (${}_{\mathrm{e}}$) and Schmid (${}_{\mathrm{s}}$) components on the original slip (${}^{\mathrm{g}}$) plane $(111)$ and the cross-slip (${}^{\mathrm{c}}$) plane $(11\overline{1})$ (Materials and Methods). The Schmid stress on the original slip plane ${\sigma }_{\mathrm{s}}^{\mathrm{g}}$ is set to zero so that the dislocation does not move prior to cross-slip (31). The effect of this stress component can be accounted for by introducing an additional term in the effective stress as discussed in refs. 11, 13, 31, and 32.

MD simulations of cross-slip are carried out using the LAMMPS package (33). The initial configuration is heated up to the target temperature $T$ using the Nosé-Hoover thermostat (NVT ensemble) while keeping a constant applied stress at ${\mathit{\tau }}_{\text{app}}=(-0.6,-0.8,0.8)\text{GPa}$ by adjusting the strain. After equilibration, the simulation continues at constant $T$ and the corresponding stress until the dislocation cross-slips (at time $t_{\text{cs}}$) and annihilates at the surface (Materials and Methods). The MD simulation is repeated 32 times at each temperature. The cross-slip rate $r_{\text{MD}}$, estimated as the inverse of the average cross-slip time ${\overline{t}}_{\text{cs}}$, is plotted against the temperature in Fig. 1C. The temperature dependence of the cross-slip rate is seen to follow the Arrhenius law,

$$\begin{array}{c}\hfill r_{\text{MD}}={\nu }_{\text{MD}}exp\left[-\frac{H_{\mathrm{c}}^{\text{MD}}}{k_{\mathrm{B}}T}\right],\end{array}$$ [2]

where $H_{\mathrm{c}}^{\text{MD}}=0.60\text{eV}$ and ${\nu }_{\text{MD}}=2.18\times {10}^{16}{\mathrm{s}}^{-1}$ are parameters obtained from fitting the MD data.

We proceed to analyze the cross-slip rates by TST. The activation enthalpy $H_{\mathrm{c}}$ represents the energy difference between the transition state (i.e., saddle point on the potential energy landscape) and the initial state of the thermally activated cross-slip. To find the transition state under the applied stress ${\mathit{\tau }}_{\text{app}}$, we first determine the minimum-energy path (MEP) using the free-end string method (34, 35). Given the MEP, the exact transition state (saddle point) is then obtained by the dimer method (36) (Materials and Methods). Fig. 1B illustrates two converged MEPs with and without the applied stress ${\mathit{\tau }}_{\text{app}}$ corresponding to the MD simulations, respectively. As expected, the applied stress lowers the activation enthalpy of cross-slip. Furthermore, the activation enthalpy of cross-slip under the applied stress, $H_{\mathrm{c}}=0.60\text{eV}$, perfectly matches the value $H_{\mathrm{c}}^{\text{MD}}$ extracted from the MD simulations (Fig. 1C). On the other hand, if we adopt the commonly used estimate for the frequency prefactor (17, 18), $\nu (L)={\nu }_{\mathrm{D}}L/L_0$, for the dislocation length ($L\approx 10\text{nm}$) considered here, we would arrive at $\nu (L)\approx {10}^{11}{\mathrm{s}}^{-1}$, which is more than five orders of magnitude lower than MD predictions (Fig. 1C). This paper’s primary purpose is to identify the physical origin of this discrepancy.

To go beyond a heuristic estimate, we use the harmonic transition state theory (HTST) to compute the rate prefactor more rigorously. In HTST, the rate prefactor is expressed as follows (14):

$$\begin{array}{c}\hfill {\nu }_{\text{HTST}}=\frac{{\prod }_{i=1}^{3N-3}{\nu }_i^A}{{\prod }_{j=1}^{3N-4}{\nu }_j^S},\end{array}$$ [3]

where ${\nu }_i^A$ and ${\nu }_i^S$ are frequencies of the eigenmodes of the initial state (A) and the transition state (S), respectively. The three rigid-body translational modes (with zero frequency) are excluded from the product in both states A and S. For state S, the mode along the reaction coordinate (with imaginary frequency) is also excluded. Although HTST is often employed to study thermally activated processes in solids at moderately low temperatures, it has never been successfully applied to dislocation cross-slip due to several challenges.

First, a direct implementation of Eq. 3 requires diagonalizing the Hessian matrix of the system to obtain the eigen-frequencies (37) (for both states A and S). The Hessian matrix is quite large (size $3N\times 3N$), and a full diagonalization is computationally very expensive. In this work, we take advantage of the fact that the product of eigen-frequencies can be obtained from the determinant of the Hessian matrix, which can be computed much more efficiently (e.g., using LU decomposition) than to obtain all the eigen-frequencies individually. To avoid the determinant becoming zero due to the rigid-body translation modes, we slightly perturb the Hessian matrix to impart a small but nonzero frequency to these modes (Materials and Methods).

Second, the harmonic approximation is not valid at room temperature or above for some of the soft vibrational modes. For example, the saddle state S contains a constriction of the stacking fault, which can be formed anywhere along the dislocation line. Motion of this constriction along the dislocation line, i.e., the so-called Goldstone mode, produces periodic energy variations with an amplitude of around $20\text{meV}$ (10), even lower than the thermal energy. In this case, approximating the periodic potential landscape by a quadratic function leads to a large error in the partition function. Here, we account for these soft vibrational modes by numerically evaluating the partition function in their eigen-directions and introduce a correction factor (${\tilde{\nu }}_{\mathrm{A}}/{\tilde{\nu }}_{\mathrm{S}}$) to the cross-slip rate prediction, where ${\tilde{\nu }}_{\mathrm{S}}$ is the correction factor for the Goldstone mode in the saddle state S and ${\tilde{\nu }}_{\mathrm{A}}$ is the correction factor for the uniform glide mode of the screw dislocation on its slip plane in state A (SI Appendix, Text I).

Using the above two methods, we can now evaluate the HTST-based rate prefactor, $\nu (L)={\nu }_{\text{HTST}}·{\tilde{\nu }}_{\mathrm{A}}/{\tilde{\nu }}_{\mathrm{S}}$. For the stress condition considered above, $\nu (L)=4.56\times {10}^{12}{\mathrm{s}}^{-1}$, which, although higher than previous estimates, is still much lower than ${\nu }_{\text{MD}}$. As a result, the predicted cross-slip rate (black line) is still 3 to 4 orders of magnitude lower than the MD results (Fig. 2B).

Fig. 2.

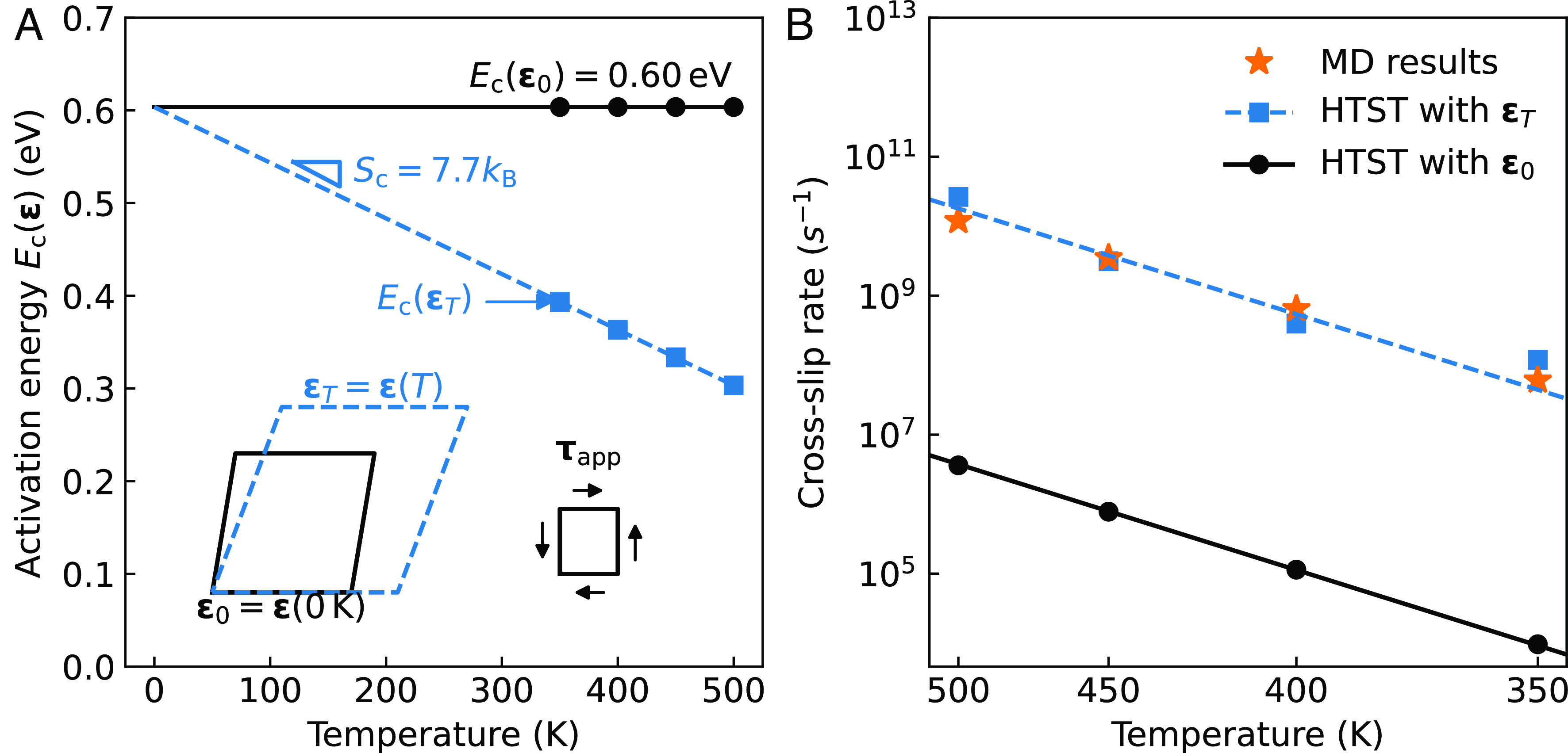
Activation entropy due to the thermal strain. (A) Activated energy calculated at zero-temperature strain ${\mathit{\epsilon }}_0$ and corresponding finite-temperature strain ${\mathit{\epsilon }}_{\mathrm{T}}$. The inset diagram schematically shows the thermal strain caused by temperature increase with the same applied stress ${\mathit{\tau }}_{\text{app}}$. (B) Estimated rates using HTST (Eq. 4) with the activation energy and prefactor evaluated at ${\mathit{\epsilon }}_0$ and ${\mathit{\epsilon }}_{\mathrm{T}}$. The benchmark average MD rates are shown as the stars (see SI Appendix, Text VII for the statistical analysis of the MD simulations).

To resolve the remaining discrepancy, we note that the activation enthalpy $H_{\mathrm{c}}$ at a given stress ${\mathit{\tau }}_{\text{app}}$ is often computed as an activation energy $E_{\mathrm{c}}$ at a given strain $\mathit{\epsilon }$ corresponding to stress ${\mathit{\tau }}_{\text{app}}$. To make this point more explicit, we express the cross-slip rate as a function of strain $\mathit{\epsilon }$ and temperature $T$,

$$\begin{array}{c}\hfill r_{\text{HTST}}(\mathit{\epsilon },T)={\nu }_{\text{HTST}}\frac{{\tilde{\nu }}_{\mathrm{A}}}{{\tilde{\nu }}_{\mathrm{S}}}exp\left[-\frac{E_{\mathrm{c}}(\mathit{\epsilon })}{k_{\mathrm{B}}T}\right].\end{array}$$ [4]

For consistency, $\mathit{\epsilon }$ should be the strain ${\mathit{\epsilon }}_T\equiv \mathit{\epsilon }({\mathit{\tau }}_{\text{app}},T)$ corresponding to stress ${\mathit{\tau }}_{\text{app}}$ at temperature $T$. However, most of the MEP methods, which are based on energy minimization, are performed at zero temperature. Let us define ${\mathit{\epsilon }}_0\equiv \mathit{\epsilon }({\mathit{\tau }}_{\text{app}},0)$ as the strain corresponding to stress ${\mathit{\tau }}_{\text{app}}$ at zero temperature. In the above, we have reported that $E_{\mathrm{c}}({\mathit{\epsilon }}_0)=H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})=0.60\text{eV}$. From Eq. 4, it can be clearly seen that an inconsistency would arise if $\mathit{\epsilon }={\mathit{\epsilon }}_T$ is used on the left-hand side and $\mathit{\epsilon }={\mathit{\epsilon }}_0$ is used on the right hand side.

While the difference between ${\mathit{\epsilon }}_T$ and ${\mathit{\epsilon }}_0$ has been implicitly assumed to be small and often neglected, here, we show that it has a pronounced effect on the predicted cross-slip rate. If the applied stress ${\mathit{\tau }}_{\text{app}}$ remains constant as temperature is increased, the strain ${\mathit{\epsilon }}_T$ increases in both the deviatoric and volumetric components, as sketched in the Inset of Fig. 2A. Fig. 2A shows that the computed activation energy $E_{\mathrm{c}}({\mathit{\epsilon }}_T)$ decreases linearly with temperature, i.e., $E_{\mathrm{c}}({\mathit{\epsilon }}_T)=E_{\mathrm{c}}({\mathit{\epsilon }}_0)-T·S_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})$, where $S_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})=7.7k_{\mathrm{B}}$ is the negative slope of the $E_{\mathrm{c}}$-$T$ curve and can be called an activation entropy. Inserting this expression of $E_{\mathrm{c}}({\mathit{\epsilon }}_T)$ into Eq. 4, we can express the HTST-based rate prediction as

$$\begin{array}{cc}& r_{\text{HTST}}({\mathit{\epsilon }}_T,T)\hfill \\ \hfill & ={\nu }_{\text{HTST}}\frac{{\tilde{\nu }}_{\mathrm{A}}}{{\tilde{\nu }}_{\mathrm{S}}}exp\left[\frac{S_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})}{k_{\mathrm{B}}}\right]exp\left[-\frac{E_{\mathrm{c}}({\mathit{\epsilon }}_0)}{k_{\mathrm{B}}T}\right].\hfill \end{array}$$ [5]

The new rate prefactor, $\nu (L)={\nu }_{\text{HTST}}·({\tilde{\nu }}_{\mathrm{A}}/{\tilde{\nu }}_{\mathrm{S}})·exp(S_{\mathrm{c}}/k_{\mathrm{B}})=$$2.71\times {10}^{16}{\mathrm{s}}^{-1}$, is in very good agreement with ${\nu }_{\text{MD}}$. Fig. 2B shows that the resulting HTST-based predictions of cross-slip rates now agree well with MD results.

Discussion

In the example considered above, we observe that the large discrepancy between previous TST-based predictions of cross-slip rate and MD results is mostly due to the change of strain with increasing temperature at a constant applied stress. Due to the thermal softening effect, the same shear stress will result in greater shear strain at higher temperature. Due to the thermal expansion effect, the volumetric strain also increases with increasing temperature. We have repeated the MD simulations and HTST calculations of cross-slip rates at two more applied stress conditions, and the results support the same conclusions (SI Appendix Text II).

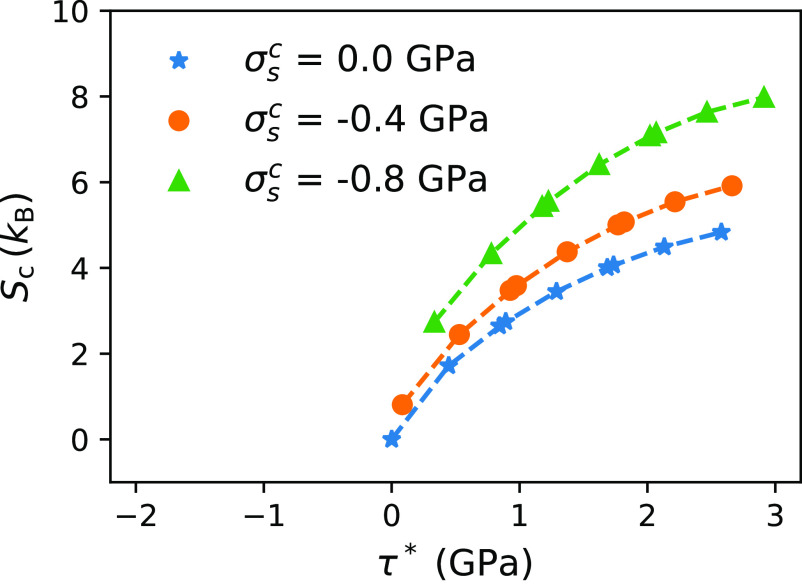
To examine how the activation entropy depends on the applied stress, we compute $S_{\mathrm{c}}$ at 27 different stress conditions (for ${\sigma }_{\mathrm{e}}^{\mathrm{g}}=0,-0.4,-0.8\text{GPa}$, ${\sigma }_{\mathrm{s}}^{\mathrm{c}}=0,-0.4,-0.8\text{GPa}$, and ${\sigma }_{\mathrm{e}}^{\mathrm{c}}=0,0.4,0.8\text{GPa}$, respectively). We have previously shown that the activation enthalpy $H_c({\mathit{\tau }}_{\text{app}})$ as a function of these three shear stress components can be expressed in terms of a one-dimension function of an effective stress (31), defined as ${\tau }^{\ast }=C_{\mathrm{e}}^{\mathrm{g}}{\sigma }_{\mathrm{e}}^{\mathrm{g}}+C_{\mathrm{e}}^{\mathrm{c}}{\sigma }_{\mathrm{e}}^{\mathrm{c}}+{(D_{\mathrm{s}}^{\mathrm{c}}{\sigma }_{\mathrm{s}}^{\mathrm{c}})}^2$, where $C_{\mathrm{e}}^{\mathrm{g}}$, $C_{\mathrm{e}}^{\mathrm{c}}$ and $D_{\mathrm{s}}^{\mathrm{c}}$ are fitting constants. Fig. 3 shows that the activation entropy $S_{\mathrm{c}}$ generally increases with the effective stress ${\tau }^{\ast }$, although it is not a function of ${\tau }^{\ast }$ alone (SI Appendix Text II).

Fig. 3.

Stress-dependent activation entropy $S_{\mathrm{c}}$. Solid dots represent the activation entropy of 27 applied Escaig–Schmid stress conditions from MEP calculations using the same method as Fig. 2A. The dashed lines are the estimated activation entropy from Eq. 6.

The empirical Meyer–Neldel (MN) compensation rule, $S_{\mathrm{c}}=H_{\mathrm{c}}/T_{\mathrm{m}}$, where $T_{\mathrm{m}}$ is the melting temperature, is often used to estimate the activation entropy (13). Because the cross-slip activation enthalpy $H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})$ is a monotonically decreasing function of ${\tau }^{\ast }$, the MN rule would predict a decreasing $S_{\mathrm{c}}$ with increasing ${\tau }^{\ast }$, which is opposite to the trend shown in Fig. 3. Our results show that the physics behind the MN rule (38), if present, plays a minor role for the rate of dislocation cross-slip. Fig. 3 clearly shows that the activation entropy $S_{\mathrm{c}}$ due to anharmonic effects becomes smaller at lower stress; in fact $S_{\mathrm{c}}$ vanishes in the zero stress limit, as we will show below. This may be a reason for neglecting the activation entropy effects in previous studies of dislocation cross-slip (10). Under the temperature and stress conditions considered here, our results show that the quasi-harmonic approximation (QHA) presented here provides a good description of dislocation cross-slip in FCC Ni, as long as the thermal expansion/softening effects and the soft-mode corrections are appropriately accounted for. At even higher temperatures, or for other materials and processes, QHA may be insufficient and other anharmonic effects may need to be considered (39–42).

We now seek a close-form expression for $S_{\mathrm{c}}$ as a function of stress, which will not only reveal more insight into the physical nature of the activation entropy but also provide a needed tool for predicting the cross-slip rate in mesoscale models such as discrete dislocation dynamics (18, 43). We begin by defining $\tilde{\mathit{\sigma }}$ as the stress of the crystal at zero temperature when subjected to the strain ${\mathit{\epsilon }}_T$, i.e., ${\mathit{\epsilon }}_T=\mathit{\epsilon }(\tilde{\mathit{\sigma }},0)=\mathit{\epsilon }({\mathit{\tau }}_{\text{app}},T)$. $\tilde{\mathit{\sigma }}$ is the stress in the simulation cell when performing MEP calculations for $E_{\mathrm{c}}({\mathit{\epsilon }}_T)$; hence, there is a one-to-one correspondence between ${\mathit{\epsilon }}_T$ and $\tilde{\mathit{\sigma }}$. At temperature $T$, the stress of the crystal subjected to strain ${\mathit{\epsilon }}_T$ is simply ${\mathit{\tau }}_{\text{app}}$. But if the temperature is set to zero with the strain fixed at ${\mathit{\epsilon }}_T$, the stress value changes, i.e., $\tilde{\mathit{\sigma }}={\mathit{\tau }}_{\text{app}}+\widehat{\sigma }\mathbf{I}+{\mathit{\tau }}_{\text{ex}}$, where $\widehat{\sigma }$ is a hydrostatic (tensile) stress and ${\mathit{\tau }}_{\text{ex}}$ is an excess shear stress. We performed 500 MEP calculations of cross-slip at different stress $\tilde{\mathit{\sigma }}$ and fit the activation energy ${\tilde{H}}_{\mathrm{c}}(\tilde{\mathit{\sigma }})=E_{\mathrm{c}}({\mathit{\epsilon }}_T)$ results as a function of $\tilde{\mathit{\sigma }}$ (SI Appendix Text IV). The functional form of ${\tilde{H}}_{\mathrm{c}}(\tilde{\mathit{\sigma }})$ is a generalization of the $H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})$ function established in our previous work (31) and reduces to $H_{\mathrm{c}}({\mathit{\tau }}_{\text{app}})$ when $\widehat{\sigma }=0$. Given the analytic function ${\tilde{H}}_{\mathrm{c}}(\tilde{\mathit{\sigma }})$, we obtain the following expression for the activation entropy (SI Appendix Text V)

$$\begin{array}{c}\hfill S_{\mathrm{c}}=-K{\alpha }_V\left(\frac{\partial {\tilde{H}}_{\mathrm{c}}}{\partial \widehat{\sigma }}\right)+\frac{1}{\mu }\left(\frac{\partial \mu }{\partial T}\right)\left(\frac{\partial {\tilde{H}}_{\mathrm{c}}}{\partial \mathit{\tau }}\right)·\mathit{\tau },\end{array}$$ [6]

where $K$ is bulk modulus, ${\alpha }_V$ is volumetric thermal expansion coefficient, and $\mu$ is shear modulus. Fig. 3 shows that Eq. 6 agrees very well with the activation entropy computed above. The two terms in Eq. 6 can be identified as the contributions from thermal expansion and thermal softening effects to the activation entropy. Both terms vanish at the zero-stress limit. If we consider a low-stress case where the local ${\sigma }_{\mathrm{g}}^{\mathrm{e}}$ is only 50 MPa, the estimated activation entropy $S_{\mathrm{c}}=0.6k_{\mathrm{B}}$ and the discrepancy between the Heuristic estimation $1\times {10}^{11}{\mathrm{s}}^{-1}$ and $5\times {10}^{12}{\mathrm{s}}^{-1}$ becomes much smaller. However, the local stress on a dislocation is the superposition of the applied stress and the stress field of all other dislocations. Therefore, the local stress on the screw dislocation can be high, leading to a large activation entropy, even when the applied stress is low.

Eq. 6, combined with Eq. 5, leads to a theoretical model that accurately predicts the cross-slip rate as a function of applied stress. It can serve as an essential input for mesoscale models such as discrete dislocation dynamics (44). Because Eq. 6 expresses $S_{\mathrm{c}}$ in terms of fundamental materials parameters and stress dependence of activation enthalpy, it is generally applicable to all stress-driven thermally activated processes in solids, such as dislocation motion in bcc metals, phase transformation, and twinning. Although the rate theory (Eqs. 5 and 6) we present here is only benchmarked against direct MD simulations at high stress/temperature conditions, it can predict the cross-slip rate over a wide range of stress and temperature conditions.

In conclusion, we have resolved a long-standing discrepancy between TST and direct MD predictions of cross-slip rate and show that the anomalously large activation entropy is ultimately caused by the increasing shear and volumetric strain with increasing temperature at constant applied stress. These anharmonic effects, i.e., thermal softening and thermal expansion, although previously ignored, can lead to orders-of-magnitude changes in the prediction of the cross-slip rate. We obtain an analytical expression for the activation entropy, which not only provides accurate predictions of cross-slip rate for mesoscale models but also shows that our findings are generally applicable to all stress-driven thermally activated processes in solids.

Materials and Methods

Prepare a Single Screw Dislocation under Applied Stress.

The dislocation structure is similar to that of our previous works (11, 31). We start with a perfect fcc nickel crystal (lattice constant $a_0=3.52$ Å) with simulation box dimension of $20[1\overline{1}0]\times 20[111]\times 10[\overline{1}\overline{1}2]$. $10\%$ of the atoms are removed on each side of the $y$-direction to create free surfaces, resulting in 78,400 atoms in the simulation cell. A single straight left-hand screw dislocation is created at the center of the $\mathit{yz}$-plane with Burger’s vector $\mathbf{b}=a_0[\overline{1}10]/2$ along the positive $x$-direction $\mathit{\xi }=[1\overline{1}0]$. The initial configuration is obtained by splitting the screw dislocation into two Shockley partial dislocations (orange arrows in Fig. 1A) with stacking fault on the gliding plane, i.e., the $(111)$ plane (31).

We perform energy minimization with applied shear stresses ${\mathit{\tau }}_{\text{app}}=({\sigma }_{\mathrm{e}}^{\mathrm{g}},{\sigma }_{\mathrm{s}}^{\mathrm{c}},{\sigma }_{\mathrm{e}}^{\mathrm{c}})$ to the dislocation structure. The Cartesian stress tensor can be calculated from the applied stress as

$$\begin{array}{cc}\hfill {\sigma }_{\mathrm{s}}^{\mathrm{g}}& ={\sigma }_{\mathit{xy}},{\sigma }_{\mathrm{e}}^{\mathrm{g}}={\sigma }_{\mathit{yz}},\hfill \\ \hfill {\sigma }_{\mathrm{s}}^{\mathrm{c}}& =\frac{2\sqrt{2}{\sigma }_{\mathit{xz}}-{\sigma }_{\mathit{xy}}}{3},\hfill \\ \hfill {\sigma }_{\mathrm{e}}^{\mathrm{c}}& =\frac{7{\sigma }_{\mathit{yz}}+2\sqrt{2}\left({\sigma }_{\mathit{zz}}-{\sigma }_{\mathit{yy}}\right)}{9},\hfill \end{array}$$ [7]

where ${\sigma }_{\mathit{zz}}=-{\sigma }_{\mathit{yy}}$ is enforced to enable a one-on-one mapping between the Cartesian stress and the Escaig–Schmid stress components, and ${\sigma }_{\mathit{xy}}$ is set to be zero to avoid the screw dislocation moving on the original slip plane.

On the one hand, due to free surfaces in the $y$-direction, stress components $({\sigma }_{\mathit{xy}},{\sigma }_{\mathit{yy}},{\sigma }_{\mathit{yz}})$ are applied by external forces ${\mathbf{f}}_y=(A/N_{\mathit{xz}})({\sigma }_{\mathit{xy}},{\sigma }_{\mathit{yy}},{\sigma }_{\mathit{yz}})$ to the first layer of atoms ($N_{\mathit{xz}}=$1,600 atoms in total) on the free surfaces, and $A=H_x{H}_z$ is the area of the surface. On the other hand, due to the periodic boundary condition on $x$- and $z$- directions, the stress components $({\sigma }_{\mathit{xx}},{\sigma }_{\mathit{zz}},{\sigma }_{\mathit{xz}})$ are controlled by adjusting the components $(H_x,H_z,H_{\mathit{xz}})$ in the simulation cell iteratively until the stresses are converged. The simulation cell matrix (cell vectors) $\mathbf{H}=\left[{\mathbf{c}}_1|{\mathbf{c}}_2|{\mathbf{c}}_3\right]$ is defined as

$$\begin{array}{c}\hfill \mathbf{H}=\left[\begin{array}{ccc}{H}_x& H_{\mathit{xy}}& H_{\mathit{xz}}\\ 0& H_y& H_{\mathit{yz}}\\ 0& 0& H_z\\ \end{array}\right].\end{array}$$ [8]

The stress of the dislocation configuration is calculated by averaging the atomic stress (45) of all the atoms 20 Å below the free surfaces to avoid the surface effect. The convergence tolerance of the stress is $\pm 0.05\text{MPa}$.

Minimum-Energy Path (MEP) Search.

To perform MEP search, we first prepare the initial state $A$ before the transition state and the final state $B$ after the transition state. The converged metastable dislocation structure from the previous section is used as the initial state $A$. The final state $B$ is prepared with the same full screw dislocation structure as state $A$, but with the middle half of the dislocation dissociated on the cross-slip plane $(11\overline{1})$, while the rest of the dislocation still dissociates on $(111)$ (31). Energy minimization is then performed to obtain the final state $B$ under the same applied shear stress ${\mathit{\tau }}_{\text{app}}$. In order to obtain a better initial guess and help with the convergence of the MEP search, the conjugate-gradient energy minimization on the final state $B$ is performed only for five iterations so that the cross-slipped dislocation does not move toward the free surface and annihilate, i.e., the state $B$ is not too far away from the transition state. Starting from a linear interpolation (32 image copies) between states $A$ and $B$ as the initial guess, the MEP search is performed using the free-end string method (34) with reparameterization and trimming (35). After the string method is converged, we use the dimer method (36) to obtain the exact transition state $S$. Starting from the two images closest to the maximum value as the initial dimer, we iteratively shrink the dimer until the distance is below $1\times {10}^{-7}$ Å. The external forces ${\mathbf{f}}_y$ and simulation cell matrix $\mathbf{H}$ from state $A$ are applied during all the energy minimization steps in state-$B$ preparation, MEP search, and dimer method to ensure the same applied stress condition ${\mathit{\tau }}_{\text{app}}$.

Molecular Dynamics (MD) Simulation.

MD simulations of dislocation cross-slip are performed using the LAMMPS package (33). To prepare the dislocation structure at finite temperature $T$ under the applied stress condition ${\mathit{\tau }}_{\text{app}}$, we start from the state $A$ with zero applied stress. The system is gradually heated up to the target temperature $T$ and equilibrated for 10 ps using the Nosé–Hoover thermostat (46) with zero stress applied, to avoid premature cross-slip. The configuration is then gradually loaded to the target stress ${\mathit{\tau }}_{\text{app}}$ and further equilibrated for 2 ps. The method to control the stress is the same as in the previous sections. After the system is equilibrated, we apply a small random perturbation (uniform distribution with the magnitude of $\pm 1\times {10}^{-4}$ Å$·{\mathrm{s}}^{-1}$) to the initial velocity before continuing the MD simulation to avoid repeated MD trajectories. The MD simulation is continued until cross-slip occurs (sudden release of the applied stress) and the cross-slip time $t_{\text{cs}}$ is recorded. A detailed discussion of the statistical analysis is provided in SI Appendix Text VII.

Harmonic Vibrational Frequencies.

The product of the harmonic vibrational frequencies in Eq. 4 is obtained from the Hessian matrices of the initial state $A$ (${\mathbf{K}}_A$) and the transition state $S$ (${\mathbf{K}}_S$). The standard approach to obtain the prefactor is to diagonalize ${\mathbf{K}}_A$ and ${\mathbf{K}}_S$. However, for our system ($N=78,400$), the Hessian matrices have a size of $3N\times 3N=235,200\times 235,200$, which requires significant computational load. Instead, we can calculate the products of the eigen-frequencies from the determinant if and only if $\mathbf{K}$ is nonsingular.

To avoid the nonsigularity from the three rigid-body translational modes (eigen-frequency $\nu =0$), we couple three soft harmonic spring forces $k$ to the $x$-, $y$-, and $z$-directions on one atom (atom #1) in both states $A$ and $S$. This is equivalent to modifying the first three diagonal elements of the Hessian matrix $\mathbf{K}$,

$$\begin{array}{c}\hfill K_{11}\to K_{11}+k;K_{22}\to K_{22}+k;K_{33}\to K_{33}+k.\end{array}$$ [9]

We then obtain the product of the eigen-frequencies by calculating the determinant of the modified Hessian matrix using the sparse LU decomposition in MATLAB. The negative eigenvalue of the Hessian matrix at state $S$ is obtained by finding the minimum eigenvalue using the “eigs” method in MATLAB. The soft spring frequencies are selected to be $k=1\times {10}^{-4}$ eV/Å, which will be canceled out while calculating the prefactor ${\nu }_{\text{HTST}}$ from taking the ratio between the determinant of state $S$ and state $A$. A detailed proof of the method is provided in SI Appendix Text VI.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Cross-slip simulation data and code have been deposited in MD++ (https://gitlab.com/micronano_public/MDpp) (47).