Abstract
Oral bioavailability is a pharmacokinetic property that plays an important role in drug discovery. Recently developed computational models involve the use of molecular descriptors, fingerprints, and conventional machine-learning models. However, determining the type of molecular descriptors requires domain expert knowledge and time for feature selection. With the emergence of the graph neural network (GNN), models can be trained to automatically extract features that they deem important. In this article, we exploited the automatic feature selection of GNN to predict oral bioavailability. To enhance the prediction performance of GNN, we utilized transfer learning by pre-training a model to predict solubility and obtained a final average accuracy of 0.797, an F1 score of 0.840, and an AUC-ROC of 0.867, which outperformed previous studies on predicting oral bioavailability with the same test data set.
Introduction
Current Studies and Available Models to Predict Oral Bioavailability
Orally administered drugs undergo first pass effect as they are metabolized by the liver before entering the systemic circulation. The fraction of drug that enters systemic circulation and reaches the pharmacological target is referred to as oral bioavailability.1 Despite displaying promising results during pre-clinical trial stages, some drug candidates may fail to advance through clinical trial stages due to having low oral bioavailability. As such, one crucial aspect during the early stages of the drug discovery process is to estimate the oral bioavailability of drug candidates. Traditionally, methods used to determine oral bioavailability involved the use of rodent or non-rodent mammalian models. However, such methods are time-consuming and expensive.2 Moreover, there are considerable interspecies differences between the metabolism pathway of animal models and humans that must be taken into consideration, hence highlighting the need of having a prediction model that can provide an accurate and reliable estimate on the human oral bioavailability of small molecules.
Over the years, different in silico methods have been developed to model such a relationship. They consist of different conventional machine-learning models and depend heavily on the use of appropriate molecular representations. To determine the prediction performance of models, studies computed and compared the accuracy of models, where the predicted labels are equivalent to the true labels. For example, Wei et al. conducted a study to predict oral bioavailability by generating 1143 2D molecular descriptors and a random forest (RF) algorithm, which resulted in an accuracy of 79.3%.2 On the other hand, using the same test data set, Falcón-Cano et al. developed models using other machine-learning algorithms such as classification and regression trees, multi-layer perceptron, Naïve Bayes, gradient-boosted trees, and support vector machines using 1337 molecular descriptors, which resulted in an accuracy of 78.3%.2,3 Despite using a larger number of molecular descriptors, the models developed by Falcón-Cano et al. did not manage to outperform the consensus model developed by Wei. As such, there is a need to carefully curate a set of molecular descriptors to be used as features during model development. This is consistent with other molecular properties’ study reported by Comesana et al,4 thus highlighting the need to search for a better way to represent molecules and an algorithm to model oral bioavailability. In addition, different machine-learning algorithms used in the two studies may have resulted in the disparity of performance obtained. Therefore, to build a machine-learning model is not a trivial task. It requires expert domain knowledge to study and select an appropriate set of molecular descriptors and machine-learning algorithm for model development.
Graph Neural Network
On the other hand, the emergence of the graph neural network (GNN) provided a new way of representing molecules as 2D molecular graphs.5 In GNN, each molecule can be represented as a graph, where each atom is represented by a node and each bond is then represented by an edge. After each convolution, the embeddings of each node change carry information of its neighbors. This aided in eliminating the problem of requiring prior knowledge to curate features to build machine-learning models.6,7 GNN enables extraction of abstract structural details of molecules, allowing knowledge of molecules to be captured automatically and be utilized in any prediction task. Presently, there are many variants of GNN-based models8−10 reporting state-of-the-art performance for predicting various molecular properties using publicly available data sets. In 2019, an attentive fingerprint (FP),8 which was based on GNN, was developed and garnered attention for its superior performance over molecular descriptors in predicting various molecular properties. However, the question of whether GNN can perform better than conventional machine-learning models using molecular descriptors remains controversial. For instance, Jiang et al. performed a study comparing GNN models and conventional machine-learning models using molecular descriptors and showed that molecular descriptors outperformed GNN models in various prediction tasks using publicly available data sets.11
Transfer Learning
Furthermore, GNN models suffer a major drawback with regard to the lack of a large data set to train a model. To alleviate this problem, transfer learning strategies can be employed.12 Generally, transfer learning allows one to share its knowledge on one task to predict another task. A strategy that was employed widely in computer vision and natural language processing task is pre-training a model using supervised learning. With this strategy, a model can be built to predict a prior task that is akin to the actual task. This allows better feature extraction and thus enables better prediction performance. In the chemistry domain, the idea of pre-training was used to generate vector embeddings of molecules. For instance, Goh et al. designed ChemNet by pre-training neural networks using large unlabeled chemical databases by treating molecules as images and SMILES.13 On the other hand, Jaeger et al. designed Mol2vec which learned vector representation of molecules represented as SMILES in an unsupervised manner which can be used for other downstream tasks.14
Project Objectives and Scope of Study
In this paper, we demonstrated that GNNs can be used as an alternative to molecular descriptors and FPs for oral bioavailability prediction. To address the issue of small data set size, we explored the use of transfer learning by pre-training the model with a larger data set on a similar task using supervised learning. Given that a close relationship exists between solubility and oral bioavailability, we hypothesized that the GNN models will be able to capture relevant information using supervised learning to predict solubility, which can be translated to oral bioavailability prediction.
Materials and Methods
Solubility Data Set and Oral Bioavailability Data Set
To develop a model for oral bioavailability prediction, we obtained a data set from Wei et al.(2) with the train data set containing 1157 molecules and the test data set containing 290 molecules that were originally obtained from four public data sources. Since there was no agreement in relation to the best cut-off value to be used for this binary classification problem, we decided to adopt the definition described by Wei et al. such that molecules with oral bioavailability more than or equal to 50% are classified as having high oral bioavailability.
For the transfer learning to be successful, we pre-trained the model with a data set that is large and exhibits a close relationship with oral bioavailability. Since GNN is prone to overfitting, training GNNs with a larger data set will allow better generalization. In addition, using a closely related data set allowed the model to learn structural details of molecules that might be transferable to oral bioavailability. We adopted a solubility data set obtained from Hou et al.(15) and the identical train, validation, and test split was used in this study. It contained a total of 9943 non-redundant molecules. However, three molecules were removed as it could not be processed, resulting in a data set consisting of 9940 molecules. Molecules’ data sets can be found in the Supporting Information.
RF and GNN-Based Models
All models were built and trained using an Intel Core i5-12600K with NVIDIA GeForce RTX3060 Ti. A Random Forest Classifier was built using Scikit-learn16 (1.2.0). RF is widely used as a baseline model in different molecular property prediction studies.17,18 RF was shown to be superior to other machine-learning algorithms with advantages when developing a quantitative structure–activity relationship model, such as being less sensitive to hyperparameters and high prediction accuracy. In essence, RF is an ensemble technique that is composed of multiple individual decision trees, and a final prediction result is obtained by averaging the results from each decision tree.
Two GNN-based models were developed using Pytorch Geometric19 (2.1.0) with CUDA (11.3) enabled. First, a graph isomorphism network (GIN) model was developed using the GINConv layer available in Pytorch Geometric. GINConv was developed by Xu et al.(20) and possessed superior representation ability than other GNN-based models such as GCN and GraphSAGE. Second, a graph transformer (GT) model was developed using the TransformerConv layer available in Pytorch Geometric. Inspired by the transformer architecture of Vaswani et al.,21 Shi et al.(22) translated the work of Vaswani et al. and developed the TransformerConv layer to allow the transformer architect to be used on graphs. In addition, another GNN-based model called Vertical GNN was developed by merging GIN and GT convolution techniques into a single model (Figure 1). Embeddings were first generated by passing the graph data into a GT convolution block and subsequently into a GIN convolution block. Finally, the prediction of class labels was obtained by passing the final embeddings into a classifier block.
Figure 1.
Architecture of Vertical GNN models using GINConv and TransformerConv layers.
Molecular Descriptors and FPs for the RF Model
A total of 208 molecular descriptors were generated using an RDKit23 (2022.09.5). Next, we removed molecular descriptors that are zero for all molecules. Molecular descriptors that have zero variance were also removed since they possess little predictive power. As a result, a set of 45 molecular descriptors was obtained for all molecules. The list of molecular descriptors used is available in the Supporting Information. MACCSKeys, Morgan FPs, and RDKit FPs were generated using RDKit. Morgan FPs were generated using a bit size of 1024 and a radius size of two. RDKit FPs were generated using a bit size of 1024 with a minPath of one and maxPath of two.
Generating Nodes and Edge Features for GNN-Based Models
Nodes and edge features were generated using DeepChem24 (2.6.1) and RDKit based on WeaveNet paper.25 Node features include the atom type, formal charge, hybridization, hydrogen bonding, aromatic, degree, number of hydrogens, and chirality. Meanwhile, edge features consist of the bond type, whether they are on same ring, conjugated, and the stereo configuration of the bond.
Hyperparameter Tuning for RF Models and GNN Models Built from Scratch
Hyperparameters for all models were tuned using the Tree-structured Parzen Estimators algorithm provided in Optuna26 (3.1.0) in 30 evaluations with the aim of reducing the loss function. For the solubility data set, the mean squared error from Pytorch Geometric was used. For the oral bioavailability data set, binary cross entropy with logits loss from Pytorch Geometric and log loss from Scikit-Learn were used, respectively, during hyperparameter tuning.
Model Training, Validating, and Testing
Training was conducted to a maximum epoch of 300 with an early stopping algorithm set at 10 epochs to prevent overfitting. All models were trained, validated, and tested using a five-fold cross validation method. The whole process was subsequently repeated five times. All hyperparameters were made available in the Supporting Information.
Transfer Learning Data Set Pre-Processing
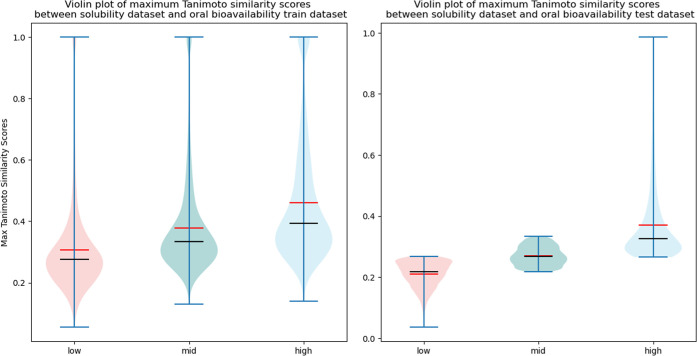
To avoid data leakage, molecules that appeared in both the solubility data set and oral bioavailability test data set were removed from the solubility data set, resulting in the solubility data set size decreasing to 9844. Next, the maximum Tanimoto similarity scores for molecules between the solubility and oral bioavailability data set were calculated using RDKit, and the median Tanimoto similarity scores with respect to the oral bioavailability train and test data set were 0.327 and 0.267, respectively. The solubility data was split up into three different sets with each set containing 5000 molecules and having a different range of similarity scores ranging from low to high. A violin plot, comprising a hybrid of a box plot and kernel density plot, was plotted to show the average, median, and distribution of Tanimoto similarity scores for molecules (Figure 2). The number of solubility molecules to include for pre-training is an empirical value that can be changed to suit different needs. In this study, we decided to use 5000 to ensure that each data set contained sufficient instances for the model to be pre-trained with sufficient information since GNNs are known to learn better with larger data sets. When compared to the oral bioavailability test data set, the median similarity scores for low, mid, and high solubility data sets were 0.217, 0.270, and 0.327, respectively. On the other hand, when compared to the oral bioavailability train data set, the median similarity scores for low, mid, and high solubility data were 0.275, 0.333, and 0.392. The solubility data sets and splitting strategy can be found in the Supporting Information.
Figure 2.
Violin plots of maximum similarity scores between the solubility data set and oral bioavailability data set. The red line indicates the average value, while the black line indicates the median value.
Transfer Learning Models
Vertical GNN was used to build transfer learning models. The classifier block was replaced with a linear block to predict solubility. Hyperparameters were obtained using the train and validation solubility data set from Hou et al. after removing molecules that appeared in the oral bioavailability test data set. Using the hyperparameters obtained previously, models were pretrained at 60 epochs using different similarity levels of the solubility data set (low, mid, high). Generally, we noted that higher epochs of pre-training resulted in better performance during validation (Table S8). However, the value of 60 epochs is empirical and can be changed to correspond to different demands. To further optimize the pre-trained model, we experimented with different learning rates and training epochs. The hyperparameters used for pre-trained models can be found in the Supporting Information.
Evaluation Metrics
Since there is no global consensus as to which metric is the best for a binary classification problem, we employed a combination of four different metrics to evaluate model performance. Log loss measures how close the predicted probability is compared to the true label. A model that correctly returns predicted probability closer to the true label will result in a lower log loss value. Accuracy (Acc) measures the exact match between the predicted label and the true labels. A model that returns predicted labels that are of exact match to the true labels would result in higher accuracy value. F1 score, or balance F-score, takes into consideration precision and recall and measures the harmonic mean between the two factors. A model with a higher F1 score suggests the model simultaneously maximizes precision and recall scores and hence a better model. Lastly, the area under the curve of a receiver operating characteristic (AUC-ROC) curve were calculated and compared. AUC-ROC considers the measure of separability. A model with a high AUC-ROC suggests that the model is capable of distinguishing between classes and is hence a better model. We calculated the four metrics and compared them. The model that did well for the greatest number of metrics was deemed as the best performing model.
Results and Discussion
Prediction Performance between RF Models
Among various features used for RF models, the model with molecular descriptors as its feature resulted in the best prediction performance (Table 1).
Table 1. Prediction Performance for the RF Models Using Different Featuresa.
| molecular descriptor | Morgan FP | RDKit FP | MACCSkeys | |
|---|---|---|---|---|
| log loss | 0.561±0.012 | 0.592 ± 0.012 | 0.610 ± 0.009 | 0.592 ± 0.010 |
| Acc | 0.722±0.016 | 0.684 ± 0.013 | 0.670 ± 0.026 | 0.687 ± 0.019 |
| F1 score | 0.761±0.015 | 0.738 ± 0.020 | 0.724 ± 0.026 | 0.738 ± 0.018 |
| AUC-ROC | 0.784±0.017 | 0.746 ± 0.017 | 0.724 ± 0.022 | 0.742 ± 0.012 |
The bold values represent the best scores. Prediction performance using the oral bioavailability test data set was reported in mean ± standard deviation.
A possible explanation could be because molecular descriptors contain more detailed information ranging from molecular weight to topological information. On the other hand, FPs mainly encode structural details of molecules into bits. Previous molecular property prediction studies had also suggested a similar conclusion whereby molecular descriptors were often better at representing molecules in prediction models. For example, Orosz et al. developed a model to predict adsorption, distribution, metabolism, elimination, and toxicity properties using molecular descriptors and FPs and compared their prediction performance. They reported that the model built using molecular descriptors resulted in superior prediction performance over the model that was built using FPs.27 In another study by Racz and Keserű, a similar conclusion was also derived where the molecular descriptor-based model outperformed the FP-based model for modeling potential drug interactions with cytochrome P450 enzymes.28
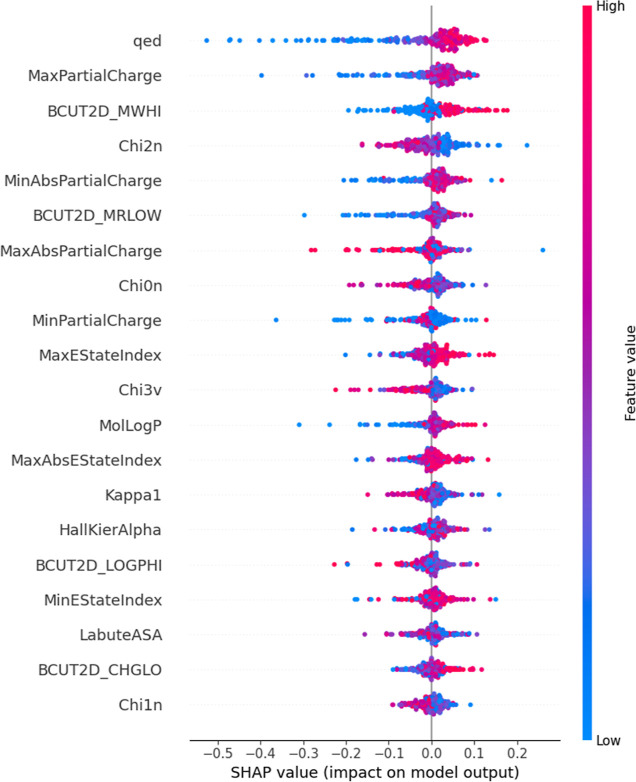
In addition, SHapley Additive exPlanations29 (SHAP) was employed to interpret the model built using molecular descriptors. Briefly, SHAP was developed using game theory. SHAP helps to connect credit allocation and local explanations by calculating Shapley values, thus allowing us to understand a prediction model’s decision. If a feature is of higher importance then a larger Shapley value will be calculated. In addition to Shapley values, Beeswarm plots were plotted to allow for a better interpretation of a model’s decision. In a Beeswarm plot, the molecular descriptors used for modeling are arranged in order of importance, with the most important descriptor being at the top (Figures 3 and S2–S5). For each descriptor in the Beeswarm plot, every molecule is represented as a point. The points are distributed horizontally according to the SHAP value. For example, quantitative estimation of drug-likeness (QED) considers the distribution of molecular properties such as molecular weight, log P, topological surface area, and number of hydrogen bond donors and acceptors and was shown to have the highest predictive power. A molecule with a large QED value (red) resulted in a higher predicted probability of having a high oral bioavailability value. This is expected since a drug-like molecule often exhibits a higher oral bioavailability. Conversely, we noted that a molecule with a small QED value (blue) resulted in a higher predicted probability of having a low oral bioavailability value. Similarly, we also observed a positive correlation between Mol log P and oral bioavailability, which is expected since a higher logP results in better drug permeation.
Figure 3.
Beeswarm plot of top 20 important molecular descriptors for the RF model toward oral bioavailability prediction using the oral bioavailability test data set. Analysis done on the model that was developed from the first fold data set produced using five-fold cross-validation.
In addition, we summarized the number of times a feature appeared within the top five positions in all five models developed during the five-fold cross-validation process. We observed that QED was the most important feature as it appeared in the top position for all five models. The other four common features that appeared the most in order after QED are BCUT2D_MWHI, BCUT2D_MRLOW, MinAbsPartialCharge, and MaxPartialCharge (Figures S6–S10).
Next, we compared the prediction performance of our models with previous studies that studied the prediction of oral bioavailability using the same train and test data set. Wei et al. constructed a consensus RF model using five RF models with 1143 molecular descriptors obtained from Mordred and obtained an average accuracy of 0.793 and an average AUC-ROC score of 0.830. Despite using the same machine-learning algorithm, the RF model constructed in this study with 45 molecular descriptors obtained from RDKit only reported an average accuracy of 0.722 and an average AUC-ROC score of 0.784. The difference in the number of molecular descriptors that were used might have an impact on the model prediction performance. This suggests that perhaps more descriptors will result in a better model. On the other hand, Falcón-Cano et al. developed a model that was based on a different algorithm and included using classification and regression trees, multi-layer perceptron, Naïve Bayes, gradient boosted trees, and support vector machine. Despite using more molecular descriptors (1337) for modeling, Falcón-Cano et al. reported a model with an average accuracy of 0.783 and an average AUC-ROC score of 0.800, which were lower than what Wei et al. had reported. This suggests that using more descriptors for modeling does not necessarily result in better prediction performance and that the machine-learning algorithm might have an impact on prediction performance. As such, this highlights the importance of possessing expert knowledge to carefully curate a set of molecular descriptors and select a relevant machine-learning algorithm to be used for modeling since both factors can affect the prediction performance of models.
Prediction Performance of GNN Models
Among all the GNN-based models, Vertical GNN resulted in the best prediction performance (Table 2). The prediction performance of GT was better than that of GIN, suggesting that the GT architecture was superior in its representation ability. When different convolution techniques were combined into a single model, higher average accuracy was recorded (0.742) compared to that of GNN models with a single convolution technique (0.630–0.663), thus highlighting that the predictive performance of GNN models can be improved using merged convolution techniques.
Table 2. Prediction Performance for Different GNN-Based Modelsa.
| GIN | GT | Vertical GNN | |
|---|---|---|---|
| log loss | 0.677 ± 0.154 | 0.618 ± 0.028 | 0.530±0.053 |
| Acc | 0.630 ± 0.125 | 0.663 ± 0.034 | 0.742±0.036 |
| F1 score | 0.611 ± 0.307 | 0.733 ± 0.027 | 0.778±0.046 |
| AUC-ROC | 0.665 ± 0.185 | 0.705 ± 0.045 | 0.807±0.033 |
Bold values represent the best scores. Prediction performance using the oral bioavailability test data set was reported in mean ± standard deviation.
Comparison between RF and GNN
First, Vertical GNN reported better average scores among the metrics used when compared to those obtained from the RF model constructed with molecular descriptors in this study. However, when standard deviations were taken into consideration, the prediction performance between both models is relatively comparable. Despite that, the benefit of using GNN is the ability to automatically extract relevant features from a raw graph input. In GNN, the molecular structure of a molecule is represented as a graph where information of atoms and bonds is encoded into nodes and edges of a graph, respectively. The training process of GNN automatically extracts relevant features toward the prediction task. This is useful especially in drug chemistry such as de-novo drug synthesis since using explainable artificial intelligence tools such as GNNExplainer30 can reveal the important substructure of the molecules toward the molecular prediction tasks.
On the other hand, developing RF models using molecular descriptors requires labor-intensive feature selection. Feature selection is important as it reduces the number of molecular descriptors and thus increases model interpretability. For example, having multiple co-related features may result in features being wrongly classified as significant during the interpretation of the model.31 Feature selection also reduces chances of overfitting from non-redundant molecular descriptors which, in turn, can improve model prediction performance.32,33 In addition, molecular descriptors are forms of mathematical representations of molecules that were derived from algorithms and may not be the best way to represent a molecule.34 For example, QED, a feature that was highlighted to be of highest importance in this study, is derived from multiple functions using eight molecular properties. However, studies revealed that QED may not be practical as a feature for modeling since the properties used to determine QED were undistinguishable between drug and non-drug molecules.35,36
Next, we also computed the computational efficiency of the model. RF demonstrated superiority in terms of computational efficiency, taking less than a second to train. On the other hand, GNN, with different model architectures, resulted in different computational efficiencies (Table 3).
Table 3. Training Runtime of Different Modelsa.
| RF |
GNN |
||||||
|---|---|---|---|---|---|---|---|
| molecular descriptors | Morgan FP | RDKit FP | MACCS-keys | GIN | GT | Vertical GNN | |
| time/s | 1.529 ± 0.024 | 1.163 ± 0.045 | 0.277 ± 0.005 | 0.687 ± 0.010 | 7.334 ± 0.609 | 17.138 ± 2.317 | 12.449 ± 0.640 |
All runs were repeated 5 times and the measured times were reported in mean ± standard deviation.
Comparing the computational times of different RF models, we noted that despite having a smaller dimension size, molecular descriptor-based RF took a longer time for training to be completed. A possible reason for such observation could be due to the max depth value. Max depth signifies the maximum depth of the tree in RF. Molecular descriptor-based RF was shown to have the highest max depth value after hyperparameter optimization, and hence, training time was recorded to be slightly longer than the rest of the RF models.
For GNN models, GT took the longest, averaging at 17.1 s per run. A possible reason could be the hidden size. GT was found to have the largest hidden size value after hyperparameter optimization as opposed to GIN and Vertical GNN. As such, it is expected that longer training is required for GT. When comparing between the best models of RF and GNN, we observed that Vertical GNN required a longer time, approximately 8 times longer, to train than the molecular descriptor-based RF model. Despite that, the time to train Vertical GNN was relatively short, finishing in an average of 12.4 s per run. Nevertheless, we should also factor in that longer time is required for feature selection in developing the RF model. In addition, having features automatically extracted by using GNN removes the need for the user to possess expert domain knowledge for feature selection, hence highlighting the need to balance the trade-off between computational efficiency, time, and knowledge required for feature selection depending on the user’s needs.
Prediction Performance of Transfer Learning Models
When the prediction performance of GNN models was compared to that of Wei et al.’s model using the same test data set, our model reported poorer average prediction performance across all metrics used. A possible explanation could be because GNN models were trained with a small data set, which resulted in poor generalizability and hence poorer performance of the model. To alleviate this problem, we explored the use of transfer learning. The aim of transfer learning is to pre-train a model with a task and transfer the knowledge gained to predict downstream tasks. We hypothesized that pre-training a model with a prior task that is similar to a downstream task can improve the prediction performance of the model. Since various studies37,38 indicated a close relationship between solubility and oral bioavailability, we pre-trained GNN models with a larger data set on predicting solubility to improve the performance toward oral bioavailability prediction.
One important aspect of transfer learning is the data set used. Therefore, we evaluated the importance of data similarity and data set size relative to the prediction performance of the model. In this section, we utilized the Vertical GNN model architecture as it reported better prediction performance among various GNN models listed above, suggesting better representation ability than the others. We froze the parameters of the feature extraction blocks (GIN + GT convolution block) while allowing the classifier block to update during training so that correct prediction can be given. We trained the pre-trained models with data sets of different similarities (low, mid, high) and different sizes (5000 vs 9844) and noted better performance when using high similarity data (Table S9). To ensure optimal performance, we fine-tuned the model further by experimenting with different numbers of training epochs before triggering the early stopping mechanism as well as contrasting learning rates to improve the prediction model performance (Table 4). As noted in the work mentioned above, high similarity data resulted in the best performance, so we decided to fine-tune the model that was pre-trained with high similarity data.
Table 4. Hyperparameter Tuning Results for the Transfer Learning Vertical Modela.
| number of training epochs | 10 | 15 | 20 | |
|---|---|---|---|---|
| learning rate ÷ 5 | log loss | 0.626 ± 0.026 | 0.636 ± 0.031 | 0.650 ± 0.034 |
| Acc | 0.647 ± 0.033 | 0.637 ± 0.055 | 0.635 ± 0.050 | |
| F1 score | 0.671 ± 0.093 | 0.646 ± 0.133 | 0.645 ± 0.124 | |
| AUC-ROC | 0.674 ± 0.042 | 0.674 ± 0.045 | 0.672 ± 0.043 | |
| learning rate ÷ 10 | log loss | 0.622±0.030 | 0.625±0.033 | 0.629±0.036 |
| Acc | 0.656±0.050 | 0.656±0.052 | 0.649±0.050 | |
| F1 score | 0.675±0.108 | 0.678±0.107 | 0.663±0.117 | |
| AUC-ROC | 0.680±0.042 | 0.681±0.044 | 0.680±0.046 |
Vertical GNN models were pre-trained with a solubility data set of high similarity levels for 60 epochs with different learning rates and trained with different epochs before triggering the early stopping mechanism. Prediction performances were reported in mean ± standard deviation using the five-fold cross-validation method and validation data set. Bold values represent the best scores across different learning rates.
We observed that using a learning rate which is 10 times smaller than the original learning rate resulted in a better performance across all training epochs during validation. This suggests that allowing model to learn at a slower learning rate may allow a pre-trained model to pick up relevant details regarding oral bioavailability while still retaining the main bulk of the information that was learnt previously. Finally, we compared the prediction performance of the transfer learning model that was tuned with the best hyperparameters with other models that were published recently (Table 5). It is worth noting that we used the same train and test data set as Wei et al. and Falcón-Cano et al. and the results were reproduced from Wei et al. Unfortunately, their results did not include standard deviations for comparison. Nevertheless, by comparing the average values, our transfer learning model reported an average accuracy of 0.797, which is a slight improvement from Wei’s and Falcón-Cano’s models. Moreover, our transfer learning model reported highest average F1 score (0.840) and AUC-ROC (0.867). When compared to the prediction performance of the Vertical GNN model that was built from scratch, we observed an improvement in prediction performance across all metrics. This suggests that transfer learning using a closely related data set such as solubility can indeed improve prediction performance of oral bioavailability prediction. The pre-trained model could potentially be used for other downstream tasks that are closely related to solubility. However, to perform transfer learning, it is noted that an additional step of pre-training is required and undoubtedly will result in an increase in computational cost and time.
Table 5. Prediction Performance for Our Best Model against Other Established Modelsa.
| Vertical GNN | transfer learning model | Wei et al2 | Falcón-Cano et al2,3 | |
|---|---|---|---|---|
| log loss | 0.530 ± 0.053 | 0.467 ± 0.007 | NA | NA |
| Acc | 0.742 ± 0.036 | 0.797 ± 0.005 | 0.793 | 0.783 |
| F1 score | 0.778 ± 0.046 | 0.840 ± 0.006 | 0.817 | NA |
| AUC-ROC | 0.807 ± 0.033 | 0.867 ± 0.003 | 0.830 | 0.800 |
Transfer learning model was pre-trained with 60 epochs using a high similarity solubility data set and subsequently trained with a learning rate that was 10 times smaller than the original learning rate and a training epoch of 15 before the trigger of early stopping mechanism. Bold values represent the best scores. Prediction performances were reported in mean ± standard deviation using the oral bioavailability test data set. Mean values were reported for Wei et al. and Falcón-Cano et al.
Analysis of Chemical Space and Applicability Domain of the Transfer Learning Model
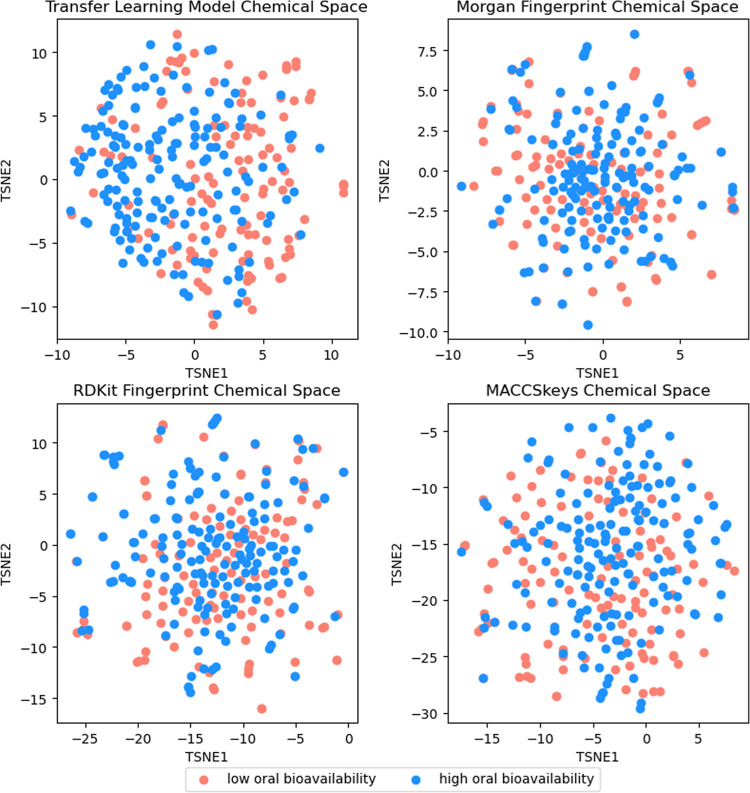
To understand the chemical space generated by the transfer learning model, we extracted the embeddings right after the graph convolution techniques were operated on the test molecules. We obtained a vector with a size of 490 for each test molecule and plotted the chemical space using T-distributed Stochastic Neighbor Embedding39 (T-SNE). T-SNE employs a technique known as Kulbeck–Liebler Divergence. T-SNE enables the distances between distributions to be reduced and hence converts high-dimensionality data to low-dimensionality data. For comparison, we also conducted a similar analysis on various FPs that encode structural information (Figure 4). Such FPs include Morgan FPs, RDKit FPs, and MACCSkeys FPs. Surprisingly, despite having a smaller vector size than Morgan and RDKit FPs, the embeddings generated by the transfer learning model showed a clearer distinction between test molecules of high and low oral bioavailability. This suggests that the transfer learning model is capable of learning and extracting information relevant to oral bioavailability that was learnt during the training process.
Figure 4.
Chemical space generated from embeddings obtained from the transfer learning model and various FPs. Dimensionality reduction conducted using T-SNE with a perplexity of 50, number of iterations of 5000, and learning rate of 10.
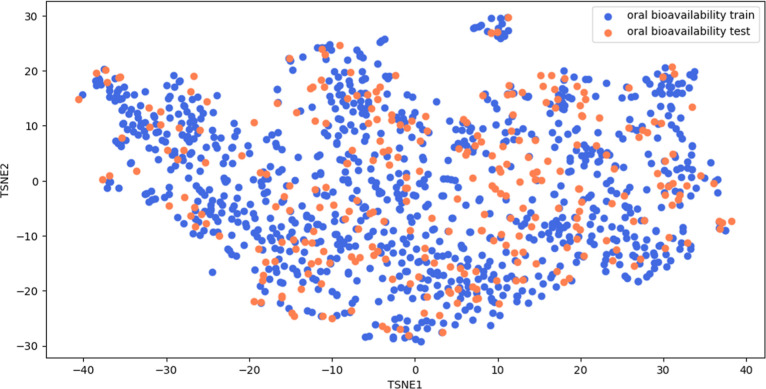
Next, we analyzed the applicability domain of the transfer learning model. We extracted the embeddings generated from the transfer learning model and reduced its dimension to two using T-SNE. We plotted the chemical space and observed that the oral bioavailability train and test molecules exist within the same chemical space (Figure 5). This indicates that reliable prediction can be made for those test molecules. However, a potential caveat of our study is that no test molecules were spotted to be distinctively located out of the chemical space of the oral bioavailability train data set. As a result, we were unable to analyze if our model can accurately predict the oral bioavailability of a molecule that exists outside the chemical space. Future work can be done to include molecules that are outside the chemical space to test the robustness of the model.
Figure 5.
T-SNE plot of oral bioavailability train and test data set with a perplexity of 50, number of iterations of 5000, and learning rate of 10.
Conclusions
In conclusion, we showed that GNN-based models can be exploited for automatic feature selection to predict oral bioavailability. This eliminates the need for expert domain knowledge and time to carry out feature selection for modeling purposes. To further improve the prediction performance of Vertical GNN, we trained Vertical GNN using a larger data set to predict solubility, allowing the model to automatically extract the important substructure of molecules. Next, we fine-tuned the same model to predict oral bioavailability and managed to achieve better prediction performance than a model that was built from scratch. Like conventional machine-learning models, GNN models are also termed as “black box” models due to their low interpretability. Similar to how SHAP analysis is carried out to explain the decision made by conventional machine-learning models, different ways have been explored to interpret GNN models. For instance, Ying et al.(30) devised a method known as GNNExplainer, which could identify important substructures of graphs that can in turn affect the prediction choices made by the model. Future works could explore the utilization of an even larger data set of higher similarity molecules to improve prediction performance. To assess the robustness of the model, future studies can include test molecules outside of the applicability domain of the model. In addition, GNNExplainer can be used to provide insights into how structures affect oral bioavailability, or other bioactivities of interest, which could aid in the drug discovery process.
Acknowledgments
This research is supported by the Ministry of Education, Singapore, under its Academic Research Fund Tier 1 RG83/20, RG82/22.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.3c00554.
Hyperparameters of RF and GNN models, list of molecular descriptors for the RF model, solubility data set splitting strategy, prediction performance for pre-training epochs and data set similarity comparison during validation and testing, and SHAP analysis of molecular descriptor-based RF models (PDF)
SMILES: Oral bioavailability and solubility data set (XLSX)
Author Contributions
S.S.S.N. is the first author, who wrote the codes and prepared most of the manuscript. Y.L. supervised the study and revised the manuscript. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Notes
All data and codes are made available on GitHub: https://github.com/sherwin97/Hob-Pred-using-Transfer-Learning.
Supplementary Material
References
- Kennedy T. Managing the drug discovery/development interface. Drug Discov. Today 1997, 2, 436–444. 10.1016/s1359-6446(97)01099-4. [DOI] [Google Scholar]
- Wei M.; Zhang X.; Pan X.; Wang B.; Ji C.; Qi Y.; Zhang J. Z. H. HobPre: Accurate Prediction of Human Oral Bioavailability for Small Molecules. J. Cheminf. 2022, 14, 1. 10.1186/s13321-021-00580-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falcón-Cano G.; Molina C.; Cabrera-Pérez M. Á. ADME Prediction with KNIME: Development and Validation of a Publicly Available Workflow for the Prediction of Human Oral Bioavailability. J. Chem. Inf. Model. 2020, 60, 2660–2667. 10.1021/acs.jcim.0c00019. [DOI] [PubMed] [Google Scholar]
- Comesana A. E.; Huntington T.; Scown C. D.; Niemeyer K. E.; Rapp V. A Systematic Method for Selecting Molecular Descriptors as Features When Training Models for Predicting Physiochemical Properties. Fuel 2022, 321, 123836. 10.1016/j.fuel.2022.123836. [DOI] [Google Scholar]
- Reiser P.; Neubert M.; Eberhard A.; Torresi L.; Zhou C.; Shao C.; Metni H.; van Hoesel C.; Schopmans H.; Sommer T.; Friederich P. Graph Neural Networks for Materials Science and Chemistry. Commun. Mater. 2022, 3, 93. 10.1038/s43246-022-00315-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshavarzi Arshadi A.; Salem M.; Firouzbakht A.; Yuan J. S. MolData, a Molecular Benchmark for Disease and Target Based Machine Learning. J. Cheminf. 2022, 14, 10. 10.1186/s13321-022-00590-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan Y.; Edwards J. S.; Dwivedi Y. K. Artificial Intelligence for Decision Making in the Era of Big Data—Evolution, Challenges and Research Agenda. Int. J. Inf. Manag. 2019, 48, 63–71. 10.1016/j.ijinfomgt.2019.01.021. [DOI] [Google Scholar]
- Xiong Z.; Wang D.; Liu X.; Zhong F.; Wan X.; Li X.; Li Z.; Luo X.; Chen K.; Jiang H.; Zheng M. Pushing the Boundaries of Molecular Representation for Drug Discovery with the Graph Attention Mechanism. J. Med. Chem. 2020, 63, 8749–8760. 10.1021/acs.jmedchem.9b00959. [DOI] [PubMed] [Google Scholar]
- Kong Y.; Zhao X.; Liu R.; Yang Z.; Yin H.; Zhao B.; Wang J.; Qin B.; Yan A. Integrating Concept of Pharmacophore with Graph Neural Networks for Chemical Property Prediction and Interpretation. J. Cheminf. 2022, 14, 52. 10.1186/s13321-022-00634-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang K.; Swanson K.; Jin W.; Coley C.; Eiden P.; Gao H.; Guzman-Perez A.; Hopper T.; Kelley B.; Mathea M.; Palmer A.; Settels V.; Jaakkola T.; Jensen K.; Barzilay R. Analyzing Learned Molecular Representations for Property Prediction. J. Chem. Inf. Model. 2019, 59, 3370–3388. 10.1021/acs.jcim.9b00237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D.; Wu Z.; Hsieh C.-Y.; Chen G.; Liao B.; Wang Z.; Shen C.; Cao D.; Wu J.; Hou T. Could Graph Neural Networks Learn Better Molecular Representation for Drug Discovery? A Comparison Study of Descriptor-Based and Graph-Based Models. J. Cheminf. 2021, 13, 12. 10.1186/s13321-020-00479-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J.; Cui G.; Hu S.; Zhang Z.; Yang C.; Liu Z.; Wang L.; Li C.; Sun M. Graph Neural Networks: A Review of Methods and Applications. AI Open 2020, 1, 57–81. 10.1016/j.aiopen.2021.01.001. [DOI] [Google Scholar]
- Goh G. B.; Siegel C.; Vishnu A.; Hodas N.. Using Rule-Based Labels for Weak Supervised Learning. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2018.
- Jaeger S.; Fulle S.; Turk S. Mol2vec: Unsupervised Machine Learning Approach with Chemical Intuition. J. Chem. Inf. Model. 2018, 58, 27–35. 10.1021/acs.jcim.7b00616. [DOI] [PubMed] [Google Scholar]
- Hou Y.; Wang S.; Bai B.; Chan H. C. S.; Yuan S. Accurate Physical Property Predictions via Deep Learning. Molecules 2022, 27, 1668. 10.3390/molecules27051668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Müller A.; Nothman J.; Louppe G.; Prettenhofer P.; Weiss R.; Dubourg V.; Vanderplas J.; Passos A.; Cournapeau D.; Brucher M.; Perrot M.; Duchesnay É.. Scikit-Learn: Machine Learning in Python. arXiv [cs.LG], 2012. [Google Scholar]
- Xie L.; Xu L.; Kong R.; Chang S.; Xu X. Improvement of Prediction Performance with Conjoint Molecular Fingerprint in Deep Learning. Front. Pharmacol. 2020, 11, 11. 10.3389/fphar.2020.606668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Random Forests. Mach. Learn. 2001, 45, 5–32. 10.1023/a:1010933404324. [DOI] [Google Scholar]
- Fey M.; Lenssen J. E.. Fast Graph Representation Learning with PyTorch Geometric, 2019. arXiv [cs.LG]. http://arxiv.org/abs/1903.02428.
- Xu K.; Hu W.; Leskovec J.; Jegelka S.. How Powerful Are Graph Neural Networks? arXiv:1810.00826, 2019. [Google Scholar]
- Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser L.; Polosukhin I.. Attention Is All You Need, 2017. https://arxiv.org/abs/1706.03762.
- Shi Y.; Huang Z.; Feng S.; Zhong H.; Wang W.; Sun Y.. Masked Label Prediction: Unified Message Passing Model for Semi-Supervised Classification. arXiv:2009.03509, 2021. [Google Scholar]
- RDKit: Open-Source Cheminformatics Software. https://www.rdkit.org (accessed 2023 03 20).
- Ramsundar B.; Eastman P.; Walters P.; Pande V.. Deep Learning for the Life Sciences: Applying Deep Learning to Genomics, Microscopy, Drug Discovery, and More; O’Reilly Media, 2019. [Google Scholar]
- Kearnes S.; McCloskey K.; Berndl M.; Pande V.; Riley P. Molecular Graph Convolutions: Moving beyond Fingerprints. J. Comput. Aided Mol. Des. 2016, 30, 595–608. 10.1007/s10822-016-9938-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akiba T.; Sano S.; Yanase T.; Ohta T.; Koyama M.. Optuna: A next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; ACM: New York, NY, USA, 2019.
- Orosz Á.; Héberger K.; Rácz A. Comparison of Descriptor- and Fingerprint Sets in Machine Learning Models for ADME-Tox Targets. Front. Chem. 2022, 10, 10. 10.3389/fchem.2022.852893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rácz A.; Keserű G. M. Large-Scale Evaluation of Cytochrome P450 2C9 Mediated Drug Interaction Potential with Machine Learning-Based Consensus Modeling. J. Comput. Aided Mol. Des. 2020, 34, 831–839. 10.1007/s10822-020-00308-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundberg S.; Lee S.-I.. A unified approach to interpreting model predictions. arXiv [cs.AI], 2017. [Google Scholar]
- Ying R.; Bourgeois D.; You J.; Zitnik M.; Leskovec J. GNNExplainer: Generating Explanations for Graph Neural Networks. Adv. Neural Inf. Process. Syst. 2019, 32, 9240–9251. [PMC free article] [PubMed] [Google Scholar]
- Strobl C.; Boulesteix A.-L.; Zeileis A.; Hothorn T. Bias in Random Forest Variable Importance Measures: Illustrations, Sources and a Solution. BMC Bioinf. 2007, 8, 25. 10.1186/1471-2105-8-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y. A Comparative Study on Feature Selection Methods for Drug Discovery. J. Chem. Inf. Comput. Sci. 2004, 44, 1823–1828. 10.1021/ci049875d. [DOI] [PubMed] [Google Scholar]
- Newby D.; Freitas A. A.; Ghafourian T. Pre-Processing Feature Selection for Improved C&RT Models for Oral Absorption. J. Chem. Inf. Model. 2013, 53, 2730–2742. 10.1021/ci400378j. [DOI] [PubMed] [Google Scholar]
- Wills T. J.; Polshakov D. A.; Robinson M. C.; Lee A. A. Impact of Chemist-in-the-Loop Molecular Representations on Machine Learning Outcomes. J. Chem. Inf. Model. 2020, 60, 4449–4456. 10.1021/acs.jcim.0c00193. [DOI] [PubMed] [Google Scholar]
- Beker W.; Wołos A.; Szymkuć S.; Grzybowski B. A. Minimal-Uncertainty Prediction of General Drug-Likeness Based on Bayesian Neural Networks. Nat. Mach. Intell. 2020, 2, 457–465. 10.1038/s42256-020-0209-y. [DOI] [Google Scholar]
- Lee K.; Jang J.; Seo S.; Lim J.; Kim W. Y. Drug-Likeness Scoring Based on Unsupervised Learning. Chem. Sci. 2022, 13, 554–565. 10.1039/d1sc05248a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink C.; Sun D.; Wagner K.; Schneider M.; Bauer H.; Dolgos H.; Mäder K.; Peters S.-A. Evaluating the Role of Solubility in Oral Absorption of Poorly Water-Soluble Drugs Using Physiologically-Based Pharmacokinetic Modeling. Clin. Pharmacol. Ther. 2020, 107, 650–661. 10.1002/cpt.1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ndayishimiye J.; Kumeria T.; Popat A.; Blaskovich M. A. T.; Falconer J. R. Understanding the Relationship between Solubility and Permeability of γ-Cyclodextrin-Based Systems Embedded with Poorly Aqueous Soluble Benznidazole. Int. J. Pharm. 2022, 616, 121487. 10.1016/j.ijpharm.2022.121487. [DOI] [PubMed] [Google Scholar]
- van der Maaten L. J. P.; Hinton G. E. Visualizing Data Using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.