Diffusion-enhanced characterization of 3D chromatin structure reveals its linkage to gene regulatory networks and the interactome

Abstract

The interactome networks at the DNA, RNA, and protein levels are crucial for cellular functions, and the diverse variations of these networks are heavily involved in the establishment of different cell states. We have developed a diffusion-based method, Hi-C to geometry (C_TG), to obtain reliable geometric information on the chromatin from Hi-C data. C_TG produces a consistent and reproducible framework for the 3D genomic structure and provides a reliable and quantitative understanding of the alterations of genomic structures under different cellular conditions. The genomic structure yielded by C_TG serves as an architectural blueprint of the dynamic gene regulatory network, based on which cell-specific correspondence between gene–gene and corresponding protein–protein physical interactions, as well as transcription correlation, is revealed. We also find that gene fusion events are significantly enriched between genes of short C_TG distances and are thus close in 3D space. These findings indicate that 3D chromatin structure is at least partially correlated with downstream processes such as transcription, gene regulation, and even regulatory networking through affecting protein–protein interactions.

The 3D architecture of chromatin is crucial to the functionality of 1D DNA sequences (Oudelaar and Higgs 2021) and is shown to be involved in many critical biological processes, such as gene regulation, cell fate decisions, and even evolution (Bonev and Cavalli 2016). Sharing fixed genetic inheritance, the organization of genomic structure is hierarchical, and the primary domains that make up the hierarchical organization, such as compartments and topologically associating domains (TADs), are largely conserved across cell types (Rao et al. 2014). On the other hand, the variations of chromatin structures among different cell states are pertinent to their distinct genomic function (Bonev and Cavalli 2016; Wang et al. 2023). The role of 3D chromatin structure in gene expression regulation has been shown through the importance of loop, TAD formation, and compartmentalization (Bonev and Cavalli 2016). Various types of genomic changes are relevant to genetic disorders and can lead to genomic diseases such as cancer (Corces and Corces 2016; Li et al. 2020). However, the concrete correlation between 3D architecture and its function has not been completely resolved.

Hi-C data provide us with genome-wide unbiased profiling of genomic structure. The great success of high-throughput sequencing technology makes it possible to obtain Hi-C data with high throughput. However, the quality and reproducibility of raw Hi-C data are affected by technical and biological bias, and the characterization of the genomic geometry requires normalization tools. A number of normalization algorithms have been developed to remove unwanted systematic bias (Imakaev et al. 2012; Knight and Ruiz 2013; Shavit and Lio 2014). However, the unpredictable technical bias that mainly comes from insufficient sampling remains unaddressed, resulting in dubiously weak contact strengths and random noise. The correlation between raw matrices and matrices normalized by different algorithms increases with the sequencing depth (Han and Wei 2017), indicating the need for sufficient sampling. Unfortunately, the randomly directed noise conceals the real biological proximity information and distorts the characterization of the chromatin structures among different cell states, which renders great difficulties to downstream studies at transcriptional and translational levels.

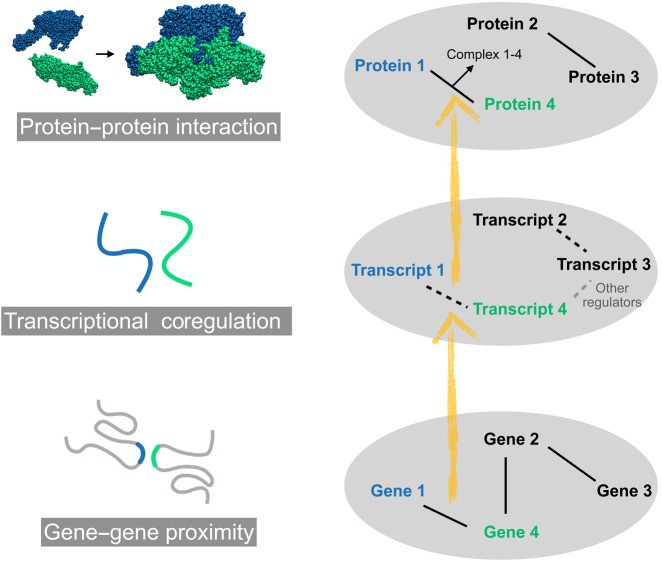
The dynamics of 3D genomic structure is related with its tissue-specific function in gene regulation (Oudelaar and Higgs 2021). The central dogma states that genetic information flows from DNA to RNA to protein. Similarly, an increasing number of novel and tissue-specific protein–protein interactions (PPIs) are also being detected (Huttlin et al. 2021; Kim et al. 2021; Swaney et al. 2021). The protein interactome shows great variance across cell types, which is important to shape cell specificity and to respond to external and internal signals. To understand the mechanisms of tissue-specific gene regulation and functionality, integrating and analyzing gene regulatory networks and the interactome at multiple levels (from DNA to RNA to protein) is necessary. The accumulation of high-throughout interactome data provides feasibility to decipher and understand the gene regulatory network.

Results

Overview of C_TG

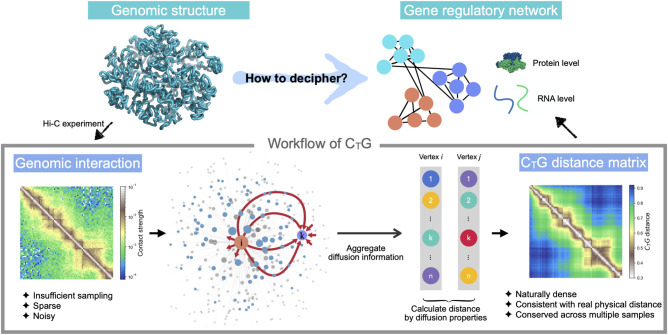
We proposed Hi-C to geometry (C_TG), a diffusion-based algorithm, to treat the technical insufficiency and uncover the geometric structure from Hi-C data (Fig. 1). There are several algorithms using a diffusion process to denoise and enhance the biological networks (Cao et al. 2014; Wang et al. 2018). Inspired by these methods, C_TG takes the Hi-C contact matrix as the adjacency matrix of a graph and outputs a C_TG distance matrix. To eliminate the impact of systematic biases, such as GC bias and restriction enzymes, the Hi-C contact matrix is normalized by ICE (Imakaev et al. 2012). The main inspiration of the C_TG algorithm stems from the physical succession of the genomic structure. It is suggested that to construct a valid Hi-C contact matrix, 80% of loci should have at least 1000 valid reads (Rao et al. 2014). The quantity of valid reads is insufficient compared with the quantity of pairs of loci. Therefore, we alleviate the insufficiency of Hi-C contact matrix by a diffusion-based method that quantifies the information transmission on the corresponding graph and integrates neighboring information. Concretely, we quantify the diffusion property of each genomic locus to all other genomic loci by integrating k-step (k = 1, 2, 3, ……) transition probability matrices derived from a Hi-C contact matrix (see Methods). Taking all other genomic loci into consideration, the diffusion property is hence defined based on global information of the Hi-C contact matrix. As Hi-C contact matrix and the graph share one-to-one correspondence, the physical succession of the genomic structure suggests that the proximal genomic loci should share similar diffusion properties. We also showed in the next section that genomic loci with a short C_TG distance are indeed proximal in physical space and vice versa. A C_TG distance matrix is constructed based on the similarity of the diffusion property between genomic loci in the Hi-C contact map. Except for self-distance, the calculation of C_TG distance (L1 distance between rows of transition probability matrix) ensures the matrix elements are nonzeros. Similar with Hi-C contact probability matrix, a C_TG contact probability matrix is constructed based on the rank of a C_TG distance matrix (see Methods) that proximal loci have higher C_TG contact probability; approximating distributions for C_TG distance are thus not required. C_TG is an entirely physical-based method that excludes external randomness as much as possible and is not limited to any subset of Hi-C data.

Figure 1.

Schematic overview of C_TG. The sparse Hi-C contact matrix is the starting data type of C_TG. Taking the Hi-C contact matrix as the adjacency matrix of a graph, C_TG uses a diffusion-based strategy to uncover the geometry of genomic structure from Hi-C data. C_TG quantifies the diffusion property of each vertex by aggregating global diffusion information from the vertex to other vertices, respectively (as the red arrows illustrate). The C_TG distance between pairwise vertices is calculated by the similarity of their diffusion properties. C_TG allows for a genome-wide insight into deciphering the gene regulation information coded in genomic structure.

Using this approach, we investigated the functionality of gene–gene proximity in genomic structure and discovered the correspondence of gene network architecture at the transcriptional and translational levels. As the functions of DNA are associated with its transcriptional and translational products, we correlate here the genomic proximity with RNA coregulation and PPIs along the flow of central dogma. We found that genes that form cancer-specific gene–gene interactions (GGIs) in genomic structure tend to be largely involved in cancer-related pathways, and their transcript products are more likely to form gene fusion. Our following results reveal a consistent interactome framework across the DNA, RNA, and protein levels. Cell-specific GGIs are related to cell-specific PPIs, whose biological functions are correlated with the establishment of cell specificity. 3D genomic structure can be crucial for understanding how the coding information on the cell type–specific PPI is stored and realized given that the interacting molecules can change significantly with the change of cellular state even for the same cell type.

Validation of C_TG

We showed below that C_TG distance faithfully reproduces spatial distance and thus provides information on the geometry of the genome. C_TG aims to recover a steady genomic structural geometry excluding any stochastic sources.

One way to test whether a sequencing-based method such as Hi-C can faithfully reproduce geometric structure information is to make a comparison with fluorescence in situ hybridization (FISH) imaging data (Su et al. 2020), as the latter provides direct spatial position information of individual loci. Su et al. (2020) provided high-resolution imaging data on the coordinates at 50-kb resolution for Chr 2 and Chr 21 of human lung fibroblast (IMR-90) cells (from the GRCh38 assembly). The median spatial distance for 700 cells between pairs of imaged loci is thus a physical distance measurement (Fig. 2A,B, right). Taking the Hi-C data of IMR-90 (Rao et al. 2014), one can perform a direct comparison between the imaging spatial distance and the inverse contact probability (with logarithm transformation), and the Pearson correlation coefficients are 0.790 and 0.897 for Chr 2 and Chr 21, respectively, which is, to some extent, satisfactory. In contrast, as shown in Figure 2C, the calculation of the C_TG distance matrix (Fig. 2A,B, left) improves its linear correlation with the physical distance measurement, and the corresponding Pearson correlation coefficients with the imaging spatial distance matrix reach 0.952 and 0.930, respectively. To exclude the impact of 1D genomic distance, we also calculated the corresponding Pearson correlation coefficients with the imaging spatial distance matrix at different 1D genomic distances; C_TG distance remains in high correlation with imaging spatial distance at ∼50 Mb. (Supplemental Fig. S1). These results show that the C_TG method provides a more accurate calibration between two different experimental methods and that the distance metrics generated by the C_TG method reproduce those observed by superresolution experiment. C_TG works on ChIA-PET as well (Supplemental Fig. S2). For Chr 2, the corresponding Pearson correlation coefficients between the C_TG distance derived from ChIA-PET data and the median spatial distance reach 0.911 and 0.877 using CTCF and RNAPII, respectively.

Figure 2.

Validation of C_TG. (A) The Hi-C contact matrix (left), C_TG distance matrix (middle), and the median spatial distance matrix (right) of Chr 2 (resolution of 50 kb). (B) The Hi-C contact matrix (left), C_TG distance matrix (middle), and the median spatial distance matrix (right) of Chr 21 (resolution of 50 kb). (C) The correlation between the C_TG distance matrix and the median spatial distance matrix of Chr 2 and Chr 21. (D) The Spearman's correlation for the genomic sequence distance (top) and for the individual genomic region (bottom) between pairwise contact matrices derived from (1) normal colon tissue samples, (2) tumor colon tissue samples, (3) different numbers of 293 cells, and (4) repeated experiments on 293 cells. (***) P-value < 10⁻³⁰⁰ (t-test). (E) The MD plots between two normal colon tissue samples in view of genomic sequence distance.

We also found that the flexible 2D binning method Serpentine (Baudry et al. 2020) performs well, and the corresponding Pearson correlation coefficient with the imaging spatial distance matrix for Chr 21 reaches 0.939. However, the program faces difficulties for a large Hi-C system (Supplemental Fig. S3). It is not suitable for ChIA-PET data as well.

The results of C_TG are also consistent with known precise cis-regulatory interactions, such as promoter-centered interactions detected by Capture Hi-C (Jung et al. 2019) and enhancer–promoter interactions from EnhancerAtlas (Gao and Qian 2019). Taking IMR-90 as an example (from the hg19 assembly), the long-range cis-regulatory interactions (greater than megabases) may be weak or even undetected in raw Hi-C data at 40-kb resolution; these interactions are more significant treated by C_TG (Supplemental Figs. S4, S5). The Hi-C contact matrix contains more details than it intuitively shows. A/B compartments and TADs can also be found from this analysis (Supplemental Fig. S6). We also transformed the coordinates of precise cis-regulatory interactions from hg19 to GRCh38 using UCSC liftOver (Kuhn et al. 2013) and performed similar analyses. As shown in Supplemental Figure S7, the results of C_TG using GRCh38 are consistent with results using the hg19 reference. We used the hg19 reference genome for following analyses.

C_TG reveals a steady genomic structural geometry

We evaluate the robustness of the C_TG contact propensity map by applications to different samples and compare the Hi-C data derived from (1) normal colon tissue samples of different individuals (Johnstone et al. 2020), (2) tumor colon tissue samples (Johnstone et al. 2020), (3) different numbers of HEK293 cells (sample 0923-2 and 0923-4), and (4) repeated experiments on HEK293 cells (sample 0923-4 and 1002-5). The robustness of C_TG is assessed by calculating the Spearman's correlation coefficient of spatial interactions from different samples at various genomic distances. Such a calculation is equivalent to calculating the Spearman's correlation coefficient of diagonal elements of Hi-C maps. For a Hi-C contact map treated after ICE normalization, the correlations between different samples decrease sharply as genomic distance increases (Fig. 2D, top), indicating that the normalized Hi-C contact map is of high confidence level at scales up to ∼5 Mb but not longer. In contrast, the correlations of C_TG contact maps are significantly higher and hardly decrease with the genomic distance. We also compared the Spearman's correlation coefficient for individual genomic regions between Hi-C and C_TG contact maps, equivalent to calculating the Spearman's correlation coefficient of each row of different contact maps (Fig. 2D, bottom), where the latter also displays a higher consistency than the former. In addition, the systematic bias between different data sets for the Hi-C and C_TG contact map was quantified by a minus, or difference, versus distance plot (MD plot) (Stansfield et al. 2018), to visualize the differences between the two data sets, accounting for the linear genomic distance between interacting genomic regions. M is defined as the fold-change between two Hi-C data sets, with its element M_ij = log₂(IF¹_ij/IF²_ij), where IF¹_ij and IF²_ij are contact strengths between pairs of genomic regions from two data sets. D is defined as the 1D genomic distance of pairwise genomic regions. In this way, the systematic bias between different data sets is reflected by the deviation of M from the M = 0 baseline. The MD plot (Fig. 2E) of the C_TG contact map is approximately symmetric to the about M = 0 baseline without any prior fitting. In contrast, for the Hi-C contact map, only 30% of nonzero elements can be faithfully calculated owing to the limitation of sparse data. The distribution obtained for the Hi-C contact map (Fig. 2E, bottom) deviates significantly from the baseline, indicating the impact of systematic bias.

We note here that the unprocessed Hi-C contact map is subject to large noise owing to incomplete statistics, and the large variance of long-range interactions (>5 Mb) among similar samples indicates that weak interactions or long-range interactions tend to be unreliable. Therefore, a genome-wide comparison between different Hi-C data sets is ambiguous, owing to the noisy and sparse data. By incorporating the genome-wide diffusion property of each genomic region into consideration, the problem associated with insufficient sampling for singular interactions is sufficiently corrected. The C_TG contact/distance maps reveal the hidden reproducibility of Hi-C data and, more importantly, reveal that the putative topologies of genomic structures are conserved across different cell numbers and even different individuals. The genomic structures recovered by the C_TG algorithm thus allow for a direct comparison for replicate experiments and even for samples from different individuals/experimental setups. Such a property of C_TG makes it suitable for characterizing the changes of genomic structures under different conditions.

C_TG characterizes the global structural changes in colorectal cancer pathogenesis

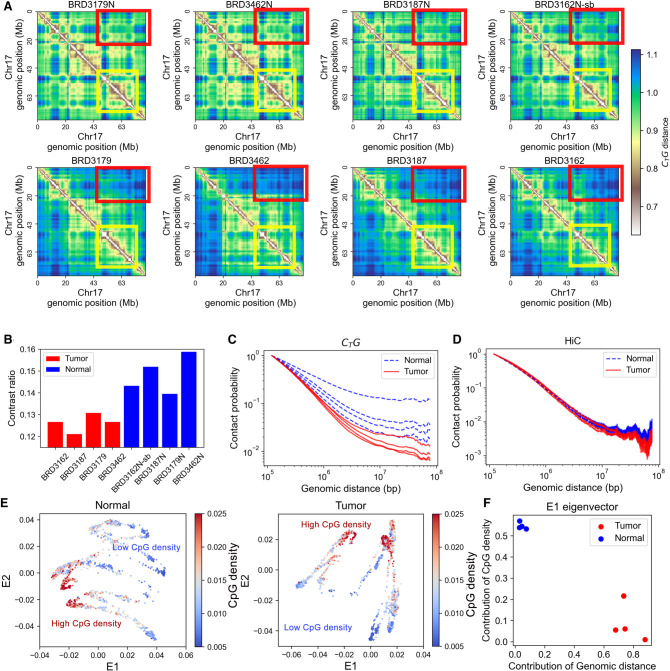
In this section, we use the C_TG method to analyze genomic structures derived from normal and tumor colon Hi-C data. Compartmental recognition was performed in a previous study (Johnstone et al. 2020) on these data sets, which associated the compartment changes during colorectal cancer pathogenesis with stemness, invasion, and metastasis of tumor. In the following, we show that C_TG allows for new insights into cancer-related changes of genomic structure. To ensure the consistency and reproducibility of our analysis, pairwise normal and tumor samples derived from four individuals were compared. We took Chromosome 17 as an example in our latter single-chromosome analysis to simplify our discussion. The conclusions are the same for other chromosomes.

As can be seen from Figure 3A, the overall pattern of C_TG distance matrices clearly distinguishes normal from tumor colon samples. From direct visualization, the fine plaid patterns of normal samples become significantly blurred in cancer, where the distinct genomic “chess-like squares” are no longer properly segregated, and the specific long-range aggregation weakens. To be more quantitative, we calculated the contrast ratio of the genomic “squares” over their proximal neighbors (Methods; Fig. 3B). The contrast ratios were found to be significantly higher for normal samples than for tumor samples (P-value = 0.0084) and were conserved across the four individuals. Such a result indicates that there is clear insulation between neighboring regions in normal tissues, the strength of which weakens in cancer samples. This change in genome insulation indicates the potential transcriptional dysregulation in carcinogenesis.

Figure 3.

Global structural patterns of colorectal cancer revealed by C_TG. (A) The C_TG distance matrix for normal (top) and tumor (bottom) colon samples. Each column represents pairwise normal and tumor samples derived from the same patient. The yellow and red squares are examples of the differences between normal and tumor samples. (B) The contrast ratio of the C_TG distance map; the blue bars correspond to normal samples, and the red bars correspond to tumor samples. (C) Contact probability as a function of genomic distance calculated from the C_TG contact map. (D) Contact probability as a function of genomic distance calculated from the Hi-C contact map. (E) The 2D Laplacian eigenmaps of C_TG distance matrices for pairwise colon normal and tumor samples. Each point represents a 40-kb genomic region. The color is used to represent the CpG density of the corresponding genomic region. (F) Contribution of sequence properties to structure-related E1 eigenvector.

Next, we calculated the reconstructed contact as a function of the 1D genomic distance (Fig. 3C). It can be seen that the tumor samples display large decay rates in the megabase scale, and the comparison between normal and cancerous C_TG distance matrices suggests the loss of specific long-range interactions in colon cancer, as revealed by Figure 3C. In comparison, the decay curve derived from Hi-C data normalized by ICE only varies more significantly over different samples (Fig. 3D), again validating the effectiveness of C_TG in revealing the consistent difference between normal and cancer cells.

Sequence properties, especially CpG density, were reported to be an important factor affecting the organization of genomic structure (Liu et al. 2018). To gain an understanding of how 1D DNA sequences affect the organization of 3D genomic structure, we performed dimensionality reduction on the C_TG distance matrix. The nonlinear Laplacian eigenmaps (see Methods) were used for dimensionality reduction, as the eigenvectors obtained by this method are interpretable and reveal information on hierarchical clustering (Fig. 3E; Supplemental Fig. S8). Sorted by eigenvalues, the leading eigenvector, E1, reflects the predominant structural patterns. We quantified the contribution of sequence properties, including sequential similarity (CpG density) and sequential distance, to genomic structure by projecting the structure-related eigenvectors on these sequence properties. Reflected by the projection of E1 (Fig. 3F), the dominant factor in structure determination changes from sequential similarity in normal cells to sequential distance in colon cancer, affecting the organization of A and B compartmental domains and probably resulting in the dysregulation of transcriptionally active or inactive states (see Discussion).

Gene coexpression and genomic proximity in colorectal cancer pathogenesis

The genomic structure is believed to play a crucial role in the precise gene expression program (Elimelech and Birnbaum 2020; Oudelaar and Higgs 2021). The genomic interactions between gene promoters and distal cis-regulatory elements have been studied extensively (Li et al. 2022). Because less attention has been paid to the function of gene–gene colocalization in genomic structures, we investigate here the physical GGIs at genomic levels, represented through the contacts between genomic bins in 40-kb resolution that contain these genes. Of special interest is whether a correlation exists between gene–gene contact in chromatin and gene coexpressions at the transcript level. The correlation network at transcript levels was characterized by Spearman's correlation coefficients of RNA-seq data, with the RNA-seq data derived from The Cancer Genome Atlas (TCGA) program, for 86 pairwise normal and tumor colon samples. The interaction network at genomic levels was quantified by C_TG distances. The two networks were aligned together in perspective of the genomic position of each gene.

To be more specific, we evaluated the one-to-one correspondence between genomic colocalization and coexpression. For both tumor and normal samples, the proximal gene pairs tend to coexpress at the transcript level (Fig. 4A), and such an inter-dependence is stronger for tumor samples than normal samples. In reverse, gene pairs that share a similar expression pattern tend to be proximal at genomic levels for tumor samples (Fig. 4B), which is again more prominent for tumor samples than for normal samples. Such a difference between tumor and normal samples indicates an increased correlation between genomic structure and gene transcription in cancers in perspective of gene–gene interplay. Compared with cancer samples, there is a weaker correlation between gene pair proximity and their expression correlation across normal samples; meanwhile, genes of large linear and spatial distances can be highly transcriptionally correlated in normal samples, suggesting other regulation mechanisms besides spatial cotranscription, such as histone modification or DNA methylation, play more important roles in normal cells than in their cancerous counterparts. The elevated dependence of gene coexpression on their spatial interaction in chromatin may suggest that gene expression regulation becomes more directly correlated with genomic structure. It was discovered recently that the RNA and protein levels become more strongly correlated in carcinogenesis, supporting that the regulation network simplifies in cancer pathogenesis (Nusinow et al. 2020). The increasing correlation in carcinogenesis may be partially owing to TAD boundary loss. HiCExplorer (Wolff et al. 2020) was used to detect TADs for four pairs of normal and tumor colon samples. If the overlap fraction of gene and TAD domain is >50% of gene length, the gene is considered as belonging to the corresponding TAD. The belonging TADs for 204 genes pairs with gene–gene proximity and gene coexpression (Pearson correlation coefficient > 0.5 in colon cancer samples) in cancer samples were detected. In addition, 48 out of 204 genes pairs are related with TAD boundary loss. They belong to different TADs in normal samples and belong to the same TADs in tumor samples; the proportion is 23.5%. Moreover, we also found, besides solid tumors, a similar correspondence of gene–gene proximity and gene coexpression in acute lymphoblastic leukemia samples (Supplemental Fig. S9).

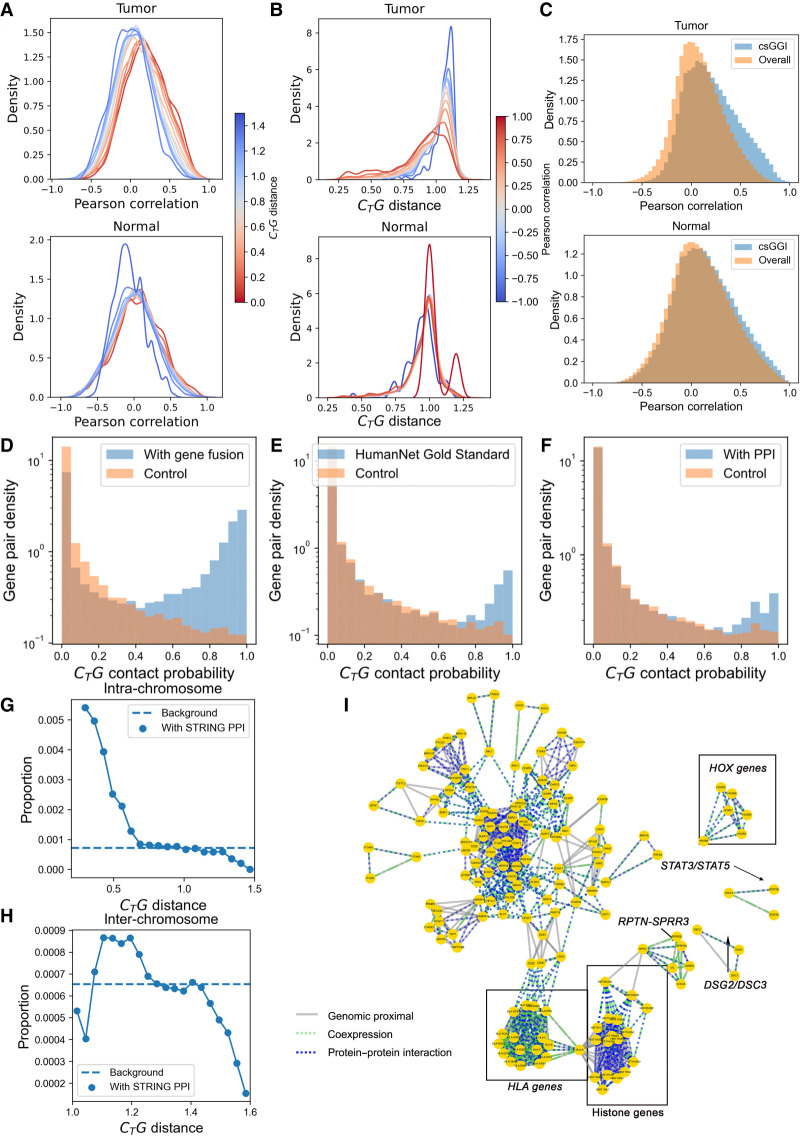
Figure 4.

Passage of gene–gene interplay from genomic level to transcription and protein levels in colorectal cancer. (A) The distribution of transcriptional Pearson correlation under different C_TG distance of the whole chromosome; the color of each line indicates the corresponding C_TG distance. (B) The distribution of C_TG distance under different Pearson correlation of the whole chromosome; the color of each line indicates corresponding Pearson correlation coefficient. (C) The distribution of correlation of gene pairs with csGGIs and overall background. (D) Distribution of C_TG contact probability for gene pairs with (blue) and without (orange) gene fusion events reported in FusionGDB2 data set. (E) Distribution of C_TG contact probability for gene pairs with (blue) and without (orange) similar biological process reported in HumanNet. (F) Distribution of C_TG contact probability for gene pairs with (blue) and without (orange) PPIs reported in STRING database (G) The proportion of intra-chromosomal gene pairs with STRING PPI at different C_TG distances in the tumor sample. The proportion refers to number of gene pairs with PPIs at fixed C_TG distance/number of all gene pairs at fixed C_TG distance. The background refers to number of gene pairs with PPIs/number of all gene pairs at all C_TG distance. (H) The proportion of inter-chromosomal gene pairs with STRING PPI at different C_TG distances in tumor sample. (I) The gene network integrates colon cancer–related gene–gene interplay at the DNA, RNA, and protein levels. The three kinds of edges indicate gene–gene interplays at three levels.

Gene fusion and functional analysis of GGI formation in cancer

Next, we analyzed the local spatial contacts in chromatin for individual genes (see Methods), where spatial GGIs are characterized. The interactions formed in cancer but not in normal tissue are referred to as cancer-specific GGIs (csGGIs). Noticeably, genes involved in csGGIs are prone to be more positively correlated in tumor samples than in normal samples compared with respective backgrounds (Fig. 4C; Supplemental Fig. S10). These csGGIs tend to be properly insulated in normal cells but not in cancer. An extreme case of the change of gene proximity in cancer development is gene fusion, which can play an important role in cancer biology. We did find that cancer-associated transcript fusions appear to associate with genomic proximity in cancer cells. Using the FusionGDB2 data set (Kim et al. 2022b), which contains approximately 90,000 gene fusions, we found that intra-chromosomal proximal genes are more likely to be involved in the gene fusion events (Fig. 4D). It is known that fusion genes are related to the downstream rewiring of protein interaction networks and therefore promote cancer (Latysheva et al. 2016). Our results showed that fusion events are related to the upstream alterations of genomic structure. Hence, the cause of the rewiring of protein interaction networks may also be traced back to the genomic level, which is analyzed in the next section. Further, we found that intra-chromosomal proximal genes are also more likely to participate in the similar biological process with their neighbors than those that are far apart, and the gold-standard gene pairs of the HumanNet v3 sharing pathway annotation (Kim et al. 2022a) are found to be more proximal than random gene pairs (Fig. 4E). Shorter C_TG distances between gene pairs are associated with higher probability of (1) gene fusion, (2) gene coexpression, and (3) interactions between the proteins coded by the two genes. In particular, the latter two occur in a cell type–specific manner and thus show a possible passage of chromatin 3D structural and networking information to the downstream products such as mRNA and proteins.

Hence, we expect the csGGIs found in genomic structures of tumor colon samples by the C_TG algorithm to play an important role in transcriptional coregulation between genes. Therefore, we further select csGGIs with notable changes in RNA correlation (tumor correlation >0.5 and normal correlation <0.1) and construct a csGGIs network. We found that the cancer-related genes (see Methods) are significantly enriched in the network, as 4.33% of genes involved in this network are cancer genes, showing 15-fold enrichment compared with the background. The cancer genes, including ERBB3, HRAS, MAP2K2, PTK6, RAC1, SDC4, TSC2, and SRC, among others, are connected with a large number (more than five) of genes and thus may play critical roles in this network (Supplemental Figs. S11–S13). Meanwhile, these cancer genes were also reported to be highly relative in colorectal cancer pathogenesis (Serebriiskii et al. 2019; Liu et al. 2021; Wang et al. 2021). We next performed functional annotation analysis on all genes connected to more than five genes in this network (Supplemental Table S1) and found these genes to be strongly involved in the epidermal growth factor receptor (ERGF) signaling pathway and proteoglycans in cancer. In addition, HRAS, RAC1, SOS2, MAPK3, and MAP2K2 directly participate in the colorectal cancer KEGG pathway. HRAS is involved in multiple cancer-related processes (Pylayeva-Gupta et al. 2011), and genes interacting with HRAS in the cancer genomic structure, for example, IFITM3, DRD4, IRF7, and NLRP6 (Hur et al. 2020), are heavily involved in the immune response. Such an analysis thus suggests a change of immune response regulation in cancer pathogenesis.

Genomic proximity is related to PPI in colorectal cancer pathogenesis

After interrogating the interplays between gene pairs at DNA levels and their transcript product, we wondered whether such information is further passed along the central dogma, such that GGIs at the chromatin level correlate with the interaction between their translational products. The interplays at protein levels were evaluated by physical PPIs derived from the STRING project (Szklarczyk et al. 2021). The genomic interactions and PPIs were aligned by genes and protein isoforms generated from corresponding genes. As Figure 4F shows, we did identify associations between the genomic structure and PPIs that have not been discussed before.

First, it can be seen from Figure 4, G and H, and Supplemental Figure S14 that the C_TG distances between gene pairs with their proteins forming known/predicted PPIs tend to be more proximal than those without PPIs, for both intra-chromosomal gene pairs with a more stable genomic structure and inter-chromosomal gene pairs with a more flexible genomic structure. The spatially proximal gene pairs are more likely to have their product proteins form PPIs. These results suggest that contact information deposited in genomic spatial structures has a tendency to pass to the protein level. Because the information passage of DNA–DNA (gene–gene) interaction to PPI goes through RNA, we next examined the correlation between different genes at the RNA and protein levels. Gene pairs forming PPIs in the STRING data set are indeed more prone to be correlated in transcription than are randomly chosen pairs, and such a tendency is found across different tumor types (Supplemental Fig. S15). Although coexpressions are a portion of gene interplays at RNA levels and PPIs in the data set are not tissue-matched, gene pairs with GGIs and PPIs are more correlated in transcription than are those only with PPIs (Supplemental Fig. S16). It is reported that gene fusion events are relevant to the rewiring of protein interaction networks in cancer (Lupiáñez et al. 2015). As shown by Figure 4, D and F, the origin of the transcript fusions may be traced back to genomic levels, and this may influence translational levels. Such results suggest that the information of the gene regulatory network is at least partially coded in 3D genomic structures and transferred to RNA and protein levels along with the central dogma, in a way beyond correct coding and functioning of single genes, but also in the message-passage level in the form of GGIs.

We integrated gene–gene interplay at the DNA, RNA, and protein levels to construct an interaction network at multiple levels. As Hi-C is a sequence-based method, the results may be influenced by repetitive regions or structural variants that show a high diversity between individuals. For example, the HLA genomic superlocus tends to show high diversity in human genomes. To exclude variation between individuals as much as possible, we determined csGGIs from the overlap in four pairs of normal and tumor colon samples. One thousand six hundred twenty-six pairs of genes are seen to be at the center of the interaction network for colon cancer (Fig. 4I). For example, STAT3/STAT5A, DSG2/DSC3, and RPTN/SPRR3 all possess genomic proximity, transcription coregulation, and potential protein interactions inferred from STRING. In fact, these genes are all reported to be involved in colorectal tumorigenesis. For example, STAT3 is a known biomarker for colon cancer as it is necessary for proliferation and survival in colon cancer–initiating cells (Lin et al. 2011), and STAT5A is reported to be involved in the regulation of colorectal cancer cell apoptosis (Du et al. 2012). The down-regulation of DSG2 and DSC3 in colon cancer cells was found to suppress colon cancer cell proliferation (Cui et al. 2011; Kamekura et al. 2014), and DSC3 is involved in tumor-suppression activity (Cui et al. 2019). Finally, the overexpression of SPRR3 is known to promote cell proliferation through AKT activation (Cho et al. 2010). Supplemental Figure S17 shows the distribution of 1D sequence distance of gene pairs integrating gene–gene interplay at the DNA, RNA, and protein levels. Gene pairs that are distal (>5 M) in 1D genome are also involved in this network; for example, CDCA8 and CDC20 are 5.7 Mb far from each other, and they are both essential regulators of cell division (Jeyaprakash et al. 2007; Yu 2007).

The interactions between multiple genes can also be observed in the chromatin structure. We downloaded the protein-complex interactions from UniProt and extracted the components of 155 protein complexes, and 118 out of 1626 gene pairs are related with protein products of the same protein complex, including the spliceosome complex (SNPNP70, SUGP1, PRPF31, PRPF38A, PRPF4, SF3A3, SF3B1), the chromatin remodeling complex (HDAC1, RBBP4, SMARCC1, PBRM1), and histocompatibility complex (HLA-A, HLA-B, HLA-C) (Fig. 4I). It is known that the relevant translational products make up the HLA class I (HLA-A, HLA-B, HLA-C) and class II (HLA-DQ, HLA-DR) complexes, which play important and distinctive roles in presenting processed peptide antigene (Giudizi et al. 1987; Choo 2007). The results indicated that not only direct protein interactions within each class of complex but also coregulation between the two complexes may be partially coded in genomic structure, although they are distant in the linear genome. C_TG provides statistically csGGIs; the related biological consequences require further experiments.

Tissue-specific coupling of PPI and genomic interactions

Functional proteins are directly involved in diverse biological processes, and proteins are shown to be strongly coregulated (Gonc et al. 2022). The associations and interactions between proteins are crucial for proper cellular homeostasis and regulations. The protein post-translational modification and the copy numbers of proteins can change with the cell states (e.g., through the cell cycle) and cell types. Meanwhile, the protein interactomes show great variety across cell types to shape cell specificity and to respond to external and internal signals, as a wide range of novel and specific PPIs are gradually detected (Huttlin et al. 2021; Kim et al. 2021; Swaney et al. 2021). The integrated STRING PPI data set contains both tissue-matched and unmatched PPIs, which allow the statistical analysis of GGI-PPI correlation but limit one from precisely matching GGIs with PPIs in a cell state–specific manner. To overcome this problem, we next performed an analysis based on the tissue-matched PPI data sets from the affinity-purification mass spectrometry (APMS) technique (see Methods).

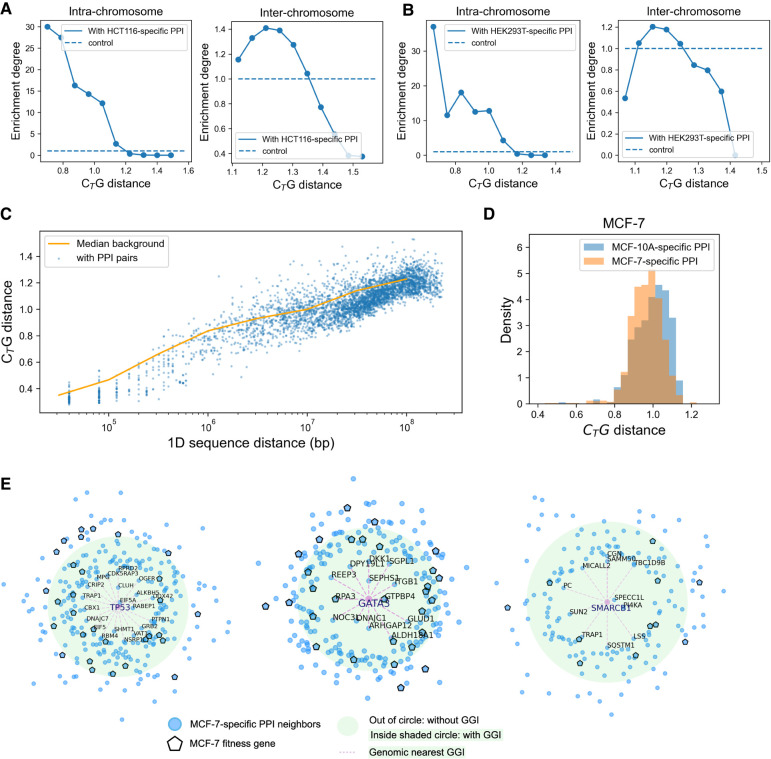
Fortunately, the BioPlex project has compiled a comprehensive data set of PPIs of HCT116 and HEK293T cells (Huttlin et al. 2021). The cell-matched BioPlex PPIs consist of about 71,000 and about 120,000 interactions, respectively, and they are all included in our analysis. Consistent with the results obtained using STRING data sets, as shown in Figure 5, A and B, genomic proximal gene pairs in HCT116 and HEK293T cells are also more likely to possess corresponding PPIs, and on the other hand, gene pairs with corresponding PPIs also tend to be spatially closer in genomic structure than those without known PPIs, although the current PPI list is probably far from being complete.

Figure 5.

The tissue-specific correspondence of PPI and genomic proximity. (A) The proportion of intra-chromosomal (left) and inter-chromosomal (right) gene pairs with HCT116-related PPI at different C_TG distances. The proportion refers to number of gene pairs with PPIs at fixed C_TG distance/number of all gene pairs at fixed C_TG distance. The background refers to number of gene pairs with PPIs/number of all gene pairs at all C_TG distance. The enrichment degree refers to the proportion/background. The control is one. (B) The proportion of intra-chromosomal (left) and inter-chromosomal (right) gene pairs with HEK293T-related PPI at different C_TG distances. (C) The C_TG distance of gene pairs in fixed 1D genomic distance. The C_TG distance between gene pairs with corresponding PPIs (blue scatters) is more proximal than the median C_TG distance of all gene pairs at all 1D genomic sequence distance (orange line). (D) C_TG distance of gene pairs with MCF-7-specific and MCF-10A-specific PPIs in MCF-7 cell. (E) TP53-, GATA3-, and SMARCB1-related MCF-7-specific PPIs. The distance to TP53 indicates the C_TG distance; the green circle indicates the background distance, the pink scatter indicates MCF-7 fitness genes, and the dashes indicate genomic proximal neighbors.

The mutual correspondence between GGI and PPI uncovers a significant correlation between genomic interactions and PPIs. The genomic proximity information appears to be partially preserved in both transcription and translation. Furthermore, the intra-chromosomal gene pairs with PPIs (Fig. 5A,B, left) displayed a tighter correlation with genomic structure than did inter-chromosomal ones (Fig. 5A,B, right). It is known that genes with related functions tend to cluster along the linear genome and in individual chromosomes (Hurst et al. 2004). The higher intra- than inter-chromosomal DNA, RNA, and protein coupling is consistent with this functional requirement. Next, to exclude the impact of 1D genomic distance within chromosomes, we evaluated GGI–PPI correlation at fixed genomic distances and found that gene pairs with corresponding PPIs tend to be more proximal in all genomic distances (Fig. 5C) than those without. Limited by a majority of weak or even undetected interactions, these signals are insignificant in raw Hi-C data sets with 90% zero elements, again showing the importance of further data processing for the Hi-C matrix. We also performed functional annotation analysis for proximal gene pairs with tissue-matched PPIs for HCT116 cells (Supplemental Tables S2 and S3), quantifying the correlation between genomic interactions and protein interactions for this colorectal carcinoma cell line. These genomic-proximal intra-chromosomal PPIs significantly correlate with cell adhesion and immune response, enriched in “interferon signaling pathway” and “antigen presentation” (HLA genes). In accordance, the interferon gene family is heavily involved in cancer-related pathways, such as those of JAK-STAT and PI3K-AKT signaling (Horvath 2004; Burke et al. 2014). Meanwhile, HLA genes play vital roles in cancer immunotherapy (Anderson et al. 2021). The interactions of HLA genes in both the genomic and protein levels in colon cancer cell lines are consistent with findings on solid colorectal cancer samples. On the other hand, the functions of genomic-proximal inter-chromosomal PPIs are relevant to RNA exosome and proteasome, which mediate the degradation of RNA and protein (Makino et al. 2013). The degradation system was shown to play important roles in cancer studies (Manasanch and Orlowski 2017; Taniue et al. 2022), and the two degradation systems may follow common principles (Makino et al. 2013). These results showed the possible roles chromatin and corresponding protein complex structures may play in the establishment of cell identity, as the structural-related PPIs are in correspondence with the cell-specific biological processes.

Next, we studied the specific genomic and protein interactions of breast cancer cell line MCF-7 and its normal counterpart MCF-10A cells (Kim et al. 2021) and compared them. The specific PPIs were quantified by overexpression APMS (PPI-score > 0.65) (Kim et al. 2021). The number of MCF-10A-specific PPIs is 559, and that of MCF-7-specific PPIs is 1325. From Figure 5D, one observes a clear tendency that gene pairs with MCF-7-specific PPIs are more likely to possess genomic interactions in MCF-7 cells rather than MCF-10A-specific PPIs, whereas in contrast, such a trend is insignificant for MCF-10A cells. In addition, gene pairs with MCF-7-specific PPIs are more distal (t-value = −16.23, P-value = 1.79 × 10⁻⁵⁷), and those with MCF-10A-specific PPIs are more proximal (t-value = 7.08, P-value = 1.99 × 10⁻¹²) in MCF-10A cells than in MCF-7 cells. These results thus reflect a tissue-specific correspondence between GGIs and PPIs. The fact that the breast cancer cell line MCF-7 displays a more significant correspondence than its normal counterpart may reflect that fewer cell-specific PPIs were identified in the normal cells than in the cancer cells. This observation may also indicate the cancer-specific PPIs to be more strongly correlated with the changes in genomic structure, although the inference requires more experimental evidence owing to the limited quantity of MCF-10A-specific PPIs. As specific and important examples, we analyzed TP53, GATA3, and SMARCB1 and their corresponding MCF-7-specific PPI neighbors. As shown in Figure 5E, the PPI neighbors of these genes, for example, CBX1/TP53, ITGB1/GATA3, and PI4KA/SMARCB1, tend to be proximal judged by comparison to their mean distances to all genes. Their proximal PPI neighbors enrich more MCF-7 fitness genes (Behan et al. 2019), such as EIF5/TP53, GTPBP4/GATA3, and PAM16/SMARCB1, than distal PPI neighbors do in genomic structure, suggesting the importance of genomic structure to cell functionality and survivability.

In summary, C_TG revealed that a proportion of genomic proximity information is directly reflected at both the transcriptional and translational levels. Such an observation suggests that the PPI information is at least partially coded through genomic proximity in the nucleus (see Discussion).

Discussion

In central dogma, the sequence information of the DNA is mapped into that of RNA and then that of proteins, effectively resulting in a passage of the linear sequence information (Wood 2005). It is well appreciated that the 1D DNA sequence information, which turns into the amino acid sequence of proteins, largely determines their 3D structures (Wang et al. 2017). Such a notion has brought great success in the prediction of protein structures, with the usage of coevolutionary information found by the alignment of protein sequences (Ovchinnikov et al. 2017). Despite the precise structure of proteins, we examined in this study whether the global interactome and regulatory framework formed by proteins is also coded in DNA levels. The linear genomic distribution of genes is fundamental to the establishment of a regulatory framework; there are many gene clusters located next to each other in a genome that are functionally coregulated and form complexes (Yi et al. 2007). Besides the fixed linear genome, the dynamic 3D genomic structures provide variability to the regulatory network and could also be relevant with the cell-specific interactomes at the protein level, as well as the regulatory network at RNA level.

The precise gene expression program through interactions between gene promoters and distal cis-regulatory elements has been widely investigated. A genome-wide interrogation on the correlations between proximal genes in genomic structure and their functions at transcriptional and translational levels, on the other hand, is still needed, partly owing to the large noise and sparsity in long-range interactions in Hi-C data. To obtain more reliable chromatin 3D structure information using Hi-C data, we developed and present here a computational method, C_TG. The genomic structure derived from C_TG was shown to be highly consistent with imaging data obtained by the FISH technique, thus validating the physical interpretation of the former. The reproducible and stable structure framework allows a consistent study of the variation of genomic structures among different samples and experiments. We found here that the genomic GGIs at DNA levels are correlated with coexpressions at RNA levels and PPIs at protein levels. The physical contact information between genes at the DNA level is thus likely transferred to the protein level for at least a subset of genes.

First, from DNA to RNA levels, genome-wide correspondence between genomic proximity and coexpression in colorectal cancer was detected. Such an observation triggers us to speculate that the long-range interactions of the genomic structure play a fundamental role in the global transcriptional regulation, ensuring that specific linearly distant genes can share similar transcription environments, such as transcription factor binding and epigenetic hallmarks, and thus are coregulated. Second, from DNA to protein levels, associations between genomic proximity and PPIs were also detected. We showed such an association on both integrated and tissue-matched PPI data sets. The genomic-proximal PPIs were found to be enriched in tissue-specific biological processes in several cell lines with available data, including HCT116, HEK293T, MCF-7, and MCF-10A. Third, from RNA to protein, it is confirmed that gene pairs with detected PPIs are prone to be positively correlated in transcription for various types of normal and cancer samples deposited in TCGA. A more comprehensive picture of the biological information passage through central dogma thus likely goes beyond the single gene (protein) and the sequence (chemical formula) level and includes more complex interaction information (Fig. 6). In this scenario, the three layers of regulatory networks (roughly speaking, DNA, or more precisely, chromatin, RNA, and protein) are inter-connected not only at the single gene level but also partially at the levels of gene–gene and protein–protein pairs. The contributions of nuclear proximity for gene expression covariations have been detected in mouse embryonic stem cells, and these covariations play a part in ensuring stoichiometry between interacting proteins (Tarbier et al. 2020), which is consistent with our results.

Figure 6.

Passage of gene–gene interplay through central dogma. Lines between pairwise genes, transcripts, and proteins represent GGI, transcriptional coregulation, and PPI, respectively.

The PPIs can change significantly with the change of cellular state even for the same cell type. It is also known that cell-specific DNA methylation and chromatin structure can be passed through different generations of cells (Wootton and Soutoglou 2021). Considering the fixed genetic inheritance, not only genetic but also epigenetic information is passed through DNA to proteins. We showed that the variable interactomes at the protein level, as well as the regulatory network at the RNA level, could be affected by the dynamic 3D genomic structures, and the latter can be passed through cell replication. On the other hand, the distinct epigenetic hallmarks affect the accessibility and TF and RNA binding preference to DNA of specific genomic regions and introduce distinct GGIs over a similar 1D DNA sequence for different tissues. These interactions are all likely to participate in the establishment of tissue-specific gene regulatory networks.

In fact, the storage and passage of interactome information in genomic structure can be crucial for tissue specificity and stability of the regulatory networks. It is known that the tissue/cell-specific PPIs play essential roles in the functional organization of regulatory networks (Huttlin et al. 2021). However, proteins can vary heavily in a number of copies, diffuse relatively freely in the cell if not anchored, and can have short lifetimes. Many of them are also required to respond quickly to external signals and other changes of cellular states. In addition, the cell is a painfully crowded and complex environment for proteins to find and associate with each other faithfully in a timely and well-organized manner, as required by signal transduction, especially if the population and distribution of individual proteins were entirely random or independent of each other. The highly responsive PPIs also impose difficulties for the proteins to maintain cell state–related information with constant disturbance as a result of cross talk with the environment. In such an environment, a coordinated production of proteins can be envisioned to facilitate their interactions, the occurrence of which at the right place and right time could be essential for the information cascade. In contrast to proteins, genes, including their copy numbers, positions on the linear DNA, and 3D chromatin, are less variable and provide a more stable information storage. This study suggests that a coordinated and cellular state–dependent, highly regulated PPI network can be achieved through the use of information stored in GGIs in 3D chromatin structure. Such an information flow is expected to result in coordinated transcription and eventually to functional PPIs. One can imagine that such PPIs involve not only pairs of proteins but also heterocomplexes formed by multiple proteins, the formation of which requires conceivably an even higher level of coordination.

In contrast to the fast accumulation of Hi-C data, high-throughput quantifications of tissue/cell-specific PPIs are still challenging. The genomic structure changes provide important knowledge and complementary information in predicting tissue-specific PPIs, which is expected to be of use in understanding the dynamic function of proteomics, as well as the resulting gene regulation network. To understand the molecular mechanisms leading to the various molecular associations, it would be necessary to thoroughly analyze the sequence and structure properties of proteins identified through chromatin structure analysis. The underlying mechanisms and functions of the passage of chromatin structure information to transcription correlation and PPI require much more experimental and computational validations and tests. For a more decisive evaluation of the GGI and PPI relationship, concurrent measurement of them in the same cells at the single-cell level would also be extremely valuable.

Methods

C_TG algorithm

W denotes the Hi-C contact map normalized by ICE. Before performing C_TG, we exclude genomic loci without any detected interactions with others (e.g., the centromere). Therefore, the matrix elements of input matrix W are either nonzero (with detected interactions) or zero (without detected interactions), and each row of the matrix is with at least one nonzero element. It is a positive symmetric matrix and is regarded as the adjacency matrix for a weighted connected network G(V,E), where the vertices V = {v₁,v₂,…v_n} denote the nonoverlapping genomic regions, and the edges E = {e_i,j} denote the contact strength between pairwise genomic regions. D is the diagonal degree matrix for the network, where the matrix element $D_{i,i}={\sum }_{j=1}^n{W}_{i,j}$. A one-step transition probability matrix P⁽¹⁾ can be derived by row-normalization of W:

$$P^{\left(1\right)}=P=D^{-1}W.$$

As W is diagonalizable, P is also diagonalizable:

$$P=U\mathrm{\Lambda }{U}^{-1}.$$

The eigenvectors U = {u₁,u₂,…,u_n} reflect the characteristics of the reference matrix P. From the perspective of spectral analysis, the eigenvectors indicate the hierarchy of the network, and the eigenvector corresponding to the largest eigenvalue indicates the most predominant hierarchy level of the network. Specific to genomic structures, the eigenvectors are, respectively, assigned to hierarchical structures, such as compartments and TAD structures. In addition, the local systematic biases are more likely to be assigned to eigenvectors of small eigenvalues, as they are not global properties.

The k-step transition probability matrix P^(k) can be written as the kth power of P⁽¹⁾:

$$P^{\left(k\right)}=P^k=U{\mathrm{\Lambda }}^k{U}^{-1}.$$

With step number k increasing, eigenvectors associated with the genomic structure are preserved. Meanwhile, for a larger k, the contributing proportion of eigenvectors (corresponding eigenvalues) changes, where eigenvectors corresponding to larger eigenvalues of Λ gradually contribute more, and P^(k) highlights the predominant hierarchy level of the network. P^(k) converges to the invariant distribution quickly, and the difference between P^(k−1) and P^(k) decreases sharply, which means P^(k) provides less and less new information with k increasing. An exponential decay is chosen to fit the convergence, and α denotes the attenuation factor. A transition propensity matrix S within k steps is defined as

$$S^{\left(k\right)}=\sum _{t=1}^k\exp (-\alpha t)P^t.$$

When k approaches infinity, S^(k) converges to S (Supplemental Methods):

$$S=U\mathrm{\Lambda }{\left[\exp \right(\alpha )I-\mathrm{\Lambda }]}^{-1}{U}^{-1}.$$

I denotes the identity matrix.

Therefore, the properties of S are independent from the value k. S_i denotes the ith row of S and represents the integrated diffusion propensity of the ith vertex. The L1 norm of S_i can be written as

$${\Vert S_i\Vert }_1=\underset{n\to \mathrm{\infty }}{\lim }\sum _k\exp (-\alpha k)={\displaystyle \frac{1}{\exp (\alpha )-1}.}$$

Considering the uniformity of the L1 norm of S_i, we quantify the similarity between pairwise genomic regions i and j by calculating the L1 distance between S_i and S_j. A C_TG distance matrix, denoted as DI, is constructed from the Hi-C contact matrix, and the distance measures the similarity of pairwise genomic regions by their diffusion propensity in a genome-wide fashion. C_TG distance DI_ij between pairwise genomic regions i and j is defined as

$$D{I}_{ij}={\Vert S_i-S_j\Vert }_1.$$

A C_TG contact probability matrix, C, is constructed by the rank of the C_TG distance to avoid approximating distributions of the C_TG distance matrix and to make comparison with Hi-C contact probability. The C_TG distance is sorted from least to greatest, and we use exponential function to normalize rank between (0,1):

$$C=\exp \left(-rank/n\right).$$

Hi-C experiment

Cell culture and fixation

HEK293 cells (American Type Culture Collection) were cultured at 37°C under 5% CO₂ in a humidified incubator. We cultured HEK293 cells in DMEM medium (Gibco 11965092) with 10% fetal bovine serum and 1% penicillin–streptomycin. To gather the cells for Hi-C processing, the cells were washed twice using PBS, detached by adding 1 mL 0.25% trypsin-EDTA (Gibco 25200056) to their culture dish, centrifuged at 500g for 5 min, and recovered in PBS buffer. The cells were counted by a cell-counter to determine the concentration. For sample 0923-4, 1000 cells were extracted to a 0.5-mL Eppendorf lobind microcentrifuge tube (Eppendorf 32119210) for each sample. For samples 1002-5 and 0923-2, 10,000 cells were extracted.

The cells were then fixed by adding formaldehyde (Sigma-Aldrich 47608) to a final concentration of 2% for 10 min at room temperature and then quenched by 0.2 M glycine (Sigma-Aldrich 50046) for 10 min. The fixed cells were centrifuged at 2500g for 5 min to discard the supernatant and washed with 0.5 mL PBS (Gibco 20012027) once.

Hi-C experiments

Hi-C experiments were performed following methods described by Rao et al. (2014) with some modifications. Briefly, the fixed cell pallet was lysed in 100 µL Hi-C lysis. The fixed cell pallet was lysed in 100 µL Hi-C lysis buffer (10 mM Tris-HCl at pH 7.6 [Rockland MB-003], 10 mM NaCl [Invitrogen AM9760G], 0.2% IGEPAL CA-720 [Sigma-Aldrich 238589], 1× cOmplete protease inhibitor [Roche 04693116001]) on ice for at least 30 min. The tubes were centrifuged to remove all the supernatant. Fifty microliters of 0.5% SDS (Invitrogen 15553027) was added to each tube and incubated for 20 min at 65°C. To quench the reaction, 25 µL of 10% Triton X-100 (Sigma-Aldrich T8787) was added and mixed by pipetting up and down several times. The tubes were then incubated for 20 min at 37°C. To perform chromatin digestion, 10 µL 10× NEBuffer2 (NEB B7002S), 10 µL 25 U/µL MboI (NEB R0147L), and 5 µL water were added to each tube and incubated with rotation for 24 h at 37°C. MboI enzyme was inactivated for 20 min at 62°C. Fill-in mix that contains 14 µL 0.4 mM biotin-dATP (Invitrogen 19518018), 0.17 µL 10 mM dTTP (NEB N0446S), 0.17 µL 10 mM dGTP (NEB N0446S), 0.17 µL 10 mM dCTP (NEB N0446S), and 3 µL 5 U/µL DNA polymerase I large (Klenow) fragment (NEB M0210V) was added and incubated for 45 min at 37°C with rotation. Next, 12 µL 10% Triton X-100, 1.5 µL 100× BSA (NEB B9000S), 5 µL 10× T4 DNA ligase reaction buffer (NEB B0202S), 2 µL 400 U/µL T4 DNA ligase (NEB M0202V), 10 µL 10 mM ATP (NEB P0756S), and 2 µL water were added to each sample, and the ligation reaction was performed by incubating with rotation for 24 h at room temperature.

Library construction

After ligation, DNA fragments were released by the addition of 15 µL 10% SDS and 30 µL Proteinase K (Qiagen 19133) to each tube followed by incubation for 3 h at 50°C. The DNA fragments were purified by Ampure XP beads (volume ratio 1:1; Beckman Coulter A63881), and the DNA fragments were eluted in 27 µL water. Tagemtation was performed by adding 4 µL 8× TD buffer (80 mM Tris-HCl at pH 7.6, 40 mM MgCl₂ [Invitrogen AM9530G], 80% N,N-dimethylformamide [Sigma-Aldrich D4551]) and 1 µL TTE mix V50 Tn5 enzyme (Vazyme TD501) to the 27-µL DNA template. The tubes were incubated for 1 h at 55°C. To stop the reaction, 8 µL 5× TS (Vazyme TD503) was added to each tube and incubated at room temperature for 5 min. To prepare Dynabeads M-280 streptavidin (Invitrogen 11206D) for the capture of ligation junctions, 25 µL streptavidin beads was washed by 1× BW buffer (5 mM Tris-HCl at pH 7.6, 0.5 mM EDTA [Invitrogen AM9260G], 1 M NaCl) and resuspended in 13 µL 4× BW buffer (20 mM Tris-HCl at pH 7.6, 2 mM EDTA, 4 M NaCl) for each sample. The beads were then mixed with 40 µL segmentation mix and incubated overnight with rotation at room temperature. The streptavidin beads were washed twice with 1× BW buffer, washed twice with 10 mM Tris-HCl (pH 7.6), and resuspended in 20 µL 10 mM Tris-HCl (pH 7.6). PCR amplification was performed by the addition of 5 µL 10 µM Nextera index mix(Vazyme TD203) and 25 µL Q5 high-fidelity 2× master mix (NEB M0492S) to the 20 µL sample. The PCR program is available in the Supplemental Methods.

Post-PCR purification was performed using Ampure XP beads (0.8 times the volume of the PCR mix) according to the manufacturer's instructions.

Library QC and sequencing

The libraries were quantified using Qubit 1× dsDNA HS assay kits (Invitrogen Q33230), and the size distribution was assessed using a 5200 fragment analyzer system (Agilent M5310AA). The qualified libraries were then quantified by qPCR and sequenced by a 2× 150-bp paired-end run on a NovaSeq 6000 system (Illumina).

Sequencing data processing

Paired-end reads were first under adaptor trimming using cutadapt (version 2.10) (Martin 2011) with default arguments. Reads <20 bp were filtered out after adapter trimming. Trimmed reads were mapped to Genome Reference Consortium Human Build 37 (hg19; downloaded from UCSC, https://hgdownload.soe.ucsc.edu/goldenPath/hg19/bigZips) and processed by HiC-Pro (version 2.11.4) (Servant et al. 2015) using default settings. The contact matrix extracted by HiC-Pro were then used in downstream analysis.

Contrast ratio

The Sobel operator is a discrete derivative operator for edge detection, which is defined as

$$S_x=\left\{\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right\},S_y=\left\{\begin{array}{ccc}-1& 0& 1\\ 2& 0& 2\\ -1& 0& 1\end{array}\right\}.$$

Convolution was performed on a distance map I with the Sobel operator as the kernel:

$$G_x=S_x\ast I,$$

$$G_y=S_y\ast I,$$

$$G=\sqrt[2]{G_x^2+G_x^2}.$$

Distinct edges will be emphasized by G for a distance map with “chess-like squares.” Therefore, G reflects the contrast ratio of the genomic “squares” with distinct edges over their proximal neighbors, and the mean of G is defined as the overall contrast ratio of the distance map.

Laplacian eigenmaps

Given a C_TG distance map I, it is transformed into weight matrix W by an exponential kernel:

$$A=\exp \left(-\mu I\right).$$

μ reflects the scale of genomic structure we focused on. A large μ amplifies weights of short distance, and a small μ amplifies weights of long distance. To avoid the impact of uneven degree distribution, the normalized Laplacian L is constructed:

$$L=I-D^{-1/2}A{D}^{-1/2},$$

where D is the degree matrix for W.

L is diagonalizable, and the bottom three eigenvectors, E0, E1, and E2, are computed. E0 is excluded as it is not informative:

$$Y=\left[\begin{array}{c}E1\\ E2\end{array}\right]D^{-1/2}.$$

The coordinates for n genomic regions {y₁|y₂|…|y_n} ∈ R² are acquired by converting the columns of Y into 2D vectors:

$$\left[y_1\right|y_2\left|\dots \right|y_n]=Y.$$

Genomic neighborhood and csGGIs

The neighborhood for a given genomic region is defined by its radial distribution function (RDF), taking a small proportion of genomic regions within the neighborhood. The diameter of the neighborhood is determined by boundary of the highest characteristic peak, where the slope of the tangent line of the cumulative RDF is calculated, and the tangent line with the largest slope is chosen as a guideline. The diameter is quantified by the point that the guideline intersects with the x-axis. The neighborhood for a given genomic region is then settled. Pairwise genomic regions within each other's neighborhood are defined to have GGIs.

The fold-change of the C_TG distance between tumor samples and normal samples is calculated, where m denotes the mean of the fold-change and σ denotes the standard deviation. The csGGIs are GGIs from tumor samples with the extreme change in C_TG distance (fold-change < m − 3σ, according to the 3σ rule).

Gene function analysis

GO enrichment analysis of all the given gene clusters in this work was conducted using DAVID (https://david.ncifcrf.gov). Individual gene functions were obtained from GeneCards (https://www.genecards.org). Cancer genes were obtained from COSMIC (https://cancer.sanger.ac.uk/cosmic).

Visualization

The PyMOL program (version 1.8, https://pymol.org/2/) was used to visualize the genomic structure (Xie et al. 2017) in Figure 1. The VMD program (Humphrey et al. 1996) was used to render the protein structure.

Data sets

Hi-C data

For normal and tumor colon samples, we used Hi-C data obtained from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) accession number GSE133928: The normal samples are BRD3162N-sb, BRD3179N, BRD3187N, and BRD3462N; the tumor samples are BRD3162, BRD3179, BRD3187, and BRD3146. For the HCT116 cell line, we used Hi-C data from GEO GSE133928. For the MCF-7 and MCF-10A cell lines, we used the sample from GEO GSE165570. Hi-C matrices were normalized using the ICE algorithm (Imakaev et al. 2012).

Gene expression data

We downloaded all available tumor–normal pairwise somatic expression data for patients from the TCGA GDC data portal (https://portal.gdc.cancer.gov) and selected expression data with more than 10 patients for 17 cancer types/subtypes. All expression data were converted to transcripts per million (TPM) format.

PPI data

To build a comprehensive protein–protein interactome, we assembled PPIs from three sources: (1) PPIs from the STRING project (https://www.string.com), (2) HCT116-related PPIs from the BioPlex project, and (3) MCF-10A-related and MCF-7-related PPIs from Kim et al. (2021). The cell-specific PPIs were determined from the second and third sources with PPI score ≥ 0.65 and eightfold or more change.

Data access

All raw and processed sequencing data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE233166. C_TG source codes and scripts are available at GitHub (https://github.com/PKUGaoGroup/CTG.git) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.