Void volume fraction of granular scaffolds

Abstract

Void volume fraction (VVF) is a global measurement frequently used to characterize the void space of granular scaffolds, yet there is no gold standard by which to measure VVF in practice. Using simulated packed particles in 3-D, we study the relationship between VVF and particles of varying size, form, and composition. Our library of VVF values reveal that VVF is more variable across replicate scaffolds relative to the number of particles parameters. We next use our simulated data to explore the relationship between microscope magnification and VVF for monodisperse spherical particles. We offer recommendations for optimizing the accuracy of approximating VVF using 2-D microscope images, which is the most common approach for computing VVF of hydrogel granular scaffolds. Lastly, we measure VVF of hydrogel granular scaffolds while varying four input parameters: image quality, magnification, analysis software, and intensity threshold. Results show that VVF is highly sensitive to these parameters. Overall, random packing results in variation of VVF among granular scaffolds comprising the same particle populations. Furthermore, while VVF is used to compare the porosity of granular materials within a study, VVF is a less reliable metric across studies that use different input parameters. VVF is a global measurement which inherently cannot describe the dimensions of local pores within granular scaffolds, and our work supports the notion that more descriptors are necessary to accurately and sufficiently characterize void space.

Graphical Abstract

The void volume fraction (VVF) of granular scaffolds is challenging to measure accurately. For real microscope images, user preference for software, magnification, and threshold parameters has significant influence on the final reported VVF. We use simulated packed particles in 3-D to study VVF for a range of granular scaffolds. With access to a ground truth, our simulated microscope images reveal relationships between VVF and magnification, z-gap, and the number of z-slices.

1. Introduction

Void volume fraction (VVF¹) is one of the most reported analyses for packed granular materials. The measurement describes the proportion of the structure that is occupied by void space between particles. In the biomaterials field, we care about understanding void space because granular materials made from microscopic particles are often designed for applications in wound healing or organ-on-chips, where cells infiltrate into and reside in the void space while they enact their therapeutic effect. VVF gives us information about particle-packing density and is one way to characterize the space available to cells. For studying the inside of granular scaffolds, the field uses light microscopy or micro-computed tomography to generate 2-D z-stack images of the sample. These slices are then either analyzed on a per-slice basis or fed into software that reconstructs a 3-D image for 3-D analysis. We are interested in studying VVF in more depth to understand how particle composition and methods of analysis affect what is being reported in the literature. Our goal is to 1) derive relationships between particles and VVF for a range of idealized particle packings, 2) expose the shortcomings of measuring VVF in practice, and 3) identify potential practical strategies that increase accuracy and reduce subjective variabilities.

1.1. Current approaches for imaging granular scaffolds and computing VVF

In the biomaterials field, confocal microscopy is a common imaging approach for visualizing and analyzing granular scaffolds, where particles are fluorescently labeled and/or void space is illuminated using fluorescently-labeled dextran. Scaffolds are imaged with a specified objective lens magnification (and corresponding numerical aperture) along the vertical axis to generate a z-stack of 2D-slice images that are typically a uniform step-size (z-gap) apart. Protocols for obtaining microscopy images vary in terms of magnification, sample thickness, z-gap, and the number of z-slices (Table 1), which can be attributed to user-preference that aims to balance image resolution, sample size, and imaging (1-7).

Table 1.

Sample microscopy parameters used in the literature for computing void volume fraction.

Magnification	Sample thickness (μm)	z-gap (μm)	Number of z-slices	Reference
unspecified	150	7.1	21	(1)	Sideris, 2016
unspecified	100	5	20	(2)	Mendes, 2021
10x	400	12	33	(3)	Caldwell, 2017
25x	100	5 (average)	20 (average)	(4)	Muir, 2021
unspecified	100	unspecified	≥ 6	(5)	Alexis, 2021
unspecified	100	1.3	77	(6)	Sheikhi, 2019
10x	200	unspecified	≥ 4	(7)	Truong, 2019

Computing VVF from microscope z-stack images can be broadly categorized as 2-D or 3-D approximations, and approaches under each umbrella use techniques from image processing that introduce user bias. The most common 2-D approach is to approximate VVF by the average void area fraction among z-slices. Fiji (ImageJ) is an image processing platform that is used to approximate VVF in this way (4, 5, 8, 9), and users must choose from 16 Auto-Threshold methods for the binarization step that influences VVF (10). The field also commonly employs MATLAB to compute average void area fraction by implementing MATLAB-native thresholding algorithms into custom code, which further adds to the variability of computing VVF (3, 6, 11). 3-D approximations require first constructing a 3-D volume prior to computing VVF. Imaris is a microscopy image analysis software that computes VVF by generating a triangulated mesh of either the particles or the void space, then computing the volume of the space enclosed by the mesh. User bias is introduced when setting the global threshold that is applied to all images in the z-stack during image processing. The 3-D aspect of Imaris (and other similar software) has made it appealing for visualizing granular scaffolds as well as computing VVF (7, 11-13)

2. Methods

2.1. Simulating granular scaffolds and computing VVF

Packed particle domains were simulated using SideFX Houdini software. Particles were randomly initialized above a funnel geometry that feeds into a 600 x 600 x 600 μm³ container. Domains were discretized on a uniform Cartesian grid. The mesh size, $dx$, for all domains was chosen to produce a total voxel count between 10⁷ and 10⁸, which produced the best trade-off between detail and memory usage. We use Houdini’s native rigid-body physics solver to simulate how particles fall, collide, and ultimately settle in the container. All parameters not otherwise stated are held constant, including particle friction. Domains containing binary mixtures are generated by first determining the number of particles for each population according to the desired volume ratio and container size, then initializing their starting positions (randomly) within a cylinder above the setup before dropping them into the container through a funnel (Supplementary Figure 1). Polydisperse particle domains are similarly generated, where particle diameters are sampled from a normal distribution with set mean and standard deviation. For non-spherical particles, we use Houdini to model ellipsoids, cylinders (rods), and nuggets, where nuggets were created by extruding a parametric curve that describes the perimeter of an egg-like shape. See Supplementary Figure 2 for relative particle dimensions.

Once a domain is simulated, the particles are rasterized to a uniform 3-D grid. For spherical particles, we output a CSV file storing the particle centers and radii, as well as the mesh size. For non-spherical particles, we label their associated voxels with a unique integer ID, then output the labeled-voxel data to a JSON file along with other fields: domain size, total particle count, total voxel count, voxel count per particle, and voxel size (mesh size).

VVF is defined as $\Phi -S∕V$, where $S$ represents void space and $V$ represents the total volume of scaffold. To avoid edge effects, we specifically define $V$ as the convex hull of particle centers, i.e., both particle and non-particle regions that lie within the interior of the scaffold, and $S$ is defined as the non-particle regions within the convex hull. See Supplementary Figure 3 for formal definitions of these terms.

2.2. Simulating magnification and studying z-slices

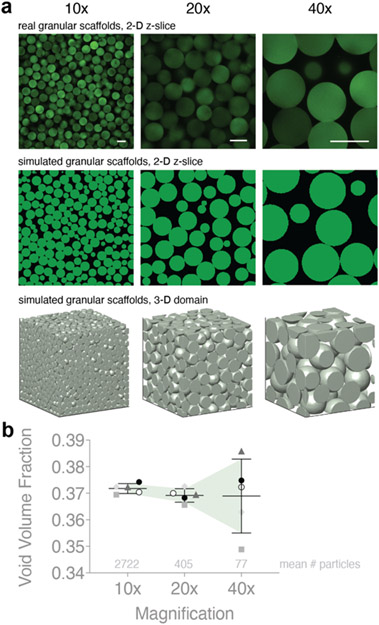
We use microscope images of real granular scaffolds comprising 100 μm diameter particles as our reference z-slice images for 10x, 20x, and 40x magnification. To start, we calibrate a simulated domain to a real image of 10x magnification by using an 800 x 800 x 800 μm³ domain of 60 μm spherical, rigid particles and cropping inward 4% in all directions using $dx$ = 2 μm. This produces a 3-D particle domain that is 736 x 736 x 736 μm³ (~5.0 x 10⁷ voxels) and subsequently 736 x 736 μm² (368 x 368 pixels) 2-D slice images. We opt for 60 μm diameter particles instead of 100 μm diameter particles because we wanted to avoid simulating particle domains that exceed 800 x 800 x 800 μm³ due to hardware constraints. This initial crop is to avoid edge effects; however, the effect of particle alignment against the walls of the container is still present (e.g., Figure 3b, for small z-slice numbers, there is a dip in relative accuracy for all scaffolds at 10x magnification; Figure 2b, the average VVF at 10x is slightly larger than 20x and 40x magnification). To generate 20x magnification, we crop the original domain inward by 27% in each direction and use $dx$ = 1 μm. This produces a 3-D particle domain that is 368 x 368 x 368 μm³ (~5.0 x 10⁷ voxels) and 368 x 368 μm² (368 x 368 pixels) 2-D slice images. This crop was chosen because a 2-fold zoom is equivalent to halving the field of view. Similarly, 40x magnification is generated by cropping the original domain 38.5% in each direction using $dx$ = 0.8 μm to produce a 3-D particle domain that is 184 x 184 x 184 μm³ (~1.2 x 10⁷ voxels) and 184 x 184 μm² (230 x 230 pixels) 2-D slice images. A $dx$ of 0.8 was used in lieu of 0.5 because of memory constraints since each run starts with the full 800 x 800 x 800 μm³ domain at the chosen $dx$ prior to cropping. Adjusting $dx$ at each simulated magnification ensures a similar voxel count. This process is repeated for four additional unique particle domains. Finally, to ensure that our simulated data reflects the real 100 μm diameter scaffolds that were used as references, we scale our reported z-gap data by ${}^{100}∕_{60}$.

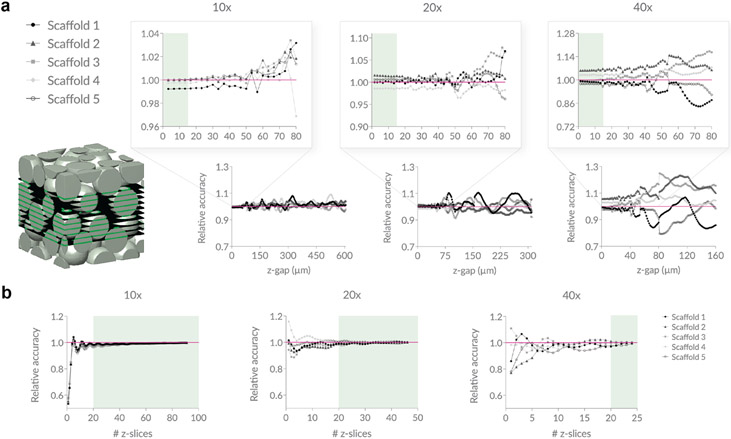
Figure 3. Studying z-gap and number of z-slices.

a, Using simulated scaffolds of 100 μm diameter particles to mimic microscope data, we approximate VVF using average void area fraction across 2-D z-slices and report how the relative accuracy of the approximation changes as a function of the step size (z-gap) taken. Z-slices are sampled within the middle 50% of each scaffold. A z-gap of less than ~15 μm ensures a stable approximation of VVF that stays within 7% accuracy for all scaffolds across all magnifications. b, We again plot the relative accuracy of average void area fraction compared to the true VVF, but this time we hold the z-gap constant at 13 μm and incrementally increase the number of z-slices starting at the bottom of the scaffold. Sampling 20 or more z-slices ensures a stable approximation of VVF that stays within 4% accuracy for all scaffolds across all magnifications. N = 5 domains. The true VVF for each scaffold at each magnification is reported in Supplementary Table 1.

Figure 2. Simulating microscope magnification.

a, Sample z-slice images from real granular scaffolds are used to calibrate our simulated scaffolds at varying magnifications. b, VVF of simulated domains is compared at different magnifications. Higher magnification yields less precise VVF. Average number of particles in 3-D domain at each magnification are shown above the x-axis. N = 5 domains for each category. Scale bars = 100 μm. Errors bars denote standard deviation.

To study how z-gap size affects average void area fraction using our simulated particle domains, we sample z-slices within the middle 50% of the scaffold that are z-gap apart and plot average void area fraction as a function of z-gap. To study how the number of z-slices affects average void area fraction, we sample an increasing number of z-slices starting from the bottom of the scaffold that are 8 μm apart. For each iteration, we compute the average void area fraction and plot as a function of the number of z-slices. We use the same particle domains as described in the previous paragraph.

2.3. Real granular scaffolds

We study how VVF measurements vary for four conditions: 1) scaffolds comprising 70 μm diameter polyethylene glycol (PEG) vs. 100 μm diameter hyaluronic acid (HA) particle scaffolds, 2) 10x, 20x, and 40x optical lens magnifications, 3) Fiji, MATLAB, Imaris, and 3-D Particle Segmentation software approaches, and 4) a reasonable range of input parameters or settings that produce a low, middle, and high VVF value. The goal of the last condition is to study the range of user bias for each software. Our protocol for determining reasonable low, middle, and high output images was as follows: low outputs showed many ‘false particle’ regions but at least one ‘false void’ region; middle output images showed both ‘false particle’ and ‘false void’ regions and was considered the ‘best’ binarization; and high output images showed many ‘false void’ regions but at least one ‘false particle’ region.

2.3.1. Polyethylene glycol Vinylsulfone microgel production

Microfluidic devices and microgels for Polyethylene glycol Vinylsulfone (PEG-VS) were produced as previously described (14). Briefly, 8 arm PEG-VS was dissolved in 0.3 M triethanolamine (Sigma) pH 8.8 and pre-reacted with K-peptide (Ac-FKGGERCG-NH2, GenScript) and Q-peptide (Ac-NQEQVSPLGGERCG-NH2, GenScript) and RGD (Ac-RGDSPGERCG-NH2, GenScript) for at least one hour at 37°C. Concurrently, the cross-linker solution was prepared by dissolving the di-thiol matrix metalloproteinase sensitive peptide (GenScript) in distilled water at 12 mM and reacted with 10 μM Alexa-Fluor 647-maleimide for 5 minutes. These solutions were filtered through a 0.22 μm sterile filter before loading into 1 ml syringes. The aqueous solutions did not mix until droplet segmentation on the microfluidic device. The pinching oil phase was a heavy mineral oil supplemented with 1% v/v Span-80. Downstream of the segmentation region, a second oil inlet with a high concentration of Span-80 (5% v/v) and Triethylamine (3% v/v) was added and mixed to the flowing droplet emulsion. These microgels were collected and allowed to gel overnight at room temperature to form microgels. The microgels were then purified and stored in HEPES buffer (pH 8.3 containing 1% Antibiotic-Antimycotic and 10 mM CaCl2) at 4 °C.

Scaffolds were made as previously described (14), where 4 U/ml of thrombin (200 U/mL in 200 mM Tris-HCl, 150 mM NaCl, 20 mM CaCl2) and 10U/ml of Factor XIII (250 U/mL) were combined with pelleted “dry” microgels and mixed and allowed to incubate at 37°C for 30 minutes to form a solid hydrogel. The scaffolds were imaged on a Nikon Ti Eclipse scanning confocal microscope equipped with a C2 laser using a 20x air objective with 0.75 numerical aperture.

2.3.2. Hyaluronic acid-norbornene microgel production

Hyaluronic acid-norbornene (HA-NB) was first synthesized as previously described (15). Briefly, HA (MW 79,000 Da) (Contipro) was activated with 4-(4,6-Dimethoxy[1.3.5]triazin-2-yl)-4-methylmorpholinium chloride (DMTMM) (MW: 294.74 Da) (TCI America, Portland, OR) at 4 molar equivalents in 200 mM MES buffer for 10 min before adding 2 molar equivalents of 5-Norbornene-2-methanamine (a mixture of isomers) (NMA) (TCI America, Portland, OR) drop-wise. HA-NB was then purified and H’NMR verified 33.5% NB functionalization.

This HA-NB was then used for microgel productions as previously described (15). Briefly, microgels were produced using a planar flow-focusing microfluidic device to create uniform particles. A 1 mL gel precursor solution was made by dissolving HA-NB in 50mM HEPES pH 7.5, di-thiol MMP sensitive linker peptide (Ac-GCRDGPQGIWGQDRCG-NH2, Genscript) (SH/HA ratio of 14), tris(2-carboxyethyl)phosphine (TCEP) (Sigma-Aldrich) (TCEP/SH ratio of 0.25) and 9.90 mM lithium phenyl(2,4,6-trimethylbenzoyl)phosphinate photo-initiator (LAP) (TCI America, Portland, OR). The final HA-NB in the precursor solution should be at 3.5% (w/v). A 5 mL BD Leur-Lok syringe was filled with 5% (v/v) Span-80 in heavy mineral oil and attached to the outer inlet of the microfluidic device. A single syringe pump was used to push the differently-sized syringes at asymmetric flow rates. A OmniCure LX500 LED Spot UV curing system controller with a OmnniCure LX500 LED MAX head at 365nm wavelength, 30% power at (20 mW/cm2) was used off chip to crosslinking the microgels. A 15 mL conical tube wrapped in foil was used to collect the HMP emulsion. Microgels were washed of any oil and left to swell in 1xPBS buffer overnight or at 4°C until stained and imaged.

Before imaging, microgels were labeled with an AlexaFluor 488 that had been previously modified with a tetrazine linker. After fluorescently tagging and washing the microgels, they were combined with 4-arm PEG-Tetrazine at a ratio of 7 Tet/HA to form scaffolds. After annealing, the scaffolds were imaged on a Nikon Ti Eclipse scanning confocal microscope equipped with a C2 laser using a 20x air objective with 0.75 numerical aperture.

2.3.3. Fiji

Fiji is an image processing program that approximates VVF by computing the average void area fraction among inputted 2-D z-slice images (16). We first convert images to 8-bit, then binarize each z-slice using built-in methods from Fiji’s Auto Threshold plugin: namely, MinError, Huang, and Default for low, middle, and high outputs, respectively. These selections were based on the sample image of cells shown in the Fiji/ImageJ online documentation (10), where we relate the circular cells to particles. MinError binarization correctly segments complete cells/particles but includes substantial particle-pixel noise, which underestimates void space. Huang produces the optimal cell/particle segmentation. Default binarization results in cells/particles that are speckled with void space pixels, which overestimates void space. These three methods reference actual settings used in the field for reporting VVF. For our analysis, we exclude blurry z-slices that appear out of focus.

2.3.4. MATLAB

Our MATLAB script uses standard built-in functions to process and binarize images, then approximates VVF by computing the average void area fraction among inputted 2-D z-slice images. Users input a parameter, γ, that divides the output of the MATLAB function graythresh (Otsu algorithm) used for binarization. We chose γ = 1 or 1.5 for our low output category, γ = 2 for our middle output category, and γ = 2.5 or 3 for our high output category. These γ values were chosen on a per-z-stack basis by observing how different γ values change the binarizations, then visually determining a ‘reasonable’ output for each category.

2.3.5. Imaris

Imaris is a microscopy image analysis software that computes VVF by binarizing z-stacks before generating a triangulated mesh of solid regions and computing VVF from the resulting 3-D surfaces. Imaris requires a user-inputted ‘absolute intensity threshold’ parameter that is globally applied to all images in the z-stack. Therefore, differential light intensity among z-stacks contributes to less accurate binarization. Light intensity cannot be easily normalized within z-slices or across z-slices in Imaris. Selecting threshold parameters for our low, middle, and high output categories was done on a per-scaffold basis and was up to user discretion following the aforementioned protocol.

2.3.6. 3-D Particle Segmentation

The complete process for our 3-D Particle Segmentation approach includes intensity compensation, binarization, distance transform, and watershed. We first convert z-stacks into 3-D intensity images then pre-process the 3-D volume to reduce the data size and improve the image quality. We resize each 3-D volume according to a specified cubic voxel size, and we compensate for intensity variation over depth by subtracting each x-y plane with its 1% percentile. We binarize the 3-D volume by selecting foreground (tentative-particle) voxels using three sequential conditions: (1) The voxel intensity is larger than a minimum intensity, $I_{min}$; (2) The voxel intensity is not lower than the mean of neighboring voxels by more than $I_{diff}$. When particles are densely packed, the gap between particles is sometimes narrow, resulting in a void region that is brighter than $I_{min}$. These void voxels are identified using relative intensity because they are significantly dimmer than neighboring voxels; (3) The voxel intensity is higher than a maximum intensity, $I_{max}$. Because the relative brightness used in Condition (2) is based on absolute intensity difference, voxels with very high intensity may show high relative intensity variation that satisfies Condition (2). Therefore, we consider voxels with very high intensity as particle voxels, regardless if they satisfy Condition (2). Foreground (tentative-particle) voxels are marked as 1 if they satisfy Condition (3) or if they satisfy Conditions (1) and (2). We consider all other voxels as background (void space) voxels, marked as 0. To generate our low, middle, and high outputs, we set $I_{min}$ to the same absolute intensity threshold that was used for the corresponding image in Imaris for each category. For the remaining parameters, we set $I_{diff}=I_{min}∕3$, and $I_{max}=I_{max}{}^{\ast }3.33$ based on reasonable test outcomes.

Next, we use watershed to segment the foreground voxels into discrete particles. We compute the 3-D distance transform of the volume, $D$, as the distance of each voxel to the nearest background voxel. We find the local maxima of $D$ as the initial seeds. To avoid finding multiple seeds within the same particle, we identify close local maxima (defined as local maxima whose distance is smaller than the mean radius of the particles). If the intensities of the voxels between the close local maxima do not drop significantly relative to the local maxima, then we remove the lower local maximum and only keep the higher one. We then use 3-D watershed seeded with the remaining local maxima to segment the volume of $-D$.

Next, we refine the segmentation results by removing small discrete volumes. For each putative segmented particle from the previous step, we calculate the surface-to-volume ratio. If the ratio is larger than a threshold of 0.5, we remove these ‘false’ particles along with their seeds. We choose a threshold of 0.5 so that 1) most small false volumes and most false volumes with irregular shapes are removed and 2) most large true volumes with regular shapes are retained. We then apply watershed to $-D$ again using the remaining seeds, which allows some original ‘false’ particles to get absorbed into nearby ‘true’ particles. We recursively apply watershed to each resulting segmented volume, as long as the surface-to-volume ratios of the smaller volumes are smaller than the threshold. Finally, we smooth the segmented regions by removing sharp boundary voxels.

2.4. Statistical methods

Statistical analysis and plotting were performed using Prism 9. For experiments in 3.1, N = 10 and N = 5 independent simulated domains for spherical and non-spherical particles, respectively. Simple linear regression is used to study VVF relationships, while one phase decay is used to study the number of particles. To test scale-independence across particle diameters, p-values were calculated from an F test. For each experiment in 3.2 and 3.3, N = 5 independent simulated domains. All error is reported as the standard deviation.

3. Results and Discussion

3.1. How does particle composition influence VVF?

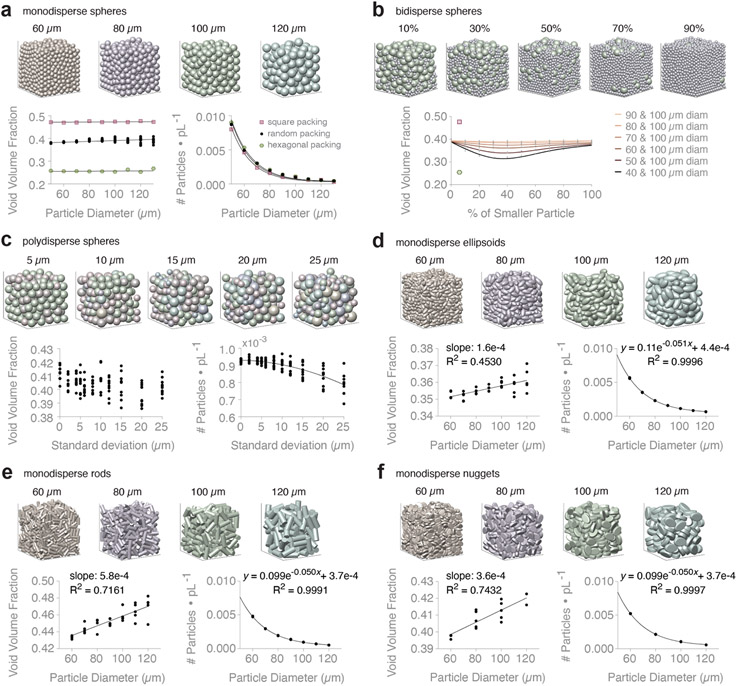
Particle packing theory tells us that VVF is scale-independent for monodisperse spheres, i.e., particle diameter should theoretically not influence VVF. However, this relationship is not always observed in real data because of particle polydispersity and stiffness, image resolution, and edge effects (11). We simulate a variety of granular scaffolds, referred to as particle domains, in order to observe how VVF changes with particle composition. VVF is defined as $\Phi =S∕V$, where $S$ is void space volume and $V$ is total volume. In our computational experiments, $S$ is the non-particle region within the convex hull, $V$, of the particle centers. Defining the void space in this way helps to reduce edge effects by focusing our computation on the interior of the scaffold. Our results for monodisperse spheres show a general trend of scale-independence for square (p-value = 0.1443), hexagonal (p-value = 0.2727), and random packing (p-value = 0.0002; slope = 3.1e-5) (Figure 1a, left). On average, Φ = 0.47, 0.26, and 0.39 for square, hexagonal, and random packing, respectively. We also fit an exponential decay for predicting the number of particles per picoliter for square (R² = 0.9967), hexagonal (R² = 0.9988), and random packing (R² = 0.9992), respectively:

$$\begin{gathered} y=0.18e^{-0.063x}+0.00042, \\ y=0.15e^{-0.057x}+0.00041, \\ y=0.15e^{-0.058x}+0.00045, \end{gathered}$$

where $x$ is particle diameter in μm (Figure 1a, right). Expanded data for these plots are shown in Supplementary Figure 4.

Figure 1. Void volume fraction (VVF) of simulated packed particles in 600 x 600 x 600 μm3 container.

a, Monodisperse spheres in square, hexagonal, and random packing configuration. Showing VVF and # of particles per picoliter (pL) for increasing particle diameter. N = 10 domains. b, Binary mixtures of spheres. Domain images are showing 40 + 100 μm diameter spheres at increasing percentage of the 40 μm diameter population (by volume). Plotting VVF of different binary mixtures (see key). For each pair of particle species, we report VVF at varying percent mixtures by volume. N = 10 domains. VVF of square packing (pink square) and hexagonal packing (green hexagon) shown for reference. c, Polydisperse spheres that follow a normal distribution with mean = 100 μm. Domain images are showing increasing polydispersity due to increasing standard deviation (σ). Showing VVF and # of particles per pL for increasing σ. N = 10 domains. d, Monodisperse ellipsoids. Showing VVF and # of particles per pL for increasing particle diameter. N = 5 domains. e, Monodisperse rods. Showing VVF and # of particles per pL for increasing particle diameter. N = 5 domains. f, Monodisperse nuggets. Showing VVF and # of particles per pL for increasing particle diameter. N = 5 domains. See Supplementary Figure 6 for simple linear regression equations of VVF data.

We next study bidisperse and polydisperse mixtures of spherical particles. For binary sphere packing, we homogeneously mix 100 μm diameter spheres with 40 to 90 μm spheres at different proportions. Details and validation of the simulation setup are shown in Supplementary Figure 1. Our outputs reveal that VVF is minimized around 35% of the smaller particle population (by volume) for all particle diameters (Figure 1b), which is consistent with the literature (17, 18). To studying polydispersity, we generate domains whose particle diameters follow a normal distribution with mean (μ) equal to 100 μm (Supplementary Figure 5). We range standard deviation (σ) from 0 to 25 μm and find that there is no clear relationship between σ and VVF (Figure 1c, left). In contrast, we see a dependence between σ and the number of particles per picoliter (R² = 6247), described by:

$$y=-0.00021x^2-0.00058x+0.93,$$

where $x$ is σ in μm (Figure 1c, right). Our results highlight the unreliability of VVF as a metric to distinguish granular scaffolds with variable polydispersity.

Lastly, we study VVF of non-spherical monodisperse particles to address less common particles used in granular biomaterials. We present data for ellipsoids, rods (cylinders), and nuggets (flattened egg-like shapes), where comparable particle diameters refer to the diameter of spheres with equivalent volume (Figure 1d-f). For each particle type, we fit a simple linear regression to VVF data. Small slopes are indicative of theoretical scale-independence for VVF, though non-spherical particles are influenced more by edge effects (Supplemental Figure 6). For comparison, the average VVF across our experimental groups is Φ = 0.39, 0.36, 0.45, 0.41 for spheres, ellipsoids, rods, and nuggets, respectively. Our results support known findings that ellipsoids can pack more tightly than spheres in random packing (19), while rods in random packing produce larger VVF compared to spheres, ellipsoids, and nuggets. Again, we can describe the relationship between particle diameter and the number of particles per picoliter for ellipsoids (R² = 0.9996), rods (R² = 0.9991), and nuggets (R² = 0.9991), respectively:

$$\begin{gathered} y=0.11e^{-0.051x}+0.00044, \\ y=0.099e^{-0.050x}+0.00037, \\ y=0.099e^{-0.050x}+0.00037, \end{gathered}$$

where $x$ is particle diameter in μm (Figure 1d-f, right). Relative to the number of particles, VVF is more variable across replicate granular scaffolds. For an in-depth review of particle packing that discusses VVF, we recommend (18).

3.2. How does microscope magnification affect VVF, and how accurate are 2-D approximations of VVF?

In the biomaterials field, computing VVF of granular scaffolds typically starts with obtaining fluorescent microscope images of the sample. Imaging techniques require setting an objective lens magnification (with corresponding numerical aperture), which affects the field of view. As magnification increases, fewer and fewer particles stay in view, and therefore, a smaller sample of void space is used when computing VVF. To study how magnification influences the accuracy of VVF, we mimic higher magnification by cropping simulated particle domains to achieve an image-enlarging effect (Figure 2a). At each magnification, we maintain a similar voxel count (10⁷), which increases the sampling rate. In this way, we see finer detail for each particle, which is what we would expect from a higher magnification lens in a real microscope. Real scaffold images at 10x, 20x, and 40x magnification are used to calibrate our crop percentages. In these computational experiments, we avoid edge effects by cropping, so we simply define void space as the non-particle regions. We simulate five different scaffolds that are cropped to 10x, 20x, and 40x magnification and report the corresponding VVF (Figure 2b). Our results reveal that VVF measured at 10x versus 40x magnification can produce greater than 5% relative difference. In general, the variability in VVF increases as magnification increases, which we expect considering that smaller regions, and therefore fewer particles, are being sampled when working at higher magnifications. We use our simulated data from Figure 1a to derive an equation for how standard deviation of VVF changes as a function of the number of particles in the sample (Supplementary Figure 7).

To isolate the influence of resolution on VVF, we range the voxel size $(dx)$ for our 10x magnification particle domain. Smaller values of $dx$ correspond to finer detail and increased resolution (Supplementary Figure 8a), which can be achieved in practice with better camera specs or image tiling. Our experiments are performed using significantly fewer pixels compared to real microscope images due to memory constraints. Nonetheless, results reveal that image resolution does not dramatically influence VVF within reasonable $dx$ (Supplementary Figure 8b,c). For example, a jump from $dx$ = 0.8 (920 pixels along x-axis) to $dx$ = 5 (147 pixels along x-axis) results in a 1.002-fold increase in VVF.

We next consider the common approach of approximating VVF of a granular scaffold by computing the average void area fraction across 2-D z-slices. We are interested in understanding how sampling 2-D z-slices influences the accuracy of the VVF approximation. To study this, we simulate five different scaffolds of 100 μm diameter particles at three magnifications and track how VVF changes as a function of the z-gap size (Figure 3a). For each z-gap size, we extract the z-slices that lie within the middle half of the scaffold and that are ‘z-gap’ apart from one another, which mimics some wet lab practices aimed at avoiding edge effects. We then compute the average void area fraction among z-slices and report the accuracy of this approximation relative to the true VVF of the scaffold at the given magnification. The true VVF values are reported in Supplementary Table 1. As expected, as z-gap increases, relative accuracy decreases, and fluctuations become more dramatic. Our results show that a z-gap of less than ~15 μm is necessary to achieve a stably accurate approximation for all magnifications, with most scaffolds converging to within 5% of the true VVF at these step sizes. Relating this to particle size, these results translate to a z-gap of less than ~15% of the average particle diameter in the scaffold.

With this information, we select a reasonable z-gap of 13 μm and study how the number of z-slices influences the relative accuracy of the VVF-approximation (Figure 3b). Starting at the bottom of the scaffold, we sample z-slices at increments of 13 μm until the entire length of the scaffold along the z-axis has been sampled. We report the relative accuracy of the average void area fraction as a function of the number of z-slices. As expected, relative accuracy improves as the number of z-slices increases. Our results show that after ~20 z-slices are taken, relative accuracy stays within 4% for all magnifications, which corresponds to a z-slice count of ~20% of the average particle diameter in the scaffold.

Our computational experiment indicates that both magnification, z-gap, and the number of z-slices play a role in the accuracy of approximating VVF with average void area fraction among 2D-slices. Our conclusions of a z-gap less than 15 μm and at least 20 z-slices (Figure 3) aligns with protocols in the field used for real granular scaffolds (11). We next explore how magnification and the method of analysis affects the precision of VVF measurements on real microscope images.

3.3. How sensitive is VVF to the method of analysis?

We move from simulated data to real granular scaffold data and study four different examples of software used to compute VVF. The first software is Fiji, an open-source image processing software that has built-in methods for processing microscope images and reporting void area fraction for each z-slice. The second method is simple in-house MATLAB code that uses built-in morphological operations to binarize and threshold 2-D z-slice images in order to compute void area fraction for each z-slice. The third software is Imaris, an image analysis software specifically designed for microscope images that converts 2-D slice data into 3-D surfaces renders and computes multiple measurements, including VVF. Lastly, we have developed a custom 3-D approach in Python for computing VVF that converts 2-D z-stack data into a 3-D matrix. The code segments and labels individual 3-D particles from 2-D microscope z-stacks, which can then be used to extract VVF. We refer to this method as 3-D Particle Segmentation.

All software that analyze real images implement techniques from image processing to classify void space versus non-void-space pixels, and these steps require user input. We are interested in studying the variability of VVF that can arise from a reasonable range of user-inputted threshold parameters or settings. For each software, we determine a user-inputted range that generates a ‘low,’ ‘medium,’ and ‘high’ version of the output image, where the categories represent the relative number of void space pixels in the final binarized image. Specifically, low output images show many ‘false particle’ regions but at least one ‘false void’ region; middle output images show both ‘false particle’ and ‘false void’ regions; and high output images show many ‘false void’ regions but at least one ‘false particle’ region.

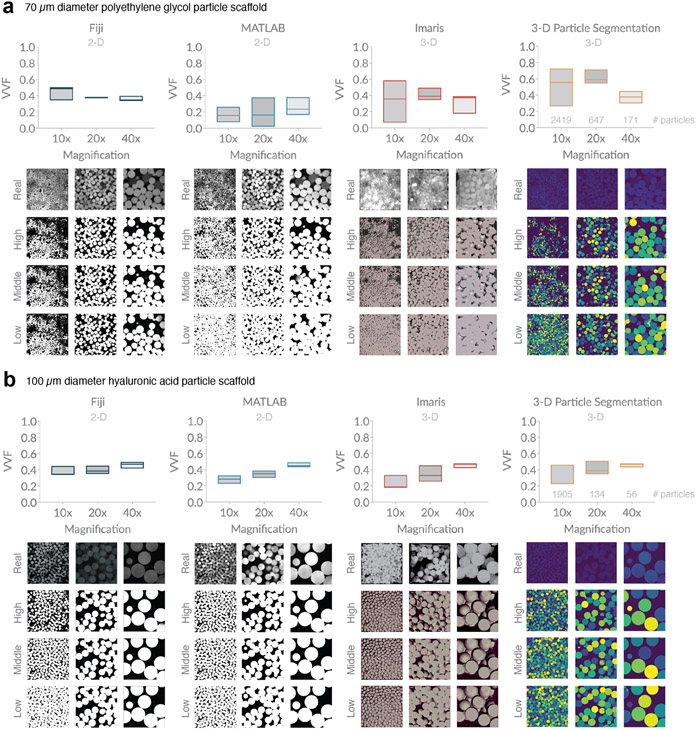
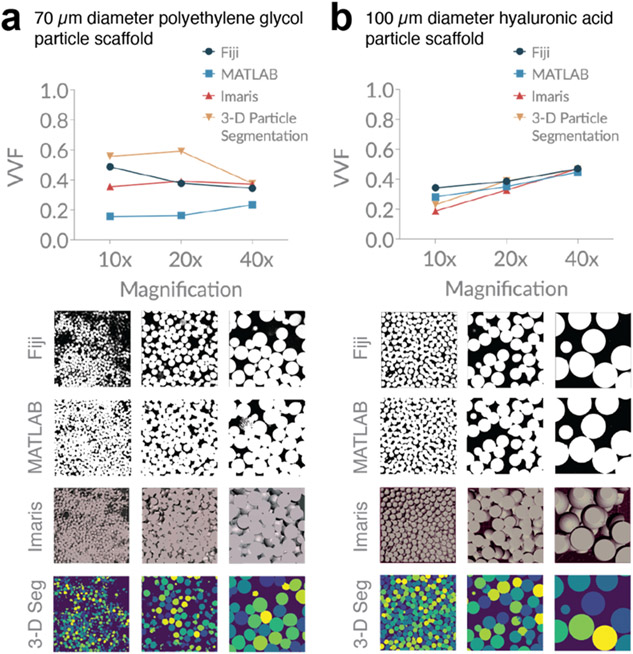
To study VVF of granular scaffolds made in lab, we have chosen to focus on fluorescently-labeled particles as opposed to fluorescently-labeled dextran (which illuminates the void space) in order to take advantage of software developed by our lab that focuses on particles. Both labeling options are conceptually the same. We study two different microporous annealed particle (MAP) scaffolds, which are a specialized type of granular scaffold comprising interlinked hydrogel microparticles (microgels) (20). The first MAP scaffold contains ~70 μm diameter microgels made of modified polyethylene glycol (14), and the second contains ~100 μm diameter microgels made of modified hyaluronic acid (15). For each piece of software, we analyze 10x, 20x, and 40x images of each scaffold and plot VVF based on input parameters that result in images classified as low, medium, and high, where the bottom, middle, and top line of each box plot corresponds to the image classifications, respectively (Figure 4). Below each software type, we show representative images from each magnification, as well as the corresponding binarized image output for our three categories. We see notable variability among different types of software, among different magnifications, and even among the reasonable range of user-inputted settings. While there is no statistical difference in VVF range (high minus low) among the four software (Supplementary Figure 9), we do notice wider box plots in our 70 μm diameter particle scaffold compared to our 100 μm diameter particle scaffold. 70 μm diameter particles will inherently be more difficult to image relative to 100 μm diameter particles because smaller particles reflect more light. In addition, discrepancies in the homogeneity of fluorescent labeling across particles will influence image quality. These results highlight how thresholding effects are impacted by image quality.

Figure 4. Variation in void volume fraction (VVF) of granular scaffolds across different software, magnification, and user-bias.

a, Scaffolds comprising 70 μm diameter polyethylene glycol (PEG) particles were analyzed for VVF using Fiji, a custom MATLAB code, Imaris software, and a custom particle segmentation code. For each magnification, we report box plots indicating a low (bottom line), middle (middle line), and high (top line) VVF that reflect variation in user-inputted parameters or settings. Below each software plot, we show sample z-slice microscope images from the sample, as well as low, middle, and high binarization outputs. Scaffolds were imaged with the following z-gap and number of z-slices: (10x) 4.075 μm, 36 slices, (20x) 1.20 μm, 118 slices, (40x) 1.00 μm, 142 slices. b, Scaffolds comprising 100 μm diameter hyaluronic acid (HA) particles were analyzed in the same manner as (a). Z-gap and number of z-slices were as follows: (10x) 3.875 μm, 40 slices, (20x) 1.20 μm, 101 slices, (40x) 1.10 μm, 192 slices. The number of particles at each magnification are approximated with the 3-D Particle Segmentation code and reported above the x-axis in the corresponding plots for (a) and (b).

For each scaffold, we also include a summary plot that compares the middle-range VVF values for all methods at each magnification (Figure 5). Our results reveal discrepancies among different magnifications, as well as different software. For example, Figure 5b shows a range (absolute measure) in VVF of ~20% among software outputs for 10x magnification.

Figure 5. Microscope magnification and analysis software influences VVF measurements.

a, Our PEG scaffolds highlight the variation in VVF that can be seen across different software when ‘middle’ range parameters and settings are used. b, Our HA scaffolds highlight the variation in VVF that can be seen across different microscope magnifications. Sample z-slice images are shown below for comparison.

We unfortunately have no way of testing the accuracy of the outputs since no gold standard exists, but our results are striking because they reveal how the most commonly-reported scaffold measurement of VVF may, in fact, be subject to substantial variance. At minimum, they reveal that VVF is highly dependent upon parameters used in their computation, including microscope magnification, the software being used, and user-inputted threshold settings. When imaging granular scaffolds, 40x magnification produces sharper particle borders, which makes void space delineation more accurate. Figure 2b indicates that 40x magnification shows the greatest variation in VVF relative to lower magnifications; however, the relative percent difference of ~10% suggests decent precision among samples. Therefore, sampling several regions of interest at 40x magnification across the scaffold and reporting the average VVF should give a reasonable approximation to true VVF. From a microscopy standpoint, VVF accuracy will be optimized by maximizing the size of the sampled region and the image resolution, such as with image tiling at high magnification. Despite the inability to determine the accuracy of VVF from microscope images, relative VVF values can be more accurately compared within an experiment by using the same method with consistent parameter settings; however, this is only true if image quality is comparable across samples.

4. Conclusion

In the biomaterials field, void space characterization is often summarized with a single reported value of VVF. Since there is currently no gold standard for measuring VVF of real granular scaffolds, we generate simulated packed particle scaffolds so we may attain the true VVF. We report the VVF for a library of 134 different categories of ideal granular scaffolds with varying particle size, form, and composition. For monodisperse scaffolds, we generally see variability in VVF across replicate scaffolds, whereas we see invariability in the number of particles per picoliter. Given parameters like particle diameter and form, we report equations to predict the VVF for monodisperse scaffolds; however, relative to VVF, our results reveal that one can more reliably predict the number of particles in a scaffold.

In practice, VVF is computed from microscope z-slice images; however, the accuracy of VVF is highly dependent upon multiple factors, including microscope magnification, the region of interest, z-slice sampling, z-intensity corrections, the software used to compute VVF, and user-selected settings. To address these issues, we analyze both ideal and experimental data. By using 3-D simulated scaffolds, we have access to the true VVF by which to compare approximations. Our deterministic study reveals how microscope magnification influences the accuracy of VVF. While average VVF is consistent, our results show that higher magnifications produce more imprecise approximations. This is true because increasing the magnification reduces the sample size. Next, we extract 2-D z-slices from our simulated scaffolds to study how the microscope step size (z-gap) and the number of sampled z-slices influence the VVF measurement. Based on the results from our study of 100 μm diameter particle scaffolds, we recommend using a z-gap of less than 15 μm (15% of the average particle diameter in the scaffold) and at least 20-slices (20% of the average particle diameter in the scaffold) for optimal sampling.

Since protocols for measuring VVF from microscope images are not standardized, we study sources for variation in VVF among techniques. We use four different software options to analyze microscope images of real granular scaffolds at different magnifications. We sample a range of user-inputted parameters or settings to obtain a reasonable range of VVF outputs for each software, and our results highlight the variation in VVF that can be attributed to magnification, software, and user-bias when selecting parameters. In contrast to our simulated results that reveal increased VVF variation at 40x magnification across multiple samples, experimental data shows decreased variation at 40x magnification across different thresholds for the same sample. Recall that 40x magnification produces the sharpest microscope images, leading to greater consistency across binarizing threshold values; however, this precision across thresholds does not speak to accuracy since we do not know the true VVF of non-simulated scaffolds. Sampling multiple regions of interest at the highest magnification or tile-stitching images will help to obtain the most accurate VVF for real granular scaffolds.

Further investigation may expand upon our work to elucidate the relationship between VVF and packed particle scaffolds, such as using soft-body simulations to capture more realistic hydrogel microparticles or considering the influence of signal-to-noise ratio in microscope image analysis. In addition, while it is important to be mindful of parameter nuances when computing and reporting VVF, our findings also highlight the need for more quantitative descriptors for characterizing the void space of granular scaffolds.