Abstract
Our understanding of the genetics of the human cerebral cortex is limited both in terms of the diversity and the anatomical granularity of brain structural phenotypes. Here we conducted a genome-wide association meta-analysis of 13 structural and diffusion magnetic resonance imaging-derived cortical phenotypes, measured globally and at 180 bilaterally averaged regions in 36,663 individuals and identified 4,349 experiment-wide significant loci. These phenotypes include cortical thickness, surface area, gray matter volume, measures of folding, neurite density and water diffusion. We identified four genetic latent structures and causal relationships between surface area and some measures of cortical folding. These latent structures partly relate to different underlying gene expression trajectories during development and are enriched for different cell types. We also identified differential enrichment for neurodevelopmental and constrained genes and demonstrate that common genetic variants associated with cortical expansion are associated with cephalic disorders. Finally, we identified complex interphenotype and inter-regional genetic relationships among the 13 phenotypes, reflecting the developmental differences among them. Together, these analyses identify distinct genetic organizational principles of the cortex and their correlates with neurodevelopment.
The human cerebral cortex is morphologically complex, with extensive interindividual and inter-regional variation associated with cognition, behavior, health, development and ageing1-4. This variation is partly genetic5-8, with several common genetic variants associated primarily (although not exclusively) with cortical thickness (CT), surface area (SA) and volume6,9-12. Less is known about the common variant genetics (including single-nucleotide polymorphisms (SNPs)) associated with more complex cortical morphometric phenotypes, such as folding or curvature or with microstructural magnetic resonance imaging (MRI) measures of cortical myelination and cytoarchitecture. We also still do not fully understand how complex cellular and molecular mechanisms of neurodevelopment give rise to these distinct cortical brain phenotypes and their links to neurodevelopmental conditions. It is also unclear if common genetic variants contribute to cephalic disorders, although the impact of de novo damaging variants has been well documented13. Finally, the role of common genetic variants in regional cortical phenotypes and organization is also unclear. This is important as regional organization may partly emerge from heterochronous regional differences in gene expression14.
To address these questions, we conducted 2,347 genome-wide association studies (GWAS) for 13 global and 2,334 regional cortical brain phenotypes in 36,663 individuals from the UK Biobank (UKB)15 and the Adolescent Brain Cognitive Development (ABCD)16 cohorts. These included eight cortical macrostructural phenotypes extracted from high-resolution anatomical MRI and five cortical microstructural phenotypes extracted from diffusion MRI, which were estimated both globally and across 180 bilaterally averaged regions based on the Human Connectome Project parcellation scheme17 (Fig. 1; Methods).
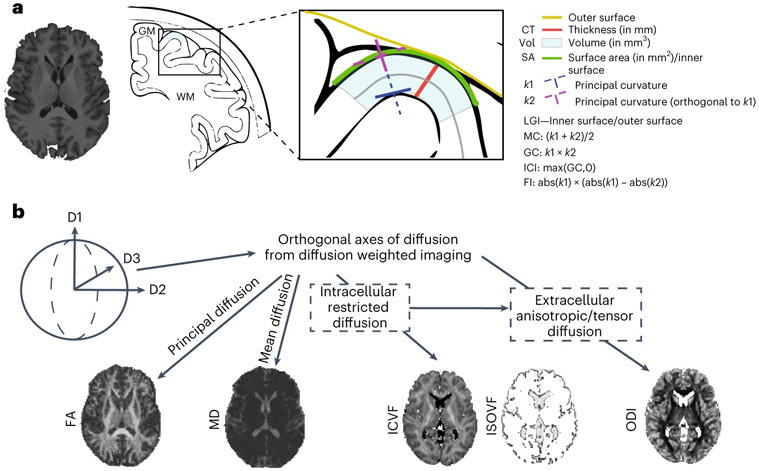
Fig. 1 ∣. Schematic overview of 13 brain MRI phenotypes and the genetic analyses.
a, We considered eight cortical macrostructural phenotypes: CT, cortical SA, please note that this is for illustrative purposes and that the SA is measured at midthickness, gray matter volume (Vol), FI, ICI, LGI, MC and GC. b, We also considered five cortical microstructural phenotypes: FA, MD, ICVF (also called neurite density index (NDI)), ISOVF and ODI. Each phenotype was measured globally (total or mean for the whole cortex) and regionally at each of 180 bilaterally averaged cortical regions defined by the Human Connectome Project parcellation scheme. We conducted genome-wide association studies of all phenotypes after removing outliers and investigated the latent structure of all phenotypes, developmental trajectories and cell type specificity and genetic organization.
Genome-wide associations of global cortical phenotypes
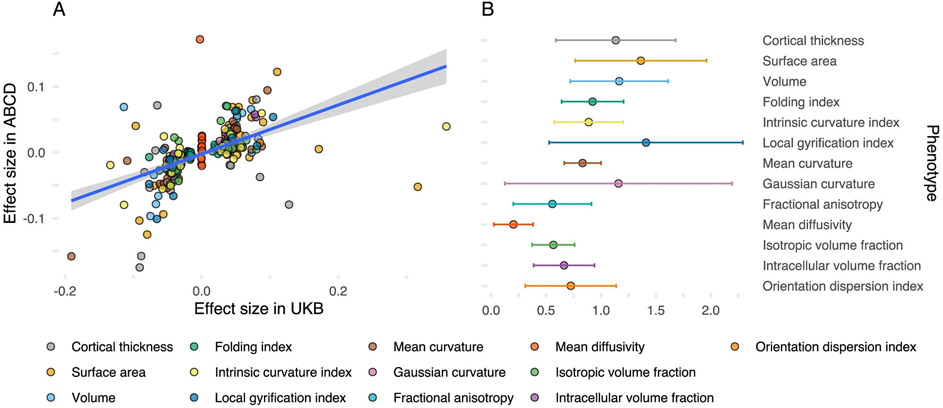
We first conducted GWAS of 13 global structural MRI cortical phenotypes (henceforth ‘global phenotypes’; Fig. 1) in the UKB (nmax = 31,797). The phenotypes include macrostructural metrics such as SA, volume, CT, folding index (FI), intrinsic curvature index (ICI), local gyrification index (LGI), mean curvature (MC) and Gaussian curvature (GC). It also includes microstructural measures such as fractional anisotropy (FA), mean diffusivity (MD), isotropic volume fraction (ISOVF), intracellular volume fraction (ICVF) and orientation diffusion index (ODI). We identified 314 independent (r2 < 0.1, 1,000 kb) genome-wide significant (P < 5 × 10−8) loci. Eighty-one of these were significant at the more stringent experiment-wide significance threshold (P < 4.58 × 10−11); Supplementary Table 1; Methods). We additionally conducted GWAS for the same 13 global phenotypes in individuals of predominantly European genetic ancestries in ABCD (nmax = 4,866). For 237 GWAS loci in UKB for which data were available in ABCD, 204 SNPs (86%) had concordant sign of genetic association (P < 0.001, two-tailed binomial sign test), compared to 119 (~50%) under the null hypothesis that only 50% of the effects have concordant direction. Furthermore, 40 (16%) of these SNPs had concordant effect direction and had P values (P) < 0.01, against an expectation of 1.18 (0.5%). Three had concordant effect direction and P < 1 × 10−5 against an expectation of <1 (0.0005%), respectively, under the null, thereby rejecting the null hypothesis. In ABCD, 34 of these SNPs were significant after false discovery rate (FDR) correction and 13 after Bonferroni correction. We identified a modest positive correlation of effect size (Pearson’s r = 0.54, 95% confidence interval (CI) 0.45–0.63; Extended Data Fig. 1). Additionally, genetic correlations between UKB and ABCD were positive and high18 (Extended Data Fig. 1 and Supplementary Table 2) for all 13 phenotypes except MD, albeit with wide CIs due to the relatively small size of the ABCD dataset. The robust replicability between two cohorts with different median ages (UKB: 64 and ABCD: 10) is notable as brain structure and its genetic influences change over time19,20.
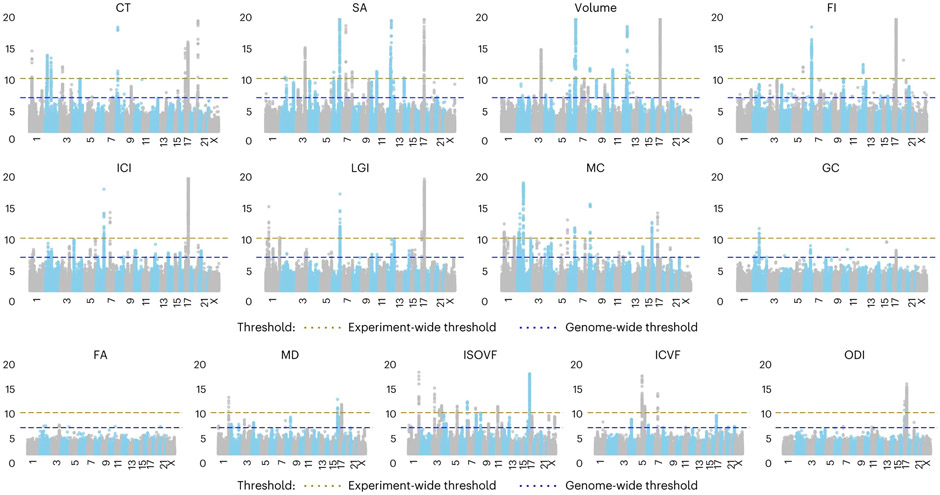
Given the observed shared genetics between UKB and ABCD, we conducted inverse-variance weighted meta-analyses21 to combine the GWAS results across both UKB and ABCD. These meta-analyses identified 367 genome-wide significant loci, of which 89 were significant at an experiment-wide threshold (Supplementary Table 3). This ranged from 50 genome-wide significant (P < 5 × 10−8) loci (18 experiment-wide significant, P < 4.58 × 10−11) for SA to six GWAS loci (with 0 experiment-wide significant) for FA (Fig. 2), with some SNPs being associated with two or more phenotypes. In total, there were 75 independent experiment-wide significant SNPs across all phenotypes. For all GWAS, the attenuation ratio (Methods) was not statistically different from 0 (Supplementary Table 4), indicating no inflation in test statistics due to uncontrolled population stratification. All phenotypes had significant SNP heritabilities (linkage disequilibrium score regression coefficient (LDSC)22: 0.06 for FA to 0.37 for SA), with higher SNP heritabilities for cortical macrostructural metrics (Supplementary Table 4) compared to cortical microstructural phenotypes.
Fig. 2 ∣. Manhattan plots of GWAS meta-analysis of 13 global MRI phenotypes.
Blue dotted line indicates the threshold for genome-wide significance (P = 5 × 10−8), and the brown dotted line indicates the threshold for experiment-wide significance (P = 4.58 × 10−11). Each dot on the x axis indicates an SNP and the y axis indicates the −log10(P values). All analyses were conducted by linear mixed models.
For SA and CT, we identified high genetic correlations with previous GWASs (SA, rg = 0.91 ± 0.03; CT, rg = 0.83 ± 0.04)6. Notably, despite the smaller sample size of the current GWAS meta-analyses, we identified a higher number of genome-wide significant loci for both SA (50 versus 19) and CT (31 versus 3) and had higher statistical power measured using mean χ2 (SA, 1.30 for current GWAS versus 1.23 for ENIGMA; CT, 1.23 for current GWAS versus 1.18 for ENIGMA). The gain in power is likely due to reduced heterogeneity in imaging and genotyping in the current study compared to ENIGMA. All three significant loci for CT and 15 of the 19 significant loci for SA from ENIGMA were significant in our GWAS with concordant effect directions.
Of the 75 independent experiment-wide significant SNPs or their proxies (r2 > 0.8 in CEU or GBR populations) only 11 were not associated with any other neuroimaging phenotype, indicating substantial pleiotropy (Supplementary Table 5).
Latent dimensions of global phenotypes
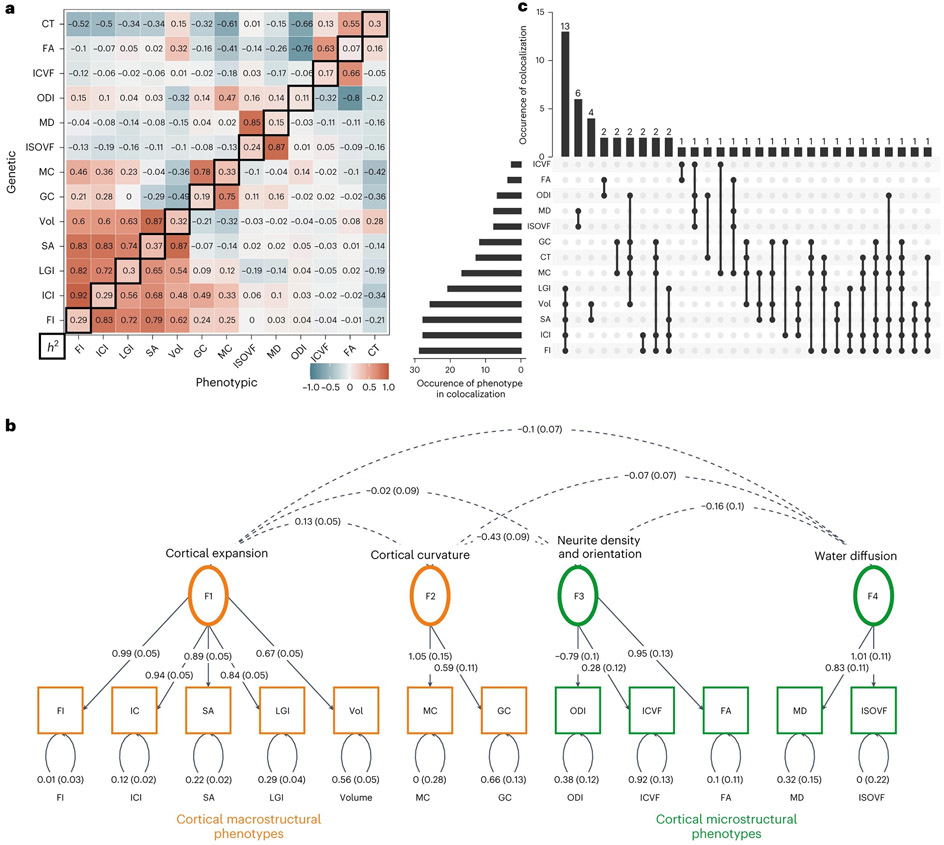
To better understand pleiotropy across the 13 global phenotypes, we estimated bivariate genetic and phenotypic correlations (Supplementary Table 6 and Fig. 3a). Patterns of genetic and phenotypic correlation across phenotypes were highly similar (Mantel’s test, r = 0.89, P = 1 × 10−4), in line with Cheverud’s conjecture23. Clustering of the genetic correlation matrix using multiple different methods consistently found that 12 of the 13 phenotypes (excluding only CT) formed four clusters relating to cortical expansion, curvature, water diffusion and neurite density and orientation (Supplementary Fig. 1). For the phenotypic correlation matrix, 11 of the 13 phenotypes formed four clusters, with CT and ICVF clustering separately (Supplementary Fig. 1).
Fig. 3 ∣. Pleiotropy among the 13 global phenotypes demonstrated by genetic/phenotypic correlations, structural equation modeling and colocalization analysis.
a, Phenotypic and genetic correlation matrices. The upper matrix triangle shows bivariate genetic correlations for each pair of phenotypes estimated using LDSC, and the lower triangle shows the pairwise phenotypic correlations (Spearman’s coefficient). The diagonal indicates the SNP heritability of each phenotype based on LDSC. Phenotypes are ordered based on hierarchical clustering of the genetic bivariate correlation (hierarchical clustering on the phenotypic correlation matrix resulted in a near identical ordering). b, Genomic SEM path diagram demonstrating the underlying latent structure of 12 of the 13 global phenotypes and the interfactor genetic correlations. Dashed lines connecting two variables, covariance relationships; double-headed arrows connecting a variable to itself, variance estimates; single-headed arrows pointing from independent variables to dependent variables, regression relationships. Circles indicate latent variables, and squares indicate measured phenotypes. The model was identified using unit variance identification such that the variance of the latent factors was set to one, and the dotted arrows across the factors can be interpreted as genetic correlation estimates. c, UpSet plot of the results of colocalization analysis demonstrating the numbers of genomic loci that colocalize between the 13 phenotypes. The dots correspond to the colocalized clusters, with the number of clusters in the vertical bars. The number of times a phenotype colocalizes is provided in the horizontal bars. Additionally, summary of clusters identified through GSEM and colocalization analyses and their relationship with other terms used in this study are also provided. Vol, gray matter volume.
Subsequently, we used genomic structural equation modeling (GSEM)24 to identify latent structures among the 13 global phenotypes. After excluding CT due to singleton-clustering and moderate genetic correlations (rg between −0.3 and −0.7 with eight of the 12 cortical phenotypes (Fig. 3a and Supplementary Fig. 1)), exploratory followed by confirmatory factor analyses identified a correlated four-factor model with the acceptable fit (comparative fit index (CFI) = 0.89, standardised root mean squared residual (SRMR) = 0.13; Supplementary Table 7 and Fig. 3b). The four factors were similar to the four clusters and relate to cortical expansion (factor 1), curvature (factor 2), neurite density and orientation (factor 3) and water diffusion (factor 4). Phenotypic factor analyses produced four similar factors, albeit only after the removal of CT that did not cluster with any phenotypes and ICI that exhibited high cross-loading onto two factors (Supplementary Note 1 and Supplementary Fig. 2).
Colocalization analysis of the experiment-wide significant associations supported the clustering and GSEM analyses and identified 56 colocalized genetic clusters among the global phenotypes (posterior probability of colocalization > 0.6). We use the term ‘cluster’ to refer to a group of phenotypes within the 13 global phenotypes that share causal variants in an LD-defined genomic region. The highest number of colocalized loci was for cortical expansion phenotypes, followed by water diffusion, neurite density and orientation phenotypes and then curvature (Supplementary Table 8 and Fig. 3c). Thus, with the exception of CT, cluster analysis, GSEM and colocalization analysis thus convergently indicate four latent factors, each phenotypically represented by two or more MRI phenotypes.
Causal relationships between cortical expansion phenotypes
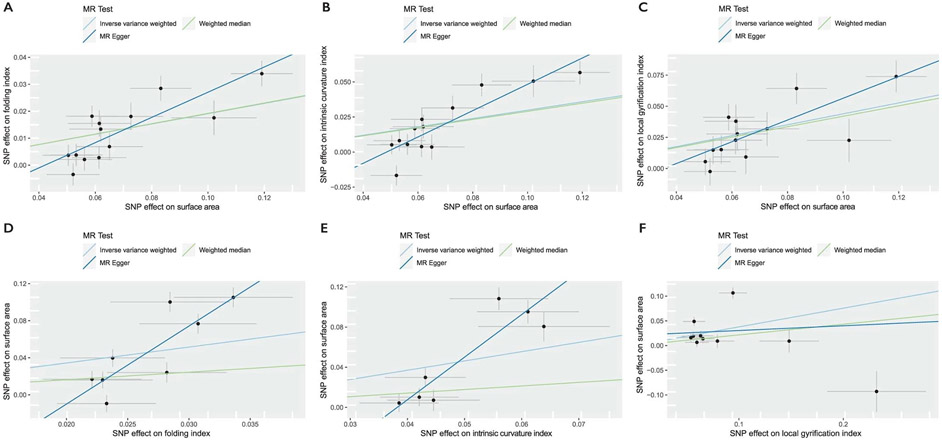
We next used Mendelian randomization (MR)25 to investigate whether the genetic relationships between phenotypes represent causal mechanisms, especially among the five cortical expansion phenotypes. We tested three theories of causation. First, consistent with the radial unit hypothesis26 which suggests that SA emerges from the number of cortical columns but thickness emerges from the number of cells within a cortical column, we would not expect causal effects between SA and CT. Indeed, we observed no significant evidence for a causal association between SA and CT. Second, because the volume is geometrically related to SA and estimated by the product of SA and CT, we expected to find a bidirectional causal relationship between SA and volume, and indeed, we found evidence for this. Third, previous research27-30 suggests that sulco-gyral folding emerges from differential tangential expansion of the cortex, partly due to the heterogeneous cortical distribution of progenitor cells31,32, suggesting a causal relationship of SA on folding (FI, LGI and ICI). Consistent with this, we found robust evidence that genetically predicted SA is associated with an increase in certain measures of folding (FI, LGI and ICI), but no evidence for reciprocally robust causal effects of folding metrics on SA (Supplementary Tables 9-11, Supplementary Note 2 and Extended Data Figs. 2 and 3). Together, these analyses suggest causal relationships between SA and some measures of folding.
Developmental and cellular profiles of global phenotypes
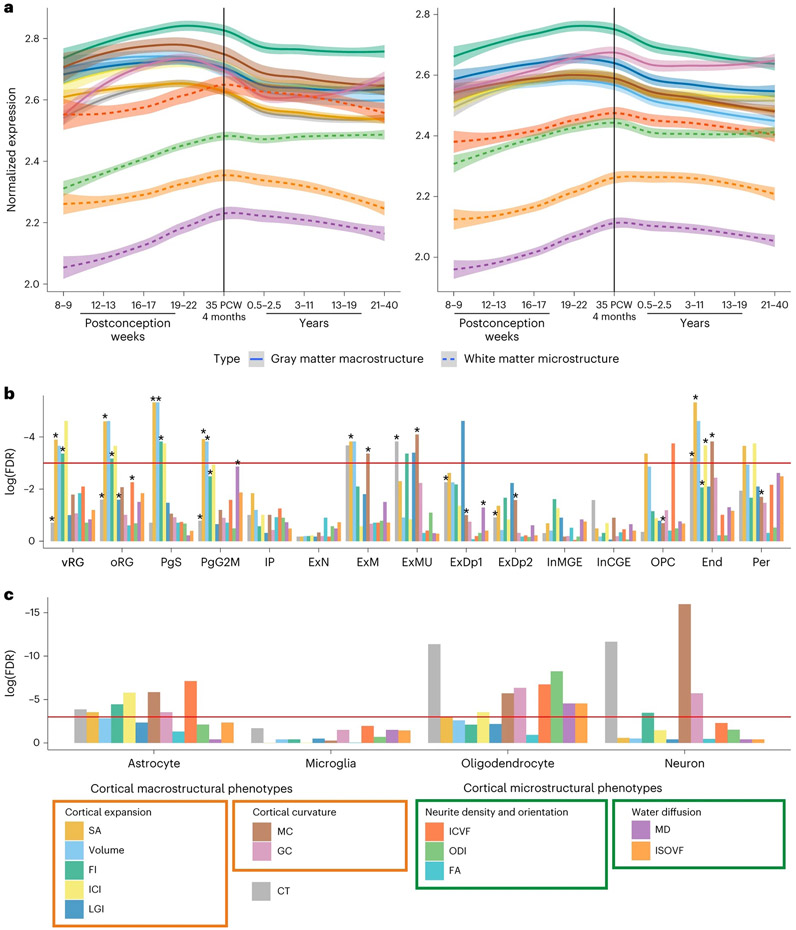
The complex genetic architecture among the 13 global phenotypes likely represents shared and distinct developmental and cellular processes. To better understand this, we aggregated SNP-based P values to gene-based P values using MAGMA33 and H-MAGMA34 and investigated if these genes exhibited specific developmental trajectories of gene expression using postmortem brain tissue data from PsychEncode35. We excluded FA due to the small number of genes identified. Genes associated with six of the seven macrostructural phenotypes had high relative expression prenatally, a peak in the late midgestation period (~19 to 22 postconception weeks (PCW)) and a decline in gene expression postnatally. In contrast, the four microstructural phenotypes were associated with genes that had peak expression at birth, followed by a less steep decline, or increased expression postnatally (Fig. 4a and Supplementary Table 12).
Fig. 4 ∣. Enrichment of GWAS signals in different cell types during development.
a, Developmental trajectories of average gene expression in cortical postmortem-bulk RNA data (PsychEncode) for all significant genes (FDR < 0.05, n = 34–1,113; Supplementary Table 12) identified using H-MAGMA (left) or MAGMA (right) for 12 of the 13 global phenotypes. Data for FA are not shown as too few genes were identified as significant. The shaded region indicates 95% confidence intervals. b, Results of enrichment analyses for cell-specific gene expression from midgestation. FDR-corrected log10(P values) for gene enrichment using genes identified from MAGMA (multiple regression) are plotted. The red line indicates the significance threshold at FDR-corrected P ≤ 0.05. Additionally, significant enrichments identified using H-MAGMA genes are indicated with an asterisk. c, Results of enrichment analyses from cell-specific epigenetic marks from postnatal cortex identified using LDSC-based enrichment. End, endothelial cells; ExDp1, excitatory deep layer neurons 1; ExDp2, excitatory deep layer neurons 2; ExM, maturing excitatory neurons; ExN, migrating excitatory neurons; ExMU, maturing excitatory neuron, upper enriched; InCGE, CGE interneuron; InMGE, MGE interneuron; IP, intermediate progenitors; OPC, oligodendrocyte precursor cells; oRG, outer radial glia; PgS and PgG2M, cycling progenitors, S phase and G2-M phase, respectively; Per, pericytes; vRG, ventral radial glia.
The different trajectories likely reflect different underlying cellular compositions for these phenotypes. Focusing on the developing brain, using sc-RNAseq data from psychENCODE14, we identified enrichment for intermediate progenitor cells for SA, volume and FI (Supplementary Table 13). To provide further temporal resolution, we investigated enrichment using scRNA-seq data from the first trimester (6–10 PCW)36 and scRNA-seq37 and scATAC-seq38 data from midgestation (marked by neural progenitor expansion)39-41. We did not identify any enrichment with cell types in the first trimester (Supplementary Table 14), but FI, volume and SA (cortical expansion phenotypes) were enriched for progenitor cells during midgestation (Supplementary Tables 15 and 16 and Fig. 4b), specifically for progenitor cells in the S phase and G2-M phases of mitosis. Additionally, CT and MC were enriched for multiple neuronal and glial cell types in both datasets, suggesting that these phenotypes are a composite of multiple cell types.
Considering the postnatal brain, there was no significant enrichment of genes in scRNA-seq data from psychENCODE (ST 17). However, analyses using epigenetic signatures of four broad cell types42 identified enrichment across multiple phenotypes (Fig. 4c and Supplementary Table 4). For instance, cortical microstructural phenotypes were primarily enriched for epigenetic markers in oligodendrocytes and astrocytes, but not neurons, consistent with the idea that these phenotypes primarily reflect myelination and related processes43. Taken together, these results demonstrate that genes underlying the 13 global phenotypes have different developmental trajectories reflecting specific cellular developmental dynamics.
Cortical expansion and neurodevelopmental conditions
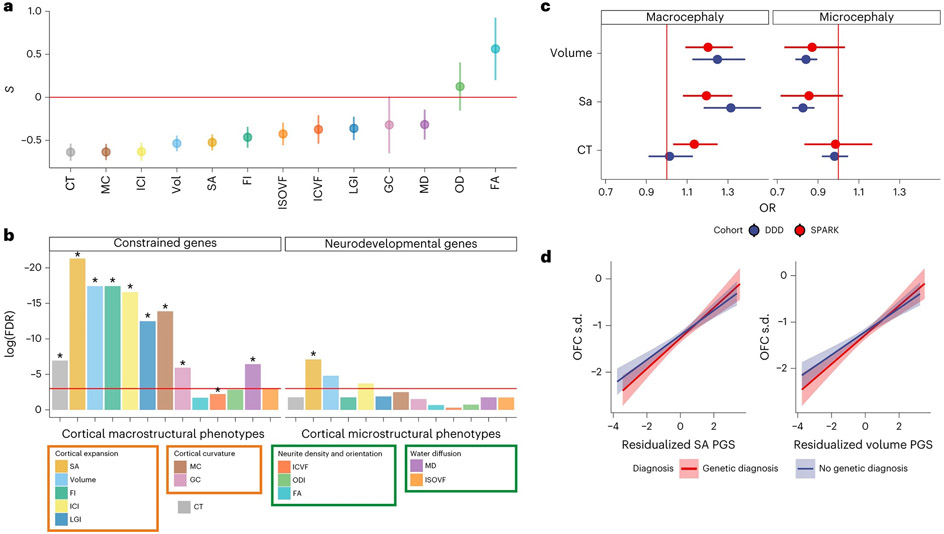
Given the enrichment of several of the global phenotypes with prenatal cellular and developmental processes, we hypothesized that these phenotypes are under negative selection pressures. Modeling the relationship between the minor allele frequency of the SNP and variance in effect size to quantify genome-wide signatures of selection using SBayesS44 suggested that the majority of the cortical macrostructural phenotypes are under significant negative selection (FDR q < 0.05; Fig. 5a and Supplementary Table 19). Additionally, we tested if the GWAS signals for the global phenotypes were enriched for constrained genes (that is, genes from which damaging variants are removed by natural selection45, genes associated with severe neurodevelopmental conditions46 or microcephaly). Cortical macrostructural phenotypes were significantly (FDR q < 0.05) enriched for highly constrained genes (pLOUEF < 0.37), and SA was enriched for genes associated with neurodevelopmental conditions (Supplementary Tables 20 and Fig. 5b). However, we identified no enrichment for genes linked to microcephaly, possibly because (1) several genes associated with microcephaly and other relevant cephalic disorders (for example, lissencephaly and holoprosencephaly) are yet to be discovered or properly documented, or (2) clinical microcephaly (and macrocephaly) might be genetically distinct from normative variation in brain size.
Fig. 5 ∣. Signatures of constraint and links to neurodevelopment for the global phenotypes.
a, Estimates of selection for the 13 cortical phenotypes. Selection coefficients (S), calculated with SBayesS, are provided as points on the y axis (points). Bars indicate 1 s.d. for the selection coefficients. Negative values indicate that lower-MAF alleles tend to have larger effect sizes. Sample sizes are sample sizes of the individual GWAS (nmax = 36,663). Vol, gray matter volume. b, Results of the enrichment analyses for constrained genes and genes associated with neurodevelopmental disorders using genes identified from MAGMA. FDR-corrected log10(P values) for gene enrichment using genes identified from MAGMA (multiple regression) are shown (y axis). The red line indicates the significance threshold at FDR-adjusted P = 0.05. Additionally, significant enrichments identified using H-MAGMA genes are indicated with an asterisk c, Odds ratio (OR; provided as points) and 95% confidence intervals (error bars) for macrocephaly and microcephaly compared to individuals with neither for 1 s.d. increase in polygenic scores for volume, SA and CT in the DDD (n = 6,916) and SPARK (n = 25,621) cohorts. d, Line of best fit plotted using the linear model between genetic principal component corrected polygenic scores (SA and volume) and standardized (compared to the general population) occipital-frontal circumference (OFC s.d.) for individuals with or without a genetic diagnosis in the DDD cohort. The shaded region indicates 95% confidence intervals.
However, polygenic scores (PGS) for SA and volume, but not CT, were associated with macrocephaly and microcephaly in the expected directions in individuals from the deciphering developmental disorders (DDD)47,48 and SPARK49 studies (Fig. 5c). Furthermore, in the DDD cohort, PGS for both volume and SA were significantly associated with occipital-frontal circumference standardized for age and sex, in both individuals with and without a genetic diagnosis (Fig. 5d). This suggests that common genetic variants associated with normative variation in brain size are also linked to clinical cephalic disorders.
Finally, we conducted bivariate genetic correlations between the 13 phenotypes and 15 different neurodevelopmental, psychiatric and cognition-related conditions. After multiple testing corrections, we identified significant genetic correlations between several cortical expansion phenotypes and measures of cognition (cognitive aptitude and educational attainment; Supplementary Table 22).
Prioritizing candidate genes
Given the previous enrichment and polygenic association with neurodevelopmental and cephalic disorders, we were interested in identifying potential causal genes from the global GWAS and investigating if these genes are associated with cephalic or neurodevelopmental conditions. We thus conducted functionally informed fine mapping of all experiment-wide significant loci using Polyfun50 to identify causal variants. For 29 of these loci, we were able to finemap to fewer than five credible variants, and for eight, a single credible variant (Supplementary Table 23). We used nine overlapping methods to identify candidate genes (Methods) and identified 181 candidate genes (Supplementary Table 24). From this list, we defined prioritized candidate genes if they were supported by at least two experimental methods, leading to 40 different prioritized candidate genes, including 19 in the 17q21.31 region (Supplementary Table 25). Of these, 29 were identified for cortical expansion phenotypes, four for curvature phenotypes, 13 for neurite density and orientation phenotypes, 14 for water diffusion phenotypes and 12 for CT, with considerable overlap between the phenotypic domains.
Several genes identified for cortical expansion phenotypes are involved in mitosis, neural progenitor proliferation and cephalic and neurodevelopmental conditions including ATR (ref. 51), CENPW52, KANSL1 (ref. 53) and HMGA2 (refs. 54-56). Mutations in ATR cause Seckel syndrome, characterized by dwarfism, severe microcephaly and intellectual disability51. KANSL1 is associated with Koolen-de Vries syndrome, characterized by global developmental delays, and with over 50% of published individuals having microcephaly53. Mutations in HMGA2 lead to macrocephaly and Silver–Russell syndrome56. The overlap between fine-mapped genes from common variants and genes implicated through rare variants suggests convergence between rare and common variants. The genes identified for the cortical expansion phenotypes were enriched for the Wnt signaling pathway (GO:1904953, q = 0.04), which regulates progenitor proliferation and cortical size57.
Some genes implicated in CT and neurite density and orientation phenotypes were involved in axogenesis and neuronal migration, including VCAN58 and MACF1 mutations, which cause lissencephaly and defects in neuronal migration and axon guidance59. Finally, genes associated with water diffusion phenotypes included MOBP, which encodes a structural component of the myelin sheath, the neuronal proline and glycine transporter gene SLC6A20, and the lipid-gated potassium channel gene KCNK2.
Genetic loci associated with regional cortical phenotypes
To identify genetic influences on regional neuroimaging measures, we conducted 2,338 GWAS using regional phenotypes measured for 180 bilaterally averaged cortical regions using the Human Connectome Parcellation scheme17. We did not adjust for global phenotypes to minimize false positives60 (Supplementary Note 3). In total, we identified 4,260 experiment-wide significant (P < 4.58 × 10−11) loci. The highest number was associated with regional SA (1,033; Supplementary Table 26). These loci were more likely to contain constrained regions of the genome61 (P = 3.97 × 10−3, one-sided Wilcoxon rank-sum test). This enrichment was driven by loci that were significant for regional cortical expansion phenotypes (P = 4.38 × 10−4, one-sided Wilcoxon rank-sum test). The 4,263 loci clustered into 456 semi-independent regions when accounting for linkage disequilibrium (LD) (r2 > 0.1, 1,000 kb) agnostic of the neuroimaging phenotype, indicating widespread pleiotropy across the regional measures.
To understand the extent to which these signals reflect genetic influences on the global phenotypes, we used the ‘GWAS-by-subtraction’ method to regress out a latent factor representing genetic variance62 on global phenotypes for 3,216 of the experiment-wide significant loci (Methods; Supplementary Table 27). In total, 1,633 (50%) of these loci remained experiment-wide significant (P < 4.58 × 10−11) and 3,049 (95%) remained genome-wide significant (P < 5 × 10−8), suggesting that the vast majority of these loci had statistically significant regional effects. In contrast, the global genetic latent trait reached experiment-wide significance for 966 of these loci (30%) and 1,499 (46%) reached genome-wide significance, suggesting that as many as half of these loci are also associated with the global genetic latent trait. However, this could be partly by design, as the global phenotypes in this study are simply the sum of the regional phenotypes.
To further identify shared genetic loci across regional and global phenotypes, we conducted colocalization analyses across all experiment-wide significant (P < 4.58 × 10−11) loci (regional and global) for each of the 13 phenotypes separately (Supplementary Table 28). We identified between 409 (for SA) and 17 (for FA) colocalized clusters, where we use the term ‘cluster’ to refer to a group of phenotypes within one of the 13 neuroimaging modalities that share causal variants in an LD-defined genomic region. The largest cluster was at chr12:65559695-67181144 (12q14.3) comprising the global SA and 156 other regional SA GWAS. This region includes the aforementioned HMGA2, associated with Silver–Russell syndrome54-56. For all phenotypes except FA and MD, larger clusters were more likely to include hits in the global GWAS (P < 0.05, one-sided Wilcoxon rank-sum test). However, there were some large clusters that comprised only regional GWAS, suggesting more localized regional effects. Visual inspection of all clusters with a cluster size of 30 + GWAS (that is, clusters based on 30 or more regional GWAS) revealed that topologically closer regions were more likely to have higher genetic colocalization (Supplementary Figs. 3 and 4). Furthermore, median geodesic distance between regions within a cluster was smaller than the median geodesic distance between regions within and outside a cluster (P < 2 × 10−16, Wilcoxon rank-sum test).
Clusters that included the global GWAS also exhibited broader regional patterns of colocalization. For example, a locus at chr6:125424383-127540461, which includes CENPW, was associated with FI and ICI both globally and in over 30 regions in the superior (dorsal) cortex (Supplementary Fig. 5). CENPW exhibits regional differences in gene expression in the developing cortex63. These analyses demonstrate that SNPs associated with global phenotypes may be associated with only some regional phenotypes.
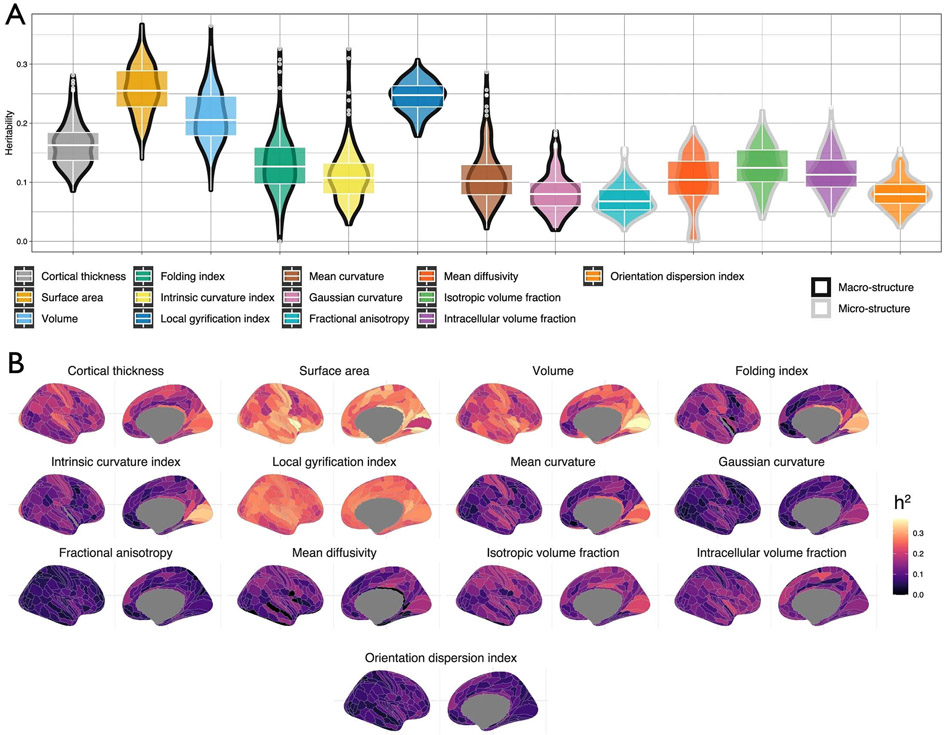
As with the global features, regional cortical macrostructural phenotypes showed an on average higher heritability compared to regional cortical microstructural phenotypes (Extended Data Fig. 4 and Supplementary Table 29; t = −19.4, P < 2 × 10−16, F(12,2327) = 420.7). We further evaluated if SNP heritability systematically varied across previously established functional (Yeo and Krienen communities)64 and morphological (Mesulam classes) parcellations65 of the cortex. Permutation analyses that account for spatial correlation between regions (spin permutation)66 revealed that only CT had relatively higher heritability in idiotypic sensory areas (Mesulam), and a similar profile was observed for the sensory-motor network (Yeo and Krienen)64 (Supplementary Table 30 and Supplementary Fig. 6). This may reflect better histological and functional demarcation of the sensory-motor regions relative to other regions. Overall, these results suggest limited evidence of SNP heritability for cortical morphology being preferentially larger or smaller in known functional and morphological organizational classes.
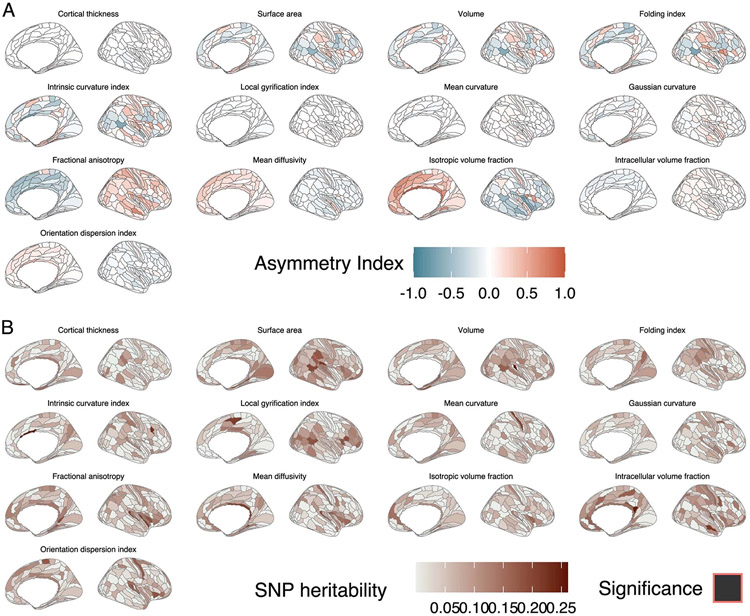
Previous research has indicated that asymmetry in some phenotypes across the cortex is modestly genetic67. In the UKB, we identified greater absolute average asymmetry for cortical expansion and cortical microstructural phenotypes compared to curvature-related phenotypes or CT. However, SNP heritability of the asymmetry index was minimal (Extended Data Fig. 5 and Supplementary Table 31) and reached statistical significance for only 21 phenotype-region combinations (q < 0.05). Together this indicates the minimal genetic contribution to asymmetry across the cortex and is suggestive of high genetic correlation across the hemispheres.
Differential regional genetic organization of the cortex
The high-resolution parcellation scheme used in this study also allowed us to evaluate the protomap hypothesis, which suggests that regional differentiation of the cortex is intrinsically (genetically) determined early in cortical development26,68. If this is true, we would expect regions that are spatially closer to each other to be genetically more similar. Partly supporting this, genetic correlations were moderately correlated with geodesic distances among the 180 regions for each of the 13 phenotypes (r = 0.57 for LGI to 0.13 for ICVF, P = 0.001 for all tests, Mantel test; Supplementary Table 32).
We further investigated if regional genetic correlations were higher within either functionally similar networks (Yeo and Krienen communities64) and morphologically similar classes of laminar differentiation (Mesulam classes65). Across multiple phenotypes we identified higher genetic correlations among Mesulam’s heteromodal association cortical regions but not in any of the Yeo and Krienen communities64 (Supplementary Table 33 and Supplementary Fig. 7).
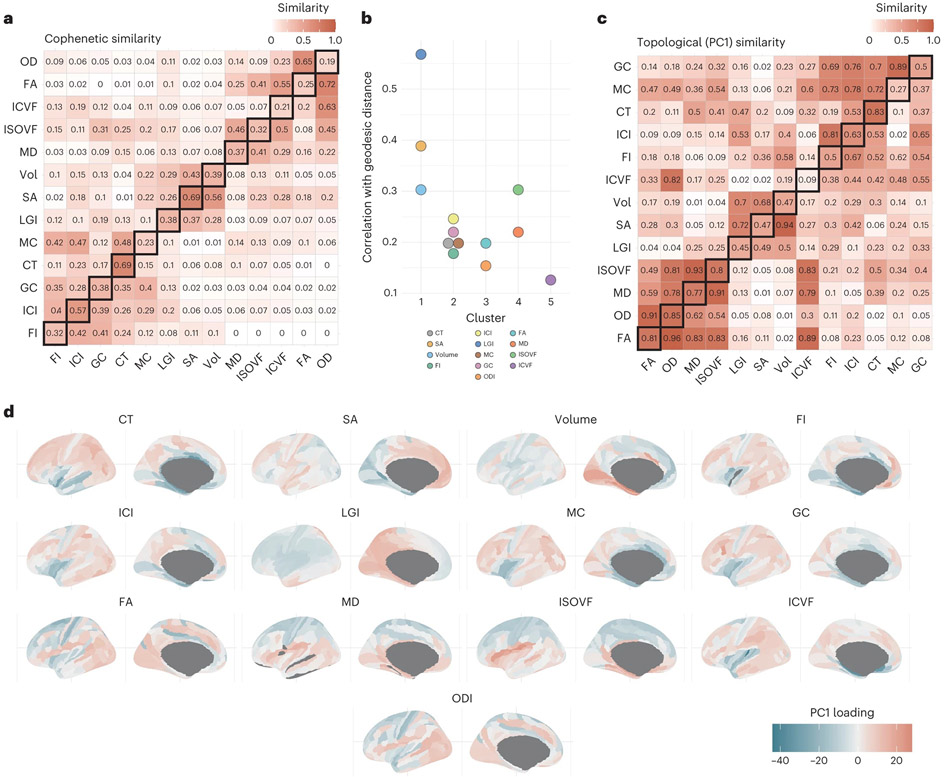
To better understand if the 13 phenotypes are similar in their pattern of regional genetic correlations, we calculated cophenetic correlation coefficients among all 13 neuroimaging modalities using the regional genetic correlation matrices. Grouping based on cophenetic correlations identified four clusters with similar regional genetic correlation patterns (cluster 1: SA, volume and LGI; cluster 2: all folding measures and CT; cluster 3: FA and OD and cluster 4: MD and ISOVF; Fig. 6a). Similar clusters were also observed when using regional phenotypic correlation matrices. These clusters differed from the clusters identified from the global phenotypes in that FI and ICI clustered together with CT and other measures of curvature. This suggests that clusters based on shared genetics of global phenotype moderately overlap with clusters based on regional genetic organization.
Fig. 6 ∣. Topographic similarity and principal component structure of cortical phenotypes.
a, Cophenetic similarity matrix depicting the similarity between the region × region similarity matrices. The upper triangle shows the cophenetic genetic similarity, the lower triangle shows the cophenetic phenotypic similarity and the diagonals show the phenotype–genotype cophenetic similarity across features. b, Correlation between network topology and geodesic distance organized by hierarchical clustering of the cophenetic similarity. c, Spatial correlation between the first principal component of each regional similarity matrix. The upper triangle shows the genetic similarity, the lower triangle shows the phenotypic similarity and the diagonals show the phenotype–genotype correlation across. d, Topology of the first genetic principal components, with color depicting the relative PCA eigenvalues. The color thus indicates to what extent regions show more homogenous similarity (that is, regions with more similar color have more similar covariance), but the actual sign and magnitude are relative within each phenotype.
These four clusters were also distinguishable based on their correlation between regional geodesic distances and genetic correlation (Fig. 6b). Cluster 1 phenotypes, which relate to progenitor proliferation, had the highest correlation between genetic correlation and geodesic distance between regions. This was followed by cluster 4 (MD and ISOVF: the water diffusion phenotypes), which both increase with age in adults69,70. We speculate that this patterning might reflect the heterochronous cellular and developmental trajectories of these phenotypes–regional differences in gene expression in the cortex exhibit a cup-shaped pattern with high regional differences in midgestation that re-emerge during adolescence and increase in adulthood14,71.
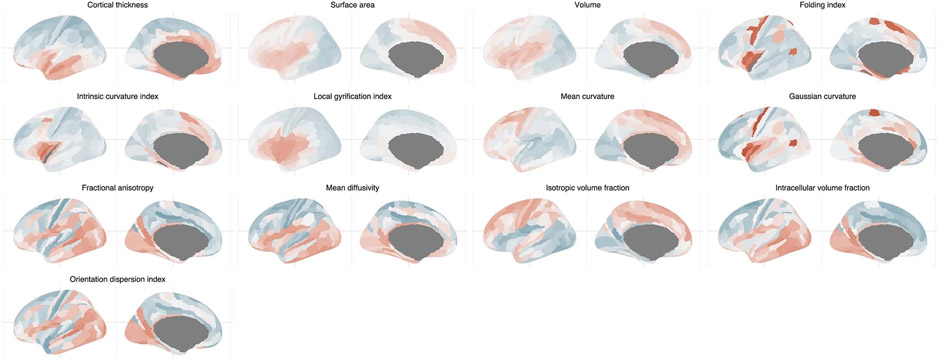
To further explore the pattern of regional organization, we extracted the first principal component from each respective genetic correlation matrix. The first principal component explained between 25% (LGI) to 62% (MD) of the variance. Clustering of the neuroimaging modalities based on the similarity of the first principal component of the region-to-region similarity was similar to the clustering based on the cophenetic correlations of the same region-to-region similarity (Fig. 6c), suggesting that the first principal component largely captures regional genetic organization. Visual inspection of the first principal component identified the following four different axes of variation: anterior–posterior (SA, volume and LGI: cluster 1 phenotypes), inferior–superior (ISOVF, MD: cluster 4 phenotypes) and a mix of primary-association and inferior–superior (CT, GC, MC, FI, ICI: cluster 2 phenotypes, and ICVF; Fig. 6d). For OD and FA (cluster 3 phenotypes), we were unable to identify a clear topological axis of variation. These are in line with the following patterns of gene expression in the human cortex: anterior–posterior gradients during development, and primary-association gradients postnatally up until adolescence and early adulthood72, and in the inferior–superior direction for water diffusion phenotypes, which are late-emerging73,74. Using the first principal component derived from regional phenotypic correlation, we identified clear axes of variation for SA, volume (anterior–posterior) and LGI, CT (inferior–superior), but not for the other phenotypes (Extended Data Fig. 6). This likely reflects the additional influence of directionless nongenetic factors in the development of cortical microstructure and curvature.
Discussion
Our results provide granular insights into the organization and development of the human cortex and links to cephalic and neurodevelopmental conditions, after testing several different hypotheses (Supplementary Table 34). We find that cortical macrostructural and microstructural phenotypes are genetically distinct, enriched for different cellular and developmental processes and provide support for the differential tangential expansion hypothesis2 ,30,31. We find that even among individuals with severe developmental disorders47,48, common genetic variants are associated with cephalic disorders, expanding our understanding of the role of common and rare genetic variants in developmental disorders.
Regionally, topologically closer regions were likely to share genetic loci and be genetically similar, suggesting that regional effects are not constrained to parcellation boundaries and supporting the protomap hypothesis26,68. We identify principal dimensions of regional genetic organizations among the phenotypes, suggesting that cortical organization is informed by distinct waves of molecular processes, some of which are highly directional.
Our analyses focused on individuals predominantly of European genetic ancestries and common genetic variants, as we were limited by sample size, computational power and methodology. There is considerable heterogeneity in MRI preprocessing and postprocessing approaches, including the application of parcellation schemes75,76. We chose a commonly used approach to increase the compatibility of our summary statistics. Finally, expanding the number of phenotypes such as functional MRI (fMRI), white matter and subcortical measures will provide a more precise atlas of the genetics of structure and function of the human brain and the genetic relationships between them.
In conclusion, by conducting and analyzing GWAS of 13 different neuroimaging modalities both globally and across 180 cortical regions we provide unprecedented insights into the genetic organization and development of the human cortex. We make this resource freely available to researchers for further analysis.
Methods
Inclusion and ethics
This research complies with all relevant ethical regulations. Ethical procedures for the UKB are controlled by the Ethics and Guidance Council (http://www.ukbiobank.ac.uk/ethics), and the study was conducted in accordance with the UKB Ethics and Governance Framework document (https://www.ukbiobank.ac.uk/media/0xsbmfmw/egf.pdf), with institutional review board approval by the North West Multicenter Research Ethics Committee. Ethical approval for ABCD was obtained from multiple institutional review boards.
Datasets
UKB
The UKB is a prospective cohort of 500,000 individuals from the UK. Of these individuals, 100,000 will undergo brain scanning5,15,77, with approximately 40,000 scans having been completed when the current study commenced. Participants were excluded from the MRI study on the basis of standard MRI safety criteria such as metal implants, recent surgery or conditions problematic for scanning such as hearing problems, breathing problems or claustrophobia.
ABCD
The ABCD study is an ongoing study of childhood and adolescence78. Participants from the general population were recruited from all over the United States across 21 sites by providing select schools with information packets to all families with 8- to 10-year-old students.
Image acquisition
Data were acquired as part of the UKB and ABCD cohort studies with the following protocols. For the UKB (https://www.fmrib.ox.ac.uk/ukbiobank/protocol/V4_23092014.pdf), T1-weighted structural imaging was obtained using the following parameters: 1.0 mm isotropic resolution, TR = 2,000 ms, TE = 2.01 ms, TI = 880 ms and flip angle 8 degrees; T2-weighted fluid-attenuated inversion recovery (FLAIR) structural imaging was obtained using the following parameters: 1.0 × 1.0 × 1.1 mm resolution, TR = 5,000 ms, TE = 395.0 ms and TI = 1,800 ms; and diffusion-weighted imaging (2.0 mm isotropic resolution) was obtained using the following parameters: MB = 3, R = 1, TE/TR = 92/3,600 ms, PF 6/8, fat sat, b = 0 s mm−2 (5× + 3× phase-encoding reversed), b = 1,000 s mm−2 (50×), b = 2,000 s mm−2 (50×), 105 + 6 time-points (PA–AP). For ABCD (https://github.com/nih-fmrif/abcd_protocols) and ref. 16, T1-weighted imaging (1.0 mm isotropic resolution) was obtained using the following parameters: TR = 2500 ms, TE = 2.88 ms, TI = 1060 ms, flip angle 8 degrees; T2-weighted imaging (1.0 mm isotropic resolution) was obtained using the following parameters: TR = 3200 ms, TE = 565 ms, flip angle variable; and diffusion-weighted imaging (1.7 mm isotropic resolution) was obtained using the following parameters: TR = 4100 ms, TE = 88 ms, flip angle 90 degrees, 500 (6-dirs); 1,000; (15-dirs) 2,000; (15-dirs) and 3,000 (60-dirs)
While not processed as part of the present analysis, we also obtained framewise displacement parameters from each individual’s accompanying resting-state fMRI scan.
Image processing
Structural minimally processed T1 and T2-FLAIR-weighted data were obtained from UKB (application 20904) and the ABCD study (via the NIH Data Archive Repository). These images were preprocessed with FreeSurfer (v6.0.1)79 using the T2-FLAIR-weighted image to improve pial surface reconstruction when available. Recon-all reconstruction included bias field correction, registration to stereotaxic space, intensity normalization, skull-stripping and white matter segmentation. A triangular surface tessellation fitted a deformable mesh model onto the white matter volume, providing gray–white and pial surfaces with >160,000 corresponding vertices registered to fsaverage standard space. When no T2-FLA1R image was available, FreeSurfer reconstruction was done using the T1-weighted image only. Given systematic variation related to the inclusion of T2 FLAIR, this was included as a confound variable in downstream analyses. Cortical surfaces were reconstructed for each individual using FreeSurfer and registered using FreeSurfer’s surface-based registration to fsaverage. The Human Connectome Project’s (HCP) multimodal parcellation v1.0 (ref. 17) was resampled from fs_LR to fsaverage using existing transformations80 and from there back to the individual’s surface meshes based on the FreeSurfer folding-based surface registration. Reconstruction quality was assessed using the Euler index81 and included as a covariate in subsequent analyses (Supplementary Note 4).
Structural diffusion-weighted imaging was obtained in processed form from UKB and ABCD in a similar fashion. As described in the UKB Brain Imaging Documentation (v1.8)82, UKB diffusion images were corrected for eddy currents, head motion and outlier slices using the Eddy tool (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/EDDY). Echo planar imaging (EPI) distortion correction was performed using a field map estimated from three (b = 0) images with standard (anterior–posterior) phase encoding and three (b = 0) images acquired with reversed-phase encoding. Similarly, ABCD diffusion images were corrected for eddy currents (12 free parameters), head motion (rigid-body registration) and EPI distortion using pairs of b = 0 with opposite phase encoding polarities83. Neurite orientation dispersion and density indices (NODDI) parameters were estimated using the accelerated microstructure imaging via convex optimization84 processing approach from the minimally processed diffusion images. The subject-specific T1-aligned (based on surface alignment procedures) parcellation template was coregistered to the diffusion-weighted image using fsl FLIRT, and regional values for FA, MD and the three NODDI parameters were extracted using AFNI’s 3dROIstats function for all of the 360 cortical regions included in the Human Connectome parcellation and averaged across the hemisphere to reduce the number of regions to 180 bilateral regions. We also evaluated a direct surface-based registration approach in line with HCP protocols for surface-based registration (Supplementary Note 4b).
In total, the following 13 different imaging-derived phenotypes were extracted using this pipeline:
Total SA of the cortex (measured at midthickness)
Total volume of the cortex (volume)
-
Average thickness of the cortex (CT)
Measures of curvature–we calculated five measures of curvature. Assuming two principal curvatures ( and ), we can define the five measures of curvature as follows.
Total . MC is typically thought to measure extrinsic curvature. In other words, this is not curvature that is intrinsic to the surface, but rather extrinsic to the surface.
Total
Total . In other words, if GC is positive, ICI is positive. If GC is negative, ICI is 0.
Total .
-
Total LGI85–gyrification index quantifies the amount of curvature that is buried within the sulcal folds and is a measure of gyrification. This is computed by calculating the ratio of the area between an outer smoother surface and an inner surface tightly wrapping the pial surface. As it is a ratio, it is a unitless measure.
These measures have consistently been found to have high test–retest reliability (intraclass correlation coefficient (ICC): ~0.8) across sites, acquisition protocols and recent FreeSurfer versions86-90. The above properties measure primarily tissue macrostructure. To better understand cortical microstructure, we calculated five measures from the diffusion-weighted images91. Because conventional diffusion parameters such as FA and MD alone are not specific to the underlying microstructure of axons and dendrites (referred to, collectively, as neurites), we also extracted NODDI measures92,93.
FA91–FA is thought to be a measure of microstructural integrity. Higher FA values are thought to indicate fiber tracts (that is, greater anisotropy). FA would be higher in areas of greater neurite density due to less isotropic water diffusion.
-
MD91–MD measures the degree of displacement (or diffusivity) of water. It can be a measure of membrane density and degree of myelination. Lower membrane density and greater myelination are thought to decrease MD.
We calculated the following three metrics using NODDI. NODDI assumes three microstructural environments for the diffusion of water–intracellular, extracellular and CSF43. The intracellular environment is anisotropic and water diffusion in this environment can be quantified using
ICVF–also referred to as neurite density index, this is a measure of the density of neurites (axons and dendrites). Higher ICVF values indicate that a greater fraction of the tissue consists of neurites.
ODI–this measures the orientation and spatial variation of the neurite fibers. Zero indicates perfectly aligned straight fibers and one for completely isotropic fibers. Thus, larger values of ODI represent highly dispersed neurites and smaller values represent highly aligned neurites.
ISOVF–this is a measure of water diffusion, typically representing cerebrospinal fluid and ventricles in the cortex.
All white matter metrics have also shown high test–retest reliability (ICC: −0.8) and scanner consistency, both in a longitudinal subset of the UKB dataset (n = 2,817, mean scan-to-scan interval 2.25 years s.d.: 0.12)90 and in a specifically designed test–retest cohort to evaluate both intervendor and scan–rescan reliability94.
We note that all phenotypes were standardized. Mean CT was calculated as the average across the 180 bilaterally averaged cortical regions. Due to this standardization, the standardized scores from the average and total values will be identical.
We calculated the hemispheric asymmetry between the regional values using the widely used asymmetry index67,95-97.
| (1) |
Genome-wide association analyses
Genetic quality control in the UKB
Genetic quality control and imputation of the UKB were done by the UKB team and described in detail elsewhere15. After this, we included only individuals of self-identified white ethnicity, and from this group of individuals, excluded individuals who were above ±5 s.d. from the means of the first two genetic principal components, and refer to this group as individuals of predominantly European genetic ancestries. We further removed individuals whose genetic sex did not match their reported sex, or had excessive genetic heterozygosity, as provided by the UKB team. For the GWAS, we used all genotyped and imputed SNPs in the UKB that had a minor allele frequency >0.01% and were in Hardy–Weinberg equilibrium (HWE; P < 1 × 10−6) and, for imputed SNPs, had an imputation r2 > 0.4. After quality control, we retained a maximum of 31,797 participants and 15,916,802 SNPs. We conducted our analyses using people of predominantly European genetic ancestries as this represented the largest, relatively genetically homogeneous group. We did not conduct GWAS for individuals in other ethnic groups as there were fewer than 400 individuals with imaging and genetic data after quality control in each of the other ethnic groups, which is insufficient sample size for linear mixed-effect models for GWAS. However, as greater data from other ethnic groups become available, we will revisit these analyses.
Genetic quality control in ABCD
Before imputation, we filtered SNPs with missingness >90% and deviations from HWE (P < 1 × 10−6). We removed individuals with missingness >5% and whose genetic sex did not match their reported sex. As HWE and heterozygosity are incorrectly calculated in populations with diverse genetic ancestries, these steps were conducted in relatively homogenous genetic ancestral groups identified using principal-component-based clustering after combining the data with the 1000 Genomes phase 3 data98. Principal components were calculated using GENESIS99 after accounting for relatedness between samples as calculated using KING100. We calculated genetic principal components using only genotyped SNPs that had passed quality control, and after pruning the SNPs to account for LD (r2 > 0.1), and after removing the MHC locus, a region of long-range LD. To identify genetically homogeneous groups, we used the first five principal components to identify clusters in the 1000 Genomes data using UMAP, identifying seven broad populations–non-Finnish Europeans, Finnish Europeans, Africans, Americans, East Asians, South Asian and Bengali. Then, using the first five PCs from the ABCD dataset, we projected individuals onto the seven clusters, identifying broadly homogeneous populations (Supplementary Fig. 8). HWE-based filtering (P < 1 × 10−6) and removing individuals with excess heterozygosity (±3 s.d.) was then conducted. After clustering into genetically homogeneous groups, we additionally calculated genetic PCs specifically in the subgroup of the ABCD participants that were predominantly of European genetic ancestries, again using a pruned set of genotyped SNPs and after excluding the MHC. The data were then merged, phased (Eagle v 2.4) and imputed (Minimac4) using the TOPMED Imputation Server. From the imputed data, we removed SNPs with poor imputation (r2 < 0.4) and minor allele frequency <0.1% (n = 14,495,763 SNPs). We restricted our analyses to individuals of predominantly European genetic ancestries (n = 4,866).
Genome-wide association analyses
In both the UKB and ABCD, we followed the same procedures outlined below. We conducted whole brain and regional GWAS analyses for the 13 phenotypes mentioned in the ‘Image Processing.’ For each region, we averaged the values bilaterally, resulting in a total of 180 regional phenotypes per phenotype. For ICI and FI, we excluded regions ‘52’, ‘PI’ and ‘PHA2’ because of no variance. In total, we conducted 2,347 GWAS using FastGWA (v1.93)101. FastGWA can simultaneously account for both relatedness and subtle population stratification in the analyses.
All phenotypes were scaled to a mean of 0 and a s.d. of 1. We removed individuals who scored above or below 5 s.d. from the mean for all phenotypes, as these are most likely technical outliers. Furthermore, these outliers skew the phenotypic scores and cannot be used in fastGWA, which can produce false positives at stringent P value or for SNPs with low minor allele frequencies101. Additionally, we visually inspected histograms of all phenotypes and further removed outliers above or below 5 median absolute deviations for phenotypes with substantial skew, primarily for MD and FI. Additionally, to ensure that the GWAS were not confounded by fine-scale population stratification, among the individuals of European ancestry identified in UKB or ABCD, we removed individuals who were above or below 5 s.d. from the mean of the first two genetic principal components. For all GWAS, we included age, age2, sex, age × sex, age2 × sex, imaging center, first 40 genetic principal components, mean framewise displacement (as obtained from the accompanying resting-state fMRI scan), maximum framewise displacement (as obtained from the accompanying resting-state fMRI scan) and Euler Index81 as covariates. In addition, for structural MRI metrics derived from T1, we included the inclusion of T2 scans as covariates as this influenced the calculation of these metrics. To ensure this inclusion did not bias our results, we also computed separate GWAS for individuals with both T1 and T2-FLAIR and individuals who only had a usable T1 but no additional T2 FLAIR. Genetic correlations between the T1-only sample and the T1 + T2-FLAIR-weighted sample were indistinguishable from 1 for all 7 GWAS, indicating that the overall genetic architecture is identical. Furthermore, effect sizes of the genome-wide significant SNP were highly correlated between the Tl-only GWAS and the combined GWAS (r = 0.9998, P < 2 × 10−16).
For the regional GWAS, we chose not to include the respective global phenotypes for three reasons. First, adjusting for heritable and highly correlated phenotypes biases the GWAS estimates60,102. All global phenotypes were substantially heritable and highly correlated with the regional phenotypes (detailed in Supplementary Note 3). Second, including highly correlated and heritable covariates may result in collider bias for downstream analyses such as MR103. Given that we wish to make the summary statistics available for researchers to conduct other analyses, including global phenotypes as a covariate can restrict the scope of downstream analyses. Finally, we were specifically interested in identifying SNPs with effects across the cortex, which may not have been possible if we had adjusted for global phenotypes. We note that methods such as genomic-SEM24, mtCOJO104 and multivariable MR105 all allow adjustment for global GWAS in downstream analyses. Here we used genomic-SEM to regress out the genetic effects of the global phenotype for the majority of experiment-wide significant SNPs (definition of which is detailed below), to identify the fraction of SNPs that remained significant. We note that modeling of global versus local genetic effects at a genome-wide level as conducted elsewhere106 is beyond the scope of this study.
We meta-analyzed results from the UKB and ABCD using inverse-variance weighted meta-analyses in Plink v1.9 (ref. 107), excluding SNPs that were absent from the UKB, given the difference in sample sizes (and consequently, statistical power) between the UKB and ABCD. We checked for inflation in summary statistics using the attenuation ratio. In fastGWA, which uses a linear mixed-effects model, the LDscore intercept is not a good indicator of inflation in test statistics due to population stratification. Instead, as recommended108, we used the attenuation ratio:
| (2) |
We investigated if our variantsor variants in high LD (r2 > 0.8 in CEU or GBP populations) were significantly associated with neuroimaging phenotypes (including quality control) metrics sequentially using the following four different databases: the Oxford Brain Imaging Genetics PheWeb (PheWeb(ox.ac.uk)), GWAS catalog (GWASCatalog(ebi.ac.uk)), GWAS ATLAS (Genome-wide association study ATLAS (ctglab.nl)) and Brain Imaging Genetics Knowledge Portal Brain Imaging Genetics Summary Statistics.
Multiple testing correction
Using matrix decomposition109, we estimated that there were 1,092 independent phenotypes. This was estimated from all 2,347 global and regional phenotypes included in the study, and thus corrects for all the tests conducted in the study. Consequently, using the total number of independent phenotypes, we used Bonferroni correction to define an experiment-wide threshold of 4.58 × 10−11 (5 × 10−8/1,092) to correct for the multiple tests conducted. To identify significant loci, we cl umped the GWAS using an r2 threshold of 0.1 over 1,000 kb. We used LD information available from a random sample of 5,000 unrelated individuals from the UKB who were included in the GWAS.
Genetic correlation and causal analyses
Genetic correlation, SNP heritability estimation, clustering and GSEM
For the global phenotypes, we used LDSC (v1.01)18,22 to compute genetic correlations and SNP heritability for the meta-analyzed GWAS statistics, using LD weights from the North West European populations. Intercepts were not constrained. Heritability and genetic correlation (among 180 regions per phenotype for all 13 phenotypes) of the regional GWAS were calculated using LDSC as incorporated within genomic-SEM24. Additionally, for the global phenotypes in the UKB, we conducted GCTA–GREML110 (v1.93) based SNP heritability using a genetic relationship matrix calculated using all imputed SNPs included in the GWAS, for 30,765 unrelated individuals (using a GCTA–GREML cutoff of 0.05) with neuroimaging GWAS. For the asymmetry indices, we calculated SNP heritability for a subset of approximately 9,650 unrelated individuals. We applied the same quality control and used the same covariates as for the GWAS.
For the global phenotypes, clustering of the phenotypic and genetic correlation matrices was conducted on the Euclidean distance. As the final hierarchical clustering is dependent on the clustering method used, we used three different clustering methods (Average, Ward D and Complete Linkage) and visualized the different clusters obtained. Cophenetic correlations (in R Stats (version 3.6.2)) were obtained by comparing the phenotypic and genetic dendrograms produced by the different clustering methods.
GSEM was conducted using genomic-SEM24 using summary GWAS statistics of the global cortical phenotypes. We conducted exploratory factor analyses using the even chromosomes, identified factor models and conducted confirmatory factor analyses using the odd chromosomes. The final model was selected after multiple iterations based on both fit indices and theoretical predictions. Fit indices and path diagrams are provided for models based on all chromosomes.
For the regional phenotypes, we conducted 1,000 spin permutations66 tests to investigate if SNP heritability of regions or genetic correlation among regions were higher in regions falling within functionally64 or morphologically similar classes65. Spin permutation accounts for spatial correspondence between regions and generates null models using random rotations across the spherical cortical surface66.
We investigated if the genetic correlation among regions was correlated with topological geodesic distances among regions using the Mantel test (within each phenotype separately). We investigated if the clustering of regions based on genetic correlations was similar between phenotypes based on cophenetic correlation.
Phenotypic correlation and principal component analysis
Comparable to region-specific genetic correlations, we also generated region-to-region phenotypic correlation matrices (‘structural covariance’) for both UKB and ABCD cohorts by taking the Pearson correlation across subjects on the scaled and filtered data. UKB and ABCD were then combined into a single meta-covariance matrix using the ‘psychmeta’ package (v 2.6.0) in R111.
We extracted the first principal component from the regional genetic correlation matrix and regional phenotypic correlation matrix for each of the 13 phenotypes separately. This principal component analysis was done using a singular value decomposition of the centered and scaled similarity matrix using the ‘stats’ package (v 3.6.3) in R.
Colocalization
To identify colocalized genomic regions among the 13 global phenotypes, we used Hyprcoloc112. Hyprcoloc is robust to participant overlap and can conduct multitrait colocalization using hundreds of GWAS. We restricted our analyses to experiment-wide significant loci and mapped these onto predefined approximately independent LD blocks in individuals of European ancestry (approximately 1.6 Mb on average)113. We did not adjust for either participant or known correlation between phenotypes, as the method gives reasonable results comparable to adjusting for correlation between phenotypes. We used the branch and bound divisive clustering algorithm incorporated in Hyprcoloc to identify clusters of phenotypes that colocalize at any given locus. We used the default variant-specific prior probabilities in Hyprcoloc112–prior 1 (probability that an SNP is associated with a single trait) as 1 × 10−4, and prior c (prior probability that the SNP is associated with a second trait) as 0.02. We identified colocalized genomic regions if the genomic regional association probability was 0.6 or higher. We used this probability of 0.6 as simulation analyses by the authors of method112 to demonstrate that at a regional association probability of 0.6, the empirical probability of identifying true clusters is greater than 90%. We used the same pipeline to investigate colocalization for 180 regional GWAS and the global GWAS for each of the 13 phenotypes conducted separately.
MR
To investigate the causal effects of SA on other cortical macrostructural phenotypes, we conducted MR analyses25 using global phenotypes. To avoid bias due to participant overlap, we randomly divided the UKB into two groups of individuals (group A: n = 15,884 of which males = 7,455; group B, n = 15,899, of which males = 7,500) and conducted GWAS analyses in each of the groups separately for the eight cortical macrostructural phenotypes using the same pipeline as detailed above. We generated instruments that consisted of SNPs with P < 5 × 10−8 in the exposure, with minor allele frequency >1%, and which were near-independent (clumping r2 = 0.001 using a 1,000 kb window using data from 5,000 unrelated individuals from the UKB). Where fewer than five SNPs met these criteria, we relaxed the P value threshold to P < 1 × 10−6. Using SA GWAS generated in group A as the exposure and the GWAS for the remaining six phenotypes in group B as the outcome, we conducted inverse-variance weighted bidirectional MR analyses. To account for pleiotropy, we additionally conducted the following sensitivity analyses: (1) median weighted MR (majority-valid114), (2) MR-Egger (accounts for pleiotropy)115; (3) MR PRESSO (detects and excludes outliers in the instrument116). Additionally, (4) for the significant MR results, to further account for correlated (vertical) pleiotropy, we conducted MR analyses using CAUSE (v1.2)117 using the following two instruments: one with of SNPs with P < 5 × 10−8, and another at a more relaxed threshold of P < 0.001. We investigated heterogeneity in the instrument using Cochran’s Q and investigated if the Egger intercept was significant. We investigated if the orientation of the causal direction was correct using Steiger analyses118 and conducted additional sensitivity analyses after removing SNPs that did not have the correct causal orientation. Finally, we inspected the scatter plot, forest plot and plots generated from leave-one-out analyses to identify if the results were driven by a subset of the SNPs. Analyses (1) and (2) and the sensitivity analyses were conducted using the R-package TwosampleMR (v.0.4.26)119.
We repeated all MR analyses except for CAUSE using instruments generated in the UKB as the exposure and ABCD as the outcome. However, this was quasi-bidirectional, in that in both directions, the exposure was instruments generated in the UKB and the outcome was SNPs in the ABCD. We did not conduct CAUSE in this instance due to a sample size imbalance that reduces statistical power.
Given substantial pleiotropy between the phenotypes, we identified significant MR associations if—(1) the P value was <0.0035 (Bonferroni-corrected threshold) in both the within UKB and the UKB–ABCD analyses for IVW, MR PRESSO and weighted median; (2) MR-Egger was in the consistent direction to the IVW (MR-Egger has lower statistical power so we did not require it to be statistically significant); (3) if Steiger analyses identified incorrect causal orientation, criteria 1 and 2 were met after Steiger filtering and (4) results were significant when MR was conducted using CAUSE, which accounts for correlated pleiotropy. Analyses were conducted using the two-sample MR package (version 0.5.6)119. Power-calculations120 were conducted assuming a s.d. in the exposure results in a 0.33 unit s.d. change in the outcome, which is a medium effect size.
Gene-based association and enrichment analyses
Gene-based association
We used MAGMA (version 1.10)33 to conduct gene-based association testing based on physical location. MAGMA assigns SNPs to the nearest gene. In line with previous analyses, we expanded the window to 35 kb upstream and 10 kb downstream of the gene to capture regulatory regions121. In addition, we used H-MAGMA34 (using MAGMA v1.08) to identify genes based on Hi-C mapping. In contrast to MAGMA, H-MAGMA is able to map SNPs to genes based on long-range interactions and can account for tissue-specific regulatory effects. To map developmental trajectories, we used Hi-C data from postnatal and prenatal human cortex34,122. Subsequently, for enrichment analyses, we used Hi-C data from the prenatal cortex given that the majority of the phenotypes were either enriched for gene expression in the prenatal cortex or did not differ in gene expression between prenatal and postnatal cortex, and because many processes investigated occurred prenatally.
Developmental trajectories
To identify patterns of gene expression across cortical prenatal and postnatal windows, we used data from PsychEncode14. The data were divided into the following nine developmental windows: Window 1, 8–9 PCW; Window 2, 12–13 PCW; Window 3, 16–17 PCW; Window 4, 19–22 PCW; Window 5, 35 PCW to 4 months; Window 6, 6 months to 2.5 years; Window 7, 3–11 years; Window 8, 13–19 years and Window 9, 21–40 years. Gene expression values were log base 2-transformed after adding a pseudocount and normalized. For 12 of the 13 phenotypes, the transformed expression values of all genes with q < 0.05 were averaged for each developmental window and smoothed LOESS curves were plotted. The excluded phenotype was FA as H-MAGMA and MAGMA identified 1 and 0 genes with q < 0.05, respectively.
Enrichment analyses
To investigate enrichment for cell types, signatures of genomic constraint and gene sets associated with neurodevelopmental and cephalic disorders, we conducted the following analyses. Within each gene set, significant results were identified after correcting for all 13 phenotypes using Benjamini–Hochberg FDR correction (q < 0.05).
To identify cell types in the prenatal and postnatal cortex, we conducted enrichment analyses using (1) single-cell gene expression data from PsychENCODE14 using prenatal (5 PCW to 125 d) and postnatal gene expression. To provide additional temporal resolution, we also conducted analyses using (2) single-cell gene expression data that spanned early cortical development (6–10 PCW)36; (3) single-cell gene expression data spanning midgestation period of cortical development (17–18 PCW)37; (4) single-cell epigenomic data (scATAC-seq) from the midgestation period of cortical development38 and (5) cell-type-specific (fluorescent-activated nuclei sorting isolated) epigenomic (ATAC-seq and ChiP–seq) data from postnatal cortex42. Analyses for datasets 1–3 were conducted using MAGMA gene-set enrichment using genes identified by MAGMA and H-MAGMA. Following previously described methods121, we filtered out genes with nonunique names and genes not expressed in any cell types. Gene expression values were log base 2-transformed after adding a pseudocount and normalized. Mean cell-type-specific gene values were calculated, and this was divided by the mean expression of the gene in all cells to get relative cell type expression. We then selected the top 10% of genes with the highest relative expression in each cell type to conduct enrichment analyses using MAGMA gene-set enrichment analyses33. Significant cell types were identified if q < 0.05 in analyses using both H-MAGMA- and MAGMA-identified genes. Analyses for datasets 4 and 5 were conducted using conditional partitioned heritability analyses in LDSC (that is, enrichment for a cell type after conditioning on all other cell types and baseline annotations)123,124.
We used the same gene-enrichment pipeline as above to investigate gene enrichment for genes that are constrained (pLOUEF < 0.37)45, genes associated with neurodevelopmental disorders46 (662 genes with FDR < 0.05) and genes associated with severe microcephaly obtained from the Genomics England Panel (244 genes, signed off on March 2, 2022: Severe microcephaly (Version 2.304; https://nhsgms-panelapp.genomicsengland.co.uk/panels/162/v2.2)). Signatures of selection were identified using SBayesS44.
PGS association analyses
Genetic quality control and PGS generation
PGS for SA, CT and volume were calculated using the meta-analyzed GWAS in a dataset of individuals with severe developmental disorders (DDD study, n = 6,916) and autistic individuals and their families (SPARK dataset, n = 25,621) using PRScs125. PRScs is a Bayesian algorithm that infers posterior effect sizes of SNPs using continuous shrinkage and does not require defining P value thresholds. Details of genetic quality control in the DDD cohort in individuals of predominantly European ancestries are provided elsewhere48. The data were re-imputed using the TOPMed reference panel, and variants with low imputation quality (minimac4 r2 < 0.8) were excluded. We kept common (minor allele frequency >1%) SNPs that are also in HapMap3 to calculate the PGS using PRScs. Genetic-ancestry QC of the SPARK dataset was conducted similar to the ABCD dataset and as detailed elsewhere126,127. We calculated PGS on individuals of predominantly European ancestries as identified by genetic principal components. All PGS were standardized with a mean zero and a s.d. of 1 for all analyses.
Defining phenotypes in DDD and SPARK
In the DDD study, we used HPO terms assigned by clinicians to define macrocephaly (n = 396 with HPO term ‘HP:0040194’, ‘HP:0000256’, ‘HP:0004482’, ‘HP:0004481’, ‘HP:0004488’ or ‘HP:0005490’) and microcephaly (n = 1,198 with HPO term ‘HP:0040195’, ‘HP:0000252’, ‘HP:0005484’, ‘HP:0004485’, ‘HP:0000253’, ‘HP:0011451’ or ‘HP:0040196’). We also analyzed occipital-frontal circumference data (n = 6,146), which were calculated as s.d. from the mean given the proband’s gestational age at birth, age at time of measurement and sex. In the SPARK dataset, information about macrocephaly and microcephaly were obtained from parental/caregiver reports of medical diagnoses.
Statistical analyses
Linear or logistic mixed-effect regressions (random intercepts for family, in SPARK) were conducted using either PGS for volume or PGS for SA and CT in a multiple regression framework. Primary analyses were conducted using logistic regression, separately for macrocephaly and microcephaly (coded as 1) compared to controls (that is, individuals in the cohort without microcephaly or macrocephaly; coded as 0). In the DDD, we also conducted linear regression using standardized occipital-frontal circumference. Additionally, we conducted linear regression with macrocephaly coded as 1, microcephaly as −1 and no diagnosis as 0. In the DDD study, we included sex, genetic diagnosis and the first ten genetic principal components as covariates. Specifically, we considered probands to be ‘diagnosed’ if they had at least one variant reported to DECIPHER that had been confirmed as pathogenic or likely pathogenic (C/LP) by a clinician, or that had been predicted as P/LP by a computational algorithm based on the American College of Medical Genetics criteria, as described in ref. 128. In SPARK, age, sex, autism diagnosis and the first ten genetic principal components were included as covariates. Significant results were identified after Benjamini–Hochberg FDR correction (q < 0.05) across all models.
Fine mapping, summary Mendelian randomization (SMR) and prioritizing candidate genes
For all exome-wide significant loci in the global GWAS (n = 90), we conducted functionally informed fine mapping using Polyfun50, using SuSiE (v 0.12.10)129 as the fine-mapping method and with up to five causal variants per locus, with each locus defined 500 kb upstream and downstream of the sentinel variant. In-sample LD was obtained from 5,000 unrelated individuals included in the GWAS from the UKB. We used precomputed prior causal probabilities from the UKB as provided in Polyfun.
To link the variants in the 95% credible sets to genes, we used Hi-C data from (1) the prenatal brain germinal zone122, (2) the prenatal brain cortical plate122, (3) neurons from postnatal cortex130 and (4) glia from postnatal cortex130. Additionally, we (5) used Ensembl Variant Effect Predictor131 to identify genes containing damaging missense (deleterious in SIFT and/or damaging/probably damaging/possibly damaging in PolyPhen) and protein-truncating variants from the list of the 95% credible sets.
To identify candidate genes using relevant eQTL and methylation data, we further conducted SMR132. SMR was conducted for all 13 phenotypes, using cis-eQTL data from postmortem (6) prenatal133 and (7) postnatal brains134, and additionally (8) methylation data from postnatal brains135. Within each phenotype, we identified significant genes by using Bonferroni correction for the total number of genes tested. We excluded significant genes with evidence to indicate that the MR association results are due to pleiotropy using the HEIDI test (HEIDI P < 0.01)132.
Finally, (9) we identified the closest gene to each sentinel variant (that is, the SNP with the lowest P value in each locus). Where the variant was intergenic, we included both the closest upstream and downstream genes. From these nine methods, we identify a list of prioritized candidate genes if they are supported by at least two methods. We conducted Gene Ontology (GO) enrichment analyses to identify biological pathways enriched for the prioritized candidate genes.
Extended Data
Extended Data Fig. 1 ∣. Consistency in genetic effects between ABCD and UKB.
(a) Correlation in effect size (regression beta from GWAS) between ABCD and UKB cohorts for all 237 genome-wide significant SNPs in the UKB: Pearson’s correlation coefficient, r = 0.54 with 95% confidence interval 0.45–0.63. (b) Genetic correlation (central point) and 95% confidence intervals (error bars) for 12 global phenotypes in the UKB and ABCD cohorts. Given the relatively small size of ABCD, the intercept has been constrained as there is no participant overlap between the UKB (Nmax = 31,797) and ABCD (Nmax = 4,866) and there is no inflation in test statistics due to uncontrolled population stratification. Consequently, estimates of genetic correlation can be above 1.
Extended Data Fig. 2 ∣. Mendelian randomization analysis for causal relationships between genetic effects on global brain phenotypes.
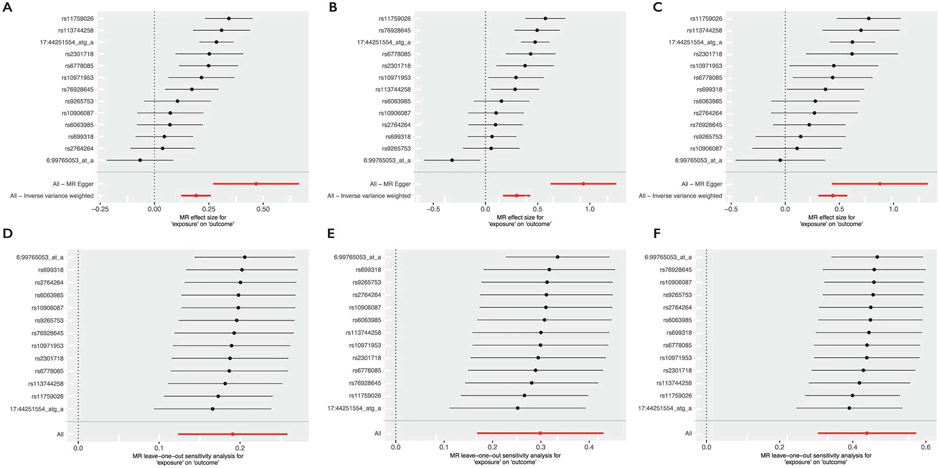
Scatter plots for the bidirectional MR effects between surface area and folding index, intrinsic curvature index, and local gyrification index. Slopes of the line (MR regression coefficient) indicate the estimated MR effect by method. Linear a, b, and c are scatter plots where surface area is the exposure, and d, e, and f are scatter plots where surface area is the outcome. All scatter plots are for MR analyses conducted by splitting the UKB into two samples of similar sample sizes. All estimates were statistically significant in scatter plots A,B, and C. Inverse-variance weighted MR failed to reach statistical significance in scatter plots d, e, and f. Number of SNPs included in the MR are provided in Supplementary Table 9. Error bars represent standard errors of the effect size (point estimates).
Extended Data Fig. 3 ∣. Forest plots and leave-one-out plots.
Forest plots (a–c) and leave-one-out (d–f) between surface area and folding index (FI, A and D), Intrinsic curvature index (ICI, B and E), and local gyrification index (LGI, C and F). Number of SNPs included in the MR are provided in Supplementary Table 9. Error bars indicate 95% confidence intervals of the effect (point estimates).
Extended Data Fig. 4 ∣. Regional heritability.
a. The distribution of the SNP heritability for the 180 bilaterally-averaged regional phenotypes of the 13 neuroimaging modalities. Maximum GWAS sample size = 36,663. Box plots indicate the median value (central line), the interquartile range, and the whiskers indicate the minimum and maximum. b. The cortical spatial topology of SNP heritability for the 13 neuroimaging modalities.
Extended Data Fig. 5 ∣. Asymmetry indices and SNP heritability of asymmetry indices for the 13 phenotypes.
a. Asymmetry indices for the 13 phenotypes. Positive values indicate leftward asymmetry. b. SNP heritabilities for asymmetry indices by region and phenotype. SNP heritability was calculated using GCTA–GREML for approximately 9,650 unrelated individuals from the UK Biobank. Significant regions were identified after FDR correction within each of the 13 phenotypes.
Extended Data Fig. 6 ∣. Topography of the first phenotypic principal components.
Color scales depict the relative eigenvector ranging from −20 to +29, in all plots the midpoint is defined as 0. It should be noted that the sign is somewhat ambiguous and that the magnitude is relative to its own scaling (in this case within each phenotype for which the PCA is performed). Thus, in this context, the color scale indicates to what extent regions show more homogenous similarity (that is, regions with more similar color have more similar covariance).
Supplementary Material
Acknowledgements
V.W. is supported by St. Catharine’s College Cambridge, funding from the Wellcome Trust (214322\Z\18\Z) and UKRI (10063472). E.-M.S. is supported by a Ph.D. studentship awarded by the Friends of Peterhouse. E.A.W.S. is supported by the National Institute for Health Research (NIHR) Cambridge Biomedical Research Center (BRC-1215-20014). The views expressed are those of the authors and not necessarily those of the NIHR or the Department of Health and Social Care. R.A.I.B. is supported by the Autism Research Trust. S.B.C. received funding from the Wellcome Trust (214322\Z\18\Z). S.B.C. also received funding from the Autism Center of Excellence, SFARI, the Templeton World Charitable Fund, the MRC and the NIHR Cambridge Biomedical Research Center. The research was supported by the NIHR Applied Research Collaboration East of England. J.S. was supported by NIMH (T32MH019112-29 and K08MH120564). E.T.B. was supported by an NIHR Senior Investigator award and the Wellcome Trust collaborative award for the Neuroscience in Psychiatry Network. A.F.A.-B. was supported by NIMH (K08MH120564). R.R.G. was supported by the EMERGIA Junta de Andalucía program (EMERGIA20_00139). S.L.V. was supported by Max Planck Gesellschaft, (Otto Hahn Award) and the Helmholtz Association’s Initiative and Networking Fund under the Helmholtz International Lab grant agreement InterLabs-0015, and the Canada First Research Excellence Fund (CFREF Competition 2, 2015–2016) awarded to the Healthy Brains, Healthy Lives initiative at McGill University, through the Helmholtz International BigBrain Analytics and Learning Laboratory (HIBALL). G.K.M. was supported by MRC (MR/W020025/1). For the purpose of open access, the authors have applied a CC BY license to any author-accepted manuscript version arising from this submission. We thank L.K. Abraham and J. Asimit for their helpful discussions. Additional acknowledgments are provided in the Supplementary Information.
Footnotes
Competing interests
A.A.-B. receives consulting income from Octave Biosciences. E.T.B. serves as a consultant for Sosei Heptares, Boehringer Ingelheim, GlaxoSmithKline, Monument Therapeutics and SR One. M.J.G. receives grant support from Mitsubishi Tanabe Pharma, unrelated to the current manuscript. The remaining authors declare no competing interests.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Online content
Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41588-023-01475-y.
Extended data is available for this paper at https://doi.org/10.1038/s41588-023-01475-y.
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41588-023-01475-y.
Data availability
All summary statistics for the GWAS meta-analyses are available for access here: https://portal.ide-cam.org.uk/overview/483. To prevent potential misuse, the data are available under controlled access after approval by the research team for educational and research purposes only. Data from the UKB and ABCD can be applied for and accessed by approved researchers. GWAS summary statistics for other brain imaging phenotypes can be obtained from: The Oxford Brain Imaging Genetics PheWeb (PheWeb (ox.ac.uk)), GWAS catalog (GWAS Catalog (ebi.ac.uk)), GWAS ATLAS (Genome-wide association study ATLAS (ctglab.nl)) and Brain Imaging Genetics Knowledge Portal Brain Imaging Genetics Summary Statistics. The SPARK dataset can be obtained by application to SFARIbase (SFARI ∣ SFARI Base). The DDD dataset can be obtained via EGA (deciphering developmental disorders (DDD)–EGA European Genome-Phenome Archive (ega-archive.org)).
Code availability
Code used are available at https://github.com/ucam-department-of-psychiatry/UKB (ref. 136), https://github.com/ucam-department-of-psychiatry/ABCD (ref. 137), vwarrier/ABCD_geneticQC (github.com; ref. 138) and vwarrier/Imaging_genetics_analyses (github.com; ref. 139).
References
- 1.Bethlehem RAI et al. Brain charts for the human lifespan. Nature 604, 525–533 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Thompson PM et al. ENIGMA and global neuroscience: a decade of large-scale studies of the brain in health and disease across more than 40 countries. Transl. Psychiatry 10, 100 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gilmore JH, Knickmeyer RC & Gao W Imaging structural and functional brain development in early childhood. Nat. Rev. Neurosci 19, 123–137 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Paus T, Keshavan M & Giedd JN Why do many psychiatric disorders emerge during adolescence? Nat. Rev. Neurosci 9, 947–957 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Elliott LT et al. Genome-wide association studies of brain imaging phenotypes in UK Biobank. Nature 562, 210–216 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grasby KL et al. The genetic architecture of the human cerebral cortex. Science 367, eaay6690 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stein JL et al. Identification of common variants associated with human hippocampal and intracranial volumes. Nat. Genet 44, 552–561 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhao B. et al. Common genetic variation influencing human white matter microstructure. Science 372, eabf3736 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Makowski C. et al. Discovery of genomic loci of the human cerebral cortex using genetically informed brain atlases. Science 375, 522–528 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jansen PR et al. Genome-wide meta-analysis of brain volume identifies genomic loci and genes shared with intelligence. Nat. Commun 11, 5606 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Smith SM et al. An expanded set of genome-wide association studies of brain imaging phenotypes in UK Biobank. Nat. Neurosci 24, 737–745 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Naqvi S. et al. Shared heritability of human face and brain shape. Nat. Genet 53, 830–839 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jayaraman D, Bae B-I & Walsh CA The genetics of primary microcephaly. Annu. Rev. Genomics Hum. Genet 19, 177–200 (2018). [DOI] [PubMed] [Google Scholar]
- 14.Li M. et al. Integrative functional genomic analysis of human brain development and neuropsychiatric risks. Science 362, eaat7615 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bycroft C. et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Casey BJ et al. The Adolescent Brain Cognitive Development (ABCD) study: imaging acquisition across 21 sites. Dev. Cogn. Neurosci 32, 43–54 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Glasser MF et al. A multi-modal parcellation of human cerebral cortex. Nature 536, 171–178 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bulik-Sullivan BK et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet 47, 1236–1241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hedman AM, van Haren NEM, Schnack HG, Kahn RS & Hulshoff Pol HE Human brain changes across the life span: a review of 56 longitudinal magnetic resonance imaging studies. Hum. Brain Mapp 33, 1987–2002 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brouwer RM et al. Genetic variants associated with longitudinal changes in brain structure across the lifespan. Nat. Neurosci 25, 421–432 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Willer CJ, Li Y & Abecasis GR METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics 26, 2190–2191 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bulik-Sullivan BK et al. LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet 47, 291–295 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sodini SM, Kemper KE, Wray NR & Trzaskowski M Comparison of genotypic and phenotypic correlations: Cheverud’s conjecture in humans. Genetics 209, 941–948 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grotzinger AD et al. Genomic structural equation modelling provides insights into the multivariate genetic architecture of complex traits. Nat. Hum. Behav 3, 513–525 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sanderson E. et al. Mendelian randomization. Nat. Rev. Methods Primers 2, 6 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rakic P. Specification of cerebral cortical areas. Science 241, 170–176 (1988). [DOI] [PubMed] [Google Scholar]
- 27.Ronan L. et al. Differential tangential expansion as a mechanism for cortical gyrification. Cereb. Cortex 24, 2219–2228 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Garcia KE, Kroenke CD & Bayly PV Mechanics of cortical folding: stress, growth and stability. Philos. Trans. R. Soc. Lond. B Biol. Sci 373, 20170321 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Richman DP, Stewart RM, Hutchinson JW & Caviness VS Jr. Mechanical model of brain convolutional development. Science 189, 18–21 (1975). [DOI] [PubMed] [Google Scholar]
- 30.Tallinen T, Chung JY, Biggins JS & Mahadevan L Gyrification from constrained cortical expansion. Proc. Natl Acad. Sci. USA 111, 12667–12672 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Reillo I, de Juan Romero C, García-Cabezas MÁ & Borrell V A role for intermediate radial glia in the tangential expansion of the mammalian cerebral cortex. Cereb. Cortex 21, 1674–1694 (2011). [DOI] [PubMed] [Google Scholar]
- 32.Kriegstein A, Noctor S & Martínez-Cerdeño V Patterns of neural stem and progenitor cell division may underlie evolutionary cortical expansion. Nat. Rev. Neurosci 7, 883–890 (2006). [DOI] [PubMed] [Google Scholar]
- 33.De Leeuw CA, Mooij JM, Heskes T & Posthuma D MAGMA: generalized gene-set analysis of GWAS data. PLoS Comput. Biol 11, e1004219 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sey N Y. A et al. A computational tool (H-MAGMA) for improved prediction of brain-disorder risk genes by incorporating brain chromatin interaction profiles. Nat. Neurosci 23, 583–593 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Akbarian S. et al. The PsychENCODE project. Nat. Neurosci 18, 1707–1712 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Eze UC, Bhaduri A, Haeussler M, Nowakowski TJ & Kriegstein AR Single-cell atlas of early human brain development highlights heterogeneity of human neuroepithelial cells and early radial glia. Nat. Neurosci 24, 584–594 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Polioudakis D. et al. A single-cell transcriptomic atlas of human neocortical development during mid-gestation. Neuron 103, 785–801 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ziffra RS et al. Single-cell epigenomics reveals mechanisms of human cortical development. Nature 598, 205–213 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Florio M & Huttner WB Neural progenitors, neurogenesis and the evolution of the neocortex. Development 141, 2182–2194 (2014). [DOI] [PubMed] [Google Scholar]
- 40.Geschwind DH & Rakic P Cortical evolution: judge the brain by its cover. Neuron 80, 633–647 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gertz CC, Lui JH, LaMonica BE, Wang X & Kriegstein AR Diverse behaviors of outer radial glia in developing ferret and human cortex. J. Neurosci 34, 2559–2570 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nott A. et al. Brain cell type-specific enhancer-promoter interactome maps and disease-risk association. Science 366, 1134–1139 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fukutomi H. et al. Neurite imaging reveals microstructural variations in human cerebral cortical gray matter. Neuroimage 182, 488–499 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zeng J. et al. Widespread signatures of natural selection across human complex traits and functional genomic categories. Nat. Commun 12, 1164 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Karczewski KJ et al. The mutational constraint spectrum quantified from variation in 141,456 humans. Nature 581, 434–443 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fu JM et al. Rare coding variation provides insight into the genetic architecture and phenotypic context of autism. Nat. Genet 54, 1320–1331 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Prevalence and architecture of de novo mutations in developmental disorders. Nature. 542, 433–438 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Niemi MEK et al. Common genetic variants contribute to risk of rare severe neurodevelopmental disorders. Nature 562, 268–271 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.SPARK Consortium. SPARK: a US cohort of 50,000 families to accelerate autism research. Neuron 97, 488–493 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Weissbrod O. et al. Functionally informed fine-mapping and polygenic localization of complex trait heritability. Nat. Genet 52, 1355–1363 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kabeche L, Nguyen HD, Buisson R & Zou L A mitosis-specific and R loop-driven ATR pathway promotes faithful chromosome segregation. Science 359, 108–114 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kaczmarczyk A & Sullivan KF CENP-W plays a role in maintaining bipolar spindle structure. PLoS ONE 9, e106464 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Koolen DA et al. The Koolen-de Vries syndrome: a phenotypic comparison of patients with a 17q21.31 microdeletion versus a KANSL1 sequence variant. Eur. J. Hum. Genet 24, 652–659, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhou X. et al. Cellular and molecular properties of neural progenitors in the developing mammalian hypothalamus. Nat. Commun 11, 4063 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kuwayama N. et al. A role for Hmga2 in the early-stage transition of neural stem-progenitor cell properties during mouse neocortical development. Preprint at bioRxiv 10.1101/2020.05.14.086330 (2021). [DOI] [Google Scholar]
- 56.De Crescenzo A. et al. A splicing mutation of the HMGA2 gene is associated with Silver–Russell syndrome phenotype. J. Hum. Genet 60, 287–293 (2015). [DOI] [PubMed] [Google Scholar]
- 57.Chenn A & Walsh CA Regulation of cerebral cortical size by control of cell cycle exit in neural precursors. Science 297, 365–369 (2002). [DOI] [PubMed] [Google Scholar]
- 58.Xiang Y-Y et al. Versican G3 domain regulates neurite growth and synaptic transmission of hippocampal neurons by activation of epidermal growth factor receptor. J. Biol. Chem 281, 19358–19368 (2006). [DOI] [PubMed] [Google Scholar]
- 59.Dobyns WB et al. MACF1 mutations encoding highly conserved zinc-binding residues of the GAR domain cause defects in neuronal migration and axon guidance. Am. J. Hum. Genet 103, 1009–1021 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Aschard H, Vilhjálmsson BJ, Joshi AD, Price AL & Kraft P Adjusting for heritable covariates can bias effect estimates in genome-wide association studies. Am. J. Hum. Genet 96, 329–339 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chen S. et al. A genome-wide mutational constraint map quantified from variation in 76,156 human genomes. Preperint at bioRxiv 10.1101/2022.03.20.485034 (2022). [DOI] [Google Scholar]
- 62.Demange PA et al. Investigating the genetic architecture of noncognitive skills using GWAS-by-subtraction. Nat. Genet 53, 35–44 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bhaduri A. et al. An atlas of cortical arealization identifies dynamic molecular signatures. Nature 598, 200–204 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Yeo BTT et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol 106, 1125–1165 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Mesulam MM From sensation to cognition. Brain 121, 1013–1052 (1998). [DOI] [PubMed] [Google Scholar]
- 66.Alexander-Bloch AF et al. On testing for spatial correspondence between maps of human brain structure and function. Neuroimage 178, 540–551 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sha Z. et al. The genetic architecture of structural left–right asymmetry of the human brain. Nat. Hum. Behav 5, 1226–1239 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Rubenstein JL & Rakic P Genetic control of cortical development. Cereb. Cortex 9, 521–523 (1999). [DOI] [PubMed] [Google Scholar]
- 69.Cox SR et al. Ageing and brain white matter structure in 3,513 UK Biobank participants. Nat. Commun 7, 13629 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sexton CE et al. Accelerated changes in white matter microstructure during aging: a longitudinal diffusion tensor imaging study. J. Neurosci 34, 15425–15436 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pletikos M. et al. Temporal specification and bilaterality of human neocortical topographic gene expression. Neuron 81, 321–332 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zhu Y. et al. Spatiotemporal transcriptomic divergence across human and macaque brain development. Science 362, eaat8077 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yoon B, Shim Y-S, Lee K-S, Shon Y-M & Yang D-W Region-specific changes of cerebral white matter during normal aging: a diffusion-tensor analysis. Arch. Gerontol. Geriatr 47, 129–138 (2008). [DOI] [PubMed] [Google Scholar]
- 74.Shi Y. et al. Diffusion tensor imaging-based characterization of brain neurodevelopment in primates. Cereb. Cortex 23, 36–48 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Coalson TS, Van Essen DC & Glasser MF The impact of traditional neuroimaging methods on the spatial localization of cortical areas. Proc. Natl Acad. Sci. USA 115, E6356–E6365 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kharabian Masouleh S. et al. Influence of processing pipeline on cortical thickness measurement. Cereb. Cortex 30, 5014–5027 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Alfaro-Almagro F. et al. Confound modelling in UK Biobank brain imaging. NeuroImage 224, 117002 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Barch DM et al. Demographic, physical and mental health assessments in the adolescent brain and cognitive development study: rationale and description. Dev. Cogn. Neurosci 32, 55–66 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Fischl B. et al. Automatically parcellating the human cerebral cortex. Cereb. Cortex 14, 11–22 (2004). [DOI] [PubMed] [Google Scholar]
- 80.Van Essen DC, Glasser MF, Dierker DL, Harwell J & Coalson T Parcellations and hemispheric asymmetries of human cerebral cortex analyzed on surface-based atlases. Cereb. Cortex 22, 2241–2262 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Rosen AFG et al. Quantitative assessment of structural image quality. Neuroimage 169, 407–418 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Alfaro-Almagro F. et al. Image processing and quality control for the first 10,000 brain imaging datasets from UK Biobank. Neuroimage 166, 400–424 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Hagler DJ Jr et al. Image processing and analysis methods for the Adolescent Brain Cognitive Development Study. Neuroimage 202, 116091 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Daducci A. et al. Accelerated microstructure imaging via convex optimization (AMICO) from diffusion MRI data. Neuroimage 105, 32–44 (2015). [DOI] [PubMed] [Google Scholar]
- 85.Schaer M. et al. How to measure cortical folding from MR images: a step-by-step tutorial to compute local gyrification index. J. Vis. Exp 2, e3417 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Knussmann GN et al. Test-retest reliability of FreeSurfer-derived volume, area and cortical thickness from MPRAGE and MP2RAGE brain MRI images. Neuroimage Rep. 2, 100086 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Haddad E et al. Multisite test-retest reliability and compatibility of brain metrics derived from FreeSurfer versions 7.1, 6.0, and 5.3. Hum. Brain Mapp 44, 1515–1532 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Hedges EP et al. Reliability of structural MRI measurements: the effects of scan session, head tilt, inter-scan interval, acquisition sequence, FreeSurfer version and processing stream. Neuroimage 246, 118751 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Madan CR & Kensinger EA Test-retest reliability of brain morphology estimates. Brain Inform. 4, 107–121 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Duff E. et al. Reliability of multi-site UK Biobank MRI brain phenotypes for the assessment of neuropsychiatric complications of SARS-CoV-2 infection: the COVID-CNS travelling heads study. PLoS ONE 17, e0273704 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.O’Donnell LJ & Westin C-F An introduction to diffusion tensor image analysis. Neurosurg. Clin. N. Am 22, 185–196 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Zhang H, Schneider T, Wheeler-Kingshott CA & Alexander DC NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61, 1000–1016 (2012). [DOI] [PubMed] [Google Scholar]
- 93.Tariq M, Schneider T, Alexander DC, Gandini Wheeler-Kingshott CA & Zhang H Bingham-NODDI: mapping anisotropic orientation dispersion of neurites using diffusion MRI. Neuroimage 133, 207–223 (2016). [DOI] [PubMed] [Google Scholar]
- 94.Andica C. et al. Scan–rescan and inter-vendor reproducibility of neurite orientation dispersion and density imaging metrics. Neuroradiology 62, 483–494 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Kong X-Z et al. Mapping cortical brain asymmetry in 17,141 healthy individuals worldwide via the ENIGMA Consortium. Proc. Natl Acad. Sci. USA 115, E5154–E5163 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Kurth F, Gaser C & Luders E A 12-step user guide for analyzing voxel-wise gray matter asymmetries in statistical parametric mapping (SPM). Nat. Protoc 10, 293–304 (2015). [DOI] [PubMed] [Google Scholar]
- 97.Leroy F. et al. New human-specific brain landmark: the depth asymmetry of superior temporal sulcus. Proc. Natl Acad. Sci. USA 112, 1208–1213 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.1000 Genomes Project Consortium. et al. A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Gogarten SM et al. Genetic association testing using the GENESIS R/bioconductor package. Bioinformatics 35, 5346–5348 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Manichaikul A. et al. Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–2873 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Jiang L. et al. A resource-efficient tool for mixed model association analysis of large-scale data. Nat. Genet 51, 1749–1755 (2019). [DOI] [PubMed] [Google Scholar]
- 102.Day FR, Loh P-R, Scott RA, Ong KK & Perry JRB A robust example of collider bias in a genetic association study. Am. J. Hum. Genet 98, 392–393 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Hartwig FP, Tilling K, Davey Smith G, Lawlor DA & Borges MC Bias in two-sample Mendelian randomization when using heritable covariable-adjusted summary associations. Int. J. Epidemiol 50, 1639–1650 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Zhu Z. et al. Causal associations between risk factors and common diseases inferred from GWAS summary data. Nat. Commun 9, 224 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Burgess S & Thompson SG Multivariable Mendelian randomization: the use of pleiotropic genetic variants to estimate causal effects. Am. J. Epidemiol 181, 251–260 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Grotzinger AD et al. Multivariate genomic architecture of cortical thickness and surface area at multiple levels of analysis. Nat. Commun 14, 946 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Purcell S. et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet 81, 559–575 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Loh P-R, Kichaev G, Gazal S, Schoech AP & Price AL Mixed-model association for biobank-scale datasets. Nat. Genet 50, 906–908 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Zheng J. et al. PhenoSpD: an integrated toolkit for phenotypic correlation estimation and multiple testing correction using GWAS summary statistics. Gigascience 7, giy090 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Yang J. et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet 42, 565–569 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Dahlke JA & Wiernik BM psychmeta: an R package for psychometric meta-analysis. Appl. Psychol. Meas 43, 415–416 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Foley CN et al. A fast and efficient colocalization algorithm for identifying shared genetic risk factors across multiple traits. Nat. Commun 12, 764 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Berisa T & Pickrell JK Approximately independent linkage disequilibrium blocks in human populations. Bioinformatics 32, 283–285 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Bowden J, Smith GD, Haycock PC & Burgess S Consistent estimation in Mendelian randomization with some invalid instruments using a weighted median estimator. Genet. Epidemiol 40, 304–314 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Bowden J, Davey Smith G & Burgess S Mendelian randomization with invalid instruments: effect estimation and bias detection through Egger regression. Int. J. Epidemiol 44, 512–525 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Verbanck M, Chen C-Y, Neale B & Do R Publisher correction: detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nat. Genet 50, 1196 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Morrison J, Knoblauch N, Marcus JH, Stephens M & He X Mendelian randomization accounting for correlated and uncorrelated pleiotropic effects using genome-wide summary statistics. Nat. Genet 52, 740–747 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Hemani G, Tilling K & Smith GD Orienting the causal relationship between imprecisely measured traits using GWAS summary data. PLoS Genet. 13, e1007081 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Hemani G. et al. The MR-base platform supports systematic causal inference across the human phenome. eLife 7, e34408 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Burgess S. Sample size and power calculations in Mendelian randomization with a single instrumental variable and a binary outcome. Int. J. Epidemiol 43, 922–929 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Bryois J. et al. Genetic identification of cell types underlying brain complex traits yields novel insights into the etiology of Parkinson’s disease. Nat. Genet 52, 482–493 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Won H. et al. Chromosome conformation elucidates regulatory relationships in developing human brain. Nature 538, 523–527 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Finucane HK et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet 47, 1228–1235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Finucane HK et al. Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat. Genet 50, 621–629 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Ge T, Chen C-Y, Ni Y, Feng Y-CA & Smoller JW Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun 10, 1776 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Warrier V. et al. Gene–environment correlations and causal effects of childhood maltreatment on physical and mental health: a genetically informed approach. Lancet Psychiatry 8, 373–386 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Warrier V. et al. Genetic correlates of phenotypic heterogeneity in autism. Nat. Genet 54, 1293–1304 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Wright CF et al. Optimising diagnostic yield in highly penetrant genomic disease. N. Engl. J. Med 388, 1559–1571 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Wang G, Sarkar A, Carbonetto P & Stephens M A simple new approach to variable selection in regression, with application to genetic fine mapping. J. R. Stat. Soc. Series B Stat. Methodol 82, 1273–1300 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Hu B. et al. Neuronal and glial 3D chromatin architecture informs the cellular etiology of brain disorders. Nat. Commun 12, 3968 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.McLaren W. et al. The ensembl variant effect predictor. Genome Biol. 17, 122 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Zhu Z. et al. Integration of summary data from GWAS and eQTL studies predicts complex trait gene targets. Nat. Genet 48, 481–487 (2016). [DOI] [PubMed] [Google Scholar]
- 133.O’Brien HE et al. Expression quantitative trait loci in the developing human brain and their enrichment in neuropsychiatric disorders. Genome Biol. 19, 194 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Yang J, Qi T, Wu Y, Zhang F & Zeng J Genetic control of RNA splicing and its distinctive role in complex trait variation. Nat. Genet 54, 1355–1363 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Qi T. et al. Identifying gene targets for brain-related traits using transcriptomic and methylomic data from blood. Nat. Commun 9, 2282 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Bethlehem RAI & Romero-Garcia R ucam-department-of-psychiatry/UKB: V1. Zenodo. 10.5281/zenodo.8051797 (2023). [DOI] [Google Scholar]
- 137.Bethlehem RAI & Romero-Garcia R ucam-department-of-psychiatry/ABCD: V1. Zenodo. 10.5281/zenodo.8051799 (2023). [DOI] [Google Scholar]
- 138.Warrier V. vwarrier/ABCD_geneticQC: v1. Zenodo. 10.5281/zenodo.8050609 (2023). [DOI] [Google Scholar]
- 139.Warrier V. vwarrier/Imaging_genetics_analyses: v1. Zenodo. 10.5281/zenodo.8050589 (2023). [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All summary statistics for the GWAS meta-analyses are available for access here: https://portal.ide-cam.org.uk/overview/483. To prevent potential misuse, the data are available under controlled access after approval by the research team for educational and research purposes only. Data from the UKB and ABCD can be applied for and accessed by approved researchers. GWAS summary statistics for other brain imaging phenotypes can be obtained from: The Oxford Brain Imaging Genetics PheWeb (PheWeb (ox.ac.uk)), GWAS catalog (GWAS Catalog (ebi.ac.uk)), GWAS ATLAS (Genome-wide association study ATLAS (ctglab.nl)) and Brain Imaging Genetics Knowledge Portal Brain Imaging Genetics Summary Statistics. The SPARK dataset can be obtained by application to SFARIbase (SFARI ∣ SFARI Base). The DDD dataset can be obtained via EGA (deciphering developmental disorders (DDD)–EGA European Genome-Phenome Archive (ega-archive.org)).
Code used are available at https://github.com/ucam-department-of-psychiatry/UKB (ref. 136), https://github.com/ucam-department-of-psychiatry/ABCD (ref. 137), vwarrier/ABCD_geneticQC (github.com; ref. 138) and vwarrier/Imaging_genetics_analyses (github.com; ref. 139).