Abstract
Liquid-liquid phase separation (LLPS) has been thought to be the biophysical principle governing the assembly of the multiphase structures of nucleoli, the site of ribosomal biogenesis. Condensates assembled through LLPS increase their sizes to minimize the surface energy as far as their components are available. However, multiple microphases, fibrillar centers (FCs), dispersed in a nucleolus are stable and their sizes do not grow unless the transcription of pre-ribosomal RNA (pre-rRNA) is inhibited. To understand the mechanism of the suppression of the FC growth, we here construct a minimal theoretical model by taking into account nascent pre-rRNAs tethered to FC surfaces by RNA polymerase I. The prediction of this theory was supported by our experiments that quantitatively measure the dependence of the size of FCs on the transcription level. This work sheds light on the role of nascent RNAs in controlling the size of nuclear bodies.
Subject terms: Supramolecular assembly, Biopolymers in vivo
Theoretical modeling and experimental tests shed light on the roles of nascent prerRNA, produced by Pol I transcription, in the assembly of the sea-island multi-phase structure in the nucleolus.
Introduction
In the interchromatin spaces of a cell nucleus, there are a variety of nuclear bodies, such as nucleoli1–4, Cajal bodies5,6, nuclear speckles7, and paraspeckles8. Many of the nuclear bodies are scaffolded by ribonucleoprotein (RNP) complexes, which are composed of RNA and RNA-binding proteins (RBPs). The class of RNAs that are essential to the assembly of specific subcellular bodies, is called architectural RNA (arcRNA)8–11. A growing number of researches suggest that nuclear bodies are assembled via liquid-liquid phase separation (LLPS), which is driven by the multivalent interaction between RBPs bound to arcRNAs8–11. Condensates produced by LLPS are spherical and increase their size by coarsening and/or coalescence to minimize the surface energy (macroscopic phase separation)12.
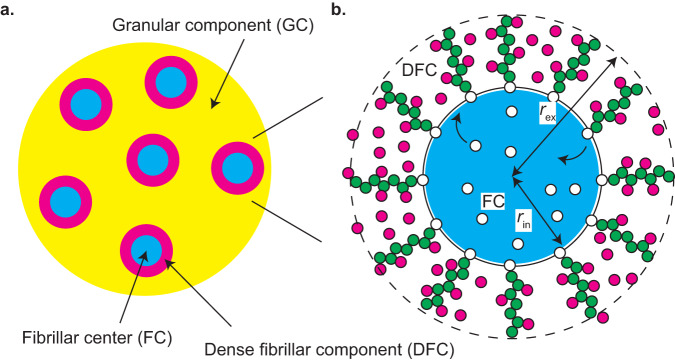
Nucleoli are nuclear bodies, where ribosome assembly takes place1,2. In the nucleoli, pre-ribosomal RNAs (pre-rRNAs) are transcribed by RNA polymerase I (Pol I) and maturated to construct ribosomes with ribosomal proteins. A nucleolus is not a uniform disordered liquid, but multiple microphases, called fibrillar centers (FCs), are dispersed in the sea of a granular component (GC) (Fig. 1a). Fibrillarin molecules (FBLs), which are RBPs interacting with pre-rRNAs, are condensed to form another phase, called the dense fibrillar component (DFC), at the interfaces between FCs and the GC. The multiphase structures of nucleoli have been thought to be assembled via simple LLPS13. However, this picture may not be complete because the FCs do not show coalescence or coarsening to increase their sizes. Indeed, when the Pol I transcription of pre-rRNA is inhibited, FCs show coalescence, as in the case of LLPS, and are excluded to the surface of the nucleolus (the excluded FCs are called nucleolar caps)14. This implies that transcription somehow suppresses the growth of FCs. Ribosomal DNA (rDNA), from which pre-rRNAs are transcribed, is a repeat sequence of coding units (10 kb) intervened by the intergenic regions (30 kb). The transcriptionally active rDNA units and Pol I are localized at the surfaces of FCs where the transcription of pre-rRNAs takes place3,14–16. The DFC layer is probably assembled by the RNP complexes of nascent pre-rRNAs and the associated RBPs, such as FBLs16. FBLs show phase separation with the physiological concentration and bind to nascent pre-rRNAs13,16. These experimental results imply that nascent pre-rRNAs may act as ‘surfactants’ that suppress the growth of FCs.
Fig. 1. Multiphase structure of a nucleolus.
a A nucleolus is composed of multiple fibrillar centers (FC) microphases in the sea of the granular component (GC). There is a layer of dense fibrillar component (DFC) between each FC and GC. b RNA polymerase I (Pol I) molecules (white particles) are entrapped in FC microphases (light blue) and the active rDNA units (black line) are localized at the surfaces of microphases. Nascent pre-rRNAs (green particles) are thus at the surfaces of the microphase and form a DFC layer with RNA-binding proteins (magenta particles). The interface between FC and DFC is located at a distance from the center and the interface between DFC and GC is located at a distance .
Paraspeckles are nuclear bodies scaffolded by NEAT1_2 arcRNAs. Analogous to FCs in the nucleolus, multiple paraspeckles are dispersed in a nucleoplasm17. Paraspeckles form the core-shell structure, where the two terminal regions of NEAT1_2 form the shell and the middle region of NEAT1_2 forms the core18,19. We have recently shown that the terminal regions of NEAT1_2 in the shell suppress the growth of paraspeckles, analogous to micelles of triblock copolymers17,20. The size of paraspeckles increases with the NEAT1_2 transcription upregulation17,21, which is distinct from the response of FCs in a nucleolus to transcription upregulation. This implies that the size control mechanism of FCs in a nucleolus is different from that of paraspeckles.
We here construct a simple theoretical model that predicts the contributions of nascent pre-rRNAs to the assembly of the multiphase structure of nucleolus. This model takes into account the phase separation, the transcription kinetics, and the interfacial effects, which are probably the minimum to account for the multiphase structure. Our theory predicts that the nascent pre-rRNAs are stretched to accommodate FBLs in the DFC layer and generate the lateral pressure that counteracts the interfacial tensions. The size of FCs is determined by the balance of the interfacial tensions and the lateral pressure. The latter activity of nascent pre-rRNAs is analogous to the surface activity of surfactants. Our theory quantitatively predicts the dependence of the size of FCs on the transcription rate. The suppression of the FC growth by the pre-rRNA transcription results from the fact that these complexes are end-grafted to the FC surfaces via Pol I, in contrast to other condensates in which arcRNAs diffuse freely and increase their sizes by the transcription upregulation. To test our prediction, we experimentally measured the FC sizes and the pre-rRNA levels while the transcription rate is changed by the dose of BMH-21 or CX-5461, which specifically inhibits the Pol I transcription. The scaling exponent predicted by our theory is consistent with our experimental results, implying that the lateral pressure generated by nascent pre-rRNAs are possible mechanism of the size control of FCs. We anticipate that this theory can be a base theory to further look into the contribution of the multiphase structure in the function of nucleoli and can be extended to study the mechanism of the size control and the functions of other nuclear bodies, such as nuclear speckles and transcriptional condensates.
Results
Model of nucleolus
We here construct a minimal model of a nucleolus to predict the size of FCs in the steady state (the list of symbols is given in Supplementary Table 1). The nucleolus is composed of a GC in which multiple spherical FCs are dispersed (Fig. 1a). Pol I molecules (shown by white particles in Fig. 1b) are entrapped in the FCs (shown by a light blue droplet in Fig. 1b). The transcriptionally active repeat units of rDNA (shown by the black line in Fig. 1b) are localized at the surfaces of the FCs. We assume that the number of Pol I molecules and the copy number of transcriptionally active rDNA units in the nucleolus are constant. Nascent pre-rRNAs (shown by chains of green particles in Fig. 1b) are localized at the surfaces of FCs and form a DFC layer (Fig. 1b). Recent experiment revealed that the 5’ terminal external transcribed spacer (ETS) regions of nascent pre-rRNAs are localized at the DFC layer and that, among the proteins localized in the DFC layer, FBLs contributed most significantly to the localization of the terminal regions of nascent pre-rRNAs in the DFC layer16. Motivated by this result, we take into account only the FBL-binding terminal regions of nascent pre-rRNAs as arcRNAs that scaffold the DFC layers and only FBLs as RBPs that bind to these regions (see also the “Discussion” section). Recent experiments also revealed that the upstream half of ETSs are localized at the DFC layer and the downstream half is localized at the FC16. This motivated us to assume that the terminal regions are spanning from the top to the bottom of the DFC layer. Some RBPs bind to the nascent pre-rRNAs and the others diffuse freely in the DFC layer (shown by magenta particles in Fig. 1b). The interface between FC and DFC is located at a distance from the center and the interface between DFC and GC is located at a distance from the center (see Fig. 1b). For simplicity, we assume that all the FCs have equal volume and the sum of the volumes of microphases is fixed to . This assumption does not seem so far off although it has not been quantified22.
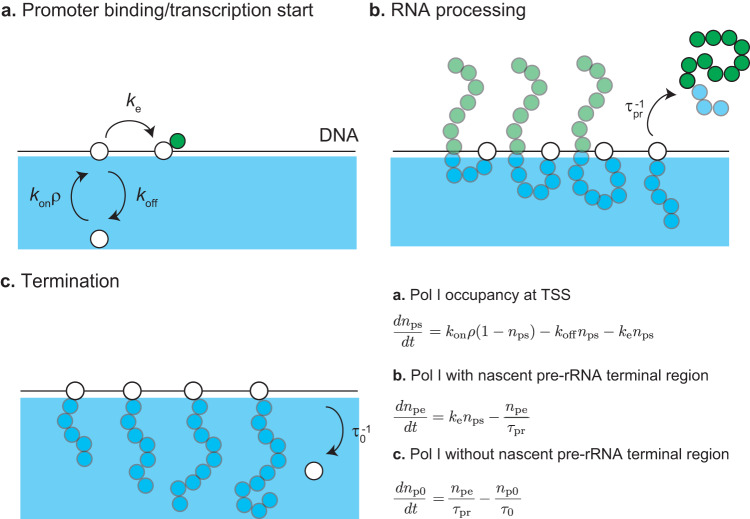
The number of nascent pre-rRNAs at the surfaces of FCs is determined by the kinetics of transcription and RNA processing. We treat the transcription dynamics of pre-rRNA by using an extension of the model used by Stasevich and coworkers23 (Fig. 2). Pol I in an FC binds to the transcription start site (TSS) of a transcriptionally active rDNA unit. The Pol I bound to the TSS starts transcription (Fig. 2a) or returns to the FC without starting transcription (Fig. 2a). The rate with which the Pol I bound to the TSS starts transcription is smaller than the rate with which this Pol I returns to the FC without starting transcription. The Pol I polymerizes a pre-rRNA while it moves uni-directionally towards the transcription termination site (TTS). The nascent pre-rRNAs are subject to co-transcriptional RNA processing (Fig. 2b). The FBL-binding terminal region is located at the ETS of pre-rRNA and is cleaved co-transcriptionally by endoribonuclease. The average time between the transcription initiation and the cleavage of the FBL-binding region is , where this time includes the elongation time to the cleavage site and the time necessary for the enzymatic reaction, see Fig. 2b and the Discussion. Pol I reaches TTS at the average elongation time and is then released to the FC (), see Fig. 2c. This model is designed to focus on the transcription of the FBL-binding terminal regions of nascent pre-rRNAs and to treat the rest of the process as simple as possible. The kinetic equations of the Pol I transcription and co-transcriptional processing are derived by taking into account the above-mentioned processes, see Fig. 2 and Eqs. (5)–(7). By solving these kinetic equations for the steady state, we found that the surface density is proportional to the radius of FCs, see Eq. (9) in Methods. We thus introduce a dimensionless parameter
| 1 |
which is proportional to the transcription rate and processing time , while it is independent of the radius . is the number of units in the terminal region of a nascent pre-rRNA (≈33)16 and b is the (Kuhn) length of RNA unit (≈4 nm)24.
Fig. 2. Model of transcription dynamics.
DNA (black solid line) is localized at the surface of an FC (cyan). a RNA polymerase I (Pol I) in a microphase binds to the transcription starting site (TSS) of an active rDNA repeat unit. The bound Pol I starts transcription with the rate or returns to the microphase without starting transcription. b During the transcription, Pol I migrates uni-directionally towards the transcription terminating site (TTS) while polymerizing a nascent pre-rRNA. The terminal region of the nascent pre-ribosomal RNA (pre-rRNA), to which FBL binds, are cleaved by the co-transcriptional RNA processing with the rate . The terminal region is released to GC. c After the cleavage of the terminal region, Pol I continues transcription until it reaches the TTS. At the TTS, Pol I is releaed to the FC with the rate .
The stability of the system is quantified by the free energy. The free energy of a DFC layer has 4 contributions: (1) the elastic free energy of nascent pre-rRNA, (2) the mixing free energy of RBPs and solvent, (3) the interaction free energy between RBPs (both freely diffusing in the DFC layer and bound to nascent pre-rRNA), and (4) the binding free energy of RBPs to the pre-rRNA terminal regions. The expressions of these free-energy contributions are shown in Eqs. (11)–(16) in Methods. The elastic free energy of flexible polymer chains, such as nascent pre-rRNAs, increases as the chains stretch because the number of possible conformations decreases12,25. The thermal fluctuation mixes the components (nascent pre-rRNA units, RBPs, and solvent) and this contribution is quantified as the mixing free energy The interaction free energy is the free-energy contribution of the multivalent interactions between RBPs. The binding free energy represents the free-energy gain due to the binding of RBPs to nascent pre-rRNA units and the thermal fluctuations that dissociate RBPs from nascent pre-rRNA units. The free energy takes into account the binding of RBPs to the terminal regions of nascent pre-rRNAs and the spherical geometry of the system in an extension of the Alexander model of polymer brush26.
The free energy of the system has the form
| 2 |
where is the interfacial energy per unit area (interfacial tension) at the interface between FC and DFC () and is the surface energy per unit area (interfacial tension) at the interface between DFC and GC (). The external radius is determined by the conservation of the number of RNA units in the DFC layer in the steady state, see Eq. (10) in Methods. The interfacial tension results from the interactions between the components of interfacing phases. We therefore assume that the surface tensions, and , are proportional the local volume fraction of RBPs at the interfaces, with the proportional coefficient , see Eqs. (17) and (18) in Methods. The free energy is a functional of the occupancy of the pre-rRNA terminal regions by RBPs, the volume fraction of RBPs freely diffusing in the DFC layer, and the volume fraction of the FBL units, where these are functions of the distance from the center of the FC. We derive these quantities by analyzing the condition of the minimum of the free energy, Supplementary Note 1. The relaxation dynamics of the terminal region of nascent pre-rRNAs is estimated to be faster than the elongation and thus its contribution is negligible, see Supplementary Note 2 and Supplementary Table 2.
Parameter estimate suggests that the terminal regions of nascent pre-rRNAs are highly stretched
The independent parameters involved in our theory and their estimates are summarized in Table 1. The kinetic constants involved in the Pol I transcription are included in , see Eq. (1). The energy gain due to the binding of RBPs to the pre-rRNA terminal regions is represented as We represent the magnitudes of the multivalent interaction between RBPs by using the Flory interaction parameter In principle, these parameters, and do not change with the suppression of Pol I transcription, but by the mutation of the RNA-binding regions and the intrinsically disordered regions of FBL, respectively. We neglect the dependence of the magnitudes of the interaction between RBPs on their binding state and also assume that solvent molecules and naked pre-rRNA units are equivalent in terms of the magnitudes of the interaction. This highlights the fact that the multivalent interaction between FBLs drives phase separation in vitro, not to lose the essence by introducing many interaction parameters. The volume fraction of RBPs in the nucleoplasm is taken into account via the chemical potential .
Table 1.
List of independent (dimensionless) parameters involved in our theory.
| Parameter | Meaning | Estimate | Value | Ref |
|---|---|---|---|---|
| ζ | Rescaled pre-rRNA surface density | <0.12 | Varied | 16 |
| Rescaled surface tension per RBP | 0.03 | 0.03 | ||
| χ | Interaction parameter | >10 | 12 | |
| ϵ | RBP-RNA-binding energy | <−10 | −12 | |
| RBP chemical potential | −10 | −10 | 13 |
The unit length b of pre-rRNA is estimated as 4 nm (≈12 b) by using the value of single-stranded DNA (23). The absolute temperature T is 300 K. The surface density was estimated by the number of Pol I (50 Pol I per rDNA, 300 copies of active rDNA repeat per cell, ~10 FCs per nucleolus, ~2 nucleoli per cell) and the typical radius of FCs (3,16). The surface tension can be estimated as (27,28), where the size of FBL is ≈4 nm (29). The number of units in the FBL-binding region of pre-rRNA is estimated by using its length ∼400 b (2,16). The chemical potential of FBL was estimated by using its concentration ~1 μM (13).
The interaction parameter and the binding energy are important quantities of polymer physics but are not experimentally well characterized. In the limit of vanishing volume fraction of nascent RNAs, , our model returns to the theory of the binary mixture of RBPs and solvent molecules12,27, see Eqs. (13)–(16) in Methods. The latter theory predicts that the phase separation happens at the threshold interaction parameter . FBL molecules show phase separation in vitro with the physiological concentration13, implying that χ > χtr0. If FBLs bind to the pre-rRNA terminal regions even in a dilute solution, it implies that ϵ < μp/(kBT). The size of the FBL-binding terminal region of a nascent pre-rRNA is ≈30 nm in the relaxed state (≈130 nm in the maximally stretched state), while the thickness of a DFC layer is ≈100 nm, implying that FBLs are highly stretched.
The multivalent interaction between FBLs localizes these RBPs to the DFC layer and stretches the terminal regions of nascent pre-rRNAs
To avoid complexity arising from the geometry of the system, we first analyze the composition of a DFC layer on a planer surface. This is indeed the limit of large FCs and the essential feature of the assembly of DFC layers is included in this analysis. In the planer geometry, the chemical potential of RBPs and the osmotic pressure are uniform, see also the asymptotic analysis in Supplementary Note 3.
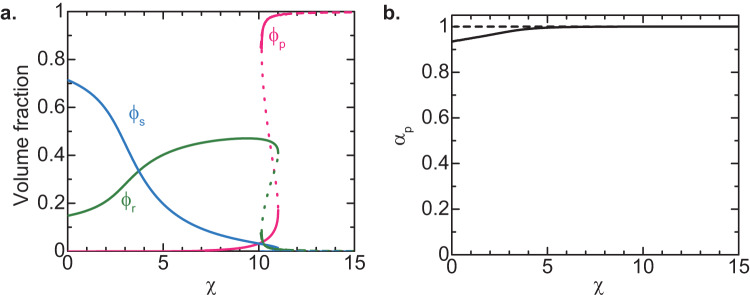
The magnitude of the multivalent interactions between RBPs (either bound to the pre-rRNA terminal regions or freely diffusing) increases with increasing the interaction parameter χ. Although it is not straightforward to experimentally control the interaction parameter χ of FBLs, it is instructive to analyze the composition of the layer occupied by the FBLs of nascent pre-rRNAs as a function of the interaction parameter χ, see Fig. 3. For cases in which the interaction parameter is small (which corresponds to self-association defective FBL ΔIDR mutant16), the major component of the layer is solvent (nucleoplasm), see the cyan line in Fig. 3. For χ < χs, the excluded volume interaction between nascent pre-rRNA units dominates the attractive interaction between RBPs bound to these nascent pre-rRNAs (good solvent regime). The interaction parameter χs at the crossover is 2 in the limit of ϵ ≪ μp/(kBT), such as the case of Fig. 3, see also Supplementary Equation (S27) for the general expression. The inverse of the volume fraction ϕr of nascent pre-rRNA is proportional to the extent of the stretching of the terminal regions of nascent pre-rRNAs. The terminal regions of these RNAs are somewhat stretched for χ ≈ 0 due to the excluded volume interaction between the pre-rRNA units. The terminal regions shrink as the magnitude χ of the attractive interaction between RBPs bound to the terminal regions of nascent pre-rRNAs, see the green line in Fig. 3. For , the attractive interaction dominates the excluded volume interaction (poor solvent regime) and the terminal regions are collapsed with RBPs bound to these regions (melt regime), see the green line in Fig. 3.
Fig. 3. Composition of planer DFC layer vs. interaction parameter χ.
a The volume fraction of pre-rRNA units (green), the volume fraction of freely diffusing RBPs (magenta), the volume fraction of solvent molecules (cyan) in a DFC layer are shown as functions of the interaction parameter . b The occupancy of pre-rRNA terminal region by RBPs is shown as a function of the interaction parameter . We used , , , and for the calculations, see also Table 1. The solid lines are derived by numerically solving Supplementary Equations (S15), (S16), and (S20). The broken lines are derived by using Supplementary Equation (S47) (shown for ).
At a threshold interaction parameter, χth ≈ −μp/(kBT), the volume fraction ϕp of freely diffusing RBPs jumps to a large value, see the magenta line in Fig. 3. In contrast, the volume fraction of the solvent (nucleosol) jumps to almost zero, see the cyan line in Fig. 3. The feature of the layer for χ > χth is analogous to the DFC layer observed experimentally (which we thus call DFC regime). The volume fraction ϕr of nascent pre-rRNA units jumps to a small value at χ ≈ χth, see the green line in Fig. 3, implying that the terminal regions of the nascent pre-rRNAs are stretched at the transition. Because the volume fraction ϕr is smaller than the case of χ = 0, the stretching is not solely due to the fact that RBPs in the DFC layer behave as an athermal solvent to the RNP complexes of RBPs and the pre-rRNA terminal regions. The terminal regions stretch so that the DFC layer can accommodate more RBPs to decrease the free energy due to the multivalent interactions between them. The stretching thus may be a transport mechanism of the ETS of pre-rRNAs towards the DFC layer.
The lateral pressure generated by nascent pre-rRNAs suppresses the growth of FCs
Now we discuss the DFC layers at the surfaces of spherical FCs to derive the radius of FCs in the steady state. In the spherical geometry, the chemical potential of RBPs and the chemical potential of pre-rRNA units, instead of the osmotic pressure, are uniform. These are the conditions of the minimum of the free energy, Eq. (2), see also Supplementary Note 1. We performed numerical and analytical calculations for the DFC regime in which the volume fraction of solvent molecules is negligibly small and the occupancy of the pre-rRNA terminal regions is approximately unity, see also Supplementary Note 4. In the spherical geometry, the volume fraction ϕr of pre-rRNA units is not uniform in the DFC layer and decreases with the distance r from the center (rin < r < rex), see the solid green line in Fig. 4. It results from the fact that the elastic stress (proportional to the number of pre-rRNAs per unit area) generated by pre-rRNA decreases with increasing r. The rest of the space in the DFC layer is filled by RBPs, see the inset of Fig. 4.
Fig. 4. Profile of volume fraction ϕr of pre-rRNA units in DFC layer.
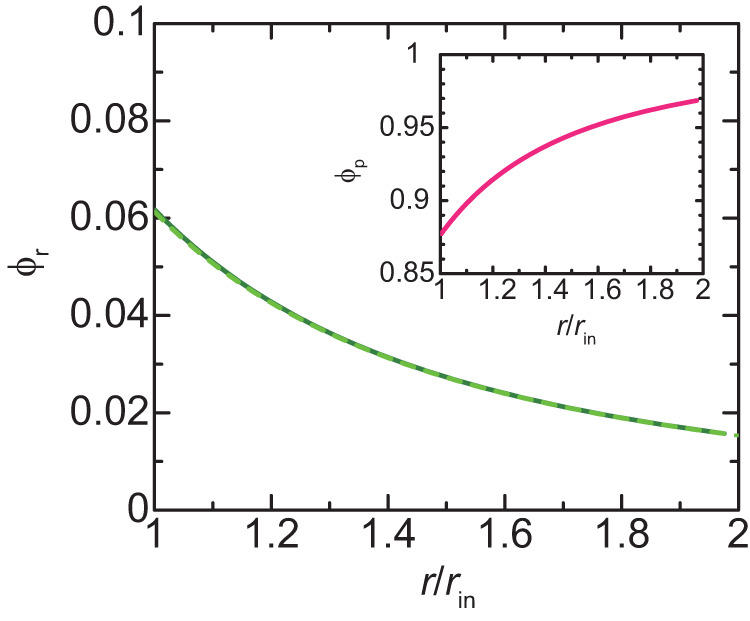
The volume fraction of nascent pre-rRNA units is shown as a function of the position in the DFC layer (). The solid dark green line is derived by numerically calculating Supplementary Equations (S13), (S15), and (S16) for with the condition that the volume fraction of solvent is zero and the occupancy of the terminal regions of pre-rRNAs by RBPs is unity. The values of other parameters are summarized in Table 1. The broken light green line is derived by using Supplementary Equation (S59) with and (which were derived from the numerical calculation to obtain the light green line). The volume fraction of freely diffusing RBPs is shown in the inset.
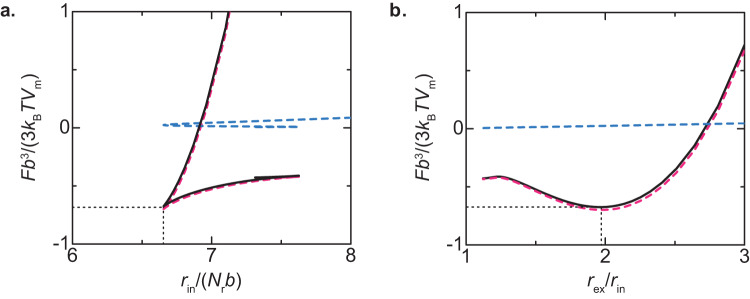
We used the profile of the pre-rRNA units to derive the free energy as a function of the radius rin of FCs. For cases in which the Pol I transcription is inhibited, the free energy of the system decreases monotonically with the radius rin, implying that, the radius of FCs increases with time by coarsening or coalescence. For cases in which the Pol I transcription is active, the free energy generated by the terminal regions of the nascent pre-rRNA is an intriguing function of rin, which has a minimum, see the solid black line in Fig. 5a. Indeed, the free energy is a simpler function of the ratio with a minimum, see Fig. 5b. Indeed, the surface free energy, the second and third terms of Eq. (2), is not significant for the values of parameters estimated in Table 1, see the broken cyan line in Fig. 5a.
Fig. 5. Free energy F of nucleolus.
The free energy of the system is shown as a function of the radius of FCs (a) and the ratio of the external radius to the internal radius (b). The black solid line is the total free energy, including the free energy of DFC layers (shown by the magenta broken line, the first term of Eq. (2)) and the surface free energy (shown by the cyan broken line, the second and third terms of Eq. (2)) for . The values of other parameters are summarized in Table 1.
One of the conditions satisfied at the minimum of the free energy has an approximate expression
| 3 |
Indeed, Eq. (3) represents the balance of the surface tensions, γin and γex, and the lateral osmotic pressure ΔΠ∥ generated in the DFC layer, see Eq. (20) for the complete form. The anisotropy in the osmotic pressure ΔΠ‖ results from the fact that the elastic stress of pre-rRNAs only acts in the radial direction. Although the isotropic osmotic pressure generated by FBLs filled in the DFC layer is balanced by the elastic stress of pre-rRNAs in the normal direction, it still acts in the lateral direction. The radius rin at the minimum of the free energy decreases with increasing the transcription rate, see Fig. 6. The radius at the minimum of the free energy has an asymptotic form
| 4 |
see also the broken line in Fig. 6. Equation (4) is derived by expanding the free energy in a power series of and by using the asymptotic form of , see Supplementary Note 4 for the details of the derivation. We also neglected the surface free energy, the second and third terms of Eq. (2), because it is not significant with our estimate in Table 1. Our theory therefore predicts that the radius of FCs decreases with the inverse of the square root of the transcription rate. At the minimum of the free energy, the ratio of the radii is , which roughly agrees with the fact that the radius of FCs and the thickness of DFC layers are the same order of length scales, , see Fig. 5b.
Fig. 6. Radius rin of FCs vs. rescaled transcription rate ζ.
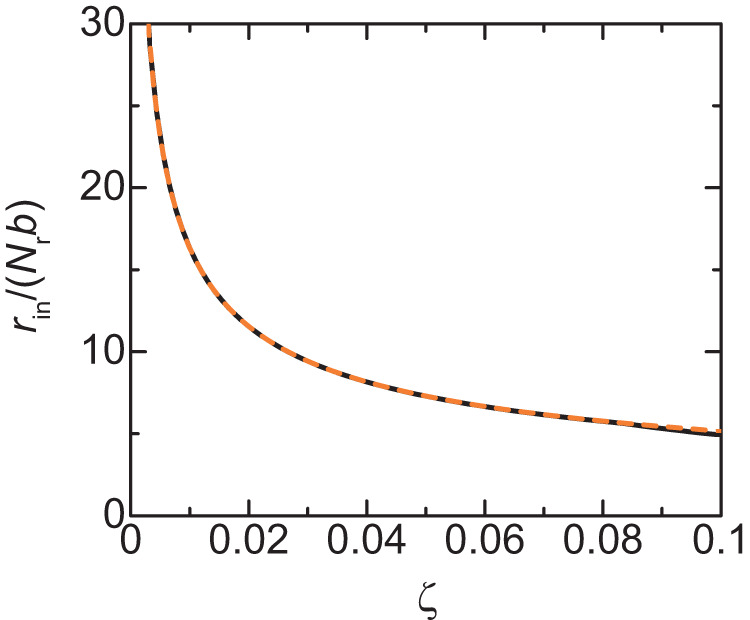
The radius of FCs at the free-energy minimum is shown as a function of rescaled transcription rate ζ. The solid dark green line is derived by numerically calculating Supplementary equations (S13), (S15), and (S16) with the condition that the volume fraction of solvent is zero and the occupancy of the terminal regions of pre-rRNAs by RBPs is unity. The orange broken line is derived by using Eq. 5. The parameters used for the calculations are summarized in Table 1.
Mild inhibition of Pol I increases the size of FCs
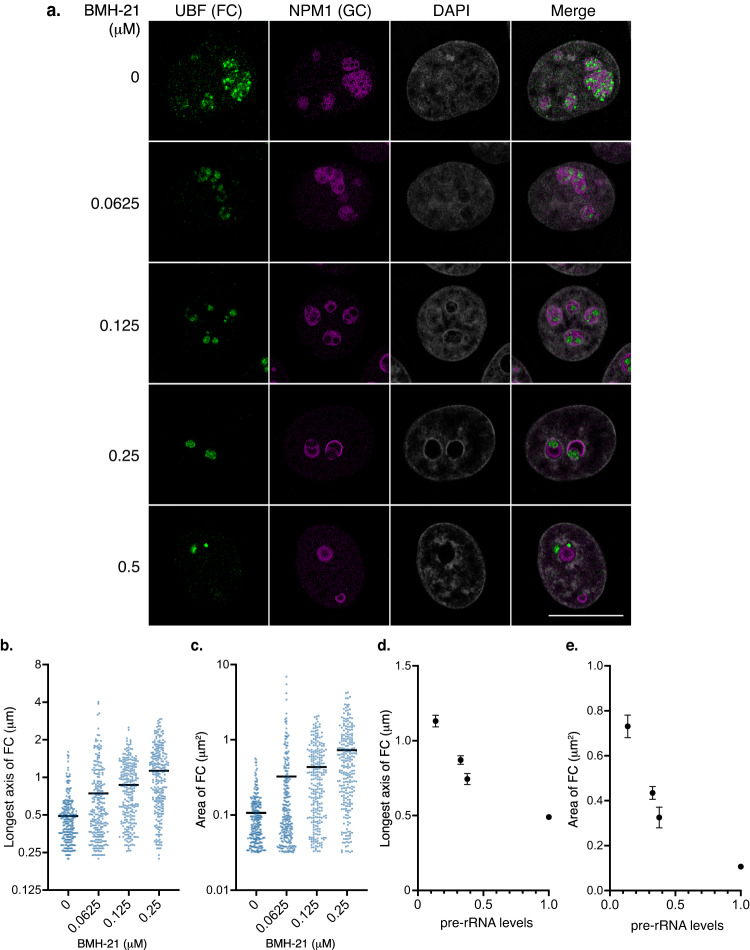
The main prediction from our theoretical model is that the size of FCs increases by reducing the expression level of nascent pre-rRNAs. To experimentally test this prediction, we used BMH-21 and CX-5461, specific Pol I inhibitors, which reduce nascent pre-rRNA levels in a dose-dependent manner28–30, see Figs. S1a, b. In untreated cells, small foci of UBF (a marker for FCs) and FBL (a marker for DFC) proteins were dispersed within the nucleoli as previously reported14, see Fig. 7a and Figs. S2a, S2b, and S3a. In contrast, UBF and FBL proteins were relocalized to nucleolar caps in the presence of high doses of BMH-21 (0.5 μM) or CX-5461 (2 μM), as reported14,28, see Fig. 7a and Figs. S2a, S2b, and S3a. Strikingly, the FCs were larger in cells treated with the medium doses of BMH-21 (0.0625, 0.125, and 0.25 μM) or CX-5461 (0.25, 0.5, and 1 μM) than in untreated cells, Fig. 7a and Figs. S2a, S2b, and S3a. The range of concentrations of BMH-21 used in our experiments is well within the subsaturation regime of Pol I transcription29. We then quantified the size of the FCs under these untreated and mildly treated conditions, see Fig. 7b, c, and Figs. S3b, S3c, and S4. Indeed, the longest axis (Lx) and area of the FCs increase with increasing the dose of BMH-21 and CX-5461. As theoretically predicted, the Lx and area of the FCs increase according to pre-rRNA level reduction, see Fig. 7d, e and Figs. S3d, e.
Fig. 7. Mild Pol I inhibition by BMH-21 increases the size of FCs.
a Immunofluorescence of UBF (FC) and NPM1 (GC) in HeLa cells with or without BMH-21 treatments. Scale bar, 10 μm. b, c Quantification of the longest axis (b) and area (c) of the FCs in cells under indicated conditions. Each scatter dot plot shows the mean (black line). Dots indicate all points of quantified data (n = 250). Mean longest axes of the FCs is shown below: 0 μM: 0.4907 μm, 0.0625 μM: 0.7440 μm, 0.125 μM: 0.8710 μm, 0.25 μM: 1.131 μm. Mean areas of the FCs are shown below: 0 μM: 0.170 μm2, 0.0625 μM: 0.3255 μm2, 0.125 μM: 0.4347 μm2, 0.25 μM: 0.7312 μm2. Statistical analyses using the Kruskal–Wallis test with Dunn’s multiple comparison test were performed and the results are shown as follows. b 0 μM vs. 0.0625 μM: P < 0.0001, 0 μM vs. 0.125 μM: P < 0.0001, 0 μM vs. 0.25 μM: P < 0.0001, 0.0625 μM vs. 0.125 μM: P < 0.0001, 0.0625 μM vs. 0.25 μM: P < 0.0001, 0.125 μM vs. 0.25 μM: P = 0.0008. c 0 μM vs. 0.0625 μM: P = 0.0003, 0 μM vs. 0.125 μM: P < 0.0001, 0 μM vs. 0.25 μM: P < 0.0001, 0.0625 μM vs. 0.125 μM: P < 0.0001, 0.0625 μM vs. 0.25 μM: P < 0.0001, 0.125 μM vs, 0.25 μM: P = 0.0010. d and e Graphs showing the mean longest axis (d) and area (e) of the FCs with SEM vs. pre-rRNA expression levels. The pre-rRNA expression level in untreated cells is defined as 1.
FC radius is a power function of the pre-rRNA transcription level with an exponent of approximately –0.5
The scaling exponent that describes the dependence of the size of FCs on the transcription level is a universal quantity that does not depend on specific values of the parameters, see Eq. (4). In polymer physics, checking such scaling exponents with experiments is the first thing to do to test theories31. To extract the scaling exponent from our experiments, we curve-fit the size of FCs (the square root of the average area of FCs, which is proportional to their radii) as a function of the transcription level by a power function, see Fig. 8. By fitting the data with a power function, we found that the scaling exponent is –0.49 for the case of the BMH-21 treatment, –0.46 for the case of the CX-5461, and –0.48 if both data are fitted. The scaling exponent predicted by our theory –0.5 reasonably agrees with our experiments, see Eq. 4.
Fig. 8. Exponent that accounts for the dependence of the size of FCs on pre-rRNA expression level.
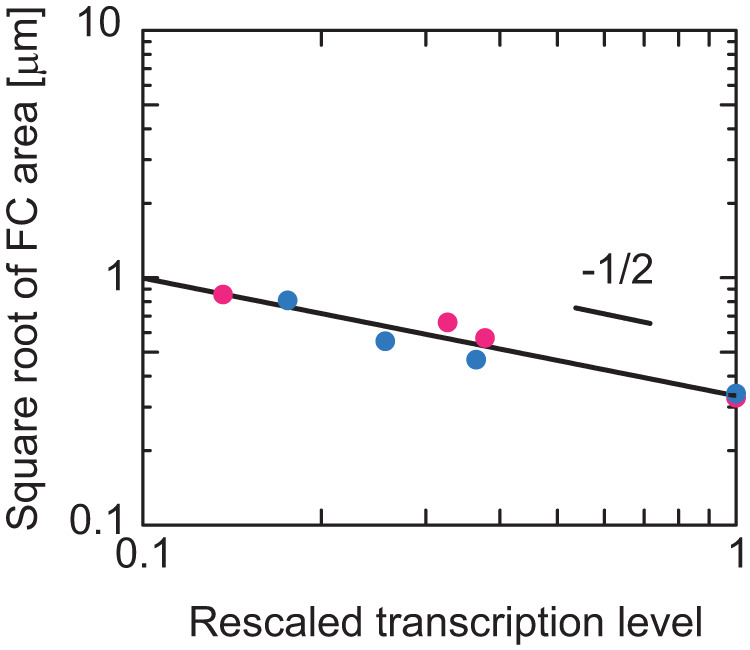
The data in Fig. 7e was shown in the double-logarithm plot and fitted with a power function. The magenta and cyan dots are the results of suppressing the Pol I transcription by using BMH-21 and CX-5461. The slope of the double-logarithm plot is the exponent that accounts for the dependence of the radius of FCs on the transcription level. The curve fitting shows that the exponent is –0.49 for the case of the BMH-21 treatment, –0.46 for the case of the CX-5461, and –0.48 if both data are fitted.
Discussion
Our theory predicts that the terminal regions of nascent pre-rRNAs at the surfaces of FC microphases in a nucleolus generate the lateral osmotic pressure and suppress the growth of microphases. This theory predicts the dependence of the radius of FCs on the transcription rate is consistent with our experiments. The lateral pressure is generated by the fact that the nascent pre-rRNAs are tethered to the surfaces of FCs via Pol I and attract FBL to the DFC layer. This pressure increases with the transcription rate by increasing the surface density of the nascent pre-rRNAs. Thus, if the Pol I transcription is continuously and slowly suppressed, the size of FCs increases following Eq. (4), see also Fig. 6. The contributions of the kinetics of transcription to the lateral pressure remain to be experimentally determined, while we estimate that its contribution is relatively small, see Supplementary Note 2. Our theory also predicts that the radius of FCs increases with increasing the pre-rRNA processing rate The inhibition of processing induced by ribosomal protein depletion, such as uL18 (RPL5) and uL5 (RPL11), changes the multiphase structure of nucleoli32. Recent experiments have demonstrated that long pre-rRNAs are accumulated in RPL5 knockdown cells and the size of FCs in such cells is smaller than that in the wild type33. The consistency between our theory and experiments suggests that the growth of FCs is suppressed by the terminal regions of nascent pre-rRNAs localized at the surfaces of FCs. This implies that the elastic energy of the terminal region is the driving force of the transport of the 5’ ETSs cleaved by RNA processing towards GC.
In many cases, the multivalent interaction between complexes of RNA and RBPs drives the growth of condensates34,35, see Fig. 9a. The size of such condensates increases with increasing the transcription rate17,21,36. In contrast, in the case of FCs in nucleoli, the multivalent interaction between the complexes of nascent RNA and RBPs rather suppresses the growth of FCs14. The size of FCs indeed decreases with increasing the transcription rate. Our theory predicts that the suppression of the growth of FCs by transcription results from the fact that pre-rRNAs are end-grafted to the surfaces of FCs via Pol I, see Fig. 9b.
Fig. 9. Summary of results.
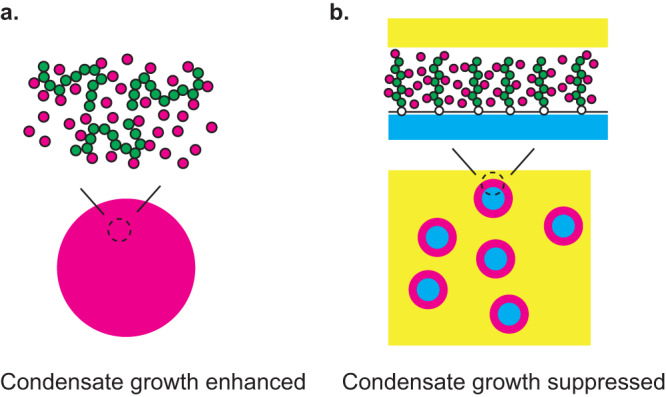
RNP complexes enhance or suppress the growth of condensates depending on whether the RNP complexes are mobile in the interior or tethered to the surfaces of the condensates. a The multivalent interaction between the RNP complexes enhances the growth of the condensates if these condensates are assembled by the RNP complexes. b The multivalent interaction between the RNP complexes suppresses the growth of the condensates if these complexes are tethered to the surfaces of the condensates assembled by other RNAs and proteins.
Our theory predicts that the function of the terminal regions of nascent pre-rRNAs is analogous to surfactants, such as lipids. If the surfactants at an interface between two immiscible liquids are dense enough to form a monomolecular liquid film, these surfactants decrease the interfacial tension to almost zero to disperse multiple droplets even in the thermodynamic equilibrium27,37. The surfactant monolayer acts as a kinetic barrier to suppress the coalescence and decreases the hydrostatic pressure of the droplet to suppress the coarsening12,27. These features are analogous to the roles of nascent pre-rRNAs predicted by our theory. The surface activity of some RNAs and proteins was also discussed in synthetic systems38,39. There are also differences between nascent pre-rRNA and surfactants. Surfactants are localized at interfaces at the thermodynamic equilibrium, while the terminal regions of nascent pre-rRNAs are localized at the FC-DFC interfaces only during the transcription, and their surface activity is regulated by Pol I transcription dynamics.
Although our theory probably could capture the essential features that are necessary to understand the assembly mechanism of the multiphase structure of nucleolus, it is not complete. First, the layers at the interface between FCs and GC are not uniform, but DFC regions are flanked by the regions, in which FBLs are not observed by super-resolution microscopy and are not visible by electron microscopy. Second, we did not take into account the downstream pre-rRNA regions that are not bound by FBLs. These downstream regions were observed in FCs16. The direct contribution of rDNAs localized at the surfaces of FCs is probably not significant, see Supplementary Discussion. Third, we did not explicitly take into account the transport dynamics of pre-rRNAs in GCs. Fourth, RNAs can be not only cleaved but also can be folded and/or chemically modified during co-transcriptional processing. The processing of pre-rRNAs in yeast has been well-documented40,41, but much less in higher eukaryotes42,43, in which the multiphase structure of nucleolus is usually observed. It is of interest to extend the present theory by taking into account the co-transcriptional RNA processing to study the biochemical role of RBPs in RNA processing44, the modulation of RBP binding by the chemical modification of pre-rRNAs, such as methylation and pseudouridylation, and the role of the RNA chemical modification in the assembly of the multiphase structure of the nucleus. Fifth, we did not take into account the modulation of the stiffness of pre-rRNAs by the binding of RBPs. Sixth, we neglect the contributions of molecular factors other than the RNP complexes of nascent pre-rRNAs and RBPs. Last, but not least, we assume that the DFC layer is a liquid layer, see also Supplementary Discussion. Indeed, recent experiments showed that long non-coding RNA SLERT facilitates the transition of the RNA helicase DDX21 to the closed conformation and ensures the fluidity of proteins in the DFC layer45.
Whether the multiphase structure of the nucleolus contributes to its function is not yet clear. It is of interest to extend our theory to understand the structure-function relationship of the nucleolus46. A peculiar process is that during the maturation of rRNAs, processed pre-rRNAs, from which ETSs are cleaved and thus have the affinity to FCs, penetrate through the DFC layer towards the GC. One possible hypothesis is that the processed pre-rRNAs pass the flanking regions of the DFC layer. These flanking regions increase the density of the terminal regions of pre-rRNAs in the DFC compartments and enhance the lateral osmotic pressure, see also Supplementary Note 4. The enhanced lateral pressure and/or the kinetic trapping of the coalescence of FCs by nascent pre-rRNAs may explain the fact that the radius of FCs observed in experiments is somewhat smaller than that predicted by our theory. However, following the approach of classical theoretical physics, our present theory should be experimentally tested before adding more assumptions that have not been experimentally explored. Identifying RBPs bound to different regions of pre-rRNAs would be useful to address the above-mentioned questions.
Our theory may provide insight into the size control mechanism of other nuclear bodies. Nuclear stress bodies (nSBs) form a sea-island multiphase structure, which is somewhat analogous to nucleoli47. nSBs are composed of HSATIII arcRNA and specific RBPs10. HSATIII is transcribed by Pol II from the pericentromeric Satellite III regions, which are enriched in tandem repeats48,49. The size of nuclear speckles increases by the suppression of transcription7. The size and stability of transcriptional condensate50–54 also depend on the transcription rate and the length of transcripts50,51. These features are common with nucleoli and thus motivate us to think of a general mechanism involved in the assembly of the multiple subcompartments. The nascent RNAs, which are produced by transcription and are modulated by RNA processing, are important elements that regulate the multiphase structures and possibly their functions of nuclear bodies.
Methods
Transcription and RNA processing
The occupancy of the TSS of the active rDNA by Pol I follows the kinetic equation
| 5 |
Equation (5) suggests that the occupancy changes due to the binding of Pol I from the FC (the first term), the unbinding of Pol I from the TSS to the FC without starting transcription (the second term), and the initiation of the elongation of Pol I (the third term), see Fig. 2a. kon is the rate constant for the binding of Pol I to TSS and ρ is the concentration of Pol I in a FC (which will be determined later). koff is the rate constant for the unbinding of Pol I from TSS. ke is the rate of the transition of Pol I from the bound state to the elongation state.
The number of elongating Pol I protein complexes with pre-processed nascent pre-rRNA follows the kinetic equation
| 6 |
Equation (6) suggests that the number changes due to the release of Pol I from TSS for elongation (the first term) and the cleavage of the FBL-binding terminal region of nascent pre-rRNA (the second term), see Fig. 2b. is the average time between the transcription initiation and the cleavage of the terminal regions of the pre-rRNA.
The number of elongating Pol I with processed nascent pre-rRNA follows the kinetic equation
| 7 |
Equation (7) suggest that the number changes due to the the cleavage of the terminal regions of pre-rRNAs (the first term) and the transcription termination (the second term), see Fig. 2c. is the average time between the cleavage of FBL-binding region and the transcription termination.
The numbers, , , and , of Pol I in each state are derived for the steady state, , by using Eqs. (5)–(7). The inverse time of the transcription initiation is much smaller than the inverse of the unbinding of Pol I from TSS, . The concentration Pol I in a FC is determined by the condition
| 8 |
that the sum of the number of Pol I during transcription (the first term) and the number of Pol I diffusing in microphases (the second term) in the system is constant. All the parameters involved in Eq. (8) do not depend on the size of FCs, see Eqs. (5)–(7). The concentration of Pol I in FCs thus does not depend on the size of FCs.
The surface density of the FBL-binding terminal regions of nascent pre-rRNAs at each FC (the number of nascent pre-rRNAs per unit area of each FC surface) is represented as
| 9 |
by assuming that the terminal regions of nascent pre-rRNA is distributed uniformly at the surfaces of FCs. We note that is the number of FCs in a nucleolus. The last form of Eq. (9) is derived by using the solution of Eqs. (5)–(7).
Thickness of DFC layer
The exterior radius (see also Fig. 1b) is determined by the relationship
| 10 |
where is the average number of units in the terminal region of a nascent pre-rRNA. It is a mean-field treatment that assumes that nascent RNAs are composed of the same number of units and is effective within the Alexander-de Gennes approximation, with which the brush height is determined by the distance between neighboring grafting points and the average number of units per chain (if one neglects the fact that the lateral fluctuations of a chain composed of units is limited to )55,56.
Free energy of DFC layer
The free energy of each DFC layer has the form
| 11 |
with
| 12 |
Equation (11) is the functional of the local volume fraction of nascent pre-rRNA units, the local volume fraction of RBPs, and the occupancy of nascent pre-rRNA units by RBPs, which are functions of the distance from the center of the FC (), see Fig. 1b. is the length of a pre-rRNA unit. This free energy is composed of 4 contributions: is the elastic free-energy density of the terminal regions of nascent RNAs, is the free-energy density due to the mixing entropy of RBPs and solvent molecules, is the free-energy density due to the interactions between RBPs, and is the free-energy density due to the binding of RBPs to the terminal regions of nascent RNAs. is the chemical potential of RBPs and is the osmotic pressure from the exterior.
The (entropic) elastic free-energy density has the form
| 13 |
where is the surface density of FBL-binding regions of nascent pre-rRNAs. for cases in which the surface of FCs is sphere and for cases in which the surface of FCs is planer (which corresponds to the limit of ). The volume fraction of pre-rRNA units decreases as the terminal regions of the nascent pre-rRNAs are stretched. Equation (13) represents the fact that the elastic free energy increases as these terminal regions are stretched. Equation (13) takes into account the spherical geometry of the system in an extension of the Alexander model (that assumes that the concentration of the terminal regions of nascent pre-rRNA is uniform in the DFC layer in the limit of ) in the spirit of the Daoud-Cotton theory57, see Supplementary Note 5 for the derivation. is the Boltzmann constant and is the absolute temperature.
The free energy due to the mixing entropy of RBPs and solvent molecules has the form
| 14 |
The mixing free energy, Eq. (14), has the contributions of the mixing entropy of RBPs (the first term) and the mixing entropy of solvent molecules (the second term).
The free energy due to the interactions between RBPs has the form
| 15 |
where is the interaction parameter that accounts for the attractive interactions. For simplicity, we assumed that RBPs bound to the terminal regions of nascent pre-rRNAs are equivalent to RBPs freely diffusing in the DFC layer and that solvent molecules are equivalent to nascent RNA units in terms of the interactions.
The free energy due to the binding of RBPs to nascent RNAs has the form
| 16 |
where is the energy increase due to the binding of RBPs to nascent RNAs. For simplicity, we assumed that each nascent RNA unit has one binding site of RBPs.
Free energy of system
The free energy of the system, Eq. (2) is derived by using the fact that the number of microphases in the system is to derive this form. The interfacial tension between GC and nucleosol is relative small3,13 and FC is excluded out from the nucleolus by the transcription inhibition3,14, implying that the interfacial tension between FC and nucleosol is even smaller. In vitro experiments suggest that the attractive interaction between FBLs is much larger than that between nucleophosmins, a major component of GC13. It implies that the interfacial tension between DFC and GC and that between DFC and FC are larger than their difference. By neglecting the difference between these interfacial tensions, the interfacial tensions γin and γex at the interior and the exterior interfaces are represented by the forms
| 17 |
| 18 |
where is the surface tension between a nucleosol and a liquid of the RBPs and is proportional to .
Lateral osmotic pressure
The lateral osmotic pressure can be defined by
| 19 |
where the derivative with respect to is taken with the condition that is constant (this increases the area of the surface of a FC without changing the composition of the DFC layer). is the lateral osmotic pressure, from which the contribution of the isotropic osmotic pressure is subtracted.
Radius of FCs at free-energy minimum
The free energy is represented as a function only of the radius of FCs if the occupancy, , and the volume fractions, and , are substituted into Eq. (2). The radius at the steady sate is derived by the condition with the condition that (this increases the area of the surfaces of FCs with the optimization of the arrangement of the active rDNA repeats). This leads to the form
| 20 |
which represent the fact that the surface tension is balanced to the surface pressure generated by the FBRs of nascent pre-rRNAs.
Cell culture, drug treatment, reverse transcription-quantitative PCR (RT-qPCR), immunofluorescence, and quantification of the size of FCs
HeLa cells were maintained in DMEM containing high glucose (Nacalai Tesque, Cat# 08458-16) supplemented with 10% FBS (Sigma) and Penicillin-Streptomycin (Nacalai Tesque). Cells were treated with BMH-21 (Selleckchem, Cat# S7718) or CX-5461 (AdooQ Bioscience) for 3 h. Quantification of nascent pre-rRNAs (forward primer: 5’-CCTTCCCCAGGCGTCCCTCG-3’, reverse primer: 5’-GGCAGCGCTACCATAACGGA-3’)14 by RT-qPCR was performed using LightCycler 480 II (Roche). These primers are located in the 5’ external transcribed spacer region of pre-rRNA, where the mature 18S, 5.8S, and 28S rRNAs do not include this region. Therefore, these primers only detect pre-rRNAs and do not detect the mature rRNAs. GAPDH mRNAs were used as a loading control17. The antibodies to UBF (Santacruz, F-9, sc-13125, mouse monoclonal antibody, 1:50 dilution), FBL (Proteintech, 16021-1-AP, rabbit polyclonal antibody, 1:500 dilution), and NPM1/Nucleophosmin (Abcam, ab183340, SP236, rabbit polyclonal antibody, 1:100 dilution) were used to visualize FCs, DFCs, and GCs in immunofluorescence, respectively. Cells were grown on coverslips (Matsunami; 18 mm round) and fixed with 4% paraformaldehyde/PBS at room temperature for 10 min. Then, the cells were washed three times with 1x PBS, permeabilized with 0.5% Triton-X100/PBS at room temperature for 5 min, and washed three times with 1x PBS. The cells were incubated with 1x blocking solution (Roche, Blocking reagent, and TBST [1x TBS containing 0.1% Tween 20]) at room temperature for 1 h. Then, the coverslips were incubated with primary antibodies in 1x blocking solution at room temperature for 1 h, washed three times with TBST for 5 min, incubated with secondary antibodies (anti-mouse IgG, Alexa Fluor 488, superclonal [Thermo Fisher Scientific, Cat#A28175], anti-rabbit IgG, Alexa Fluor 568 [Thermo Fisher Scientific, Cat#A11036]) at room temperature for 1 h, and washed three times with TBST for 5 min. The coverslips were mounted with a Vectashiled hard-set mounting medium with DAPI (Vector, H-1500). Super-resolution images were acquired using ZEISS LSM900 with Airyscan 2. Quantification of the FCs marked by UBF staining within the nucleoli labeled by NPM1 staining was performed using NIS Elements Advanced Research (NIKON). “FillArea” and “MaxFeret” of the UBF foci (FCs) detected with an intensity threshold were quantified as area and Lx of the FCs, see Fig. S4.
Statistics and reproducibility
Statistical analyses were performed using the Kruskal–Wallis test with Dunn’s multiple comparison test for Fig. 7b, c, and Fig. S3b, c. The calculated p-values are described in the figure legends. No statistical method was used to pre-determine the sample size, but our sample sizes are similar to those reported in previous publications. All experiments were performed independently two or three times with similar results obtained. Prism 8 software (GraphPad) was used for the statistical analyses.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Acknowledgements
This research was supported by KAKENHI grants from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan [to T. Yamamoto (20H05934, 21K03479, 21H00241), T. Yamazaki (21H00253, 22H02545), K.N. (19K06478, 22K06083), and T.H. (20H00448, 20H05377,21H05276)], J.S.T., PRESTO Grant Number JPMJPR18KA (to T. Yamamoto), the Mochida Memorial Foundation for Medical and Pharmaceutical Research (to T. Yamazaki), the Naito Foundation (to T. Yamazaki), the Takeda Science Foundation (to T. Yamazaki), and JST CREST Grant Number JPMJCR20E6 (to T.H.). T. Yamazaki thanks Toyofumi Kameoka (NIKON SOLUTIONS CO., LTD.) and Takayuki Funato (NIKON SOLUTIONS CO., LTD.) for support of microscopic image analyses. T. Yamamoto acknowledges the fruitful discussion with Noriko Saito (Japanese Foundation for Cancer Research), Yuma Ito (Tokyo Institute of Technology), Satoru Ide (National Institute of Genetics), Tsutomu Suzuki (Univ. of Tokyo), Takehiko Kobayashi (Univ. of Tokyo), Yutetsu Kuruma (JAMSTEC), Shintaro Iwasaki (Univ. of Tokyo), Sumio Sugano (Chiba Univ.), Haruhiko Siomi (Keio Univ.), Hideaki Matsubayashi (Tohoku Univ.), and Naomichi Takemata (Kyoto Univ.).
Author contributions
T. Yamamoto, T. Yamazaki, K.K., and T.H. designed the research and wrote/revised the manuscript. T. Yamamoto developed the theoretical model and performed the calculations. T. Yamazaki performed the experiments.
Peer review
Peer review information
Communications Biology thanks the anonymous reviewers for their contribution to the peer review of this work. Primary handling editors: Krishnananda Chattopadhyay and Anam Akhtar. A peer review file is available.
Data availability
The data of the numerical calculations available in figshare with the identier (10.6084/m9.figshare.16599446)58.
Code availability
The Mathematica file used for the numerical calculations is available in figshare with the identier (10.6084/m9.figshare.16599446).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Tetsuya Yamamoto, Tomohiro Yamazaki.
Contributor Information
Tetsuya Yamamoto, Email: tyamamoto@icredd.hokudai.ac.jp.
Tomohiro Yamazaki, Email: tyamazaki@fbs.osaka-u.ac.jp.
Supplementary information
The online version contains supplementary material available at 10.1038/s42003-023-05519-1.
References
- 1.Klinge S, Woolford J., Jr Ribosome assembly coming into focus. Nat. Rev. Mol. Cell Biol. 2019;20:116–131. doi: 10.1038/s41580-018-0078-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McStay B, Grummt I. The epigenetics of rRNA genes: from molecular to chromosome biology. Annu. Rev. Cell Dev. Biol. 2008;24:131–157. doi: 10.1146/annurev.cellbio.24.110707.175259. [DOI] [PubMed] [Google Scholar]
- 3.Lafontaine D, Riback J, Bascetin R, Brangwynne C. The nucleolus as a multiphase liquid condensate. Nat. Rev. Mol. Cell Biol. 2021;22:165–182. doi: 10.1038/s41580-020-0272-6. [DOI] [PubMed] [Google Scholar]
- 4.Berry J, Weber S, Vaidya N, Haataja M, Brangwynne C. RNA transcription modulates phase transition driven nuclear body assembly. Proc. Natl Acad. Sci. USA. 2015;112:E5237–E5245. doi: 10.1073/pnas.1509317112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cioce M, Lamond AI. Cajal bodies: a long history of discovery. Annu. Rev. Cell Dev. Biol. 2005;21:105–131. doi: 10.1146/annurev.cellbio.20.010403.103738. [DOI] [PubMed] [Google Scholar]
- 6.Nizami Z, Deryusheva S, Gall JG. The Cajal body and histone locus body. Cold Spring Harb. Perspect. Biol. 2010;2:a000653. doi: 10.1101/cshperspect.a000653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lamond A, Spector D. Nuclear speckles: a model for nuclear organelles. Nat. Rev. Mol. Cell Biol. 2003;4:605–612. doi: 10.1038/nrm1172. [DOI] [PubMed] [Google Scholar]
- 8.Hirose T, Ninomiya K, Nakagawa S, Yamazaki T. A guide to membraneless organelles and their various roles in gene regulation. Nat. Rev. Mol. Cell Biol. 2023;24:288–304. doi: 10.1038/s41580-022-00558-8. [DOI] [PubMed] [Google Scholar]
- 9.Nakagawa S, Yamazaki T, Hirose T. Molecular dissection of nuclear paraspeckles: towards understanding the emerging world of the RNP milieu. Open Biol. 2018;8:180150. doi: 10.1098/rsob.180150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chujo T, Yamazaki T, Hirose T. Architectural RNA (arcRNAs): A class of long noncoding RNAs that function as the scaffold of nuclear bodies. Biochim. Biophys. Acta. 2015;1859:139–146. doi: 10.1016/j.bbagrm.2015.05.007. [DOI] [PubMed] [Google Scholar]
- 11.Yamazaki T, Nakagawa S, Hirose T. Architectural RNAs for membraneless nuclear body formation. Cold Spring Harb. Symp. Quant. Biol. 2019;84:227–237. doi: 10.1101/sqb.2019.84.039404. [DOI] [PubMed] [Google Scholar]
- 12.Doi, M. Soft Matter Physics. (Oxford University Press, Oxford, UK, 2013).
- 13.Feric M, et al. Coexisting liquid phases underlie nucleolar subcompartments. Cell. 2016;165:1686–1697. doi: 10.1016/j.cell.2016.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ide S, Imai R, Ochi H, Maeshima K. Transcriptional suppression of ribosomal DNA with phase separation. Sci. Adv. 2020;6:eabb5953. doi: 10.1126/sciadv.abb5953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maiser A, et al. Super-resolution in situ analysis of active ribosomal DNA chromatin organization in the nucleolus. Sci. Rep. 2020;10:7462. doi: 10.1038/s41598-020-64589-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yao R, et al. Nascent pre-rRNA sorting via phase separation drives the assembly of dense fibrillar components in the human nucleolus. Mol. Cell. 2019;76:767–783. doi: 10.1016/j.molcel.2019.08.014. [DOI] [PubMed] [Google Scholar]
- 17.Yamazaki T, et al. Paraspeckles are constructed as block copolymer micelles. EMBO J. 2021;40:e107270. doi: 10.15252/embj.2020107270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Souquere S, Beauclair G, Harper F, Fox A, Pierron G. Highly ordered spatial organization of the structural long noncoding Neat1 RNAs within paraspeckle nuclear bodies. Mol. Biol. Cell. 2010;21:4020–4027. doi: 10.1091/mbc.e10-08-0690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.West J, et al. Structural, super-resolution microscopy analysis of paraspeckle nuclear body organization. J. Cell Biol. 2016;214:817–830. doi: 10.1083/jcb.201601071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yamamoto T, Yamazaki T, Hirose T. Triblock copolymer micelle model of spherical paraspeckles. Front. Mol. Biosci. 2022;9:925058. doi: 10.3389/fmolb.2022.925058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hirose T, et al. NEAT1 long noncoding RNA regulates transcription via protein sequestration within subnuclear bodies. Mol. Biol. Cell. 2014;25:169–183. doi: 10.1091/mbc.e13-09-0558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tchelidze P, et al. Nucleolar sub-compartments in motion during rRNA synthesis inhibition: contraction of nucleolar condensed chromatin and gathering of fibrillar centers are concomitant. PLoS ONE. 2017;12:e0187977. doi: 10.1371/journal.pone.0187977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stasevich T, et al. Regulation of RNA polymerase II activation by histone acetylation in single living cells. Nature. 2014;516:272–275. doi: 10.1038/nature13714. [DOI] [PubMed] [Google Scholar]
- 24.Roth E, Azaria AG, Girshevitz O, Bitler A, Garini Y. Measuring the conformation and persistence length of single-strand DNA using a DNA origami structure. Nano Lett. 2018;18:6703–6709. doi: 10.1021/acs.nanolett.8b02093. [DOI] [PubMed] [Google Scholar]
- 25.de Gennes, P. G., Scaling Concepts in Polymer Physics. (Cornell Univ. Press, NY, US.), (1979).
- 26.Alexander S. Adsorption of chain molecules with a polar head a scaling description. J. Phys. Fr. 1980;38:983–987. doi: 10.1051/jphys:01977003808098300. [DOI] [Google Scholar]
- 27.Safran, S. A., Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. (Westview Press, CO, USA., 2003).
- 28.Peltonen K, et al. A targeting modality for destruction of RNA polymerase I that possesses anticancer activity. Cancer Cell. 2014;25:77–90. doi: 10.1016/j.ccr.2013.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jacobs RQ, Huffines AK, Laiho M, Schneider DA. The small-molecule BMH-21 directly inhibits transcription elongation and DNA occupancy of RNA polymerase I in vivo and in vitro. J. Biol. Chem. 2022;298:101450. doi: 10.1016/j.jbc.2021.101450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Drygin D, et al. Targeting RNA polymerase I with an oral small molecule CX-5461 inhibits ribosomal RNA synthesis and solid tumor growth. Cancer Res. 2011;71:1418–1430. doi: 10.1158/0008-5472.CAN-10-1728. [DOI] [PubMed] [Google Scholar]
- 31.de Gennes, P. G., Brochard-Wyart, F., and Quéré, D. Wetting phenomena Drops, Bubbles, Pearls, Waves. (Springer, NY, US., 2004).
- 32.Nicolas E, et al. Involvement of human ribosomal proteins in nucleolar structure and p53-dependent nucleolar stress. Nat. Commun. 2016;7:11390. doi: 10.1038/ncomms11390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Matsumori H, et al. Ribosomal protein L5 facilitates rDNA-bundled condensate and nucleolar assembly. Life Sci. Alliance. 2022;5:e202101045. doi: 10.26508/lsa.202101045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Banani S, Lee H, Hyman A, Rosen M. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017;18:285–298. doi: 10.1038/nrm.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shin Y, Brangwynne C. Liquid phase condensation in cell physiology and disease. Science. 2017;357:eaaf4382. doi: 10.1126/science.aaf4382. [DOI] [PubMed] [Google Scholar]
- 36.Yamamoto T, Yamazaki T, Hirose T. Phase separation driven by production of architectural RNA transcripts. Soft Matter. 2020;16:4692–4698. doi: 10.1039/C9SM02458A. [DOI] [PubMed] [Google Scholar]
- 37.Langevin D. Microemulsion. Acc. Chem. Res. 1988;21:255–260. doi: 10.1021/ar00151a001. [DOI] [Google Scholar]
- 38.Folkmann AW, Putnam A, Lee CF, Seydoux G. Regulation of biomolecular condensates by interfacial protein clusters. Science. 2021;373:1218–1224. doi: 10.1126/science.abg7071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Navarro MGJ, et al. RNA is a critical element for the sizing and the composition of phase-separated RNA-protein condensates. Nat. Commun. 2019;10:3230. doi: 10.1038/s41467-019-11241-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Turowski TW, Tollervery D. Cotranscriptional events in eukaryotic ribosome synthesis. WIREs RNA. 2015;6:129–139. doi: 10.1002/wrna.1263. [DOI] [PubMed] [Google Scholar]
- 41.Barandun J, Hunziker M, Klinge S. Assembly and structure of the SSU processome–a nucleolar precursor of the small ribosomal submit. Curr. Opin. Struct. Biol. 2018;49:85–93. doi: 10.1016/j.sbi.2018.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tomecki R, Sikorski PJ, Zakrzewska-Placzek M. Comparison of preribosomal RNA processing pathways in yeast, plant, and human cells–focus on coordinated action of endo- and exoribonulease. FEBS Lett. 2017;59:1801–1850. doi: 10.1002/1873-3468.12682. [DOI] [PubMed] [Google Scholar]
- 43.Scull CE, Schneider DA. Coordinated control of rRNA processing by RNA polymerase I. Trends Genet. 2019;35:724–733. doi: 10.1016/j.tig.2019.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Houseley J, Tollervey D. The many pathways of RNA degradation. Cell. 2009;136:763–776. doi: 10.1016/j.cell.2009.01.019. [DOI] [PubMed] [Google Scholar]
- 45.Wu M, et al. lncRNA SLERT controls phase separation of FC/DFCs to facilitate Pol I transcription. Science. 2021;373:547–555. doi: 10.1126/science.abf6582. [DOI] [PubMed] [Google Scholar]
- 46.Tartakoff A, et al. The dual nature of the nucleolus. Genes Dev. 2022;36:765–769. doi: 10.1101/gad.349748.122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kawaguchi T, et al. SWI/SNF chromatin-remodeling complexes function in noncoding RNA-dependent assembly of nuclear bodies. Proc. Natl Acad. Sci. USA. 2015;112:4304–4309. doi: 10.1073/pnas.1423819112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ninomiya K, et al. LncRNA-dependent nuclear stress bodies promote intron retention through SR protein phosphorylation. EMBO J. 2020;39:e102729. doi: 10.15252/embj.2019102729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ninomiya K, Hirose T. Short tandem repeat-enriched architectural RNAs in nuclear bodies: functions and associated disease. Non-Coding RNA. 2020;6:6. doi: 10.3390/ncrna6010006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Henninger J, et al. RNA-mediated feedback control of transcriptional condensates. Cell. 2021;184:207–225. doi: 10.1016/j.cell.2020.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hilbert L, et al. Transcription organizes euchromatin via microphase separation. Nat. Commun. 2021;12:1360. doi: 10.1038/s41467-021-21589-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Nozaki T, et al. Dynamic organization of chromatin domains revealed by super-resolution live-cell imaging. Mol. Cell. 2017;67:282–293. doi: 10.1016/j.molcel.2017.06.018. [DOI] [PubMed] [Google Scholar]
- 53.Sabari B, et al. Coactivator condensation at super-enhancers links phase separation and gene control. Science. 2018;361:eaar3958. doi: 10.1126/science.aar3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wei M, et al. Nucleated transcriptional condensates amplify gene expression. Nat. Cell Biol. 2020;22:1187–1196. doi: 10.1038/s41556-020-00578-6. [DOI] [PubMed] [Google Scholar]
- 55.Wang H, Boisvert D, Kim KK, Kim R, Kim SH. Crystal structure of a fibrillarin homologue from Methanococcus jannaschii, a hyperthermophile, at 1.6 Å resolution. EMBO J. 2000;19:317–323. doi: 10.1093/emboj/19.3.317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.de Gennes PG. Conformation of polymers attached to an interface. Macromolecules. 1980;13:1069–1075. doi: 10.1021/ma60077a009. [DOI] [Google Scholar]
- 57.Daoud M, Cotton J. Star shaped polymers: a model for the conformation and its concentration dependence. J. Phys. Fr. 1982;43:531–538. doi: 10.1051/jphys:01982004303053100. [DOI] [Google Scholar]
- 58.Yamamoto, T., Yamazaki, T., Ninomiya, K., & Hirose, T. Numerical and experimental data–Nascent ribosomal RNA act as surfactant that suppresses growth of fibrillar centers in nucleolus [Data set]. figshare 10.6084/m9.figshare.16599446 (2021). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data of the numerical calculations available in figshare with the identier (10.6084/m9.figshare.16599446)58.
The Mathematica file used for the numerical calculations is available in figshare with the identier (10.6084/m9.figshare.16599446).