Adaptive Covariance Estimation of Non-stationary Processes and its Application to Infer Dynamic Connectivity from fMRI

Abstract

Time-varying covariance is an important metric to measure the statistical dependence between non-stationary biological processes. Time-varying covariance is conventionally estimated from short-time data segments within a window having a certain bandwidth, but it is difficult to choose an appropriate bandwidth to estimate covariance with different degrees of non-stationarity. This paper introduces a local polynomial regression (LPR) method to estimate time-varying covariance and performs an asymptotic analysis of the LPR covariance estimator to show that both the estimation bias and variance are functions of the bandwidth and there exists an optimal bandwidth to minimize the mean square error (MSE) locally. A data-driven variable bandwidth selection method, namely the intersection of confidence intervals (ICI), is adopted in LPR for adaptively determining the local optimal bandwidth that minimizes the MSE. Experimental results on simulated signals show that the LPR-ICI method can achieve robust and reliable performance in estimating time-varying covariance with different degrees of variations and under different noise scenarios, making it a powerful tool to study the dynamic relationship between non-stationary biomedical signals. Further, we apply the LPR-ICI method to estimate time-varying covariance of functional magnetic resonance imaging (fMRI) signals in a visual task for the inference of dynamic functional brain connectivity. The results show that the LPR-ICI method can effectively capture the transient connectivity patterns from fMRI.

I. Introduction

BIOLOGICAL systems and signals are usually characterized as non-stationary with time-varying structures, behaviors, and functions. For example, the human brain processes sensory and cognitive information evoked by an external stimulus in the order of milliseconds [1]. However, how to mathematically describe and identify non-stationary processes of biological systems is still largely an open question. Specifically, there are few studies on the theoretical treatment and estimation of time-varying covariance, which is an important metric to measure the statistical dependence between multiple non-stationary biological processes. The lack of theory and methods for non-stationary processes is mainly due to the fact that most of conventional statistical analysis tools (such as asymptotic analysis) are based on the assumption of stationarity and are not applicable to non-stationary processes. The theory of locally stationary process is an emerging and promising topic in statistics [2]. By assuming the non-stationary processes are stationary locally in time while there are still infinite number of samples in locally stationary intervals, classical asymptotic analysis can be well applied to non-stationary processes.

Estimation of locally stationary processes (including estimation of time-varying covariance between locally stationary processes) can usually be achieved by conventional stationary methods on windowed data segments where the assumption of stationarity holds, though alternative approaches, such as basis expansion and adaptive filtering, exist [3]. By using a window or kernel with a specific bandwidth to assign large weights on data around the current time and small weights on remote data, the parameters of interest (such as mean, variance, covariance, etc.) at the current time can be estimated from weighted data samples using conventional methods. By sliding the window along time, we can estimate the time-varying parameters of the non-stationary process. Such a sliding-window approach has been proved to be simple and effective in many applications [3]. But, one problem that has not been well addressed is how to select the appropriate window bandwidth to achieve the optimal estimation. This problem is not trivial because it stems from the fundamental bias-variance tradeoff problem in the estimation theory.

In statistics, an estimator with the least possible mean square error (MSE), which is the sum of squared bias and variance, is commonly considered as optimal. For locally stationary processes, even an estimator is asymptotically unbiased for stationary processes, it contains an excessive bias caused by neighboring data samples with different statistical properties. Generally, a longer window including more remote data increases the excessive bias due to non-stationarity but decreases the variance. On the contrary, a smaller window decreases the excessive bias at the expense of increased variance. Therefore, it is crucial to select variable window bandwidth for optimal estimation (in the sense of minimum MSE) of locally stationary processes.

In our previous studies, we have investigated the statistical properties of several types of locally stationary processes, such as piecewise smooth signals and images [4] and [5], time-varying linear system [6] and time-varying autoregressive processes [7], and have proposed a local polynomial modeling method for estimating various parameters of these processes. We have also developed many practical applications by estimating real-world locally stationary processes. These applications include: image smoothing [5], time-frequency analysis of electroencephalography (EEG) [7], power quality monitoring [6] and [8], etc. However, above studies only focused on the estimation of one locally stationary process, and the investigation of relationship between two or more local stationary processes is still lacking.

In biomedical research, it is significant to explore the statistical relationship between multiple non-stationary biological signals or systems. Recent years have witnessed a major shift in biomedical research from functional segregation (i.e., how each biological system functions independently) towards functional integration (how biological systems coordinate to perform specific functions). For example, the study of functional connectivity (i.e. the statistical dependence) among distributed brain regions from neuroimaging data (such as EEG and functional magnetic resonance imaging [fMRI]) has been drastically advancing our knowledge on the organization of brain networks [9] and [10]. At present, covariance is still a fundamental and popular statistic to measure the relationship between multiple biological processes due to its simplicity and effectiveness. However, how to estimate time-varying covariance between multiple locally stationary processes is seldom explored. In [11]–[13], the sliding-window approach was employed to estimate time-varying covariance from short-time data segments within a window. But the key issues to be addressed include what the asymptotic properties of the sliding-window covariance estimates are (more specifically, how the window bandwidth affects the bias and variance of the covariance estimate) and how to adaptively select the bandwidth for the optimal estimate.

This paper is aimed (1) to address above key issues by deriving asymptotic properties of the sliding-window-based local covariance estimation, and (2) to develop a new biomedical application (i.e., the interference of dynamic functional connectivity from fMRI data) of time-varying covariance estimation

Firstly, we adopt the local polynomial regression (LPR) method [14] and [15], which fits polynomials to the inner products of two non-stationary processes within a sliding window having variable bandwidth, to estimate time-varying covariance. We derive the asymptotic expressions for the bias and variance of the LPR estimator using the theory of locally stationary processes, and show that the bias increases while variance decreases as the bandwidth increases. Hence, there exists an optimal bandwidth to minimize the MSE of the time-varying covariance estimator locally. This asymptotic analysis is important to justify the applicability of conventional adaptive bandwidth selection methods for the estimation of time-varying covariance. Subsequently, we adopt an intersection of confidence intervals (ICI) technique [16]–[19] to adaptively select the optimal variable bandwidth for the LPR. Extensive simulation results show that the LPR-ICI method can obtain robust and accurate estimation of time-varying covariance for various types of non-stationary processes and at different levels of noise. Therefore, the LPR-ICI method is particularly suitable for the analysis of biomedical signals, of which the characteristics (such as the amount of noise and the degree of non-stationarity) are unknown.

Secondly, we develop an important application of time-varying covariance estimation: to infer dynamic functional connectivity of fMRI data in task-related experiments. In fMRI study, the functional connectivity is often inferred from temporal dependency (e.g., covariance, correlation, mutual information) between fMRI time-series data in different brain regions [20] and [21]. Conventional functional connectivity analysis approaches implicitly assume sustained changes of connectivity throughout the experiments. This assumption seriously limits our understanding of the dynamic functional organization of brain network, because dynamics of functional connectivity could be prominent during a task and even in the resting state [22]. In the present study, we use the proposed LPR-ICI method to adaptively estimate the time-varying covariance among fMRI signals from brain regions activated in a visual task, and to verify whether task related connectivity changes can be reliably detected. Compared with our previous work in [23], the present study (1) provides an asymptotic analysis of the bias and variance of the time-varying covariance estimator; (2) extends the kernel smoothing estimator in [23] to LPR (kernel smoothing is equivalent to LPR with an order of 0); (3) adopts a faster ICI method instead of the plug-in method in [23] for adaptive bandwidth selection.

The rest of this paper is organized as follows. The theory of locally stationary processes and the asymptotic properties of sliding-window covariance estimation are introduced in Section II. In Section III, we adopt the LPR method for estimating the time-varying covariance and the ICI technique for adaptively selecting the variable bandwidth in LPR. Section IV is devoted to the practical applications of the LPR-ICI method to biomedical research (specifically, in the inference of connectivity from fMRI). The performance of LPR-ICI is tested on various simulated signals in Section V. In Section VI, we extend this method to estimate dynamic functional connectivity from fMRI in a visual task. Finally, conclusions are drawn in Section VII.

II. Local Covariance Estimation

A. Locally Stationary Processes

As mentioned in the Introduction, conventional asymptotic analysis usually investigates limiting behaviors of a stationary process by considering the number of samples in the process approaches infinity. In order to extend such asymptotics to non-stationary processes, we need new ways to describe such non-stationary processes and investigate their properties and connections with conventional stationary approaches so that one can proceed with their estimation and characterization. One such approach is called the theory of locally stationary processes, which is based on the framework of infill asymptotics, in which time is rescaled to the unit interval and the unit interval is sampled over a finer and finer grid as the sampling points grow denser and denser. That is to say, the asymptotic consideration that the number of samples tends to infinity does not mean extending the samples to the future, but means that we have more and more samples for each value of the process. By assuming the non-stationary processes are stationary locally in time while there are still infinite number of samples in locally stationary intervals, infill asymptotics can resolve the contradiction between time-varying statistics of non-stationary processes and the assumptions of infinity and homogeneity in asymptotics. As a consequence, asymptotic analysis can be applied to locally stationary processes for a rigorous theoretical investigation of statistical properties of such processes.

The definition of locally stationary processes in terms of the time-varying spectral representation is given in [2]. A sequence of stochastic process $X_{n,N},\left(n=1,···,N\right)$, is called locally stationary with transfer function $\tilde{A}$ if there exists a representation

$$X_{n,N}=\underset{-\pi }{\overset{\pi }{\int }}exp\left(i\lambda n\right){\tilde{A}}_{n,N}\left(\lambda \right)d\xi \left(\lambda \right),$$ (1)

where $\xi \left(\lambda \right)$ is a stochastic process on $\left[-\pi ,\pi \right]$ with $\overline{\xi \left(\lambda \right)}=\xi \left(-\lambda \right)·\xi \left(\lambda \right)$ satisfies $\text{cum}\left\{d\xi \left({\lambda }_1\right),···,d\xi \left({\lambda }_J\right)\right\}=\eta \left({\sum }_{j=1}^J{\lambda }_j\right)g_k\left({\lambda }_1,···,{\lambda }_{J-1}\right)d{\lambda }_1···d{\lambda }_J$, where $\text{cum}\left\{\cdots \right\}$ denotes the cumulant of $J$th order, $g_1=0$, $g_2\left(\lambda \right)=1,\left|g_k\left({\lambda }_1,···,{\lambda }_{J-1}\right)\right|\le cons{t}_J$ for all $J$ and $\eta \left(\lambda \right)={\sum }_{j=\infty }^{\infty }\delta \left(\lambda +2\pi j\right)$ is the period $2\pi$ extension of the Dirac delta function. In addition, there exists a constant $L$ (independent of $T$) and a $2\pi$-periodic function $A:\left[0,1\right]\times \Re \to \text{\hspace{0.17em}Çt}C$ with $\overline{A\left(u,\lambda \right)}=A\left(u,-\lambda \right)$ and $\underset{n,\lambda }{\text{sup}}\left|{\tilde{A}}_{n,N}\left(\lambda \right)-A\left(n/N,\lambda \right)\right|\le L{N}^{-1}$ for all $N$, which is needed for rescaling and to impose necessary smoothness conditions. That is, by denoting $u=n/N\in \left(0,1\right]$, $A\left(u,\lambda \right)$ is assumed to be smooth and continuous in the rescaled time $u$, which guarantees (asymptotically) that the process has a locally stationary behavior. The function $f\left(u,\lambda \right)={\left|A\left(u,\lambda \right)\right|}^2$ is called the time-varying spectral density of the process. More details about the definition and assumptions of locally stationary processes can be referred to [2].

B. Asymptotics of Time-varying Covariance of Locally Stationary Processes

Suppose we have two locally stationary processes: $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ with transfer functions ${\tilde{A}}^{\left(i\right)}$ and time-varying spectral densities $f^{\left(i\right)}\left(u,\lambda \right)={\left|A^{\left(i\right)}\left(u,\lambda \right)\right|}^2$, $i=1,2$ respectively. In addition, the time-varying cross-spectrum of $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ is $g\left(u,\lambda \right)=\left|A^{\left(1\right)}\left(u,\lambda \right)A^{\left(2\right)}\left(u,\lambda \right)\right|$. The time-varying covariance (or, more precisely, cross-covariance) between $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ at time $u$ with lag $l$ is defined as

$$c\left(u,l\right)=\underset{-\pi }{\overset{\pi }{\int }}exp\left(i\lambda l\right)g\left(u,\lambda \right)d\lambda ,$$ (2)

and can be estimated from windowed neighboring samples as

$${\widehat{c}}_N\left(u,l\right)=\frac{1}{N}{\sum }_n{K}_h\left(\frac{n}{N}-u\right)X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)},$$ (3)

where $K_h\left(\frac{n}{N}-u\right)=\frac{1}{h}K\left(\frac{1}{h}\left(\frac{n}{N}-u\right)\right)$ is a window used to control the number and weights of neighboring samples around $u$ on the estimation of ${\widehat{c}}_N\left(u,l\right)$. $K_h\left(·\right)$ can be obtained by scaling a basis window $K\left(·\right)$ by a bandwidth parameter $h$. Here, we assume $\int K\left(x\right)dx=1$ and $\int xK\left(x\right)dx=0$.

We are interested in the asymptotic expressions of the bias and variance as functions of the bandwidth $h$ when the number of samples is sufficiently large. To this end, we allow $h$ to tend to zero so that we can employ the Taylor series expansion to reveal their order of dependence as $h\to 0$. Meanwhile, $N$ is still assumed to be large so that $hN\to \infty$ to guarantee there are infinite data samples locally for asymptotic analysis. We will further assume the time-varying cross-spectrum $g\left(u,\lambda \right)$ is twice differentiable in $u$ with uniformly bounded derivative. Then, the expectation of ${\widehat{c}}_N\left(u,l\right)$ can be calculated as

$$\begin{array}{l}E\left({\widehat{c}}_N\left(u,l\right)\right)=\frac{1}{hN}{\sum }_{n}K\left(\frac{1}{h}\left(\frac{n}{N}-u\right)\right)\\ \times \underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right){\tilde{A}}_{n,N}^{\left(1\right)}\left(\lambda \right){\tilde{A}}_{n+l,N}^{\left(2\right)}\left(\lambda \right)d\lambda \\ =\frac{1}{hN}{\sum }_{n}K\left(\frac{1}{h}\left(\frac{n}{N}-u\right)\right)\\ \times \underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right)A^{\left(1\right)}\left(\frac{n}{N},\lambda \right)A^{\left(2\right)}\left(\frac{n+l}{N},\lambda \right)d\lambda +O\left(N^{-1}\right)\\ =\frac{1}{hN}{\sum }_{n}K\left(\frac{1}{h}\left(\frac{n}{N}-u\right)\right)\\ \times \underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right)g\left(\frac{n}{N},\lambda \right)d\lambda +O\left(N^{-1}\right).\end{array}$$ (4)

By a second order Taylor series expansion of $g\left(u,\lambda \right)$ around $u$, we have

$$\begin{array}{l}E\left({\widehat{c}}_N\left(u,l\right)\right)=\frac{1}{hN}{\sum }_{t}K\left(\frac{1}{h}\left(\frac{n}{N}-u\right)\right)\\ \times \underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right)\left[g\left(u,\lambda \right)+\left(\frac{n}{N}-u\right)g^{\prime }\left(u,\lambda \right)\right.\\ \left. +\frac{1}{2}{\left(\frac{n}{N}-u\right)}^2{g}^{″}\left(u,\lambda \right)+o\left({\left(\frac{n}{N}\right)}^2\right)\right]d\lambda \\ +O\left(N^{-1}\right).\end{array}$$ (5)

Next, making $x=\frac{1}{h}\left(\frac{n}{N}-u\right)$ and using the assumptions of $\int K\left(x\right)dx=1$ and $\int xK\left(x\right)dx=0$, one gets

$$\begin{array}{l}E\left({\widehat{c}}_N\left(u,l\right)\right)=c\left(u,l\right)+\frac{1}{2}{h}^2\underset{-\infty }{\overset{\infty }{\int }}{x}^{2}K\left(x\right)dx\underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right)g^{″}\left(u,\lambda \right)d\lambda \\ +o\left(h^2\right)+O\left(T^{-1}\right)\\ =c\left(u,l\right)+\frac{1}{2}{h}^2\varphi c^{″}\left(u,l\right)+o\left(h^2\right)+O\left(T^{-1}\right),\end{array}$$ (6)

where $c^{″}\left(u,l\right)=\underset{-\pi }{\overset{\pi }{\int }}\text{exp}\left(i\lambda l\right)g^{″}\left(u,\lambda \right)d\lambda$ and $\varphi =\underset{-\infty }{\overset{\infty }{\int }}{x}^{2}K\left(x\right)dx$. So, the bias of the local covariance estimator (3) is

$$\begin{array}{l}Bias\left({\widehat{c}}_N\left(u,l\right)\right)=E\left({\widehat{c}}_N\left(u,l\right)\right)-c\left(u,l\right)\\ =\frac{1}{2}{h}^2\varphi c^{″}\left(u,l\right)+o\left(h^2\right).\end{array}$$ (7)

It can be seen that the bias depends on the non-stationary term $c^{″}\left(u,l\right)$ and the bandwidth $h$. Actually, by considering (3) as a Nadaraya-Watson kernel regression estimator of samples $X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)}$ and making use of the assumption of $\underset{n,\lambda }{\text{sup}}\left|{\tilde{A}}_{n,N}\left(\lambda \right)-A\left(n/N,\lambda \right)\right|\le L{N}^{-1}$, the asymptotic bias can be directly obtained from the well-established asymptotic properties of kernel estimation [14].

The asymptotic variance of the local covariance estimate can be obtained similarly as

$$\mathit{\text{Var}}\left({\widehat{c}}_N^2\left(u,l\right)\right)=\frac{1}{hN}\psi {\sigma }^2\left(u,l\right)+o\left(h^{-1}\right),$$ (8)

where $\psi =\underset{-\infty }{\overset{\infty }{\int }}K{\text{(}x\text{)}}^{2}dx$ and ${\sigma }^2\left(u,l\right)=\mathrm{var}\left(X_{u,N}^{\left(1\right)}{X}_{u+l,N}^{\left(2\right)}\right)$.

The asymptotic expressions of bias (7) and variance (8) are meaningful since they illustrate how the components involved affect the bias and variance of the local covariance estimation. Importantly, the bias is an increasing function of the bandwidth $h$, while the variance is a decreasing function of $h$. As a result, there exists an optimal bandwidth to minimize the MSE

$$\begin{array}{l}\mathit{\text{MSE}}\left({\widehat{c}}_N^2\left(u,l\right)\right)=\hspace{0.17em}\mathit{\text{Bia}}{s}^2\left({\widehat{c}}_N^2\left(u,l\right)\right)+Var\left({\widehat{c}}_N^2\left(u,l\right)\right)\\ =\frac{1}{4}{h}^4{\varphi }^2{\left[c^{″}\left(u,l\right)\right]}^2+\frac{1}{hT}\psi c^2\left(u,l\right)+o\left(h^4+h^{-1}\right).\end{array}$$ (9)

By setting the derivative of $\mathit{\text{MSE}}\left({\widehat{c}}_N^2\left(u,l\right)\right)$ with respect to $h$ to zero, we get the optimal bandwidth as

$$h^{opt}\left(u,l\right)={\left[\frac{\psi }{{\varphi }^2}·\frac{{\sigma }^2\left(u,l\right)}{c^{″}{(u)}^2}\right]}^{1/5}.$$ (10)

In above equation, $\psi$ and $\varphi$ are determined by the window type and are easy to calculate. However, since quantities ${\sigma }^2\left(u,l\right)$ and $c^{″}\text{(}u,l\text{)}$ are unknown and difficult to be approximated, it is still difficult to calculate the optimal bandwidth directly from (10). In the next section, we will introduce a more general local polynomial regression method to estimate the time-varying covariance and an empirical bandwidth selection method to approximate the variable optimal bandwidth.

III. Local Polynomial Regression and Variable Bandwidth Selection

A. Local Polynomial Regression

The time-varying covariance estimator of (3) can be considered to belong to a more general local polynomial regression (LPR) method [15]. That is, the time-varying covariance estimate can be obtained by locally fitting a $p$th degree polynomial to the samples $X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)}$, and the estimator of (3) is actually equivalent to the LPR estimator with $p=0$.

In LPR, we regard the samples $m\left(n,l\right)=X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)}$ as being generated from the following model

$$m\left(n,l\right)=c\left(n,l\right)+e\left(n,l\right),$$ (11)

where $e\text{(}n,l\text{)}$ is the estimation residual with zero mean and variance ${\sigma }^2\left(n,l\right)$ and it is independent of $c\text{(}n,l\text{)}$. Since $c\text{(}n,l\text{)}$ is assumed to be a smooth function, we can approximate it locally as a degree-$p$ polynomial at time $\tau$ as

$$\begin{array}{c}c\left(n,l\right)\approx {\sum }_{k=0}^p\frac{1}{k\text{!}}{c}^{\left(k\right)}\left(\tau ,l\right){\text{(}n-\tau \text{)}}^k\\ ={\sum }_{k=0}^p{\beta }_k\left(\tau ,l\right){\text{(}n-\tau \text{)}}^k\end{array},$$ (12)

where ${\beta }_k\left(\tau ,l\right)=c^{\left(k\right)}\left(\tau ,l\right)/k\text{!}\left(k=0,1,\cdots ,p\right)$ is the $k$th polynomial coefficient.

By minimizing a locally weighted least-squares (WLS) solution criterion as

$${\sum }_{n=1}^{N-1}{K}_h\left(n-\tau \right){\left[X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)}-{\sum }_{k=0}^p{\beta }_k\left(\tau ,l\right){\text{(}n-\tau \text{)}}^k\right]}^2,$$ (13)

one gets the estimates of the polynomial coefficients as

$$\widehat{\mathit{\beta }}={\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\mathit{Y}}^T\mathit{W}\mathit{m}\text{,}$$ (14)

where $\widehat{\mathit{\beta }}={\left[{\widehat{\text{β}}}_0\text{,}{\widehat{\text{β}}}_1,\cdots \text{,}{\widehat{\text{β}}}_p\right]}^T$, $\mathit{m}={\left[X_{1,N}^{\left(1\right)}{X}_{1+l,N}^{\left(2\right)},\cdots ,X_{N-l,N}^{\left(1\right)}{X}_{N,N}^{\left(2\right)}\right]}^T$, $\mathit{Y}=\left[\begin{array}{cccc}1& \left(1-\tau \right)& \cdots & {\left(1-\tau \right)}^p\\ 1& \left(2-\tau \right)& \cdots & {\left(2-\tau \right)}^p\\ ⋮& ⋮& \ddots & ⋮\\ 1& \left(N-l-\tau \right)& \cdots & {\left(N-l-\tau \right)}^p\end{array}\right]\text{and}$$\mathit{W}=diag\left[K_h\left(1-\tau \right),\cdots ,K_h\left(N-1-\tau \right)\right]$. Note that $\widehat{\mathit{\beta }}$, $\mathit{X}$, $\mathit{W}$, and $\mathit{m}$ are all functions of time $\tau$ and lag $l$, but the indices $\tau$ and $l$ are omitted in (14) and in the following for notational simplicity when there is no ambiguity. The covariance at time $\tau$ with lag $l$ is finally obtained as $\widehat{c}\left(\tau ,l\right)={\widehat{\beta }}_0\left(\tau ,l\right)$.

Since the asymptotic analysis of the classical LPR estimator in [15] is applicable to the local covariance estimator of (14), here we only provide the asymptotic bias and variance of $\widehat{\mathit{\beta }}$ without proof. The asymptotic bias and variance are expressed as

$$\mathit{B}\left(\widehat{\mathit{\beta }}\right)={\mathit{H}}^{-1}{\mathit{S}}^{-1}{\mathit{c}}_p{\beta }_{p+1}{h}^{p+1}\left\{1+o_P\left(1\right)\right\},$$ (15)

$$\mathit{V}\left(\widehat{\mathit{\beta }}\right)=\frac{{\sigma }^2\left(\tau ,l\right)}{d\left(\tau \right)Nh}{\mathit{H}}^{-1}{\mathit{S}}^{-1}{\mathit{S}}^{*}{\mathit{S}}^{-1}{\mathit{H}}^{-1}\left\{1+o_P\left(1\right)\right\},$$ (16)

where $\mathit{H}=\hspace{0.17em}\mathit{\text{diag}}\left(1,h,\cdots ,h^p\right)$, $\mathit{S}={\left({\mu }_{j+l}\right)}_{0\le j,l\le p}$ with ${\mu }_j=\int x^{j}K\left(x\right)dx$, ${\mathit{S}}^{*}={\left(v_{j+l}\right)}_{0\le j,l\le p}$ with $v_j=\int x^j{K}^2\left(x\right)dx$, ${\mathit{c}}_p={\left[{\mu }_{p+1},\cdots ,{\mu }_{2p+1}\right]}^T$, ${\beta }_{p+1}=c^{\left(p+1\right)}/\left(p+1\right)\text{!}$, and $d\left(\tau \right)$ is the sampling density around $\tau$. It can be clearly seen that the bias increases while variance decreases as $h$ increases. So, at each time $\tau$, there exists a locally optimal (in the sense of minimum MSE) bandwidth for the LPR-based covariance estimator. Because the unknown quantities in (15) and (16) make it difficult to directly calculate the optimal bandwidth, we will adopt an empirical data-driven technique for variable bandwidth selection.

B. Variable Bandwidth Selection

The intersection of confidence intervals (ICI) method [16] is employed in this study to determine the optimal bandwidth in the LPR covariance estimator at each time point and each lag. The ICI method was originally proposed in [16] for adaptive window selection in LPR, and such a LPR-ICI estimator has been proved to be nearly optimal by asymptotic analysis in [16]. The LPR-ICI method was firstly applied in the field of signal processing in [17] to filter a signal given with an additive noise. Because of its effectiveness in adaptively selecting suitable window size for local estimation, the LPR-ICI method has gained popularity in many related fields, in particular, image processing [18] and [19]. The theory and derivation of the ICI method are omitted to save space, and the readers can be referred to [17] for details. Here, we only briefly introduce the algorithm of the ICI method.

Given a finite set of bandwidth parameters in an ascending order as

$$\tilde{H}=\left\{h_1<h_2<\cdots <h_{\text{Γ}}\right\},$$ (17)

where $\text{Γ}$ is the number of candidate bandwidths, the ICI method selects the best bandwidth from $\tilde{H}$ by comparing the confidence intervals of the estimate ${\widehat{\beta }}_k\left(\tau ,l\text{;\hspace{0.17em}}{h}_{\gamma }\right)$ with different bandwidths $h_{\gamma }$, $\gamma =1,2,\cdots ,\text{Γ}$, in $\tilde{H}$. Consider a series of confidence intervals $D_{\gamma }=\left[L_{\gamma },U_{\gamma }\right]$ with

$$U_{\gamma }={\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)+\kappa \cdot SD\left({\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)\right),$$ (18)

$$L_{\gamma }={\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)-\kappa \cdot SD\left({\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)\right),$$ (19)

where $SD\left({\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)\right)$ are the square roots of the diagonal elements of $\mathit{V}\left(\widehat{\mathit{\beta }}\left(\tau \text{, }l\text{;\hspace{0.17em}}{h}_{\gamma }\right)\right)$, and $\kappa$ is a threshold to adjust the width of the confidence intervals and can be chosen by the cross-validation criterion [16]. The ICI method examines the following quantities from the confidence intervals

$$\begin{array}{c}{\overline{L}}_{\gamma }=max\left[{\overline{L}}_{\gamma -1},L_{\gamma }\right]\text{, \hspace{0.17em}}for \gamma =2,3,\cdots ,\text{Γ},\\ {\underset{¯}{U}}_{\gamma }=min\left[{\underset{¯}{U}}_{\gamma -1}\text{,\hspace{0.17em}}{U}_{\gamma }\right], for \gamma =2,3,\cdots ,\text{Γ},\\ {\overline{L}}_1={\underset{¯}{U}}_1=0,for \gamma =1.\end{array}$$ (20)

${\overline{L}}_{\gamma }$ is the largest upper bound of the confidence interval for bandwidth up to $h_{\gamma }$, while ${\underset{¯}{U}}_{\gamma }$ is the corresponding lower bound. The largest $\gamma$ for which ${\underset{¯}{U}}_{\gamma }\ge {\overline{L}}_{\gamma }$ gives the ICI-selected optimal bandwidth ${\widehat{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$. When $h$ is increased beyond ${\widehat{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$, the bias will suddenly increase while the variance will gradually decrease. Hence, the confidence intervals will no longer intersect above ${\widehat{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$.

In the ICI method, $\mathit{V}\left(\widehat{\mathit{\beta }}\left(\tau \text{,\hspace{0.17em}}l\right)\right)$ has to be approximated to construct the confidence intervals in (18) and (19). Assuming local homoscedasticity, a finite sample approximation of the covariance matrix of $\widehat{\mathit{\beta }}$ ($\tau$ and $l$ are omitted for notational simplicity) can be derived from (14) as

$$\begin{array}{l}\mathit{V}\left(\widehat{\mathit{\beta }}\right)=E\left\{\left[\widehat{\mathit{\beta }}-E\left(\widehat{\mathit{\beta }}\right)\right]{\left[\widehat{\mathit{\beta }}-E\left(\widehat{\mathit{\beta }}\right)\right]}^T\right\}\\ ={\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\mathit{Y}}^T\mathit{W}E\left[\left(\mathit{c}-\mathit{m}\right){\text{(}\mathit{c}-\mathit{m}\text{)}}^T\right]\mathit{W}\mathit{Y}{\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}\\ ={\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\mathit{Y}}^T\mathit{W}{\mathit{\Sigma }}_{\sigma }\mathit{W}\mathit{Y}{\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}\\ ={\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\mathit{Y}}^T\mathit{W}\mathit{W}\mathit{Y}{\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\sigma }^2,\end{array}$$ (21)

where $c={\text{[}c\left(1\text{,\hspace{0.17em}}l\right)\text{,}\cdots \text{,\hspace{0.17em}}c\left(N-l\text{,\hspace{0.17em}}l\right)\text{]}}^T$ and ${\sum }_{\sigma }=\hspace{0.17em}\mathit{\text{diag}}\left\{{\sigma }^2\left(1\text{,\hspace{0.17em}}l\right)\text{,}\cdots \text{,}{\sigma }^2\left(N-l\text{,\hspace{0.17em}}l\right)\right\}$. The residual variance ${\sigma }^2\left(\tau \text{,\hspace{0.17em}}l\right)$ can be estimated as the normalized weighted residual sum of squares [15]

$${\widehat{\sigma }}^2\left(u\text{,\hspace{0.17em}}\tau \right)=\frac{{‖\mathit{W}\left(\mathit{m}-\mathit{Y}\widehat{\mathit{\beta }}\right)‖}_2^2}{\mathit{\text{tr}}\left\{\mathit{W}-\mathit{W}\mathit{Y}{\left({\mathit{Y}}^T\mathit{W}\mathit{Y}\right)}^{-1}{\mathit{Y}}^T\mathit{W}\right\}}.$$ (22)

With (21) and (22), the variance of ${\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)$ can be obtained and the ICI technique can be implemented to select a nearly optimal bandwidth from the set $\tilde{H}$. It is important to note that, there is a local ICI bandwidth parameter ${\widehat{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$ for each $k$th derivative at each time $\tau$ and for each lag $l$.

As observed in [4], the variable optimal bandwidth estimated by the ICI technique usually exhibits considerable variability since it is based on a finite sample approximation of the local noise variance. Hence, ${\widehat{h}}_k^{\mathit{\text{opt}}}\left(\tau \text{,\hspace{0.17em}}l\right)$ should be slightly smoothed (say, using a window with the minimum bandwidth in $\tilde{H}$ ) in the time domain to reduce the variance.

C. LPR-ICI

Now we summarize the LPR with ICI (LPR-ICI) method for the estimation of time-varying covariance between two locally stationary processes in the following table.

It should be noted that the LPR-ICI is applicable to signals that satisfy the following requirements: the bias of window-based local estimation is an increasing function of the window bandwidth while the estimation variance is a decreasing function of the bandwidth. This paper has proved an asymptotic analysis of the second-order statistics (i.e., covariance) to show that LPR-ICI is applicable to the estimation of time-varying covariance. Although it is plausible that the sliding window-based estimation of local higher-order statistics also satisfies the requirements of LPR-ICI, an asymptotic analysis of the relationship between local estimation of higher-order statistics and bandwidth (i.e., to derive asymptotic expressions of estimation bias and variance as functions of bandwidth) is very difficult. Therefore, we have not pursued such a direction in the current study. The LPR-ICI method can also be used for variance estimation, and the results are provided in Appendix I of the Supplementary Materials (http://www.eee.hku.hk/~zgzhang/publication/tbiocas2013_supp.pdf).

IV. Biomedical Applications

We now study the practical applications of the LPR-ICI method for estimating time-varying covariance of real-world biomedical signals. Several practical issues such as parameter selection and complexity will be discussed first. Then, we will introduce the application of the LPR-ICI method for the inference of functional connectivity from fMRI.

A. Practical Issues

1). Computational Complexity:

The arithmetic complexity of the LPR estimator in (14) at each time point is $O\left\{N\right\}$, where $N$ is the number of samples in the whole period. This complexity of LPR can be reduced if the window has a limited support so that the number of actual samples included in the window is finite. Denote the number of samples included in $K_h\left(x\right)$ as $N_K$, then the complexity of the LPR estimator is $O\left(N_K\right)$. Since $N_K$ increases with the bandwidth parameter $h$, a large bandwidth will increase the computational complexity. The LPR-ICI method has a complexity of ${\sum }_{\gamma =1}^{\text{Γ}}O\left\{N_K^{\left(\gamma \right)}\right\}+O\left\{N_K^{opt}\right\}$, where ${\sum }_{\gamma =1}^{\text{Γ}}O\left\{N_K^{\left(\gamma \right)}\right\}$ is the total complexity to calculate LPR with each bandwidth in the bandwidth set $\tilde{H}$ and $O\left\{N_K^{opt}\right\}$ is the complexity to calculate LPR with the optimal bandwidth ${\widehat{h}}_k^{\text{opt}}$. The elapsed time of LPR-ICI and other methods in simulation is provided in Appendix II of the Supplementary Materials.

In addition, it is possible to extend the LPR-ICI method for online calculation by using one-sided window in LPR and recursively updating the adaptive bandwidth of the windows used in the ICI method [5]. This recursive implementation of LPR-ICI can decrease the processing time and memory requirement caused by excessive buffering of the data in conventional LPR with two-sided windows.

2). Parameter Selection in LPR:

We now consider the window type and model order in LPR. In the study we employ the Epanechnikov window

$$K\left(x\right)=\left\{\begin{array}{cc}\frac{3}{4}\left(1-|x{|}^2\right)& \left|x\right|<1,\\ 0& \left|x\right|\ge 1,\end{array}\right.$$ (23)

because it has high efficiency and is with finite support [15]. The property of finite support is particularly favored because it can reduce the computational complexity of LPR. For an Epanechnikov window with bandwidth $h$, $K_h\left(x\right)=\frac{1}{h}K\left(x/h\right)$, only the samples included in the interval($x-h$, $x+h$) are used for local estimation. Other types of windows, such as Gaussian and Hanning windows, can also be used in LPR, but it has been shown in [15] that the window type has very limited impact on the performance of LPR.

The only parameter to be pre-specified in LPR is the model order $p$. A larger $p$ gives the polynomial more approximation power and hence a smaller bias. However, it also increases the variability of the estimates because more variables (namely $p+1$ ) are to be estimated. On the other hand, the number of variables should be smaller than the number of measurements $N_K$ in the smallest window to make sure (14) is solvable. Hence, a large $p$ also requires a larger window. As recommended in [15], an appropriate selection of model order is $p=v+1$, where $\nu$ is the order of derivative of interest.

3). Parameter Selection in ICI:

The variable bandwidth $h_k^{opt}\left(\tau \text{,\hspace{0.17em}}l\right)$ and the threshold parameter $\text{Γ}$ used in ICI are both automatically determined from a grid of candidate parameters. The grid should cover possible ranges of parameters to make sure the optimal parameter is in the range defined by the grid. As a result, the parameter selection problem is reduced to how to determine a grid of parameters. For the threshold parameter $\text{Γ}$ in ICI, the values of the grid can be {0.67 0.84 1.04 1.28 1.44 1.65 1.96 2.58 2.81 3.29}, which are associated with confidence levels of {50.0 60.0 70.0 80.0 85.0 90.0 95.0 99.0 99.5 99.9}% [8].

The candidate bandwidth set $\tilde{H}$ could largely influence the performance of the LPR-ICI method and should be carefully specified. The minimum bandwidth, $h_1$, in $\tilde{H}$ should be chosen to ensure that the number of samples in the interval ($\tau -h_1$, $\tau +h_1$) is equal to or larger than the number of variables to be estimated,($p+1$), so that the least-squares solution to (14) exists. Suppose the signal is uniformly distributed at a sampling rate of $f_s$, then we get the following condition for the bandwidth: $h\ge \left(p+1\right)/\left(2f_s\right)$. On the other hand, the maximum bandwidth $h_{\text{Γ}}$ can be arbitrarily large (say, to make the estimation window as large as the recording time), but too large a bandwidth will result in a high computational complexity. It was suggested in [15] that the maximum bandwidth $h_{\text{Γ}}$ could be set as half of the recording time so that the resulting Epanechnikov window can cover all data samples. In practice, the maximum bandwidth could be determined from the prior knowledge about the transient properties of the processes under study. For example, in task fMRI study, the largest bandwidth can be chosen to cover one full cycle of the stimulation, because data from one cycle should be sufficient to estimate meaningful dynamics with the lowest degree of non-stationarity.

In addition, we generally select 3–4 bandwidths between $h_1$ and $h_{\text{Γ}}$ for generating $\tilde{H}$ to achieve a tradeoff between performance and complexity. Intensive experimental results show that the proposed selection of parameters gave satisfactory results in practice.

4). Estimation of Covariance Matrix and Correlation:

Finally, it should be noted that the LPR-ICI method can also be applied to estimate auto-covariance of a locally stationary process. The time-varying covariance matrix of multiple ($>2$) locally stationary processes can also be estimated using LPR-ICI by calculating pairwise covariance. Although it is reasonable to use different bandwidth parameters for elements that have different degrees of variations in the covariance matrix of multiple processes, the positive definiteness of the whole covariance matrix may not be guaranteed. As a result, the correlation (cross-covariance normalized by auto-covariance) may be out of the range[−1, 1]. To partially solve this problem, we can approximate a universal bandwidth for the whole covariance matrix as the average of the ICI-selected optimal local bandwidths for all elements in the matrix. A theoretically optimal bandwidth selection method that can handle different degrees of variations of elements while keeping the time-varying covariance matrix positive-definite will be left for future study.

B. Application to Dynamic Connectivity Analysis of fMRI

Functional connectivity is an important tool to characterize brain mechanisms and investigation of functional connectivity from fMRI has been drawing increasing interests recently [9]. However, the conventional connectivity analysis approaches, such as psychphysiological interaction [24] and dynamic causal modeling [25], are usually model-based and implicitly assume a sustained change of connectivity throughout the task condition. Hence, conventional functional connectivity analysis based on the assumption of stationarity may not be sufficient to capture the dynamic characteristics of functional connectivity and seriously limits our understanding of the dynamic functional organization of the brain. A non-parametric data-driven method, which does not assume any prior structural or biophysical knowledge, is needed to justify whether connectivity changes in the task is sustained over time.

Covariance is a commonly used measure of functional connectivity, and the sliding-window approach is a simple but useful technique to estimate the time-varying covariance between fMRI signals. The selection of window size is critical to the inference of dynamic functional connectivity. A short window can help detect more transient events but, because of only a few samples used, its variability may be large, which implies spurious transient events may also be detected. A long window could decrease the variability of functional connectivity at a higher risk of smoothing out meaningful transient patterns. The window bandwidth should be adaptively and locally selected so that important dynamic information of the connectivity will not be overlooked while spurious patterns will not be wrongly identified. To the best of our knowledge, current sliding-window analyses of dynamic functional connectivity in the resting state all rely on an empirically-selected constant window size, ranging from 30 s to60 s [22], while there is no study of dynamic functional connectivity in a task. In this study, the LPR-ICI method is used to estimate the time-varying covariance between fMRI from brain regions activated by a visual task. The LPR-ICI method, which is more “data-driven”, has an evident advantage over other “model-based” functional connectivity analysis methods when a prior model is not precisely given or unavailable.

The proposed dynamic connectivity analysis of fMRI data in task-related experiments consists of three steps: (1) data pre-processing (realignment, coregistration, normalization, smoothing, etc.); (2) identification of activation regions using the general linear model (GLM); (3) estimation of time-varying covariance between fMRI signals of activation regions using the LPR-ICI method.

The first two steps are processing routines for task fMRI signals and can be easily implemented using popular software such as SPM. The third steps can be implemented using the LPR-based algorithm in Table I.

TABLE I.

The LPR-ICI Method for Time-varying Covariance Estimation

Step 1.	Calculate the inner product of two locally stationary processes as $m\left(n\text{,\hspace{0.17em}}l\right)=X_{n,N}^{\left(1\right)}{X}_{n+l,N}^{\left(2\right)}$
Step 2.	At each time instant $\tau$, estimate ${\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{h}_{\gamma }\right)$ as in (14) by a $p$th order LPR with each bandwidth $h_{\gamma }$ in the set $\tilde{H}$.
Step 3.	Approximate the residual variance ${\sigma }^2\left(\tau \text{,\hspace{0.17em}}l\right)$ and the covariance $\text{V}\left(\widehat{\beta }\left(\tau \text{,\hspace{0.17em}}l\right)\right)$ as in (21) and (22).
Step 4.	Calculate the optimal bandwidth ${\widehat{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$ using the ICI method as in (18 – 20).
Step 5.	Smooth ${\widehat{h}}_k^{\text{opt }}\left(\tau \text{,\hspace{0.17em}}l\right)$ slightly to reduce the variance, resulting in a smoothed variable bandwidth ${\tilde{h}}_k^{\text{opt }}\left(\tau \text{,\hspace{0.17em}}l\right)$.
Step 6.	Perform a $p$th order LPR with bandwidth ${\tilde{h}}_k^{\text{opt}}\left(\tau \text{,\hspace{0.17em}}l\right)$ to obtain ${\widehat{\beta }}_k\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{\tilde{h}}_k^{\text{opt }}\left(\tau \text{,\hspace{0.17em}}l\right)\right)$. ${\widehat{\beta }}_0\left(\tau \text{,\hspace{0.17em}}l\text{;\hspace{0.17em}}{\tilde{h}}_0^{\text{opt }}\left(\tau \text{,\hspace{0.17em}}l\right)\right)$ is the final estimate of time-varying covariance $\widehat{c}\left(\tau \text{,\hspace{0.17em}}l\right)$.

In the framework of LPR-ICI [16], it is assumed that the signal to be estimated is a $p$-differentiable smooth function where $p$ is the order of LPR) while the additive noise is a zero-mean Gaussian process. In the application of covariance estimation of fMRI signals, it is reasonable to assume the covariance of two fMRI signals is a smooth function because the hemodynamic response function is smooth so that fMRI signals in response to stimulation or events as well as their covariance are smooth. Although it is difficult to accurately describe the property of noise component in the covariance estimation of fMRI signals, it has been demonstrated in [26] that the ICI method can still achieve accurate and reliable results even in the cases of some heavy-tailed types of noise, such as the Laplacian noise and uniform noise. Therefore, we conclude that the LPR-ICI method is applicable to the problem of time-varying covariance estimation of fMRI signals.

V. Simulation Results

In this section, we evaluate the performance of the LPR-ICI method on simulated signals with different types of time-varying covariance structures and at different levels of signal-to-noise ratio (SNR).

A. Signals with Jumping Covariance

We first test the LPR-ICI method using simulated signals with jumping covariance, as shown in Fig. 1 (c). Signals $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ are both piecewise constant functions with $N=500$. The covariance between $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ contains extreme types of variations (constant and jump discontinuity) so that this simulation can effectively illustrate the results of variable bandwidth selection for estimating covariance with different degrees of variations.

Fig. 1.

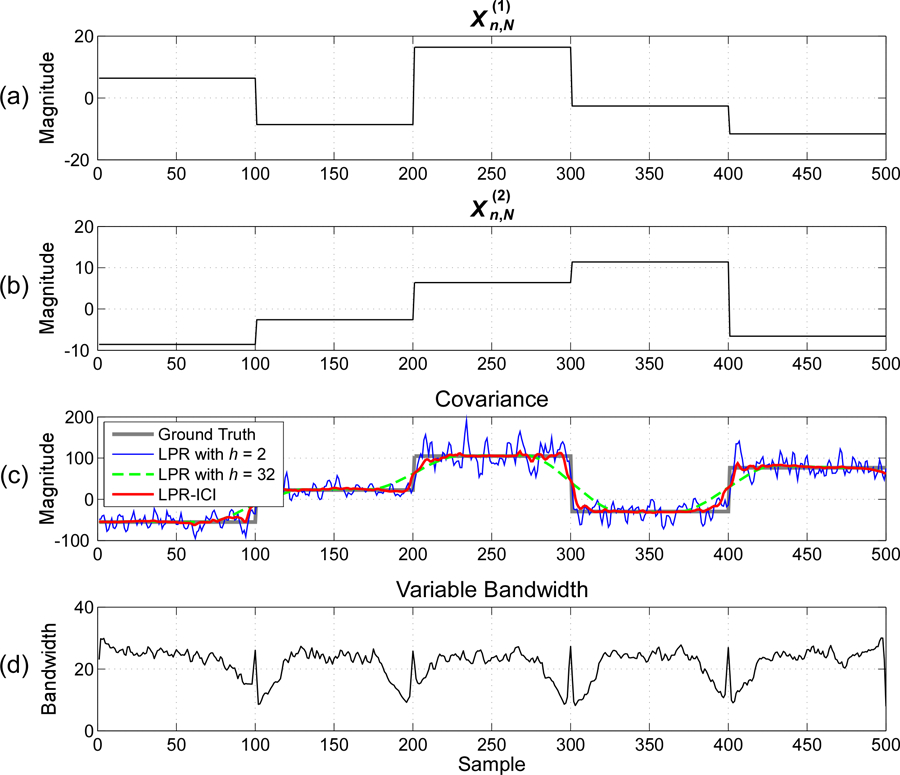
Estimation of time-varying covariance between two signals with jumping covariance and an SNR of 10dB : (a) Simulated signal $X_{n,N}^{\left(1\right)}$, (b) Simulated signal $X_{n,N}^{\left(2\right)}$, (c) Time-varying covariance estimated by different methods; (d) Variable bandwidths used in LPR-ICI. The model order for LPR is $p=1$.

Zero mean white Gaussian noise with SNR (0dB, 0dB, 5dB, 10dB, or 20dB) is added to $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ independently to assess the performance of the LPR-ICI under different noise scenarios.

Note that since the product of two independent zero mean Gaussian variables also has a zero mean, the assumption for the residual in (11) (zero mean and independence of $X_{n,N}^{\left(1\right)}{X}_{n,N}^{\left(2\right)}$) holds in the simulation. The Epanechnikov kernel is employed and the bandwidth set for ICI is chosen as $\tilde{H}=\left\{2,4,8,16,32\right\}$. The polynomial order used in LPR is $p=0,1$, or 2. The LPR-ICI method is compared with LPR using a constant bandwidth 2, 4, 8, 16, or 32 in the whole period. Only the covariance at zero $lag\left(l=0\right)$ is estimated.

Fig. 1 illustrates the time-varying covariance estimates and the variable bandwidth selection in one realization of the simulation with an SNR of 10dB and an LPR order of 1. It can be clearly seen from Fig. 1 that: 1) a small bandwidth $\left(h=2\right)$ can accurately estimate the jump changes of covariance, but it leads to large estimation variations for constant covariance; 2) a large bandwidth $\left(h=32\right)$ can obtain smooth estimates when the covariance varies slowly or even remains constant, but it cannot well estimate the fast changes of covariance; 3) the LPR-ICI method could obtain satisfactory results for both slowly-varying covariance and fast-varying covariance by employing small bandwidths for jump discontinuities and large bandwidths for constant covariance.

The MSE for covariance estimate at each time sample can be approximated by means of Monte-Carlo simulations. Suppose we perform $M$ independent Monte-Carlo realizations of the simulation, and denote $c\left(n\right)$, $\widehat{c}\left(n\text{;}m\right)$, and $\overline{c}\left(n\right)$ respectively as the true covariance, the estimated covariance, and the average of the estimated covariance $\left(\overline{c}\left(n\right)=\frac{1}{M}{\sum }_{m=1}^M\hat{c}\left(n\text{;}m\right)\right)$ at time $n$ of the $m$th realization. The bias, variance, and MSE of the covariance estimates at time $n$ can be approximated from $M$ independent realizations as

$$\mathit{\text{Bias}}\left(n\right)=\overline{c}\left(n\right)-c\left(n\right),$$ (24)

$$MSE\left(n\right)=\frac{1}{M}{{\sum }_{m=1}^M\left[\widehat{c}\left(n;m\right)-c\left(n\right)\right]}^2,$$ (25)

The squared bias, variance, and MSE approximated from 50 independent Monte-Carlo realizations are illustrated in Fig. 2. We can see that, the estimation bias for a small $h$ is much smaller than that for a large $h$ around jump discontinuities (sample 100, 200,300, and 400); while at flat areas the estimation bias is rather small. On the other hand, the estimation variance for a large $h$ is much smaller than that for a small $h$. For the MSE, we can see that a small $h$ has small MSE values around the jump discontinuities, while a large $h$ has small MSE values on the flat areas. The local variable bandwidths, which are small around the jump discontinuities and large on the flat areas, can obtain satisfactory results for the whole period.

Fig. 2.

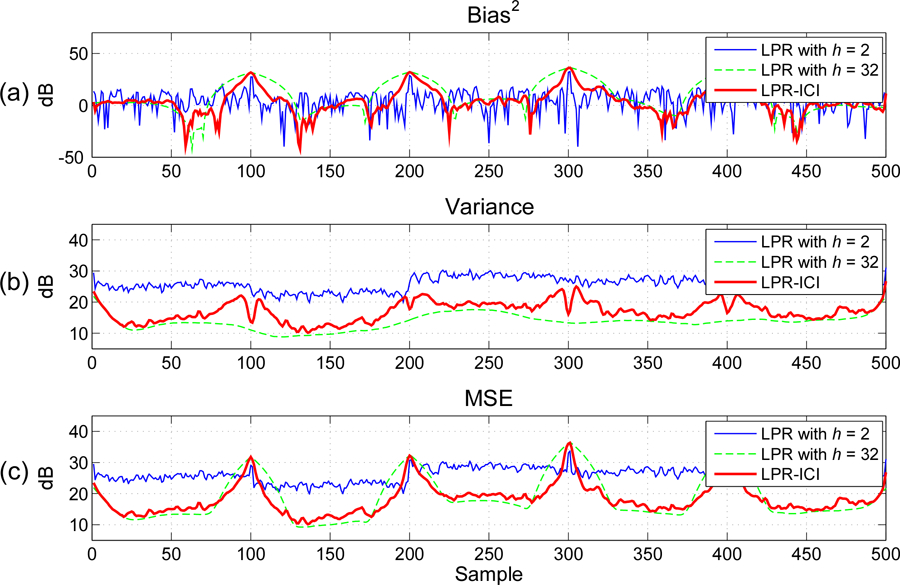
(a) Squared bias, (b) variance and (c) MSE of time-varying covariance estimates between two signals with jumping covariance and an SNR of 10dB. The model order for LPR is $p=1$.

Furthermore, we calculate the ensemble MSE (EMSE) of the $m$th realization as

$$EMSE\left(m\right)=\frac{1}{N}{\sum }_{n=1}^N{\left[c\left(n\right)-\widehat{c}\left(n;m\right)\right]}^2,$$ (26)

for quantitatively comparing the performance of various methods in the whole time period. Table II shows the EMSE values averaged from 50 independent Monte-Carlo realizations. First, we can see from Table II that the “optimal” global bandwidth (with the minimum EMSE under one certain SNR) decreases with the SNR. That is, when the amount of noise is large, the optimal bandwidth should be large, which agrees with the theoretical results of (10) (where the optimal bandwidth is proportional to the noise variance). Second, the LPR-ICI method can always achieve good results that are not far from the “optimal” one under different testing scenarios. The robust and consistent performance of the LPR-ICI method is very useful for practical applications, where the ground truth is unknown and there is no means to find the optimal bandwidth. Third, a small $p$ is more suitable for a signal with a low SNR, because large noise could be incorrectly modeled by using excessive order. Forth, the LPR with the plug-in method for bandwidth selection can also achieve good performance but its computational complexity is much higher than LPR-ICI (see Appendix II in the Supplementary Materials)

TABLE II.

EMSEs of Different Covariance Estimation Methods for Two Signals with Jumping Covariance (Unit: Decibels)

Methods	SNR = 0	SNR = 5	SNR = 10	SNR = 20
LPR ($p=1$, $h=2$)	38.00	31.94	26.65	17.53
LPR ($p=1$, $h=4$)	34.74	28.78	23.83	17.50†
LPR ($p=1$, $h=8$)	31.88	26.39	22.56†	19.44
LPR ($p=1$, $h=16$)	29.45	25.35†	23.27	22.11
LPR ($p=1$, $h=22$)	28.54†	26.21	25.39	25.06
LPR-ICI ($p=0$)	28.75*	25.32*	22.89	19.86
LPR-ICI ($p=1$)	29.23	25.35	22.52*	19.53
LPR-ICI ($p=2$)	35.73	30.01	24.88	16.60*
LPR w. plug-in ($p=1$)	28.58	25.36	22.27	15.85

^†The minimum EMSE of LPR over all fixed bandwidths under one certain SNR is marked with

^*The minimum EMSE of LPR-ICI over all model orders under one certain SMR is marked with.

B. Signals with Randomly Varying Covariance

We further test the performance of the LPR-ICI method on more general signals with randomly varying covariance. Signal $X_{n,N}^{\left(1\right)}$ and $X_{n,N}^{\left(2\right)}$ are generated by filtering white Gaussian signals with zero mean and unit variance using low-pass filters. The resultant signals (with $N=500$ ) and their covariance vary randomly over time and the degree of variations is determined by the cutoff frequency of the low-pass filter. Four cutoff frequencies $f_c$:0.005, 0.01, 0.02, and 0.05, are used to simulate different degrees of covariance variations. These examples can be used to demonstrate the effectiveness of the LPR-ICI method in estimating randomly varying covariance, which is more similar to real-world signals. Zero mean white Gaussian noises with different SNRs (0, 5, 10, and 20 dB) are added to simulate different noise conditions. Here, we also compare the LPR-ICI method with LPR using a constant bandwidth (2, 4, 8, 16, or 32). Other parameters for the LPR are the same as those in the previous simulation.

Table III lists the EMSE values of different methods averaged over 50 independent Monte-Carlo realizations, and Fig. 3 shows the estimation results of different methods for signals generated with $f_c=0.01$ and $SNR=10 dB$ in one realization. It can be seen from Fig. 3 that a large bandwidth over-smooths fast-varying covariance while a small bandwidth results in large variance in the covariance estimation. The LPR-ICI method can avoid the deficits of using a constant bandwidth and obtain more accurate estimates of time-varying covariance. We can further observe the following from Table III. First, for signals with one certain degree of variations (indicated by $f_c$ ), the “optimal” constant bandwidth (having the minimum EMSE) increases with the amount of noise, which is similar to the observation in previous simulation. Second, at a certain noise level, the “optimal” fixed bandwidth decreases with the degree of the signal variations (indicated by $f_c$ ). That is, if the variation of signals is large, the “optimal” fixed bandwidth is small, which can be seen from the theoretical result of (10) (where the optimal bandwidth is inverse proportional to $c^{″}\left(u\right)$, the second-order derivative of covariance). Third, even at large noise level and signal variation, the LPR-ICI method provides good estimation results, which are not far from the best results from an “optimal” fixed bandwidth. Forth, a higher $p$ can achieve better performance when the signal has a higher degree of non-stationarity and the additive noise is small. But in most scenarios, a model order of $p=1$ can achieve good performance, which agrees with the recommendation in the literature [15].

TABLE III.

EMSEs of Different Covariance Estimation Methods for Two Signals with Randomly Varying Covariance (Unit: Decibels)

Methods	$f_c=0.005$
	SNR = 0	SNR = 5	SNR = 10	SNR = 20
LPR ($p=1$, $h=2$)	−39.98	−46.13	−51.67	−61.75
LPR ($p=1$, $h=4$)	−43.31	−49.63	−55.06	−65.09
LPR ($p=1$, $h=8$)	−46.20	−52.76	−57.98	−67.87†
LPR ($p=1$, $h=16$)	−48.76	−55.53†	−59.98†	−65.95
LPR ($p=1$, $h=22$)	−49.99†	−54.48	−55.51	−56.20
LPR-ICI ($p=0$)	−49.21	−54.59	−57.61	−63.14
LPR-ICI ($p=1$)	−49.27*	−55.08*	−58.68*	−66.88*
LPR-ICI ($p=2$)	−42.51	−48.44	−53.85	−63.92
LPR w. plug-in ($p=1$)	−49.14	−55.20	−59.49	−67.79
Methods	$f_c=0.01$
	SNR = 0	SNR = 5	SNR = 10	SNR = 20
LPR ($p=1$, $h=2$)	−40.41	−46.66	−51.92	−62.10
LPR ($p=1$, $h=4$)	−43.79	−49.98	−55.28	−65.34
LPR ($p=1$, $h=8$)	−46.76	−52.83	−57.92†	−65.55†
LPR ($p=1$, $h=16$)	−48.87†	−53.38†	−55.94	−57.32
LPR ($p=1$, $h=22$)	−46.70	−47.75	−48.08	−48.19
LPR-ICI ($p=0$)	−47.74	−51.67	−55.35	−59.91
LPR-ICI ($p=1$)	−47.89*	−52.47*	−56.81*	−64.36*
LPR-ICI ($p=2$)	−42.94	−48.85	−54.02	−64.07
LPR w. plug-in ($p=1$)	−48.34	−53.60	−58.04	−65.36
Methods	$f_c=0.02$
	SNR = 0	Methods	SNR = 0	Methods
LPR ($p=1$, $h=2$)	−27.82	−33.86	−39.36	−49.44
LPR ($p=1$, $h=4$)	−31.17	−37.27	−42.70	−51.81†
LPR ($p=1$, $h=8$)	−33.99	−39.42†	−43.19†	−45.94
LPR ($p=1$, $h=16$)	−34.07†	−36.10	−36.73	−36.95
LPR ($p=1$, $h=22$)	−30.77	−31.20	−31.30	−31.32
LPR-ICI ($p=0$)	−32.92	−36.38	−39.41	−43.10
LPR-ICI ($p=1$)	−33.17*	−37.10*	−40.95	−47.46
LPR-ICI ($p=2$)	−30.10	−35.92	−41.13*	−50.75*
LPR w. plug-in ($p=1$)	−33.59	−38.85	−43.55	−51.74
Methods	$f_c=0.005$
	SNR = 0	SNR = 5	SNR = 10	SNR = 20
LPR ($p=1$, $h=2$)	−18.75	−24.77	−30.37	−39.45†
LPR ($p=1$, $h=4$)	−21.80	−27.07†	−30.69†	−33.24
LPR ($p=1$, $h=8$)	−22.10†	−24.19	−24.87	−25.13
LPR ($p=1$, $h=16$)	−20.97	−21.66	−21.83	−21.90
LPR ($p=1$, $h=22$)	−20.81	−21.19	−21.27	−21.30
LPR-ICI ($p=0$)	−21.43	−22.87	−24.97	−25.14
LPR-ICI ($p=1$)	−21.54*	−23.52	−27.53	−32.04
LPR-ICI ($p=2$)	−20.61	−25.76*	−30.32*	−34.48*
LPR w. plug-in ($p=1$)	−21.03	−25.93	−30.96	−38.64

^†The minimum EMSE of LPR over all fixed bandwidths under one certain SNR is marked with.

^*The minimum EMSE of LPR-ICI over all model orders under one certain SMR is marked with.

Fig. 3.

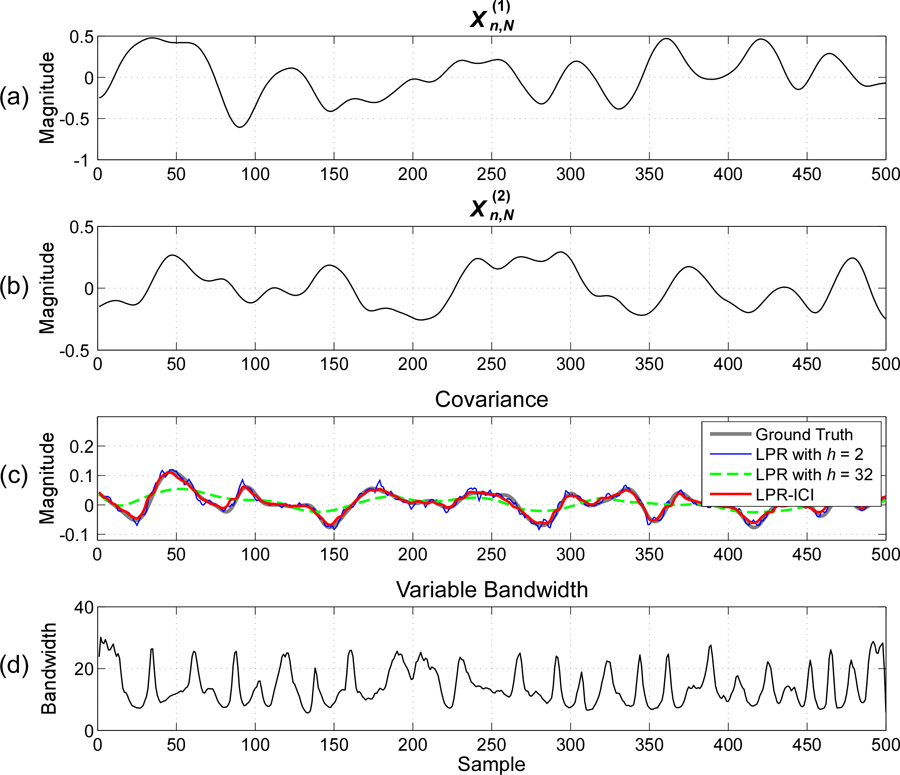
Estimation of time-varying covariance between two signals with randomly varying covariance ($f_c=0.01$) and an SNR of 10dB: (a) simulated signal $X_{n,N}^{\left(1\right)}$, (b) simulated signal $X_{n,N}^{\left(2\right)}$, (c) time-varying covariance estimated by different methods; (d) variable bandwidths used in LPR-ICI.

To sum up, we can see from these simulation results that the LPR-ICI method can adaptively select variable bandwidths so that it can achieve good performance for signals with different degrees of covariance variations and under different SNR. Although LPR with a fixed bandwidth may outperform the LPR-ICI method for certain signals and SNRs, its performance is limited in practice especially when the signal property is varying or unknown. Therefore, the LPR-ICI method provides a reliable and accurate estimator for estimating time-varying covariance in practical applications.

VI. Application to Infer Dynamic Brain Connectivity

In this section, we use the LPR-ICI method to explore visually induced connectivity changes when subjects were viewing checkerboard flickering. The fMRI data from the enhanced Nathan Kline Institute (NKI)/Rockland sample of the international neuroimaging data-sharing initiative (INDI) (http://fcon_1000.projects.nitrc.org/indi/enhanced/) are analyzed. Only the visual checkerboard data with a TR of 645 ms and the MPRAGE (magnetization-prepared rapid acquisition with gradient echo) anatomical images are used in the current analysis. The enhanced NKI Rockland sample consists of a community sample of originally 181 subjects. We include 26 subjects (8 females) who do not have any mental or physical disease that could affect brain functions. Age range is restricted to 18 to 60 years (mean of 31.7 years). Subjects’ data with large head motions (> 3 mm or 3°) are also deleted. As a result, 26 subjects’ data are included in the current analysis (8 females). The mean age of the subjects is 31.7 years (18.4 – 59.9 years). The task used for this data set is a simple checkerboard visual task. The checkerboard stimuli are presented in the center of the screen with a flickering frequency of 4 Hz. With a block design, the scan starts with a 20 s rest condition and then a 20 s checkerboard condition with three repetitions. After the third checkerboard block, there is a 35 s rest condition. The total scan time is about 2 m 35 s with totally 240 images acquired. The MPRAGE images are scanned using the following parameters: TR, 1900 ms; TE, 2.52 ms; flip angle, 9 deg; voxel size, 1 mm³ isotropic. The fMRI data are scanned using the following parameters: TR, 645 ms; TE, 30 ms; flip angle, 60 deg; voxel size, 3 mm³ isotropic, 40 slices. In particular, the TR of fMRI is relatively shorter than conventional fMRI studies and is more suitable for studying the dynamic connectivity.

The fMRI data are preprocessed using SPM8 (h)ttp://www.fil.ion.ucl.ac.uk/spm/)) under MATLAB (version 7.6, MathWorks) environment. First, the first 14 functional images are discarded (9 s). The remaining images are motion corrected, and coregisterd to subject’s high resolution anatomical image. The anatomical images are segmented using the new segment routine in SPM8. Then, the deformation field obtained from the segmentation step is applied to the functional images to normalize them into standard MNI space (Montreal Neurological Institute). Finally, all the functional images are smoothed using an 8 mm Gaussian kernel. GLM is used to get activations relating to the checkerboard condition. Based on the activation maps (Fig. 4), four ROIs are defined: the right middle occipital gyrus (MOG), left MOG, right fusiform gyrus (FuG), and left FuG. The fMRI time series data from the four ROIs are extracted after removing head motion parameters and signals from the white matter and cerebrospinal fluid.

Fig. 4.

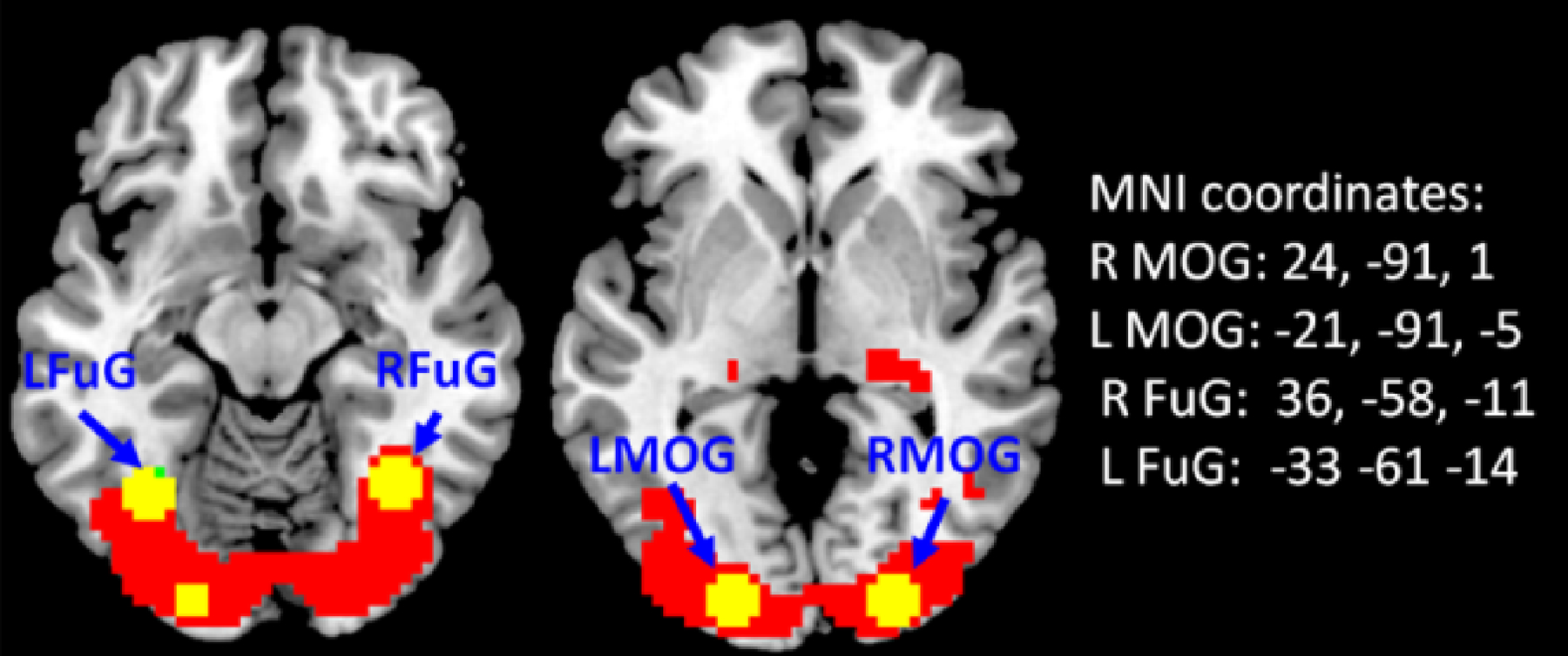
The group activation map for the checkerboard stimuli. Four ROIs identified by GLM are labeled.

Next, the LPR-ICI method is used to estimate pairwise time-varying covariance between each pair of the ROIs during the whole scan and for each subject. The bandwidth set for ICI is chosen as cycles (one cycle of stimulation has a period of 40 s: 20 s checkerboard viewing and 20 s rest). The largest bandwidth of 1/2 cycle is selected to make the largest window cover a full cycle of stimulation, while the smallest bandwidth of 1/16 cycle is set to ensure the least-squares solution exist. Other parameters for the LPR are the same as those in the previous simulation. Here, we compare the LPR-ICI method with LPR using a fixed bandwidth (1/16 or 1/2). Fig. 5 shows BOLD signals and the time-varying covariance estimates averaged across three repetitions and all subjects and the time interval under analysis is the pre-stimulus rest condition (−10 s to 0 s, the baseline interval) and the whole checkerboard condition (0 s to 20 s, the activation interval). It can be seen that the time-varying covariance estimated by LPR-ICI is very stable in the pre-stimulus interval (which is reasonable because there is no stimulation before stimulation and the functional connectivity should be in a steady state) and shows prominent dynamic patterns and tendency in the activation interval (transient increases shortly after the stimulus onset and decreases afterwards can be observed from time-varying covariance of most pairs of ROIs). A large bandwidth ($h=1/2$) results in very flat covariance estimates, so it is difficult to see any dynamic pattern in the activation interval from the over-smoothed results. On the other hand, a small bandwidth ($h=1/16$) has large variations in the covariance estimates and thus some meaningless transient information may mislead our understanding of the brain connectivity. For example, the covariance estimates obtained with $h=1/16$ exhibits considerable variations in the pre-stimulus rest interval, which is difficult to be interpreted. As the functional connectivity in the pre-stimulus rest interval should be stable, it is highly possible that such large temporal variation in functional connectivity is caused by using LPR with a too short window. Considering the LPR-ICI method can achieve robust performance in different simulation scenarios, we conclude that the LPR-ICI method has more accurate estimates than the LPR with a fixed bandwidth for real-world fMRI signals in task-related experiments.

Fig. 5.

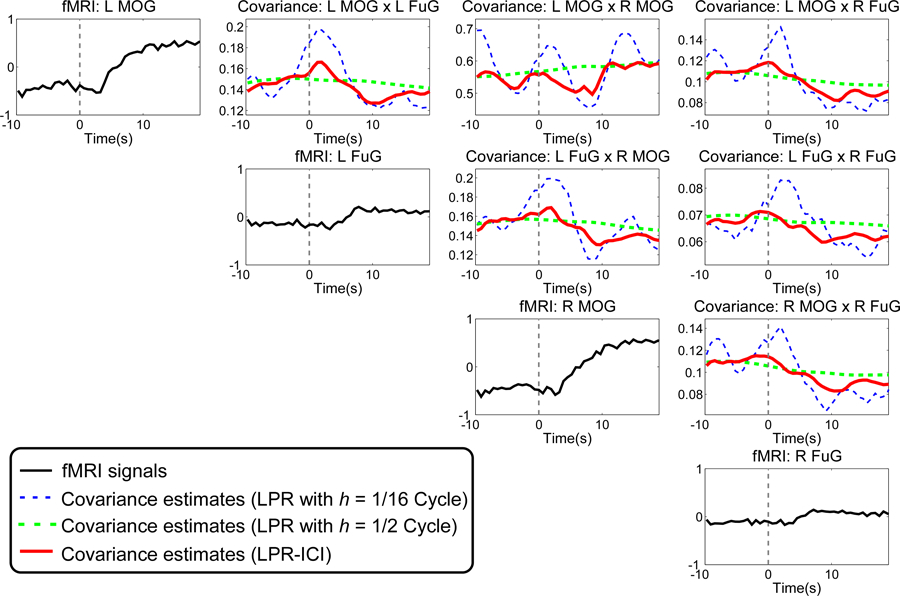
fMRI signals from four ROIs and their time-varying covariance estimates in the baseline interval (−10 s to 0 s) and the activation interval (0 s to 20 s ). All the fMRI signals and time-varying covariance estimates are averaged across three repetitions and 26 subjects.

Further, we take a close examination of the time-varying covariance between left MOG and left FuG (lower and higher visual areas in the same hemisphere) in Fig. 6. To find out whether and when the fMRI signals and time-varying covariance within the activation interval are significantly different from those within the baseline interval, the following statistical analysis is performed. For each fMRI signal or time-varying covariance (averaged across three repetitions and all subjects), the probability density function of the samples in the baseline interval (−10 s to 0 s) is estimated using kernel density estimation [26]. For each sample within the activation interval (0 s to 20 s), its significance level, indicating the rejection of the null hypothesis of no change in the sample compared to the baseline interval, is obtained by locating it under the probability density function estimated from the baseline interval. To address the problem of multiple comparisons, the $p$-value is corrected using a false discovery rate (FDR) procedure [28].

Fig. 6.

Statistical difference between samples in the activation interval (0 s to 20 s) and samples in the baseline interval (−10 s to 0 s) in the fMRI signals from left MOG and left FuG and in their time-varying covariance. Samples with significant difference ($p<0.05$, FDR corrected) with respect to baseline interval are indicated by gray background.

The fMRI data show a hemodynamic delay about 4–5 s after stimulation, which has been repeatedly observed in literature. It can be clearly seen that the time-varying covariance estimated using LPR-ICI exhibits a dynamic pattern: a quick increase after the stimulus onset followed by a decrease. The transient connectivity changes may reflect adaptation or decreases of predictive values of the visual stimuli. Most interestingly, the adaption only occurs on functional connectivity, but the fMRI activities sustain over the block for all the regions.

All these results suggest that the LPR-ICI method could be a powerful technique to estimate dynamic changes of connectivity and to avoid arbitrarily selection of window bandwidth that may lead to misleading and uninterpretable results. Importantly, these results provide the first evidence that the functional connectivity in a task condition measured by fMRI is not stationary but highly dynamic.

VII. Conclusions

This paper examines the asymptotic properties of time-varying covariance between two non-stationary processes and shows that there exists a local optimal bandwidth to achieve the best bias-variance tradeoff. To adaptively select the variable bandwidth for the optimal estimate of time-varying covariance, the LPR-ICI method is adopted. We use extensive simulation results to show that the LPR-ICI method offers good performance for signals with various degrees of covariance variations and under different SNRs. Since covariance is essential for many data analysis techniques, such as principal component analysis and factor analysis, the LPR-ICI method has the potential to improve the performance of these data analysis techniques, in which covariance estimation is essential, when dealing with non-stationary processes. The LPR-ICI method offers an effective method to address the difficult problem of window selection and time-varying estimation such as the covariance in practical biomedical applications as it is more consistent and reliable than using constant bandwidth which may lead to un-interpretable or misleading results. To illustrate the usefulness of the LPR-ICI method, it is further applied to the analysis of dynamic functional connectivity from fMRI in a visual task. We found that the functional connectivity, which is usually assumed as static in most of conventional fMRI studies, is remarkably dynamic during the task. The dynamics of functional connectivity may convey important information about the underlying physiological and psychological states of the subjects. We believe that the proposed time-varying covariance estimation based the LPR-ICI method is expected to find various applications in biomedical signals and systems, such as estimating the dynamic connectivity between multimodal biomedical signals.