Perspectives on Computational Enzyme Modeling: From Mechanisms to Design and Drug Development

Abstract

Understanding enzyme mechanisms is essential for unraveling the complex molecular machinery of life. In this review, we survey the field of computational enzymology, highlighting key principles governing enzyme mechanisms and discussing ongoing challenges and promising advances. Over the years, computer simulations have become indispensable in the study of enzyme mechanisms, with the integration of experimental and computational exploration now established as a holistic approach to gain deep insights into enzymatic catalysis. Numerous studies have demonstrated the power of computer simulations in characterizing reaction pathways, transition states, substrate selectivity, product distribution, and dynamic conformational changes for various enzymes. Nevertheless, significant challenges remain in investigating the mechanisms of complex multistep reactions, large-scale conformational changes, and allosteric regulation. Beyond mechanistic studies, computational enzyme modeling has emerged as an essential tool for computer-aided enzyme design and the rational discovery of covalent drugs for targeted therapies. Overall, enzyme design/engineering and covalent drug development can greatly benefit from our understanding of the detailed mechanisms of enzymes, such as protein dynamics, entropy contributions, and allostery, as revealed by computational studies. Such a convergence of different research approaches is expected to continue, creating synergies in enzyme research. This review, by outlining the ever-expanding field of enzyme research, aims to provide guidance for future research directions and facilitate new developments in this important and evolving field.

Introduction

Enzymes differ from conventional catalysts in their ability to accelerate chemical reactions, often exceeding a million-fold.¹⁻¹¹ This unparalleled catalytic power makes them indispensable for carrying out a vast array of biological functions that would not otherwise be possible.¹² However, enzymes are not ordinary catalysts; they exhibit exceptional selectivity in recognizing and binding specific substrates, ensuring efficient catalysis while preventing wasteful or undesirable side reactions.¹³⁻¹⁷ What further distinguishes enzymes is that they are regulated by multiple and customized mechanisms so that each chemical process occurs with exquisite timing within the relevant cellular context.¹⁸⁻²¹ Throughout evolution, these unique features of enzymes have exerted evolutionary pressure, resulting in the optimization of their functions and even the development of new capabilities.²²⁻²⁹ In addition, the design of robust enzymes has received considerable attention in recent years.³⁰ Therefore, a comprehensive understanding of the mechanisms of enzyme action has become essential to maximize their potential in a wide range of applications, from biotechnology³¹⁻³⁴ to medicine.³⁵⁻⁴² This understanding has also contributed significantly to our broader understanding of chemical processes in biology and life.

Extensive computational studies have been devoted to elucidating the role of enzymes in catalyzing reactions.^3,43−48 Initially, much of this research focused on understanding how enzymes stabilize the high-energy transition state (TS) of a reaction—a concept famously theorized by Pauling.⁴⁹⁻⁵¹ This stabilization effectively reduces the activation free energy required for reactions to proceed, resulting in a significant increase in the reaction rates. However, as scientific investigation has progressed, several alternative mechanisms have been proposed, including reactant-state destabilization,^45,52 coupled dynamics,⁵³⁻⁵⁶ chemical control,⁵⁷ chemical dynamics,^58,59 and others.^60,61 Recently, many investigations have focused on understanding protein allostery in the context of regulation of enzyme function.^{25,56,62−67} In principle, allosteric regulation involves the binding of effector molecules at sites other than the enzyme’s active site, thereby affecting its catalytic activity. Understanding these regulatory mechanisms has not only provided valuable insights into how enzymes respond to specific cellular demands, such as in cellular signaling,^19,68,69 but has also shed light on the underlying factors contributing to the development of various human diseases and therapeutic strategies to target them.^38,39,41,70

The mechanisms of ligand binding have also been extensively studied, leading to an ongoing debate between the induced-fit¹³ and conformational selection mechanisms.^{15,27,62,71−74} In the induced-fit model, the enzyme undergoes a conformational change upon binding of its substrate, rearranging its active site to accommodate the ligand. In contrast, the conformational selection model, also known as the population-shift model, assumes that the enzyme has multiple pre-existing conformations, one of which is a favorable fit to the ligand. While computational studies have played a central role in the investigation of these mechanisms,⁷⁵⁻⁷⁷ the search for the definitive mechanism behind ligand binding remains an active area of research. Moreover, molecular recognition extends beyond substrates and cofactors to include allosteric regulators, target proteins, and even drug binding. Therefore, developing the ability to theoretically model these processes will allow a more detailed exploration of how enzymes recognize and bind ligands and ultimately help to better understand these essential biological interactions.

Within the context of the topics outlined above, this review discusses the current state of several important areas within the field of computational enzymology (Figure 1). The discussion begins with a brief overview of recent advances, with particular emphasis on the enzyme systems that have been the focus of recent research from our laboratories. We then discuss the challenges inherent in studying complex enzymes, engineering enzymes for non-natural reactions, and developing innovative drugs targeting enzymes. Throughout this discussion, our goal is to highlight recent advances while recognizing the ongoing challenges that continue to drive research in the field. It is anticipated that this review will provide guidance for future directions and developments in the field.

Figure 1.

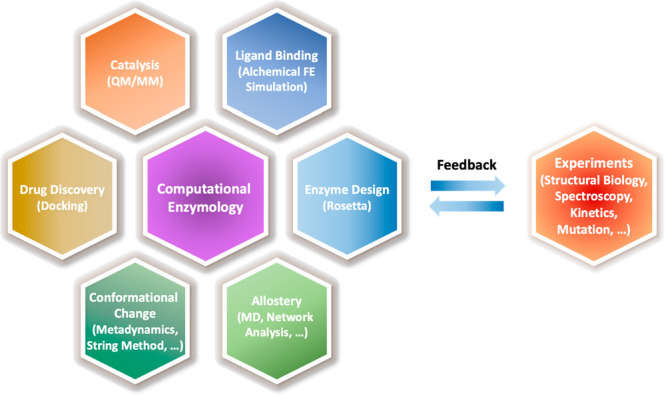
Topics in computational enzymology covered in this review and representative computational approaches. The synergistic connection with experiments is also indicated. Abbreviations: MD: molecular dynamics; QM/MM: quantum mechanical and molecular mechanical method; FE: free energy.

Modeling of Complex Enzyme Catalytic Mechanisms

While transition-state (TS) stabilization remains a fundamental principle,^12,50,51,78 it represents only the tip of the iceberg underlying the full spectrum of catalytic strategies employed by enzymes.^45,61,79,80 These strategies include, but are not limited to, acid–base catalysis,^11,81 covalent catalysis,^11,61,82 solvation/desolvation,⁸³⁻⁸⁵ reactant-state (RS) destabilization,^45,52 strain distortion,^86,87 near-attack conformation,^61,88 chemical control,^89,90 quantum tunneling,⁹¹⁻⁹³ promoting vibration,^60,94,95 and coupled dynamics.^3,96−98 Some of these strategies, such as acid–base catalysis and covalent catalysis, are enzyme-specific, while others contribute more generally to catalytic acceleration. However, their impact on catalytic efficiency (i.e., k_cat) varies and depends on the context (e.g., reactions and enzymes), with TS stabilization often being the most significant contributor. Furthermore, recognizing that many enzymes involve small- to large-scale conformational motions, recent studies,^53,99−104 including our own,^98,105 have investigated the interplay between protein dynamics and enzymatic catalysis, revealing how these motions contribute to enzyme catalysis and regulation (see the discussion in the section “Conformational Substrates and Their Role in Enzyme Activity”). Taken together, these mechanisms unraveled by computational studies have greatly enriched our understanding of how life orchestrates chemical reactions and evolves new functionalities.^23,27,106 From the perspective of enzyme design and evolution, this mechanistic understanding also has important implications for further enhancing enzyme activity.

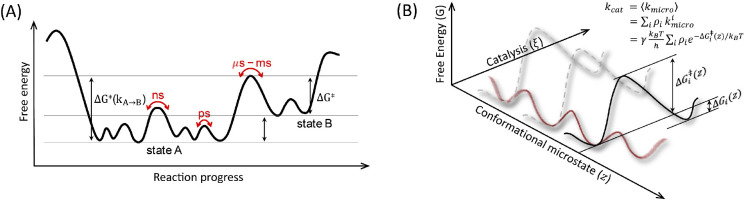
Computational studies in the area typically begin by determining the catalytic barriers associated with different chemical reaction steps (Figure 2).^44,45,107 These barriers can be compared to experimental reaction rates through transition state theory (TST),^44,108 as described by the equation:

1

In this equation, γ represents the generalized transmission coefficient and β = (k_BT)⁻¹, where k_B is the Boltzmann constant and T is the temperature. The term ν^‡, according to gas-phase reaction theory, is equal to (βh)⁻¹, where h is Planck’s constant, and characterizes the inverse time for transitioning from the transition state to the product state (PS). Since the classical (recrossing) contribution to γ is typically in the range of 0.5 to 1.0,^109−112 its contribution to the reaction rate is often ignored in most studies. Enzymes, which play a significant role, are primarily limited to reactions involving proton and/or hydride transfers with pronounced quantum mechanical effects, such as tunneling.^{8,91−93,113}

Figure 2.

(A) Free energy landscapes visualizing the hierarchy of protein motions on different time scales. State A represents the reactant state in which multiple substates exist in equilibrium. The rate constants for exchange between substates occur on time scales ranging from picoseconds (ps) to nanoseconds (ns). The catalytic reaction takes place on microsecond (μs) ∼ millisecond (ms) time scales, forming products represented as state B. (B) Enzyme catalysis from the perspective of conformational substates, where the free energy landscape is plotted as a function of the catalytic reaction coordinate (ξ) and conformational substate (z). In each substate, the catalytic barrier and reaction free energy can be calculated by applying the QM/MM free energy simulation methods. Then, the overall reaction rate can be expressed as the sum of the population-weighted rates (eq 3).

The activation free energy, denoted as ΔG^‡ in eq 1, is defined as the free energy difference between the transition state and the reactant state. In practical applications, it is often approximated as the difference between the potentials of mean force (PMFs) for TS and RS, as

2

where W(ξ_X) represents the PMF value at a given reaction coordinate value ξ = ξ_X, where X refers to either TS or RS.⁴⁵ The calculation of PMF is commonly performed using enhanced sampling techniques, such as umbrella sampling¹¹⁴ and variants thereof,^48,115 with stratification into narrow simulation windows to facilitate configuration sampling. Data-reweighting can be accomplished with the weighted histogram analysis method (WHAM),¹¹⁶ the multistate Bennett acceptance ratio (MBAR),^117,118 the variational free energy profile (vFEP) method,^119,120 and the dynamic histogram analysis method (DHAM).¹²¹ In recent years, methods such as metadynamics,^122−124 string methods,^125,126 and their variants^127−132 have emerged as valuable tools for determining the minimum free energy paths (MFEP) and the corresponding PMF values along these paths. Nonetheless, these simulation techniques must be combined with hybrid quantum mechanical and molecular mechanical (QM/MM) potentials, using both semiempirical (SE) and ab initio/density functional theory (AI/DFT) methods as QM methods, to enable bond breaking and formation.^133−140 Recent studies have also explored machine learning potentials (MLPs) employing deep learning techniques, which show great promise in speeding up calculations by using potentials that are surrogates for time-consuming QM methods,^141−148 as well as approaches that use low-level QM theories to drive the QM/MM molecular dynamics (MD) simulations while high-level QM theories are used to provide corrections to the energy on the fly^138,149 or as a posterior correction.^150−163 Alternatively, the low-level QM potentials are reparameterized to reproduce results at high-level QM theories.^{135,164−168} While each approach has its own strengths and weaknesses—e.g., speed versus transferability in MLPs and reparameterized SE-QM models—the ultimate goal may be to incorporate high-level QM energies and forces directly into the simulations, e.g., by applying multiple time step approaches, to overcome the limitations of MLPs and SE-QM/MM methods without significantly increasing the overall computational cost.^{138,149,169,170}

Despite substantial progress in free energy barrier calculations, elucidating the complete mechanism of enzymes remains a formidable theoretical challenge.^45,171−173 To begin with, experimentally determined rates, such as k_cat, derived by fitting the Michaelis–Menten equation, provide only apparent values that are collective reporters of the overall reaction without providing insights into the microscopic steps in catalysis. This limitation can lead to misleading interpretations of the specifics of reaction steps and underlying mechanisms, especially when catalytic turnover involves multiple reaction steps. To address this problem, integrated approaches combining various methods such as kinetics,^174,175 high-throughput microfluidic kinetics,¹⁷⁶ kinetic isotope effects,^87,113,177 single-molecule spectroscopy,^{73,100,178−180} vibrational spectroscopy,^9,181 X-ray crystallography,^182−185 and nuclear magnetic resonance (NMR) spectroscopy^{7,97,186−192} have been used in conjunction with simulations to characterize individual steps and associated transient intermediates. NMR spectroscopy, in particular, has the advantage of providing both quantitative and qualitative insights into protein dynamics across time-scales ranging from picoseconds (ps) to hours, and at atomic resolution.^7,189 An example demonstrating this is a study of the dynamics of a transition state mimic bound to the nucleoside monophosphate kinase UmpK.¹⁹³ Based on the results, the authors proposed that the transition state is a rigid, low entropy state that can facilitate the chemical reaction while suppressing unproductive structural fluctuations. NMR-derived order parameters have also been used to estimate residue-specific contributions to entropy for the binding of substrate molecules to proteins;^194−196 the estimated binding entropy can serve as a benchmark for computationally derived order parameters, such as those from MD simulations.^71,197 Despite these advantages, NMR spectroscopy has limitations. For example, NMR spin relaxation rates include contributions from all of the parallel processes occurring during enzymatic reactions, which complicates their interpretation. Under these circumstances, biochemical tuning, such as the use of nonhydrolyzable ATP analogues¹⁹⁸ or amino acid substitutions,^199,200 can be used to study each process separately, which can also be combined with molecular simulations to provide more detailed insights into each process. Another widely used experimental approach is isothermal titration calorimetry (ITC), which can quantify the enthalpic and entropic contributions to the binding step in catalysis. However, this methodology provides only total contributions and can separate neither the contributions of protein versus water solvent in molecular recognition nor the contributions of individual residues.

From a computational point of view, the computational cost increases rapidly as the complexity of a reaction mechanism increases.^120,201 For example, many enzymes catalyze their reactions through complex multistep processes, requiring the evaluation of the catalytic barrier for each step to identify the rate-determining step (RDS) and the underlying mechanisms.^57,201,202 When alternative mechanisms are possible, each mechanism must be thoroughly investigated and compared with experimental rates or product distributions.^{57,90,201−203} This situation highlights the importance of being able to simulate multiple reaction steps within a single simulation framework to expedite the exploration of these mechanisms. Therefore, traditional methods such as umbrella sampling are less applicable, and new, more efficient approaches are needed. In addition, improving the efficiency of filtering out unrealistic mechanisms at low computational cost, as exemplified by EnzyDock’s consensus docking of reaction mechanisms,²⁰⁴ can significantly reduce the number of mechanisms and reaction steps that require computationally intensive investigation. Together, these innovations will serve to bridge the gap between experimental and computational approaches in enzyme mechanism studies.

Having identified the reaction mechanisms, the logical next step in exploring the catalytic power of an enzyme is to dissect its individual contributions to both the catalytic barrier and the overall free energy of the reaction.^205,206 This can be done by decomposing the free energy values, including enthalpy–entropy decomposition,^48,207,208 specifying the contributions of individual residues,^{203,209−220} and taking into account the electrostatic solvation effects of the enzyme and the surrounding solvent.^164,221 While computational methods, some of which are reviewed in ref (222), have been instrumental in providing detailed insights into these aspects, they require experimental validation. To this end, a widely used experimental approach is to introduce amino acid substitutions into the enzyme and measure their effects on catalytic activity.^{105,223−225} These perturbations then provide feedback on computational predictions and accuracy of the simulation models. Likewise, simulations complement these efforts by providing additional perspectives on enzyme mechanisms. A notable example of this synergy between computation and experiment is our recent study of adenylate kinase.^98,105 In this study, we investigated the role of catalytic residues in facilitating the key catalytic step of the enzyme using both QM/MM simulations and amino acid replacements to characterize the effects of individual residues on the kinetic parameters of the enzyme. Interestingly, this investigation revealed that these catalytic residues also have a significant effect on the global dynamics of the enzyme. This finding demonstrates the interplay between enzyme activity and protein dynamics that underlies the robust catalytic activity of this enzyme and the importance of combining simulations and experiments.

Hierarchy of Functional Protein Motions

Enzymes are inherently dynamic, involving a variety of motions on different time and length scales to coordinate their biological functions (Figure 2A).^{5,6,8,51,226−228} Among these motions, fast time-scale motions, such as bond vibrations and bending motions, manifest as fluctuations around the average enzyme structures during reactions and contribute to the overall entropy of these processes. MD simulations have proven powerful in exploring these fast time-scale motions and have provided valuable insights into their role in enzymatic function.^43,226,229 For example, numerous QM/MM MD simulation studies have shown that active site residues of enzymes rearrange rapidly following catalytic reactions, providing transition state stabilization and thereby facilitating the catalytic transformation from reactant to product.^{3,44,98,174,203,220,230−234} Consequently, mutations in these residues directly impact their catalytic processes, which can be readily explored using both experiments and simulations.^{95,105,174,181,217,234,235}

In contrast, large-scale collective protein motions, which occur on time scales ranging from microseconds (μs) to milliseconds (ms), play distinctive roles in enzyme function.^{53,186,190,198,227,236} Perhaps, their most prominent role is to bridge different conformational states of an enzyme, achieved by driving interconversion between them during processes such as ligand binding,^{180,198,237−240} allosteric activation,^241−244 and even the chemical reaction.^{98,101,102,105} While their role in modulating enzymes’ conformational states is easy to conceptualize, understanding how they influence catalytic mechanisms remains elusive. For example, functional links between large-scale protein motions and key enzymatic processes may exist in enzymes with active sites located at flexible hinges.²⁴⁵ Particularly, in these enzymes, active sites undergo open–closed conformational transitions that accompany ligand binding and release,^{179,186,198,246} as well as catalysis.¹⁰⁰ Numerous simulation studies, including long MD simulations using all atom potentials,^{229,247−250} have explored their role in enzyme function and provided valuable insights into protein dynamics relevant to conformational changes. Nevertheless, studying these large-scale motions and their involvement in the catalytic process remains a theoretical challenge and requires further development of advanced, enhanced sampling techniques to efficiently characterize their complex free energy landscapes.^{229,248,251−254} In addition, in recent years, the proposed involvement of protonation state changes during protein conformational change and function^255−259 has added complexity to simulation studies. Such studies require the application of constant pH MD (CpMD) simulation techniques²⁶⁰ and/or the simulations must be performed at different protonation states.

The mechanisms governing large-scale conformational changes in enzymes have been studied extensively, particularly in the context of substrate binding and product release.^{15,27,71,73,74,76,237,240} This has led to the development of two widely discussed models: the induced-fit model¹³ and the conformational selection model.^62,72,73,261 In the induced-fit model, enzymes are postulated to adopt an open conformation in their apo state. Upon ligand binding, the molecules undergo a conformational transition to a closed state. Following the reaction and subsequent release of the reaction products, the enzymes return to their open conformation, completing the catalytic cycle. In contrast, the conformational selection model assumes that enzymes populate multiple conformations including the conformation with optimal geometry for ligand binding even in the absence of ligands (e.g., substrates) and that ligand binding occurs predominantly with the closed conformation. In theory, these two models can be distinguished by examining the accessibility of the closed conformation in the apo state and/or by investigating the time scales of conformational changes between the enzyme in the apo versus holo states.^240,262,263 For real enzymes, however, complications arise because most experimentally measured opening and closing rates reflect the residence times of the enzyme in its respective closed and open states rather than the actual time scales of conformational motions.^{73,180,187,198} Furthermore, as we have recently pointed out, caution must be exercised when comparing protein opening/closing motions in the presence of natural substrates versus non-natural substrates or inhibitors.^105,240 For example, using adenylate kinase as a model enzyme, we demonstrated differences in the opening rates of the enzyme between the two ligand-binding subdomains, and these rates were significantly affected by the nature of the ligands (i.e., reactants, products, or inhibitors).^98,240 These studies were carried out by applying the string free energy simulation method¹²⁶ to simulate the opening of the enzyme and the concurrent release of ligands, which clearly showed a three-step process in enzyme opening and ligand release and differences in the free energy barriers of enzyme opening between the reactant and product states. These results suggest a measurable influence of active site residues on modulating the free energy of enzyme opening. In addition, the sequence of opening events differed between the apo- and holo-state enzymes.²⁴⁰ These results suggest that the conformational changes of the enzyme are more complex than those captured by a simple two-state model. Therefore, interpreting experimental data by fitting them to a two-state model may potentially lead to a misleading understanding of the underlying mechanism of enzyme opening and closing.^240,264 Furthermore, for enzymes to exhibit robust activity, they must have evolved to minimize the closed-to-open conformational transitions during catalytic reactions. Ideally, they should remain in the closed conformation and transition to the open state only when products are released.¹⁰⁵ In such scenarios, even if the chemical step is the actual rate-limiting step, experimentally measured rates may overlap with enzyme opening rates if they represent residence times. In addition, if these enzymes are small, the two events, i.e., conformational change and enzymatic catalysis, may not be completely separable, as the enzyme must share the same functional/structural units to perform both tasks as we have shown in adenylate kinase.^98,105 In this case, therefore, it is possible that there exists a connection between large-scale protein motions and enzymatic processes, at least at the mechanistic level.

Conformational Substrates and Their Role in Enzyme Activity

In recent years, the existence of conformational substates within enzyme–substrate complexes and their role in enzymatic activity has been increasingly recognized.^{14,21,265−274} In essence, this concept proposes that enzymes do not function exclusively in a single, well-defined conformation in the holo-state. Instead, they exist in a dynamic equilibrium of multiple similar conformations, each associated with different degrees of catalytic activity. Early evidence supporting this idea came from a single-molecule experiment performed by English et al. in 2006.¹⁷⁸ In their study, the authors observed a wide range of waiting times between catalytic events of the enzyme β-galactosidase. These variations, however, could not be explained by simple diffusion of the substrate to and from the enzyme alone. Instead, the authors proposed fluctuations in the catalytically relevant conformations of the enzyme, characterized by conformational transition time scales slower than those of substrate binding and catalysis.^178,275

This observation can also be understood as a mechanistic coupling between large-scale conformational fluctuations and enzymatic catalysis (Figure 2B). However, due to the disparate time scales between the two, this coupling does not necessarily occur dynamically during the catalytic process. Instead, the enzyme continuously explores its conformational landscapes and establishes an equilibrium distribution along these landscapes. During this exploration, catalytic events proceed as expected, but with different catalytic barriers depending on the conformational state of the enzyme.^{99,273,276,277} In this scenario, the overall catalytic rate can be expressed as the sum of the population-weighted rates, represented as

3

where ρ represents the population at the conformational coordinate z along which conformational fluctuations occur, and k_micro denotes the (microscopic) rate constant of each conformational state (Figure 2B). If the substates are discrete, as implied in the case of β-galactosidase mentioned above,¹⁷⁸ the integral can be replaced by a summation over the accessible substates. A pertinent example of such dynamic motions involves low-frequency hinge motions observed in enzymes with active sites located at their hinges.^98,103,278 In these cases, motions along the hinges can modulate the relative orientations of the reacting species, transitioning between optimal and suboptimal orientations for catalysis or bringing them close together. These hinge motions can also contribute to the establishment of (discrete) conformational substates in the catalytic conformations of the enzyme. To computationally study this scenario, it is necessary to incorporate a conformational coordinate z into the reaction coordinate alongside the chemical events. This approach has recently been exploited by our group⁹⁸ and others.¹⁰⁴ In these studies, while the conformational coordinate z was restrained to discrete values, QM/MM simulations were performed to determine the catalytic free energy profiles and to compare the effects of restraints on the catalytic barrier. These simulations clearly show impacts on the catalytic barrier and/or reaction free energy in response to the restrained slow protein motions, supporting the proposed mechanistic coupling between the two events. Alternatively, QM/MM simulations can be performed for multiple protein conformations, which are sampled prior to the QM/MM simulations using enhanced sampling techniques, as demonstrated for dihydrofolate reductases.²⁷⁷ In addition, conformational substates and their role in catalysis can be studied by designing amino acid substitutions that selectively perturb either the catalytic barrier or the population distribution; in some cases, both aspects can be affected simultaneously, as recently demonstrated by Yabukarski et al. using ketosteroid isomerase as a model enzyme.²⁷³ However, despite these valuable studies, gaining a concrete understanding of the full spectrum of these conformational substates and their associated time scales remains an important subject for further investigation.

Protein Allostery for Enzyme Activity Regulation

Since the introduction of the term “allostery” in 1961,²⁶¹ the concept has evolved to encompass long-range communication within proteins that affects activities at the active sites, as well as the influence of effector molecule binding.^{38,63,67,68,279} In the case of multimeric enzymes, this mode of communication is often manifested as positive or negative cooperativity.^21,56,64,280 For instance, consider F₁-ATPase, whose activity responds cyclically to the rotation of a central γ-subunit.^281,282 Despite the substantial separation of more than 50 Å between the three active sites of the enzyme, they exhibit negative cooperativity, ensuring that only one active site functions at any given time to achieve high energy conversion efficiency.²³⁹ This phenomenon highlights the communication between spatially separated active sites within the enzyme. Another important example is found in protein kinases, where allosteric regulation plays a central role in cell signaling.^19,23,283 Because of its importance, protein allostery has been studied extensively.^{23,64,243,249,284−287} While more comprehensive reviews are available elsewhere,^21,65,66,279 our discussion here focuses on protein allostery within the context of protein dynamics and conformational landscapes.

Allosteric communication can occur through two primary mechanisms: conformationally driven and entropically driven.^{21,286,288,289} The conformationally driven mechanism, which is often associated with changes in protein structure, is relatively straightforward to study using structural biology techniques such as X-ray crystallography. This type of allostery, similar to ligand binding, can result from conformational changes resembling the induced-fit model, or it can involve transitions between different conformational states, such as population shift.^103,290 Consequently, the principles established to explain ligand binding mechanisms can be readily applied to understand conformational allostery, while the investigation of the conformational change mechanism is largely left for computational studies. Notable examples of such studies include the Markov state modeling (MSM) studies of cSrc protein kinase,²⁴¹ the metadynamics simulations of cyclin-dependent protein kinase 5²⁹¹ and adenylyl cyclase,²⁷⁴ the string method simulation study of insulin receptor kinase (IRK),²⁴⁴ and the alchemical free energy simulation study of insulin-like growth factor 1 kinase (IGF-1RK).²⁴³ However, in contrast to the structure prediction problem, which can be approached using pairwise interactions, allosteric networks are generally orders of magnitude more complex and rely on clusters of interacting networks on multiple levels.¹⁰ In addition, the energetic separation between microscopic structural states in allosteric mechanisms can be minute, on the order of a few “k_BT”,⁹⁷ and therefore difficult to accurately quantify with existing computational approaches and force fields.

The entropically driven mechanism is characterized by minimal or no discernible changes in protein structure.^{286,288,290,292} Instead, it operates by modifying the dynamic behavior of enzymes, such as correlated protein dynamics (that can be characterized by covariance analysis^293,294), to induce entropic effects and resultant changes in the free energy landscapes of the enzyme as discussed below. Notably, since no conformational changes are involved, these changes occur through the adjustment of protein–ligand and intraprotein interaction networks in response to ligand binding/release. Theoretical studies of this mechanism, however, have been challenging, which has led to the development of various approaches,^295,296 such as principal component and covariance analyses,^293,294,297 network models,^298,299 normal mode/elastic network models,^300−302 statistical coupling analysis,³⁰³ rigid residue scan^304,305 and machine learning approaches,^306,307 as well as through the determination of free energy profiles along the allosteric conformational change pathways.^241,244,252 These methods have allowed the investigation of protein allostery in protein activation,^{238,244,249,308} ligand binding/recognition,^{187,238,285,309,310} and even catalysis,^187,243,311 which revealed the complex role of protein dynamic motions in these functions and allosteric hotspots.^305,310 In parallel, experimental techniques, such as amino acid substitutions^223,312 and NMR spectroscopy,^{191,284,292,313} have been used to quantify changes in protein dynamics attributable to allosteric effects. This collaborative effort between experimental and theoretical methods serves as a powerful tool for understanding the intricate mechanisms underlying protein allostery and its role in biological processes.³¹⁴ One particular example of the synergy between simulation and experiment can be found in our study of F₁-ATPase.²³⁹ In this study, we used single-molecule spectroscopy data measured for the enzyme^315,316 and previous computational results^317,318 to construct free energy profiles of the enzyme along the entire 360° rotation cycle. The determined free energy profiles, together with covariance analyses of the enzyme,³¹⁹ can explain the molecular events associated with the enzyme’s power-stroke process and the overall energy conversion efficiency achieved by modulating the free energy of substrate vs product binding during the rotational cycle of the enzyme.

Interestingly, these two types of allostery need not be mutually exclusive. Our recent computer simulation studies examining the activation mechanism of IRK and IGF-1RK have shown that they can indeed coexist within a single protein fold, each operating in distinct functional steps (Figure 3).^243,244 For example, the conformational activation of these kinases is modulated by conformational allostery. In particular, phosphorylation of their activation loop (A-loop) restricts access to their inactive conformation, while the kinase predominantly adopts this inactive conformation in the inactive state. In contrast, allostery in the catalytic and ligand-binding steps is driven by entropic effects resulting from altered coordinated protein dynamics upon activation loop phosphorylation.^243,311 Similarly, in the Src kinase, binding of its regulatory domain to the C-terminal tail of the kinase induces changes in the dynamics of the enzyme as demonstrated by using MD simulations.³²⁰ These changes then propagate to modulate the coupled dynamics between the two regulatory subdomains of the enzyme, ultimately leading to the association or dissociation of these regulatory subdomains from the kinase domain. Likewise, the catalytic activity of spleen tyrosine kinase (Syk) is regulated via modulation of the conformational dynamics (i.e., entropy) of the linker connecting the two regulatory domains of the kinase. This effect is mediated by phosphorylation in the linker which is located remotely from the regulatory domains binding surfaces and solvent exposed,³²¹ and was probed by a combined application of MD simulations, isothermal calorimetry and NMR spectroscopy. These findings suggest that due to the structural similarities among protein kinases, these principles of allostery may be applicable to other protein kinases. However, further studies are needed to thoroughly examine and confirm this idea.

Figure 3.

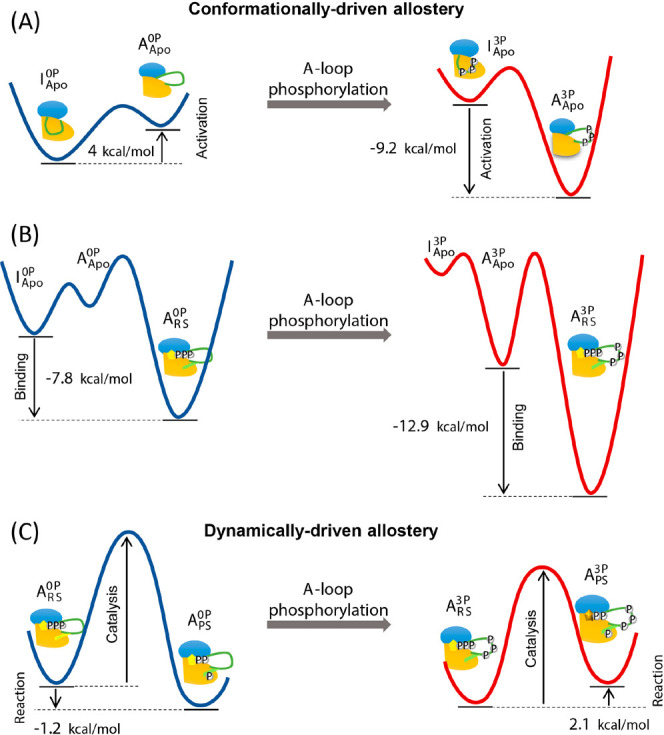
Schematic representation of the free energy changes and thus, the allosteric mechanisms of (A) the IGF-1RK conformational change that is shifted toward the activated state following phosphorylation, (B) increased substrate binding affinity following phosphorylation, and (C) increased phosphoryl transfer reaction partly caused by changes in underlying protein dynamics after phosphorylation. In each diagram, the changes of the free energy are indicated with the arrow, and the red and blue lines represent the free energy profiles of fully activated and inactive form kinases, respectively. Adapted with permission from ref (243). Copyright 2017 Royal Society of Chemistry.

De Novo Enzyme Design and Evolution

The ultimate goal in enzyme design is to engineer entirely new enzymes equipped with catalytic capabilities that match or even surpass those of their natural counterparts while catalyzing novel chemical reactions. Substantial progress has been made toward this goal over the past few decades, largely driven by the development of computational enzyme design strategies.^31,322−334 Typically, de novo enzyme design begins with the creation and fine-tuning of “theozymes”, which comprise essential side chains positioned to stabilize reaction transition states.³³⁵ This initial design is followed by the selection of enzyme scaffolds capable of accommodating the theozyme configurations, forming the active site of the designed enzyme; recent development even allows the design of the scaffold proteins through deep learning approaches.^336−339 Subsequently, sequence optimizations are performed to maximize the compatibility of the active site with the reaction mechanism of the theozyme while preserving the overall stability of the designed enzyme. Sequences produced through these processes are then subjected to experimental characterization to evaluate their catalytic efficiencies, often measured as the specificity constant k_cat/K_M. When necessary, the selected sequences, once their catalytic efficiency has been measured, undergo further refinement to enhance their catalytic performance and improve properties like thermostability. These strategies have been successfully employed to generate de novo enzymes with the capacity to catalyze a range of organic reactions, including Kemp eliminase,³²³ retro-aldolase,^340,341 Diels–Alderase,³⁴² esterase,^327,343,344 and luciferase.³⁴⁵ Alternatively, existing enzymes or sequences are repurposed to catalyze increasingly complex chemical reactions,^{329,332,346−348} including poly(ethylene terephthalate) (PET) hydrolysis.^349−352

Despite these successes, the designed enzymes have shown relatively modest catalytic activities, with k_cat/K_M values being several orders of magnitude lower than those of natural enzymes.^326,353,354 To further enhance the catalytic potential of these designed enzymes, experimental approaches, e.g., directed evolution, have been employed.^{324,330,355−357} This combined approach, starting with computational design followed by experimentally directed evolution, has resulted in designed enzymes with catalytic efficiencies approaching those of their natural counterparts. It also provided valuable insights into the structural determinants of efficient catalysis. In particular, directed evolution introduces variations of active site residues, including the catalytic residues that were originally designed. Amino acid replacements from directed evolution can improve catalysis, for example, by introducing new catalytic groups, optimizing catalytic contacts and ligand-binding modes and enhancing transition-state complementarity within the binding pocket.³⁴⁸ In some cases, replacements are introduced at positions remote from the active site, affecting ligand-binding properties and/or populations of conformational substates.^323,354,358 These observations, together with relatively poor selectivity of substrates in the designed enzymes, point to potential limitations of current computational methods and highlight the need for further development of computational enzyme design algorithms.^272,341,354 Such improvements should aim to improve the accuracy of modeling catalytic and ligand-binding interactions while allowing the efficient exploration of the vast sequence space. In addition, the full spectrum of mechanisms contributing to enzyme catalysis, beyond the simple transition state stabilization, needs to be considered in the design of new enzymes to reach the catalytic activity of natural enzymes.

In recent years, the application of machine learning techniques has revolutionized the field of protein structure prediction,^359,360 protein design,^{334,338,339,345,361} and enzyme engineering.^{334,361−366} These techniques focus primarily on either structure prediction or activity prediction. On the structure side, achievements such as AlphaFold2³⁵⁹ and RoseTTAFold2³⁶⁰ have significantly improved the accuracy of protein structure prediction. These structure prediction techniques have the potential to greatly improve our ability to design robust enzymes with high success rates.³⁶⁷ Nevertheless, challenges remain, including the need to incorporate aspects of protein dynamics,^272,368 allostery and entropy-enthalpy compensation into enzyme design principles,^333,369 as well as the design of enzymes capable of catalyzing multistep reactions.^330,367 From the perspective of computational enzymology, the physics-based computational methods discussed above have proven instrumental in exploring these complexities of enzymes and understanding their mechanisms.³²⁹ Consequently, these methods need to be fully integrated with machine learning techniques into the enzyme design framework to streamline the effective refinement of the catalytic properties of the designed enzymes.^{30,272,329,330,333,367,370,371} On the activity prediction side, regression models, including linear regression and neural networks, have long been used to decipher the sequence–activity relationship of enzymes. Such relationships have then been used to guide (a) the optimization of enzyme variants^372,373 and (b) the directed evolution of enzyme activity^362,374,375 and product enantioselectivity.^376,377

A compelling question related to enzyme design principles is how nature evolved enzymes to achieve the remarkable catalytic capabilities found in modern enzymes.^{28,67,106,272,332,353,358,368,371,378} To address this question, ancestral sequence reconstruction (ASR) algorithms^379,380 can be combined with protein structure prediction algorithms to test evolutionary design principles, such as those governing their catalytic activities and thermal adaptation, and to rapidly evaluate hypotheses.^{331,332,381,382} This idea has already been adopted, where the high accuracy of proteins structure predictions such as AlphaFold2 and RoseTTAFold2 have been used to evaluate the structures of the ASR-generated sequences, followed by biochemical/biophysical characterization and structural elucidation.^383−385 Notable examples of such studies include the study of monooxygenases’ functional diversification, which revealed relatively few mutations could be sufficient to induce diversification of the catalytic function of the enzyme,³⁸⁴ and the development of multiple xylulose isomerases by combining big data, ASR, and adaptive laboratory evolution techniques for biotechnology.³⁸⁵ We expect that this combined approach will be used more frequently to provide new opportunities for researchers. Furthermore, these approaches can also be applied to further evolve enzymes for biomedical and biotechnological applications. In these applications and in the development of new enzyme-design approaches, advanced physics-based computational methods, such as those discussed in this review, can provide a fundamental understanding of their working mechanisms and thereby help advance the field of enzyme design and its biotechnological applications.³²⁹

Emergence of Covalent Drugs and In Silico Docking Strategies

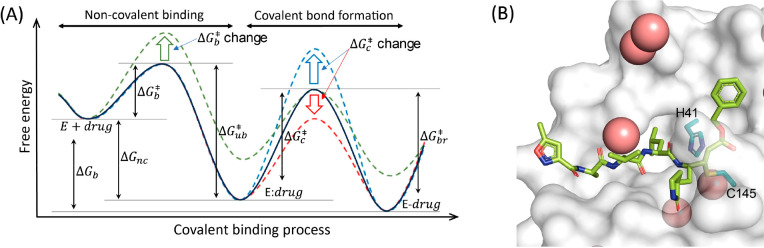
While drugs that form covalent bonds with protein targets have been known for more than a century, such as aspirin and penicillin, recent successes have renewed efforts to develop covalent drugs.^386−389 Notable examples of these drugs include remdesivir^390,391 and nirmatrelvir^392,393 for COVID-19 and the G12C K-Ras inhibitor sotorasib,^394,395 where K-Ras has long been considered undruggable. Compared to the conventional noncovalent drugs,^396,397 the main advantage of covalent drugs is their ability to produce long-lasting pharmacological effects even at low doses, and they can even irreversibly inactivate target proteins, reducing the frequency of administration. For this advantage, numerous computational studies have been conducted to elucidate the chemical mechanism underlying the covalent bond formation (Figure 4).^41,398−410 However, despite this recent interest in the development of covalent drugs, the lack of effective strategies remains a current technical challenge to the widespread development of covalent inhibitors.^{387,388,397,408,411−419}

Figure 4.

(A) Proposed two-step binding of a covalent ligand. The first step is noncovalent binding with barrier ΔG^⧧_b, and the second step is covalent bond formation with ΔG^⧧_c as the associated barrier. The effectiveness of the covalent binders can be determined by the free energy barrier (ΔG^⧧_c) of the second step relative to the noncovalent binding free energy (ΔG_nc) and/or the unbinding free energy barrier (ΔG^⧧_ub). Too high a barrier can result in premature release of the binder prior to covalent bond formation, while too low a barrier renders the binder reversible or ineffective as a covalent inhibitor. In the latter case, the warhead may be too reactive, leading to nonspecific binding. Therefore, modulation of both ΔG_nc and ΔG^⧧_c is critical for the design of effective covalent binders, where the binding pocket of the target protein/enzyme provides an environment for nonspecific binding and functional modifications of the warhead control the reactivity of the binders. (B) SARS-CoV-2 Mpro with bound ligand, N3 inhibitor (PDB ID: 7BQY). The bound ligand is colored yellow, and water molecules are pink. The protein surface appears in gray. The Cys 145-His41 dyad is shown in deep teal. Adapted with permission from ref (404). Copyright 2021 American Chemical Society.

From the point of view of enzymatic catalysis, covalent drugs follow the general mechanism analogous to the Michaelis–Menten mechanism (Figure 4A).^389,413 In essence, they first bind noncovalently and reversibly to the target protein, followed by the formation of a covalent bond between the ligand and the target residue. In this context, the first step corresponds to the substrate binding step, and the second step is analogous to the enzymatic catalysis step, where the enzyme environment and protein dynamics play a critical role in achieving high catalytic efficiency and specificity in substrate recognition. Therefore, in addition to achieving high binding affinity of the drug (in a noncovalent form), efforts in covalent drug design must take into account: (a) the reactivity of the “warheads”, i.e., the reactive functional groups of the drug, and (b) the presence of susceptible residues on the target proteins, such as cysteine (Cys) residues, among others.^387,420,421 In particular, the reactivity of the warheads should be sufficient to react with the target residues, but not overly reactive to minimize off-target reactivity.^415,420,422 For this reason, most known warheads are weak electrophiles. Upon binding, the warheads must also be properly oriented to react effectively with the nucleophile of the protein.⁴¹¹ While the first consideration requires quantum mechanical treatment,^409,421 the second can be partially addressed using conventional, noncovalent drug docking approaches. For example, docking can be performed with restraints that position the warheads in proximity to the target residue and predict the docked poses driven by noncovalent interactions.^{411,413,417,423} The approach can then be switched to a QM/MM potential to optimize the docked poses in the presence of a covalent bond between the warhead and the protein.^{408,413,424,425} However, the actual binding of covalent drugs involves reaction transition states, whose barriers influence the time scale of the reaction. Understanding this process is therefore necessary to gain insight into the reactivity of the warheads and the reversibility of the covalently bound drugs.^{405,406,426−428} In this regard, knowledge gained from the study of enzyme catalysis can be applied to identify potential binding poses and subsequent reactions with target proteins.^{70,204,426,428} Furthermore, given the shared principles between enzyme catalysis and covalent drug binding, the multiscale computational approaches developed to study enzyme mechanisms (Figure 1) can be effectively applied to understand both covalent and noncovalent drug binding. For a similar reason, rational covalent drug design shares the same challenges as enzyme design. However, unlike enzyme design, where the goal is to maximize the catalytic activity of the designed enzymes, the challenge in covalent drug design lies in the modulation of the reactivity of the warheads specifically for the target residues while ensuring that they react within a reasonable time frame of noncovalent binding/unbinding.

Finally, similar to the case of enzyme design, machine learning algorithms have shown potential to improve the accuracy and efficiency of molecular docking.^429−433 These machine learning, particularly deep learning, techniques include multilayer perceptrons, convolutional neural networks, and graph neural networks. Many of these methods have focused on virtual screening of ligand libraries,^433,434 which can be helpful in identifying new lead molecules as inhibitors. Other methods have focused on improving the accuracy or efficiency of scoring functions. Deep learning methods for binding site identification have also been proposed. However, these methods have mostly focused on noncovalent compounds. Therefore, although they can be helpful for computational enzymologists to quickly generate initial structures, they have not been specifically designed toward generating high-quality guesses for Michaelis complex needed for enzyme modeling. Hence, as with any general docking tool, computational enzymologists should use these methods with caution and consider the docking results as initial guesses that should be refined using multiscale methods as defined in this review (Figure 1).

Future Perspectives

In this review, we have discussed several topics within the field of computational enzymology while highlighting several emerging frontiers that deserve future exploration. These include:

• Computational approaches for complex enzymatic processes: Enzymatic catalysis involves interrelated events spanning multiple temporal and spatial scales, encompassing substrate binding, multistep catalysis, and product release. Exploring this complexity requires the development of advanced computational methods capable of integrating multiple levels of theory within a unified free energy simulation framework. While such methods have yet to reach full development, they remain a compelling theoretical challenge.

• Real-time enzyme observations: The field of structural biology is advancing toward the real-time unraveling of dynamic molecular processes. Techniques, such as room-temperature X-ray free-electron laser (XFEL), time-resolved X-ray crystallography, cryo-electron microscopy, and single-molecule approaches, combined with molecular simulations, have the potential to transform the field by enabling real-time observation of enzymatic processes.

• Conformational substates in enzymes: The study of conformational substates within enzyme–substrate complexes is an evolving field. The full spectrum of these substates, their temporal dynamics and their impact on enzyme mechanisms remain to be characterized.

• Advanced enzyme design strategies: The development of robust enzyme design algorithms is an important frontier. These algorithms should improve the accuracy of modeling catalytic and ligand-binding interactions, while rapidly exploring the vast sequence and protein conformational space. To this end, the incorporation of machine learning techniques has shown the potential to significantly accelerate enzyme prediction and design. In addition, the development of enzyme design principles that incorporate our knowledge of protein dynamics, entropy and allostery is essential for improving the mechanistic properties of designed enzymes, such as catalytic activity, substrate specificity, and thermal stability.

• Covalent drug design strategies: Developing effective strategies for the widespread development of covalent inhibitors is an ongoing technical challenge. Advancing our understanding of covalent drug interactions, warhead reactivity, and potential binding poses represents an emerging frontier where the integration of QM/MM methodologies can have an impact by providing more accurate descriptions of drug–protein interactions and the reaction transition states that govern the binding and reactivity of covalent drugs.

Together, these frontiers represent areas where ongoing research and innovation promise significant advances in our understanding of enzymes, protein dynamics, and drug and enzyme design. They also offer exciting opportunities to push the boundaries of what is currently achievable in these fields. Finally, we note that the synergistic integration of experimental and computational methods will continue to play a central role in providing valuable insights into enzymatic mechanisms and protein–ligand interactions.

The authors declare no competing financial interest.