Abstract
Ab initio multireference second-order perturbation theory computations are used to explore the photochemical behavior of two ion pairs constituted by a chloride counterion interacting with either a rhodopsin or bacteriorhodopsin chromophore model (i.e., the 4-cis-γ-methylnona-2,4,6,8-tetraeniminium and all-trans-nona-2,4,6,8-tetraeniminium cations, respectively). Significant counterion effects on the structure of the photoisomerization paths are unveiled by comparison with the paths of the same chromophores in vacuo. Indeed, we demonstrate that the counterion (i) modulates the relative stability of the S0, S1, and S2 energy surfaces leading to an S1 isomerization energy profile where the S1 and S2 states are substantially degenerate; (ii) leads to the emergence of significant S1 energy barriers along all of the isomerization paths except the one mimicking the 11-cis → all-trans isomerization of the rhodopsin chromophore model; and (iii) changes the nature of the S1 → S0 decay funnel that becomes a stable excited state minimum when the isomerizing double bond is located at the center of the chromophore moiety. We show that these (apparently very different) counterion effects can be rationalized on the basis of a simple qualitative electrostatic model, which also provides a crude basis for understanding the behavior of retinal protonated Schiff bases in solution.
Keywords: ab initio, counterion, conical intersection, protonated Schiff base
Retinal proteins (1-4) include the retina visual pigment rhodopsin (Rh) and the bacterial proton-pump bacteriorhodopsin (bR). The biological activity of these pigments is triggered by the ultrafast light-induced cis-trans isomerization of their chromophores. These correspond to the 11-cis (PSB11) and all-trans (PSBT) stereoisomers of the protonated Schiff base (PSB) of retinal respectively. Recently, we have reported (5-7) the computed photoisomerization path of different models of PSB11 and PSBT in vacuo. It has been shown that, invariably, the excited state branch of the path develops entirely along a charge transfer state (that can be related to the 1Bu, i.e., hole pair, state of polyenes) that corresponds to the first singlet excited state (S1) of the system and ends at a peaked conical intersection (CI) where the S1 and ground (S0) state energy surfaces cross. Because the CI features an ≈90° twisted double bond, its geometrical and electronic structure is consistent with that of a twisted intramolecular charge transfer (TICT) state (5-7). The corresponding S1 isomerization coordinate, starting at a planar Franck-Condon (FC) point, is bimodal being sequentially dominated by two uncoupled modes. The first corresponds to a stretching mode involving C-C bonds order inversion. The second mode breaks the planar symmetry and is dominated by a one-bond-flip (OBF) (8, 9) twisting of the reacting double bond.
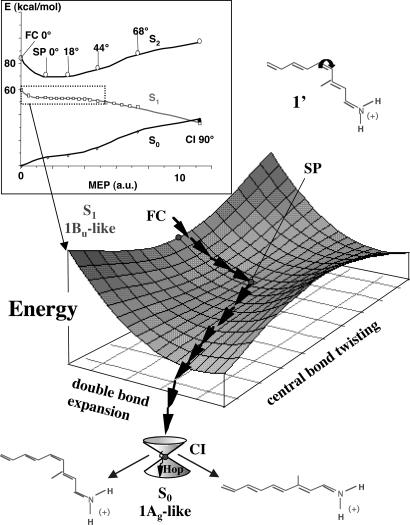
In Fig. 1, we report the computed energy profiles and give a pictorial view of the structure of the S1 energy surface of the PSB11 model 4-cis-γ-methylnona-2,4,6,8-tetraeniminium cation (1′). As shown in the figure, the path switches from the stretching to the torsional mode in the region of the planar structure stationary point (SP) located at the center of a rather long energy plateau. The same data indicate that the path is either barrierless or displays, along the plateau, a small (<1.0 kcal·mol-1) barrier. Computed absorption and fluorescence maxima (6) changes in dipole moments and simulated resonance Raman spectra (10) are consistent with the corresponding experimental quantities, providing a validation of the quality of the investigated models as well as of the two-state/two-mode (6) reaction coordinate described above.
Fig. 1.
The Inset displays the energy profiles along the photoisomerization minimum energy path (MEP) computed on the S1 (1Bu-like) energy surface for the PSB11 model in vacuo (1′) (see ref. 6). A schematic illustration of the bimodal reaction coordinate (stream of arrows) along the MEP in the dotted box is reported below. Point SP corresponds to a flat planar stationary point on S1, where the torsional deformation (leading to the TICT S1/S0 CI) begins.
As mentioned above, the previously reported isomerization paths are based on isolated PSB11 or PSBT models. No environmental factors (e.g., the solvent or protein cavities) have been included in the computations. However, such factors are known to affect both spectroscopic and photochemical properties (11). First, the absorption maximum in the protein (500 and 568 nm for Rh and bR, respectively) appears to be red-shifted with respect to the one observed in solution (440 nm). Second, time-resolved spectroscopic observations indicate that the excited state lifetimes of Rh and bR are ≈150 and 200 fs, respectively. It is also shown that their photoisomerization is stereoselective leading, exclusively, to the all-trans and 13-cis chromophore stereoisomers, respectively, with high (≈67%) quantum yield (QY) (12, 13). In contrast, in solution (e.g., in methanol or hexane) the excited state decay of PSBT features a biexponential dynamics with a dominant (almost 20-fold longer) 2-ps component (12, 14, 15) and leads to production of a mixture of different stereoisomers, with smaller (≈25%) QY (12, 16). Finally, an excited state energy barrier has been observed for PSBT in solution (14). This finding has been used by Anfinrud and coworkers (17, 18) to support a three-state (S0, S1, and S2) model of bR photoisomerization, as an alternative to the two-state (S0, S1) model (19-22) supported by our computations in vacuo (5, 6).
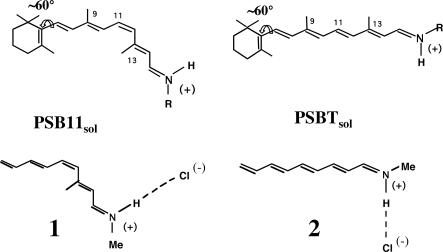
Among other possible environmental effects, the interaction of the cationic retinal chromophore with its counterion is expected to play a crucial role in tuning its photochemical and photophysical properties. Indeed, because S1 is (with respect to S0) a charge transfer (Bu-like) state (5, 6), its energy is expected to depend on the interaction with the counterion. In the present work, the isolated (i.e., gas-phase) models 1 and 2 (Scheme 1) are taken as qualitative (first order) models for contact ion pairs of PSB11 and PSBT. In fact, both computational (23-26) and experimental (27, 28) results indicate an ≈60° twisted (i.e., quasi-deconjugated) 6-s-cis β-ionone ring for retinal chromophores, supporting the use of five conjugated double bond models.‡‡ Furthermore, the small difference between the absorption maxima of PSBT and PSB11 in polar and apolar solvents (440 nm in methanol and 460 nm in hexane) suggests the existence of strong chromophore/counterion interaction (i.e., of a contact ion pair) not only for solvents of low polarity but also for polar solvents. Possible alternative explanations for this fact are provided in the literature (29-32), where it is proposed that a polarizable environment as well as charge induced dipoles orientation in polar solvents may yield a virtual counterion in contact with the positive N-head even when the ion pair is loose. Because of these missing effects, the isolated (i.e., gas-phase calculations) ion pair can provide only a crude model for retinal in solution.
Scheme 1.
The retinal chromophore/counterion interaction has been widely investigated in the past (29, 33-36) by using different theoretical treatments and, mainly, within the protein environment (e.g., the electrostatic effect of the environment has been treated by using dielectric models (29, 33), explicit point charges (36), and specifically parametrized semiempirical quantum chemical methods). Semiempirical quantum chemical studies (including a polarizable environment) dealing with the effect of the counterion position on the retinal chromophore isomerization path have been pioneered by Warshel (37). Here, we report the first ab initio multiconfigurational second-order perturbation theory computational study of the isolated retinal chromophore/chlorine ion pair with the aim to establish the basic effects of a bare counterion on the photochemistry of an isolated retinal chromophore. In other words, we derive at the highest and unbiased level of theory possible a reference model for the effect of the only counterion and, in turn, for the comprehension of any superimposed environmental effect. Accordingly, as mentioned above, 1 and 2 are investigated to provide information on the structure of the photoisomerization path of contact ion pairs. The Cl(-) counterion (that results from the Schiff base protonation with HCl) is placed along the N-H axis as suggested by NMR simulations (38, 39) and to mimic the hydrogen bond of crystal structures of related compounds (40-43). Most importantly, to relate the behavior of the isolated ion pair with the behavior in solution, the N─Cl distance is fixed at 5.25 Å. This is the distance required to reproduce (computationally) the observed absorption maximum in solution (425 nm in methanol) (28) of the 5,6-dihydroretinal chromophore analogue of model 1. Although this relatively large distance [yielding an ≈4.25-Å-long N-H(+)─Cl(-) hydrogen-bonded salt bridge] does reflect the lack of the solvent dielectric constant in our “solvent” model, its value seems to be consistent with that estimated for retinylidene iminium salts in solution by Blatz (40) and Honing (44).
Below, we show that the interaction with the counterion leads to the emergence of a long segment of the S1 isomerization path featuring nearly degenerate S2 and S1 states and that may contain flat energy minima and transition structures. Furthermore, we show that the counterion may change the topology of the bottom of the S1 potential energy surface turning the TICT S1/S0 CI feature to a true S1 energy minimum. Such finding seems to be in line with the longer S1 lifetime observed for PSB11 and PSBT in the solvent environment.
Methodology
Consistently with previous work (5, 6), the presented excited state isomerization paths are computed in terms of MEPs carried out at the complete active space-self consistent field (CAS-SCF)/6-31G* level of theory, with an active space constituted by 10 electrons in the 10 π-orbitals of the conjugated backbones of 1 and 2 (45). Multiconfigurational second-order perturbation theory reevaluation of the energy carried out with the complete active space second-order perturbation theory (CASPT2) method (46) is then used to increase the accuracy of the path energy profile (see supporting information, which is published on the PNAS web site, for further details).
Results and Discussion
A schematic view of the S0, S1 and S2 energy profiles along the computed S1 branch of the photoisomerization path of 1′ (5, 6) is shown in Fig. 2A. Notice that the steepness of the initial part of the path is higher for the S2 covalent state (see also Fig. 1) (47). Because the position of the positive charge along the chain depends on the nature of the electronic state (i.e., it is located near the N-head for ground and covalent Ag-like states and near the C-tail for the charge transfer Bu-like state), a different stabilization is expected when a chloride is placed near the N-head (as in 1 and 2). In particular (see Fig. 2B), S1 is destabilized (i.e., because of a larger chloride/positive charge distance) and S2 is stabilized (i.e., because of a shorter counterion/positive charge distance) with respect to S0. This leads to a blue-shifted (S0 → S1) absorption maximum (interestingly, an ≈0.38-eV solvatochromic blue-shift has been estimated for retinal PSBs in solvent with respect to isolated conditions) (25) and, depending on the magnitude of the destabilization, to a S1/S2 crossing near FC. As a consequence, the energy profile along the S1 state may show regions with a covalent Ag-like character similar to that documented for neutral polyenes (47-49). Accordingly, point SP may feature a diradical rather than closed-shell structure. Eventually, a second crossing could arise [leading to an avoided crossing transition state (TS)] along the S1 path that will recover the initial Bu-like (charge transfer) character and end at the TICT state.
Fig. 2.
Schematic illustration of the S0, S1, and S2 energy profiles along the retinal S1 photoisomerization coordinate in vacuo (A) and in a tight ionic pair (B).
The same qualitative model predicts a different effect related to the change in magnitude of the charge transfer along the S1 path. In fact, according to previous computations (5, 6), only a partial (≈30%) positive charge translocation from the head to the tail occurs upon S0 → S1 vertical transition. The remaining charge still resides near the N-head, and only later (i.e., upon twisting of the reactive bond) migrates to the C-tail ultimately yielding a 100% charge transfer at the TICT state. Thus, chloride destabilization of the Bu-like charge transfer state will not occur with the same intensity along the S1 path. In particular, the model predicts an effect that is smaller at FC (i.e., the vertically excited structure) but higher at twisted points, resulting (see Fig. 2b) in a decrease of the slope of the S1 energy profile.
Finally, the same model can be used to predict the counterion effects on the S1-S0 energy gap at the TICT state. In fact, because of counterion destabilization of the Bu-like state, TICT states do not correspond anymore to the CI seen in isolated retinal chromophore models (Fig. 2A) but to true energy minima (TM in Fig. 2B).§§
The S1 isomerization paths computed for models 1 and 2 are reported in Figs. 3 and 4, respectively. It is immediately apparent that a behavior consistent with that predicted in Fig. 2 is demonstrated. In fact:
Fig. 3.
Computed MEPs along the central C4═C5 S1 photoisomerization coordinate (A) (for comparison, the corresponding path in vacuo is also reported; see dotted lines) (6), and C2═C3 S1 photoisomerization coordinate (B) of 1. Energy profiles have been scaled to match CASPT2 energies. The structures (geometrical parameters in Å and degrees) document the progression of the molecular structure along the coordinate. FC1 is the Franck-Condon structure, SP1 corresponds to the covalent-like S1 skeletal relaxed species, CI1 and TM1 are the TICT (≈90° twisted) S1/S0 CI funnel and twisted minimum, respectively, and TS11 and TS21 are the transition states located along the paths. Ionic- and covalent-like S1 surfaces (as resulting from the analysis of the CAS-SCF wave functions) are illustrated by a white and gray background, respectively. The bar diagrams give the S0 (black), S1 (light gray), and S2 (dark gray) CAS-SCF/6-31G* Mulliken charges for the twisting left and right moieties (the dotted line represents the border between the two moieties) of 1 along the illustrated photoisomerization paths.
Fig. 4.
Computed MEPs along the central C4═C5 S1 photoisomerization coordinate (A), and C2═C3 S1 photoisomerization coordinate (B) of 2 (for comparison, the corresponding paths in vacuo are also reported; see dotted lines) (7). Energy profiles have been scaled to match CASPT2 energies. The structures (geometrical parameters in Å and degrees) document the progression of the molecular structure along the coordinate. FC2 is the Franck-Condon structure, SP2 corresponds to the covalent-like S1 skeletal relaxed species, CI2 and TM2 are the TICT (≈90° twisted) S1/S0 CI funnel and twisted minimum, respectively, and TS12 and TS22 are the transition states located along the paths. Ionic- and covalent-like S1 surfaces (as resulting from the analysis of the CAS-SCF wave functions) are illustrated by a white and gray background, respectively. The bar diagrams give the S0 (black), S1 (light gray), and S2 (dark gray) CAS-SCF/6-31G* Mulliken charges for the twisting left and right moieties (the dotted line represents the border between the two moieties) of 2 along the illustrated photoisomerization paths.
Destabilization (due to the counterion) of the original charge transfer Bu-like state creates a marked blue-shifted absorption and an extended segment of the paths where the Bu- and Ag-like excited states are substantially degenerate (effectively an S1/S2 intersection space is created) (50). This extended degeneracy is a consequence of the tendency of the charge transfer and covalent states to cross and recross repeatedly along the path (as predicted in Fig. 2).
Along the S1/S2 segments, the assignment of the electronic structure of the path (including that of the original SPs) is substantially impossible. Indeed, because the two states are nearly degenerate, their wave functions arbitrarily mix. As a consequence, the amount of charge transfer or covalent character of the states cannot be defined (51). On the other hand, minimum energy structures (indicated as SP1 and SP2 for models 1 and 2, respectively) have been located.
Shallow energy barriers, controlling the S1 isomerization, have also been located along the S1/S2 reaction path segments that may play a role in the excited state isomerization.
Further evolution beyond the TSs leads to the splitting of the S1/S2 degeneracy. This reconstitutes the original charge transfer Bu-like character of the S1 state as in the isolated chromophore. Consistently, we find that, in all cases, the S1 isomerization path terminates at a TICT state. Notice that such a state corresponds to a peaked S1/S0 CI (CI1 and CI2) only when the isomerizing─C═C─double bond is the one closer to the anion. In contrast, when the isomerizing bond is the central one the TICT state corresponds to a real energy minimum (TM1 and TM2) in full agreement with the qualitative prediction in Fig. 2.
The chosen distance between the chloride and chromophore models (5.25 Å) seems to represent a borderline value for the selection of the electronic character of the S1 energy surface along the isomerization path. In fact, for values below this threshold we expect, because of enhanced destabilization of the charge transfer (Bu-like) state, a nondegenerate covalent (Ag-like) planar minimum SP and a higher-energy TS. On the other hand, at longer distances a charge transfer (Bu-like) SP is expected, similar to the situation found in vacuo. This information might be useful in the design of photodriven devices based on the cis-trans isomerization of PSBs (52). We stress here that these results strictly apply only to the isolated (i.e., gas-phase) ion pair or when this represents an acceptable model of the condensed phase.
The energy barriers computed for 2 (1.2 and 1.8 kcal/mol at TS22 and TS12, respectively) are of the same magnitude of the experimental value reported for the PSBT in methanol solution (1.7 kcal·mol-1) by El-Sayed and coworkers (14). Because of the minimal character of our model, the agreement may be coincidental (here, we tentatively extend our gas-phase results to the condensed phase environment). However, it is worth to notice that the computed barriers would provide a rationalization for the photoproduct distributions observed for PSB11 and PSBT in solution. In fact, whereas PSB11 gives PSBT as the only product, the latter generates a mixture of the PSB11 and PSB13 (i.e., the 13-cis) stereoisomers (16). Because the PSB11 model 1 displays a substantially barrierless path for the central double bond isomerization (see Fig. 3A) but a barrier (≈1.8 kcal·mol-1 at TS21) controlled path for the adjacent double bond isomerization, the first is expected to dominate consistently with PSBT as the major product. Because the isolated PSB11 (7) displays a preferential 11-cis bond photoisomerization, it appears that this is more an intrinsic property of the chromophore than a directional effect of the external charge. On the other hand, model 2 features similar barriers (1.8 and 1.2 kcal/mol) for the paths of Fig. 4 A and B consistently with production of a mixture of PSB11 and PSB13 stereoisomers.
The existence of extended energy plateaus (where S1 and S2 are degenerate) and energy barriers along the S1 isomerization paths of 1 and 2 may provide a rationale for the slower radiationless deactivation (i.e., picosecond vs. subpicosecond decay) and, in turn, for the smaller photoisomerization QY observed in solution as compared with the visual receptor Rh [in fact, the QY has been shown to increase when the deactivation time scale (actually, the product appearance time) decreases] (53). Because of the possible S1/S2 crossing and recrossing processes along the degenerate plateau and the effect of the shallow barriers, the chromophore evolution is slowed down with respect to the maximum possible speed that, presumably, one has in the protein. Notice that recent CASPT2//CAS-SCF/Amber quantum mechanics/molecular mechanics computations (54, 55) indicate that, because of a specific point charge distribution in the Rh cavity, the retinal chromophore “sees” an environment more similar to gas-phase than to that of its counterion. A similar effect has also been seen in bR (56). This effect leads to nondegenerate S1 and S2 surfaces, no barriers, and steeper paths, as computed for the photoisomerization of the isolated chromophore (5, 6). Therefore, the “unperturbed” (i.e., in vacuo; Fig. 2A) and “perturbed” (i.e., ion pair; Fig. 2B) retinal chromophore provides a crude model for the investigation of the photoisomerization in the protein and solution, respectively.
The central double bond twisting in 1 and 2 involves, according to our computations, population of TICT energy minima (TM1 and TM2), which should result in thermal equilibration on S1, delayed deactivation, and increased photoproduct appearance times. On the other hand, we have seen (see supporting information) that the S1-S0 energy gap at TM1 and TM2 can be tuned by moving the counterion along the chain: When the anion gets closer to the twisted bond, the S1-S0 energy gap decreases, and eventually, a S1/S0 CI emerges (this situation corresponds to the one depicted in Figs. 3B and 4B, where the twisting C═C bond is closer to the anion). Thus, a repositioning of the counterion could, at least partially, remove the S1-S0 gap. Strictly speaking, this conclusion applies only to the gas-phase ion pair. Nevertheless, if the solvent polarizability and oriented dipoles act as a virtual counterion (29, 30, 32), one may tentatively extend such a result to weakly bound ion pairs in a polar solvent.
Conclusions
We have provided computational evidence that a bare counterion strongly affects the energetic and photoreactivity of retinal chromophores. In particular, we have shown that a qualitative electrostatic model, when applied to the isomerization path of the isolated retinal chromophore (see Fig. 2A), can successfully predict the structural changes of the excited state energy surface. Namely, it is predicted that the charge transfer Bu-like state and the covalent Ag-like excited state may become degenerate and cross repeatedly (see Fig. 2B). The reported unbiased, state-of-the-art photoisomerization path computations on 1 and 2 demonstrate that such behavior is indeed found. We have also provided computational evidence in favor of the validity of the idea that ion pairs constitute zeroth-order models for the PSB11 and PSBT chromophores in solution. In particular, the computationally documented flat and S2/S1 degenerate potential energy region seems consistent with the slower decay observed in solution with respect to the more gas-phase-like protein environment (54, 55).
The two- vs. three-state model has been widely discussed in the past by various authors (5, 6, 17-22, 57). Specifically, the presence of an energy barrier was proposed to support a three-state model for the retinal chromophore (excited state) isomerization where both a Bu-like and an Ag-like state contributed, sequentially, to the description of the electronic character of the excited state reaction path (17, 18). Whereas in previous studies, carried out with the same level of theory and focusing on the isolated chromophore or on the protein-embedded chromophore, the results excluded such possibility pointing to a two-state reactivity model, this does not seem to be the case for the isolated ion pair. In fact, the documented existence of Bu- and Ag-like real crossings and nearly degenerate regions along the path support the idea that a three-state model may more closely represent the situation even in solution (recent ab initio QM/MM computations for the PSB11 in solution confirm a very close placement of the S1 and S2 states) (55), although in a different way than reported in the literature. Indeed, the Bu-like electronic character is recovered for the reaction path driving the decay to the ground state.
Supplementary Material
Acknowledgments
We thank Consorzio Interuniversitario per il Calcolo Automatico dell'Italia Nord Orientale and Consorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali for granted calculation time. This work was supported by the University of Bologna (Funds for Selected Research Topics), the Ministero dell'Istruzione, dell'Università e della Ricerca (funds ex 60%), and the Ministero dell'Università e della Ricerca Scientifica e Tecnologica Cofin 2003 (projects Reazioni stereoselettive promosse da nuovi sistemi catalitici e loro modellistica). M.O. is grateful for the support of the Human Frontier Science Program (Grant RG 0229/2000-M), Fondo per gli Investimenti della Ricerca di Base (FIRB) (Grant RBAU01EPMR), and the Università di Siena (Grant PAR 02/04). M.G. is grateful for the support of FIRB (Grant RBAU01L2HT).
Author contributions: F.B. and M.G. designed research; A.C. performed research; M.O. and M.G. analyzed data; and M.O. and M.G. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: bR, bacteriorhodopsin; FC, Franck-Condon; CI, conical intersection; CAS-SCF, complete active space-self consistent field; MEP, minimum energy path; PSB, protonated Schiff base; QY, quantum yield; Rh, rhodopsin; SP, stationary point; TICT, twisted intramolecular charge transfer; TM, true energy minima; TS, transition state.
Footnotes
Obviously, the residual β-ionone ring conjugation and its alkyl inductive effects are not accounted for in our models.
Because translocation of the counterion to the central position of the chromophore chain (i.e., above the central double bond of models 1 and 2) is predicted to leave the original energy gap unchanged (due to an equivalent stabilization of the charge transfer and covalent states), a systematic trend may be expected at the TICT points, with decreasing S1-S0 energy separation as decreasing the distance between the twisted central double bond and the counterion (see ref. 11).
References
- 1.Kandori, H., Shichida, Y. & Yoshizawa, T. (2001) Biochemistry (Moscow) 66, 1197-1209. [DOI] [PubMed] [Google Scholar]
- 2.Needleman, R. (1995) in CRC Handbook of Organic Photochemistry and Photobiology, eds. Horspool, W. M. & Song, P.-S. (CRC, Boca Raton, FL), pp. 1508-1515.
- 3.Wald, G. (1968) Science 162, 230-239. [DOI] [PubMed] [Google Scholar]
- 4.Mathies, R. & Lugtenburg, J. (2000) in Molecular Mechanism of Vision, eds. Stavenga, D. G., DeGrip, W. J. & Pugh, E. N. J. (Elsevier, New York), Vol. 3, pp. 55-90. [Google Scholar]
- 5.Garavelli, M., Vreven, T., Celani, P., Bernardi, F., Robb, M. A. & Olivucci, M. (1998) J. Am. Chem. Soc. 120, 1285-1288. [Google Scholar]
- 6.Gonzalez-Luque, R., Garavelli, M., Bernardi, F., Merchan, M., Robb, M. A. & Olivucci, M. (2000) Proc. Natl. Acad. Sci. USA 97, 9379-9384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.De Vico, L., Page, C. S., Garavelli, M., Bernardi, F., Basosi, R. & Olivucci, M. (2002) J. Am. Chem. Soc. 124, 4124-4134. [DOI] [PubMed] [Google Scholar]
- 8.Turro, N. J. (1991) Modern Molecular Photochemistry (Benjamin Cummings, Menlo Park, CA).
- 9.Gilbert, A. & Baggott, J. (1991) Essentials of Molecular Photochemistry (Blackwell, Oxford).
- 10.Garavelli, M., Negri, F. & Olivucci, M. (1999) J. Am. Chem. Soc. 121, 1023-1029. [Google Scholar]
- 11.Cembran, A., Bernardi, F., Olivucci, M. & Garavelli, M. (2004) J. Am. Chem. Soc. 126, 16018-16037. [DOI] [PubMed] [Google Scholar]
- 12.Hamm, P., Zurek, M., Roschinger, T., Patzelt, H., Oesterhelt, D. & Zinth, W. (1996) Chem. Phys. Lett. 263, 613-621. [Google Scholar]
- 13.Kandori, H., Sasabe, H., Nakanishi, K., Yoshizawa, T., Mizukami, T. & Shichida, Y. (1996) J. Am. Chem. Soc. 118, 1002-1005. [Google Scholar]
- 14.Logunov, S. L., Song, L. & ElSayed, M. A. (1996) J. Phys. Chem. 100, 18586-18591. [Google Scholar]
- 15.Kandori, H., Katsuta, Y., Ito, M. & Sasabe, H. (1995) J. Am. Chem. Soc. 117, 2669-2670. [Google Scholar]
- 16.Freedman, K. A. & Becker, R. S. (1986) J. Am. Chem. Soc. 108, 1245-1251. [Google Scholar]
- 17.Gai, F., Hasson, K. C., McDonald, J. C. & Anfinrud, P. A. (1998) Science 279, 1886-1891. [DOI] [PubMed] [Google Scholar]
- 18.Hasson, K. C., Gai, F. & Anfinrud, P. A. (1996) Proc. Natl. Acad. Sci. USA 93, 15124-15129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rosenfeld, T., Honig, B. & Ottolenghi, M. (1977) Pure Appl. Chem. 49, 341-351. [Google Scholar]
- 20.Hurley, J. B., Ebrey, T. G., Honig, B. & Ottolenghi, M. (1977) Nature 270, 540-542. [DOI] [PubMed] [Google Scholar]
- 21.Mathies, R. A., Cruz, C. H. B., Pollard, W. T. & Shank, C. V. (1988) Science 240, 777-779. [DOI] [PubMed] [Google Scholar]
- 22.Weiss, R. M. & Warshel, A. (1979) J. Am. Chem. Soc. 101, 6131-6133. [Google Scholar]
- 23.Froese, R. D. J., Komaromi, I., Byun, K. S. & Morokuma, K. (1997) Chem. Phys. Lett. 272, 335-340. [Google Scholar]
- 24.Buss, V., Kolster, K., Frank, T. & Vahrenhorst, R. (1998) Angew. Chem. Int. Ed. 37, 1893-1895. [Google Scholar]
- 25.Rajamani, R. & Gao, J. (2002) J. Comput. Chem. 23, 96-105. [DOI] [PubMed] [Google Scholar]
- 26.Terstegen, F. & Buss, V. (1998) J. Mol. Struct. 430, 209-218. [Google Scholar]
- 27.Albeck, A., Livnah, N., Gottlieb, H. & Sheves, M. (1992) J. Am. Chem. Soc. 114, 2400-2411. [Google Scholar]
- 28.Arnaboldi, M., Motto, M. G., Tsujimoto, K., Balogh-Nair, V. & Nakanishi, K. (1979) J. Am. Chem. Soc. 101, 7082-7084. [Google Scholar]
- 29.Warshel, A. (1976) Nature 260, 679-683. [DOI] [PubMed] [Google Scholar]
- 30.Warshel, A. (1979) J. Phys. Chem. 83, 1640-1652. [Google Scholar]
- 31.Houjou, H., Sakurai, M. & Inoue, Y. (1996) Chem. Lett. 1075-1076.
- 32.Houjou, H., Inoue, Y. & Sakurai, M. (1998) J. Am. Chem. Soc. 120, 4459-4470. [Google Scholar]
- 33.Warshel, A., Chu, Z. T. & Hwang, J. K. (1991) Chem. Phys. 158, 303-314. [Google Scholar]
- 34.Saam, J., Tajkhorshid, E., Hayashi, S. & Schulten, K. (2002) Biophys. J. 83, 3097-3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tavan, P. & Schulten, K. (1986) Biophys. J. 50, 81-89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tallent, J. R., Hyde, E. Q., Findsen, L. A., Fox, G. C. & Birge, R. R. (1992) J. Am. Chem. Soc. 114, 1581-1592. [Google Scholar]
- 37.Warshel, A. (1978) Proc. Natl. Acad. Sci. USA 75, 5250-5254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Han, M., DeDecker, B. S. & Smith, S. O. (1993) Biophys. J. 65, 899-906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Han, M. & Smith, S. O. (1995) Biochemistry 34, 1425-1432. [DOI] [PubMed] [Google Scholar]
- 40.Blatz, P. E., Mohler, J. H. & Navangul, H. V. (1972) Biochemistry 11, 848-855. [DOI] [PubMed] [Google Scholar]
- 41.Zelnik, R., Haraguchi, M., Matida, A. K., Lavie, D., Frolow, F. & Weis, A. L. (1986) J. Chem. Soc. Perkin Trans. 1 2051-2053.
- 42.Elia, G. R., Childs, R. F., Britten, J. F., Yang, D. S. C. & Santarsiero, B. D. (1996) Can. J. Chem. 74, 591-601. [Google Scholar]
- 43.Santarsiero, B., James, M., Mahendran, M. & Childs, R. F. (1990) J. Am. Chem. Soc. 112, 9416-9418. [Google Scholar]
- 44.Honig, B., Greenberg, A. D., Dinur, U. & Ebrey, T. G. (1976) Biochemistry 15, 4593-4599. [DOI] [PubMed] [Google Scholar]
- 45.Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Zakrzewski, V. G., Montgomery, J. A., Jr., Stratmann, R. E., Burant, J. C., et al. (1998) gaussian 98 (Gaussian, Pittsburgh), Revision A.6.
- 46.Andersson, K., Blomberg, M. R. A., Fülscher, M. P., Karlström, G., Lindh, R., Malmqvist, P.-Å., Neogrády, P., Olsen, J., Roos, B. O., Sadlej, A. J., et al. (1999) molcas 5.0 (Lund University, Lund).
- 47.Fuss, W., Haas, Y. & Zilberg, S. (2000) Chem. Phys. 259, 273-295. [Google Scholar]
- 48.Hudson, B. S., Kohler, B. E. & Schulten, K. (1982) in Excited States (Academic, New York), Vol. 6, pp. 1-99. [Google Scholar]
- 49.Robb, M. A., Garavelli, M., Olivucci, M. & Bernardi, F. (2000) Rev. Comput. Chem. 15, 87-146. [Google Scholar]
- 50.Migani, A., Sinicropi, A., Ferré, N., Cembran, A., Garavelli, M. & Olivucci, M. (2004) Faraday Discuss. Chem. Soc. 127, 179-191. [DOI] [PubMed] [Google Scholar]
- 51.Atchity, G. J., Xantheas, S. S. & Ruedenberg, K. (1991) J. Chem. Phys. 95, 1862-1876. [Google Scholar]
- 52.Ruiz, D. S., Migani, A., Pepi, A., Busi, E., Basosi, R., Latterini, L., Elisei, F., Fusi, S., Ponticelli, F., Zanirato, V. & Olivucci, M. (2004) J. Am. Chem. Soc. 126, 9349-9359. [DOI] [PubMed] [Google Scholar]
- 53.Kochendoerfer, G. G., Verdegem, J. E., van der Hoef, I., Lugtenburg, J. & Mathies, R. A. (1996) Biochemistry 35, 16230-16240. [DOI] [PubMed] [Google Scholar]
- 54.Ferré, N. & Olivucci, M. (2003) J. Am. Chem. Soc. 125, 6868-6869. [DOI] [PubMed] [Google Scholar]
- 55.Andruniów, T., Ferré, N. & Olivucci, M. (2004) Proc. Natl. Acad. Sci. USA 101, 17908-17913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Vreven, T. & Morokuma, K. (2003) Theor. Chem. Acc. 109, 125-132. [Google Scholar]
- 57.Warshel, A. & Chu, Z. T. (2001) J. Phys. Chem. A 105, 9857-9871. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.