Drug dependence in cancer is exploitable by optimally constructed treatment holidays

Abstract

Cancers with acquired resistance to targeted therapy can become simultaneously dependent upon the presence of that drug for survival, suggesting that intermittent therapy may slow resistance. However, relatively little is known about which tumors are likely to become dependent and how to schedule intermittent therapy optimally. Here, we characterized drug dependence across a panel of over 75 MAPK inhibitor (MAPKi) resistant BRAF^V600E mutant melanoma models at the population and single clone levels. Melanocytic differentiated models exhibited a much greater tendency to give rise to drug dependent progeny than their dedifferentiated counterparts. Mechanistically, acquired loss of microphthalmia-associated transcription factor (MITF) in differentiated melanoma models drives ERK-JunB-p21 signaling to enforce drug dependence. We identified the optimal scheduling of “drug holidays" using simple mathematical models which we validated across short and long timescales. Without detailed knowledge of tumor characteristics, we found that a simple adaptive therapy protocol can produce near-optimal outcomes using only measurements of total population size. Finally, a spatial agent-based model (ABM) demonstrated that optimal schedules derived from exponentially growing cells in culture remain nearly optimal in the context of tumor cell turnover and limited environmental carrying capacity. These findings may guide the implementation of improved evolution-inspired treatment strategies for drug dependent cancers.

Introduction

In unresectable or metastatic BRAF^V600E melanoma, patients are commonly treated in the first line with a combination of CTLA-4 and PD-1 immunotherapy, yielding 5-year survival rates over 50%¹. Patients who fail to respond, develop resistance to immunotherapy, or cannot remain on therapy because of toxicity commonly switch to MAPK inhibitor (MAPKi) therapy targeting BRAF plus MEK, further improving clinical outcomes^2,3. Unfortunately, the eventual emergence of resistance to MAPKi is a common outcome in these patients⁴. Interestingly, numerous reports have revealed that upon resistance to targeted BRAF plus MEK inhibitors, BRAF^V600E mutant melanomas may become dependent on these inhibitors for survival^5-9. Mechanistically, it was found that withdrawing MAPKi treatment in resistant tumors hyperactivates ERK1/2 through derepressed BRAF activity combined with the intrinsic and adaptive resistance mechanisms employed to survive treatment⁸. Overstimulation of ERK2 induces the AP-1 transcription factors JunB and FRA1, which were discovered to drive p21-dependent cell cycle arrest following MAPKi withdrawal in drug dependent models^7,9. These pioneering preclinical studies suggest that incorporating "drug holidays" might effectively slow disease progression in MAPKi-resistant patients. A large-scale phase 2 clinical trial compared continuous vs. intermittent BRAF plus MEK inhibition for patients with BRAF^V600E melanoma to further test this idea. Disappointingly, in this trial intermittent dosing did not improve the primary endpoint of progression-free survival in patients compared to continuous therapy¹⁰.

One potential explanation for the discrepancy between preclinical and clinical outcomes for intermittent therapy is our incomplete understanding of the factors contributing to the drug dependence phenotype. As a result, it is currently impossible to select patients whose tumors are most likely to develop drug dependence and are most likely to respond to intermittent therapy. BRAF^V600E mutant melanomas exhibit substantial phenotypic heterogeneity¹¹. These tumors are transcriptionally classified across a continuous spectrum of differentiation states, which include melanocytic, transitory, neural crest-like, and undifferentiated¹². A unique transcriptional signature defines each differentiation state but can be identified via relative levels of governing transcription factors (MITF, SOX10, and SOX9) and receptor tyrosine kinases (AXL, NGFR, and EGFR). Differentiated melanoma is considered more proliferative and is defined by MITF^high, SOX10^high, AXL^low, and EGFR^low. Undifferentiated melanoma has a transcriptional signature resembling epithelial-to-mesenchymal transition (EMT), is thought to be more invasive, and is defined by being MITF^low, SOX10^low, AXL^high, and EGFR^high. Although melanoma differentiation states are known to alter phenotypic responses to both immunotherapy^13-15 and targeted therapy^16-18, it is poorly understood if they contribute to drug dependence.

A second potential explanation for the clinical failure of intermittent therapy in patients with BRAF^V600E mutant melanoma is the possibility that the intermittent dosing schedule employed in the trial was suboptimal. This intermittent dosing schedule was adapted from studies performed in a preclinical immunodeficient mouse model with single-agent BRAF inhibition rather than the combination of BRAF plus MEK inhibition used in the trial^5,10. It is possible that an alternative scheduling approach may have worked better, though it is uncertain how such an approach would be designed.

Recently, there has been a movement toward evolution-informed therapies^19-21. These therapies aim to treat cancers (and other diseases) as heterogeneous, ecologically diverse, evolving populations²². For example, recent laboratory work in cancer and bacteria aims to take advantage of drug sensitivities that evolve due to the initial treatment, a phenomenon known as "collateral sensitivity"^23-26. More ecologically inspired therapies take advantage of the competition for resources between distinct clonal populations, hypothesizing that more treatable clones may win out in a competition for shared resources^27,28. Evolutionary game theory has also been leveraged to quantify and exploit distinct interactions between clonal populations^29-31. Still, much of the existing literature on evolution-based therapies is theoretical. It is unclear how an evolution-inspired therapy might optimally treat a cancer cell population that includes drug dependent cells.

In this work, we take an essential step toward understanding the frequency of drug dependence in BRAF^V600E mutant melanoma, the factors that determine a tumor's propensity to acquire drug dependence, and how intermittent therapeutic strategies may be optimally administered to mixed cancer cell populations to minimize population growth over time.

Results

Melanoma differentiation state correlates with drug dependence

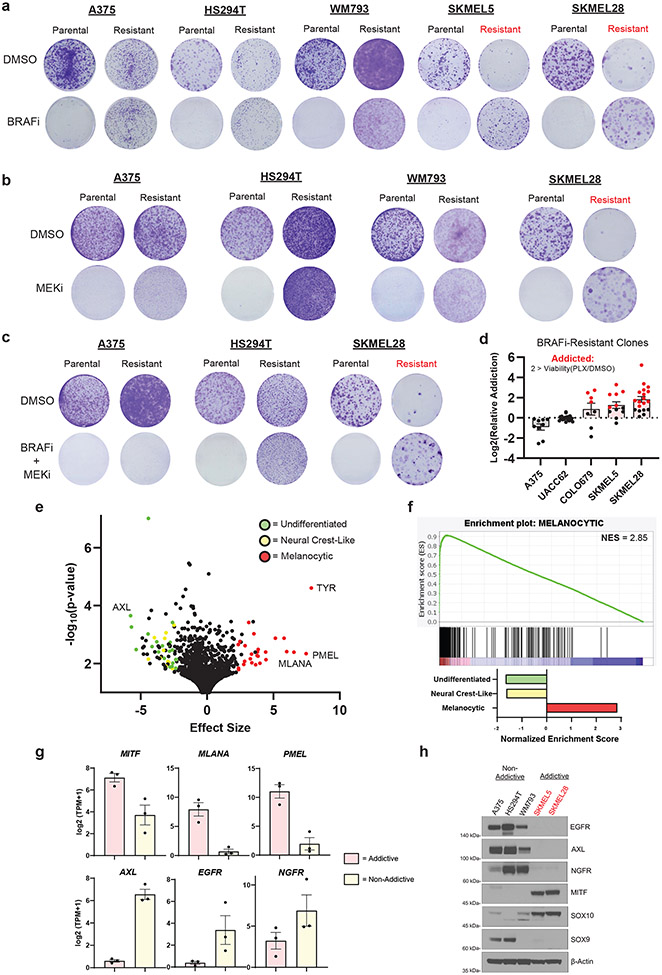
We began investigating drug dependence by deriving resistance to single agent or combination BRAF (PLX4720) and MEK (AZD6244) inhibition across BRAF^V600E mutant melanoma cell lines (Supplemental Fig. 1a). We chose A375, HS294T, WM793, SKMEL5, and SKMEL28 BRAF^V600E mutant models as they are well characterized in the literature^32,33 and the Cancer Dependency Map Project (DepMap)³⁴. We maintained a pooled population of each resistant model to preserve phenotypic diversity. Once the resistant populations began proliferating through high-dose MAPKi, we assessed their dependence on the treatment (Fig. 1a-1c). We defined drug dependence as the ability of MAPKi resistant cells to proliferate at least twice as rapidly in the presence of MAPKi than without it. We found mixed evidence of drug dependence across MAPKi resistant cell lines at the population level. Whereas SKMEL5 and SKMEL28 cell lines exhibited a strong drug dependence phenotype (Fig. 1a-1c), A375, HS294T, and WM793 cell lines did not (Fig. 1a-1c).

Fig 1: Melanocytic melanoma is primed for addiction to MAPK inhibition upon resistance.

a, Parental and PLX4720-resistant melanoma cell lines were seeded at a 1000 cells/mL concentration and treated every 72 hrs with DMSO or 3 μM PLX4720 (BRAFi). b, Parental and AZD6244-resistant melanoma cell lines were seeded at a 1000 cells/mL concentration and treated every 72 hrs DMSO or 3 μM AZD6244 (MEKi). c, Parental and PLX4720 + AZD6244-resistant melanoma cell lines were seeded at a 1000 cells/mL concentration and treated every 72 hrs DMSO or 3 μM PLX4270 + 3 μM AZD6244. a-c, Crystal violet staining was performed when the DMSO-treated parental group reached confluency. Drug dependent conditions are highlighted with red color. d, Individual PLX4720-resistant clones from the specified cell lines were subjected to identical experimental conditions as in a. Drug dependent clones are highlighted in red. Data are representative of the following number of biologically independent samples: A375 n = 9, UACC62 n = 19, COLO679 n = 8, SKMEL5 n = 12, and SKMEL28 n = 19. e, Two-class comparison of the DepMap Expression (Public 22Q4) dataset between ‘in-group’ addictive (COLO679, SKMEL5, and SKMEL28), and ‘out-group’ non-addictive (WM793, A375, and HS294T) cell lines. The top 100 differentially expressed genes involved in melanoma differentiation states are highlighted with the indicated color. Refer to methods for detailed statistical information f, GSEA results from the ranked gene list from e. Enrichment plot of the melanocytic differentiation gene set and associated statistics (top panel). Normalized enrichment scores of melanoma differentiation gene sets (bottom panel). g, DepMap Expression (Public 22Q4) comparison between addictive (COLO679, SKMEL5, and SKMEL28 (n = 3)) and non-addictive (WM793, A375, and HS294T (n = 3)) cell lines of the specified genes. h, Western blot of the indicated proteins in the parental melanoma cell lines. a-c, h, The data are representative of three biologically independent experiments (n = 3). a, g Data are presented as mean ± SEM.

Next, we sought to understand why specific BRAF^V600E mutant models gave rise to drug dependence. Initial experiments were performed with 12 pooled populations of resistant clones, and we hypothesized that drug dependent cell lines were selected for a unique drug resistance mechanism that dominated the pooled population and gave rise to drug dependence. To investigate this question, we quantified drug dependence across over 65 individual MAPKi resistant clones in A375, UACC62, COLO679, SKMEL5, and SKMEL28 BRAF^V600E mutant cell lines (Fig. 1d). We found no emergence of drug dependent clones in either A375 or UACC62 cell lines despite the fact that A375 cells are known to give rise to a multitude of resistance mechanisms³⁵ (Fig. 1d). Interestingly, we found almost all resistant clones from COLO679, SKMEL5, and SKMEL28 cell lines became MAPKi dependent upon resistance (Fig. 1d). These data suggest that no specific resistance mechanism is associated with drug dependence, a point observed by others⁹, and that rather, a difference in the baseline characteristics of the cell lines may contribute to the emergence of MAPKi dependence.

Next, we compared the drug-naive gene expression profiles of cell lines that give rise to resistant-dependent progeny (COLO679, SKMEL5, and SKMEL28) to those of cell lines that give rise to resistant-non-dependent progeny (A375, HS294T, and WM793) in DepMap. Strikingly, the top 100 differentially expressed genes (DEGs) between the former and latter groups were enriched in processes related to melanoma differentiation (Fig. 1e). Using melanoma differentiation gene sets previously identified¹², we found cell lines that give rise to drug resistant-dependent progeny are significantly enriched in the melanocytic gene expression signature (Fig. 1f). We confirmed that these cell lines were more differentiated at baseline, as defined by their increased expression of MITF, SOX10, MLANA, and PMEL and their decreased expression of EGFR, NGFR, AXL, and SOX9 (Fig. 1g-1h). Reciprocally, we found that cell lines that give rise to resistant-MAPKi non-dependent progeny exhibited neural crest-like and undifferentiated characteristics, as defined by their inverse expression of these markers (Fig 1g-1h). Together these data suggest that the drug-naive differentiation state of melanoma is tightly correlated with the ability to become MAPKi dependent upon resistance.

Dedifferentiated melanoma is resistant to ERK-induced cell cycle arrest

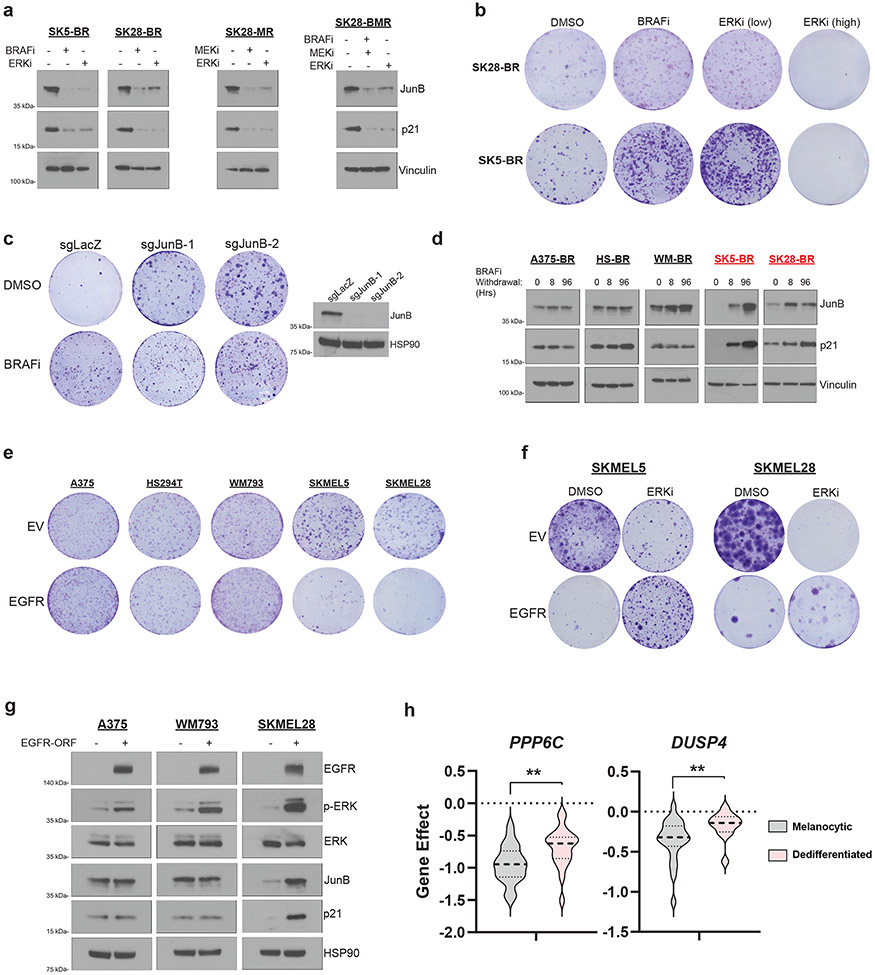
Drug dependence in BRAF^V600E melanoma is driven by the ERK2-JunB/FRA1-p21 signaling axis^6,7,9. Specifically, removing MAPKi from drug dependent cell lines hyperactivates ERK2, inhibiting cell cycle progression through JunB/FRA1-dependent accumulation of p21. We therefore hypothesized that melanoma cell differentiation state modulates ERK2-JunB/FRA1-p21 signaling. To investigate this, we first validated that the drug dependent, melanocytic, MAPKi resistant SKMEL5 and SKMEL28 models induce JunB-p21 in an ERK-dependent manner following the withdrawal of the drug (Fig. 2a). We found p21 accumulation in the drug dependent models to be associated with a significant accumulation of cells in G1 phase (Supplemental Fig. 1b) and an increase in β-galactosidase (β-gal) staining (Supplemental Fig. 1c). p21-dependent cell cycle arrest was reversed by low-dose ERK inhibitor (SCH772984) treatment, which rescued cell proliferation to levels equal to that observed in the context of BRAFi treatment (Fig. 2a-2b). Additionally, we confirmed that knockout of JunB with CRISPR/Cas9 rescued cell proliferation upon drug removal (Fig. 2c). Interestingly, we did not observe clear evidence of increased phosphorylation of FRA1 following drug removal in drug dependent models relative to drug non-dependent models (Supplemental Fig. 1d). Together these data confirm previous reports demonstrating that the ERK-JunB-p21 pathway drives cell cycle arrest in drug dependent models^7,9.

Fig 2: Dedifferentiated melanoma is resistant to ERK-induced cell cycle arrest.

a, Western blot of indicated proteins in SKMEL5-BRAFi Resistant (SK5-BR), SKMEL28- BRAFi Resistant (SK28-BR), -MEKi Resistant (SK28-MR), and -BRAFi + MEKi resistant (SK28-BMR) cell lines treated with the specified doses of DMSO, 3 μM PLX4720 (BRAFi), 3 μM AZD6244 (MEKi), or 50 nM SCH772984 (ERKi) for 96hrs. b, SK28-BR and SK5-BR cells were treated every 72hrs with the indicated drug. Crystal violet staining was performed when each cell line reached confluency. c, (Left) SK5-BR cells with two sgRNAs targeting JunB and one non-targeting control were treated with DMSO or 3 μM PLX4720 every 72hrs. Crystal violet staining was performed on day 14 following seeding. (Right) Western blot validation of JunB knockout. d, Western blot analysis of indicated proteins in BRAFi-resistant A375 (A375-BR), HS294T (HS-BR), WM793 (WM-BR), SK5-BR, and SK28-BR cell lines following BRAFi withdrawal for the specified time. Drug dependent models are highlighted in red. e, Melanoma cell lines with empty vector (EV) or EGFR-ORF construct were seeded in media that contained 2.5 ng/ml of EGF. Crystal violet staining was performed when each cell line's EV condition reached confluency. f, SKMEL5 and SKMEL28 EV and EGFR-ORF transduced cell lines treated with DMSO or 50 nM SCH772984 (ERKi), refreshed every 72hrs. Cells were seeded in media containing 2.5 ng/ml of EGF. g, Western blot analysis of melanoma cell lines transduced with EV or EGFR-ORF following 96 hrs of treatment with 5 ng/ml EGF. h, (Left) Analysis of PPP6C DepMap CRISPR gene score across melanocytic (n = 26) and dedifferentiated (n = 21) MAPK-mutant melanoma. (Right) Analysis of DUSP4 and gene effect across melanocytic (n = 23) and dedifferentiated (n = 12) MAPK-mutant melanoma using the DepMap RNAi (Achilles + DRIVE + Marcotte, DEMETER2) dataset. Two-tailed unpaired t-test, p-values; * <.05 and ** <.01 a-g, The data represent three independent experiments (n =3).

The non-dependent and dedifferentiated A375, HS294T, and WM793 resistant models did not induce JunB-p21 signaling (Fig. 2d), G1 arrest (Supplemental Fig. 1b), or β-gal staining (Supplemental Fig. 1c) following MAPKi withdrawal. Furthermore, A375, HS294T, and WM793 MAPKi resistant models demonstrated phospho-ERK rebound upon drug withdrawal and remained sensitive to SCH772984, suggesting that resistance in these models is indeed driven by ERK reactivation (Supplemental Fig. 1e-1f) rather than an ERK-independent mechanism³⁶. We next tested if dedifferentiated melanoma models were resistant to direct activation of ERK-JunB-p21 signaling. To activate ERK, wild-type epidermal growth factor receptor (EGFR) was ectopically expressed in A375, HS294T, WM793, SKMEL5, and SKMEL28 parental cell lines, and growth kinetics were measured. Compared to matched controls, melanocytic melanoma cell growth (SKMEL5 and SKMEL28) was significantly inhibited following EGFR expression (Fig. 2e). Interestingly, EGFR expression did not affect proliferation in dedifferentiated melanoma models (A375, HS294T, and WM793s) (Fig. 2e). The sensitivity to EGFR expression and activation of JunB-p21 in the melanocytic cell lines was rescued by low-dose SCH772984 treatment, confirming ERK hyperactivation-dependent growth inhibition (Fig. 2f and Supplemental Fig. 2a). Furthermore, hyperactivation of ERK via EGFR expression induced JunB-p21 in melanocytic but not dedifferentiated cells (Fig. 2g). Collectively, these data indicate that dedifferentiated melanoma models are resistant to JunB-p21 dependent cell cycle arrest following ERK hyperactivation.

To further understand the impact of differentiation state on sensitivity to ERK-JunB-p21 hyperactivation, we performed single sample Gene Set Enrichment Analysis (ssGSEA) on every BRAF- and NRAS-mutant melanoma cell line annotated in DepMap. Based on their transcriptomic profile, we classified lines as 'melanocytic' or 'dedifferentiated'. We included neural crest-like and undifferentiated differentiation states into the 'dedifferentiated' grouping. Interestingly, dedifferentiated melanoma was significantly more resistant to loss of dual specificity phosphatase 4 (DUSP4) and protein phosphatase 6 catalytic subunit (PPP6C) when compared to melanocytic melanoma (Fig. 2h). DUSP4 and PPP6C are phosphatases that negatively regulate ERK signaling in MAPK mutant melanoma. Genetic silencing of either gene leads to hyperactivation of ERK^37-39, which suggests that across a broad panel of models, melanocytic differentiated melanomas are sensitive to ERK hyperactivation while dedifferentiated melanomas are relatively resistant.

Manipulation of differentiation state modulates MAPKi dependence

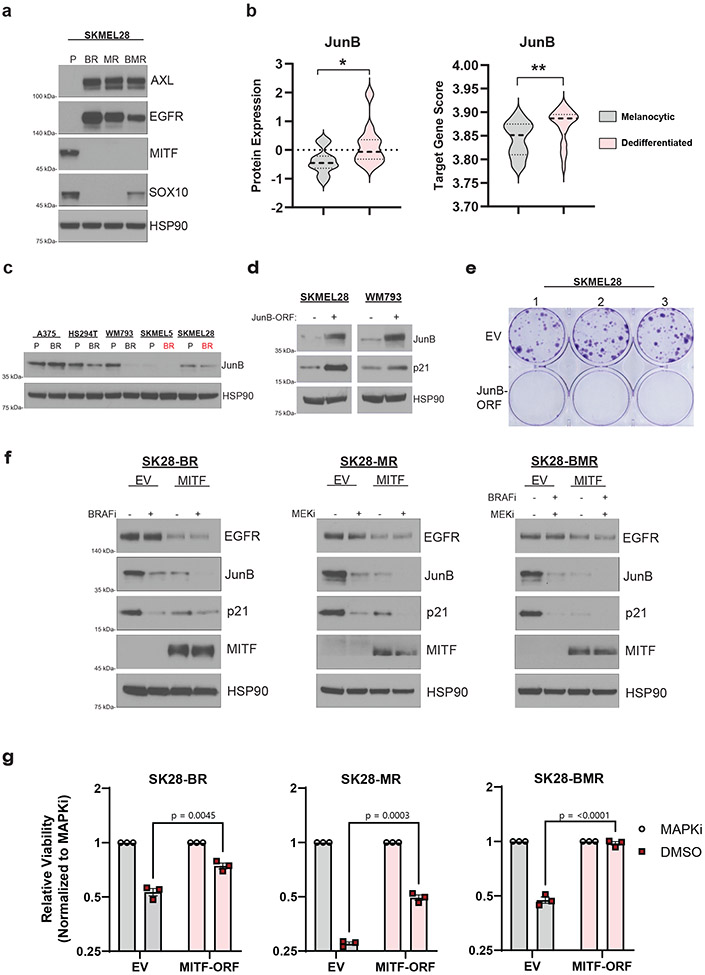
Next, we sought to investigate the mechanistic basis for the observed correlation between melanoma differentiation state and drug dependence. Melanocytic melanoma is defined by its expression of MITF and SOX10. Interestingly, it is known that acquired resistance to MAPKi can occur through dedifferentiation via the loss of MITF^16,40. Consistent with this concept, SKMEL28 cells dedifferentiated into a MITF^low, SOX10^low, EGFR^high, and AXL^high state upon MAPKi resistance (Fig. 3a), which has been previously characterized in this model¹⁶. We measured cell surface EGFR levels in the parental and BRAFi-resistant SKMEL28 cells and found no evidence of EGFR^high clones in the parental population (Supplemental Fig. 2b), suggesting that the evolution of resistance in this case may not involve selection for an intrinsically resistant, EGFR^high clone, but rather an adaptive dedifferentiation process, consistent with previous work^41-43.

Fig 3: Adaptive loss of MITF is a driver of drug dependence in MAPKi resistant melanoma.

a, Western blot analysis of the indicated proteins in parental (P), BRAFi-resistant (BR), MEKi-resistant (MR), or BRAFi- and MEKi-resistant (BMR) derivatives of SKMEL28 cells. b, (Left) JunB protein level analysis of melanocytic (n = 17) and dedifferentiated (n = 9) MAPK-mutant melanoma cell lines using the DepMap Proteomics dataset. (Right) JunB target gene expression score across melanocytic (n = 36) and dedifferentiated (n = 26) MAPK-mutant melanoma cell lines using the DepMap Expression (Public 22Q4) dataset. Two-tailed unpaired t-test, p-values; ** <.01. c, Western blot analysis of the indicated protein across the specified parental (P) and BRAFi-resistant (BR) cell lines. d, Western blot of SKMEL28 and WM793 parental cells transduced with an empty vector (EV) or JunB expression construction (MOI = 1). e, Clonogenic assay of SKMEL28 cells from experiment d. f, SKMEL28 BRAFi-resistant (SK28-BR), MEKi-resistant (SK28-MR), and BRAFi- and MEKi-resistant (SK28-BMR) cell lines were transduced with an empty (EV) or a full-length MITF (MITF) expression vector and treated with DMSO or the indicated MAPKi for 96 hrs before western blot analysis. g, SK28-BR, SK28-MR, and SK28-BMR were transduced with an empty (EV) or a full-length MITF (MITF-ORF) expression vector. After selection, the cell lines were seeded at 10,000 cells/ml and treated with DMSO or the specific MAPKi therapy to which they evolved resistance. The drug was refreshed every 72hrs. After 10 days, the cells were counted, and the MAPKi counts were normalized to the DMSO counts. Two-tailed unpaired t-test, p-values included in figure. Data are presented as mean ± SEM. a, c-g, These data represent three independent experiments (n =3).

As MAPKi forces dedifferentiation in the SKMEL28 model, it was surprising that these cells were drug dependent and sensitive to ERK-JunB-p21 signaling. We hypothesized the MAPKi resistant SKMEL28 cells retained molecular features of the melanocytic parental state which would explain their continued sensitivity to ERK hyperactivation. We first assessed JunB and FRA1 protein levels across all DepMap melanoma cell lines and observed a significant increase in levels of JunB, but not FRA1, protein in dedifferentiated melanoma compared to melanocytic melanoma cell lines (Fig. 3b and Supplemental Fig. 2c-2d). To understand if this increase in protein expression was correlated with JunB transcriptional activity, we created a JunB transcriptional signature by taking the top 100 upregulated genes from a recent JunB overexpression experiment in A375 melanoma cells⁴⁴. We performed ssGSEA with the JunB target gene signature on ~1400 available cell lines in DepMap to give each cell line a JunB target score and found a significant positive correlation between JunB mRNA with the JunB target gene score across all cell lines (Supplemental Fig. 2e), which suggests the target gene signature appropriately represents JunB transcriptional activity. We then identified that dedifferentiated melanoma has a transcriptional profile significantly enriched for JunB target genes compared to melanocytic melanoma (Fig. 3b). Interestingly, the MAPKi resistant SKMEL28 model maintained JunB protein levels equal to their drug-naive melanocytic parents (Fig. 3c). To test if melanocytic melanoma are specifically vulnerable to switching from a JunB^low to a JunB^high transcriptional state, we ectopically expressed JunB in the melanocytic SKMEL28 cell lines and found it robustly induced p21-acculmulation when compared to dedifferentiated WM793 cells overexpressing JunB (Fig. 3d). Accordingly, we found switching melanocytic melanoma from a JunB^low to a JunB^high transcriptional state inhibited cellular proliferation (Fig. 3e). This finding suggests that molecular characteristics of the drug-naïve differentiation state, including vulnerability to JunB induction, are retained following MAPKi resistance and contribute to drug dependence.

To determine whether something about the adaptive dedifferentiation process drives SKMEL28’s dependence on MAPKi, we ectopically expressed MITF and SOX10 in SKMEL28 models with acquired resistance to BRAF inhibitor monotherapy, MEK inhibitor monotherapy, or the combination. MITF activity was functionally confirmed by observing its inhibition of EGFR expression (Fig. 3f)⁴⁰. Following the withdrawal of MAPKi, MITF expression, but not SOX10 expression, entirely blocked the induction of the JunB-p21 signaling axis (Fig. 3f and Supplemental Fig. 2f). MITF expression also rescued the inhibited cell growth following the withdrawal of MAPKi in resistant SKMEL28 models (Fig. 3g). Together, these mechanistic data demonstrate that the loss of MITF in melanocytic differentiated melanomas facilitates not only dedifferentiation and drug resistance, but also JunB-p21 dependent growth inhibition following drug removal-induced ERK hyperactivation.

Drug holidays can minimize growth in drug dependent models

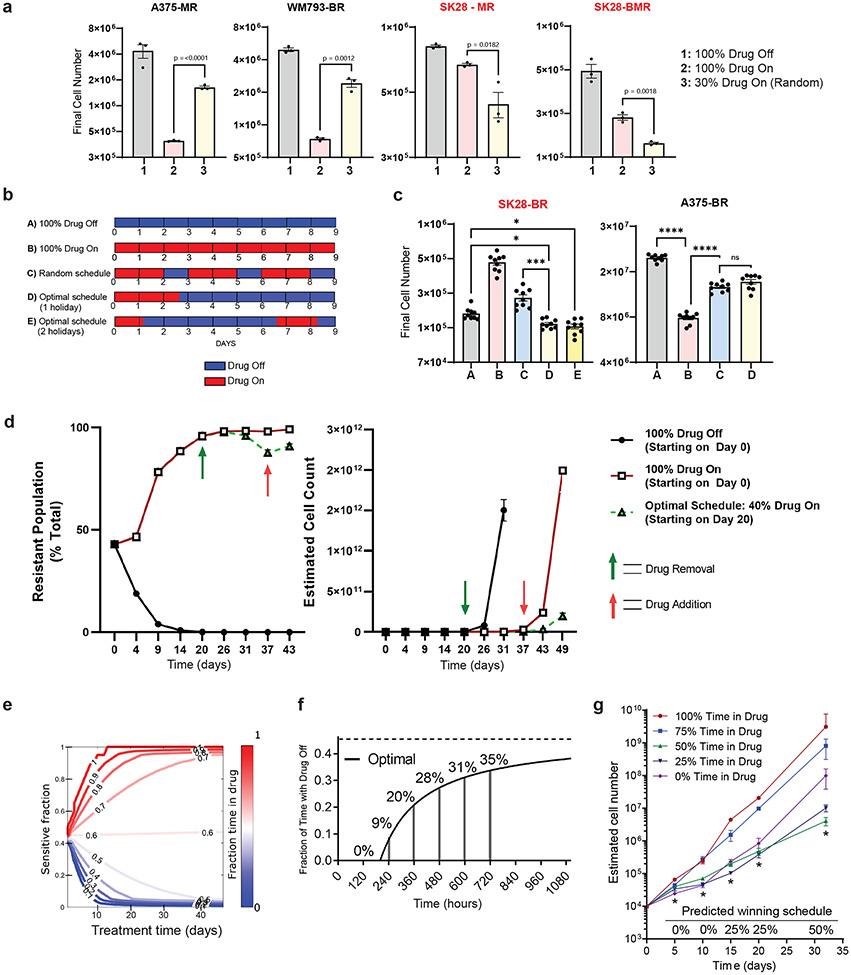
The poor growth of drug dependent-resistant cells in drug-free environments suggests that population growth may be minimized by incorporating drug-free "holidays“ into treatment schedules^7,45. However, heuristics guiding the proper design of optimal drug holiday regimens need to be clarified, as these may depend on the population's initial properties (e.g., the ratio of sensitive to resistant cells) and the growth characteristics of different subpopulations. To investigate this question, we seeded a growth experiment with a panel of BRAFi-resistant (BR), MEKi-resistant (MR) or BRAFi- and MEKi-resistant (BMR) BRAF^V600E melanoma cell lines. The resistant cells were mixed at a 9:1 ratio with their matched parental cells, loosely mimicking a progressing tumor that has become dominated by resistant cells. We then measured population size in each population after 9 days of exposure to one of 3 different treatment schedules: 1) 100% DMSO (“Drug Off”), 2) 100% MAPKi (“Drug On”), or 3) a random intermittent therapy in which MAPKi was applied 30% of the time. We found the periodic dosing schedules outperformed either the drug-free or the drug-only treatments, but not both. Specifically, total population size was minimized by schedule 3 in the populations containing drug dependent (SK28-MR and SK28-BMR) resistant subpopulations and by schedule 2 in the populations with non-dependent resistant subpopulations (A375-MR and WM793-BR) (Fig. 4a). To investigate whether a more judiciously chosen treatment schedule may further reduce growth, we considered a simple mathematical model of exponentially growing subpopulations (sensitive and resistant cells) whose growth rates depend on the environment (with or without drugs; see SI). On long timescales, we expect static treatments to eventually select the subpopulation with the highest growth rate in that environment. However, in the presence of time-dependent treatments that switch between drug and no-drug epochs, it may be possible to maintain a heterogeneous population of both cell types–each one suboptimal in one environment, optimal in the other–that leads to reduced growth of the total population. Indeed, in the limiting case where cells do not interact, a treatment strategy will maintain co-existing populations of both cell types when the drug treatments comprise a fraction ($f_{ON}$) of the total treatment time $T$,

$$f_{ON}=\frac{1}{1+\gamma }$$ (1)

where $\gamma \equiv \frac{k_{1,ON}-k_{2,ON}}{k_{2,OFF}-k_{1,0FF}}$ is a dimensionless parameter that depends only on the growth characteristics ($k_{i,ON}$ and $k_{i,OFF}$) of the different subpopulations; $k_{i,ON}$ ($k_{i,OFF}$) is the per capita growth rate of population $i$ in the presence (absence) of drug. The value of $k_{i,ON}$ depends on the concentration of drug, which we assume is fixed throughout the experiment (during all ON epochs). More generally, the parameter values ($k_{i,ON}$ and $k_{i,OFF}$) will depend on drug concentration, cell line, and culture conditions, but they are straightforward to measure in a given experiment. In our experiments, we choose a particular drug concentration up front and directly measure the growth parameters ($k_{i,ON}$ and $k_{i,OFF}$) for those conditions. We then assume these parameters remain fixed throughout the experiment (that is, $k_{i,ON}$ and $k_{i,OFF}$ are independent of time, but we relax these assumptions below). This simple model suggests that we can maintain population heterogeneity by incorporating drug-free epochs when $\gamma >0$; that is, when sensitive cells grow faster than resistant cells without the drug, while resistant cells grow faster than sensitive cells with the drug. In the long-term limit ($T\to \infty$), this treatment strategy yields a constant ratio of the different cell types, independent of the initial composition of the population. In addition, the growth of this heterogenous population is optimal; that is, it is smaller than growth in either static with-drug or static drug-free environments if

$$\begin{gathered} k_{2,ON}-k_{2,OFF}>0 \\ {k}_{1,OFF}-k_{1,ON}>0 \end{gathered}$$ (2)

Fig 4: Scheduling drug exposure can optimize growth inhibition in dependent cell lines.

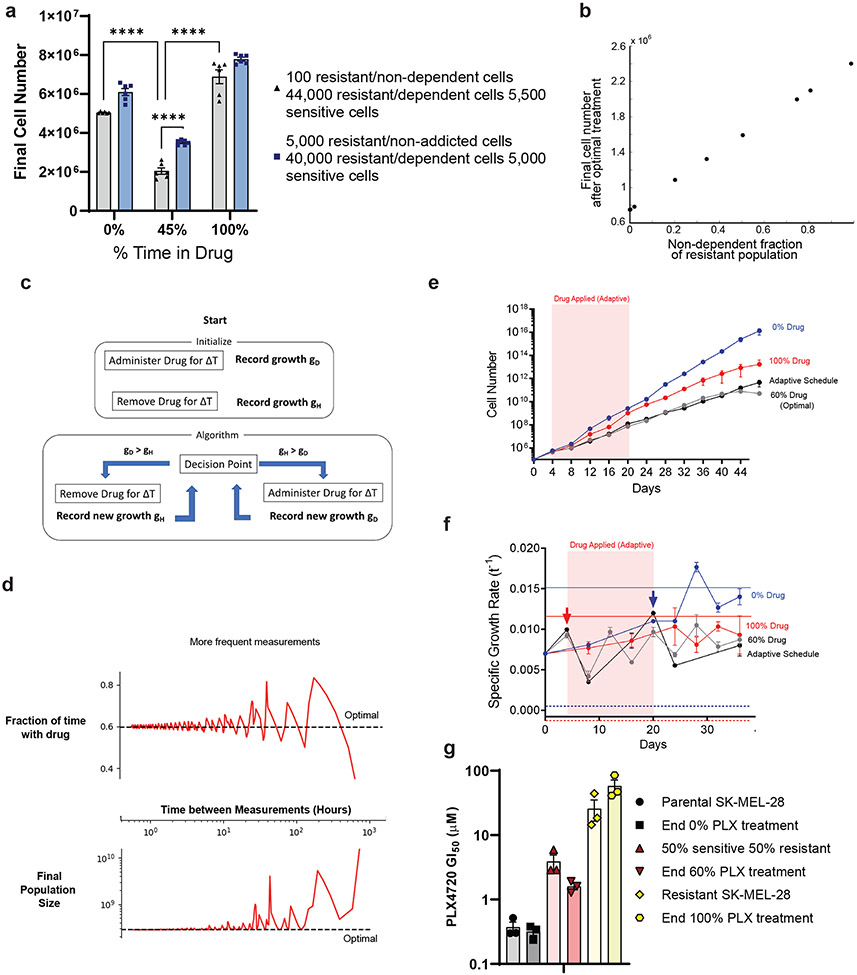
a, A375 MEKi-resistant (A375-MR), WM793 BRAFi-resistant (WM-BR), SKMEL28 MEKi-resistant (SK28-MR), and SKMEL28 BRAFi- and MEKi-resistant (SK28-BMR) cell lines were mixed with their parental counterparts at a ratio of 18000 resistant: 2000 parental cells and were treated with 1 μM of drug as described for 9 days before counting. Two-tailed unpaired t-test, p-values included in figure. Drug dependent cell lines are indicated by red font. b, Schematic of five different drug schedules: A) 100% Drug Off (DMSO), B) 100% Drug On (1 μM PLX4720), C) random periodic schedule, D) Optimal schedule up front, and E) Optimal schedule split into two epochs. c, (Left) 2,000 parental and 18,000 SKMEL28 BRAFi-resistant cells and (Right) 2,000 parental and 18,000 A375 BRAFi-resistant cells treated according to the schematic in b. On the ninth day, cells were counted. One-way ANOVA with Tukey’s multiple-comparison test. p-values; ns, not significant, * <.05, *** <.01, and **** <0.0001. d, The data represent nine independent experiments (n =9) d, SKMEL28 parental (EGFR^null) and BRAFi-resistant (EGFR^high) populations were mixed and treated with continuous DMSO (100% Drug Off) or continuous 1 μM PLX4720 (100% Drug On) for 20 days before splitting into the specified drug treatment schedule. (Left) Cell surface expression of EGFR^high populations on every split day of the experiment. (Right) Estimated cell counts on every split day of the experiment. e, Empirically constrained simulations show the optimal fraction of time exposed to the drug as the ratio of sensitive to drug dependent cells and total treatment time is varied. f, Algorithm predicted optimal percent drug holiday as total treatment time increases. The optimal asymptote is represented with a dashed line. g, A mixture of 2,500 parental and 7,500 SKMEL28 BRAFi-resistant cells were treated with the indicated schedule of 1 μM PLX4720 24 hours later. The algorithm-predicted optimal ('winning') schedule is indicated along the x-axis, and time points that conform to predicted values are indicated with an asterisk. a, d, g These data represent three independent experiments (n =3). a, c-d, g Data are presented as mean ± SEM.

Equation (2) says that one cell type (i=2) must grow faster with drug than without, while the other cell type (i=1) must grow faster without a drug than with; these are the precise conditions that define drug dependent resistance. In summary, in this simple model, one can maintain heterogeneity as long as sensitive cells are favored during drug-free epochs. Furthermore, that heterogeneity leads to minimal growth only when the resistant cells grow faster with the drug than without (i.e. when they are drug dependent). Importantly, the model predicts an optimal treatment that is highly dependent on (experimentally accessible) growth rates, which depend on the cell line, drug concentration, and environment.

Equation (1), along with experimentally measured growth rates of parental and resistant lines with and without drug, predicts an optimal schedule with $f_{ON}=0.29$ (holiday 71 percent of the time) for the SKMEL28 (drug dependent) population and $f_{ON}=1$ (drug-only) for the A375 (non-dependent) population. Based on these predictions, we experimentally compared five different treatment schedules: A) 100% Drug Off ($f_{ON}=0$); B) 100% Drug On ($f_{ON}=1$); C) a random schedule; D) an optimal schedule with $f_{ON}\approx 0.29$ where drug was given for 2.6 days on followed by 6.4 days off; and E) an optimal schedule with $f_{ON}\approx 0.29$ where drug was given for 1.1 days on, 5.5 days off, 1.5 days on, and 0.9 days off. Consistent with predictions of the model, the optimal schedules (D and E) outperformed other treatments in the populations with drug dependent resistance (SK28-BR) but were outperformed (by schedule B) in the populations with non-dependent resistance (A375-BR) (Fig. 4c). We found no significant difference between schedules D-E, consistent with the fact that schedules should depend only on $f_{ON}$ (not the specific timing of the holidays) when subpopulations are acting approximately independently.

To further understand the effectiveness of optimal therapy scheduling at forestalling resistance, we created a mixed population of resistant-dependent (~43%) and parental (~57%) SKMEL28 cells. Long-term population dynamics were tracked by cell surface expression of EGFR, with EGFR^high status indicating the dependent-resistant population (Fig. 4d, left). Following 20 days of continuous PLX4720 treatment, the population was ~95% resistant-dependent cells (Fig. 4d, left), and at this point, we split this population into treatment groups that used 40% drug (optimal schedule, $f_{ON}=0.4$) or 100% drug ($f_{ON}=1$). The optimal schedule group significantly slowed population growth (Fig. 4d, right).

The optimal schedule is dependent on the treatment length

On sufficiently long time horizons, we expect that the optimal treatment will be independent of the initial composition of the tumor. However, many real-world applications will likely involve finite-time treatments where these asymptotic results are invalid. Under these conditions (see SI), the growth of the population will be minimized when

$$f_{ON}=\frac{1}{1+\gamma }+\frac{1}{T}\log \left(\frac{n_1(k_{1,OFF}-k_{1,ON})}{n_2(k_{2,ON}-k_{2,OFF})}\right)$$ (3)

Equation (3) reduces to equation (1) when $T\to \infty$. However, on shorter time horizons, the optimal treatment will depend on the total treatment duration $T$ (Fig. 4e). To test this prediction experimentally, we plated a mixed population of 10⁵ cells comprised of 25 percent resistant-dependent SKMEL28 cells. The cells were treated with one of five schedules with drug holidays ranging from 0 (static with-drug treatment) to 100 percent (static drug-free treatment). The treatment schedules were broken into 5-day blocks so that the cells could be counted every 5 days for an indeterminate length of time and remain on schedule. Based on the results of the model (Fig. 4f), we hypothesized that the treatment performing optimally would vary over time, with static drug treatments minimizing growth at early times while treatments with increasing drug holidays (asymptotically approaching the long-time optimal of approximately 45 percent drug holiday, $f_{ON}=0.55$) minimizing growth on longer timescales.

Indeed, experiments confirmed that growth was initially (e.g., days 5 and 10) minimized in the static drug (PLX4720) treatment (Fig. 4g). However, by day 15, the treatment with 25 percent holiday ($f_{ON}=0.75$) was optimal, while the treatment with 50 percent drug holiday–which most closely corresponds to the predicted long-time optimum–led to minimal growth by day 30. These results underscore the notion that the optimal strategy for drug holidays will initially vary over time–a phenomenon tied to the transient behavior of the population as it approaches a steady state composition–but for sufficiently long treatment periods approaches an optimum that is independent of the initial population composition.

Presence of non-dependent resistant cells does not alter optimality

Because parental melanoma tumors potentially give rise to both drug dependent and non-dependent resistant lineages, we asked how the presence of both resistance types would impact the optimal treatment schedule. To answer this question, we treated two different mixed populations containing drug sensitive, drug resistant-dependent, and drug resistant-non-dependent derivatives of UACC62 with one of three treatments: 1) static drug-free treatment, 2) static treatment with PLX4720, or 3) a model-inspired (approximately) optimal treatment with $f_{ON}=0.45$ (55 percent of the time in drug holiday). The two mixed populations comprised approximately constant ratios of drug sensitive to drug dependent resistant cells. However, one population initially contained 0.2 percent non-dependent resistant cells and the other 10 percent non-dependent resistant cells. In both populations, the model-inspired therapy– which contains drug holidays calculated without knowledge of the non-dependent populations – significantly outperformed the static therapies (Fig. 5a), as one might intuitively expect. However, the population sizes become much larger in populations that started with more non-dependent resistant cells, consistent with predictions of the model (Fig. 5b). This result highlights a more general principle: in cases where non-dependent resistant cells grow at similar rates in the presence and absence of drug, these cells are not expected to alter the choice of optimal therapy. However, their presence can significantly limit the utility of intermittent therapy in cases where these cells grow faster than the average growth rate of the drug holiday-optimized population of sensitive and drug dependent cells.

Fig 5: Optimal scheduling can be approximated with a mixed cell population of unknown growth rates.

a, A mixture of the specified ratios of UACC62 cells were treated with 1 μM PLX4720 at the indicated schedules 24 hours later. Cells were counted on day 9. One-way ANOVA with Tukey’s multiple-comparison test. p-values; **** <0.0001. The data represent six independent experiments (n =6) b, Using empirically constrained simulations, we plot the total population count as the fraction of non-dependent resistant cells varying from 0% to 100% of the resistant population. c, A cartoon schematic of the blind adaptive therapy algorithm. d, (Top) Using empirically measured growth rates, we simulate the fraction of time spent exposed to a drug following the blind adaptive therapy (solid red line) and compare it to the true optimal (dotted black line) as a function of how frequently population-level growth rates can be measured. (Bottom) The same simulations as above but now showing the final cell count of the population (solid red line) is compared to what is projected from the optimal schedule (black dotted line). e, Results of the blind adaptive therapy experiment. Cell counts over time were recorded, and the shaded red region highlights the time the drug was applied. f, Growth rates for each schedule at the indicated time points. The growth rate of parental SKMEL28 cells in DMSO (solid blue line) and BRAFi (blue dashed line) is indicated. Arrows indicate time points when the treatment condition was changed due to the measurement. The growth rate of PLX-resistant pooled SKMEL28 cells in 1 μM PLX4720 (solid red line), and DMSO (red dashed line) is indicated. The red region highlights the period the drug was applied. g, The PLX4720 GI₅₀ values of the ending cell populations in e compared to the PLX4720 GI₅₀ values of the indicated known mixtures of parental and resistant SKMEL28 cells. e, g, These data represent three independent experiments (n =3). a, e-g, Data are presented as mean ± SEM.

Adaptive therapy based on population size approximates optimal schedule

In a clinical setting, detailed measurements of growth parameters for different cell types is not typically possible. Therefore, we attempted to develop an adaptive therapy method that approximates the optimal holiday schedule without detailed growth rate information about the individual subpopulations (Fig. 5c, Methods). Briefly, we began by administering the drug for one treatment window, followed by the removal of the drug for one treatment window. The growth rates of each treatment window were recorded, and the treatment that led to a lower growth rate was then continued. This treatment protocol was continued until the growth rate of the population surpassed that of the opposite treatment type, as recorded by the most recent treatment window of that type. At that time, the treatment is switched. This process continued until the treatment ended.

We tested the performance of this approach computationally using empirically measured growth rates from the previous experiments (Fig. 5d). Simulations revealed that the performance of the blind adaptive therapy approaches that of true optimal therapy, provided that one can make sufficiently frequent measurements of total population size. To test this approach experimentally, we established a mixed population comprised of sensitive and resistant dependent SKMEL28 cells and exposed replicate populations to one of four drug schedules: 1) static no-drug schedule ($f_{ON}=0$), 2) static PLX4720 (constant drug) schedule ($f_{ON}=1$), 3) the optimal schedule ($f_{ON}=0.6$, 40 percent drug holiday) based on measured growth rates of the different cell populations, and 4) the adaptive schedule described above. Treatments were applied in 4-day blocks for a total of 48 days. As predicted by the model, the optimal therapy (treatment 3) performed considerably better than the two static therapies. In addition, the adaptive therapy and the calculated optimal schedule performed almost identically over 48 days (Fig. 5e-5f). To determine if we had achieved the goal of maintaining population heterogeneity, we took the final cell population from each schedule and measured the GI₅₀ of each population to PLX4720 (Fig. 5g). As a benchmark, we compared these GI₅₀ values to those of freshly made mixtures containing 100% sensitive, 50% sensitive/50% resistant, and 100% resistant populations. We found that the populations treated with 0% PLX4720 (100% PLX4720) exhibited GI₅₀ values similar to those of fully sensitive (resistant) populations, consistent with the prediction that static therapies eventually lead to homogeneous populations (Fig. 5g, blue and red bars). By contrast, populations treated with the optimal schedule exhibited GI₅₀ values similar to, but slightly smaller than, those of an equally mixed population of 50% sensitive/50% resistant cells (Fig. 5g, gray bars). These results suggest that reaching near-optimal treatment outcomes with incomplete population dynamics information may be possible.

Well-mixed model approximates an agent-based model

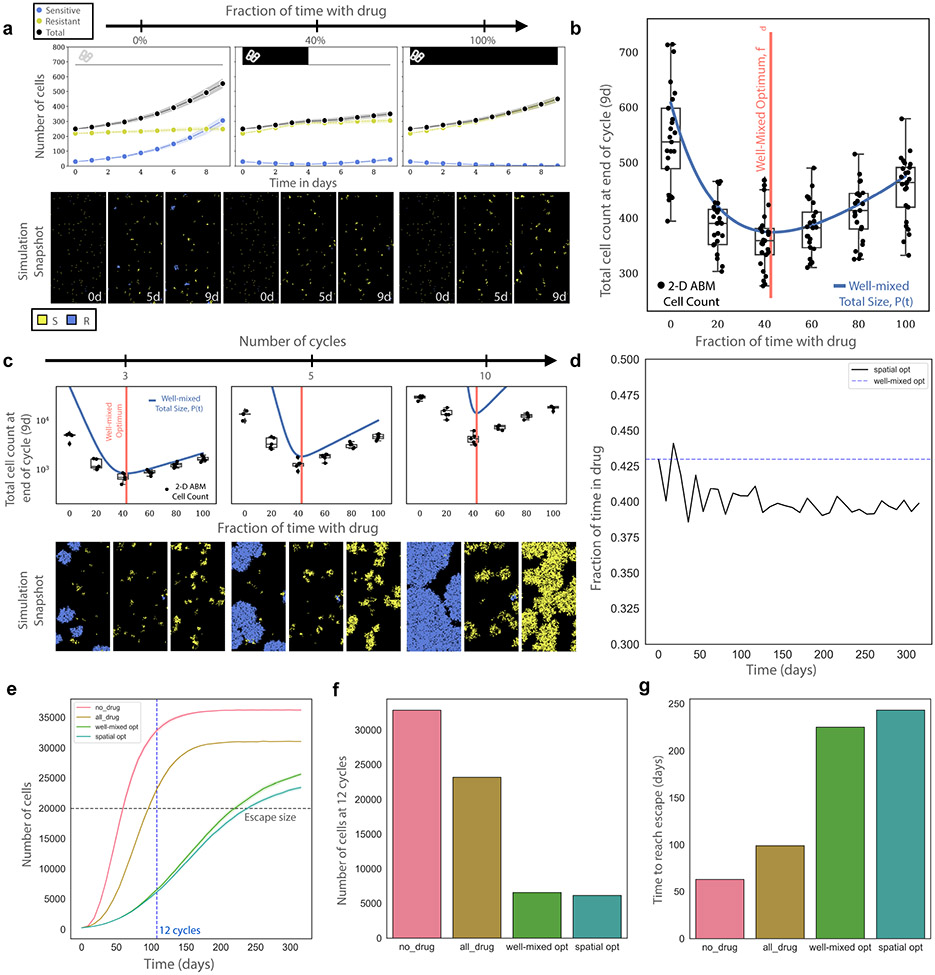
The “well-mixed” model above neglects complicating features—for example, stochasticity, cell death/turnover, and spatial competition—that may be necessary to predict scheduling in a more realistic in vivo environment. To explore how these features impact our predictions, we implemented a 2-D, on-lattice, agent-based model (ABM, Methods). We began with a sparsely seeded, mixed population of sensitive and drug dependent resistant cells. Each population divides with an effective proliferation rate informed by their birth rate (determined by in vitro experiments) and a constant death rate to simulate in vivo cell turnover. We then simulated a variety of drug holiday schedules (Fig. 6a-6b). Simulations that employed a drug holiday similar to the predicted optimal led to smaller tumor population at the end of a 9-day simulated treatment (Fig. 6b), consistent with predictions of the simpler model. The success of the simple model is not altogether unexpected, because it predicts that the optimal $f_{ON}$ depends only on a ratio of growth rate differences, not the absolute values. As a result, environmental factors that impact all cell types approximately equally—for example, by scaling all growth rates by a constant factor—will not change the predicted optimal.

Fig 6: Optimal schedules derived from a well-mixed model approximate those derived from an agent-based model incorporating cell turnover, spatial competition, and carrying capacity.

a, Representative ABM simulations depicting 0% drug treatment, 40% drug treatment, and 100% drug treatment schedules for one drug cycle, or 9 days. Blue cells (lines) represent sensitive cells while yellow cells (lines) represent resistant and dependent cells. Cell death/turnover is equal for all cell types and drug concentrations and is equal to half the sensitive populations drug-free growth rate. b, Similar to a but with 25 replicates and additional treatment schedules (0, 20, 40, 60, 80, 100 percent time in drug). ABM simulations (black dots, box and whisker plots) show broad agreement with the well-mixed model experimental model prediction (blue line). The predicted well-mixed optimal (red vertical line) captures the simulations well. Data is presented as such; mean is center solid line and the 95% confidence interval is the shaded band above and below the mean c, Simulations similar to a and b, but the simulations continue for 3, 5, and 10 cycles of treatment (each cycle is one 9-day schedule). d, Using the data from c we calculate the optimal treatment after each 9 day treatment schedule and how it varies as the populations compete for space. This result is deemed the “spatial optimal.” e, Simulations comparing the total population size over time using the well-mixed optimal, spatial optimal, 100% drug, and 0% drug. f, Comparison of total cells after 12 cycles (blue dotted line in e, the last cycle before the worst condition reaches carrying capacity) reveals an ~8% decrease in cell count of the spatial optimal in comparison to the well-mixed optimal. g, Comparison of the time to reach treatment escape (grey horizontal line in e) reveals the spatial optimal extends treatment success for an additional ~8%. b, c, Box plot elements are defined as follows: centre line, median; box limits, upper and lower quartiles; whiskers, 1.5 × interquartile range.

We next investigated simulations over longer treatment periods, where cell crowding may introduce non-intuitive effects. We repeated the previous experiment but administered treatment for three, five and ten 9-day cycles. We found that the optimal treatment schedule remains optimal across all treatment lengths, but the final tumor burdens predicted by the well-mixed model become increasingly inaccurate (Fig. 6c). Deviations between the ABM and well-mixed model appear well before the tumor reaches carrying capacity (Supplemental Fig. 3a), suggesting the effect is due to local cell crowding, similar to what occurs in other tumor models⁴⁶.

During each nine-day optimal cycle, the population experiences one epoch in drug and one without. As a result, each nine-day cycle allows us to extract effective growth rates ($k_{i,ON}$ and $k_{i,OFF}$) for the previous period; with these measurements, we can therefore calculate a (now time-dependent) optimal drug dose $f_{ON}(t)$ for each nine-day period (Fig. 6d, black line). As expected, the time-dependent optimal initially agrees with the well-mixed optimal (Fig. 6d, blue line), but over time the optimal requires less drug than predicted by the simple model (Supplemental Fig. 3b). We confirmed that the optimal, $f_{ON}(t)$, calculated in this way indeed out-performs the static, well-mixed optimal (Fig. 6e-g). To compare performance between optimal treatments prescribed by the well-mixed and spatial models, we compared total population sizes across treatment arms after twelve cycles (108 days, the last cycle before carrying capacity is reached in the largest population; Fig. 6e, blue vertical line). In addition, we measured how long each treatment arm contained the population below a given threshold (“escape size”) for the first time (Fig. 6e, grey horizontal line). Across both tests, we found that the spatial optimal out-performed the well-mixed optimal by approximately 8% (Fig. 6f-g).

Discussion

Our work complements a broad set of recent studies ranging from purely theoretical evolutionary therapy to clinical trials which have attempted to harness intermittent drug treatment schedules. Importantly, it demonstrates that while drug holidays can improve tumor growth control, they must be designed and implemented using strategies like the adaptive treatment regimen described here, which account for the evolutionary dynamics of cells within the tumor—which harbor potentially different drug response and dependency characteristics—as well as the variation in these properties across individual patients. Additionally, this work suggests that the heterogeneity of differentiation states found in melanoma tumors is a predictive and mechanistic factor associated with drug dependence in MAPK mutant melanoma. The lack of incorporation of these elements may be at least partially responsible for the failure of recent trials regarding intermittent therapy^10,47. Together these findings support melanocytic tumors as prime candidates for optimized, intermittent MAPKi therapy to slow disease progression when other options are unavailable.

Interestingly, MITF loss has previously been described in the literature as a contributing factor to MAPKi addiction in melanoma models⁹. In that report, it was discovered that withdrawal of MAPKi from drug dependent models activated ERK2-JunB, which led to subsequent loss of MITF protein and cell cycle arrest. In this scenario, drug resistance emerging in melanocytic differentiated models that have remained in this differentiation state during the acquisition of resistance is associated with drug removal-induced MITF loss. Indeed, we observed this proposed mechanism in BRAFi resistant SKMEL5 cells upon withdrawal of MAPKi (Supplemental Fig. 2g). In the current study, we describe a distinct scenario where melanocytic differentiated melanoma cells undergo MITF loss and associated dedifferentiation during the acquisition of drug resistance, and we show that such cells retain sensitivity to ERK hyperactivation-induced JunB-p21 activation (Supplemental Fig. 4). Both cases underscore the notion that MITF is a key regulator of the drug dependence phenotype, supporting our discovery that melanocytic melanoma tumors are primed for MAPKi-addiction.

In order to capture more potential features of in vitro evolution such as stochasticity, cell death/turnover, spatial competition, and carrying capacity, we translated our system into a 2-D, on-lattice ABM. We found, somewhat surprisingly, that predictions from the simple model were largely robust against these additional complexities. Specifically, we observed that cell death/turnover did not affect the optimal schedule, as long as the intrinsic turnover rate was approximately equal for each cell type. In addition, the well-mixed model perfectly recapitulated the results from the spatial simulations at low densities, but at large densities, we observed an asymmetric impact on growth rates that led to modest changes in the optimal treatment schedule—a schedule we could infer by updating the estimates of cell growth rates over time. This time-dependent ABM optimal schedule led to an approximately 8% decrease in tumor size as well as 8% increase in population escape time over the well-mixed optimal. Taken together, these results suggest that while spatial effects can play an important role in fine-tuning the optimal schedule, the well-mixed model remains a surprisingly accurate approximation for our experimental system.

It is also important to address several potential limitations in our approach. For example, our models ignored the potential impacts on drug resistance from the host environment, specific resistance mutations, and ecological interactions within the tumor. In addition, we ignore the role of de novo mutations in evolutionary adaptation, which would likely play a role in informing the optimal treatment, at least in small populations (see Supplemental Information for a brief discussion on mutation rates). However, even in this well-controlled laboratory setting, calculating an optimal schedule is challenging. As a result, it is notable that such a simple mathematical model captures the main qualitative features necessary to define optimal therapy schedules. Further, it is significant that empirical adaptive scheduling can produce near-optimal results when frequent tumor growth surveillance is performed, a concept that is becoming increasingly feasible with the broad adoption of minimally invasive, blood-based monitoring of circulating tumor DNA levels. To be clear, the model in its current form is not meant to be directly applicable in the clinic. But its surprising success in in vitro an in silico experiments—which already include numerous biological complexities neglected in the model—give hope that similarly simple “minimal” models may aid in understanding which melanoma tumors are primed for drug dependence and how one might optimally treat such tumors in realistic clinical scenarios. Finally, although holiday-based schedules cannot entirely prevent disease progression, they are a promising therapeutic approach to slow progression that may eventually lead to improved treatment outcomes for a subset of patients with drug dependent metastatic disease.

Methods

Cell lines

A375, COLO679, UACC-62, WM793, HS294T, SKMEL5, and SKMEL28 cells were grown in RPMI 1640 (Life Technologies Corporation, Carlsbad, CA) supplemented with 10% fetal bovine serum (Sigma-Aldrich Corporation, St. Louis, MO) and 1% penicillin/streptomycin (Life Technologies Corporation). SKMEL28 cell lines were obtained from L. Garraway (Harvard University, Dana-Farber Cancer Institute). All other cell lines were purchased from the American Type Culture Collection. All lines were submitted to STR profiling by the Duke University DNA Analysis Facility to confirm their authenticity. The cells routinely tested negative for mycoplasm with the MycoAlert^™ Mycoplasma Detection Kit (Lonza # LT07-318).

Chemicals

All inhibitors were purchased from Selleck Chemicals (Houston, TX) and prepared at 100 mM stock solutions in DMSO.

GI₅₀ assay

Wherever GI₅₀ values of specific inhibitors are indicated, they were determined as follows. Cells were seeded at 5,000 cells/well in 96-well plates in normal tissue culture conditions. After a 24-hour incubation, diluent (typically DMSO) or concentrated 10-fold dilutions of the indicated inhibitors (at 1:1000) were added to the cells to yield the highest concentration of 200 μM (all other inhibitors). After a three-day incubation with the treatment, cell viability was assessed with the CellTiter-Glo luminescent viability assay (Promega Corporation, Durham, NC) according to the manufacturer's instructions. Growth inhibition was calculated as a percentage of diluent-treated cells, and GI₅₀ values were determined to correspond to the inhibitor concentration that resulted in half-maximal growth inhibition.

Immunoblotting

Western blot procedure was followed as previously described⁴⁸. Primary antibodies were all purchased from Cell Signaling Technology and diluted at 1:1000. The catalog numbers are as follows: phospho-ERK (#9101), ERK (#4695), EGFR (#4267), PARP (#9542), vinculin (#4650), Beta-actin (#4970), AXL (#8661), p75NTR (#4201), MITF (#12590), SOX10 (#89356), SOX9 (#82630), JunB (#3753), p21 (#2947), HSP90 (#4874), FRA1 (#5281), and p-FRA1 (#3880).

Cell Surface Flow Cytometry

Pelleted cells were resuspended in 100 μL of Flow Cytometry Staining Buffer (eBioscience^™, #00-4222-26) at a concentration of 100,000 cells/ml. APC anti-human EGFR Antibody (Biolegend, #352906) or APC Mouse IgG1, κ Isotype Ctrl (FC) Antibody (Biolegend, #400122) was added at 2000x to the suspended cells, and the reaction was left to incubate at room temperature for 30 minutes. Cells were washed thrice with 1 ml of Flow Cytometry Staining Buffer. Data were acquired with a FACSCanto II (BD Biosciences) flow cytometer, and the results were analyzed in Flowjo (TreeStar).

Lentivirus preparation and DNA constructs

All expression plasmids were prepared in lentiviral form as previously described⁴⁹. In brief, expression constructs, psPAX2 (addgene, #12260), and pMD2.g (addgene, #12259) were transfected into AAVpro^® 293Ts (Takara, #632273) using Lipofectamine 2000 (Thermo Fisher Scientific, #11668500) according to the manufacturers protocol. Following a four hour incubation, the transfection media was removed and replaced with harvest media containing 30% FBS. The virus-containing media was collected after 48 or 72 hours, filtered with a 0.45 μm filter, and stored at −80°C until use with 8 μg/mL polybrene (Sigma-Aldrich). pHAGE-EGFR was a gift from Gordon Mills & Kenneth Scott (Addgene plasmid #116731 ; http://n2t.net/addgene:116731 ; RRID:Addgene_116731). pHAGE_puro was a gift from Christopher Vakoc (Addgene plasmid #118692 ; http://n2t.net/addgene:118692 ; RRID:Addgene_118692). FUW-Sox10 was a gift from Bob Weinberg (Addgene plasmid #36978; http://n2t.net/addgene:36978; RRID: Addgene_36978). TFORF2346 was a gift from Feng Zhang (Addgene plasmid #142043; http://n2t.net/addgene:142043; RRID: Addgene_142043).

Generation of CRISPR/Cas9 knockouts

lentiCRISPR v2 (LCV2) was a gift from Feng Zhang (Addgene plasmid # 52961 ; http://n2t.net/addgene:52961 ; RRID:Addgene_52961). sgRNAs were chosen from the TKOv3 genome-wide library⁵⁰ (JunB-1: GTGTAGAGAGAGGCCACCAG and JunB-2: ACTCCTGAAACCGAGCCTGG) and were cloned into LCV2 using the protocol provided by the maker. Lentivirus containing the plasmid were generated as described above. Cells were spinfected with a mixture of virus, 8 μg/mL polybrene, and media at 2250 rpm for 1 hour, followed by incubation at 37 degrees overnight in the transduction mixture. The following day the transduction mixture was removed and 2 μg/ml of puromycin was added to the cells. 48 hours later the surviving cells were seeded into the described experiments.

In vitro, adaptation of inhibitor-resistant cells

PLX4720-, AZD6244- or PLX4720 and AZD6244-resistant cell lines were produced by one of two methods as previously described⁴⁹. Briefly, parental cells were either exposed to escalating inhibitor doses or exposed to a high dose (3 μM) of inhibitor until logarithmic growth resumed. The resultant resistant clones were expanded and cultured. Parental cell lines were cultured concurrently with DMSO. Resistant cell lines were maintained in routine culture with 3 μM MAPKi drug. All resistant and DMSO parental control lines were submitted to STR profiling by the Duke University DNA Analysis Facility to confirm their authenticity upon the acquisition of resistance.

Clonogenic growth assay

To measure the ability of cell lines to form colonies from a single cell, clonogenic growth assays were performed as previously described⁴⁹. Briefly, 1000-5000 cells were seeded per well in 6 or 12-well tissue culture plates in standard growth media. After 24 hours, the indicated treatments were added, and the assay was incubated for 14-21 days with fresh media and inhibitors every 72-96 hrs. Cells were fixed and stained with 0.5% (w/v) crystal violet in 6.0% (v/v) glutaraldehyde (Thermo Fisher Scientific, Waltham, MA). Quantifications of the surface area covered were used to estimate cell viability and were performed in ImageJ software with the ColonyArea plugin⁵¹.

Cell cycle analysis

To analyze the progression of cells through the cell cycle, cells were plated in triplicate at 20,000 cells per well in six-well plates. The following day, the growth media was removed and replaced with fresh media containing the indicated dose of drug or diluent (typically DMSO). After a 72-hour incubation in the drug, cells were counted. The cells were washed twice in PBS and stained with a solution of 50 μg/μL RNase A, 20 μg/μL propidium iodine, 0.05% TritonX-100 in PBS (Sigma-Aldrich). 1x10⁶ cells were washed twice with PBS and then fixed in 70% ethanol. DNA content of the cell population was determined and quantified by flow cytometry. Gating was defined using untreated/unstained cells, and treatments were evaluated at 20,000 counts using BD FACSVantage SE.

Senescence-associated β-galactosidase assay

To determine the effect of treatment on the induction of senescence, cells were plated in triplicate in 6-well plates at a density that would achieve 80-90% confluency at 10 days of growth, typically between 1,000 and 50,000 cells. After 24 hours of culture, the growth media was removed and replaced with fresh media containing the indicated drug or diluent. After 10 days of treatment, media was removed, and the cells were stained with the kit, Senescence b-Galactosidase Staining Kit (Cell Signaling Technology), according to the manufacturer's instructions. Bright-field images were taken at 100x magnification at five random locations in each well. Representative images are shown.

DepMap Analyses

Addictive vs. non-addictive RNAseq comparison:

Using the custom analysis feature on DepMap.org, we performed a two-class comparison of Expression Public 22Q4 data with our addictive cell lines (COLO679, SKMEL5, and SKMEL28) as our “in” group and our non-addictive cell lines (A375, HS294T, and WM793) as our “out” group. The resulting data is found in the supplementary materials. We performed GSEA analysis⁵² on this data using melanocytic, neural crest-like, and undifferentiated gene signatures that were previously defined¹² and can also be found in the supplemental material.

Melanocytic or Dedifferentiated Melanoma Classification:

We performed ssGSEA on all 63 BRAF- and NRAS-mutant melanoma cell lines annotated in the DepMap Expression Public 22Q4 database with the melanocytic gene signature using the GenePattern platform^52-54. MAPK-mutant melanoma with an enrichment score >2500 was classified as melanocytic. All MAPK-mutant cell lines with an enrichment score <2500 were classified as dedifferentiated. The enrichment scores for each cell line are in the supplementary material. We used these classifications to compare DUSP4 and PPP6C dependency scores and JunB protein levels via the DepMap custom analyses feature.

Definition of JunB Transcriptional Signature:

We selected the top 100 upregulated genes from a JunB overexpression experiment in melanoma⁴⁴, found in the supplemental materials. Using this signature, we assigned every available cell line in DepMap an enrichment score using ssGSEA. We correlated this score with the JunB expression to validate the signature. Following validation, we compared the enrichment score of melanocytic and dedifferentiation melanoma. Both analyses were performed in the DepMap custom analyses feature.

Growth rate calculation

To calculate growth rates, cell populations were used at low passage numbers with measured drug resistance. Cells were plated in triplicate in 10 cm plates at 3,000 cells per plate in standard growth media. The following day, cells were treated with drug or DMSO. Six days later, the cells were lifted with 0.25% trypsin (Life Technologies) and counted using a Z2 Coulter Particle Count and Size Analyzer (Beckman Coulter, Pasadena, CA). Effective growth rates ($\mu$) were calculated from the number of cells plated (${\mathrm{N}}_0$) and the number counted ($\mathrm{N}$) according to the equation:

$$\text{ln}N=\text{ln}{N}_0+\mu \tau$$

where $\tau$ is the elapsed time (168 hours).

Drug scheduling assay

After measuring growth rates, we plated cells in 15 cm plates with growth media and no drug. The following day, we added drug (or not) based on the indicated drug schedule. Cells were counted at the end of each completed schedule and replated as indicated. All drug schedules were established based on the interval between counts; for example, if cells were treated with 75% drug and counted every four days, they would be treated with the drug for three days and diluent for one day, counted, and replated for the duration of the experiment. If a portion of cells was discarded before replating, growth rates ($\mu$) were calculated over the period from the number of cells plated at the beginning of the period (${\mathrm{N}}_0$) and the number counted at the end of the period (N) according to the equation above. These growth rates were then used to predict the total cell number as if no cells had been discarded. After the initial plating, which was always diluent only, cells were replated into treatment determined by their schedule.

Statistics

All results are shown as means ± SD. To compare groups, unless noted otherwise, P-values were determined using unpaired, two-tailed Student's t-tests.

“Blind” adaptive therapy algorithm

We started by administering drug for some time ΔT and estimating the growth rate during that period. This period is followed by removing the drug for the same ΔT, and the drug-free (or 'holiday') growth rate is estimated. We then administered the condition (drug or no drug) corresponding to the lower growth rate and recorded the growth rate for each ΔT that passes. If the growth rate for the most recent ΔT surpasses that of the opposite condition, we switched the treatment condition for the next time window. We repeated this process for the remainder of the treatment time, recording new values for the population growth in drug and during treatment holidays and switching between treatments as they become optimal.

Spatial agent-based model

We employ a 2-D, on-lattice, ABM using the Hybrid Automata Library (HAL)⁵⁵. The cells can be divided into sensitive and resistant populations and do not allow for mutation between cell types. All simulations are performed with a 200x200 lattice size with no flux boundary conditions. Cells are assumed to be randomly distributed to start. Sensitive and resistant cells attempt to divide at a constant rate determined by their environment (drug on or off). If at least one site in the cell’s neighborhood is empty, then the cell will divide and a daughter will now occupy the empty site. The neighborhood size is assumed to be von Neumann (cells not impacted by the boundary have four neighbors). Cells die a constant rate, which we assume (for simplicity) is equal for sensitive and resistant cells. Cell movement/migration is not allowed, and the drug environment is assumed to be homogenous. Dead cells are immediately removed from the lattice.

Data availability

All data generated or analyzed during this study are included in this published article (and its supplementary information files).

Code availability

All code used in this study will be available on GitHub.