Brain cell-type shifts in Alzheimer’s disease, autism, and schizophrenia interrogated using methylomics and genetics

Abstract

Few neuropsychiatric disorders have replicable biomarkers, prompting high-resolution and large-scale molecular studies. However, we still lack consensus on a more foundational question: whether quantitative shifts in cell types—the functional unit of life—contribute to neuropsychiatric disorders. Leveraging advances in human brain single-cell methylomics, we deconvolve seven major cell types using bulk DNA methylation profiling across 1270 postmortem brains, including from individuals diagnosed with Alzheimer’s disease, schizophrenia, and autism. We observe and replicate cell-type compositional shifts for Alzheimer’s disease (endothelial cell loss), autism (increased microglia), and schizophrenia (decreased oligodendrocytes), and find age- and sex-related changes. Multiple layers of evidence indicate that endothelial cell loss contributes to Alzheimer’s disease, with comparable effect size to APOE genotype among older people. Genome-wide association identified five genetic loci related to cell-type composition, involving plausible genes for the neurovascular unit (P2RX5 and TRPV3) and excitatory neurons (DPY30 and MEMO1). These results implicate specific cell-type shifts in the pathophysiology of neuropsychiatric disorders.

Analysis of cell-type composition from 1270 brains across three diagnoses implicates endothelial cell loss in Alzheimer’s disease.

INTRODUCTION

Most neuropsychiatric disorders lack biomarkers that can provide insights into pathophysiology, inform clinical diagnosis, or guide management (1). High-throughput genomic profiling technologies—applied to bulk tissue or single cells—may provide insights at scale: interrogating genome-wide molecular features (e.g., gene expression or DNA methylation) across large numbers of brain samples. Despite these technical advances, however, our understanding of the cell types, cell states, and molecular mechanisms contributing to the pathophysiology for most neuropsychiatric disorders remains limited. Most fundamentally, the impact of cell-type proportion (CTP) shifts has not been robustly established, despite these being important intermediate traits that may reflect cellular vulnerability or activation states underlying pathogenesis. In neurological disorders, for example, loss of dopaminergic neurons and oligodendrocytes are hallmarks of Parkinson’s disease (2) and multiple sclerosis (3), respectively. Furthermore, when observed, it has been difficult to infer whether CTP changes reflect causality or consequence using cross-sectional data. Causal inference methods from statistical genetics (4) may offer inroads into addressing these fundamental questions.

Leveraging the growing number of large-scale, multi-omic profiling studies conducted using postmortem human brain tissue from donors diagnosed with neuropsychiatric disorders (5–9), methods have been devised to infer CTPs from bulk tissue genomic readouts, particularly RNA sequencing (RNA-seq) and methylomic data (10, 11). Below, we summarize important considerations for CTP deconvolution efforts.

The first consideration is the deconvolution algorithm method, which can be reference-based (supervised) or reference-free (unsupervised). The success of reference-free methods [which typically implement variations of sparse principal components analysis (PCA) (12) or surrogate variable analysis (SVA) (10, 13)] reflects the fact that subtle differences in cell-type composition across samples drive substantial variance in bulk genomic datasets including DNA methylation (14) and RNA-seq (7). However, reference-based methods that identify specific cell types—typically implementing non-negative matrix factorization or similar approaches (15–17)—are necessary for biological inference.

A second issue in deconvolution is the choice of omics data type to best inform biological inference. There is rich literature comparing CTP deconvolution methods for DNA methylation (10) and RNA-seq data (11). Overall, DNA methylation data are more amenable to deconvolution as the data are scaled between 0 and 1 (whereas RNA-seq has a much greater dynamic range), and, unlike RNA, DNA content is constant across cells (two copies for diploid organisms) (18). Furthermore, methylation profiling captures a greater proportion of the genome than RNA-seq and can identify “upstream” regulatory elements known to drive cell-type identity (19). Practically, methylation has demonstrated great efficacy in distinguishing neuron populations (20, 21). In contrast, RNA-based deconvolution pipelines often poorly quantify CTPs as they capture transcriptional activity (18) and—instead of tagging nuclei—can also capture neuropil, which includes material originating from distant brain regions. Other approaches count brain cell types more directly, such as immunohistochemistry (IHC) of bulk data, and cell sorting methods (including single-cell approaches). However, these approaches can be difficult to scale. Cell sorting also induces other experimental biases: Physical stress from bulk tissue dissociation alters epigenetic profiles, structurally fragile cell types become underrepresented, physical characteristics of cells affect library preparation (19), and the reliance on cell markers (or their absence) for gating methods may not be sufficiently specific, resulting in heterogeneity within sorted populations. These biases help to explain why single-nucleus RNA-seq (snRNA-seq) appears to oversample neuronal and oligodendrocyte proportions (22) compared to IHC counts.

A third issue for reference-based bulk deconvolution relates to the quality of the reference: Whether the reference (i) captures the full complement of cell types (11), (ii) is appropriately matched to the bulk sample [e.g., cell lines may have epigenetic differences compared to donor tissue (10)], and (iii) whether specific, high-fidelity cell-type markers have been selected (9, 10).

While DNA methylation has advantages for deconvolution (18, 23), its uptake has been limited by the availability of high-quality reference datasets. Furthermore, single-cell technology is less mature for DNA methylation (compared to RNA-seq), which has restricted the granularity of reference cell-type panels. On balance, with a high-quality DNA methylation reference dataset, results from bulk deconvolution may be more robust than single-cell or cell sorting experiments and more scalable. Overall, it can be concluded that brain CTP deconvolution has not yet been optimized due to limitations in omics technologies and available data.

Here, we uniformly processed and integrated bulk DNA methylation and single-nucleotide polymorphism (SNP) genotypes from 1270 postmortem human brain samples, including from donors diagnosed with Alzheimer’s disease (n = 300), autism spectrum disorder (ASD) (n = 31), and schizophrenia (n = 186) across the life span (0 to >90 years; Fig. 1). Leveraging recent high-quality single-cell methylome profiling in the neurotypical brain (24), we developed a cell type–specific reference panel for CTP deconvolution, which we validated and contrasted with previously developed—but less specific—reference-based and reference-free approaches (Fig. 1A) (25), as well as with other deconvolution modalities. We observed substantial CTP shifts across diagnoses, age, and sex. Finally, integration with genetic data highlighted genetic contributions to brain CTP shifts [through genome-wide association study (GWAS)], while polygenic score (PGS) and mediation analyses facilitated causal inference about diagnosis-associated brain CTP changes.

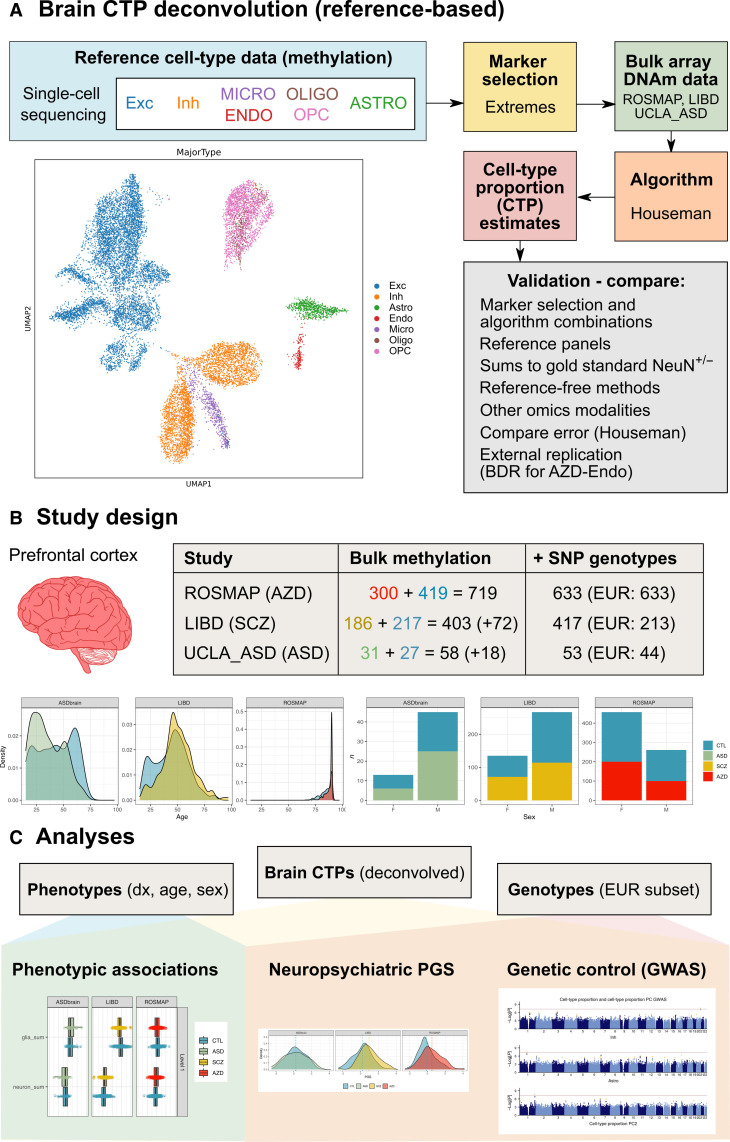
Fig. 1. Overview of study design and analyses.

(A) An overview of the pipeline developed for reference-based deconvolution of CTPs from bulk brain methylation data. UMAP shows 7 major brain cell types clustered by single cell methylome profiles. (B) Bulk prefrontal cortex DNA methylation data was integrated from three studies: ROSMAP (ascertained for Alzheimer’s disease), LIBD (ascertained for schizophrenia), and UCLA_ASD (ascertained for ASD). Table shows the number of participants: Second column shows individuals with bulk DNA methylation data in each study; blue text for the number of individuals without the diagnosis of interest; red (Alzheimer’s disease), yellow (schizophrenia), and green (ASD) are for those with the diagnosis; the numbers in brackets indicates the number of people excluded for case/control analyses to balance study design by age and sex; third column shows the number of people with matching SNP genotypes, with individuals of European ancestry shown in brackets. Density plot shows age distribution for each constituent study, and bar plots show breakdown by sex. (C) Downstream analyses involving deconvolved brain CTPs, phenotype and genotype data. EUR, European; Exc, excitatory neurons; Inh, inhibitory neurons; Astro, astrocytes; Endo, endothelial cells; Micro, microglia; Oligo, oligodendrocyte, OPC, oligodendrocyte precursor cells.

RESULTS

Deconvolution of cell types and validation

Following careful quality control, outlier removal, and normalization (Materials and Methods), we aggregated genome-wide methylation profiling of homogenate prefrontal cortex brain tissue samples from 1270 unique subjects across datasets [ROSMAP (5), UCLA_ASD (26), and LIBD (6)] (table S3). In parallel, using methylome data from 15,030 single cells from adult human prefrontal cortex (24), we assembled a cell type–specific reference panel for seven major brain cell types: excitatory neurons, inhibitory neurons, astrocytes, endothelial cells, microglia, oligodendrocytes, and oligodendrocyte precursor cells (OPCs) (Fig. 1). We compared and validated a variety of cell-type deconvolution pipelines, evaluating the final deconvolution quality based on several criteria as described in note S1 (figs. S1 to S13 and tables S4 to S6).

We ultimately selected a reference-based pipeline: the reference being the single-cell methylation sequencing-based panel devised here with marker probe selection based on “extremes” of methylation (Materials and Methods) and the deconvolution via a non-negative matrix factorization algorithm implemented previously (Fig. 2, figs. S1 to S13, and table S7) (15). In validation, we found excellent concordance among CTP estimates from alternative reference profiles and deconvolution pipelines for bulk methylation, including with whole-genome bisulfite sequencing reference profiles from sorted cell populations [“WGBS/FACS” (fluorescence-activated cell sorting)] (27) and with EpiSCORE RNA reference-based deconvolution (fig. S6 and note S1) (28). The consistency of these results is notable as the reference profile can strongly influence the deconvolution (29). Our deconvolution pipeline performed strongly when benchmarked against external sorted cell populations (fig. S8 and note S1). We further compared our results with reference-free methods including smartSVA (13) and MethylNet (figs. S5, S9, and S10) (30) and observed strong correlations between surrogate variable(s) and oligodendrocyte proportion, suggesting that gray/white matter dissection is a major driver of variation in DNA methylation profiles and CTPs. Finally, we compared our deconvolved CTPs (from bulk DNA methylation) against matched CTP estimates from orthogonal omics technologies (single cell, bulk RNA-seq, and IHC) and found modest concordance (figs. S12 and S13; details in note S1). These comparisons demonstrate the systematic differences in how different omics technologies can infer CTPs. Notably, bulk RNA-seq approaches provided less specific estimates as they also capture neuropil (which constitutes the majority of brain tissue), rather than nuclear material alone (23). We provide extensive detail on our comparison of methods and evaluation of the optimal method in note S1.

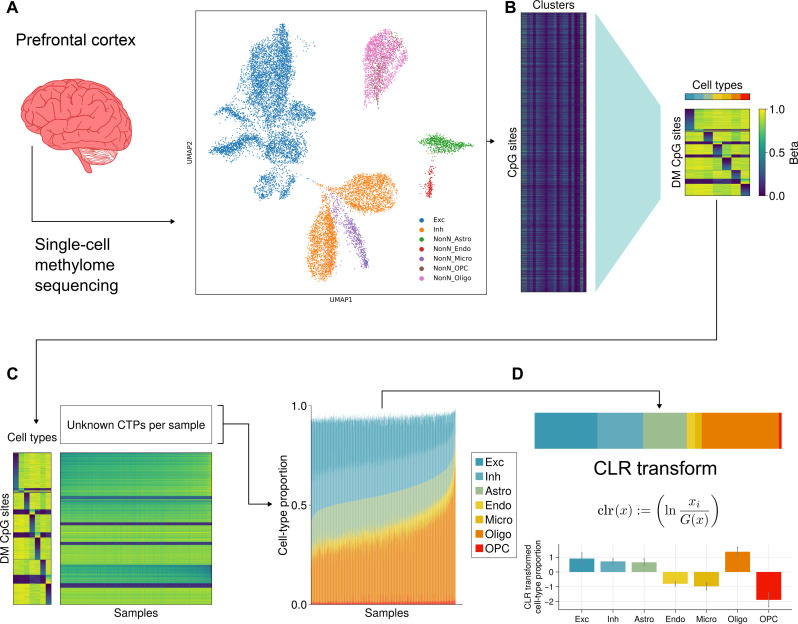
Fig. 2. Overview of deconvolution method.

(A) Single-cell methylome sequencing was performed on 15,030 single cells from postmortem human frontal cortex. (B) Reference panel of marker sites was created from the methylome data to capture differentially hypermethylated and hypomethylated sites for each of the seven major brain cell types. (C) With this reference panel, bulk methylation data from ROSMAP, LIBD, and UCLA_ASD was deconvolved using non-negative matrix factorization as implemented by the Houseman algorithm. (D) We applied the clr-transformation to the seven major brain CTPs. Bar plot below shows the average clr-transformed CTPs (± SE).

Associations between neuropsychiatric diagnoses and brain CTPs

Within each of the bulk DNA methylation datasets, we tested for associations between the seven brain CTPs and neuropsychiatric diagnoses (Alzheimer’s disease for ROSMAP, ASD for UCLA_ASD dataset, and schizophrenia for LIBD; Fig. 3A and fig. S14) (full dataset subset to n = 1179 in this diagnosis-based analysis to balance study design by age; see Materials and Methods).

Fig. 3. Brain cell type shifts are observed across neuropsychiatric diagnoses, age, and sex.

(A) Boxplot of deconvolved brain CTPs, stratified by study. (B) Diagnosis coefficients (±95% CI) from linear models of brain CTP (clr-transformed) ~ diagnosis + age + age² + sex + batch. This model was run within each study (UCLA_ASD, n = 58; ROSMAP, n = 715; LIBD, n = 402). Labeled results indicate nominally-significant results (P ≤ 0.05). (C) Age effect coefficients (±95% CI) from linear models of brain CTP (clr-transformed) ~ diagnosis + age + sex + batch; coefficients for sex from linear models of brain CTP (clr-transformed) ~ diagnosis + age + age² + sex + batch. This model was run as a mega-analysis including all participants (with and without neuropsychiatric diagnoses) across all studies (n = 1270). (D) Age trajectories of brain CTPs (clr-transformed) aggregating across all studies, correcting for batch effects. (E) Boxplot of endothelial cell proportion (clr-transformed) by final clinical consensus cognitive diagnosis: no cognitive impairment (NCI) versus mild cognitive impairment (MCI) versus Alzheimer’s disease (AZD) versus other primary cause of dementia (Other). (F) Scatterplot of endothelial cell CTP (clr-transformed) versus Braak score (representing histopathological severity of Alzheimer’s disease), demonstrating replication across the ROSMAP and BDR datasets. (G) Increased microglia are replicated in ASD using snRNA-seq count data (n = 60). ASD diagnosis coefficients (±95% CI) from linear models of brain CTP (clr-transformed) ~ diagnosis + age + age² + sex + brain region.

It is difficult to interpret diagnostic associations with CTPs using standard statistical tools—whether such an association represents a quantitative cell-type difference or, alternatively, shifts in other cell types. Hence, we employed compositionally aware methods, which are underused despite being necessary for correct inference. The first compositionally aware approach applied the centered log-ratio (clr) transformation to CTPs before regressing against diagnosis and baseline covariates [CTP (clr-transformed) ~ diagnosis + age + age² + sex + batch] (Fig. 3B and tables S8 and S9). The clr-transformation accounts for compositionality by comparing proportions relative to the geometric mean; unlike other methods, it retains all compositions for analysis. The second compositional approach involved generating compositionally aware principal components (CTP_PCs), where each CTP_PC represents a “balance” or “ratio” of the seven CTPs. These methods are explained in detail in note S2.

We identified diagnostic associations between Alzheimer’s disease and decreased endothelial cells (b = −0.039, SE = 0.007, P = 2.1 × 10⁻⁷, Bonferroni significant), increased excitatory neurons (b = 0.04, SE = 0.01, P = 3.1 × 10⁻³, Bonferroni significant) and inhibitory neurons (b = 0.028, SE = 0.008, P = 5.3 × 10⁻⁴, Bonferroni significant), ASD and increased microglia (b = 0.06, SE = 0.03, P = 2.1 × 10⁻²), and schizophrenia and decreased oligodendrocytes (b = −0.10, SE = 0.03, P = 5.4 × 10⁻⁴, Bonferroni significant). As expected, these associations were consistent with sensitivity analyses excluding covariates (fig. S15).

We further explored the association between measures of Alzheimer’s disease severity and loss of endothelial cells within the ROSMAP dataset, as this association appeared to be particularly strong. We similarly found significant associations between decreased endothelial cells and both clinical [“final clinical consensus diagnosis”; analysis of variance (ANOVA) F = 6.6, P = 1.8 × 10⁻⁴, adjusted for baseline covariates; Fig. 3E] and neuropathological (Braak score; b = −0.011, SE = 0.005, P = 1.9 × 10⁻², adjusted for covariates) measures of Alzheimer’s disease severity (Fig. 3F). As an indicator of biological significance, we found that endothelial CTP (clr-transformed) explained 3.4% of variance (Nagelkerke R²) in Alzheimer’s disease diagnosis within the ROSMAP dataset, which was comparable to the variance explained by APOE genotype (Nagelkerke R² = 3.7%), greater than the effects of sex (Nagelkerke R² = 0.4%) and years of education (Nagelkerke R² = 0.02%) but less than age effects (Nagelkerke R² = 10.7%; ROSMAP age range: 66 to >90).

Second, we tested whether global cell-type compositional shifts were associated with significant variation in diagnosis (beyond that explained by a model with baseline covariates including age, age², sex and batch) using a likelihood ratio test. Within each dataset, we quantified global cell-type compositional shifts by generating compositionally-aware PCs of the CTPs (CTP_PCs; table S8 and note S2), where each PC represents a ratio of cell types. We then took the first CTP_PCs explaining ≥95% of the variation to fit as additional variables in the likelihood ratio test (fig. S16 and Materials and Methods). CTP_PCs (calculated within each dataset) were necessary to use in this analysis, as raw CTPs are correlated (by nature of being a proportion), and singularity errors make it impossible to simultaneously include all CTPs (raw or clr-transformed) in this model. For Alzheimer’s disease (ROSMAP dataset: n = 300 AZD and n = 418 undiagnosed), cell-type compositional shifts significantly improved the model fit (χ² = 27.7, P = 1.4 × 10⁻⁵, df = 4). This association was driven by increased CTP_PC3 (reflecting increased excitatory neurons and decreased microglia) and reduced CTP_PC4 (reflecting increased endothelial cells and astrocytes and decreased microglia and neurons) (fig. S16C). For schizophrenia (LIBD dataset subset balanced for age: n = 185 SCZ and n = 217 undiagnosed), CTP_PCs explained significantly more variance in diagnosis than the baseline covariate model (χ² = 23.8, P = 8.7 × 10⁻⁵, df = 4). This association was driven by increased CTP_PC2, whose loadings represent reduced oligodendrocytes, and increased OPCs and endothelial cells (fig. S16B). For ASD diagnosis (UCLA_ASD dataset subset balanced for age differences: n = 31 ASD and n = 27 undiagnosed), including the CTP_PCs in the model demonstrated marginal improvement in model fit (χ² = 6.28, P = 9.9 × 10⁻², df = 4). This association was driven by increased microglia and decreased excitatory neurons and oligodendrocytes (CTP_PC2; fig. S16A). Overall, these results demonstrate that global cell-type compositional shifts are associated with diagnosis of these three neuropsychiatric conditions.

These unsupervised PCs yielded consistent CTP ratios within each dataset and in aggregation, indicating that they capture consistent biology and not artifact. For example, the first CTP_PC represented ratios of neurons and astrocytes against microglia, oligodendrocytes, and OPCs. For each study, there was also a CTP_PC interpretable as the “neurovascular unit” with a ratio of endothelial cells and astrocytes against neurons and microglia (aggregated CTP_PC5, ROSMAP CTP_PC4, LIBD CTP_PC4, and UCLA_ASD CTP_PC3; fig. S16). Hypothesizing that Alzheimer’s disease may be related to this neurovascular unit, we found a significant association between ROSMAP CTP_PC4 and Alzheimer’s disease diagnosis (b = −0.036, SE = 0.009, P = 3.9 × 10⁻⁵).

We did not find that other clinical variables (e.g., comorbidities, medications, and cause of death) were potential confounders of these CTP associations (note S3).

Replication using external datasets and with orthogonal omics technologies

As further validation, we performed replication using external datasets. The independent and large Brains for Dementia Research (BDR) dataset—ascertained for Alzheimer’s disease—includes bulk prefrontal cortex DNA methylation data for n = 597 individuals (31). For replication in BDR, we focused on Braak score (as there are relatively few controls in this dataset) and again identified a significant association between reduced endothelial cells and increased Braak score (b = −0.028, SE = 0.006, P = 9.6 × 10⁻⁶) (Fig. 3F), indicating that this CTP change is robust. Within BDR, the variance in Braak stage (R² = 4.1%) associated with endothelial CTP was similar to ROSMAP, whereas age and sex had lesser associations (R² = 0%), likely due to ascertainment.

We next compared diagnostic associations using matched data from orthogonal omics technologies, noting the inherent limitations of this approach (note S1) (23). There were matched single-nucleus RNA-seq counts for a subset of UCLA_ASD (32) and ROSMAP (33) participants and matched deconvolved bulk RNA-seq CTPs for a subset of the LIBD and UCLA_ASD participants from PsychENCODE (7). Using the single-cell datasets, we replicated the association between increased microglia and ASD diagnosis (b = 0.36, SE = 0.16, P = 3.0 × 10⁻², n = 60) (Fig. 3g and fig. S17) (34). The Alzheimer’s disease single-cell RNA-seq dataset (n = 48) did not detect endothelial cell loss (fig. S18), which likely reflects technical difficulties in capturing this very low-prevalence cell type in single-cell experiments without experimental enrichment or capture techniques (35). Compared to bulk methylation deconvolution, bulk RNA-seq deconvolution (n = 473) had weaker signal for diagnostic associations but consistent directions of effect: There was a trend-level association between increased microglia and ASD diagnosis (b = 0.29, SE = 0.15, P = 5.9 × 10⁻²) and no significant association between decreased oligodendrocytes and schizophrenia diagnosis (b = −2.1 × 10⁻², SE = 4.8 × 10⁻², P = 0.65) (fig. S19).

Last, we internally recapitulated the association between Alzheimer’s disease and endothelial cells using deconvolutions derived from alternative pipelines applied to the same bulk datasets (note S1). We focused on two pipelines: a recent WGBS DNA methylation atlas reference from Loyfer et al. (27) with methylation profiles from a total of 39 FACS-sorted cell types including some brain cell types (WGBS/FACS) and another from Zhu et al. (28), which inferred DNA methylation cell-type profiles from single-cell RNA-seq (“EpiSCORE RNA based”). We again observed a significant association between Alzheimer’s disease and reduced endothelial cells within the ROSMAP dataset when using both the WGBS/FACS-based reference (β = −8.5 × 10⁻², SE = 1.6 × 10⁻², P = 2.4 × 10⁻⁷, Bonferroni significant) and the EpiSCORE RNA-based deconvolution (b = 4.9 × 10⁻², b = 2.5 × 10⁻², P = 4.7 × 10⁻²).

Mega-analysis of cell proportion shifts across the life span and between sexes

To investigate associations between CTPs, age, and sex, we mega-analyzed all n = 1270 participants across studies and diagnoses. With increasing age, we found Bonferroni significant patterns of decreasing endothelial cells (b = −1.8 × 10⁻³, SE = 2.1 × 10⁻⁴, P = 6.2 × 10⁻¹⁸) and microglia (b = −5.1 × 10⁻³, SE = 3.4 × 10⁻⁴, P = 1.7 × 10⁻⁴), increasing excitatory neurons (b = 2.1 × 10⁻³, SE = 6.0 × 10⁻⁴, P = 4.0 × 10⁻⁴), and marked early-life increases in oligodendrocytes (b = 5.8 × 10⁻³, SE = 5.6 × 10⁻⁴, P = 1.8 × 10⁻²³) alongside decreases in inhibitory neurons (b = −2.5 × 10⁻³, SE = 2.4 × 10⁻⁴, P = 2.6 × 10⁻²³) (Fig. 3, C and D). Furthermore, age effects accounted for substantial proportions of variance in CTPs (fig. S20). Male sex was associated with increased microglia (b = 2.8 × 10⁻², SE = 8.8 × 10⁻³ P = 1.4 × 10⁻³) and reduced endothelial cells (b = −2.8 × 10⁻², SE = 5.4 × 10⁻³, P = 2.9 × 10⁻⁷) after Bonferroni correction (Fig. 3C and fig. S21). To ensure that results were robust, we confirmed that mega-analysis effects were consistent across the three constituent studies and also confirmed that these age and sex effects persisted in the subset of n = 741 undiagnosed participants (fig. S22). We note that sex and age covaried in ROSMAP (males tend to be younger: b = −1.89, SE = 0.36, P = 2.4 × 10⁻⁷) and LIBD datasets (males younger: b = −5.5, SE = 1.9, P = 4.5 × 10⁻³), and this association likely reflects the relationship between female sex and increased life expectancy. Regardless, stratification by sex did not meaningfully alter the age-CTP associations (fig. S23).

Brain CTPs are associated with PGSs for neuropsychiatric traits

These observed disorder-associated cell-type shifts could reflect either a causal process or simply a consequence. To begin to differentiate these distinct interpretations, we leveraged PGSs as a directional genetic anchor. We uniformly processed genome-wide SNP genotypes among donors with matched brain methylation profiling (n = 1098). Focusing on individuals of European ancestry (n = 878; fig. S24), we calculated PGSs for multiple neuropsychiatric traits, including ASD (36), schizophrenia (37), Alzheimer’s disease (38), major depressive disorder (39), and educational attainment (40), as well as height (41) as a negative control (tables S8 and S9 and fig. S25). As a validation, we found that PGS significantly predicted diagnostic status for both schizophrenia and Alzheimer’s disease within their respective cohorts (Fig. 4A and fig. S25). This was not the case for ASD PGS, which likely reflects insufficient power of the training weights from GWAS as well as the small sample size of the UCLA_ASD cohort. There were weak associations for the relationships for height versus ASD and schizophrenia diagnosis and educational attainment, potentially reflecting ascertainment (fig. S25).

Fig. 4. Polygenic scores for neuropsychiatric traits predict brain cell-type shifts.

(A) Distributions of PGS within each study, comparing individuals with and without the neuropsychiatric diagnosis of interest. (B) Neuropsychiatric trait PGS coefficients (±95% CI) from linear models for brain CTP (clr-transformed) ~ neuropsychiatric trait PGS + age + age² + diagnosis + sex + batch + genotyping PC1–3, subsetting for individuals with the diagnosis of interest (i.e., one of ASD, schizophrenia, or Alzheimer’s disease) and undiagnosed controls. Analyses included individuals with the diagnosis of interest and all controls: n = 531 for the ASD_PGS analysis, n = 591 for the SCZ_PGS analysis, and n = 763 for the AZD_PGS analysis. The White Matter Hyperintensity on MRI (WMH_PGS) PGS analysis included the same n = 763 individuals as for Alzheimer’s disease. (C) Schematic of causal analyses (mediation analysis and SMR). For the mediation analysis, statistics for effect sizes, 95% CI and P value are provided. ACME, average causal mediation effect; ADE, average direct effect.

We next estimated effect sizes for relationships between brain CTPs and PGS for neuropsychiatric diagnoses and traits (Fig. 4B). There remained significant associations between increased Alzheimer’s disease PGS and decreased endothelial cells (b = −0.008, SE = 0.003, P = 7.0 × 10⁻³; adjusting for baseline covariates plus diagnosis) and between higher schizophrenia PGS and decreased astrocytes (b = −0.015, SE = 0.007, P = 2.8 × 10⁻²; baseline covariates plus diagnosis) (Fig. 4B and fig. S26). The former result was particularly notable as these genetic results corroborated the phenotypic association between Alzheimer’s disease diagnosis and decreased endothelial CTP (Fig. 3, B, E, and F). In sensitivity analyses, we showed that the association between Alzheimer’s disease PGS and endothelial cells persisted when we restricted our analysis to undiagnosed participants (leaving n = 503 of European ancestry) (b = −0.008, SE = 0.003, P = 3.1 × 10⁻²; baseline covariates), suggesting that genetic effects on endothelial cell loss in Alzheimer’s disease precede clinical diagnosis (fig. S27). Alzheimer’s disease PGS was most predictive of endothelial cell loss among older individuals (fig. S28 and note S4). There was no significant relationship between Alzheimer’s disease PGS and the neurovascular unit CTP_PC5 (in the aggregated dataset) after correcting for Alzheimer’s disease diagnosis and baseline covariates (b = 0.003, SE = 0.003, P = 0.40). In the broader context, one interpretation is that endothelial cell loss may be a specific etiological factor, whereas broader scale neurovascular changes may occur relatively downstream.

To clarify the putative causal association between endothelial cell loss and Alzheimer’s disease, we performed a mediation analysis quantifying the contribution of endothelial cell loss to the association between Alzheimer’s PGS and Alzheimer’s diagnosis (i.e., Alzheimer’s disease PGS → endothelial cells → Alzheimer’s disease diagnosis). We identified statistically significant mediation in models with covariates {mediating effect of endothelial cells (ACMEs) = 8.9 × 10⁻³, 95% confidence interval (CI) (2.6 × 10⁻³, 2.0 × 10⁻²), P ~ 0; effect of Alzheimer’s PGS on Alzheimer’s disease [average direct effect (ADE)] = 0.15, 95% CI (0.11, 0.19), P ~ 0)} and without covariates (Materials and Methods). Notably, we lacked statistical power to perform more stringent Mendelian randomization analyses to corroborate a causal effect of endothelial cell loss on Alzheimer’s disease as there was an insufficient number of valid genetic instruments; however, we did not find evidence for the reverse causal effect of Alzheimer’s disease on endothelial cell loss despite having adequate power (note S5).

As a form of validation, we calculated PGS for white matter hyperintensities (WMHs) detected on brain magnetic resonance imaging (MRI) (42)—this is a marker for cerebral small-vessel disease including endothelial dysfunction. WMHs are strongly associated with vascular risk factors (e.g., smoking, hypertension, diabetes, and hypercholesterolaemia) and are a well-known risk factor for dementia and stroke (43–45). Consistently, the WMH PGS was nominally predictive of reduced endothelial cells (b = −6.9 × 10⁻³, SE = 3.4 × 10⁻³, P = 0.04) (Fig. 4B).

Given this evidence for a relationship between endothelial cell loss and polygenic risk for Alzheimer’s disease, we investigated associations between endothelial cell loss and APOE ε4 genotypes—the single largest genetic risk factor for Alzheimer’s disease. In this analysis, we included the Alzheimer’s disease cases and all undiagnosed controls across the three studies, with 15 of the 775 individuals carrying homozygous APOE ε4 alleles (Materials and Methods). There was a nominally significant association between endothelial cell loss and APOE ε4 homozygous genotype (b = −9.6 × 10⁻², SE = 4.3 × 10⁻², P = 2.7 × 10⁻²), which remained when restricting to only controls (b = −9.9 × 10⁻², SE = 4.7 × 10⁻², P = 4.3 × 10⁻²; n = 511), adjusting for baseline covariates. Together, these results support a potential causal relationship of endothelial cell loss in the progression and severity of Alzheimer’s disease that is underpinned by common genetic risk, including APOE ε4 alleles.

Genetic control of brain CTPs

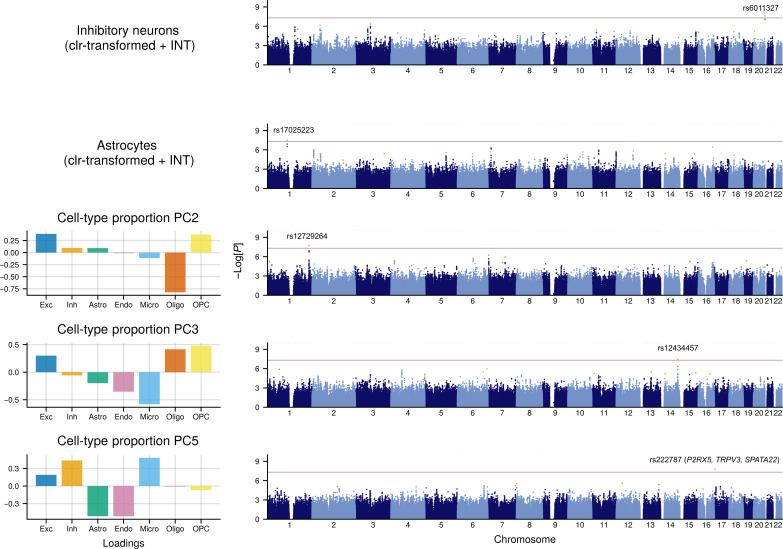
To identify individual genetic loci underlying these cell proportion associations, we next performed GWAS meta-analyses—each including more than 5 million SNPs—among the n = 873 unrelated participants of European ancestry (Materials and Methods). We performed two sets of GWAS to aid interpretation of the proportional data (note S2): (i) taking the brain CTPs (with clr-transformation followed by ranked inverse normal transformation; the latter being typical in GWAS) as the phenotype (Fig. 5 and fig. S29) and (ii) as a secondary analysis, capturing “axes” of CTP shifts with compositionally aware PCs (CTP_PCs; with inverse normal transformation) (fig. S30). We included as covariates age, age², sex, batch, and five within-study genotyping PCs for population stratification. In addition to standard quality control (QC) procedures, we filtered out SNPs that were not present in all three studies, had P < 0.001 for Cochran’s Q test for heterogeneity, or had a minor allele frequency (MAF) < 0.05 (Materials and Methods). In total, we identified five genome-wide significant (GWS) loci (P < 5 × 10⁻⁸) that were independently associated with specific brain CTP changes (Table 1) including one for inhibitory neurons (rs6011327; P = 2.3 × 10⁻⁸), one for astrocytes (rs17025223; P = 3.3 × 10⁻⁸), and three for various CTP_PCs (Fig. 5, Table 1, and figs. S29 to S32).

Fig. 5. Manhattan plots for genome-wide association studies for brain CTPs and composition.

Manhattan plots correspond to GWAS meta-analyses (n = 873), with signficant (P < 5 × 10⁻⁸) hits: inhibitory neuron CTP, astrocyte CTP, CTP_PC2 (↓Oligo / ↑OPC + Exc), CTP_PC3 (↓Micro / ↑Oligo + OPC), and CTP_PC5 (↓Astro + Endo / ↑Exc + Inh + Micro). Left barplots denote the relative loadings of cell types related to the CTP_PC variables. GWAS was performed in a linear model framework, including as covariates age, age², sex, batch, and diagnosis. Red dotted line denotes the P < 5 × 10⁻⁸ threshold.

Table 1. Annotation of significant GWAS SNPs (P < 5 × 10⁻⁸).

SNP	CHR	BP (hg38)	Z	P	MAF	Phenotype	Nearest Gene	Region	SMR associations
rs6011327	20	64182740	−5.58	2.32 × 10−8	0.06	Inhibitory neuron proportion	MYT1	Intronic	–
rs17025223	1	109947719	−5.52	3.30 × 10−8	0.10	Astrocyte proportion	CSF1	Intergenic	–
rs12729264	1	232502590	−5.63	1.86 × 10−8	0.10	CTP PC2: ↓Oligo / ↑OPC + Exc	SIPA1L2	Intronic	–
rs12434457	14	95547914	−5.48	3.63 × 10−8	0.26	CTP PC3: ↓Micro / ↑Oligo + OPC	GLRX5	Intergenic	–
rs222787	17	3625320	5.64	1.68 × 10−8	0.49	CTP PC5: ↓Astro + Endo / ↑Exc + Inh + Micro	SHPK, SHPK-TRPV1	Intronic	P2RX5, TRPV3, SPATA22

To gain further insights into the genetic architecture of CTP traits in this relatively underpowered dataset, we identified independent loci at a relaxed P value threshold (P < 1 × 10⁻⁵) in a conditional and joint analysis framework using the software package GCTA-COJO (46, 47). We found 11 independent loci for excitatory neurons, 14 for inhibitory neurons, 17 for astrocytes, 9 for endothelial cells, 14 for microglia, 11 for oligodendrocytes, and 13 for OPCs (Fig. 5). In the corresponding CTP_PC analysis (GCTA-COJO, P < 1 × 10⁻⁵), we found 18 for CTP_PC1, 10 for CTP_PC2, 11 for CTP_PC3, 5 for CTP_PC4, and 6 for CTP_PC5. We also attempted to perform a multi-ancestry analysis; however, this introduced heterogeneity due to confounding between covariates and brain CTPs (note S6 and figs. S33 and S34), and we therefore focused on the European subset.

To identify the putative genes underlying the loci identified by CTP GWAS (GWAS, P < 1 × 10⁻⁶), we performed summary data–based Mendelian randomization (SMR) (table S10) in conjunction with the HEIDI test to exclude associations due to genetic linkage (where genetic variants influence CTP through other genes) (48). Figures S35 to S41 provide LocusZoom plots for the genomic regions and forest plots to demonstrate consistent effects across studies.

We identified a relationship between the neurovascular unit CTP_PC5 locus on chromosome 17 (GWAS index SNP rs222787; P = 1.68 × 10⁻⁸), with the expression of genes including P2RX5 (p_SMR = 7.95 × 10⁻⁵, p_HEIDI = 0.31), TRPV3 (p_SMR = 3.54 × 10⁻³, p_HEIDI = 0.09) and SPATA22 (p_SMR = 1.77 × 10⁻³, p_HEIDI = 0.09) (fig. S42). CTP_PC5 may be interpreted as a representation of the cerebrovascular system/blood-brain barrier (high ratio of astrocytes and endothelial cells relative to neurons and microglia), so it is notable that these genes have related roles. P2RX5 encodes the P2X5 purinergic receptor, a ligand-gated ion channel activated by ATP, which contributes to endothelial cell differentiation and autocrine regulation (49, 50), and has functional roles in adult mouse astrocytes (51). Common genetic variation plausibly contributes to P2X5 receptor function: Due to a SNV that promotes exon skipping, only a proportion of the human population express fully functional P2X5 receptors, and amino acid substitutions within this gene can markedly affect the receptor’s responsiveness to its ATP ligand (52). TRPV3 is a nonselective cation channel, whose activation induces endothelium-mediated vasodilation of cerebral arteries (53) and cerebral parenchymal arterioles, which regulate blood flow from larger pial arteries on the brain surface to capillary beds (54). There is also evidence to suggest that TRPV3 overactivity exacerbates cerebral ischaemia/reperfusion injury in stroke by promoting neural excitotoxicity (55).

For the top GWAS locus in excitatory neurons (GWAS index SNP rs13425083; P = 8.43 × 10⁻⁷), we identified associations with DPY30 expression (p_SMR = 1.47 × 10⁻⁵, p_HEIDI = 0.18)—which has been identified as an important regulator of neural progenitor cells and their proliferation and differentiation (56)—and MEMO1 expression (p_SMR = 8.43 × 10⁻³, p_HEIDI = 0.46), which mediates radial glia tiling and subsequent neuronal migration (fig. S42) (57).

For the other GWS loci (P < 5 × 10⁻⁸; Fig. 5 and Table 1), there was no strong evidence for underlying relationships with gene expression. For the GWS brain CTP SNPs, we also performed colocalization (58) using large-scale human brain expression and splicing quantitative trait locus (QTL) resources, including MetaBrain, THISTLE, and a recent single-cell QTL human brain resource (59), but did not identify any significant associations.

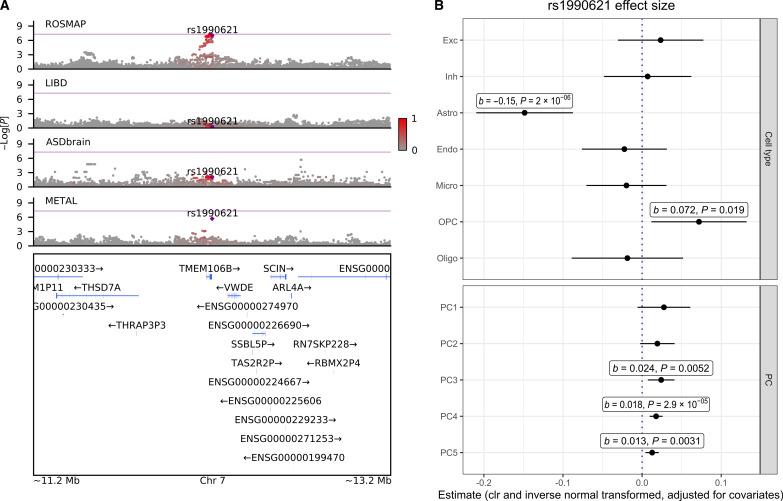
Lastly, we investigated the TMEM106B locus, as previous studies have implicated rs1990621 (within the TMEM106B gene region) and nearby SNPs on neuronal proportion deconvolved from ROSMAP bulk RNA-seq samples (60, 61). Here, we observed a GWS association between rs1990621 and increased astrocyte proportion within the ROSMAP cohort (b = 0.21, SE = 0.03, P = 8.9 ×10⁻⁸, n = 621) (Fig. 6A), although these results did not remain GWS in the full meta-analysis. In contrast to the previous RNA-seq deconvolution results, this SNP was not associated with neuronal proportions in our dataset (Fig. 6B). We hypothesize that the specificity of this rs1990621/astrocyte association to the ROSMAP dataset may reflect a cohort-specific effect, for example, related to a gene-by-environment interaction in the context of neurodegeneration.

Fig. 6. Investigation of TMEM106B locus, focusing on the ROSMAP dataset.

(A) LocusZoom plot comparing GWAS results on astrocyte CTP at the TMEM106B locus within the ROSMAP, LIBD, UCLA_ASD, and meta-analyzed datasets (METAL). (B) rs1990621 GWAS SNP effect size (±95% CI) in the ROSMAP dataset across the seven CTPs and the five CTP_PCs.

DISCUSSION

Here, we present a comprehensive and granular investigation of brain cell-type composition, its developmental regulation, sexual dimorphism, genetic regulation, and association with neuropsychiatric disorders, leveraging a large-scale integrated genetic and methylomic dataset from 1270 brain tissue samples. To quantify cellular shifts, we constructed a deconvolution pipeline using a single-cell methylome-based human brain reference panel to estimate proportions for 7 major brain cell types, which is available to the broader research community (github.com/gandallab/brain_CTP_deconv). We identified significant brain CTP shifts for three neuropsychiatric diagnoses (Fig. 3), using PGSs to aid causal inference (Fig. 4).

We identified a potential causal role of endothelial cell loss on Alzheimer’s disease. This result was robust: to external replication; multiple sensitivity analyses; and demonstrated a dose-response relationship across the spectra of genetic risk, clinical progression, and neuropathological severity. Notably, the variance explained by endothelial CTP in diagnosis was comparable to APOE genotype status within the ROSMAP dataset. These findings are consistent with a recent human brain vascular atlas study which found endothelial cell loss and blood brain-barrier impairment in Alzheimer’s disease using snRNA-seq and immunostaining approaches (35), as well as evidence that brain endothelial cells mediate microglial activation and cognitive decline in mouse models (62). Our results advance these findings through an orthogonal approach, extending to a much larger sample size, and by using clinically meaningful measures of Alzheimer’s disease severity alongside extensive sensitivity analyses to ensure robustness. Furthermore, we identified relationships with other clinical variables related to Alzheimer’s disease including APOE ε4 genotype and brain MRI WMHs.

We also found relative increases in excitatory and inhibitory cells associated with Alzheimer’s disease diagnosis but not with genetic risk, suggesting that this CTP shift may be associated with a downstream disease process (or that our PGS analysis was underpowered). This seems paradoxical, as neuron death is observed in Alzheimer’s disease; however, it is important to note that these proportional data should be interpreted as a relative decrease in neuronal populations compared to the glial proportions. In a re-analysis of snRNA-seq data (33) and IHC data with clr-transformation (22), we also identified similar trends, and these are also reflected in recent work (63). While there is a well-established association between microglial activation and Alzheimer’s disease, we found no significant shift in microglial proportion. This stands in contrast to RNA-seq based deconvolution results in Alzheimer’s disease, which we suspect misconstrue microglial activation as an increase in cell proportion (64). Thus, Alzheimer’s disease-related microglial activation may reflect altered cellular state rather than a shift in microglia quantity.

Schizophrenia diagnosis was associated with decreased oligodendrocytes which, importantly, replicates previous findings from histological (65–67), neuroimaging (68) and transcriptomic studies (69). Increased schizophrenia PGS was associated with lower astrocyte CTP, whereas schizophrenia diagnosis was associated with increased astrocyte CTP although not to statistical significance. Previous gene expression studies have also found associations between schizophrenia diagnosis and proxies for increased astrocytes (69, 70), so it is possible that astrocyte CTP changes may reflect a compensatory process unrelated to genetic risk.

In line with previous findings of neural-immune activation in ASD (70, 71), we confirmed that ASD diagnosis was associated with increased microglia CTP. We did not find a genetic association between ASD PGS and microglia, but cannot rule out a causal effect because the ASD PGS is relatively underpowered.

There were substantial shifts in brain cell-type composition with increasing age and between sexes (Fig. 3, C and D), and these trends were consistent across studies and when excluding individuals with a neuropsychiatric diagnosis. The striking increase in oligodendrocytes during the first 20 years of life fits with extensive myelination occuring through adolescence and early adulthood (72). The decreasing trajectory of inhibitory neuron CTPs was also predominantly confined to early life. In contrast, there were more gradual compositional shifts with aging toward increased excitatory neurons and reduced microglia and endothelial cells. Regarding sex differences, males across cohorts tended to have relatively higher microglia CTP (Fig. 1B), as well as reduced excitatory neurons and increased inhibitory neurons.

Through GWAS, we identified common genetic variants associated with brain CTPs (Fig. 5). Despite the relatively small EUR sample size (n = 873) by GWAS standards, we identified significant associations for inhibitory neurons and astrocytes and for broader cell-type compositional shifts including one representing the neurovascular unit. Some of the GWS SNPs could be fine-mapped to genes with credible evidence of cell type–specific expression or functions [e.g., excitatory neurons: (DPY30 and MEMO1) and the neurovascular unit (P2RX5 and TRPV3)]. We hypothesize that markers of cell identity may be distinct from genes that affect cell-type composition, as they do not necessarily relate to cell proliferation and development.

Previous brain cell-type genetic analyses applied to RNA-seq data (primarily from the ROSMAP dataset) (60, 61) have suggested that neuronal CTPs are associated with variants within TMEM106B, a gene that is associated with frontotemporal dementia. In our analysis, SNPs proximal to TMEM106B were not associated with neuronal proportions, but did exhibit trending association with astrocytes (rs1990621; P = 1.98 × 10⁻⁶), a signal driven entirely within the ROSMAP dataset (Fig. 6). The lack of association in the smaller LIBD and UCLA_ASD datasets may be due to limited power or may reflect a cohort-specific bias within ROSMAP (noting that we ensured that older age did not drive this association). We propose a few other explanations for this disparity. With respect to differences between DNA methylation and RNA-seq deconvolution, it is possible that TMEM106B variants may, in fact, be associated with increased neuronal transcriptional activity [which RNA-seq deconvolution is sensitive to (18, 64)], rather than CTPs (which DNA methylation is better suited for). Compositionally aware data analysis may play a role: In the Li et al. analysis (60), the predominant cell type was astrocytes, and analyses of overlapping datasets found that astrocytes and neuronal proportions generally shifted in opposing directions (73). Thus, without a compositionally aware analytical framework, the TMEM106B locus that has previously been associated with neuronal proportion may reflect astrocyte proportion, which would be consistent with our findings.

Our careful validation of our brain CTP estimates is a major strength of our study. First, DNA methylation appears to be the most appropriate omics data modality for robust investigation of brain CTPs. This is because—in addition to favorable biological characteristics of DNA methylation that specifically sample nuclei and are unrelated to cellular activity—bulk deconvolution of brain CTPs is cost-effective to perform at scale, which ameliorates the large sampling biases that accompany postmortem brain dissection (23). Second, to ensure that our reference-based CTP estimates are robust, we performed extensive comparisons of references, marker selection methods, and deconvolution algorithms (note S1). We tested five independent reference panels, motivated by previous evidence that the reference is more important for accurate brain cell-type deconvolution than the method choice (29). We were reassured by the consistent estimates across these pipelines and good performance in external benchmarking (figs. S4 to S11). Third, we found strong relationships between reference-based estimates and reference-free approaches (figs. S9 and S10), which is notable as these approaches operate under entirely different assumptions. Last, we extensively compared our results to deconvolution from other omics modalities (bulk RNA-seq, single-cell RNA-seq, and IHC) (figs. S12 and S13 and S17 to S19), noting caveats to these comparisons.

The quality of our analysis was also aided by multiple sensitivity analyses, external replication, and our careful use of compositional data analysis techniques, as is appropriate. We advocate for greater uptake of compositional analysis to avoid false positives and violation of statistical assumptions. We provide more information about our approach and choices in note S2.

There are also limitations to this work. First, there is a lack of reasonably large gold standard benchmarking datasets to compare deconvolved CTPs to, as all existing modalities that count or deconvolve CTPs have limitations. Our approach to this problem was to triangulate an optimal cell-type deconvolution by comparing many different combinations of methods and modalities. However, the ideal dataset for comparison would benchmark multiple omics modalities derived from the exact same sample. Second, although this is one of the largest analyses of brain CTPs to date, it is still underpowered to perform genetic analyses. Ideally, the genetic analyses would include sensitivity analyses excluding participants with a neuropsychiatric diagnosis; however, this was not possible here given our small sample size (by GWAS standards). Third, we only analyzed CTPs from prefrontal cortex samples; this may not generalize to other cortical regions (which may also require dedicated reference panels). Fourth, there were substantial batch effects in the LIBD and ROSMAP datasets and batch-diagnosis interactions in LIBD. We accounted for potential batch effect confounders via statistical correction at the risk of overcorrection and losing diagnostic effects. Last, our conclusions are restricted to quantifications of cell types; it is possible that cell types may undergo diagnosis-related functional changes, without changes in proportions.

In conclusion, we deconvolved brain CTPs in 1270 participants and found changes in cell-type composition related to neuropsychiatric diagnoses (Alzheimer’s disease, ASD, and schizophrenia). Leveraging measures of genetic risk, we found evidence of a potential causal relationship between Alzheimer’s disease and loss of endothelial cells. We also replicate previous associations between ASD and increased microglia and between schizophrenia and reduced oligodendrocytes using orthogonal methods in larger datasets than previously. These results advance our understanding of the biology of neuropsychiatric traits, and they direct efforts to investigate and prioritize specific cell types as contributors to neuropsychiatric diagnoses.

MATERIALS AND METHODS

Experimental design

For the main analysis, we deconvolved brain CTPs for a total of n = 1270 prefrontal cortex samples after QC, aggregated from the ROSMAP (n = 300 diagnosed with Alzheimer’s disease and n = 419 undiagnosed), LIBD (n = 186 diagnosed with schizophrenia, n = 217 undiagnosed, and n = 72 donors under age 18 that were removed from the analysis for diagnosis to improve age and sex matching between cases and controls, but which were included in the analysis of age and sex), and UCLA_ASD studies (n = 31 diagnosed with ASD, n = 27 undiagnosed, and 18 donors removed to improve age and sex matching when testing for diagnostic associations but which were included in age and sex analyses). We characterized brain CTP shifts associated with diagnosis, age, and sex. We then leveraged genetic data available for a subset of n = 873 participants of European ancestry to identify associations between brain CTPs and PGSs and also to perform a GWAS. A schematic of experimental design is provided in Fig. 1.

Ethics

Our analysis used publicly available de-identified postmortem human brain data, and our analysis was therefore considered exempt from Institutional Review Board approval.

Bulk methylation data QC

For the ROSMAP and LIBD studies, we took raw .idat files (see the “Data and materials availability” section in Acknowledgment) and performed functional normalization using the meffil (74) pipeline, which outputs a normalized methylation beta matrix. For the UCLA_ASD study, we used the normalized beta matrix from the prefrontal cortex samples, available at https://doi.org/10.7303/syn8263588. All studies used the Illumina 450K DNA methylation array. We visualized batch effects using PCA. The ASD brain data had less noticeable batch effects (possibly because the downloaded data had already been batch corrected), but the ROSMAP and LIBD datasets had persisting, larger batch effects after functional normalization.

For the reference-free approaches [such as smartSVA (13) and MethylNet (30)], we sought to ensure that the identified drivers of variance or network effects were not related to batch effects. For this purpose, we performed ComBat (75) normalization [implemented in the sva (76) R package], batch correcting by plate while protecting the variables diagnosis, age, and sex. In some cases, this caused some beta values to become negative, which induces errors in cell-type deconvolution algorithms; for these values, we re-adjusted them to equal zero. Otherwise, for reference-based deconvolution approaches, we did not perform ComBat normalization on the bulk methylation data, and batch was instead corrected for as a covariate in the linear regression analyses. The rationale here was that the reference-based approaches were more robust to batch effects, and reference-based deconvolution algorithms do not handle negative methylation beta values.

Excluded probes

Using the normalized beta matrix, we subset to autosomal probes only and also excluded MASK probes (77).

Excluded samples

We excluded n = 32 samples (n = 16 from LIBD and n = 16 from ROSMAP) that failed the following meffil QC (default) filters: <0.1 of probes failing threshold of three beads, <0.1 of probes failing detection P < 0.01, <0.1 samples failing threshold of three beads, <0.1 samples failing detection P < 0.01, <5 SDs in determining whether the sample is a sex outlier, and <0.8 concordance threshold to determine whether the sample is an outlier. We also excluded samples to better balance study design in the analyses of relationships between brain CTPs and diagnosis. For the UCLA_ASD and LIBD study, we noted that the ASD and schizophrenia groups were significantly different in age from the within-study neurotypical groups. Hence, for analyses involving diagnostic comparisons, we excluded the 12 youngest participants (all in the ASD group) and the 6 oldest participants (all participants in the neurotypical group) to better balance the study design. For these same reasons, we also excluded n = 73 participants from the LIBD study (n = 72 not diagnosed with schizophrenia and n = 1 diagnosed with schizophrenia) using an age threshold of <18 years. However, these samples were still included in mega-analyses investigating the relationships between brain CTPs as well as age and sex.

Overall, with regards to sample size, we deconvolved brain CTPs for a total of n = 1270 individuals (n = 76 from UCLA_ASD, n = 475 from LIBD, and n = 719 from ROSMAP). We included all individuals in age and sex analyses, but only 1179 were included in the diagnostic comparisons to match by age.

Reference-based (supervised) cell-type deconvolution with sequencing reference data

For reference-based deconvolution, we extensively tested a variety of reference datasets, marker probe selection approaches, and deconvolution algorithms (Fig. 1B). Further details on other combinations of methods that we tested are provided in note S1.

Primary deconvolution pipeline

Reference dataset: Single-cell methylome sequencing

We used single-cell methylome sequencing data from Luo et al. (24), who applied single-nucleus methylcytosine, chromatin accessibility, and transcriptome sequencing (snmCAT-seq) to 15,030 cells derived from postmortem human frontal cortex tissue from n = 2 healthy male donors in their 20s. This dataset identified a total of 20 major cell subtypes, of which 9 were excitatory neuronal, 8 were inhibitory neuronal, and 5 were glial or non-neuronal (astrocytes, endothelial cells, microglia, oligodendrocytes, and OPCs). It included counts of methylated and unmethylated cytosine bases across the genome. The cell subtypes had been identified by applying a chi-squared test to a multirow contingency table of the methylated/unmethylated cytosine base counts, as previously described (24). Using this sequencing dataset, we summed read counts across cell subtypes, such that our final dataset had methylated and unmethylated cytosine counts for seven cell types: excitatory neurons, inhibitory neurons, astrocytes, endothelial cells, microglia, oligodendrocytes, and OPCs.

We subset the methylation sequencing data to CpG sites overlapping with the Illumina 450K array and then summed reads within a ±50-bp window around these CpG sites [on the basis of methylation being highly locally correlated, so this approach improves genome coverage (78)]. Then, we took sites with coverage >10 read counts across all seven cell types, leaving n = 58,352 methylation sites from which to identify cell-type markers (Fig. 1B).

We QCed these reference data of methylated/unmethylated cytosine sequencing read counts using the following steps: (i) taking cytosine sites with >10 read counts and (ii) excluding cytosine sites on sex chromosomes or overlapping with MASK probes on the Illumina 450K array, which have been demonstrated to have quality issues including cross-hybridization (77).

Marker selection: Based on extremes

In the primary analysis, we identified reference cell-type DNA methylation markers based on how extreme their methylation profiles were relative to the other cell types. For this, we converted the filtered methylation sequencing counts into beta values (methylated read counts per total read counts). Marker sites were those where one cell-type had beta ≤ 0.4, whereas all other cell types had beta ≥ 0.6 (down-methylated marker site) or vice versa (up-methylated marker site). We selected this 0.4/0.6 split as this provided at least ~100 marker sites for each of the cell types. We were left with n = 983 excitatory neurons markers, n = 99 inhibitory neuron markers, n = 499 astrocyte markers, n = 682 endothelial cell markers, n = 763 microglia markers, n = 423 oligodendrocyte markers, and n = 838 OPC markers. Most of the marker sites were unmethylated for all cell types except for inhibitory neurons (fig. S1), which is consistent with previous findings (20). The inhibitory neuron reference had fewer marker sites than other cell-type references, but we found that relaxing criteria to increase the number of marker sites destabilized the deconvolution. We additionally experimented with marker selection for the sequencing reference using a chi-squared statistic approach but found that this was inferior (fig. S7C).

Validation of marker selection

We visualized the beta values for these markers within the reference dataset to check that they captured differentially methylated sites between cell types (fig. S1). We confirmed that the probes were able to distinguish between the array reference of sorted cell-type populations (fig. S2). We checked that the probes had relatively consistent effects across all bulk DNA methylation samples and were not susceptible to strong batch effects (fig. S3).

Deconvolution: Houseman algorithm

The classic Houseman method applies non-negative matrix factorization and quadratic programming to bulk methylation data to estimate CTPs (15). We used the minfi implementation (79).

Comparison with alternative reference-based deconvolution pipelines

1. methylCC

Comparison is shown in fig. S5.

Reference dataset:

Single-cell methylome sequencing from Luo et al. 2023 (24) as described above.

Marker selection:

The methylCC algorithm models marker sites as being fully methylated or unmethylated (0 or 1, respectively), with variation around that modeled as a random variable to capture platform-specific effects. Hence, for methylCC deconvolution, we converted the reference marker probes beta values into binarized 0/1 coding, depending on which extreme they were closest to.

Deconvolution algorithm:

Deconvolving array-based bulk data from sequencing-based reference data may not account for cross-platform differences (17). The methylCC package (17) was designed for this and extended the conventional Houseman (15) approach to account for cross-platform differences. It does this by selecting the probes with the strongest biological signal (i.e., differentially methylated) and then in the deconvolution algorithm, includes a random effect to model platform-specific variation. Within each study, we additionally deconvolved within each batch before aggregating the deconvolved cell types together and correcting for batch post hoc (explained further in note S1 and fig. S4A).

2. CelFiE

Comparison is shown in fig. S5.

Reference dataset:

Single-cell methylome sequencing from Luo et al. 2023 (24) as described above.

Marker selection

As described in the primary analysis.

Deconvolution algorithm:

CelFiE (78) involves an expectation maximization algorithm and is optimized for sequencing reference and target data as well as for circumstances where the cell-type mixture is highly heterogeneous (i.e., in the case of circulating cell-free DNA in the blood). One advantage of CelFiE is that it also models a specified number of unknown cell types.

3. NeuN^+/− (the historical benchmark)

To benchmark the performance of deconvolution to granular cell types, we estimated CTPs using the most commonly used NeuN^+/− reference. We then compared the sum of glial cell types (astrocytes, endothelial cells, microglia, oligodendrocytes, and OPCs) to the NeuN⁻ proportion and the sum of neuronal cell types (excitatory/glutamatergic and inhibitory/GABAergic) to the NeuN⁺ proportion (fig. S5).

Reference dataset:

Methylation Illumina 450K array data from Guintivano et al. (80), available on Bioconductor as FlowSorted.DLPFC.450k, providing n = 29 NeuN+ and n = 29 NeuN⁺ methylome profiles. We QCed this reference dataset using the minfi (79) implementation of functional normalization and excluded from cell type–specific probe selection those that were on sex chromosomes, MASK_general probes [which are known to cross-hybridize and have other quality issues (77)], or that were also SNPs. We also confirmed that the methylomes clustered as expected by plotting the first three PCs and generating Uniform Manifold Approximation and Projection for Dimension Reduction (UMAP) plots.

Marker selection

Using the eBayes t test implemented in the TOAST package (16) to select marker probes (100 up-methylated and 100 down-methylated)

Deconvolution algorithm:

Houseman algorithm.

4. WGBS/FACS

This reference dataset is similar to that used in the primary analysis; however, the deconvolution is less granular and includes non–brain cell types that are used as proxies. Comparison is shown in fig. S6.

Reference dataset and marker selection:

Publicly-available DNA methylation atlas with reference markers derived from methylation whole genome bisulfite sequencing (WGBS) of FACS sorted cell populations (27). From this reference panel, we included both brain-specific cell types (neurons, oligodendrocytes), and “proxy” cell types (macrophages/monocytes to represent microglia, and endothelial cells to represent brain endothelial cells).

Deconvolution algorithm:

We used the accompanying published deconvolution algorithm to estimate brain CTPs, which uses a non-negative least squares approach.

5. EpiSCORE RNA-based pipeline

The advantage of using single-cell RNA-seq profiles is that it permits higher cell-type resolution than what is typically possible with single-cell DNA methylation. This deconvolution pipeline permitted deconvolution of neurons, astrocytes, endothelial cells, microglia, oligodendrocytes, and OPCs. Comparison shown is in fig. S6.

Reference dataset and marker selection:

Publicly available cell-type DNA methylation markers inferred from single-cell RNA-seq profiles (28).

Deconvolution algorithm:

EpiSCORE deconvolution algorithm (28).

6. Methylation array reference pipeline

Comparison is shown in figs. S7 and S11.

Reference dataset:

We gathered Illumina 450K methylation array profiles from seven cell types: glutamatergic neurons (n = 5, GSE50853) (20), GABAergic neurons (n = 5, GSE50853) (20), astrocytes (n = 2, GSE40699 and GSE92462) (81), endothelial cells (n = 3, GSE137830) (82), oligodendrocytes [n = 45; (63)] (31, 83), and OPCs (n = 1, GSE92462) (81). In the absence of publicly available microglia datasets, we used monocytes as a proxy as they share a developmental lineage. For this, we obtained monocyte methylome profiles from the FlowSorted.Blood.450k data available on Bioconductor (84).

Marker selection:

We compared eBayes t test versus row t test marker selection for the array reference (fig. S7), settling on the eBayes t test.

Deconvolution algorithm:

Houseman algorithm.

Benchmarking and evaluation of deconvolution quality

Benchmarking of deconvolutions against pure cell-type populations

As a key benchmark for these alternative reference datasets and deconvolution algorithms, we applied our deconvolution method to FACS-sorted brain cell-type populations profiled using DNA methylation array (63). Therefore, we would expect these data to represent “pure” cell-type populations sorted on the basis of two cell markers: NeuN positive (neurons), Sox10 positive (oligodendrocytes/OPCs), and NeuN and Sox10 negative or “double negative” (for all other cell types) (fig. S8).

Comparison to reference-free deconvolution

We used unsupervised approaches as an orthogonal form of validation for the supervised approach (figs. S9 and S10).

smartSVA

We applied the smartSVA algorithm (13) to data that had been batch-corrected using ComBat (75, 76) (protecting the variables diagnosis, age, and sex, and zeroing any negative values induced by batch correction). In the smartSVA analysis, we removed probes with any not applicable (NA) values across the samples and protected the variable corresponding with diagnosis. We looked for correlation between sSVs and reference-based methods (fig. S9).

MethylNet

We used a variational autoencoder (VAE) deep learning method as implemented in the MethylNet package(30) to compress the data into salient variables (embeddings) in a nonlinear framework. The package trains a VAE to encode the β values of a sample into an embedding in a lower dimensional latent space and reconstructs the original β values from the embedding. Using the launch_hyperparameter_search command of the package, we generated 50 models each with 2 and 10 latent variables, generating different neural network topologies with varied hyperparameters such as learning rate, weight decay, disentanglement, and number of layers. The model with the lowest validation loss for each number of latent variables was chosen to generate embeddings. The VAEs were trained on bulk methylation datasets aggregated across the three studies. We looked for correlation between these embeddings and reference-based methods (fig. S10). The final hyperparameters were n_epochs = 700, best_epoch = 669, min_loss = 129526199.314208, min_val_loss = 14275442.5, min_val_kl_loss = 9555.58544921875, min_val_recon_loss = 14265887, min_loss-batchsize_adj = 131109297.305827, min_val_loss-batchsize_adj = 14418196.925, min_val_kl_loss-batchsize_adj = 9651.14130371093, min_val_recon_loss-batchsize_adj = 14408545.87, min_val_beta-adj_loss = 14265906.1111709, n_input = 388841, n_latent = 10, hidden_layer_encoder_topology = [200, 200, 100], learning_rate = 0.00005, weight_decay = 0.0001, beta = 500, kl_warm_up = 20, train_batch_size = 50, and val_batch_size = 50.

CETGYO error metric (RMSE) calculation

We calculated the CETGYO error metric (85) (a RMSE measure) for the Houseman deconvolutions (fig. S11). Here, the CETGYO error metric was calculated by multiplying the reference cell-type methylation profiles by the estimated CTP, to “reconstitute” the initial beta matrix. In general, CETGYO error ≤ 0.10 indicates good quality deconvolution.

Comparison to CTP representations from orthogonal omics technologies

We used Pearson’s correlation coefficient to evaluate associations between CTPs derived from different technology platforms on matching individuals, described in turn below. In all cases, for the CTP variables, we converted counts to proportions (for the single-cell data) and then performed clr-transformation to account for compositionality.

1. RNA-seq WGCNA module eigengenes representing cell types (UCLA_ASD, LIBD) (70): We leveraged previously generated WGCNA network modules, which had previously been generated using RNA-seq data, for matching brains in the UCLA_ASD (n = 49) and LIBD (n = 394) studies. These network modules were annotated to cell types based on the presence of cell-type marker genes within these networks. For matching brains across the RNA-seq and bulk methylation datasets, we then compared module eigengenes (interpreted as a quantification of that cell type) to the methylation deconvolved CTPs (fig. S12).

2. Comparison to deconvolved proportions from bulk RNA-seq data (UCLA_ASD, LIBD) (7): These CTPs had previously been derived from non-negative matrix factorization on bulk RNA-seq data using markers from single cell data. We used data from n = 473 samples that had matching methylation data in UCLA_ASD and LIBD from the PsychENCODE dataset (fig. S12).

3. Comparison to proportions from single cell counts (ROSMAP) (33): These CTPs were derived from counting cell types from single-cell data sequenced from n = 48 ROSMAP participants, including n = 37 individuals who were included in our bulk DNA methylation dataset (fig. S13). The raw cell counts were converted into proportions.

4. Comparison to IHC proportions (ROSMAP) (22): These CTPs were previously derived from IHC proportions (22) from n = 49 ROSMAP participants who were also included in our bulk DNA methylation dataset (fig. S13).

5. Comparison to proportions from single cell counts (UCLA_ASD) (32): These CTPs were derived from counting cell types from single-cell data sequenced from n = 60 samples from UCLA_ASD, including n = 17 individuals who overlapped with our bulk DNA methylation dataset (fig. S13). The raw cell counts were converted into proportions.

We also attempted to account for variation in CTPs that could be due to dissection of different tissue specimens from the same brain donor. We achieved this by removing the oligodendrocyte proportion and rescaling the neuronal cell populations to sum to 100% (tables S11 and S12). The rationale for this is that different depths of gray matter dissection would capture variable quantities of white matter, reflected in variable oligodendrocyte proportion. As other glial cells are expected to be relatively evenly distributed throughout white and gray matter, only the neuronal cell population was scaled, so that the total sum of CTPs (excluding oligodendrocytes) summed to 100%.

Consistency and comparison to expectation

In determining the optimal deconvolution method, we also considered whether the deconvolution was relatively consistent across methods and ensured that the CTPs were concordant with expectation; for example, that neurons and oligodendrocytes were the major cell types (63) and that endothelial cells, microglia, and OPCs were of low abundance.

Phenotype data

Our primary variables of interest were neuropsychiatric diagnoses: Alzheimer’s disease, schizophrenia, and ASD. Within the ROSMAP dataset, we also leveraged continuous measures of Alzheimer’s disease severity based on clinical (based on final consensus diagnosis) and neuropathological (Braak score; corresponding to histopathological progression of neurofibrillary tangles) assessments. The final consensus diagnosis measure is based on a physician’s overall cognitive diagnostic category following full review by a neurologist of all available clinical data (but no postmortem histological data). It is scored as 1: no cognitive impairment (NCI), 2: mild cognitive impairment (MCI) and no other cause of cognitive impairment (CI), 3: MCI with other cause of CI, 4: Alzheimer’s dementia and no other cause of CI, 5: Alzheimer’s dementia with other cause of CI, and 6: other primary cause of dementia. We regrouped these categories into NCI, MCI, AZD, and other primary cause of dementia for statistical analysis and regressed against endothelial cell proportion in an ANOVA model.

As covariates, we focused on age, age², sex, and batch variables in our analyses, as these were common across all three datasets. For brevity, these are referred to as baseline covariates in the main text. Where there were multiple batch variables, we selected the single batch variable with the strongest effect after careful exploration of the data, indicating that this was sufficient: For ROSMAP, this was the batch variable corresponding to a different thermocycler being used; for LIBD, this was plate; and for UCLA_ASD, this was the processing batch variable. For ROSMAP, the age data were censored, whereby participants aged over 90 were assigned to be “90+.” For these individuals, we imputed age to be 90.

Testing for group differences in CTPs

We performed statistical testing to address two questions:

1. What are the effect sizes of each cell-type on diagnosis, and

2. Whether there are any global shifts in CTPs with diagnosis.

We were careful to use compositional data analysis approaches, whose importance are summarized in note S2.

First, to quantify the effect sizes of each cell-type on ASD diagnosis, we applied a clr-transformation to the CTP data and set the lowest value to equal 0.001 (the “offset”) to handle the log transformation. This analysis then becomes compositionally aware as proportions become interpreted relative to the geometric mean (with log transformation). However, while more easily interpretable, the clr-transformation has limitations compared to the compositional PCA approach (described below), including that the chosen offset value can affect the results.

Second, to test for global shifts in CTPs, we performed logistic regression for two models and tested for the contribution of CTPs by comparing these two models in a likelihood ratio test:

$$\text{Model} 0:\text{Diagnosis}\sim \text{age}+\text{sex}+\text{batch}$$

$$\text{Model} 1:\text{Diagnosis}\sim \text{age}+\text{sex}+\text{batch}+{\displaystyle \sum _{n=1}^i}\mathrm{P}{\mathrm{C}}_n^{\text{CTP}}$$

To quantify the variance in diagnosis associated with cell-type shifts, we performed compositionally aware PCA (using an Aitchison transformation) on the matrix of estimated CTPs per sample. Briefly, the rationale for this is that CTPs are a form of compositional data; by summing up to 100%, this induces correlations between estimates. In contrast, PCs of compositional data are orthogonal variables, which can then be input as dependent variables in conventional linear models. We took the first i PCs that explained >95% of the variance and input these as covariates in model 1 above.

Sensitivity analysis: Robustness of diagnostic associations to batch effects

Given that the LIBD and ROSMAP datasets had large batch effects, we also performed within-batch sensitivity analyses, regressing clr-transformed CTPs against diagnosis and covariates and focusing on the cell types with statistically significant diagnostic associations.

For the LIBD dataset, there was confounding between plate and diagnosis for two plates (plate Lieber_30 had schizophrenia patients only, and Lieber_104 had undiagnosed individuals only), so we performed these sensitivity analyses within the three batches, which had both schizophrenia and undiagnosed groups. For diagnostic associations with endothelial cells and oligodendrocytes, two plates had consistent directions of effect with nominal or trend-level significance; for OPCs, the relationship appeared to be driven by one plate (plate Lieber_244).

For the ROSMAP dataset, the directions of effect were consistent across batches for endothelial cells, excitatory neurons, and inhibitory neurons. The effects tended to be driven by batch 1, although this may be related to power (batch_1: n = 453 versus batch_0: n = 265).

External replication of phenotypic associations

We drew upon the BDR (31) dataset to replicate the association between reduced endothelial cells and Alzheimer’s disease that had initially been identified in ROSMAP. The replication BDR dataset included DNA methylation array data for n = 597 donors of prefrontal cortex samples, with QC performed previously (31). We used Braak score as the clinical variable for replication as the BDR dataset was essentially ascertained for Alzheimer’s disease (and therefore has few controls) and has systematically collected data on neurohistopathology and also because these histological changes would be expected to be a more “biologically proximal” process to brain CTP shifts.

Mega-analysis for age and sex

We performed a mega-analysis to identify age and sex associations with brain CTPs. In this analysis, we included the n = 7 UCLA_ASD and n = 73 LIBD participants that had previously been excluded to balance the study design. For the age (and age²) analysis, we included sex and batch as covariates. For the sex analysis, we included age, age², and batch as covariates.

Genotyping QC

General QC

In general, we applied the same QC filters to each of the datasets. Additional details that are specific to each dataset are described below. Genotyped SNPs were removed if they fulfilled any of the following criteria: HWE P < 1 × 10⁻⁶, MAF < 0.01, individuals with missingness > 0.1, and variants with missingness > 0.05. Pre-imputation QC was performed using the Will Rayner pre-imputation genotyping toolbox (www.well.ox.ac.uk/~wrayner/tools/). Autosomal SNPs were imputed using Minimac4 TOPMed Imputation Server (86, 87). The choice of imputation panel depended on the ancestry make-up of the dataset. After imputation, the following filters were applied: HWE P < 1 × 10⁻⁶, MAF > 0.01, genotype missingness < 0.05, and INFO score > 0.3. We performed lift-over of datasets to the hg38 build.

ROSMAP

We extracted biallelic SNPs from ROSMAP whole-genome sequencing (WGS) data and imputed to the Haplotype Reference Consortium reference panel (88). We used WGS data rather than the ROSMAP SNP genotyping data, as there was high genotype missingness across samples, leading to considerable sample drop out among the participants with overlapping bulk methylation data. There were n = 6 individuals with duplicate WGS samples passing QC, so we excluded the following samples: SM-CTEIJ, SM-CTEMN, SM-CTEI8, SM-CTEN3, SM-CTED9, and SM-CTEE2. After applying the aforementioned QC filters, there were n = 633 individuals and n = 7,753,174 SNPs, of which n = 623 people were genetically inferred to be of European ancestry, and of which n = 621 had complete data for all covariates.

LIBD

The LIBD genotyping data were collected across two arrays: the Illumina 1M array (n = 329) and the Illumina h650 array (n = 133). We chose the TOPMed reference panel (89) for imputation as the dataset included people of both European (EUR) and African (AFR) ancestry. After QC and merging data from the two genotyping panels together and filtering for individuals with matching bulk methylation data, there were n = 462 individuals (EUR, n = 220; AFR, n = 216; SAS, n = 1; and other/admixed, n = 25) and 15,518,464 SNPs. After examining for population stratification among Europeans using genotyping PCs using a genetic relatedness matrix (GRM) calculated using linkage disequilibrium (LD) pruned SNPs, we excluded an additional n = 3 participants. Overall, after genotyping QC for GWAS, there were 7,845,067 SNPs, including n = 210 individuals of European ancestry.

UCLA_ASD

This dataset had a total of n = 105 individuals, with imputation to the Haplotype Reference Consortium reference panel (88). There were n = 53 individuals (EUR, n = 44; AFR, n = 2; SAS, n = 2; EAS, n = 1; and other/admixed, n = 4) with matching bulk methylation data including those who were excluded in case/control analyses to balance the study design. For PGS analyses, we considered the 44 individuals of European ancestry, of which n = 35 were included for direct comparisons of diagnostic groups to balance for age differences. For GWAS, genotyping QC was modified to avoid the MAF filter excluding excessive numbers of SNPs in this small study. Specifically, we applied the aforementioned QC filters to both the full n = 105 multi-ancestry dataset and the subset of n = 88 genetically inferred Europeans before filtering again to the n = 44 individuals of European ancestry with matching bulk methylation data. To examine for population stratification, we generated genotyping PCs using a GRM calculated using LD pruned SNPs and excluded n = 2 participants. After genotyping QC for GWAS, there were 6,051,638 SNPs, of which n = 42 people were of European ancestry.

Merged genotypes

We merged the above three datasets together, and performed additional PLINKv1.9 (90) QC on this dataset using the following flags: --geno 0.05, --hwe 1 × 10⁻⁶, --maf 0.01. There were n = 1113 people across ancestries with matching bulk methylation data (EUR, n = 900; AFR, n = 181; SAS, n = 3; EAS, n = 1; and other/admixed, n = 28). We filtered for people of European ancestry (see “Ancestry inference and relatedness” below; n = 885) and then subset to unrelated individuals (relatedness coefficient < 0.05), leaving n = 878 individuals of European ancestry (ROSMAP, n = 623; LIBD, n = 211; and UCLA_ASD, n = 44) and 4,857,536 SNPs.

Ancestry inference and relatedness

We built a GRM based on the merged genotypes. Ancestry was inferred by projecting the samples onto the first two PCs from the 1000G reference (filtering for common HapMap3 SNPs with MAF > 0.05 in the 1000G reference) (fig. S24). Ancestry was assigned on the basis of being within 4 standard deviations of the 1000G reference population.

For downstream genetic analysis, we focused on the subset with European ancestry (n = 877), as there were too few non-European participants to perform a sufficiently powered genetic analysis (n = 480) and also because the available GWAS summary statistics for polygenic scoring were from European populations and therefore have poorer prediction accuracy in non-European target populations.

To capture population stratification in the European subset for use as covariates, we built a GRM, filtered for unrelated participants (relatedness coefficient < 0.05), filtered for LD pruned SNPs (flag --indep 50 5 2, corresponding to settings: 50-kb window, step size of 5, and variance inflation factor (VIF) threshold of 2), and then calculated genotyping PCs. For the GWAS meta-analysis, we calculated genotyping PCs representing population stratification for the aggregated European subset across the ROSMAP, LIBD, and UCLA_ASD datasets (used in the PGS analysis; fig. S24) and also within each dataset (used in the GWAS analysis).

Polygenic scores

We calculated PGS weights for ASD (36), schizophrenia (37), Alzheimer’s disease [specifically using the Marioni et al. (38) GWAS summary statistics for reasons described previously (91)], WMHs (42), major depressive disorder (39), years of education (also referred to as educational attainment) (40), and height (41) as a negative control. After filtering the summary statistics for HapMap3 SNPs that were also in the target dataset, we calculated SNP weights using SBayesR (92) and the UK Biobank banded LD reference download from the GCTB website (https://cnsgenomics.com/software/gctb/). We used the same pi and gamma settings for each phenotype (--pi 0.95,0.03,0.01,0.01, --gamma 0,0.01,0.1,1) but changing the heritability setting between traits: ASD --h2 0.5; schizophrenia --h2 0.7, Alzheimer’s disease --h2 0.7, major depressive disorder --h2 0.4, years of education --h2 0.4, height --h2 0.8. For binary traits with odds ratio summary statistics, we took the log transformation as the input effect size. Using these SBayesR weights, we then calculated PGSs for each European participant by multiplying the SNP weights by that individual’s allele dosage using the --score function in PLINKv1.9 (90).

Prediction of diagnosis and CTP traits using PGS

We used linear models to identify associations between PGS and both diagnosis categories (for ASD, schizophrenia and Alzheimer’s disease) and brain CTP traits. For the diagnostic associations, we performed analyses within each study, including as covariates age, age², sex, and three genotyping PCs representing population stratification (fig. S25). For the brain CTP associations, we included all controls and cases for the PGS of interest, including covariates for age, age², sex, diagnosis, and three genotyping PCs. We also explored whether the inclusion of 3 genotyping PCs was sufficient, finding that the inclusion of 10 genotyping PCs made negligible difference to results.

Mediation analysis

We performed mediation analysis for AZD PGS → endothelial CTP → AZD within the ROSMAP dataset, using the R mediation package. This generates two estimates: the average causal mediation effect (ACME)—which represents the mediating effect of endothelial cells—and the average direct effect (ADE)—which represents the direct effect of Alzheimer’s PGS → Alzheimer’s diagnosis.

Mendelian randomization

We performed Mendelian randomization (MR) using GWAS summary statistics to test for causal associations between endothelial CTP → Alzheimer’s disease, and Alzheimer’s disease → endothelial CTP. As different methods operate under slightly different assumptions, we tested multiple MR methods, as is typical: CAUSE, IVW, MR-Egger, weighted median, weighted mode, GSMR (93–98). To identify instrumental SNPs for Alzheimer’s disease, we used conventional P value thresholds (P < 1 × 10⁻³; P < 1 × 10⁻⁸ for all other methods). The endothelial CTP GWAS has no GWS SNPs (which violates a core MR assumption), so we used a more relaxed P value threshold for instrumental SNPs (P < 1 × 10⁻³ for CAUSE; P < 1 × 10⁻⁵ for all other methods). We also performed power calculations using https://sb452.shinyapps.io/power/ for analyses in both causal directions.

APOE genotype imputation

We imputed the APOE genotype from the SNPs rs429358 and rs7412, as previously described in www.snpedia.com/index.php/APOE according to table S13.

Genome-wide association study

We took a meta-analysis approach to identify genetic variants associated with brain CTPs. We chose meta-analysis over mega-analysis to mitigate batch effects and because each study had variable demographic characteristics that could confound results. For the phenotype data, we applied an inverse normal transformation (as is typical in GWAS) to each clr-transformed CTP or CTP_PC.

As we were performing one GWAS per study for meta-analysis, we also recalculated a per-study GRM and regenerated genotyping PCs among the European participants. In this genotyping PC-based QC step, from UCLA_ASD, we excluded AN01093_BA9 and AN00764_BA9 for being genotyping PC outliers; from LIBD, we excluded Sample137/Br1878, Sample153/Br1876, Sample487/Br1113, Sample631/Br1427, Sample541/Br2090, and Br1684/Sample664 for being genotyping PC outliers, and from ROSMAP, we excluded SM-CJFOM, SM-CJGIK, SM-CJK4S, SM-CJK5A, SM-CTDR9, SM-CTDRF, and SM-CTED9 based on the rel < 0.05 filter in GCTA (in addition to the n = 6 duplicate samples excluded earlier: SM-CTEIJ, SM-CTEMN, SM-CTEI8, SM-CTEN3, SM-CTED9, and SM-CTEE2). After this genotyping PC-based QC, this left n = 873 individuals for GWAS.

We performed a linear model GWAS meta-analysis, implemented in the GCTA (47) fastGWA module. We included the following covariates: age, age², sex, batch, diagnosis, and five population stratification genotyping PCs from that dataset. We used METAL (99) to combine the per-study test statistics and SEs and then filtered for SNPs that were present in all of the studies, with heterogeneity (Cochran’s Q test) P < 0.001 and MAF > 0.05 in all datasets. This left more than 4 million SNPs per CTP GWAS (excitatory neurons: 4,052,158; inhibitory neurons: 4,047,728; astrocytes: 4,033,521; endothelial cells: 4,044,819; microglia: 4,057,334; oligodendrocytes: 4,017,933; and OPCs: 4,063,783). We then identified independent loci among SNPs with P < 1 × 10⁻⁵ using GCTA-COJO (46, 47), which applies conditional and joint analysis to summary statistics. We used the individual-level genotyping data as a LD reference, and used the following settings: --cojo-slct, --cojo-actual-geno, --cojo-p 1e-5. Manhattan and LocusZoom plots were visualized using GeneticsMakie v0.1.5 (100).

SMR analysis

We performed Summary-data-based Mendelian Randomization (SMR) analysis (48) using cis-eQTL summary statistics from the BrainMeta dataset (101). As SMR instruments, we selected SNPs with GWAS P < 1 × 10⁻⁶ and then performed SMR within the chromosome for these SNPs. We used default SMR settings.

Colocalization analysis

For the GWS SNPs without a statistically significant SMR association, we also performed colocalization analysis (102). This method takes a Bayesian approach, assigning posterior probabilities to various hypotheses. We focused on PPH4 statistics, which represents the posterior probability that the two traits are genetically associated and share the same causal variant. As reference eQTL and sQTL datasets, we used MetaBrain (103), PsychENCODE (7), BrainMeta (101), and a cell type–specific eQTL dataset (59).

Supplementary Materials

This PDF file includes:

Notes S1 to S6

Figs. S1 to S42

Legends for tables S1 to S13

References

Other Supplementary Material for this manuscript includes the following:

Tables S1 to S13