Continuous measurement of dynamic classroom social interactions

Abstract

Human observations can only capture a portion of ongoing classroom social activity, and are not ideal for understanding how children’s interactions are spatially structured. Here we demonstrate how social interaction can be investigated by modeling automated continuous measurements of children’s location and movement using a commercial system based on radio frequency identification. Continuous location data were obtained from 16 five-year-olds observed during three 1-h classroom free play observations. Illustrative coordinate mapping indicated that boys and girls tended to cluster in different physical locations in the classroom, but there was no suggestion of gender differences in children’s velocity (i.e., speed of movement). To detect social interaction, we present the radial distribution function, an index of when children were in social contact at greater than chance levels. Rank-order plots indicated that children were in social contact tens to hundreds of times more with some peers than others. We illustrate the use of social ties (higher than average levels of social contact) to visualize the classroom network. Analysis of the network suggests that transitivity is a potential lens through which to examine male, female, and mixed-sex cliques. The illustrative findings suggest the validity of the new measurement approach by re-examining well-established gender segregation findings from a new perspective.

Current understanding of early classroom social interaction relies primarily on experts’ manual coding of interactions. However, the quantity of data that experts can extract in any given observation period is limited. The interaction partners of each child in the class-room are typically observed sequentially rather than concurrently. Sequential observations do not allow for continuous capture of the social behavior of all children in the classroom. This paper explores an alternative approach that captures each child’s interaction with every other child—objective, continuous measurement of class-room behavior—using commercially available location-based tracking. Here we validate the approach by providing objective measurements of gender-specific social interaction (Martin, Fabes, & Hanish, 2018), while offering novel perspective on features of classroom interactions such as the heterogeneous distribution of children’s social contacts.

Expert observation of young children’s classroom interactions underscores the importance of mutual proximity to social affiliation (Daniel, Santos, Peceguina, & Vaughn, 2013; Santos, Daniel, Fernandes, & Vaughn, 2015; Schaefer, Light, Fabes, Hanish, & Martin, 2010). When children are in high mutual proximity, they are likely to direct social attention, interaction bids, and friendship nominations to each other. There are two central approaches to the automated measurement of child proximity. Egocentric (child-centered) approaches measure a child’s social contact without respect to spatial location. Allocentric (location-based) approaches measure a child’s social contacts within classroom space.

Using an egocentric approach to social contact, children wear badges that record contact when a child is physically proximal to another. In a recent example, Veiga et al. (2016) found that the mean duration of a child’s contact with other children was positively associated with teacher ratings of the child’s social competence. While promising, badge-based technologies have several notable limitations. First, badges do not provide a principled means for inferring the distance at which children are in social contact. The distance at which A and B are deemed to be in social contact is based on a priori parameters defined by the badge manufacturer’s firmware. Relatedly, badges provide only an egocentric (A is near B) view of social interaction, but do not indicate where that interaction occurs in the classroom. This leaves open the possibility that A is near B because both prefer the reading area. More formally, egocentric tracking cannot dissociate social preference from location preference.

A promising alternative is an allocentric approach that involves automated recordings of children’s location produced by a tag-based radio-frequency identification (RFID) system. Irvin, Crutchfield, Greenwood, Kearns, and Buzhardt (2017) validated the three-dimensional spatial location measurements provided by a RFID system (manufactured by Ubisense) using a stationary tag (average SD = 13.9 cm) and a moving child walking a predetermined course (average SD = 11.8 cm). The spatial measurements were then used to visualize two children’s predilections for different areas of a classroom during a 90-min observation. Recent reports suggest the feasibility of employing this approach in the preschool classroom (Killijian, Pasqua, Roy, Trédan, & Zanon, 2016). However, automated allocentric measurement of multiple children interacting within a classroom has not yet been described, nor has a principled means of social contact from distance been proposed. Here we provide an approach to inferring and analyzing preschool social interactions based on a commercial system for tracking children’s movements.

We use the well-documented social phenomenon of children’s sex segregation as proof of concept for our novel application of automated measurements in the classroom. Kindergarten children tend to form gender-segregated, transitive social ties (Daniel et al., 2013; Schaefer et al., 2010). By 4–5 years of age, both boys and girls interact with same sex peers three to four times more often than with other sex peers (Martin et al., 2013). Sex differences in the use of classroom space have also been documented (Torrens & Griffin, 2013). Expert coding of the social activity and location of each child via a geographic information system interface indicated that boys tended to pursue social and nonsocial activities in different classroom areas while girls exhibited a more mixed use of space. However, the time-consuming nature of such an approach means that much is unknown about the spatial underpinnings of children’s social interactions in the classroom.

The present study illustrates how conventional and novel measures of classroom social activity can be efficiently measured using commercially available continuous measurement technology. The technology provides the physical location of each child multiple times per second. To investigate spatial indices of sex segregation, we document where boys and girls cluster in the classroom (the probability distributions of their location). Children initiate and terminate social contact by moving toward and away from peers. Velocity indexes the speed of this movement and shows sex differences. Boys are slightly (and somewhat variably) faster than girls in timed runs between four and six years of age (Thomas & French, 1985). To illustrate the rich data provided by objective classroom measurements, we measured velocity during everyday classroom activities to better understand similarities and differences in boys’ and girls’ movement parameters.

A fundamental task for objective measurement approaches is indexing social contact. Using children’s observed movement patterns, we introduce a bottom-up, data-driven measure of social contact, the radial distribution function. Importantly, the radial distribution function estimates when social contact occurs at greater than chance levels. This, in turn, allows for examination of the distribution of children’s social contacts. That is, we ask whether children have relatively equal levels of social contact with their peers or whether they prefer some peers to others, and to what degree (Hartup, Laursen, Stewart, & Eastenson, 1988; Santos & Vaughn, 2018). We use the term “prefer” to indicate social contact between two peers where social contact refers to greater than chance levels of colocation.

Social tie networks describe the strength of affiliations between members of a classroom based on the frequency of their social interaction (Moreno & Jennings, 1938). Transitivity describes the likelihood that two children have a social tie if they have a social tie with a third child (Holland & Leinhardt, 1970). Gender-based social tie networks and gender-driven transitivity effects are well-established in the literature (Martin, Fabes, Hanish, & Hollenstein, 2005). We examine these phenomena using continuous assessments of social interaction, validating our procedure by grounding it in the extant literature.

Children’s classrooms networks have been explored through expert coding (Schaefer et al., 2010) and teacher reports of peer preference (Chen, Lin, Justice, & Sawyer, 2017), but not through objective measures of affiliation. We illustrate construction of a classroom network based on each child’s time in social contact with every other child. Visualization of the network illustrates gender differences in social affinity—distinct male and female cliques with modest gender integration. Finally, we examine the transitivity of social contact—the tendency of children with friends in common to also be friends with each other. Overall, we seek to show that automated location-based measurement can efficiently provide new insights into classroom interactions.

Classroom Case Example

Participants

To collect an illustrative dataset, we tracked the location of 16 children (eight female) with a mean age of 61.8 months (SD = 8.1 months) in a kindergarten classroom in Southern Germany during free play for 1 h on each of three days over a 10-day period in 2014. Attendance varied between 14 children (observations one and three) and 13 children (observation two). Eleven children were present at all three observations (Table S1). Measurement occurred at the beginning of the morning routine (09:00–10:00) during a time interval regularly designated as a free-play period. Kindergarten teachers were asked to let the children play as they wished, and to refrain from giving instructions. Parents gave their written informed consent for their children’s participation in the study and children verbally assented to wearing a tag on their wrists.

Location Measurement

Child location was measured at 6 Hz to an accuracy of 15 cm within the classroom (6.01 m × 7.23 m × 2.5 m) using RFID, which relies on electromagnetic fields to automatically identify and track tags worn by the participants. RFID was implemented with an Ubisense 7000 System, Tag Module Research with Research Upgrade. The system consists of the tracking tags (Figure S1a), a dedicated server housing Ubisense software, and four sensors in the classrooms’ corners (Figure S1b). Sensors tracked radio impulses emitted by the active tags worn by children and teachers. Each tag sent out an ultra-wide-band signal to the sensors that allowed the system to locate each child in $XYZ$ (three-dimensional) space by means of triangulation (angle of arrival = $AoA$) and time differences in arrival ($TDoA$). The $XYZ$-data in combination with the respective time-stamps were written to a .csv file. Software routines for using the data to investigate classroom interactions are provided in Code S1 in the Supplementary Material.

Velocity

Movies S1–S3 rendered children’s movements in classroom space for each observation day. For each child, velocity was computed as the difference in location between consecutive 1-s intervals. More precisely, velocity was calculated as the temporal derivative of displacement using the finite difference method. The mean velocity of boys’ and girls’ movement within the classroom was compared for the three observation days. Neither mean velocity nor the SD of velocity differed by gender (see Table S2).

Location Distributions

To understand where children tended to reside in the classroom, we visualized their spatial location. In doing so, we assumed that measurement error from individual child tags was randomly distributed around a Gaussian centroid. Specifically, we digitized classroom space into a 0.1 m × 0.1 m grid and measured the total duration $P_i(x,y)$ spent by each child $i$ in each gridded location ($x$, $y$). This duration, $P_i(x,y)$ was divided by the total observational time such that the overall probability for each child equaled 1. Guided by earlier reports of gender differences in classroom spatial location (Torrens & Griffin, 2013), we separately calculated and displayed the normalized probability of girls and boys, ${\rho }_f(x,y)$ and ${\rho }_m(x,y)$, being present in each classroom location ($x$, $y$). (Specifically, ${\rho }_f(x,y)=\sum _{i=\text{ female}}{P}_i(x,y)/N_f$ and ${\rho }_m(x,y)=\sum _{\begin{array}{l}i=\text{male}\\ \end{array}}{P}_i(x,y)/N_m$ measure the normalized duration time in classroom locations, averaged over females and males, where $N_f$ and $N_m$ are normalization factors indexing the total number of girls and boys, respectively.)

Location Visualizations

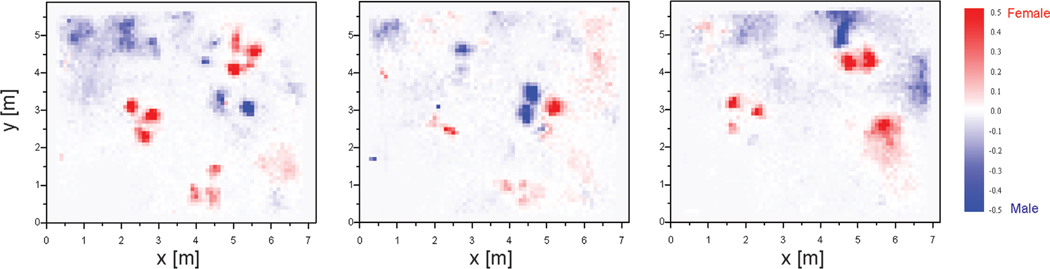
Female and male spatial probability distributions in the classroom for each day of observation are displayed in Figure S2. Visual inspection suggests girls and boys were unlikely to occupy the same classroom locations on any given day. To pursue this observation, we calculated and visualized the difference between the female and male distributions in Figure 1. Specifically, the male probability distribution was subtracted from the female distribution for each classroom location, ${\rho }_f(x,y)-{\rho }_m(x,y)$. In each observation, some areas of the classroom are occupied predominantly by boys and other areas predominantly by girls. However, some areas of the classroom occupied predominantly by girls and other areas occupied predominantly by boys were proximal to one another on observation days 2 and 3. The visualizations suggest the spatial probability distributions of boys and are girls are largely distinct with some areas of potential contact.

Figure 1. Spatial probability distributions by gender.

The difference between female and male spatial distributions throughout the classroom is displayed. Darker red indicates a high density of females to males; darker blue indicates a higher density of males to females. The spatial probability distributions of males and females are largely distinct (see also Figure S2). Axes are in meters.

The Social Contact Radius

Having determined overall location preferences in the classroom, we determined a radius of social contact. To this end, we disentangled social preferences from preferences for specific areas of the classroom. For each pair of children (A and B), we calculated their joint spatial distribution $P_{AB}(r)$. This is a measure of the total time that A and B were separated by radius $r=\sqrt{{\left(x_A-x_B\right)}^2+{\left(y_A-y_B\right)}^2}$. We compare this to a null model $P_{AB,-NULL}$ in which the radius $r$ separating A and B is the product of the probability distributions of each child’s individual location preference. If Child A and Child B move entirely independently, their positions are not affected by one another’s position. In this case, the null probability $P_{AB,NULL}(r)$ equals the product of A and B’s location probabilities for a given radius $r$. When $P_{AB}$ is greater than $P_{AB,NULL}$ for a given $r$, the children are closer together than expected by chance. When $P_{AB}$ is less than the null, the children are further away from one another than expected by chance.

Radial Distribution Function

To calculate the social contact radius for the entire class, the ratio of the mean $P_{AB}$ for all pairs of children was divided by the mean $P_{AB,NULL}$ for all pairs of children. This ratio is calculated at all distances of $r$. These quotients defines the radial distribution function $g(r)$, the relative ratio of the observed joint probability to the null model, $g(r)=P_{AB}(r)P_{AB,NULL}(r)$. It indexes the likelihood of finding a pair of children separated at distance $r$, relative to a random distribution that encodes each child’s individual (but not joint) location preference. Put another way, $g(r)$ indexes the distance between children at which social affinity influences individual location.

Radial Distribution Example

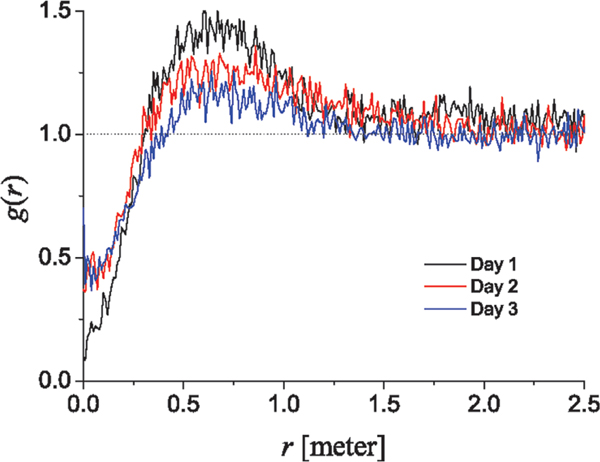
The radial distribution function for the three classroom observations exhibited similar distributions (see Figure 2). Where $r<0.3$ meter, $g(r)<1$ and observed colocation was less than that expected by chance. Where $g(r)=1$, children’s joint location preferences do not differ from their random (individual) preferences. In fact, when $r>1$ meter, $g(r)$ converged to 1, implying that social affinity had a limited range and did not impact movement when children were further than 1 m apart. Where $g(r)>1$, between 0.3 and 1 m, colocation was greater than chance, and affinity can be inferred. Based on these empirical findings, we defined a social contact radius $\left(r_c\right)$ when a pair of children were within 1 m of one another, $r<1$ meter, ignoring the rare low probability instances when $r<0.3$. The social contact radius represents a data-driven inference (rather than an a priori rule) indicating when children were affected by each other, i.e., when they were interacting.

Figure 2. The radial distribution function.

The radial distribution function, $g(r)$, is the ratio of the observed distance between children divided by the distance expected by chance. Chance is based the expected distance between children based on their individual location distribution. When $g(r)>1$, children are clustered more closely than expected by chance. The distribution of $g(r)$ was relatively stable over the three observations. Social contact was defined as children being within a radius, $r$, of 1 m, encompassing the peaks of $g(r)$.

Calculating a Social Contact Distribution

The social contact radius allows us to quantify children’s social ties. For each pair of children (A and B), we measured the total amount of time $T_{AB}$ they were in social contact (e.g., the total duration of time they were within 1 m of each other). We next calculated the social contact frequency $f_{AB}=T_{AB}/T$ as time $T_{AB}$ normalized by total observation time $T$. To determine the social contact distribution for each child, we measured their contact frequencies $f$ with each of their peers. Each child has $n-1$ peers. We ordered these $n-1$ contact frequencies by rank, $k$, and averaged over $k$ for males and for females. That is, we took the mean of contact frequencies over each child’s first most preferred peer, second most preferred peer, and so on. This defines the social contact distribution $f_k$, which measures the reduction of contact frequency $f$ with rank $k$.

Social Contact Distribution Example

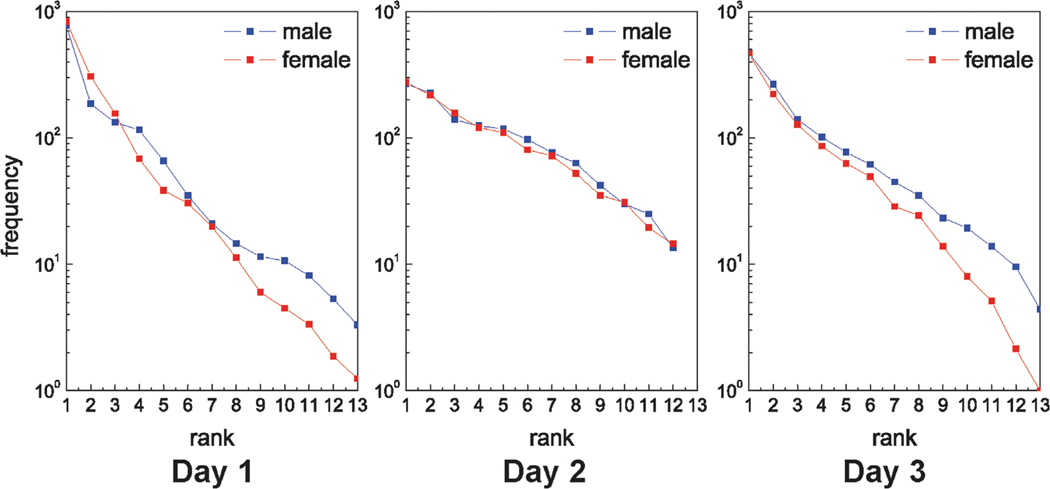
The semi-log plot depicted in Figure 3 depicts social contact frequency by the rank of the contacted peer. The social contact distributions of males and females were similar. There was a rapid decrease in social contacts as rank increased, indicating heterogeneity in the amount of contact time that individual children have with peers in the classroom. Social contact with the most contacted peer was consistently ten to hundreds of times greater than social contact with the least contacted peer.

Figure 3. Contact frequency.

Semi-log plots of the mean frequency of children’s social contacts by ordinal rank. Rank 1 indicates the most contacted peer, Rank 2 the second-most, through the least-most contacted peer. On Day 1 and Day 3, 14 children were in attendance and each child had 13 peers. On Day 2, 13 children were in attendance and each child had 12 peers. Mean contact frequency by rank is displayed for males and females. Both males and females consistently show levels of social contact with their most contacted peers that are ten to hundreds of time higher than levels of contact with their least contacted peers.

Social Tie Network

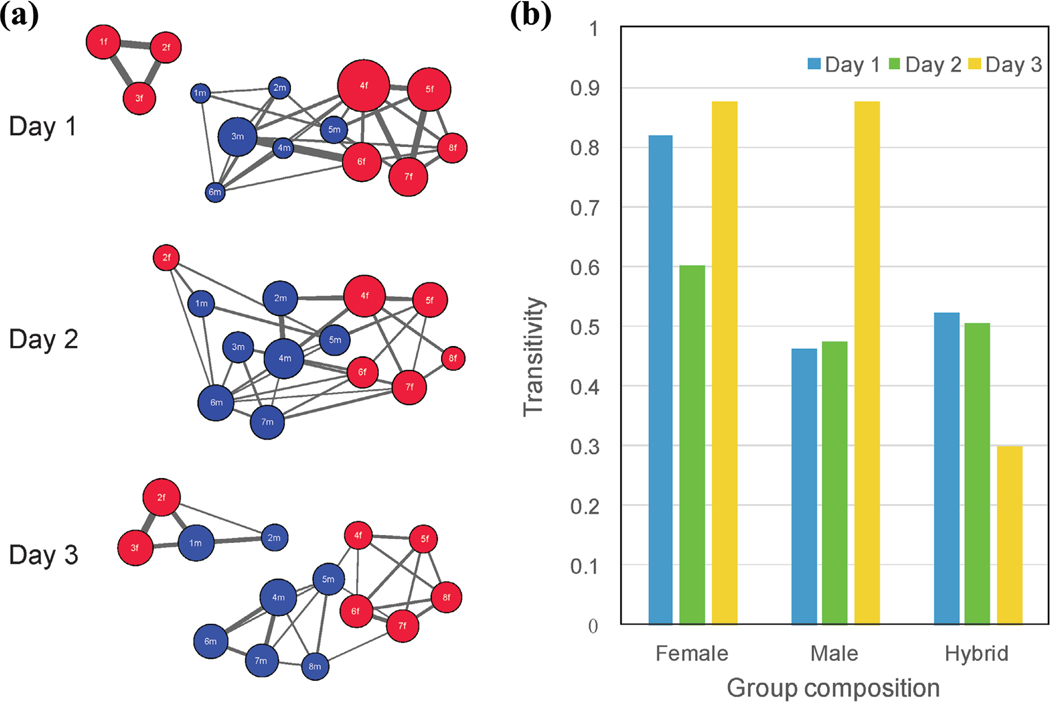
To fully characterize the ensemble of social contacts between males and females, we created a network of peer interactions for each day of observation. Each child was a node in the network. Boys were colored blue and girls red. Social ties between children were denoted as edges (lines) when that pair of children’s contact frequency was greater than the mean of all pairs on a given day. The thickness of the edges is proportional to the frequency of social contact between the children. Figure 4a displays these social tie networks for the three observation days, showing nontrivial topological structures.

Figure 4. Social networks and transitivity.

(a) Red nodes (circles) represent female children and blue nodes represent male children. Node diameter is proportional to the duration of contact with all other children. Edges (lines between circles) connect children when the contact frequency between those two children was greater than the mean contact frequency of all pairs of children on a given day. The width of edges connecting circles is proportional to the duration of contact between the two connected children. Males and females appear to form male-only, female-only, and mixed groups. (b) Transitivity occurs when children who share a social contact are themselves in social contact. To quantify transitivity, each day’s network is considered as a set of triplets of three children. A triplet is composed of three nodes with two or three edges connecting the nodes. The proportion of three-edged triplets indexes transitivity. Transitivity is shown for all-female, all-male, and hybrid (mixed) triplets for each day of observation.

Stability

The classroom social network exhibited structural changes over closely spaced observation days (see Figure 4a). To assess stability, we correlated the duration of each child’s contact with every other child over observation days. The mean of all the pairs of correlations (Day 1 to Day 2: 0.45, Day 1 to Day 3: 0.44, and Day 2 to Day 3: .15) was 0.38, suggesting moderate to weak stability in social contact over observations.

Illustrating Transitivity

The networks exhibited transitivity. Transitivity is the likelihood that two children have a social tie if they each have a social tie with a third child. More colloquially, transitivity can be described as the predilection of friends of friends to also be friends. For example, on Day 1, three girls (1f, 2f, and 3f), are shown in the top left corner of Figure 4a. Edges between their nodes are transitive—each is in contact with each. By comparison, on Day 3, two girls and a boy (2f, 3f, and 2 m), are shown in the top left corner. While 3f and 2 m are each in contact with 2f, 3f and 2 m are not themselves in contact (lack of transitivity).

Quantifying Transitivity

To quantify transitivity, we considered the network as a set of triplets of three children. A triplet is composed of three nodes with two or three edges connecting the nodes. Consider the triplet formed by three children, $ijk$, and imagine that child $i$ has social ties with $j$ and $k$. When the triplet has a transitive relation, $j$ and $k$ are also connected; they have a social tie and the subgraph ($ijk$) forms a triangle, a closed triplet (e.g., 1f, 2f, and 3f on Day 1). If $j$ and $k$ are not connected, the triplet is open (e.g., 2f, 3f, and 2 m on Day 3). For each observation, we enumerated the total number of open and closed triplets, $O$ and $C$, respectively. The transitivity ratio is defined as the fraction of observed closed triplets among all connected triplets, i.e., $T=C/(C+O)$ (Wasserman & Faust, 1994; Watts & Strogatz, 1998). Overall, the social tie networks had substantial transitivity values over the three observations. Values, ranging from 0.5 to 0.65, indicated the proportion of closed triplets.

Gender Transitivity

To explore potential gender associations with transitivity, we examined groups of three children (triplets), which we categorized as boys-only, girls-only, and gender-integrated (hybrid) triplets. Formally, triplet vertices consisted of females-only ($f$), males-only ($m$), and hybrid ($h$). We enumerated the number of closed and open triplets, $O_{\alpha }$ and $C_{\alpha }$, for different classes $\alpha$, where a $\alpha \in \{\text{f},m,h\}$ and calculated the corresponding transitivity $T_{\alpha }=C_{\alpha }/\left(C_{\alpha }+O_{\alpha }\right)$ for each class. Figure 4b compares $T_{\alpha }$ for all groups over the three observations. All-female triplets displayed greater transitivity than all-male triplets on observations 1 and 2, and displayed greater transitivity than hybrid triplets in all observations. This observation suggests that all-girl groups may be more likely than groups including boys (all boy or hybrid groups) to form closed triplets where all three children have social ties.

Discussion

Recent advances in commercially available systems using RFID for allocentric human tracking have opened new avenues of research for scholars interested in precision measurements of social networks (Irvin, Crutchfield, Greenwood, Kearns, & Buzhardt, 2017; Killijian et al., 2016). Here we provide guidance and software routines for using such a system to investigate classroom interactions. To do so, we analyzed children’s real-time location and movement in their kindergarten classroom during three 50-min observations of free play (raw data may be obtained from the first author). We focus on children’s location distributions and velocity, inferring and plotting the distribution of their social contacts, and transitivity in their social networks. Our results replicate and extend well-established findings of gender differences in preschool class-rooms, providing new insights into children’s use of physical space and the distribution of their social contact with their peers. In so doing, we help validate the use of RFID technology in a classroom setting and point the way for future investigators to adapt the technology to explore new measures of classroom behavior.

Movement and position are straightforward metrics for understanding classroom activity, which can only be measured efficiently via automated tracking. One novel use of these measures is the assessment of velocity, the overall speed of movement. Despite meta-analytic evidence for greater male than female velocity in timed trials (Thomas & French, 1985), we found no indication of sex differences in classroom mean velocity or its SD. This finding underlines the potential of objective measurements to suggest similarities as well as differences in boys’ and girls’ class room behavior. In future research, velocity measures might serve to distinguish different classroom activities, individual differences between children, or the speed of successful and unsuccessful social approach attempts.

Visualization of aggregated measurements of children’s location across an observation indicated that boys and girls clustered in different areas of classroom space on each observation day (see Figure 1). Torrens and Griffin (2013) noted that boys and girls tended to occupy different areas of the classroom but did not measure overall spatial segregation. Self-reports of friends and preferred playmates are strongly linked to the amount of time that children are observed to spend together during free time (Hartup, Laursen, Stewart, & Eastenson, 1988; McCandless & Marshall, 1957; Shin, Kim, Goetz, & Vaughn, 2014). Thus it is likely that observed gender segregation in social partners (Martin et al., 2018) reflects differences in spatial location. Nevertheless, the current report represents the most direct evidence that sex-based social segregation is reflected in boys’ and girls’ spatial preferences. In future research, spatial visualizations might be employed to examine the geographic integration of children with and without disabilities in inclusion classrooms.

Although expert observers frequently use proximity as an index of interaction, there has been no objective criterion for inferring interaction. Badge-based technologies apply an a priori criterion for inferring social contact. Allocentric RFID tracking allows users to determine an index of social contact, but does not provide a principled approach for doing so (Killijian et al., 2016). To address this issue, we introduce a data-driven measure of social contact, the radial distribution function. The radial distribution function compares observed distances between pairs of children to distances expected based on each child’s individual location distribution. Calculated for all distances and all pairs of children, the radial distribution function estimates the distances at which contact is due to social affinity. The radial distribution function, $g(r)$, was relatively consistent over each day of observation (see Figure 2), allowing for a consistent, empirical criterion for ascertaining social contact (1 m).

We recognize that colocation at greater than chance levels does not guarantee social contact. One can imagine circumstances in which children in proximity and oriented toward one another are actually engaged in solitary play (e.g., sitting at a table and coloring). Likewise, children at some distance might be playing tag or one child might be fetching blocks to complete a co-constructed tower. Thus, the current approach indexes social contact but does not adjudicate its presence as would a human expert (though, of course, human experts are not infallible). Moreover, the current approach allows for continuous observation of all children in the classroom, which is not possible with human experts. Moreover, data derived from continuous observations, open new opportunities such as the ability to accurately measure behavioral cascades in real-time, and the network factors that impede or propel their spread between peers (Fowler & Christakis, 2010).

Establishing a principled criterion for social contact allows investigators to examine the distribution of social ties among children. It is axiomatic that children prefer some peers to others. However, we know of no overall quantitative description of the distribution of children’s social contact among peers. Here, we visualized that distribution with respect to the frequency of contact—from the most to the least preferred peer (the most to the least contacted peer). Visualization over three days of observations indicate substantial heterogeneity, meaning that both boys and girls are in contact with some peers at least 100 times more than others (see Figure 3). We believe this to be the first quantification of this heterogeneity, indicating that some dyads show orders of magnitude more social contact than do others.

Social network analysis based on expert observations indicate that preschoolers select same-sex playmates who in turn influence them to engage in gender-typed activities (Martin et al., 2013). Here, using the data-driven measure of social contact, naturalistic classroom networks were visualized for each day of observation. Clusters of boys and clusters of girls were evident, with variable levels of cross-sex ties. Visualization of the networks suggested a tendency for children to form ties with same-sex peers, although some mixed sex ties were also evident (see Figure 4a). These network analyses revealed male and female cliques with limited gender integration. Confidence in our criterion for social contact is bolstered by these findings, which replicate those previously obtained with conventional expert observation procedures.

Network analyses provide an overview of the web of social contacts in the classroom and can be subject to a wide range of analyses focusing on the connectivity of individual children, groups of children, or the network as a whole. We focused on transitivity, the tendency of children with a common social contact to also be in social contact. To illustrate how gender might structure the network, we described transitivity in different types of triples over the three days of observation. All-female triplets (triads of girls) displayed somewhat greater transitivity than all-male triplets and consistently greater transitivity than hybrid (gender-integrated) triplets (see Figure 4b). This illustration suggests potentially fruitful directions and methods for classroom researchers interested in group differences in social networks.

There are several limitations of the approach described here. No attempt, for example, was made to model the effect of specific physical structures such as classroom tables. More generally, social contact was based on proximity as determined by the data-driven radial distribution function. Future investigations might supplement proximity with measures of physical orientation. Orientation could be assessed by equipping children with both a right and a left trackable tag (Killijian et al., 2016). One could then define social contact using both distance (e.g. 1 m) and relative orientation (e.g., within 45°) criteria. Finally, contact and/or orientation might be supplemented by automated measures of other interactive parameters such as vocalizations (Sangwan, Hansen, Irvin, & Greenwood, 2015), or with expert observations of interaction. It should be noted that all these measures of social contact can be used as input to the analyses of the distribution of children’s social contacts, as well as to the creation of social networks, which are presented here.

A single classroom of 14 children was observed for an hour on three different occasions. Correlational analyses indicated moderate to weak stability of children’s social contacts over observations. This finding suggests the importance of repeated observations of classroom networks to produce stable measures of individual children’s sociality.

Although the current data are not sufficient for longitudinal analysis, two analytic alternatives for future longitudinal investigations bear mention. First, network analyses involving multiple classrooms might profit from stochastic modeling techniques such as SIENA (Ripley, Snijders, Boda, Vörös, & Preciado, 2016). At present (Niezink & Snijders, 2017), SIENA models social ties discretely (presence versus absence) and so cannot take full advantage of the continuous measurements of social contact strength afforded by objective measurements. A complementary approach would involve multilevel modeling—in which observations are nested within children—of continuous parameters such as the quantity of children’s social contacts. These models produce intraclass correlations, which quantify the stability of children’s contacts, while an age term would assess linear or other developmental changes. Using multilevel models, a child’s level of social contact might be predicted by time-varying covariates such as velocity or by child-level traits such as gender.

In conclusion, we have described approaches to visualizing and modeling the rich data provided by a commercially available RFID tracking system suitable for tracking children’s position in a class-room. Procedures for calculating velocity and location distributions illustrated the potential of these metrics to investigate individual differences in the classroom. The radial distribution function provided a measure of social contact that controlled for individual location preferences. This measure was used to illustrate quantitative differences in the distribution of children’s social contact with individual peers. Finally, using the social contact measures, networks were created to capture sex differences in the full set of classroom relationships. The resulting illustrative findings replicate well-established sex-differences while suggesting new insights into children’s location preferences (boys and girls inhabited geographically distinct areas of the classroom) and social proclivities (both boys and girls associated up to hundreds of times more with some peers than others). Future scholars are encouraged to harness the continuous measurement tools described here to generate a deeper understanding of children’s classroom-based activity.