Design of intrinsically disordered protein variants with diverse structural properties

Abstract

Intrinsically disordered proteins (IDPs) perform a broad range of functions in biology, suggesting that the ability to design IDPs could help expand the repertoire of proteins with novel functions. Computational design of IDPs with specific conformational properties has, however, been difficult because of their substantial dynamics and structural complexity. We describe a general algorithm for designing IDPs with specific structural properties. We demonstrate the power of the algorithm by generating variants of naturally occurring IDPs that differ in compaction, long-range contacts, and propensity to phase separate. We experimentally tested and validated our designs and analyzed the sequence features that determine conformations. We show how our results are captured by a machine learning model, enabling us to speed up the algorithm. Our work expands the toolbox for computational protein design and will facilitate the design of proteins whose functions exploit the many properties afforded by protein disorder.

Algorithm to design intrinsically disordered proteins with specific conformational properties expands the protein design toolbox.

INTRODUCTION

Intrinsically disordered proteins and regions (from here on collectively termed IDPs) represent a diverse class of proteins that carry out a wide range of functions and are characterized by extreme but often nonrandom structural heterogeneity (1, 2). Their distinct amino acid composition and sequences (3) differ from those of natively folded proteins and prevent the formation of stably folded conformations. Thus, IDPs are best described by ensembles of heterogeneous conformations that interconvert rapidly (4, 5). The disordered and dynamic nature of IDPs is often central for their biological and biochemical functions. They can be linkers separating functional domains, regulating the interaction between the latter (6), or they can play roles as spacers that impair undesirable protein-protein interactions (7, 8). IDPs are often involved in mediating molecular interactions including via so-called short-linear motifs (9), and their large capture radius may give rise to faster binding kinetics compared to that of folded proteins (10). Thus, IDPs are, for example, commonly found in signaling molecules (11) and transcription factors (12). Furthermore, the interactions within and between IDPs and other biomolecules have emerged as an important factor in the spatial organization of cellular matter. Through their ability to encode multivalent interactions, IDPs can aid in or drive the formation of membraneless organelles, which typically consist of a wide range of biomolecules and compartmentalize many biological processes (13, 14). In vitro, many IDPs have been shown to undergo a phase separation (PS) process that leads to the coexistence of a protein-rich dense phase that separates from a dilute phase when the concentration of the protein reaches the so-called saturation concentration (c_sat) (14). Thus, at concentrations above c_sat, the protein is found in both a dilute phase and a coexisting dense phase that macroscopically may appear liquid-like and, at the molecular level, may behave as a fluid with viscoelastic properties (14, 15).

Similarly to the long-lasting quest for predicting the native structure of folded proteins from their sequences (16), a field that has recently witnessed substantial advances (17–19), there is interest in understanding the sequence determinants for the conformational properties of IDPs (3, 20–26) and how these are related to their functions (25, 27). For both folded and disordered proteins, the ability to predict structure(s) from sequences may help infer their functional properties. Accurate structure prediction may also support or sometimes replace the need for experimental studies of protein structure. Last, rapid structure prediction enables proteome-wide analyses and can aid in protein design.

In parallel with our continuously improving ability to predict structures of folded proteins, there has been substantial development in our ability to design sequences that fold into specific three-dimensional folded structures (28–30). Given the multitude of functions and properties of IDPs, there would be great potential in designing IDPs with targeted properties (31). Such proteins could potentially find applications as linkers in multidomain enzymes (32), signaling molecules, or using IDPs as biomaterials (33). In contrast to the developments for folded proteins, computational design of IDPs with specific properties remains more limited. This is because characterizing and predicting the structural properties of IDPs is a complicated task given that we know less about the sequence-ensemble relationships for IDPs. The native structure of folded proteins can be experimentally determined at atomic resolution, and the availability of many high-resolution structures has been one key driving force for understanding and predicting how sequences encode structures (17). On the other hand, characterizing the ensemble of conformations that an IDP adopts generally requires the integration of experiments and simulation methods (4, 5). Collecting such data is, however, difficult and their interpretation is often ambiguous. As a consequence, there are only limited examples of detailed structural characterizations (34). Thus, there are still many open questions about how the sequence of an IDP translates into a structural ensemble and function (35). Despite these limitations, a number of rules that govern the local and global conformational properties of IDPs have emerged. For example, the content (21, 22) and patterning (36) of charged residues have been related to the global expansion of an IDP in solution (25, 26) as well as their propensity to undergo PS (37–39). Similarly, hydrophobicity and, in particular, the number and patterning of aromatic residues influence the compaction of an IDP and its propensity to phase separate (40–42). In some cases, the resulting sequence-ensemble rules have been used to modify sequences to change, for example, their level of compaction (43–45) or propensity to undergo PS (46, 47).

A number of different approaches have recently led to the development of accurate yet highly computationally efficient physics-based coarse-grained models for molecular simulations of the global conformational properties of IDPs (48–53). These simulation methods make it possible to generate conformational ensembles from sequences on timescales that are compatible with screening a large number of sequences, e.g., all IDPs in the human genome (25). Building on these developments, we here present an algorithm to generate sequences of IDPs with predefined conformational properties. The central idea is to search sequence space and to use efficient coarse-grained simulations to link each sequence to conformational properties (54). Specifically, we use the CALVADOS (Coarse-graining Approach to Liquid-liquid phase separation Via an Automated Data-driven Optimisation Scheme) model, which has been optimized by targeting small-angle x-ray scattering (SAXS) and paramagnetic relaxation enhancement nuclear magnetic resonance (NMR) experiments on IDPs in solution (49) and which has been extensively validated using independent experimental data (25). In some aspects, our algorithm is conceptually similar to previously described approaches that sample sequence space using, for example, genetic algorithms; these sequences can then be evaluated using simulations to generate structures with, for example, a defined helical structure (55), properties correlated with propensities to PS (56, 57), or sensor peptides for curved lipid bilayer membranes (58). We show how the combination of a Monte Carlo algorithm, an efficient coarse-grained model, and alchemical free-energy calculations enables large-scale exploration of the sequence-structure space, and we validate the results experimentally.

We begin by studying four IDPs with different sequence compositions and characteristics. Starting from each sequence, we design new sequences with different levels of compaction while keeping the amino acid composition constant. The results show that—even with the restriction of having a fixed amino acid composition—it is possible to achieve conformational ensembles with highly diverse properties. We show that this is mainly, but not solely, due to differences in the patterning of charged residues. We used the low complexity domain of hnRNPA1 (hereafter A1-LCD) to study the relationship between sequence patterning, single-chain properties, and the propensity to undergo PS. We selected five variants of A1-LCD for experimental characterization and find good agreement between the experiments and predictions. Together, our results show that the algorithm that we have developed is efficient and can be used to design IDP sequences with novel properties. The algorithm is fully general and can therefore also be used to design sequences with varying amino acid composition and for other target properties than chain dimensions.

RESULTS

Algorithm to design novel IDPs

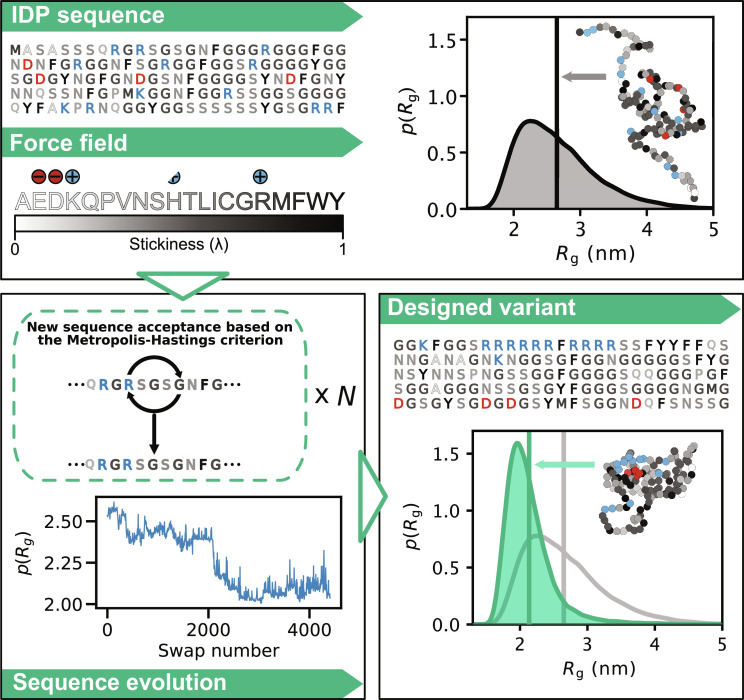
To design IDP sequences with specific conformational properties, it is necessary to be able to predict these properties from sequences accurately and rapidly. Therefore, the first question that we address is if it is possible to use state-of-the-art simulation-based approaches to develop a generalizable method for IDP design. Recent studies have established efficient machine learning–based methods to predict average conformational properties from sequences (25, 26), but these methods do not predict full conformational ensembles and have not been tested experimentally on novel sequences. Instead, we employed a simulation-based approach where we use a coarse-grained model to generate a conformational ensemble for a given sequence (Fig. 1).

Fig. 1. Outline of our algorithm for designing sequences of IDPs with targeted conformational properties.

As the starting point, we here use naturally occurring IDP sequences, although this is not a requirement of the approach. We use MD simulations with the coarse-grained CALVADOS force field to describe the IDPs and to generate a conformational ensemble. New sequences are proposed through an MCMC scheme. We evolve the sequences by consecutive swaps in positions between two randomly selected residues and evaluate if the sequences get closer or further away from the design target—here chain compaction. During sequence optimization, we calculate the conformational properties for a given sequence by either direct simulations or alchemical calculations that rely on conformational ensembles of previously sampled sequences. The conformations shown have the same radius of gyration as the average of the conformational ensemble.

We combine coarse-grained molecular dynamics (MD) simulations using the CALVADOS model (49) with alchemical free-energy calculations in an algorithm that sequentially generates new sequences and characterizes their conformational ensembles in a time-efficient manner. While MD simulations with a coarse-grained model can rapidly produce conformational ensembles from which structural features can be directly calculated, screening a large number of different IDPs sequentially with only MD simulations would still be computationally difficult. Alchemical free-energy calculations, on the other hand, can predict conformational properties of newly proposed sequences from conformational ensembles generated by simulations of different sequences. Our algorithm thus combines simulations and alchemical free-energy calculations in an optimization process that, in some ways, is analogous to what has been proposed in the context of force field optimization (59–61).

While the overall sequence composition of an IDP is known to affect its conformational properties (25), we here aimed to explore the more subtle and difficult-to-extract effects of sequence patterning (23, 36, 41, 62–65). Therefore, we apply our design algorithm to generate sequences of IDPs with diverse structural properties while preserving the overall amino acid composition. In this way, we also test and possibly expand our understanding of how the patterning of specific residues in a sequence influences its conformational properties. Early pioneering studies focused on the role of charge patterning on conformational properties and propensity to phase separate (36–38, 43). Other studies have linked the number and patterning of amino acids, in particular aromatic and arginine residues, to both conformational properties and propensity to phase separate (39, 41, 42, 66).

Nonetheless, even restricting the sequence space to sequences of fixed composition, the number of possible sequences is enormous; for example, there are ~10¹²⁷ unique sequences with the amino acid composition of the disordered domain of the fused in sarcoma (FUS) protein. Thus, sampling even a tiny part of this space is unfeasible. To circumvent this problem, our algorithm drives the exploration of the sequence space toward sequences resulting in a target conformational property. This is achieved via a Markov chain Monte Carlo (MCMC) sampling scheme that iteratively generates sequence variants and predicts their conformational properties (through MD simulations and alchemical free-energy calculations) in search of specific arrangements of amino acids that determine a certain structural feature (see Materials and Methods for a more detailed description of the algorithm and its components).

To exemplify and demonstrate the power of our algorithm, we generate variants of IDPs with either increased or decreased chain dimensions, measured by their radius of gyration (R_g), while keeping a fixed amino acid composition. To this aim, at each iteration, the algorithm swaps the positions of two randomly selected residues to generate a variant (from here on called a swap variant). We compare the R_g before and after the swap (evaluated from either MD simulations or alchemical free-energy calculations), and the Monte Carlo move is accepted or rejected based on the Metropolis-Hastings criterion (Fig. 1). Although we here have focused on the difficult problem of changing conformational properties while keeping a fixed amino acid composition, the algorithm is versatile and other criteria can be used to propose changes in the sequences (e.g., single amino acid substitutions) as well as selecting for other structural features than the R_g.

Design of IDPs with conformational ensembles that vary in compaction

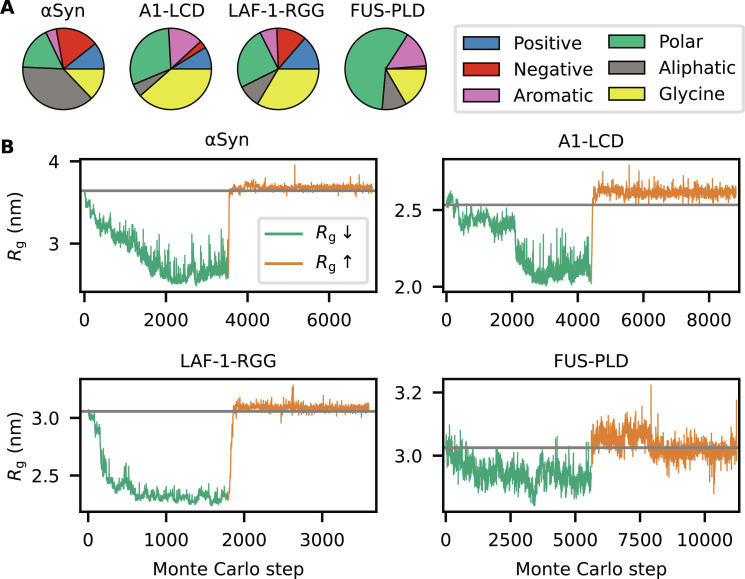
The second question that we address is: Starting from a natural IDP, how much more compact or expanded can it become when only changing the positions of the amino acids in its sequence? To answer this question, we selected four IDPs with different sequence compositions: α-synuclein (αSyn), the low complexity domain from hnRNPA1 (A1-LCD), the prion-like domain of FUS (FUS-PLD), and the R-/G-rich domain of the P granule protein LAF-1 (LAF-1-RGG) (Fig. 2A). We used our sequence design algorithm in a simulated annealing protocol to let the sequences evolve in search of amino acid arrangements that result in more compact ensembles. The results show that we can generate sequence permutations of αSyn, A1-LCD, and LAF-1-RGG that are substantially more compact than the wild-type (WT) sequence (Fig. 2B, green lines). In contrast, for FUS-PLD, we only find variants that are modestly more compact than the WT protein. To demonstrate that the algorithm can also find sequences of increased expansion, we began from the compact designs and instead targeted greater R_g values. For αSyn, A1-LCD, and LAF-1-RGG, we find that the algorithm quickly generates sequences with WT-like dimensions (Fig. 2B, orange lines). In all cases, the algorithm only finds sequences that are modestly more expanded than the WT sequence, although the algorithm was tuned to expand the protein as much as possible. We repeated these calculations starting also from the WT sequences and obtained similar results (fig. S1).

Fig. 2. Designing sequences with varied compaction.

(A) Pie chart of the sequence composition of αSyn, A1-LCD, LAF-1-RGG, and FUS-PLD. Amino acids are grouped as negative (D and E), positive (R and K), aromatic (Y, W, and F), polar (S, T, N, Q, H, and C), aliphatic (A, V, I, L, M, and P), and glycine. (B) Design of compact (green lines) and expanded (orange lines) variants for αSyn, A1-LCD, LAF-1-RGG, and FUS-PLD. Each accepted Monte Carlo step thus gives rise to a sequence that differs from the previous by the position of the two swapped residues. Each Monte Carlo step therefore corresponds to a different sequence, whose ensemble averaged R_g is evaluated by either MD simulations or alchemical free-energy calculations. The gray horizontal line indicates the R_g of the WT sequence.

Sequence features that determine the compaction of the designs

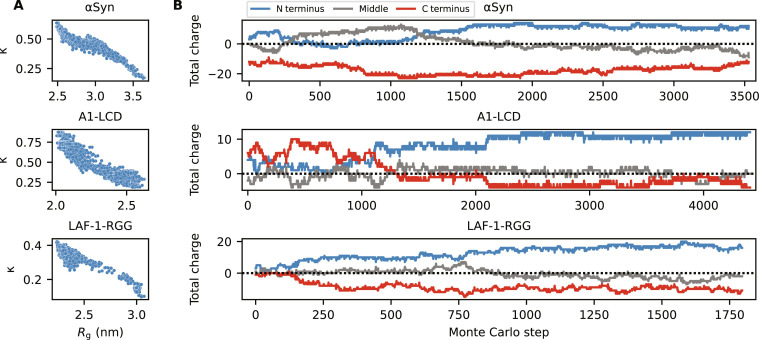
In the calculations above, we observed that, while thousands of swap moves are required for the algorithm to reach the most compact ensembles, a much smaller number of moves were required to recover sequences with WT-like dimensions (Fig. 2B). As the moves swap two randomly selected positions, we speculate that there is an entropic barrier in sequence space in finding the arrangement of amino acids that determines compact ensembles. This suggests that compaction is driven by some kind of specific ordering of the amino acid sequences. The next question we addressed was therefore: What are the sequence determinants of IDP compaction in the generated sequences? As described above, we were able to generate substantially more compact variants for αSyn, A1-LCD, and LAF-1-RGG but not for FUS-PLD. We therefore aimed to identify which sequence features led to this compaction and assessed if the same features were responsible in all three cases. We calculated a number of sequence features for the variants of αSyn, A1-LCD, and LAF-1-RGG and examined the correlation with the R_g (Fig. 3A and fig. S2). In all cases, we observe a strong correlation between the patterning of the charged amino acid residues, as captured by the κ parameter (Fig. 3A) (36) and R_g. The κ parameter captures if the positively and negatively charged residues are well mixed together (low κ) or if they tend to be found in blocks of like charges (high κ) (36). For all three proteins, we observe that the positively charged residues tend to be clustered in the N-terminal third of the sequence and the negatively charged residues in the C-terminal third as the sequences get increasingly compact during the sequence design (Fig. 3B). Because the N terminus carries a positive charge and the C terminus carries a negative charge, it is likely that the charged termini contribute to the overall charge segregation. We stress that we did not directly drive this charge clustering during the sequence design algorithm but that the analysis shows that clustering of the charges occurs as the algorithm explores sequence space to generate compact structures. The formation of charge-clustered sequences is in line with the hypothesis above of an “entropic bottleneck” during the sequence design and that it is easier to disrupt such patterns than to generate them by randomly swapping amino acid residues.

Fig. 3. Charge patterning drives compaction.

(A) Correlation between R_g and κ (a high κ indicates segregated clusters of residues with the same charge, and a low κ indicates that charges are well mixed along the sequence). (B) We divided the sequences of αSyn, A1-LCD, and LAF-1-RGG into three sections covering the N-terminal third (blue), the middle third (gray), and the C-terminal third (red) of the sequence and calculated the total charge in each of these sections.

We also examined other sequence features including patterning of aromatic and hydrophobic residues and found that they generally have a weaker correlation with the R_g (fig. S2). For LAF-1-RGG, we, however, found that the patterning of hydrophobic residues may also contribute to compaction similarly to the patterning of charged residues (fig. S2). This suggests that, while charge patterning captures most of the variation in compaction of the permuted sequences, it is difficult to find individual sequence descriptors that fully explain the chain dimensions of these IDPs and that combinations of features may be needed to predict compaction (25, 26, 65, 67). The importance of charge patterning also helps to explain why we were not able to obtain swap variants of FUS-PLD that are more compact than the WT because FUS-PLD has only two negatively charged and no positively charged residues.

Relating sequence, compaction, and propensity to phase separate of designed variants

Theory, simulations, and experiments show that the compaction of an IDP is related to its propensity to self-associate and to undergo different forms of phase transitions (68). Conceptually, this can be understood by the fact that the intramolecular interactions that drive sequence compaction are the same as the intermolecular interactions that drive self-association and PS. It would be useful to be able to design proteins with predefined propensities to undergo PS and participate in the formation of biomolecular condensates. Building on previous studies in this area (56, 57), the fourth question that we sought to answer is: Are the changes in single-chain compaction of the designed swap variants accompanied by a change in their propensity to phase separate? To examine this question, we chose to study A1-LCD in more detail because the relationship between sequence and PS of A1-LCD has been studied extensively by experiments, theory, and simulations (39, 41, 49, 69).

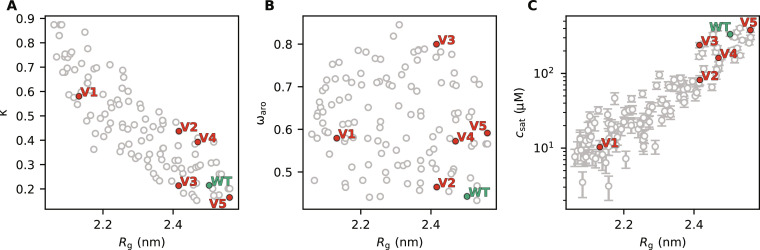
To improve statistics, we performed nine additional runs of the design algorithm to generate a larger and more diversified pool of A1-LCD variants with different levels of compaction (fig. S3). We then grouped these sequences by their R_g (in bins of 0.05-nm width), clustered the sequences (see Supplementary Materials), and used the centroid of each cluster for further analyses. In this way, we removed sequences that are very similar to each other (there are many similar sequences within each run of sequence design because the design algorithm evolves sequences by consecutive position swaps of two residues) and only use one representative sequence for each cluster. We then performed 1-μs-long simulations of each centroid sequence to reevaluate their R_g values. We do this to validate the accuracy of the alchemical free-energy calculations in predicting the R_g of variants proposed by the design algorithm. In line with preliminary tests (fig. S4; see Materials and Methods), we find an average error on the predicted R_g values of 1.5% (fig. S5). We then rebinned the centroids based on the R_g from simulations, and for each bin, we selected up to 15 sequences that are diverse in the patterning of charged and aromatic residues. In this way, we selected 120 A1-LCD variants (including the WT) with diverse sequence features and compaction (Fig. 4, A and B). Of the 119 swap variants, 113 have less than 30% sequence identity to the WT protein (fig. S6).

Fig. 4. Characterization of the 120 A1-LCD variants.

We show the relationship between R_g and (A) κ, (B) ω_aro (patterning of aromatic residues; a high ω_aro values indicate clustering of aromatic residues), and (C) the c_sat calculated from simulations of 100 chains in slab geometry. We highlight the WT sequence of A1-LCD in green and five variants selected for experimental characterization in red. Error bars of the average R_g are not shown as their size is negligible.

To examine the propensity of the designed A1-LCD variants to phase separate, we ran simulations of these variants (one at a time) consisting of 100 copies in a “slab” geometry and estimate their c_sat from the concentration of the dilute phase in the simulation box (70). As previously observed for a model system (37), we find a logarithmic relationship between R_g and c_sat, with compact variants showing a stronger propensity to PS (low c_sat) and expanded variants showing a weaker propensity to PS (high c_sat) (Fig. 4C). Despite this expected correlation between single-chain properties and the propensity to phase separate, we find some sequences with similar R_g values whose c_sat values differ by up to one order of magnitude. This observation suggests that, while the single-chain behavior can be very similar, other features encoded in the sequences of heteropolymers can cause diversity in the PS properties. Overall, this correlation between R_g and c_sat not only further supports a strong link between single-chain properties and PS propensity that can be used to extrapolate PS propensity from single-chain compaction but also suggests that other sequence features that do not substantially change the single-chain R_g might have an effect on PS.

Experimental characterization of A1-LCD variants

Above we have described an approach for designing IDPs and examine how the arrangement of amino acids in the primary sequences can influence their behavior. While the coarse-grained model that we use in our algorithm (49) has been extensively validated on naturally occurring proteins and variants thereof (25), it has not been used as a generative model and tested on novel, designed sequences. We thus asked if the accuracy of CALVADOS for predicting R_g and c_sat for natural proteins also extends to sequences that show little sequence identity to natural proteins and, for example, show substantial charge patterning. Thus, a fifth question that we asked was: How accurate are our computational predictions of chain dimensions and propensity to phase separate for the designed variants?

We therefore sought to test our predictions by experiments. We focused our experiments on 15 swap variants of A1-LCD, selected from the 120 sequences analyzed above, that represent a range of chain dimensions and sequence properties. We focused on A1-LCD because the WT protein is already relatively compact and because its propensity to phase separate is rather strong for a protein of its length (39, 41). Thus, we speculated that the ability to make it even more compact and endow it with a lower c_sat without changing the amino acid composition would be a powerful test of our design algorithm and the CALVADOS model.

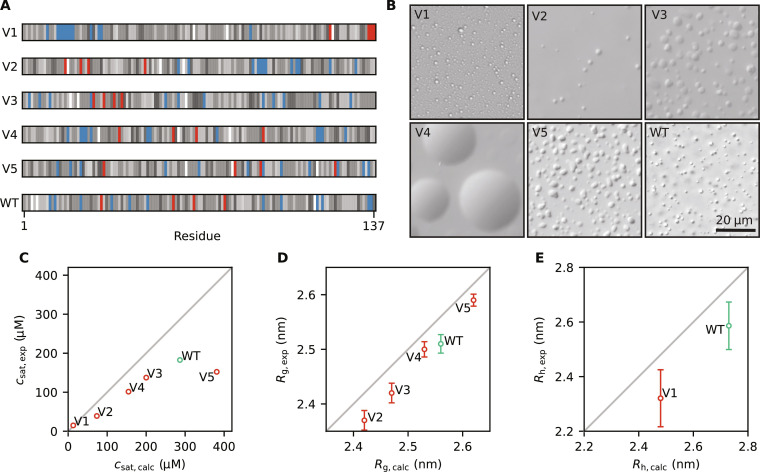
Out of the 15 variants that we selected, we successfully expressed and purified five variants (red points in Fig. 4 and fig. S7) and the WT A1-LCD protein. We ran new simulations of the selected variants under the conditions of the experiments and including a glycine-serine pair at the N terminus that is present in the experimental constructs (table S1). We name these variants V1 to V5, sorted by their calculated R_g, with V1 predicted to be the most compact and most strongly phase-separating variant, with a marked segregation of positive and negative charges at the termini (Fig. 5A). We induced PS by adding 150 mM NaCl and visualized the resulting condensates by differential interference contrast (DIC) microscopy (Fig. 5B). We measured the c_sat of the five variants and the WT and compared the experimental results with those predicted from multichain simulations. We find a high correlation between predicted and observed values of c_sat (Fig. 5C), with the only outlier being V5, which is the sole variant expected to be more expanded than the WT. To investigate possible reasons for the discrepancy in PS propensity of V5, we ran additional simulations. The calculated c_sat values that we compare to experiments (Fig. 5C) are averages over the c_sat values calculated from three independent simulations. We obtained comparable results from the three independent replicates, demonstrating that the differences are not due to lack of convergence of the simulations (fig. S8). We also ran simulations with different setups: one with twice as many chains to address potential finite size effects and another with the updated CALVADOS 2 model (53). All three simulation setups gave comparable values for c_sat (fig. S8). We also repurified and remeasured c_sat values for V5 and obtained comparable results.

Fig. 5. Experimental characterization of WT A1-LCD and five designed variants.

(A) Diagram of the arrangement of amino acids in A1-LCD and the five designed variants. Negative and positive charges are colored in red and blue, respectively. The neutral residues are colored by a gray scale that reflects their hydrophobicity (corresponding to the λ parameter in CALVADOS), with the least hydrophobic residues in white and the most hydrophobic residues in black. (B) Visualization of condensates of WT A1-LCD and the five variants by DIC microscopy; these images are only meant to illustrate the formation of condensates and not necessarily differences between the variants. (C) Comparison of experimental and calculated values of c_sat at 298 K. (D) Comparison of experimental and calculated values of R_g for WT A1-LCD and V2 to V5. (E) Comparison of experimental and calculated values of R_h at 307 K for WT A1-LCD and V1. Error bars whose sizes are comparable to those of the markers are not shown.

We used previously described methods to measure SAXS data for proteins close to their solubility limit (71) to test our predictions of chain dimensions for the designed variants. Like for c_sat, we find a high correlation between the R_g values derived from SAXS and those from simulations (Fig. 5D) and a good agreement between the experimental and calculated SAXS curves with ${\mathrm{\chi }}_r^2$ values around 1 to 2 (fig. S9). Given the low c_sat of V1 (15 μM), we were not able to obtain a sufficient signal-to-noise ratio at a protein concentration below c_sat. We instead turned to diffusion NMR experiments at low protein concentrations to measure the hydrodynamic radius (R_h) of V1 and WT A1-LCD. We thus acquired NMR data for WT A1-LCD and V1 at 307 K, where the measured c_sat of V1 is 34 μM (compared to 15 μM at 298 K). At this temperature, we find that V1 is substantially more compact than WT A1-LCD (Fig. 5E). We note that, for both R_g and R_h, there appears to be a small, but systematic, offset between the predicted and experimentally determined values. Some of these differences may indicate remaining errors in the CALVADOS force field but may also reflect uncertainty in how R_g and R_h are estimated from experiments and simulations (72–75).

We find that both simulations and experiments show that V3 is more compact than V4 (Fig. 5D), while V4 has a lower c_sat than V3 (Fig. 5C). Previously, it has been shown that changes in the formal net charge may break the correlation between R_g and c_sat (39, 49), but the case of V3 and V4 shows that certain sequence features can break this symmetry even without changing the amino acid composition and that this is captured by CALVADOS. Examining the sequence features of V3 and V4, we note that V4 has a greater value of κ (indicating that negatively and positively charged residues are not well mixed) (Fig. 4A), while the high value of ω_aro in V3 shows that the aromatic residues are highly segregated (Fig. 4B), a feature that has previously been correlated with an increased propensity to form amorphous aggregates (41). If these or other sequence features cause the “symmetry breaking” between R_g and c_sat for V3 and V4 will be an interesting topic for future analyses.

Designing variants with specific contact maps

Having demonstrated and experimentally validated that we can design sequences with specified levels of compaction, we asked the question if our algorithm could also be used to design sequences with conformational requirements that are more complex than the average chain dimension. We therefore implemented a version of our algorithm that targets a prespecified contact map during the sequence optimization. As above, we use simulations and alchemical calculations to score the agreement between the designed sequence and the target contact map.

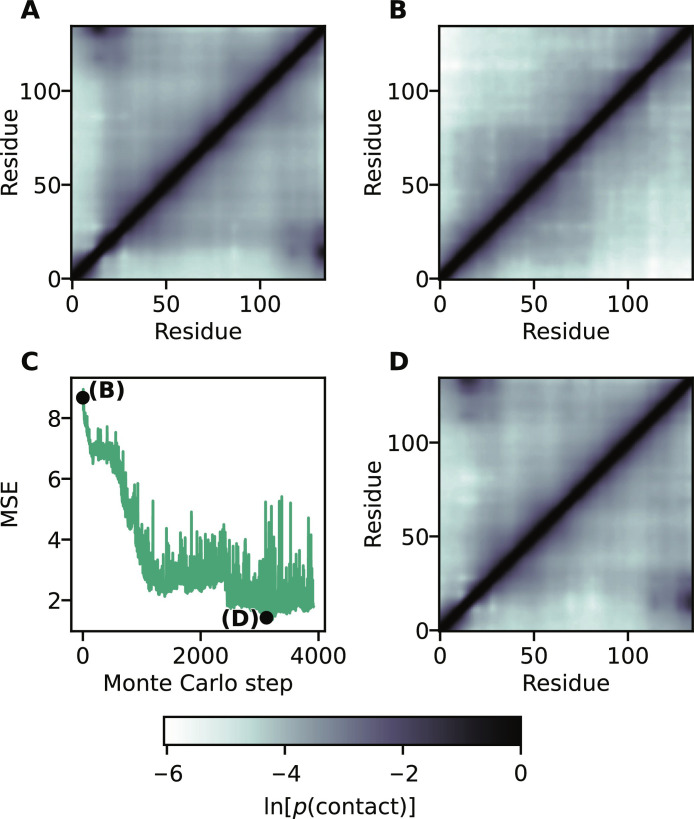
As an example of this more complex design target, we selected the simulated contact map for the compact V1 variant of A1-LCD (Fig. 6A). Starting from the sequence of WT A1-LCD, we used the design algorithm to find sequences with the same composition as A1-LCD with predicted contact maps resembling V1. We selected the contact map of V1 as the target and the A1-LCD sequence as the starting point because the two proteins have substantially different contact maps (Fig. 6, A and B) but the same amino acid composition. Our results show that we can generate variants with a predicted contact map that is similar to that of the target (Fig. 6, C and D). We find that the sequences generated via this procedure also show increased charge segregation (compared to A1-LCD) and have increased sequence similarity to V1 (fig. S10).

Fig. 6. Designing variants with a target contact map.

(A) Contact map of the compact V1 variant of A1-LCD. (B) Contact map of A1-LCD. (C) Design of A1 variants targeting the contact map in (A). The similarity between contact maps is measured with the MSE. (D) Contact map of the variant with the lowest observed MSE.

Designed variants in the context of the human disordered proteome

The results described above show that we can design IDPs with specific conformational properties and that charge segregation emerges as an important determinant of compaction of the designed sequences. This result is in line with previous observations from theory, simulation, and experiments (36, 63, 68). Recently, we have performed simulations of all IDPs from the human proteome (the IDRome) and found that chain dimensions of this broad range of natural sequences is governed by a complex interplay between average hydrophobicity, net charge, and charge patterning (25). Motivated by these observations, we examined the sequences generated by our design algorithm in the context of the properties of natural disordered sequences in the human proteome.

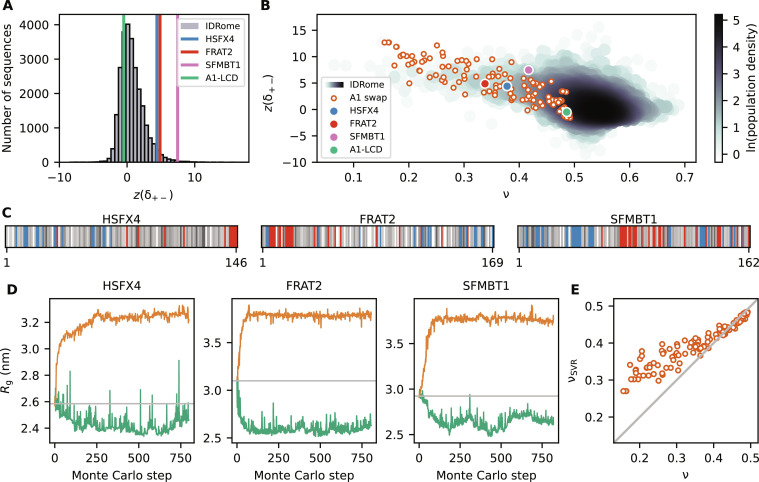
The first aspect that we examined was inspired by our observation that we could generate more compact variants of αSyn, A1-LCD, and LAF-1-RGG but not expand these proteins much (Fig. 2). As discussed above, we speculated that this observation was due to the fact that the charged residues in these proteins are well mixed so that it is possible to compact them by segregating positive and negative charges but more difficult to expand them by further mixing these charged residues. Similarly, we hypothesized that the small number of charged residues in FUS-PLD was the cause of the inability to change the compaction substantially. These observations led us to hypothesize that it would be possible to increase the compaction of natural proteins with stronger charge segregation. We therefore turned to calculations of the z(δ₊₋) score, which is analogous to the κ score for charge segregation but is defined in a way that makes it more appropriate for comparisons across sequences of different lengths and compositions (65). We thus examined the distribution of z(δ₊₋) scores across the human IDRome (25) and find that, for example, A1-LCD has a well-mixed arrangement of charges as indicated by z(δ₊₋) ≈ 0 (Fig. 7A).

Fig. 7. Designed swap variants in the context of the IDRome.

(A) Histogram of the sequences in the IDRome grouped based on their charge clustering. We use z(δ₊₋) to compare the degree of charge clustering for sequences of different lengths and composition, with high values of z(δ₊₋) indicating high segregation (65). z(δ₊₋) for the WT A1, HSFX4, FRAT2, and SFMBT1 are indicated in green, blue, red, and pink, respectively. (B) Comparison of 120 swap variants of A1-LCD (orange) with the IDRome by compaction (ν) and charge clustering [z(δ₊₋)]. (C) Diagram of the sequences of disordered regions in HSFX4, FRAT2, and SFMBT1 that we extracted from the IDRome as representative naturally occurring IDPs that show strong charge clustering. Negative and positive charges are colored in red and blue, respectively. The neutral residues are colored by a gray scale that reflects their hydrophobicity (corresponding to the λ parameter in CALVADOS), with the least hydrophobic residues in white and the most hydrophobic residues in black. (D) Design of more expanded and more compact swap variants starting from the WT sequences of the disordered domains of HSFX4, FRAT2, and SFMBT1. (E) Comparison of ν calculated from MD simulations [with CALVADOS 2 (53)] and predicted via an SVR machine learning model (ν_SVR) (25) for 120 representative A1-LCD variants.

To examine if charge patterning and compaction of the designed variants reflect the same rules as for natural proteins, we turned to the calculation of apparent scaling exponents (ν) as a length-independent measure of compaction. For a so-called “ideal-chain” polymer, protein-protein, protein-water, and water-water interactions are balanced, and ν = 0.5; smaller values of ν indicate more compact sequences, and an expanded, excluded-volume random coil has ν ≈ 0.6. We calculated ν for the designed A1-LCD variants and find that they follow the overall general relationship between charge segregation [z(δ₊₋)] and sequence compaction (ν) observed for natural proteins (Fig. 7B). For a few proteins, we find nominal scaling exponents below the value of 0.33 expected for compact globules (76); these unusual values reflect that these proteins are not homopolymers and arise from how we calculate scaling exponents.

To explore these aspects further, we selected three naturally occurring human IDPs (the disordered domains of HSFX4, FRAT2, and SFMBT1) whose compaction can be explained by their strong segregation of positively and negatively charged residues (Fig. 7C). Building on our hypothesis of why we could not expand the well-mixed sequences of αSyn, A1-LCD, and LAF-1-RGG (Fig. 2), we asked if we could design sequences resulting in more expanded conformational ensembles if we started from these charge segregated sequences. When we applied our design algorithm with the WT sequences of HSFX4, FRAT2, and SFMBT1 as starting points, we were able to obtain substantially more expanded sequences as well as also modestly more compact sequences (Fig. 7D). Together, these results support the notion that—for fixed sequence composition—modulation of the distribution of the positively and negatively charged residues is a key determinant of compaction and our ability to change this.

While charge segregation is important for fixed sequence composition, we previously found a more complex interplay between a wider range of sequence properties and chain compaction (25). These observations, in turn, enabled us to train a support vector regression (SVR) machine learning model to predict scaling exponents from sequences (ν_SVR). Given that the SVR model was trained on natural sequences, we asked how well our machine learning model was able to predict chain compaction for designs that have properties that are less common in natural sequences. Overall, we find a high correlation between predicted (ν_SVR) scaling exponents and those obtained directly from simulations (ν) of the 120 A1-LCD variants (Fig. 7E). The average absolute error of the predictions (19%) is somewhat greater than the value found across the IDRome [2.3% (25)], although these values are not fully comparable due to the different ranges of scaling exponents in the two datasets. We again note that defining and calculating the apparent scaling exponents are most robust for proteins that behave more like long homopolymers and that the specific structural properties in the most compact sequences make the average scaling exponent less representative of the conformational ensemble.

Efficient sequence design by machine learning

The results above demonstrate that we can design sequences of disordered proteins using an algorithm that combines molecular simulations with a coarse-grained model and alchemical free-energy calculations. Although the coarse-grained simulations are efficient and the free-energy calculations decrease the requirements for simulations, the design algorithm still requires substantial computational resources. Thus, a single run of ~4500 iterations for a protein such as A1-LCD (Fig. 3) takes about 20 days on a machine equipped with a current graphics processing unit (see Materials and Methods).

As also described above, we have developed an SVR model that can predict scaling exponents directly from the sequence (25), and our results show that this model is relatively accurate for the A1-LCD variants that we designed using molecular simulations (Fig. 6). This observation suggests that we could circumvent the computationally expensive simulations in the design of variants with changed compaction by using the scaling exponents from the SVR model instead of evaluating chain compaction by simulations. It has previously been demonstrated that such proxies can be used to drive the design of disordered proteins with specific properties (43, 45, 55, 58).

We therefore developed an alternative design procedure that replaces the MD simulations with the SVR model to predict chain compaction (ν). We demonstrate the utility of this model by designing variants of the seven proteins we studied above (Figs. 2 and 6) with either decreased or increased values of ν (fig. S11). The results recapitulate the observations from the simulation-driven designs, and simulations of the resulting sequences using CALVADOS confirm the accuracy of the SVR model in capturing chain compaction (fig. S11). Because of the efficiency of this approach, it can be run using easily available resources such as via Google Colab, for which we provide an easy to use implementation (see Materials and Methods).

DISCUSSION

IDPs play important roles in a range of biological processes and convey functions that complement those of folded proteins. Thus, the ability to design disordered sequences could substantially expand our ability to design proteins with novel functions and properties, in the same way as biology exploits combinations of order and disorder (31). Combinations of experiments and simulations has led to an improved understanding of the conformational properties of IDPs, which, in turn, has enabled improved models to generate conformational ensembles directly from sequence via molecular simulations (48, 77). These models have enabled previous applications to design IDPs (55–58) and genome-wide studies of sequence-ensemble relationships (25, 26). Our understanding of sequence-ensemble relationships may, in some cases, be encoded in simple relationships between sequence properties and, for example, compaction, and these relationships have been used in sequence design (43–47).

Here, we describe a general approach for designing IDPs that exploits a computationally efficient simulation model. Instead of using rules for sequence-ensemble relationships, our design algorithm is based on MCMC sampling of sequence space, where each sequence is structurally characterized by combining CALVADOS-based MD simulations (49) and alchemical free-energy calculations (78). In some aspects, our algorithms are similar to others previously used to generate sequences with specified conformational or functional propensities (43–47, 55–58). Our MCMC sampling guides the sequence toward a design target, here compaction or contact maps, and uses the MD simulations and alchemical calculations to predict the conformational ensembles of candidate sequences. Together, this leads to an efficient algorithm that we have successfully used to generate a wide range of sequences with diverse structural features.

We experimentally characterized five designed variants of A1-LCD and find good agreement between experiments and simulations in terms of both the target property (compaction) and the propensity of the sequences to undergo PS. These findings are, in our view, important. First, we selected A1-LCD because it is one of the most compact IDPs that have been characterized experimentally, and thus making it even more compact is, we thought, nontrivial. Second, we restricted our optimization algorithm to maintain sequence composition and show that we can find substantially more compact sequences even with this restriction. Third, the high correlation between the experimental and calculated radii of gyration demonstrates that CALVADOS remains accurate even for highly unnatural sequences whose properties are well outside those it has previously been trained and benchmarked on. This is a strong validation of our approach of using a physics-based model to drive the sequence design algorithm. We note, however, that the CALVADOS force field we used could have been readily reparameterized to improve predictions of single-chain compaction, in case our experiments had revealed discrepancies with simulation predictions (49, 59). Fourth, we show that our designs not only match the experiments for the design target (compaction) but also have propensities to phase separate that generally match the predictions from simulations. We note, however, that V5 appears to be an outlier because its experimental c_sat value is lower than the prediction from CALVADOS and deviates from the observed trend of increasing c_sat with increasing R_g. The origin of the discrepancy for the c_sat value is unclear, and we note that we accurately predict the R_g of V5.

We initially selected 15 variants of A1-LCD for experimental characterization. Ten of these variants (table S2) could not easily be expressed in Escherichia coli, and further investigation will be necessary to shed light on sequence features that might impair either transcription or translation of such synthetic constructs. We did not find sequence features related to patterning of charged and aromatic residues that differed clearly between the variants that expressed and those that did not (fig. S7), and sequences with similar properties are also found among naturally occurring disordered proteins (25). Many of the compact designed sequences have large charge segregation including stretches of positively charged amino acids, and we note that such polybasic regions may slow down translation (79); however, we also note that V1 contains seven consecutive basic (lysine or arginine) residues so that this property does not alone explain which proteins could be expressed.

In addition to developing an algorithm to design IDPs with different levels of compaction, our work also sheds light on sequence-ensemble relationships that can help us understand how natural evolution shapes IDPs. We found that we could generate more compact structures for proteins with the same composition as αSyn, A1-LCD, and LAF-1-RGG, but not for FUS-PLD, and that we could not generate substantially more expanded conformations for protein sequences with any of these compositions. Our results show that these effects are mainly due to the number and patterning of charged residues in these proteins. Thus, while global sequence composition may be an important factor in the evolution of IDPs (80–82), our results support the notion that patterning also plays a key role. The results from these analyses are in line with previous bioinformatics analyses that show that most natural IDPs have relatively high mixing of positively and negatively charged residues (83). Nevertheless, we and others have previously shown that some natural IDPs are compact due to strong segregation of positively and negatively charged residues (25, 26, 36, 84), and we show that, for sequences such as the disordered domains of HSFX4, FRAT2, and SFMBT1, we can generate more expanded sequences by disrupting this charge patterning. If the high mixing of charged residues is due to entropic effects in sequence space together with the fact that IDPs have a large tolerance for sequence variation (85–88) or is due to effects, e.g., on solubility or preventing erroneous interactions, is an interesting question for future studies.

Looking ahead, our results show that the accuracy of CALVADOS appears to extrapolate also to outside of the realm of natural proteins and variants thereof, on which the model was trained. This suggests that even more extensive sampling of sequence space might be useful. While our MCMC-based approach enables a fine-grained and substantial sampling of the sequence space, it may be combined with or replaced by other approaches to guide the sequence design. We and others have recently shown that it is possible to encode the sequence-ensemble relationships from coarse-grained simulations in machine learning methods (25, 26, 67); we suggest that such methods for predicting properties from sequences may be used together with, for example, reinforcement learning (89, 90) or Bayesian optimization (91) to explore sequence space even more efficiently. Such rule-based methods have previously been used, for example, to design sequences with modified chain dimensions (43, 44) or propensity to undergo PS (46, 47). We here provide an initial proof of principle of this approach using our SVR model to drive the sequence design algorithm; similar ideas have recently been presented in related works using a machine learning model to drive the sequence design of disordered proteins (45, 58).

We expect that combinations of machine learning and simulations will, in particular, be important when designing for structural observables that are more complex than single-chain compaction, where simulations could be more expensive and alchemical free-energy calculations might be less efficient. Our algorithm can be applied to design for other structural features than single-chain dimensions and can be adapted to other ways of sampling sequence space. As an initial proof of principle, we here have also demonstrated that it is possible to design sequences with a target contact map. The range of applications can therefore be extended to studies focused on understanding the effect of the patterning of specific residues or groups of residues or to design for, e.g., binders for disordered therapeutic targets.

In summary, we have developed, applied, and validated an algorithm for designing disordered sequences with specified conformational properties. We show that we can design IDPs with substantially increased compaction even with fixed amino acid composition and find that our algorithms mostly exploit the relationship between charge patterning and compaction. We also explain why some sequences are difficult to expand when the positively and negatively charged residues are well mixed. Our experimental validation highlights the accuracy of the coarse-grained model with prospective testing of novel sequences. Together, our results show that it is now possible to design sequences of disordered proteins, thus expanding our toolbox for designing proteins with novel or improved functions.

MATERIALS AND METHODS

MCMC sampling for IDP design

We used an MCMC algorithm to generate sequences of IDPs. We here targeted the compaction of the chain (as quantified by the R_g) and kept the composition constant during the sequence sampling by using swaps of a randomly selected pair of residues as our MCMC move (92). We evaluated the R_g of the new sequence, either by running an MD simulation or by reweighting (see below) and used the Metropolis-Hastings criterion to evaluate the probability of acceptance (A_k−1→k)

$$A_{k-1\to k}=\left\{\begin{array}{cc}\text{exp}\left[-\frac{\mid \mathrm{\Delta }{R}_{\mathrm{g},k}\mid -\mid \mathrm{\Delta }{R}_{\mathrm{g},k-1}\mid }{c}\right],\hfill & \mid \mathrm{\Delta }{R}_{\mathrm{g},k}\mid >\mid \mathrm{\Delta }{R}_{\mathrm{g},k-1}\mid \hfill \\ 1,\hfill & \mid \mathrm{\Delta }{R}_{\mathrm{g},k}\mid \le \mid \mathrm{\Delta }{R}_{\mathrm{g},k-1}\mid \hfill \end{array}\right.$$

Here, ∣ΔR_g,k∣ is the cost function that quantifies the absolute difference between the R_g of the sequence at the MCMC step k and a target R_g (∣ΔR_g,k∣ = ∣R_g,k − R_g,target∣), and c is a control parameter. R_g,target is set to 0 nm to design for more compact IDPs and to 10 nm to design for more expanded IDPs. The starting value for c is 0.014, corresponding to A_k−1→k = 0.5 for ∣ΔR_g,k ∣ − ∣ ΔR_g,k−1∣ = 0.01 nm. We apply simulated annealing using an approach where c is decreased by 1% every 2l MCMC steps, where l is the number of amino acids in the IDP sequence.

We used the same scheme as above for designing sequences targeting a contact map. For targeting contact maps, the starting value for c was set to 0.049. As the cost function, we use the mean square error (MSE) to the target contact map. We calculate the contact map as

$$p\left(C_{\mathit{ij}}\right)=N^{-1}{\displaystyle \sum _n^N}‍0.5-0.5 \text{tanh}\left[\left(d_{\mathit{ij},n}-1\right)/0.3\right]$$

Here, N is the number of simulation frames and d_ij,n is the distance between interaction sites i and j in the nth simulation frame. We excluded neighboring residue pairs from the MSE calculations.

Although, in this work, we focus on the specific application of generating variants with fixed amino acid composition, the algorithm and our software accommodates other user-specified MCMC moves (e.g., single-site or multisite amino acid substitutions, substitutions restricted to specific positions and specific residue types). Furthermore, other observables that can be calculated from the simulations can be used as the design target. A scheme of the design algorithm is shown in fig. S12.

MD simulations

We ran coarse-grained MD simulations using the CALVADOS M1 (49) C_α-based model. Instead, when comparing ν from simulations to ν predicted with the SVR model, we used the CALVADOS 2 (53) model because the SVR model was trained on CALVADOS 2 simulations. Single-chain simulations in the design algorithm were run for 500 ns with a 10-fs time step. Simulation conditions were set to reproduce 298 K, 150 mM ionic strength, and pH 7. Other single-chain simulations that are not in the context of the design were run for 1 μs and, when simulations are compared to experiments, under the experimental conditions.

Multichain simulations to study the PS propensity of the A1-LCD variants were performed in slab geometry with the CALVADOS M1 model. One hundred chains were assembled in a simulation box 150 nm long and with a cross section of 15 nm × 15 nm. Multichain simulations were run for 20 μs. For multichain simulations of experimental constructs, three replicates were run for a total simulation time of 120 μs (one replicate 20 μs long and two replicates 50 μs long).

The cutoff used for nonbonded nonionic interactions was 4 nm for single-chain simulations and 2 nm for multichain simulations (53). Charge-charge interactions were truncated and shifted at a cutoff of 4 nm in all simulations.

Alchemical free-energy calculations with MBAR

When proposing a new sequence, the design algorithm attempts to predict the R_g by reweighting simulations generated at previous steps of the MCMC algorithm using the multistate Bennett acceptance ratio (MBAR) method (78). Because the simulations are performed with a C_α-based coarse-grained model, changing the amino acid type in a position of the sequence simply means changing the force field parameters and possibly the charge of the bead representing the residue at that position. Thus, it is easy to evaluate the per-frame potential energy of a new sequence for an ensemble of conformations sampled with another protein sequence. MBAR takes as input an energy matrix defined by frames coming from n simulations of different sequences (MBAR pool) and the potential energy functions from each sequence. We calculate the potential energies of the frames of the simulations for a new sequence proposed by the MCMC algorithm and use MBAR to obtain the Boltzmann weights to estimate the weighted average of the R_g of the new sequence without running a new simulation.

The reweighting is most accurate when there is substantial overlap between the potential energy functions of the simulations in the MBAR pool and that of the new sequence. We quantify how much the energies of the frames from the simulations in the MBAR pool are compatible with the potential energy function of the new sequence by calculating the number of effective frames (N_eff) that contributes to the averaging

$$N_{\text{eff}}=N \text{exp}\left[-{\displaystyle \sum _i^N}{w}_i\text{ln}\left(w_{i}N\right)\right]$$

where N is the total number of frames from the simulations in the MBAR pool and w_i is the weight of the ith frame obtained from MBAR to calculate the R_g of the new sequence. By generating test datasets where we compare the simulated R_g with the predicted R_g from MBAR weights, we assessed the relationship between N_eff and the accuracy of the predicted R_g (fig. S4). In light of this analysis, we set a threshold for N_eff to 20,000. When the weights obtained by MBAR result in a N_eff below this threshold, the algorithm initiates a new simulation and uses the R_g from this simulation when evaluating the acceptance probability in the MCMC sampling scheme.

The ability to estimate the R_g of new sequences by reweighting makes the design algorithm more efficient as it decreases the number of MD simulations that are needed. Because of the large size of the energy matrix, we still need to keep the number of simulations in the MBAR pool relatively low so that the calculations are efficient. With a test dataset, we also assessed how the efficiency of the algorithm would change varying the size of the MBAR pool. In general, the larger the pool, the less simulations are required by the algorithm (i.e., it occurs less frequently that the N_eff drops below 20,000). In light of these observations, we set the maximum size of the MBAR pool to 10 (fig. S4). When the size of the pool is at its maximum and the N_eff drops below the threshold, a new simulation is performed and added to the pool, while the oldest simulation is discarded from the MBAR pool.

Small-angle X-ray scattering

SAXS experiments (fig. S13 and table S3) were performed at BioCAT (beamline 18ID at the Advanced Photon Source, Chicago) with in-line size exclusion chromatography to separate protein from aggregates, contaminants, and storage buffer components, thus ensuring optimal data quality (fig. S14) as previously reported (39, 41, 71). Samples were loaded onto a Superdex 75 Increase 10/300 GL column (Cytiva), which was run at 0.6 ml/min by an AKTA Pure FPLC (GE), and the eluate, after passing through the ultraviolet monitor, was flown through the SAXS flow cell. The flow cell consisted of a 1.0-mm inside diameter quartz capillary with ~20-μm walls. All protein solutions were measured at room temperature in 20 mM Hepes (pH 7.0), 150 mM NaCl, and 2 mM dithiothreitol. A coflowing buffer sheath was used to separate the sample from the capillary walls, helping to prevent radiation damage (93). Scattering intensity was recorded using an Eiger2 XE 9M (Dectris) detector, which was placed 3.685 m from the sample, giving us access to a q range of 0.0029 to 0.42 Å⁻¹. Exposures of 0.5 s were acquired every 1 s during elution, and data were reduced using BioXTAS RAW 2.1.4 (94). Buffer blanks were created by averaging regions flanking the elution peak and subtracted from exposures selected from the elution peak to create the I(q) versus q curves (scattering profiles) used for subsequent analyses. RAW was used for buffer subtraction, averaging, and Guinier fits. Scattering profiles were additionally fit using an empirically derived molecular form factor (95) (used to calculate the experimental R_g values in Fig. 5).

Diffusion-ordered NMR spectroscopy

We carried out diffusion-ordered spectroscopy experiments (96) at 307 K to measure translational diffusion coefficients for WT A1-LCD and the V1 variant by fitting intensity decays of individual signals selected between 0.5 and 2.5 parts per million (97) with the Stejskal-Tanner equation (98). Spectra were recorded on a Bruker 600-MHz spectrometer equipped with a cryoprobe and Z-field gradient and were obtained over gradient strengths from 5 to 95% (32 points) for A1-LCD and from 5 to 75% (16 points) for V1 (γ = 26,752 rad s⁻¹ G⁻¹) with a diffusion time (Δ) of 50 ms and a gradient length (δ) of 6 ms. We used 1,4-dioxane (0.10% v/v) as the internal reference for the R_h [2.27 ± 0.04 Å (75)]. We acquired 80 scans for A1-LCD and 480 scans for V1. Translational diffusion coefficients were fitted in Dynamics Center v2.5.6 (Bruker) and were used to estimate the R_h for the proteins (99), with error propagation using the diffusion coefficients of both the protein and dioxane.

Supplementary Materials

This PDF file includes:

Supplementary Materials and Methods

Figs. S1 to S14

Tables S1 to S3

References