Statistical Analysis of Self-Reported Health Conditions in Cohort Studies: Handling of Missing Onset Age

Abstract

Objective:

This paper discusses methodological challenges in epidemiological association analysis of a time-to-event outcome and hypothesized risk factors, where age/time at the onset of the outcome may be missing in some cases, a condition commonly encountered when the outcome is self-reported.

Study Design and Setting:

A cohort study with long-term follow-up for outcome ascertainment such as the Childhood Cancer Survivor Study (CCSS), a large cohort study of 5-year survivors of childhood cancer diagnosed in 1970-1999 in which occurrences and age at onset of various chronic health conditions (CHCs) are self-reported in surveys. Simple methods for handling missing onset age and their potential bias in the exposure-outcome association inference are discussed. The interval-censored method is discussed as a remedy for handling this problem. The finite sample performance of these approaches is compared through Monte Carlo simulations. Examples from the CCSS include four CHCs (diabetes, myocardial infarction, osteoporosis/osteopenia, and growth hormone deficiency).

Results:

The interval-censored method is usable in practice using the standard statistical software. The simulation study showed that the regression coefficient estimates from the ‘Interval censored’ method consistently displayed reduced bias and, in most cases, smaller standard deviations, resulting in smaller mean square errors, compared to those from the simple approaches, regardless of the proportion of subjects with an event of interest, the proportion of missing onset age, and the sample size.

Conclusion:

The interval-censored method is a statistically valid and practical approach to the association analysis of self-reported time-to-event data when onset age may be missing. While the simpler approaches that force such data into complete data may enable the standard analytic methods to be applicable, there is considerable loss in both accuracy and precision relative to the interval-censored method.

1. Introduction

Self-reporting of health conditions plays a pivotal role in epidemiological research due to its methodological feasibility through questionnaires and interviews and its ability to reflect the participants’ perspectives. However, self-reported conditions often involve a temporal dimension, specifically the condition’s onset, which depends on the participants’ memory and recall abilities. This reliance can lead to missing onset ages, producing interval-censored data, i.e., the onset is known to fall within a time interval but its exact time is unknown, and posing a methodological challenge for epidemiologists seeking to infer associations between exposures and health outcomes.

Cox regression offers a robust framework for estimating the associations of covariates with the hazard rate of event occurrence and is a widely used statistical method in epidemiology (Cox, 1972; Hosmer et al., 2008). However, standard implementations of Cox regression in statistical software typically exclude interval-censored data from the analysis, which reduces the sample size and potentially introduces bias to the results.

This paper aims to describe and illuminate intricacies in association analysis of self-reported time-to-event data with missing onset age information, using examples from a large cohort study of childhood cancer survivors: see Section S1 of Supplementary Materials. Section 2 describes the research aims and presents the study/data structure. Section 3.1 explores simple approaches that may be employed to address the issue of missing onset age. To overcome the limitations, we discuss the utilization of interval censoring as a practical methodology for handling missing onset age in Section 3.2. Section 4 compares the interval-censored method with the simple approaches through Monte Carlo simulations, providing insights into their realistic performance differences. Utilizing examples from the analysis of chronic health conditions (CHCs) in childhood cancer survivors, Section 5, illustrates the complexities and inherent limitations of the simple approaches. Discussion on related methodological issues is given in Section 6.

2. Research Aims and Motivating Data Structure

In the CCSS, survivors are asked in longitudinally- administered questionnaires if they have ever been told by a doctor or other health care professional that they have, or have had, each of many CHC conditions of interest and, if yes, when the age at onset was. Of 25,656, the percentages of survivors who self-reported having had four CHCs we consider here, diabetes, MI, osteoporosis/osteopenia, and GHD, are 3.0%, 1.2%, 8.0%, and 22.5%, respectively. For GHD, the percentage is among those who had brain radiation during cancer therapy (n = 7177) as they are the at-risk population and the target of clinical investigation.

Table 1 shows the percentages of those who have experienced each condition and, among those who had, the percentage with a reported onset age.

Table 1:

Descriptive summary of diabetes controlled by insulin shot, myocardial infarction (MI), osteoporosis or osteopenia, and growth hormone deficiency (GHD) conditions among survivors of the Childhood Cancer Survivor Study

Conditions		Had the event		Have not had the even
	N	Onset reported	Onset not reported
Diabetes	25656	432 ( 2.0%)	227 (1.0%)	24997 (97.0%)
Myocardial infarction	25656	254 ( 1.0%)	43 (0.20%)	25359 (98.8%)
Osteoporosis/Osteopenia	25656	1279 ( 5.0%)	744 (3.0%)	23633 (92.0%)
Growth hormone deficiency	7177	636 ( 8.9%)	981 (13.6%)	5560 (77.5%)

As shown in Table 1, among those who experienced the conditions, some didn’t report the onset age, which is missing information.

Our research objective is to evaluate associations between each of the four CHC conditions and its hypothesized risk factors.While the standard implementations of Cox regression are widely used for studying the associations of covariates with event hazard rates, they require complete information on the onset age of the event of interest. In the next section, we briefly describe some simple methods for handling missing onset-age information that can be considered in epidemiological research. Then, we describe utilizing an interval-censored approach as an alternative.

3. Statistical methods for handling missing onset age

It’s essential to acknowledge that missing onset age is not missing data in the usual sense. This type of missing data occurs exclusively in participants who report having experienced an event, i.e., the missingness occurs only in a subset of the participants. Since the survivor reported the event’s occurrence at the time of the survey, the missing onset age is interval-censored and known to fall within the interval between the start of the at-risk time (or the survey completion date of the preceding questionnaire if any) and the completion date of the survey that reported the occurrence of the event, but its exact time is unknown (see the Section S3 of Supplementary Material for detailed statistical modeling.) Furthermore, in long-term childhood cancer survivors’ surveys, treatment influence on non-reporting causes informative censoring (Zhang and Sun, 2010; Mirzaei Salehabadi and Sengupta, 2016). The challenge associated with missing onset age is intricately tied to the occurrence of events. This special form of missingness complicates how we handle the missing onset age problem in practice: see further discussion in Supplementary Materials: Missing onset age.

We explore alternative approaches in this manuscript, focusing on practical and feasible options for epidemiological research.

3.1. Simple methods

If the percentage of missing onset age is small, it may seem reasonable to create a complete dataset in a rather crude fashion and use Cox regression. Otherwise, practical analysis often involves removal, imputation, or assuming event non-occurrence by the study end, despite the complexities introduced by interval censoring. Two broad categories of simple approaches may be considered for missing onset age.

3.1.1. Deletion-based methods

The ‘deletion-based’ method encompasses two simple deletion approaches.

Approach (a): The ‘observation-deletion’ method was employed by researchers such as Smarr et al. (2021), who investigated preconception exposure to environmental pollutants to identify key risk factors for incident human chorionic gonadotropin (hCG) pregnancy loss: they excluded observations from approximately 150 women (out of 501) who did not report the time to pregnancy loss when they indicated a loCoss at the survey time. This follows the commonly employed ‘complete-data analysis’ approach above, introducing bias by removing participants who experienced the event but did not provide the age at onset.

Approach (b): The ‘event-deletion’ method treats events with no reported onset age as reporting errors and assumed that they did not occur. In other words, the observation of the individual is retained but assumes that the incompletely-reported events did not occur. The underlying concept of this approach is that the incompleteness in reporting an event, specifically the absence of its onset age, is an indication of an error in reporting the event itself and lead to a presumption that the event had not occurred. For example, Suh et al. (2020) used the CCSS data to assess the association of various risk factors with the occurrence of chronic health conditions. In the CCSS, if a condition is reported without specifying the age at onset, a team of experts reviews all available medical information, including medications, to validate the reported event. If they can confirm the event occurrence through other sources, they assign the survey time to the missing onset age (see 3.1.2 below). If the occurrence cannot be verified, the observation for that survivor is retained, assuming the event did not occur: this is the ‘event-deletion’ method.

These approaches use events only if they were reported with an onset age and remove events without an onset age, i.e., they are conservative in using the reported events, and their event count is smaller than the count of the reported events. Both approaches facilitate the ‘complete-data’ availability, enabling Cox regression for association inference.

3.1.2. Simple replacement method

‘Simple replacement’ method, applied by researchers such as Dixon et al. (2023) who used the CCSS data to assess cardiovascular risk factors, replaces the missing time-to-event with survey time when the age at onset of those cardiovascular conditions are missing. This approach keeps the event count as reported, but the missing onset age is assumed to be the latest possible time, the survey in which the event was reported. This approach also facilitates the ‘complete-data’ availability and enables Cox regression for association inference.

Because they facilitate complete data, many study investigators opt to use them utilizing standard statistical software (i.e., coxph in R, stcox in Stata, or PHREG in SAS (Gómez et al. (2009); Allison (2010)) in practice.

In practice, the ‘Simple methods’ utilize the traditional Cox regression, which requires exact event times, allowing the risk set at each event time to be constructed. However, these ‘Simple methods’ that force the use of the traditional Cox regression are not a statistically valid approach for interval-censored data.

3.2. Interval-censored regression model

The self-reported onset ages are susceptible to censoring Padez (2003); Mirzaei-Salehabadi et al. (2015). In cases where a participant doesn’t report the onset age, the information is confined to an interval from the beginning of the at-risk period (or, the survey completion date of the preceding questionnaire if any) to the completion date of the survey in which the participant reported having had an event without specifying the onset age. This incomplete data falls under the ‘interval-censored’ data category because we know the event occurred within a specific interval but do not know the exact age of onset. This limitation complicates the calculation of the risk set because it cannot be precisely determined, thus necessitating specialized statistical methods that can accommodate interval-censored data to enable valid statistical analysis. Regression analysis of interval-censored data under the proportional hazard model has been studied. Finkelstein (1986) addressed this issue by proposing a maximum likelihood estimation method to jointly estimate regression parameters and the baseline hazard function using a Newton-Raphson-based algorithm. Subsequent developments in the interval-censored regression model include works by Groeneboom and Wellner (1992); Satten (1996); Goggins et al. (1998); Cai and Betensky (2003); Li and Ma (2013); Shao et al. (2014). Since these methods are either computationally intensive or methodologically complex in practical applications, they are beyond the scope of this paper. Nevertheless, we provide some relevant R packages in Section 6.

Wang et al. (2016) proposed a method for analyzing interval-censored data under the proportional hazards model using a monotone spline approximation of the cumulative baseline hazard function. This approach is flexible, accurate, computationally efficient, and user-friendly. For a detailed explanation of the proposed likelihood, refer to Finkelstein (1986); for the optimization method, see Wang et al. (2016). Both are briefly described in the Section S3 of Supplementary Material. Additionally, a companion R package ‘icenReg’ had been developed to facilitate their method by Anderson-Bergman (2017). We have used this R package for the analyses based on the interval-censored approach in this study.

4. Monte Carlo simulation to evaluate inferential performance

To assess the performance of methods described in Section 3, we conducted a comparative analysis of the estimated coefficients for the risk factors through Monte Carlo simulation: see Section S4 of Supplementary Materials for the details according to the approach proposed by Morris et al. (2019). The assessment included estimates from ‘observation-deletion,’ ‘event-deletion,’ ‘Simple replacement,’ and ‘Interval-censored’ approaches. Standard Cox regression software can be used for the first three. The ‘Interval-censored’ approach used the ic_sp’ function in icenReg package of R, fitting a semi-parametric Cox proportional model with 50 bootstrap iterations to estimate covariance matrix for the regression coefficients.

We run 500 simulations for each of the combinations of parameters mentioned in the Supplementary Materials for sample sizes n = 300, 1000, and 5000 to compute the empirical bias, the standard deviation (Stdev), the mean squared error (MSE), and the mean of standard error (SE) for the estimates of regression coefficients, based on the four methods described above.

Figures 1 and 2 show, for event frequencies (a) 10% and (b) 30%, respectively, plots of the bias (the left column) and the standard deviation (Stdev) (the right column) for the estimated regression coefficients in three scenarios: 1) Equal Reporting/Non-reporting (the top panel), 2) Reporting Dominance (the middle panel), and 3) Non-Reporting Dominance (the bottom panel), for n = 5000. In both event frequencies, the estimates from the ‘Interval-censored’ method have a smaller bias and Stdev than those from the other methods. A considerable bias is evident with deletion-based or ‘Simple replacement’ methods, particularly for the binary covariate. However, when using continuous covariate, the Stdev of ‘Simple replacement’ and ‘Interval-censored’ are comparable.

Figure 1:

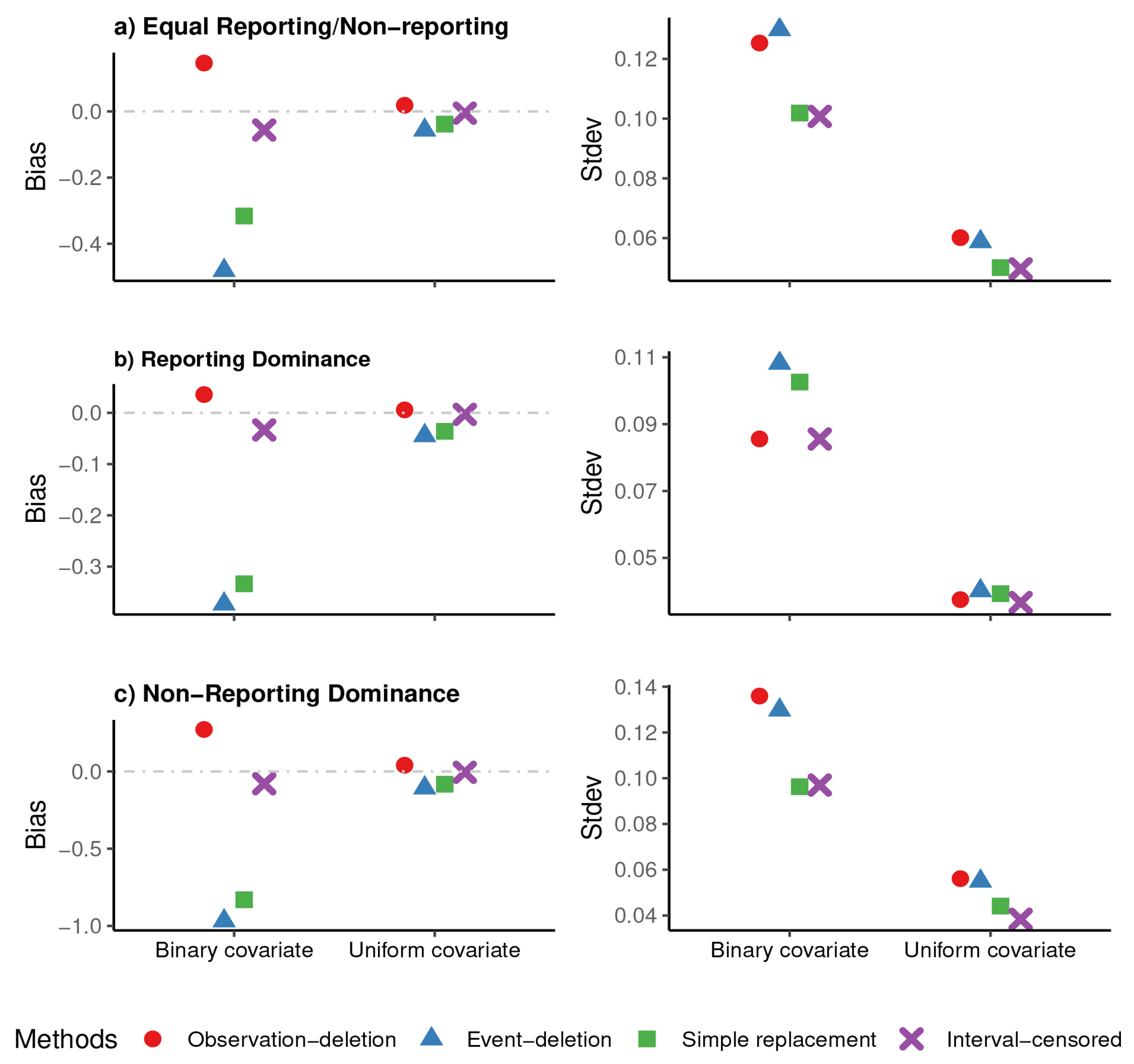
Plots of observed bias in the left column, and standard deviation (Stdev) in the right column of the estimated risk factor’s coefficient in ‘observation-deletion’, ‘event-deletion’, ‘Simple replacement’, and ‘Interval-censored’ scenarios, for a) ‘Equal Reporting/Non-reporting’ (the top panel), b) ‘Reporting Dominance’ (the middle panel), and c) ‘Non-Reporting Dominance’ (the bottom panel), for n=5000 in 500 simulations when about 10% of individuals have experienced the event by the time of survey.

Figure 2:

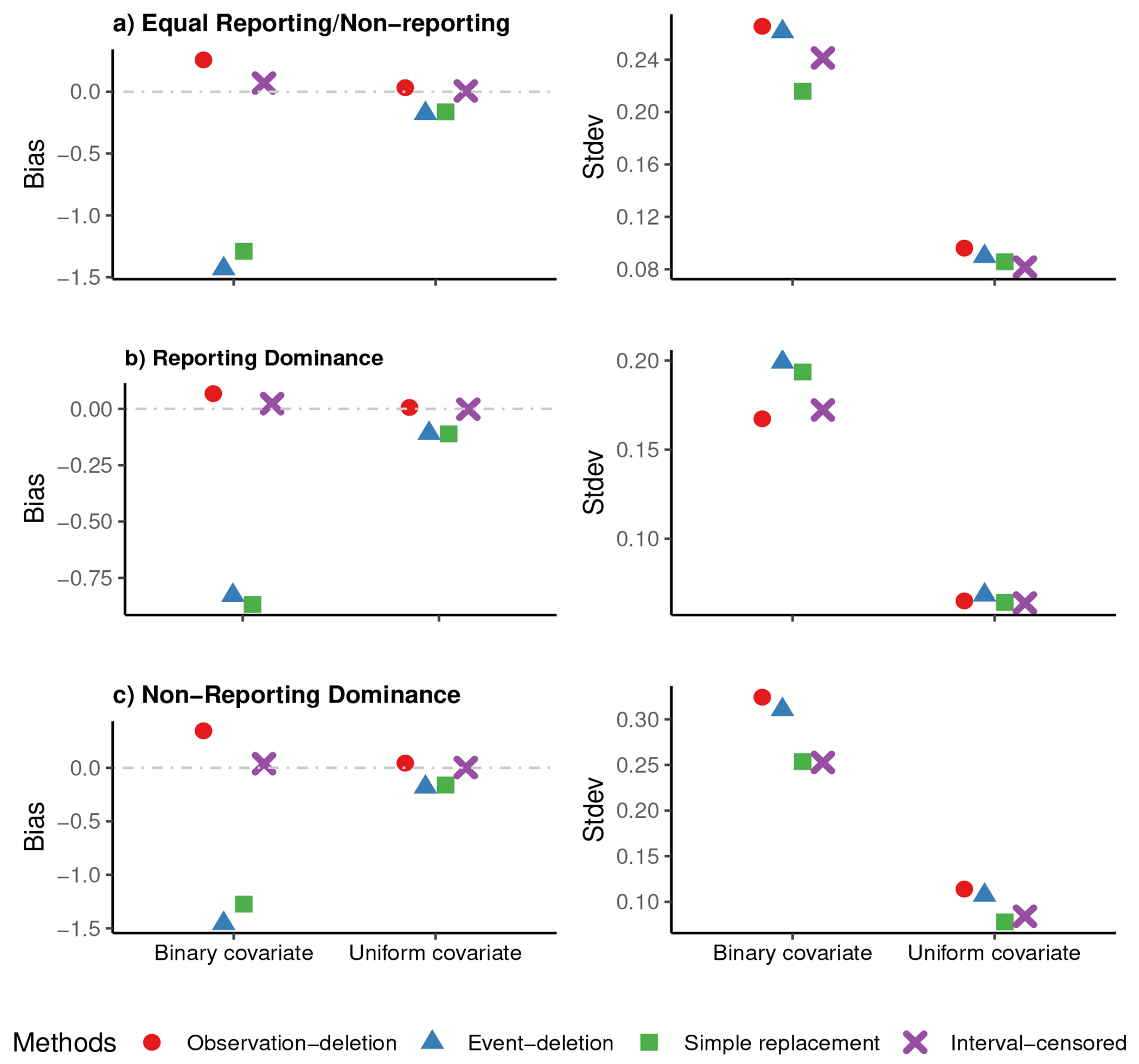
Plots of observed bias in the left column, and standard deviation (Stdev) in the right column of the estimated risk factor’s coefficient in ‘observation-deletion’, ‘event-deletion’, ‘Simple replacement’, and ‘Interval-censored’ scenarios, for a) ‘Equal Reporting/Non-reporting’ (the top panel), b) ‘Reporting Dominance’ (the middle panel), and c) ‘Non-Reporting Dominance’ (the bottom panel), for n=5000 in 500 simulations when about 30% of individuals have experienced the event by the time of survey.

Plots similar to Figures 1 and 2 for n = 300 and 1000 are given in the Supplementary Material (see Figures S1–S4). Across the varying sample sizes, the superior performance of the ‘Interval-censored’ method remained as n = 5000. The results are consistent across the three missingness proportion scenarios. The better performance of the ‘Interval-censored’ method supports its use when there is missing age at onset in the self-reported time-to-event data. The results also show that the empirical standard deviation of parameter estimates are close to the mean of standard error estimates of parameter estimates for all the methods, confirming the validity of standard error estimates in three different scenarios. The results of the simulations are detailed in Tables S1–S6 of Supplementary Material.

5. Epidemiological Analysis Applications

We examined the set of risk factors for diabetes and GHD that have been discussed in the literature on childhood cancer survivors. In both examples, the follow-up time commences five years after childhood cancer diagnosis until the first occurrence of the event of interest, death, or the last survey time. The time axis is denoted as years since the 5-year post-diagnosis. Models have been adjusted for age at diagnosis. See also Supplementary Materials: Two other examples.

5.1. Example 1: Diabetes controlled by insulin shots

The percentage of survivors who self-reported having a diabetes condition that needs to be controlled by insulin shots in the CCSS surveys was 3.0%. Among them, 34.5% didn’t report the age at onset and left it blank in the survey. Friedman et al. (2020) identified the variables in Table 2 as risk factors, whose associations with the outcome are estimated here using the four methods described in Section 3. Table 2 summarizes the findings, including estimates of the hazard ratios (HRs) and their 95% confidence intervals (CI).

Table 2:

Estimated hazard ratios and their 95% confidence intervals (CIs) of risk factors associated with the onset of diabetes

Parameter	Observation-deletion (N=25429)		Event-deletion (n=25656)		Simple replacement (n=25656)		Interval censored (n=25656)
	HR	95% CI	HR	95% CI	HR	95% CI	HR	95% CI
BMI-Normal	Ref.		Ref.		Ref.		Ref.
BMI-Underweight	1.16	(0.78, 1.70)	1.15	(0.78, 1.70)	1.38	(1.02, 1.86)	1.32	(0.97, 1.80)
BMI-Overweight	1.57	(1.22, 2.01)	1.56	(1.22, 2.00)	1.60	(1.31, 1.94)	1.61	(1.34, 1.93)
BMI-Obese	3.64	(2.89, 4.59)	3.62	(2.87, 4.56)	3.04	(2.50, 3.68)	2.94	(2.44, 3.54)
No Panc.T radiation	Ref.		Ref.		Ref.		Ref.
Panc.T RT (0,10) Gy	0.94	(0.76, 1.17)	0.94	(0.75, 1.16)	0.97	(0.82, 1.14)	1.03	(0.87, 1.23)
Panc.T RT [10, 15) Gy	3.19	(2.36, 4.31)	3.20	(2.37, 4.32)	2.23	(1.71, 2.91)	2.31	(1.74, 3.06)
Panc.T RT [15, 20) Gy	2.77	(1.61, 4.77)	2.77	(1.61, 4.78)	2.13	(1.32, 3.44)	2.34	(1.41, 3.91)
Panc.T RT 20+ Gy	2.83	(1.81, 4.43)	2.80	(1.79, 4.38)	2.21	(1.50, 3.26)	2.57	(1.75, 3.78)
Age at diagnosis	1.01	(0.92, 1.11)	1.00	(0.91, 1.10)	1.18	(1.10, 1.28)	1.18	(1.11, 1.25)

Diabetes conditions can happen at any time after surviving cancer, posing higher risks with advancing age. For those who reported the onset age, the mean onset age was 14.7 with a standard deviation of 9.4. While there’s a noticeable percentage of individuals not reporting their onset age, the overall prevalence of reported diabetes is relatively low. Substituting missing onset ages with survey age produces hazard ratio estimates comparable to the ‘Interval-censored’ method. However, results differ appreciably from the observation/event deletion-based approaches. For example, doses of pancreas tail radiation above 10 Gy, especially 10-15 Gy, show higher estimated hazard ratios from the observation/event deletion-based approaches than the ‘Simple replacement’ and ‘Interval-censored’ methods. Age at diagnosis appears not statistically significant in the observation/event deletion-based approaches, while the ‘Simple replacement’ and ‘Interval-censored’ methods identified its associations with diabetes statistically significant among survivors.

5.2. Example 2: Growth hormone deficiency

The salient feature of this example is that 22.5% of survivors self-reported experiencing GHD, with 60.7% of them not providing information on the age at onset. Previous studies, such as those by Chemaitilly et al. (2015); van Iersel et al. (2019) identified the variables in Table 3 as risk factors associated with GHD. In our analysis, we employed the same covariates, utilizing brain radiation dose as a categorical covariate, BMI with the standard categories, gender as a binary covariate, and age at diagnosis as a continuous covariate. The findings are summarized in Table 3.

Table 3:

Estimated hazard ratios and their 95% confidence intervals (CIs) of risk factors associated with the onset of GHD

Parameter	Observation-deletion (N=6196)		Event-deletion (n=7177)		Simple replacement (n=7177)		Interval censored (n=7177)
	HR	95% CI	HR	95% CI	HR	95% CI	HR	95% CI
BMI-Normal	Ref.		Ref.		Ref.		Ref.
BMI-Underweight	1.42	(1.12, 1.81)	1.24	(0.97, 1.57)	1.57	(1.35, 1.83)	1.48	(1.25 1.76)
BMI-Overweight	0.82	(0.67, 1.01)	0.86	(0.70, 1.06)	0.78	(0.68, 0.88)	0.81	(0.72, 0.91)
BMI-Obese	0.67	(0.52, 0.85)	0.72	(0.56, 0.92)	0.75	(0.65, 0.87)	0.74	(0.64, 0.84)
Brain RT [0,20) Gy	Ref.		Ref.		Ref.		Ref.
Brain RT [20,30) Gy	1.14	(0.91, 1.42)	1.14	(0.91, 1.43)	0.71	(0.60, 0.85)	0.94	(0.82, 1.09)
Brain RT [30,50) Gy	2.39	(1.85, 3.08)	1.98	(1.53, 2.55)	2.33	(1.95, 2.78)	2.65	(2.26, 3.12)
Brain RT 50+ Gy	3.07	(2.51, 3.77)	2.00	(1.63, 2.45)	4.17	(3.65, 4.77)	4.51	(3.99, 5.10)
Female	Ref.		Ref.		Ref.		Ref.
Male	1.49	(1.26, 1.75)	1.51	(1.28, 1.78)	1.27	(1.15, 1.40)	1.20	(1.09, 1.32)
Age at diagnosis	0.28	(0.25, 0.32)	0.29	(0.25, 0.33)	0.51	(0.48, 0.55)	0.51	(0.48, 0.54)

The GHD example stands out due to a substantial proportion of missing onset age among those experiencing GHD. This results in distinct behaviors observed in the two deletion-based approaches compared to the ‘Simple replacement’ and ‘Interval-censored’ methods. Furthermore, over 95% of individuals reporting GHD onset age in CCSS reported the onset within five to 18 years post-diagnosis (the average onset age of 3.6 with 3.1 standard deviation), indicating an early post-therapy manifestation. Consequently, applying the ‘Simple replacement’ and ‘Interval-censored’ methods in this example leads to different results. For instance, brain radiation dose of 20-30 Gy shows a protective association with GHD according to the ‘Simple replacement’ method (HR [95% CI]: 0.71 [0.60, 0.85]), compared to brain radiation of < 20 Gy, but not statistically significant difference between < 20 Gy and 20-30 Gy according to the ‘Interval censored’ method (HR [95% CI]: 0.94 [0.82,1.09]).

In our first example, we observe a diverse post-treatment interval (between five years post-diagnosis and up to about 40 years) for the onset of the specific CHCs, akin to the survey time range among those with the condition who did not report onset age. This similarity results in comparable performance between the ‘Simple replacement’ and ‘Interval-censored’ methods. However, in the second example, the majority of survivors reporting their CHC experienced it within 18 years post-diagnosis -a range notably distinct from the survey time range among those with a GHD who did not report onset age.

6. Discussion

This study described association analysis methods for self-reported time-to-event data when onset age may be missing, comparing practical approaches to enhance the association inference. Two key findings are: 1) the presence of considerable bias when relying solely on ad-hoc complete data or employing a straightforward substitution for missing onset age, and 2) a notable improvement in association inference accuracy achieved by employing the ‘Interval-censored’ method. The practical application of interval censoring, explored in diabetes, MI, osteoporosis/osteopenia, and GHD conditions, illustrated the magnitude of differences that could be seen in real applications. It’s important to note that while the paper focuses on association rather than baseline distribution estimate, the deletion or ad-hoc complete data method impacts the cumulative incidence of the event (or baseline hazard).

In the simulations, regardless of the proportion with an event of interest, the proportion of missing onset age, and sample size, regression coefficient estimates from the ‘Interval censored’ method consistently displayed reduced bias and, in most cases, smaller standard deviation, resulting in a smaller mean square error, compared to the three simple approached. Notably, when grappling with missing onset ages, opting for the simple deletion of corresponding observations proves more advantageous in mitigating bias compared to alternative strategies such as substituting survey times for missing onsets or treating participants as if they had not experienced the event.

Furthermore, under certain CHCs evaluated in Section 5 and Supplementary Materials, particularly when a higher proportion of participants who experienced the condition reported their onset age, the simple approaches and the ‘Interval-censored’ approach gave comparable standard deviations in the estimated effect of covariates. Equally noteworthy, when faced with an equal or higher proportion of individuals reporting their onset ages, as observed in CHCs occurring between five years post-diagnosis and up to 40 years thereafter (analyzed in Subsections 5.1 and examples in Supplementary Materials), ‘Simple replacement’ aligns closely with the performance of the ‘Interval-censored’ approach in terms of standard deviation. However, in scenarios where the occurrence of a condition is anticipated to be earlier, such as shortly after cancer therapy (i.e., GHD), ‘Simple replacement’ may lead to bias in estimating the effects of risk factors because it assumes the onset at survey which is an unreasonable assumption for such conditions that occur soon after cancer therapy. This underscores the critical need for handling missing onset age in such cases when the onset age may not be uniformly scattered in the interval in which the onset is possible (in our example, the interval from the start of the follow-up to the survey time).

It’s worth emphasizing that in situations with large sample sizes, as demonstrated in our examples, the differences between ‘observation-deletion’ and alternative methods may be less apparent. However, in studies with smaller sample sizes, one might observe discernible distinctions among these approaches.

This study should be of particular interest to researchers dealing with incomplete onset age data in observational studies similar to the CCSS. Key outcomes in these studies often include event occurrences and age at the event occurrence may be missing when an event is reported. On the other hand, similar situations are encountered in cancer clinical trials where time to progression (TTP) is a crucial endpoint but the exact time of progression is often unknown and typically assigned to the date of the clinical visit or imaging assessment when progression is identified Dancey et al. (2009); Stone et al. (2011), for example, used this approach and it is similar to the ‘Simple replacement’ method discussed here. Unlike CCSS in which we have both reported and missing onset ages, the exact TTP in clinical trials is unknown for all participants. Additionally, clinical trials may have uniform assessment times common to all participants, whereas, in observational studies, survey or assessment times may differ across subjects, adding complexity to the analysis.

For fitting proportional hazards models with interval-censored data, R, SAS, and Stata offer various package/procedures. In R, aside from icenReg package, there are other packages, including SmoothHazard and intcox, which provide tools for analyzing regression models with interval-censored data. These packages primarily differ in how they estimate the baseline hazard but serve a common purpose in conducting association analyses with interval-censored data. Similarly, the ‘PROC ICPHREG’ procedure in SAS is designed for fitting Cox proportional hazards models with interval-censored data. Stata does not have a dedicated package for Cox regression with interval-censored data, but some researchers apply an estimation command ‘stint’ in Stata based on the maximum likelihood estimation proposed by Zeng et al. (2016) to fit the Cox regression model to interval-censored event-time data. The choice between these software packages depends on user familiarity, specific analysis requirements, and the availability of specialized tools.

In this paper, while we discussed the ‘Interval-censored’ approach, we focused specifically on situations where the missingness of onset age is non-informative, meaning the missingness is assumed to be unrelated to when the event occurred. We recognize that this assumption may be untenable in long-term cancer survivors’ surveys where non reporting of onset age may depend on when it occurred and the cancer treatment received which potentially affects their memory. If the CHC happened a long time before the survey, there is a higher chance of recall bias impacting the accuracy of reported onset ages. We did not address this complex situation. We acknowledge the importance of this assumption in our discussion, and its potential violation needs to be addressed in future research.

Data sharing

Despite some limitations in this study: not registered or with an EQUATOR network guideline, all the data are shared on the St. Jude Cloud Survivorship Portal at http://survivorship.stjude.cloud.