Is there a ubiquitous spectrolaminar motif of local field potential power across primate neocortex?

Summary

Mendoza-Halliday, Major et al., 2024 (“The Paper”)¹ advocates a local field potential (LFP)-based approach to functional identification of cortical layers during “laminar” (simultaneous recordings from all cortical layers) multielectrode recordings in nonhuman primates (NHPs). The Paper describes a “ubiquitous spectrolaminar motif” in the primate neocortex: 1) 75–150 Hz power peaks in the supragranular layers, 2) 10–19 Hz power peaks in the infragranular layers and 3) the crossing point of their laminar power gradients identifies Layer 4 (L4). Identification of L4 is critical in general, but especially for The Paper as the “motif” discovery is couched within a framework whose central hypothesis is that gamma activity originates in the supragranular layers and reflects feedforward activity, while alpha-beta activity originates in the infragranular layers and reflects feedback activity. In an impressive scientific effort, The Paper analyzed laminar data from 14 cortical areas in 2 prior macaque studies and compared them to marmoset, mouse, and human data to further bolster the canonical nature of the motif. Identification of such canonical principles of brain operation is clearly a topic of broad scientific interest. Similarly, a reliable online method for L4 identification would be of broad scientific value for the rapidly increasing use of laminar recordings using numerous evolving technologies. Despite The Paper’s strengths, and its potential for scientific impact, a series of concerns that are fundamental to the analysis and interpretation of laminar activity profile data in general, and local field potential (LFP) signals in particular, led us to question its conclusions. We thus evaluated the generality of The Paper’s methods and findings using new sets of data comprised of stimulus-evoked laminar response profiles from primary and higher-order auditory cortices (A1 and belt cortex), and primary visual cortex (V1). The rationale for using these areas as a test bed for new methods is that their laminar anatomy and physiology have already been extensively characterized by prior studies, and there is general agreement across laboratories on key matters like L4 identification. Our analyses indicate that The Paper’s findings do not generalize well to any of these cortical areas. In particular, we find The Paper’s methods for L4 identification to be unreliable. Moreover, both methodological and statistical concerns, outlined below and in the supplement, question the stated prevalence of the motif in The Paper’s published dataset. After summarizing our findings and related broader concerns, we briefly critique the evidence from biophysical modeling studies cited to support The Paper’s conclusions. While our findings are at odds with the proposition of a ubiquitous spectrolaminar motif in the primate neocortex, The Paper already has, and will continue to spark debate and further experimentation. Hopefully this countervailing presentation will lead to robust collegial efforts to define optimal strategies for applying laminar recording methods in future studies.

Evaluation of the FLIP method in new data sets.

We applied The Paper’s main analytic strategy, Frequency-based Layer Identification Procedure (FLIP), to three data sets recorded from primary (A1) and belt (secondary) auditory cortex (2 monkeys) and V1 (2 monkeys). These areas were chosen because: 1) their laminar field potential, current source density (CSD) and multiunit activity (MUA) profiles have been thoroughly characterized by a number of labs, 2) they exhibit robust sensory-evoked responses with laminar activation patterns that reliably identify the positions of the supragranular, granular and infragranular layers ^2–7 and 3) there is general agreement across labs on this point ^3,8–11. The Paper contends that the crossing point between high and low frequency relative power gradients marks the location of cortical Layer 4 (L4). To identify this location, FLIP uses a linear regression approach, iterating over combinations of recording probe channels’ signals. The laminar region with the highest goodness-of-fit value (G) for low vs high frequency power regression lines with slopes of opposite signs determines the range of probe channels to be used as the “regression region” within which to search for the location where the power gradients cross. We encountered several problems with this approach.

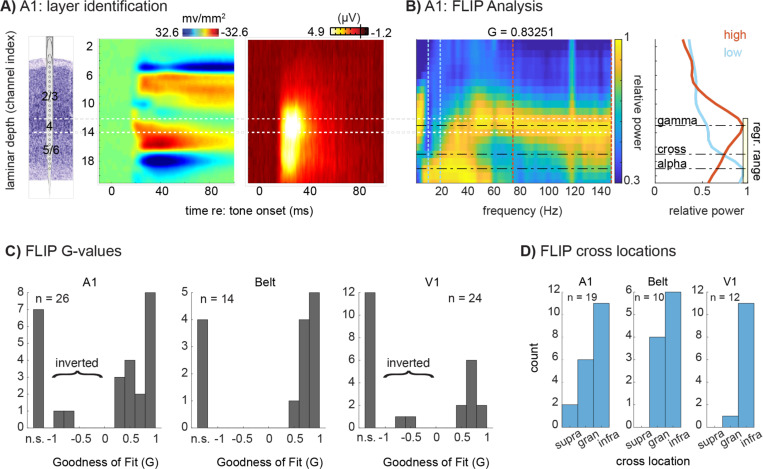
First, FLIP does not reliably identify L4. Figures 1A-C show findings from a representative site in A1 where current source density (CSD) and multiunit activity (MUA) profiles were used to identify the position of L4 (white lines), for comparison with FLIP-defined layer locations (Fig 1A). Based on laminar distributions of relative LFP power in the 75–150Hz and 10–19 Hz ranges for this site, time-locked to the stimulus and normalized to the channel with maximal power, the FLIP-defined laminar power gradient crossing falls outside of (in this case below) L4 (Fig 1B). Quantification of FLIP-defined L4 locations for the subset of profiles it is able to fit (Fig 1C) and registered in the framework of the CSD/MUA-defined layer scheme at each site for our A1, auditory belt and V1 data sets (Fig 1D), shows that this finding is general across areas: for cases in which the FLIP algorithm could find a fit (64% overall), the power gradient crossing falls in L4 in only 29% of the cases overall (32% in A1, 40% in belt and 8% in V1). In the majority of cases (71%), the FLIP-defined power gradient crossing point falls in the infragranular layers.

Fig 1 –

Frequency-based Layer Identification Procedure (FLIP) analysis in auditory and visual cortices. A) Representative tone-evoked CSD and MUA profiles used to identify cortical layers in A1; Layer 4 is outlined in white. Laminar identification used methods established by prior studies. Specifically, the electrode array was positioned to straddle the region exhibiting significant (non-overlapping trial-wise confidence intervals between the pre- and post-stimulus periods) CSD activation. Layer 4’s location was defined as the channel in the middle third portion of the active region with the earliest current sink onset, within 100 microns (+/− 1 channel in this case) of the peak amplitude MUA site. B) Relative LFP power at each frequency, epoched −300 to 300 ms around stimulus onset, displayed as a color plot (left) with the associated goodness of fit (G) value generated by the FLIP algorithm; line plots (right) depict the laminar power gradients for alpha-beta (blue line, 10–20 Hz) and broadband gamma (red line; 75 – 150 Hz). The dashed lines indicate low and high frequency peaks picked by FLIP, and the power gradient crossing point. The yellow box indicates the FLIP-selected range of channels over which it conducts the regression. C) Goodness of fit (G-values) resulting from FLIP for A1, Belt, and V1. Values could be not significant (“n.s.”), negative (inverted motif), or positive. D) FLIP-defined power gradient crossing locations for the subset of sites with significant fits by FLIP, for A1, Belt cortex, and V1, binned into CSD/MUA-defined supragranular, granular, or infragranular compartments.

Second, FLIP’s fitting process is variable and error prone. While FLIP was able to find an adequate ‘fit’ for 64% of sites overall (comparable to The Paper’s findings), the values were highly variable across areas, with 73% of A1 sites and 71% of auditory belt sites, but only 50% of V1 sites (Fig 1C). Note that a similar degree of variability was also evident in the shared dataset accompanying The Paper (Table S-1). Note also, that in our data sets, FLIP finds 2 cases each in A1 and V1 where the G value is negative, implying that the laminar array penetrated cortex from the white matter surface, producing an “inverted” motif (Fig 1C) as reported in The Paper. Such inverted penetration is possible for peripheral V1 representations lying in the inner folds of the Calcarine Sulcus, and it produces clearly recognizable inversions of LFP, CSD and MUA profiles (see ref ³ Fig 4). However, this scenario is anatomically implausible for our data sets, since our A1 and V1 samples came entirely from areas lying on flat, unfolded cortical planes, and electrode penetrations were all made through the pial surface of the cortex. Observation of these “motif inversion errors” raises concern about interpretation of motif inversions in The Paper (Supplement, Table 1).

Consideration of the vFLIP method.

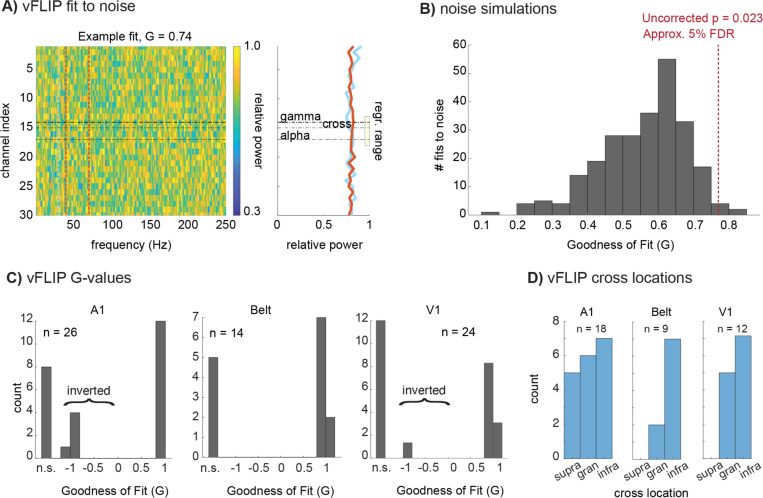
The second quantitative algorithm used in The Paper is “vFLIP,” a frequency-variable version of FLIP. vFLIP first runs the FLIP process over a large space of potential frequency bands and picks the best fit bands instead of using preset frequency bands the way FLIP does. This approach produces a multiple comparison problem and the threshold used for vFLIP must be adjusted accordingly. The Paper does not specify the threshold used for vFLIP, but it states that vFLIP identifies 81% of penetrations showing “opposing gradients of 10–19 Hz and 75–150 Hz power” across laminae, while FLIP identifies 64%. The determination of an appropriate threshold is critical, because vFLIP can find relatively high goodness of fit (G) values for random noise (Fig 2A). We analyzed data from noise simulations using vFLIP to determine the “G” threshold equivalent to the .265 threshold used for FLIP in The Paper (Fig 2B); this equivalent threshold corresponds to a single penetration p-value of approximately p<.03 for noise simulations and a false discovery rate of approximately .05 in the shared dataset that accompanies The Paper (see Supplement; 1.). When we applied this appropriate threshold, vFLIP identifies approximately 3% fewer penetrations than FLIP does (rather than 17% more) in that shared dataset. Notably, vFLIP findings agree with FLIP findings in only 49% of cases in the shared dataset (i.e., the data from figures 1-6 of The Paper). “49%” refers specifically to: 1) agreement between FLIP and vFLIP on whether a penetration is “fit” (identified as having opposing gradients), 2) when both methods identify a particular penetration as fit, they specify the same (upright/inverted) orientation and 3) the electrode channels identified as the crossover by the two methods are within 200 microns of one another; this “agreement” becomes only 56% if the criterion is lowered to 500 microns. Allowance for some variation in peak alpha-beta and gamma frequencies is a key strength of vFLIP. However, a significant factor in the divergence of FLIP and vFLIP results for the same data set is that vFLIP tends to find very narrow bands (the vast majority of bands are at the 10 Hz minimum allowed by the code) for both alpha-beta and gamma (Fig S-1); this also has negative consequences for vFLIP’s wider use in the study of neuronal oscillations.

Figure 2 –

Variable Frequency-based Layer Identification Procedure (vFLIP) analysis. A) Representative relative power map of 1/f noise samples (30 channels, 1000 time points, 75 trials) displayed as a color plot (left) with the associated goodness of fit (G) value from vFLIP, 0.74. B) A histogram depicts the G-values produced by vFLIP when fit to 1/f noise 250 times. A red line depicts the statistical threshold used to attain a 5% False-discovery rate, which was then applied to the vFLIP results in auditory and visual cortices. C) as in Fig. 1, vFLIP cross locations determined by co-registration with CSD and MUA profiles for areas A1, Belt auditory cortex, and V1, and binned into supragranular, granular, or infragranular compartments. D) as in Fig. 1, G-values for A1, Belt, and V1, which could be not significant (“n.s.”), negative (inverted motif), or positive.

Evaluation of vFLIP in new data sets.

Application of vFLIP to our data sets re-iterates the critical problems seen with FLIP. First, like FLIP, vFLIP’s identification of Layer 4 is unreliable. For the 61% of penetrations overall that vFLIP is able to fit (Fig 2C), it correctly identifies Layer 4 in well under 1/2 of the cases in A1 (33%), auditory belt (22%) and V1 (42%), (Fig 2D). Second, vFLIP incorrectly labels penetrations as “inverted” (Fig 2C). While FLIP was the primary analyses of the non-human primate data in The Paper, concerns about vFLIP are significant, as vFLIP was the primary method used for the interspecies generalization analyses.

Broader concerns about The Paper’s approach

The specific analytic problems noted above connect to broader concerns about The Paper’s approach and its conclusions. We address two related and consequential concerns here and defer others to the supplement (4.1-4.5).

First, The Paper used an image similarity metric to support the idea that results of vFLIP are equivalent both within and across species, however, this metric is meant to compare similarity of images based on human perceptual biases and is highly vulnerable to artifacts when it is used for comparing spectrolaminar motifs. Effects of systematically increasing the degree of blur in a pair of images on the image similarity metric used in The Paper suggests that values found in Figure 8 of The Paper are well within a pure noise range (Fig S-2).

A second concern is that both FLIP and vFLIP analyze on LFPs recorded against a distant reference, a practice that is relatively imprecise in its spatial localization of signal origins, and thus, at odds with the objective of precisely locating L4 and differentiating activity in superficial versus deep layers of cortex^11–13. Studies that localize field potentials using bipolar and CSD derivations ^11,13,14 (Fig S-4; see also The Paper’s Supplemental Fig 9) outline a paradox: alpha/beta LFP power peaks in the infragranular layers, but the strongest generators (transmembrane currents that set-up the field potential distribution in the extracellular medium) are in the supragranular layers. Volume conduction effects with a distant reference pose the risk that LFP measures can mis-localize neural activity not only across cortical layers, but also across cortical areas^15–17. A search for a functional method that reliably identifies specific cortical layers, and that generalizes across areas should start with methods having the best available signal localization qualities (i.e., the highest spatial resolution). LFP quantification measures like FLIP and the image similarity metric used in The Paper produce increasing false positive rates as the spatial resolution of the measure decreases. While the thresholds used in The Paper are appropriate when spatial resolution is high, they are not adjusted for the lower spatial resolution of LFP measured against a distant reference. In the latter case the risk of false positive outcomes increases significantly (Fig S-3), leaving unclear the real, quantifiable percentage of laminar motifs that have the pattern referred to as “ubiquitous.” Note that the false positive rate is reduced with bipolar and CSD derivations.

Going forward – in-silico experiments to inform and extend in-vivo findings.

Near The Paper’s end, the authors discuss Neuronal Mass Modeling in an attempt to resolve the paradox between unipolar FP analysis and bipolar/CSD derivations¹⁸. However, the model does not seem to reproduce The Paper’s experimental data well. While the increasing relative LFP power gradient for the low-frequencies from superficial to deep was somewhat approximated by the model, the model does not reproduce the high-frequency component of the LFP, which peaks in the granular instead of the supragranular layers (this is noted by the authors¹⁸). Furthermore, the model CSD shows a peak in the granular layers for both the slow and fast frequencies. This is in conflict with the CSD measure derived from the data, which shows a decreasing gradient from supragranular to deep for both the high and low frequencies. Since the model does not reproduce the experimental LFP/CSD patterns, the alternative to a volume conduction interpretation, proposed by The Paper, lacks support. These discrepancies may be due to limitations in the design of the model, for instance, its sparse neurobiological detail, which can be avoided by using publicly available, detailed biophysical models (see Supplement; 5.).