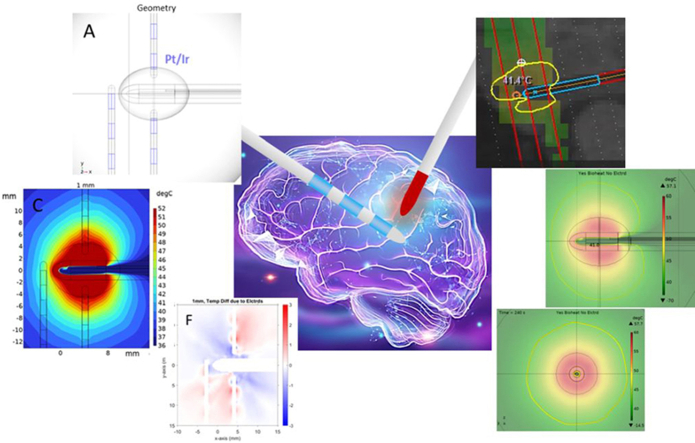
Abstract
Laser thermal ablation has become a prominent neurosurgical treatment approach, but in epilepsy patients it cannot currently be safely implemented with intracranial recording electrodes that are used to study interictal or epileptiform activity. There is a pressing need for computational models of laser interstitial thermal therapy (LITT) with and without intracranial electrodes to enhance the efficacy and safety of optical neurotherapies. In this paper, we aimed to build a biophysical bioheat and ray optics model to study the effects of laser heating in the brain, with and without intracranial electrodes in the vicinity of the ablation zone during the LITT procedure. COMSOL Multiphysics finite element method (FEM) solver software was used to create a bioheat thermal model of brain tissue, with and without blood flow incorporation via Penne's model, to model neural tissue response to laser heating. We report that the close placement of intracranial electrodes can increase the maximum temperature of the brain tissue volume as well as impact the necrosis region volume if the electrodes are placed too closely to the laser coupled diffuse fiber tip. The model shows that an electrode displacement of 4 mm could be considered a safe distance of intracranial electrode placement away from the LITT probe treatment area. This work, for the first time, models the impact of intracranially implanted recording electrodes during LITT, which could improve the understanding of the LITT treatment procedure on the brain's neural networks a sufficient safe distance to the implanted intracranial recording electrodes. We recommend modeling safe distances for placing the electrodes with respect to the infrared laser coupled diffuse fiber tip.
Keywords: Finite element method, Multiphysics, Bioheat modeling, Ray optics, Neurosurgical laser interstitial thermal therapy, Neurotherapy safety, Intracranial electrodes
Graphical abstract
Highlights
-
•
Biophysical bioheat and optics model with and without intracranial electrodes for neurological laser thermal treatments
-
•
Close placement of intracranial electrodes increases the maximum temperature of the brain tissue volume
-
•
Presence of intracranial electrodes close to the laser coupled diffuse fiber tip can impact the necrosis region volume
-
•
Recommended safe distance of 4 mm for placing the electrodes with respect to the infrared laser coupled diffuse fiber tip is reported
Abbreviations:
- CFD
computational fluid dynamics
- CO2
carbon dioxide
- EPS
expanded polystyrene
- FEM
finite element method
- LITT
laser interstitial thermal therapy
- MRI
magnetic resonance imaging
- MRgLITT
magnetic resonance imaging guided laser interstitial thermal therapy
- MRT
magnetic resonance thermometry
- MTLE
medically intractable mesial temporal lobe epilepsy
- NIR
near infrared
- PDMS
polydimethylsiloxane
- PEEK
polyether ether ketone
- Pt/Ir
platinum-iridium alloy
- sEEG
stereoelectroencephalography
- SiO2
silicon dioxide
- UIHC
University of Iowa Hospitals and Clinics
1. Introduction
Laser Interstitial Thermal Therapy (LITT) (Barot et al., 2022)is becoming a prominent optical neurotherapy for minimally invasive neurosurgical treatment procedures, such as tumor ablation and intractable epilepsy requiring ablation of a pathological brain site causing seizures. LITT ablation relies on near-infrared (NIR) (980 nm and 1064 nm wavelengths) laser technology to perform thermal ablation of pathological brain tissue(Landazuri et al., 2020; Le et al., 2018). The advantage of LITT is that it is a minimally invasive procedure that can be used by neurosurgeons to target focal brain regions by advancing a probe through a small craniotomy to a brain area for controlled laser thermal ablation. LITT can be conducted in combination with Magnetic Resonance Imaging (MRI) for both targeting and thermometry to control thermal ablation around the tip of the LITT probe(Barot et al., 2022). LITT provides a less invasive complement to “gold standard” resection surgery, such as anterior temporal lobectomy and amygdalo-hippocampectomy, in the management of patients with medically intractable mesial temporal lobe epilepsy (MTLE). MTLE is the most common type of focal epilepsy in adults, accounting for approximately one third of all treatment-resistant focal epilepsies(Gonzalez-Martinez et al., 2014; Widjaja et al., 2019). However, LITT treatment for epilepsy is not yet comparable to the seizure-free outcomes of resection surgery reliant on direct neurosurgical resection requiring larger cranial openings(Gonzalez-Martinez et al., 2014; Gupta et al., 2020; Hawasli et al., 2014; Tao et al., 2018). LITT treatment or resection surgery typically follows a period of epilepsy patient monitoring with intracranially implanted electrodes that are used to identify the epileptogenic site(s) requiring ablation or resection.
Being able to conduct the LITT treatment with intracranial electrodes during and after the LITT treatment procedure could allow evaluating epileptiform activity changes before and after the LITT treatment (including interictal event abnormalities(Taylor et al., 2022)). However, placing intracranial electrodes that are composed of metallic structures (spaced by polymer materials) could interact with the high-power laser probe inserted in the brain during LITT treatment, and cause burn lesions in unintended intracranial locations– making the placement of electrodes unsafe during LITT treatments. However, if a safe distance for the placement of the intracranial electrodes, which results in minimal undesired interaction between the electrodes and the LITT probe, can be determine, it would enable low risk intraoperative neuromonitoring during LITT procedures. Therefore, a biophysical model of LITT with and without intracranially implanted electrodes is urgently needed to allow determination of the safe distance for the placement of the intracranial electrodes during LITT procedures.
In this paper, we utilize Finite Element Method (FEM) (Bathe, 2007)to accurately model the LITT procedure with and without electrodes to understand how their presence influences heat transfer and distribution in brain tissue during the laser ablation process. Two modeling studies are reported in this paper: Study I and Study II. Study I analyzes the difference between modeling the LITT procedure in the brain with and without blood flow, and with and without three intracranial electrode probes 1 mm away from a model laser coupled diffuse fiber tip. Study II includes both blood flow and electrode probes to determine the differences in temperature distribution when the electrodes were incrementally displaced from the laser. Finally, the results of Study I are compared for accuracy with respect to the ground truth utilizing MR thermometry data collected during a LITT procedure at the University of Iowa Hospitals Clinics (UIHC), indicating a reasonable match between the modeled and in vivo surgical ablation zone parameters.
2. Methods
2.1. COMSOL Overview
COMSOL is a multiphysics FEM software ("COMSOL Multiphysics - https://www.comsol.com/," 2023) that allows for coupled multiphysics analyses to be performed on the same physical model, including time-dependent and frequency-dependent studies. The three primary types of COMSOL multiphysics utilized in this work are optics (Geometric Optics), thermodynamics (Theory for Heat Transfer in Solids, 2022), and fluid dynamics (Laminar Flow).
2.1.1. Finite element analysis and meshing
COMSOL's solver uses a FEM approach to break down the full physical volume of the problem into smaller finite elements in a process called meshing. COMSOL can then solve the appropriate system of equations for each element of that mesh. The smaller the elements of the mesh, the higher the results' resolution. However, more mesh elements result in longer computation times because of increased degrees of freedom to solve. To strategically limit the computation time, we set the mesh sizes for different portions of the computed geometry (Fig. 1), according to the desired data resolution in different regions, as shown in Fig. S1. The shells on the sEEG electrodes and the inlet and outlet coolant tubes had the smallest feature size, and so were meshed first by resolving their edges and then sweeping that along their length. Proximal to the laser probe, the mesh element size ranged from 75 μm to 1.75 mm, because this was the region of interest for thermal ablation and studying the impact of intracranial electrodes. Medial to the laser probe, the elements had a size which ranged from 50 mm to 10 mm. Distal to the laser probe, the elements size ranged from 0.9 mm to 5 mm at the 2.5 cm volume boundary of the geometry where resolution was not as important given the far distance from the laser probe.
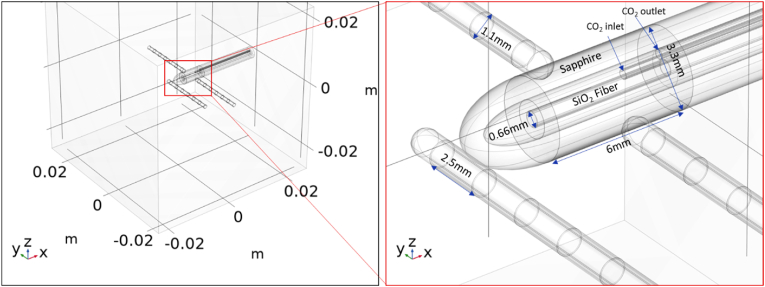
Fig. 1.
Annotated images of the utilized LITT FEM model captured from COMSOL to illustrate (left) the 5x5x5 cm3 brain phantom volume that simulates brain tissue. The 1064-nm NIR laser coupled 3.3-mm diameter diffuse fiber tip is placed in the center and surrounded by the electrodes.
2.1.2. Multiphysics coupling
There are currently two commonly used stereotactic LITT surgical systems for intracranial ablations: NeuroBlate® (Monteris, Plymouth, Minnesota, USA) ("Neuroblate(R) System - https://www.monteris.com/healthcare-professionals/neuroblate-system/,")and Visualase™ (Medtronic, Minneapolis, Minnesota, USA)("Visualase™ - MRI-guided laser ablation (https://www.medtronic.com/us-en/healthcare-professionals/products/neurological/laser-ablation/visualase.html) - 2022,"). Both systems serve to provide the same end results (i.e., target ablation), using a ∼3.3 mm diffuse-tip probe coupled to a high-power NIR laser (NeuroBlate®: 1064 nm wavelength emission, up to 12 W pulsed laser output power and Visualase™: 980 nm wavelength emission, 15 W continuous wave laser output power) (Lagman et al., 2017)that generates a uniform ellipsoid ablation zone around the center of the probe tip. There is only a slight (∼10%) difference in brain tissue penetration depth of 980 nm and 1064 nm NIR wavelengths, (Genina et al., 2019)where 1064 nm has higher ∼10% penetration depth, therefore optically the LITT procedure outcomes between the two leading systems should be similar. Moreover, it has been shown that the two have no statistically significant difference in treatment efficacy(Lagman et al., 2017). In this work, we conduct optical and bioheating modeling assuming the operational parameters of the Monteris Medical's NeuroBlate® 3.3 mm FullFire® probe system since that is the system used at the University of Iowa Hospitals and Clinics (UIHC) neurosurgery department for MRgLITT procedures.
COMSOL's heat transfer module ("Heat Transfer Module - https://www.comsol.com/Heat Transfer Module (2022),") models basic principles of thermodynamics to model heat transfer in solids, fluids, and other media ("Theory for Heat Transfer in Solids - https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.07.html (2022),"). We implemented the Heat Transfer in Solids interface and defined a Biological Tissue node (Bost, 2024) therewithin to model the bioheat transfer in our LITT FEM model. The Biological Tissue node allows the user to add tissue properties, such as heat capacity at constant pressure, density, thermal conductivity, and relative permittivity, among others. In all models in this work, Biological Tissue properties were set assuming a 1:3 ratio of gray to white matter. Additionally, to properly model the effect of laser-generated joule-heating, Ray Heat Source multiphysics available within.
COMSOL was used("Ray Heat Source - https://doc.comsol.com/5.5/doc/com.comsol.help.roptics/roptics_ug_multiphysics.7.3.html," 2022). These physics interfaces allow for accurate simultaneous simulation of the joule-heating due to optical absorption and the heat transfer within living human brain tissue. The interface uses the equations of the selected heat transfer interface, except it adds a radiative heat source as discussed below.
We implemented the Laminar Flow physics node from COMSOL's computational fluid dynamics (CFD) module to model carbon dioxide (CO2) flow that cools the laser fiber probe tip. Fig. S2 shows the results of the laminar flow modeling, where we tested a range of different CO2 flowrates and found that 26.6 m/s (300 sccm) results in temperature profiles similar to those measured via magnetic resonance thermometry (MRT) during procedures at UIHC. The flow lines shown in Fig. S2 confirm that the coolant flows uniformly across the tube cross-section to maintain the modeled laser fiber probe's temperature. The laminar flow physics was coupled with the Nonisothermal Flow Multiphysics node within the Heat Transfer in Solids module, which models heat transfer in fluid domains. With the Laminar Flow node modeling fluid transport and the Heat Transfer in Solids node modeling fluid thermodynamics, the forced convection of the coolant (CO2) is fully accounted for.
2.1.3. Heat transfer in solids
The Heat Transfer in Solids physics option in COMSOL solves for a version of the heat balance Eq. (1)("Theory for the Heat Transfer Module - https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.01.html," 2022):
| (1) |
where, Qexch is the exchanged heat rate and EΩ is the internal energy, both defining quantities at the microscopic level due to the atomic vibrations and similar microscopic phenomena that are felt as heat. Pstr is the thermal stress power that is converted into heat by dissipation. Eq. (1) is derived considering the first law of thermodynamics, commonly referred to as the principle of conservation of energy, to simulate the transfer of heat through conduction, convection, and radiation.
The more detailed version of the heat transfer in solids Eq. (2) is as follows ("Ray Heat Source - https://doc.comsol.com/5.5/doc/com.comsol.help.roptics/roptics_ug_multiphysics.7.3.html," 2022):
| (2) |
where is the density (SI unit: kg/m3), is the specific heat capacity at constant stress (SI unit: J/(kg·K)), is the absolute temperature (SI unit: K), is the velocity vector of translation motion (SI unit: m/s), is the heat flux by conduction (SI unit: W/m2), is the heat flux by radiation (SI unit: W/m2), is the coefficient of thermal expansion (SI unit: 1/K), is the second Piola-Kirchhoff stress tensor (Rossmanna and Haemmerich, 2014) (SI unit: Pa), and defines additional heat sources (SI unit: W/m3). The first term on the right-hand side of Eq. (2) is an expression to define thermoelastic damping and accounts for thermoelastic effects in solids(Ezzat, 2020). For a steady-state problem the temperature does not change with time and the terms with time derivatives disappear.
2.1.4. Geometric Optics & Ray Heat Source
The Geometric Optics physics node uses ray propagation Eq.s (3), (4) (below), which describe the relationships between ray position (SI units: ), and wave vector (SI units: ), to calculate how rays of light propagate through various types of media and across various boundaries.
| (3) |
| (4) |
As rays pass through media, they can be absorbed and converted into heat. Heat generated in any medium by absorbed light depends on that medium's refractive index, specifically the imaginary component called the extinction coefficient , as shown in Eq. (5). This can be used to calculate the absorption coefficient (SI units: cm−1) [Eq. (6)], which describes how much light is absorbed as it passes through a given length of medium.
| (5) |
| (6) |
The energy in the absorbed light rays can be converted to atomic or molecular energy in many ways. When light in the NIR spectrum is absorbed, it is converted into molecular vibrations i.e., heat. The Ray Heat Source Multiphysics node couples this absorbed energy into a heat source within a Heat Transfer physics node, which can also model heat generation and transfer in living tissue.
Biological tissue is mainly composed of water, which has a high absorption coefficient at a wavelength of 1064 nm ( (Hale and Querry, 1973)), which means that laser light is quickly absorbed after penetrating a short distance into the tissue. In addition to biological tissue, we also modeled the material properties of the laser probe in the NeuroBlate® system, which comprises of a sapphire tube that holds the laser fiber, which is cooled by a CO2 based refrigerant(for more details refer to Section 2.2). In contrast to the biological tissue, sapphire is transparent to these wavelengths, and so it has a low absorption coefficient ( (Querry, 1985)) at 1064 nm and is relatively transparent. So, the NIR laser light exits the fiber within the sapphire tube, pass through the CO2 refrigerant and sapphire without attenuating, and into the tissue. The tissue then absorbs the light and converts it into heat, which can then be conducted through the tissue, applicator, or electrodes according to standard heat transfer.
2.1.5. Heat transfer in biological tissue
The Heat Transfer in Solids interface allows the user to define domains composed of living biological tissue. Heat transfer within such media is different from that within standard homogeneous solids in that living biological tissue generates its own metabolic heat, and perfused fluids, such as blood convects heat. The Biological Tissue node recognizes and accounts for these mechanisms given user-defined values of: blood temperature (SI unit: K), blood heat capacity (SI unit: J/(kg·K)), blood perfusion rate (SI unit: s−1), blood density (SI unit: kg/m3), and metabolic heat source (SI unit: W/m3). These terms are related with a version of the heat transfer equation (Eq. (7)) which implements Pennes’ approximation("Theory for Heat Transfer in Solids - https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.07.html (2022),"). Specifically, it includes heat sources from blood perfusion and metabolism in the classical heat transfer equation (Eq. (2))(Hackett, 2018).
| (7) |
Depending on the type of tissue, the heat generated from metabolism can vary quite a lot., because of the variable metabolic activity in different parts of the human anatomy(Gerasimov, 1998). In brain tissue, metabolic heat generated can be orders of magnitude higher than average tissue, partly because neurons require 300–2500 more power (0.5–4.0 nW) to function than an average body cell (1.6 pW)(Kiyatkin, 2010). Cerebral blood flow in the brain tissue is also on average higher (68.50 ± 17.64∗∗ ml/min/100 g, p = 0.038∗∗) than global body flow rate (56.65 ± 10.87∗ ∗∗ ml/min/100 g, p < 0.0005∗) (Mintun et al., 2001) that supports maintaining the brain tissue's temperature around normal body temperature of (Corbett et al., 1997; Nybo et al., 2002; H. Wang et al., 2014). In addition to accounting for the metabolism and convective temperature regulation, the Biological Tissue node can calculate thermal damage to tissue given values of: damage temperature (SI unit: K), damage time (SI unit: s), necrosis temperature (Si unit: K), and enthalpy change (SI unit: J/kg). These parameters are used to calculate the damaged tissue indicator (unitless) [Eq. (8)] and instant necrosis tissue indicator (unitless) [Eq. (9)] based on the ratio of time spent above the damage temperature (unitless), and the overall fraction of necrotic tissue (unitless) [Eq. (10)] using the equations below.
| (8) |
| (9) |
| (10) |
The rate of damage progression (Eq. (11)) can also be expressed for this tissue hyperthermia using the polynomial Arrhenius equation given values for the frequency factor (SI unit: s−1), and activation energy (SI unit: J/mol) which vary with the type of tissue:
| (11) |
In which case, the fraction of necrotic tissue can then be expressed as, Eq. (12):
| (12) |
For optically absorbing media, an additional heat source term is added to both the heat transfer equations above, i.e. Eq.s (2), (7), and is proportional to the absorption coefficient, (SI unit: m−1), as(Pennes, 1948):
| (13) |
where (SI unit: W/m2) is the intensity of the incident radiation. Given a user-defined ray source, in the Geometric Optics physics node, with defined power/intensity, all the parameters within COMSOL are set to model quantity of energy absorbed and converted into heat in the modeled brain tissue.
2.2. Geometry
2.2.1. Objects
Fig. 1 shows the objects used in the FEM LITT model including the 1064 nm NIR laser coupled diffuse fiber tip probe, three electrodes, and the brain tissue. The diffuse fiber tip probe was modeled based on the 3.3-mm diameter NeuroBlate® Optic FullFire® laser fiber probe. The intracranial electrodes were modeled based on DIXI Medical Microdeep® sEEG electrodes with 1.1-mm outer diameter, 2.5-mm long, and 55-μm thick platinum/iridium (Pt/Ir) multiple macro-contacts ("Theory for Bioheat Transfer - The Bioheat Equation (https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.14.html), (2022),"). The external sapphire shell has an outer diameter of 3.3 mm and a thickness of 0.9 mm. Its ellipsoid tip has a major axis radius of 3 mm. A hollow chamber exists between the sapphire and silicon dioxide (SiO2) fiber allowing for coolant CO2 to flow and regulate the fiber's temperature. The fiber has a SiO2 core with a radius of 300 μm and a diffuse SiO2 cladding with thickness 30 μm. At the boundary between the 6 mm active region and the inactive region behind it, two 0.2 mm radius tubes provide an inlet and outlet for the coolant which span the length of the inactive region (17.35 mm). While the opening of the CO2 outlet tube is flush with the in/active boundary, the inlet protrudes 1.5 mm into the hollow chamber. Along the inactive region, the sapphire is coated with 0.1 mm of PEEK (polyether ether ketone), and the previously hollow space between the fiber and sapphire is filled with thermal/electrical insulation assumed to be EPS (expanded polystyrene) in these simulations. The electrodes have an inner core of PDMS (polydimethylsiloxane) with radius 0.55 mm and outer 55-μm thick shells of Pt/Ir which are 2.5 mm long and spaced by 1.5 mm of PDMS also 55-μm thick. Each electrode tip is the union of a 0.55-mm radius hemisphere and 0.95-mm long cylinder with the same radius. Several simplifications and assumptions were made in this geometry. First, we assumed that only the three (instead of the full 18) closest sets of electrode contacts to the laser coupled diffuse fiber tip were included for each electrode probe. This was done to reduce computation time after revealing the excluded contacts had no effect on the results of the simulations. The diffuse fiber tip was assumed to terminate as a perfectly cylindrical boundary. Also, the CO2 inlet and outlet were assumed to have the size previously stated, and to be on opposite sides of the fiber and equidistant between the fiber and sapphire surfaces. Lastly, to make our model as general-purpose as possible, the nearby brain was simply modeled by a 125-cm3 cube of brain tissue with the laser coupled diffuse fiber tip centered in the middle.
2.2.2. Orientation
As described above, the active region of the laser coupled diffuse fiber tip was 6 mm long, and its tip was placed at the center of the brain tissue cube. The remainder of the laser coupled diffuse fiber tip was considered inactive. “Active” here means the surface releases light rays when the laser is in the ON period of the pulsed waveform. The electrode probe orientations of interest were perpendicular to the fiber axis and placed either near the sides of the diffuse fiber or near its termination, as shown in Fig. 1. The side electrode probes were placed such that they lined up with the mid-length point of the active elements of the laser coupled diffuse fiber tip. In Study I, when electrode probes were included in the simulation, they were always placed 1 mm from the laser coupled diffuse fiber probe. For Study II, the electrode probes remained on their same axes but were incrementally displaced from the laser coupled diffuse fiber tip to determine a safety range.
2.2.3. Boundary
The brain tissue cube volume was made sufficiently large (5 cm × 5 cm x 5 cm dimensions) such that no heat from the laser reached the exterior surface of the volume during simulation; therefore, boundary conditions on the exterior of the cube did not influence the results. The emissivity of the surface of the cube and the heat flux across this boundary were set to zero.
2.2.4. Additional shapes
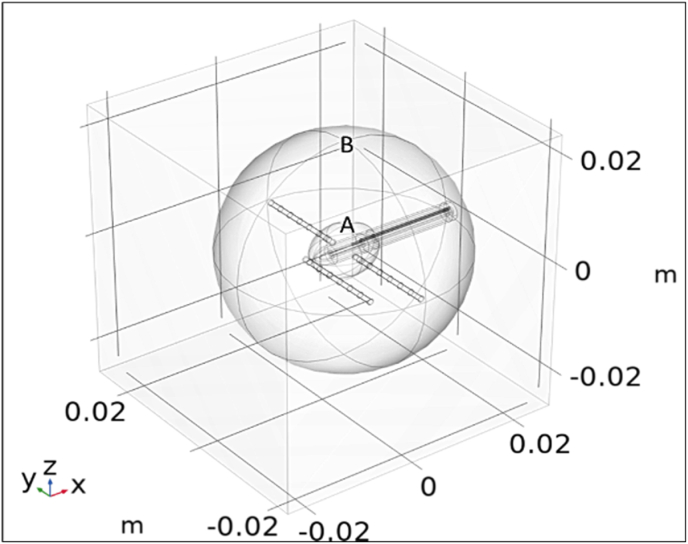
To better characterize the distribution of heat throughout the brain tissue cube post-simulation, two additional surfaces, one sphere and one ellipsoid, were added to the geometry as shown in Fig. 2. These surfaces were defined to be completely transparent to heat transfer and light propagation. Both surfaces encapsulated the areas of interest, so the mesh was made finer inside their volumes (for more accurate results).
Fig. 2.
COMSOL rendered geometrical representation of Surface A: an ellipsoid with semi-axis dimensions of 5.9x4.5 × 4.5 mm which simulates the inted ablation zone, and Surface B: a larger 20 mm radius sphere to study and quantify tissue damage outside the intended ablation zone.
The inner surface, an ellipsoid (Surface A), was added to mimic the intended ablation zone. Through literature review of typical reported LITT ablation zone size and volume, (Hoppe et al., 2017; "Microdeep (R) micro-macro depth electrodes - https://diximedical.com/products/microdeep-micro-macro-depth-electrodes," 2022; Mohammadi and Schroeder, 2014; "Theory for Bioheat Transfer - The Bioheat Equation (https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.14.html), (2022),")the ablation zone was approximated to be an ellipsoid with semiaxis dimensions of 5.9 mm, 4.5 mm, and 4.5 mm placed at the center of the brain tissue cube. Surface A allowed for measurements both including, and excluding, the region of tissue which was expected to be ablated. Without defining this, taking volumetric measurements over all tissue would skew the data when looking at whether unintended damage was occurring.
The outer surface, Surface B, was a sphere of radius 20 mm and was concentric with the ablation zone ellipsoid. This surface was used to quantify the heat and tissue damage outside of the intended ablation zone but still in the immediate vicinity of the laser coupled diffuse fiber tip. This area was of interest because it had the highest likelihood of absorbing and transferring heat away from the ablation zone.
3. LITT models
Two studies were performed using the general modeling structure described in Section 2 Methods. All models used a time dependent study due to the time dependent nature of heat transfer. The frequency of the NIR laser was fixed corresponding to the ablation wavelength of 1064 nm, so no frequency dependent studies were performed.
3.1. Description of models
Study I investigated the difference in heating and distribution when using the Heat Transfer in Solids interface with and without bioheat transfer. This study also included simulations with and without the electrodes placed 1-mm away from the laser coupled diffuse fiber tip. In total, four models were run as detailed in Table 1.
Table 1.
Models for study I.
| Model | Purpose |
|---|---|
| Heat transfer in solids without electrode probes | Control study for baseline comparison |
| Heat transfer in solids with electrode probes | Understand how the heat transfer is influenced by the presence of electrodes when no heat sump (blood) is used |
| Bioheat transfer without electrode probes | Understand how blood flow affects the bioheat transfer and directly compare isothermal contours between the model and MRI thermometry measured during NeuroBlate® based LITT surgery |
| Bioheat transfer with electrode probes | Most biologically accurate case for determining the safety of the presence of electrode probes |
In all appropriate Study I models, the three electrodes were placed 1 mm away from the laser coupled diffuse fiber tip. This distance was chosen as a compromise between having the electrode probes close enough to affect the heat transfer, while also not being so close such that the difference from adding bioheat transfer was not apparent.
As will be discussed in Results, it was determined that a simulation of 4 min was more than enough time to discern the differences between models.
3.2. Parameterization
Study II investigated how incrementally increasing the distance between the electrodes and the laser coupled diffuse fiber tip affected heating and distribution. There were 8 model variations in this study. The model was simulated for the following distances between the electrodes and laser coupled diffuse fiber tip: 0.5 mm, 1 mm, 2 mm, 3 mm, 4 mm, 5 mm, 10 mm, and infinity (electrodes absent). For the majority of the simulation results, the incremental distance variations between the electrodes and the laser coupled diffuse fiber tip above showed clear trends that could be interpolated if desired.
As was the case in Study I, the set of models for Study II were evaluated for 4 min of LITT procedure time. Most measurements reached a steady state, or the relationship between varying models was clear in this time.
3.3. User-specified physics parameters
3.3.1. Laser
The simulated laser used a pulsed waveform with a pulse duration of 2 s with 0.4 s between pulses and a power output of 12 W. The pulsed waveform information was provided to us by the Monteris engineer and the power output value was provided by the UIHC neurosurgery department; taken from their standard LITT surgical procedures. Because the laser was pulsed on a small-time scale relative to the ablation time, we needed to ensure the COMSOL solver did not miss any transitions. Therefore, we used the Events interface to toggle the laser power on and off.
The laser had an internal CO2 flow-based cooling mechanism that could keep the laser coupled diffuse fiber tip between 11 °C and 14 °C. The instructions manual for the NeuroBlate system indicated the laser would be given time to come to a steady temperature before the procedure would begin. Hence the need for modeling the non-isothermal fluid dynamics of gaseous CO2 entering and exiting the laser probe chamber. This coolant was assumed to enter at 26.6 m/s (300 sccm) and −70 °C and exit to atmospheric pressure.
The initial temperatures of the fiber and CO2 were assumed to be 12 °C and the sapphire shell was assumed to be 37 °C, the same as the tissue.
3.3.2. Electrodes
It was assumed that the electrode probes were at the same temperature as the tissue at the beginning of the simulation. The boundary conditions were defined based on standard heat transfer, as previously mentioned, which depends on material properties such as density, thermal conductivity, and heat capacity.
3.3.3. Brain tissue
The optical and thermal properties of all materials in the model, including those of human brain tissue, are divided into two tables below, Table 2, Table 3. Table 2 contains parameters for standard modeling of optics and heat transfer, while the second contains additional parameters for modeling blood flow, metabolic heat generation, and hyperthermia damage, all relevant for Bioheat Transfer. In all models, the brain tissue was assumed to be a 1:3 ratio of gray to white matter.
Table 2.
User-specified thermal and optical model parameter values.
Estimated to be small enough to be negligible with respect to brain tissue.
Approximated from that of water.
Approximated from that of pure Pt.
Weighted average of 2% Styrene () (Zhang et al., 2020) and 98% air.
Table 3.
User-specified Bioheat Transfer model parameter values.
| Parameter | Blood |
|---|---|
| Arterial blood temperature [°C] | 37 |
| Blood perfusion rate [1/s] | 0.009022 (Roberts et al., 1994) |
| Metabolic heat source, brain [W/m3] | 10460 (Nybo et al., 2002) |
| Damage temperature [°C] | 43 (Ashraf et al., 2018; Mensel et al., 2006) |
| Damage time [s] | 360 |
| Necrosis temperature [°C] | 60 (Ashraf et al., 2018; Mensel et al., 2006) |
Table 2 parameters are necessary for both standard Heat Transfer in Solids and Bioheat Transfer. While it is easy to parameterize the thermal and optical properties of Pt/Ir, PDMS, and SiO2, it is not so easy for brain tissue. These parameters vary widely across demographics and types of tissue. To generalize this breadth of values, it is common to assume brain tissue has absorption properties similar to water since as reported in literature, (Johansson, 2010; Shah et al., 2022)white matter contains around 70% absolute water content and gray matter contains around 80% in both female and male human brains.
Table 3 parameters are necessary to model Bioheat Transfer, but they also accounted for thermal damage by using temperature-threshold, hyperthermia analysis to determine fraction of damage of the tissue.
For models without the Bioheat Transfer node, no such blood flow or damage parameters were specified. However, both interfaces included a thermal insulation boundary around the outer surface of the brain tissue cube.
3.4. Executing models
Computation time was a limiting factor in the number of simulations we could produce. Each simulation took over 30 h to compute, not including any initial model set-up or subsequent post-processing. To decrease computation time, we used varying sized meshes throughout the model. In areas of high interest or smaller geometries, it was important to use smaller mesh elements to properly resolve the equations. In large areas that were not significant to consider, we used a coarser mesh.
Overall, the required computation time and memory depended greatly on both the mesh resolution and how many points in time we wanted to simulate. Because our pulse is on the order of 100ms, one may think our time interval step size would need to be on the same order of magnitude, so all transitions are accounted for. However, COMSOL's events interface ("The Events Interface," 2023) allowed us to use much larger step sizes because in the events interface settings, an event can be explicitly defined by the exact time when the event occurs. When an event occurs, the solver takes smaller time steps in order to accurately model the transient phenomena. As the transient behavior subsides, the solver takes larger time steps to model large spans of steady-state behavior quickly. Through this method, the time steps taken by the solver are not the same as those specified by the user. This is to simulate the model more accurately. These time steps increase the amount of time needed to accurately run the simulation, but their solutions are not stored in the results. Only the solutions at the time steps specified by the user are stored in the results which are then post-processed. This has the added benefit of reducing the results file size. Moreover, by limiting simulation time to that required for the model results to reach steady state or show an obvious trend, overall computation time was effectively reduced.
4. Modeling results
Due to the risk posed to patients, the impact of the presence of intracranial electrodes during MRgLITT cannot be tested in vivo. An alternative approach is to conduct tests with a brain phantom material implanted with electrodes in vitro, and to simulate the LITT procedure while taking temperature measurements of the various phantom regions(Packett et al., 2017). However phantom materials do not account for the heat extraction that occurs due to blood flow in the brain tissue in vivo, providing only a worst-case scenario of bioheating during LITT procedures. Blood perfusion is a very important parameter in quantifying the heat distribution and intensity around and inside the ablation zone, because of the high heat capacity of flowing blood and its active role in thermal regulation of the brain. The impact of blood perfusion and the various optical and thermal parameters that it impacts are studied in this work (Study I).
Typically, the temperature distribution of the LITT procedure is measured by overlaying thermometry data on MRI images (Odéen and Parker, 2019; Rieke and Butts Pauly, 2008) by tracking resonant frequency changes in the voxels and relating them to tissue temperature changes in brain tissue via the Arrhenius model(Arnold et al., 1981). A model that is widely used in thermal therapy is the thermal dose model, (Sapareto and Dewey, 1984)which is based on the Arrhenius-damage integral, this model quantifies damage using temperature and time in a nonlinear fashion and relates it to an equivalent heating time at 43 °C. The thermal dose required for total necrosis ranges from 25 to 240 min at 43 °C for biological tissues (Rieke and Butts Pauly, 2008). Based on a variety of factors driven by anatomical structures, the software calculates the expected thermal damage zones and overlays outlines on the MRI image in the form of thermal-damage-threshold isocontours. There is currently little to no research investigating the safety of having intracranial electrodes present during MRgLITT procedure.
4.1. Analyses for study I and II
Because of COMSOL's capability to derive other variables from those directly computed in any given study, a variety of analysis figures were generated during Study I and II. In general, we were interested in the measurements listed in Table 4.
Table 4.
Summary of analyses conducted in Study I & II.
| Analyzed parameters | Purpose |
|---|---|
| Maximum temperatures | Instant necrosis happens at 60 °C; therefore, any volume of tissue that reaches this threshold at least once is considered ablated. |
| Average temperatures | Understand the overall distribution of heat within the tissue over time |
| Final temperatures | Expected temperatures during steady state |
| Constant temperature (isothermal) contours | Understand how the ablation zone expands |
| Necrosis volume | Defines the minimum volume of ablated tissue |
| Isothermal surface of 60 °C | Very conservative estimate of the ablation zone shape and volume; useful for models without a necrosis calculation (heat transfer in solids)a |
Assumes necrosis volume increases at the same rate as tissue temperature ≥60 °C.
4.2. Studies
Next, we discuss the specifics of Study I and Study II. As explained previously, Study I analyzed the difference between modeling the LITT procedure in the brain with and without blood flow. As a step towards Study II, we also explored the same scenarios as Study I, except we added the three electrode probes 1-mm away from the laser coupled diffuse fiber tip, as described in Section 3 Models. The second study included both blood flow and electrode probes. We analyzed the differences in temperature distribution when the electrodes were incrementally displaced from the laser.
4.2.1. Study I: bioheating
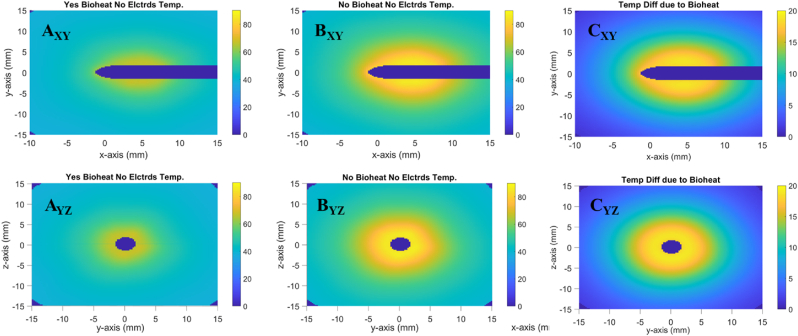
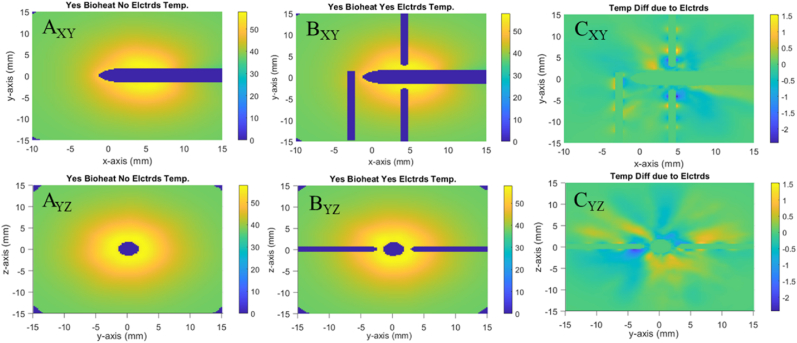
Fig. 3 shows that models which include bioheat transfer in the tissue have lower overall temperature than those without. While subfigures AXY and AYZ show a max temperature , subfigures BXY and BYZ show a max . Moreover, subfigures CXY and CYZ show that the maximum difference between A and B is . As shown in Fig. 3, when bioheat transfer is accounted for, the average temperature within the volume of ellipsoid A after 4 min is approximately 62oC. In contrast, when not accounting for bioheat transfer, the same average temperature exceeds 80oC. This difference extends to the total necrotic volume, which is for cases with bioheat and for cases without. See Fig. S4 for further details. This is because the tissue with bioheat experiences a heat sump effect due to the blood flow. The Fullfire probe is modeled identically in all scenarios, and so the simulated brain tissue is receiving the same amount of energy from the 1064 nm NIR laser for all scenarios. By the end of the simulated 4 min, the models with blood flow reach an equilibrium point where the heat entering the system through the laser is balanced by the heat leaving the system through blood perfusion. The models without blood flow showed no sign of reaching an equilibrium state within the 4-min simulation time.
Fig. 3.
Difference in tissue temperature due to bioheat. (A) shows the temperature profile with bioheat. (B) shows the temperature profile without bioheat. (C) shows a profile of the difference in temperature between A & B. Subfigure labels' subscripts indicate viewing plane.
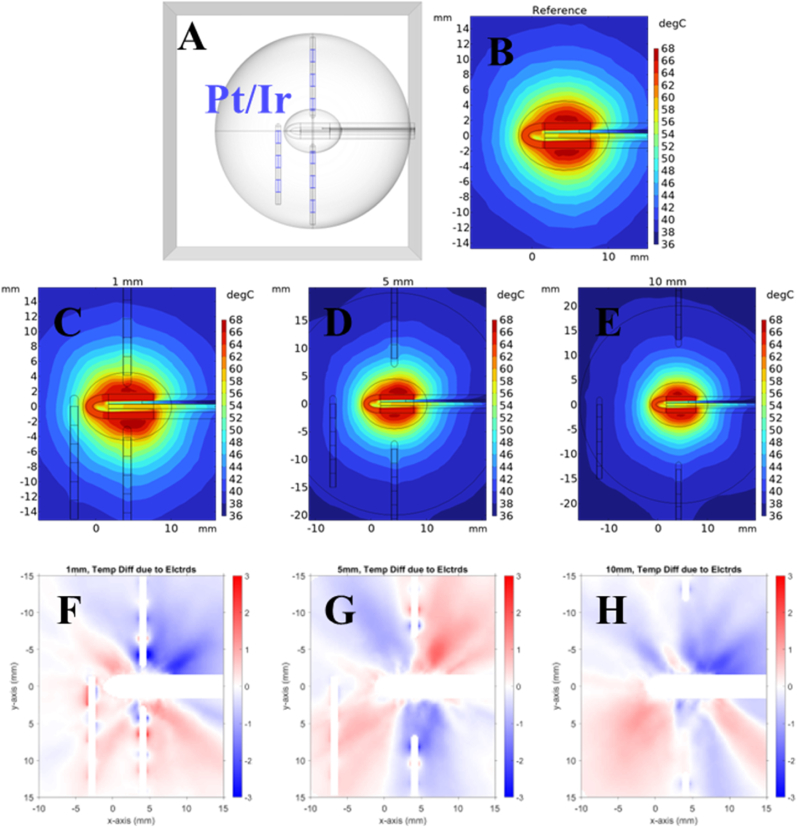
As expected, the presence of electrode probes had virtually no impact on either the maximum or the total volume average temperature over time (Fig. S3). However, as shown in Fig. 4 the Pt/Ir shells did cause temperature differences of 2–3 °C localized around their edges. While the temperature profiles in subfigures AXY & BXY and AYZ & BYZ appear similar, ignoring the dark blue electrodes themselves, subfigures CXY & CYZ show small temperature differences localized around the edges of the Pt/Ir shells. For each shell, cold blue regions occur proximally to the laser probe while hot yellow regions occur distally. These differences are due to the metal's high thermal conductivity, which causes the temperature of the entire metal shell to be the average of its surroundings. The tissue in contact is the same temperature, which results in a temperature difference between the cases with/out electrodes at the tissue in contact with the metal. This observation confirms that the electrodes being present during a LITT procedure could impact the ablation zone shape. Since the electrodes will conduct laser probe heat to other unintended tissue causing further ablation. These factors will be crucial for understanding the safe distance of the electrodes during LITT procedures.
Fig. 4.
Difference in tissue temperature due to electrodes. (A) shows the temperature profile without electrodes. (B) shows the temperature profile with electrodes. (C) shows profiles of the temperature difference between A & B. Subfigure labels' subscripts indicate viewing plane.
Study I's results indicate that modeling with recording electrodes present during the LITT procedure resulted in minimal change to the shape and size of the ablation zone than without. However, modeling with blood flow had a much more substantial influence on the necrotic volume so conducting in vitro brain phantom studies without an effective simulated heat sump mechanism, does not accurately translate to actual surgical conditions.
4.2.2. Comparison with surgical LITT MR thermometry data
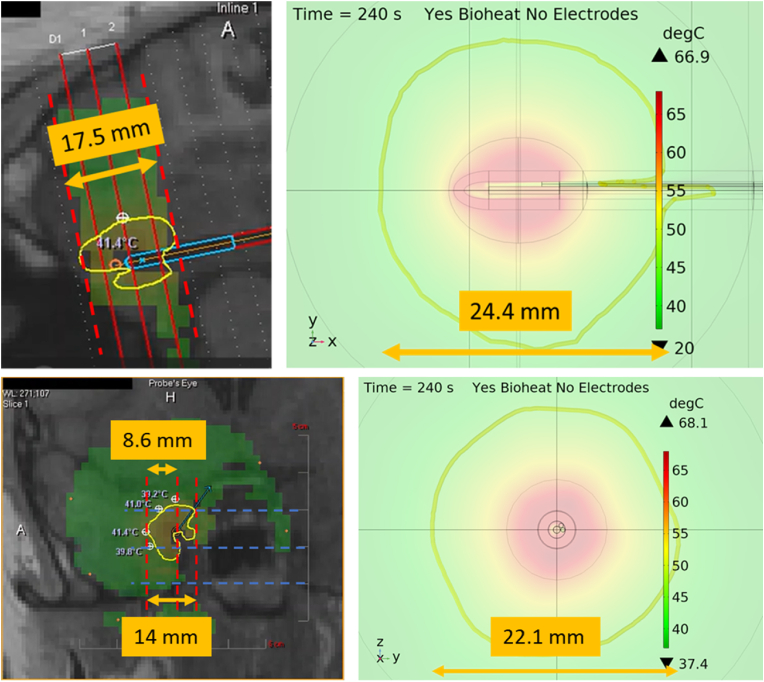
To compare our bioheat modeled data for LITT with MRT data collected via LITT surgical procedures at UIHC, we took time snapshots of a surgical video at 240 s for both XY and YZ views. The results in Fig. 5 indicate that there is a significant difference in the size of the 41 °C isothermal contours between the MRT and COMSOL data. This suggests that either the modeled laser power settings or tissue absorption coefficient are unrealistic. However, the laser power was modeled based on the 12 W reported in the MRT software, and the absorption coefficient was approximated based on that of water and the water content of the tissue. It should be noted that the value of 12 W does not account for power lost between the laser diode and the applicator probe, which could explain the difference in isothermal contours between the MRT and COMSOL data. This difference aside, the maximum dimensions of the contours are very consistent. In the top MRT image, the maximum contour diameter is 17.5 mm, and in the bottom the maximum contour radius is 8.6 mm. Similarly, the maximum diameters of the modeled contours are 24.4 mm and 22.1 mm, respectively. The MRT contours in both perspectives are less circular than the modeled contours, because of the brain tissue heterogeneity. Heterogenous features in brain tissue like blood vessels and cerebrospinal fluid would act as additional local heat sinks, thus deforming the isothermal contours. This indicates that for future efforts, tissue heterogeneity will need to be accounted for and our current presented work will provide an initial view on the safety of the intracranial electrodes during LITT procedures. It is worth noting that the MRT data is limited to a resolution of 1 mm3, and that it omits temperature data in voxels which contact the applicator tip which should be the hottest. In contrast, the model has much higher resolution, particularly in ellipsoid A which contains the tissue volume directly surrounding the applicator tip. As a result of this, the maximum tissue temperature of 60 °C reported from MRT disagrees with the 68 °C from the model.
Fig. 5.
The top row (left) compares the MR thermometry data collected during a LITT procedure at UIHC using the Neuroblate system and (right) the modeled COMSOL Multiphysics results. The bottom row compares the (left) MR thermometry view from the YZ view and (right) modeled YZ view. Both perspectives show significant differences in the isothermal contours due to the differences in laser coupling efficiency and tissue heterogeneity.
4.2.3. Study II: electrode placement
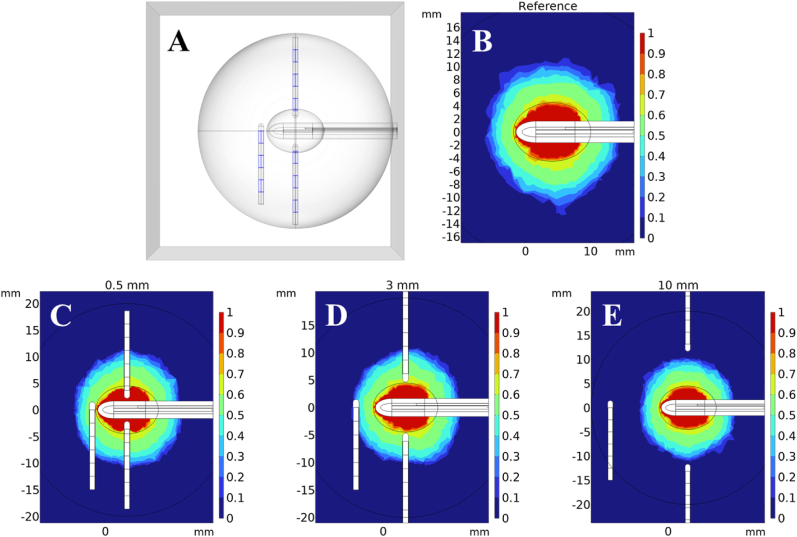
To understand the results of the parameterized electrode and laser coupled diffuse fiber tip displacement simulations we compared our results to the reference case of no electrodes with bioheat transfer in the brain tissue phantom volume. Fig. 6(A) shows the geometry of the model. In particular, it depicts the sEEG electrode metal shells which are colored blue. Fig. 6(B–E) show temperature profiles of the reference case (Ref) and three cases with electrodes placed at various distances from the probe (1, 5, 10 mm). Below Fig. 6(F–H) show the differences in temperature between the corresponding case above and the reference case. For similar information regarding other electrode distances not shown here (0.5, 2, 3, 4 mm), see Supplementary Fig. S5. Consider the 1-mm case (C), one can see how the temperature contours are warped around the Pt/Ir shells on the electrodes. The electrodes have high thermal conductivity and low heat capacity, so they maintain a much more even temperature along their length than the PDMS. The tissue in contact with the metal is also the same temperature, and so the contacting tissue at the ends of each metal shell are similar in temperature as that in the middle. These local volumes of contacting tissue are hotter or colder than their equivalent volumes in the reference case. Generally, tissue along the proximal edges of metal shells tends to be colder than in the case without electrodes while distal tissue tends to be hotter. Looking again at Fig. 6(F–H), smearing of red and blue around these hot/cold spots represents the thermal gradients around them caused by thermal conduction through the tissue. Small differences in temperature can also be seen particularly in the 10-mm case across the profile. These are far from any electrodes and thus have no significant relation and are only minor computational artifacts. The closer the metals shells are to the probe; the more local temperature differences can be observed. From these results it can be further speculated that longer shells would produce larger local differences in temperature at their proximal and distal edges.
Fig. 6.
For selected cases of electrode displacement in Study 2, (A) shows the geometry of the 1-mm case including the Pt/Ir electrode shells, highlighted blue. (B–E) show FEM model temperature profiles after 4 min with color legend denoting temperature in °C. (F–H) show differences in temperature (°C) between the given case and the reference without electrodes. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 7 shows the resulting estimated necrosis volumes for various electrode distances in the case of brain tissue with bioheat. For similar information regarding other electrode distances not shown here (1, 2, 4, 5 mm), see Supplementary Fig. S6. The color scales represent the overall fraction of necrotic tissue, described as in Section 2.1.5. The tissue that is colored red has experienced instant necrosis after exceeding 60 °C, but the surrounding green tissue has not yet reached 60 °C and instead has experienced gradual necrosis due to being hotter than 43 °C. The surrounding dark blue tissue has not reached 43 °C, and so is undamaged. Fig. 7(A) shows the model geometry again, particularly depicting the Pt/Ir electrode shells (colored blue). Notice how the contours in Fig. 7(C–E) bend at the edges of the metal shells. As discussed previously, the temperature around each shell is largely constant because of its high thermal conductivity. As a byproduct, the fraction of damage is also largely constant around the metal shells; especially when compared to the bare PDMS. This can be seen in how the damage contours bend around the edges of the metal shells but not around the bare PDMS in Fig. 7(C–E). Aside from the differences due to electrodes, there are no significant differences in the damage volumes shape or size, because the extent and degree of damage are due to the absorptive properties of the tissue, the power of the laser, and the amount of time the model was simulated, which are all constant between the separate cases. One such example of this is the sharp damage boundary at around 10 mm on the y-axis, which is sharp because the tissue beyond this point doesn't reach the threshold for thermal damage (). Any small differences between the profiles away from the electrode-tissue boundary, such as in the roughness of the damage contours, are likely computational artifacts which largely depend on the mesh resolution of the model.
Fig. 7.
Changes in fraction of thermal damage due to electrodes. (A) the geometry of the model, Pt/Ir shells are blue. (B–E) show FEM model thermal damage fraction after 4 min. Colorbars indicate said fraction, ranging from 0 (no damage) to 1.0 (complete necrosis). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
5. Discussion
During the MRgLITT procedure a high power NIR diode laser (several watts of optical power) is coupled to an optical fiber for delivery of high power NIR radiation into the brain via a robotic system to induce hyperthermia within epileptic foci or to disconnect the pathways to the epileptic foci (Hoppe et al., 2017). Before surgery, however, neurosurgeons need to identify the foci of these signals (Burns et al., 2012). To help identify epileptic foci in patients with medically refractory seizures, and monitor levels of activity, electrodes are implanted in the brains of epilepsy patients. Traditionally, these electrodes are implanted before and removed up to months prior to the LITT surgery (Yuan et al., 2012). However, there are diagnostic benefits to keeping the intracranial electrodes during and after the MRgLITT procedure, to enable continued monitoring of the electrical activity and to better understand the impact of MRgLITT surgery on MTLE and other forms of refractory epilepsy(Bhattacharyya et al., 2017; Cobourn et al., 2018). The interaction between the electrodes, brain tissue, and laser energy needs to be well understood to ensure the safety of the presence of electrodes during MRgLITT. One challenge of having intracranial electrodes during MRgLITT is that the metal electrodes interfere with MRI signals and MR thermometry data becomes unreliable or even unavailable. Another challenge is that the electrodes’ metal construction makes them more thermally conductive than brain tissue (see Table 2). An anticipated risk of performing the LITT procedure with implanted intracranial electrodes, is the transfer of heat away from the intended ablation zone, due to the thermal conductivity of the metal electrodes interdigitated in polymer materials. Depending on the size of the electrodes and the amount of energy the electrodes absorb, the ablation zone may change shape or temperature. This could result in thermal damage to brain tissue outside of the laser-ablated zone and possibly a change in the outcomes of the tissue inside the laser-ablated zone.
We expect that our study's results will, generally, be applicable for other similar stereotactic LITT systems that utilize NIR lasers for ablation such as the Visualase system. This is because our model accounts for the scattering and absorption of NIR laser light in the brain tissue surrounding the fiber probe tip, which acts as the primary heat source in this ablation.
FEM modeling presented in this work can now be implemented as part of digital workflows for mapping epileptogenic zone networks (e.g., Wang et al., Science Translational Medicine, 2023; others relevant here). The advantage of the FEM modeling for planning neurosurgical patient treatment is that it can allow, as we have shown, modeling of the heat transfer to the tissue in a way that can be compared with MRI thermometry and post-LITT MRI anatomical confirmation of the ablation zone. Although we have focused on the FEM modeling of LITT with implanted electrodes, to have a neurophysiological measure of LITT impact on interictal abnormalities (Taylor et al., 2022), the FEM modeling approach taken here can be integrated into other digital workflow pipelines and be expanded to model patient treatment. FEM modeling could be expanded in the following key ways to improve epilepsy patient treatment options. For example, FEM models of epileptic seizures on the neuronal level to the whole brain promise the ability to develop individualized treatment plans for epilepsy patients (Fabrizi et al., 2007; Schreiner and Mardal, 2022; Sip et al., 2022). FEM models of post surgical treatments of epilepsy, such as repetitive transcranial magnetic stimulation (rTMS) can also help understand the effectiveness of such approaches without having the patients involved.
COMSOL FEM solver software could import and sufficiently mesh these scans and account for the variation in material properties across the different types of brain tissue. The computed results could then be combined with other information like that in the VEP (H. E. Wang et al., 2023), for more effective treatment. While the methods in this work assume the tissue to be homogeneous, using imported MRI scans or other three-dimensional maps, such as brain atlases (H. E. Wang et al., 2021) would account for the brain's heterogeneity, and dramatically improve the accuracy of its predicted ablation. In the future, imaging methods, such as MRI which distinguish different types of tissue could be used to develop personalized models of a patient's brain to predict highly specific and accurate outcomes before surgery (H. E. Wang et al., 2023). Future models could also be developed into applications which could be evaluated in minutes or seconds instead of days, reducing computational costs and increasing accessibility to the physicians.
6. Conclusion
In conclusion, we present results on the impact of included blood flow as a heat sump in analytical models of LITT. We also study the impact of electrode placement during LITT procedures and report that electrodes can increase the maximum temperature of the brain tissue volume as well as impact the necrosis region volume if the electrodes are placed too closely to the laser coupled diffuse fiber tip. We expect that an electrode displacement of at least 4 mm or higher could be considered safe for placing electrodes during the LITT procedure.
Code, data, and materials availability
All modeling data is available upon request from the corresponding for academic research purposes. Use of data for commercial purposes requires permission from the corresponding author before use.
CRediT authorship contribution statement
Daniel W. Keefe: Formal analysis, Methodology, Software, Visualization, Writing – original draft. David T. Christianson: Conceptualization, Writing – review & editing. Greyson W. Davis: Formal analysis, Methodology, Software. Hiroyuki Oya: Conceptualization, Writing – review & editing. Matthew A. Howard: III, Conceptualization, Supervision, Resources, Writing – review & editing. Christopher I. Petkov: Conceptualization, Supervision, Validation, Resources, Writing – review & editing. Fatima Toor: Conceptualization, Formal analysis, Methodology, Project administration, Supervision, Validation, Resources, Data curation, Writing – review & editing.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Fatima Toor reports was provided by The University of Iowa. Editor-in-Chief Dr. Chris Petkov is a co-author of this manuscript and should be recused from serving as an editor for this manuscript. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research was supported in part through computational resources provided by The University of Iowa High Performance Computing (HPC) system. All computation times estimated included the use of HPC system resources. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.crneur.2024.100139.
Appendix A. Supplementary data
The following is the Supplementary data to this article.
References
- Abdulrazaq Hilal Amir H.Z.A. Comparison between heat conductivity of EPS (expanded polystyrene) and XPS (extruded polystyrene) IJRRCME. 2018;4:24–31. [Google Scholar]
- Annealed 90-Platinum 10-Iridium Alloy . MakeitFrom.com. 2018. . 09/20/2018. [Google Scholar]
- Arnold M., Veress G., Paulik J., Paulik F. The applicability of the Arrhenius model in thermal analysis. Anal. Chim. Acta. 1981;124:341–350. [Google Scholar]
- Ashraf O., Patel N.V., Hanft S., Danish S.F. Laser-Induced thermal therapy in neuro-oncology: a review. World Neurosurgery. 2018;112:166–177. doi: 10.1016/j.wneu.2018.01.123. [DOI] [PubMed] [Google Scholar]
- Barot N., Batra K., Zhang J., Klem M.L., Castellano J., Gonzalez-Martinez J., Bagic A. Surgical outcomes between temporal, extratemporal epilepsies and hypothalamic hamartoma: systematic review and meta-analysis of MRI-guided laser interstitial thermal therapy for drug-resistant epilepsy. Journal of Neurology, Neurosurgery & Psychiatry. 2022;93:133. doi: 10.1136/jnnp-2021-326185. [DOI] [PubMed] [Google Scholar]
- Bathe K.J. Wiley Encyclopedia of Computer Science and Engineering. 2007. Finite element method; pp. 1–12. [Google Scholar]
- Bhattacharyya P.K., Mullin J., Lee B.S., Gonzalez-Martinez J.A., Jones S.E. Safety of externally stimulated intracranial electrodes during functional MRI at 1.5T. Magn. Reson. Imag. 2017;38:182–188. doi: 10.1016/j.mri.2017.01.012. [DOI] [PubMed] [Google Scholar]
- Bost C. Heat transfer in biological tissue with thermal damage analysis. 2024. https://www.comsol.com/blogs/heat-transfer-in-biological-tissue-with-thermal-damage-analysis Vol. 2024.
- Burns S.P., Sritharan D., Jouny C., Bergey G., Crone N., Anderson W.S., Sarma S.V. 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2012. A network analysis of the dynamics of seizure; pp. 4684–4687. [DOI] [PubMed] [Google Scholar]
- Cobourn K., Fayed I., Keating R.F., Oluigbo C.O. Early outcomes of stereoelectroencephalography followed by MR-guided laser interstitial thermal therapy: a paradigm for minimally invasive epilepsy surgery. Neurosurg. Focus. 2018;45 doi: 10.3171/2018.6.FOCUS18209. [DOI] [PubMed] [Google Scholar]
- Corbett R., Laptook A., Weatherall P. Noninvasive measurements of human brain temperature using volume-localized proton magnetic resonance spectroscopy. J. Cerebr. Blood Flow Metabol. 1997;17:363–369. doi: 10.1097/00004647-199704000-00001. [DOI] [PubMed] [Google Scholar]
- Expanded Polystyrene (EPS) Technical Data. In. A. A. U. Styrene (Ed.).
- Ezzat M.A. Fractional thermo-viscoelastic response of biological tissue with variable thermal material properties. J. Therm. Stresses. 2020;43:1120–1137. [Google Scholar]
- Fabrizi L., Horesh L., McEwan A., Holde D. World Congress on Medical Physics and Biomedical Engineering 2006: August 27–September 1, 2006 COEX Seoul, Korea “Imaging the Future Medicine. Springer; 2007. A feasibility study for imaging of epileptic seizures by EIT using a realistic FEM of the head; pp. 3874–3877. [Google Scholar]
- Fused Quartz. In. MatWeb.com.
- Genina E.A., Bashkatov A.N., Tuchina D.K., Dyachenko Timoshina P.A., Navolokin N., Shirokov A., Khorovodov A., Terskov A., Klimova M., Mamedova A., Blokhina I., Agranovich I., Zinchenko E., Semyachkina-Glushkovskaya O.V., Tuchin V.V. Optical properties of brain tissues at the different stages of glioma development in rats: pilot study. Biomed. Opt Express. 2019;10:5182–5197. doi: 10.1364/BOE.10.005182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerasimov V. 1998. Information Processing in Human Body. Website: [Google Scholar]
- Gonzalez-Martinez J., Vadera S., Mullin J., Enatsu R., Alexopoulos A.V., Patwardhan R., Bingaman W., Najm I. Robot-assisted stereotactic laser ablation in medically intractable epilepsy: operative technique. Operative Neurosurgery. 2014;10:167–173. doi: 10.1227/NEU.0000000000000286. [DOI] [PubMed] [Google Scholar]
- Gowrishankar T., Stewart D.A., Martin G.T., Weaver J.C. Transport lattice models of heat transport in skin with spatially heterogeneous, temperature-dependent perfusion. Biomed. Eng. Online. 2004;3:1–17. doi: 10.1186/1475-925X-3-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta K., Cabaniss B., Kheder A., Gedela S., Koch P., Hewitt K.C., Alwaki A., Rich C., Ramesha S., Hu R., Drane D.L., Gross R.E., Willie J.T. Stereotactic MRI-guided laser interstitial thermal therapy for extratemporal lobe epilepsy. Epilepsia. 2020;61:1723–1734. doi: 10.1111/epi.16614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett R.M. In: Hyperelasticity Primer. Hackett R.M., editor. Springer International Publishing; Cham: 2018. Stress measures; pp. 29–48. [Google Scholar]
- Hale G.M., Querry M.R. Optical constants of water in the 200-nm to 200-μm wavelength region. Appl. Opt. 1973;12:555–563. doi: 10.1364/AO.12.000555. [DOI] [PubMed] [Google Scholar]
- Hasgall P.A.D.G.F., Baumgartner C., Neufeld E., Lloyd B., Gosselin M.C., Payne D., Klingenböck A., Kuster N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues. 1 ed. 2022. p. 4. [Google Scholar]
- Hawasli A.H., Kim A.H., Dunn G.P., Tran D.D., Leuthardt E.C. Stereotactic laser ablation of high-grade gliomas. Neurosurg. Focus. 2014;37 doi: 10.3171/2014.9.FOCUS14471. [DOI] [PubMed] [Google Scholar]
- Haynes W.M. CRC press; 2016. CRC Handbook of Chemistry and Physics. [Google Scholar]
- Heat Transfer Module 2022. https://www.comsol.com/heat-transfer-module .
- Hoppe C., Witt J.-A., Helmstaedter C., Gasser T., Vatter H., Elger C.E. Laser interstitial thermotherapy (LiTT) in epilepsy surgery. Seizure. 2017;48:45–52. doi: 10.1016/j.seizure.2017.04.002. [DOI] [PubMed] [Google Scholar]
- Johansson J. Spectroscopic method for determination of the absorption coefficient in brain tissue. J. Biomed. Opt. 2010;15 doi: 10.1117/1.3495719. [DOI] [PubMed] [Google Scholar]
- Khashan M.A., Nassif A.Y. Dispersion of the optical constants of quartz and polymethyl methacrylate glasses in a wide spectral range: 0.2–3 μm. Opt Commun. 2001;188:129–139. [Google Scholar]
- Kiyatkin E.A. Brain temperature homeostasis: physiological fluctuations and pathological shifts. Front Biosci (Landmark Ed) 2010;15:73–92. doi: 10.2741/3608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagman C., Chung L.K., Pelargos P.E., Ung N., Bui T.T., Lee S.J., Voth B.L., Yang I. Laser neurosurgery: a systematic analysis of magnetic resonance-guided laser interstitial thermal therapies. J. Clin. Neurosci. 2017;36:20–26. doi: 10.1016/j.jocn.2016.10.019. [DOI] [PubMed] [Google Scholar]
- Landazuri P., Shih J., Leuthardt E., Ben-Haim S., Neimat J., Tovar-Spinoza Z., Chiang V., Spencer D., Sun D., Fecci P., Baumgartner J. A prospective multicenter study of laser ablation for drug resistant epilepsy – one year outcomes. Epilepsy Res. 2020;167 doi: 10.1016/j.eplepsyres.2020.106473. [DOI] [PubMed] [Google Scholar]
- Le S., Ho A.L., Fisher R.S., Miller K.J., Henderson J.M., Grant G.A., Meador K.J., Halpern C.H. Laser interstitial thermal therapy (LITT): seizure outcomes for refractory mesial temporal lobe epilepsy. Epilepsy Behav. 2018;89:37–41. doi: 10.1016/j.yebeh.2018.09.040. [DOI] [PubMed] [Google Scholar]
- Malitson I.H. Interspecimen comparison of the refractive index of fused silica. Josa. 1965;55:1205–1209. [Google Scholar]
- Mateck Sapphire (Al2O3). In. MatWeb.com.
- Mensel B., Weigel C., Hosten N. Minimally Invasive Tumor Therapies. 2006. Laser-induced thermotherapy; pp. 69–75. [Google Scholar]
- Mintun M.A., Lundstrom B.N., Snyder A.Z., Vlassenko A.G., Shulman G.L., Raichle M.E. vol. 98. Proceedings of the National Academy of Sciences; 2001. pp. 6859–6864. (Blood Flow and Oxygen Delivery to Human Brain during Functional Activity: Theoretical Modeling and Experimental Data). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohammadi A.M., Schroeder J.L. Laser interstitial thermal therapy in treatment of brain tumors – the NeuroBlate System. Expet Rev. Med. Dev. 2014;11:109–119. doi: 10.1586/17434440.2014.882225. [DOI] [PubMed] [Google Scholar]
- Neuroblate(R) System - https://www.monteris.com/healthcare-professionals/neuroblate-system/. In. (Vol. 2022).
- Nybo L., Secher N.H., Nielsen B. Inadequate heat release from the human brain during prolonged exercise with hyperthermia. J. Physiol. 2002;545:697–704. doi: 10.1113/jphysiol.2002.030023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odéen H., Parker D.L. Improved MR thermometry for laser interstitial thermotherapy. Lasers Surg Med. 2019;51:286–300. doi: 10.1002/lsm.23049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overview of materials for Polyetheretherketone, Unreinforced. In.: MatWeb.com.
- Packett R.D., Brown P.J., Popli G.S., Scott Gayzik F. Development and validation of a brain phantom for therapeutic cooling devices. J. Biomech. Eng. 2017;139 doi: 10.1115/1.4036215. [DOI] [PubMed] [Google Scholar]
- PDMS (Polydimethylsiloxane). In. 6.777J/2.751J Material Property Database: Massachusetts Institute of Technology (MIT).
- Pennes H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948;1:93–122. doi: 10.1152/jappl.1948.1.2.93. [DOI] [PubMed] [Google Scholar]
- Poly(dimethylsiloxane) 2017. Chemical Retrieval on the Web (CROW) . [Google Scholar]
- Pt-10% Ir Alloy, Annealed. In. (Vol. vol. 2023): MatWeb.
- Querry M.R. Missouri Univ-Kansas City; 1985. Optical Constants. [Google Scholar]
- Rieke V., Butts Pauly K. MR thermometry. J Magn Reson Imaging. 2008;27:376–390. doi: 10.1002/jmri.21265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts D.A., Detre J.A., Bolinger L., Insko E.K., Leigh J.S. Quantitative magnetic resonance imaging of human brain perfusion at 1.5 T using steady-state inversion of arterial water. Proc. Natl. Acad. Sci. USA. 1994;91:33–37. doi: 10.1073/pnas.91.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossmanna C., Haemmerich D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Crit. Rev. Biomed. Eng. 2014;42:467–492. doi: 10.1615/critrevbiomedeng.2015012486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sapareto S.A., Dewey W.C. Thermal dose determination in cancer therapy. Int. J. Radiat. Oncol. Biol. Phys. 1984;10:787–800. doi: 10.1016/0360-3016(84)90379-1. [DOI] [PubMed] [Google Scholar]
- Schreiner J., Mardal K.-A. Simulating epileptic seizures using the bidomain model. Sci. Rep. 2022;12 doi: 10.1038/s41598-022-12101-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah N.J., Abbas Z., Ridder D., Zimmermann M., Oros-Peusquens A.-M. A novel MRI-based quantitative water content atlas of the human brain. Neuroimage. 2022;252 doi: 10.1016/j.neuroimage.2022.119014. [DOI] [PubMed] [Google Scholar]
- Sip V., Guye M., Bartolomei F., Jirsa V. Computational modeling of seizure spread on a cortical surface. J. Comput. Neurosci. 2022;50:17–31. doi: 10.1007/s10827-021-00802-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao J.X., Wu S., Lacy M., Rose S., Issa N.P., Yang C.W., Dorociak K.E., Bruzzone M., Kim J., Daif A., Choi J., Towle V.L., Warnke P.C. Stereotactic EEG-guided laser interstitial thermal therapy for mesial temporal lobe epilepsy. Journal of Neurology, Neurosurgery & Psychiatry. 2018;89:542. doi: 10.1136/jnnp-2017-316833. [DOI] [PubMed] [Google Scholar]
- Taylor P.N., Papasavvas C.A., Owen T.W., Schroeder G.M., Hutchings F.E., Chowdhury F.A., Diehl B., Duncan J.S., McEvoy A.W., Miserocchi A., de Tisi J., Vos S.B., Walker M.C., Wang Y. Normative brain mapping of interictal intracranial EEG to localize epileptogenic tissue. Brain. 2022;145:939–949. doi: 10.1093/brain/awab380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Events Interface. In. (2023) (Vol. 2023).
- Theory for Heat Transfer in Solids 2022. https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.heat/heat_ug_theory.07.07.html .
- Torvi DA, Dale JD. A finite element model of skin subjected to a flash fire. J. Biomech. Eng. 1994;116(3) doi: 10.1115/1.2895727. [DOI] [PubMed] [Google Scholar]
- Visualase™ - MRI-guided laser ablation (https://www.medtronic.com/us-en/healthcare-professionals/products/neurological/laser-ablation/visualase.html)-2022. In.
- Wang H., Wang B., Normoyle K.P., Jackson K., Spitler K., Sharrock M.F., Miller C.M., Best C., Llano D., Du R. Brain temperature and its fundamental properties: a review for clinical neuroscientists. Front. Neurosci. 2014;8 doi: 10.3389/fnins.2014.00307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.E., Scholly J., Triebkorn P., Sip V., Medina Villalon S., Woodman M.M., Le Troter A., Guye M., Bartolomei F., Jirsa V. VEP atlas: an anatomic and functional human brain atlas dedicated to epilepsy patients. J. Neurosci. Methods. 2021;348 doi: 10.1016/j.jneumeth.2020.108983. [DOI] [PubMed] [Google Scholar]
- Wang H.E., Woodman M., Triebkorn P., Lemarechal J.-D., Jha J., Dollomaja B., Vattikonda A.N., Sip V., Medina Villalon S., Hashemi M., Guye M., Makhalova J., Bartolomei F., Jirsa V. Delineating epileptogenic networks using brain imaging data and personalized modeling in drug-resistant epilepsy. Sci. Transl. Med. 2023;15 doi: 10.1126/scitranslmed.abp8982. [DOI] [PubMed] [Google Scholar]
- Werner W.S.M., Glantschnig K., Ambrosch-Draxl C. Optical constants and inelastic electron-scattering data for 17 elemental metals. J. Phys. Chem. Ref. Data. 2009;38:1013–1092. [Google Scholar]
- Widjaja E., Papastavros T., Sander B., Snead C., Pechlivanoglou P. Early economic evaluation of MRI-guided laser interstitial thermal therapy (MRgLITT) and epilepsy surgery for mesial temporal lobe epilepsy. PLoS One. 2019;14 doi: 10.1371/journal.pone.0224571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaroslavsky A., Schulze P., Yaroslavsky I., Schober R., Ulrich F., Schwarzmaier H. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Phys. Med. Biol. 2002;47:2059. doi: 10.1088/0031-9155/47/12/305. [DOI] [PubMed] [Google Scholar]
- Yuan J., Chen Y., Hirsch E. Intracranial electrodes in the presurgical evaluation of epilepsy. Neurol. Sci. 2012;33:723–729. doi: 10.1007/s10072-012-1020-2. [DOI] [PubMed] [Google Scholar]
- Zhang X., Qiu J., Li X., Zhao J., Liu L. Complex refractive indices measurements of polymers in visible and near-infrared bands. Appl. Opt. 2020;59:2337–2344. doi: 10.1364/AO.383831. [DOI] [PubMed] [Google Scholar]
- Zhao Y., Wang F., Li A., Liu B., Wu Z., Zhang D., Liu S., Yi M. Cross-linkable fluorinated poly(ether ether ketone) polymers for optical waveguide devices. Mater. Lett. 2004;58:2365–2368. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.