Abstract
The ubiquitous smart meters are expected to be a central feature of future smart grids because they enable the collection of massive amounts of fine-grained consumption data to support demand-side flexibility. However, current smart meters are not smart enough. They can only perform basic data collection and communication functions and cannot carry out on-device intelligent data analytics due to hardware constraints in terms of memory, computation, and communication capacity. Moreover, privacy concerns have hindered the utilization of data from distributed smart meters. Here, we present an end-edge-cloud federated split learning framework to enable collaborative model training on resource-constrained smart meters with the assistance of edge and cloud servers in a resource-efficient and privacy-enhancing manner. The proposed method is validated on a hardware platform to conduct building and household load forecasting on smart meters that only have 192 KB of static random-access memory (SRAM). We show that the proposed method can reduce the memory footprint by 95.5%, the training time by 94.8%, and the communication burden by 50% under the distributed learning framework and can achieve comparable or superior forecasting accuracy to that of conventional methods trained on high-capacity servers.
Subject terms: Electrical and electronic engineering, Energy management, Energy grids and networks, Energy supply and demand
Smart meters collect detailed consumption data but struggle with on-device analytics due to hardware and privacy issues. The authors propose an end-edge-cloud federated split learning framework to introduce edge intelligence, reducing memory, training time, and communication burden while maintaining accuracy.
Introduction
Electric power systems account for more than 40% of global carbon dioxide emissions1,2. Accommodating high penetration of renewable energy is an essential way to decarbonize power systems and thus alleviate climate change. Harnessing demand-side flexibility is a cost-effective strategy for promoting renewable energy accommodation3, where smart meters play a pivotal role in this process. Smart meters are the core of the advanced metering infrastructure in power systems, which are supported by sensors, control devices, and dedicated communication infrastructure4. Smart meters can record real-time energy information, including voltage, frequency, and energy consumption, from the demand side and can enable bidirectional communication between system operators and end-users5. The advanced functions of smart meters provide a strong foundation for harnessing demand-side flexibility in terms of data and hardware platforms6,7. On the one hand, smart meter data enable the estimation of demand response potential8 and dynamic pricing design9 to integrate renewable energy. On the other hand, smart meters can act as agents for home energy management systems to monitor distributed renewable energy generation, storage, and consumption10.
The construction of smart grids has increased the adoption of smart meters, and the number of smart meters is expected to exceed 1.2 billion globally by the end of 202411; the global penetration of smart meters will increase to nearly 59% by 202812. The ubiquity of smart meters will enable them to become a central feature of future smart grids by enabling the collection of massive fine-grained consumption data to support demand-side flexibility7,13. However, current smart meters are not smart enough. They are incapable of conducting on-device intelligent data analytics and can only transmit collected data to a data management system6, which can result in potential privacy leakage, heavy transmission burdens, and low efficiency in demand-side management. Enabling on-device intelligence for smart meters without additional investment in computational facilities is an economical way to help consumers manage flexible resources more autonomously and efficiently. Moreover, enabling smart meter intelligence can reduce the need for uploading local data, which may alleviate privacy concerns and increase consumers’ willingness to adopt smart meters14–16, thus facilitating the digitalization of electric grids a step forward.
On-device load forecasting is one of the key components of smart meter intelligence, as it can provide consumers with valuable information and a foundation for optimal decision-making in a peer-to-peer energy market17,18, building energy and household appliance management19,20, electric vehicle charging/discharging and local storage scheduling21,22, etc. Deep learning-based methods for accurate load forecasting have been investigated in numerous studies23–25. The success of these load forecasting methods relies heavily on the training of complex neural networks with extensive data as input, which are traditionally carried out in a data-centralized manner on servers with abundant computational resources. However, these methods are not applicable to smart meters due to limitations in terms of data availability and hardware resources: (1) smart meter data involve consumer privacy, which creates a data barrier that hinders the utilization of distributed big data26; and (2) smart meters have insufficient memory, computational power, and communication resources to support complicated model training. Therefore, it is worth investigating how to effectively utilize distributed data resources to train complex models for accurate load forecasting on resource-constrained smart meters. Such an investigation will help to intellectualize the end infrastructure of power systems at a low cost and to obtain maximal value from smart meter data.
Recently, researchers have focused on harnessing the potential of edge data and computational resources by pushing artificial intelligence toward end devices, giving rise to the concept of “edge intelligence" (EI)27–29. Considering the data privacy concerns regarding smart meters, as well as their hardware constraints in terms of memory, computation, and communication capacity, achieving EI on smart meters requires a privacy-enhancing framework with high efficiency. First, to address the memory and computational power limitations of end devices, studies have considered computation offloading to transfer computation-intensive tasks from end devices to edge or cloud servers30,31. The split learning approach32,33 enables a deep neural network to be split, allocated, and trained across multiple entities, thereby opening up opportunities for addressing the resource constraints of end devices. Second, to make full use of smart meters and distributed data while helping preserve privacy, federated learning (FL) is a promising solution, as it allows multiple clients to collaboratively develop high-performance global models34,35. The success of FL has been achieved in several fields, such as healthcare36–38, finance39,40, and energy41–43. In FL, model development involves intensive information exchange (including the exchange of model parameters and gradients) between clients and a server, making communication overhead a crucial concern. In the scenario of the large-scale deployment of smart meters, the transmission of massive numbers of parameters generated by deep learning models will impose a significant burden on communication networks and can even cause network congestion44,45. Another problem in implementing FL is that the overall computation speed is subjected to the model aggregation process. In practice, smart meters may have different training speeds depending on the computing power and task occupancy of each meter. The vanilla FL method adopts a synchronous approach in model aggregation, which slows convergence since it needs to wait for the slowest meter to complete model updates in each communication round46,47. Several studies have investigated FL for edge intelligence, such as refs. 48–52. However, these studies mainly utilize smart meter data to carry out simulation experiments instead of implementing their methods on resource-constrained smart meter hardware. There is still a lack of a unified framework that considers all perspectives of model accuracy, on-device memory footprint, computation speed, and communication overhead to fully achieve on-device intelligence.
Previous edge intelligence studies cannot be applied to the smart grid since the ubiquitous smart meters present distinctive challenges and opportunities. Our work provides a comprehensive solution tailored for smart meter hardware that translates theoretical methods into practical, real-world applications. This paper focuses on two critical questions in achieving on-device intelligence: “How can we efficiently utilize distributed data?" and “How can we train models on resource-constrained devices?". To answer these questions, we present an end-edge-cloud framework that combines federated learning and split learning to intellectualize resource-constrained smart meters for on-device load forecasting in a privacy-enhancing manner. This work overcomes the constraints inherent to smart meter environments, ensuring that our approaches are not only theoretically sound but also viable for on-the-ground deployment. Figure 1 compares the characteristics of mainstream learning methods, highlighting that our framework consolidates several properties: higher accuracy, reduced memory footprint, faster computation speed, smaller communication overhead, and enhanced privacy. In particular, we develop an optimal splitting strategy, collaborative knowledge distillation mechanism, and semi-asynchronous aggregation approach in our framework to tackle the issues of computation offloading, device collaboration, and heterogeneous aggregation for smart meter intelligence. We provide a theoretical analysis for guaranteeing the convergence of the proposed distributed method and set up a hardware platform to validate the proposed method by performing individual building and household load forecasting on smart meters. The experimental results demonstrate that our method can reduce the memory footprint by 95.5%, the training time by 94.8%, and the communication overhead by 50% in the distributed learning framework and can achieve comparable or even superior forecasting accuracy to that of conventional methods trained on high-capacity servers. This implementation of complex model training on smart meters represents a pioneering effort in EI concepts within smart grids. It bridges the gap between theory and practice, fostering the utilization of demand-side flexibility to enhance the efficiency and reliability of smart grids.
Fig. 1. Comparison among mainstream energy data analytics methods.

The excellent, good, fair, and poor coordinate points represent the general performance of different methods in various dimensions. Our proposed federated split learning integrates the advantages of federated learning and split learning methods, achieving exceptional performance across all dimensions.
Results
Overall framework
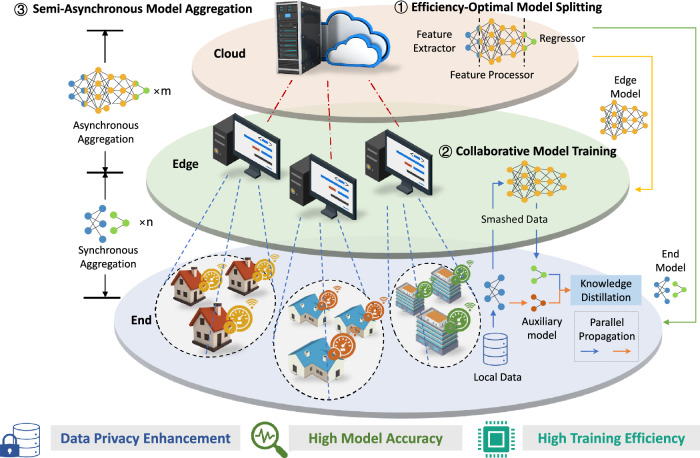
We first present a concise overview of the proposed end-edge-cloud framework for intellectualizing smart meters. As shown in Fig. 2, the framework consists of a hierarchy with three levels: smart meters, edge servers, and a cloud server. The proposed framework is capable of collaboratively training the model deployed on different entities with distributed data in a privacy-enhancing manner to address the challenges posed by the resource constraints and insufficient data of individual smart meters. To enable accurate on-device load forecasting with memory, computation, and communication efficiency, our framework incorporates three critical phases, namely, model splitting, model training, and model aggregation.
In the model splitting phase, the cloud server determines an efficiency-optimal model split ratio for each smart meter and edge server pair. This aims to minimize the training time while avoiding memory overflow on smart meters. Consequently, the model is split into three components: a feature extractor, a feature processor, and a regressor. The feature extractor and regressor involve private raw data and thus are deployed on smart meters, while the feature processor requires complex computations and thus is deployed on edge servers. In this way, most of the resource burden of the model training is transferred to edge servers.
In the model training phase, the smart meters and edge servers collaboratively train the model deployed on them. We introduce a small auxiliary network as an extra regressor on smart meters to update the end- and edge-side models in parallel. This parallelism significantly reduces the computation time and communication overhead. To enhance the model accuracy, a knowledge distillation-based mechanism is employed to guarantee objective consistency between the two split models throughout the training process.
In the model aggregation phase, the cloud server and the edge servers aggregate the trained models in a hierarchical way. We first adopt a hardware-aware clustering algorithm to designate smart meters with similar training times to the same edge server. This allows the models of intra-cluster smart meters to be synchronously aggregated by edge servers. Subsequently, the aggregated models of each edge server can be asynchronously uploaded to update the global model via the cloud server. This two-stage semi-asynchronous approach effectively reduces the delay time without compromising accuracy by combining the benefits of the synchronous and asynchronous methods.
Fig. 2. Overview of the end-edge-cloud framework for on-device load forecasting.
We develop a federated split learning approach under this framework, which mainly incorporates three phases: (1) model splitting, in which the cloud server splits the large model and assigns a small portion to smart meters and a larger portion to the edge servers; (2) model training, in which multiple smart meters collaborate with edge servers to train the complete model; (3) model aggregation, in which the trained models are hierarchically aggregated by the edge servers and the cloud server to update the global model.
Experimental setup
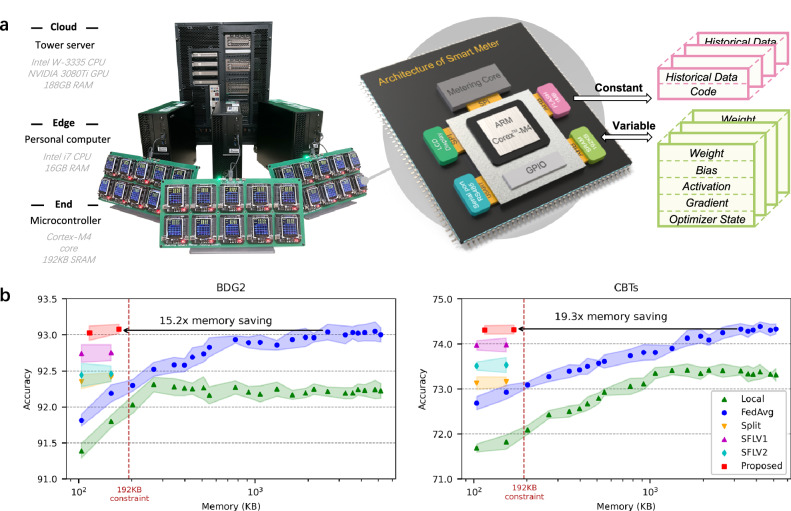
We established a hardware platform instantiating the end-edge-cloud framework to verify the effectiveness of our method for smart meter intelligence and on-device load forecasting. As illustrated in Fig. 3a, this hardware platform comprises one tower server, three personal computers (PCs), and thirty microcontroller units (MCUs). Specifically, the tower server and PCs function as the cloud server and edge servers in our framework, respectively. In addition to the metering core, the internal MCU of the smart meter is primarily used for computation and storage functionalities. Therefore, we employ an ARM Cortex-M4 series microchip, which is a representative MCU in smart meters53,54. The smart meter faces considerable constraints in terms of memory, computational, and communication resources. Training deep learning-based models typically requires the storage of numerous variable parameters and massive amounts of constantly collected data. The constants, such as preloaded datasets, can be stored in nonvolatile FLASH memory. The variables, such as the weights and gradients involved in model training, are cached in volatile SRAM memory. However, the limited memory budget of 192 KB SRAM and 1 MB FLASH in smart meters is inadequate for inference, let alone for training. Furthermore, the Cortex-M4 processor, with a maximum frequency of only 168 MHz, struggles to carry out computationally intensive model training. In addition, the communication rates of wired modes such as RS485 in smart meters are restricted to a relatively low level (115.2 kbps in subsequent experiments) to ensure transmission stability.
Fig. 3. Hardware demonstration for on-device load forecasting in our framework.
a Schematic of the hardware platform. The established platform instantiates the proposed end-edge-cloud framework for comprehensive experiments. The memory-constrained smart meter cannot match the requirement of numerous variable parameters and massive amounts of constantly collected data for model training. b Comparison of forecasting accuracy versus memory usage on smart meters for our method and benchmark methods with different model sizes. The average forecasting accuracy with 95% confidence intervals is presented with five independent experiments. Source data are provided as a Source Data file.
We conduct comprehensive experiments on two open smart meter datasets. The first dataset BDG255, contains hourly-resolution load profiles for different types of buildings across North America and Europe, spanning from January 2016 to December 2017. The second dataset, CBTs56, contains load data at a 30-min resolution for Irish residences from July 2009 to December 2010. Adjacent half-hour data values in CBTs are averaged to obtain hourly load values. In our experiments, data from 30 randomly selected buildings and residences are imported into each MCU as the load record. We divide the load data into two parts: the data of the first full year are used to train the model and the data of the subsequent half-year are used to test the model. Considering the unavailability of weather data for smart meters, the input features include only historical load and calendar information (month, weekday, day, and hour).
Three common metrics are selected to evaluate the forecasting accuracy: mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE). Since residential loads are near zero at some moments, we adopt the symmetric mean absolute percentage error (sMAPE) instead of the MAPE to avoid extremes in evaluating forecasting performance on the CBTs dataset. The accuracy of load forecasting is expressed as 1-MAPE. In addition, three model efficiency metrics are of significant interest and are crucial for smart meter intelligence: the memory footprint, training time, and communication overhead. The peak memory footprint determines whether the model can be trained without overflowing the SRAM of smart meters. A reduction in training time can effectively improve the response speed of the smart grid, thus enabling regular updates of the model on smart meters. A reduction in the communication overhead of distributed smart meters can effectively alleviate network congestion and delay, thus improving the reliability of communication in smart grids.
Performance evaluation
We compare the proposed method with several benchmarks, including privacy-invasive centralized learning (Cen), local learning (Local), two versions of federated learning (FedAvg57 and FedProx58), split learning (Split)32, and two versions of split federated learning (SFLV1 and SFLV2)33. Cen collects private load data from smart meters and trains the forecasting model on the cloud server. Local allows each smart meter to train the forecasting model with locally measured data. FedAvg and FedProx leverage a server to aggregate model parameters to train the forecasting model with data from distributed smart meters. Split trains the large forecasting model on smart meters with the assistance of servers. The proposed method, SFLV1, and SFLV2, enable smart meters to collaborate with edge servers to train the large forecasting model with multiple data sources. A basic multilayer perception (MLP) is applied as the baseline model to forecast the next 4-h electricity loads.
As a hard constraint, the limited memory resources on smart meters make it challenging to train a high-performing large-scale model with large amounts of data. We first investigate model accuracy versus on-device memory footprint for the local and distributed learning methods in Fig. 3b. The results show that Local consistently underperforms the other methods. This can be attributed to the inability of smart meters to effectively utilize either large models or extensive data. Interestingly, increasing the model size would lead to overfitting and a subsequent decrease in accuracy due to the insufficient amount of local data. Owing to the benefits derived from multiple data resources, FedAvg achieves greater accuracy than Local. However, the memory constraints of smart meters prevent the small model from accurately characterizing the volatile individual load well. In contrast, Split enables smart meters to train a powerful large model on smart meters with minimal memory footprint. However, model generalization is hindered by the limited data from a single smart meter, resulting in unsatisfactory accuracy. SFLV1 and SFLV2, which combine federated learning and split learning, significantly improve model accuracy. Remarkably, compared to the benchmark methods, our proposed method achieves the best performance within the 192 KB memory constraint and saves the memory footprint of smart meters by 15.2 times with similar accuracy.
We next compare the performance of our method with eight benchmark methods in terms of accuracy, memory, training time, and communication. We design two models of different sizes: a small model with a single hidden layer and a large model with multiple hidden layers. Due to the limited resources of smart meters, Local, FedAvg, and FedProx can only support the training of the small model. In contrast, the split learning-based methods can effectively train the large model under a memory constraint of 192 KB. Although training the large model on resource-constrained smart meters is an overwhelming task in local and federated frameworks, we simulate the experimental results to illustrate the superiority of our method. From the results in Table 1, we find that the forecasting performance of our method exhibits varying degrees of improvement compared to other device-friendly alternatives in terms of all accuracy metrics. For instance, the proposed method outperforms Split, FedAvg-S, FedProx-S, and Local-S by achieving 5.62%, 7.27%, 9.46%, and 11.07% improvements in the MAE for the BDG2 dataset, respectively. Compared with SFLV1 and SFLV2, our method achieves comprehensive improvements in both accuracy and efficiency metrics, with only a slight increase in the memory footprint. Moreover, the accuracy of our on-device training method is similar to or even superior to that of the conventional methods trained on high-capacity servers. Importantly, the migration of the model training burden provides substantial savings of 22.4 × memory footprint, 2.02 × communication overhead, and 19.23 × training time. These results indicate that the proposed method enables resource-constrained smart meters to execute resource-intensive intelligence algorithms effectively.
Table 1.
Performance of different methods on BDG2 and CBTs in terms of accuracy, memory, training time, and communication overhead per round
| Method | BDG2 | CBTs | Memory (KB) | Training Time (s) | Communication (KB) | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAPE | MAE | RMSE | MAPE | MAE | ||||
| Cen | 22.82 | 8.41 | 8.20 | 0.4780 | 26.98 | 0.2727 | 2578.42 (1.0 ×) | 586.42 (2.05 ×) | – |
| Local-S | 23.56 | 8.13 | 8.12 | 0.4698 | 28.19 | 0.2726 | 152.53 (16.9 ×) | 41.19 (29.14 ×) | – |
| FedAvg-S | 22.79 | 7.67 | 7.98 | 0.4681 | 27.04 | 0.2699 | 152.53 (16.9 ×) | 46.49 (28.80 ×) | 5.50 (27.18 ×) |
| FedProx-S | 22.58 | 7.71 | 7.91 | 0.4668 | 27.17 | 0.2678 | 152.53 (16.9 ×) | 46.49 (28.80 ×) | 5.50 (27.18 ×) |
| Local-M | 22.84 | 7.75 | 8.03 | 0.4645 | 26.67 | 0.2682 | 2578.42 (1.0 ×) | 1187.15 (1.01 ×) | – |
| FedAvg-M | 22.25 | 6.96 | 7.48 | 0.4614 | 25.81 | 0.2637 | 2578.42 (1.0 ×) | 1200.44 (1.0 ×) | 149.50 (1.0 ×) |
| FedProx-M | 22.21 | 7.16 | 7.62 | 0.4622 | 25.76 | 0.2639 | 2578.42 (1.0 ×) | 1200.44 (1.0 ×) | 149.50 (1.0 ×) |
| Split | 23.27 | 7.68 | 7.96 | 0.4679 | 26.83 | 0.2687 | 103.75 (24.8 ×) | 96.00 (12.50 ×) | 91.25 (1.63 ×) |
| SFLV1 | 22.34 | 7.25 | 7.68 | 0.4647 | 26.03 | 0.2664 | 103.75 (24.8 ×) | 96.49 (12.44 ×) | 96.75 (1.54 ×) |
| SFLV2 | 22.76 | 7.53 | 7.89 | 0.4674 | 26.49 | 0.2683 | 103.75 (24.8 ×) | 96.49 (12.44 ×) | 96.75 (1.54 ×) |
| Proposed | 22.17 | 6.98 | 7.44 | 0.4630 | 25.74 | 0.2636 | 115.07 (22.4 ×) | 62.41 (19.23 ×) | 74.43 (2.01 ×) |
1The best-performing and second-best-performing methods are bolded and underlined, respectively.
2-S and -M indicates that the model has single and multiple hidden layers, respectively.
Model effectiveness
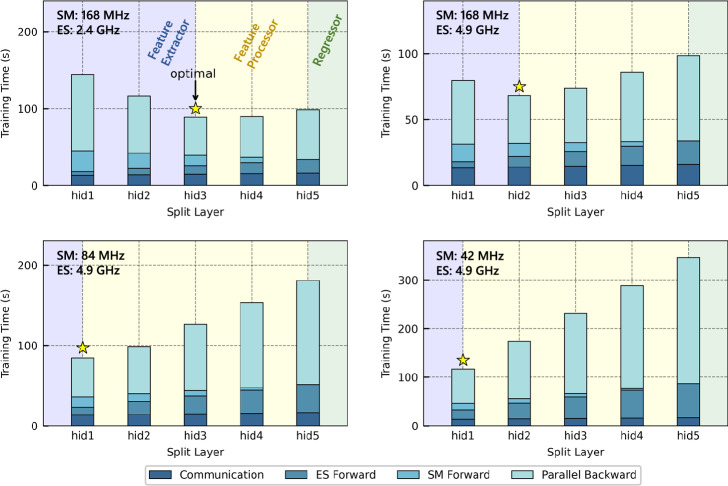
Next, we verify the effectiveness of three important techniques in our method, namely, efficiency-optimal model splitting, knowledge distillation-based model training, and semi-asynchronous model aggregation. We first investigate the impact of our efficiency-optimal splitting strategy. The proposed method requires two split layers to split the model into three components. The subsequent split point is fixed as the last hidden layer. Here we only discuss how to determine the previous split layer. The implemented MLP model consists of 5 hidden layers, with the lower and upper bounds for the split ratio being the first and fifth hidden layers, respectively. The experimental results in Supplementary Fig. 4 reveal that splitting at different hidden layers does not affect the forecasting accuracy of the model. However, the training time varies depending on the chosen split layer due to the differences in computational resources between smart meters and edge servers. We report the total training time under four distinct configurations of the computational power of the edge servers and smart meters in Fig. 4. We can observe that the proposed efficiency-optimal split ratio can serve as a guideline for how to split the model to minimize the training time. By adopting the proposed splitting strategy, the allocation of the complete model can benefit from up to 2.97 × shorter training time.
Fig. 4. Effectiveness of the efficiency-optimal model splitting strategy.
Each hidden layer is considered a candidate split layer. The split layers that yield the best efficiency are annotated. The hidden layers contained in the feature extractor, feature processor, and regressor after the optimal splitting are indicated with different colors. The total training times under four distinct hardware configurations when choosing different split layers are provided. The stacked histograms represent the measured times for communication, forward propagation of the edge server and smart meter, and parallel backward propagation, arranged from bottom to top. Source data are provided as a Source Data file.
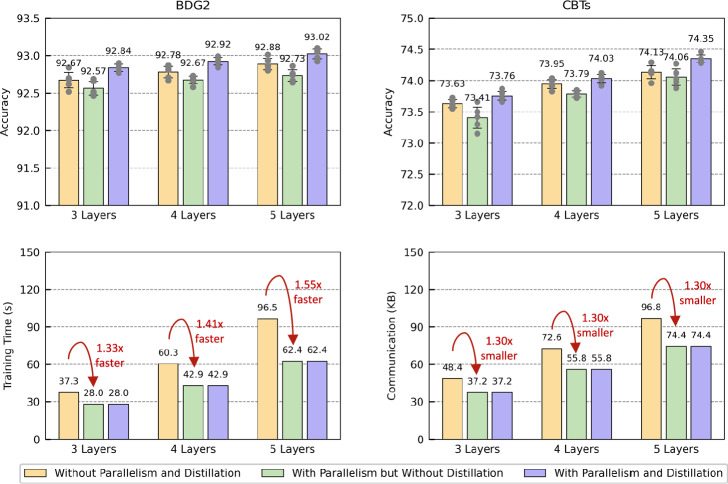
We further conduct an ablation study on parallelism and knowledge distillation in model training. We compare the accuracy, training time, and communication per round for the proposed method and two ablated variants. The results of the ablation experiments in Fig. 5 show that the integration of the parallelism mechanism decreases the training time by up to 1.55 × and the communication overhead by 1.3 × . This is mainly due to the benefit of parallelizing the model training on smart meters and edge servers. However, the parallel training leads to instability in the convergence processes of the two models, which subsequently impairs the convergence accuracy. We find that our method employing knowledge distillation exceeds the accuracy of the nonparallelized method at no extra memory cost. This improvement can be primarily attributed to the knowledge incorporated into the loss function, which enables the two models to guide each other during training and helps them avoid becoming trapped in local optima.
Fig. 5. Effectiveness of the collaborative model training method.
We compare the model performance in terms of accuracy, training time, and communication per round when the parallelism and knowledge distillation mechanisms are removed. The mean accuracy with 95% confidence intervals is presented with five independent experiments. Source data are provided as a Source Data file.
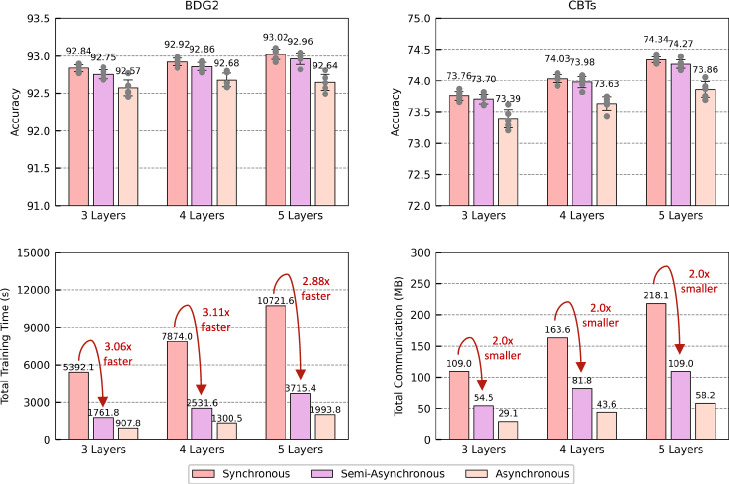
We also conduct a performance comparison between the proposed method and two widely used methods in federated learning (synchronous aggregation and asynchronous aggregation) in a heterogeneous smart meter scenario. To create device heterogeneity, we set the MCUs in our experiment to have different operation frequencies that determine the computation speed. As shown in Fig. 6, the synchronous approach results in a considerable waiting time due to the different training times of heterogeneous meters. Nonblocking updates in asynchronous aggregation substantially shorten the delay time and diminish the communication overhead. However, this approach also reduces the convergence accuracy due to the stochasticity of a single model’s gradient. In contrast, the proposed method strikes a good trade-off between accuracy and training efficiency. Specifically, our semi-asynchronous method can reduce the total training time by 3.11 × and the communication overhead by 2.0 × with minimal sacrifice in accuracy. This suggests that our two-stage approach combines the strengths of both methods while suppressing the effects of their weaknesses. Follow-up experiments illustrate that choosing an appropriate number of clusters can enable our method to achieve almost the same accuracy as the synchronous method with a greater training speed and smaller communication overhead (see Supplementary Fig. 9).
Fig. 6. Effectiveness of the semi-asynchronous model aggregation method.
We compare the model performance in terms of the accuracy, total training time, and communication overhead of the proposed method with the, synchronous, asynchronous, and semi-asynchronous model aggregation methods. Source data are provided as a Source Data file.
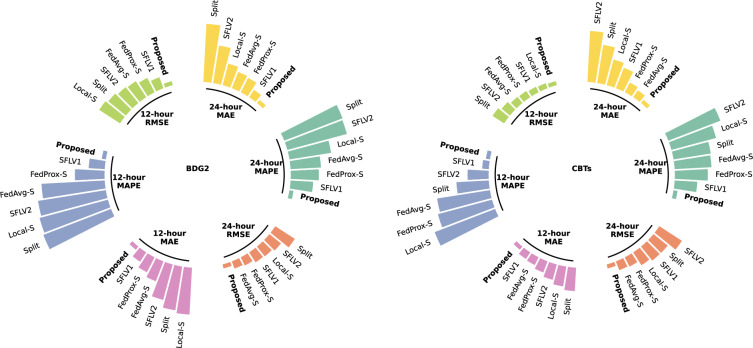
Considering additional forecasting scenarios in smart grids, we evaluate the accuracy of our method compared with other device-friendly methods on different forecasting ranges and different neural network backbones. We first visualize the performance improvement on all accuracy metrics obtained by the proposed method for 12 h ahead and 24 h ahead forecasting in Fig. 7. Compared to the best-performing benchmarks in each task, our proposed model has improvements of 1.33%, 2.19%, and 3.27% in terms of the RMSE, MAPE, and MAE, respectively. This highlights the superior ability of our method to handle forecasting tasks at different scales. We also implement our method and the benchmarks with several common deep learning-based backbones in load forecasting, including a convolutional neural network (CNN), recurrent neural network (RNN), gate recurrent unit (GRU), and long short-term memory (LSTM). Our proposed method surpasses other feasible on-device methods on both BDG2 and CBTs datasets, which shows that our method is model-agnostic and performs well with different neural networks as the backbone (see Supplementary Fig. 11). Recalling the results presented in Table 1, we see that the basic deep-learning model MLP even achieves higher forecasting accuracy. The possible reason is that MLP with simple architectures can accommodate more neurons than models with complex architecture in limited memory space, thus achieving a stronger representation capacity. In summary, we can conclude that the proposed method consistently maintains high performance in handling various real-world forecasting scenarios.
Fig. 7. Performance evaluation of the proposed model for different forecasting ranges.
We present the accuracy improvement of our method compared with other device-friendly methods for 12 h ahead and 24 h ahead forecasting. Source data are provided as a Source Data file.
Impact on energy management
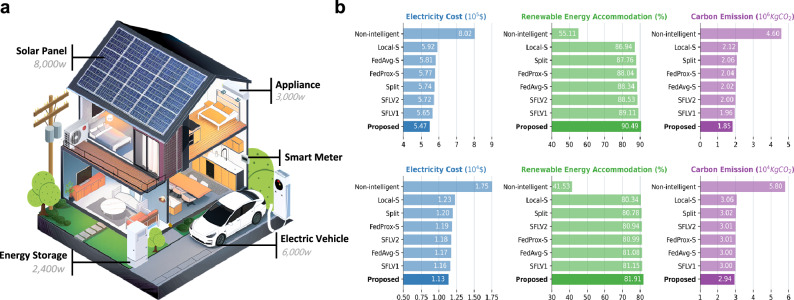
Load forecasting facilitates consumers to gain deeper insights into future energy consumption patterns, thereby supporting tailored energy management decisions. In addition to conducting accuracy analysis, we explore the impact of forecasting errors on the downstream decision-making process. Figure 8(a) illustrates a representative home that features distributed flexible energy resources, including solar panels, controllable appliances, electric vehicles, and energy storage systems. Note that a building can be regarded as a multi-household collective with larger-scale distributed resources. Building energy management (BEM) and home energy management (HEM) are typically achieved through two stages: (1) short-term scheduling and (2) real-time balancing. Briefly, short-term scheduling aims to minimize electricity costs while ensuring a balance between forecast demand and supply by scheduling various flexible resources for upcoming periods. To this end, the smart meter installed on each building/home first predicts the future load using a pre-trained forecasting model and retrieves the time-of-use tariff information from the grid operator’s cloud platform. On this basis, the smart meter can determine the operating strategies of storage systems and household appliances and recommend strategies for participating in the energy market. To save electricity costs, storage systems, and electric vehicles can be charged during off-peak tariff periods, while grid-connected electricity sales can be conducted during peak solar generation periods. However, due to prediction errors, smart meters may require further adjustments to achieve the real-time supply and demand balance. In this case, a higher predicted load implies that consumers discard unused generated renewable energy, while a lower predicted load means that consumers have to temporarily purchase electricity in the energy market. Both situations are unfavorable for efficient energy management. In short, accurate forecasting results contribute to low additional grid electricity purchases and a high accommodation ratio of solar generation, thus reducing total carbon emissions.
Fig. 8. Impacts of different forecasting methods on individual energy management.
a Schematic diagram of edge home energy management for flexible energy resources. Edge intelligence enables smart meters to manage local energy storage, controllable household appliances, electric vehicle charging, and energy market participation based on predicted loads. b Comparison of the electricity cost, renewable energy accommodation ratio, and carbon emission for a non-intelligent strategy and various edge intelligent methods. The experiments were conducted on 30 buildings and houses in the BDG2 and CBTs datasets for 180 test days. Source data are provided as a Source Data file.
We conducted comprehensive experiments on the BDG2 and CBTs datasets to showcase the effectiveness of the proposed method in enhancing decision-making for BEM and HEM. Figure 8b provides a performance comparison of a non-intelligent strategy and various edge intelligent methods in terms of the electricity cost, renewable energy accommodation ratio, and carbon emission. In the non-intelligent strategy, smart meters without edge intelligence cannot provide any assistance or support for customers to schedule flexible energy resources. The results clearly show that introducing edge intelligence to smart meters can, on average, reduce electricity costs by 31.79%, increase renewable energy accommodation by 35.38%, and reduce carbon emissions by 59.78% for each building. These improvements brought to each house can be found at 35.42%, 40.38%, and 49.31%, respectively. By adopting our approach, electricity cost savings of $1,176.11 per building and electricity cost savings of $18.93 per household can be expected annually. Importantly, the proposed method, which has the highest forecasting accuracy among all intelligent methods, also achieves a significant performance improvement in individual energy management. Compared to the best-performing benchmarks, our approach saves electricity costs, boosts renewable energy consumption, and reduces carbon emission for buildings and houses, reaching values of 3.08%, 1.38%, 5.42%, 2.41%, 0.76%, and 1.96%, respectively. Interestingly, the prediction error is not strictly monotone with the downstream decision cost. For instance, SFLV2 outperforms FedAvg-S in residential load forecasting, but its performance in subsequent energy management is unsatisfactory.
Discussion
In this work, we have proposed a unified end-edge-cloud framework that integrates the strengths of federated learning and split learning to introduce edge intelligence into smart meters. The core of the proposed method is to collaboratively train a model deployed on different distributed entities with distributed data in a privacy-enhancing manner, thus facilitating accurate energy analysis on resource-constrained and data-scarce smart meters. This paradigm can increase the digital intelligence of ubiquitous smart meters through synergy between hierarchical grid devices. Moreover, with the implementation of customized model splitting, model training, and model aggregation strategies, our method can greatly improve the efficiency and practicality of smart meter intelligence in terms of memory, communication, and training time compared to existing decentralized methods, especially in large-scale heterogeneous scenarios. In summary, this work provides a feasible, efficient, and adaptable approach for application to existing smart meter systems without the need for additional investment in computational facilities.
The effectiveness and practicability of the proposed method have been validated by comprehensive experiments on two real-world datasets on a hardware platform. The experimental results demonstrate that our method can reduce the memory footprint by 95.5%, the training time by 94.8%, and the communication overhead by 50% in the distributed learning framework and can achieve comparable or even superior forecasting accuracy to that of the server-trained results. In addition, the proposed approach is a general method that performs well in different forecasting ranges and with different models as the backbone. More importantly, the forecasts produced by the proposed method have been proven to provide excellent support for energy management, achieving a 31.79% reduction in electricity cost, a 35.38% increase in renewable energy accommodation, and a 59.78% reduction in carbon emissions.
However, some aspects also need to be further explored. First, devices with poor-quality data or unstable communication may affect the accuracy and efficiency of the proposed method. Thus, it is necessary to develop active device selection methods to choose representative, well-conditioned devices for collaboration. Second, smart meters collect new data continuously, and there is a need to update the model frequently. For these reasons, online mechanisms to ensure timely and efficient model updates are of interest for further study. Third, the extensive use of smart meters will lead to problems of data heterogeneity and device heterogeneity, where a single global model with a fixed structure will be insufficient to meet all conditions. Thus, it is of further interest to develop personalization approaches for automatic model design and to improve model performance on individual devices.
The work in this paper is the first attempt to achieve smart meter-based intelligence in smart grids, laying the foundation for broader EI applications. The proposed framework is not limited to load forecasting tasks but also has wide applicability to on-device monitoring and on-device control, which provides benefits for both consumers and distribution system operators (DSOs). For consumers, the proposed framework can be extended to enable smart meters to carry out local energy management, household appliance control, electric vehicle charging/discharging scheduling, autonomous energy market participation, etc. This will help consumers better exploit flexible resources to reduce costs and accommodate more distributed renewable energy. For DSOs, the proposed framework has the potential to achieve on-device electricity theft detection and allocation, demand response, distributed renewable energy management, etc. This will enable DSOs to better observe the system’s status and manage the system to decrease operation costs and improve the reliability of the energy supply. In addition, the proposed framework can effectively help preserve data privacy, which will increase consumers’ willingness to adopt smart meters, thus promoting smart meter penetration and contributing to the digitalization and consequent decarbonization of smart grids.
This study provides the following takeaway messages. First, implementing edge intelligence algorithms on smart meters should primarily consider hardware resource availability for the feasibility of grid applications. Second, smart meters can collaborate through federated learning to improve energy analytics performance in edge intelligence by orchestrating the cooperation of distributed data resources. Third, smart meters can split large-scale models with the assistance of high-capacity servers to improve energy analytics performance in edge intelligent systems by orchestrating the cooperation of hierarchical computational resources. Finally, edge intelligence on smart meters can substantially optimize energy management, promote sustainable energy development, and thereby advance the decarbonization of power and energy systems.
Despite the end-edge-cloud framework bringing advancements in smart meter intelligence, this study has two concerns that should be addressed in industrial applications. First, the adopted clustering algorithm is designed for the computing resources of heterogeneous devices, without considering the geographical location and physical connection characteristics of smart meters in smart grids. Second, the established experimental platform only selects one representative hardware configuration for the smart meter. Implementing smart meter intelligence should consider the compatibility of devices equipped with varying core models and communication technologies.
Methods
Efficiency-optimal model splitting
Let denote the size of the parameters. Since the model is split and allocated in the proposed method, we define α as the split ratio between the number of network parameters for the model deployed on the smart meter and that for the complete model, i.e., (Fig. 2). α determines the peak memory footprint M of the model deployed on smart meters and also influences the overall training time T. To this end, we aim to find an optimal split ratio α* that minimizes T subject to the memory constraints Msm of smart meters, which can be formulated as
| 1 |
Analysis of peak memory footprint M(α)
The peak memory footprint for training a neural network on smart meters consists of three main components59. We analyze how these three types of sources contribute to the memory footprint of the i-th layer as follows. Model memory is the memory space allocated to store the fundamental network parameters wi, i.e., the weights and biases of each layer of the network. The number of network parameters for various common layers can be found in Supplementary Table. 1. Some nonparametric layers, such as the activation layer, do not impose any burden on the model memory. In addition, intermediate memory comprises two parts: the memory footprint required for the activations of each layer ai during the forward pass, and the memory footprint required for the gradients of ai and wi during the backward pass. Note that the same intermediate memory needs to be assigned for each sample in batch B, and this memory consumes most of the storage resources in model training. The number of intermediate parameters for various common layers is also provided in Supplementary Table 2. Furthermore, the optimizer memory refers to the memory used to store the optimizer states. For instance, the standard SGD needs to cache the momentum values of wi, while the Adam optimizer requires buffer memory for the first- and second-moment estimates of wi. In general, all parameters are statically allocated to memory and stored as single precision floating point numbers for smart meters. Consider the example of a complete model with L layers using the Adam optimizer. Once we know the total number of parameters for each layer of the end-side model, the peak memory footprint M(α) can be calculated by multiplying this number by 32-bit as follows:
| 2 |
where denotes the maximum number of layers in the end-side model, the network parameters of which do not exceed the α of the complete model.
Analysis of training time T(α)
The overall training time T includes the computation time and communication time. We consider a collaboration setting involving one edge server and K smart meters. Let Psm, Pes, and R denote the computational power of the smart meters, the computational power of the edge server, and the transmission rate of communication between the smart meters and the edge server respectively. For simplicity, we assume that the dataset size of each smart meter and the number of neurons s in each split layer are identical.
First, we analyze the time spent on computation, including forward and backward propagation. The amount of computation required for each parameter is assumed to be equal and is denoted as n. Since ∣w∣ is typically much larger than ∣a∣ in (2), the computational complexity of the complete model training can be represented as for the entire dataset. Therefore, the total amount of computation in the training process can be characterized as n∣D∣∣w∣. Let β denote the fraction of computation used for forward propagation. Initially, smart meters concurrently perform forward propagation on their local models, which takes time of . Similarly, the edge server then carries out forward propagation on the edge-side models for each smart meter, which takes time of . In our training method detailed later, the smart meters and edge server backpropagate their respective models in parallel. The parallel propagation time is determined by the maximum value for the model of the smart meters and edge server, which can be expressed as .
Second, we analyze the time spent on communication. In each round, the smart meters communicate with the edge server to upload and download the weights of the end-side model, with each process requiring time of . Since the complete model is split into three parts, the intermediate activations of the split layers need to be transmitted twice between the smart meters and edge server for forward propagation, which will take time of . In our method detailed later, the edge server no longer returns the gradient of the split layer to the smart meters. Thus, the smart meters send the gradients of the activations of the split layer back to the edge server, taking the time of .
In summary, the overall training time T(α) used per round can be formulated as:
| 3 |
Solution for optimal split ratio α*
First, we can calculate an upper bound αupper for the split ratio that ensures that M(α) remains within the memory constraints Msm, which can be formulated as:
| 4 |
Second, as mentioned earlier, the input and output layers, i.e., the first and last layers, must be deployed on the ED for load data protection, so we can calculate a lower bound αlower for the split ratio, which can be formulated as:
| 5 |
To this end, we can solve the optimization problem (1) by piecewise dissection. Theorem 1 offers guidance for determining the efficiency-optimal split ratio α*. The proof is provided as Supplementary Proof. 1.
Theorem 1
(Efficiency-optimal split ratio): If , we have
| 6 |
If , we have
| 7 |
If , we have
| 8 |
Collaborative model training
To perform collaborative training of the split model in our framework, information needs to be exchanged between the smart meters and edge servers during the forward and backward propagation processes. However, the transmission of split-layer activations and gradients results in a large amount of communication, and the sequential propagation severely limits computational efficiency. To address this, we design a communication-efficient and computation-efficient training method geared to the split learning setup with parallelism and knowledge distillation mechanisms.
Parallelism
Distributed optimization enables parallel solving of subproblems across multiple computing nodes, thereby significantly improving efficiency. Inspired by this, we parallelize the training process of the end-side and edge-side models. As shown in Fig. 9, an extra auxiliary network wa is added as another regressor connected to the feature extractor we. Thus two trainable models are formed, namely the main model and the auxiliary model . Let f(⋅) denote the output of the corresponding model. The smart meter first utilizes historical data x as inputs to obtain the extracted representation he = f(we, x). Next, the feature processor wp in the edge server further refines the representations hp = f(wp, he), and the smart meter then calculates the prediction ys of the main model as ys = f(wr, hp). In tandem, the smart meter can directly calculate the prediction of the local auxiliary model as yc = f(wa, he). Note that the introduction of the auxiliary model produces an extra loss function ℓc in addition to the loss function ℓs. In contrast to traditional split training methods, the gradients of we in the proposed method are calculated based on ℓc rather than ℓs. As a result, the backward propagation process is divided into two parallel subprocesses: (1) the main model ws except for we are propagated based on the loss ℓs through the interaction between smart meters and edge servers; (2) the auxiliary model wc is locally propagated in the smart meter based on the extra loss ℓc.
Fig. 9.
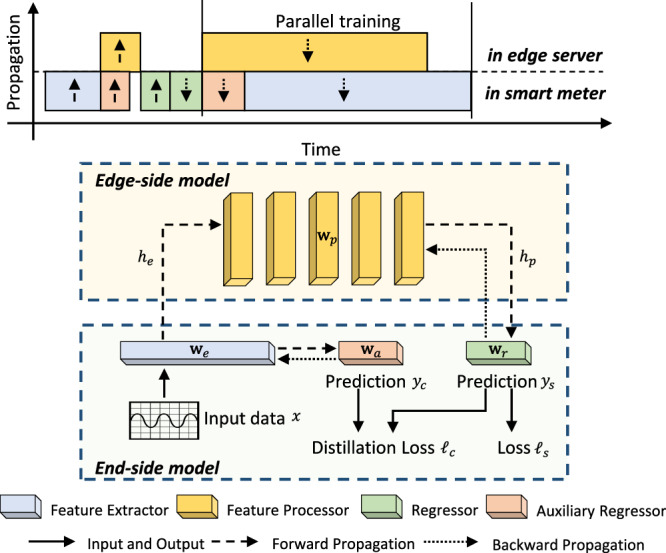
Illustration of the process and pipeline in collaborative model training.
There are two distinct advantages of the proposed method. First, the gradient computation of we is independent of that of wp. In other words, the edge server does not have to send the returned gradient to the smart meters, which eliminates a quarter of the communication overhead. Second, the gradients of we and wr can be calculated in parallel, which saves nearly half of the computation time required for backpropagation (the vast majority of computation in model training). The auxiliary regressor introduces almost no memory footprint.
Knowledge distillation
To achieve accurate forecasting, our goal is to find the optimal parameters to minimize the loss of the main model and the extra loss of the auxiliary model for dataset D, which can be formulated as:
| 9 |
| 10 |
There is a difficulty in solving this optimization problem. As a shared component of the main model ws and the auxiliary model wc, updating the feature extractor, we will change the results of ℓs and ℓc. Thus, the parameter optimization we aims to minimize the objective loss in both (9) and (10). However, we serve as a decision variable only in (10). In other words, we are optimized based on the loss ℓc in (10) and is independent of the loss ℓs in (9). This lack of correlation means that the converged optimal solution to we in (10) will generate a considerable loss in (9). Generally, knowledge transfer promotes the exchange of gainful information between multiple models60. Inspired by this, we redesign the loss function by incorporating knowledge distillation to introduce the convergence of (9) as an objective into the optimization of we. The specific formulations of ℓs and ℓc are as follows:
| 11 |
| 12 |
where y denotes the true label, μ and γ denote the weights of the label loss and knowledge distillation loss, respectively. Here ℓ is the basic loss function, which can be L2 loss for deterministic load forecasting or pinball loss for probabilistic load forecasting. Intuitively, knowledge distillation brings the prediction of wc closer to that of ws.
In addition, as we can obtain the forecasting outputs ys and yc from the main model and auxiliary model, respectively, our method shows great adaptivity during the inference stage under different communication conditions. When the communication network is working properly, ys is preferred as the forecasting result because the main model has more hidden layers and typically has better performance than the auxiliary model. To further enhance the forecasting robustness, an ensemble learning strategy can also be adopted for the main and auxiliary models. When the communication network is poor and hinders the parameter transmission of the main model, smart meters can still make forecasts based on the local auxiliary model, which can conduct inferences without communication.
Semi-asynchronous model aggregation
To train a global model with extensive data from distributed smart meters, the network parameters of the end-side model and edge-side model are aggregated in a federated manner. Due to the device heterogeneity of smart meters, the completion time of model training may vary significantly. In addressing this problem, two widely used aggregation methods have advantages and disadvantages. The synchronous method realizes stable global model updates but causes delays that depend on the smart meter with the longest arrival time. The asynchronous approach virtually eliminates the waiting delay but results in lower model accuracy due to the stochastic gradient of the single end-side model. To overcome this dilemma, we combine the advantages of the two methods and design a two-stage semi-asynchronous method, which includes end-edge synchronous model aggregation and edge-cloud asynchronous model aggregation.
End-edge synchronous aggregation
In our proposed framework shown in Fig. 2, each edge server interacts with a certain cluster of smart meters and aggregates their models to form the complete model. Then, the powerful cloud server interacts with all edge servers to update the final global model. To reduce the aggregation delay for each cluster, we adopt a hardware configuration-based clustering algorithm to designate smart meters with similar training times to the same edge server. As analyzed in (3), the overall training time T is related to two variables of smart meters, namely, Psm and R. Therefore, smart meters can be grouped into M clusters based on their feature vectors , where the number of smart meters designated to the i-th edge server is denoted as Ki. Here, we recommend utilizing the balanced k-means algorithm to ensure that the numbers of smart meters in each cluster are similar and to avoid overloading and no-loading of the edge server in any cluster. After all intra-cluster smart meters have completed model training, the edge server aggregates these models synchronously as follows:
| 13 |
where denotes the aggregated model at the i-th edge server in round t + 1 and denotes the model of the k-th smart meter in round t + 1.
Edge-cloud asynchronous aggregation
Although clustering-based end-edge synchronous aggregation significantly reduces the delay in intra-cluster aggregation, the training time still differs between clusters. Therefore, asynchronous aggregation over edge servers is performed on the cloud server to further minimize the delay time. Since the designation of smart meters for each cluster is independent of the data distribution, the aggregated gradient for each cluster can be regarded as an unbiased estimator of the full gradient for all smart meters. Thanks to the robustness of the intra-cluster aggregated model, our method effectively mitigates the problem of accuracy degradation in asynchronous aggregation. As soon as the aggregated model is received from the i-th edge server, the cloud server updates the global model asynchronously as follows:
| 14 |
where wt denotes the aggregated model at the cloud server in round t and is the weight of in the asynchronous update phase.
Convergence analysis
As shown in (10), we update the parameters not based on the gradient of ws. Therefore, we discuss the convergence of two models, ws and wc, respectively. In each round, takes the as input, which is time-varying following the distribution of . Let denote the output distribution of with optimal parameters. We define the squared Euclidean distance between two distributions as . Here three common assumptions are considered for convergence analysis61.
Assumption 1
(Lipschitz continuity): The loss functions of the main model and auxiliary model are L-smooth, i.e.,
for all w1 and w2.
Assumption 2
(Bounded gradient): The expected squared norm of stochastic gradients is upper bounded, i.e.,
for all k = 1,2, …,.
Assumption 3
(Robbins-Monro conditions): The learning rates satisfy
Theorem 2
(Model convergence): If Assumption 1, 2, and 3 holds, the auxiliary model converges as
| 15 |
and the main model converges as
| 16 |
The right-hand side of both (15) and (16) converge to a constant as T grows, so our algorithm is convergent. The proof of Theorem 2 is provided in Supplementary Proofs 2 and 3.
Supplementary information
Source data
Acknowledgements
This work is supported in part by the National Key R&D Program of China (No. 2022YFE0141200, Y.W.), the Research Grants Council of the Hong Kong SAR (No. CRF-YCRG C1002-23Y and HKU 27203723, Y.W.), and the School of Engineering and Applied Science and the Andlinger Center for Energy and the Environment of Princeton University (H.V.P.). We would also like to acknowledge the high-performance computing facilities and smart meter hardware platforms provided by the Energy Digitalization Laboratory at The University of Hong Kong.
Author contributions
Y.L. and Y.W. conceived the idea and designed the framework. Y.L. and D.Q. established the platform and performed the experiments. Y.L., Y.W., and H.V.P. analyzed and discussed the experiential results. All authors contributed to writing and revising the paper.
Peer review
Peer review information
Nature Communications thanks Xiaoyu Xia and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The BDG2 dataset is available at https://github.com/buds-lab/building-data-genome-project-2. The CBTs dataset is available from the ISSDA website https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ by emailing a form request. The above-mentioned datasets have been processed and deposited in our GitHub repository https://github.com/hkuedl/Make-Smart-Meter-Really-Smart. Source data are provided with this paper.
Code availability
The code for the experiments is publicly available on our GitHub repository https://github.com/hkuedl/Make-Smart-Meter-Really-Smart and archived at the Zenodo https://zenodo.org/doi/10.5281/zenodo.1377708062.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Yehui Li, Dalin Qin.
Contributor Information
H. Vincent Poor, Email: poor@princeton.edu.
Yi Wang, Email: yiwang@eee.hku.hk.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53352-9.
References
- 1.Carbon Dioxide Emissions From Electricity. https://world-nuclear.org/information-library/energy-and-the-environment/carbon-dioxide-emissions-from-electricity.aspx (2024).
- 2.CO2 Emissions in 2022. https://iea.blob.core.windows.net/assets/3c8fa115-35c4-4474-b237-1b00424c8844/CO2Emissionsin2022.pdf (2023).
- 3.O’Shaughnessy, E., Shah, M., Parra, D. & Ardani, K. The demand-side resource opportunity for deep grid decarbonization. Joule6, 972–983 (2022). [Google Scholar]
- 4.Avancini, D. B. et al. Energy meters evolution in smart grids: A review. J. Clean. Prod.217, 702–715 (2019). [Google Scholar]
- 5.Mohassel, R. R., Fung, A., Mohammadi, F. & Raahemifar, K. A survey on advanced metering infrastructure. Int. J. Electr. Power Energy Syst.63, 473–484 (2014). [Google Scholar]
- 6.Barai, G. R., Krishnan, S. & Venkatesh, B. Smart metering and functionalities of smart meters in smart grid-a review. In 2015 IEEE Electrical Power and Energy Conference (EPEC), 138–145 (IEEE, 2015).
- 7.Wang, Y., Chen, Q., Hong, T. & Kang, C. Review of smart meter data analytics: Applications, methodologies, and challenges. IEEE Trans. Smart Grid10, 3125–3148 (2019). [Google Scholar]
- 8.Dyson, M. E., Borgeson, S. D., Tabone, M. D. & Callaway, D. S. Using smart meter data to estimate demand response potential, with application to solar energy integration. Energy Policy73, 607–619 (2014). [Google Scholar]
- 9.Cai, Q., Xu, Q., Qing, J., Shi, G. & Liang, Q.-M. Promoting wind and photovoltaics renewable energy integration through demand response: Dynamic pricing mechanism design and economic analysis for smart residential communities. Energy261, 125293 (2022). [Google Scholar]
- 10.Zhou, B. et al. Smart home energy management systems: Concept, configurations, and scheduling strategies. Renew. Sustain. Energy Rev. Reviews61, 30–40 (2016). [Google Scholar]
- 11.Wood Mackenzie. Global smart meter total to double by 2024 with Asia in the lead. https://www.woodmac.com/news/editorial/global-smartmeter-total-h1-2019 (2019).
- 12.Navigant Research. The global penetration rate of smart meters is expected to near 60% by 2028. https://guidehouseinsights.com/news-andviews/the-global-penetration-rate-of-smart-meters-is-expected-to-near-60-by-2028 (2019).
- 13.Sun, H., Hatziargyriou, N., Poor, H. V., Carpanini, L. & Fornié, M. A. S. Smarter Energy: From Smart Metering to the Smart Grid (2016).
- 14.Véliz, C. & Grunewald, P. Protecting data privacy is key to a smart energy future. Nat. Energy3, 702–704 (2018). [Google Scholar]
- 15.Balta-Ozkan, N., Boteler, B. & Amerighi, O. European smart home market development: Public views on technical and economic aspects across the United Kingdom, Germany and Italy. Energy Res. Social Sci.3, 65–77 (2014). [Google Scholar]
- 16.Hmielowski, J. D., Boyd, A. D., Harvey, G. & Joo, J. The social dimensions of smart meters in the united states: Demographics, privacy, and technology readiness. Energy Res. Social Sci.55, 189–197 (2019). [Google Scholar]
- 17.Morstyn, T., Farrell, N., Darby, S. J. & McCulloch, M. D. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy3, 94–101 (2018). [Google Scholar]
- 18.Pena-Bello, A. et al. Integration of prosumer peer-to-peer trading decisions into energy community modelling. Nat. Energy7, 74–82 (2022). [Google Scholar]
- 19.Langevin, J. et al. Us building energy efficiency and flexibility as an electric grid resource. Joule5, 2102–2128 (2021). [Google Scholar]
- 20.Wang, N. Transactive control for connected homes and neighbourhoods. Nat. Energy3, 907–909 (2018). [Google Scholar]
- 21.Schuller, A., Flath, C. M. & Gottwalt, S. Quantifying load flexibility of electric vehicles for renewable energy integration. Appl. Energy151, 335–344 (2015). [Google Scholar]
- 22.Wolinetz, M., Axsen, J., Peters, J. & Crawford, C. Simulating the value of electric-vehicle–grid integration using a behaviourally realistic model. Nat. Energy3, 132–139 (2018). [Google Scholar]
- 23.Almalaq, A. & Edwards, G. A review of deep learning methods applied on load forecasting. In 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), 511–516 (IEEE, 2017).
- 24.Kuster, C., Rezgui, Y. & Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc.35, 257–270 (2017). [Google Scholar]
- 25.Hong, T. & Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast.32, 914–938 (2016). [Google Scholar]
- 26.Asghar, M. R., Dán, G., Miorandi, D. & Chlamtac, I. Smart meter data privacy: A survey. IEEE Commun. Surv. Tutor.19, 2820–2835 (2017). [Google Scholar]
- 27.Zhou, Z. et al. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proc. IEEE107, 1738–1762 (2019). [Google Scholar]
- 28.Gooi, H. B., Wang, T. & Tang, Y. Edge intelligence for smart grid: A survey on application potentials. CSEE J. Power Energy Syst.9, 1623–1640 (2023). [Google Scholar]
- 29.Deng, S. et al. Edge intelligence: The confluence of edge computing and artificial intelligence. IEEE Internet of Things J.7, 7457–7469 (2020). [Google Scholar]
- 30.Lin, L., Liao, X., Jin, H. & Li, P. Computation offloading toward edge computing. Proc. IEEE107, 1584–1607 (2019). [Google Scholar]
- 31.Min, M. et al. Learning-based computation offloading for iot devices with energy harvesting. IEEE Trans. Veh. Technol.68, 1930–1941 (2019). [Google Scholar]
- 32.Vepakomma, P., Gupta, O., Swedish, T. & Raskar, R. Split learning for health: Distributed deep learning without sharing raw patient data. Preprint at 10.48550/arXiv.1812.00564 (2018).
- 33.Thapa, C., Arachchige, P. C. M., Camtepe, S. & Sun, L. Splitfed: When federated learning meets split learning. In Proceedings of the AAAI Conference on Artificial Intelligence, 8, 8485–8493 (2022).
- 34.McMahan, B., Moore, E., Ramage, D., Hampson, S. & Arcas, B. A. Communication-efficient learning of deep networks from decentralized data. In Artificial Intelligence and Statistics, 1273–1282 (PMLR, 2017).
- 35.Yang, Q., Liu, Y., Chen, T. & Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol.10, 1–19 (2019). [Google Scholar]
- 36.Kalra, S., Wen, J., Cresswell, J. C., Volkovs, M. & Tizhoosh, H. Decentralized federated learning through proxy model sharing. Nat. Commun.14, 2899 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pati, S. et al. Federated learning enables big data for rare cancer boundary detection. Nat. Commun.13, 7346 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bercea, C. I., Wiestler, B., Rueckert, D. & Albarqouni, S. Federated disentangled representation learning for unsupervised brain anomaly detection. Nat. Mach. Intell.4, 685–695 (2022). [Google Scholar]
- 39.Chatterjee, P., Das, D. & Rawat, D. B. Federated learning empowered recommendation model for financial consumer services. IEEE Trans. Consum. Electron.70, 2508–2516 (2024). [Google Scholar]
- 40.Byrd, D. & Polychroniadou, A. Differentially private secure multi-party computation for federated learning in financial applications. In Proceedings of the First ACM International Conference on AI in Finance, 1–9 (2020).
- 41.Wang, R. et al. Adaptive horizontal federated learning-based demand response baseline load estimation. IEEE Trans. Smart Grid15, 1659–1669 (2024). [Google Scholar]
- 42.Liu, H. & Wu, W. Federated reinforcement learning for decentralized voltage control in distribution networks. IEEE Trans. Smart Grid13, 3840–3843 (2022). [Google Scholar]
- 43.Wang, X., Xie, H., Tang, L., Chen, C. & Bie, Z. Decentralized privacy-preserving electricity theft detection for distribution system operators. IEEE Trans. Smart Grid15, 2179–2190 (2023).
- 44.Chen, M., Shlezinger, N., Poor, H. V., Eldar, Y. C. & Cui, S. Communication-efficient federated learning. Proc. Natl. Acad. Sci.118, e2024789118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cao, X. et al. Communication-efficient distributed learning: An overview. IEEE J. Sel. Areas Commun.41, 851–873 (2023). [Google Scholar]
- 46.Chen, Y., Ning, Y., Slawski, M. & Rangwala, H. Asynchronous online federated learning for edge devices with non-iid data. In 2020 IEEE International Conference on Big Data (Big Data), 15–24 (IEEE, 2020).
- 47.Xie, C., Koyejo, S. & Gupta, I. Asynchronous federated optimization. Preprint at 10.48550/arXiv.1903.03934 (2019).
- 48.Fekri, M. N., Grolinger, K. & Mir, S. Distributed load forecasting using smart meter data: Federated learning with recurrent neural networks. Int. J.Electr. Power Energy Syst.137, 107669 (2022). [Google Scholar]
- 49.Fekri, M. N., Grolinger, K. & Mir, S. Asynchronous adaptive federated learning for distributed load forecasting with smart meter data. Int. J. Electr. Power Energy Syst.153, 109285 (2023). [Google Scholar]
- 50.Hudson, N. et al. A framework for edge intelligent smart distribution grids via federated learning. In 2021 International Conference on Computer Communications and Networks (ICCCN), 1–9 (IEEE, 2021).
- 51.Wang, Y., Gao, N. & Hug, G. Personalized federated learning for individual consumer load forecasting. CSEE J. Power Energy Syst.9, 326–330 (2022). [Google Scholar]
- 52.Taïk, A. & Cherkaoui, S. Electrical load forecasting using edge computing and federated learning. In ICC 2020-2020 IEEE International Conference on Communications (ICC), 1–6 (IEEE, 2020).
- 53.Electricity metering data exchange - The DLMS/COSEM suite - Part 1-0: Smart metering standardisation framework. Standard IEC 62056, International Electrotechnical Commission (IEC). https://webstore.iec.ch/publication/6397 (2014).
- 54.Protocol Specification for ANSI Type 2 Optical Port. Standard ANSI C12.18, American National Standards Institute (ANSI). https://webstore.ansi.org/standards/nema/ansic12182006r2016 (2006).
- 55.Miller, C. et al. The building data genome project 2, energy meter data from the ASHRAE Great Energy Predictor III competition. Sci. Data7, 368 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Commission for Energy Regulation (CER). CER smart metering project - electricity customer behaviour trial. https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ (2012).
- 57.Li, X., Huang, K., Yang, W., Wang, S. & Zhang, Z. On the convergence of fedavg on non-iid data. International Conference on Learning Representations10.48550/arXiv.1907.02189 (2019).
- 58.Li, T. et al. Federated optimization in heterogeneous networks. In Proceedings of Machine Learning and Systems, 429–450 (2020).
- 59.Sohoni, N. S., Aberger, C. R., Leszczynski, M., Zhang, J. & Ré, C. Low-memory neural network training: A technical report. Preprint at 10.48550/arXiv.1904.10631 (2019).
- 60.Gou, J., Yu, B., Maybank, S. J. & Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis.129, 1789–1819 (2021). [Google Scholar]
- 61.Belilovsky, E., Eickenberg, M. & Oyallon, E. Decoupled greedy learning of cnns. In International Conference on Machine Learning, 736–745 (PMLR, 2020).
- 62.Li, Y., Qin, D., Poor, H. & Wang, Y. Introducing edge intelligence to smart meters via federated split learning. 10.5281/zenodo.13777080 (2024). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The BDG2 dataset is available at https://github.com/buds-lab/building-data-genome-project-2. The CBTs dataset is available from the ISSDA website https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ by emailing a form request. The above-mentioned datasets have been processed and deposited in our GitHub repository https://github.com/hkuedl/Make-Smart-Meter-Really-Smart. Source data are provided with this paper.
The code for the experiments is publicly available on our GitHub repository https://github.com/hkuedl/Make-Smart-Meter-Really-Smart and archived at the Zenodo https://zenodo.org/doi/10.5281/zenodo.1377708062.