HIV dynamics with multiple infections of target cells

Abstract

The high incidence of multiple infections of cells by HIV sets the stage for rapid HIV evolution by means of recombination. Yet how HIV dynamics proceeds with multiple infections remains poorly understood. Here, we present a mathematical model that describes the dynamics of viral, target cell, and multiply infected cell subpopulations during HIV infection. Model calculations reproduce several experimental observations and provide key insights into the influence of multiple infections on HIV dynamics. We find that the experimentally observed scaling law, that the number of cells coinfected with two distinctly labeled viruses is proportional to the square of the total number of infected cells, can be generalized so that the number of triply infected cells is proportional to the cube of the number of infected cells, etc. Despite the expectation from Poisson statistics, we find that this scaling relationship only holds under certain conditions, which we predict. We also find that multiple infections do not influence viral dynamics when the rate of viral production from infected cells is independent of the number of times the cells are infected, a regime expected when viral production is limited by cellular rather than viral factors. This result may explain why extant models, which ignore multiple infections, successfully describe viral dynamics in HIV patients. Inhibiting CD4 down-modulation increases the average number of infections per cell. Consequently, altering CD4 down-modulation may allow for an experimental determination of whether viral or cellular factors limit viral production.

In a significant shift from the prevalent paradigm of HIV infection that individual target cells are generally infected with single HIV virions, recent studies have demonstrated that multiple infections of cells occur far more frequently than single infections both in vivo (1, 2) and in vitro (2–4). For instance, CD4⁺ cells from the spleens of two HIV-infected individuals were found to harbor up to eight proviruses with three or four proviruses per cell on average (1). Multiple infections of cells with virions containing diverse genomes is a prerequisite for the evolution of recombinant forms of HIV, which may be resistant to multidrug therapy or that may escape specific host immune responses (5–7). Of great interest, therefore, is to establish the mechanisms that underlie the high incidence of multiple infections of cells by HIV and to understand their implications for HIV evolution and therapy.

Following the observations by Jung et al. (1), recent studies have examined quantitatively how multiple infections might be orchestrated during HIV infection. Dang et al. (3) found that cells are doubly infected in vitro at rates significantly higher than expected from random infection events. At the same time, HIV infection follows single-hit kinetics. Dang et al. (3) argue that cell subpopulations with variable susceptibilities to infection present a scenario where nonrandom frequencies of double infection may arise despite infection following single-hit kinetics. Chen et al. (4) suggest that the HIV-1 entry pathway contributes to the frequency of multiple infections but is not solely responsible for nonrandom infections. Levy et al. (2) investigated the kinetics of multiple infections and found that the fraction of cells that are coinfected with two distinctly labeled viruses scales with the square of the total fraction of cells infected. Remarkably, this scaling is independent of the relative viral and cell densities, the time after the onset of infection, and whether the experiment is conducted in vitro or in SCID-hu mice.

Standard models of HIV dynamics implicitly assume that target cells are infected by single HIV virions (8, 9). These models successfully describe viral load evolution in HIV infected individuals and provide insights into HIV replication kinetics in vivo and the effects of therapy (10–14). With growing evidence of the predominance of multiple infections, however, the success of standard models in describing HIV dynamics is intriguing. Currently, no models describe HIV dynamics with multiple infections.

In a recent study aimed at understanding the kinetics of HIV recombination, Bretscher et al. (15) considered a framework where cells are either singly or doubly infected by HIV. This framework provides useful insights into HIV recombination, challenging the widespread notion that recombination facilitates the emergence of drug resistance. A more recent study presents evidence for positive epistasis in HIV-1, further challenging the fitness advantage conferred by recombination (16). The underlying description of multiple infections, however, remains to be tested. More recently, we have developed a probabilistic description of multiple infections and CD4 down-modulation (17) that accounted for the distribution of proviral copy number in infected splenocytes measured by Jung et al. (1). We found that in the chronically infected steady state, two scenarios are able to quantitatively predict the observed distribution, one where multiple viral genomes are acquired by target cells in a series of sequential infectious contacts with cell-free virions and infected cells, each contact resulting in the transmission of one genome, and the other where multiple genomes are acquired in single infectious contacts of target cells with infected cells. Whether these scenarios also predict the kinetics of multiple infections remains unknown.

In this work, we present a model of HIV dynamics with a detailed description of multiple infections. The model captures several experimental observations and provides key insights into the mechanisms that underlie multiple infections of cells by HIV.

HIV Dynamics with Multiple Infections

We consider experiments where HIV virions are added to CD4⁺ target cells in vitro and the time evolution of the number of multiply infected cells is followed. Let T be the number of CD4⁺ target cells, V the number of virions, and 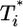the number of cells (multiply) infected i times at time t after the onset of infection. Typically, in in vitro experiments, virion numbers are several orders of magnitude larger than target cell numbers. Under these circumstances, infections by cell-free virions should dominate; cell–cell transmission may be neglected (18). Building on standard viral dynamics models (8, 9), we write the time evolution of virus and cell numbers in vitro as follows:

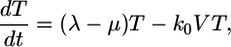[1]

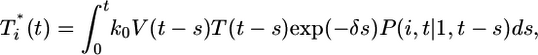[2]

[3]

The initial conditions for these equations are , and V(0) = V₀, where T₀ and V₀ are the cell and virion numbers, respectively, at the onset of infection.

In Eq. 1, λ and μ are the first-order birth and death rates of target cells in vitro, and k₀ is the second-order rate constant for the infection of uninfected cells, i.e., with normal CD4 expression levels, yielding the rate k₀VT of the formation of infected cells. Eq. 1 has been shown to capture target cell dynamics in vitro (19). The difference of this description from in vivo dynamics lies in the birth process, which in in vivo settings includes a thymic source (8, 9, 20) and possible density-dependent proliferation (21) as opposed to the first-order birth term in Eq. 1.

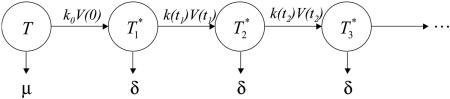
Eq. 2 describes the evolution of multiply infected cell subpopulations. In an infinitesimal interval of time ds near time t - s ≥ 0, where t = 0 marks the onset of the experiment, the number of uninfected cells that become singly infected is k₀V(t - s)T(t - s)ds. We define the quantity P(i, t|1, t - s) as the probability that a cell infected singly at a time t - s is multiply infected with i genomes at time t, provided it survives the intervening interval of duration s. The survival probability is exp(-δs), where δ is the death rate of infected cells. In Fig. 1, we present a schematic of how a cell infected singly at time t = 0 is multiply infected at later times. In general, δ will depend on the multiplicity of infection, i. Accumulation of unintegrated DNA, seen by the host cell as DNA damage, and the expression of toxic viral gene products induce apoptotic and/or cytotoxic effects, which are expected to increase δ with i (22–24). In contrast, greater down-modulation of CD4 and MHC class I molecules may promote immune evasion and decrease δ at higher i (25–27). How these competing effects determine the dependence of δ on i remains unknown. Here, as an approximation, we assume that δ is independent of i. The integrand in Eq. 2 thus quantifies the fraction of cells first infected at t - s that survive and possess i genomes at time t. Integration from time 0 to t gives the total subpopulation of cells, , that are infected with i genomes at time t.

Fig. 1.

Schematic of a target cell undergoing multiple infections by HIV. An uninfected cell, T, is infected by a virion at time t = 0 and forms a singly infected cell, , which in turn is infected at times t₁, t₂, etc. to form doubly infected cells, 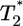, triply infected cells, 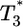, etc. The infection rate of uninfected cells is k₀V(0), where k₀ is the second-order infection rate constant in the absence of CD4 down-modulation and V(t) is the viral load at time t. The rates for subsequent infections are k(t_i)V(t_i), where k(t_i) = k₀exp(-t_i/t_d), with t_d the characteristic time for CD4 down-modulation. Infected cells die at rate δ, whereas uninfected cells die at rate μ. (Not shown is the formation of new target cells at rate λ and the production and clearance of free virions according to Eq. 3.)

Note that in Eq. 2, we ignore the proliferation of infected cells because the death rate of infected cells is nearly twice their proliferation rate (19). Infected cell proliferation is easily incorporated, however, by replacing δ in Eq. 2 with the net death rate, i.e., the difference of the infected cell death and proliferation rates.

Evolution of the free virion population is described by Eq. 3. Cells infected with i genomes release N_i progeny virions during the average infected cell lifetime, 1/δ. Free virions are cleared with a first-order rate constant, c, which is assumed to include natural decay and loss through infection. Letting N_i depend on i constitutes a generalized description of viral production. Here, because of the lack of precise information, we examine the consequences of assuming that N_i is independent of i.

To evaluate the quantity P(i, t|1, t - s), consider a cell that is first infected at time t - s. The probability that the cell is infected again during an infinitesimal interval of time Δτ near τ, where t - s ≤ τ ≤ t, is 1 - exp(-kV(τ)Δτ) ≈ kV(τ)Δτ, where

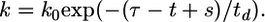[4]

Eq. 4 quantifies the reduced susceptibility of the cell to infection at time τ due to CD4 down-modulation (22, 28, 29), which appears to proceed exponentially with a characteristic timescale, t_d, after the first infection of the cell (17,29) (see Supporting Text and Fig. 6, which are published as supporting information on the PNAS web site). Accordingly, k = k₀ at τ = t - s, and k → 0 as τ → ∞. The probability that the cell has i genomes at time τ + Δτ is then given by P(i, τ + Δτ|1, t - s) = P(i - 1, τ|1, t - s)kV(τ)Δτ + P(i, τ|1, t - s)(1 - kV(τ)Δτ), provided the cell survives the interval Δτ. The first term on the right-hand side of this equation is the probability that the cell has i - 1 genomes at time τ and is infected in the interval Δτ. The second term is the probability that the cell has i genomes at time τ and is not infected in the interval Δτ. The interval Δτ is chosen to be arbitrarily small so that at most one infection can occur during the interval. Rearranging this equation, dividing by Δτ, and letting Δτ → 0, we get

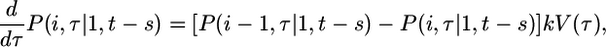[5]

where we define P(0, τ|1, t - s) = 0. That a cell first infected at t - s has exactly one genome at t - s gives the initial conditions P(1, t - s|1, t - s) = 1 and P(i > 1, t - s|1, t - s) = 0.

Eqs. 1–5 present a model of HIV dynamics with multiple infections. The equations are strongly coupled, and below we develop a technique that simplifies their solution.

Consider the total population of infected cells,

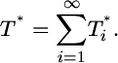Summing Eq. 2 over i, and recognizing that

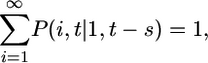we get

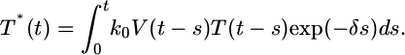[6]

Eq. 6 can be shown to be identical to

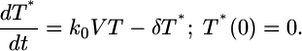[7]

Simultaneously, Eq. 3 can be simplified by writing

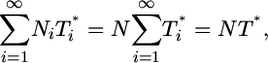where N is the average viral burst size for the total infected cell population. Note that N is a constant in the limit where the burst size is independent of the multiplicity of infection, i.e., N_i = N. When the burst size depends on i, N is expected to vary with time. Here, as an approximation, we assume that N remains constant. Eq. 3 then becomes

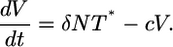[8]

With this approximation, Eqs. 1, 7, and 8 can be solved independently for V, T, and T^*. Knowledge of V then allows the straightforward solution of Eqs. 2 and 5 for .

Model Calculations

We use the following representative parameter values for our calculations, following in vitro estimates (19, 30): The birth and death rate of target cells in vitro, λ = 0.624 day^-1 and μ = 0.018 day^-1; the death rate of infected cells, δ = 1.44 day^-1; the viral burst size, N = 1000; and the clearance rate of free virions, c = 0.35 day^-1. The infection rate constant k₀ and the timescale of CD4 down-modulation, t_d, are not well known, and we vary these parameters to examine their influence on the dynamics of multiple infections. Typical target cell numbers used in in vitro experiments are T₀ = 10⁶, which we fix in our calculations. We vary initial virion numbers over the experimental range, V₀ ≈ 10⁸ to 10¹⁰ (2). (Thus, in a 1- to 10-ml sample volume, these values yield cell and virion number densities of 10⁵ to 10⁶ ml^-1 and 10⁷ to 10⁹ ml^-1, respectively.)

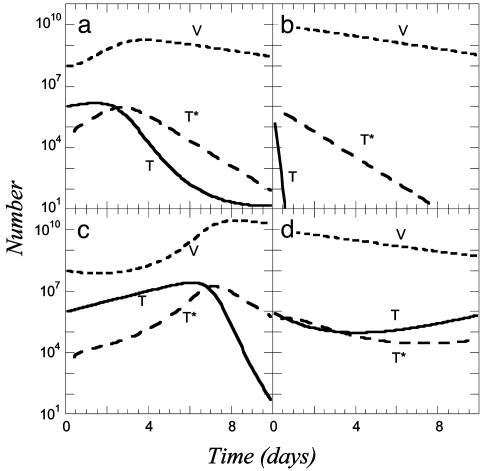
In Fig. 2a, we present the time evolution of T, V, and T^* by solving Eqs. 1, 7, and 8 for k₀ = 2 × 10^-9 day^-1 and V₀ = 10⁸. Note that the solution is independent of t_d, the characteristic time for CD4 down-modulation. Changes in t_d alter the distribution of infected cells into subpopulations of multiply infected cells but leave the size of the infected cell pool unaltered. We find in Fig. 2 that T, V, and T^* all evolve in two dominant phases, an initial rise and a subsequent fall. To understand these phases, we note that in the absence of infection (V = 0), Eq. 1 predicts that T will monotonically increase at an exponential rate determined by the difference in the birth and death rates, λ - μ. The initial rise in T corresponds to the net proliferation of target cells. The presence of infectious virus (V > 0) causes a loss in T and a corresponding increase in T^* at rate k₀VT. The proliferation of T initially outweighs this loss by infection. Eventually, virus production from T^* increases V sufficiently that the loss of target cells by infection outweighs target cell proliferation. A drop in T therefore results, which in Fig. 2a begins at t ≈ 2 days. By t ≈ 10 days, the population of target cells nearly vanishes. This drop in T decreases the rate of formation of T^*. Accordingly, a peak in T^* results at t ≈ 3 days, after which T^* decays asymptotically exponentially at the death rate δ (Fig. 2a). The drop in T^* diminishes virus production causing V to decay eventually at the clearance rate, c.

Fig. 2.

Time evolution of virion (V), target cell (T), and total infected cell (T^*) numbers obtained by solving Eqs. 1, 7, and 8 for k₀ = 2 × 10^-9 day^-1 and V₀ = 10⁸ (a); k₀ = 2 × 10^-9 day^-1 and V₀ = 10¹⁰ (b); k₀ = 2 × 10^-10 day^-1 and V₀ = 10⁸ (c); and k₀ = 2 × 10^-10 day^-1 and V₀ = 10¹⁰ (d). The values of the other parameters used are as follows: λ = 0.624 day^-1, μ = 0.018 day^-1, δ = 1.44 day^-1, N = 1,000, c = 0.35 day^-1, and T₀ = 10⁶.

To examine how this dynamics varies with V₀, we let V₀ = 10¹⁰. Increasing V₀ by two orders of magnitude drastically increases the loss rate of target cells by infection (Fig. 2b). In t ≈ 0.5 day, the target cell pool is fully depleted and T^* attains its asymptotic decline at the exponential rate δ. In Fig. 2 c and d, the same calculations as in Fig. 2 a and b are shown but for a lower value of k₀ = 2 × 10^-10 day^-1. The dynamics is now considerably slower than in Fig. 2 a and b, and we find that T^* attains a maximum at t ≈ 6 days and 1 day, respectively (Fig. 2 c and d).

In all cases, T^* exhibits two-phase dynamics with an initial rise (note that T^* = 0 at t = 0) and subsequent fall, with possible minor variations. [The target cell pool in Fig. 2d does not vanish but eventually rises again following predator–prey dynamics (9), so T^* also has a late rise.] This overall two-phase dynamics is similar to the infected cell dynamics observed in in vitro experiments (2). With the overall dynamics thus qualitatively mimicking experiments, we employ this description to investigate the dynamics of multiple infections.

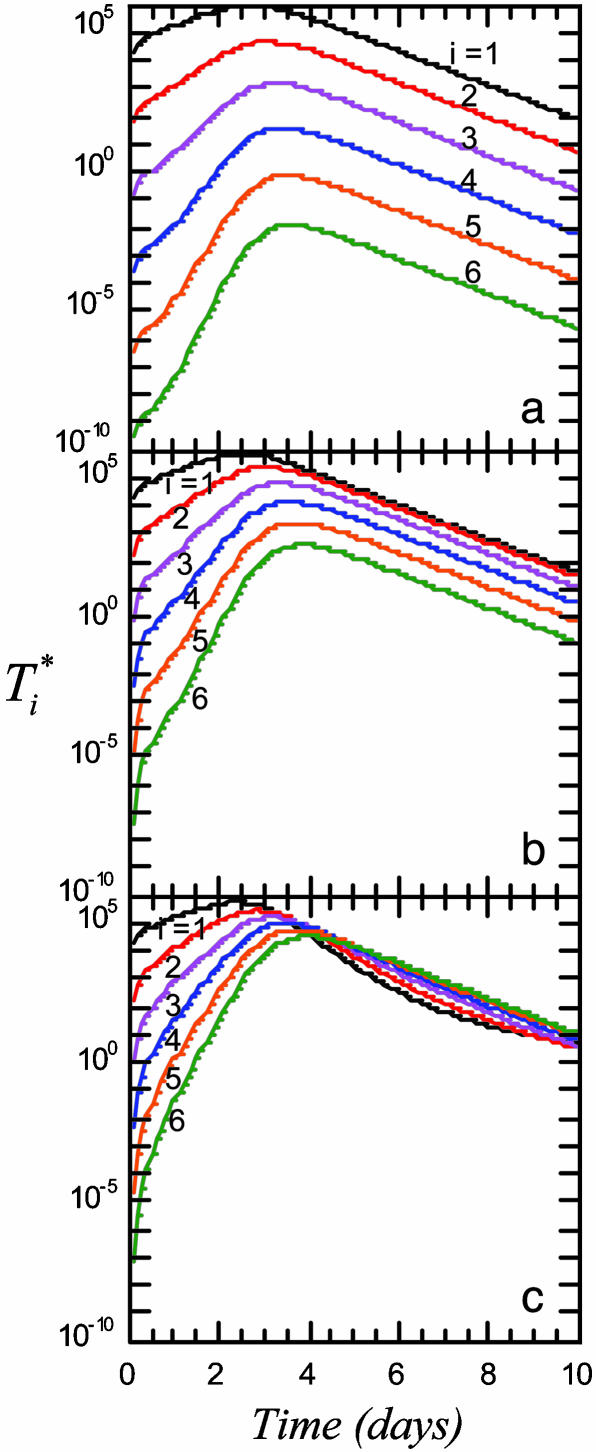
We present in Fig. 3 the evolution of 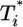by solving Eqs. 2 and 5, 6, 7, 8 for characteristic CD4 down-modulation times, t_d = 0.028, 0.28, and 2.8 days, respectively, with k₀ = 2 × 10^-9 day^-1 and V₀ = 10⁸ (as in Fig. 2a). We choose this range for t_d as Nef-induced down-modulation appears to occur rapidly with a timescale t_d ≈ 0.028 day, but overall down-modulation may be several orders of magnitude slower (see Supporting Text). In all cases, 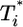also display two-phase dynamics with an initial increase and a subsequent fall. Changes in t_d, however, alter the distribution of 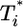significantly. For t_d = 0.028 day, we find that 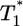is nearly two orders of magnitude larger than 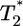, which in turn is much larger than 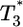, and so on, at all times. For t_d = 0.28 day, the same trend, i.e., 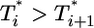, is maintained, but the difference between 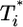and 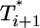is much smaller than for t_d = 0.028 day. Indeed, after the maximum at t ≈ 3 days, 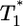is only marginally larger than 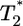. For t_d = 2.8 days, not only is the difference between 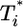and 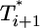still smaller before the maximum at t ≈ 3 days, but the trend is reversed following the maximum and 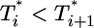up to t ≈ 9 days.

Fig. 3.

Time evolution of multiply infected cell subpopulations (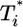) obtained by solving Eqs. 2 and 5 for parameter values used in Fig. 2a and t_d = 0.028 day (a), 0.28 day (b), and 2.8 days (c).

These calculations describe how subpopulations of multiply infected cells evolve during HIV infection. In particular, they demonstrate that the fraction of multiply infected cells consistently increases with the characteristic time for CD4 down-modulation, t_d. When CD4 down-modulation is rapid, cells are largely singly infected. As t_d increases, cells down-modulate CD4 receptors at slower rates. Infected cells remain susceptible to further infections for longer periods and therefore undergo more infections on average.

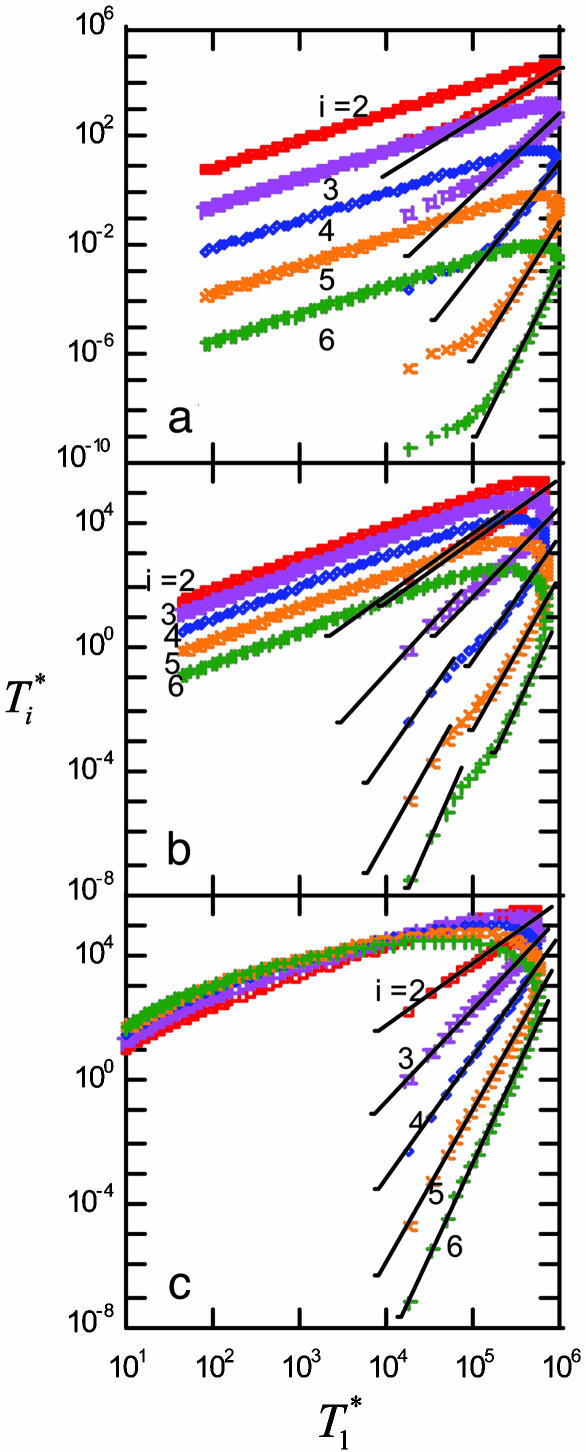
We next examine whether the above dynamics captures the scaling law observed in experiments. In Fig. 4, we present the data in Fig. 3 as parametric plots of 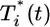vs. 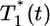. Recall that Levy et al. (2) found that coinfected cells, presumably mostly 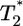, are proportional to 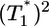. (Note that 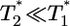in their experiments except near peak infection so that 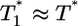.) Here, we reproduce this scaling but not under all conditions. Fig. 4a (t_d = 0.028 day) shows that 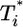scales as 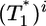for all i (i = 2,...,5 shown) (as indicated by the black straight line power law markers) during the first phase of 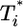evolution when 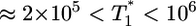. The growth rate of 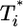is smaller than this power law when 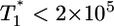. When t_d = 0.28 day, the power law scaling, 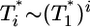, also is observed for small values of 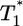, i.e., 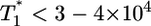, and again when 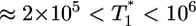(Fig. 4b). However, for intermediate values of 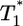, i.e., 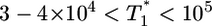, growth rates smaller than the power law scaling are observed. For t_d = 2.8 days, the power law scaling is observed for all values of 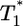in the first phase (Fig. 4c). In the second phase of 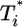evolution, i.e., following its maximum, 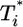scales linearly with 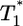. (An exception occurs in Fig. 4c, where a slight curvature is introduced because of the higher susceptibility of infected cells as t_d = 2.8 days.) This linear scaling arises because the uninfected cell pool is nearly completely depleted and all infected cells die at the rate δ.

Fig. 4.

Parametric plots of 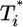vs. 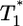with the data in Fig. 3 (symbols). Traversing counter-clockwise on any curve, as 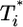rises and falls, marks increasing time. The solid black lines are power law markers, y ∼ xⁱ, to guide the eye.

These calculations thus reproduce the scaling law observed by Levy et al. (2) but also suggest that the scaling is not universal. As shown in Supporting Text, power law scaling emerges from our model under the following three circumstances: (i) at small times after the onset of infection, t < min(t_s, t_d, 1/δ), where t_s is the timescale over which V and T vary, t_d is the timescale for CD4 down-modulation, and 1/δ is the average lifetime of infected cells; (ii) at large times, t > t_eq, when T^* is sufficiently large that V is in pseudo-steady state with T^*, i.e., V ≈ NδT^*/c, and when CD4 down-modulation is rapid, t >> t_d; and (iii) at large times, t > t_eq, and when CD4 down-modulation is slow, t << t_d. These cases explain the various regimes observed in Fig. 4 (see Supporting Text). To test the robustness of our finding, we consider the case when k₀ = 2 × 10^-10 day^-1, t_d = 0.28 day, and V₀ = 10⁸ or 10¹⁰ (Fig. 5). As illustrated by the black power law marker lines, we again find power law scaling regimes that are well described by the three cases above (see Supporting Text).

Fig. 5.

Predicted change in multiply infected cell populations with time after infection and corresponding time-parameterized curves showing how the level of multiply infected cells, 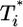, varies with the level of singly infected cells, 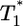. (a and b) Time evolution of multiply infected cell subpopulations (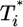) (a) and the corresponding parametric plots of 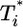vs. 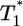for the parameter values used in Fig. 2c and t_d = 0.28 day (b). (c and d) Similar plots for the parameter values used in Fig. 2d and t_d = 0.28 day.

Discussion

Standard HIV dynamics models implicitly assume that target cells are infected with single HIV virions. However, growing evidence both in vivo and in vitro points to the predominance of multiple infections of cells in HIV infection. No models exist that describe HIV dynamics with multiple infections. Here, we have presented a model of HIV dynamics that incorporates a detailed description of multiple infections and keeps track of events since the time of first infection of cells. Such a description is essential because after their first infection, cells down-modulate their surface CD4 molecules, rendering further infections difficult. In other words, cells retain “memory” of their first infection. Because cells are infected asynchronously, describing multiple infections requires keeping track of when each cell is first infected. This goal is accomplished by using an integral equation formalism (Eq. 2). Evolution of uninfected cell and viral populations is described as in standard virus dynamics models. The resultant integro-differential equation model predicts the dynamics of virus, uninfected cell, and all multiply infected cell populations during HIV infection.

We have calculated the evolution of subpopulations of multiply infected cells under conditions that are representative of recent in vitro experiments. In particular, we have considered the experiments by Levy et al. (2), who observed that the fraction of coinfected cells scales as the total number of infected cells squared. Our model predicts this scaling under the assumption that most coinfected cells are doubly infected and shows that cells with higher multiplicities of infection also exhibit a power law scaling with an exponent equal to the multiplicity of infection. [The experiments of Levy et al. (2) are unable to distinguish cells with higher multiplicities of infection.] More importantly, our calculations show that power law scaling is not universal but depends on several parameters, namely the infectivity of the virus population, relative virion and cell numbers, the CD4 down-modulation timescale, and for a given set of parameter values on the time after the onset of infection. Indeed, parameter values exist that yield the power law scaling over entire periods of observation. The values of these parameters corresponding to the experiments of Levy et al. (2) remain unknown and thus preclude a direct comparison with their data.

Several other limitations arise when making a quantitative comparison of our calculations with the experiments of Levy et al. (2). First, not all cells in their cultures are susceptible to infection by HIV. Thus, for the highest virion numbers used, the maximum fraction of cells infected was ≈20% (2). In contrast, we assume in our model that all cells are susceptible and close to 100% of the cells are infected for high virion numbers. Further, resting cells are activated in their experiments by regular addition of the cytokine IL-2. More sophisticated descriptions are necessary to account for resting and activated cells and their effects on virus dynamics. Second, Levy et al. (2) detected infected cells by fluorescence measurements. Cells are infected with equal populations of yellow and cyan fluorescent viruses, which presumably have identical infection and replication characteristics. Cells that are positive for both yellow and cyan are counted as coinfected. Such a count places cells infected with two cyan or two yellow viruses in the singly infected subpopulation. Thus, the technique underestimates the frequency of coinfection. Probabilistically, the number of cells infected with two yellow viruses will be half the number of cells infected with a yellow and a cyan virus. Thus, the measured number of coinfected cells is only half the actual number of coinfected cells, assuming that the number of cells infected with more than two viruses is small. However, because this correction is a numerical factor, the power law scaling still holds. Quantitative comparisons of our calculations with the experiments of Dang et al. (3) and Chen et al. (4), who determine odds ratios characterizing multiple infections, are also not possible, because they, too, detected coinfected cells by infecting cells with two kinds of viruses and counting cells positive for both, which excludes cells that are doubly infected with the same kind of virus and errs by a factor of 2.

Despite these limitations, the qualitative agreement obtained between our calculations and the measurements of Levy et al. (2) is remarkable. The evolution of multiply infected cell populations in vitro follows two-phase dynamics, with an initial rise and a subsequent fall. The duration of the first phase decreases upon increasing the number of virions used to infect cells. The fraction of infected cells that are coinfected increases from <1% at the onset of infection to up to 40% (to within a factor of 2; see above) at peak infection. All these observations are reproduced by our model calculations in addition to the power law scaling, indicating that our model captures much of the underlying physics governing the dynamics of multiple infections of cells by HIV.

In the in vivo measurements of Jung et al. (1), the average multiplicity of infection was found to be ≈3–4. In the present calculations and in the observations of Levy et al. (2), the number of multiply infected cells is generally smaller than the number of singly infected cells. Two possibilities could explain this discrepancy. First, the virion numbers considered in the latter studies may be lower than those found in vivo in lymphoid tissue. Second, infection may proceed in vivo not only by means of virus–cell interactions but also by means of cell–cell transmission, where cell–cell contact may result in the simultaneous transmission of multiple viral genomes (4). In the experiments of Levy et al. (2) the number of virions used was up to four orders of magnitude higher than the number of cells, which suggests that virion–cell infection may be the major mode of infection. Also, our earlier analysis of the Jung et al. (1) experiments showed that a model that includes cell–cell transmission captures the observations of Jung et al. better than a model that only considers infection by free virions (17).

Interestingly, Levy et al. (2) also conducted in vivo experiments with SCID-hu mice, where they found that the power law scaling remains valid. Thus, cell–cell transmission appears to affect multiple infections quantitatively but not qualitatively. Indeed, we show in our analysis (see Supporting Text) that the Poisson process of infection, which captures the observations of Jung et al. (1), also yields the power law scaling according to our model when virion numbers are proportional to infected cell numbers (pseudo-steady state) and CD4 down-modulation is rapid compared with changes in virion numbers. The proportionality between virion and infected cell numbers suggests that the scaling law predicted by our model might extend to the case where infection also occurs by cell–cell transmission. Extension of our model to incorporate cell–cell transmission is beyond the scope of the present work.

Our model also suggests why standard viral dynamics models, which ignore multiple infections, are able to describe viral load evolution in HIV-infected individuals. Remarkably, when the viral burst size, which is the number of progeny virions released by an infected cell during its lifetime, is independent of the multiplicity of infection, virus and cell dynamics in our model are decoupled from the dynamics of multiple infections. The evolution of virus, uninfected cell, and total infected cell numbers (Eqs. 1, 7, and 8) is then identical to that predicted by standard viral dynamics models (8, 9, 19). This similarity arises because by producing the same number of progeny virions, multiply infected cells contribute no more to the virion pool than singly infected cells. Thus, replacing all multiply infected cells with singly infected cells will not alter viral dynamics, which is in essence what standard viral dynamics models do and therefore successfully capture viral load evolution.

Whether the burst size is independent of the multiplicity of infection is unknown. However, if it is, it implies that virus production is limited by cellular rather than viral trait(s). All cellular and viral traits that control virus production have not been identified. Our model suggests a way of determining whether cellular or viral traits limit virus production. The CD4 down-modulation timescale, t_d, which determines the distribution of the infected cell population into subpopulations of multiply infected cells, is governed by three viral genes, nef, env, and vpu (28). If by altering the expression of one or more of these genes t_d is altered, the average multiplicity of infection will change. If the burst size is independent of the multiplicity of infection, virus dynamics will be unaffected by this alteration. If, however, the burst size depends on the multiplicity of infection, virus dynamics will be altered significantly by changing t_d. Experiments along these lines are yet to be conducted.

An important consequence of multiple infections of cells by HIV is the emergence of recombinant forms of HIV, which may be resistant to multidrug therapy or possess the ability to evade specific host immune responses. The predominance of multiple infections suggests that rampant recombination has been a constant underlying force driving HIV evolution (1, 31). A mechanistic understanding of recombination is therefore crucial not only to understand HIV evolution but also for the development of effective antiretroviral therapy. A limitation has been the poor understanding of how multiple infections are orchestrated during HIV infection. Our model provides a description of HIV dynamics with multiple infections and establishes a framework for a quantitative understanding of HIV recombination.