Effects of threshold choice on biological conclusions reached during analysis of gene expression by DNA microarrays

Abstract

Global analysis of gene expression by using DNA microarrays is employed increasingly to search for differences in biological properties between normal and diseased tissue. In such studies, expression that deviates from defined thresholds commonly is used for creating genetic signatures that characterize disease vs. normality. Although it is axiomatic that the threshold parameters applied to microarray analysis will alter the contents of such genetic signatures, the extent to which threshold choice can affect the fundamental conclusions made from microarray-based studies has not been elucidated. We used gabriel (Genetic Analysis By Rules Incorporating Expert Logic), a platform of knowledge-based algorithms for the global analysis of gene expression, together with conventional statistical approaches, to examine the sensitivity of conclusions to threshold choice in recently published microarray-based studies. An analysis of the effects of threshold decisions in one of these studies [Ramaswamy, S., Ross, K. N., Lander, E. S. & Golub, T. R. (2003) Nat. Genet. 33, 49–54], which arrived at the important conclusion that the metastatic potential of primary tumors is encoded by the bulk of cells in the tumor, is the focus of this article. We discovered that support for this conclusion highly depends on the threshold used to create gene expression signatures. We also found that threshold choice dramatically affected the gene function categories represented nonrandomly in signatures. Our results suggest that the robustness of biological conclusions made by using microarray analysis should be routinely assessed by examining the validity of the conclusions by using a range of threshold parameters.

DNA microarrays, which enable the expression of thousands of genes to be assessed simultaneously at the transcriptional level, have become an important tool for research in the biological and biomedical sciences to produce genetic “signatures” for human disease (1–9). Whereas it is axiomatic that the threshold used to determine whether gene expression is altered will affect the list of genes comprising the genetic signature, and the effects of parameter choice have been examined in other fields of study (10), the consequences of threshold decisions on the interpretation of data obtained during microarray studies has not been elucidated. Genetic Analysis By Rules Incorporating Expert Logic (gabriel), a platform of knowledge-based algorithms that apply domain-specific and procedural knowledge systematically for the assessment of data from DNA microarrays, has the ability to make the consequences of changes in analytical parameters readily apparent (11–15). We used gabriel together with other analytical tools to investigate the effects of threshold choice on microarray-based conclusions.

The principal data set used for our investigation of the effects of threshold decisions was collected by Ramaswamy et al. (16) in an important study of the origin of cancer metastases, which underlie the lethality of almost all cancers (17). Whether the genetic alterations that lead to metastasis occur in a small fraction of cells in primary tumors or are present more generally has been controversial (16, 18, 19). The format of the Ramaswamy et al. analysis (16) was to define a collection of genes showing the greatest differential expression in metastatic tumors vs. primary tumors as a “metastasis signature” and then to use the occurrence of this signature to classify, by hierarchical clustering, separate groups of patients having primary lung adenocarcinoma, prostate adenocarcinoma, medulloblastoma, or large B cell lymphoma according to whether the metastasis signature was present or absent in a sample of the primary tumor. They then determined that the primary tumor patients having a metastasis signature showed a statistically significant decrease in survival. Their discovery of such a decrease in patients having tumors with a metastasis signature led them to conclude that the bulk of cells in primary tumors have the genetic potential for metastasis. Others have reached similar conclusions independently from examination of data sets comparing gene expression in normal and tumor tissues (20).

We found that the ability to classify tumors according to the data of Ramaswamy et al. data set is profoundly influenced by the threshold used to compile the metastasis signature and that the effects of threshold choice on microarray-based classification apply similarly to other published data sets that we have analyzed. During our investigations, we additionally observed that threshold choice, and, consequently, the number of genes in genetic signatures, also dramatically affects the gene function categories represented nonrandomly in signatures. Our results suggest a need for routine assessment of the robustness of microarray-based biological conclusions by evaluation of the conclusion's statistical validity under a range of threshold parameters.

Methods

Design and Validation of FDR and FNR Algorithms. Because experimental variability commonly differs among microarray data sets, estimates of false discovery rate (FDR; the rate of false inclusion of genes whose expression is not truly altered) and false negative rate (FNR; the rate of false exclusion of genes whose expression is truly altered) during microarray-based analysis of gene expression require data set-specific assessment of random fluctuation (11, 21–25). In addition, the frequencies of true positives and true negatives usually are not known during microarray-based studies, requiring estimation of FDR and FNR by a strategy that is independent of such prior knowledge. To estimate FDR for output resulting from the application of gabriel rules, we adopted and incorporated into gabriel a computational approach [Significance Analysis of Microarray (sam); refs. 11 and 21–25] that randomized the original data and then determined the frequency at which the conditions used for gene selection were satisfied by the random data sets (see Fig. 2 and Supporting Text, which are published as supporting information on the PNAS web site). To generate FNR values, we designed a computational approach that estimates both experimental variability (noise) and the true expression level (signal) in the data set being analyzed; the extent of experimental variability is then estimated by randomizing the data, for example, by randomly flipping the numerical signs of data points. The signal was estimated by averaging values for the expression of genes that satisfy t score thresholds. FNR was then defined as the frequency at which the observed level of expression would be overlooked as a consequence of adding the estimated experimental variability to the estimated signal.

Because the signal-to-noise ratio and probability distributions of signals and noise are unknown in real biological data sets, we tested FDR and FNR algorithms by applying them to data sets in which the identities of positive genes and negative genes were defined by simulation and, therefore, were known. By applying different levels of noise and signal, we found that FDR and FNR estimates deviated from actual values and that the deviation increased as the signal-to-noise ratio or number of experimental repeats decreased. In general, deviation of FNR estimates from actual values approximated the deviation of FDR estimates from actual values reported in previous studies (26) (Table 4, which is published as supporting information on the PNAS web site).

Analytical Procedures. We used exactly the same procedures reported by Ramaswamy et al. (16) to preprocess data, choose metastasis signatures, and carry out two-way hierarchical clustering and Kaplan–Meier analysis. We also compiled additional signatures by using a range of threshold values not included in the Ramaswamy et al. report. The full data set was further analyzed by using the K-means clustering function of the cluster program (4) at K = 2 and a randomized iteration process of 100,000 iterations that identifies similarly expressed genes based on correlation coefficient.

Gene Ontology Category Analysis. We used the Gene Ontology go:termfinder program to classify genes by biological process, molecular function, or cellular component and to calculate the statistical significance of the resulting groupings (27, 28). This program estimates the FDR for go categorization by using computer generated random simulations to calculate the likelihood that the frequency of genes in a category exceeds randomness (27) as compared with the distribution frequency of all of the genes on the microarray. The human gene annotation association file was downloaded from European Bioinformatics Institute (www.ebi.ac.uk/GOA). We determined nonrandom representation in a category by using a range of FDR cutoffs.

Results and Discussion

Threshold-Dependent Relationship of Metastasis Signature and Clinical Outcome. Our analysis used the 128 gene and 17 gene metastasis signatures compiled by Ramaswamy et al. and also metastasis signatures of 256, 512, and 1,024 genes that we compiled by using the same procedure with different thresholds to define altered expression (Table 1, top section).

Table 1. P values of the differences between survival curves of the two clusters of patient samples for lung adenocarcinoma, prostate adenocarcinoma, medulloblastoma, and large B cell lymphoma data sets.

No. of signature genes*	SNR threshold overexpressed/underexpressed	P value in lung adenocarcinoma	P value in prostate adenocarcinoma	P value in medullo blastoma	P value in large B cell lymphoma
Equal number of underexpressed and overexpressed genes
128	0.483/-0.403	0.000966	0.275	0.382	0.409
256	0.442/-0.369	0.598	0.269	0.498	0.388
512	0.400/-0.314	0.0657	0.118	0.88	0.197
1,024	0.347/-0.258	0.00243	0.242	0.941	0.119
17	N/A†	0.136	0.0413	0.0868	0.303
Signatures compiled with equal SNR thresholds for overexpressed and underexpressed genes
21/3*	0.55/-0.55	0.0512	0.77	0.198	0.869
51/14*	0.5/-0.5	0.997	0.473	0.173	0.556
109/30*	0.45/-0.45	0.885	0.473	0.134	0.245
250/80*	0.4/-0.4	0.00279	0.275	0.403	0.206
474/168*	0.35/-0.35	0.069	0.275	0.941	0.245
P values by using clusters derived by K-means clustering (K = 2)
128	0.483/-0.403	0.469	1	0.798	0.938
256	0.442/-0.369	0.74	0.487	0.969	0.969
512	0.400/-0.314	0.138	0.487	0.969	0.969
1,024	0.347/-0.258	0.0007	0.487	0.711	0.119
17	N/A†	0.044	0.0017	0.217	0.479

The data sets (16) were downloaded from Ramaswamy's supplemental information web site. We did not analyze the breast cancer data set because of unavailability of gene identifiers. In the top section, the 128, 256, 512, and 1,024 gene signatures are chosen based on the SNR in the Global Map data set of 64 primary tumors and 12 metastasis tumors. Each of them contains an equal number of overexpressed and underexpressed genes. The two signal to-noise thresholds in each row define the threshold for selecting overexpressed and underexpressed genes, respectively. The 17-gene signature is from Ramaswamy et al. (16) which is a subset of the 128-gene signature selected based on the SNR in the lung adenocarcinoma data set. The calculation of P values is described in Methods. When the hierarchical clustering dendrogram could be divided in different ways, we show here the division that yields the lowest P value.

^*Signature genes are listed by number of overexpressed/underexpressed genes.

^†N/A, not applicable.

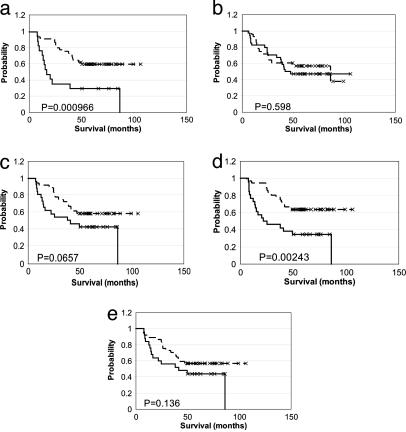
The conclusion by Ramaswamy et al. that metastatic potential resides in the bulk of cells in primary tumors depended on their finding that the list of genes they defined as a metastasis signature was statistically predictive of poor survival by Kaplan–Meier analysis (17). A 128-gene metastasis signature in their lung adenocarcinoma data set was used to arrive at this conclusion. However, using identical procedures but different thresholds to compile signatures of different sizes from the same data set, we found that the statistical significance (P value) of the conclusion that the two groups of patients they delineated by hierarchical clustering showed differences in survival was influenced strongly by the number of genes included in the signature and, thus, depended largely on threshold choice (Table 1 and Fig. 1). For example, whereas the 128-gene metastasis signature yielded statistically different survival rates between lung adenocarcinoma patients that did or did not have the signature (P < 0.01), the 256-gene signature yielded a P value of 0.598 for these same patients. The loss of statistical significance and predictive ability for the 256-gene signature vs. the 128-gene signature does not result from inclusion of a larger fraction of uninformative genes as signature size increases, because the P value decreased to 0.0657 for a 512-gene signature. Thus, the relationship between threshold choice and significance of the biological conclusion reached is not linear.

Fig. 1.

Kaplan–Meier survival analysis of the clusters of lung adenocarcinoma individuals defined by the gene signature of different sizes. The dashed line represents the individuals without the metastasis signature delineated by hierarchical clustering, and the solid line represents the individuals with the metastasis signature. The plots are generated by the winstat software (R. Fitch Software, Staufen, Germany). Shown are the clusters for the following gene signatures: 128 (a), 256 (b), 512 (c), 1,024 (d), and 17 (e).

By using their 17-gene metastasis signature to classify cancer patients, Ramaswamy et al. concluded that the presence or absence of this signature in primary tumor samples has general value in predicting patient outcome. We used their procedures to examine the same prostate adenocarcinoma, medulloblastoma, and B cell lymphoma data sets by employing a range of thresholds to define “overexpression” and “underexpression (Table 1, top section); whereas the 17-gene signature yielded a low P value for the distinction between poor survival and good survival curves for prostate adenocarcinoma and medulloblastoma patients whose tumors have or lack metastasis signatures (P = 0.0413 and 0.0868, respectively), as reported by Ramaswamy et al., signatures of other sizes failed to statistically support this distinction for the same data sets (P > 0.1). No evidence of the ability of the 17-gene signature to predict clinical outcome for B cell lymphomas was observed by either us or Ramaswamy et al. For the lung adenocarcinoma data set, the P value we obtained for the 17-gene signature was different from the one reported by Ramaswamy et al., possibly due to the nonunique ordering of hierarchical clustering output (4).

Ramaswamy et al. included equal numbers of overexpressed and underexpressed genes in each metastasis signature, and we initially followed this practice in compiling signatures. To determine whether the observation that threshold choice influences the biological conclusion applies also to signatures that are not constrained in this way, we additionally compiled signatures consisting of overexpressed and underexpressed genes selected at equal threshold values and contained unequal numbers of overexpressed and underexpressed genes. We found that when these “metastasis signatures” were used to predict patient survival (Table 1, middle section), the P value of the difference between the survival data also varied nonlinearly with the threshold. We also determined whether the effects we observed depended on the method of clustering we used, namely, hierarchical clustering. We applied K-means clustering to the same data set (Table 1, bottom section) and again found that the P value of the difference between the survival data of the patients varied nonpredictably with the signature size.

The effects of parameter choice on microarray investigations were, as expected, not restricted to the Ramaswamy et al. cancer metastasis data set. We found (unpublished data) that changes in the parameters used to analyze microarrays also had important effects on gene lists obtained in our own studies of gene expression during the Streptomyces coelicolor life cycle (13) and the replicative senescence in human fibroblasts and mammary epithelial cells (14).

Estimates of FDR and FNR for Metastasis Signatures. To assess statistical confidence in the signatures compiled at various thresholds, we used gabriel to estimate the FDR and FNR (see Methods) for overexpressed and underexpressed genes in signatures by applying a range of signal-to-noise ratio (SNR) thresholds to define “over” and “under”-expression (Table 1). FNR, which bears a largely reciprocal relationship to FDR, commonly is increased when thresholds for defining perturbed expression are increased in stringency, leading to a correspondingly greater chance of not identifying genes whose expression is genuinely affected by the event being studied. The results of this analysis (Table 2; see also Fig. 3, which is published as supporting information on the PNAS web site) indicated that genes overexpressed in these tumors show estimated FDR and FNR values (in the range of 0.144∼0.191 and 0.245∼0.295, respectively) for all signatures compiled within the range of SNR thresholds we examined, but that signatures for underexpressed genes were associated with an FDR value >0.5 over a range of thresholds, indicating a high likelihood of false discovery among this gene group. When equal SNR threshold values were applied for identification of overexpressed and underexpressed genes, a much larger number of overexpressed genes was observed. For example, as shown in Table 1, at an SNR threshold of 0.35, 474 overexpressed genes but only 168 underexpressed genes were selected. We also observed an excess of overexpressed genes vs. underexpressed genes in metastatic tumors in another published metastasis data set (29).

Table 2. FDR and FNR estimates associated with metastasis signatures containing different numbers of genes.

No. genes (SNR threshold)	FDR	FNR
Overexpressed genes
64 (0.483)	0.144	0.295
128 (0.442)	0.161	0.287
256 (0.400)	0.171	0.262
512 (0.347)	0.191	0.245
Underexpressed genes
64 (-0.408)	0.577	0.638
128 (-0.369)	0.546	0.626
256 (-0.314)	0.62	0.612
512 (-0.258)	0.641	0.564

Analysis was done by using gabriel and the Ramaswamy et al. data set (16). We calculated the SNR thresholds corresponding to each size signature and showed them in the parentheses.

We extensively tested our FDR algorithm on simulated data sets and as well as on other published data sets (e.g., a replicative senescence data set; ref. 14) and found that the overexpressed and underexpressed genes in these data sets had similar FDRs, indicating that the calculated difference between the FDRs of overexpressed and underexpressed genes in the Ramaswamy et al. data set is not a result of a methodological artifact. The surprising difference between FDR estimates for overexpressed and underexpressed genes in the Ramaswamy et al. data set found by gabriel analysis was also observed when we used sam (21) (data not shown).

Analysis of Biological Categories Represented Nonrandomly in Metastasis Signatures. During our investigations, we observed that signature size, as determined by threshold choice, also had surprising effects on the identification of functional categories considered to be represented nonrandomly during classification of genes by their annotated biological role or cellular function. Nonrandom representation, or enrichment, of a particular class of genes was determined by comparison with the expected random incidence of genes in that category by using computer simulated data (see Methods). Some nonrandomly enriched categories detected at an FDR cutoff of 5% for the 128-, 256-, 512-, or 1,024-gene metastasis signatures are shown in Table 3; analogous results but different categories of nonrandom enrichment were obtained at FDR cutoff values of 1% and 10% (data not shown). Whereas in general, larger size signatures resulted in nonrandom enrichment of more categories (e.g., genes related to transcription were enriched in 1,024-gene signature but not in the 128-gene signature), some categories (e.g., macromolecule biosynthesis) showed greater enrichment for a smaller size signature showed than for a larger one. Additionally, genes annotated as encoding a cellular component of fibrillar collagen were represented nonrandomly in metastasis signatures that contain 256 and 512 genes (FDR < 5%) but not in signatures of other sizes. Collectively, our findings indicate that conclusions about nonrandom representation of certain biological processes and cellular components in gene signatures identified by microarray analysis can depend significantly on the SNR threshold used to select these genes, and the relationship between category representation and threshold choice is neither linear nor predicable. This effect may result from possible nonlinearity of the ratio between the total number of genes identified and the number of genes in a particular category.

Table 3. Gene Ontology analysis for metastatic signature gene in Ramaswamy et al. data set.

	Gene signature size
	128		256		512		1024
Category	No. gene	FDR, %	No. gene	FDR, %	No. gene	FDR, %	No. gene	FDR, %
(BP) transcription	18	27.33	27	50.29	53	3.50	113	0.00
(BP) macromolecule biosynthesis	8	24.95	11	52.85	27	3.54	40	17.27
(CC) fibrillar collagen	2	16.67	3	2.00	4	0.00	4	9.60
(BP) metabolism	53	2.00	98	0.00	190	0.00	355	0.00

The table shows selected Gene Ontology biological processes or cellular components nonrandomly represented in different sizes of signatures. Each of the categories listed is nonrandomly represented in at least one of the four sizes of signatures. Nonrandom representation is defined by FDR ≤5%. The FDRs in bold are the ones ≤5%. BP, biological process; CC, cellular component.

Collectively, the results reported here argue strongly that microarray-based gene classifications be carried out routinely by using a range of threshold conditions to assess the sensitivity of biological conclusions to threshold choice and the overall robustness of the conclusions.