Programmable Lipid Bilayer Tension–Control Apparatus for Quantitative Mechanobiology

Abstract

The biological membrane is not just a platform for information processing but also a field of mechanics. The lipid bilayer that constitutes the membrane is an elastic body, generating stress upon deformation, while the membrane protein embedded therein deforms the bilayer through structural changes. Among membrane-protein interplays, various channel species act as tension-current converters for signal transduction, serving as elementary processes in mechanobiology. However, in situ studies in chaotically complex cell membranes are challenging, and characterizing the tension dependency of mechanosensitive channels remains semiquantitative owing to technical limitations. Here, we developed a programmable membrane tension-control apparatus on a lipid bilayer system. This synthetic membrane system [contact bubble bilayer (CBB)] uses pressure to drive bilayer tension changes via the Young–Laplace principle, whereas absolute bilayer tension is monitored in real-time through image analysis of the bubble geometry via the Young principle. Consequently, the mechanical nature of the system permits the implementation of closed-loop feedback control of bilayer tension (tension-clamp CBB), maintaining a constant tension for minutes and allowing stepwise tension changes within a hundred milliseconds in the tension range of 0.8 to 15 mN·m^–1. We verified the system performance by examining the single-channel behavior of tension-dependent KcsA and TREK-1 potassium channels under scheduled tension time courses prescribed via visual interfaces. The result revealed steady-state activity and dynamic responses to the step tension changes, which are essential to the biophysical characterization of the channels. The apparatus explores a frontier for quantitative mechanobiology studies and promotes the development of a tension-operating experimental robot.

Cell membranes are an integrated system of lipid bilayers and membrane proteins.¹⁻⁷ The mechanical interplay between the lipid bilayer and membrane proteins founds the basis of mechanobiology.⁸⁻¹¹ The elastic lipid bilayer exerts a force on membrane-embedded proteins (force-from-lipid principle),¹²⁻¹⁶ while membrane proteins deform the bilayer (force-from-proteins or hydrophobic mismatch),¹⁷⁻²³ with the deformation transferring both locally and over long distances.^24,25 In this membrane system, the ability to sense membrane tension changes and yield signals is crucial for establishing the mechanical integrity. This is where the tension-dependent or mechanosensitive ion channel plays a pivotal role.

The mechanosensitive channels were discovered several decades ago: a cell-membrane patch isolated by a glass pipet (patch-clamp method) was subjected to negative pressure to extend a patch membrane, increasing membrane tension and opening the channel.²⁶ Since then, the patch-clamp method has become the gold standard for examining tension-sensitive channels²⁷⁻³² as other methods cannot simultaneously evaluate tension and channel activity.³³⁻³⁷ However, the in situ patch-clamp method has limitations regarding reproducibility and quantitative evaluation of membrane tension.^26,38,39 These issues are inherent to the physical nature of the giga-sealed patch membranes, adhered to the glass surface,⁴⁰⁻⁴³ and cannot be overcome by technical challenges.^32,44,45

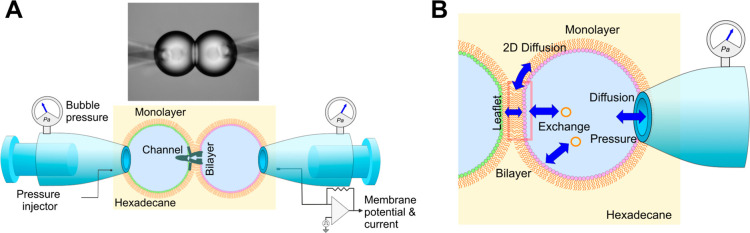
Alternatively, we introduced a membrane reconstitution system called the contact bubble bilayer (CBB) for performing more controlled mechanobiology experiments (Figure 1A).^46,47 On the CBB, a membrane’s absolute tension is evaluated and manipulated freely, allowing characterization of tension-dependent channels,⁴⁶⁻⁵² which surpasses patch-clamp’s semiquantitative experiments.^47,51,53 To enhance the advantage of the CBB system, here we developed a programmable tension-control system using a feedback control circuit (Figure 2). The system performs under stable tension for minutes, and rapid stepwise tension changes can be applied within a hundred milliseconds. These experimental features are a solid basis for quantitatively characterizing tension-dependent channels but have never been attained in the previous methods.⁵⁴ To overview the feedback system for membrane tension control, we summarize the basic physicochemical principles of the CBB system and relevant mechanical principles.

Figure 1.

CBB system. (A) CBB system for membrane tension experiments. In this setup, bubble pressure is finely tuned manually to maintain the bubble size (30–50 μm in radius) and membrane tension while continuously monitoring the bubble pressure within the range of 1000 Pa. Previously, bubble geometry was analyzed off-line, and bilayer tension was evaluated by integrating the bubble pressure and geometric data. In the tension-clamp CBB system, a stepping motor fine-tunes the bubble pressure, while bilayer tension is monitored in real-time using an image-analysis program, enabling automatic tension control via feedback. (B) Open CBB system. An electrolyte bubble lined by a lipid monolayer is immersed in the bulk organic solvent, and the bubble electrolyte is diffusible to the pipet solution. The bilayer leaflet and bubble monolayer form a continuous phase, allowing lipid diffusion between them. Monolayer and leaflet lipids are also supplied from liposomes dispersed in the bubble electrolyte phase, ensuring that the leaflet is quasi-equilibrated with the surrounding phases. The objectives of the feedback control are such a fragile and nonequilibrium system.

Figure 2.

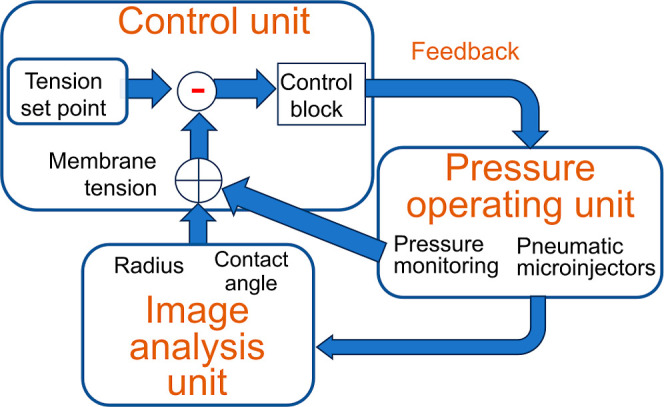
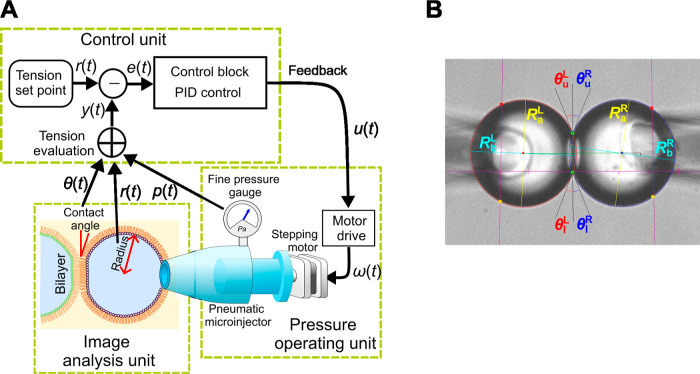
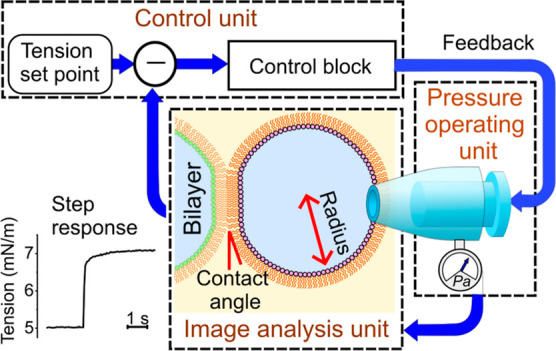
General schematic of the membrane tension-clamp system established on the CBB system. Here, each bubble system is depicted, which is integrated to manage bilayer tension in the CBB. The bubble system comprises three subsystems: the pressure-operating unit (for pressure measurement and application), the image analysis unit, and the control unit. To clamp membrane tension, real-time tension evaluation is essential. Image-processing techniques are used to deduce bubble geometry (radius of bubbles and contact angle between bubbles). The bubble geometry data and pressure values are combined to assess leaflet and bilayer tension. In the control unit, deviations of measured values from a set point value are processed through the control block, involving the proportional-integral-derivative (PID) controller, yielding feedback signals. The feedback signals are sent to the bubble pressure controller (a pneumatic microinjector), finely tuning the bubble pressure via a stepping motor.

In the CBB, water bubbles are inflated from pipettes into an organic solvent, and monolayers formed at the oil–water interfaces are docked for bilayer formation (Figure 1A). Bubbles are maintained by applying pressure, and changes in pressure yield membrane-tension changes governed by the Young–Laplace principle. Pressure-driven tension control differs in principle from that applied in biological membranes, but it is promising for developing a pressure-controlled experimental apparatus. Moreover, the CBB is an open and dynamic system,^46,48,50,52 which facilitates experiments under various chemical and physical perturbations on the one hand but needs fine-tuning of bubble pressure on the other (Figure 1B).^55,56 Bubbles are fragile and interacting (Figure 1A), where the underlying physicochemical and mechanical principles of each bubble and interacting bubbles are composite.⁵⁰ Monolayer tension of each bubble is directly controllable, whereas bilayer tension is locally equilibrated by the force balance between the monolayers and bilayer, which is out of control.

Controlling bilayer tension needs feedback for a stable operation. Accordingly, the current manual tuning of membrane tension in CBB is replaced with automatic feedback control, ensuring stable and stepwise changes in membrane tension through dynamically controlling bubble pressure (Figure 2).^50,52,53 This system is named the tension-clamp CBB, functioning similarly to the voltage clamp used in electrophysiology.^57,58 Feedback control of such a fragile and open system requires sophisticated maneuvers. To build up the tension-clamp CBB, we established real-time tension monitoring and fine-tuning of bubble pressure, which are integrated into a closed-loop feedback system (image-mechanical feedback). Relevant principles and detailed methods are described in the Methods section. In the Results section, we present the performance of the tension-clamp system for quasi-equilibrium lipid bilayers and embedded channels. We also developed a program for scheduling tension changes via a visual interface, allowing for automatic operation in practical tension-clamp experiments. Single-channel current recordings of the tension-dependent KcsA and TREK-1 potassium channels under this tension protocol verified the performance of the tension-clamp CBB. The reliability and accuracy of the tension-clamp CBB were thoroughly tested and corroborated. The tension-clamp CBB enables long-term stable tension experiments with rapid stepwise changes, allowing the biophysical characterization of mechanosensitive channels at single-molecule levels and renovating quantitative mechanobiology studies.

Results

Free-Running CBB

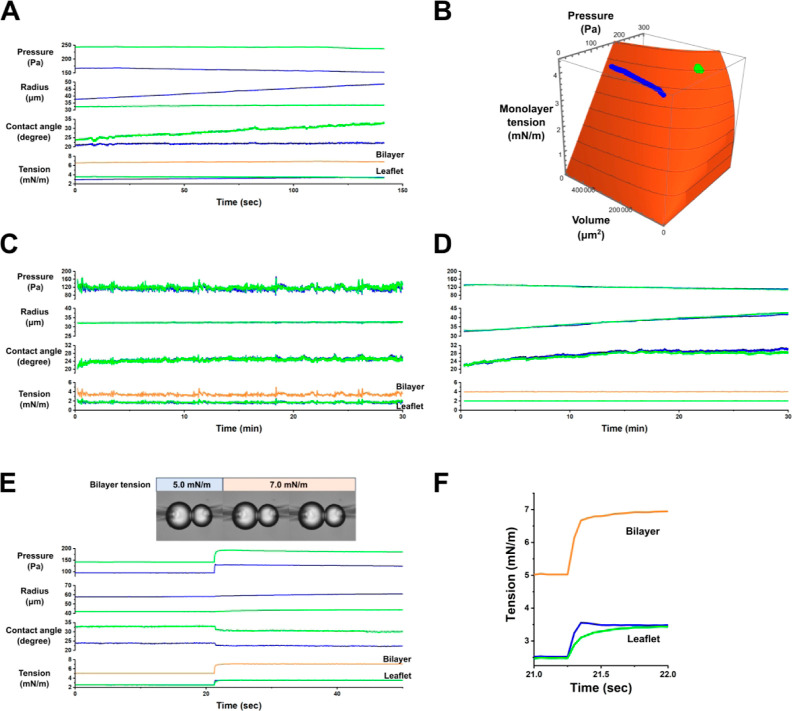
We first examined the physical characteristics of a free-running CBB by using our developed real-time monitoring system without feedback control. The CBB was formed from azolectin in a hexadecane organic phase (see the Methods section). The bubbles were left untouched to observe their spontaneous changes. Representative traces of bubble parameters, such as pressure, volume, and monolayer and bilayer tensions, are shown in Figure 3A, recorded at a frequency of 10 Hz. Over time, the bubbles gradually changed in size and associated parameters. The size and monolayer tension of each bubble were plotted on a 3D surface (monolayer tension as a function of bubble pressure and volume, governed by the Young–Laplace principle; Figure 3B; see Methods and Figure 6): the left bubble (blue) gradually inflated, while the right bubble (green) slightly shrunk. These spontaneous changes result from the slow partitioning of lipids into and from the monolayer and bulk phase liposomes (Figure 1B). In the case of manual control, we intercepted these spontaneous changes by fine pressure manipulation to maintain bubble size or bilayer tension. The time course of parameter changes indicates that such manipulations are infrequent.

Figure 3.

Time courses of bubbles and membrane tension. (A) Free running of a CBB. Spontaneous changes were allowed in the system without controlling the bubble pressure. In this scenario, the right bubble (blue) inflated while the left bubble (green) remained nearly constant in volume, with slight increases in the contact angle over time. Consequently, the leaflet tension increased slightly. The time course of the parameters is shown at 10 Hz. (B) 3D Trajectory. This plot shows the contrasting behaviors of the two bubbles. (C) Steady size-clamp. The average radii of the bubbles were maintained with pressure controllers operating frequently, as evidenced by fine and frequent fluctuations in bubble pressures, contact angles, and tensions. (D) Steady tension-clamp. Symmetrical bubble sizes and pressures were set to achieve a bilayer tension of 4 mN·m^–1. The membrane tension was clamped for 30 min. During this period, bubble pressure gradually decreased, bubble size expanded, and the contact angle increased slightly. These trends are frequently observed and explained by a gradual increase in lipid density in the monolayers via slow partitioning. Green: left; blue: right; and orange: bilayer. The traces of the left and right leaflets are nearly overlapped. (E) Step tension change and its response under tension-clamp. The bilayer tension was changed stepwise with each simultaneous leaflet tension change of 1 mN·m^–1. The feedback control gain (k_p and k_d) was set to fast for a quick response. The contact angles changed immediately according to the force balance of the monolayers and leaflets. The bubble volume changed gradually at the tension step due to the slow bulk flow of the pipet solution toward the bubble. The inset shows captured images of the bubbles at the tension step (see the video in the Supporting Information). The temporal resolution was 20 Hz. (F) Time course of the tension (leaflets and bilayer) changed on an expanded time scale. The 90% rise time was less than 100 ms (see the video in the Supporting Information). Parameters are shown for the left (blue) and right (green) bubbles.

Figure 6.

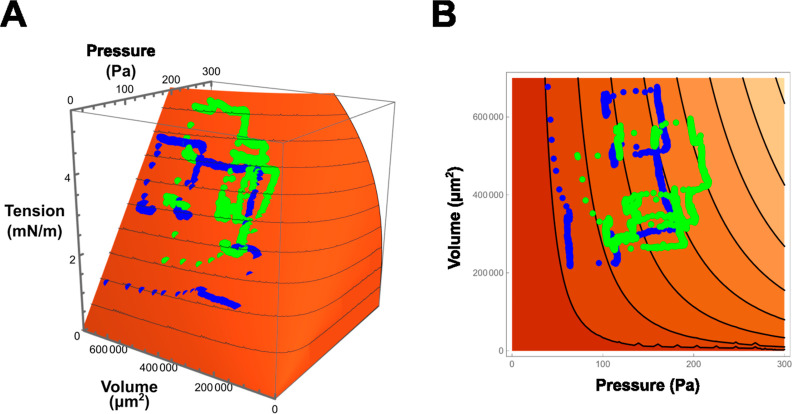
Volume–pressure–tension relationship of a bubble. The Young–Laplace relation is transformed to a bubble volume-based representation rather than a radius-based one by assuming a spherical bubble. Accordingly, the monolayer tension is depicted as a function of bubble pressure and volume and is shown as a 3D plot (A) and a contour map (B). Representative trajectories of bubble changes with measured pressure and volume are superimposed on the 3D surface (blue and green for each bubble). When bubble pressure increases, the monolayer tension rises linearly, followed by a delayed volume increase due to bulk volume flow. For a small bubble, the monolayer tension increases moderately with rising pressure.

Bubble-Size Clamp Experiments

Next, we conducted bubble-size clamp experiments to keep the bubble size constant. Figure 3C presents representative traces from these experiments, showing that both bubble sizes were maintained over a long period. The monolayer and bilayer tensions fluctuated slightly, which were synchronized to pressure fluctuations under feedback driving.

Tension-Clamp Experiments

Stability of the Bilayer Tension

The tension-clamp system (Figure 2) was experimentally verified by examining the geometrical and mechanical features of the lipid bilayer. As shown in Figure 3D, the membrane tension remained constant for more than 30 min. One or both bubbles might gradually change in size due to decreased monolayer tension, resulting from further lipid transfer into the monolayer. The bilayer tension can be varied between 0.8 and 15 mN·m^–1. The membrane breakdown tension⁵⁹⁻⁶¹ was relatively high in this system.

Tension Step Responses

The time course of step tension changes was examined (Figure 3E), showcasing the precision of the tension-clamp system, akin to step voltage changes in the voltage-clamp method. The control parameters [k_p and k_f (eq 9) of the proportional-integral-derivative (PID) controller; Figure 7A] in the control block (Figure 2) were optimized to achieve rapid step changes without causing ringing or breaking bubbles.⁶²Figure 3F presents experimental results for a step tension change of 2 mN·m^–1, with each leaflet tension changing simultaneously of 1 mN·m^–1. As shown in the video with the 20 Hz video rate (see Supporting Information, Video 1), the bubbles swung slightly upon a step change, relaxing their positions under pipet-hanged configurations. Each leaflet tension exhibited a distinct time course, while the bilayer tension transitioned stepwise smoothly without ringing, reaching a steady level within 0.1 s (Figure 3F). The time course of other bubble parameters is shown in Figure 3E, where the contact angles responded immediately and simultaneously, reaching a new force balance between the leaflets and monolayers (eqs 6 and 7). In contrast, the bubble volume changed slowly without stepwise alterations due to the slow bulk flow of the pipet solution toward the bubble. These results validate the bilayer tension control via independent leaflet control through simultaneous step changes. The demonstrated overall performance of the tension-clamp CBB system highlighted its ability to exhibit fast and reliable dynamic responses.

Figure 7.

System diagram and operation apparatus of the membrane tension-clamp system. (A) System diagram. The system comprises three units: control, pressure-operating, and image analysis. In the pressure-operating unit, a pneumatic microinjector for manual control is driven by a stepping motor for fine-tuning the bubble pressure. This configuration is convenient because it allows for easy switching between manual and automatic operations. A fine pressure gauge continuously measures the bubble pressure. The image analysis unit processes time-series bubble images (10–20 fps) to determine bubble radii and contact angles in real-time. The control unit integrates monitored pressure data and bubble geometry analyzed by the image analysis unit. The evaluated tension value is compared with the preset value. The system operates as a negative feedback (NFB) system with signals processed in the control block using a proportional-integral-differential (PID) method, which serves as a feedback signal for the motor driver. Bubble geometry, pressure, and membrane tension are displayed in real-time. The electrophysiological unit, crucial for single-channel current recordings, operates independently of the other units but is shielded effectively to minimize noise from the pressure-operating stepping motor. (B) Extraction of the geometric parameters of the two bubbles. The captured frame focuses on the bubbles, while the pipettes away from the focal plane are out of focus. R_a^L, R_b^L, R_a^R, and R_b^R represent the bubble radii. θ_u^L, θ_l^L, θ_u^R, and θ_l^R denote the upper and lower contact angles, from which θ^L and θ^R in eq 3 are calculated as θ^L = (θ_u^L + θ_l^L)/2 and θ^R = (θ_u^R + θ_l^R)/2.

Experimental Verification of the Tension Clamp Using the Tension-Dependent KcsA Channel

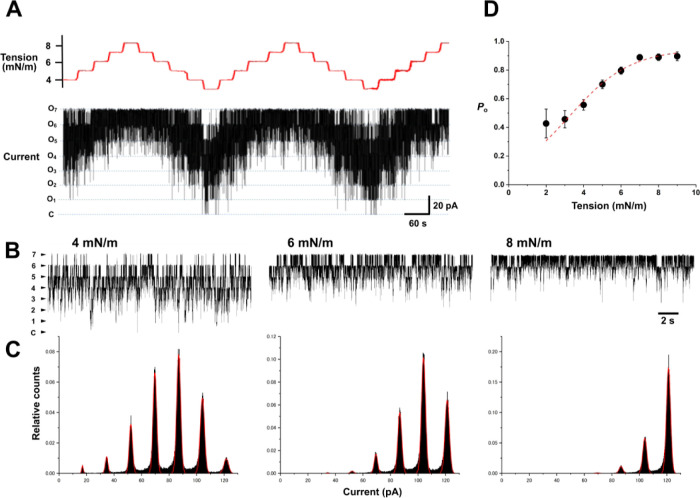
The membrane tension-clamp system was experimentally verified with ion channels, using the tension-dependent KcsA potassium channel as a reporter for membrane tension changes (Figure 4).^{23,51−53,63} The KcsA channel is nonmechanosensitive under neutral intracellular pH levels, remaining locked in the resting state.^37,53 However, it becomes responsive to tension when in the ready-to-activate state at acidic intracellular pH levels.^51,53 The KcsA channel has two gates in series: an activation gate and an inactivation gate. The activation gate exclusively responds to tension;⁵³ thus, single-channel current recordings of the noninactivated mutant E71A represent activation gating behavior.^64,65 The E71A mutant was reconstituted in an asymmetric membrane^52,66 with POPG in the inner leaflet and POPC in the outer leaflet with an acidic intracellular solution to render the channel ready for activation (see the Methods section in detail).

Figure 4.

Tension-clamp experiments for a KcsA potassium channel with simultaneous single-channel current recordings. (A) Single-channel current trace in varied membrane tension. To investigate the tension dependency of the activation gate of the KcsA channel, the noninactivating mutant E71A was applied. Experiments were performed in an asymmetric membrane with POPG in the inner leaflet and POPC in the outer leaflet to activate the channel. Bilayer tension was stepwise changed from 3 to 9 mN·m^–1 with a step of 1 mN·m^–1. Representative KcsA channel currents showed that seven channels were incorporated into the membrane and remained active throughout the 30 min recording period. Independent and stochastic behavior of each channel was evident, exhibiting up to seven active channels at the highest tension. For automatic tension control, the tension step changes were set to a “slow” rate (0.2 mN·m^–1·s^–1) to ensure stable transitions across a wide tension range. Each tension step was maintained for 30 s. (B) Single-channel current traces in expanded time scale at 4 mN·m^–1 (left), 6 mN·m^–1 (middle), and 8 mN·m^–1 (right), respectively. (C) Amplitude histograms at varied tension. Histograms were fitted with a binomial distribution, assuming seven active channels embedded in the membrane. The estimated open probability was 0.673, 0.837, and 0.948, respectively. (D) Tension dependence of the open probability. Data were collected from different membranes containing different numbers of active channels. Data are presented as means with error bars (SEM, n = 3–22), which were fitted with the Boltzmann function (broken line; see the Methods section). The fitting deduced the free energy difference of the open and closed conformations (ΔG) as 4.833 kJ/mol, and the cross-sectional area expansion upon openings (ΔA) was 2.5 nm².

In these tension-clamp experiments, a wide range of tension changes was necessary to characterize the tension dependency of the KcsA channel in a steady state (Figure 4 upper). Each tension level was maintained for 30 s to ensure steady-state channel activity. The speed of the tension step was set to “slow” (0.2 mN·m^–1·s^–1, see the Methods section in detail) to prevent instability of the CBB system during long-run experiments with repeated up-and-down tension changes. Rapid step changes could destabilize the system due to the mechanical coupling of the bubbles caused by their swelling and shrinkage.

These experimental parameters were configured in the Chart program, where tension levels, duration, and speed of changes were set through a visual interface (see Supporting Information, Figure S3). The protocol involved repeated up-and-down changes in the bilayer tension over 30 min. Bilayer tension was varied stepwise from 3 to 9 mN·m^–1, with each step maintained for 30 s, covering mostly tension-dependent activation of the KcsA channel. The tension-up and tension-down cycles were repeated.

In the CBB experiments, an arbitrary number of channels were spontaneously reconstituted in the membrane, and the active channels were retained at a steady state. Figure 4 shows a representative current trace of the E71A mutant of the KcsA channel under repeated up and down step changes in the bilayer tension for over 30 min. Several active channels were discernible as discrete transitions between numbers of current levels. As shown in Figure 4B, expanded current traces indicate the stochastic gating transitions of independently active channels at different tensions.²³ Despite the frequent operation of the stepping motors throughout the recordings, the background noise was negligible.

Amplitude histograms for the above current traces at varied membrane tensions are shown in Figure 4C. At high channel activity at the repeated highest tension of 8 mN·m^–1, seven channels are recognized with high open probability, indicating that a total of seven active channels are reconstituted in this membrane throughout the recording.⁶⁷ Given the total channel number, the histograms were fitted with a binomial distribution for evaluating the channel open probability. The tension-dependent open probability of the KcsA channel activity obtained from different membranes was plotted and fitted with the Boltzmann function (Figure 4D), reproducing the previous data.^23,51 The tension-clamp experiments enabled efficient, reproducible, and quantitative experiments under steady-state tension conditions, advancing biophysical mechanobiological studies.

Experimental Verification of Tension Steps Using the Tension-Dependent TREK-1 Channel

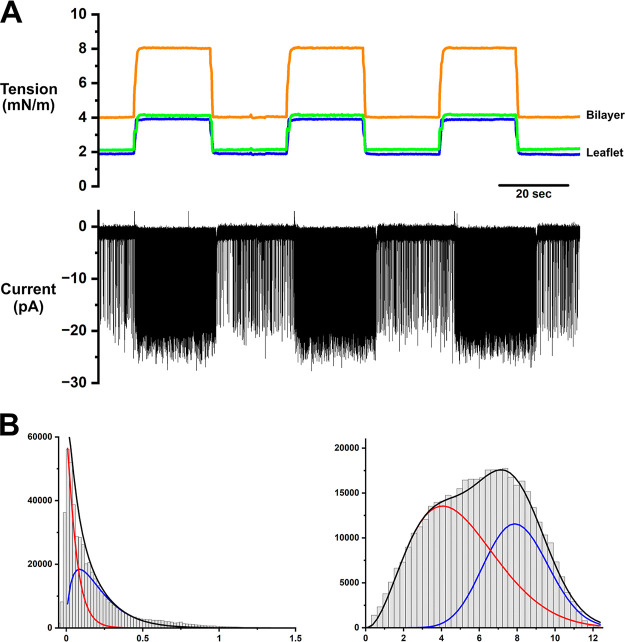
We explored the system’s responses to a range of tension jumps in the presence of TREK-1 channels (Figure 5). TREK-1 is a tension-sensitive channel,⁶⁸⁻⁷⁰ and a purified human TREK-1 channel was incorporated into a CBB (see the Methods section).

Figure 5.

Automatic repeated stepwise tension-clamp and single-channel responses of the TREK-1 channel. (A) The bilayer tension was repeatedly changed between 4 and 8 mN·m^–1 (orange) by simultaneously driving the leaflet tension (blue and green). Typical flicker gating of single-channel TREK-1 was recorded at −100 mV. At 4 mN·m^–1 tension, the TREK-1 channel exhibited infrequent flicker gating. The flicker gating frequency immediately increased after the tension was increased to 8 mN·m^–1. The single-channel currents were Bessel filtered at the cutoff frequency of 5 kHz and were sampled at 25 kHz, which are further digitally filtered (Bessel filter) at 1 kHz cutoff frequency for display. (B) Flicker gating analysis by the BPoF method.⁷¹ The amplitude histograms are shown for the low- and high-tension traces (see the Methods section). The histograms were compiled from the first-order filtered current data (cutoff frequency of 3 Hz for low tension and 10 Hz for high tension). Subsequent fitting with one beta-distribution was unsuccessful, whereas two beta-distributions (blue and red) successfully reproduced the amplitude histogram. Accordingly, two distinct flickerings underly the gating of the TREK-1 channel. Two sets of flickering rates were estimated by assuming two independent flickering relevant to two beta distributions. The estimated rate constants for opening, k_co, and closing, k_oc, were 0.02 and 2.07 ms^–1 for the major component and 0.018 and 5.89 ms^–1 for the minor component for the low tension; k_co and k_oc for the high tension were 0.89 and 1.31 ms^–1 for the major component and 0.21 and 0.64 ms^–1 for the minor component.

Bilayer tension was repeatedly jumped at such a big step from 4 to 8 mN·m^–1, programmed using Chart. The speed of the tension jumps was set to moderate to ensure reproducibility, reaching a steady level within 1 s. Still, the bubbles retained their integrity. The current trace indicates typical flicker gating of the TREK-1 channel having only one channel in the membrane throughout the recording (Figure 5A). The single-channel current of the TREK-1 channel exhibited an infrequent flicker gating at 4 mN·m^–1. Upon increasing the tension to 8 mN·m^–1, the channel activity promptly transitioned to much more frequent flickering. When the tension was reduced to 4 mN·m^–1, the frequent flickering reverted immediately to the original infrequent flickering, retaining its steady low activity. These reproducible and rapid responses in single-channel current have never been attained, substantiating the tension-clamp performance.

Our recently developed flicker analysis method (beta distribution-based analysis by adaptive postfiltering; BPoF) allowed the evaluation of underlying fast flicker rate constants of single-channel current recordings.⁷¹ As shown in Figure 5B, single-channel amplitude histograms compiled from the first-order filtered current traces were fitted with two beta-distribution functions, suggesting two flicker components underly. Two flicker modes were seen in our previous reports⁷¹ and also reported for the other two-pore-domain TRAAK channel⁷²⁻⁷⁵ but have yet to be reported for the TREK-1 channel. The open probability was estimated to be 0.02 at low tension and 0.65 at high tension by assuming two independent gating modes. The TREK-1 responses to tension were consistent with previously reported data using macroscopic current data.^39,54 However, further quantification of the tension dependency of the TREK-1 channel is reserved for future studies because the previous BPoF analysis method needs to accommodate more complicated flicker gating.⁷¹

The step tension protocol in the tension-clamp CBB enabled the quantitative evaluation of channel gating from single-channel recordings in response to the bilayer tension. This demonstrated the validation of the tension-clamp CBB system under a predefined tension time course using the Chart program, further solidifying its efficacy and reliability of the tension-clamp system.

Discussion

We established a tension-clamp CBB system that promises to promote quantitative mechanobiology experiments. The tension-clamp CBB can maintain steady membrane tension for several tens of minutes over a tension range of 0.8 to 15 mN·m^–1 and execute stepwise changes within a hundred milliseconds. Feedback control of such delicate objects had never been considered before. The stable, dynamic, quantitative, and reproducible performance of the tension-clamp CBB under single-channel current recordings surpasses any other method in mechanobiology studies. Its underlying principles are straightforward, involving surface chemistry and essential feedback control. Absolute tension value evaluation has been reliable since the CBB was first used for tension sensitivity experiments in 2018,⁵³ with more sophisticated tension evaluation methods incorporating bubble pressure measurements introduced in 2021.⁵¹ The tension-clamp CBB allows for more sophisticated tension-related experiments than previously possible since asymmetric membranes are readily formed.^52,66 In contrast, the conventional patch-clamp method³⁹ and the recently developed “freestanding lipid bilayer tensiometer” system⁵⁴ face difficulties in maintaining constant tension due to the relaxation characteristics of glass-sealed patch membranes⁴⁰⁻⁴³ and the bulged planar lipid bilayers.⁵⁴ The tension-clamp CBB was validated using KcsA and TREK-1 potassium channels, demonstrating reproducible channel responses to repeated tension changes over a long time course.

The tension-clamp CBB system has significant potential for further development. The tension step speed was set to moderate in the long-run experiments (Figure 6) compared with the short-run experiment (Figure 5). However, it can be speeded up by finely tuning the feedback parameters while maintaining bubble integrity. Practical applications include loading sinusoidal and other tension variations, enabling the examination of frequency responses of tension-dependent channel activity. The system also serves as a test platform for evaluating tension-sensitive dyes.⁷⁶⁻⁷⁸ Additionally, it can form membranes with arbitrary lipid compositions and asymmetric bilayers,⁵² allowing distinct tension to be applied to each leaflet—a feature reserved for future studies. Unlike other static systems, the lipid compositions of a bilayer or leaflet are immediately changed through the “membrane perfusion” method.^48,52 The “Chart” software allows tension time courses to be designed and operated automatically. The size-clamp system stabilizes experiments by maintaining the bubble size, preventing spontaneous size changes. This method also has critical additional applications, such as replacing surface chemistry experiments conducted with the pendant drop method⁷⁹ under size-clamp conditions. Moreover, the size clamp also enables automatic CBB formation via the Chart program, such that slow blowing of bubbles at the beginning to avoid breakage secures automatic bubble formation and maintenance. The entire control system is moving toward establishing a CBB robot for automated lipid bilayer formation and manipulation, simultaneously evaluating membrane tension and single-channel behavior.

Study Limitations

Various methods for membrane-tension experiments have been developed. For the tension measurements, membrane tether pulling from cell membranes has a solid physical basis, evaluating in situ membrane tension as low as 0.01 mN·m^–1.³⁵ This method is, however, confined to tension measurements without tension manipulations and channel activity measurements. Patch-clamp methods can evaluate membrane tension while applying tension during single-channel current measurements. However, the unknown tension is applied upon giga-seal formation, which cannot be evaluated precisely, and evaluating the small curvature of the patch membrane is technically challenging for precise evaluation of absolute membrane tension.³⁹ The solvent injection assay to droplet lipid bilayer³⁷ is straightforward, but underlying physicochemical processes upon volume expansion are complex. Freestanding lipid bilayer tensiometer⁵⁴ drives tension changes by applying hydrostatic pressure, and tension can be evaluated from membrane curvature. However, a freestanding torus containing a bulk organic solvent supports the freestanding lipid bilayer. After bulging of the membrane that includes the torus upon hydrostatic pressure application, equilibration and relaxation between the bilayer and bulk torus phases spontaneously occur, which prevents steady maintenance of membrane tension.

In contrast, tension-clamp CBB is based on simple physicochemical principles, and rapid changes in leaflet tension are immediately equilibrated compared to the above systems. Real-time feedback control has never been considered in tension control experiments. Among others, distinct tension control in each leaflet is a specific feature of the tension-clamp CBB, which has never been attained. One limitation of the system is the fragile objectives of mechanical control, which are especially prominent at very low tension. Below 0.8 mN·m^–1, stable maintenance of bubbles is challenging, which could, however, be overcome in future studies.

Conclusions

While the CBB is an open system regarding chemical equilibrium, it is a straightforward mechanical system driven by bubble pressure manipulations. In contrast, the bilayer tension is governed by the force balance between monolayers and leaflets (Young principle) and is not directly driven by the bubble pressure. Separate manipulation of each bubble drives monolayer tension directly, leading to leaflet tension control via feedback control, which is integrated into controlled bilayer tension and constituting the tension-clamp system. The tension-clamp CBB has an impact on mechanobiology studies, as does the impact of the voltage-clamp introduced into electrophysiology. The tension-clamp CBB extends the frontier for quantitative mechanobiology by characterizing the biophysical properties of membranes and mechanosensitive channels.

Methods

Building the tension-clamp CBB system requires a solid understanding of the physicochemical principles and mechanical operations of the CBB.⁵⁰ Thus, we begin by examining these principles.

Principles of the CBB System

We first describe the CBB system, including the formation processes, which help us understand the underlying physicochemical and mechanical principles. The CBB is formed using the following process.^46,47,52 Electrolyte bubbles are blown into an organic solvent, typically hexadecane, from a fine glass pipet with a tip diameter of 30 μm (Figure 1). Phospholipids, dispersed as liposomes in the pipet solution, spontaneously migrate to the surface of the newly formed bubble, creating a lipid monolayer. The bubble size (30–50 μm in radius) is maintained by fine-tuning the bubble pressure using a pneumatic injector connected to the pipet. This pressure line is equipped with a precise gauge that measures bubble pressure below 1000 Pa. Each bubble is physically bound to a supporting pipet, and two bubbles interact mechanically via the bilayer because two membrane leaflets adhere to each other. The bubbles push and pull upon mechanical changes in the bubbles. These mechanical stresses can be relieved by adjusting the pipet distance.

Due to its design, the CBB is a metastable open system (Figure 1B). Factors influencing the time-dependent lipid density in each monolayer substantially affect the bubble stability. Consequently, the bubble size can change spontaneously, affecting the bilayer tension. The system’s metastable open systems involve the following: (i) Open Bubble System: each bubble is an open system connected to a supporting pipet that maintains the bubble pressure (holding pressure). Bubble pressure is under equilibrium with that of the pipet and capable of pressure manipulation, yielding monolayer tension changes governed by the Young–Laplace principle. Bubbles are also open in chemical compositions. Electrolytes within the bubble can freely diffuse into the bulk pipet solution. (ii) Lipid exchanges: each leaflet is continuous with the respective bubble monolayer, forming a bulk reservoir in equilibrium with the leaflet. Lipids in monolayers and leaflets are also supplied to and from liposomes dispersed in the bubble solution.⁸⁰ (iii) Interleaflet interactions: the two leaflets interact through adhesion energy,^81,82 which varies substantially, such as at applied membrane potentials. These chemical and physical interactions between the leaflets and the surrounding media alter the lipid density in a leaflet, preventing the system from reaching a true equilibrium. For instance, the slow partitioning of lipids into a monolayer gradually decreases the monolayer tension, causing the bubble to expand slowly. Maintaining bubble size and bilayer tension requires precise control of bubble pressure in this metastable system as pressure is the only adjustable parameter.

Young–Laplace Principle

Bubbles were maintained by the steady application of holding pressure, governed by the Young–Laplace principle

1

where P is the bubble pressure, γ_m is the monolayer tension, R₁ and R₂ are the principal radii of the bubble, and R_avg is the harmonic average of the bubble radii

2

This Young–Laplace relation can be transformed from a pressure-radius relation to a pressure–volume relation by assuming spherical bubbles

3

Thus, γ_m is shown as a function of P and V in a 3D plot (Figure 6). Here, γ_m varies linearly with P, while the slope depends on V. The bubbles expand and contract in quasi-equilibrium on this 3D surface. Representative experimental trajectories, keeping or jumping monolayer tension, are superimposed on the surface.

Young Principle

At the contact of two bubbles, bilayer tension is generated owing to interfacial force balance. The Young principle states that leaflet tension is determined from the monolayer tensions via a contact angle, θ,

4

The bilayer tension is then simply the sum of the two leaflet tension values

5

Although the monolayer tension is directly controlled by pressure (eq 1), the contact angle is governed by the force balance between the monolayers and the bilayer

6

In parallel, adhesion energy is expressed as

7

Adhesion energy is related to the contact angle,^81,82 which is influenced by factors such as monolayer tension, organic solvents, and membrane lipids. The force balance between monolayers and a bilayer is not directly manipulable. Therefore, while the bubble-size clamp is straightforward, the tension clamp involves two physical processes: changes in the monolayer tension followed by changes in the bilayer tension via alterations in the contact angle.

Generally, as contact angles increase, the bubbles interact intimately and the two leaflets are stabilized by the adhesion energy. However, this study uses hexadecane as a bulk organic solvent, where the contact angles are small. Accordingly, the adhesion energy is minimal, and the bubbles behave nearly independently.

Tension Measurement Procedure

Determining the bubble pressure, radius, and contact angle between the two bubbles is necessary to measure the bilayer tension. The bubble geometry was analyzed by fitting a contour with an ellipse (see the Supporting Information), which provided the principal radii. Additionally, the contact angles between the two bubbles were measured. From the bubble radii and pressure, the monolayer tension was calculated by using the Young–Laplace principle (eq 1). The leaflet tension of each bilayer was then derived from the monolayer tension and contact angle using Young’s principle (eq 4). Consequently, the bilayer tension was determined as the sum of the tensions of the two leaflets (eq 5).

System Design for the Size- and Tension-Clamp

The tension-clamp system was developed based on the well-established CBB system. To build a feedback system, we initially configured a bubble-size clamp system due to its straightforward design. Figures 2 and 7 illustrate the feedback system for a single bubble. Maintaining a constant bubble pressure alone is insufficient in the CBB to sustain a constant bubble size as the monolayer tension varies. The system comprises three units: a pressure-operating unit, an image analysis unit, and a control unit.

The pressure-operating unit includes a fine pressure gauge that monitors the bubble pressure below 1000 Pa. Concurrently, the bubble pressure is manipulated using a pneumatic microinjector driven by a stepping motor. For the size clamp, the image analysis unit captures bubble-shape images with a video camera and extracts the geometrical parameters of the bubble radii using image analysis techniques. The control unit compares the measured and preset bubble size, processes this data in the control block, and feeds it to the motor driver to fine-tune the bubble pressure. For the tension clamp, the image analysis unit also provides data on the contact angles. The control unit collects both bubble pressure and geometrical data to calculate the membrane tension, which is then used for feedback control of the bubble pressure. The objective of the control is bilayer tension, and an uncontrollable contact angle intervenes between monolayer and leaflet tension. The closed-loop feedback control allows the accommodation of bilayer tension. In this study, we manipulate two bubbles simultaneously.

Image Analysis Unit

The image analysis unit, as depicted in Figure 7, extracts the geometric parameters of the two contact bubbles captured by a video camera on an inverted microscope. Figure 7B presents a representative photograph of a frame captured by the camera, showing a pair of bubbles and glass pipettes. The vertical positions of the bubbles were manually adjusted to be horizontally aligned, ensuring that the bubble edges were in focus while the pipettes, being out of the focal plane, appeared blurred. The bubbles are small (R: 30–50 μm), so gravitational effects on shape deformation are negligible (R ≪ capillary length: 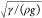, where ρ is the liquid density and g is the gravitational acceleration).⁷⁹ Each bubble forms an oblate or prolate spheroid due to forces such as bilayer adhesion energy^81,82 and mechanical constraints from the pipet positions along the polar axis across the bubbles. Consequently, the bubble shape in the focal plane is a truncated ellipse.

First, we detected the boundaries of the bubbles and the corner points where the left and right boundaries meet (see Supporting Information, Figure S2). Boundaries and corner points are identified using suitable edge and corner detection operators from fundamental image-processing techniques.⁸³ Since the bubble shapes can be accurately modeled with a slanted ellipse, their geometric parameters are obtained by fitting each boundary to the parametric equation of an ellipse

8

Coefficients a–e are determined using the least-squares technique. From these coefficients, the geometric parameters of the bubbles are readily derived, including the bubble center (c_x, c_y), the radii of the major and minor axes (r_a and r_b), and the tilt angle φ from the polar axis across the bubbles. The contact angles where the two ellipses merge were also evaluated. These geometric features and the ellipses fitted using eq 8 were superimposed on the bubble image.

Bubble Pressure Operation Unit

Bubble Pressure Monitoring Unit

A fine pressure gauge (DP103; Validyne Engineering, Los Angeles, CA, USA) was connected to a glass pipet holder to monitor bubble pressure continuously. The pressure readings were amplified by using a signal amplifier (PA701; Krone, Tokyo, Japan). The amplified signals were digitized with a 16 bit analog-to-digital converter and transmitted to a personal computer (PC) for analysis.

Bubble Pressure Control Unit

Fine-tuning of the bubble pressure is essential for maintaining stable bilayer tension. The pressure was controlled using a pair of pneumatic microinjectors (IM-11-2, NARISHIGE Co., Ltd., Japan; Figure S1), initially designed for manual operation. A stepping motor (PKP523N12B, ORIENTAL MOTOR Co., Ltd., Japan) was mounted to the injector’s rotational axis, as depicted in Figure 7A (see Supporting Information, Figure S1), to enable computer control. The stepping motor rotates in response to pulse counts from the PC, with a pulse count of 10,000 rotating the motor axis by 360°. This setup allows for seamless switching between feedback and manual control, enhancing experimental flexibility.

Control Unit

By integration of geometrical parameters and bubble pressures, bilayer tension was numerically evaluated in real-time. Simultaneously, stepping motors allowed precise adjustment of bubble pressure controlled by a control unit. We aimed to control the bubble pressure to maintain a constant bubble size (size-clamp) or bilayer tension (tension-clamp). This section first describes bubble-size clamping and then extends to tension clamping. Figure 7A presents a block diagram of the control system. Signals within the diagram include the following: r(t): the reference or clamping target value for size or tension; y(t): the measured bubble size or tension; e(t): the error or difference in size or tension; u(t): the control block output; ω(t): the rotation angle of the injector’s stepping motor; p(t): the bubble pressure; r(t): the bubble radius; and θ(t): the contact angle.

First, using a negative feedback control technique, we developed a size-clamp system to maintain a constant bubble radius. The control objective is the harmonic average of the bubble radii, R_avg (eq 2). Here, r(t) is the reference (clamping target) value for y(t), and e(t) is the error within the closed loop [e(t) = r(t) – y(t)]. We employed a simple PID control technique in the control block.⁶² The control block outputs are based on error e(t), where k_p and k_d are proportional constants

9

The output u(t) was sent to the pressure-operating unit as a pulse count to rotate the axis. The motor drive then produced the rotation angle, ω(t), for the stepping motor. A fine pressure gauge continuously monitored changes in the bubble pressure p(t). Simultaneously, the image analysis unit retrieved the bubble radii [R_avg(t)], which were fed back into the size-clamp system.

Our ultimate goal is a membrane tension-clamp system, which can be achieved by changing the control target from R_avg to the membrane bilayer tension γ_bil (eq 5). An additional geometric parameter, the contact angle, was extracted from image analysis to calculate γ_bil (eqs 1, 4, and 5). Referring to the preset γ_bil, e(t) was processed in the control block to yield u(t).

For simplicity, all time-dependent variables are represented as continuous functions of t. In reality, the temporal variable t is discretized, converting the continuous control system into a discrete one. For instance, u(t) represents the temporal density of the pulse count before the discretization. The Supporting Information provides detailed feedback on the control system information, including its digital counterpart.

Electrical Interference of the Control System to the Electrophysiological System

In the tension-clamp system, the primary task is to examine the single-channel activity of the membrane-reconstituted channels. The electrophysiological unit, consisting of an amplifier, is susceptible to electrical background noise. Consequently, electrical background noise can arise from the equipment, particularly the stepping motor, which necessitates proper shielding.

Graphical Interface for Tension-Control Experiments (Chart Program)

We developed a user-friendly interface program named the Chart program to manage the experimental protocol for tension-control experiments. This graphical interface allows users to set and edit the time course of the bilayer tension changes. Using a mouse, users can specify the start and end times for a particular tension level, which the system reproduces during the experiment (see Supporting Information, Figure S3). Feedback parameters such as k_p and k_d can be adjusted for situations requiring a rapid step response to prevent ringing and to avoid bubble bursting.

CBB Experiments

The CBB method was previously reported.^46,47 For the KcsA channel experiments, asymmetric membranes with acidic lipids in the inner leaflet are necessary to maintain channel activity. The bubble on the outer leaflet side (pH 7.4) contained liposomes of POPC,²³ whereas the bubble on the inner leaflet side contained liposomes of POPG, reconstituted with the E71A mutant KcsA channel (proteoliposomes). The two pipet solutions contained 200 mM of KCl electrolyte, where the solutions on the inner and outer leaflet sides had pH values of 4 and 7.4, respectively. The TREK-1 channel was reconstituted into azolectin liposomes, and single-channel recordings of the TREK-1 channel were performed in a symmetrical solution of 200 mM KCl and 10 mM HEPES (pH 7.4).

Conventional Single-Channel Current Recordings

Single-channel currents were recorded using an analogue amplifier (Axopatch 200B, Molecular Devices, USA). A four-pole Bessel filter with a cutoff frequency f_c^Bessel of 1 kHz (−3 dB) for KcsA and 5 kHz for TREK-1 channels was employed, and the sampling frequency was set to 5 kHz and 25 kHz for KcsA and TREK-1, respectively.

Tension-Dependent Analysis of KcsA Channels

The amplitude histograms were compiled from current traces of multichannel activity of 30 s (Figure 4), which were fitted with multiple Gaussian distributions. The number of channels embedded in a membrane is evaluated from that at the highest tension (8 mN·m^–1), where the open probability reaches more than 0.9. Then, open channel probability was evaluated from the relative contribution of each current level through fitting with a binomial distribution, given the number of active channels in the membrane.

The tension-dependent open probability was fitted with the Boltzmann function

10

where ΔG is the free energy difference for open and closed channels, γ is the bilayer tension, ΔA is changes in the channel cross-sectional area upon opening, k_B is the Boltzmann constant, and T is the absolute temperature.

BPoF Analysis for Flicker Gating of the TREK-1 Channel

The BPoF method is described in detail in a previous report.⁷¹ Conventionally recorded single-channel current data (Bessel-filtered at the cutoff frequency of 5 kHz and the sampling rate of 25 kHz) are digitally filtered through a first-order filter at a certain cutoff frequency.⁷¹ A current amplitude histogram is compiled from the filtered trace, which is fitted with the beta distribution function, yielding underlying flicker rate constants.

Materials

Reagents

The phospholipids used for the KcsA study were 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(10-rac-glycerol) (sodium salt) (16:0–18:1 PG, POPG) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (sodium salt) (16:0–18:1 PC, POPC). These lipids were purchased from Avanti Polar Lipids (Birmingham, AL, USA). For the TREK-1 experiments, azolectin (l-α-phosphatidylcholine type IV-S) was used, which was purchased from Sigma-Aldrich (St. Louis, MO, USA). All other chemicals were procured from Nacalai Tesque (Kyoto, Japan).

KcsA Channel

The expression and purification of the E71A mutant of the KcsA channel have been previously described.⁶³ Liposomes and channel-incorporated liposomes (proteoliposomes) were prepared following established protocols.⁶⁶ POPC and POPG (2 mg/mL) in chloroform were dried and dispersed in a 200 mM KCl solution (pH 7.4 or 4.0) to produce a liposome suspension. Purified channel proteins were incorporated into liposomes by dilution at a lipid–protein weight ratio of 2000:1.

TREK-1 Channel

Cloning, Expression, and Purification of hTREK-1

The Homo sapiens TREK-1 complementary DNA was codon-optimized for Saccharomyces cerevisiae and synthesized by Thermo Fisher Scientific (Pittsburgh, PA, USA). The optimized TREK-1 DNA, encoding amino acids 21-322 with N95 and N122 replaced with glutamine, was fused to double ProteinA tags at the N terminus, separated by a PreScission protease recognition sequence, and cloned under the control of the S. cerevisiae GAL1 promoter into the plasmid pDDGFP_LEU 2d, a gift from Simon Newstead (RRID: Addgene_58352).⁸⁴ The constructed plasmid, named pProA-TREK-1, was sequence-verified. The pProA-TREK-1 plasmid was introduced into the S. cerevisiae strain obtained from the National BioResource Project (NBRP ID: BY20173, strain alias: CB018; MATa Δpep4::HIS3 prb1::hisG prc1::hisG ade2-1 can1-100 his3-11,15 leu2-3,112 trp1-1 ura3-1), using the LiAc/Single-stranded carrier DNA/PEG method.⁸⁵

Yeast cells were grown on an SD plate with dropout supplements (-Ura, Takara Bio Co., Ltd., Shiga, Japan) at 30 °C. Colonies were propagated in SD medium with dropout supplements (−Ura/–Leu, Takara Bio Co., Ltd.) at 30 °C to saturation. Harvested cells from a 25 mL SD −Ura/–Leu medium culture were used to inoculate 500 mL of expression medium [1% yeast extract, 2% peptone, 2% (w/v) sodium lactate, and 3% (w/v) glycerol] at 30 °C. When OD₆₀₀ reached 0.6, TREK-1 protein expression was induced by adding 50 mL of 20% galactose and incubating at 30 °C for 20 h.

After centrifugation, the cell pellet was resuspended in lysis buffer [20 mM HEPES-KOH (pH 7.4), 400 mM KCl, 1 mM dithiothreitol, 20% (v/v) glycerol, 0.5 mM EDTA, 1 mM phenylmethylsulfonyl fluoride; 3 mL per 1 g cells]. Cells were lysed using glass beads (425–600 μm) (Sigma-Aldrich, St. Louis, MO, USA) in a vortex mixer (Electro Scientific Industries, Inc., Beaverton, OR, USA) at 4 °C with 2 cycles of 7 min on and 7 min off. Cell debris was removed by centrifugation at 3000g for 10 min at 4 °C, and the supernatant was ultracentrifuged using an S50A rotor (Eppendorf Himac Technologies Co., Ltd., Ibaraki, Japan) at 150,000g for 1 h at 4 °C. The membrane pellet was resuspended in lysis buffer containing 2% (w/v) n-dodecyl-β-d-maltoside (DDM) (Dojindo, Kumamoto, Japan) (1.5 mL per 1 g cells) and solubilized at 4 °C for 4 h with agitation. Then, the insoluble material was removed by ultracentrifugation at 150,000g for 30 min at 4 °C. The solubilized membrane fraction was mixed with Rabbit-IgG agarose (Sigma-Aldrich, St. Louis, MO, USA) (1 mL of resin slurry per 20 mL of lysate) at 4 °C for 2 h with agitation. The resin was transferred to a prewashed bio-Spin column (Bio-Rad, Hercules, CA., USA) and washed with 10 bed volumes of wash buffer [10 mM HEPES-KOH (pH 7.4), 200 mM KCl, 20% (v/v) glycerol, and 0.06% (w/v) DDM]. The resin was then suspended in half a volume of wash buffer containing 5 U/mL of PreScission protease (Takara Bio Co., Ltd.) and incubated overnight at 4 °C. The elution sample was mixed with Ni-NA agarose (FUJIFILM Wako, Osaka, Japan) for 1 h at 4 °C to remove PreScission protease.

Reconstitution of hTREK-1 into Liposomes

The hTREK-1-reconstituted liposomes were prepared by the dilution method using azolectin (l-α-phosphatidylcholine type IV-S, Sigma-Aldrich, St. Louis, MO, USA) and a purified hTREK-1 channel, following a previous report.⁵³ The lipid–protein ratio of the reconstituted liposome was 2000:1 (weight/weight). The liposome suspension contained 200 mM KCl and 10 mM HEPES (pH 7.4) with a lipid concentration of 2 mg/mL.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.4c09017.

• Additional experimental details and mathematical handling of the feedback control (PDF)

• CBB images upon a tension-jump experiment (AVI)

Author Contributions

S.O. and M.I. conceived the basic idea. S.O., T.Y., and M.I. developed the method. Y.M., T.M., M.T., M.I., and S.O. performed the experiments. The manuscript was written through contributions from all authors. All authors have approved the final version of the manuscript.

The authors declare no competing financial interest.