CaY@C_2n: Exploring Molecular Qubits with Ca–Y Metal–Metal Bonds

Abstract

Metal–metal bonding is crucial in chemistry for advancing our understanding of the fundamental aspects of chemical bonds. Metal–metal bonds based on alkaline-earth (Ae) elements, especially the heavier Ae elements (Ca, Sr, and Ba), are rarely reported due to their high electropositivity. Herein, we report two heteronuclear di-EMFs CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀, which contain unprecedented single-electron Ca–Y metal–metal bonds. These compounds were characterized by single-crystal X-ray crystallography, electron paramagnetic resonance (EPR) spectroscopy, and DFT calculations. The crystallographic study of CaY@C_s(6)-C₈₂ shows that Ca and Y are successfully encapsulated into the carbon cage with a Ca–Y distance of 3.691 Å. The CW-EPR study of both CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀ exhibits a doublet, suggesting the presence of an unpaired electron located between Ca and Y. The combined experimental and theoretical results confirm the presence of a Ca–Y single-electron metal–metal bond with substantial covalent interaction, attributed to significant overlap between the 4s4p orbitals of Ca and the 5s5p4d orbitals of Y. Furthermore, pulse EPR spectroscopy was used to investigate the quantum coherence of the electron spin within this bond. The unpaired electron, characterized by its s orbital nature, is effectively protected by the carbon cage, resulting in efficient suppression of both spin–lattice relaxation and decoherence. CaY@C_s(6)-C₈₂ behaves as an electron spin qubit, displaying a maximum decoherence time of 7.74 μs at 40 K. This study reveals an unprecedented Ae–rare-earth metal–metal bond stabilized by the fullerene cages and elucidates the molecular qubit properties stemming from their unique bonding character, highlighting their potential in quantum information processing applications.

Introduction

Metal–metal bonds are of great significance in expanding our understanding of the nature of chemical bonding.¹⁻³ Over the past two decades, a number of remarkable discoveries like Zn–Zn,⁴ Cr–Cr,⁵ Mg–Mg,⁶ and Be–Be⁷ bonds, have been reported, attracting great attention to metal–metal bonding. To date, the studies of metal–metal bonding are mainly focusing on the main⁸ and transition group⁹ elements. Metal–metal bonds based on alkaline-earth (Ae) elements, especially the heavier Ae elements (Ca, Sr, and Ba), are rarely reported due to their high electropositivity. In this case, only a few examples of metal–metal bonds involving Ae metals have been reported so far. All of these bonds are formed between Ae and main-group^1,10−14 or transition metals^1,15−17 with the exception of Be–Be and Mg–Mg bonds. In particular, the formation of metal–metal bonds between Ae metals and rare-earth (Re) metals is challenging with conventional synthetic methods due to the high electropositivity of both Ae and Re metals. To the best of our knowledge, this kind of metal–metal bond has not been reported to date.

Metal atoms can be encapsulated into the internal cavities of fullerenes to form endohedral metallofullerenes (EMFs), which are stabilized by transferring electrons from the metals to the carbon cages. Di-EMFs, i.e., carbon cages encapsulating two metal atoms, are considered as an ideal model for investigating metal–metal bonding. On the one hand, carbon cages can protect metal dimers from external influences. On the other hand, the Coulomb repulsion between the metal ions can be limited by the confinement effect of the carbon cages, which can shorten the distance between the metals and thus facilitate the formation of metal–metal bonds.¹⁸ Indeed, recent studies have indicated that direct metal–metal bonds can be formed between the metal ions encapsulated in di-EMFs, such as M₂@C₈₂ (M₂ = Sc₂,¹⁹ Y₂,¹⁸ Er₂,²⁰ Lu₂,²¹ and ScY²²) and M₂@C₈₀ (M₂ = U₂²³ and Th₂²⁴).

In particular, single-electron metal–metal bonds can also be obtained in the form of dimetallofullerene derivatives²⁵⁻³⁰ or azafullerenes.³¹⁻³⁴ With the encapsulated [Ln-e-Ln] bonding motifs (Ln = Dy, Gd, and Tb), these di-EMFs exhibit excellent magnetic properties.²⁹ Such special properties of single-electron metal–metal bonds have also been found in organometallic chemistry. Recently, Gould et al. reported the dilanthanide complexes (Cp^iPr5)₂Ln₂I₃ with single-electron Ln-Ln bonds (Ln = Gd, Tb, or Dy), which displayed the highest 100 s blocking temperatures among all reported single-molecule magnets up to date.³⁵

Recently, we reported a series of mixed-valence di-EMFs with single-electron actinide-lanthanide metal–metal bonds, namely, ThDy@C_2n (2n = 72, 76, 78, and 80) and ThY@C_2n (2n = 72 and 78).³⁶ Surprisingly, these di-EMFs are stable in their pristine form and do not require any derivatization. A similar case was reported by Yang et al., who synthesized the endofullerene LaTi@C_2n.³⁷ Both fullerene families share a common feature: the two encapsulated metal atoms have an odd sum of valence electrons, which appears to facilitate the formation of the single-electron metal–metal bonds inside the pristine fullerene cages. This inspires us to explore the possibility of an Ae–Re metal–metal bond, in which alkaline-earth elements possess two valence electrons and rare-earth elements possess three valence electrons.

Herein, we report the successful synthesis and characterizations of Ca-based heteronuclear di-EMFs, i.e., CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀. These novel compounds were characterized by single-crystal X-ray crystallography, UV–vis–NIR spectroscopy, electron paramagnetic resonance (EPR) spectroscopy, and theoretical calculations. We identified the formation of an unprecedented Ca–Y single-electron metal–metal bond inside a carbon cage. Moreover, the electron in this bond exhibits significant spin coherence at relatively high temperatures, behaving as a qubit with potential utility for quantum information science.

Results and Discussion

CaY@C_2n (2n = 80 and 82) were synthesized by a modified Krätschmer–Huffman DC arc discharge method.³⁸ In brief, 0.33 g of CaO, 0.67 g of Y₂O₃, and 2.13 g of graphite powder (molar ratio of Ca:Y:C = 1:1:30) were packed in each graphite rod (6.7 g, without filling). About 300 graphite rods were vaporized in the arcing chamber under a 200 Torr He atmosphere. The resulting carbon soot was extracted by CS₂ for 24 h. Then, a multiple-step HPLC procedure was employed to isolate and purify CaY@C_2n (2n = 80 and 82). The purity of CaY@C_2n (2n = 80 and 82) was confirmed by the single peaks in the HPLC chromatogram and matrix-assisted laser desorption/ionization time-of-flight mass spectrometry (MALDI-TOF-MS). The MALDI-TOF-MS spectra of CaY@C₈₂ and CaY@C₈₀ show single peaks at m/z = 1112.898 and 1088.856, respectively, and their isotopic distributions agree well with the calculated ones (Figure S3). The estimated yields of CaY@C₈₀ and CaY@C₈₂ are ca. 0.20 and 0.22 mg, respectively.

Ca-based heteronuclear di-EMFs have rarely been reported before. The only study of the synthesis of CaHo@C₈₂ was reported in 2007.³⁹ However, lacking characterization and quantum-chemical studies, the molecular and electronic structure of this compound has never been identified. In this study, black block cocrystals of CaY@C₈₂·[Ni^II(OEP)]·2C₆H₆ (OEP = 2,3,7,8,12,13,17,18-octaethylporphyrin anion) were obtained by slow diffusion from a benzene solution of Ni^II(OEP) into a CS₂ solution of CaY@C₈₂. The molecular structure of CaY@C₈₂ was unambiguously determined by single-crystal X-ray diffraction and refined as CaY@C_s(6)-C₈₂, which was monoclinic with the C2/m space group (Figure 1).

Figure 1.

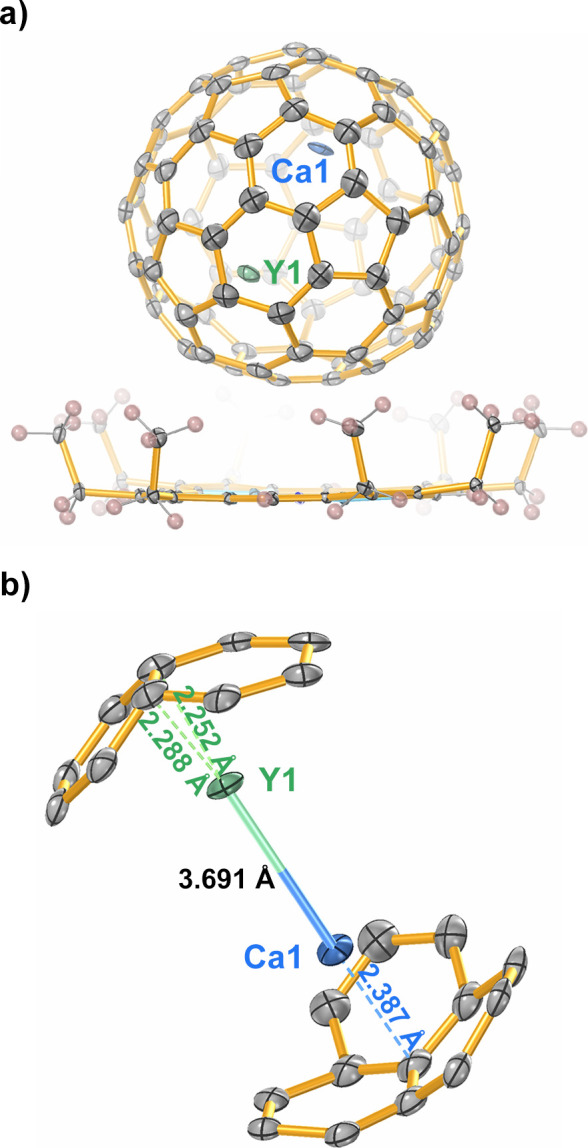
(a) ORTEP drawing for CaY@C_s(6)-C₈₂·[Ni^II(OEP)] with 15% thermal ellipsoids. Only one cage orientation and the major Ca and Y sites are shown. For clarity, the solvent molecule and minor metal sites are omitted. (b) Detailed structure of the major Ca and Y sites interacting with the closest fragments of the C_s(6)-C₈₂ cage.

Due to the crystallographic mirror plane of the C2/m space group, the carbon cage of CaY@C_s(6)-C₈₂ has two equivalent orientations with the same occupancy of 0.5. The metal atoms inside the carbon cage exhibit some degree of disorder. Ca1 and Y1 were identified as the major sites for Ca and Y atoms, respectively, with an occupancy of 0.3157(17) for both. Ca1_m and Y1_m are generated from Ca1 and Y1 through the crystallographic mirror plane. The minor sites, namely, Ca2, Ca3, Y2, and Y3, are all located on the crystallographic mirror plane. Ca2 and Y2 have the same occupancy (0.172(3)) as well as for Ca3 and Y3 (0.196(3)). For clarity, only one orientation of the carbon cage and the major sites of internal metal atoms, i.e., Ca1 and Y1, are selected for further analysis.

Similar to the position of Y3 in Y₂@C_s(6)-C₈₂,¹⁸ Y1 resides over the [6,6] carbon bond with the shortest Y cage distances ranging from 2.252 to 2.288 Å, which is in good agreement with the density functional theory (DFT) calculations (2.345–2.357 Å, Figure S6). This Y cage distance is slightly shorter than that in Y₂@C_s(6)-C₈₂ (ranges from 2.323 to 2.331 Å in the X-ray structure and from 2.407 to 2.421 Å at the DFT level), which suggests that the Y cage interaction is enhanced by replacing the other Y atom with a Ca atom. Furthermore, when a Y atom is replaced with a Ca atom, the position of the respective metal atom within the carbon cage is altered. Different from Y5 in Y₂@C_s(6)-C₈₂, which is located near the [5,6] bond, Ca1 in CaY@C_s(6)-C₈₂ is located at the junction of the three hexagons with the Ca cage shortest distance of 2.387 Å. A similar phenomenon has been observed when a Sc atom replaces a Y atom in Y₂@C_3v(8)-C₈₂.²² The distance of Ca1–Y1 is determined to be 3.691 Å (vs 3.705 Å in calculations), which is comparable to the Y–Y distance in Y₂@C_s(6)-C₈₂ (3.635 Å vs 3.613 Å in calc.)¹⁸ and the Sc–Y distance in ScY@C_3v(8)-C₈₂ (3.674 Å).²² Considering the presence of metal–metal bonds in both Y₂@C_s(6)-C₈₂ and ScY@C_3v(8)-C₈₂, this Ca–Y distance might indicate that there is a bonding interaction between Ca and Y.

The electronic features of CaY@C_2n (2n = 80 and 82) were studied by UV–vis–NIR spectroscopy (Figure S5). The spectrum of CaY@C_s(6)-C₈₂ exhibits absorption peaks at 765, 828, and 1190 nm, which are similar to those of M₂@C_s(6)-C₈₂ (M = Lu,²¹ Y,¹⁸ and Er²⁰). It is well-known that the UV–vis–NIR spectra of EMFs with the same isomer structure and formal charge state of the carbon cage are almost identical due to π→π* transitions of the cage.⁴⁰ Consequently, this UV–vis–NIR spectrum suggests that CaY@C_s(6)-C₈₂ has the same electronic configuration with M₂@C_s(6)-C₈₂ (M = Lu, Y, and Er), namely, (CaY)⁴⁺@C₈₂^4–. The spectrum of CaY@C₈₀ exhibits a major absorption peak at 672 nm, which is similar to the one observed in the spectrum of Sc₂O@C_2v(5)-C₈₀.⁴¹ This suggests that the C_2v(5)-C₈₀ isomer is the same as the cage isomer of CaY@C₈₀, which can be formally described as (CaY)⁴⁺@C₈₀^4–.

To analyze the electronic structure and the Ca–Y bonding interaction, DFT calculations at the PBE0/TZP/D3⁴²⁻⁴⁸ level were performed for CaY@C_2n (2n = 80 and 82) cages, showing a spin-doublet ground electronic state for both of them (see computational details for more information). Different positions of Ca and Y atoms within the C_2v(5)-C₈₀ and C_s(6)-C₈₂ cages were computed to analyze the most likely location of the metals inside the cages (see Tables S3 and S4 and Figures S8 and S9). Our calculations show that the lowest-energy structure of CaY@C_s(6)-C₈₂ corresponds to the one observed in the X-ray structure. Other positions of the metals show a relative energy of 3.5 kcal·mol^–1 (orientation B in Table S4 and Figure S9) and around 9 kcal mol^–1 (C–E), which confirm the somewhat degree of disorder found in experiments. DFT optimizations of the crystallographic Ca2–Y2 and Ca3–Y3 positions evolve to orientation C (Figure S14). For CaY@C_2v(5)-C₈₀, the lowest-energy arrangement of the metals corresponds to their positioning analogous to the sites occupied by Sc atoms in Sc₂O@C_2v(5)-C₈₀.⁴¹ If the metal atoms exchange their positions, the relative energy increases to 4.2 kcal·mol^–1. Other positions of the metal atoms are found at higher energies (>12.2 kcal·mol^–1).

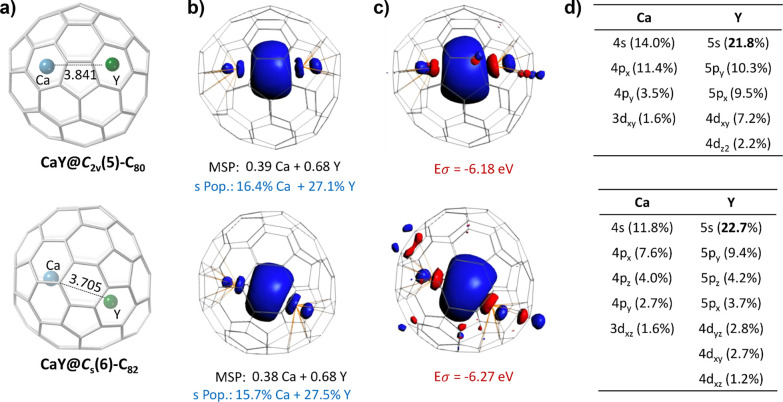
The following description corresponds to the lowest-energy geometries of CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂ (Figure 2). The optimized Ca–Y distances are 3.841 and 3.705 Å for CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂, respectively, resulting in the latter to be very close to experiments (3.691 Å). For CaY@C_2v(5)-C₈₀, the Ca and Y are both located at [6,6] bonds of pyracylene motifs, showing that the Y metal–cage distances (2.357 Å) are closer than those of Ca (2.473 Å) (Figure S7). In CaY@C_s(6)-C₈₂, the Ca is located at the center of a hexagon from an s-indacene motif with the closest metal–cage distance of 2.490 Å (vs 2.387 Å in experiments), while the Y is placed on top of a [6,6] bond of a pyracylene motif with metal–cage distances of 2.345–2.357 Å (Figure S6), slightly larger than those from experiments (2.252–2.288 Å). The position of Y in a pyracylene motif in CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂ is in accordance to the largest molecular orbital contribution of the LUMO+1 of neutral C_2v(5)-C₈₀ and C_s(6)-C₈₂ cages, as well as to the most negative region of the potential electrostatic maps of C_2v(5)-C₈₀^4– and C_s(6)-C₈₂^4– anions (see Figures S10 and S11, respectively).

Figure 2.

For CaY@C_2v(5)-C₈₀ (top) and CaY@C_s(6)-C₈₂ (bottom); (a) DFT-optimized structure, where the Ca–Y distance (in Å) is indicated. (b) Spin density distribution with an isosurface of ±0.002 au, Mulliken spin populations (MSP), and amount of s spin density population (s Pop.) of the metals. (c) Molecular orbital (MO) isosurface (±0.03 au) for the delocalized σ orbital a₁ for the α-spin with the corresponding MO energy (in eV). (d) Molecular orbital contributions of the σ-type bonding orbital formed essentially by ns, np, and (n – 1)d metal orbitals.

Figure 2b shows the spin density distributions for CaY@C_2n, indicating that the unpaired electron is delocalized between the two metal atoms. Additionally, Figure 2c illustrates that the unpaired electron resides in an a₁ sigma-type orbital, which results from a significant overlap between the 4s4p orbitals of Ca and 5s5p4d of Y (Figure 2d). Despite the fairly symmetric appearance of the spin density distribution and the sigma a₁ orbital representation, the atomic Mulliken spin populations of approximately 0.4 e for Ca and 0.7 e for Y indicate that the metal–metal bond displays a certain degree of polarization. This polarization is primarily driven by the s-type orbitals, with associated s spin density populations of around 16% for Ca and 27% for Y.

These data indicate that the formal oxidation states would be close to 1.5+ for Ca and 2.5+ for Y, if the unpaired electrons were equally shared. Thus, there is an electron transfer of four electrons from the CaY cluster to the C_2n cage, resulting in an electronic structure of (CaY)⁴⁺@(C_2n)^4– according to the ionic model. The molecular orbital (MO) diagrams for the ground spin-doublet state of CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂ are provided in the Supporting Information (SI). As mentioned, a delocalized sigma-bonding orbital a₁ is observed in both CaY@C_2n cages (Figure 2c) with the energy depending on the metal–metal bond length. Specifically, the shorter the Ca–Y distance (3.841 vs 3.705 Å), the lower the energy of the σ-bonding orbital (−6.18 vs −6.27 eV, respectively). In addition, both oxidation and reduction⁴⁹ of CaY@C_s(6)-C₈₂ are predicted to take place on the carbon cage, with the one-electron Ca–Y σ-bond remaining essentially unaltered (Figure S15).

Two notable features distinguish this novel Ae–Ln bond from the recently detected one-electron σ bond in ThLn@C_2n (Ln = Y and Dy).³⁶ (i) It exhibits some degree of polarization due to the larger electronegativity difference between Y (Pauling, 1.22) and Ca (1.00). (ii) There is minimal involvement of the 3d orbitals from Ca (Figure 2d). Additionally, this direct Ca–Y interaction clearly demonstrates that under specific conditions, the Ca orbitals can indeed participate in covalent interactions.

To further characterize the Ae(Ca)–Ln(Y) bond interaction, we performed the Bader’s quantum theory of atoms in molecules⁵⁰ analysis. Bader postulated the bond critical point (bcp) between two atoms as a necessary and sufficient condition for the atoms to be bonded. The corresponding values of the electron density (ρ) and the Laplacian of the electron density (∇²ρ) at the bcp for CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂ are provided in Table 1, which verify the presence of an accumulation of charge density in the center of the metal–metal bond. The electron density values of both CaY@C_2n systems closely resemble those of other reported systems, such as ThY@D_3h(5)-C₇₈,³⁶ Y₂@C₈₀-CH₂Ph,²⁷ and Y₂@C₇₉N³¹ as well as the hypothetical SrY@C_2v(5)-C₈₀ and SrY@C_s(6)-C₈₂ cages (see Table 1). It is worth noting that CaY@C_2n systems present slightly lower electron density values compared to the corresponding SrY@C_2n endohedral fullerenes, which show smaller metal–metal distances. All these systems present a negative sign in the Laplacian of the electron density; however, M–Y (M = Ca and Sr) systems show lower absolute values than for the other calculated EMFs. Larger absolute values of ∇²ρ are found for Ca–Y compared to Sr–Y systems, consistent with the fact that the Sr–Y σ bonds are somewhat more polarized. Interestingly, the CaY@C_2n systems exhibit the largest ρ values among other experimental reported Ca–X (X = Al, Sn, Co, and Fe) complexes.^10,14,16,51 Therefore, for instance, a Ca–Fe bond with a bond length of 2.98 Å⁵¹ displays a charge density of 0.022 e/ų, considerably lower than that observed for Ca–Y, even though the latter has a significantly longer bond length (Table 1). Furthermore, the Ca–Y bond shows a negative sign on the ∇²ρ, consistent with the Ca–Y covalent interaction deduced from the singly occupied delocalized σ orbital. The Ca–Y bonds characterized in this study can be considered as the bonds with the highest degree of covalent character involving a calcium atom reported to date.

Table 1. Computed EPR and Electronic and Structural Parameters for Different XY@C_2n Systems^g.

	CaY@C2v(5)-C80	SrY@C2v(5)-C80	CaY@Cs(6)-C82	SrY@Cs(6)-C82	ThY@D3h(5)-C78	Y2@C80-CH2Ph	Y2@C79N
g-value	1.983 (1.983)	1.972	1.979 (1.982)	1.969	1.803 (1.825)	1.978	1.975 (1.974)
Aa	236 (252)	266	245 (260)	275	206 (200)	204 (224)	203 (224)
d(Y–X)b	3.841	3.750	3.704 (3.147)	3.657	4.137 (4.144)	3.879	3.863
spin Yc	0.68	0.72	0.68	0.73	0.59	0.53	0.53
spin Xc	0.39	0.34	0.38	0.34	0.43	0.52	0.52
s Pop.d	27.1	30.0	27.5	30.7	22.4	21.4	21.3
εσLUMOe	–3.50	–3.34	–3.59	–3.38	–3.68	–3.95	–4.01
ρbcpf	0.091	0.106	0.100	0.112	0.107	0.108	0.109
∇2ρbcpf	–0.063	–0.027	–0.026	–0.015	–0.194	–0.204	–0.201

^aHyperfine coupling (in MHz).

^bMetal–metal distance (in Å).

^cAtomic Mulliken spin densities for Y and X.

^dAmount of the s spin density population on Y (in %).

^eEnergies of the sigma LUMO (beta) orbital (in eV).

^fElectron density and Laplacian of the electron density at the bond critical points are given in [e Å^–3] and [e Å^–5], respectively.

^gExperimental values are in parentheses.

Continuous-wave (CW) EPR spectroscopy experiments were also performed on CaY@C_2n (2n = 80 and 82) to obtain further information on their open-shell electronic structure. As is shown in Figure 3, the EPR spectra of purified CaY@C_2n (2n = 80 and 82) in a CS₂ solvent show, for each compound, a doublet at 290, 270, 250, 220, and 190 K, which indicates hyperfine coupling between an unpaired electron and an ⁸⁹Y nucleus (nuclear spin I = 1/2 of ⁸⁹Y, 100% natural abundance, while the nuclear spin of ⁴⁰Ca is 0 in 96.941% natural abundance). As the temperature decreases, the high magnetic field signal becomes increasingly more dominant compared to the low magnetic field signal. Such a kind of paramagnetic anisotropy results from insufficient rotational averaging due to the restricted motion of the Y nucleus and the unpaired electron.⁵² At 150 K, the hyperfine structure disappears, and the spectrum exhibits a single broad peak since the nonglassy CS₂ solvent freezes at this temperature, causing molecular aggregation where spin–spin dipolar interaction dominates over the hyperfine interaction. Fitting of the EPR spectra collected at 290 K revealed that the hyperfine coupling constants (abbreviated as hfcc or A below) of CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀ are 260 and 252 MHz, respectively (Figure S16). These hfcc constants are significantly larger than those found for Y@C₈₂ whose electron spin mainly resides on the carbon cage.⁵³ Thus, the strong hyperfine coupling in CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀ indicates that their unpaired electrons are mainly metal-centered, as confirmed by the spin density distribution (Figure 2b).⁵⁴ The Lorentzian line shape of EPR spectra indicates negligible hyperfine coupling from ¹³C, which is consistent with the result obtained from pulse EPR characterization (vide infra). The isotropic g-values of CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀ are 1.9819 and 1.9827, respectively, which are comparable to those of Y₂@C₇₉N (g = 1.9740)³¹ and Y₂@C₈₀(CH₂Ph) (g = 1.9733), as well as their spin densities.²⁷ Thus, EPR experiments also indicate the formation of a single-electron metal–metal bond between Ca and Y.

Figure 3.

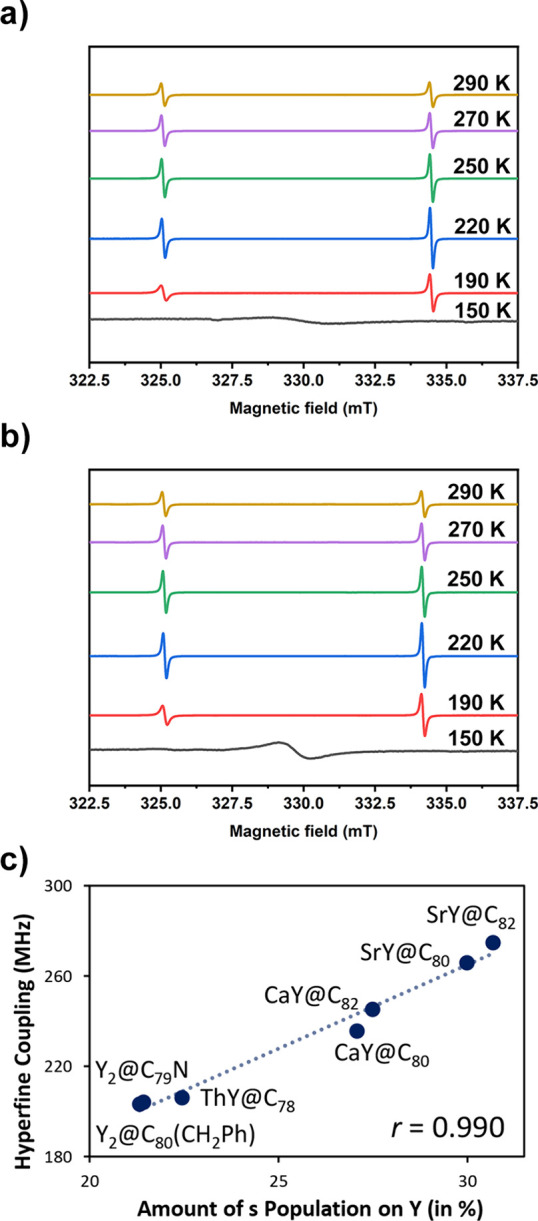
EPR X-band spectra of CaY@C_s(6)-C₈₂ (a) and CaY@C_2v(5)-C₈₀ (b) measured in CS₂ solution at 290, 270, 250, 220, 190, and 150 K. (c) Representation of the correlation between the hyperfine coupling constant (in MHz) and the amount of the s spin density population located on the Y atom (in %) for all the XY@C_2n systems shown in Table 1. The correlation coefficient r is also given.

DFT calculations are in full agreement with experiments (Table 1). The calculated g-values for CaY@C_2v(5)-C₈₀ and CaY@C_s(6)-C₈₂ are 1.983 and 1.979, respectively, nearly identical with the experimental values. The calculated hfcc are 236 MHz for CaY@C_2v(5)-C₈₀ and 245 MHz for CaY@C_s(6)-C₈₂, in good agreement with the experimental values (vs 252 and 260 MHz, respectively). The spin density located on the Y atom is the same for both CaY@C_2n cages (0.68 e). The slightly larger hfcc in CaY@C_s(6)-C₈₂ than in CaY@C_2v(5)-C₈₀ is most likely related to the larger amount of the s spin density population located on yttrium (27.5 vs 27.1%). These data are consistent with the electronic structure, as they indicate that the unpaired electron is confined to yttrium and delocalized on calcium, suggesting the formation of a polarized single-electron bond between Y and Ca atoms.

To further explore the electronic structure and EPR parameters on CaY@C_2n systems, a computational study involving other XY@C_2n families was performed. Table 1 provides the most relevant data from this DFT study. We have worked with some previously reported systems ThY@D_3h(5)-C₇₈,³⁶ Y₂@C₈₀(CH₂Ph),²⁷ and Y₂@C₇₉N,³¹ as well as with the hypothetical SrY@C_2n (2n = 80 and 82) family, where the Ca is replaced with a Sr atom in the corresponding CaY@C_2n (2n = 80 and 82) cages. Our calculations reproduce very well the experimental g-values and the hfcc of all of the systems analyzed herein, as seen in Table 1. ThY@D_3h(5)-C₇₈ shows the lowest g-value among these systems, and its hfcc is significantly lower than those of CaY@C_2n cages but very similar to Y₂@C₈₀(CH₂Ph) and Y₂@C₇₉N. This fact is related to the spin density of Y as well as the amount of the s spin density population located on the Y atom. For ThY@D_3h(5)-C₇₈, Y₂@C₈₀(CH₂Ph), and Y₂@C₇₉N, all of these values are very similar. CaY@C_2n cages show larger values of Mulliken spin density on Y (0.68 vs ∼0.59) and a larger amount of the s population on Y (27% vs ∼22%). Therefore, larger values of hfcc are observed in the CaY@C_2n cages. For the SrY@C_2n (2n = 80 and 82) family, although similar g-values are found, this hypothetical family displays the largest hfcc (266 MHz for SrY@C_2v(5)-C₈₀ and 275 MHz for SrY@C_s(6)-C₈₂), which is also in line with the larger values of Mulliken spin density of Y (∼0.72 e) and the amount of the s spin density population on Y (∼30%). Interestingly, a good correlation exists between the hfcc and the amount of the s population on the Y atom (Figure 3c). A reasonably acceptable correlation is still found if hfcc values are plotted with respect to the total spin population on Y (see Figure S13). We note that all of these systems present a two-center single-electron σ bond.

The demonstration of single-electron bonds in CaY@C_2n inspired us to investigate their potential as electron spin qubits. A spin qubit should possess a long spin–lattice relaxation time (T₁) and decoherence time (T₂) at relatively high temperatures (above 77 K) to facilitate its implementation in quantum information technologies.⁵⁵ As revealed by the DFT calculations (Table 1), the partially distributed electrons on both Ca and Y exhibit significant s orbital character. Because the s electron is free of orbital angular momentum, its spin–orbit coupling is naturally quenched, giving rise to slow spin–lattice relaxation.^56,57 Since T₁ serves as the upper limit to T₂, T_2,max = 2T₁, the electron spin with s orbital character likely maintains quantum coherence at relatively high temperatures. Such an effect has manifested itself in an Y²⁺-based coordination complex, [K(2,2,2-cryptand)][Y(C₅H₄SiMe₃)₃], whose ²S_1/2-like ground state shows microsecond-scale T₁ and T₂ at room temperature.⁵⁶ In addition, the carbon cage provides a rigid, isolated, and almost nuclear spin-free environment to the endohedral electron spin, which suppresses spin–lattice relaxation and decoherence.⁵⁸ As a result, fullerenes encompassing spin centers could exhibit an excellent qubit performance. For instance, Sc₃C₂@C₈₀ maintains coherence at room temperature in solution,⁵⁹ Gd₂@C₇₉N behaves as a qudit with a large ground spin state (S = 15/2),⁶⁰ and functionalized N@C₆₀ displays an exceptionally long T₂ (tens of microseconds at 77 K) and multiple addressable quantum states that enable quantum error correction and simultaneous operations of two quantum logic gates.⁶¹ It is also noteworthy that Y@C₈₂ displays coherence up to 130 K albeit its electron spin distributes dominantly on the carbon cage.⁶² Putting together, the electron residing on the Ca–Y bond should display slow spin–lattice relaxation and maintain coherence at elevated temperatures.

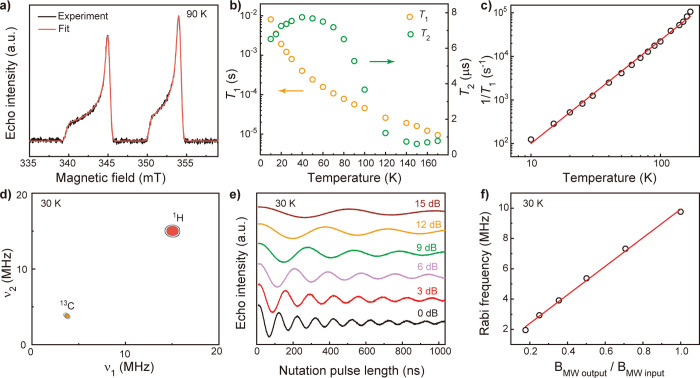
We chose CaY@C_s(6)-C₈₂ as an example and characterized its electron spin dynamics by X-band pulse EPR spectroscopy. To avoid the molecular aggregation observed in the CS₂ solution, we dissolved this compound in toluene, which is a glassy solvent. The echo-detected field sweep (EDFS) spectrum (Figure 4a) collected at 90 K shows features of g-anisotropy. Fitting of this spectrum revealed g_∥ = 1.99948(6) and g_⊥ = 1.97259(1) as well as anisotropic hyperfine splitting constants with A_∥ = 296.1(5) MHz and A_⊥ = 249.6(1) MHz. These values translate to isotropic g_iso = 1.98159 and A_iso = 266.0 MHz, which are consistent with the above-mentioned results of solution-phase CW-EPR and DFT calculations. The anisotropy and hyperfine coupling together give rise to four addressable EPR transitions, which likely exhibit comparable spin dynamics according to the previous study on [K(2,2,2-cryptand)][Y(C₅H₄SiMe₃)₃].⁵⁶ Thus, we focused on the transition centered at approximately 354 mT in the following studies (the exact magnetic field varies with the microwave frequency used for the specific experiment).

Figure 4.

X-band pulse EPR of CaY@C_s(6)-C₈₂ dissolved in toluene. (a) Echo-detected field sweep (EDFS) spectrum at 90 K under a microwave frequency of 9.656 GHz. (b) Temperature dependence of T₁ and T₂. (c) Corresponding 1/T₁ versus temperature. The red line is a fit to the data by the Raman relaxation process, 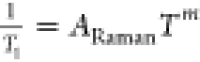, where A_Raman and T are the weighting coefficient and temperature, respectively. The fitted exponent m is 2.37. (d) HYSCORE spectrum collected at 30 K. (e) Rabi oscillations using various microwave attenuations. (f) Relationship between the Rabi frequency and B_MW output/B_MW input, where B_MW output and B_MW input represent the magnetic field of the output microwave and input microwave, respectively, the latter of which is equal to 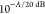(A represents the microwave attenuations in the unit of dB). The red line is a linear fit to the data.

We were able to acquire T₁ and T₂ of CaY@C_s(6)-C₈₂ from 10 to 170 K (Figures S17–S19 and Table S5); toluene melting and fast relaxation prevented measurements above 170 K. As shown in Figure 4b, T₁ gradually decreases with an increasing temperature from 8.09 ms at 10 K to 9.5 μs at 170 K. The persistence of T₁ up to 170 K is mainly attributed to the s orbital character of the Ca–Y single-electron bond as discussed above.⁵⁶ The relaxation rate, 1/T₁, is proportional to T^2.37 (T represents temperature, Figure 4c), which may be attributed to the Raman relaxation mechanism in the high-temperature regime. When the experimental temperature is much higher than the Debye temperature (T_D), i.e., T ≫ T_D, all acoustic phonons are thermally accessible, giving rise to 1/T₁ ∝ T² behavior that is consistent with our experimental observation.^63,64 This indicates that T_D ≪ 10 K, which is significantly lower than those of conventional inorganic solid-state materials that are typically hundreds of Kelvin. The exceptionally small T_D is likely the result of weak intramolecular interaction between the Ca–Y moiety and the C₈₂ cage as well as weak intermolecular interaction between the C₈₂ cage and toluene.^24,63,65 Thus, the temperature dependence of T₁ reinforces our hypothesis that the carbon cage protects the Ca–Y single-electron bond from the environment.

The coherence of the toluene solution of CaY@C_s(6)-C₈₂ is mainly limited by nuclear spin flip-flops and spin relaxation. The T₂ is dramatically shorter than the T₁ from 10 to 170 K, indicating that the dominant sources of decoherence are environmental nuclear spins. Under 40 K, the T₂ gradually increases from 6.52 to 7.74 μs with an increasing temperature (Figure 4b). This phenomenon is likely associated with rotation of the methyl group in toluene, which facilitates the nuclear spin flip and reduces T₂. Such enhancement of decoherence may be the most significant at a temperature lower than 10 K when the rotation resonates with the Larmor precession of nuclear spins, and it weakens at higher temperatures as a result of detuning, leading to a positive relationship between T₂ and temperatures above 10 K.^62,64 As the temperature increases above 40 K, the T₂ first gradually decreases to 7.18 μs at 70 K. It then drops sharply above 70 K and reaches 1.22 μs at 120 K. These trends imply that the spin relaxation starts to limit coherence above 40 K.⁶² Finally, the T₂ tends to level off above the glass temperature of toluene (T_glass = 113 K), and it becomes unmeasurable above the melting point of toluene (T_melt = 178.2 K). With the quantum coherence at 170 K, CaY@C_s(6)-C₈₂ joins Sc@C₈₂, Y@C₈₂, La@C₈₂, Sc₂@C₈₀(CH₂Ph), and Sc₃C₂@C₈₀ to form a subclass of high-temperature EMF qubits that are compatible with a liquid nitrogen-cooled environment.^59,62,66 Another subclass, e.g., Eu@C_2n (2n = 74, 80, 82, and 84), Gd@C₈₂, animated Gd@C₈₂, and Gd₂@C₇₉N, displays coherence at much lower temperatures (below 20 K) likely due to the f orbital character of their unpaired electrons.^60,67,68 Their operation requires liquid-helium cooling or other sophisticated cryogenic technologies.

To gain a deeper understanding of the spin decoherence mechanism, we studied the nuclear spin bath of CaY@C_s(6)-C₈₂ by hyperfine spectroscopy. Specifically, we conducted remotely detected combination-peak electron spin echo envelope modulation (CP-ESEEM) experiments at 30 K (Figure S20a).^69,70 This sequence probes the modulation of electron spin precession by nearby nuclear spins; therefore, it could reveal Larmor frequencies of nuclear spins and their hyperfine interactions with the electron spin. The CP-ESEEM spectrum displays two peaks located at 7.56 and 30.0 MHz (Figure S20b). They correspond to twice the Larmor frequencies of ¹³C and ¹H nuclei, respectively. We further characterized details of hyperfine interactions by a remotely detected hyperfine sublevel correlation (HYSCORE) experiment conducted at 30 K. The HYSCORE spectrum displays two signals located at 3.75 and 15.0 MHz that are consistent with ¹³C and ¹H nuclear spins, respectively. These signals do not exhibit apparent correlation ridges, indicating a negligibly weak hyperfine coupling (Figure 4d). Neither CP-ESEEM nor HYSCORE spectra show signals corresponding to ⁸⁹Y, probably due to the strong hyperfine coupling of this nucleus, as revealed by the CW-EPR and EDFS measurements. As weakly coupled nuclear spins tend to behave as magnetic noises to undermine coherence, we speculate that ¹³C on the C₈₂ cage and ¹³C and ¹H in toluene are major sources of decoherence to CaY@C_s(6)-C₈₂. In contrast, ⁸⁹Y resides within the nuclear diffusion barrier, so it has little contribution to decoherence.⁷¹ This indicates that deuteration of toluene may help improve T₂, as demonstrated for Sc@C₈₂, Y@C₈₂, and La@C₈₂.⁶² The T₂ may be further improved by dynamic decoupling methods, such as the Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence, as shown in Sc₂@C₈₀(CH₂Ph) and Sc₃C₂@C₈₀.^59,66 These coherence enhancement strategies will be investigated in future studies.

To prove the ability of coherent manipulation of the electron spin in CaY@C_s(6)-C₈₂, we conducted nutation experiments at 30 K under various microwave powers. The nutation pulse rotates the electron spin on the Bloch sphere, with the rotation angle determined by the pulse length and microwave power, giving rise to iconic Rabi oscillations shown in Figure 4e. The fast Fourier transform (FFT) of the Rabi oscillation at each power reveals the corresponding Rabi frequency (Figure S21), which exhibits a linear dependence on the relative microwave magnetic field strength (B_MW output/B_MW input) (Figure 4f). This indicates that the electron spin of CaY@C_s(6)-C₈₂ behaves as a qubit that satisfies the Rabi relationship: ℏω_Rabi = gμ_ΒSB₁, where ℏ is Planck's constant, ω_Rabi is the Rabi frequency, μ_Β is the Bohr magneton, and B₁ is the microwave magnetic field strength. As the nutation pulse implements a single-qubit quantum logic gate, these experiments demonstrate the potential of CaY@C_s(6)-C₈₂ for quantum information science.

Conclusions

In summary, unprecedented Ca–Y single-electron metal–metal bonds were formed inside heteronuclear di-EMFs, namely, CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀. The single-crystal X-ray crystallographic study unambiguously determined that the Ca ion and Y ion were encapsulated inside C_s(6)-C₈₂ with a Ca–Y distance of 3.691 Å. The UV–vis–NIR spectra as well as DFT computations suggest that four of the five valence electrons of the internal metals are formally transferred to the carbon cage. The CW-EPR study of both CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀ exhibits a doublet and implies that an unpaired electron is located between Ca and Y. The theoretical studies further confirm the existence of a Ca–Y single-electron metal–metal bond with substantial covalent interaction, attributed to significant overlap between the 4s4p orbitals of Ca and 5s5p4d orbitals of Y. With the s orbital character unpaired electron well-protected by the carbon cage, CaY@C_s(6)-C₈₂ behaves as an electron spin qubit, showcasing excellent coherence even at relatively high temperatures. Its potential applications in quantum information science warrant further exploration.

This study reveals the unexpected capacity of fullerenes to stabilize the Ae–Re bond, a target that remains challenging to achieve using conventional synthesis methods. Furthermore, it validates that by encapsulating two metal atoms with an odd sum of valence electrons, single-electron metal–metal bonds can be stabilized in the pristine fullerene cages. This paves the way for a novel method to achieve metal–metal bonding within fullerene structures, encouraging further investigation into the stabilization of metal–metal bonds with metals that typically resist bond formation. It is also reasonable to assume that compounds containing these novel single-electron metal–metal bonds could exhibit distinctive molecular magnetic properties, potentially leading to their applications in the field of molecular magnets as well as quantum information processing.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c04720.

• Experimental details, HPLC separation of CaY@C_s(6)-C₈₂ and CaY@C_2v(5)-C₈₀, crystallographic information, computational results, and pulse EPR results (PDF)

Author Contributions

^# J.Q., L.A., and X.D. contributed equally to this work.

The authors declare no competing financial interest.