Abstract
Securing optimal work functions for two-dimensional (2D) nanomaterials in Organic Light-Emitting Diodes (OLEDs) is crucial for enhancing the internal quantum efficiency of a device. However, the conventional approach to material discovery, which relies on empirical methods and iterative experimentation, is often time-consuming and inefficient. Here, we propose a target-driven material design framework that combines high-throughput virtual screening and interpretable machine learning (ML) to accelerate the discovery of transparent OLED anode materials. We developed an ML regression model (CatBoost), which accurately predicts work functions for 2D nanomaterials with a mean absolute error (MAE) of 0.20 eV. Remarkably, global and local model interpretation based on the SHapley Additive exPlanations (SHAP) method revealed that the space group is the decisive factor in work function prediction for most materials, while atomic-scale features of the material composition are the dominant factors for other materials, refreshing the traditional understanding of the nature of material work functions. Certain space groups (Pmn2_1 and P6̄m2) tend to exhibit relatively higher work functions (>7 eV), while some other space groups (P4/mmm and P1̄) often present relatively lower work functions (<4 eV). Our methodology, combining robust ML models, multi-condition screening, and DFT calculations, has identified a promising 2D nanomaterial—PS. The material demonstrates exceptional conductivity (σ > 106 S m−1), high transparency (transmittance > 90%), and favorable work function (>5 eV), significantly outperforming the commonly used indium tin oxide (ITO), emerging as a potential candidate for transparent OLED anodes. This study provides new insights into the intrinsic mechanisms affecting the work function of 2D nanomaterials, and provides a cost-effective design framework for identifying other high-performance materials.
A target-driven material design framework for the rapid work function prediction of AB-type 2D nanomaterials is proposed to accelerate the discovery of transparent OLED anode materials.
1. Introduction
The 2023 Nobel Prize in Chemistry was awarded to three scientists who have made remarkable contributions to the field of quantum dots, which serve as the basic materials of quantum light-emitting diodes (QLEDs). This honor further underscores the outstanding position of LED technology in the chemistry and materials science fields. Organic light-emitting diodes (OLEDs), another further development of LED technology, are also significant in the field of display technology owing to their unique self-luminous properties.1–3 When displaying dark or black content, OLED screen pixels can operate independently without the need for a backlight panel, whereas QLEDs require constant backlighting, which leads to lower power consumption, as compared with QLEDs.4–6 Furthermore, the efficiency of OLEDs is not solely dependent on energy consumption; the efficient transport of carriers within the device is another important aspect. Accordingly, the OLED anode material plays a crucial role. However, the design and use of OLED anode materials face significant challenges. Conventional transparent indium tin oxide (ITO) conductive anodes exhibit excellent electrical conductivities and high light transmittances; however, the work function of deposited ITO thin films is typically low, ranging from 4.3 to 4.7 eV.7 This low work function cannot match the highest occupied molecular orbital (HOMO) energy level of most organic materials, leading to low hole injection efficiency. Therefore, the improvement in energy conversion efficiency is limited. Moreover, ITO is prone to bending and breaking and its high manufacturing costs restrict its widespread application in flexible OLEDs.8
Researchers have replaced fragile ITO with silver nanowires,9 graphene,10–12 carbon nanotubes,7,13 conductive polymers,14 and MXenes (transition metal carbides, carbonitrides, and nitrides)15 to fabricate high performance transparent conductive films. However, their work functions are relatively low, and surface treatment is required to engineer their work functions or improve their contact with organic materials. Two-dimensional (2D) nanomaterials have emerged as the most promising alternatives to ITO owing to their unique characteristics.10,16 These materials possess a tunable band gap, high carrier mobility, resistance to short-channel effects, high transparency, and mechanical flexibility, making them highly attractive for next-generation electronics and optoelectronics,17,18 particularly in the design and optimization of OLED anode materials. Accordingly, the quest for 2D nanomaterials with appropriate work functions has become imperative.19
Density functional theory (DFT) is crucial for the investigation of 2D nanomaterials, enabling the prediction of their geometries, electronic structures, and various properties.20 DFT possesses the capability to accurately predict the work function of 2D nanomaterials, rendering it a valuable and indispensable tool for guiding experimental investigations. For example, the effects of atomic adsorption, applied electric fields, and layer engineering on the work function of borophene can be effectively investigated using DFT. Accordingly, researchers can fine-tune the electronic structure and properties of these materials. The optimization of electronic structure and properties is highly beneficial for enhancing the performance of electronic, optoelectronic, and energy-related devices.21,22 However, there are still some challenges in the study of 2D nanomaterials for targeted applications. In particular, the search for structures with optimal properties in large-scale target-driven material screening faces challenges including vast search spaces and intensive DFT calculations for numerous candidate structures. This involves structural optimization and electronic properties calculations. Furthermore, calculations are often parallelized and executed on high-performance computing systems; however, the process is time consuming, resulting in reduced efficiency. A recent study performed using DFT identified over 6000 2D nanomaterials that are anticipated to be exfoliated from their layered bulk (2DMatpedia database).23 Traditional experimental and computational methods cannot meet the rapidly growing demand for target-driven 2D nanomaterial research. Therefore, more efficient approaches to accelerate the discovery of 2D nanomaterials beyond traditional DFT technology must be developed to unlock their full potential for various technological applications.
Machine learning (ML), which enables the provision of surrogate algorithms for material development, has gained enormous attention in recent years for effectively predicting physical and chemical properties, establishing the structure–property relationships, and navigating the chemical space for guiding chemical synthesis.24–26 Substantial progress has been made in studying the work functions of materials using ML techniques. Schindler et al. employed a physics-based surface feature approach to develop an ML model (random forest model) to rapidly predict the extremely low or high work functions of surfaces.27 Hashimoto et al. used Gaussian process regression and Bayesian optimization to quickly screen the top ten materials with the highest and lowest work functions from a database of 27271 materials using first-principles simulations.28 However, research focusing on the data-driven modeling of the work function of 2D materials is still in its infancy.29,30 Furthermore, material screening is closely related to DFT calculations and ML algorithms, that is, it still relies on DFT calculations. Unfortunately, the computational cost of DFT calculations is significant, though high-performance computing resources are becoming increasingly available. Intriguingly, recent studies have explored the combination of ML algorithms with high-throughput computations to accelerate the discovery of materials with a target performance.26,31,32 However, the acquisition of datasets and training of ML models still require a substantial amount of basic data. Additionally, owing to the lack of effective descriptors, the accuracy of the trained models relies heavily on the quality of the training set.
A novel target-driven material screening framework is proposed for the first time in this study to accelerate the discovery of 2D nanomaterials with excellent performance and specific work function values by incorporating high-throughput virtual screening (HTVS) and ML techniques. The training set consisted of 1681 AB-type 2D nanomaterials. An efficient ML regression model was trained using structure- and composition-based features to rapidly predict the work functions of 2D nanomaterials. Global and local model interpretation results based on the SHapley Additive exPlanations (SHAP) method reveal that the space group is the decisive factor in predicting the work functions for most 2D nanomaterials, while atomic-scale features of the material composition (elemental radius, electron affinity energy, ionization energy, etc.) are the dominant factors for the other materials, which refreshes the traditional understanding of the nature of material work functions. Furthermore, certain space groups (Pmn2_1 and P6̄m2) tend to exhibit relatively higher work functions (>7 eV), while some other space groups (P4/mmm and P1̄) often present relatively lower work functions (<4 eV). Finally, by combining the ML model with HTVS, which consumes minimal time (≈103 faster than DFT) and computational resources, 100 2D OLED anode candidate materials with suitable work functions (>5 eV), excellent photoelectric properties, and high thermodynamic stabilities were identified from more than 6000 2D nanomaterials in the 2DMatpedia database. Further DFT calculations confirmed an excellent transparent OLED anode candidate (PS) with transmittance > 90% in the visible region and electrical conductivity > 106 S m−1, superior to traditional ITO.
2. Computational details
2.1. Computational details
All geometric structure and electronic property calculations for the investigated 2D nanomaterials were performed using the Vienna ab initio simulation package (VASP). The Perdew–Burke–Ernzerhof (PBE)33 exchange–correlation functional within the framework of the generalized gradient approximation (GGA)34 was employed to describe the electronic interactions. Furthermore, a convergence criterion of 10−2 eV Å−1 was set for the forces on each atom, and a total energy convergence criterion of 5 × 10−5 eV was used. The plane-wave cutoff energy for the calculations was set to 500 eV. The k points were automatically generated using the VASPKIT tool.35 The density was set to 2π × 0.02 Å−1, according to the Gamma scheme, ensuring an appropriate sampling of the Brillouin zone for accurate optical property calculations. The optical transmittance was first investigated by calculating the frequency-dependent function. The imaginary part of the dielectric function can be determined using eqn (1).
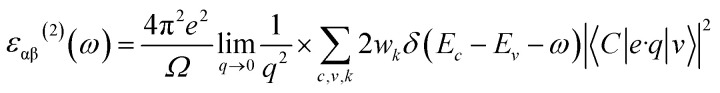 |
1 |
where ω represents the photon frequency, |〈C|e·q|v〉| is the integrated optical transition from the valence state (v) to the conduction state (c), e is the polarization direction of the photon, and q is the electron momentum operator. The integration over k was performed by summing over special k-points with a corresponding weighting factor wk.35 Considering the Kramers–Kronig transformation,36 the real part of the dielectric function can be obtained using eqn (2).
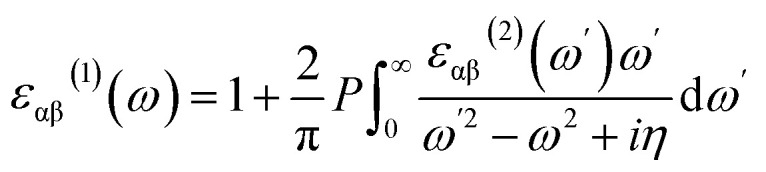 |
2 |
where P is the principal value and η is the complex shift parameter. The normalized transmittance (T(ω)) can thus be determined using the widely used formula shown in eqn (3).
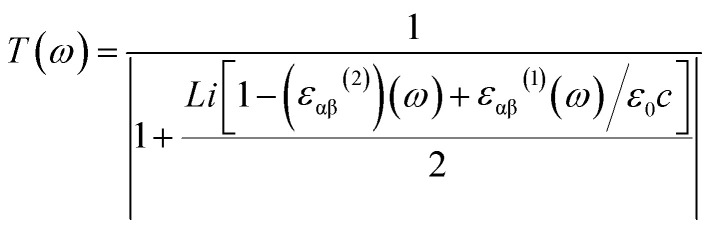 |
3 |
where L is the slab thickness in the simulation cell, ε0 is the permittivity of vacuum, and c is the speed of light.35
The calculation of the electrical transport properties employs the semi-classical Boltzmann transport theory using the BoltzTrap2 software.37σ was obtained by solving the Boltzmann transport equation.
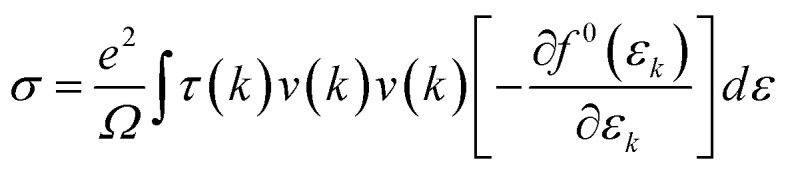 |
4 |
where e, Ω, εk, τ(k), v(k), and f0 are the electron charge, volume of the orthonormal cell, Fermi level, relaxation time, group velocity, and Fermi–Dirac distribution, respectively. The relaxation time of electrons is calculated based on the deformation potential theory.38 It can be expressed by the formula shown in eqn (5).
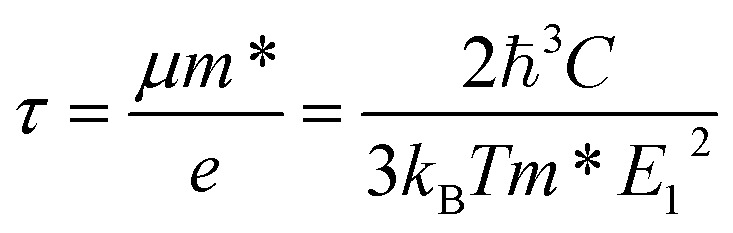 |
5 |
where h, kB, and μ are respectively the reduced Planck constant, the Boltzmann constant, and the mobility. The effective mass m*, the elastic constant C, and the deformation potential constant E1 are respectively expressed by:38
| m* = ℏ2/(∂2E/∂k2) | 6 |
| C = [∂2E/∂(Δa/a0)2]/S0 | 7 |
| E1 = ∂Eedge/∂(Δa/a0) | 8 |
where E1, Δa, S0, and Eedge are respectively the total energy of the cell under uniaxial strain, the change in the lattice constant relative to the relaxed lattice constant, the area of the orthogonal cell on the surface, and the shift of the conduction band minimum (CBM) and valence band maximum (VBM).
2.2. ML model evaluation
Four indices, namely, R2, RMSE, MSE, and MAE, were chosen to estimate the prediction errors to evaluate the performance of each ML model, as shown in eqn (9)–(12):
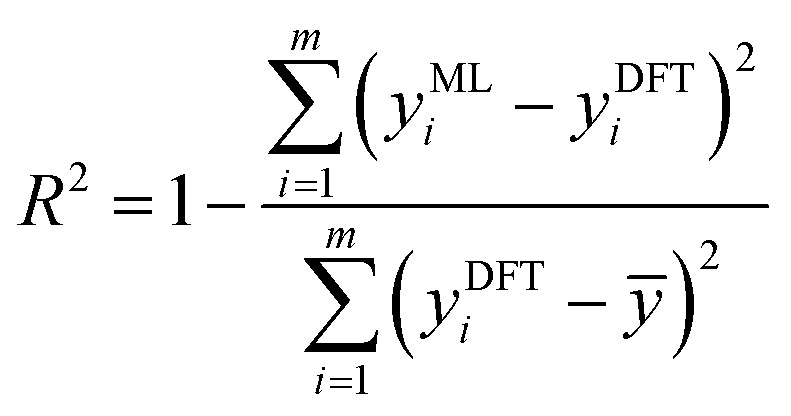 |
9 |
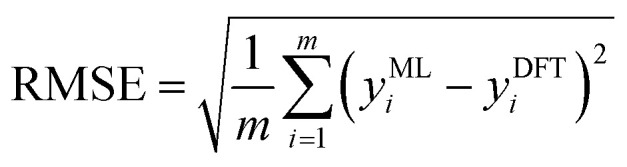 |
10 |
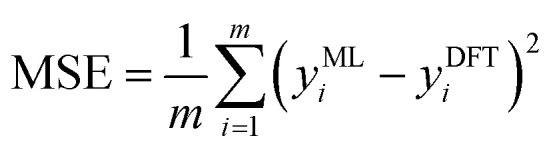 |
11 |
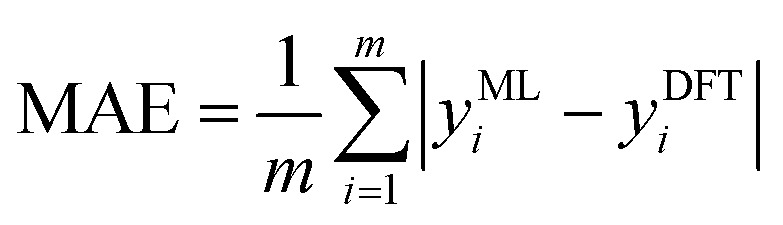 |
12 |
where m is the total amount of data, yMLi is the ML-predicted value for sample i, yDFTi is the DFT-calculated value for sample i, and ȳ is the average DFT-calculated value. An R2 value closer to 1 indicates the higher prediction accuracy of the ML model. RMSE, MSE, and MAE were used to measure the loss between the ML-predicted and DFT-calculated values. A small loss indicates high accuracy.
2.3. ML model interpretation
To evaluate the contribution of each feature to the target variable (work function) and improve the interpretability of the model, the SHAP method, developed by Shapley in the field of game theory, was used to calculate the SHAP value of each feature for the best ML model,39 which is the weighted average of all possible differences. The SHAP value for feature x (out of n total features), given the prediction p, can be calculated using eqn (13).
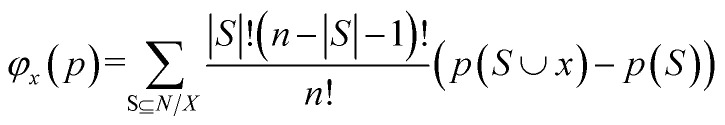 |
13 |
where n represents the total number of features, S is the subset of all features with feature x, p(S∪x) denotes the value predicted by the selected ML model considering feature x, and p(S) denotes the prediction without considering feature x. The differences among all possible subsets of S⊆n were calculated because of the dependency of the effect of withholding a feature on other features in the chosen ML model. The SHAP value of each feature quantifies its positive or negative contributions; a feature with a higher absolute SHAP value has a greater contribution to the prediction result.
3. Results and discussion
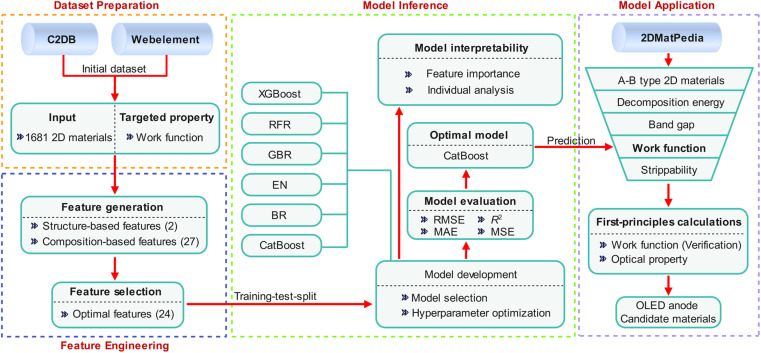
The proposed target-driven material-screening framework is shown in Fig. 1, and consists of four consecutive parts. (i) Data set preparation. An initial dataset consisting of 1681 different 2D nanomaterials from the C2DB database, which were obtained using the lattice decoration of known crystal structure prototypes, was used to address the lack of datasets in the field of 2D nanomaterials. Subsequently, the selected ML models were employed to fit or train the dataset with the work function of the materials serving as the target property. (ii) Feature engineering. The appropriate features, that is, vectors of uniform length, for 2D nanomaterials with specific work function values must be found for input into the ML model. In this study, the complete initial dataset was characterized using feature generation, resulting in a series of composition- and structure-based features representing each compound. After generating these features, the size of the input feature vector was further reduced using a series of feature selection techniques to avoid the curse of dimensionality. The optimal features obtained using feature engineering were used for the subsequent ML model training. (iii) Model inference. The performance of several ML models was compared during model development using the above-mentioned structure- and composition-based features as the only known inputs to the regression models. Once the best ML model was selected, a random grid search method was used to adjust the hyperparameters of the model to achieve optimal performance. The SHAP method was then used to enhance the model interpretability. Additionally, the importance of the features was ranked based on the optimal model to determine the features that significantly affect the work function values of 2D nanomaterials, and the effects of these features on the work function values of individual materials were analyzed. (iv) Model application. After building an ML model to predict the work function of 2D nanomaterials, an effective screening strategy was proposed to identify materials with specific work function values in a 2D nanomaterial database as an application of a high-throughput material discovery process.
Fig. 1. Target-driven material screening framework.
3.1. Dataset preparation
This study employed two open-source databases of 2D materials, namely C2DB and 2DMatPedia. C2DB serves as the source of our training set for our predictive model, thanks to its extensive collection of work function values. Meanwhile, the 2DMatPedia was employed as a resource for high-throughput screening, expanding the scope of our analysis and discovering materials with the desired work function.
The C2DB database integrates the comprehensive properties of more than 4000 2D nanomaterials, including structural, elastic, thermodynamic, electronic, magnetic, and optical properties. Calculations of the material properties in C2DB were performed using state-of-the-art DFT and many-body methods, following a high-throughput, semi-automated workflow. The Python-based atomic simulation environment (ASE) was used to manage the workflow, and all DFT and many-body calculations were performed using the projected augmented wave (PAW) code GPAW (Table S1†).40,41
The 2DMatPedia database is a large-scale 2D material database that includes more than 6000 monolayer structures, which were obtained using top-down and bottom-up discovery processes.23 In the top-down approach, the inorganic bulk crystals in the Materials Project dataset are screened by a topology-based algorithm for layered structures, which are then theoretically exfoliated to 2D monolayers. Via systematic elemental substitution of these 2D monolayers, that is, the bottom-up approach, new unary and binary 2D materials are generated. Additionally, the structural, energetic, and electronic properties of all the 2D nanomaterials in the 2DMatPedia database were calculated using the same automation process and parameter settings, providing a reliable database for material screening, data mining, data analysis, and artificial intelligence applications. Detailed computational parameters are provided in Section S1.1 in the ESI.†
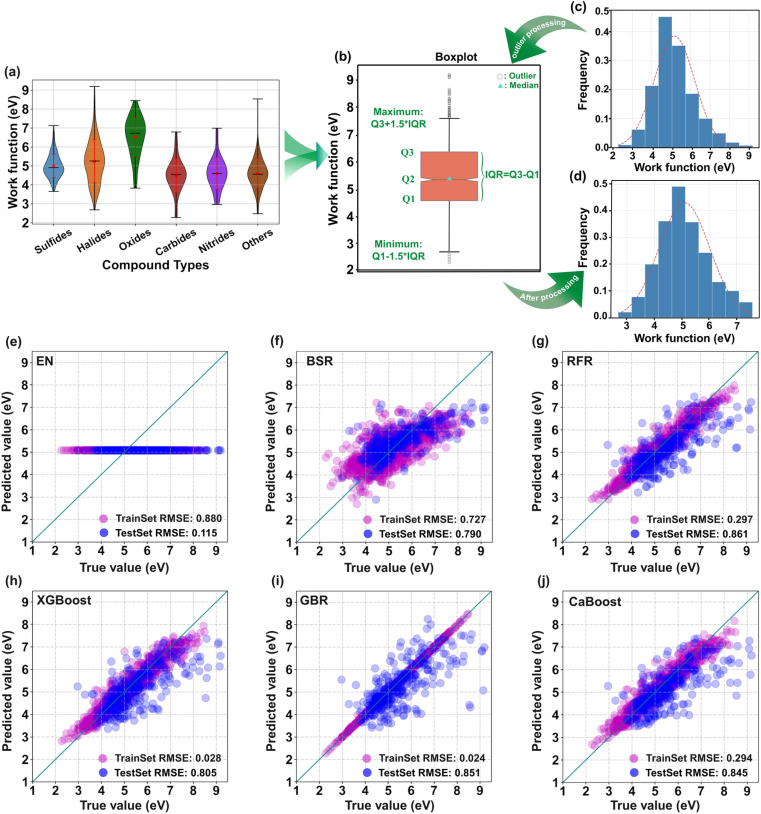
High-quality and diverse input datasets are crucial for the development of efficient ML models. In this study, 1681 2D nanomaterials were selected from the C2DB database as the initial dataset. Fig. 2a illustrates the distributions of the work functions for different types of compounds. Each violin plot exhibits a unimodal and symmetric shape, indicating a relatively concentrated and symmetric distribution of the work functions for each type of compound. Except for the oxides, the average work functions of the other series of compounds were approximately 5 eV. Moreover, the oxide violin plot exhibited the highest median, suggesting that this compound type likely possesses a relatively higher work function than the other types of compounds. In contrast, the halide violin plot exhibited longer extremal lines and error bars, indicating the presence of significant deviations or outliers in their work function values. Outliers were treated by combining boxplots and subjective judgments to ensure the robustness of the model. As depicted in Fig. 2b, data points exceeding the specified threshold were removed, reducing the dataset size to 1637 samples. Fig. 2c and d show the statistical histograms of the work function before and after the removal of outliers, respectively. The work function values after treating the outliers exhibited a Gaussian distribution with an average value of approximately 5 eV. The highest work function value frequency was observed at 4.5–5 eV, encompassing approximately 50% of the data. Information regarding the properties of the elements was obtained from WebElements (https://www.webelements.com/). Furthermore, all initial indicator data was standardized.
Fig. 2. (a) Work function violin plots of different types of 2D compounds. The black horizontal lines in the middle and at the ends represent the median and extreme values, respectively. The red dots in the middle and the length of the vertical red line represent the mean and variance, respectively. (b) Box plots for outlier processing. Statistical histograms of the work function values (c) before and (d) after outlier processing. (e) Elastic net regression (EN), (f) Bayesian regression (BSR), (g) random forest regression (RFR), (h) XGBoost, (i) gradient boosting regression (GBR), and (j) category boosting (CatBoost) scatter plots of the fitting effects for the 29 descriptors and work function values; TrainSetRMSE and TestSetRMSE are the RMSE values of the models on the training and test sets, respectively.
3.2. Descriptors
The design of a set of descriptors to predict the work function of AB-type 2D nanomaterials is equivalent to creating a set of quantitative expressions. These expressions should not only uniquely define each material in the dataset but should also be correlated with the fundamental physical and chemical properties that influence the target variable (work function). Composition-based features were sought to obtain features that contain prior knowledge of the materials without being overly complex.42 This is because the physical and chemical properties of the constituent atoms largely determine the properties of the corresponding materials. These features directly affect the macroscopic properties of the molecular and crystal structures. The effectiveness of this strategy, that is, using such atomic-scale features in constructing ML models, has already been validated in the rapid and accurate prediction of adsorption energy, band gap, and optical properties.43,44 These atomic-scale features include atomic radius, electronegativity, ionic radius, electron affinity energy, and ionization energy.43,44 Therefore, atomic-scale features were notably considered in the feature generation process. As shown in Table 1, 29 descriptors, including various features reflecting the atomic size, geometric features, physical properties, and thermal properties, were selected to construct the initial feature set in this study.
29 Feature descriptors and symbols of the initial dataset for the investigated AB-type 2D nanomaterials. A and B represent the first and second elements in the chemical formula, respectively.
| Symbol | Feature |
|---|---|
| S | Space group |
| SN | Space group number |
| AN/BN | Element amount of A or B |
| AIP/BIP | Ionization energy of A or B |
| ARa/BRa | Atomic radius of A or B |
| ARi/BRi | Ionic radius of A or B |
| AP/BP | Density of A or B |
| AEA/BEA | Electron affinity energy of A or B |
| ARC/BRC | Covalent radius of A or B |
| AE | Elastic modulus of A |
| Aq/Bq | Conductivity of A or B |
| Ac/Bc | Specific heat capacity of A or B |
| AH/BH | Heat of evaporation of A or B |
| ATB/BTB | Boiling point of A or B |
| ATM/BTM | Melting point of A or B |
| AV/BV | Atomic volume of A or B |
The feature generation process primarily leverages the Python Materials Genomics (pymatgen),45 a robust Python library that is intimately integrated with the Materials Project. This library facilitates accessing and processing of a vast amount of data stored in the Materials Project database. The periodic properties of elements (atomic radius, ionic radius, electron affinity energy, etc.) were obtained via the Element or Species class in pymatgen. Furthermore, script customization was utilized to acquire specific attributes like space group, element amount, density, and elastic modulus, thanks to the customization capability of the above-mentioned process, enhancing the flexibility in feature generation.
3.3. Model inference
To address the challenges posed by the dispersed characteristics of our dataset, we strategically selected six leading models that span the domains of ensemble learning, probabilistic modeling, and regularized linear modeling. Furthermore, in order to place a higher weight on larger errors and achieve a linear perspective on the overall predictive accuracy, Root Mean Square Error (RMSE), Mean Square Error (MSE), and Mean Absolute Error (MAE) were utilized as three error metrics of model evaluation.46 In addition, the coefficient of determination (R2) was employed to effectively quantify the fit effect of models on the input features and target variable.47
The defined 29 descriptors were used as the features for six ML models, namely, XGBoost, elastic net regression (EN), gradient boosting regression (GBR), Bayesian regression (BSR), category boosting (CatBoost), and random forest regression (RFR). The entire dataset was randomly divided into training and test sets at a 4 : 1 ratio. The training set was used to fit the relationship between the features and work function values, whereas the test set was used to evaluate the performance of the models. Four indices, namely, R2, RMSE, MSE, and MAE, were used to describe the prediction accuracy of the models. Fig. 2e–j show the fitting effects of the true and predicted values of the six ML models under the initial parameters, as well as the RMSE values of each model on the training and test sets. The linear models (EN (Fig. 2e) and BSR (Fig. 2f)) exhibited a poor fitting performance, indicating that the relationship between the 29 descriptors and work function values was nonlinear and relatively complex. The RFR model (Fig. 2g) exhibited an improved fitting performance, as compared with the EN and BSR models, but the prediction accuracy was still unfavorable (TestSet RMSE value of 0.861). The fitting effects of XGBoost (Fig. 2h), GBR (Fig. 2i), and CatBoost (Fig. 2j) on the 29 features and work function values were relatively ideal and superior to the fitting effects of the first three models (TestSet RMSE values of 0.805, 0.851, and 0.845, respectively). Interestingly, all three models were based on gradient boosting algorithms, which excel in handling complex data and nonlinear relationships, thereby enabling accurate data fitting and target prediction. They can automatically manage nonlinear relationships between features and enhance model performance through ensemble learning. Moreover, these models include mechanisms, such as regularization and pruning, to prevent overfitting. The complexity of the model can be controlled by adjusting the parameters.
3.4. Feature engineering and parameter optimization
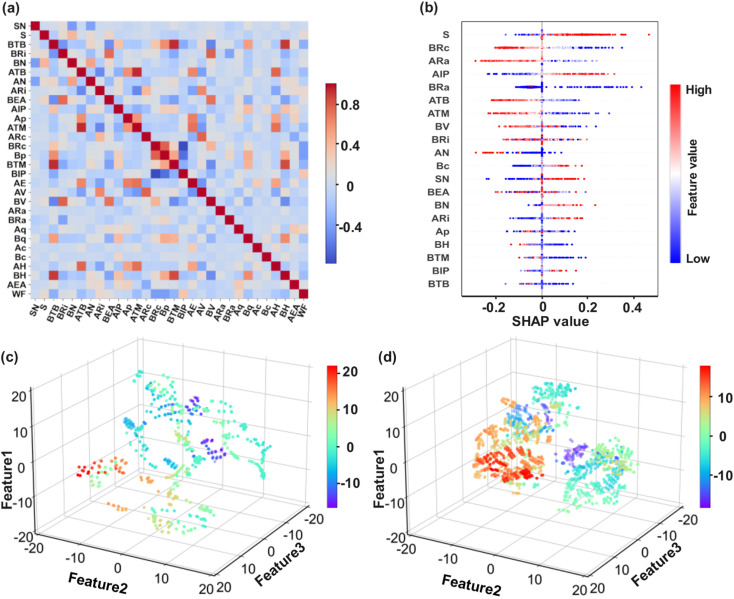
The Pearson correlation coefficients (detailed in Section S1.2 in the ESI†) between every pair of features were computed in this study (Fig. 3a). Combined with the importance ranking of features based on SHAP values (Fig. 3b), which also enhances the global interpretability of the model (detailed in the Model interpretability Section), features with correlation coefficients > 0.8 and low importance were then eliminated. Removing highly correlated features not only reduces the model training time, allowing for the testing of more hyperparameters at a given computational cost, but also creates a more stable and generalized model. Finally, a simplified subspace containing 24 features was generated (Table S3†). Furthermore, to minimize any potential order-related correlations or biases, the shuffle function (detailed in Section S1.3 in the ESI†) in Python was used to shuffle the dataset. This process effectively randomizes the order of elements within the dataset, eliminating any inherent ordering or patterns that may influence subsequent operations. The dimensionality of the features was successfully reduced to 3D (Fig. 3c and d) and 2D (Fig. S1†) by employing the t-distributed stochastic neighbor embedding (t-SNE) algorithm (detailed in Section S1.4 in the ESI†). The spatial distributions of the input variables were visualized after the dimensions were reduced. The dataset showed significant clustering after data processing and feature engineering (Fig. 3d), as compared to the original data (Fig. 3c). Furthermore, a larger number of sample points was observed, as shown in Fig. 3d. This can be attributed to the effective removal of noise and redundant information, leading to an increase in data concentration and regularity. Consequently, the sample points exhibited a tighter distribution, indicating a more organized and structured dataset, which helps the models to learn the essential characteristics of the data better, improving both the prediction accuracy and generalization ability of the model. A random grid search method was employed to optimize the XGBoost, CatBoost, and GBR models. The selection of the hyperparameters focused on four key parameters, as detailed in Table S4.† The number of iterations was set to 5000 to ensure efficient exploration of the hyperparameter space, allowing for the identification of optimal hyperparameters within a reasonable timeframe.
Fig. 3. (a) Heat map of the Pearson correlation coefficient matrix between the selected features. (b) Importance ranking of the top 20 features. Three-dimensional (3D) spatial visualization of (c) the original data and (d) the data after feature engineering and data processing. Feature1, Feature2, and Feature3 represent the values of the corresponding three features of the dataset after dimensionality reduction. The different material sample point colors represent the Feature1 values.
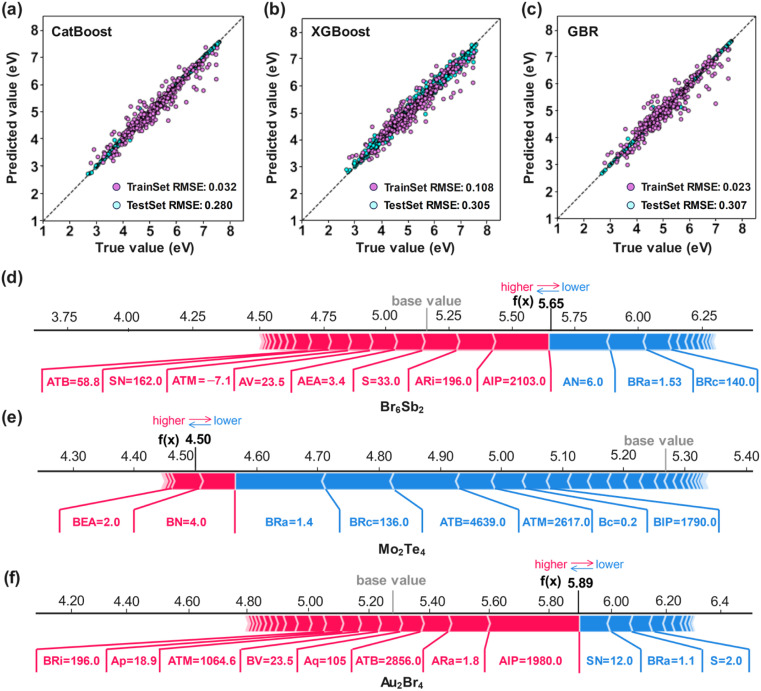
After the optimal hyperparameters were obtained, the models were retrained and evaluated on the test set. The results showed that the CatBoost model exhibited the best performance on the test set and reached the expected performance level with an MAE, RMSE, and R2 of 0.20 eV, 0.28 eV, and 0.92, respectively (Fig. 4a–c and Table 2). Furthermore, 20 AB-type 2D nanomaterials were randomly selected from the dataset, and the ML-predicted work functions (CatBoost) were compared with the corresponding DFT-calculated results in the C2DB dataset. The results demonstrated that the ML-predicted work function values agreed well with the DFT-calculated values, with an average relative error of only 0.29% (Fig. S3†). Moreover, the ML model showcases an accelerated capability for predicting the work function of 2D nanomaterials, achieving speeds approximately three orders of magnitude swifter than those achieved by DFT calculations. To further validate the stability and generalization ability of the CatBoost model, 5-fold cross validation was conducted using RMSE as the performance evaluation indicator. The results demonstrated that the model was stable for different data subsets (Fig. S2†), confirming its strong stability and generalization ability. Therefore, CatBoost can establish nonlinear mapping between the input features and work function values, predict unexplored new datasets, and assist in the high-throughput screening of materials with specific work function values.
Fig. 4. Fitting effects of the (a) CatBoost, (b) XGBoost, and (c) GBR model-predicted and true work functions on the test set. Individual SHAP plots of the CatBoost model predictions for (d) Br6Sb2, (e) Mo2Te4, and (f) Au2Br4. The SHAP positive (red) and negative (blue) feature weights are given for the three materials. The bar size represents the SHAP value. The base value is the mean value of the work function in the training data. The output value f(x) represents the predicted work function of the three materials.
RMSE, MAE, MSE, and R2 values from CatBoost, GBR, and XGBoost models for the work function prediction of AB-type 2D nanomaterials on the training and the test sets after parameter optimization.
| Model | RMSE (eV) | MAE (eV) | MSE (eV) | R 2 | ||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| CatBoost | 0.03 | 0.28 | 0.02 | 0.20 | 0.00 | 0.08 | 0.99 | 0.92 |
| GBR | 0.02 | 0.31 | 0.05 | 0.22 | 0.00 | 0.09 | 0.99 | 0.90 |
| XGBoost | 0.09 | 0.30 | 0.04 | 0.21 | 0.00 | 0.09 | 0.98 | 0.90 |
3.5. Model interpretability
Explaining the explicit relationship between the features and output of a black-box ML model is challenging. The SHAP method, which has emerged as an effective solution for unraveling this complex relationship, can provide insightful explanations. SHAP not only ranks feature importance, but also reflects the positive and negative contributions of each feature, providing both global (feature importance) and local (individual instance) interpretability for the best ML model. SHAP comprehensively measures the feature importance and uses game theory to explain the contribution of each feature to the output of the ML model.39 Each feature is assigned a unique weight in the global model interpretation. Fig. 3b summarizes the SHAP explanations for the CatBoost model and shows the top 20 features. Each point corresponds to a compound in the dataset; red and blue indicate higher and lower feature values, respectively. The negative and positive contributions of each feature were identified using the SHAP value. S is clearly the most important feature, in which most of the higher values have a significant positive impact on the model output, whereas several lower values have a negative influence. To further explain the influence of the selected features on the work function output of the compound, the CatBoost model provides individual SHAP plots for predicting several different types of 2D nanomaterials, as shown in Fig. 4d–f. The base value is the average output value of the ML model in the whole training set. The positive and negative contributions are represented by red and blue arrows, respectively, corresponding to the influence of different features on driving the work function value away from and closer to the base value. The contribution of the features increases with the length of the corresponding arrow. The local interpretation results show that each feature plays a different role in different materials. For example, ATB has a negative impact on Mo2Te4 with a SHAP value of 4636.0, whereas it has a positive impact on Br6Sb2 and Au2Br4 with SHAP values of 58.8 and 2856.0, respectively. Therefore, once the total positive contributions of all the features are higher than the negative contributions, the final predicted value of the work function value is greater than the base value. This indicates that the work function values are the result of the synergistic interplay of multiple factors rather than being solely determined by a single factor. Furthermore, the impact of a single factor on the final work function value is not fixed and can exert either a positive or negative influence.
The space group is the most important feature (Fig. 3b) because it describes the positions and symmetry of atoms in the crystal, including geometric structural information such as the lattice parameters, cell shape, and locations of atoms in the lattice. Symmetry within a crystal can affect the band structure, density of states, and electron wave function of the crystal, thereby exerting a significant influence on the work function prediction.48
Previous explorations of the intrinsic mechanisms of work function variations for a nanomaterial primarily focused on the properties of systems, including changes in the surface dipole and intrinsic bulk electronic structure of the material, as well as their effects on the vacuum and Fermi levels.22,49,50 However, investigations focusing on the influence of the properties of the constituent atoms on the work function of 2D nanomaterials are rare, particularly for AB-type 2D nanomaterials. Herein, apart from the above-mentioned material-based feature, that is, the space group, a series of composition-based features at the atomic scale, such as atomic radius, electron affinity energy (EA), and ionization energy (IE), were confirmed to play vital roles in work function prediction by employing local and global feature analyses based on the SHAP method.
The elemental radius (atomic, ionic, and covalent radius) and atomic volume are also crucial features. They reflect the size of an atom or ion and directly affect the corresponding lattice morphology, arrangement of atoms, distribution of electron clouds, bond length, and bond strength, thus influencing the work function prediction of 2D nanomaterials. In particular, the atomic radius refers to the average distance between the atomic nucleus and the outermost electrons in the electron cloud. This is related to factors such as the charge number of the atomic nucleus, number of electron layers, arrangement of atoms, and distance and interaction between atoms. A larger atomic radius leads to a looser lattice structure and more relaxed atomic arrangement, thereby influencing the defect density, surface activity, and mechanical and chemical properties of the material, ultimately impacting the work function of the material.51 The covalent radius, which is half of the distance between two identical atomic nuclei bound by a covalent single bond, reflects the strength and length of the covalent bond.52 The length and strength of the chemical bond directly impact the work function prediction of a material. Shorter chemical bonds result in an increased overlap of electron clouds, stronger interactions, and a higher energy level for valence electrons. This, in turn, affects the electronic interactions within the material, electron state density, and band structure, ultimately affecting the work function of the material. The ionic radius affects the distance between ions in a material with ionic bonds. The electrostatic Coulomb force, which is inversely proportional to the square of the ionic distance, plays a crucial role in internal interactions. The interaction energy increases with a decreasing ionic distance. This change in the ionic radius directly affects the interionic distance, influencing the interaction energy within the ionic bonds. The interionic distance decreases with a decreasing ionic radius, leading to an increase in the interaction energy. Consequently, the material exhibits a stronger attraction to electrons on its surface.53
Additionally, atomic volume is also an important feature in the work function of 2D nanomaterials. Both the atomic volume and elemental radius are physical quantities used to describe the size of an atom or ion. However, the underlying influence mechanisms of the two features on the work functions of materials are quite different. The elemental radius reflects the size of atoms in a crystal structure and the length and strength of covalent or ionic chemical bonds, thereby affecting the surface chemical properties of the materials. In contrast, the atomic volume mainly reflects the space occupied by an atom, which affects the density of the material, shielding effect of surface electrons, and strength of the chemical bonds. A larger atomic volume generally lowers the density of the material, decreasing the shielding effect experienced by the surface electrons. Consequently, less energy is required for surface electrons to escape from the material surface, leading to a lower work function.
The IE and EA of an element are closely related to its “electron-donating” and “electron-attracting” abilities.22 Therefore, they significantly affect the electron configuration of the system, resulting in variations in the Fermi level, thus affecting the work function (detailed in Section S1.5 in the ESI†). This conclusion was confirmed by a recent study, in which the work function of adatom-borophene (M/BBP) systems (M = Li–Cs; Be–Ba) is nearly linearly dependent on the IE, with R2 values of 0.80 and 0.91, respectively. However, the IEs and EAs of the constituent atoms are not the only factors contributing to the work function of the system. Apart from the IE or EA, both the structure-based and a series of composition-based features are key factors that affect the work function. This, in turn, indicates the relatively poor linear relationship between the work functions of M/BBP and IE (R2 = 0.80–0.91), that is, multiple factors, including material-based and a series of composition-based features, affect the work functions of nanomaterials.
The boiling and melting points of the constituent atoms of compounds have an intrinsic relationship with the electronic band structure of the material and surface chemical environment. These factors play significant roles in predicting the work function. Materials with larger band gaps generally exhibit higher boiling and melting points. This is because the electrons within materials require higher energy to move; thus, higher temperatures are needed to overcome the energy barrier and transition to higher energy states, resulting in the transition of materials from a solid to a gas or liquid phase. Therefore, the boiling and melting points provide important information regarding the electronic activity and electron transport properties of a material for work function prediction. Moreover, the boiling and melting points reflect the characteristics of the material surface. The energy of the surface of a material, as compared with the bulk phase, is higher, and the interactions between surface atoms or molecules and the external environment are more complex (such as adsorption and catalytic reactions), which also have an important impact on the work function prediction. In summary, the boiling and melting points, both of which are crucial factors in work function prediction, provide valuable insights into the electronic properties and surface characteristics of materials.
3.6. OLED anode candidate materials
The contact between the electrodes and organic materials in OLED devices is a key factor influencing device performance. Therefore, the selection of suitable electrode materials is crucial to achieve high-performance OLED devices. Fig. S4a† illustrates the luminescence mechanism of OLEDs, where holes are injected from the Fermi level of the anode into the HOMO level of the hole transport layer (HTL).54,55 The injection efficiency depends on the degree of matching between the work function of the anode and the HOMO level of the HTL; a higher matching degree results in a lower potential barrier at the interface, leading to an increased hole transmission efficiency. Most organic materials currently used in OLED devices have HOMO levels greater than 5 eV (Fig. S4b†).56,57 Therefore, anode materials with considerable work function values are required. An ML model (CatBoost) was employed for the high-throughput screening of 2D nanomaterials in the 2DMatPedia database to identify the best OLED anode candidate materials.
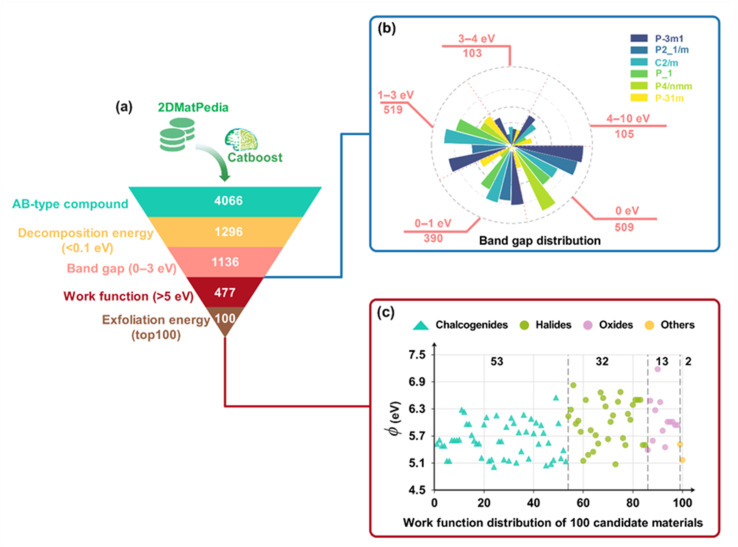
The screening process was semi-automated based on python. Furthermore, the screening conditions were primarily based on the theoretical work function, band gap, thermodynamic stability, and strippability of the materials (Fig. 5a). All the AB-type compounds were selected from the database in the first round of screening. These compounds have a large chemical space, relatively simple chemical composition, and are easy to synthesize and characterize, making them convenient for subsequent research. The first round of screening yielded 4066 AB-type 2D nanomaterials. The thermodynamic stability was regarded in the second round of screening as a key consideration, and the screening criterion was set to a decomposition energy of <0.1 eV per atom. This criterion was set based on the fact that the decomposition energies of the 59 2D nanomaterials synthesized in the experiment were all <150 meV per atom (Fig. S5†).58–60 The second round of screening yielded 1296 stable AB-type 2D nanomaterials. The band gap was the main consideration in the third round of screening, and the screening criterion was set to a band gap of <3 eV. Materials with a band gap in this range usually have relatively good conductivity and can effectively inject holes into organic materials (a more detailed discussion on conductivity follows). The third round of screening yielded 1136 stable AB-type 2D nanomaterials. Furthermore, the third round of screening revealed that the P3̄m1 space group was prevalent among the stable compounds (Fig. 5b). This indicates that this type of structure is relatively stable in AB-type 2D compounds, which may be related to the symmetry of the crystal, atomic arrangement, and bonding method and is irrelevant to the band gap. The screening criterion was set to work function values > 5 eV owing to the above-mentioned work function requirement for HTL materials (Fig. S4b†). The fourth screening round yielded 477 2D candidate materials. Finally, after sorting by exfoliation energy, 100 candidate OLED anode materials were obtained. These materials mainly include chalcogenides, halides, and oxides, with work functions of approximately 6 eV.
Fig. 5. (a) High-throughput screening flow in the 2DMatPedia database. Statistical plots of (b) the space group distribution of various stable 2D materials with different band gap ranges and (c) work functions (ϕ) of 100 candidate materials.
In addition to the appropriate work function, the transparency and conductivity of the OLED anodes stand as pivotal performance metrics. An anode with exceptional transparency and conductivity is anticipated to propel the device to its optimal performance. However, there is often a nuanced equilibrium between the transparency and conductivity within prospective materials. Enhancing a material's conductivity typically leads to reduced transparency, given that materials with high conductivity tend to possess significant light absorption capabilities. Conversely, diminishing the material's thickness bolsters its transparency, but an overly thin material can hinder conductivity by interrupting the electron transport pathway.61 Therefore, striking a harmonious balance in the design and optimization of OLED materials is crucial, one that fosters robust conductivity while maintaining sufficient transparency.
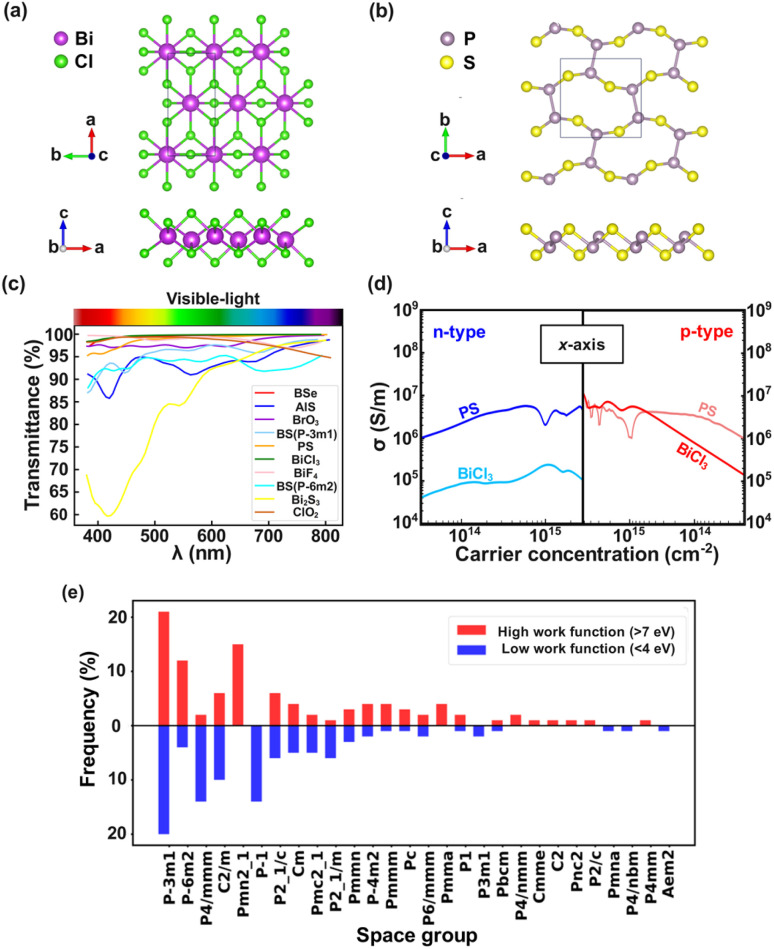
Following the exclusion of systems containing d-block, f-block, and precious metal elements, which detrimentally impact OLED performance and escalate costs, we assessed the optical properties of ten alternative materials (Table S5†). Fig. 6a and b reveal that the transmittances of nine candidates exceed 85%, underscoring their considerable promise as anode materials for OLED devices, particularly in terms of transparency. When appraising materials for conductivity, the band gap offers only a glimpse into their conductive properties, as narrower band gaps are conducive to electron migration to the conduction band. Therefore, our attention centered on two exemplary 2D materials, PS (Fig. 6a) and BiCl3 (Fig. 6b), for meticulous electrical conductivity analyses. This entailed calculating the conductivity-to-relaxation time ratio (σ/τ) via Boltzmann transport theory and deducing τ by evaluating the elastic constants, deformation potential constants, and effective mass through deformation potential theory (Table S6†). While BiCl3 presents a conductivity slightly lower than that of the commonly utilized ITO (σ > 105 S m−1), PS exhibits a remarkable 10-fold increase (ranging from 106 to 107 S m−1, Fig. 6d) in conductivity compared to the frequently used ITO, showcasing outstanding conductivity capability. Collectively, considering transparency, conductivity, and work function, PS demonstrates significant potential for application as an OLED transparent anode.
Fig. 6. Top and side views of (a) BiCl3 and (b) PS structures. Transmittances of (c) BSe, AlS, BrO3, BS (P3̄m1), PS, BiCl3, BiF4, BS (P6̄m2), Bi2S3, and ClO2 in the visible region. (d) The electrical conductivities (σ) of different carrier concentrations for PS and BiCl3 along the x-axis at 300 K. (e) The frequency distribution of space groups for materials with work functions greater than 7 eV and less than 4 eV generated by high-throughput screening.
Based on the global SHAP model interpretation results (Fig. 3b), it is evident that for the entire dataset, the space group is the most important feature and plays a decisive role in work function prediction. To elucidate the decision mechanisms related to space groups in work function prediction, we analyzed the frequency distribution of space groups among materials generated during high-throughput screening. Fig. 6e shows the distribution of space groups for 2D nanomaterials with work functions greater than 7 eV and less than 4 eV. Red and blue represent the high and low work function regions, respectively. Remarkably, among the six space groups with the highest frequency distribution, P3̄m1 and C2/m appear in both the high (red) and low (blue) work function regions with considerable frequencies. In contrast, Pmn2_1 and P6̄m2 show higher frequencies in the high work function regions, while P4/mmm and P1̄ are more frequent in the low work function regions. Therefore, we can deduce that for materials exhibiting space groups P3̄m1 and C2/m, the space group does not serve as a decisive factor for their work function. Conversely, for materials with space groups Pmn2_1 and P6̄m2, as well as P4/mmm and P1̄, the work function is a critical factor. To further explore this observation and validate the global analysis conclusions, a local SHAP-based model interpretation was performed on randomly selected materials BeI2 (P3̄m1), Al2Se5 (C2/m), TaTe2 (P6̄m2), GeSe (Pmn2_1), Be2Cd (P4/mmm), and TaI5 (P1̄) from the high-throughput screening results. Clearly, the space group significantly influences work function prediction in TaTe2 (P6̄m2), GeSe (Pmn2_1), Be2Cd (P4/mmm), and TaI5 (P1̄) (Fig. S6c–f†), consistent with the global analysis results (Fig. 3b). Conversely, atomic radius, covalent radius, electron affinity, and boiling point are the most significant contributors to work function prediction in BeI2 (P3̄m1) and Al2Se5 (C2/m) (Fig. S6a and b†), confirming that these features, rather than the space group, are the primary factors for predicting work functions, which is inconsistent with the global interpretation (Fig. 3b).
Combining the local and global interpretations with the frequency distribution of space groups for these materials, we can gain these significant new insights into the work functions of 2D nanomaterials: (i) work function is determined not only by structure-based factors but also by atomic-level features, refreshing the traditional understanding of the nature of material work functions, i.e., work function variations for a nanomaterial primarily originated from the changes in the surface dipole and intrinsic bulk electronic structure of the material, as well as their effects on the vacuum and Fermi levels, from a new dimension. (ii) From a holistic view, the space group stands out as a significant factor of work function prediction. However, for certain materials, such as BeI2 (P3̄m1) and Al2Se5 (C2/m), the determining factor for their work function is not the space group but the atomic-level features. (iii) Materials with the P6̄m2 and Pmn2_1 space groups generally exhibit relatively higher work functions, while those with the P4/mmm and P1̄ space groups tend to present relatively lower work functions.
4. Conclusion
This study proposes a target-driven framework for material design to accelerate the discovery of potential transparent OLED anode materials. This framework combines the HTVS and ML techniques to enhance the efficiency of the discovery process. A robust ML regression model (CatBoost) was successfully trained using model comparison and hyperparameter optimization. This model demonstrated a remarkable ability to directly predict the work functions of AB-type 2D nanomaterials, with R2 and RMSE values of 0.92 and 0.28 on the test set, respectively, eliminating the requirement for time-consuming DFT calculations (≈103 faster than DFT). Global and local model interpretation results based on the SHAP method reveal that the space group is the decisive factor in predicting the work function for most materials, while atomic-scale features of the material composition (elemental radius, electron affinity energy, ionization energy, etc.) are the dominant factors for other materials. Certain space groups (Pmn2_1 and P6̄m2) tend to exhibit relatively higher work functions (>7 eV), while some other space groups (P4/mmm and P1̄) often present relatively lower work functions (<4 eV). Finally, CatBoost was applied to high-throughput screening, resulting in a comprehensive list of OLED anode materials with thermodynamic stability (dissociation energy <0.1 eV per atom), narrow band gap (0–3 eV) and specific work functions (>5 eV) from the 2DMatPedia database. Significantly, further DFT computations reveal that the PS nanomaterial displays superb transparency (transmittance > 90%) and elevated conductivity (σ > 106 S m−1). This positions PS as an exceptionally promising candidate for transparent OLED anodes, surpassing the conventional ITO.
This study provides new insights into the intrinsic mechanisms affecting the work function of 2D nanomaterials, and the proposed design framework offers an efficient approach for exploring optoelectronic materials. The research paradigm that deeply analyzes the relationship between features and target properties by employing interpretable ML techniques is poised to become a significant driver in the future exploration of material properties, offering new perspectives and breakthroughs in uncovering the fundamental nature of materials and their performance.
Data availability
The data set for training a 2D nanomaterial function prediction model in this study can be sourced from the C2DB database and is publicly available at https://cmr.fysik.dtu.dk/c2db/. The high-throughput screening data can be obtained from the 2DMatPedia database, accessible at https://www.2dmatpedia.org/. Further ESI data is included in the ESI.†
Author contributions
Liying Cui: conceptualization, investigation, methodology, formal analysis, data curation, software, visualization, writing – original draft. Qing Li: methodology, data curation. Yanchang Zhang: data curation. Jiao Zhang: data curation. Zhe Wang: data curation. Jiankang Chen: data curation. Bing Zheng: conceptualization, funding acquisition, supervision, writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 21601054), the Project funded by China Postdoctoral Science Foundation (No. 2020M670935), the Heilongjiang University Special Project of the Fundamental Research Funds for the Provincial Universities (Program for Technological Innovation, 2024), and the Training Program of Innovation and Entrepreneurship for Undergraduates of Heilongjiang Province (No. S202310212187).
Electronic supplementary information (ESI) available: Calculation details of the 2DMatPedia database, Pearson correlation coefficient, t-SNE algorithm, shuffle function, and work function (Section S1); 2D dataset visualization, cross validation, the work function values predicted by ML and DFT, OLED's luminous mechanism, level of common organic materials, decomposition energies of previous 2D materials, the frequency distribution of space groups, and individual SHAP plots of the CatBoost for the structures with different space groups (Section S2); material's properties and corresponding methods of C2DB and 2DMatPedia, descriptors of the ML model, parameter optimization details and performance tests of models, and transport property calculation results (Section S3). See DOI: https://doi.org/10.1039/d4sc05598e
References
- Hong G. Gan X. Leonhardt C. Zhang Z. Seibert J. Busch J. M. Bräse S. A Brief History of OLEDs-Emitter Development and Industry Milestones. Adv. Mater. 2021;33:2005630. doi: 10.1002/adma.202005630. [DOI] [PubMed] [Google Scholar]
- Song J. Lee H. Jeong E. G. Choi K. C. Yoo S. Organic Light-Emitting Diodes: Pushing Toward the Limits and Beyond. Adv. Mater. 2020;32:1907539. doi: 10.1002/adma.201907539. [DOI] [PubMed] [Google Scholar]
- Salehi A. Fu X. Y. Shin D. H. So F. Recent Advances in OLED Optical Design. Adv. Funct. Mater. 2019;29:1808803. doi: 10.1002/adfm.201808803. [DOI] [Google Scholar]
- Baek G. W. Seo S. G. Hahm D. Kim Y. J. Kim K. Lee T. Kim J. Bae W. K. Jin S. H. Kwak J. Optimum Design Configuration of Thin-Film Transistors and Quantum-Dot Light-Emitting Diodes for Active-Matrix Displays. Adv. Mater. 2023;35:2304717. doi: 10.1002/adma.202304717. [DOI] [PubMed] [Google Scholar]
- Efros A. L. Brus L. E. Nanocrystal Quantum Dots: From Discovery to Modern Development. ACS Nano. 2021;15:6192–6210. doi: 10.1021/acsnano.1c01399. [DOI] [PubMed] [Google Scholar]
- Meng T. T. Zheng Y. T. Zhao D. L. Hu H. l. Zhu Y. B. Xu Z. W. Ju S. M. Jing J. P. Chen X. Z. Gao H. J. Yang K. Y. Guo T. L. Li F. S. Fan J. P. Qian L. Ultrahigh-Resolution Quantum-Dot Light-Emitting Diodes. Nat. Photonics. 2022;16:297–303. doi: 10.1038/s41566-022-00960-w. [DOI] [Google Scholar]
- Ou E. C. W. Hu L. B. Raymond G. C. R. Soo O. K. Pan J. S. Zheng Z. Park Y. Hecht D. Irvin G. Drzaic P. Gruner G. Surface-Modified Nanotube Anodes for High Performance Organic Light-Emitting Diode. ACS Nano. 2009;3:2258–2264. doi: 10.1021/nn900406n. [DOI] [PubMed] [Google Scholar]
- Ahn J. H. Hong B. H. Graphene for Displays That Bend. Nat. Nanotechnol. 2014;9:737–738. doi: 10.1038/nnano.2014.226. [DOI] [PubMed] [Google Scholar]
- Kim T. H. Kang S. W. Heo J. W. Cho S. S. Kim J. W. Choe A. Walker B. Shanker R. Ko H. H. Kim J. Y. Nanoparticle-Enhanced Silver-Nanowire Plasmonic Electrodes for High-Performance Organic Optoelectronic Devices. Adv. Mater. 2018;30:10. doi: 10.1002/adma.201800659. [DOI] [PubMed] [Google Scholar]
- Sharif P. Alemdar E. Ozturk S. Caylan O. Haciefendioglu T. Buke G. Aydemir M. Danos A. Monkman A. P. Yildirim E. Gunbas G. Cirpan A. Oral A. Rational Molecular Design Enables Efficient Blue TADF-OLEDs with Flexible Graphene Substrate. Adv. Funct. Mater. 2022;32:14. doi: 10.1002/adfm.202207324. [DOI] [Google Scholar]
- Park I. J. Kim T. I. Yoon T. Kang S. Cho H. Cho N. S. Lee J. I. Kim T. S. Choi S. Y. Flexible and Transparent Graphene Electrode Architecture with Selective Defect Decoration for Organic Light-Emitting Diodes. Adv. Funct. Mater. 2018;28:10. [Google Scholar]
- Han T. H. Lee Y. Choi M. R. Woo S. H. Bae S. H. Hong B. H. Ahn J. H. Lee T. W. Extremely Efficient Flexible Organic Light-Emitting Diodes with Modified Graphene Anode. Nat. Photonics. 2012;6:105–110. doi: 10.1038/nphoton.2011.318. [DOI] [Google Scholar]
- Graf A. Murawski C. Zakharko Y. Zaumseil J. Gather M. C. Infrared Organic Light-Emitting Diodes with Carbon Nanotube Emitters. Adv. Mater. 2018;30:6. doi: 10.1002/adma.201706711. [DOI] [PubMed] [Google Scholar]
- Wang Z. Y. Gao L. Wei X. Z. Zhao M. Miao Y. Q. Zhang X. F. Zhang H. X. Wang H. Hao Y. Y. Xu B. S. Guo J. J. Energy Level Engineering of PEDOT:PSS by Antimonene Quantum Sheet Doping for Highly Efficient OLEDs. J. Mater. Chem. C. 2020;8:1796–1802. doi: 10.1039/C9TC06049A. [DOI] [Google Scholar]
- Li H. A. Li Y. Aljarb A. Shi Y. M. Li L. J. Epitaxial Growth of Two-Dimensional Layered Transition-Metal Dichalcogenides: Growth Mechanism, Controllability, and Scalability. Chem. Rev. 2018;118:6134–6150. doi: 10.1021/acs.chemrev.7b00212. [DOI] [PubMed] [Google Scholar]
- Ahn S. Han T. H. Maleski K. Song J. N. Kim Y. H. Park M. H. Zhou H. Y. Yoo S. Gogotsi Y. Lee T. W. A 2D Titanium Carbide MXene Flexible Electrode for High-Efficiency Light-Emitting Diodes. Adv. Mater. 2020;32:7. doi: 10.1002/adma.202000919. [DOI] [PubMed] [Google Scholar]
- Liao L. P. Kovalska E. Regner J. Song Q. L. Sofer Z. Two-Dimensional Van Der Waals Thin Film and Device. Small. 2023;20:2303638. doi: 10.1002/smll.202303638. [DOI] [PubMed] [Google Scholar]
- Akinwande D. Petrone N. Hone J. Two-Dimensional Flexible Nanoelectronics. Nat. Commun. 2014;5:5678. doi: 10.1038/ncomms6678. [DOI] [PubMed] [Google Scholar]
- Jeong S. Y. Jeon Y. Kim E. Lee G. B. Oh Y. W. Ahn C. W. Cho E. H. Lee Y. H. Choi K. C. Highly Air-Stable, Flexible, and Water-Resistive 2D Titanium Carbide MXene-Based RGB Organic Light-Emitting Diode Displays for Free-Form Electronics Article. ACS Nano. 2023;17:10353–10364. doi: 10.1021/acsnano.3c00781. [DOI] [PubMed] [Google Scholar]
- Saha S. Ananthram K. S. Hassan N. Ugale A. Tarafder K. Ballav N. Ag Nanoparticles-Induced Metallic Conductivity in Thin Films of 2D Metal-Organic Framework Cu3(HHTP)2. Nano Lett. 2023;23:9326–9332. doi: 10.1021/acs.nanolett.3c02522. [DOI] [PubMed] [Google Scholar]
- Zheng B. He J. Wang Z. Xie Y. Qian Y. Y. Zhang J. Tang Y. N. Cui L. Y. Wu Y. M. Yang L. Yu H. T. Ultra-Stable Metallic Freestanding Multilayer Borophene with Tunable Work Function. Appl. Surf. Sci. 2023;612:155842. doi: 10.1016/j.apsusc.2022.155842. [DOI] [Google Scholar]
- He J. Zheng B. Xie Y. Qian Y. Y. Zhang J. Wang K. Yang L. Yu H. T. Effects of Adatom Species on the Structure, Stability, and Work Function of Adatom-α-Borophene Nanocomposites. Phys. Chem. Chem. Phys. 2022;24:8923–8939. doi: 10.1039/D2CP00506A. [DOI] [PubMed] [Google Scholar]
- Zhou J. Shen L. Costa M. D. Persson K. A. Ong S. P. Huck P. Lu Y. Ma X. Chen Y. Tang H. Feng Y. P. 2DMatPedia, an Open Computational Database of Two-Dimensional Materials from Top-Down and Bottom-Up Approaches. Sci. Data. 2019;6:86. doi: 10.1038/s41597-019-0097-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. Z. Xu S. H. Shabani S. Zhao Y. Q. Fu M. Millis A. J. Fogler M. M. Pasupathy A. N. Liu M. Basov D. N. Machine Learning for Optical Scanning Probe Nanoscopy. Adv. Mater. 2022;35:2109171. doi: 10.1002/adma.202109171. [DOI] [PubMed] [Google Scholar]
- López C. Artificial Intelligence and Advanced Materials. Adv. Mater. 2023;35:2208683. doi: 10.1002/adma.202208683. [DOI] [PubMed] [Google Scholar]
- Liu C. Lüer L. Corre V. L. Forberich K. Weitz P. Heumüller T. Du X. Y. Wortmann J. Zhang J. Y. Wagner J. Ying L. Hauch J. Li N. Brabec C. J. Understanding Causalities in Organic Photovoltaics Device Degradation in a Machine-Learning-Driven High-Throughput Platform. Adv. Mater. 2023;36:2300259. doi: 10.1002/adma.202300259. [DOI] [PubMed] [Google Scholar]
- Schindler P. Antoniuk E. R. Cheon G. Zhu Y. B. Reed E. J. Discovery of Stable Surfaces with Extreme Work Functions by High-Throughput Density Functional Theory and Machine Learning. Adv. Funct. Mater. 2024;34:2401764. doi: 10.1002/adfm.202401764. [DOI] [Google Scholar]
- Hashimoto W. Tsuji Y. Yoshizawa K. Optimization of Work Function via Bayesian Machine Learning Combined with First-Principles Calculation. J. Phys. Chem. C. 2020;124:9958–9970. doi: 10.1021/acs.jpcc.0c01106. [DOI] [Google Scholar]
- Wei X. Wang J. Wang C. Zhu S. Wang L. Guan S. Prediction of Electronic Work Function of the Second Phase in Binary Magnesium Alloy Based on Machine Learning Method. J. Mater. Res. 2022;37:3792–3802. doi: 10.1557/s43578-022-00752-6. [DOI] [Google Scholar]
- Li N., Zong T. X. and Zhang Z. G., Presented in Part at the 2021 IEEE 6th International Conference on Big Data Analytics (ICBDA), 2021 [Google Scholar]
- Li J. L. Hu W. Yang J. L. High-Throughput Screening of Rattling-Induced Ultralow Lattice Thermal Conductivity in Semiconductors. J. Am. Chem. Soc. 2022;144:4448–4456. doi: 10.1021/jacs.1c11887. [DOI] [PubMed] [Google Scholar]
- Wang H. S. Feng J. Dong Z. H. Jin L. j. Li M. M. Yuan J. Y. Li Y. Y. Efficient Screening Framework for Organic Solar Cells with Deep Learning and Ensemble Learning. npj Comput. Mater. 2023;9:200. doi: 10.1038/s41524-023-01155-9. [DOI] [Google Scholar]
- Paier J. Hirschl R. Marsman M. Kresse G. The Perdew-Burke-Ernzerhof Exchange-Correlation Functional Applied to The G2-1 Test Set Using a Plane-Wave Basis Set. J. Chem. Phys. 2005;122:234102. doi: 10.1063/1.1926272. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Burke K. Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997;77:38653–38868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Wang V. Xu N. Liu J. C. Tang G. Geng W. T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021;267:108033. doi: 10.1016/j.cpc.2021.108033. [DOI] [Google Scholar]
- Moscowitz A. Theoretical Aspects of Optical Activity Part One: Small Molecules. Adv. Chem. Phys. 1962;4:67–112. doi: 10.1002/9780470143506.ch2. [DOI] [Google Scholar]
- Madsen G. K. Carrete J. Verstraete M. J. BoltzTraP2, a Program for Interpolating Band Structures and Calculating Semi-Classical Transport Coefficients. Comput. Phys. Commun. 2017;231:140–145. doi: 10.1016/j.cpc.2018.05.010. [DOI] [Google Scholar]
- Bardeen J. Shockley W. S. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950;80:72–80. doi: 10.1103/PhysRev.80.72. [DOI] [Google Scholar]
- Lundberg S. M. Lee S. I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017;30:4768–4777. [Google Scholar]
- Haastrup S. Strange M. Pandey M. Deilmann T. Schmidt P. S. Hinsche N. F. Gjerding M. N. Torelli D. Larsen P. M. Riis-Jensen A. C. Gath J. Jacobsen K. W. Mortensen J. J. Olsen T. Thygesen K. S. The Computational 2D Materials Database: High-Throughput Modeling and Discovery of Atomically Thin Crystals. 2D Mater. 2018;5:042002. doi: 10.1088/2053-1583/aacfc1. [DOI] [Google Scholar]
- Gjerding M. N. Taghizadeh A. Rasmussen A. Ali S. Bertoldo F. Deilmann T. Knosgaard N. R. Kruse M. Larsen A. H. Manti S. Pedersen T. G. Petralanda U. Skovhus T. Svendsen M. K. Mortensen J. J. Olsen T. Thygesen K. S. Recent Progress of the Computational 2D Materials Database (C2DB) 2D Mater. 2021;8:044002. doi: 10.1088/2053-1583/ac1059. [DOI] [Google Scholar]
- Isayev O. Oses C. Toher C. Gossett E. Curtarolo S. Tropsha A. Universal Fragment Descriptors for Predicting Properties of Inorganic Crystals. Nat. Commun. 2017;8:15679. doi: 10.1038/ncomms15679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bang K. Hong D. Park Y. Kim D. Han S. S. Lee H. M. Machine Learning-Enabled Exploration of the Electrochemical Stability of Real-Scale Metallic Nanoparticles. Nat. Commun. 2023;14:3004. doi: 10.1038/s41467-023-38758-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M. Tikhonov E. Tudi A. Kruglov I. Hou X. Xie C. Pan S. Yang Z. Target-Driven Design of Deep-UV Nonlinear Optical Materials via Interpretable Machine Learning. Adv. Mater. 2023;35:2300848. doi: 10.1002/adma.202300848. [DOI] [PubMed] [Google Scholar]
- Ong S. P. Richards W. D. Jain A. Hautier G. Kocher M. Cholia S. Gunter D. Chevrier V. L. Persson K. A. Ceder G. Python Materials Genomics (pymatgen): A Robust, Open-Source Python Library for Materials Analysis. Comput. Mater. Sci. 2013;68:314–319. doi: 10.1016/j.commatsci.2012.10.028. [DOI] [Google Scholar]
- Karunasingha D. S. K. Root Mean Square Error or Mean Absolute Error? Use Their Ratio As Well. Inf. Sci. 2022;585:609–629. doi: 10.1016/j.ins.2021.11.036. [DOI] [Google Scholar]
- Chicco D. Warrens M. J. Jurman G. The Coefficient of Determination R-Squared is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021;7:24. doi: 10.7717/peerj-cs.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bykov M. Bykova E. Ponomareva A. V. Tasnádi F. Chariton S. Prakapenka V. B. Glazyrin K. Smith J. S. Mahmood M. F. Abrikosov I. A. Goncharov A. F. Realization of an Ideal Cairo Tessellation in Nickel Diazenide NiN2: High-Pressure Route to Pentagonal 2D Materials. ACS Nano. 2021;15:13539–13546. doi: 10.1021/acsnano.1c04325. [DOI] [PubMed] [Google Scholar]
- Shan B. Cho K. First Principles Study of Work Functions of Single Wall Carbon Nanotubes. Phys. Rev. Lett. 2005;94:236602. doi: 10.1103/PhysRevLett.94.236602. [DOI] [PubMed] [Google Scholar]
- Zheng B. Wang Z. He J. Zhang J. Qi W. B. Zhang M. Y. Yu H. T. Structure and Work Function of Alkaline (Earth) Metal-Bilayer α-Borophene Nanocomposite: A Theoretical Study. Acta Chim. Sin. 2023;81:1357–1370. doi: 10.6023/A23050210. [DOI] [Google Scholar]
- Zhang S. B. Cohen M. L. Determination of AB Crystal Structures from Atomic Properties. Phys. Rev. B: Condens. Matter Mater. Phys. 1989;39:1077–1080. doi: 10.1103/PhysRevB.39.1077. [DOI] [PubMed] [Google Scholar]
- Pyykkö P. Additive Covalent Radii for Single-, Double-, and Triple-Bonded Molecules and Tetrahedrally Bonded Crystals: A Summary. J. Phys. Chem. A. 2015;119:2326–2337. doi: 10.1021/jp5065819. [DOI] [PubMed] [Google Scholar]
- Agmon N. Isoelectronic Theory for Cationic Radii. J. Am. Chem. Soc. 2017;139:15068–15073. doi: 10.1021/jacs.7b07882. [DOI] [PubMed] [Google Scholar]
- Kumar P. Aggrawal N. Choudhary S. D. Gautam A. K. Highly-Efficient Solution Processed Yellow Organic Light Emitting Diode With Tungsten Trioxide Hole Injection/Transport Layer. IEEE Trans. Nanotechnol. 2020;19:61–66. [Google Scholar]
- Huang F. Liu H. L. Li X. G. Wang S. R. Enhancing Hole Injection by Processing ITO Through MoO3 and Self-Assembled Monolayer Hybrid Modification for Solution-Processed Hole Transport Layer-Free OLEDs. Chem. Eng. J. 2022;427:131356. doi: 10.1016/j.cej.2021.131356. [DOI] [Google Scholar]
- Huang Q. L. Evmenenko G. A. Dutta P. Lee P. Armstrong N. R. Marks T. J. Covalently Bound Hole-Injecting Nanostructures. Systematics of Molecular Architecture, Thickness, Saturation, and Electron-Blocking Characteristics on Organic Light-Emitting Diode Luminance, Turn-on Voltage, and Quantum Efficiency. J. Am. Chem. Soc. 2005;127:10227–10242. doi: 10.1021/ja051077w. [DOI] [PubMed] [Google Scholar]
- Perumal A. Faber H. Yaacobi-Gross N. Pattanasattayavong P. Burgess C. Jha S. McLachlan M. A. Stavrinou P. N. Anthopoulos T. D. Bradley D. D. High-Efficiency, Solution-Processed, Multilayer Phosphorescent Organic Light-Emitting Diodes with a Copper Thiocyanate Hole-Injection/Hole-Transport Layer. Adv. Mater. 2015;27:93–100. doi: 10.1002/adma.201403914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang B. Clark G. Navarro-Moratalla E. Klein D. Cheng R. Seyler K. L. Zhong D. Schmidgall E. Mcguire M. A. Cobden D. H. Layer-Dependent Ferromagnetism in a Van Der Waals Crystal down to the Monolayer Limit. Nature. 2017;546:270. doi: 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
- Xu S. Han Y. Chen X. Wu Z. Wang N. Van Der Waals Epitaxial Growth of Atomically Thin Bi2Se3 and Thickness-Dependent Topological Phase Transition. Nano Lett. 2015;15:2645–2651. doi: 10.1021/acs.nanolett.5b00247. [DOI] [PubMed] [Google Scholar]
- Li J. Guan X. Wang C. Cheng H. C. Duan X. Synthesis of 2D Layered BiI3 Nanoplates, BiI3/WSe2 Van Der Waals Heterostructures and Their Electronic, Optoelectronic Properties. Small. 2017;13:1701034. doi: 10.1002/smll.201701034. [DOI] [PubMed] [Google Scholar]
- Chen Z. B. Yang S. D. Huang J. H. Gu Y. F. Huang W. B. Liu S. Y. Lin Z. Q. Zeng Z. P. Hu Y. G. Chen Z. M. Yang B. R. Gui X. C. Flexible, Transparent and Conductive Metal Mesh Films with Ultra-High FoM for Stretchable Heating and Electromagnetic Interference Shielding. Nano-Micro Lett. 2024;16:13. doi: 10.1007/s40820-023-01239-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data set for training a 2D nanomaterial function prediction model in this study can be sourced from the C2DB database and is publicly available at https://cmr.fysik.dtu.dk/c2db/. The high-throughput screening data can be obtained from the 2DMatPedia database, accessible at https://www.2dmatpedia.org/. Further ESI data is included in the ESI.†