Abstract
Quantum computing has emerged as a powerful computational paradigm capable of solving problems beyond the reach of classical computers. However, today’s quantum computers are noisy, posing challenges to obtaining accurate results. Here, we explore the impact of noise on quantum computing, focusing on the challenges in sampling bit strings from noisy quantum computers and the implications for optimization and machine learning. We formally quantify the sampling overhead to extract good samples from noisy quantum computers and relate it to the layer fidelity, a metric to determine the performance of noisy quantum processors. Further, we show how this allows us to use the conditional value at risk of noisy samples to determine provable bounds on noise-free expectation values. We discuss how to leverage these bounds for different algorithms and demonstrate our findings through experiments on real quantum computers involving up to 127 qubits. The results show strong alignment with theoretical predictions.
Subject terms: Quantum information, Applied mathematics
In this study, the authors investigate the impact of noise on quantum computing with a focus on the challenges in sampling bit strings from noisy quantum computers, which has implications for optimization and machine learning.
Main
Quantum computing is a new computational paradigm that promises to impact many disciplines, ranging from quantum chemistry1,2, quantum physics3 and material sciences4 to machine learning5–7, optimization8–12 and finance13. However, leveraging near-term quantum computers is difficult due to the noise present in the systems. Ultimately, this needs to be addressed by quantum error correction, which exponentially suppresses errors by encoding logical qubits in multiple physical qubits14.
In near-term devices, implementing error correction is infeasible. We must find other ways to handle the noise. A promising approach to bridge the gap between noisy and error-corrected quantum computing is error mitigation. Here, we leverage multiple noisy estimates to construct a better approximation of the noise-free result. The most prominent examples are probabilistic error cancellation (PEC)15,16 and zero-noise extrapolation (ZNE)17. While error mitigation in general scales exponentially15, a combination of PEC and ZNE has been impressively demonstrated recently in a 127-qubit experiment at a circuit depth beyond the reach of exact classical methods18,19. The rate of the exponential cost of error mitigation directly relates to the errors in the quantum devices. It is expected that these errors can be reduced to a level at which noisy devices with error mitigation can already perform practically relevant tasks even before error correction20. PEC and ZNE mitigate the errors in expectation values. While this finds many applications (for example, in quantum chemistry and physics), most quantum optimization algorithms8,10,21 and many quantum machine learning algorithms6,22 build directly on top of measured samples from a quantum computer. In optimization, having access to an objective value but not the samples corresponds to knowing the value of an optimal solution but not how to realize it. Obtaining these samples is thus a key problem to scale sample-based algorithms on noisy hardware.
In this paper, we examine the impact of noise on sampling bit strings from a noisy quantum computer and quantify the required sampling overhead to extract good solutions—for example, in the context of optimization. It turns out that the sampling overhead is substantially lower than, for example, estimating expectation values via PEC. Furthermore, we connect our findings to the conditional value at risk (CVaR, also known as expected shortfall), an alternative loss function introduced in ref. 23. We show that the CVaR is robust against noise and can generate meaningful results from noisy samples also for expectation values. The noise robustness of the CVaR had already been conjectured but had not been shown formally23. Our work closes this gap and shows that the CVaR evaluated on noisy samples achieves provable bounds on noise-free observables.
The CVaR offers important advantages over PEC and ZNE when bounds on expectation values are sufficient: unlike PEC, which requires costly noise learning15, the CVaR can be implemented using a much cheaper fidelity estimation protocol24 and requires less restrictive assumptions on the noise model. Additionally, the CVaR leads to a substantially lower sampling overhead than PEC. ZNE involves amplifying the noise to extrapolate to the zero-noise limit. This amplification can be achieved by repeating certain gates or calibrating special pulses, both difficult to scale, or by first learning the noise as in PEC18 and then amplifying it. Further, ZNE is usually heuristic without the theoretical guarantees of PEC or the CVaR. These properties render the CVaR a promising approach for extracting properties of expectation values and a practical loss function for training variational quantum algorithms23,25.
We demonstrate our theoretical results on a real quantum computer applied to fidelity estimations on up to 100 qubits as well as optimization problems on up to 127 qubits, where we find close agreement between the experiments and theory. In particular, this allows us to apply the known noise-free performance bounds for the quantum approximate optimization algorithm (QAOA) for MaxCut on 3-regular graphs8,26. Thus, our work results in provable performance guarantees for a variational algorithm on noisy hardware.
Results
Consider a noise-free quantum state ρ and the corresponding noisy quantum state , when preparing ρ on a noisy quantum computer. There are different ways to model the noise and characterize its strength. A practical and efficient way is by estimating the layer fidelity (LF) of a circuit24, which essentially is equal to the probability of no error happening. Alternatively, assuming the Pauli–Lindblad noise model, it is possible to learn the noise explicitly15. The strength of the noise can be characterized by the parameter γ, which determines the cost to mitigate the noise using PEC, where 1/√γ represents the probability of no error, that is, is equal to the LF.
This allows us to relate the probability of sampling a bit string x ∈ {0, 1}n when measuring ρ (px) and () as
| 1 |
In other words, taking √γ (or 1/LF) more samples guarantees that a noisy state generates bit strings with at least the same probability as the corresponding noise-free state.
Further, if we have a Hamiltonian H and are interested in the expectation value tr(ρH), we can show that the CVaR at level α with α = 1/√γ allows us to generate provable lower bounds (and upper bounds, denoted by ) on noise-free expectation values using only samples from the noisy state . In the following, we discuss these results in the context of different algorithms and applications and demonstrate them on real quantum computers using up to 127 qubits. The theoretical details are provided in Methods.
Applications
We now discuss the presented theory on sampling probabilities and the CVaR in the context of different applications: first, fidelity-based algorithms, such as quantum support vector machines (QSVMs)5,27,28 as well as variational quantum time evolution (VarQTE)7,29–34, and second, quantum optimization8,10,21,23,35. These are illustrative examples; the theory presented here is applicable to many other domains, such as quantum chemistry and physics.
Fidelity estimation
Several quantum algorithms leverage fidelity estimation between two quantum states as a subroutine. In the following, we first discuss how to leverage the CVaR bounds to approximate fidelities on noisy quantum computers and then how this impacts two concrete classes of algorithms: QSVMs and VarQTE.
Suppose we have n-qubit quantum circuits U and V that define |ψ〉 = U|0〉 and |ϕ〉 = V|0〉, respectively. A common approach to estimate the state fidelity between |ψ〉 and |ϕ〉 is the compute–uncompute method given by
| 2 |
F is thus the probability of measuring |0〉 for the state V†U|0〉. This is also equal to the expectation value tr(ρH) for the state ρ = V†U|0〉 and the diagonal Hamiltonian H = |0〉 〈0|. Thus, we can use to obtain an upper bound of the noise-free fidelity. Here the resulting random variable follows a Bernoulli distribution, as the expectation value counts the number of measured instances of |0〉 and ignores all other outcomes. Since the variance of the CVaR for a Bernoulli random variable scales with 1/α (Conditional value at risk), we can set α = 1/√γ and use equation (13) to upper bound the fidelity with a sampling overhead of √γ, compared with the γ2 required by PEC to obtain an unbiased estimation. We demonstrate this on a concrete example in Experiments.
QSVMs leverage a quantum feature map to define a quantum kernel and provably outperform classical computers on certain tasks36. The quantum feature map is a parameterized quantum circuit that takes a classical feature vector x as an input to prepare a corresponding quantum state |ϕ(x)〉. The corresponding quantum kernel is then defined via the Hilbert–Schmidt inner product of |ϕ(x1)〉 and |ϕ(x2)〉 for two classical data points x1 and x2 from some training set, which is equal to F(|ϕ(x1)〉, |ϕ(x2)〉), and thus falls exactly into the case above.
VarQTE for real or imaginary time evolution assumes a given parameterized quantum state |ψ(θ)〉 and then projects the exact state evolution to the parameter evolution of the ansatz. This approximates the desired time evolution in the subspace that the ansatz can represent. The exact projection requires the evaluation of the quantum geometric tensor (QGT)29–31. However, this quickly becomes prohibitive as the number of parameters increases. Thus, multiple approximate variants of VarQTE have been proposed that work around the evaluation of the QGT32–34. Many of these approximations leverage the fact that the Hessian of the fidelity ∣〈ψ(θ)∣ψ(θ + δθ)〉∣2 with respect to δθ is proportional to the QGT of |ψ(θ)〉 up to higher-order terms. They either use the simultaneous perturbation stochastic approximation to estimate the Hessian from evaluations of the fidelity as approximations of the QGT, or they construct alternative loss functions that directly leverage the mentioned fidelity without constructing an approximate QGT. In all variants, the parameter disturbances δθ are small, which implies fidelities close to one. Thus, this is in the regime where the noisy CVaR is very close to the noise-free expectation value, that is, the sweet spot of the introduced approximation.
Quantum optimization
Many (variational) quantum algorithms have been proposed to solve discrete optimization problems, such as quadratic unconstrained binary optimization. Most of them have similar structures and interpret every measured bit string as a potential solution to the problem. Proposals that derive variable values from expectation values9,37 are, however, outside the focus of our work.
Consider a generic unconstrained binary optimization problem of the form
| 3 |
where is an objective function on n binary variables. For instance, a quadratic unconstrained binary optimization has f(x) = xTQx with . In the case of quadratic unconstrained binary optimization, we can apply a change of variables xi = (1 − zi)/2 for zi ∈ { −1, +1} and replace zi by the Pauli Zi matrix on qubit i and products zizj by Zi ⊗ Zj to define a diagonal Hamiltonian H and translate equation (3) into a ground-state problem38
| 4 |
As mentioned in Conditional value at risk, we can transform any generic function to a Hamiltonian where f(x) defines the diagonal element of H at the position of the computational basis state |x〉 (ref. 21).
Most variational quantum algorithms for binary optimization are defined via a parameterized ansatz |ψ(θ)〉 with parameters , a loss function that maps parameter values to a loss value, and an optimizer to solve
| 5 |
After the final parameters θ* are determined, the resulting state |ψ(θ*)〉 is measured and the sampled bit strings are used as potential solutions to the problem. Samples obtained during the execution of the algorithm can also be considered as solutions in case they achieve better objective values than the final samples.
If we set for some ansatz |ψ(θ)〉, we obtain the variational quantum eigensolver1. Further, if we define the ansatz as
| 6 |
we obtain the QAOA8, where p defines the depth, and the angles are the variational parameters. H and with Pauli matrices Xi define a phase separating and a mixing Hamiltonian, respectively.
Our theoretical results (Methods) can be immediately applied to the QAOA. Suppose we already have a quantum circuit that, when executed and measured in an ideal noise-free setting, produces good solutions to a considered optimization problem. Then, when executed on a noisy device, a sampling overhead of √γ is sufficient to extract solutions of the same quality as in the noise-free case. In certain cases it might be feasible to determine θ* classically39–41 and only use the quantum computer to sample good solutions, since evaluating (local) expectation values might be easier than sampling from the full circuit. However, in cases where we must train the parameterized quantum circuit we can replace the expectation value by the CVaR23,25. Our results provide guidance on how to choose α and the required sampling overhead to obtain good results from a noisy device. We illustrate this on concrete examples in Experiments.
Our results allow us to apply proven performance guarantees for the QAOA without noise to noisy hardware. For MaxCut on 3-regular graphs, the QAOA achieves a worst-case performance of 0.692 for p = 1 (ref. 8), 0.7559 for p = 2 and (under certain assumptions) 0.7924 for p = 3 (ref. 26). With a √γ sampling overhead these guarantees are recovered even in the noisy regime. Furthermore, for 3-regular graphs, we can always train the QAOA with p ≤ 3 classically by simulating at most 30 qubits at a time11: that is, we can determine the optimal parameters via classical simulation and then sample good solutions with a √γ overhead from the quantum computer. Since γ grows exponentially with the circuit size the sampling overhead introduced to combat noise may exceed the cost of a brute-force search. A simple back of the envelope calculation, discussed in Supplementary Information, ‘Relation to brute-force search’, determines a minimum LF required to apply a depth-p QAOA.
The quantum alternating operator ansatz (QAOA′) is a generalization of the QAOA8,42. The QAOA′ allows for constraints on the set of feasible solutions, such as a fixed Hamming weight (that is, a fixed number of ones in a bit string), which it enforces by starting in a superposition of feasible states43,44 and changing the mixing Hamiltonian to preserve and interfere with such states45–47. More generally, the QAOA′ allows different mixing Hamiltonians and initial states to be used (unlike the original QAOA), and typically uses the same phase-separating Hamiltonian that encodes the classical optimization problem of interest. Thus, if the QAOA′ is executed noise free, all resulting samples must satisfy the given constraint. This is an example of a filter function (for example, post-select on samples with the correct Hamming weight) that can help to improve the CVaR bounds on the corresponding expectation value (Methods).
Experiments
We now demonstrate the introduced theory in the context of the discussed applications. First we show how to estimate state fidelities with the CVaR, and second we study two optimization problems from the literature. We run the circuits on the ibm_sherbrooke and ibm_kyiv quantum devices48 and find good sagreement between our theory and the experimental results.
Both ibm_sherbrooke and ibm_kyiv are 127-qubit superconducting qubit devices with echoed cross-resonance gates as two-qubit gates49. This gate is equivalent to a controlled NOT (CNOT) gate up to single-qubit gates. We let the transpiler map our CNOT gates to echoed cross-resonance gates and thus write about CNOT gates for better readability. All circuits are implemented in Qiskit50 and run using the SamplerV2 primitive of Qiskit IBM Runtime51 with enabled dynamical decoupling and Pauli twirling for CNOT gates. We use the built-in capabilities with XY4 dynamical decoupling and Pauli twirling with 64 randomizations per circuit, that is, the stated number of shots is distributed equally over all twirls. Further, we apply M3 measurement error mitigation52 to every experiment.
Fidelity estimation
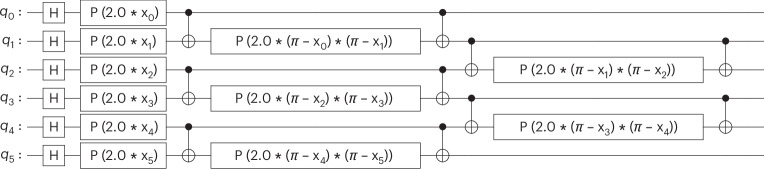
As mentioned in Applications, estimating fidelities F(|ψ〉, |ϕ〉) for given quantum states |ψ〉 and |ϕ〉 is relevant for several algorithms, such as QSVMs and VarQTE. To demonstrate the introduced theory in this context, we consider the hardware-native ZZ Feature Map53 that has been introduced in the context of QSVMs5. More precisely, we consider n-qubit parameterized quantum states |ψ(x)〉 = U(x)|0〉, , with the parameterized unitary U as illustrated in Fig. 1. Further, we randomly sample two data points x, y ~ U([0, 1]n) and aim to estimate F(|ψ(x)〉, ψ(x + δy)〉) for varying to illustrate the behavior of the theory for a representative range of parameter values.
Fig. 1. ZZ Feature Map5,53 for n = 6.
A data point x is mapped to an exponentially higher-dimensional feature space by applying Hadamard gates H, phase gates P that depend on x, and CNOT gates.
We study this setting for a line of n = 50 qubits on the ibm_sherbrooke device48. We evaluate the fidelity F(|ψ(x)〉, ψ(x + δy)〉) using the compute–uncompute method, that is, we prepare the state U†(x + δy)U(x)|0〉 and estimate the probability of measuring |0〉. The circuit is simple enough to classically simulate with a matrix product state (MPS) simulator for validation54.
The considered circuits have two distinct layers of CNOT gates with the LFs estimated as 0.7217 (starting on qubit 0, with 25 CNOT gates) and 0.7340 (starting on qubit 1, with 24 CNOT gates), which implies a total fidelity of 0.7217 × 0.7340 = 0.5397. We take the geometric average over the total number of CNOT gates and derive the CNOT fidelity as FCX = (0.5397)1/(25+24) = 0.9871. This allows us to compute the error per layered gate (EPLG)24 as 1 − FCX = 0.01288. Since both layers of CNOT gates appear four times in total in the compute–uncompute circuit, the overall circuit fidelity is 0.0787, which corresponds to γ = 161.0568. This allows us to use to compute an upper bound on the state fidelity for different δ. While the CVaR would also allow us to compute a lower bound, this is usually equal or close to zero, and thus we omit it here. At the end of this section, we discuss when to expect tight bounds and when not.
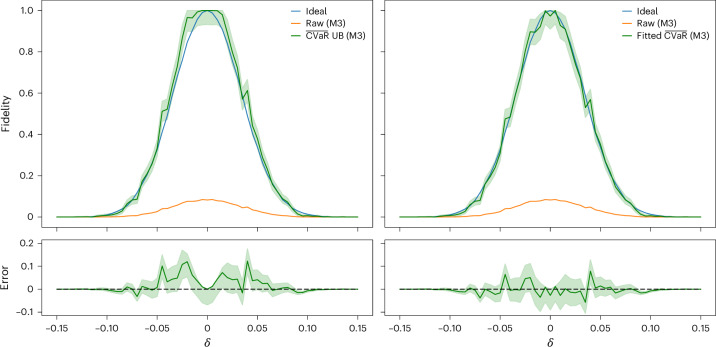
We vary δ from −0.15 to 0.15 in steps of 0.005. To improve the hardware results, we leverage the symmetry of F, that is, we run U†(x + δy)U(x)|0〉 as well as U†(x)U(x + δy)|0〉, with 10,000 shots each, and take the average of the resulting state fidelity estimates. Thus, we use 20,000 shots for each circuit. For each δ, we compute with α = 0.0787. The upper bounds hold and provide a good estimate of the noise-free fidelities (Fig. 2, left column).
Fig. 2. Fidelity estimates on 50 qubits.
Top left: ideal results from noise-free simulation, raw fidelity estimates using only M3 readout error mitigation, and the upper bounds (UB) and corresponding 95% confidence intervals (shaded area). Bottom left: difference between upper bounds and ideal noise-free results and corresponding 95% confidence intervals (shaded area). Top right: same as top left but with fitted values. Bottom right: same as bottom left but for fitted values.
The variance amplification of the CVaR is only 1/α = √γ = 12.6908. By contrast, the variance amplification of PEC is γ2 = 25,939.3. Given the quality of the CVaR bounds shown here, PEC would thus require three orders of magnitudes more samples to obtain similar results—although with the guarantee of an unbiased estimator.
Suppose that exact values for some data points are given—for example, by a classically efficient Clifford simulation. Then, we can carry out a least-squares fit of the CVaR to the data by varying α. In the present case, since we know the exact state fidelities for each δ, we can test this and fit the CVaR to the ideal data. This results in α = 0.0849, which translates to an effective EPLG of 0.01250. This is slightly lower than the measured EPLG, which indicates that our experiment is sensitive to most but not all errors that can occur. The results are shown in Fig. 2 (right column). This provides a very close approximation of the fidelity with substantially smaller overhead than PEC and may be used as a building block in the aforementioned algorithms.
Results for experiments with 100 qubits are reported in Supplementary Information, ‘100-qubit fidelity estimation’. There, we also find a nice agreement between theory and experiment; however, the confidence intervals are substantially larger due to the increasing sampling overhead.
It may seem surprising that the upper bounds for state fidelities are very tight, while the CVaR lower bounds are trivial. The following discussion offers some insights into when these bounds are expected to be tight. We measure the fidelity between a noisy state prepared on hardware and the projector |0〉 〈0|. This projector is an observable with two eigenvalues: 0 and 1. The eigenspace of eigenvalue 1 is one dimensional, corresponding to the eigenstate |0〉, while the eigenspace of eigenvalue 0 is highly degenerate, with a dimension of 2n − 1 for n qubits, spanned by all computational basis states except |0〉. This makes it more likely for an error to move the state out of the eigenspace of eigenvalue 1 than out of the eigenspace of eigenvalue 0. More formally, consider a state ρ on n qubits with F(ρ, |0〉 〈0|) = f0. Further, consider a simplified illustrative noise model that maps ρ to , where we assume that σ is a state with F(σ, |0〉 〈0|) = 0. Let us now define a random variable X ∈ {0, 1}, where we set X = 1 if measuring results in the all-zero bit string and X = 0 otherwise. Then, it is easy to see that , that is, we have not only an upper bound, but equality. By contrast, unless γ is very small and f0 is large, the lower bound CVaR1/√γ(X) is typically zero. Given the initial discussion, it can be seen that fidelity estimation resembles this idealized scenario. We generally expect F(σ, |0〉 〈0|) to be very small, if not zero, which explains why the upper bounds are very tight while the lower bounds are trivial.
Quantum optimization
In this section, we demonstrate the CVaR bounds for QAOA circuits. First we analyze smaller but deeper circuits, and second we analyze larger but shallower circuits. In both experiments we determine the angles of the QAOA circuits classically, and only focus on the sampling behavior for fixed circuits.
We start by examining the QAOA for MaxCut on a random 3-regular graph with 40 nodes, that is, 40 qubits, on ibm_sherbrooke. We take the problem instance from ref. 11 and optimize the parameters classically for the QAOA with p = 1 and p = 2 using light-cone simplifications. This allows us to evaluate the required noise-free 2-local expectation values by simulating maximally 14 qubits at a time11. The circuits and optimal parameters are further discussed in Supplementary Information, ‘40-qubit QAOA circuits’.
The circuits are constructed such that they consist of only two different layers of CNOT gates on a line of 40 qubits, denoted by q0, …, q39. The first layer is composed of 20 CNOT gates on qubits (qi, qi+1) for i even and the second composed of 19 CNOT gates on (qi, qi+1) for i odd. Using the technique introduced in ref. 24, the measured LFs for these two layers are LF1 = 0.7510 and LF2 = 0.7919, respectively, which implies a total fidelity of LF = LF1 × LF2 = 0.5947. We take the geometric average over the total number of CNOT gates and derive FCX = LF1/39 = 0.9868 and a corresponding EPLG of 1 − FCX = 0.0132. We also define γCX = 1/FCX2 = 1.0270. In total, the circuits for p = 1 and p = 2 have 461 and 922 CNOT gates, respectively, all in the form of the aforementioned layers. We can thus compute the sampling overheads for p = 1 and p = 2 as √γ1 = 465.3 and √γ2 = 216,539.2, respectively, which corresponds to α1 = 2.149 × 10−3 and α2 = 4.620 × 10−6, respectively. A regularly measured EPLG evaluated over a chain of 100 qubits is provided for ibm_sherbrooke in the IBM Quantum Platform48. At the time of the experiment the backend reported an EPLG of 0.028, that is, a little higher than our measured EPLG, which is expected, since we are restricted to 40 qubits. In any case, the EPLG reported by the backend is a good proxy to estimate the LF and resulting γ when executing a particular circuit on a device.
To apply the CVaR bounds, we run the circuits for p = 1 with 105 shots and for p = 2 with 107 shots. This corresponds to 215 and 46 samples that remain to estimate the CVaR after sorting them and keeping the best α1 and α2 fraction, respectively. The data confirm that provides an upper bound (since MaxCut is a maximization problem) to the noise-free expectation values, as predicted (Fig. 3 and Table 1). The CVaR upper bound exceeds the noise-free value by 2.1% for p = 1 and by 6.3% for p = 2.
Fig. 3. QAOA results for 40 qubits.
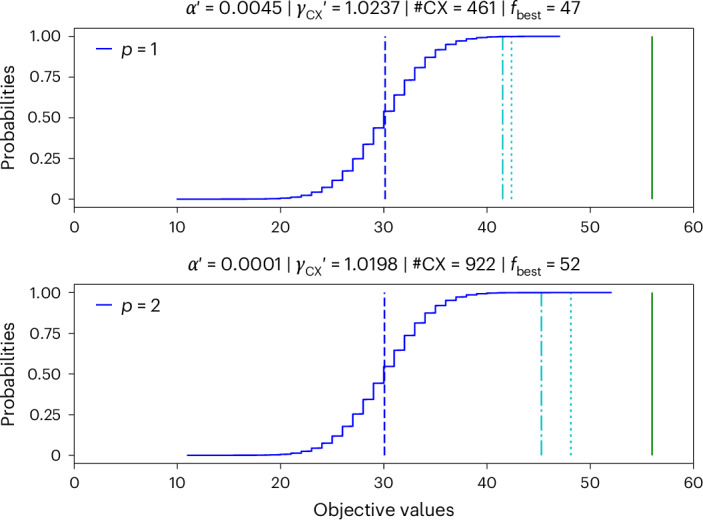
The curve is the cumulative distribution function resulting from sampling the circuits for a MaxCut instance executed on ibm_sherbrooke for p = 1 with 105 shots (top) and p = 2 with 107 shots (bottom), both applying M3 measurement error mitigation. The vertical lines show the corresponding noisy expectation values (blue dashed), the noise-free expectation values evaluated using light-cone optimized classical simulation (cyan dashed–dotted), the (cyan dotted) and the globally optimal solution equal to 56 (green solid). The title shows the fitted αp′ and corresponding γCX′ (cf. main text) such that the are equal to the noise-free expectation values (that is, cyan dashed–dotted line). Further, the titles show the number of CNOT gates (#CX) and the best sampled objective value (fbest) for p = 1, 2.
Table 1.
QAOA results for 40 qubits on ibm_sherbrooke: the different results for p = 1 and p = 2 when running the QAOA on the introduced 40-qubit MaxCut instance
| p = 1 | p = 2 | |
|---|---|---|
| Global optimum | 56 | |
| 30.1 | 30.1 | |
| 41.5 | 45.3 | |
| 42.4 | 48.1 | |
| fbest | 47 | 52 |
| Number of CNOT gates | 461 | 922 |
| √γp | 465.3 | 216,539.2 |
| αp | 2.149 × 10−3 | 4.620 × 10−6 |
| αp′ | 4.510 × 10−3 | 1.200 × 10−4 |
| γCX | 1.0270 | |
| γCX,p′ | 1.0237 | 1.0198 |
The table shows the noisy () and noise-free () expectation values as well as the CVaR estimates (), best sampled values (fbest) and the global optimal value. Further, it shows the total number of CNOT gates, the overall √γp for the circuits, the αp derived from the LF as well as the αp′ derived from calibrating the CVaR on the noise-free expectation values, and the corresponding γCX and γCX,p′ as defined in the main text.
We also use the noise-free expectation values obtained from the light-cone simulation to calibrate an α such that the CVaR matches the noise-free result exactly, denoted by αp′. This allows us to derive an induced effective γCX,p′ and compare it with the true γCX. We find that γCX,p′ is quite stable for the different p and substantially smaller than γCX (Table 1). This may imply that the observable of interest is not affected by all the errors that may occur. Crucially, this observation may allow us to calibrate α for a particular application and choose larger values than implied by the LF—for example, by running circuits of similar structure but with known noise-free results. This may reduce the sampling overhead in certain scenarios while still achieving good results. However, in general, the lower/upper bounds proven in Methods will not hold anymore for α > 1/√γ.
Comparing the and the best samples with the globally optimal solution, we find that they achieve approximation ratios of 0.757 (CVaR) and 0.839 (best sample) for p = 1, and 0.859 (CVaR) and 0.929 (best sample) for p = 2. All these numbers exceed the corresponding theoretical performance lower bounds for the QAOA of 0.692 (p = 1) and 0.756 (p = 2) discussed in Applications.
We now show results of running the QAOA on higher-order spin glass models. Originally described in refs. 55,56, these models are designed for a heavy-hex connectivity graph57 of IBM Quantum’s Eagle devices48, such as ibm_sherbrooke and ibm_kyiv.
We define a minimization problem for the following cost Hamiltonian corresponding to a random coefficient spin-glass problem with cubic terms and a connectivity graph that is defined to be compatible with an arbitrary heavy-hex lattice graph G = (V, E) (Supplementary Fig. 3):
| 7 |
As G is a connected bipartite graph with vertices V = {0, …, n − 1}, it is uniquely bipartitioned as V = V2⊔V3 with E ⊂ V2 × V3, where Vi consists of vertices of degree at most i. With W ⊆ V2 in (7), we denote the subset of vertices in V2 of degree exactly 2. Each node l in W has two neighbors, denoted by n1(l) and n2(l). Thus dv, di,j and are the coefficients representing the random selection of the linear, quadratic and cubic coefficients, respectively. The random coefficients are chosen from {+1, −1} with equal probability. An example of such a random higher-order Ising model is in Supplementary Fig. 3.
We use the qubits in V2 to compute and uncompute parities into, for the ZZ and ZZZ terms in which they are contained (cf. ref. 55). The unitaries e−iγZZ and e−iγZZZ are then realized with Rz(2γ) rotations on these parity qubits. Computing and uncomputing parities needs 1 + 1 and 2 + 2 CNOT gates for the quadratic and cubic terms, respectively; however, the CNOT gates for and can be subsumed into the CNOT gates for .
Furthermore, G as a bipartite graph of maximum degree 3 admits a 3-edge coloring due to Kőnig’s line coloring theorem, meaning that these 2 + 2 CNOT gates can be scheduled simultaneously for all terms in just 3 + 3 non-overlapping layers55. Depth-p QAOA circuits for these problems thus have a CNOT depth of only 6p, independent of the system size n. Further circuit details are given in Supplementary Information, ‘127-qubit QAOA circuits’.
Leveraging parameter transfer of QAOA angles for problems with the same structure but varying numbers of qubits allows us to obtain good angles for these 127-qubit QAOA circuits for p = 1, …, 5, without on-device variational learning58. Additionally, we utilize converged MPS simulations with a bond dimension of χ = 2,048 to verify that the fixed QAOA angles produce good expectation values58, for all circuits. The hardware-compatible circuits are run on the ibm_kyiv device. The optimal solutions of the higher-order Ising models were computed using CPLEX58,59.
As before, we only have a small number of unique layers of CNOT gates. Since we want to cover a graph of degree three, we need at least three layers (Supplementary Information, ‘127-qubit QAOA circuits’), with 144 CNOT gates in total. The measured LFs for the three layers are LF1 = 0.2190, LF2 = 0.1579 and LF3 = 0.2590. These fidelities are substantially smaller than for the 40-qubit circuits. The reason is that the qubits and gates on a 127-qubit device are not all the same; there are always some better and some worse. For 40 qubits, we could select the best line of 40 qubits (Supplementary Information, ‘40-qubit QAOA circuits’), while for 127 qubits we use the whole chip. From this we can again compute FCX = (LF1 × LF2 × LF3)1/144 = (0.008956)1/144 = 0.967784, EPLG = 0.032216 and γCX = 1.067683. The results for evaluating the circuit on ibm_kyiv, each with 2 × 105 shots, are provided in Fig. 4 and Table 2. With the substantially lower fidelities, the numbers of shots required to apply the analytic CVaR bounds are substantially higher and mostly impractical to run. However, as before, we see that the effective γCX is substantially smaller, even smaller than for the longer 40-qubit circuits. Further, we see that the best samples are improving from p = 1 to p = 5.
Fig. 4. QAOA results for sampling a random hardware-compatible higher-order Ising model (minimization combinatorial optimization problem) on 127 qubits.
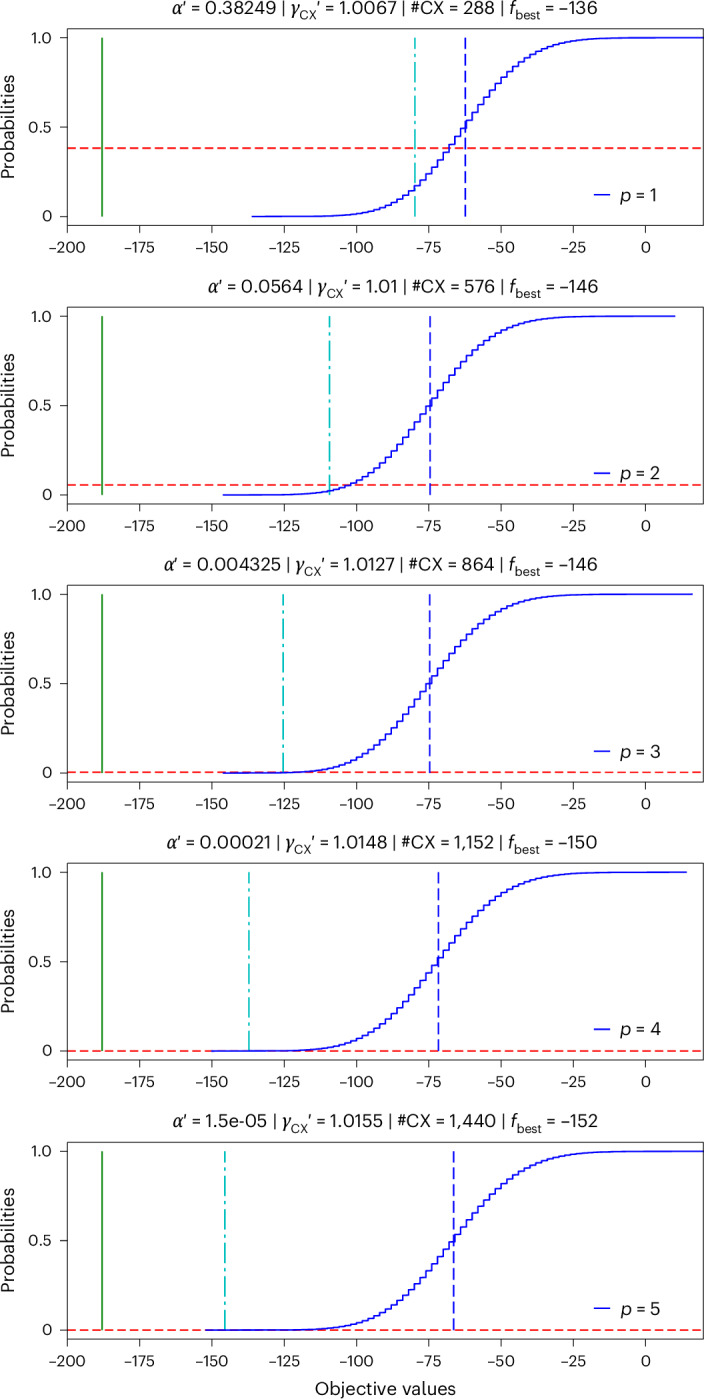
The resulting distributions from 127-qubit circuits executed on ibm_kyiv for p = 1, …, 5 (top to bottom). The cumulative distribution functions show the values of the resulting samples from 105 shots for every p. The vertical lines show the corresponding noisy expectation values (dashed blue), the noise-free expectation values evaluated using MPS simulation (cyan dashed–dotted) and the globally optimal solution equal to −188 (green solid). The titles show the fitted αp′ and corresponding γCX′ (cf. main text) such that the are equal to the noise-free expectation values (that is, cyan dashed–dotted line). The corresponding αp′ are indicated by the horizontal dashed red line. Further, the titles show the number of CNOT gates (#CX) and the best sampled objective value (fbest) for p = 1, …, 5.
Table 2.
QAOA results for 127 qubits on ibm_kyiv: the different results for p = 1, …, 5 when running the QAOA on the introduced 127-qubit spin-glass instance
| p | No. of CNOTs | tr(ρH) | fbest | √γp | αp | αp′ | γCX,p′ | |
|---|---|---|---|---|---|---|---|---|
| 1 | 288 | −79.79 | −62.37 | −136 | 1.247 × 104 | 8.021 × 10−5 | 0.3825 | 1.0067 |
| 2 | 576 | −109.35 | −74.56 | −146 | 1.554 × 108 | 6.434 × 10−9 | 0.0564 | 1.0100 |
| 3 | 864 | −125.37 | −74.67 | −146 | 1.938 × 1012 | 5.161 × 10−13 | 0.0043 | 1.0127 |
| 4 | 1,152 | −137.22 | −71.69 | −150 | 2.415 × 1016 | 4.140 × 10−17 | 0.1 × 10−4 | 1.0148 |
| 5 | 1,440 | −145.54 | −66.39 | −152 | 3.011 × 1020 | 3.321 × 10−21 | 1.5 × 10−5 | 1.0155 |
The table shows the number of CNOT gates per circuit, the noise-free (tr(ρH)) and noisy () expectation values and the best sampled values (fbest). Further, it shows the overall √γp for the circuits and corresponding αp derived from the LF as well as the γCX,p′ and αp′ derived from calibrating the CVaR on the noise-free expectation values as defined in the main text.
Finally, we use bootstrapping to confirm the scaling of the CVaR variance with respect to α. More precisely, we uniformly sample 105 values from the results collected using ibm_kyiv and estimate the CVaR for the five values of αp′ reported in Table 2. We repeat this 104 times to estimate the variance of the resulting CVaR estimators. The results are provided in Extended Data Fig. 1 and are in line with the theory presented in Methods.
Extended Data Fig. 1. Variance of CVaR estimates.
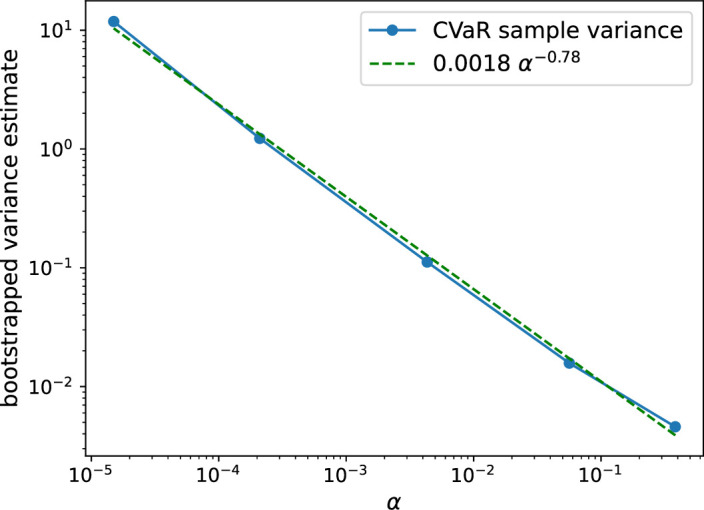
Variance of CVaR estimates: We draw 105 uniform samples from the original data to estimate the CVaR for , p = 1, …5, cf. Table 2, and repeat this 104 times to get an estimate of the variance of the CVaR estimator. The dashed green line is fitted to the results and is in line with the predicted upper bound of .
Discussion
The primary focus here was the errors occurring during circuit execution. However, other error sources, notably state preparation and measurement (SPAM) errors, also affect performance on noisy devices. The methodologies developed in this paper can be adapted to account for SPAM errors by increasing sampling overhead instead of applying, for example, statistical measurement error mitigation, as we did here. The latter may allow us to mitigate certain errors with lower sampling overhead but requires additional calibration circuits and possibly expensive classical post-processing. Investigating the impact of SPAM errors and comparing different mitigation strategies remains an intriguing direction for future research.
In addition, there are several promising research directions for studying the CVaR in an algorithmic context. These include using the introduced approach for state fidelity estimation as well as using the CVaR as a loss function—for example, in training of QAOA circuits on quantum devices. Additionally, filtering or post-selecting samples to strengthen the CVaR bounds for expectation values opens up opportunities to leverage natural symmetries or to model problems to introduce certain properties that can be leveraged accordingly. To conclude, the techniques introduced in this Article provide a alternative perspective on addressing noise in quantum computers across various domains and may help advance quantum computing toward useful applications.
Methods
Sampling from noisy quantum computers
Consider an initial n-qubit quantum state ρ0, a quantum operation and the resulting . On a real quantum computer, we usually have access not to the ideal operation but only to a noisy version , which we model by , where Λ denotes the noise operation and ∘ denotes the composition of operators; that is, we assume that applies first Λ and then . We denote the resulting noisy state by .
To simplify the presentation and to relate to existing literature, we assume the Pauli–Lindblad noise model15
| 8 |
Here, denotes the index set for (local) Pauli error terms Pk, and for corresponding model coefficients λk that determine the strength of the noise. The assumption of Pauli noise can be justified by applying Pauli twirling60–62: see Supplementary Information, ‘Pauli twirling’ for more details. However, our results also hold for more general ‘reasonable’ noise models with a non-zero probability that no error is occurring24.
In general, a quantum circuit is not a single operation but a concatenation of layers , i = 1, …, l. Their noisy versions are with corresponding noise models Λi. Crucially, this allows us to learn the noise model for each layer independently15. A common assumption is that the layers consist of non-overlapping CNOT gates (or other hardware-native two-qubit Clifford gates) and that these layers are possibly alternating with layers of single-qubit gates. Single-qubit gates are assumed to be noise free since their errors are usually an order of magnitude smaller than those of two-qubit gates. Therefore, only the noise of the two-qubit gate layers is considered.
Assuming the above layer structure and that the noise model of the quantum processor is sparse allows us to efficiently learn the λk (ref. 15). A property of Λ that characterizes the overall strength of the noise is . This has a direct operational interpretation, since γ2 defines the sampling overhead of applying PEC to mitigate the noise in the context of estimating an expectation value15,17.
Here, we first focus on sampling from noisy quantum computers instead of estimating expectation values. Suppose that we prepare a quantum state and afterwards measure the qubits. Then, the probability of sampling a bit string x ∈ {0, 1}n is given by px = tr(ρ|x〉 〈x|) for the noise-free state ρ and by for the noisy state . The noise model introduced in equation (8) can also be interpreted as follows: with a probability of 1/√γ = ∏kwk we sample a bit string from ρ and with probability 1 − 1/√γ we sample from a state where at least one error has occurred. Here, we assume λk ≪ 1 such that we can leverage . It immediately follows that , and thus 1/√γ = ∏kwk. Then, the law of total probability63 implies the lower bound:
| 9 |
In other words, if ρ is approximated by prepared through a noisy process characterized by γ, we need a multiplicative sampling overhead of √γ to guarantee at least the same probability of sampling x as for the noise-free state. Thus, as long as we are only interested in generating relevant bit strings that we can efficiently evaluate classically, we can deal with the noise by measuring √γ times more often. This is in contrast to the multiplicative sampling overhead γ2 introduced by PEC when we are interested in estimating expectation values. Interestingly, if we apply PEC and then determine only the sampling probabilities, without evaluating an expectation value, we find that the sampling probabilities are lower bounded by px/γ, that is, PEC ‘amplifies’ the noise to achieve an unbiased estimation of expectation values (see Supplementary Information, ‘PEC & sampling’ for more details).
The sampling overhead √γ can be derived from the learned noise model15. However, in the present context, we are not interested in the full description of the noise model, only in the probability of no error occurring, that is, in 1/√γ. Recently, ref. 24 introduced the LF, a metric to measure noise present in the hardware when executing a circuit. The LF also assumes the layered gate structure mentioned above and determines the resulting fidelity for each layer of gates. When assuming the Pauli–Lindblad noise model, it holds that LFi = 1/√γi, where γi characterizes the noise of layer i. However, the LF does not require this assumption and also applies to more general noise models24. For multiple layers we can rewrite equation (9) as
| 10 |
Further, the LF has the advantage that it is very cheap to evaluate when compared with learning the full noise model. Thus, for a given circuit, the LF allows us to efficiently determine the sampling overhead to compensate for the noise.
Other types of error not mentioned so far are SPAM errors. SPAM errors can also be modeled as Pauli errors64–66, thus, in principle, one could also determine a probability of no error and compensate for SPAM errors by increasing the number of samples. However, there also exist other protocols to mitigate measurement errors—for example, via statistical corrections52,67. Within this Article, we apply the M3 readout error mitigation technique52. A systematic study of the pros and cons of alternative approaches to account for SPAM errors would be interesting for future research.
Conditional value at risk
Sampling from noisy quantum computers shows that we can sample bit strings of interest, x, that is, corresponding to the noise-free state ρ, by taking √γ times more samples from the noisy state . However, we usually do not know which samples correspond to the noise-free state and which samples have been affected by noise. We now leverage these insights and show that the CVaR can provide provable bounds to noise-free expectation values from noisy samples. The CVaR has already been suggested as a loss function and observable in ref. 23, but on the basis of only intuition and without theoretical justification.
Consider an integrable real-valued random variable X with cumulative distribution function . Then, the (lower) CVaR at level α ∈ (0, 1] is defined as
where . In the case when FX(xα) = α, this definition simplifies to , that is, we are considering the expectation of X when we are conditioning X to take values in its bottom α quantile. Accordingly, we define the upper CVaR as
| 11 |
Therefore, we are considering the expectation of X conditioned on values in its upper α quantile. This allows us to prove the following lemma.
Lemma 1
Consider a random variable X with probabilities for . Further, consider another random variable as well as a given constant C ≥ 1 such that . Then we have
| 12 |
for all α ≤ 1/C. Thus, the lower and upper CVaRs of with α ≤ 1/C define lower and upper bounds, respectively, of the expectation value of X.
Proof
By monotonicity of in α, it suffices to show the claim for α = 1/C. Let x1 < … < xn denote the support of . Take k ≤ n such that , then
Clearly, the p minimizing and satisfying for all x is also supported on {x1, …, xn} and satisfies
From this, the claim is immediate by using the above to lower bound . The upper bound follows by applying the lower bound to −X and in place of X and . □Next, let us consider again a noise-free n-qubit quantum state ρ, its noisy version and the corresponding γ. Further, consider a diagonal Hamiltonian H, which can also be interpreted as a function . Let us define the random variables as the result of measuring ρ and , respectively. Then, Lemma 1 and equation (9) immediately imply
| 13 |
for all α ≤ 1/√γ. Since for a diagonal H we have , equation (13) implies that the lower/upper CVaRs computed from the noisy samples ρ provide lower/upper bounds for the noise-free expectation value of ρ. Further, suppose that ρ is the ground state of the diagonal H. Then, cannot achieve any values smaller than tr(ρH) and the left inequality in equation (13) is an equality. Thus, the noisy lower CVaR is equal to the ground-state energy (similarly for the upper CVaR if ρ were to correspond to the maximally excited state of H). Further, we also know that if the noisy CVaR were to be equal to the ground-state energy the fidelity between the noise-free state ρ and the noisy state would be lower bounded by the considered α, that is, .
Diagonal Hamiltonians arise, for example, in optimization problems or in the form of projectors |x〉 〈x|, as can be used, for example, for fidelity estimations. This is discussed in more detail in Applications. However, many applications also involve non-diagonal Hamiltonians, most prominently applications in quantum chemistry and physics1. Consider a non-diagonal Hamiltonian H = ∑iciPi, where Pi denote Pauli terms and ci the corresponding weights. Then, we can decompose H into a sum of Hamiltonians consisting of subsets of Pauli strings H = ∑jHj, where we assume that each Hj can be diagonalized. This can be achieved, for example, if all Pauli terms in Hj commute qubit-wise, in which case they can be simultaneously diagonalized via single-qubit Pauli rotations68. Thus, we can assume that the Hj are diagonal without loss of generality. We define the corresponding functions as well as noise-free and noisy random variables , respectively, resulting from measuring the quantum states with the corresponding post-rotations to diagonalize the Hamiltonians Hj. This implies
| 14 |
for all α ≤ 1/√γ, which extends the previous result to non-diagonal Hamiltonians. Note that, in contrast to diagonal Hamiltonians, we cannot draw conclusions anymore about the ground-state energy or the fidelity between the noisy state and ground state. For instance, the lower bound in equation (14) can be strictly smaller then the ground-state energy.
The CVaR can be estimated using Monte Carlo sampling. The variance of this estimator depends on the type of distribution considered but is always bounded by . However, for instance, for normal and Bernoulli distributions it can even be shown that in the present context the analytic behavior of the variances of the CVaR for α → 0 is , where for Bernoulli we assume that the success probability p satisfies , which is the relevant case here (cf. Applications). The derivation for the variance bounds for CVaR estimation is provided in Supplementary Information, ‘Variance of estimating the CVaR’. Thus, in these cases and for α = 1/√γ, the variance increases as . This renders the CVaR a very promising noise-robust loss function for variational quantum algorithms. The variance is amplified substantially less than for PEC, where it increases as . However, we need to recall that PEC comes with much stronger theoretical guarantees, that is, provides an unbiased estimator instead of a bound. Thus, depending on the application, the CVaR might not be applicable.
In the remainder of this section we discuss improvements to the lower and upper bounds for cases where we have more information about the noise-free state, that is, properties that the bit strings measured from the noise-free state must have but that might not persist under noise. Examples of such properties are particle preservation in quantum chemistry69,70 and constraint satisfaction in quantum optimization23.
Consider a function that determines whether a bit string x has a required property. Here, indicates the presence of the property. Further, consider a given Hamiltonian H and, for simplicity, let us assume it is diagonal and defined by a function . From this, we can construct a modified Hamiltonian defined by the function
| 15 |
where M is a given constant. We thus have in the noise-free case for any M, since all noise-free samples x satisfy . Next, we assume constants Ml and Mu that satisfy Ml ≤ h(x) ≤ Mu for all x with . Samples with must be affected by noise, which allows us to filter out samples where the noise destroys the required property. Although there might still be noisy samples that are feasible, the post-selection reduces the impact of noise. Owing to the equality of expectation values in the noise-free case and the choice of Ml and Mu, we immediately obtain
| 16 |
for all α ≤ 1/√γ. This can lead to substantially better bounds since we can leverage the additional information about the considered problem to filter out more noisy samples. For non-diagonal Hamiltonians (equation (14)), it is possible to define a filter function for each Hj.
Another implication of our results is that the average over the post-selected noisy samples must lie between the lower and upper bounds resulting from the filtered CVaR due to the monotonicity of the CVaR with respect to α. Thus, the CVaR allows us to bound the bias that post-selection may introduce and provide a quality measure for the estimated expectation value.
Supplementary information
Supplementary Figs. 1–4, Discussion and Proofs.
Source data
Raw data for Fig. 2.
Raw data for Fig. 3.
Raw data for Fig. 4.
Raw data for Extended Data Fig. 1.
Acknowledgements
We thank A. Carrera Vazquez, J. Gacon, Y. Kim, D. McKay, D. Ristè, D. Sutter, K. Temme, M. Tran and J. Wootton for discussions and recommendations to improve the theoretical and experimental results as well as the whole manuscript. M.L. and S.W. acknowledge the support of the Swiss National Science Foundation, SNF grant 214919. E.P., A.B. and S.E. acknowledge the support of (1) the Beyond Moore’s Law thrust of the Advanced Simulation and Computing Program (NNSA ASC) at Los Alamos National Laboratory (LANL), which is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the US Department of Energy (contract 89233218CNA000001), and (2) LANL’s Institutional Computing program. LANL report LA-UR-23-33295. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. We acknowledge the use of IBM Quantum services for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.
Extended data
Author contributions
All authors contributed to the discussions of theory and results and to writing the manuscript. S.V.B. and S.W. ran the experiments. S.W. created and optimized the circuits for the fidelity estimation experiments. D.J.E. created and optimized the circuits for the 40-qubit QAOA experiments. E.P., A.B. and S.E. created and optimized the circuits for the 127-qubit QAOA experiments. M.L. derived the theory on the variance when estimating the CVaR. S.W. conceived the idea and coordinated the project.
Peer review
Peer review information
Nature Computational Science thanks Dong-Ling Deng and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Data availability
Source data for Figs. 2, 3 and 4 and Extended Data Fig. 1 are available from Zenodo (10.5281/zenodo.13738011)71.
Code availability
Code to generate and execute all quantum circuits, to generate all data and to create all figures and tables presented in this Article is available from Zenodo (10.5281/zenodo.13738011)71.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
is available for this paper at 10.1038/s43588-024-00709-1.
Supplementary information
The online version contains supplementary material available at 10.1038/s43588-024-00709-1.
References
- 1.Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun.5, 4213 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ollitrault, P. J., Miessen, A. & Tavernelli, I. Molecular quantum dynamics: a quantum computing perspective. Acc. Chem. Res.54, 4229–4238 (2021). [DOI] [PubMed] [Google Scholar]
- 3.Di Meglio, A. et al. Quantum computing for high-energy physics: state of the art and challenges. PRX Quantum5, 037001 (2024). [Google Scholar]
- 4.Barkoutsos, P. K. et al. Quantum algorithm for alchemical optimization in material design. Chem. Sci.12, 4345–4352 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Havlicek, V. et al. Supervised learning with quantum-enhanced feature spaces. Nature567, 209–212 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Zoufal, C., Lucchi, A. & Woerner, S. Quantum generative adversarial networks for learning and loading random distributions. npj Quantum Inf.5, 103 (2019). [Google Scholar]
- 7.Zoufal, C., Lucchi, A. & Woerner, S. Variational quantum Boltzmann machines. Quantum Mach. Intell.3, 7 (2021). [Google Scholar]
- 8.Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at 10.48550/arXiv.1411.4028 (2014).
- 9.Bravyi, S., Kliesch, A., Koenig, R. & Tang, E. Obstacles to variational quantum optimization from symmetry protection. Phys. Rev. Lett.125, 260505 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Egger, D. J., Mareček, J. & Woerner, S. Warm-starting quantum optimization. Quantum5, 479 (2021). [Google Scholar]
- 11.Sack, S. H. & Egger, D. J. Large-scale quantum approximate optimization on nonplanar graphs with machine learning noise mitigation. Phys. Rev. Res.6, 013223 (2024). [Google Scholar]
- 12.Abbas, A. et al. Quantum optimization: potential, challenges, and the path forward. Preprint at 10.48550/arXiv.2312.02279 (2023).
- 13.Egger, D. J. et al. Quantum computing for finance: state-of-the-art and future prospects. IEEE Trans. Quantum Eng.1, 3101724 (2020). [Google Scholar]
- 14.Lidar, D. A. & Brun, T. A. Quantum Error Correction (Cambridge Univ. Press, 2013).
- 15.van den Berg, E., Minev, Z. K., Kandala, A. & Temme, K. Probabilistic error cancellation with sparse Pauli–Lindblad models on noisy quantum processors. Nat. Phys.19, 1116–1121 (2023). [Google Scholar]
- 16.Piveteau, C., Sutter, D. & Woerner, S. Quasiprobability decompositions with reduced sampling overhead. npj Quantum Inf.8, 12 (2022). [Google Scholar]
- 17.Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett.119, 180509 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Kim, Y. et al. Evidence for the utility of quantum computing before fault tolerance. Nature618, 500–505 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Anand, S., Temme, K., Kandala, A. & Zaletel, M. Classical benchmarking of zero noise extrapolation beyond the exactly-verifiable regime. Preprint at 10.48550/arXiv.2306.17839 (2023).
- 20.Bravyi, S., Dial, O., Gambetta, J. M., Gil, D. & Nazario, Z. The future of quantum computing with superconducting qubits. J. Appl. Phys.132, 160902 (2022). [Google Scholar]
- 21.Zoufal, C. et al. Variational quantum algorithm for unconstrained black box binary optimization: application to feature selection. Quantum7, 909 (2023). [Google Scholar]
- 22.Letcher, A., Woerner, S. & Zoufal, C. From tight gradient bounds for parameterized quantum circuits to the absence of barren plateaus in QGANs. Quantum8, 1484 (2024). [Google Scholar]
- 23.Barkoutsos, P. K., Nannicini, G., Robert, A., Tavernelli, I. & Woerner, S. Improving variational quantum optimization using CVaR. Quantum4, 256 (2020). [Google Scholar]
- 24.McKay, D. C. et al. Benchmarking quantum processor performance at scale. Preprint at 10.48550/arXiv.2311.05933 (2023).
- 25.Sachdeva, N. et al. Quantum optimization using a 127-qubit gate-model IBM quantum computer can outperform quantum annealers for nontrivial binary optimization problems. Preprint at 10.48550/arXiv.2406.01743 (2024).
- 26.Wurtz, J. & Love, P. MaxCut quantum approximate optimization algorithm performance guarantees for p > 1. Phys. Rev. A103, 042612 (2021). [Google Scholar]
- 27.Gentinetta, G., Thomsen, A., Sutter, D. & Woerner, S. The complexity of quantum support vector machines. Quantum8, 1225 (2024). [Google Scholar]
- 28.Gentinetta, G., Sutter, D., Zoufal, C., Fuller, B. & Woerner, S. Quantum kernel alignment with stochastic gradient descent. In 2023 IEEE International Conference on Quantum Computing and Engineering (QCE) 256–262 (IEEE, 2023).
- 29.McArdle, S. et al. Variational ansatz-based quantum simulation of imaginary time evolution. npj Quantum Inf.5, 75 (2019). [Google Scholar]
- 30.Yuan, X., Endo, S., Zhao, Q., Li, Y. & Benjamin, S. C. Theory of variational quantum simulation. Quantum3, 191 (2019). [Google Scholar]
- 31.Zoufal, C., Sutter, D. & Woerner, S. Error bounds for variational quantum time evolution. Phys. Rev. Appl.20, 044059 (2023). [Google Scholar]
- 32.Gacon, J., Zoufal, C., Carleo, G. & Woerner, S. Simultaneous perturbation stochastic approximation of the quantum Fisher information. Quantum5, 567 (2021). [Google Scholar]
- 33.Gacon, J., Zoufal, C., Carleo, G. & Woerner, S. Stochastic approximation of variational quantum imaginary time evolution. In 2023 IEEE International Conference on Quantum Computing and Engineering (QCE) 129–139 (IEEE, 2023).
- 34.Gacon, J., Nys, J., Rossi, R., Woerner, S. & Carleo, G. Variational quantum time evolution without the quantum geometric tensor. Phys. Rev. Res.6, 013143 (2024). [Google Scholar]
- 35.Weidenfeller, J. et al. Scaling of the quantum approximate optimization algorithm on superconducting qubit based hardware. Quantum6, 870 (2022). [Google Scholar]
- 36.Liu, Y., Arunachalam, S. & Temme, K. A rigorous and robust quantum speed-up in supervised machine learning. Nat. Phys.17, 1013–1017 (2021). [Google Scholar]
- 37.Fuller, B. et al. Approximate solutions of combinatorial problems via quantum relaxations. IEEE Trans. Quantum Eng.5, 3102615 (2024). [Google Scholar]
- 38.Lucas, A. Ising formulations of many NP problems. Front. Phys.2, 5 (2014). [Google Scholar]
- 39.Streif, M. & Leib, M. Training the quantum approximate optimization algorithm without access to a quantum processing unit. Quantum Sci. Technol.5, 034008 (2020). [Google Scholar]
- 40.Sack, S. H. & Serbyn, M. Quantum annealing initialization of the quantum approximate optimization algorithm. Quantum5, 491 (2021). [Google Scholar]
- 41.Ozaeta, A., van Dam, W. & McMahon, P. L. Expectation values from the single-layer quantum approximate optimization algorithm on Ising problems. Quantum Sci. Technol.7, 045036 (2022). [Google Scholar]
- 42.Hadfield, S. et al. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms12, 34 (2019). [Google Scholar]
- 43.Bärtschi, A. & Eidenbenz, S. Short-depth circuits for Dicke state preparation. In 2022 IEEE International Conference on Quantum Computing & Engineering (QCE) 87–96 (IEEE, 2022).
- 44.Bärtschi, A. & Eidenbenz, S. Grover mixers for QAOA: shifting complexity from mixer design to state preparation. In 2020 IEEE International Conference on Quantum Computing & Engineering (QCE) 72–82 (IEEE, 2020).
- 45.Wang, Z., Rubin, N. C., Dominy, J. M. & Rieffel, E. G. XY mixers: analytical and numerical results for the quantum alternating operator ansatz. Phys. Rev. A101, 012320 (2020). [Google Scholar]
- 46.Cook, J., Eidenbenz, S. & Bärtschi, A. The quantum alternating operator ansatz on maximum k-vertex cover. In 2020 IEEE International Conference on Quantum Computing & Engineering (QCE) 83–92 10.1109/QCE49297.2020.00021 (IEEE, 2020).
- 47.Golden, J., Bärtschi, A., Eidenbenz, S. & O’Malley, D. Numerical evidence for exponential speed-up of QAOA over unstructured search for approximate constrained optimization. In 2023 IEEE International Conference on Quantum Computing & Engineering (QCE) 496–505 10.1109/QCE57702.2023.00063 (IEEE, 2023).
- 48.IBM Quantum IBM Quantum Platform—Compute Resourceshttps://quantum-computing.ibm.com/services/resources (2023).
- 49.Sheldon, S., Magesan, E., Chow, J. M. & Gambetta, J. M. Procedure for systematically tuning up cross-talk in the cross-resonance gate. Phys. Rev. A93, 060302 (2016). [Google Scholar]
- 50.Javadi-Abhari, A. et al. Quantum computing with Qiskit. Preprint at 10.48550/arXiv.2405.08810 (2024).
- 51.qiskit-ibm-runtime API reference (IBM, accessed 30 July 2024); https://docs.quantum.ibm.com/api/qiskit-ibm-runtime
- 52.Nation, P. D., Kang, H., Sundaresan, N. & Gambetta, J. M. Scalable mitigation of measurement errors on quantum computers. PRX Quantum2, 040326 (2021). [Google Scholar]
- 53.ZZFeatureMap (IBM, accessed 23 July 2024); https://docs.quantum.ibm.com/api/qiskit/qiskit.circuit.library.ZZFeatureMap
- 54.AerSimulator (IBM, accessed 30 July 2024); https://docs.quantum.ibm.com/api/qiskit/0.40/qiskit_aer.AerSimulator
- 55.Pelofske, E., Bärtschi, A. & Eidenbenz, S. Quantum annealing vs. QAOA: 127 qubit higher-order Ising problems on NISQ computers. In High Performance Computing. ISC High Performance 2023 (eds Bhatele, A. et al.) 240–258 (Springer, 2023).
- 56.Pelofske, E., Bärtschi, A. & Eidenbenz, S. Short-depth QAOA circuits and quantum annealing on higher-order Ising models. npj Quantum Inf.10, 30 (2024). [Google Scholar]
- 57.Chamberland, C., Zhu, G., Yoder, T. J., Hertzberg, J. B. & Cross, A. W. Topological and subsystem codes on low-degree graphs with flag qubits. Phys. Rev. X10, 011022 (2020). [Google Scholar]
- 58.Pelofske, E., Bärtschi, A., Cincio, L., Golden, J. & Eidenbenz, S. Scaling whole-chip QAOA for higher-order Ising spin glass models on heavy-hex graphs. Preprint at 10.48550/arXiv.2312.00997 (2023).
- 59.IBM IBM ILOG CPLEX Optimization Studio: CPLEX User’s Manual v.22.1 https://www.ibm.com/products/ilog-cplex-optimization-studio (2024).
- 60.Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A77, 012307 (2008).
- 61.Dankert, C., Cleve, R., Emerson, J. & Livine, E. Exact and approximate unitary 2-designs and their application to fidelity estimation. Phys. Rev. A80, 012304 (2009). [Google Scholar]
- 62.Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett.106, 180504 (2011). [DOI] [PubMed] [Google Scholar]
- 63.Kokosaka, S. & Zwillinger, D. CRC Standard Probability and Statistics Tables and Formulae (CRC Press, 2000).
- 64.Zhang, Z., Chen, S., Liu, Y. & Jiang, L. A generalized cycle benchmarking algorithm for characterizing mid-circuit measurements. Preprint at 10.48550/arXiv.2406.02669 (2024).
- 65.Koh, J. M., Koh, D. E. & and Thompson, J. Readout error mitigation for mid-circuit measurements and feedforward. Preprint at 10.48550/arXiv.2406.07611 (2024).
- 66.Hines, J. & Proctor, T. Pauli noise learning for mid-circuit measurements. Preprint at 10.48550/arXiv.2406.09299 (2024).
- 67.van den Berg, E., Minev, Z. K. & Temme, K. Model-free readout-error mitigation for quantum expectation values. Phys. Rev. A105, 032620 (2022).
- 68.Gokhale, P. et al. Minimizing state preparations in variational quantum eigensolver by partitioning into commuting families. Preprint at 10.48550/arXiv.1907.13623 (2019).
- 69.Bonet-Monroig, X., Sagastizabal, R., Singh, M. & O'Brien, T. E. Low-cost error mitigation by symmetry verification. Phys. Rev. A98, 062339 (2018). [Google Scholar]
- 70.Choquette, A. et al. Quantum-optimal-control-inspired ansatz for variational quantum algorithms. Phys. Rev. Res.3, 023092 (2021). [Google Scholar]
- 71.Woerner, S. stefan-woerner/provable_bounds_cvar: provable bounds for noise-free expectation values computed from noisy samples. Zenodo10.5281/zenodo.13738011 (2024). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figs. 1–4, Discussion and Proofs.
Raw data for Fig. 2.
Raw data for Fig. 3.
Raw data for Fig. 4.
Raw data for Extended Data Fig. 1.
Data Availability Statement
Source data for Figs. 2, 3 and 4 and Extended Data Fig. 1 are available from Zenodo (10.5281/zenodo.13738011)71.
Code to generate and execute all quantum circuits, to generate all data and to create all figures and tables presented in this Article is available from Zenodo (10.5281/zenodo.13738011)71.