Abstract
Spectral clustering views the similarity matrix as a weighted graph, and partitions the data by minimizing a graph-cut loss. Since it minimizes the across-cluster similarity, there is no need to model the distribution within each cluster. As a result, one reduces the chance of model misspecification, which is often a risk in mixture model-based clustering. Nevertheless, compared to the latter, spectral clustering has no direct ways of quantifying the clustering uncertainty (such as the assignment probability), or allowing easy model extensions for complicated data applications. To fill this gap, we propose the Bayesian forest model as a generative graphical model for spectral clustering. This is motivated by our discovery that the posterior connecting matrix in a forest model has almost the same leading eigenvectors, as the ones used by normalized spectral clustering. To induce a distribution for the forest, we develop a “forest process” as a graph extension to the urn process, while we carefully characterize the differences in the partition probability. We derive a simple Markov chain Monte Carlo algorithm for posterior estimation, and demonstrate superior performance compared to existing algorithms. We illustrate several model-based extensions useful for data applications, including high-dimensional and multi-view clustering for images.
Keywords: Graphical Model Clustering, Model-based Clustering, Normalized Graph-cut, Partition Probability Function
1. Introduction
Clustering aims to partition data into disjoint groups. There is a large literature ranging from various algorithms such as K-means and DBSCAN (MacQueen, 1967; Ester et al., 1996; Frey and Dueck, 2007) to mixture model-based approaches [reviewed by Fraley and Raftery (2002)]. In the Bayesian community, model-based approaches are especially popular. To roughly summarize the idea, we view each as generated from a distribution , where are drawn from a discrete distribution , with as the probability weight, and as a point mass at . With prior distributions, we could estimate all the unknown parameters (’s, ’s, and ) from the posterior.
The model-based clustering has two important advantages. First, it allows important uncertainty quantification such as the probability for cluster assignment , , as a probabilistic estimate that comes from the th cluster . Different from commonly seen asymptotic results in statistical estimation, the clustering uncertainty does not always vanish even as . For example, in a two-component Gaussian mixture model with equal covariance, for a point at nearly equal distances to two cluster centers, we would have both and close to 50% even as . For a recent discussion on this topic as well as how to quantify the partition uncertainty, see Wade and Ghahramani (2018) and the references within. Second, the model-based clustering can be easily extended to handle more complicated modeling tasks. Specifically, since there is a probabilistic process associated with the clustering, it is straightforward to modify it to include useful dependency structures. We list a few examples from a rich literature: Ng et al. (2006) used a mixture model with random effects to cluster correlated gene-expression data, Müller and Quintana (2010); Park and Dunson (2010); Ren et al. (2011) allowed the partition to vary according to some covariates, Guha and Baladandayuthapani (2016) simultaneously clustered the predictors and use them in high-dimensional regression.
On the other hand, model-based clustering has its limitations. Primarily, one needs to carefully specify the density/mass function , otherwise, it will lead to unwanted results and difficult interpretation. For example, Coretto and Hennig (2016) demonstrated the sensitivity of the Gaussian mixture model to non-Gaussian contaminants, Miller and Dunson (2018) and Cai et al. (2021) showed that when the distribution family of is misspecified, the number of clusters would be severely overestimated. It is natural to think of using more flexible parameterization for , in order to mitigate the risk of model misspecification. This has motivated many interesting works, such as modeling via skewed distribution (Frühwirth-Schnatter and Pyne, 2010; Lee and McLachlan, 2016), unimodal distribution (Rodríguez and Walker, 2014), copula (Kosmidis and Karlis, 2016), mixture of mixtures (Malsiner-Walli et al., 2017), among others. Nevertheless, as the flexibility of increases, the modeling and computational burdens also increase dramatically.
In parallel to the above advancements in model-based clustering, spectral clustering has become very popular in machine learning and statistics. Von Luxburg (2007) provided a useful tutorial on the algorithms and a review of recent works. On clustering point estimation, spectral clustering has shown good empirical performance for separating non-Gaussian and/or manifold data, without the need to directly specify the distribution for each cluster. Instead, one calculates a matrix of similarity scores between each pair of data, then uses a simple algorithm to find a partition that approximately minimizes the total loss of similarity scores across clusters (adjusted with respect to cluster sizes). This point estimate is found to be not very sensitive to the choice of similarity score, and empirical solutions have been proposed for tuning the similarity and choosing the number of clusters (Zelnik-Manor and Perona, 2005; Shi et al., 2009). There is a rapidly growing literature of frequentist methods on further improving the point estimate [ Chi et al. (2007); Rohe et al. (2011); Kumar et al. (2011); Lei and Rinaldo (2015); Han et al. (2021); Lei and Lin (2022); among others], although, in this article, we focus on the Bayesian perspective and aim to characterize the probability distribution.
Due to the algorithmic nature, spectral clustering cannot be directly used in model-based extension, or produce uncertainty quantification. This has motivated a large Bayesian literature. There have been several works trying to quantify the uncertainty around the spectral clustering point estimate. For example, since the spectral clustering algorithm can be used to estimate the community memberships in a stochastic block model, one could transform the data into a similarity matrix, then treat it as if generated from a Bayesian stochastic block model (Snijders and Nowicki, 1997; Nowicki and Snijders, 2001; McDaid et al., 2013; Geng et al., 2019). Similarly, one could take the Laplacian matrix (a transform of the similarity used in spectral clustering) or its spectral decomposition, and model it in a probabilistic framework (Socher et al., 2011; Duan et al., 2023).
Broadly speaking, we can view these works as following the recent trend of robust Bayesian methodology, in conditioning the parameter of interest (clustering) on an insufficient statistic (pairwise summary statistics) of the data. See Lewis et al. (2021) for recent discussions. Pertaining to Bayesian robust clustering, one gains model robustness by avoiding putting any parametric assumption on within-cluster distribution ; instead, one models the pairwise information that often has an arguably simple distribution. Recent works include the distance-based Pólya urn process (Blei and Frazier, 2011; Socher et al., 2011), Dirichlet process mixture model on Laplacian eigenmaps (Banerjee et al., 2015), Bayesian distance clustering (Duan and Dunson, 2021a), generalized Bayes extension of product partition model (Rigon et al., 2023).
This article follows this trend. Instead of modeling ’s as conditionally independent (or jointly dependent) from a certain within-cluster distribution , we choose to model as dependent on another point that is close by, provided and are from the same cluster. This leads to a Markov graphical model based on a spanning forest, a graph consisting of multiple disjoint spanning trees (each tree as a connected subgraph without cycles). The spanning forest itself is not new to statistics. There has been a large literature on using spanning trees and forests for graph estimation, such as Meila and Jordan (2000); Meilă and Jaakkola (2006); Edwards et al. (2010); Byrne and Dawid (2015); Duan and Dunson (2021b); Luo et al. (2021). Nevertheless, a key difference between graph estimation and graph-based clustering is that — the former aims to recover both the node partition and the edges characterizing dependencies, while the latter only focuses on estimating the node partition alone (equivalent to clustering). Therefore, a distinction of our study is that we will treat the edges as a nuisance parameter/latent variable, while we will characterize the node partition in the marginal distribution.
Importantly, we formally show that by marginalizing the randomness of edges, the point estimate on the node partition is provably close to the one from the normalized spectral clustering algorithm. As the result, the spanning forest model can serve as the probabilistic model for the spectral clustering algorithm — this relationship is analogous to the one between the Gaussian mixture model and the K-means algorithm (MacQueen, 1967). Further, we show that treating the spanning forest as random, as opposed to a fixed parameter (that is unknown), leads to much less sensitivity in clustering performance, compared to cutting the minimum spanning tree algorithm (Gower and Ross, 1969). On the distribution specification on the node and edges, we take a Bayesian non-parametric approach by considering the forest model as realized from a “forest process” — each cluster is initiated with a point from a root distribution, then gradually grown with new points from a leaf distribution. We characterize the key differences in the partition distribution between the forest and classic Pólya urn processes. This difference also reveals that extra care should be exerted during model specification when using graphical models for clustering.Lastly, by establishing the probabilistic model counterpart for spectral clustering, we show how such models can be easily extended to incorporate other dependency structures. We demonstrate several extensions, including a multi-subject clustering of the brain networks, and a high-dimensional clustering of photo images.
2. Method
2.1. Background on Spectral Clustering Algorithms
We first provide a brief review of spectral clustering algorithms. For data , let be a similarity score between and , and denote the degree . To partition the data index into sets, , we want to solve the following problem:
| (1) |
This is known as the minimum normalized cut loss. The numerator above represents the across-cluster similarity due to cutting off from the others; and the denominator prevents trivial solutions of forming tiny clusters with small .
This optimization problem is a combinatorial problem, hence has motivated approximate solutions such as spectral clustering. To start, using the Laplacian matrix with the diagonal matrix of ’s, and the normalized Laplacian , we can equivalently solve the above problem via:
where . It is not hard to verify that . We can obtain a relaxed minimizer of , by simply taking as the bottom eigenvectors of (with the minimum loss equal to the sum of the smallest eigenvalues). Afterward, we cluster the rows of into groups (using algorithms such as the K-means), hence producing an approximate solution to (1).
To clarify, there is more than one version of the spectral clustering algorithms. An alternative version to (1) is called “minimum ratio cut”, which replaces the denominator by the size of cluster . Similarly, continuous relaxation approximation can be obtained by following the same procedures above, except for clustering the eigenvectors of the unnormalized . Details on comparing those two versions can be found in Von Luxburg (2007). In this article, we focus on the one based on (1) and the normalized Laplacian matrix . This version is also commonly referred to as “normalized spectral clustering”.
2.2. Probabilistic Model via Bayesian Spanning Forest
The next question is if there is some partition-based generative model for , that has the maximum likelihood estimate (or, the posterior mode in the Bayesian framework) almost the same as the point estimate from the normalized spectral clustering.
We found an almost equivalence in the spanning forest model. A spanning forest model is a special Bayesian network that describes the conditional dependencies among . Given a partition of the data index , consider a forest graph , with each a component tree (a connected subgraph without cycles), the set of nodes and the set of edges among . Using and a set of root nodes with , we can form a graphical model with a conditional likelihood given the forest:
| (2) |
where we refer to as a “root” distribution, and as a “leaf” distribution; and we use to denote the other parameter; and we use simplified notation to mean that is an edge of the graph . Figure 1 illustrates the high flexibility of a spanning forest in representing clusters. It shows the sampled based on three clustering benchmark datasets. Note that some clusters are not elliptical or convex in shape. Rather, each cluster can be imagined as if it were formed by connecting a point to another nearby. In the Supplementary Materials S4.8, we show two different realizations of spanning forest.
Fig. 1.

Three examples of clusters that can be represented by a spanning forest.
Remark 1. To clarify, the point estimation on a spanning forest (as some fixed and unknown graph) has been studied (Gower and Ross, 1969). However, a distinction here is that we consider as the parameter of interest, but the edges and roots as latent variables. The performance differences are shown in the Supplementary Materials S4.6.
The stochastic view of is important, as it allows us to incorporate the uncertainty of edges and avoids the sensitivity issue in the point graph estimate. Equivalently, our clustering model is based on the marginal likelihood that varies with the node partition :
| (3) |
where is the latent variable distribution that we will specify in the next section. We can quantify the marginal connecting probability for each potential edge
| (4) |
Similar to the normalized graph cut, there is no closed-form solution for directly maximizing (3). However, closed-form does exist for (4) (see Section 4). Therefore, an approximate maximizer of (3), , can be obtained via computing the matrix and searching for diagonal blocks (after row and column index permutation) that contain the highest total values of ’s. Specifically, we can extract the top leading eigenvectors of and cluster the rows into groups.
This approximate marginal likelihood maximizer produces almost the same estimate as the normalized spectral clustering does. This is because the two sets of eigenvectors are almost the same. Further, it is important to clarify that such closeness does not depend on how the data are really generated. Therefore, to provide some numerical evidence, for simplicity, we generate from a simple three-component Gaussian mixture in with means in (0, 0), (2, 2), (4, 4) and all variances equal to . Figure 2 compares the eigenvectors of the matrix and the normalized Laplacian (that uses and to specify , with details provided in Section 4). Clearly, these two are almost identical in values. Due to this connection, the clustering estimates from spectral clustering can be viewed as an approximate estimate for in (3).
Fig. 2.
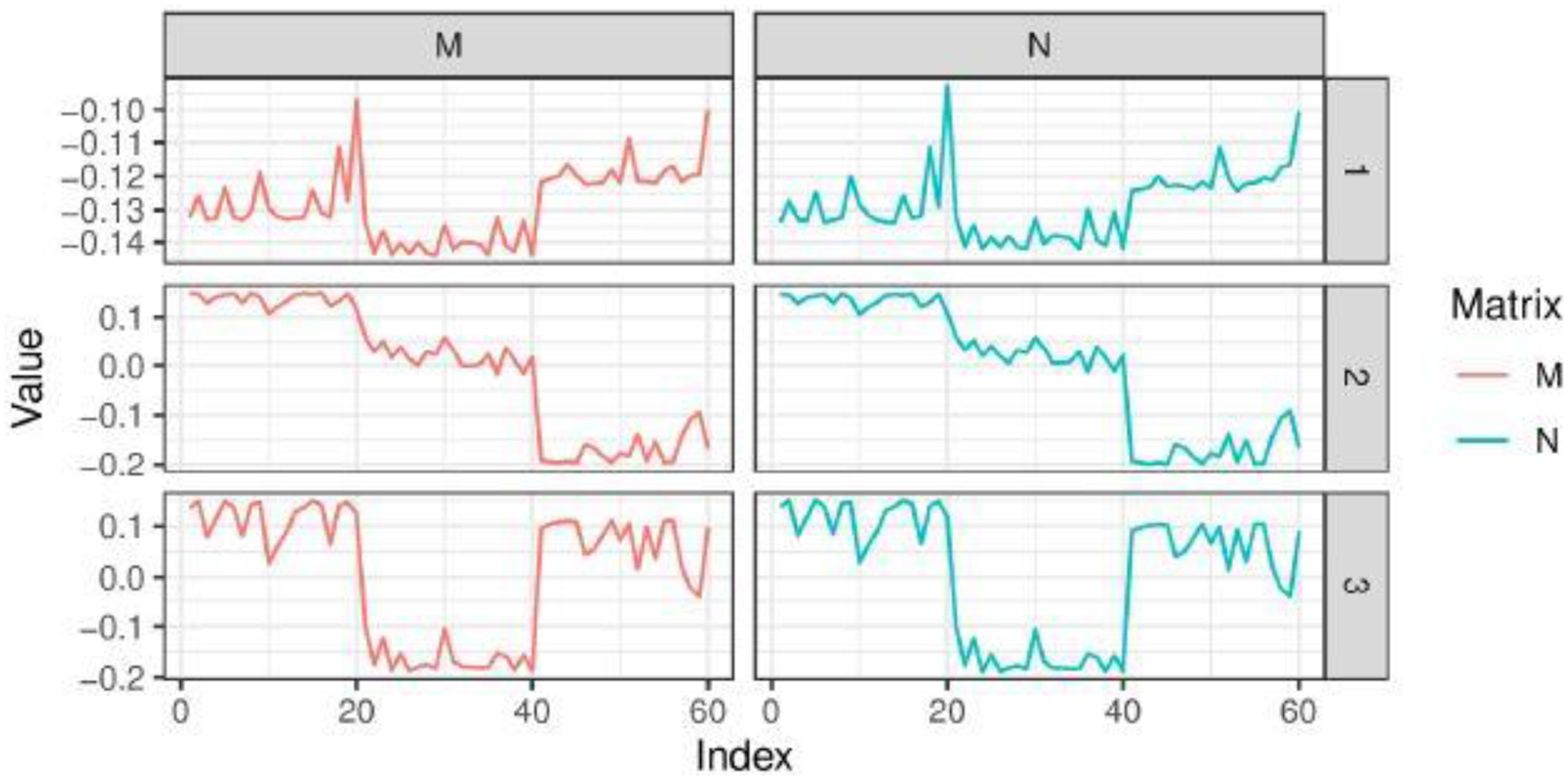
Comparing the eigenvectors of a marginal connecting probability matrix and the ones of normalized Laplacian .
We now fully specify the Bayesian forest model. For simplicity, we now focus on continuous . For ease of computation, we recommend choosing as a symmetric function , so that the likelihood is invariant to the direction of each edge; and choose as a diffuse density, so that the likelihood is less sensitive to the choice of a node as root. In this article, we choose a Gaussian density for and Cauchy for .
| (5) |
where and are scale parameters. As the magnitudes of distances between neighboring points may differ significantly from cluster to cluster, we use a local parameterization , and will regularize via a hyper-prior.
Remark 2. In (5), we effectively use Euclidean distances . We focus on Euclidean distance in the main text, for the simplicity of presentation and to allow a complete specification of priors. One can replace Euclidean distance with some others, such as Mahalanobis distance and geodesic distance. We present a case of high-dimensional clustering based on geodesic distance on the unit-sphere in the Supplementary Materials S1.1.
2.3. Forest Process and Product Partition Prior
To simplify notations as well as to facilitate computation, we now introduce an auxiliary node 0 that connects to all roots . As the result, the model can be equivalently represented by a spanning tree rooted at 0:
In this section, we focus on the distribution specification for . The distribution, denoted by can be factorized according to the following hierarchies: picking the number of partitions , partitioning the nodes into , forming edges and picking one root for each . To be clear on the nomenclature, we call as the “latent variable distribution”, as the “partition prior”.
| (6) |
Remark 3. In Bayesian non-parametric literature, is known as the partition probability function, which plays the key role in controlling cluster sizes and cluster number in model-based clustering. However, when it comes to graphical model-based clustering (such as our forest model), it is important to note the difference — for each partition , there is an additional probability due to the multiplicity of all possible subgraphs formed between the nodes in .
For simplicity, we will use discrete uniform distribution for . Since there are possible spanning trees for nodes [ if , otherwise 0], and possible choice of roots. We have .
We now discuss two different ways to complete the distribution specification. We first take a “ground-up” approach by viewing as from a stochastic process where the node number could grow indefinitely. Starting from the first edge , we sequentially draw new edges and add to , from
| (7) |
with some probability vector that adds up to one. We refer to (7) as a forest process. The forest process is a generalization of the Pólya urn process (Blackwell and MacQueen, 1973). For the latter, would make node take the same value as node , [although in model-based clustering, one would use notation , and ]; would make node draw a new value for from the base distribution. Due to this relationship, we can borrow popular parameterization for from the urn process literature. For example, we can use the Chinese restaurant process parameterization for , and with some chosen . After marginalizing over the order of and partition index [see Miller (2019) for a simplified proof of the partition function], we obtain:
| (8) |
Compared to the partition probability prior in the Chinese restaurant process, we have an additional term that corresponds to the conditional prior weight of for each possible given a partition .
To help understand the effect of this additional term on the posterior, we can imagine two extreme possibilities in the conditional likelihood given a . If the conditional is skewed toward one particular choice of tree [that is, is large when , but is close to zero for other values of ], then acts as a penalty for a lack of diversity in trees. On the other hand, if is equal for all possible ’s, then we can simply marginalize over and be not be subject to this penalty [since ].
Therefore, we can form an intuition by interpolating those two extremes: if a set of data points (of size ) are “well-knit” such that they can be connected via many possible spanning trees (each with a high conditional likelihood), then it would have a higher posterior probability of being clustered together, compared to some other points (of the same size ) that have only a few trees with high conditional likelihood.
With the “ground-up” construction useful for understanding the difference from the classic urn process, the distribution (8) itself is not very convenient for posterior computation. Therefore, we also explore the alternative of a “top-down” approach. This is based on directly assigning a product partition probability (Hartigan, 1990; Barry and Hartigan, 1993; Crowley, 1997; Quintana and Iglesias, 2003) as
| (9) |
where the cohesion function effectively cancels out the probability for each . To assign a prior for , we assign a probability
supported on with , with , multiplying the terms according to (6) leads to
| (10) |
which is similar to a truncated geometric distribution and easy to handle in posterior computation, and we will use this from now on. In this article, we set .
Remark 4. We now discuss the exchangeability of the sequence of random variables generated from the above forest process. The exchangeability is defined as the the invariance of distribution under any permutation (Diaconis, 1977). For simplicity, we focus on the joint distribution with as given, and hence omit here. There are three categories of random variables associated with each node : the first drawn edge that points to a new node (whose sequence forms ), the cluster assignment of a node (whose sequence forms ), and the data point . It is not hard to see that, since each component tree encodes an order among , the joint distribution of the data and the forest is not exchangeable. Nevertheless, as we marginalize out each to form the clustering likelihood in (3), and all priors presented in this section only depend on the number and sizes of clusters, the joint distribution of the data and cluster labels is exchangeable, with its form provided soon in (14). Lastly, we see that is exchangeable after marginalizing over .
2.4. Hyper-priors for the Other Parameters
We now specify the hyper-priors for the parameters in the root and leaf densities. To avoid model sensitivities to scaling and shifting of the data, we assume that the data have been appropriately scaled and centered (for example, via standardization), so that the marginally and for . To make the root density close to a small constant in the support of the data, we set and .
For in the leaf density , in order to likely pick an edge with as a close neighbors of (that is, with small ), we want most of to be small. We use the following hierarchical inverse-gamma prior that shrinks each , while using a common scale hyper-parameter to borrow strengths among , s,
where is the scale parameter for the exponential. To induce a shrinkage effect a priori, we use and for a likely small hence a small . Further, we note that the coefficient of variation ; therefore, we set to have most of near in the prior. We use these hyper-prior settings in all the examples presented in this article.
In addition, Zelnik-Manor and Perona (2005) demonstrate good empirical performance in spectral clustering via setting to a low order statistic of the distances to . We show a model-based formalization with similar effects in the Supplementary Materials S5.
2.5. Model-based Extensions
Compared to algorithms, a major advantage of probabilistic models is the ease of building useful model-based extensions. We demonstrate three directions for extending the Bayesian forest model. Due to the page constraint, we defer the details and numeric results of these extensions in the Supplementary Materials S1.1, S1.2 and S1.3.
Latent Forest Model:
First, one could use the realization of the forest process as latent variables in another model for data ,
where and denote the other needed parameters. For example, for clustering high-dimensional data such as images, it is often necessary to represent each high-dimensional observation by a low-dimensional coordinate (Wu et al., 2014; Chandra et al., 2023). In the Supplementary Materials, we present a high-dimensional clustering model, using an autoregressive matrix Gaussian for and a sparse von Mises-Fisher for the forest model.
Informative Prior-Latent Variable Distribution:
Second, in applications it is sometimes desirable to have the clustering dependent on some external information , such as covariates (Müller et al., 2011) or an existing partition (Paganin et al., 2021). From a Bayesian view, this can be achieved via taking an -informative distribution:
In the Supplementary Materials, we illustrate an extension with a covariate-dependent product partition model [PPMx, Müller et al. (2011)] into the distribution of .
Hierarchical Multi-view Clustering:
Third, for multi-subject data for , we want to find a clustering for every . At the same time, we can borrow strength among subjects, by letting subjects share some similar partition structure on a subset of nodes (while differing on the other nodes). This is known as multi-view clustering. On the other hand, a challenge is that a forest is a discrete object subject to combinatorial constraints, hence it would be difficult to partition the nodes freely while accommodating the tree structure. To circumvent this issue, we propose a latent coordinate-based distribution that gives a continuous representation for .
Consider a latent for each node , we assign a joint prior–latent variable distribution for and :
| (11) |
where are the weights that vary with and , and is the matrix form. Equivalently, the above assigns each node a location parameter , drawn from a hierarchical Dirichlet distribution with shared atoms and probability (Teh et al., 2006). Further, one could let vary over node according to some functional using a hybrid Dirichlet distribution (Petrone et al., 2009).
Using a Gaussian mixture kernel on , we can now separate ’s into several groups that are far apart. To make the parameters identifiable and have large separations between groups, we fix ’s on the -dimensional integer lattice with (hence ); and we use and in this article.
Remark 5. To clarify, our goal is to induce between-subject similarity in the node partition, not the tree structure. For example, for two subjects and , when and are both near for all , then both the spanning forest and will likely cluster the nodes in together, even though and associated with may be different.
3. Posterior Computation
3.1. Gibbs Sampling Algorithm
We now describe the Markov chain Monte Carlo (MCMC) algorithm. For ease of notation, we use an matrix , with (for convenience, we use 0 to index the last row/column), , and to represent the adjacency matrix of . We have the posterior distribution
| (12) |
Note the above form conveniently include the prior term for the number of clusters, , via the number of edges adjacent to node 0.
Our MCMC algorithm alternates in updating and , hence is a Gibbs sampling algorithm. To sample given , we take the random-walk covering algorithm for weighted spanning tree (Mosbah and Saheb, 1999), as an extension of the Andrei–Broder algorithm for sampling uniform spanning tree (Broder, 1989; Aldous, 1990). For this article to be self-contained, we describe the algorithm below. The above algorithm produces a random sample following the full conditional proportional to (12). It has an expected finish time of . Although some faster algorithms have been developed (Schild, 2018), we choose to present the random-walk covering algorithm for its simplicity.
Algorithm 1.
Random-walk covering algorithm for sampling the augmented tree
| Start with and , and set : |
| while do |
| Take a random walk from to with probability . |
| if then |
| Add to . Add to . |
| Update . |
We sample using the following steps,
To update , we use the form of the multivariate Cauchy as a scale mixture of over . We can update via
We run the MCMC algorithm iteratively for many iterations. And we discard the first half of iterations as burn-in.
Remark 6. We want to emphasize that the Andrei–Broder random-walk covering algorithm (Broder, 1989; Aldous, 1990; Mosbah and Saheb, 1999) is an exact algorithm for sampling a spanning tree . That is, if were fixed, each run of this algorithm would produce an independent Monte Carlo sample . Removing the auxiliary node from will produce disjoint spanning trees. This augmented graph technique is inspired by Boykov et al. (2001).
In our algorithm, since the scale parameters in are unknown, we use Markov chain Monte Carlo that updates two sets of parameters, (i) and (ii) from iteration to . Therefore, rigorously speaking, there is a Markov chain dependency between and induced by . Nevertheless, since we draw in a block via the random-walk covering algorithm, we empirically find that and are substantially different. In the Supplementary Materials S4.4, we quantify the iteration-to-iteration graph changes, and provide diagnostics with multiple start points of .
3.2. Posterior Point Estimate on Clustering
In the field of Bayesian clustering, for producing point estimate on the partition, it had been a long-time practice to simply track , then take the element-wise posterior mode over as the point estimate for . Nevertheless, this was shown to be sub-optimal due to that: (i) label switching issue causes unreliable estimates on ; (ii) the element-wise mode can be unrepresentative of the center of distribution for (Wade and Ghahramani, 2018). These weaknesses have motivated new methods of obtaining point estimate of clustering, that transform an pairwise co-assignment matrix into an assignment matrix (Medvedovic and Sivaganesan, 2002; Rasmussen et al., 2008; Molitor et al., 2010; Wade and Ghahramani, 2018). More broadly speaking, minimizing a loss function based on the posterior sample (via some estimator or algorithm) is common for producing a point estimate under some decision theory criterion. For example, the posterior mean comes as the minimizer of the squared error loss; in Bayesian factor modeling, an orthogonal Procrustes-based loss function is used for producing the posterior summary of the loading matrix from the generated MCMC samples (Aßmann et al., 2016).
We follow this strategy. There have been many algorithms that one could use. For a recent survey, see Dahl et al. (2022). In this article, we use a simple solution of first finding the mode of from the posterior sample, then doing a -rank symmetric matrix factorization on and clustering into groups, provided by RcppmL package (DeBruine et al., 2021).
4. Theoretical Properties
4.1. Convergence of Eigenvectors
We now formalize the closeness of the eigenvectors of matrices and (shown in Section 2.2), by establishing the convergence of the two sets of eigenvectors as increases.
To be specific, we focus on the normalized spectral clustering algorithm using the similarity , with . On the other hand, for the specific form, can be any density satisfying can be any density satisfying . For the associated normalized Laplacian , we denote the first bottom eigenvectors by , which correspond to the smallest eigenvalues.
Let be the matrix with for and . The Kirchhoff’ tree theorem (Chaiken and Kleitman, 1978) gives an enumeration of all ,
| (13) |
where is the Laplacian matrix transform of the similarity matrix denotes the th smallest eigenvalue. Differentiating its logarithmic transform with respect to ,
Let be the top eigenvectors of , associated with eigenvalues , and . And we can compare with the leading eigenvectors of . Using and to denote two matrices, we now show they are close to each other.
Theorem 1. There exists an orthonormal matrix and a finite constant ,
with probability at least .
Remark 7. To make the right-hand side go to zero, a sufficient condition is to have all with . We provide a detailed definition of the bound constant in the Supplementary Materials S2.
To explain the intuition behind this theorem, our starting point is the close relationship between Laplacian and spanning tree models — multiplying both sides of Equation (13) by shows that the non-zero eigenvalue product of the graph Laplacian is proportional to the marginal probability of data points from a spanning forest-mixture model. Starting from this equality, we can write the marginal inclusion probability matrix of as a mildly perturbed form of the normalized Laplacian matrix. Intuitively, when two matrices are close, their eigenvectors will be close as well (Yu et al., 2015).
Therefore, under mild conditions, as , the two sets of leading eigenvectors converge. In the Supplementary Materials S4.7, we show that the convergence is very fast, with the two sets of leading eigenvectors becoming almost indistinguishable starting around .
Besides the eigenvector convergence, we can examine the marginal posterior , which is proportional to
| (14) |
where is the unnormalized Laplacian matrix associated with matrix . Imagine that if we put all indices in one partition , then would be very small due to those close-to-zero eigenvalues. Applying this deduction recursively on subsets of data, it is not hard to see that a high-valued would correspond to a partition, wherein each has away from 0 for any . Further, since , a permutation in corresponds to congruent and simultaneous permutations of rows and columns of each , which does not change each determinant. Therefore, the joint distribution of is exchangeable.
4.2. Consistent Clustering of Separable Sets
We show that clustering consistency is possible, under some separability assumptions when the data-generating distribution follows a forest process. Specifically, we establish posterior ratio consistency, as the ratio between the maximum posterior probability assigned to other possible clustering assignments to the posterior probability assigned to the true clustering assignments converges to zero almost surely under the true model (Cao et al., 2019).
To formalize the above, we denote the true cluster label for generating by (subject to label permutation among clusters), and we define the enclosing region for all possible as for for some true finite . And we refer to as the “null partition”. By separability, we mean the scenario that are disjoint and there is a lower-bounded distance between each pair of sets. As alternatives, regions could be induced by from the posterior estimate of . For simplicity, we assume the scale parameter in is known and all equal .
Number of clusters is known. We first start with a simple case when we have fixed . For regularities, we consider data as supported in a compact region , and satisfying the following assumptions:
(A1, diminishing scale) for some and .
(A2, minimum separation) , for all with some positive constant such that for all and is known for some constant .
(A3, near-flatness of root density) For any , for all .
Under the null partition, is maximized at , which contains trees with each being the minimum spanning tree (denoted by subscript “MST”) within region . Similarly, for any alternative is maximized at the .
Theorem 2. Under (A1, A2, A3), we have almost surely, unless for some permutation map .
Number of clusters is unknown: Next, we relax the condition by having a not necessarily equal to . We show the consistency in two parts for 1) , and 2) separately. In order to show posterior ratio consistency in the second part, we need some finer control on :
(A3’) The root density satisfies for some .
In this assumption, we essentially assume the root distribution to be flatter with a larger . Then we have the following results.
Theorem 3. 1) If , under the assumptions (A1, A2, A3), we have almost surely.
2) If , under the assumptions (A1, A2, A3’), we have almost surely.
The above results show posterior ratio consistency. Furthermore, when the true of clusters is known, the ratio consistency result can be further extended to show clustering consistency, which is proved in the Supplementary Materials S3.
5. Numerical Experiments
To illustrate the capability of uncertainty quantification, we carry out clustering tasks on those near-manifold data commonly used for benchmarking clustering algorithms. In the first simulation, we start with 300 points drawn from three rings of radii 0.2, 1 and 2, with 100 points from each ring. Then we add some Gaussian noise to each point to create a coordinate near a ring manifold. We present two experiments, one with noises from , and one with noises . As shown in Figure 3, when these data are well separated (Panel a, showing posterior point estimate), there is very little uncertainty on the clustering (Panel b), with the posterior co-assignment close to zero for any two data points near different rings. As noises increase, these data become more difficult to separate. There is a considerable amount of uncertainty for those red and blue points: these two sets of points are assigned into one cluster with a probability close to 40% (Panel d). We conduct another simulation based on an arc manifold and two point clouds (Panels e-h), and find similar results. Additional experiments are described in the Supplementary Materials S4.2.
Fig. 3.
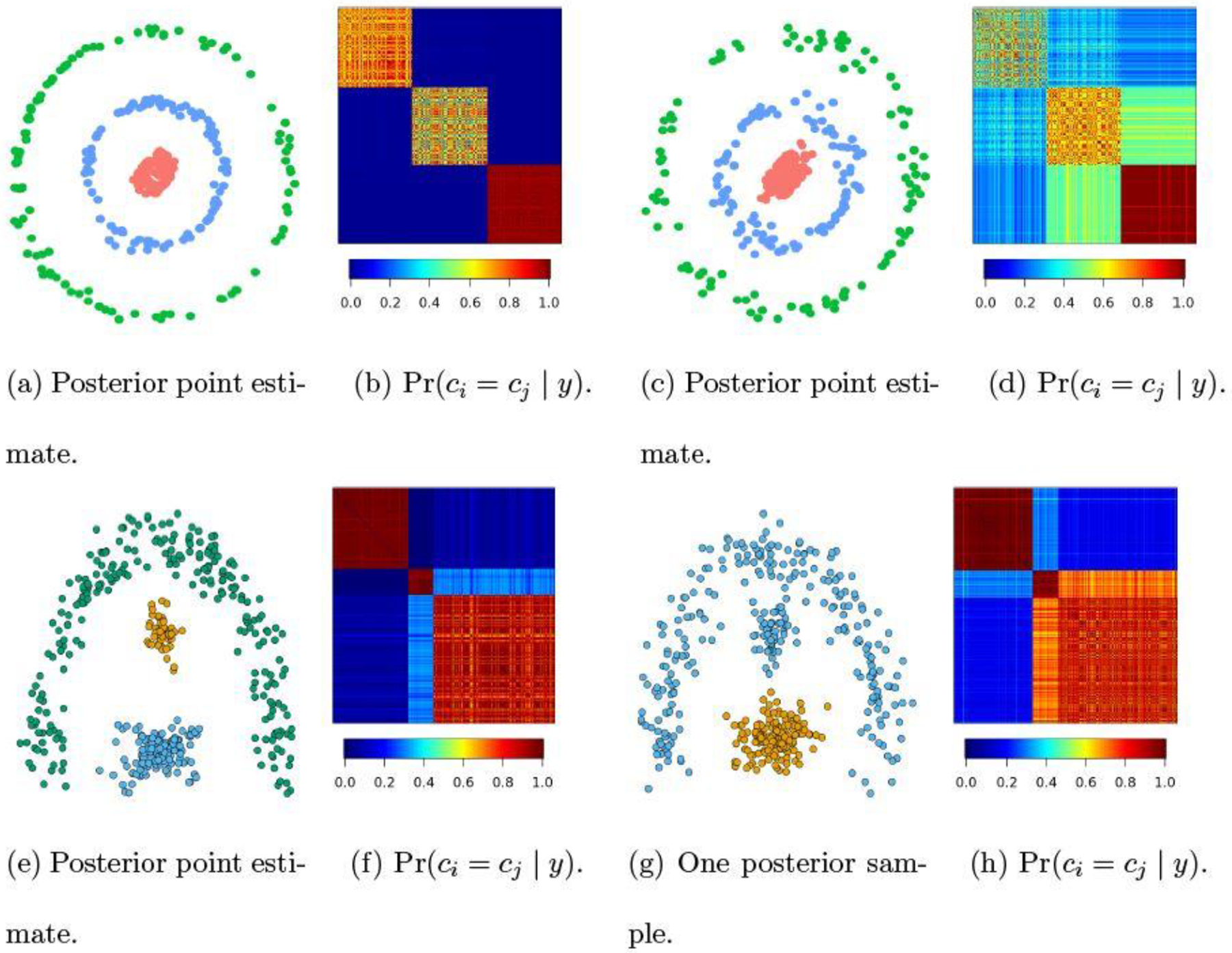
Uncertainty quantification in clustering data generated near three manifolds. When data are close to the manifolds (Panels a,e), there is very little uncertainty on clustering in low between points from different clusters (Panels b,f). As data deviate more from the manifolds (Panel c,g), the uncertainty increases (Panels d,h). And in Panel g, the point estimate shows a two-cluster partitioning, while there is about 20% of probability for three-cluster partitioning.
In the Supplementary Materials S4.1 and S4.3, we present some uncertainty quantification results, for clustering data that are from mixture models. We compare the estimates with the ones from Gaussian mixture models, which could correspond to correctly/erroneously specified component distribution. Empirically, we find that the uncertainty estimates on and from the forest model are close to the ones based on the true data-generating distribution; whereas the Gaussian mixture models suffer from sensitivity in model specification, especially when is not known.
6. Application: Clustering in Multi-subject Functional Magnetic Resonance Imaging Data
In this application, we conduct a neuroscience study for finding connected brain regions under a varying degree of impact from Alzheimer’s disease. The source dataset is resting-state functional magnetic resonance imaging (rs-fMRI) scan data, collected from subjects at different stages of Alzheimer’s disease. Each subject has scans over regions of interest using the Automated Anatomical Labeling (AAL) atlas (Rolls et al., 2020; Shi et al., 2021) and over time points. We denote the observation for the th subject in the th region by .
The rs-fMRI data are known for their high variability, often characterized by a low intraclass correlation coefficient (ICC), , as the estimate for the proportion of total variance that can be attributed to variability between groups (Noble et al., 2021). Therefore, our goal is to use the multi-view clustering to divide the regions of interest for each subject, while improving our understanding of the source of high variability.
We fit the multi-view clustering model to the data, by running MCMC for 5, 000 iterations and discarding the first 2, 500 as burn-in. As shown in Figure 4, the hierarchical Dirichlet distribution on the latent coordinates induces similarity between the clustering of brain regions among subjects on a subset of nodes, while showing subtle differences on the other nodes. On the other hand, some major differences can be seen in the clusterings between the healthy and diseased subjects. Using the latent coordinates (at the posterior mean), we quantify the distances between and for each pair of subjects . As shown in Figure 5(a), there is a clear two-group structure in the pairwise distance matrix formed by , and the separation corresponds to the first 64 subjects being healthy (denoted by ) and the latter 102 being diseased (denoted by ).
Fig. 4.
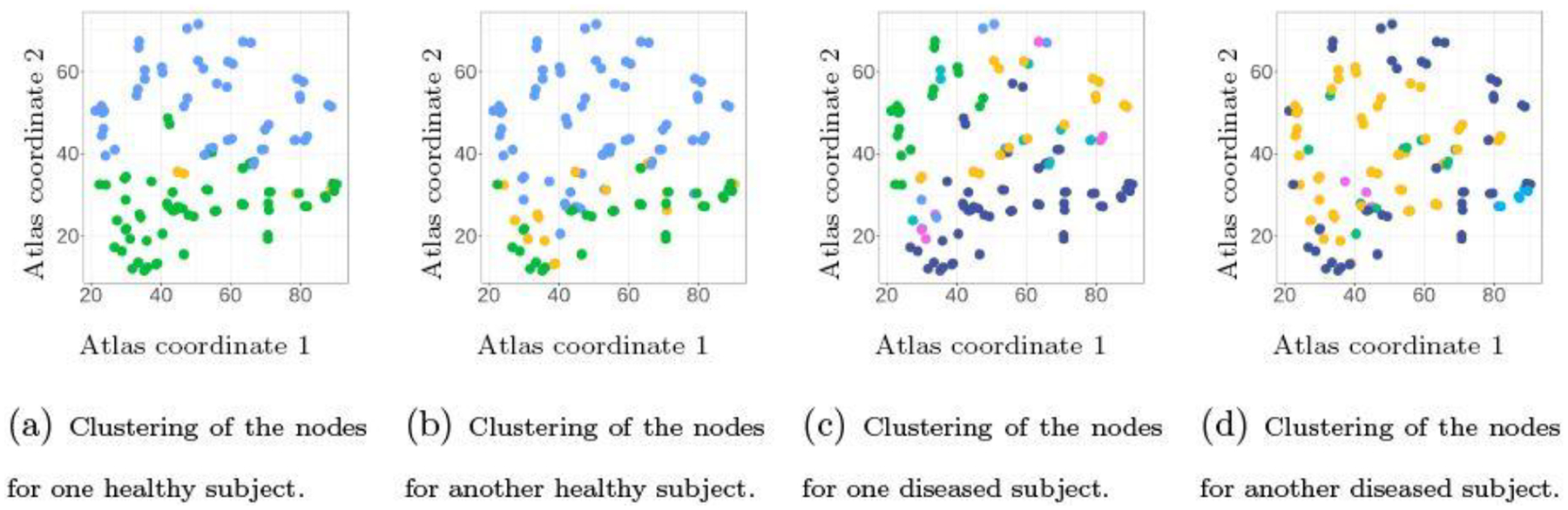
Results of brain region clustering (lateral view) for four subjects taken from the healthy and diseased groups. The multi-view clustering model allows subjects to have similar partition structures on a subset of nodes, while having subtle differences on the others (Panels a and b, Panels c and d). At the same time, the healthy subjects show less degree of variability in the brain clustering than the diseased subjects.
Fig. 5.
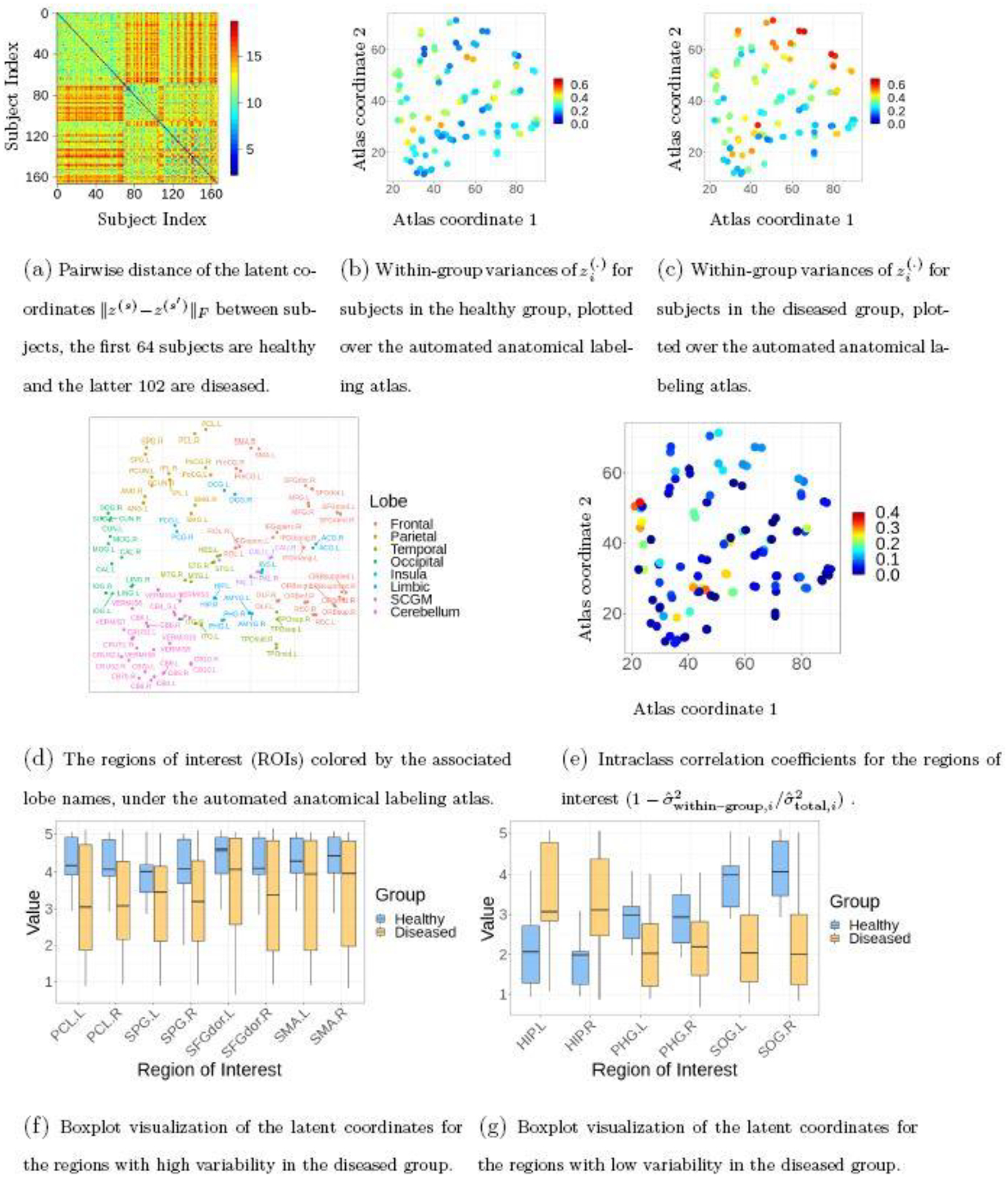
Using the latent coordinates to characterize the heterogeneity within the subjects.
Next, we compute the within–group variances for these two groups, using , for and 2, and plot the variance over each region of interest on the spatial coordinate of the atlas. Figure 5(b) and (c) show that, although both groups show some degree of variability, the diseased group shows clearly higher variances in some regions of the brain. Specifically, the paracentral lobule (PCL) and superior parietal gyrus (SPG), dorsolateral superior frontal gyrus (SFGdor), and supplementary motor area (SMA) in the frontal lobe show the highest amount of variability. Indeed, those regions are also associated with very low ICC scores [Figure 5(e)] calculated based on the variance of , with pooled estimates and On the other hand, some regions such as the hippocampus (HIP), parahippocampal gyrus (PHG), and superior occipital gyrus (SOG) show relatively lower variances within each group, hence higher ICC scores.
To show more details on the heterogeneity, we plot the latent coordinates associated with those ROIs using boxplots. Since each is in two-dimensional space, we plot the linear transform . Interestingly, those 8 ROIs with high variability still seem quite informative for distinguishing the two groups (Figure 5(f)). To verify, we concatenate those latent coordinates and form an matrix, and fit them in a logistic regression model for classifying the healthy versus diseased states. The Area Under the Curve (AUC) of the Receiver Operating Characteristic is 86.6%. On the other hand, when we fit the 6 ROIs with low variability in logistic regression, the AUC increases to 96.1%.
An explanation for the above results is that Alzheimer’s disease does different degrees of damage in the frontal and parietal lobes (see the two distinct clusterings in Figure 4 (c) and (d)), and the severity of the damage can vary from person to person. On the other hand, the hippocampus region (HIP and PHG), important for memory consolidation, is known to be commonly affected by Alzheimer’s disease (Braak and Braak, 1991; Klimova et al., 2015), which explains the low heterogeneity in the diseased group. Further, to our best knowledge, the high discriminability of the superior occipital gyrus (SOG) is a new quantitative finding, that could be meaningful for a further clinical study.
For validation, without using any group information, we concatenate those ’s over all and form an matrix and use lasso logistic regression to classify the two groups. When 12 predictors are selected (as a similar-size model to the one above using 6 ROIs), the AUC is 96.4%. Since ’s are obtained in an unsupervised way, this validation result shows that the multi-view clustering model produces meaningful representation for the nodes in this Alzheimer’s disease data. We provide further details on the clusterings, including the number of clusters, and the posterior co-assignment probability matrices in the Supplementary Materials S4.5.
7. Discussion
In this article, we present our discovery of a probabilistic model for popular spectral clustering algorithms. This enables straightforward uncertainty quantification and model-based extensions through the Bayesian framework. There are several directions worth exploring. First, our consistency theory is conducted under the condition of separable sets, similar to Ascolani et al. (2022). For general cases with non-separable sets, clustering consistency (especially on estimating ) is challenging to achieve; to our best knowledge, existing consistency theory only applies to data generated independently from a mixture model (Miller and Harrison, 2018; Zeng et al., 2023). For data generated dependently via a graph, this is still an unsolved problem. Second, in all of our forest models, we have been careful in choosing densities with tractable normalizing constants. One could relax this constraint by using densities and , with some similarity function, and potentially intractable. In these cases, the forest posterior becomes . Therefore, one could choose an appropriate (equivalent to choosing some value of ), without knowing the value of or ; nevertheless, how to calibrate still requires further study. Third, a related idea is the Dirichlet Diffusion Tree (Neal, 2003), which considers a particle starting at the origin, following the path of previous particles, and diverging at a random time. The data are collected as the locations of particles at the end of a time period. Compared to the forest process, the diffusion tree process has the conditional likelihood given the tree invariant to the ordering of the data index, which is a stronger property compared to the marginal exchangeability of the data points. Therefore, it is interesting to further explore the relationship between those two processes.
Supplementary Material
Acknowledgment:
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada.
Footnotes
Conflict of interest statement: The authors report that there are no competing interests to declare.
References
- Aldous DJ (1990). The Random Walk Construction of Uniform Spanning Trees and Uniform Labelled Trees. SIAM Journal on Discrete Mathematics 3 (4), 450–465. [Google Scholar]
- Ascolani F, Lijoi A, Rebaudo G, and Zanella G (2022). Clustering Consistency With Dirichlet Process Mixtures. arXiv preprint arXiv:2205.12924. [Google Scholar]
- Aßmann C, Boysen-Hogrefe J, and Pape M (2016). Bayesian Analysis of Static and Dynamic Factor Models: An Ex-Post Approach Towards the Rotation Problem. Journal of Econometrics 192 (1), 190–206. [Google Scholar]
- Banerjee S, Akbani R, and Baladandayuthapani V (2015). Bayesian Nonparametric Graph Clustering. arXiv preprint arXiv:1509.07535. [Google Scholar]
- Barry D and Hartigan JA (1993). A Bayesian Analysis for Change Point Problems. Journal of the American Statistical Association 88 (421), 309–319. [Google Scholar]
- Blackwell D and MacQueen JB (1973). Ferguson Distributions via Pólya Urn Schemes. The Annals of Statistics 1 (2), 353–355. [Google Scholar]
- Blei DM and Frazier PI (2011). Distance Dependent Chinese Restaurant Processes. Journal of Machine Learning Research 12 (8). [Google Scholar]
- Boykov Y, Veksler O, and Zabih R (2001). Fast Approximate Energy Minimization via Graph Cuts. IEEE Transactions on pattern analysis and machine intelligence 23 (11), 1222–1239. [Google Scholar]
- Braak H and Braak E (1991). Neuropathological Stageing of Alzheimer-Related Changes. Acta Neuropathologica 82 (4), 239–259. [DOI] [PubMed] [Google Scholar]
- Broder AZ (1989). Generating Random Spanning Trees. In Annual Symposium on Foundations of Computer Science, Volume 89, pp. 442–447. [Google Scholar]
- Byrne S and Dawid AP (2015). Structural Markov Graph Laws for Bayesian Model Uncertainty. The Annals of Statistics 43 (4), 1647–1681. [Google Scholar]
- Cai D, Campbell T, and Broderick T (2021). Finite Mixture Models Do Not Reliably Learn the Number of Components. In International Conference on Machine Learning, pp. 1158–1169. PMLR. [Google Scholar]
- Cao X, Khare K, and Ghosh M (2019). Posterior Graph Selection and Estimation Consistency for High-Dimensional Bayesian DAG Models. The Annals of Statistics 47 (1), 319–348. [Google Scholar]
- Chaiken S and Kleitman DJ (1978). Matrix Tree Theorems. Journal of Combinatorial Theory, Series A 24 (3), 377–381. [Google Scholar]
- Chandra NK, Canale A, and Dunson DB (2023). Escaping the Curse of Dimensionality in Bayesian Model Based Clustering. Journal of Machine Learning Research 24, 1–42. [Google Scholar]
- Chi Y, Song X, Zhou D, Hino K, and Tseng BL (2007). Evolutionary Spectral Clustering by Incorporating Temporal Smoothness. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 153–162. [Google Scholar]
- Coretto P and Hennig C (2016). Robust Improper Maximum Likelihood: Tuning, Computation, and a Comparison With Other Methods for Robust Gaussian Clustering. Journal of the American Statistical Association 111 (516), 1648–1659. [Google Scholar]
- Crowley EM (1997). Product Partition Models for Normal Means. Journal of the American Statistical Association 92 (437), 192–198. [Google Scholar]
- Dahl DB, Johnson DJ, and Müller P (2022). Search Algorithms and Loss Functions for Bayesian Clustering. Journal of Computational and Graphical Statistics 31 (4),1189–1201. [Google Scholar]
- DeBruine ZJ, Melcher K, and Triche TJ Jr (2021). Fast and Robust Non-Negative Matrix Factorization for Single-Cell Experiments. bioRxiv, 2021–09. [Google Scholar]
- Diaconis P (1977). Finite Forms of de Finetti’s Theorem on Exchangeability. Synthese 36, 271–281. [Google Scholar]
- Duan LL and Dunson DB (2021a). Bayesian Distance Clustering. Journal of Machine Learning Research 22, 1–27. [PMC free article] [PubMed] [Google Scholar]
- Duan LL and Dunson DB (2021b). Bayesian Spanning Tree: Estimating the Backbone of the Dependence Graph. arXiv preprint arXiv:2106.16120. [Google Scholar]
- Duan LL, Michailidis G, and Ding M (2023). Bayesian Spiked Laplacian Graphs. Journal of Machine Learning Research 24 (3), 1–35. [Google Scholar]
- Edwards D, De Abreu GC, and Labouriau R (2010). Selecting High-Dimensional Mixed Graphical Models Using Minimal AIC or BIC Forests. BMC Bioinformatics 11 (1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ester M, Kriegel H-P, Sander J, and Xu X (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, pp. 226–231. AAAI Press. [Google Scholar]
- Fraley C and Raftery AE (2002). Model-Based Clustering, Discriminant Analysis, and Density Estimation. Journal of the American Statistical Association 97 (458), 611–631. [Google Scholar]
- Frey BJ and Dueck D (2007). Clustering by Passing Messages Between Data Points. Science 315 (5814), 972–976. [DOI] [PubMed] [Google Scholar]
- Frühwirth-Schnatter S and Pyne S (2010). Bayesian Inference for Finite Mixtures of Univariate and Multivariate Skew-Normal and Skew-t Distributions. Biostatistics 11 (2), 317–336. [DOI] [PubMed] [Google Scholar]
- Geng J, Bhattacharya A, and Pati D (2019). Probabilistic Community Detection With Unknown Number of Communities. Journal of the American Statistical Association 114 (526), 893–905. [Google Scholar]
- Gower JC and Ross GJ (1969). Minimum Spanning Trees and Single Linkage Cluster Analysis. Journal of the Royal Statistical Society: Series C (Applied Statistics) 18 (1), 54–64. [Google Scholar]
- Guha S and Baladandayuthapani V (2016). A Nonparametric Bayesian Technique for High-Dimensional Regression. Electronic Journal of Statistics 10 (2), 3374–3424. [Google Scholar]
- Han X, Tong X, and Fan Y (2021). Eigen Selection in Spectral Clustering: A Theory-Guided Practice. Journal of the American Statistical Association, 1–13.35757777 [Google Scholar]
- Hartigan JA (1990). Partition Models. Communications in Statistics-Theory and Methods 19 (8), 2745–2756. [Google Scholar]
- Klimova B, Maresova P, Valis M, Hort J, and Kuca K (2015). Alzheimer’s Disease and Language Impairments: Social Intervention and Medical Treatment. Clinical Interventions in Aging, 1401–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosmidis I and Karlis D (2016). Model-Based Clustering Using Copulas With Applications. Statistics and Computing 26 (5), 1079–1099. [Google Scholar]
- Kumar A, Rai P, and Daume H (2011). Co-regularized Multi-view Spectral Clustering. In Shawe-Taylor J, Zemel R, Bartlett P, Pereira F, and Weinberger K (Eds.), Advances in Neural Information Processing Systems, Volume 24. Curran Associates, Inc. [Google Scholar]
- Lee SX and McLachlan GJ (2016). Finite Mixtures of Canonical Fundamental Skew t-Distributions. Statistics and Computing 26 (3), 573–589. [Google Scholar]
- Lei J and Lin KZ (2022). Bias-Adjusted Spectral Clustering in Multi-Layer Stochastic Block Models. Journal of the American Statistical Association, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei J and Rinaldo A (2015). Consistency of Spectral Clustering in Stochastic Block Models. The Annals of Statistics 43 (1), 215–237. [Google Scholar]
- Lewis JR, MacEachern SN, and Lee Y (2021). Bayesian Restricted Likelihood Methods: Conditioning on Insufficient Statistics in Bayesian Regression. Bayesian Analysis 16 (4), 1393–1462. [Google Scholar]
- Luo Z, Sang H, and Mallick B (2021). A Bayesian Contiguous Partitioning Method for Learning Clustered Latent Variables. Journal of Machine Learning Research 22. [Google Scholar]
- MacQueen J (1967). Classification and Analysis of Multivariate Observations. In 5th Berkeley Symp. Math. Statist. Probability, pp. 281–297. [Google Scholar]
- Malsiner-Walli G, Frühwirth-Schnatter S, and Grün B (2017). Identifying Mixtures of Mixtures Using Bayesian Estimation. Journal of Computational and Graphical Statistics 26 (2), 285–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDaid AF, Murphy TB, Friel N, and Hurley NJ (2013). Improved Bayesian Inference for the Stochastic Block Model With Application to Large Networks. Computational Statistics & Data Analysis 60, 12–31. [Google Scholar]
- Medvedovic M and Sivaganesan S (2002). Bayesian Infinite Mixture Model Based Clustering of Gene Expression Profiles. Bioinformatics 18 (9), 1194–1206. [DOI] [PubMed] [Google Scholar]
- Meilă M and Jaakkola T (2006). Tractable Bayesian Learning of Tree Belief Networks. Statistics and Computing 16 (1), 77–92. [Google Scholar]
- Meila M and Jordan MI (2000). Learning With Mixtures of Trees. Journal of Machine Learning Research 1 (Oct), 1–48. [Google Scholar]
- Miller JW (2019). An Elementary Derivation of the Chinese Restaurant Process From Sethuraman’s Stick-Breaking Process. Statistics & Probability Letters 146, 112–117. [Google Scholar]
- Miller JW and Dunson DB (2018). Robust Bayesian Inference via Coarsening. Journal of the American Statistical Association 114 (527), 1113–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JW and Harrison MT (2018). Mixture Models With a Prior on the Number of Components. Journal of the American Statistical Association 113 (521), 340–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molitor J, Papathomas M, Jerrett M, and Richardson S (2010). Bayesian Profile Regression With an Application to the National Survey of Children’s Health. Biostatistics 11 (3), 484–498. [DOI] [PubMed] [Google Scholar]
- Mosbah M and Saheb N (1999). Non-Uniform Random Spanning Trees on Weighted Graphs. Theoretical Computer Science 218 (2), 263–271. [Google Scholar]
- Müller P and Quintana F (2010). Random Partition Models With Regression on Covariates. Journal of Statistical Planning and Inference 140 (10), 2801–2808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller P, Quintana F, and Rosner GL (2011). A Product Partition Model With Regression on Covariates. Journal of Computational and Graphical Statistics 20 (1), 260–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neal RM (2003). Density Modeling and Clustering Using Dirichlet Diffusion Trees. Bayesian Statistics 7, 619–629. [Google Scholar]
- Ng S-K, McLachlan GJ, Wang K, Ben-Tovim Jones L, and Ng S-W (2006). A Mixture Model With Random-Effects Components for Clustering Correlated Gene-Expression Profiles. Bioinformatics 22 (14), 1745–1752. [DOI] [PubMed] [Google Scholar]
- Noble S, Scheinost D, and Constable RT (2021). A Guide to the Measurement and Interpretation of fMRI Test-Retest Reliability. Current Opinion in Behavioral Sciences 40, 27–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowicki K and Snijders TAB (2001). Estimation and Prediction for Stochastic Blockstructures. Journal of the American Statistical Association 96 (455), 1077–1087. [Google Scholar]
- Paganin S, Herring AH, Olshan AF, and Dunson DB (2021). Centered Partition Processes: Informative Priors for Clustering. Bayesian Analysis 16 (1), 301–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J-H and Dunson DB (2010). Bayesian Generalized Product Partition Model. Statistica Sinica, 1203–1226. [Google Scholar]
- Petrone S, Guindani M, and Gelfand AE (2009). Hybrid Dirichlet mixture models for functional data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71 (4), 755–782. [Google Scholar]
- Quintana FA and Iglesias PL (2003). Bayesian Clustering and Product Partition Models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65 (2), 557–574. [Google Scholar]
- Rasmussen C, Bernard J, Ghahramani Z, and Wild DL (2008). Modeling and Visualizing Uncertainty in Gene Expression Clusters Using Dirichlet Process Mixtures. IEEE/ACM Transactions on Computational Biology and Bioinformatics 6 (4), 615–628. [DOI] [PubMed] [Google Scholar]
- Ren L, Du L, Carin L, and Dunson DB (2011). Logistic Stick-Breaking Process. Journal of Machine Learning Research 12 (1). [PMC free article] [PubMed] [Google Scholar]
- Rigon T, Herring AH, and Dunson DB (2023). A Generalized Bayes Framework for Probabilistic Clustering. Biometrika, 1–14. [Google Scholar]
- Rodríguez CE and Walker SG (2014). Univariate Bayesian Nonparametric Mixture Modeling With Unimodal Kernels. Statistics and Computing 24 (1), 35–49. [Google Scholar]
- Rohe K, Chatterjee S, and Yu B (2011). Spectral Clustering and the High-Dimensional Stochastic Blockmodel. The Annals of Statistics 39 (4), 1878–1915. [Google Scholar]
- Rolls ET, Huang C-C, Lin C-P, Feng J, and Joliot M (2020). Automated Anatomical Labelling Atlas 3. Neuroimage 206, 116189. [DOI] [PubMed] [Google Scholar]
- Schild A (2018). An Almost-Linear Time Algorithm for Uniform Random Spanning Tree Generation. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, pp. 214–227. [Google Scholar]
- Shi D, Zhang H, Wang S, Wang G, and Ren K (2021). Application of Functional Magnetic Resonance Imaging in the Diagnosis of Parkinson’s Disease: A Histogram Analysis. Frontiers in Aging Neuroscience 13, 624731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi T, Belkin M, and Yu B (2009). Data Spectroscopy: Eigenspaces of Convolution Operators and Clustering. The Annals of Statistics, 3960–3984. [Google Scholar]
- Snijders TA and Nowicki K (1997). Estimation and Prediction for Stochastic Blockmodels for Graphs With Latent Block Structure. Journal of Classification 14 (1), 75–100. [Google Scholar]
- Socher R, Maas A, and Manning C (2011). Spectral Chinese Restaurant Processes: Nonparametric Clustering Based on Similarities. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, pp. 698–706. JMLR Workshop and Conference Proceedings. [Google Scholar]
- Teh YW, Jordan MI, Beal MJ, and Blei DM (2006). Hierarchical dirichlet processes. Journal of the American Statistical Association 101 (476), 1566–1581. [Google Scholar]
- Von Luxburg U (2007). A Tutorial on Spectral Clustering. Statistics and Computing 17 (4), 395–416. [Google Scholar]
- Wade S and Ghahramani Z (2018). Bayesian Cluster Analysis: Point Estimation and Credible Balls. Bayesian Analysis 13 (2), 559–626. [Google Scholar]
- Wu S, Feng X, and Zhou W (2014). Spectral Clustering of High-Dimensional Data Exploiting Sparse Representation Vectors. Neurocomputing 135, 229–239. [Google Scholar]
- Yu Y, Wang T, and Samworth RJ (2015). A Useful Variant of the Davis–Kahan Theorem for Statisticians. Biometrika 102 (2), 315–323. [Google Scholar]
- Zelnik-Manor L and Perona P (2005). Self-Tuning Spectral Clustering. In Advances in Neural Information Processing Systems, Volume 17. [Google Scholar]
- Zeng C, Miller JW, and Duan LL (2023). Consistent Model-based Clustering using the Quasi-Bernoulli Stick-breaking Process. Journal of Machine Learning Research 24, 1–32. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


