Protein translation can fluidize bacterial cytoplasm

Abstract

The cytoplasm of bacterial cells is densely packed with highly polydisperse macromolecules that exhibit size-dependent glassy dynamics. Recent research has revealed that metabolic activities in living cells can counteract the glassy nature of these macromolecules, allowing the cell to maintain critical fluidity for its growth and function. While it has been proposed that the crowded cytoplasm is responsible for this glassy behavior, a detailed analysis of the size-dependent nature of the glassy dynamics and an explanation for how cellular activity induces its fluidization remains elusive. Here, we use a combination of computational models and targeted experiments to show that entropic segregation of the protein synthesis machinery from the chromosomal DNA causes size-dependent spatial organization of molecules within the cell, and the resultant crowding leads to size-dependent glassy dynamics. Furthermore, Brownian dynamics simulations of this in silico system supports a new hypothesis: protein synthesis in living cells contributes to the metabolism-dependent fluidization of the cytoplasm. The main protein synthesis machinery, ribosomes, frequently shift between fast and slow diffusive states. These states correspond to the independent movement of ribosomal subunits and the actively translating ribosome chains called polysomes, respectively. Our simulations demonstrate that the frequent transitions of the numerous ribosomes, which constitute a significant portion of the cell proteome, greatly enhance the mobility of other macromolecules within the bacterial cytoplasm. Considering that ribosomal protein synthesis is the largest consumer of ATP in growing bacterial cells, the translation process can serve as the primary mechanism for fluidizing the cytoplasm in metabolically active cells.

Significance Statement.

This manuscript offers a mechanistic analysis of size-dependent organization and dynamics of cellular components in bacterial cytoplasm. It reveals that entropic segregation of chromosomal DNA and ribosomes partitions the cytoplasm into nucleoid and nucleoid-free zones, with molecular components distributing according to their size-dependent segregation from the nucleoid meshwork. Localized molecular crowding in this segregated cytoplasm results in size-dependent glassy dynamics. A computational model proposes physical mechanisms controlling cytoplasmic fluidity, with translational activity, in the form of polysome-to-ribosome switching mechanism, playing a key role in enhancing macromolecular mobility. This framework provides alternate mechanism into how bacterial cells maintain critical cytoplasmic fluidity despite high molecular density.

Introduction

In the absence of cytoskeletal filaments and motor proteins, biomolecular reactions within the bacterial cytoplasm are predominantly constrained by diffusion. Recent experiments involving single molecule tracking in living cells have highlighted the prominent role of diffusion-limited search times as the determining factor for reaction kinetics (1–4). As a result, comprehending the mechanisms that influence the diffusional properties of various cytoplasmic components is crucial for grasping the spatiotemporal organization of biomolecular reactions within individual bacterial cells.

The dynamics of various cellular entities in the bacterial cytoplasm exhibit significant variability and frequently deviate from simple diffusion (3, 5–7). The bacterial cytoplasm represents a densely populated environment comprising a multitude of polydisperse entities (8–13), ranging in size from a few nanometers (such as small proteins, ribosomes, metabolites, etc.) to micrometers (including DNA, polysomes, large proteins, etc.). This polydisperse crowding has been demonstrated to influence the dynamics of individual components in a size-dependent manner (14, 15). A recent study by Parry et al. (16) further reveals that the mode of dynamics also relies on the size of the particle under examination. In aggregate, their findings suggest that the bacterial cytoplasm displays dynamics reminiscent of glass-like behavior, where smaller components exhibit liquid-like dynamics and larger components exhibit solid-like dynamics.

The highly crowded and polydisperse nature of the cytoplasm is expected to underlie the size-dependent glassy dynamics observed in cytoplasmic particles. At significantly high crowder densities, particles can become entrapped and unresponsive to external perturbations, resembling solids. While in a monodisperse system, this scenario could lead to crystallization, in a complex and polydisperse system like the bacterial cytoplasm, the dynamics turn chaotic and glassy, which aligns with observations made by Parry et al. (16).

However, comprehending the mechanistic intricacies governing these glassy dynamics would benefit from computational investigations, which enable precise control and consideration of confounding perturbations. This contrasts with experimental settings where apparently straightforward perturbations might trigger various unpredictable changes in biomolecular states, complicating the identification of intended direct effects. In this study, we endeavor to address this challenge using a Brownian dynamics model of the bacterial cytoplasm. This model allows for systematic exploration of diverse factors that could impact the dynamics of cytoplasmic components.

Parry et al. (16) also discovered that in metabolically active cells, the dynamics of larger components are fluidized by cell metabolism, potentially playing a critical role in determining their enzymatic activity. However, the mechanism underlying the metabolic activity-dependent fluidization of the glassy cytoplasm remains unclear. An earlier investigation by Weber et al. (17) demonstrated that ATP-dependent nonequilibrium fluctuations contribute to the macro-molecular motion in cells, enhancing their mobility. In line with this observation, Parry et al. identified ATP as a pivotal factor in fluidizing the dynamics of various cytoplasmic components. Numerous potential mechanisms of ATP-dependent fluidization have been proposed (including protein conformational changes, nonequilibrium fluctuations, fluid displacement, etc.). However, to align with experimental observations, such a mechanism should exhibit strong ATP dependence and induce fluidization or glassification of cytoplasmic components in a size-dependent manner.

In this study, we propose a hypothesis that underscores the role of ATP-dependent translation activity in metabolically active cells as the primary force for cytoplasmic fluidization. Translation stands as the primary ATP consumer within the cell, with ribosomes being the central players which are large molecular machines highly concentrated in the cytoplasm (13, 18). The presence or absence of ATP could shift the state of these abundant molecular machines from primarily engaged in translation to predominantly free diffusion (11, 13). Such a state transition is distinctly different from the effects of translation-inhibiting antibiotics, such as chloramphenicol, which causes drastic changes in the internal organization of the cytoplasm (11, 13). Therefore, the specific effects of translation are difficult to be tested experimentally, but can be simulated computationally.

Through computer simulations, here we have delved into how macromolecular crowding triggers glassy dynamics in the cytoplasm and assess whether the dynamic fluctuations in ribosome diffusivity, dictated by their activity, could sufficiently perturb the remaining cytoplasm to induce fluid-like motion. Our simulations demonstrate that molecular crowding indeed leads to size-dependent glassy dynamics of cytoplasmic particles. This phenomenon stems from the size-dependent spatial organization of the cytoplasm, which we have also experimentally tested and validated in this work. Subsequently, we develop a model to describe ribosome state switching during translation (initiation: fast to slow and termination: slow to fast). Our findings highlight that the substantial changes in the dynamics of numerous ribosomes during translation initiation and termination can effectively disrupt the motion of other cytoplasmic entities, promoting fluidic behavior. To provide further substantiation, we conduct additional computational and bioinformatics investigations to elucidate why ribosomes and their biochemical states are uniquely suited to serve as the primary driving force behind the transformation of the inherently glassy cytoplasm.

Results and discussion

Modeling the effects of molecular crowding in the bacterial cytoplasm

We initiate our exploration by creating a model of the bacterial cytoplasm to investigate the effects of various configurations on molecular dynamics. The bacterial chromosome is represented as a ring polymer with interconnections between segments, established using inter-gene contact probabilities derived from Hi-C experiments (19). This is combined with a polymer-physics-based framework within a spherocylindrical confinement (see the Model and method section for further details).

To simulate an excessively crowded condition resembling the bacterial cytoplasm, the simulated cell is densely packed with monomeric ribosomes (50S and 30S) as well as 13-bead polymer chains representing 70S ribosomes, referred to as polysomes. This is set in an 80:20 polysome–ribosome ratio (11, 13). While ensuring bonded connectivity within the chromosome, we employ soft excluded volume interactions to model the mutual interactions among all species coexisting within the cell. The dynamics of each constituent particle within this densely populated cell adhere to Brownian dynamics. All length and time measurements are described in reduced units relative to the diameter of the DNA bead $(\sigma )$ and Brownian time $({\tau }_B)$, respectively (as detailed in the Model and methods section).

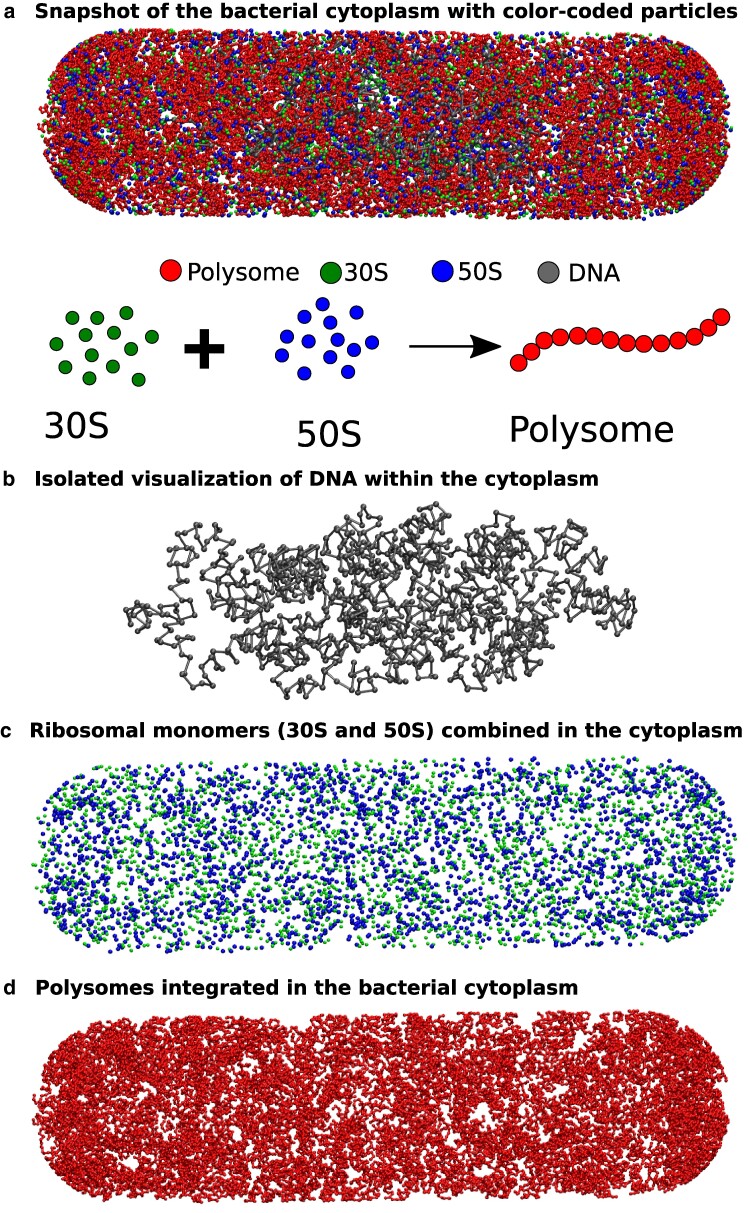
In Fig. 1a, a representative snapshot of Escherichia coli cytoplasm is presented, with color-coded beads representing various particles. Additionally, for enhanced visualization of their spatial distribution, we have individually plotted each of the components (Fig. 1b–d).

Fig. 1.

A representative snapshot of the model bacterial cytoplasm. The upper figure a) depicts a snapshot of the bacterial cytoplasm, enclosed by the cell wall, where different types of particles are distinguished by color-coded beads. The lower schematic illustrates two states of ribosomes: (i) separated into 50S and 30S monomers, and (ii) combined into 70S and integrated within a polysome. To enhance visualization, we extracted the distinct particle types from the snapshot and presented them individually (from top to bottom: b) DNA, c) 30S and 50S combined, d) and polysomes.

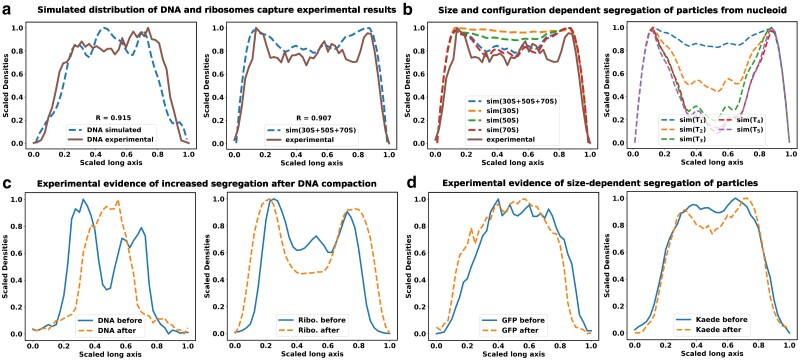
As affirmed by superresolution experiments (11–13) and validated by our previous computational model (11, 20), our current model consistently illustrates a significant spatial separation between ribosomes and DNA, as shown in Fig. 2a. In an effort to preserve configurational entropy, DNA tends to condense away from the cell walls, consequently creating distance between itself and large particles like ribosome subunits and ribosome polymers. These ribosome particles are predominantly situated within the end-cap region of the bacterial cytoplasm, an area where DNA is relatively sparse. This segregation phenomenon is notably pronounced for ribosome chains, known as polysomes.

Fig. 2.

Size-dependent spatial distribution of cytoplasmic particles. The figure shows the linear density profiles of DNA and ribosomal subunits a) Here, solid lines correspond to experimental data, while dashed lines represent simulated densities. The R value denotes the Pearson correlation coefficient between the experimental and simulated data. The experimental linear density data have been adapted from reference (12). b) Species-specific segregation various ribosome moities are shown in comparison with the total ribosomes (left). Polysomes (70S) are more segregated from the nucleoid, compared to the individual 30S and 50s subunits. Figures (b-right) depicts the linear density profiles of tracer particles $(T_1-T_5)$ with respect to the nucleoid. Similar to ribosomes, large tracer particles also exhibit noticeable segregation from the nucleoid, with the extent of this segregation being contingent on their respective sizes. c) Density profiles of DNA and ribosomes along the long axis of the cell are computed from images of corresponding fluorescently tagged stains. Blue solid line refers to the distributions in untreated cells, while the orange dashed lines refer to distributions after treatment with translation-inhibiting drug chloramphenicol. The extent of segregation of ribosomes from the nucleoid increases after the chloramphenicol induced nucleoid compaction. d) Distribution of fluorescence signal from GFP and Kaede are compared with and without chloramphenicol treatment. Distribution of Kaede signal shows moderate segregation from nucleoid after nucleoid compaction, while the distribution for GFPs remain unchanged.

When comparing the spatial distribution profiles of polysomes to the nucleoid, a clear segregation pattern emerges. This pattern closely mirrors experimental results obtained under relevant growth conditions, as documented in Mohapatra’s studies (12). This finding aligns with our earlier work’s polysome-nucleoid demixing hypothesis (11, 20). Notably, polysomes, being chains of ribosomes, exhibit a lower likelihood of intermixing with DNA chains when compared to individual 30S and 50S ribosome subunits Fig 2b. This reduced intermingling is due to the significant loss of configurational entropy involved.

Size-dependent spatial distribution of cytoplasmic particles

In the following investigation, we delve into the spatial distribution of cytoplasmic particles in relation to the nucleoid and ribosomes within our model cytoplasm. Our aim is to ascertain whether the distribution of these particles correlates with their individual sizes. To explore this, we introduced five distinct tracer particles, each characterized by varying diameters $(T_1=10$ nm, $T_2=20$ nm, $T_3=30$ nm, $T_4=40$ nm, and $T_5=50$ nm). These cytoplasmic particles interact with each other and the rest of the cytoplasmic components through excluded volume interactions (see Method and Supplementary material).

In Fig. 2b, we present a comparison of the individual particle distributions along the long axis of the bacterial cytoplasm. The density profile of the nucleoid, as displayed in Fig. 2a, serves as a reference point for assessing the relative segregation of these tracer proteins from the nucleoid. Much like ribosomes, large tracer particles also exhibit noticeable segregation from the nucleoid, and the extent of this segregation depends on their respective sizes. The compacted nucleoid seems to act as a sieve, effectively segregating the proteins from its core. Consequently, proteins are predominantly located in the end-cap region of the cytoplasm. Notably, larger tracer particles are strongly excluded from the nucleoid and tend to congregate in the ribosome-rich regions at the cytoplasm’s end cap. Since the tracer particles are introduced here in small numbers, their presence does not lead to additional compaction of the nucleoid (Figure S1).

In order to experimentally verify the size-dependent nature of protein segregation, we have measured the distribution of nucleoid in individual bacterial cells, using a DNA stain (SYTOX Orange (11)) and compared the axial distribution of three proteins of three different sizes in the cell (ribosome, GFP, and Kaede). Kaede is a tetramer of GFP-like units, and therefore four times larger in size. In untreated regular cells (blue traces in Fig. 2c), ribosomes are strongly segregated from the nucleoid along the long axis of the cell. The rich growth media used in these experiments leads to two nucleoid lobes in an average cell, and as a result there are two dips in the distribution of ribosomes along the long axis, mirroring the two peaks in the nucleoid distribution. The distribution of GFP and Kaede do not show significant segregation from the nucleoid at this condition, consistent with our superresolution measurements (21). Next, we treated cells with translation-inhibiting antibiotic chloramphenicol. Chloramphenicol leads to compaction of the nucleoid (11), which leads to stronger segregation of ribosomes from the nucleoid. In chloramphenicol-treated cells, Kaede distribution shows significant segregation from the nucleoid, while the smaller GFP molecules can maintain relatively uniform distribution (Fig. 2d). This size-dependent extent of segregation of these three particles from the bacterial nucleoid is consistent with the simulations results.

Molecular crowding causes size-dependent glassy dynamics of proteins in cytoplasm

To scrutinize the impact of molecular crowding on observed dynamics, we conduct a comparative analysis of the dynamics of individual components in the presence and absence of all other cellular constituents. To comprehensively account for the diverse range of crowding species found in the bacterial cytoplasm, it is imperative to consider additional crowding particles apart from the nucleoid and ribosomes. However, attempting to simulate the entire bacterial cytoplasm with the vast number of crowding entities poses significant computational challenges, rendering simulations excessively sluggish and unwieldy. For example, to model the entire cytoplasm under the same conditions as the cubical box (which we will discuss later), in would require simulation of approximately $\mathrm{340,000}$ particles in multiple replicate.

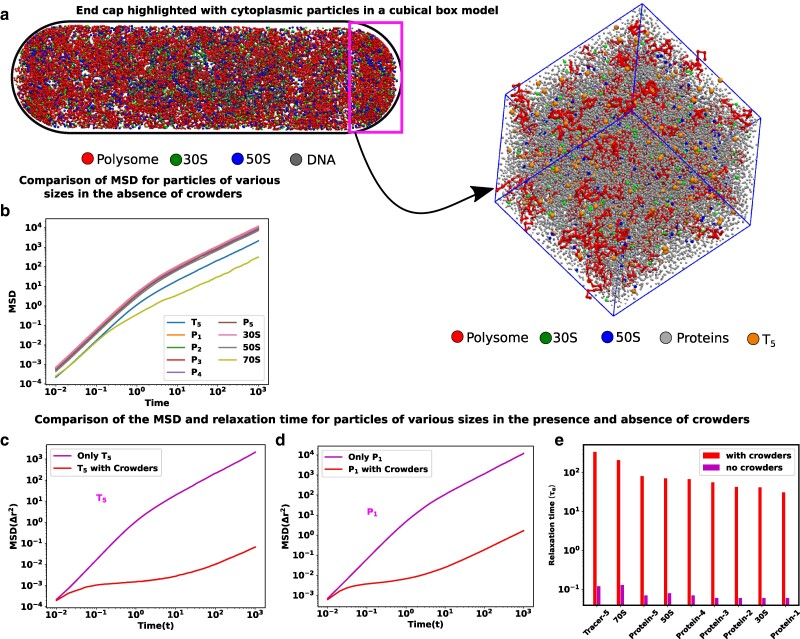
Considering that the experimental research (16) has demonstrated that only larger tracer particles typically exhibit glassy dynamics, our subsequent analysis focusses on particles exceeding 10 nm in size. As evidenced in Fig. 2c, these larger particles are exclusively concentrated within the ribosome-rich regions of the end cap (Fig. 3a). Consequently, our primary focus lies in the dynamic analysis of particles situated within the end-cap region. Therefore, our present focus centers on detailed simulations of a representative volume sharing similar dimensions and composition with the cytoplasmic end cap. In order to achieve a high packing fraction representative of the cytoplasm ($pf=$ 0.57), we introduce five distinct types of polydisperse protein particles $(P_1-P_5)$ with sizes ranging from 13 to 18 nm. Since the primary purpose of the $(P_1-P_5)$ particles are to achieve high packing fraction, we selected large particle size, to reduce the system size from having a large number of small particles. However, the size range was kept below 20 nm, since ribosomes (20 nm) are likely to be the largest high density particles in the cytoplasm.

Fig. 3.

Size-dependent glassy dynamics of particles in a crowded cytoplasm. a) The end cap of the cells is highlighted by the small rectangle. Considering a cubical box with a volume akin to that of the cell’s end cap, we have inserted the different types of cytoplasmic particles inside it. b) MSD as a function of time for different components in our simulations in the absence of crowders. c and d) The MSD for different particle sizes is compared in the presence and absence of crowders for $T_5$, and $P_1$, respectively. In the presence of crowders, all the components show a ballistic region and diffusive region in very short and longer time scales, respectively and these two regions are separated by a plateau which is an indicator of glassy dynamics. e) Bar plots of structural relaxation time for different sizes of particles both in the presence and in the absence of the crowders. The relaxation times are larger in the presence of crowders, and this effect is also dependent on particle size.

Moreover, we have also simulated them individually. For these simulations, we have chosen a very low copy number $(100)$ of each individual monomeric component to ensure that the components do not become overcrowded by themselves, while still providing sufficient data for statistical analysis of dynamic properties. We compare the dynamics of individual components in the presence and absence of all the other components. Detailed descriptions of the models and corresponding calculations of mean-squared displacements can be found in the Model and methods section.

In the absence of any crowding agents, the dynamics of the proteins and tracer particles exhibit super-diffusion on a remarkably short timescale, while also demonstrating the expected linear scaling of MSD at a very long time scale (Fig. 3b). When these moieties are placed in the crowded environment of the simulated cytoplasm, their dynamics can no longer be described as simple diffusion. Even for the smallest proteins, the mean squared displacement slows down over longer periods of time. For proteins and tracer particles $(T_5)$, a clear presence of an intermediate plateau is evidenced and indicates the glass transition (Fig. 3c and d). At shorter timescales, these moieties explore the local environments in a superdiffusive manner without being aware of the crowded neighborhood. At the intermediate timescales, they encounter immediate neighborhood obstacles and become caged. At longer timescales, they can escape the cage and their motion mimics an effective diffusive motion, which is much slower than their thermal diffusion constant in this media. This two-step dynamic is a hallmark of glass transition and is seen in the entire range of particles explored here. To analyze the short-time behavior of the particles, we fitted the MSD values with $\text{MSD}(t)=a{t}^{\delta }$, where $D=a/6$ is the diffusion constant, and δ is the MSD exponent. A value of $\delta >1$ indicates superdiffusive motion, which is only observed at very short timescales (Figure S2a-d). At these timescales, particles move without many collisions, allowing them to maintain their directed motion from the previous collision. This behavior occurs within intervals shorter than the typical collision times.

To further investigate the potential relaxation dynamics typically associated with a glassy matrix, we calculate the structural relaxation time $({\tau }_{\alpha })$ for particles of varying sizes, both in the presence and absence of crowding agents. This calculation involves assessing the overlap function (for detailed information, refer to the Materials and methods sections). The relaxation time is typically determined from a two-point density-density autocorrelation function. This parameter provides valuable insights into how the system gradually loses its memory over time. In Fig. 3e, we present bar plots illustrating $({\tau }_{\alpha })$ for particles of different sizes in descending order, denoted by red (in the presence of crowding) and magenta (in the absence of crowding) colors. Notably, in the presence of crowding, the relaxation times for all particles are significantly extended compared to their values in the absence of crowding. Furthermore, the relaxation times are notably influenced by the particle sizes, particularly when crowding is present.

Dynamic heterogeneity and non-Gaussian distribution of displacements

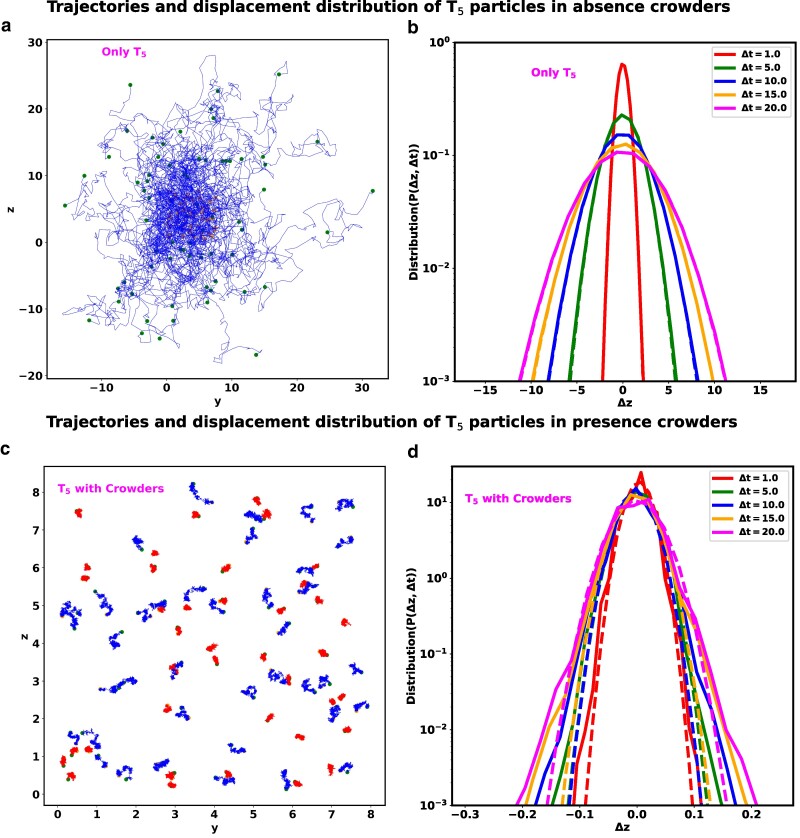
Beyond just looking at the overall behavior of the tracer particles as a group, as evidenced from mean squared displacements, examining the individual paths of these particles clearly reveals that their dynamics is specifically influenced by the molecular crowding in the system. As an illustration, we have plotted the trajectories of the $(T_5)$ particles in (yz) plane in the absence (Fig. 4a) and in the presence (Fig. 4c) of crowders, respectively. The start and end point of these trajectories are marked by magenta and green circles. In the absence of any crowder, the shape of individual trajectories are reminiscent of Brownian motion and sample a large space uniformly. However, in the presence of crowders, the variation of trajectory sizes of $T_5$ within the same time period shows that there are co-existence of fast (blue) and slow (red) moving particles. Such behavior is a signature of dynamic heterogeneity (DH). DH is a prominent feature of glassy dynamics, indicating significant variations in local particle dynamics. It implies the coexistence of regions with both highly mobile and less mobile particles (22, 23).

Fig. 4.

Comparison of Dynamic heterogeneity (DH) and non-Gaussian distribution between $T_5$ particle. a) The trajectory of $(T_5)$ particles in the absence of crowders. Each trajectory spans the same time period $(6.0{\tau }_B)$. These particles move more quickly and uniformly, filling up more of the cytoplasm. b) Distribution of displacement $(\mathrm{\Delta }z)$ for $T_5$ with different delay times $\mathrm{\Delta }t$ in the absence of crowders. c) The trajectory of $(T_5)$ in the presence of crowders. Each trajectory of $T_5$ span the time period $(1000.0{\tau }_B)$. However, from the variation of trajectory sizes of $T_5$ within the same time period, we can argue that there are co-existence of fast (blue) and slow (red) moving particles, supporting the strong indication of dynamic heterogeneity. d) Distribution of displacement $(\mathrm{\Delta }z)$ for $T_5$ with different delay times $\mathrm{\Delta }t$ in the presence of crowders. In all figures (a and c), the start and end points of the respective trajectories are denoted by magenta and green colored scatter points. In all plots of (b) and (d), the simulated data are represented by solid lines, while the fits of a Gaussian function are depicted by dotted lines.

To quantitatively compare the observed dynamics with the expected dynamics of diffusive particles, we have examined the particle displacement distributions, inspired by the experimental study by He et al. (22). We have calculated the displacement of the $T_5$ particles (z component) as $\mathrm{\Delta }z(\mathrm{\Delta }t)=[\overrightarrow{r}(t+\mathrm{\Delta }t)-\overrightarrow{r}(t){]}_z$, where $\overrightarrow{r}(t)$ is the position of the particle at time t and $\mathrm{\Delta }t$ is the delay time. Figure 4b and d illustrates the distribution of $\mathrm{\Delta }z$ for $T_5$ particles in the absence and in the presence of crowders, respectively, with different delay time $\mathrm{\Delta }t$. In all these plots, the solid lines represent the simulated data, while the dotted lines depict the fits to a Gaussian function represented as $P(\mathrm{\Delta }z)=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}(-\frac{(\mathrm{\Delta }z-\mu {)}^2}{2{\sigma }^2})$, where σ and μ correspond to the standard deviation and mean of $\mathrm{\Delta }z$, respectively. When the tracer particles are placed in isolation, the distribution of displacement closely matches a Gaussian distribution, as expected from Brownian motion. In the presence of the crowder the distributions deviate from the Gaussian function, which is another salient feature of glassy dynamics.

Translation can fluidize the glassy cytoplasm

The experimental investigations by Weber et al. (17) and Parry et al. (16) have indicated that the metabolic activities of living cells can fluidize the glassy dynamics of large cytoplasmic particles. Specifically, the research from both groups has shown that the presence and abundance of ATP is a key determinant of this metabolic activity-dependent fluidization.

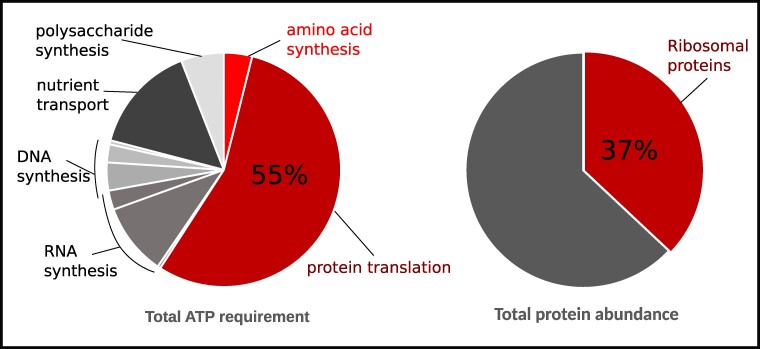
In living cells, a substantial portion of ATP is devoted to translation, specifically for aminoacylating tRNAs and regenerating GTPs. This energy expenditure is substantial, as translation activities consume approximately two-thirds of the total ATP pool within cells, significantly exceeding the demands of other energy-dependent cellular processes like nutrient transport, RNA, and DNA synthesis (24–27) (see Box 1). Consequently, translation emerges as a prime candidate whose rate and frequency could be profoundly influenced by ATP availability.

Box 1. Proteins translation requires the largest portion of metabolic energy. The protein translation machinery ribosomes are the most abundant proteins in bacterial cytoplasm. Ribosomes are large and undergo large change ($10\times$) in diffusivity during the switch of their state from subunits to actively transcribing functional units in a polysome.

Interestingly, ribosomes, the essential machinery for translation, occupy a substantial portion of the cellular proteome and significantly contribute to cellular crowding. This crowding, in turn, governs the compaction of the nucleoid and the segregation of the remaining cytoplasmic components (11). Any ATP-dependent alterations in ribosomal activity could lead to substantial changes in cytoplasmic crowding dynamics, potentially impacting the cytoplasm’s glassy nature.

What adds to the intrigue is the unique connection between ribosome mobility and their activity. Actively translating ribosomes form polysomes, groups of multiple ribosomes operating on the same mRNA strand. Polysomes exhibit slow diffusion within the cytoplasm and maintain strong segregation from the nucleoid. Conversely, freely diffusing ribosome subunits move rapidly and can traverse the nucleoid with ease. Notably, the diffusion rate of ribosome subunits is at least an order of magnitude faster than their actively engaged counterparts. The transition between these two states can lead to substantial alterations in the cytoplasm’s caging dynamics in an ATP-dependent manner. Taken together, these factors position the combination of ribosomes and translation activity as a suited candidate for mediating metabolic activity-dependent fluidization of the cytoplasm.

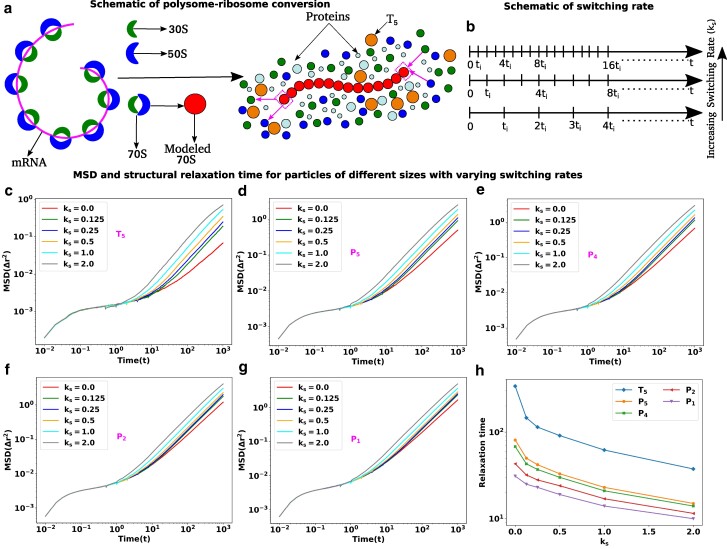
We aimed to explore the impact of metabolic activity, particularly polysome–ribosome inter-conversion, on the diffusion of various biomacromolecules within E. coli (28–30). As illustrated in Fig. 5a, we modeled this inter-conversion as follows: at specific intervals $t_i$, we randomly selected $\sim 26\mathrm{\%}$ of polysomes for conversion, or “switching,” into monomeric ribosomes. In our model, this state transition involved the removal and addition of a single 70S subunit from and to the polysome simultaneously. Figure 5a visually represents these switching schemes, where a 70S monomer dissociates into two subunits (30S and 50S) at one end of the polysome, while two subunits (30S and 50S) from the nearby cytoplasmic region join to the other end of the polysome to form a single subunit (70S). This process repeats after the same interval $(t_i)$. The corresponding switching rate is denoted as $k_s=1/t_i$ in units of ${\tau }_B^{-1}$.

Fig. 5.

Translation activities can escalate the dynamics of cytoplasmic particles. a) Schematic representation of polysome–ribosome conversion. The magenta color thread represents the mRNA chain, with the ribosomal subunits located along its length. Two ribosomal subunits (30S and 50S) associate to create another subunit called 70S and polysome is the threads of 70S. The polysome–ribosome conversion has been modeled as follows: a 70S bead from one end of the polysome dissociates into two beads (30S and 50S) and two beads (30S and 50S) from the nearby region join to the other end by forming a single bead (70S). b) Schematic representation of switching rate. The entire trajectory is represented by the time $(0-t)$, and in between switching happens at regular intervals of $(t_i)$. The switching rate will increase if there are more switching occurrences within the same interval. MSD as a function of time with various switching rates for different sizes particles in descending order c) $(T_5)$, d) $(P_5)$, e) $(P_4)$, f) $(P_2)$ and g) $(P_1)$, respectively. For all the particles, the MSD curves are showing ballistic, diffusive, and caging regions which are the hallmarks of the glassy dynamics and the length of cages diminishes with the increase in switching rate. In contrast, for the smaller particles$(P_1)$ and $(P_2)$, the switching effects are less prominent. h) Structural relaxation time $({\tau }_{\alpha }$) as a function of switching rate $(k_s)$ for particles of different sizes.

Figure 5b presents a schematic representation of switching rates. The total trajectories cover the time span $(0-t)$, with switching events occurring at regular intervals of $(t_i)$. Depending on various cellular factors such as ATP-mediated energy, ribosomal interactions, translation elongation velocity, and more (4, 31–34), the switching rate can vary. An “increasing switching rate” implies a higher frequency of switching events within the same time interval. The dotted lines suggest that there are additional switching events in the remaining intervals, which are not depicted in the diagram.

Figure 5c–g depicts the Mean Squared Displacement (MSD) curves for various species as a function of time. These curves are generated for different switching rates ($k_s$) for $T_5$ and various protein sizes, arranged in descending order of their diameter. In the absence of any switching, the MSD curve for all particle sizes exhibits distinct regions: a ballistic phase at shorter timescales, followed by a diffusive phase at longer timescales, with a plateau separating the two. This plateau signifies that the tagged particles are confined by neighboring particles, a hallmark of glassy dynamics.

Interestingly, the introduction of polysome–ribosome inter-conversion leads to a reduction in the duration of the plateau as the switching rate increases. Simultaneously, the diffusion of these particles accelerates, indicating a gradual improvement in cytoplasmic fluidity. However, these effects are less pronounced for smaller proteins $(P_1$ and $P_2)$ compared to larger particles.

To gain deeper insights into the relationship between relaxation time and switching rate for particles of different sizes, we calculated the structural relaxation time $({\tau }_{\alpha })$ and plotted it as a function of $k_s$ for different sizes of particles, as shown in Fig. 5h. The results revealed that as the switching rate increases, the relaxation time decreases for all particle sizes. To understand the impact of switching rates on fluidity, we calculated the difference in relaxation time between the presence and absence of switching (Table S1). These differences are more pronounced for larger particles compared to smaller ones, suggesting that the conversion between polysomes and ribosomes has a greater impact on the dynamics of larger particles, which exhibit glassy dynamics in the absence of switching.

High copy number and large molecular mass of ribosomes makes them effective disruptors

In the preceding section, we investigated the effects of switching dynamics on different particles with varying sizes. Now, we turn our attention to a different aspect: How does the size of the switching particle itself influence the degree of fluidization? To explore this question, we conducted a new series of simulations, manipulating the size of ribosomal subunits (30S and 50S) and polysome particles (70S). The modular structure of our computational model affords us the flexibility to design such “control” scenarios, allowing us to tune the size of the switching ribosomes.

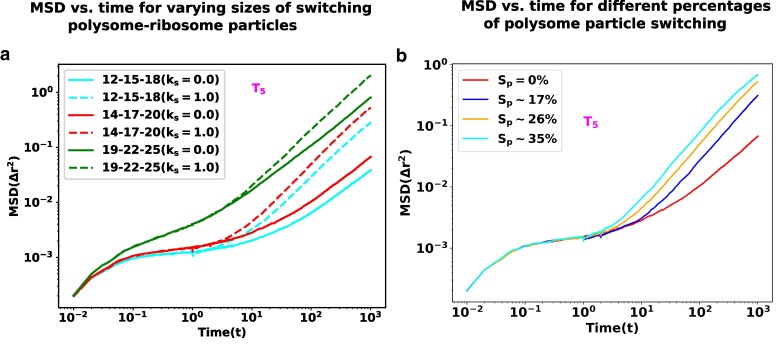
Essentially, we designed two types of control simulations. In the first setup, we altered the size of the ribosomal subunits and polysome particles to smaller dimensions (i.e. ${\sigma }_{30\mathrm{S}}=12$ nm, ${\sigma }_{50\mathrm{S}}=15$ nm, and ${\sigma }_{70\mathrm{S}}=18$ nm). In the second setup, we increased the size of the ribosomal subunits and polysome particles (i.e. ${\sigma }_{30\mathrm{S}}=19$ nm, ${\sigma }_{50\mathrm{S}}=22$ nm, and ${\sigma }_{70\mathrm{S}}=25$ nm). To maintain a consistent packing fraction in the cytoplasm, as per the original simulation settings, we added or removed additional protein particles ($P_1$-$P_5$). These systems are denoted as “12-15-18” and “19-22-25” based on the sizes of the 30S, 50S, and 70S particles. The original system is referred to as “14-17-20” according to the sizes used in the original system.

Figure 6a represents the MSDs of a the large tracer particle $T_5$ as a function of time, for different combinations of switching particles. For each combination, we have compared the MSD trends at a switching rate $k_s=1.0{\tau }_B^{-1}$ and with a switching rate $k_s=0.0{\tau }_B^{-1}$ (no switching). We note that increasing the size of ribosome-polysome particles results in a notable change in dynamics. Specifically, as the size of the ribosome-polysome particles increases, the tagged particles $(T_5)$ show enhanced diffusion. Remarkably, in the case of the larger ribosome-polysome system (“19-22-25”), the extent of the caging effect becomes less pronounced, leading to even higher diffusion compared to all other scenarios. In our simulation setup, the nonbonded interactions between all the particles are repulsive. Consequently, larger-sized particles experience stronger repulsive forces compared to their smaller counterparts. This result signifies the likely importance of the large size of ribosome particles in providing sufficient disruption to their local surroundings to cause fluidization.

Fig. 6.

The impact of switching particle sizes. a) MSD as a function of time is presented for polysome–ribosome systems of varying sizes, both with and without the presence of the switching effect. Notably, as the sizes of the switching particles increase, the tracer particles $T_5$ exhibit enhanced diffusion. b) MSD as a function of time for different percentages of polysome particle switching. As the percentage of switching $(S_p)$ increases the tracer particles $T_5$ show a systematic escalation in their mobility.

Finally, we delved into the role played by the density of the disruptor moiety, exemplified by the ribosome, in the disruption of glassy states. To analyze this, we manipulated the fraction $(S_p)$ of polysomes undergoing state transitions within a fixed switching rate $(k_s=1.0)$ and observed its impact on the Mean Squared Displacement (MSD) of the tracer particle $T_5$ (Fig. 6b). As anticipated, an increase in the fraction of switching particles led to a rapid escalation in the mobility of the tracer particle, concurrently diminishing the plateau associated with caging. In a metabolically active cell, a substantial number of ribosomes continuously transition between states, commencing or concluding rounds of translation. As one of the largest copy-number molecules housing an extensive molecular machinery within the cell, ribosomes disturb the local organization of crowders, facilitating mobility for other cellular machineries.

While the bacterial cytoplasm contains proteins with higher copy numbers, such as EFTu (35, 36), it is conceivable that EFTu molecules also undergo state transitions dependent on protein synthesis. This arises from their binding and unbinding interactions with translating ribosomes, potentially amplifying the effect of fluidizing the cytoplasm. The fraction or frequency of switching among translating ribosomes and their associated machinery is anticipated to be contingent on the cell’s metabolism, thereby presenting a mechanism for activity-dependent fluidization.

Concluding remarks

Put together, our model and experiments elucidates how glassy dynamics can emerge in the apparently moderately crowded bacterial cytoplasm and why it is size-dependent. We find that the spatial organization of the bacterial cytoplasm is a key factor in causing localized increase in crowding, which causes glassy dynamics. This organization is primarily orchestrated by the entropic segregation of ribosomes from the bacterial chromosomal DNA. This segregation likely plays a critical role in localizing activities to increase concentration and reduce search times, and leads to a size-dependent arrangement of cytoplasmic particles, a phenomenon stemming from the sieve-like structure of the compacted bacterial nucleoid. The resultant localized increase in packing density leads to extreme crowding in parts of the cytoplasm, which causes caging and glassy dynamics. Translation activities of ribosomes play a key role in this nucleoid-dependent spatial organization of the cytoplasm, as the state of ribosomes determine the extent of their mixing and resultant degree of compaction of the nucleoid (37). Intriguingly, the activity of the very same ribosomes serves as a dynamic force that disrupts the system, alleviating the confining effects. This activity-driven fluidization is of paramount importance for preserving the enzymatic functions of the cell.

In growing cells, protein translation stands as the most energy-consuming process, and the translation machinery ribosomes and the multitude of proteins associated with them undergo substantial changes in their dynamics when transitioning from an active translation state to a state of free diffusion. This frequent shift in the dynamic behavior of the translation-related proteins, which represent a significant portion of the bacterial proteome, disrupts their local surroundings sufficiently to loosen the constraints on the caged particles, ultimately promoting fluidity in their immediate vicinity. To experimentally test if protein translation could be the key energy-dependent process underlying the metabolic activity-dependent fluidization of bacterial cytoplasm, one needs to specifically perturb the translation process while keeping the packing fraction of the system unchanged. However, as shown in our current experiments, halting translation can significantly impact the spatial organization of the cytoplasm, by altering the compaction of the nucleoid and resultant size-dependent segregation of proteins. Therefore, the associated changes in local packing fraction from translation-halting drugs could affect the local dynamics, and thereby confound the analysis. Notably, a recent experimental study by Bellotto et al. (38) found that halting translation with chloramphenicol treatment leads to size-dependent reduction in diffusion constant of cytoplasmic particles, which is in strong concordance with the predictions from the current analysis.

In the field of active glass, activity is typically modeled by adding an active force to the equation of motion, and the particles behave like self-propelled particles (39, 40). The increase in activity leads to the fluidization of the system. However, bacteria lack traditional motor proteins that generate directed motion, meaning ATP-dependent biological activity cannot be modeled as a conventional self-propelled active force (41). Here, we have proposed a novel mechanism that relies on state-switching of the ribosomes during active protein translation and generates enough disturbance to fluidize the glassy cytoplasm. The mechanisms of switching-induced activity are analogous to the dynamics observed in epithelial tissues and tumor evolution, where cell division, death, and growth rates provide activity that inhibits glassy dynamics (42–44). Alternative models of metabolism-dependent fluidization has been proposed in recent literature. One such mechanism, proposed by Oyama et al. (41), involves conformational changes in proteins, where cytoplasmic protein particles alter their conformation by changing their radius of gyration. However, this study was conducted using an unrealistically high packing fraction $(pf\approx 0.94)$, and was restricted to two dimensions. Future studies should focus on analyzing relative importance of these alternative underlying mechanisms in realistic 3D environments. It is also conceivable that other metabolism-independent modes of fluidization exist in bacteria, and play important roles in different conditions of metabolic deprivation. Recent study by Shi et al. (45) found that sudden starvation did not lead to change in diffusivity of particles, in contrast to the observations by Zhu et al. (46), where cells were gradually starved. These results suggest that in metabolically inactive states, the cytoplasm can be kept fluidized by alternative mechanisms, that are possibly triggered by abrupt starvation. A systematic analysis that integrates the regulatory processes in the bacterial cells with their spatial organization will lead to further insights into the underlying causes of condition-dependent organization and mobilization of the cytoplasm.

Materials and methods

Model and method

The cytoplasm of E. coli is a highly complex environment and the exact constituents are still unknown. However, it consists of DNA, RNA, polysomes, ribosomes, and numerous poly-disperse proteins, etc. Here we have modeled the E. coli chromosome as a bead-spring polymer chain with each bead representing $5\times {10}^3$ basepair (5 kbp) and encodes Hi-C-derived contact probability matrix (19), as described in our previous works (47–52). In brief, the bonded interactions between adjacent beads have been modeled by harmonic springs with a spring constant $k_{\mathrm{spring}}=300k_{B}T/{\sigma }^2$, and the nonbonded interactions are modeled by the repulsive part of Lenard–Jones (LJ) potential i.e. $V_{nb}(r)=4ϵ(\sigma /r{)}^{12}$ with diameter and mass given by σ, and m, respectively (in real units $\sigma =67.31$ nm and $m=3245\mathrm{kDa}$). The Hi-C-derived inter-genomic contacts are modeled as harmonic springs with probability-dependent distance and distance-dependent force constants (see Supplementary material, method section). Unlike our previous model (47, 48), in our current study, we have incorporated polysome and ribosomes. Each 30S, 50S, and 70S ribosomal subunits have been modeled as spherical particles with different diameters $({\sigma }_{30\mathrm{S}}=14$ nm, ${\sigma }_{50\mathrm{S}}=17$ nm, and ${\sigma }_{70\mathrm{S}}=20$ nm) and each polysome is modeled by 13-mer of 70S ribosomal subunits which behave like a freely jointed chain. To investigate the spatial arrangement of DNA and ribosomal subunits, we conducted simulations within a spherocylindrical confinement that emulates the cell wall. In this simulation environment, all cytoplasmic particles interact through excluded volume interactions, and their behavior is described by the repulsive component of the LJ potential, with the exception of DNA and ribosomal subunits. Our observations indicate that a modest attractive interaction between DNA and ribosomal subunits is required to achieve a simulated linear density that closely approximates experimental data. This finding implies that cytoplasmic crowders exhibit some level of noninert behavior. Detailed values for the parameters $ϵ$ and σ for all particles can be found in the Supplementary material.

In a similar way, we have also introduced 2,000 copies of tracer particles $(T_1$ to $T_5)$ one at a time in ascending order of their diameter (10–50) nm. These tracer particles engage in interactions among themselves as well as with the other cytoplasmic components, characterized by excluded volume interactions governed by the repulsive component of the Lennard–Jones (LJ) potential. Similar to polysomes, large tracers also exhibit pronounced segregation from the nucleoid, with the extent of segregation dependent on their size.

The bacterial cytoplasm not only contains polysomes and ribosomes but there are also numerous other protein particles. To delve into the impact of molecular crowding on the length scale of the whole cell, the number of moieties will be huge. Thus, our focus is directed toward analyzing the dynamics of particles within the end-cap region, where a majority of polysomes and larger tracer particles reside. To initiate this study, we initially quantified the number of 30S, 50S, 70S, and $T_5$ particles within the end cap regions from our previous simulations. These particles were subsequently placed within a cubical box, its volume comparable to that of the cell’s end cap. Additionally, to achieve a desired packing fraction ($pf=0.57$), we introduced five distinct types of polydisperse protein particles ($P_1-P_5$) with sizes ranging from 13 to 18 nm. These protein particles also interact with each other and the rest of the cytoplasmic particles via the repulsive component of the LJ potential. In this context, a seminal simulation study by Kang et al. (53) demonstrated that the confinement-induced increase in packing fraction initiates the glass transition in eukaryotic chromosomes.

All the components of our model follow the Brownian dynamics and we performed the simulations in reduced units using open-source Software GROMACS 5.0.6 (54) with simulation time step $dt={10}^{-4}{\tau }_B$. We have modified the source code to introduce spherocylindrical confinement. Here all simulation length, time, and energy are in the unit of σ (the diameter of the DNA bead), ${\tau }_B$ and $k_{B}T$, respectively, and we have kept the $k_{B}T=0.55$. The mass, diameter, and the details modeling aspect of each component are given in (Table S2). We mapped the reduced unit of simulation to the physical units by taking the real value of the diameter of each DNA bead $(\sigma =67.31$ nm) (48), temperature $(T=303\mathrm{K})$, and viscosity of the cytoplasm $(\eta =17.5\mathrm{Pa}.\mathrm{s})$ (55, 56). In real physical unit, the value of ${\tau }_B$ becomes $\frac{3\pi \eta {\sigma }^3}{k_{B}T}\approx 12\mathrm{s}$. In our simulations, we selected 16 different initial configurations for the system. After thorough equilibration, each system was run for $\mathrm{1,000}{\tau }_B$ for production runs. All static quantities were averaged over all frames and across the 16 runs, while all dynamic quantities were averaged across the 16 runs.

Experiments and analysis

Ribosome distribution measurements were performed on strain MSG192, as described in our previous work (11). The effects of nucleoid compaction on Kaede and GFP were quantified using strains JCW11 and JCW1, respectively (21, 57). For imaging nucleoid morphology, SYTOX Orange was added to mid-log phase cultures (OD 0.2–0.4) at a final concentration of 500 nM from a 50 $\mu$M stock solution (58).

Cell cultures were grown in LB medium overnight with shaking in a ${37}^{\circ }$C water bath. Subcultures were prepared by diluting the overnight culture 1:100 into fresh LB. For SYTOX Orange staining, cells were incubated with the stain for 15 min, centrifuged twice to remove the stained media, and resuspended in fresh LB. Chloramphenicol treatments were conducted at 300 $\mu$g/mL (20 × MIC) using a 30 mg/mL stock solution.

E. coli cells were imaged using a Nikon Eclipse Ti inverted microscope equipped with an oil immersion objective (Nikon CFI Plan Apo Lambda, DM 100× Oil, 1.45 NA). Fluorescence and phase-contrast images were recorded alternately using a back-illuminated EMCCD camera (iXon DV-897, Andor Technology, Connecticut). A 488 nm Ar+ laser (Melles Griot, Carlsbad, CA, USA) was used to image GFP and unactivated Kaede, while a 514 nm Ar+ laser was used for ribosomal protein S2-YFP in MSG192. SYTOX Orange-stained DNA was imaged with a 561 nm laser (CrystaLaser, Reno, Nevada).

Image processing involved separating interleaved fluorescence and phase-contrast images. To analyze fluorescence images, we determined the cell orientation by fitting an ellipse to the binary mask from the phase-contrast image, using the principal axes of the ellipse as the cell’s coordinate system. Fluorescence images were projected along the x-axis (long axis) or y-axis (short axis) for analyzing nucleoid morphology and the spatial distribution of ribosomes, Kaede, and GFP inside the cell (11).

Dynamic quantities

Mean squared displacement

$$\mathrm{\Delta }{r}^2(t)=⟨\frac{1}{N}{\displaystyle \sum _{i=1}^N}{|{\overrightarrow{r}}_i(t)-{\overrightarrow{r}}_i(0)|}^2⟩$$ (1)

where $\overrightarrow{r}$ and N are the position of the particle and number of particles, respectively and $⟨..⟩$ represents the ensemble average.

Structural relaxation time $({\tau }_{\alpha })$

Generally, relaxation time is calculated from a two-point density–density autocorrelation function, defined as

$$C(t)=⟨\int \rho (\overrightarrow{r},0)\rho (\overrightarrow{r},t)d\overrightarrow{r}⟩,$$ (2)

where $\rho (\overrightarrow{r},t)$ is the density at position $\overrightarrow{r}$ at time t and $⟨\cdots ⟩$ is the ensemble average. But, here we have used a popular variant of $C(t)$, which is known as the overlap function and is defined as (59–61)

$$Q(t)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}w(|{\overrightarrow{r}}_i(t)-{\overrightarrow{r}}_i(0)|),$$ (3)

where w is the window function, $w(r)=1$ if $r<a_0$ and 0 otherwise, and $a_0$ is the cutoff distance at which the root mean squared displacement (RMSD) of the particles exhibits a plateau. In our study, we have chosen the $a_0=0.115\sigma$, to neglect small de-correlation because of the vibration of the particles in their respective cages. The structural relaxation time ${\tau }_{\alpha }$ is defined as $Q(t={\tau }_{\alpha })=1/e$.

Supplementary Material

Supplementary material is available at PNAS Nexus online.

Funding

We acknowledge the computation facilities provided by TIFR Centre for Interdisciplinary Sciences, India. We acknowledge the support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007 and Core Research grants provided by the Department of Science and Technology (DST) of India (CRG/2023/001426) to J.M. The work by S.B. was supported by the Wellcome Trust Award (grant number RG89305).

Author Contributions

Palash Bera (Data curation, Software, Formal Analysis, Validation, Methodology, Writing—original draft, Writing—review & editing), Abdul Wasim (Conceptualization, Formal Analysis, Validation, Writing—review & editing), Somenath Bakshi (Conceptualization, Formal Analysis, Supervision, Funding acquisition, Validation, Methodology, Writing–original draft, Writing—review & editing), Jagannath Mondal (Conceptualization, Resources, Supervision, Project administration, Writing—review & editing).

Preprints

This manuscript was posted on a preprint: https://www.biorxiv.org/content/10.1101/2024.01.16.575857v1.abstract.

Data Availability

All data are included in the manuscript and/or supporting information. The simulations were conducted using the open-source software GROMACS 5.0.6 (54). The corresponding scripts and input files are available on GitHub, accessible via the following: https://github.com/palash892/protein_translation_final