Abstract
Photoacoustic tomography, a novel non-invasive imaging modality, combines the principles of optical and acoustic imaging for use in biomedical applications. In scenarios where photoacoustic signal acquisition is insufficient due to sparse-view sampling, conventional direct reconstruction methods significantly degrade image resolution and generate numerous artifacts. To mitigate these constraints, a novel sinogram-domain priors guided extremely sparse-view reconstruction method for photoacoustic tomography boosted by enhanced diffusion model is proposed. The model learns prior information from the data distribution of sinograms under full-ring, 512-projections. In iterative reconstruction, the prior information serves as a constraint in least-squares optimization, facilitating convergence towards more plausible solutions. The performance of the method is evaluated using blood vessel simulation, phantoms, and in vivo experimental data. Subsequently, the transformation of the reconstructed sinograms into the image domain is achieved through the delay-and-sum method, enabling a thorough assessment of the proposed method. The results show that the proposed method demonstrates superior performance compared to the U-Net method, yielding images of markedly higher quality. Notably, for in vivo data under 32 projections, the sinogram structural similarity improved by ∼21 % over U-Net, and the image structural similarity increased by ∼51 % and ∼84 % compared to U-Net and delay-and-sum methods, respectively. The reconstruction in the sinogram domain for photoacoustic tomography enhances sparse-view imaging capabilities, potentially expanding the applications of photoacoustic tomography.
Keywords: Photoacoustic tomography, Non-invasive imaging techniques, Sparse-view, Reconstructions, Sinogram domains, Diffusion models
1. Introduction
Photoacoustic imaging is a novel non-invasive modality in biomedical imaging, combining the advantages of high contrast of optical imaging and high resolution of acoustic imaging in deep tissues [1], [2], [3], [4]. Photoacoustic tomography (PAT), a significant branch of photoacoustic imaging, demonstrates substantial clinical translational potential and promising prospects for widespread application. Nevertheless, current PAT imaging techniques and systems face several limitations, such as limited number of transducer array elements, restricted detection angles, and constrained bandwidth [5], [6], [7], [8]. These challenges lead to significant artifacts, low resolution, and limited imaging depth in photoacoustic images.
In PAT imaging, conventional reconstruction methods such as back-projection [9], [10], time reversal [11], [12], and delay-and-sum [13], [14] (DAS) tend to degrade image quality and imaging depth when the photoacoustic signal data acquisition is sparse. Model-based iterative methods [15], [16], [17], [18], [19] can mitigate these issues to some extent. Nevertheless, these methods are computationally expensive, time-consuming, and the reconstruction quality heavily depends on the selection of prior models and regularization methods. In recent years, deep learning has emerged as a preferred method in medical imaging, showing immense potential for efficiently reconstructing high-quality images [20], [21], [22], [23].
Currently, most deep learning-based PAT reconstruction methods function within the image domain. Davoudi et al. proposed a U-Net-based sparse-view reconstruction method that removes artifacts in photoacoustic images by training end-to-end from sparse-view to full-view images [6]. Guan et al. introduced a FD-Unet method for sparse reconstruction [24], which incorporates dense blocks into a standard U-Net architecture, significantly enhancing the feature extraction capabilities of the network and effectively eliminating artifacts. Another common type of reconstruction method is the direct reconstruction of sinograms into photoacoustic images. Feng et al. proposed an end-to-end Res-UNet method [25], which is trained on pairs of sinograms and their corresponding photoacoustic images, enabling direct reconstruction of photoacoustic images from sinograms. Guan et al. also developed a pixel-level deep learning (Pixel-DL) method for sparse-view reconstruction [26], employing sinogram pixel-level interpolation based on photoacoustic wave propagation physics as input for a deep learning network to directly output reconstructed images. However, there are few studies focused solely on sparse-view reconstruction in the sinogram domain. By implementing direct reconstruction in the sinogram domain, thus improving the results of inverse problems and inherently reducing distortions in image reconstruction methods [27], [28]. Awasthi et al. proposed an enhanced U-Net network that reconstructs super-resolution sinograms from degraded sinograms and use a linear back-projection method for the final PAT image reconstruction [28].
In recent years, the development of generative models [29], [30], [31], [32], [33], [34] has shown significant potential for generating high-quality data. During the parameter learning process, generative models acquire prior information that can be utilized for restore degraded images. Score-based generative models [34] have adopted more efficient sampling methods, further enhancing their generative capabilities. Score-based models learn the probability distribution of given samples, deriving probabilistic models to generate target images that fit the characteristics of the samples. Inspired by this, a novel sinogram domain sparse-view reconstruction method for photoacoustic tomography based on an enhanced score-based diffusion model was proposed. This method harnesses the capability of generative models to learn prior information, focusing on sparse reconstruction in the sinogram domain. During the training phase, an enhanced diffusion model is employed to learn the prior distribution of sinograms under full-ring 512 projections. During reconstruction, the prior information serves as a constraint in the least-squares optimization, facilitating the generation of missing data in sparse sinograms. Then, the reconstructed sinograms are transformed into the image domain using the DAS method. The contribution of this work is summarized as follows:
-
•
It is the first time a sinogram domain prior-guided method exploiting enhanced score-based diffusion model has been proposed. By implementing direct reconstruction in the sinogram domain, it improves the results of inverse problems and inherently reducing distortions in image-domain reconstruction methods.
-
•
The proposed enhanced diffusion model network is equipped with a parallel auxiliary network. It enables the network to learn prior information from both full-view and sparse-view sinograms, resulting in higher-quality reconstruction compared to the original diffusion model using only the backbone network.
-
•
The proposed method is compared with the state-of-the-art methods, demonstrating high reconstruction precision. Even under extremely sparse conditions with only 32 projections, the proposed method performs exceptionally well. Additionally, the proposed method also greatly improves structural similarity for in vivo experimental data.
2. Method
2.1. Photoacoustic tomography principle
In PAT imaging, pulse lasers are typically directed at the target tissue area, and ultrasound detectors capture the photoacoustic signals. By considering the relative positions of the transducers and the tissue, along with other imaging system parameters, the structural information of the tissue can be reconstructed, ultimately forming a photoacoustic image of the target tissue. The initial acoustic pressure at each sound source can be calculated using the corresponding formula, represented by Eq. (1):
| (1) |
where is the dimensionless Gruneisen parameter, representing the efficiency of converting optical energy into thermal energy, denotes the optical absorption coefficient, and represents the optical fluence. Centered at a point in the tissue excited by the laser, the mathematical model of the photoacoustic signal propagation equation at a distance from the point can be expressed by Eq. (2):
| (2) |
where is the heating function, is the speed of sound, is the specific heat capacity of the tissue, is the thermal expansion coefficient, and is the acoustic pressure at position and time . can be determined using the Green's function method, as shown in Eq. (3):
| (3) |
Eq. (3) delineates the propagation process of acoustic waves in PAT imaging. In real-world scenarios, sparse sampling is typically used to acquire photoacoustic signals (i.e., sinograms), as illustrated in Eq. (4):
| (4) |
where represents the photoacoustic signal detected by the transducer. denotes the photoacoustic signal under full view. is a binary extraction mask, where the value of each row represents the sampling strategy under the corresponding projection. A value of 0 indicates no sampling, while a value of 1 indicates sampling. The sparse sampling can be regarded as the process that is sampled to obtain via an extraction mask . In this paper, the sparse reconstruction process can be succinctly summarized as utilizing to restore the .
2.2. Enhanced score-based diffusion model
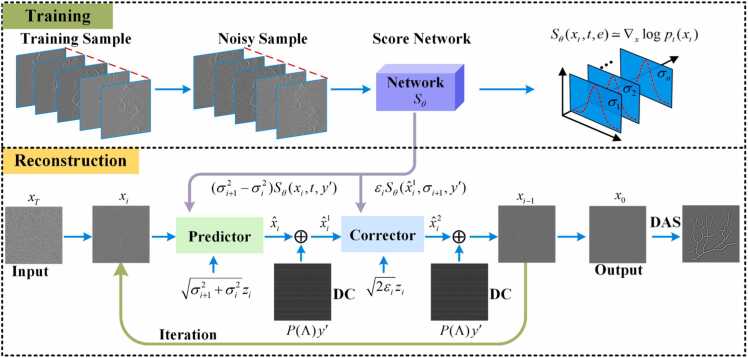
The score-based diffusion model treats the data within the training dataset as independent and identically distributed samples drawn from a common distribution . To estimate the parameters of the unknown data distribution , a neural network is employed to model its probability structure, yielding an estimated distribution with known parameters [34]. The distribution closely approximates , the distribution of the training data. Furthermore, the score-based diffusion model employs the score function , defined as the gradient of the log-probability density function, to characterize data distribution. This model reframes the task of estimating the data distribution as a process of training a neural network to approximate the score function of data distribution .
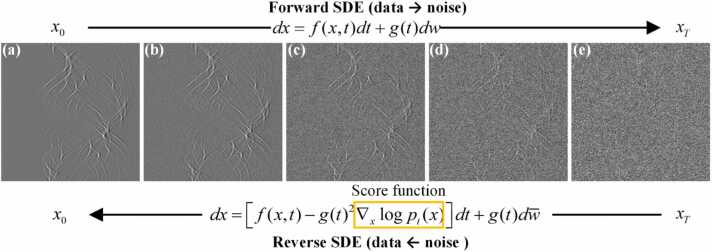
In score-based diffusion model, the diffusion process is modeled as a dynamic system influenced by random noise using stochastic differential equations (SDE). The diffusion model consists of a forward SDE process and a corresponding reverse SDE process, as depicted in Fig. 1. The forward process progressively injects Gaussian noise into the data distribution. This gradual process transforms the original data distribution through a series of intermediate distributions, ultimately converging to a simple, known prior distribution (typically a standard Gaussian). The reverse process, governed by the backward SDE, systematically removes the injected noise, thereby transforming the simple prior distribution through a sequence of intermediate distributions, ultimately approximating the original data distribution. The process effectively enables sampling from the learned data distribution.
Fig. 1.
(a)→(e) The forward diffusion process of the SDE. The forward process gradually adds Gaussian noise to the original sinogram. (e)→(a) The reverse diffusion process of the SDE. The reverse process is the inverse of the forward process, progressively reconstructing the original sinogram from a state filled with noise.
The model utilizes Brownian motion to describe the forward diffusion process, as represented by Eq. (5).
| (5) |
where represents the drift coefficient, represents the diffusion coefficient, denotes the Brownian motion, is the infinitesimal time step, and represents the increment of the data within . The forward SDE process aims to train a score network to obtain a known distribution approximating the data probability distribution without relying on specific structural interpretations. Noise-disturbed data distribution obtained from the forward process is used as training data to train the score network, which estimates the scores of the data distribution. These scores are then employed in solving the reverse SDE to generate data from noise. The reverse SDE process solves for samples, as show in Eq. (6):
| (6) |
where denotes the reverse Brownian motion. The specific structure of the SDE can be constructed by selecting different and . This work employs variance exploding (VE) SDEs to generate samples of superior quality, as depicted in Eq. (7).
| (7) |
where is a monotonically increasing noise scale function over time . During the training phase, the parameters of the score network are optimized according to Eq. (8):
| (8) |
The trained score network satisfies , also called denoising score matching. The input to the score network includes the noise-disturbed image , the time , and the prior information e containing information of . It can approximate the solution to Eq. (6) within a specified time , achieving image restoration corresponding to the noise scale , as depicted in Eq. (9).
| (9) |
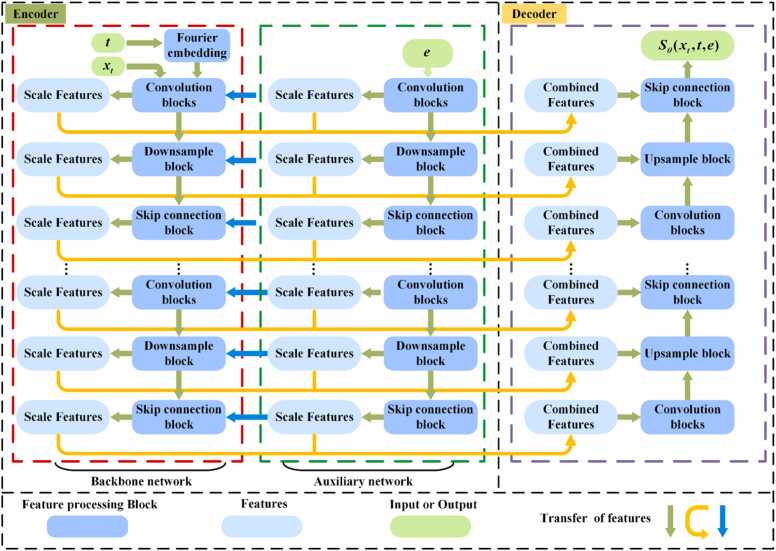
In this paper, the score-based diffusion model was enhanced by changing the original network, with introducing an independent prior e containing information of into the score network, thereby alleviating the issue of insufficient prior information for sparse reconstruction in PAT. Fig. 2 illustrates the structure of the enhanced score network.
Fig. 2.
The structure of the enhanced score network. The red dashed box encompasses the original encoder structure (backbone network). The green dashed box denotes the introduced auxiliary network within the encoder. The purple dashed box represents the decoder structure. t, the time step for the reverse SDE. , the noise-disturbed of full-view sinograms. e, the sparse-view sinograms prior after the nearest-neighbor interpolation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Based on the original score network structure, the enhanced score network introduces an auxiliary network that runs parallel to the original encoder (backbone network). The auxiliary network is designed to encode multi-scale features of . In the encoder section, encoded via Fourier embedding and intermediate image are input into the backbone network for multi-scale feature extraction. The inputs are processed through residual convolution blocks consisting of convolution layers, group normalization, dropout, and an activation function. Scale features extracted by the auxiliary network are concatenated with those from the backbone network at the combined layers, forming the input for the next layer, and are made available to the upsampling stage via skip connections. The parallel auxiliary network notably extracts global image structure information, supplying features for subsequent smaller-scale extraction in the backbone network. In the decoder section, the scale features extracted at various scales by both the backbone network and the auxiliary network in the encoder are fused and utilized for upsampling purposes. Between the encoder and decoder, a single-layer self-attention mechanism is applied to process the features, while all other feature extraction stages are handled by convolution layers. The final output of incorporates the prior information of , , and , therefore enhancing the accuracy of denoising score matching.
2.3. Sinogram domain sparse reconstruction of PAT based on diffusion model
In scenarios of extreme sparse-view sampling, the application of the original diffusion model to reconstruct sparse data frequently induces pixel-level distortions, consequently yielding ill-posed solutions in sinogram reconstruction. The phenomenon also occurs in analogous applications of diffusion models [35], [36], [37]. Inspired by the utilization of sketches to guide diffusion models in the generation of high-resolution images [38], the proposed method incorporates as the aforementioned prior input . is obtained through nearest-neighbor interpolation from the sparse sinogram . can be considered as a low-resolution sketch, offering prior information for the score network, and thereby enhancing the accuracy of denoising score matching. The optimization problem in sparse reconstruction can be formulated as Eq. (10):
| (10) |
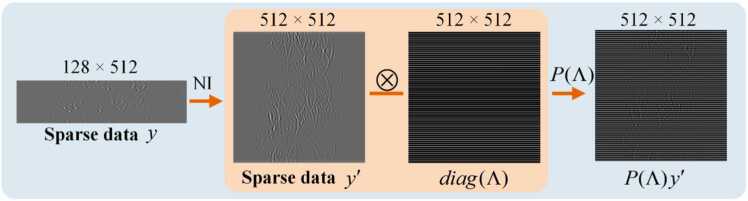
where is the data consistency (DC) term, ensuring that the generated data remains consistent with the original data in certain specific aspects. The nearest-neighbor interpolation (NI) is used to obtain a sparse sinogram of size 512×512 from a sparse sinogram . represents an extraction mask for the sinogram, transforming the sparse sinogram to , which is suitable for network processing, as detailed in Fig. 3. During the reconstruction stage, the intermediate results are processed by the operator to obtain the corresponding components with , thereby ensuring data consistency between and via the L2-norm. Due to sparse sampling, the ill-posedness of the optimization problem is exacerbated, increasing the non-uniqueness of the solution. Incorporating a high-quality prior as a regularization term can lead to faster and more accurate convergence in the problem-solving process. The regularization term is implemented through the enhanced score-based diffusion model, which allows the proposed method to overcome the ill-posedness of the optimization problem by learning high-quality prior.
Fig. 3.
The process of mask-based extraction from the sinogram. is the extraction operator. NI, nearest-neighbor interpolation.
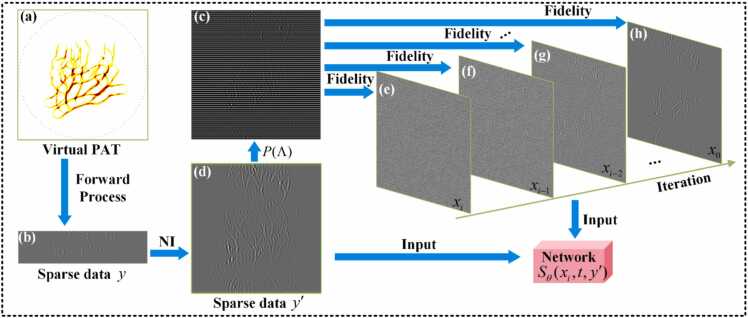
Fig. 4 illustrates the network input and replacement fidelity methods during the reconstruction phase. As shown in Figs. 4(a) and 4(b) the original sparse sinogram is obtained through the forward process by the k-Wave toolbox. The k-Wave toolbox is widely employed in PAT [39], [40]. In each iteration, elements of the network output are selectively replaced by corresponding elements from through replacement fidelity. The updated then serves as the input for the next iteration, as illustrated in Fig. 4(c). Fig. 4(d) displays , which is the result of applying nearest-neighbor interpolation to the sparse sinogram . Figs. 4(e)-4(h) show the results after the replacement operation. The final sparse reconstruction conforms to the prior distribution , thus achieving high-quality sparse reconstruction.
Fig. 4.
Schematic diagram of the fidelity input to the score network and the method of iteration replacement fidelity during the reconstruction phase. (a) The forward process in photoacoustic imaging simulated by the k-Wave toolbox. b) The original sparse data . (c) The result of mask sampling on through . (d)The sparse sinogram after nearest-neighbor interpolation. (e)-(h) The sinograms after the replacement fidelity. NI, nearest-neighbor interpolation.
The training process for sparse reconstruction in the sinogram domain is depicted in the upper part of Fig. 5. During training, replaces the unknown to realize the stepwise noise addition based on . is obtained by applying Gaussian perturbation centered at , where represents the gradient of the log-likelihood function of the current state with respect to . The score network is trained to estimate the gradient, achieving denoising score matching as described in Eq. (11).
| (11) |
Fig. 5.
Sparse reconstruction flowchart in the sinogram domain for PAT. Top: The training process for learning the gradient distribution of sinograms using denoising score matching. Noise is added to training samples to create disturbed inputs for the score network , which is trained to estimate the score using the time step t and the sparse-view sinogram prior e. Bottom: Sparse reconstruction using a numerical SDE solver. Pure noise is denoised by the Predictor and Corrector using the reverse SDE. Data consistency ensures fidelity. directs score estimation for sparse reconstruction. The final output is projected into the image domain. DC, data consistency.
The enhanced diffusion model achieves iterative reconstruction of sinograms through two pivotal steps: prediction and correction, as shown in the lower part of Fig. 5.
Predictor: Prediction is conducted based on Eq. (12) to generate the target sinogram from the learned prior distribution, followed by replacement fidelity to derive , as shown in Eq. (13):
| (12) |
| (13) |
where is the noise scale, is the number of iterations, and is Gaussian white noise with zero mean.
Corrector: The further improved sinogram is obtained using the Langevin Markov Chain Monte Carlo correction algorithm [41], as depicted in Eq. (14). Subsequently, replacement fidelity is applied to obtain , as shown in Eq. (15).
| (14) |
| (15) |
By employing prediction-correction sampling and replacement fidelity, iterative generation achieves high-quality sparse reconstruction. Algorithm 1 outlines the pseudocode for the training and reconstruction process. During the training stage, the network learns the prior distribution of the object sinogram dataset. In the reconstruction stage, the algorithm operates in two nested loops: (1) The outer loop utilizes the learned prior distribution to predict and applies replacement fidelity on sparse sinograms. (2) The inner loop employs the correction algorithm to further refine the sinograms and perform replacement fidelity again.
Algorithm 1
. Training for prior learning
 |
2.4. Dataset and network configuration
In this paper, the sparse reconstruction performance of the proposed method was validated using both simulated and experimental data. A virtual PAT system was simulated using the k-Wave toolbox, enabling the simulation of forward acoustic wave propagation for arbitrary projection angles [39]. The entire computational area is set to 50.1 mm × 50.1 mm, with a total grid of 506 × 506 pixels. And the reconstruction grid is set to 256 × 256 pixels. The ultrasound transducers are set with a central frequency of 2.25 MHz and a bandwidth of 70 %. They are positioned at a radial distance of 22 mm from the grid center. The sound velocity is set to 1500 m/s, and the surrounding medium is water with a density of 1000 kg/m³.
The simulation dataset from the public retinal vessel datasets RAVIR and DRIVE [42]. Following data augmentation operations such as rotation and cropping, a total of 1688 images were obtained. These images were split into training and test sets in an 8:1 ratio, with 1500 images allocated for training and 168 images for testing. The experimental datasets consist of public circular phantom and in vivo mouse datasets [6], both acquired under full-ring 512 projections. After augmentation, the circular phantom dataset comprises 1600 images, with 1422 images used for training and 178 images for testing. The in vivo mouse dataset contains 800 images, with 711 images for training and 89 for testing. During experimentation, the training sets were imported into the virtual PAT to generate sinograms under full-ring 512 projections. The test sets were processed using the virtual PAT to obtain sinograms under varying projections (32, 64, 128 and 512 projections). Sinograms acquired under 32, 64, and 128 projections were utilized as sparse data for reconstruction purposes, while sinograms obtained under 512 projections served as the ground truth (GT).
The training process utilized the Adaptive Moment Estimation (Adam) optimization method with a learning rate set to 2×10–4. For the iterative reconstruction phase, the number of noise scale (number of iterations) was set to 2000, with images sized at 512×512 pixels. Gaussian noise perturbation was introduced with noise values ranging from 0.6 to 300, which indicate the range of Gaussian noise perturbations. The number of noise scale corresponds to the number of levels into which the noise is categorized. Noise scales are equivalent to the number of iterations in reconstruction phase. The noise scale determines the granularity of noise values divisions and influences the accuracy of score estimation for denoising, which transitions from the noise distribution to the training data distribution. The learning rate controls the magnitude of parameter updates in each iteration. The model was developed using the PyTorch framework, predominantly within a Python environment. All computations were executed on a GeForce RTX 3060Ti GPU equipped with 8 GB of memory and an Intel Core (TM) i7-12700.
2.5. Baseline methods
In this paper, the proposed method was rigorously compared against the Cycle-GAN [43], Attention-based U-Net (At-Unet) [44], diffusion model (DM, using only the backbone network), U-Net [28], iterative model-based [17] methods to highlight its superior performance. GANs are a powerful class of generative models that learn the distribution of data through the continuous adversarial process and optimization between the generator and the discriminator, enabling the generation of high-quality data. Lu et al. employed a Cycle-GAN-based method, called PA-GAN [45], for PAT sparse reconstruction in image domain. In the following, Cycle-GAN will be used to evaluate its reconstruction performance in sinogram domain. Wang et al. proposed an Attention-based U-Net [44], which integrates local-global self-attention and external attention mechanisms by introducing a hybrid Transformer module. The network architecture effectively captures long-range dependencies between data samples, demonstrating strong performance in medical image processing tasks, which will be used to evaluate its reconstruction performance in sinogram domain as one of baseline methods. In addition, the reconstruction performance of the original diffusion model using only the backbone network will also be discussed to validate the advantages of introducing a parallel auxiliary network. In previous work [17], an advanced image domain sparse reconstruction method combining model-based iteration and diffusion model was proposed, wherein the prior learned by the diffusion model serves as the regularization term. The performance of the proposed method in the image domain will be compared with that of the model-based method (model-based DM). U-Net is widely recognized for its effectiveness in image segmentation tasks. Awasthi et al. enhanced the U-Net architecture by substituting Relu activation functions with Elu to better accommodate the bipolar characteristics in sinogram data [28]. The model-based DM method is trained in image domain, while the other methods are trained in sinogram domain. The datasets used for the baseline methods are identical. During the training phase, the sparse sinograms size of P×512 (with P being 32, 64, or 128) pixels are resized to 512×512 pixels using the nearest-neighbor interpolation. These resized sinograms serve as inputs to the network, while corresponding sinograms captured under 512 projections act as the target images. In the reconstruction stage, sparse sinograms, after undergoing nearest-neighbor interpolation, are input into the network to generate reconstructed sinograms.
3. Outcomes
3.1. Results of simulation blood vessels
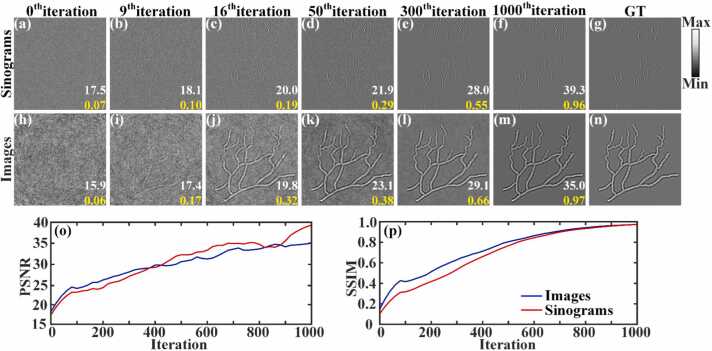
In the reconstruction stage, the reconstruction iterating starts from a pure noise image, and the simulated sparse sinograms are input into the network as the data fidelity term. Fig. 6(a)-6(f) show the iterative reconstruction of the sinograms under 64 projections, processing from 0 to 1000 iterations. The white numbers at the bottom of the figures are the peak signal-to-noise ratio (PSNR) values, and the yellow numbers are the structural similarity (SSIM) values. Figs. 6(h)-6(m) showcase the corresponding blood vessel images reconstructed by the DAS method. Figs. 6(g) and 6(n) is the GTs of the sinograms and the blood vessel images, respectively. By the 9th iteration, the outlines of both the sinograms and vessels begin to emerge from the noise. As the iterations progress from the 16th to the 300th, the noise gradually decreases, leading to clearer outlines of the sinograms and vessels. Furthermore, the curves of PSNR and SSIM steadily rise with the number of iterations, as depicted in Figs. 6(o) and 6(p). At the 1000th iteration, the noise is nearly eliminated, and the reconstructions of both sinograms and vessels stabilize. The PSNR and SSIM values for the sinograms at this stage are 39.3 dB and 0.96, respectively. The vessel images achieve PSNR and SSIM values of 35.0 dB and 0.97, respectively. This iterative process demonstrates significant improvement in image quality and fidelity as the reconstruction algorithm refines its output through successive iterations.
Fig. 6.
The iterative reconstruction process for simulated blood vessels under 64 projections. (a)-(f) The iterative reconstruction process of the sinograms from the 0th to the 1000th iterations. (h)-(m) The corresponding blood vessel images were reconstructed from the sinograms using the DAS method. (g) and (n) The GT for the sinograms and blood vessel images, respectively. (o) and (p) The PSNR and SSIM iteration carves, respectively.
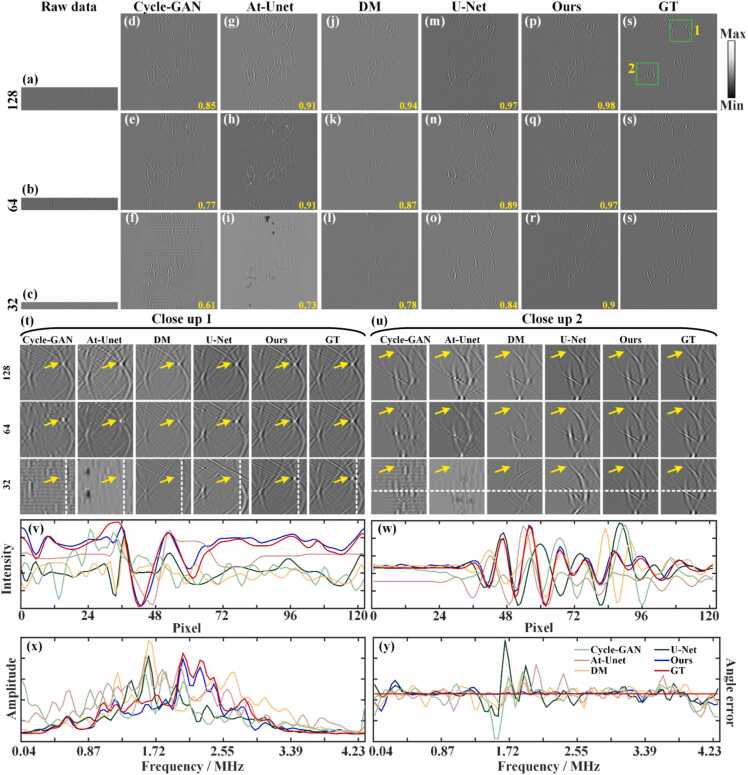
Fig. 7 shows the comparison of reconstruction results from different sparse projection sinograms using the Cycle-GAN, At-Unet, DM, U-Net and the proposed methods. Figs. 7(a)-7(c) show the sinograms (raw data) under 128, 64, and 32 projections, respectively. Figs. 7(d)-7(r) show the reconstruction results using the baseline methods and the proposed method, respectively. The SSIM values are annotated in yellow at the bottom. Fig. 7(s) show corresponding GT sinogram. As the number of projections decreases, the results of the Cycle-GAN method are the worst, and the results of At-Unet have serious signal distortion. The DM and U-Net methods have shown some improved, but under relatively sparse projections of 64 and 32, the sinograms have a certain degree of distortion. In contrary, the proposed method demonstrates robust performance across varying projections. Notably, even under extremely sparse 32 projections, the proposed method maintains accurate sinogram structures. Figs. 7(t) and 7(u) show the close-up images indicated by green boxes 1 and 2 in Fig. 7(s), highlighting more precise details reconstructed by the proposed method (indicated by the yellow arrows) compared to the baseline methods. Figs. 7(v) and 7(w) present the signal intensity distributions along white dashed lines in close-ups 1 and 2 under 32 projections. The signal distribution from the proposed method closely aligns with the GT, underscoring its effectiveness under sparse conditions. Spectra and phase residuals of the signals along the white dashed lines in close-up 2 are shown in Figs. 7(x) and 7(y), respectively. It can be observed that the frequency composition of the proposed method is closest to that of the GT, and it exhibits the smallest phase deviation. Quantitative analysis further supports the superiority of the proposed method. Under the 128 projections, the SSIM of the proposed method reaches 0.98, which is comparable to the U-Net method and significantly higher than other methods. Under 64 projections, the proposed method achieves a SSIM of 0.97, surpassing the U-Net, DM, At-Unet and Cycle-GAN methods by 0.08, 0.1, 0.06, and 0.2, respectively. It indicates the advantages of the proposed method in sparse reconstruction. When the number of projections is further reduced to 32, the SSIM of the proposed method achieves 0.90, which is 0.06, 0.12, 0.17 and 0.29 higher than the U-Net, DM, At-Unet and Cycle-GAN methods, respectively. It underscores the superior reconstruction performance of the proposed method even under highly sparse projection conditions.
Fig. 7.
Reconstruction results of sinograms of simulation blood vessels using different methods under different projections. (a)-(c) Sparse sinograms (raw data) under 128, 64, and 32 projections, respectively. (d)-(f) Reconstructed sinograms using the Cycle-GAN method. (g)-(i) Reconstructed sinograms using the Attention-based U-Net method. (j)-(l) Reconstructed sinograms using the diffusion model method. (m)-(o) Reconstructed sinograms using the U-Net method. (p)-(r) Reconstructed sinograms using the proposed method. (s) Ground truth sinogram for reference. The yellow numbers at the bottom of each figure are the SSIM values. (t) and (u) The close-up images indicated by the green boxes 1 and 2 in (s), respectively. Yellow arrows highlight differences in reconstructed details between methods. (v) and (w) Signal intensity distributions along the white dashed lines in close-ups 1 and 2 under 32 projections, respectively. (x) and (y) Spectra and phase residuals of the signals along the white dashed lines in close-ups 2, respectively.
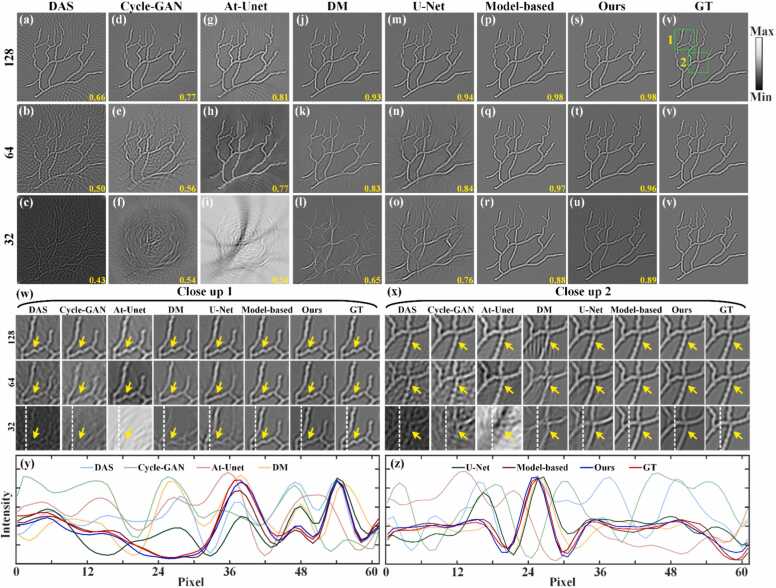
To further evaluate the results, the sinograms in Fig. 7 were processed into the image domain using the DAS method, as shown in Fig. 8. It is worth noting that the model-based DM method is also included in the comparison to evaluate the performance of the proposed method and the image-domain method. Figs. 8(a)-8(c) show the reconstruction results using only the DAS method under 128, 64, and 32 projections, respectively. It is obvious that there are serious artifacts under different sparse projections. The SSIM values denoted in yellow at the bottom of each figure. Figs. 8(d)-8(u) show the reconstruction results of the baseline methods and the proposed method, respectively. Fig. 8(v) depict the GT image for reference. Obviously, compared with the DAS method, the Cycle-GAN and At-Unet methods only remove a small amount of artifacts, and the images are even worse under 32 projections. The DM and U-Net methods have achieved substantial improvement in reconstruction. However, artifacts are still visible, particularly around blood vessels. It is worth noting that both the model-based DM method and the proposed method exhibit exceptional performance across different projections. Even under the highly sparse condition of 32 projections, artifacts are significantly reduced and the structures of blood vessels remain clearly discernible. Additionally, Figs. 8(w) and 8(x) show the close-up images indicated by the green boxes 1 and 2 in Fig. 8(v). Compared to the DAS, Cycle-GAN, At-Unet, DM and U-Net methods, both the model-based DM method and the proposed method demonstrate significantly reduced artifacts, complete vessel structures, and richer detail information, as indicated by the yellow arrows. Figs. 8(y) and 8(z) show the signal intensity distributions along the white dashed lines in close-ups 1 and 2 under 32 projections. It is evident that the signal distribution of both the model-based DM method and the proposed method closely aligns with the GT, outperforming the other methods. Quantitative analysis further confirms the above phenomenon. Under 128 projections, the SSIM of both the model-based DM method and the proposed method reach 0.98, which is 0.04, 0.05, 0.17, 0.21 and 0.32 higher than that of the U-Net, DM, At-Unet, Cycle-GAN and DAS methods, respectively. Under the 64 projections, the SSIM of the proposed method reaches 0.96, which is comparable to the model-based DM method and is 0.12, 0.13, 0.19, 0.4 and 0.46 higher than the U-Net, DM, At-Unet, Cycle-GAN and DAS methods, respectively. Even under the extremely sparse condition of 32 projections, the SSIM value of the proposed method is comparable to that of the model-based DM method and far exceeds other methods. These metrics underscore the superior reconstruction capabilities of the proposed method in the image domain, particularly under extremely sparse projection conditions. Moreover, the proposed method, by directly reconstructing in sinogram domain, not only greatly reduces the computational complexity but also shows performance as good as that of state-of-the-art methods in the image domain.
Fig. 8.
Reconstruction results of simulated blood vessels images using different methods under different projections. (a)-(c) The reconstruction results of the DAS method under 128, 64, and 32 projections, respectively. (d)-(f) Reconstruction results using the Cycle-GAN method. (g)-(i) Reconstruction results using the Attention-based U-Net method. (j)-(l) Reconstruction results using the diffusion model method. (m)-(o) Reconstruction results using the U-Net method. (p)-(r) Reconstruction results using the model-based DM method. (s)-(u) Reconstruction results using the proposed method. (v) Ground truth image for reference. The yellow numbers at the bottom of each figure indicate the SSIM values. (w) and (x) The close-up images indicated by the green boxes 1 and 2 in (v), respectively. Yellow arrows highlight differences in reconstructed details among the methods. (y) and (z) Signal intensity distributions along the white dashed lines in close-ups 1 and 2 under 32 projections, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
To strengthen the claims, additional tests were conducted on six simulated blood vessels images. The sinogram-domain and image-domain reconstruction results for two of the test images are shown in Fig. 9, Fig. 10, respectively. The reconstruction performance on the additional test images is consistent with the results and analysis presented above. The proposed method demonstrates an overwhelming advantage in sinogram domain compared to other methods. Moreover, despite having lower computational complexity than the model-based DM method, the proposed method exhibits comparably outstanding performance.
Fig. 9.
Reconstruction results of sinograms of two additional simulated blood vessels using different methods under different projections.
Fig. 10.
Reconstruction results of two additional simulated blood vessels images using different methods under different projections.
A cross-correlation (CC) [46], [47] image evaluation metric has been introduced to quantify the degree of correlation between the reconstructed images and the GT image. By calculating the sum of the products of corresponding elements as one matrix slides over another, a new cross-correlation matrix is obtained. The normalized maximum value of the cross-correlation matrix serves as the quantitative measure of correlation., while 0 indicates no correlation, and 1 indicates perfect correlation. The averages of SSIM and CC values for the reconstruction results of the seven simulated blood vessels images in both the sinogram domain and image domain using different methods are presented in Table 1, Table 2, respectively. Side-by-side comparisons highlight the excellent performance and robustness of the proposed method.
Table 1.
The average SSIM and CC values for the reconstruction results of the simulated vascular sinograms.
| Number of projections | 32 |
64 |
128 |
|||
|---|---|---|---|---|---|---|
| Method/Metric | SSIM | CC | SSIM | CC | SSIM | CC |
| Cycle-GAN | 0.7584 | 0.2294 | 0.8090 | 0.4124 | 0.8803 | 0.6205 |
| At-Unet | 0.7591 | 0.2613 | 0.8078 | 0.4472 | 0.9315 | 0.6723 |
| DM | 0.7790 | 0.2911 | 0.9169 | 0.6153 | 0.9574 | 0.7029 |
| U-Net | 0.8829 | 0.5606 | 0.9198 | 0.6503 | 0.9792 | 0.8223 |
| Ours | 0.9435 | 0.7127 | 0.9796 | 0.7777 | 0.9897 | 0.7895 |
Table 2.
The average SSIM and CC values for the reconstruction results of the simulated vascular images.
| Number of projections | 32 |
64 |
128 |
|||
|---|---|---|---|---|---|---|
| Method/Metric | SSIM | CC | SSIM | CC | SSIM | CC |
| DAS | 0.4388 | 0.4431 | 0.5242 | 0.6033 | 0.6599 | 0.7843 |
| Cycle-GAN | 0.5219 | 0.1148 | 0.5929 | 0.2627 | 0.7137 | 0.5652 |
| At-Unet | 0.6079 | 0.0742 | 0.6780 | 0.4359 | 0.8122 | 0.8064 |
| DM | 0.6776 | 0.4451 | 0.8917 | 0.8229 | 0.9559 | 0.9014 |
| U-Net | 0.8175 | 0.6794 | 0.8786 | 0.8233 | 0.9617 | 0.9294 |
| Model-based DM | 0.9308 | 0.8943 | 0.9714 | 0.9115 | 0.9801 | 0.9233 |
| Ours | 0.9467 | 0.8876 | 0.9809 | 0.9443 | 0.9887 | 0.9563 |
3.2. Results of experimental phantoms
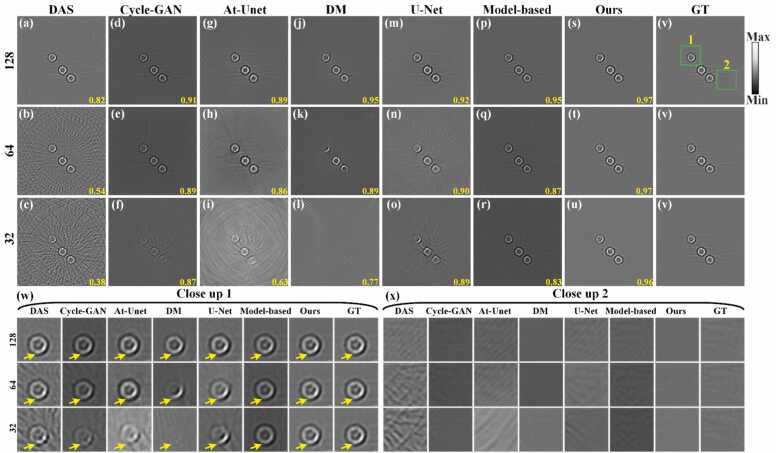
To validate the effectiveness of the proposed method on experimental data, Fig. 11 presents a comparative of reconstruction performance achieved using the different method on circular phantom experimental data under varying projections. Figs. 11(a)-11(c) show the sparse sinograms under 128, 64, and 32 projections, respectively. Figs. 11(d)-11(r) show the reconstruction results using the Cycle-GAN, At-Unet, DM, U-Net and the proposed methods, respectively. The SSIM values provided at the bottom of each figure. The baseline methods show good reconstruction capability under 128 projections but exhibits limitations as the number of projections decreases. The proposed method effectively reconstructs signals from missing projections across different sparse conditions and maintains high-quality reconstruction even under extremely sparse 32 projections. Fig. 11(s) present the GT sinogram for reference. Figs. 11(t) and 11(u) show the close-up images indicated by the green boxes 1 and 2 in Fig. 11(s). Compared to the baseline methods, the proposed method accurately reconstructs missing projection signals and preserves detailed information in the sinograms (highlighted by yellow arrows). Quantitative analysis confirms the superiority of the proposed method. Under 128, 64, and 32 projections, the SSIM values for the proposed method are 0.94, 0.94, and 0.93, respectively. With the extremely sparse condition of 32 projections, it represents improvements of 0.14, 0.29, 0.22 and 0.08 over the Cycle-GAN, At-Unet, DM, and U-Net methods, respectively. It substantiates that the proposed method outperforms these mainstreaming methods in reconstructing circular phantom sinograms, particularly under conditions of extremely sparse views.
Fig. 11.
Reconstruction results of sinograms of circular phantom using different methods under different projections. (a)-(c) Original sinograms (raw data) under 128, 64, and 32 projections, respectively. (d)-(f) Reconstructed sinograms using the Cycle-GAN method. (g)-(i) Reconstructed sinograms using the Attention-based U-Net method. (j)-(l) Reconstructed sinograms using the diffusion model method. (m)-(o) Reconstructed sinograms using the U-Net method. (p)-(r) Reconstructed sinograms using the proposed method. (s) Ground truth sinogram for reference. Yellow numbers at the bottom of each figure are the SSIM values. (t) and (u) The close-up images indicated by the green boxes 1 and 2 in (s), respectively. Yellow arrows highlight differences in reconstructed details between methods. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The reconstruction results of circular phantom in the image domain are shown in Fig. 12. Fig. 12(a)-12(c) depict the reconstruction results using only the DAS method under 128, 64, and 32 projections, respectively, noted with SSIM values in yellow at the bottom. As projections decreases, blurring of circular phantoms worsens, accompanied by increased artifacts. Figs. 12(d)-12(u) display the results of baseline methods and the proposed method, respectively. It is obvious that almost all methods can effectively reduce artefacts under 128 projections. However, under sparser projections, the results of Cycle-GAN, At-Unet, U-Net, and the model-based DM method still retain a relatively large number of artefacts. Moreover, the reconstruction results of the DM method exhibit severe distortion. In contrast, the proposed method not only significantly removes the artefacts, but also exhibits very high image reconstruction quality under different degrees of sparse views. Fig. 12(v) is the GT image. Close-ups (green boxes 1 and 2 in Fig. 12(v)) in Figs. 12(w) and 12(x) highlight the proposed method's ability to preserve structure and detail while effectively eliminating artifacts. Quantitative analysis validates its superiority. Under 128 projections, the proposed method achieves SSIM of 0.97, surpassing DAS, Cycle-GAN, At-Unet, DM, U-Net and model-based DM methods by 0.15, 0.06, 0.08, 0.02, 0.05 and 0.02, respectively. Under 64 projections, SSIM of the proposed method remains 0.97, outperforming the baseline methods by 0.43, 0.08, 0.11, 0.07, 0.1, respectively. Under 32 projections, the SSIM still reaches 0.96, which is far superior to that of the other methods. The reconstruction results of the circular phantom further demonstrate the efficacy of the proposed method under different projections.
Fig. 12.
Reconstruction results of circular phantom images using different methods under different projections. (a)-(c) The reconstruction results of the DAS method under 128, 64, and 32 projections, respectively. (d)-(f) Reconstruction results using the Cycle-GAN method. (g)-(i) Reconstruction results using the Attention-based U-Net method. (j)-(l) Reconstruction results using the diffusion model method. (m)-(o) Reconstruction results using the U-Net method. (p)-(r) Reconstruction results using the model-based DM method. (s)-(u) Reconstruction results using the proposed method. (v) Ground truth image for reference. The yellow numbers at the bottom of each figure indicate the SSIM values. (w) and (x) The close-up images indicated by the green boxes 1 and 2 in (v), respectively. Yellow arrows highlight differences in reconstructed details among the methods. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.3. Results of experimental in vivo mouse
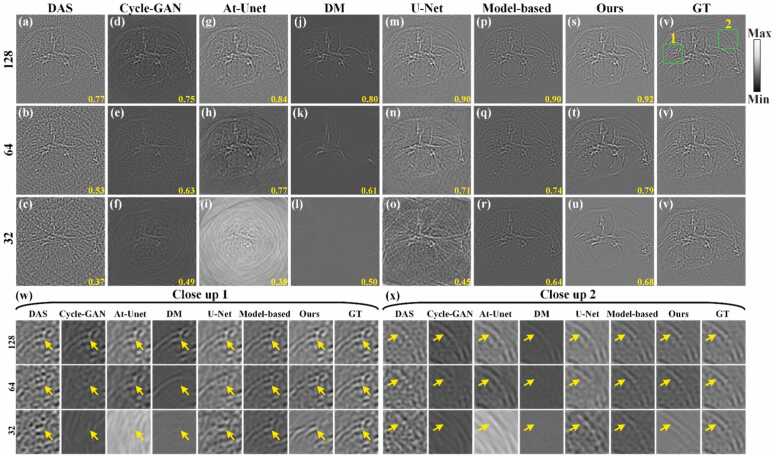
To further validate the effectiveness of the proposed method on in vivo data, experimental data from in vivo mouse abdomen with more complex structures were utilized for reconstruction, as shown in Fig. 13. Figs. 13(a)-13(c) show sinograms under 128, 64, and 32 projections, respectively. Figs. 13(d)-13(r) show the reconstruction results using the baseline methods, with SSIM values indicated at the bottom of each figure. With the decreases of the projections, the quality of the reconstructed sinograms using the baseline methods notably deteriorates. Figs. 13(p)-13(r) show the reconstruction results using the proposed method. Under 128 projections, the proposed method reconstructs missing projection signals with high fidelity. However, under sparser projections (e.g., the 64 and 32 projections), some structural details are lost in the sinograms. Fig. 13(s) show the GT sinogram for reference. Close-up images from green boxes 1 and 2 in Fig. 13(s) are shown in Figs. 13(t) and 13(u), respectively. The proposed method reconstructs more detailed reconstruction than the baseline methods, as indicated by yellow arrows in Figs. 13(t) and 13(u). Additionally, the proposed method achieves higher SSIM values compared to the baseline methods. Specifically, under 64 projections, the SSIM of the proposed method reaches 0.82, showing an improvement of 0.11, 0.03, 0.12 and 0.08 by the Cycle-GAN, At-Unet, DM, and U-Net methods, respectively. Under the sparser 32 projections, the SSIM of the proposed method is 0.74, indicating an enhancement of 0.22, 0.19, 0.17 and 0.13 over these methods, respectively. These results underscore the capability of the proposed method to achieve robust reconstruction of complex experimental data, even under highly sparse projection conditions.
Fig. 13.
Reconstruction results of sinograms of in vivo mouse abdomen using different methods under different projections. (a)-(c) Original sinograms (raw data) under 128, 64, and 32 projections, respectively. (d)-(f) Reconstructed sinograms using the Cycle-GAN method. (g)-(i) Reconstructed sinograms using the At-Unet method. (j)-(l) Reconstructed sinograms using the DM method. (m)-(o) Reconstructed sinograms using the U-Net method. (p)-(r) Reconstructed sinograms using the proposed method. (s) Ground truth sinogram for reference. Yellow numbers at the bottom of each figure are the SSIM values. (t) and (u) The close-up images indicated by the green boxes 1 and 2 in (s), respectively. Yellow arrows highlight differences in reconstructed details between methods. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The reconstruction results of in vivo mouse abdomen in the image domain are shown in Fig. 14. Figs. 14(a)-14(c) show the reconstruction results using only the DAS method under 128, 64, and 32 projections, respectively, with SSIM values indicated at the bottom in yellow. The artifacts are aggravated as the number of projections decreases, making it challenging to discern the mouse abdomen's outline under 64 and 32 projections. Figs. 14(d)-14(r) show the reconstruction results of the baseline methods under 128, 64, and 32 projections, respectively. Under the 64 and 32 projections, serious artifacts overwhelm image details, resulting in poor quality. Figs. 14(s)-14(u) show the reconstruction results using the proposed method. The proposed method effectively mitigates artifacts, allowing more structure and detail in the image to be observed even under 32 projections. Fig. 14(v) corresponds to the GT image. Additionally, Figs. 14(w) and 14(x) show the close-up images indicated by the green boxes 1 and 2 in Fig. 14(v). Comparative analysis reveals significant advantages of the proposed method in artifact reduction compared to the baseline method, as highlighted by yellow arrows in Figs. 14(w) and 14(x). Quantitative evaluations further corroborate these findings. Under the 128 projections, the SSIM of the proposed method reaches 0.92, representing improvements of 0.15, 0.17, 0.08, 0.12, 0.02 and 0.02 over the DAS, Cycle-GAN, At-Unet, DM, U-Net and model-based DM methods, respectively. Under the 64 projections, the proposed method achieves a SSIM of 0.79, surpassing the other methods by 0.26, 0.16, 0.02, 0.18, 0.08 and 0.05, respectively. Even with a further reduction to 32 projections, the proposed method maintains a competitive SSIM of 0.68, outperforming the baseline methods by 0.31, 0.19, 0.3, 0.18, 0.23 and 0.04, respectively. These results underscore the excellent sparse reconstruction performance of the proposed method, particularly evident in complex small animal data.
Fig. 14.
Reconstruction results of in vivo mouse abdomen images using different methods under different projections. (a)-(c) The reconstruction results of the DAS method under 128, 64, and 32 projections, respectively. (d)-(f) Reconstruction results using the Cycle-GAN method. (g)-(i) Reconstruction results using the Attention-based U-Net method. (j)-(l) Reconstruction results using the diffusion model method. (m)-(o) Reconstruction results using the U-Net method. (p)-(r) Reconstruction results using the model-based DM method. (s)-(u) Reconstruction results using the proposed method. (v) Ground truth image for reference. The yellow numbers at the bottom of each figure indicate the SSIM values. (w) and (x) The close-up images indicated by the green boxes 1 and 2 in (v), respectively. Yellow arrows highlight differences in reconstructed details among the methods. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Conclusion and discussion
In summary, to address the challenge of low-quality PAT image reconstruction from sparse views using conventional methods, this paper introduces a sinogram domain sparse-view reconstruction method based on an enhanced score-based diffusion model. The proposed method utilizes an enhanced diffusion model trained through denoising score matching to capture prior information from sinograms acquired under 512 projections. In the iterative reconstruction process, the Predictor-Corrector (PC) operation incorporates noise reduction and generates intermediate images as the iteration progresses. Each intermediate image undergoes a fidelity replacement step, ensuring consistency with the sparse data and refining the reconstruction while preserving data fidelity. After the fidelity enforcement, both the updated intermediate images and the nearest-neighbor interpolation derived solely from the sparse data function as essential inputs for the subsequent iteration of the diffusion model's score network. The integrated method leverages the learned sinograms prior distribution, enabling the model to progressively sample from its prior knowledge, guided by the sparse data fidelity and interpolations, to achieve a sparse reconstruction that accurately captures the underlying image structure associated with a specific sinograms. Subsequently, the reconstructed sinograms are transformed into the image domain using the DAS method to assess reconstruction performance. The proposed method effectively separates the reconstruction tasks between the sinogram and image domains in PAT.
Reconstruction experiments using simulated and experimental data validate the strong artifact removal capability of the proposed method. Quantitative analysis demonstrates its superior performance. In in vivo experiments, the proposed method performs comparably to U-Net under 128 projections. Under 64 projections, it achieves SSIM values of 0.82 for sinograms and 0.79 for images, which are both 0.08 higher than U-Net. With even sparser 32 projections, SSIM values of 0.74 for sinograms and 0.68 for images show improvements of 0.13 and 0.23, respectively, compared to U-Net. Moreover, compared to the conventional DAS method, the proposed method enhances SSIM by 0.26 (∼ 49 %) and 0.31 (∼ 84 %) for images reconstructed under 64 and 32 projections, respectively. These results underscore the proposed method's ability to deliver high-quality reconstructions of experimental data, even under extremely sparse conditions.
Diffusion models estimate an unknown score function by training a score-based network. During training, Gaussian noise is added to the datasets to effectively learn the underlying data distribution, making it a time-consuming process. The duration of training primarily hinges on the size and quantity of training datasets employed, as well as the graphics processor configuration. In the experiment, one checkpoint is saved after every 20,000 epochs, which takes ∼ 60 minutes. A total of 20 checkpoints were saved throughout the experiment, from which the optimal training model (the score network) was selected. Hence, the whole training process took ∼ 20 hours. The reconstruction is an iterative process, and the reconstruction time correlating closely with the number of iterations. As demonstrated in Figs. 6(o) and 6(p), both PSNR and SSIM stabilize about the 1000th iteration. Consequently, each iteration, contributes to an overall reconstruction time of ∼ 33 minutes (each iteration takes ∼ 2 seconds). Combined with the DAS method, photoacoustic images can be reconstructed quickly (in seconds). DAS is a mainstream and straightforward reconstruction method that demonstrates satisfactory reconstruction performance when the quality of the sinograms is sufficiently. In previous work [17], an advanced image domain sparse reconstruction method combining model-based iteration and diffusion model was proposed, wherein the prior learned by the diffusion model serves as the regularization term. However, the model-based DM method requires invoking the k-Wave toolbox to compute the A and A* operators [48] in each iteration, which results in each iteration taking ∼5 seconds. Consequently, obtaining the optimal result under the same computation conditions requires ∼1000 iterations, taking ∼83 minutes, which is ∼2.5 times longer than the proposed method. Both Cycle-GAN and U-Net are non-iterative methods with lower computational complexity, taking ∼1 second to reconstruct a single image. Utilizing more powerful computing units (e.g., NVIDIA GeForce RTX 4090) can further reduce the reconstruction time for each method. It is noteworthy that the output results of the proposed method surpassed the SSIM of the DAS method by the ∼200th iteration, as shown in Figs. 6(o) and 6(p). If the results had been output at that point, the reconstruction time would have been further reduced to ∼6 minutes. In terms of image quality improvement, the comparison of experimental results with numerous methods indicates that the proposed approach exhibits outstanding performance in sparse reconstruction for PAT. The proposed method is designed to emphasize the precise generation and recovery of the original data, particularly excelling in the restoration of high-frequency details in the signals. The model-based DM method reconstructs images directly from the sinograms by establishing a physical model of the PAT system, approaching the least-squares optimal solution through multiple iterations, and demonstrating excellent reconstruction performance in image domain. The simple structure of U-Net has limited receptive fields in its convolution layers, which hinder its ability to learn global features when processing sparse sinograms, making it less effective than diffusion models. While Cycle-GAN excels in facilitating the transition between different domains, its ability to recover details in single samples is relatively weaker. In summary, the proposed method exhibits outstanding performance in image quality, while the model-based DM method demands higher requirements on computational units. U-Net and Cycle-GAN have moderate computational complexity, whereas DAS has the lowest computational complexity but yields the poorest image quality. Readers can choose the most suitable method based on their specific conditions.
The proposed method has certain limitations, specifically in terms of reconstruction time and generalization. Since the proposed method is an iterative generation method, it requires ∼33 minutes for 1000 iterations in the current operating environment. It limits the applicability in scenarios with high real-time requirements. In addition, the experimental data in this work are obtained from the same PAT system and a relatively homogeneous imaging object. It is essential to consider improving the generalizability of the proposed method when dealing with data from different PAT systems or various types of imaging objects. In future work, faster diffusion models such as the Mean-Reverting diffusion model [49], [50] will be explored, as it can achieve satisfactory results within 100 iterations. Additionally, the experimental datasets will be augmented to enhance the generalizability of the proposed method. And the augmented datasets will include sinograms of various kind of samples obtained from different PAT systems.
Funding
National Natural Science Foundation of China (62265011, 62122033); Jiangxi Provincial Natural Science Foundation (20224BAB212006, 20232BAB202038); Training Program for Academic and Technical Leaders of Major Disciplines in Jiangxi Province (20243BCE51138); Key Research and Development Program of Jiangxi Province (20212BBE53001).
CRediT authorship contribution statement
Jiahong Li: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Yiguang Wang: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Jiabin Lin: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Zilong Li: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Xianlin Song: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Qiegen Liu: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Xuan Liu: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Yubin Cao: Writing – review & editing, Writing – original draft, Visualization, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Wenbo Wan: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Biographies

Zilong Li received the bachelor degree in Electronic Information Engineering from Guilin University of Electronic Technology, Guilin, China. He is currently studying in Nanchang University for master’s degree in Electronic Information Engineering. His research interests include optical imaging, deep learning and photoacoustic tomography.

Jiabin Lin is currently studying for bachelor degree in Automation Science in Nanchang University, Nanchang, China. His research interests include optical imaging, deep learning and photoacoustic tomography

Yiguang Wang received the bachelor degree in Biomedical Engineering from Gannan Medical University, Ganzhou, China. He is currently studying in Nanchang University for master's degree in Biomedical Engineering. His research interests include image processing, deep learning and photoacoustic microscopy.

Jiahong Li received the bachelor degree in Electronic Information Engineering from Yanshan University, Qinhuangdao, China. He is currently studying in Nanchang University for master’s degree in Electronic Information Engineering. His research interests include optical imaging, deep learning and photoacoustic tomography.

Yubin Cao received the bachelor degree in Biomedical Engineering from Gannan Medical University, Ganzhou, China. He is currently studying in Nanchang University for master's degree in Biomedical Engineering. His research interests include optical imaging, deep learning and photoacoustic microscopy.

Xuan Liu received the bachelor degree in Electronic Information Engineering from Pingxiang University, Pingxiang, China. He is currently studying in Nanchang University for master’s degree in Information and Telecommunications Engineering. His research interests include single-pixel imaging, deep learning and image processing.

Wenbo Wan received his Ph.D. degree in Biomedical engineering from Tianjin University, China in 2019. He joined School of Information Engineering, Nanchang University as an assistant professor in Nov. 2019. He has published more than 10 publications. His research topics include optical imaging and computational imaging.

Qiegen Liu received his Ph.D. degree in Biomedical Engineering from Shanghai Jiao Tong University, Shanghai, China in 2012. Currently, he is a professor at Nanchang University. He is the winner of Excellent Young Scientists Fund. He has published more than 50 publications and serves as committee member of several international and domestic academic organizations. His research interests include artificial intelligence, computational imaging and image processing.

Xianlin Song received his Ph.D. degree in Optical Engineering from Huazhong University of Science and Technology, China in 2019. He joined School of Information Engineering, Nanchang University as an assistant professor in Nov. 2019. He has published more than 20 publications and given more than 15 invited presentations at international conferences. His research topics include optical imaging, biomedical imaging and photoacoustic imaging.
Contributor Information
Qiegen Liu, Email: liuqiegen@ncu.edu.cn.
Xianlin Song, Email: songxianlin@ncu.edu.cn.
Data availability
Our code is publicly available at https://github.com/yqx7150/PAT-Sinogram-Diffusion.
References
- 1.Wang L.V. Tutorial on photoacoustic microscopy and computed tomography. IEEE J. Sel. Top. Quantum Electron. 2008;14(1):171–179. [Google Scholar]
- 2.Wang L.V., Yao J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods. 2016;13(8):627–638. doi: 10.1038/nmeth.3925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou Y., Yao J., Wang L.V. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016;21(6):61007. doi: 10.1117/1.JBO.21.6.061007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jathoul P., Laufer J., Ogunlade O., Treeby B., Cox B., Zhang E., et al. Deep in vivo photoacoustic imaging of mammalian tissues using a tyrosinase-based genetic reporter. Nat. Photonics. 2015;9(4):239–246. [Google Scholar]
- 5.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Fully dense UNet for 2D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health Inf. 2019;24(2):568–576. doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 6.Davoudi N., Deán-Ben X., Razansky D. Deep learning optoacoustic tomography with sparse data. Nat. Mach. Intell. 2019;1(10):453–460. [Google Scholar]
- 7.Waibel D., Gröhl J., Isensee F., Kirchner T., Maier-Hein K., Maier-Hein L. Reconstruction of initial pressure from limited view photoacoustic images using deep learning. Proc. SPIE. 2018;10494 [Google Scholar]
- 8.Gutta S., Kadimesetty V.S., Kalva S.K., Pramanik M., Ganapathy S., Yalavarthy P.K. Deep neural network-based bandwidth enhancement of photoacoustic data. J. Biomed. Opt. 2017;22(11) doi: 10.1117/1.JBO.22.11.116001. [DOI] [PubMed] [Google Scholar]
- 9.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;71(1) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 10.Zeng L., Xing D., Gu H., Yang D., Yang S., Xiang L. High antinoise photoacoustic tomography based on a modified filtered backprojection algorithm with combination wavelet. Med. Phys. 2007;34(2):556–563. doi: 10.1118/1.2426406. [DOI] [PubMed] [Google Scholar]
- 11.Treeby B.E., Zhang E.Z., Cox B.T. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Probl. 2010;26(11) [Google Scholar]
- 12.Cox B.T., Treeby B.E. Artifact trapping during time reversal photoacoustic imaging for acoustically heterogeneous media. IEEE Trans. Med. Imaging. 2010;29(2):387–396. doi: 10.1109/TMI.2009.2032358. [DOI] [PubMed] [Google Scholar]
- 13.Matrone G., Savoia A., Caliano G., Magenes G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imaging. 2015;34(4):940–949. doi: 10.1109/TMI.2014.2371235. [DOI] [PubMed] [Google Scholar]
- 14.Ma X., Peng C., Yuan J., Cheng Q., Xu G., Wang X., et al. Multiple delay and sum with enveloping beamforming algorithm for photoacoustic imaging. IEEE Trans. Med. Imaging. 2020;39(6):1812–1821. doi: 10.1109/TMI.2019.2958838. [DOI] [PubMed] [Google Scholar]
- 15.Hauptmann A., Lucka F., Betcke M., Huynh N., Adler J., Cox B., et al. Model-based learning for accelerated limited-view 3-D photoacoustic tomography. IEEE Trans. Med. Imaging. 2018;37(6):1382–1393. doi: 10.1109/TMI.2018.2820382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang T., He M., Shen K., Liu W., Tian C. Learned regularization for image reconstruction in sparse-view photoacoustic tomography. Biomed. Opt. Express. 2022;13(11):5721–5737. doi: 10.1364/BOE.469460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Song X., Wang G., Zhong W., Guo K., Li Z., Dong J., et al. Sparse-view reconstruction for photoacoustic tomography combining diffusion model with model-based iteration. Photoacoustics. 2023;33 doi: 10.1016/j.pacs.2023.100558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Song X., Zhong W., Li Z., Peng S., Zhang H., Wang G., et al. Accelerated model-based iterative reconstruction strategy for sparse-view photoacoustic tomography aided by multi-channel autoencoder priors. J. Biophoton. 2024;17(1) doi: 10.1002/jbio.202300281. [DOI] [PubMed] [Google Scholar]
- 19.Gutta S., Kalva S.K., Pramanik M., Yalavarthy P.K. Accelerated image reconstruction using extrapolated Tikhonov filtering for photoacoustic tomography. Med. Phys. 2018;45(8):3749–3767. doi: 10.1002/mp.13023. [DOI] [PubMed] [Google Scholar]
- 20.Tian L., Hunt B., Bell M.A.L., Yi J., Smith J.T., Ochoa M., et al. Deep learning in biomedical optics. Lasers Surg. Med. 2021;53(6):748–775. doi: 10.1002/lsm.23414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shen C., Nguyen D., Zhou Z., Jiang S.B., Dong B., Jia X. An introduction to deep learning in medical physics: advantages, potential, and challenges. Phys. Med Biol. 2020;65(5) doi: 10.1088/1361-6560/ab6f51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Razzak M.L., Naz S., Zaib A. in: Classification BioApps. Springer; Cham, Switzerland: 2018. Deep learning for medical image processing: overview, challenges and the future; pp. 323–350. [Google Scholar]
- 23.Shen D., Wu G., Suk H.I. Deep learning in medical image analysis. Ann. Rev. Biomed. Eng. 2017;19:221–248. doi: 10.1146/annurev-bioeng-071516-044442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Fully dense UNet for 2D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health Inf. 2020;24:568–576. doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 25.Feng J., Deng J., Li Z., Sun Z., Dou H., Jia K. End-to-end Res-Unet based reconstruction algorithm for photoacoustic imaging. Biomed. Opt. Express. 2020;11(9):5321–5340. doi: 10.1364/BOE.396598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Limited-view and sparse photoacoustic tomography for neuroimaging with deep learning. Sci. Rep. 2020;10(1):8510. doi: 10.1038/s41598-020-65235-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lutzweiler C., Meier R., Razansky D. Optoacoustic image segmentation based on signal domain analysis. Photoacoustics. 2015;3(4):151–158. doi: 10.1016/j.pacs.2015.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Awasthi N., Jain G., Kalva S.K., Pramanik M., Yalavarthy P.K. Deep neural network-based sinogram super-resolution and bandwidth enhancement for limited-data photoacoustic tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2020;67(12):2660–2673. doi: 10.1109/TUFFC.2020.2977210. [DOI] [PubMed] [Google Scholar]
- 29.Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S. Generative adversarial networks. Commun. ACM. 2020;63(11):139–144. [Google Scholar]
- 30.Moreno-Pino F., Olmos P.M., Artés-Rodríguez A. Deep autoregressive models with spectral attention. Pattern Recognit. 2023;133 [Google Scholar]
- 31.Kingma D.P., Dhariwal P. Glow: generative flow with invertible 1×1 convolutions. J. Inf. Process. Syst. 2018;31 [Google Scholar]
- 32.C. Doersch, Tutorial on variational autoencoders," arXiv, arXiv: 1606.05908 (2016).
- 33.Ho J., Jain A., Abbeel P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020;33:6840–6851. [Google Scholar]
- 34.Y. Song, J. Sohl-Dickstein, D.P. Kingma, A. Kumar, S. Ermon, and B. Poole, Score-based generative modeling through stochastic differential equations," arXiv, arXiv:2011.13456 (2020).
- 35.Saharia C., Ho J., Chan W., Salimans T., Fleet D.J., Norouzi M. Image super-resolution via iterative refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2022;45(4):4713–4726. doi: 10.1109/TPAMI.2022.3204461. [DOI] [PubMed] [Google Scholar]
- 36.Wang Z., Cun X., Bao J., Zhou W., Liu J., Li H. Uformer: a general U-shaped transformer for image restoration. in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2022:17683–17693. [Google Scholar]
- 37.Kawar B., Vaksman G., Elad M. Snips: solving noisy inverse problems stochastically. Proc. Adv. Neural Inf. Process. Syst. (NeurIPS) 2021:21757–21769. [Google Scholar]
- 38.Q. Wang, D. Kong, F. Lin, and Y. Qi, DiffSketching: sketch control image synthesis with diffusion models, arXiv, arXiv:2305.18812 (2023).
- 39.Treeby B.E., Cox B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave-fields J. Biomed. Opt. 2010;15(2) doi: 10.1117/1.3360308. -021314. -021314. [DOI] [PubMed] [Google Scholar]
- 40.Lan H., Gong J., Gao F. Deep learning adapted acceleration for limited-view photoacoustic image reconstruction. Opt. Lett. 2022;47(7):1911–1914. doi: 10.1364/OL.450860. [DOI] [PubMed] [Google Scholar]
- 41.Parisi G. Correlation functions and computer simulations. Nucl. Phys. B. 1981;180(3):378–384. [Google Scholar]
- 42.Staal J., Abramoff M.D., Niemeijer M., Viergever M.A., Van Ginneken B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging. 2004;23(4):501–509. doi: 10.1109/TMI.2004.825627. [DOI] [PubMed] [Google Scholar]
- 43.Zhu J., Park T., Isola P., Efros A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. IEEE Int. Conf. Comput. Vis. ICCV. 2017:2223–2232. [Google Scholar]
- 44.H. Wang, S. Xie, L. Lin, Y. Iwamoto, X. Han, Y. Chen, R. Tong, Mixed transformer U-Net for medical image segmentation, arXiv, arXiv:2111.04734 (2021).
- 45.Lu M., Liu X., Liu C., Liu C., Li B., Gu W., Jiang J., Ta D. Artifact removal in photoacoustic tomography with an unsupervised method. Biomed. Opt. Express. 2021;12(10):6284–6299. doi: 10.1364/BOE.434172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhao F., Huang Q., Gao W. Image matching by normalized cross-correlation. IEEE Int. Conf. Acoust. Speech Signal. Process. Proc. 2006;2 (II-II) [Google Scholar]
- 47.Zebende G.F. DCCA cross-correlation coefficient: quantifying level of cross-correlation. Phys. A. 2011;390(4):614–618. [Google Scholar]
- 48.Hauptmann A., Cox B. Deep learning in photoacoustic tomography: current approaches and future directions J. Biomed. Opt. 2020;25(11) -112903. -112903. [Google Scholar]
- 49.Z. Luo, F.K. Gustafsson, Z. Zhao, J. Sjölund, and T.B. Schön, Image restoration with mean-reverting stochastic differential equations, arXiv preprint arXiv:2301.11699 (2023).
- 50.Cao Y., Lu S., Wan C., Wang Y., Liu X., Guo K., Cao Y., Li Z., Liu Q., Song X. Mean-reverting diffusion model-enhanced acoustic-resolution photoacoustic microscopy for resolution enhancement: toward optical resolution. J. Innov. Opt. Health Sci. 2024:2450023. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Our code is publicly available at https://github.com/yqx7150/PAT-Sinogram-Diffusion.