Robustness of circadian rhythms with respect to molecular noise

Abstract

We use a core molecular model capable of generating circadian rhythms to assess the robustness of circadian oscillations with respect to molecular noise. The model is based on the negative feedback exerted by a regulatory protein on the expression of its gene. Such a negative regulatory mechanism underlies circadian oscillations of the PER protein in Drosophila and of the FRQ protein in Neurospora. The model incorporates gene transcription into mRNA, translation of mRNA into protein, reversible phosphorylation leading to degradation of the regulatory protein, transport of the latter into the nucleus, and repression of gene expression by the nuclear form of the protein. To assess the effect of molecular noise, we perform stochastic simulations after decomposing the deterministic model into elementary reaction steps. The oscillations predicted by the stochastic simulations agree with those obtained with the deterministic version of the model. We show that robust circadian oscillations can occur already with a limited number of mRNA and protein molecules, in the range of tens and hundreds, respectively. Entrainment by light/dark cycles and cooperativity in repression enhance the robustness of circadian oscillations with respect to molecular noise.

Circadian rhythms characterized by a period close to 24 h are observed in nearly all living organisms from cyanobacteria to Neurospora, plants, insects such as Drosophila, and mammals. The molecular mechanism of these rhythms relies on negative autoregulatory feedback on gene expression (1–4). Theoretical models for circadian rhythms based on such control mechanisms have been proposed (5–11). The question arises (12, 13) as to the biological validity of these models when the numbers of mRNA and protein molecules involved in the regulatory mechanism are small, as may occur in cellular conditions. Here we use a core molecular model proposed for circadian rhythms in Drosophila to assess its robustness with respect to molecular noise. By means of stochastic simulations we show that robust circadian oscillations already can be produced by the autoregulatory mechanism when the maximum numbers of mRNA and protein molecules are in the order of tens and hundreds, respectively. The robustness of circadian oscillations increases with both the number of molecules and the degree of cooperativity of the repression process, and entrainment by light/dark (LD) cycles stabilizes the phase of the oscillations with respect to molecular noise.

Core Molecular Model for Circadian Oscillations

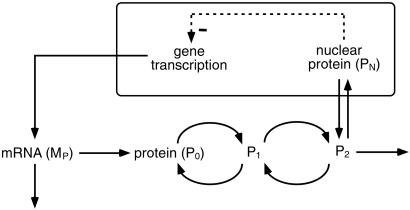
The model, schematized in general form in Fig. 1, is based on the negative feedback exerted by a protein (which will be referred to below as clock protein) on the expression of its gene. This model, previously proposed for circadian oscillations of the PER protein and per mRNA in Drosophila, is described by a set of five kinetic equations (see refs. 5 and 6 and Appendix, which is published as supporting information on the PNAS web site, www.pnas.org). It accounts for the occurrence of sustained oscillations in continuous darkness, phase shifting by light pulses, and entrainment by LD cycles. Similar results have been obtained in more detailed models incorporating additional clock gene products such as TIM and CLOCK (7–11), but for simplicity we will focus on the model based on the regulation exerted by PER alone. The model of Fig. 1 thus will serve as a core model capable of generating circadian oscillations and does not aim at representing the current, more complex view of the molecular mechanism of the Drosophila circadian clock, which is known to involve a larger number of interacting proteins (1–3). In this simple form the model can apply also to the case of Neurospora (8), in which circadian rhythms originate from the negative feedback exerted by the FRQ protein on the expression of its gene (1).

Figure 1.

Core model for circadian rhythms. The model represents a prototype for the molecular mechanism of circadian oscillations based on negative autoregulation of gene expression. The model incorporates gene transcription, transport of mRNA (M_P) into the cytosol where it is translated into the clock protein (P₀) and degraded. The clock protein can be reversibly phosphorylated from the form P₀ into the forms P₁ and P₂, successively. The latter form is degraded or transported into the nucleus (P_N), where it exerts a negative feedback of cooperative nature on the expression of its gene. The model accounts for circadian oscillations of per mRNA and PER protein in Drosophila (5, 6) but does not aim at providing a detailed picture of the mechanism of circadian rhythmicity in this organism, where additional gene products are at work (1–3). Similar results are obtained in a more extended model incorporating the formation of complexes between various clock proteins (7–11). The model can apply also to circadian oscillations of frq mRNA and FRQ protein in Neurospora (8).

Molecular Noise and Stochastic Simulations

The decrease in the total number, N, of molecules in a system of chemical reactions is accompanied by a rise in the amplitude of fluctuations around the state predicted by the deterministic evolution of this chemical system. These fluctuations reflect intrinsic molecular noise of amplitude proportional to 1/√N. Molecular fluctuations can be taken into account by describing the chemical reaction system as a birth-and-death stochastic process governed by a master equation (14). In a given reaction step, molecules of participating species are either produced (birth) or consumed (death). Each step is associated with a transition probability proportional to the numbers of molecules of involved chemical species and to the chemical rate constant of the corresponding deterministic model.

A numerical algorithm that implements such a master equation approach to stochastic chemical dynamics has been introduced by Gillespie (15, 16). Besides other approaches (17–19), this method of the Monte Carlo type is widely used to determine the effect of molecular noise on the dynamics of chemical (18, 19), biochemical (20), or genetic systems (21). The Gillespie method associates a probability with each reaction; at each time step the algorithm stochastically determines the reaction that takes place according to its probability as well as the time interval to the next reaction. The numbers of molecules of the different reacting species as well as the probabilities are updated at each time step. In this approach (see refs. 15 and 16 and Appendix), a parameter denoted Ω permits the modulation of the number of molecules present in the system. To assess the effect of molecular noise on circadian oscillations we have used this method to perform stochastic simulations of the core deterministic model described above after decomposing it into detailed reaction steps (see Appendix, Decomposition of the Deterministic Model into Elementary Reaction Steps).

Influence of Molecular Noise on Circadian Oscillations

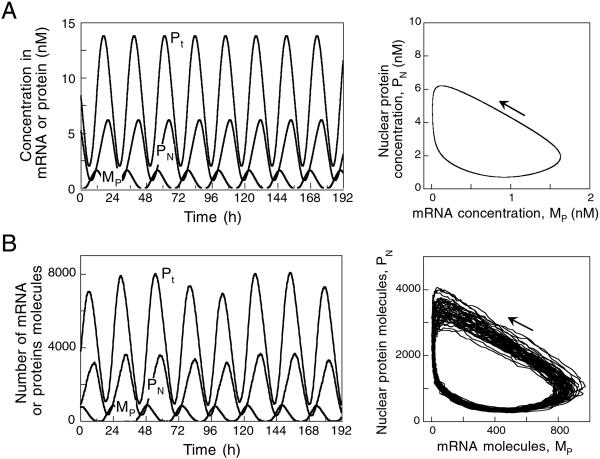
We first wish to check whether for sufficiently large numbers of molecules, stochastic simulations of the detailed reaction system produce results similar to those obtained with the deterministic model. Shown in Fig. 2A (Left) are circadian oscillations of mRNA (M_P) and nuclear (P_N) and total (P_t) clock protein obtained with the deterministic model under conditions of continuous darkness. These sustained oscillations correspond to the evolution toward a limit cycle, which is shown in Fig. 2A (Right) as a projection onto the (M_P, P_N) plane. Corresponding results from stochastic simulations performed with the detailed reaction system for Ω = 500 are shown in Fig. 2B. For this value of Ω, robust circadian oscillations are obtained in which the number of mRNA molecules varies in the range of 0–1,000, whereas the numbers of nuclear and total clock protein molecules oscillate in the range of 200–4,000 and 800–8,000, respectively. The effect of molecular noise is merely to induce variability in the maxima of the oscillations. This effect is reflected by the noisy appearance of the limit cycle and a thickening of its upper portion linking the maximum in mRNA with the maximum in nuclear (or total) clock protein.

Figure 2.

Circadian oscillations predicted by the negative-feedback model schematized in Fig. 1. (A) Oscillations obtained in the absence of noise. The curves are generated by numerical integration of the five kinetic equations governing the time evolution of the deterministic model (see refs. 5 and 6 and Appendix). Sustained oscillations of mRNA (M_P) and nuclear (P_N) and total clock (P_t) protein presented (Left) correspond to the evolution toward a limit cycle shown as a projection onto the (M_P, P_N) plane (Right). (B) Oscillations generated by the model in the presence of noise for Ω = 500 and n = 4. The results shown correspond to those obtained in A for the deterministic model. The data, expressed in numbers of molecules of mRNA and of nuclear and total clock protein, are obtained by stochastic simulations of the detailed reaction system corresponding to the deterministic model schematized in Fig. 1. Here the number of mRNA molecules oscillates between a few and 1,000, whereas nuclear and total clock protein oscillate in the ranges of 200–4,000 and 800–8,000, respectively. Robust circadian oscillations occur in these conditions despite the presence of molecular noise, with a mean period of 24.4 h and a standard deviation of 1.3 h. The decomposition of the deterministic model into elementary steps, the method of stochastic simulation, and parameter values are listed in Appendix.

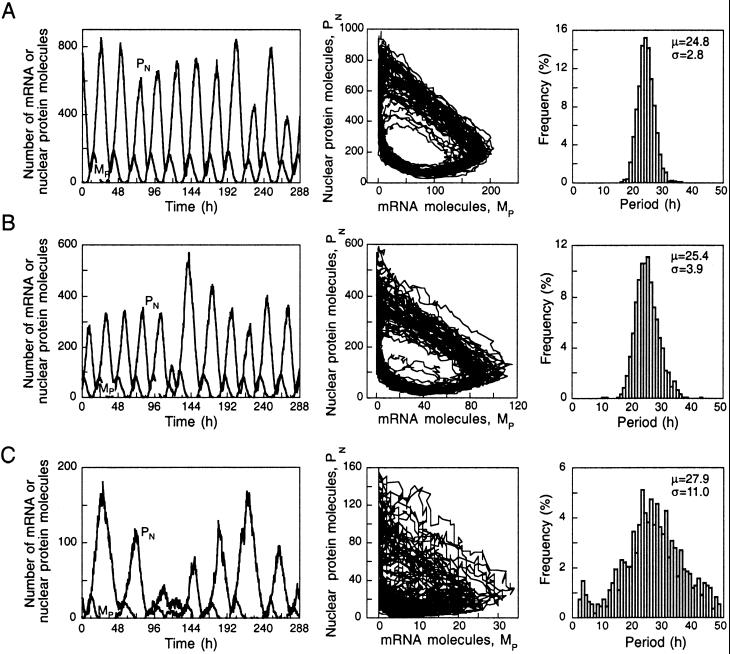
To assess the robustness of circadian oscillations at lower numbers of molecules we determined the dynamics of the detailed genetic control network by stochastic simulations for decreasing values of Ω. The results in Fig. 3 show that robust circadian oscillations occur in continuous darkness for Ω = 100 (A) or 50 (B) when the number of mRNA molecules oscillates from 0 to 200 (A) or 0 to 120 (B), whereas the number of nuclear clock protein molecules oscillates in the range of 20–800 (A) or 10–600 (B). The limit cycles are more noisy, but the period histograms calculated for some 1,200 successive cycles indicate that the distribution remains narrow with a mean free running period μ close to a circadian value. The standard deviation σ remains small with respect to the mean period but slightly increases as the number of molecules diminishes.

Figure 3.

Effect of number of molecules on the robustness of circadian oscillations. Shown in rows A–C are the oscillations in the numbers of molecules of mRNA and nuclear clock protein (Left), the projection of the corresponding limit cycle, and the histogram of periods of 1,200 successive cycles for Ω varying from 100 (A) to 50 (B) and 10 (C). The curves are obtained by stochastic simulations as described for Fig. 2B for n = 4. For period histograms, the period was determined as the time interval separating two successive upward crossings of the mean level of mRNA or clock protein. In A and B, the decrease in the numbers of mRNA and protein molecules still permits robust circadian oscillations [see histograms in which the mean value (μ) and standard deviation (σ) of the period are indicated in h], whereas at still lower numbers of molecules (C) noise begins to obliterate rhythmic behavior. For the oscillations in A, an average of one molecule of mRNA is produced every 2.5 min, whereas one molecule of clock protein is synthesized per mRNA molecule every 30 min; the average number of mRNA molecules is of the order of 60.

It is for still smaller numbers of molecules that circadian rhythmicity becomes obliterated by noise. Fig. 3C illustrates the results of stochastic simulations performed with Ω = 10. Highly irregular oscillations occur, during which the number of mRNA molecules varies from 0 to 30, whereas the number of nuclear protein molecules oscillates in the range of 5–160. Even for such reduced numbers of mRNA and protein molecules, however, oscillations are not destroyed fully by noise. The histogram of periods indicates that the mean is still close to a circadian value, but the standard deviation is increased greatly.

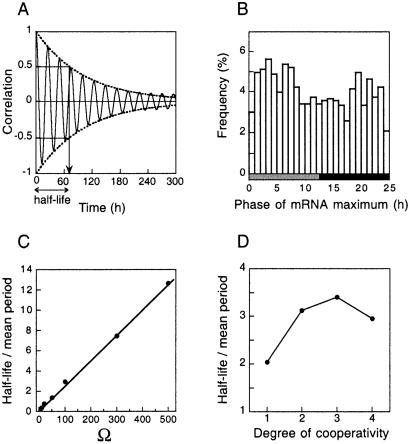
The robustness of circadian oscillations with respect to molecular noise can be quantified further by the autocorrelation function that measures the degree of periodicity of the time evolution of a given variable. In the presence of noise, the more periodic the evolution, the more slowly the autocorrelation function goes to zero. In the absence of noise, the autocorrelation function for a periodic system keeps oscillating between 1 and −1. Shown in Fig. 4A is the time course of the autocorrelation function for the oscillations illustrated in Fig. 3A, in which Ω = 100. The envelope of the function decreases exponentially, and the half-life corresponding to 50% decrease yields a measure of the robustness of periodic oscillations with respect to noise. Here, the half-life is close to 3 times the mean period of circadian oscillations. The loss of correlations primarily is due to the phenomenon of phase diffusion (18, 19); because of noise the phase of free-running oscillations varies in such a way that eventually it covers the whole range of possible values over a period (Fig. 4B).

Figure 4.

Robustness of circadian oscillations measured by half-life of autocorrelations. (A) Time evolution of the autocorrelation function, with indication of half-life time, for the oscillations obtained for Ω = 100 and n = 4 in Fig. 3A. (B) Phase of maximum in mRNA in the presence of molecular noise. The histogram is obtained under free-running conditions for 1,200 successive periods for the case considered in A. (C) Half-life of autocorrelations increases in a linear manner with the parameter Ω that provides a measure of the number of molecules present in the system. The oscillations corresponding to Ω = 500, 100, 50, and 10 are shown in Figs. 2B and 3A–C, respectively. (D) Influence of the degree of cooperativity of repression on the robustness of circadian oscillations. The half-life of autocorrelations is determined as a function of n for the case Ω = 100. In A–C, as well as in other figures, the degree of cooperativity n is equal to 4. In D, the standard deviation σ of the period distribution (shown for n = 4 in Fig. 3A) goes from 7.7 h (mean period μ = 26.9 h) for n = 1 to 2.6 h (μ = 21.2 h), 1.9 h (μ = 20.3 h), and 2.7 h (μ = 24.8 h) for n = 2, 3, and 4, respectively.

Robustness increases in proportion to the number of molecules present in the system. The ratio of the half-life of the correlations divided by the mean period indeed increases in a linear manner with parameter Ω (Fig. 4C), which is in agreement with analytical predictions on the effect of noise on limit cycle oscillations (22). When Ω rises from 50 to 500, the half-life of correlations goes from ≈1.8 to 12 times the mean period. The half-life becomes smaller than the mean period for values of Ω below 40, reflecting the takeover of periodicity by noise even though some remnant of circadian behavior is still noticeable for values of Ω as low as 10 (see Fig. 3C).

Effect of Cooperativity on Robustness of Circadian Oscillations

In the above simulations, we have considered that four molecules of nuclear protein must bind successively to the gene promoter to repress transcription. To allow for positive cooperativity, which often characterizes repression (23), we assume (see Appendix, Parameter Values for Stochastic Simulations) that the affinity of binding increases with the number of protein molecules already bound. Cooperativity, however, is not required for oscillatory behavior. Circadian oscillations indeed can occur if repression involves the binding of a single molecule of nuclear protein. To investigate the effect of cooperativity on robustness of circadian oscillations with respect to molecular noise, we performed stochastic simulations with Ω =100 for values of n ranging from 1 to 4, where n denotes the total number of protein molecules that bind to the promoter to repress transcription. For the parameter values considered, n is also the degree of cooperativity equal to the maximum Hill coefficient characterizing the sigmoidal decrease of the promoter activity as a function of nuclear protein in the deterministic model. The results (Fig. 4D) indicate that robustness, as measured by the ratio of the half-life of correlations divided by the mean period, significantly increases when n passes from 1 (absence of cooperativity) to values of 2 and above. The ratio remains in a narrow range for n = 2–4 and passes through a maximum for n = 3. The variation in half-life as well as changes in standard deviation of the period show that cooperative repression enhances the robustness of circadian oscillations with respect to molecular noise.

Entrainment by LD Cycles in the Presence of Molecular Noise

Circadian rhythms are permanently subjected to periodic forcing by the external LD cycle. The questions arise as to whether entrainment by the LD cycle can occur in the presence of low numbers of molecules and what the effect is of periodic forcing on the robustness of circadian oscillations with respect to molecular noise. By means of stochastic simulations for the case of Ω = 100 corresponding to the oscillations obtained in conditions of continuous darkness in Fig. 3A, we determine in Fig. 5 the characteristics of oscillations after entrainment by a 12:12-h LD cycle. The effect of light is incorporated by considering that light enhances degradation of the clock protein, as observed in Drosophila (1–3).

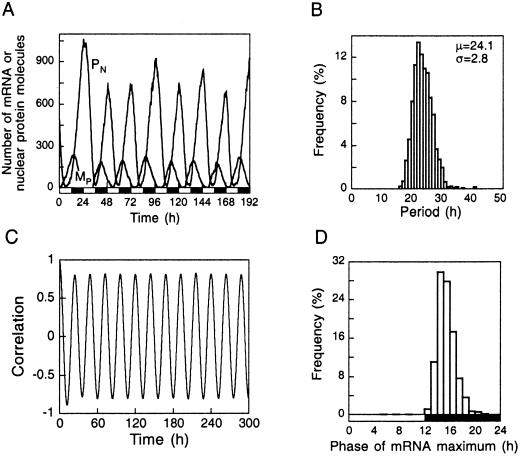
Figure 5.

Effect of molecular noise on circadian oscillations under conditions of periodic forcing by an LD cycle. The data are obtained for Ω = 100 and n = 4 and should be compared with the results shown in Figs. 3A and 4 A and B in the case of continuous darkness. (A) Circadian oscillations in the numbers of mRNA and nuclear clock protein molecules. (B) Histogram of periods with mean value (μ) and standard deviation (σ) indicated in h. (C) Time course of the autocorrelation function. (D) Histogram of the time corresponding to the maximum number of mRNA molecules over a period. In A, periodic forcing is achieved by doubling during each light phase the value ascribed during the dark phase to the parameter (k_d3) measuring the probability of the protein degradation step (see Table 1, which is published as supporting information on the PNAS web site). Histograms and autocorrelations are determined for some 1,200 successive cycles.

The results (A and B) indicate that the circadian clock mechanism can be entrained by the 24-h LD cycle in the presence of molecular noise. The mean period indeed is shifted from 24.8 h before entrainment (Fig. 3A) to 24.1 h (Fig. 5A). The standard deviation of the period is not affected significantly by entrainment (compare Fig. 5B with Fig. 3A Right). The most striking effect of periodic forcing is to stabilize the phase of the oscillations. Thus, instead of spanning the whole period (Fig. 4B), the distribution of the phase of maximum mRNA has a mean close to 15.4 h after the beginning of the light phase (Fig. 5D), which is in agreement with experimental observations that indicate (24, 25) that in Drosophila the peak in per mRNA occurs ≈4 h after the onset of darkness. The increased robustness caused by locking of the phase of circadian oscillations after entrainment is reflected also by the autocorrelation function that oscillates with constant amplitude (Fig. 5C) instead of exponentially decreasing to zero (Fig. 4A).

Discussion

Previous reports raised doubts as to whether the oscillations produced by deterministic models for circadian rhythms based on negative autoregulatory feedback remain robust in the presence of molecular noise (12, 13). In one brief study (12), stochastic simulations produced highly irregular oscillations characterized by the rapid vanishing of autocorrelations even though the maximum numbers of mRNA and protein molecules were rather large, of the order of 3,000 and 10,000, respectively. In contrast, our results demonstrate that robust oscillations can occur already with maximum numbers of mRNA and protein molecules of the order of tens and hundreds, respectively (see Figs. 3 and 4), whereas robustness is enhanced further at larger numbers of molecules (Fig. 2B). This conclusion validates the use of deterministic models to study the molecular mechanism of circadian rhythms and explains why such models provide a reliable picture of the working of circadian clocks in a variety of organisms.

Robustness is used commonly with another meaning to denote the persistence of a certain type of dynamic behavior over a significant range of parameter values. In deterministic models, sustained circadian oscillations only occur in a precise region of parameter space (5–11). We have verified that a similar conclusion is reached with stochastic simulations. The latter show that sustained oscillations occur in a sizeable domain of parameter values and that outside this domain the numbers of mRNA and clock protein molecules fluctuate around steady-state levels. The results presented here have been obtained far from a bifurcation point, well inside the domain of sustained oscillations. For a given value of Ω, the disrupting effect of molecular noise becomes more significant when the system is close to the bifurcation point corresponding to the onset of sustained oscillations beyond a critical parameter value (unpublished data).

The passage through a bifurcation point can be observed for all parameters of the model including the rate constants a_i and d_i that characterize the binding of the repressor to and dissociation from the gene promoter (reaction steps 1–8 in Table 1). The study of a deterministic differential system based on the detailed sequence of reaction steps listed in Table 1 indicates that when a_i and d_i (i = 1,… 4) are decreased without changing the equilibrium dissociation constants K_i = d_i/a_i, the oscillations disappear when the parameters are decreased by some 3 orders of magnitude with respect to the case considered in Fig. 2. The system then reaches a stable, excitable steady state. Stochastic simulations show that in these conditions molecular noise induces large excursions away from the steady state corresponding to irregular, large-amplitude peaks in mRNA and clock protein. This result may explain the lack of robustness reported by other authors (12) who considered smaller values for the bimolecular rate constants characterizing the association of the regulatory protein to the gene promoter on DNA (see Appendix, Parameter Values for Stochastic Simulations).

Besides assessing the robustness of circadian oscillations with respect to molecular noise, we showed that the persistence of circadian rhythmicity is enhanced by the cooperative nature of repression. The role of cooperativity in the oscillatory mechanism is supported by the formation of complexes between various clock proteins in Drosophila and mammals as well as in Neurospora (1–4, 26, 27). Periodic forcing by LD cycles, which acts as natural synchronizer for circadian rhythms, also has the effect of enhancing their robustness at low numbers of molecules by stabilizing the phase of the oscillations (Fig. 5D). As indicated by the stochastic study (D. Forger and C. Peskin, unpublished data) performed with similar numbers of molecules on a closely related model (7) incorporating the formation of a PER⋅TIM regulatory complex, other factors such as the formation of a complex between different clock proteins may contribute further to the stability of circadian rhythmicity with respect to molecular noise. Robustness may be enhanced also by the interaction between multiple feedback loops, as suggested by a model (12) in which the negative feedback on gene expression is of indirect rather than direct nature.

The present results show that robust circadian oscillations based on autoregulatory feedback and strengthened by cooperativity and environmental forcing can occur even at reduced numbers of mRNA and clock protein molecules near the lower limits encountered in cells. In Drosophila, precise intracellular levels of protein and mRNA molecules for the various clock genes still are unknown, and only relative values of protein levels have been measured thus far (28). It would be interesting to know the absolute numbers of mRNA and protein molecules involved in the oscillatory mechanism in Drosophila and mammals. In Neurospora, the number of FRQ molecules has been estimated to be in the range of only a few tens per nucleus (29). At such low numbers our results indicate that rhythmicity still exists but begins to be affected markedly by noise. A conspicuous feature of Neurospora is its syncitial morphology. The nucleocytoplasmic nature of the circadian oscillator implies that in Neurospora, the different nuclei within a cell may be coupled through a common variable, cytosolic FRQ. Such a coupling might enhance the robustness of circadian oscillations with respect to molecular noise even in the presence of reduced amounts of this protein within each nucleus. Other forms of coupling, between oscillating cells (30), similarly may enhance the robustness of circadian rhythms in other organisms such as Drosophila and mammals.

Abbreviation

LD

light/dark