Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Nov;73(5):2393–2403. doi: 10.1016/S0006-3495(97)78268-7

How are model protein structures distributed in sequence space?

E Bornberg-Bauer 1
PMCID: PMC1181141  PMID: 9370433

Abstract

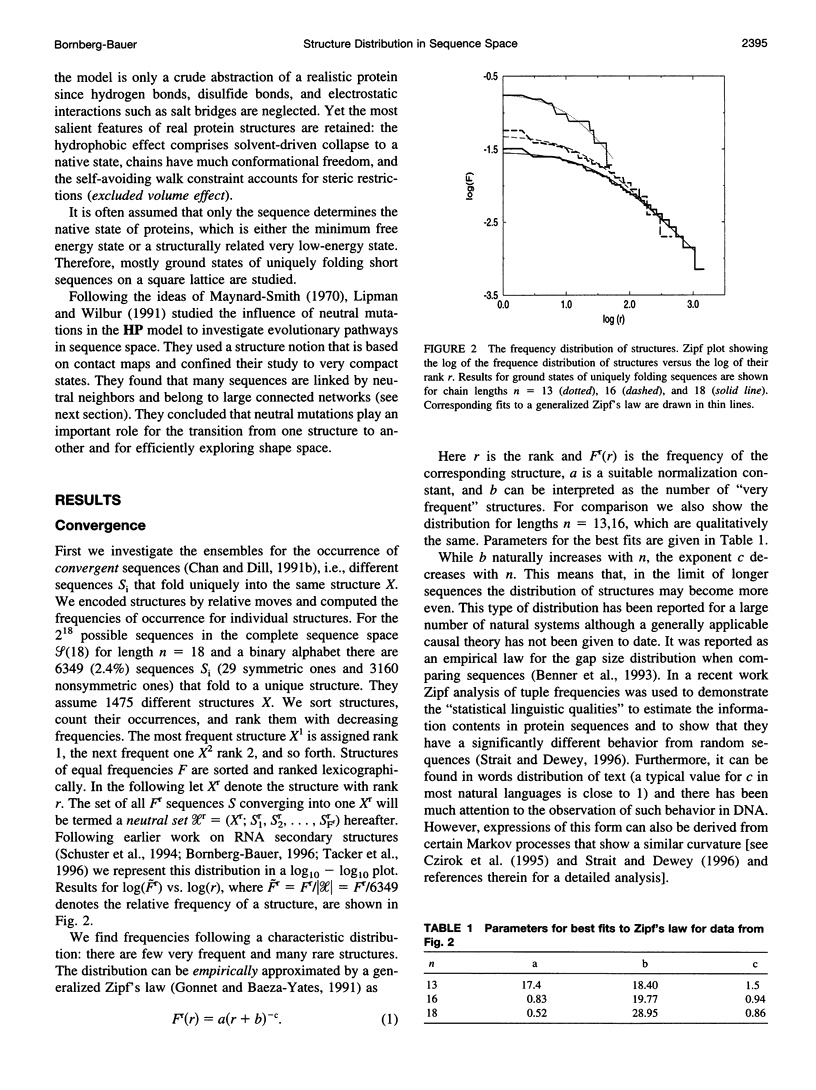
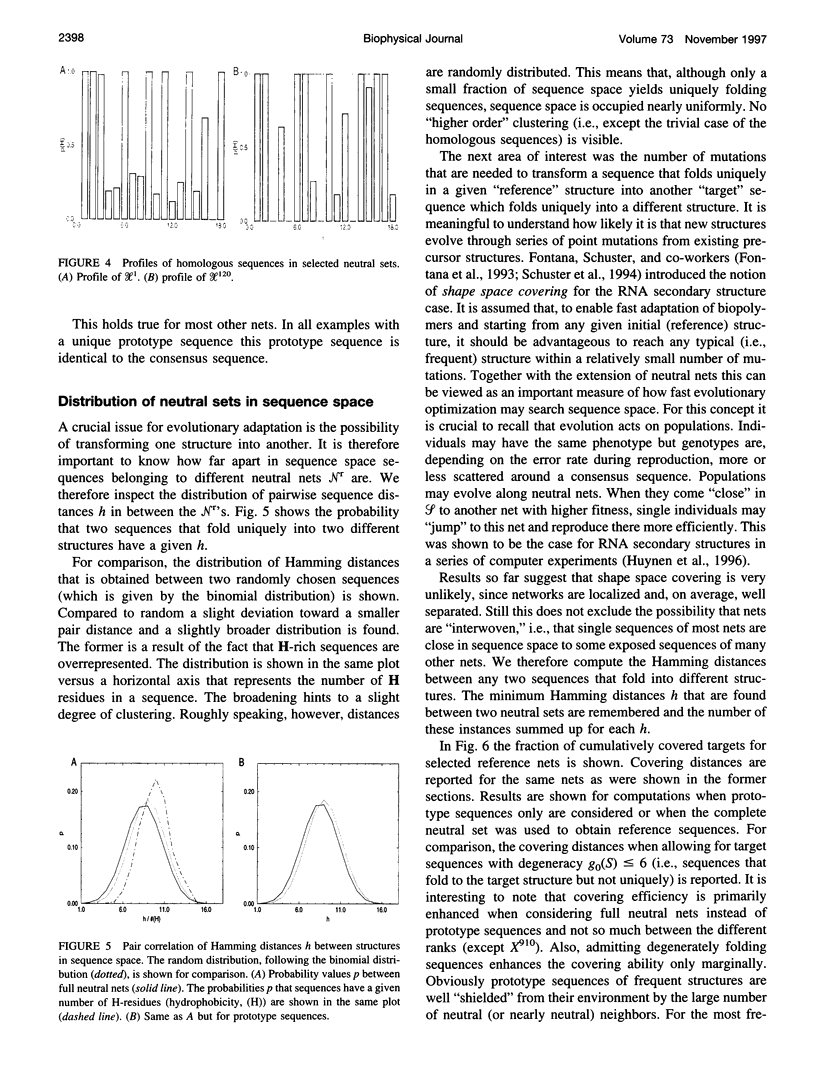
The figure-to-structure maps for all uniquely folding sequences of short hydrophobic polar (HP) model proteins on a square lattice is analyzed to investigate aspects considered relevant to evolution. By ranking structures by their frequencies, few very frequent and many rare structures are found. The distribution can be empirically described by a generalized Zipf's law. All structures are relatively compact, yet the most compact ones are rare. Most sequences falling to the same structure belong to "neutral nets." These graphs in sequence space are connected by point mutations and centered around prototype sequences, which tolerate the largest number (up to 55%) of neutral mutations. Profiles have been derived from these homologous sequences. Frequent structures conserve hydrophobic cores only while rare ones are sensitive to surface mutations as well. Shape space covering, i.e., the ability to transform any structure into most others with few point mutations, is very unlikely. It is concluded that many characteristic features of the sequence-to-structure map of real proteins, such as the dominance of few folds, can be explained by the simple HP model. In analogy to protein families, nets are dense and well separated in sequence space. Potential implications in better understanding the evolution of proteins and applications to improving database searches are discussed.

Full text

PDF
2393

Images in this article

2398FIGURE 4
on p.2398

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Abkevich V. I., Gutin A. M., Shakhnovich E. I. How the first biopolymers could have evolved. Proc Natl Acad Sci U S A. 1996 Jan 23;93(2):839–844. doi: 10.1073/pnas.93.2.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Benner S. A., Cohen M. A., Gonnet G. H. Empirical and structural models for insertions and deletions in the divergent evolution of proteins. J Mol Biol. 1993 Feb 20;229(4):1065–1082. doi: 10.1006/jmbi.1993.1105. [DOI] [PubMed] [Google Scholar]
  3. Bryngelson J. D., Wolynes P. G. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci U S A. 1987 Nov;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Camacho CJ, Thirumalai D. Minimum energy compact structures of random sequences of heteropolymers. Phys Rev Lett. 1993 Oct 11;71(15):2505–2508. doi: 10.1103/PhysRevLett.71.2505. [DOI] [PubMed] [Google Scholar]
  5. Casari G., Sippl M. J. Structure-derived hydrophobic potential. Hydrophobic potential derived from X-ray structures of globular proteins is able to identify native folds. J Mol Biol. 1992 Apr 5;224(3):725–732. doi: 10.1016/0022-2836(92)90556-y. [DOI] [PubMed] [Google Scholar]
  6. Chan H. S., Dill K. A. Comparing folding codes for proteins and polymers. Proteins. 1996 Mar;24(3):335–344. doi: 10.1002/(SICI)1097-0134(199603)24:3<335::AID-PROT6>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
  7. Chan H. S., Dill K. A. Polymer principles in protein structure and stability. Annu Rev Biophys Biophys Chem. 1991;20:447–490. doi: 10.1146/annurev.bb.20.060191.002311. [DOI] [PubMed] [Google Scholar]
  8. Chothia C. Proteins. One thousand families for the molecular biologist. Nature. 1992 Jun 18;357(6379):543–544. doi: 10.1038/357543a0. [DOI] [PubMed] [Google Scholar]
  9. Cordes M. H., Davidson A. R., Sauer R. T. Sequence space, folding and protein design. Curr Opin Struct Biol. 1996 Feb;6(1):3–10. doi: 10.1016/s0959-440x(96)80088-1. [DOI] [PubMed] [Google Scholar]
  10. Czirók A, Mantegna RN, Havlin S, Stanley HE. Correlations in binary sequences and a generalized Zipf analysis. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1995 Jul;52(1):446–452. doi: 10.1103/physreve.52.446. [DOI] [PubMed] [Google Scholar]
  11. Davidson A. R., Lumb K. J., Sauer R. T. Cooperatively folded proteins in random sequence libraries. Nat Struct Biol. 1995 Oct;2(10):856–864. doi: 10.1038/nsb1095-856. [DOI] [PubMed] [Google Scholar]
  12. Dill K. A., Bromberg S., Yue K., Fiebig K. M., Yee D. P., Thomas P. D., Chan H. S. Principles of protein folding--a perspective from simple exact models. Protein Sci. 1995 Apr;4(4):561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fontana W, Stadler PF, Bornberg-Bauer EG, Griesmacher T, Hofacker IL, Tacker M, Tarazona P, Weinberger ED, Schuster P. RNA folding and combinatory landscapes. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1993 Mar;47(3):2083–2099. doi: 10.1103/physreve.47.2083. [DOI] [PubMed] [Google Scholar]
  14. Goldstein R. A., Luthey-Schulten Z. A., Wolynes P. G. Optimal protein-folding codes from spin-glass theory. Proc Natl Acad Sci U S A. 1992 Jun 1;89(11):4918–4922. doi: 10.1073/pnas.89.11.4918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Goodsell D. S., Olson A. J. Soluble proteins: size, shape and function. Trends Biochem Sci. 1993 Mar;18(3):65–68. doi: 10.1016/0968-0004(93)90153-e. [DOI] [PubMed] [Google Scholar]
  16. Govindarajan S., Goldstein R. A. Why are some proteins structures so common? Proc Natl Acad Sci U S A. 1996 Apr 16;93(8):3341–3345. doi: 10.1073/pnas.93.8.3341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Huang E. S., Subbiah S., Levitt M. Recognizing native folds by the arrangement of hydrophobic and polar residues. J Mol Biol. 1995 Oct 6;252(5):709–720. doi: 10.1006/jmbi.1995.0529. [DOI] [PubMed] [Google Scholar]
  18. Hunt N. G., Gregoret L. M., Cohen F. E. The origins of protein secondary structure. Effects of packing density and hydrogen bonding studied by a fast conformational search. J Mol Biol. 1994 Aug 12;241(2):214–225. doi: 10.1006/jmbi.1994.1490. [DOI] [PubMed] [Google Scholar]
  19. Huynen M. A., Stadler P. F., Fontana W. Smoothness within ruggedness: the role of neutrality in adaptation. Proc Natl Acad Sci U S A. 1996 Jan 9;93(1):397–401. doi: 10.1073/pnas.93.1.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kamtekar S., Schiffer J. M., Xiong H., Babik J. M., Hecht M. H. Protein design by binary patterning of polar and nonpolar amino acids. Science. 1993 Dec 10;262(5140):1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
  21. Kimura M. Evolutionary rate at the molecular level. Nature. 1968 Feb 17;217(5129):624–626. doi: 10.1038/217624a0. [DOI] [PubMed] [Google Scholar]
  22. King J. L., Jukes T. H. Non-Darwinian evolution. Science. 1969 May 16;164(3881):788–798. doi: 10.1126/science.164.3881.788. [DOI] [PubMed] [Google Scholar]
  23. Koshi J. M., Goldstein R. A. Mutation matrices and physical-chemical properties: correlations and implications. Proteins. 1997 Mar;27(3):336–344. doi: 10.1002/(sici)1097-0134(199703)27:3<336::aid-prot2>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
  24. Li H., Helling R., Tang C., Wingreen N. Emergence of preferred structures in a simple model of protein folding. Science. 1996 Aug 2;273(5275):666–669. doi: 10.1126/science.273.5275.666. [DOI] [PubMed] [Google Scholar]
  25. Lipman D. J., Wilbur W. J. Modelling neutral and selective evolution of protein folding. Proc Biol Sci. 1991 Jul 22;245(1312):7–11. doi: 10.1098/rspb.1991.0081. [DOI] [PubMed] [Google Scholar]
  26. Lupas A. Coiled coils: new structures and new functions. Trends Biochem Sci. 1996 Oct;21(10):375–382. [PubMed] [Google Scholar]
  27. Onuchic J. N., Wolynes P. G., Luthey-Schulten Z., Socci N. D. Toward an outline of the topography of a realistic protein-folding funnel. Proc Natl Acad Sci U S A. 1995 Apr 11;92(8):3626–3630. doi: 10.1073/pnas.92.8.3626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Orengo C. A., Jones D. T., Thornton J. M. Protein superfamilies and domain superfolds. Nature. 1994 Dec 15;372(6507):631–634. doi: 10.1038/372631a0. [DOI] [PubMed] [Google Scholar]
  29. Reidhaar-Olson J. F., Sauer R. T. Combinatorial cassette mutagenesis as a probe of the informational content of protein sequences. Science. 1988 Jul 1;241(4861):53–57. doi: 10.1126/science.3388019. [DOI] [PubMed] [Google Scholar]
  30. Sali A., Shakhnovich E., Karplus M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J Mol Biol. 1994 Feb 4;235(5):1614–1636. doi: 10.1006/jmbi.1994.1110. [DOI] [PubMed] [Google Scholar]
  31. Schulman B. A., Kim P. S. Proline scanning mutagenesis of a molten globule reveals non-cooperative formation of a protein's overall topology. Nat Struct Biol. 1996 Aug;3(8):682–687. doi: 10.1038/nsb0896-682. [DOI] [PubMed] [Google Scholar]
  32. Schuster P., Fontana W., Stadler P. F., Hofacker I. L. From sequences to shapes and back: a case study in RNA secondary structures. Proc Biol Sci. 1994 Mar 22;255(1344):279–284. doi: 10.1098/rspb.1994.0040. [DOI] [PubMed] [Google Scholar]
  33. Skolnick J., Kolinski A. Simulations of the folding of a globular protein. Science. 1990 Nov 23;250(4984):1121–1125. doi: 10.1126/science.250.4984.1121. [DOI] [PubMed] [Google Scholar]
  34. Smith J. M. Natural selection and the concept of a protein space. Nature. 1970 Feb 7;225(5232):563–564. doi: 10.1038/225563a0. [DOI] [PubMed] [Google Scholar]
  35. Strait B. J., Dewey T. G. The Shannon information entropy of protein sequences. Biophys J. 1996 Jul;71(1):148–155. doi: 10.1016/S0006-3495(96)79210-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Yee D. P., Chan H. S., Havel T. F., Dill K. A. Does compactness induce secondary structure in proteins? A study of poly-alanine chains computed by distance geometry. J Mol Biol. 1994 Aug 26;241(4):557–573. doi: 10.1006/jmbi.1994.1531. [DOI] [PubMed] [Google Scholar]
  37. Yue K., Fiebig K. M., Thomas P. D., Chan H. S., Shakhnovich E. I., Dill K. A. A test of lattice protein folding algorithms. Proc Natl Acad Sci U S A. 1995 Jan 3;92(1):325–329. doi: 10.1073/pnas.92.1.325. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES