Determination of the folding transition states of barnase by using Φ_I-value-restrained simulations validated by double mutant Φ_IJ-values

Abstract

The protein barnase folds from the denatured state into its native conformation via a high-energy intermediate. Using Φ_I-values determined experimentally from single-point mutations as restraints in all-atom molecular dynamics simulations, we have determined ensembles of structures corresponding to the transition states for the formation of the folding intermediate and its conversion into the native state. We have also introduced a stringent validation of the approach used to calculate such structures by predicting interaction Φ_IJ-values determined experimentally from a series of double-mutant cycles. The ensembles that we have obtained illustrate the heterogeneity in the nucleation-condensation process by which barnase folds. Obligatory steps of this process include the sequential formation of two folding nuclei, which correspond to the two main hydrophobic cores of the protein. Nonobligatory steps include the elongation of the strand β1 and the formation of the helix α2. The results confirm that the use of experimental observables such as Φ_I-values as restraints in molecular dynamics simulations is a powerful general strategy to characterize the relatively heterogeneous structural ensembles that populate nonnative regions of the energy landscapes of proteins.

A detailed characterization of the energy landscapes of proteins is an extremely valuable tool for increasing our understanding of important biological processes such as protein folding and aggregation (1). Crucial information about the extent of formation of interresidue interactions in transition states for folding, the saddle points on the energy landscape of proteins, is provided by Φ-values, parameters determined from a combination of kinetic measurements and protein engineering experiments (2, 3). The folding transition states of several small proteins have been characterized in detail by using the Φ_I-value approach (4–9) and have revealed fundamental details about the mechanism of protein folding (10). The realization that Φ_I-values bear the same relationship to molecular simulations of elusive states as do nuclear Overhauser effects to the structural determination of stable states by NMR spectroscopy has enabled transition states and folding pathways to be analyzed at atomic resolution (11–14). Indeed, Φ_I-values have been used directly as experimental restraints in computer simulations to calculate ensembles of structures representing the transition states of folding of several single-domain proteins, including acylphosphatase (12, 15), a fibronectin type III domain (16), two immunity proteins (17), and a series of SH3 domains (18). These studies have enabled important features of these ensembles to be recognized, including a description of the critical role of certain key residues in establishing the topology of the native state through a nucleation-condensation mechanism.

In this work, we use Φ_I-values as restraints in molecular dynamics (MD) simulations of a protein with a complex folding pathway, barnase, a 110-residue ribonuclease from Bacillus amyloliquefaciens. Barnase folds via a multistate mechanism in which a high-energy intermediate is populated during folding (19, 20). The folding process has been characterized in particularly high detail by a combination of experimental and computational techniques (13, 21). Folding initiates from a denatured state that contains some residual native-like structure, as shown both by NMR experiments and MD simulations (22–24); the protein then populates transiently a high-energy intermediate between two successive transition states (TS1 and TS2) before reaching the fully native structure (19).

Evidence in support of the modular character of the folding of barnase stems from experimental studies made on selected barnase C-terminal fragments, which show that a significant degree of native-like structure can be formed even in the absence of many of the interactions that define the complete protein fold (25). Moreover, the extent of native-like structure in the C-terminal fragment increases significantly in the presence of fragments corresponding to the N-terminal helix α1 (26). The actual rate-limiting step in the folding of the intact barnase molecule depends on the concentration of chemical denaturant; at high concentrations the rate-determining step in the folding reaction is associated with TS2, between the high-energy intermediate and the native state, whereas at low concentrations it is associated with TS1, which separates the unfolded state from the high-energy intermediate (19, 20).

The folding mechanism of barnase proposed originally (27) postulated a kinetically detectable intermediate and at least one further low-energy dead-time (submillisecond) intermediate. Bai and coworkers (28–30), on the basis of being unable to find protection against hydrogen exchange that is attributable to the dead-time intermediate, and finding a smoothly curved dependence of the logarithm of unfolding rate constant against concentration of denaturant, suggested that there is no intermediate on the folding pathway of barnase, but rather that the protein folds according to two-state kinetics but with a gradual movement of the transition state as the denaturant concentration varies. Fersht and coworkers (19, 20), however, have demonstrated that the denaturant dependence of the unfolding kinetics is sigmoidal, thus showing the existence of a high-energy intermediate, and detected directly a low-energy intermediate in submillisecond continuous-flow experiments. The Φ_I-value analysis of the major transition state (TS2), measured from the unfolding kinetics at high denaturant concentration, is unaffected by these findings, but we can now interpret definitively that the observed rate constant for folding under these conditions is that for the process of going from the low-energy submillisecond intermediate (the unfolded state under refolding conditions), which has a significant amount of residual structure (23, 31), to the high-energy intermediate (20), thus allowing characterization of TS1.

In the present study, we have determined the structures of the TS1 and TS2 ensembles using Φ_I-values as restraints in MD simulations. Φ_I-values from point mutations are a measure of the gain in native interactions in the transition state for folding, relative to those interactions that already formed in the denatured state (4). In addition, we have benchmarked our calculations against Φ_IJ-values for tertiary interactions determined from double mutant cycles, providing a stringent procedure for validating the methods that we have used for determining the structures of transition states. Analysis of these ensembles provides further insight into the mechanism by which the native fold of barnase is achieved.

Methods

Determination of the Structures. Previous computational studies of transition states by using Φ_I-values as restraints in computer simulations made the simplifying assumption that the probability of the formation of native contacts was negligible in the denatured state (15–18). This assumption is appropriate when it is known experimentally that the extent of residual structure in the denatured state is low and the degree of structure in the transition state is high. The average Φ_I-value for the first transition state of barnase is, however, very low (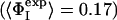), and the degree of residual structure present in the denatured state, whether formed by reducing the pH, increasing the temperature, or adding chemical denaturants, is significant (22). In the present study, we have therefore taken into account the existence of native contacts in the denatured state (D) of barnase. We use the definition 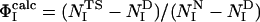where the calculated Φ_I-value of residue I (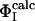) depends on the number of native contacts made by residue I in the native state (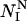) and on the number of native contacts made in the TS (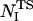) and in the denatured state (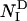) (32). N_I is calculated as

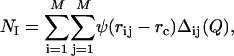[1]

where M is the number of nonhydrogen side-chain atoms in barnase, and Δ_ij(Q) = 1 if atoms i and j are closer than a threshold distance r_c and more than Q residues away in the sequence; otherwise, Δ_ij(Q) = 0. In all of the simulations carried out in this work, we set r_c = 5.5 Å and Q = 2 as described in ref. 15. To smooth the contact threshold and facilitate the calculation of the forces, we used the sigmoidal function ψ(r) = 1/(1 + exp(βr)), where β = 5 (15). Native contacts were computed from the crystal structure of barnase (see Fig. 1), and 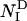was calculated as the average number of native contacts in an ensemble of configurations generated in 20 cycles of MD simulated annealing. In each cycle, the temperature of the system was first raised to 600 K to unfold the native structure and increase the efficiency of the sampling of conformational space and then slowly decreased to 300 K to restore the correct weights for the interatomic interactions under physiological conditions. At the end of each cycle, the configuration of the system was stored for subsequent analysis. In these simulations, the radius of gyration of the unfolded protein was biased to be close to 16.5 Å, the value corresponding to the end point of the thermal denaturation trajectories obtained by MD simulations by Daggett and coworkers (24).

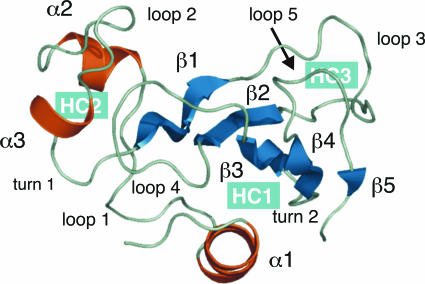
Fig. 1.

Native structure of barnase [PDB ID code 1a2p (54)]. The secondary structure elements are α1 (7–17), α2 (27–32), α3 (42–45), β1 (50–55), β2 (71–75), β3 (87–91), β4 (96–99), and β5 (107–108). The native state of the protein contains two relatively independent domains and is stabilized by the formation of three hydrophobic cores (highlighted in blue). The first domain includes hydrophobic cores 1 and 3, α1, and the C-terminal β-sheet. Hydrophobic core 1 is formed by the docking of α1 on to the centre of the C-terminal β-sheet. The second domain is formed by the association of α2 and α3. Hydrophobic core 2, which involves α2, α3, and loop 4, is the only core involving residues of both domains and hence it acts to stabilize the interface between them (46).

The restrained MD simulations were performed with the program charmm (33) using an all-atom model of the protein (34) and an implicit model for the solvent (35). An initial model for the transition state was obtained by using biased MD techniques as described in ref. 15, and the configurational search within the transition state ensemble was carried out by using repeated simulated annealing cycles, employing a similar protocol to that used for the generation of the structures of the unfolded state. The restraints were implemented as a harmonic potential that minimizes the function ρ, where

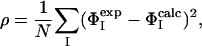[2]

where N is the number of Φ^exp restraints used in the calculation. In the presence of parallel folding pathways (36), the procedure that we described should be implemented by using ensemble-averaged simulations (17, 37), by imposing the Φ_I-value restraints on P copies of the protein molecule. When parallel folding pathways are not present, as in the case of barnase, we have shown that it is sufficient to use P = 1 (17, 37).

The efficiency of the sampling of conformational space was optimized with respect to the maximum temperature of the simulated annealing cycle. For any given transition state, using a maximum temperature for the cycle that is inversely proportional to 〈Φ^exp〉 ensures that the configurational search is extensive. Based on this criterion, the upper temperature in the simulated annealing cycle for the determination of TS1 was set to 500 K (〈Φ^exp〉 = 0.2), and to 400 K for TS2 (〈Φ^exp〉 = 0.6); in both cases, the structures of the transition states were defined to be those present when the final temperature of 300 K was reached. Ensembles of 40 structures representative of the two transition state were analyzed by using methods described in ref. 15.

Validation of the Structures. An important step in any process of structure determination is to assess the validity of the resulting structural models by testing their ability to predict the results of experiments that are not used as restraints. For this purpose, we used the structural ensembles for TS1 and TS2, obtained by using the restrained MD simulations, to predict the results of experimental double-mutant cycle measurements (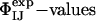) (38–41). The high level of agreement described below between the Φ_IJ-values predicted from structures determined in the absence of such data and those measured experimentally is a stringent validation of the structural models presented in this work. An alternative validation procedure, in which the probability of folding (P_fold) of the putative members of the TS ensemble is computed by using Monte Carlo simulations and the Go model, and compared with its theoretical value (0.5), has recently been discussed by Hubner et al. (42).

Double-mutant cycle experiments were used to determine the strength of the interaction between two specific side chains (I and J) in the native state of a protein (38–41, 43). By measuring the change in stability of a single mutant of each residue (ΔΔG_I→A and ΔΔG_J→A) and of a double-mutant (ΔΔG_I→A,J→A), it is possible to calculate the free energy of interaction between residues I and J (ΔG_IJ) by using the thermodynamic cycle ΔΔG_IJ =ΔΔG_I→A +ΔΔG_J→A – ΔΔG_I→A,J→A. This method can be extended to the characterization of the transition state for folding as a comparison ΔΔG_IJ with its kinetic equivalent 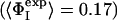enables 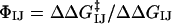to be defined, where Φ_IJ expresses the extent to which the side chains of residues I and J interact in the transition state relative to the native state. Φ_IJ-values have the potential to provide high-resolution information and are therefore a powerful method for cross-validation purposes. Moreover, the caveat in defining Φ_I-values that any structure present in the denatured state must be unchanged by mutation does not apply to Φ_IJ-values because both partners in an interaction are mutated and any perturbation of the denatured state cancels out (38). Following the contact-based definition of Φ_I-values, we define the calculated Φ_IJ-value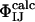s () as 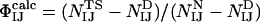, where N_IJ is calculated as

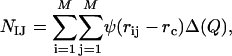[3]

and only the interatomic contacts between residues I and J are considered in the calculation of 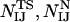, and .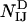

Results

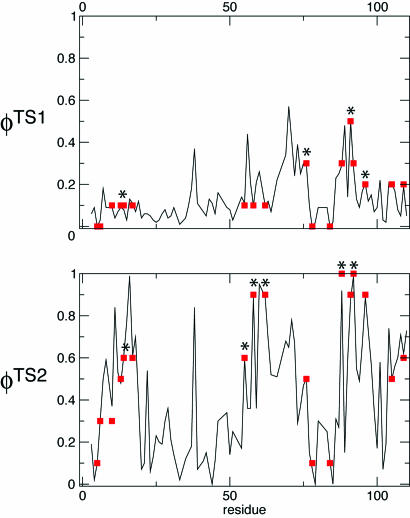
Determination of the Ensembles of TS1 and TS2. We have determined ensembles of protein structures corresponding to the first (TS1) and second (TS2) transition states of barnase using the 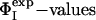measured for each state (5, 44) (A.R.F., unpublished results). The ensembles that we obtained fulfill all of the experimental restraints with high accuracy (Fig. 2) as illustrated by the high correlation between the experimental and calculated Φ_I-values (the Pearson correlation coefficient is 0.99 for both TS1 and TS2).

Fig. 2.

Comparison between 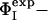and 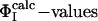for TS1 and TS2. The Φ-values of the key residues for folding (see text) are identified by an asterisk.

TS1 and TS2 have similar radii of gyration and are both slightly expanded when compared with the native state (13.9 ± 0.4 Å for TS1, 14.0 ± 0.4 Å for TS2, and 13.5 ± 0.1 Å for N). They also have significantly higher solvent-accessible areas than the native protein (6,510 ± 240 Ų for TS1, 6,420 ± 240 Ų for TS2, and 5,850 ± 80 Ų for N). The rms deviation of TS1 from the native state is 11.0 ± 1.5 Å, whereas TS2 is considerably more native-like, with an rms deviation of 7.2 ± 1.1 Å.

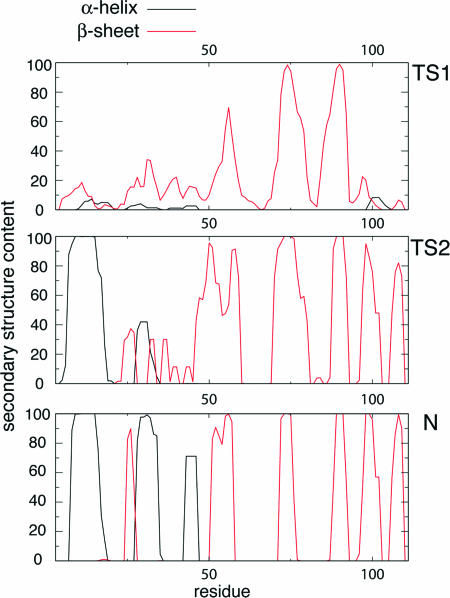
The average secondary structure content in TS1 is limited to the presence of the three central strands (β2–β4) of the native-like β-sheet, as shown in Fig. 3; the extent of secondary structure in TS2 is much higher, and all of the strands (β1–β5) of the native β-sheet are present. The difference in helical content between TS1 and TS2 is also significant because no persistent helices are present in TS1, whereas helix α1 is completely formed in TS2. In ≈40% of the structures that were determined for TS2 helix α2 is also formed; helix α3, by contrast, is completely unfolded in the ensemble. Interestingly, in both transition states, the region of sequence that corresponds to helices α2 and α3 in the native state adopts nonnative β-strand secondary structure in a significant number of structures (see below).

Fig. 3.

Secondary structure content of the transition and native states of barnase. The percentage of secondary structure was computed by using dsspcont (55).

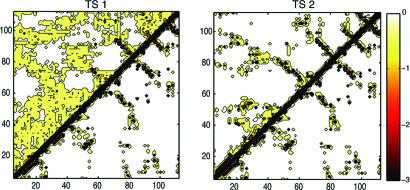
Analysis of the average interaction energies between residue pairs formed in TS1 (see Fig. 4) shows that the only persistent contacts are those between strands β2 and β3 and strands β3 and β4. The hydrophobic cores (see Fig. 1) that stabilize the native structure of barnase are evident in the interaction map, but the corresponding interaction energies are low and suggest that these structural elements are weak and nonpersistent. The situation in TS2 is very different. All of the interactions that stabilize the native β-sheet are essentially present, and there are significant nonnative interactions due to a slight lengthening of some β-strands, particularly β1; by contrast, helix α2 is only marginally formed, and helix α3 is completely unfolded in this transition state, causing strand β1 to extend into this otherwise relatively unstructured part of the sequence.

Fig. 4.

Average residue–residue interaction energy maps (15) for TS1, TS2, and the native state (N) of barnase (below the diagonal).

Key Residues Define the Transition State. In proteins that fold via a nucleation-condensation mechanism (45) the residues with the highest Φ_I-values are often, but not always, involved in the formation of the folding nucleus (6, 12). One method for identifying the residues that form the critical interactions that stabilize the nucleus is to determine the minimal set of 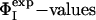restraints that must be used as restraints to generate an ensemble that allows the 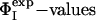of the unrestrained residues to be predicted (12, 16). Application of this method to the case of barnase shows that the network of interactions that characterizes TS1 is largely determined by four key residues, Ile-12, Ile-74, Ser-89, and Ile-94. The 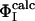profile obtained by using only the 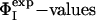of these four residues as restraints was compared with the Φ^calc profile determined by using all of the 20 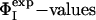as restraints. The resulting cross-validated correlation coefficient is 0.79, indicating that all 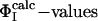can be well predicted by using only the restraints involving these four key residues. As shown in Fig. 1, these residues are all involved in the stabilization of hydrophobic core 1 (46).

An analogous procedure reveals that the residues that are most important in defining the network of interactions that characterizes TS2 are Leu-14, Ile-55, Asn-58, Lys-62, Ile-88, and Ser-92. The cross-validated correlation coefficient in this case is 0.84. This set of six residues is involved in the stabilization of both hydrophobic cores 1 and 3 in the native state; Asn-56 and Lys-60, in particular, stabilize hydrophobic core 3 by the formation of a network of hydrogen bonds.

Structure Validation Using Double-Mutant Cycles. We used the ensembles TS1 and TS2 to predict the results of double-mutant experiments carried out for barnase (38–41). Double-mutant cycles measure the degree of interaction between two side chains, I and J (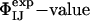), in the native state through the construction of a thermodynamic cycle (38); this approach can be extended to the study of the transition state if the cycle is constructed with activation parameters. A comparison of these two quantities provides an unambiguous measure of the extent of interaction between two specific side chains in the transition state for folding (41, 43).

Because the 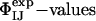have not been used as restraints in the determination of TS1 and TS2, they offer a stringent test for structure validation. The comparison between 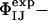and 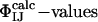is shown in Table 1. There is a significant statistical error in the computation of the 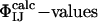because both ensembles, especially TS1, are structurally heterogeneous. Nevertheless the calculated values reproduce well the experimental values in all cases, showing that the present structure determination procedure is able to generate valid ensembles of structures for each TS.

Table 1. Comparison between calculated and experimental Φ_IJ-values obtained by using double-mutant cycles.

Residue		TS1		TS2
I	J	ΦIJexp	ΦIJcalc	ΦIJexp	ΦIJcalc
Asp-8	Arg-110	0.1	0.1 ± 0.3	0.6	0.7 ± 0.4
Asp-12	Arg-110	0.0	0.0 ± 0.2	0.6	0.6 ± 0.3
Thr-13	Tyr-17	0.1	0.2 ± 0.1	0.8	0.8 ± 0.1
Tyr-16	Tyr-17	0.2	0.2 ± 0.2	0.9	0.8 ± 0.2
His-18	Trp-94	0.1	0.1 ± 0.2	0.9	0.7 ± 0.3
Arg-69	Asp-93	0.3	0.1 ± 0.3	0.7	0.6 ± 0.3

The Φ_IJ-values were not used as restraints in the structure determination process. The interactions between Asp-8 and Arg-110 and between Asp-12 and Asp-110 report on the proximity of the N and C termini; those between Thr-13 and Tyr-17 and between Tyr-16 and Tyr-17 report on the interactions in α1; those between His-18 and Trp-94 report on the interaction between C-terminus of α1 and the turn in the β3-β4 hairpin; and finally the interactions between Arg-69 and Asp-93 link the turn in the β3-β4 hairpin to the loop between β1 and β2. See refs. 38–41 for further details.

Discussion

Transition states for folding are structurally heterogeneous ensembles, because a significant fraction of the interactions that stabilize the native state have yet to form (12, 18, 47, 48). The only structural feature common to all members of the ensemble is the presence of the folding nucleus of the nucleation-condensation mechanism (6, 46, 49); as a consequence, the variability between the structures tends to reside in regions outside the nucleus (12). One important aspect of the procedure that we have used to determine the structures of the transition states is that an ensemble of protein configurations compatible with the Φ_I-values is calculated rather than a single structure (15–18). It is therefore possible to carry out a statistical analysis of the properties of the transition states and to characterize not only those interactions that are common to all members of the transition state ensemble but also the variability of other structural features within it.

The First Transition State. Although the degree of helicity of the region of the sequence that corresponds to α1 in the native structure is very low in TS1, prenucleation events such as the formation of helix turns can be observed in the ensemble of structures that we determined. These helix-nucleation attempts are, however, not productive because they do not lead to the formation of helix α1, most likely because the tertiary contacts with the β-sheet that are necessary for the stabilization of this helix (26) are not yet completely established. The weakness of the interhelical interactions is illustrated in Fig. 4, where it is apparent that there are less of these tertiary contacts in TS1 relative to the native state. Moreover, in several conformations that contribute to the TS1 ensemble, residues in the region of the sequence corresponding to helix α1 in the native state are found to form nonnative β-strand structures, as shown in Fig. 3. There is, in addition, no significant degree of formation of native-like secondary structure in the region of the sequence corresponding to helices α2 and α3 in the native state (see Fig. 3). By contrast, the average secondary structure content of this region indicates a degree of nonnative β-strand formation that peaks at ≈35% for residues Glu-27 through Gln-29. Inspection of Fig. 5 reveals that this structure is due in part to the spontaneous extension of the native β-strands in some members of the ensemble, most likely due to the energetic advantage imparted by the formation of hydrogen bonds in this otherwise highly unfolded part of the polypeptide chain.

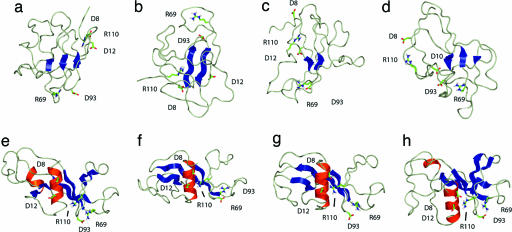
Fig. 5.

The four most representative structures determined for TS1 (structures a–d) and for TS2 (structures e–h) obtained by using a clustering procedure (15). Only the side chains of those residues involved in electrostatic side-chain-to-side-chain interactions probed by the Φ_IJ-values are shown to illustrate their variability in the transition state ensemble. Only those elements of secondary structure than span at least two residues have been highlighted.

The contacts formed by residues Leu-14, Ile-76, Ser-91, and Ile-96 are sufficient to determine the network of interactions that characterizes the first transition state in the folding of barnase. Three of these residues (Leu-14, Ile-76, and Ile-96) have side chains that point toward the interface between helix α1 and the β-sheet in the native structure, which form the main hydrophobic core of the protein. The fourth residue (Ser-91) is essential for the stability of the β-turn formed by residues Ser-91 to Ile-96, which is known to be partially formed in the chemical, thermal, and simulated denatured states of barnase (22, 23, 50). The importance of Ile-76 for folding highlights the fact that the formation of TS1 involves the transformation of the β-hairpin found in the denatured state into a three-stranded β-sheet through the formation of weak but essential contacts with residues that belong to α1 in the native state. Hydrophobic core 1 is therefore the first core formed in the folding of barnase. The interactions that stabilize this core are between residues that are found near the termini of the sequence of this protein, indicating that the first productive structural rearrangement in the folding pathway of barnase is the approach of the N and C termini to form the main hydrophobic core and, in the process, significantly reduce the configurational entropy of the polypeptide backbone.

The Second Transition State. The ensemble of structures obtained for the second transition state of barnase is much less heterogeneous than that obtained for the first (the average pairwise rms deviation in TS2 is ≈4 Å, compared with a value of ≈11 Å in TS1) and much more native-like (the average rms deviation from the native structure is of ≈11 Å in TS1 and ≈7 Å in TS2), especially in the structural region formed by the C-terminal β-sheet and the region corresponding to α1 in the native state. The map of the pairwise interactions present in TS2 shows that the native contacts within this major domain are essentially formed (see Fig. 4). Some of the β-strands, as shown in Fig. 3, extend to nonnative lengths into the secondary domain formed by helices α2 and α3.

In terms of secondary structure formation, the most important difference between TS1 and TS2 is the consolidation of the entire β-sheet, in particular the formation of the strands β1 and β5, and the complete formation of helix α1. The fact that these events take place concomitantly with the formation of contacts between helix α1 and the β-sheet reveals that they are strongly coupled in agreement with experiment (26). The native secondary structure of the domain formed by helices α2 and α3 is not, however, yet present in TS2 (see Fig. 3). Inspection of the most representative structures of the ensemble (see Fig. 5) reveals that the secondary structure in the region of the sequence that corresponds to helices α2 and α3 in the native state is very heterogeneous. Some structures (Fig. 5e) show a significant content of native-like α-helical secondary structure, but there are also members of the ensemble (Fig. 5 f and g) for which a significant amount of nonnative β-strand secondary structure is present. The second transition state of barnase has also been characterized by MD unfolding simulations that gave results in good agreement with the experimental Φ_I-values (11, 24). One apparent discrepancy was, however, observed in that helix α2 was found to be substantially formed in the simulations, although the experimental Φ_I-values corresponding to Ala to Gly mutations in this part of the sequence are low. The present analysis shows that hydrophobic core 2, which involves mainly helices α2 and α3, folds independently from the other two hydrophobic cores. Mutations carried out in the helical domain affect the degree of formation of helices α2 and α3 but not their rate of folding, which is determined by the structure present in the major domain (51); therefore, the structures selected from these high-temperature thermal denaturations (11, 24) are compatible with those determined in the present study, although the former represent only a subset of the transition state ensemble. Structural elements, such as helix α2, that are not indispensable for the formation of TS2 are present only in some of the conformations making up the ensemble.

As pointed out above, the formation of the native-like tertiary interactions of just six residues is sufficient to determine the network of interactions that stabilizes TS2. Most of these residues have important roles in the stabilization of the native structure of barnase: Leu-14 and Ile-88 are part of the main hydrophobic core, Ser-91 stabilizes the β-turn, which is the initiation site for folding (22), and Asn-58 and Lys-62 contribute to the stability of hydrophobic core 3 (Fig. 1) (46). Ile-55 is not involved in the stabilization of either of the hydrophobic cores of the protein but is at the edge of the β-sheet, in strand β1; the fact that its interactions are crucial to the formation of TS2 shows that most of the β-sheet structure of the domain is present in this transition state.

Concluding Remarks

The determination of the structures of the transition states for folding is extremely difficult because they represent regions of the free energy landscape that are populated only transiently. The fact that the structure determination procedure that we used in this work is successful is a reflection of both experimental and theoretical observations that indicate that folding transition states have a native-like topology (18, 52) and are stabilized by the formation of relatively few native-like interactions involving a subset of highly connected residues (53) in the folding nucleus (10, 49). The application of this methodology to a protein with a relatively complex structure and folding process such as barnase reveals, in agreement with the essential features of the nucleation-condensation mechanism, that the formation of the folding nucleus is sufficient to capture most of the structural features of the transition state for folding. Indeed, the fact that side-chain-to-side-chain interactions not used as restraints in the simulations can be accurately predicted from the ensemble of structures representing each transition state represents a powerful validation of both the specific results of the present study and of the general approach of using experimental data as restraints in MD simulations to characterize nonnative regions of the energy landscape or proteins.