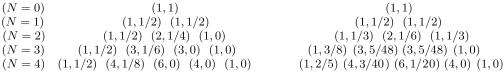Abstract
Phase space can be constructed for N equal and distinguishable subsystems that could be probabilistically either weakly correlated or strongly correlated. If they are locally correlated, we expect the Boltzmann-Gibbs entropy SBG ≡ -k Σi pi ln pi to be extensive, i.e., SBG(N) ∝ N for N → ∞. In particular, if they are independent, SBG is strictly additive, i.e., SBG(N) = NSBG(1), ∀N. However, if the subsystems are globally correlated, we expect, for a vast class of systems, the entropy Sq ≡ k[1 - Σi pqi]/(q - 1) (with S1 = SBG) for some special value of q ≠ 1 to be the one which is extensive [i.e., Sq(N) ∝ N for N → ∞]. Another concept which is relevant is strict or asymptotic scale-freedom (or scale-invariance), defined as the situation for which all marginal probabilities of the N-system coincide or asymptotically approach (for N → ∞) the joint probabilities of the (N - 1)-system. If each subsystem is a binary one, scale-freedom is guaranteed by what we hereafter refer to as the Leibnitz rule, i.e., the sum of two successive joint probabilities of the N-system coincides or asymptotically approaches the corresponding joint probability of the (N - 1)-system. The kinds of interplay of these various concepts are illustrated in several examples. One of them justifies the title of this paper. We conjecture that these mechanisms are deeply related to the very frequent emergence, in natural and artificial complex systems, of scale-free structures and to their connections with nonextensive statistical mechanics. Summarizing, we have shown that, for asymptotically scale-invariant systems, it is Sq with q ≠ 1, and not SBG, the entropy which matches standard, clausius-like, prescriptions of classical thermodynamics.
The entropy Sq (1) is defined through§,¶
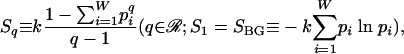 |
[1] |
where k is a positive constant (k = 1 from now on) and BG stands for Boltzmann-Gibbs. This expression is the basis of nonextensive statistical mechanics (16-18) (see http://tsallis.cat.cbpf.br/biblio.htm for a regularly updated bibliography), a current generalization of BG statistical mechanics. For q ≠ 1, Sq is nonadditive (hence nonextensive) in the sense that for a system composed of (probabilistically) independent subsystems, the total entropy differs from the sum of the entropies of the subsystems. However, the system may have special probability correlations between the subsystems such that extensivity is valid, not for SBG, but for Sq with a particular value of the index q ≠ 1. In this paper, we address the case where the subsystems are all equal and distinguishable. Their correlations may exhibit a kind of scale-invariance. We may regard some of the situations of correlated probabilities as related to the remark (see refs. 19-23 and references therein) that Sq for q ≠ 1 can be appropriate for nonlinear dynamical systems that have phase space unevenly occupied. We return to this point later.
We shall consider two types of models. The first one involves N binary variables (N = 1, 2, 3,...), and the second one involves N continuous variables (N = 1, 2, 3). In both cases, certain correlations that are scale-invariant in a suitable limit can create an intrinsically inhomogeneous occupation of phase space. Such systems are strongly reminiscent of the so called scale-free networks (24, 25), with their hierarchically structured hubs and spokes and their nearly forbidden regions.
Discrete Models
Some Basic Concepts. The most general probabilistic sets for N equal and distinguishable binary subsystems are given in Fig. 1 with
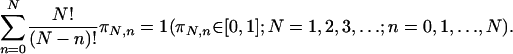 |
[2] |
Fig. 1.
Most general sets of joint probabilities for N equal and distinguishable binary subsystems.
Let us from now on call Leibnitz rule the following recursive relation:
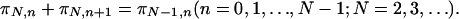 |
[3] |
This relation guarantees what we refer to as scale-invariance (or scale-freedom) in this article. Indeed, it guarantees that, for any value of N, the associated joint probabilities {πN,n} produce marginal probabilities which coincide with {πN-1,n}. Assuming π10 + π11 = 1, and taking into account that the Nth row has one more element than the (N - 1)th row, a particular model is characterized by giving one element for each row. We shall adopt the convention of specifying the set {πN,0 ∈ [0, 1], ∀N}. Everything follows from it. There are many sets {πN,0} that satisfy Eq. 3. Let us illustrate with a few simple examples:
(i) πN,0 = (2π10)N/N + 1 (0 ≤ π10 ≤ 1/2; N = 1, 2, 3,...). We have that all 2N states have nonzero probability if 0 < π10 ≤ 1/2. The particular case π10 = 1/2 recovers the original Leibnitz triangle itself (26) (see Fig. 2).
Fig. 2.
The left numbers within the parentheses correspond to Pascal triangle. The right numbers correspond to the Leibnitz harmonic triangle (d = N).
(ii) πN,0 = (π10)Nα (α ≥ 0; N = 1, 2, 3...). The α = 1 instance corresponds to independent systems, i.e., πN,n = (π10)N-n (1 - π10)n. If 0 < π10 < 1, then all 2N states have nonzero probability. The α = 0 instance corresponds to πN,0 = π10, πN,n = 0 (n = 1, 2,..., N - 1) and πN,N = 1 - π10. If 0 < π10 < 1, then only two among the 2N states have nonzero probability, ∀N, namely the states associated with πN,0 and πN,N.
We may relax the Leibnitz rule to some extent by considering those cases where the rule is satisfied only asymptotically, i.e.,
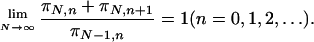 |
[4] |
Such cases will be said to be not strictly but asymptotically scale-invariant (or asymptotically scale-free). This is, for a variety of reasons, the situation in which we are primarily interested. The main reason is that what vast classes of natural and artificial systems typically exhibit is not precisely power-laws, but behaviors which only asymptotically become power-laws (once we have corrected, of course, for any finite size effects). This is consistent with the fact that within nonextensive statistical mechanics Sq is optimized by q-exponential functions (see ref. 1 and references therein and refs. 27 and 28), which only asymptotically yield power-laws. It is consistent also with a new central limit theorem that has been recently conjectured (29) for specially correlated random variables.∥
Let us now introduce a further concept, namely q-describability. A model constituted by N equal and distinguishable subsystems will be called q-describable if a value of q exists such as Sq(N)is extensive, i.e., limN→∞ Sq(N)/N <∞. If that special value of q equals unity, this corresponds to the usual BG universality class. If that value of q differs from unity, we will have nontrivial universality classes. If the subsystems {Ai} are not necessarily equal, the system is q-describable if an entropic index q exists such that limN→∞ 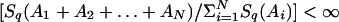 . It should be clear that we could equally well demand the extensivity of say S2-q [or even of SQ(q), where Q(q) is some monotonically decreasing function of q satisfying Q(1) = 1] instead of that of Sq. This would of course have the effect of having nontrivial solutions for q > 1 whenever we had solutions for q < 1 if the extensivity that was imposed was that of Sq.
. It should be clear that we could equally well demand the extensivity of say S2-q [or even of SQ(q), where Q(q) is some monotonically decreasing function of q satisfying Q(1) = 1] instead of that of Sq. This would of course have the effect of having nontrivial solutions for q > 1 whenever we had solutions for q < 1 if the extensivity that was imposed was that of Sq.
Finally, let us point out that we might consider the subsystems of a probabilistic system to be either strongly (or globally) correlated or weakly (or “locally”) correlated. The trivial case of independence, i.e., when the subsystems are uncorrelated, is of course a particular case of weakly correlated. Let us make these notions more precise. A system is weakly correlated if for every generic (different from zero and from unity) joint probability 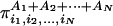 a set of individual probabilities
a set of individual probabilities 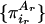 exists such that limN→∞
exists such that limN→∞ 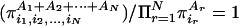 . Otherwise, the system is said to be strongly correlated. The particular case of independence corresponds to
. Otherwise, the system is said to be strongly correlated. The particular case of independence corresponds to
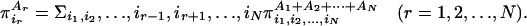 |
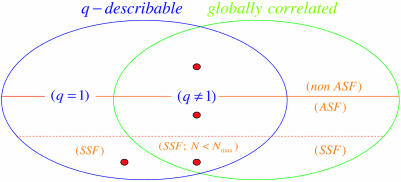
If the subsystems are equal and binary, this definition becomes as follows: a system is weakly correlated if, for generic πN,n, a probability p0 exists such that limN→γ 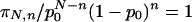 . Otherwise the system is said to be strongly correlated. The particular case of independence corresponds to p0 = π10. In the present sense, weakly correlated systems could also be thought and referred to as asymptotically uncorrelated. The interplay of scale-invariance, q-describability, and global correlation is schematized in Fig. 3.
. Otherwise the system is said to be strongly correlated. The particular case of independence corresponds to p0 = π10. In the present sense, weakly correlated systems could also be thought and referred to as asymptotically uncorrelated. The interplay of scale-invariance, q-describability, and global correlation is schematized in Fig. 3.
Fig. 3.
Scheme representing the systems that are q-describable, globally correlated, asymptotically scale-free (ASF), and strictly scale-free (SSF). The q = 1 region corresponds to “locally” correlated systems. The Leibnitz rule is strictly satisfied for SSF, but only asymptotically satisfied for ASF. Below (above) the continuous red line we have the ASF (non ASF) systems. The SSF systems (below the dashed red line) constitute a subset of the ASF subset. The red spots correspond to the four families of discrete systems illustrated in the present paper: q ≠ 1 non ASF (upper spot; Eqs. 12 and 14); q ≠ 1 ASF but non SSF (middle spot; Eqs. 17 and 24); q ≠ 1 SSF (right bottom spot; Eq. 8); q = 1 SSF (left bottom spot; examples i and ii in the text).
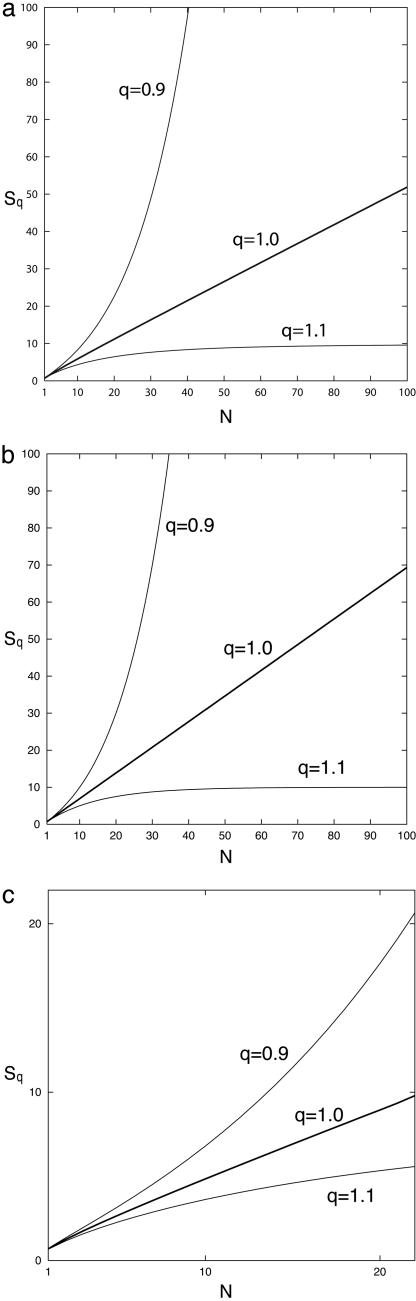
We have verified that all systems illustrated in i and ii above belong to the q = 1 class (see examples in Fig. 4). We next address q ≠ 1 systems.
Fig. 4.
Sq(N) for the Leibnitz triangle [the explicit expression πN,n = 1/(N + 1) (N - n)!n!/N! has been used to calculate Sq(N)] (a) α = 1 (i.e., independent subsystems) with π10 = 1/2 [the explicit expression πN,n = (π10)N-n (1 - π10)n has been used to calculate Sq(N) (b) and α = 1/2 with π10 = 1/2 [the recursive relation 3 has been used to calculated Sq(N)] (c). Only for q = 1 we have a finite value for limN → ∞ Sq(N)/N; it vanishes (diverges) for q > 1 (q < 1).
A Discrete Model That Is Not Asymptotically Scale-Invariant. Let us consider the probabilistic structure indicated in Fig. 5, where, for given N, only the d + 1 first elements are different from zero, with d = 0, 1, 2,..., N.
Fig. 5.
Probabilistic models with d = 1 (Left) and d = 2 (Right).
As we see, 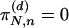 for N ≥ d + 1 and n = d + 1, d + 2,..., N. The total number of states is given by W(N) = 2N (∀d), but the number of states with nonzero probability is given by
for N ≥ d + 1 and n = d + 1, d + 2,..., N. The total number of states is given by W(N) = 2N (∀d), but the number of states with nonzero probability is given by
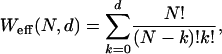 |
[5] |
where eff stands for effective. For example, Weff(N, 0) = 1, Weff(N, 1) = N + 1, Weff(N, 2) = ½N(N + 1) + 1, Weff(N, 3) = ⅙N(N2 + 5) + 1, and so on. For fixed d and N → ∞ we have that
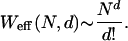 |
[6] |
Let us now make a simple choice for the nonzero probabilities, namely equal probabilities. In other words,
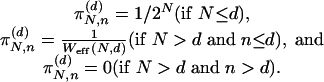 |
[7] |
See Fig. 6 for an illustration of this model.
Fig. 6.
Uniform distribution model with d = 1 (Left) and d = 2 (Right).
The entropy for this model is given by
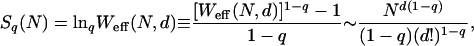 |
[8] |
where we have used now Eq. 6. Consequently, Sq is extensive [i.e., Sq(N) ∝ N for N → ∞] if and only if
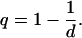 |
[9] |
Hence, if d = 1, 2, 3..., the entropic index monotonically approaches the BG limit from below. We can immediately verify in Fig. 6 (and using Eq. 7) that this model violates the Leibnitz rule for all N, including asymptotically when N → ∞. Consequently, it is neither strictly nor asymptotically scale-free. However, it is q-describable (see Fig. 3).
An Asymptotically Scale-Invariant Discrete Model. Starting with the Leibnitz harmonic triangle, we shall construct a heterogeneous distribution 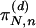 . The Leibnitz triangle is given in Fig. 2 and satisfies
. The Leibnitz triangle is given in Fig. 2 and satisfies
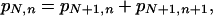 |
[10] |
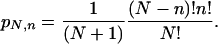 |
[11] |
We now define
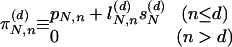 |
[12] |
where the excess probability 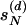 and the distribution ratio
and the distribution ratio 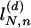 (with 0 < ε < 1) are defined through
(with 0 < ε < 1) are defined through
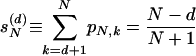 |
[13] |
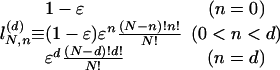 |
[14] |
(see Fig. 7). We have verified for d = 1, 2, 3, 4 and N → ∞ a result that we expect to be correct for all d < N/2, namely that 0 < πN,n+1 << πN,n ∼ πN-1,n << 1, hence
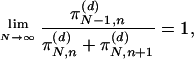 |
[15] |
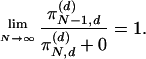 |
[16] |
Fig. 7.
Leibnitz-triangle-based ε = 0.5 probability sets: d = 1 (Left), and d = 2 (Right).
In other words, the Leibnitz rule is asymptotically satisfied for the entire probability set {πN,n}, i.e., this system has asymptotic scale invariance. Its entropy is given by
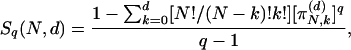 |
[17] |
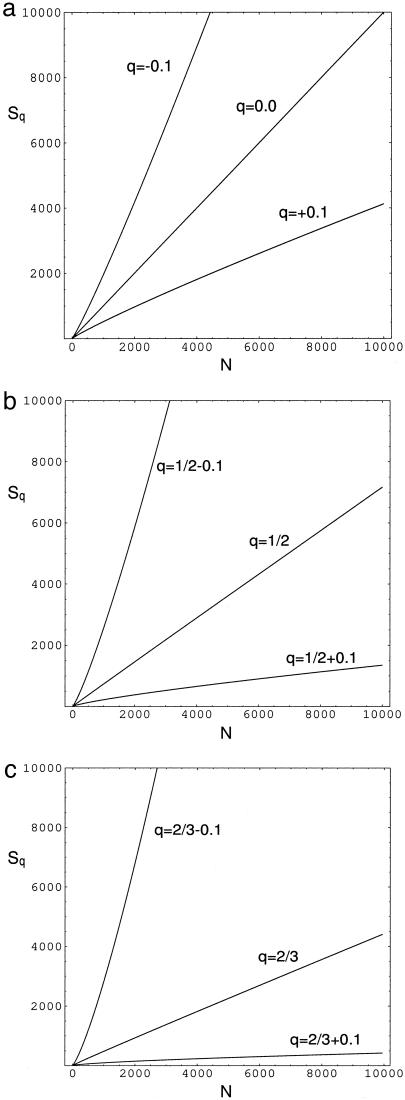
and we verify that a value of q exists such that limN→∞ Sq(N,d)/N is finite. Our numerical results suggest that, for 0 < ε < 1 (see Fig. 8),
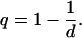 |
[18] |
Fig. 8.
Illustrations of the extensivity of Sq for the q ≠ 1 ASF model (with ε = 0.5): (a) d = 1; (b) d = 2; and (c) d = 3. Notice that the minimal value of N equals d - 1. limN → ∞ Sq(N)/N vanishes (diverges) if q > 1 - 1/d (q < 1 - 1/d), whereas it is finite for q = 1 - 1/d.
For a description of a strictly scale-invariant discrete model and a continuous model, see Supporting Text and Figs. 9-17, which are published as supporting information on the PNAS web site.
Final Remarks
Let us now critically re-examine the physical entropy, a concept which is intended to measure the nature and amount of our ignorance of the state of the system. As we shall see, extensivity may act as a guiding principle. Let us start with the simple case of an isolated classical system with strongly chaotic nonlinear dynamics, i.e., at least one positive Lyapunov exponent. For almost all possible initial conditions, the system quickly visits the various admissible parts of a coarse-grained phase space in a virtually homogeneous manner. Then, when the system achieves thermodynamic equilibrium, our knowledge is as meager as possible (microcanonical ensemble), i.e., just the Lebesgue measure W of the appropriate (hyper) volume in phase space (continuous degrees of freedom), or the number W of possible states (discrete degrees of freedom). The entropy is given by SBG(N) ≡ k ln W(N) [Boltzmann principle (34)].** If we consider independent equal subsystems, we have W(N) = [W(1)]N, hence SBG(N) = NSBG (1). If the N subsystems are only locally correlated, we expect W(N) ∼ μN (μ ≥ 1), hence limN→∞ SBG(N)/N = μ, i.e., the entropy is extensive (i.e., asymptotically additive).
Consider now a strongly chaotic case for which we have more information, e.g., the set of probabilities {pi} (i = 1, 2,..., W) of the states of the system. The form SBG ≡ -k 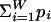 ln pi yields SBG (A + B) = SBG(A) + SBG(B) in the case of independence
ln pi yields SBG (A + B) = SBG(A) + SBG(B) in the case of independence 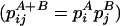 . This form, although more general than klnW (corresponding to equal probabilities), still satisfies additivity. It frequently happens, though, that we do not know the entire set {pi}, but only some constraints on this set, besides the trivial one
. This form, although more general than klnW (corresponding to equal probabilities), still satisfies additivity. It frequently happens, though, that we do not know the entire set {pi}, but only some constraints on this set, besides the trivial one 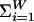 pi = 1. The typical case is Gibbs' canonical ensemble (Hamiltonian system in longstanding contact with a thermal bath), in which case we know the mean value of the energy (internal energy). Extremization of SBG yields, as well known, the celebrated BG weight, i.e., pi ∝ e-βEi, with β ≡ 1/kT and {Ei} being the set of possible energies. This distribution recovers the microcanonical case (equal probabilities) for T → ∞.
pi = 1. The typical case is Gibbs' canonical ensemble (Hamiltonian system in longstanding contact with a thermal bath), in which case we know the mean value of the energy (internal energy). Extremization of SBG yields, as well known, the celebrated BG weight, i.e., pi ∝ e-βEi, with β ≡ 1/kT and {Ei} being the set of possible energies. This distribution recovers the microcanonical case (equal probabilities) for T → ∞.
Let us now address more subtle physical systems (still within the class associated with strong chaos), namely those in which the particles are indistinguishable (bosons, fermions). This new constraint leads to a substantial modification of the description of the states of the system, and the entropy form has to be consistently modified, as shown in any textbook. These expressions may be seen as further generalizations of SBG, and the extremizing probabilities constitute, at the level of the one-particle states, generalizations of the just mentioned BG weight, recovered asymptotically at high temperatures. It is remarkable that, through these successive generalizations (and even more, since correlations due to local interactions might exist in addition to those connected with quantum statistics), the entropy remains extensive. Another subtle case is that of thermodynamic critical points, where correlations at all scales exist. There we can still refer to SBG, but it exhibits singular behavior.††
Finally, we address the completely different class of systems for which the condition of independence is severely violated (typically because the system is only weakly chaotic, i.e., its sensitivity to the initial conditions grows slowly with time, say as a power-law, with the maximal Lyapunov exponent vanishing). In such systems, long range correlations typically exist that unavoidably point toward generalizing the entropic functional, essentially because the effective number of visited states grows with N as something like a power law instead of exponentially. We exhibited here such examples for which (either exact or asymptotic) scale-invariant correlations are present. There the entropy Sq for a special value of q ≠ 1 is extensive, whereas SBG is not.
Weak departures from independence make SBG lose strict additivity, but not extensivity. Something quite analogous is expected to occur for scale-invariance in the case of Sq for q ≠ 1. Amusingly enough, we have shown (see also refs. 29 and 38) that the “nonextensive” entropy Sq—indeed nonextensive for independent subsystems—acquires extensivity in the presence of suitable asymptotically scale-invariant correlations. Thus arguments presented in the literature that involve Sq (with q ≠ 1) concomitantly with the assumption of independence should be revisited. In contrast, those arguments based on extremizing Sq, without reference to the composition of probabilities, remain unaffected. Although reference to “nonextensive statistical mechanics” still makes sense, say for long-range interactions, we see that the usual generic labeling of the entropy Sq for q ≠ 1 as “nonextensive entropy” can be misleading.
The asymptotic scale invariance on which we focus appears to be connected with the asymptotically scale-free occupation of phase space that has been conjectured (1) to be dynamically generated by the complex systems addressed by nonextensive statistical mechanics (see also refs. 39 and 40). Extensivity—together with concavity, Lesche-stability (41-43), and finiteness of the entropy production per unit time—increases the suitability of the entropy Sq for linking, with no major changes, statistical mechanics to thermodynamics.
Last but not least, the probability structure of our discrete cases is, interestingly enough, intimately related to both the Pascal and the Leibnitz triangles.
Supplementary Material
Acknowledgments
We are grateful to R. Hersh for pointing out to us that the joint-probability structure of one of our discrete models is analogous to that of the Leibnitz triangle. We have also benefited from very fruitful remarks by J. Marsh and L. G. Moyano. Y.S. was supported by the Postdoctoral Fellowship at Santa Fe Institute. Support from SI International and AFRL is acknowledged as well. Finally, the work of one of us (M.G.M.) was supported by the C.O.U.Q. Foundation and by Insight Venture Management. The generous help provided by these organizations is gratefully acknowledged.
Author contributions: C.T. and M.G.-M. designed research; C.T. and Y.S. performed research; C.T., M.G.-M., and Y.S. analyzed data; and C.T. and M.G.-M. wrote the paper.
Footnotes
In the field of cybernetics and control theory, the form 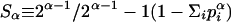 was introduced in ref. 2, and was further discussed in ref. 3. With a different prefactor, it was rediscovered in ref. 4, and further commented in ref. 5. More historical details can be found in refs. 6-8. This type of entropic form was rediscovered once again in 1988 (16-18) and it was postulated as the basis of a possible generalization of Boltzmann-Gibbs statistical mechanics, nowadays known as nonextensive statistical mechanics.
was introduced in ref. 2, and was further discussed in ref. 3. With a different prefactor, it was rediscovered in ref. 4, and further commented in ref. 5. More historical details can be found in refs. 6-8. This type of entropic form was rediscovered once again in 1988 (16-18) and it was postulated as the basis of a possible generalization of Boltzmann-Gibbs statistical mechanics, nowadays known as nonextensive statistical mechanics.
Many entropic forms are related with Sq. A special mention is deserved by the Renyi entropy 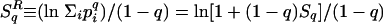 , and by the Landsberg-Vedral-Abe-Rajagopal entropy (or just normalized Sq entropy)
, and by the Landsberg-Vedral-Abe-Rajagopal entropy (or just normalized Sq entropy) 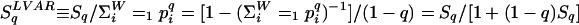 . The Renyi entropy was, according to ref. 9, first introduced in ref. 10, and then in ref. 11. The Landsberg-Vedral-Abe-Rajagopal entropy was independently introduced in ref. 12 and in ref. 13. Both
. The Renyi entropy was, according to ref. 9, first introduced in ref. 10, and then in ref. 11. The Landsberg-Vedral-Abe-Rajagopal entropy was independently introduced in ref. 12 and in ref. 13. Both 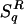 and
and 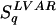 are monotonic functions of Sq; consequently, under identical constraints, they are all optimized by the same probability distribution. A two-parameter entropic form was introduced in ref. 14 which reproduces both Sq and Renyi entropy as particular cases. This scheme has been recently enlarged elegantly in ref. 15. SBG and Sq (as well as a few other entropic forms that we do not address here) are concave and Lesche-stable for all q > 0, and provide a finite entropy production per unit time;
are monotonic functions of Sq; consequently, under identical constraints, they are all optimized by the same probability distribution. A two-parameter entropic form was introduced in ref. 14 which reproduces both Sq and Renyi entropy as particular cases. This scheme has been recently enlarged elegantly in ref. 15. SBG and Sq (as well as a few other entropic forms that we do not address here) are concave and Lesche-stable for all q > 0, and provide a finite entropy production per unit time; 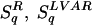 , the Sharma-Mittal, and the Masi entropic forms (as well as others that we do not address here) violate all of these properties.
, the Sharma-Mittal, and the Masi entropic forms (as well as others that we do not address here) violate all of these properties.
On the basis of what we have called here the Leibnitz rule, L. G. Moyano, C.T., and M.G.-M. (44) obtained interesting preliminary numerical results based on the so called q-product (30, 31) and its relation to the possible q-generalization of the central limit theorem. More precisely, imposing the Leibnitz rule with πN,0 -1 = p -1 ⊗ q p -1 ⊗ q... ⊗ q 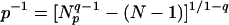 (with πN,0 = pN for q = 1), one verifies for p = 1/2 that, as N increases, the distribution probability appears to approach a q-generalized Gaussian P(n, N). The centered and rescaled distribution P(n, N) N/2 gradually becomes (say for even N) proportional to (1 - x2)1/(1 - qexp), where x ≡ [n - (N/2)]/(N/2). Numerically, the exponent appears to satisfy qexp = 2 - (1/q). This relation is obtained by applying the q → (2 - q) transformation after the q → 1/q transformation (notice that this relation can be rewritten as q = 1/(2 - qexp), which is the application of the same two transformations in the other possible order). The combinations of these two transformations define an interesting mathematical structure which might well be at the basis of the q-triplet conjectured in (32) and recently confirmed (33) with data received from the spacecraft Voyager 1 in the distant heliosphere. The q-triplet observed in the solar wind is given by qsen ≃ - 0.6 ± 0.2, qrel ≃ 3.8 ± 0.3, and qstat ≃ 1.75 ± 0.06 (33). These values are consistent with qrel + (1/qsen) = 2 and qstat + (1/qrel) = 2, hence 1 - qsen = [1 - qstat]/[3 - 2qstat]. Therefore, we expect only one q of the triplet to be independent. The most precisely determined value in ref. 33 is qstat = 1.75 = 7/4. It immediately follows that qsen = -1/2 (neatly consistent with -0.6 ± 0.2) and qrel = 4 (neatly consistent with 3.8 ± 0.3). There may be some difficulties with this approach, and efforts are being made to clear up the situation.
(with πN,0 = pN for q = 1), one verifies for p = 1/2 that, as N increases, the distribution probability appears to approach a q-generalized Gaussian P(n, N). The centered and rescaled distribution P(n, N) N/2 gradually becomes (say for even N) proportional to (1 - x2)1/(1 - qexp), where x ≡ [n - (N/2)]/(N/2). Numerically, the exponent appears to satisfy qexp = 2 - (1/q). This relation is obtained by applying the q → (2 - q) transformation after the q → 1/q transformation (notice that this relation can be rewritten as q = 1/(2 - qexp), which is the application of the same two transformations in the other possible order). The combinations of these two transformations define an interesting mathematical structure which might well be at the basis of the q-triplet conjectured in (32) and recently confirmed (33) with data received from the spacecraft Voyager 1 in the distant heliosphere. The q-triplet observed in the solar wind is given by qsen ≃ - 0.6 ± 0.2, qrel ≃ 3.8 ± 0.3, and qstat ≃ 1.75 ± 0.06 (33). These values are consistent with qrel + (1/qsen) = 2 and qstat + (1/qrel) = 2, hence 1 - qsen = [1 - qstat]/[3 - 2qstat]. Therefore, we expect only one q of the triplet to be independent. The most precisely determined value in ref. 33 is qstat = 1.75 = 7/4. It immediately follows that qsen = -1/2 (neatly consistent with -0.6 ± 0.2) and qrel = 4 (neatly consistent with 3.8 ± 0.3). There may be some difficulties with this approach, and efforts are being made to clear up the situation.
A. Einstein: “Usually W is set equal to the number of ways (complexions) in which a state, which is incompletely defined in the sense of a molecular theory (i.e. coarse grained), can be realized. To compute W one needs a complete theory (something like a complete molecular-mechanical theory) of the system. For that reason it appears to be doubtful whether Boltzmann's principle alone, i.e. without a complete molecular-mechanical theory (Elementary theory) has any real meaning. The equation S = k log W + const. appears [therefore] without an Elementary theory—or however one wants to say it—devoid of any meaning from a phenomenological point of view.” [translated by E. G. D. Cohen (34)]. A slightly different translation also is available: [“Usually W is put equal to the number of complexions.... In order to calculate W, one needs a complete (molecular-mechanical) theory of the system under consideration. Therefore it is dubious whether the Boltzmann principle has any meaning without a complete molecular-mechanical theory or some other theory which describes the elementary processes. 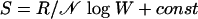 . seems without content, from a phenomenological point of view, without giving in addition such an Elementartheorie” (35)].
. seems without content, from a phenomenological point of view, without giving in addition such an Elementartheorie” (35)].
References
- 1.Gell-Mann, M. & Tsallis, C., eds. (2004) Nonextensive Entropy: Interdisciplinary Applications (Oxford Univ. Press, New York), pp. 1-422.
- 2.Harvda, J. & Charvat, F. (1967) Kybernetica 3, 30-35. [Google Scholar]
- 3.Vajda, I. (1968) Kybernetika 4, 105-110 (in Czech). [Google Scholar]
- 4.Daroczy, Z. (1970) Inf. Control 16, 36-51. [Google Scholar]
- 5.Wehrl, A. (1978) Rev. Mod. Phys. 50, 221-260. [Google Scholar]
- 6.Tsallis, C. (1995) Chaos Solitons Fractals 6, 539-559. [DOI] [PubMed] [Google Scholar]
- 7.Abe, S. & Okamoto, Y., eds. (2001) Nonextensive Statistical Mechanics and Its Applications, Lecture Notes in Physics (Springer, Heidelberg).
- 8.Tsallis, C. (2002) Chaos Solitons Fractals 13, 371-391. [Google Scholar]
- 9.Csiszar, I. (1974) in Transactions of the Seventh Prague Conference on Information Theory, Statistical Decision Functions, Random Processes, and the European Meeting of Statisticians, 1974 (Reidel, Dordrecht), pp. 73-86.
- 10.Schutzenberger, P.-M. (1954) Publ. Inst. Statist. Univ. Paris 3, 3. [Google Scholar]
- 11.Renyi, A. (1961) Proc. Fourth Berkeley Symp. 1, 547-561 (See also A. Renyi, A. (1970), Probability Theory (North-Holland, Amsterdam).) [Google Scholar]
- 12.Landsberg, P. T. & Vedral, V. (1998) Phys. Lett. A 247, 211-217. [Google Scholar]
- 13.Rajagopal, A. K. & Abe, S. (1999) Phys. Rev. Lett. 83, 1711-1714. [Google Scholar]
- 14.Sharma, B. D. & Mittal, D. P. (1975) J. Math. Sci. 10, 28-40. [Google Scholar]
- 15.Masi, M. (2005) Phys. Lett. A 338, 217-224. [Google Scholar]
- 16.Tsallis, C. (1988) J. Stat. Phys. 52, 479-487. [Google Scholar]
- 17.Curado, E. M. F. & Tsallis, C. (1991) J. Phys. A 24, L69-L72, and errata (1991) 24, 3187 and (1992) 25, 1019. [Google Scholar]
- 18.Tsallis, C., Mendes, R. S. & Plastino, A. R. (1998) Physica A 261, 534-554. [Google Scholar]
- 19.Lyra, M. L. & Tsallis, C. (1998) Phys. Rev. Lett. 80, 53-56. [Google Scholar]
- 20.Borges, E. P., Tsallis, C., Ananos, G. F. J. & Oliveira, P. M. C. (2002) Phys. Rev. Lett. 89, 254103-1-254103-4. [DOI] [PubMed] [Google Scholar]
- 21.Ananos, G. F. J. & Tsallis, C. (2004) Phys. Rev. Lett. 93, 020601-1-20601-4. [DOI] [PubMed] [Google Scholar]
- 22.Mayoral, E. & Robledo, A. (2005) Phys. Rev. E 72, 026209-1-026209-7. [DOI] [PubMed] [Google Scholar]
- 23.Casati, G., Tsallis, C. & Baldovin, F. (2005) Europhys. Lett., in press.
- 24.Watts, D. J. & Strogatz, S. H. (1998) Nature 393, 440-442. [DOI] [PubMed] [Google Scholar]
- 25.Albert, R. & Barabasi, A.-L. (2002) Rev. Mod. Phys. 74, 47-98. [Google Scholar]
- 26.Polya, G. (1962) Mathematical Discovery (Wiley, New York), Vol. 1, p. 88. [Google Scholar]
- 27.Plastino, A. R. & Plastino, A. (1995) Physica A 222, 347-354. [Google Scholar]
- 28.Tsallis, C. & Bukman, D. J. (1996) Phys. Rev. E 54, R2197-R2200. [DOI] [PubMed] [Google Scholar]
- 29.Tsallis, C. (2005) Milan J. Math. 73, in press.
- 30.Nivanen, L., Le Mehaute, A. & Wang, Q. A. (2003) Rep. Math. Phys. 52, 437-444. [Google Scholar]
- 31.Borges, E. P. (2004) Physica A 340, 95-101. [Google Scholar]
- 32.Tsallis, C. (2004) Physica A 340, 1-10. [Google Scholar]
- 33.Burlaga, L. F. & Vinas, A. F. (2005) Physica A 356, 375-384. [Google Scholar]
- 34.Cohen, E. G. D. (2005) Pramana J. Phys. 64, 635-642. [Google Scholar]
- 35.Pais, A. (1982) Subtle Is the Lord: The Science and the Life of Albert Einstein (Oxford Univ. Press, New York).
- 36.Robledo, A. (2004) Physica A 344, 631-636. [Google Scholar]
- 37.Robledo, A. (2005) Mol. Phys., in press.
- 38.Tsallis, C. (2005) in Complexity, Metastability and Nonextensivity, eds. Beck, C., Benedek, G., Rapisarda, A. & Tsallis, C. (World Scientific, Singapore), pp. 13-32.
- 39.Soares, D. J. B., Tsallis, C., Mariz, A. M. & Silva, L. R. (2005) Europhys. Lett. 70, 70-76. [Google Scholar]
- 40.Thurner, S. & Tsallis, C. (2005) Europhys. Lett. 72, 197-203. [Google Scholar]
- 41.Lesche, B. (1982) J. Stat. Phys. 27, 419-422. [Google Scholar]
- 42.Abe, S. (2002) Phys. Rev. E 66, 046134-1-046134-6. [Google Scholar]
- 43.Lesche, B. (2004) Phys. Rev. E 70, 017102-1-017102-4. [DOI] [PubMed] [Google Scholar]
- 44.Moyano, L. G., Tsallis, C. & Gell-Mann, M. (2005) arXiv: cond-mat/0509229.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.