Abstract
Formation of a water-expelling nonpolar core is the paradigm of protein folding and stability. Although experiment largely confirms this picture, water buried in “hydrophobic” cavities is required for the function of some proteins. Hydration of the protein core has also been suggested as the mechanism of pressure-induced unfolding. We therefore are led to ask whether even the most nonpolar protein core is truly hydrophobic (i.e., water-repelling). To answer this question we probed the hydration of an ≈160-Å3, highly hydrophobic cavity created by mutation in T4 lysozyme by using high-pressure crystallography and molecular dynamics simulation. We show that application of modest pressure causes approximately four water molecules to enter the cavity while the protein itself remains essentially unchanged. The highly cooperative filling is primarily due to a small change in bulk water activity, which implies that changing solvent conditions or, equivalently, cavity polarity can dramatically affect interior hydration of proteins and thereby influence both protein activity and folding.
Keywords: hydrophobic effect, T4 lysozyme
Internal protein hydration, its contribution to folding mechanisms, and the polarity of the protein interior in general are fundamental to protein structure and function. Despite the general success of hydrophobic models (1–3), attempts to determine the interior “hydrophobicity” of proteins have often given conflicting results (2, 4–10). Some proteins seem to require water at least transiently in nonpolar cavities for their function (11, 12). Moreover, the responses of proteins to pressure are not in accord with simple hydrophobic models (13); as a result, hydration of the protein core has been suggested as the mechanism of pressure-induced unfolding (14).
Additional progress will require direct measurement of the free energy needed to insert water molecules into a nonpolar protein cavity. Such an experiment requires sufficient structural resolution to unambiguously locate water molecules, the ability to resolve small changes in structure and occupancy, and the means to bias the occupancy while minimally perturbing the protein. Protein crystallography can detect changes in cavity hydration directly, but the temperature or chemical perturbations useful in solution thermodynamic measurements frequently damage crystals. We have found that high pressures of up to several hundred megapascals generally do not damage crystals (15, 16). High-pressure crystallography makes it possible to shift the equilibrium to interesting, unexplored protein states.
The ≈160-Å3 cavity containing mutant L99A of T4 lysozyme studied here was originally produced to probe the stabilizing interactions between buried nonpolar residues (2, 17). The Leu-99 → Ala mutation creates a large cavity that destabilizes the folded protein because of lost interactions between side chains and the reduced free-energy cost of exposing alanine (instead of leucine) to water (17). L99A T4 lysozyme has also been the subject of ligand- and noble-gas–binding studies (18–20) and is believed to be entirely empty under ambient conditions. Under pressure, one may expect a large cavity, similar to that produced by the L99A mutation, to collapse. Indeed, this was the original impetus to study this mutant under pressure. Instead, we find this cavity to be remarkably rigid and to fill with water at ≈150 MPa. It provides an excellent system in which to examine the interactions of water with surrounding protein.
Methods
High-Pressure Crystallography. Crystals were grown in space group P3221 as described (2). Crystallographic experiments were performed by using a beryllium cell described by Urayama et al. (15). The cell is a rod that is 6.35 mm in diameter and 25 mm long with a 1 × 19-mm bore on axis. The bore is sized to hold a glass capillary containing 0.7- to 1-mm crystals surrounded by a mixture of Sephadex and mother liquor, which supports and transmits pressure to the crystals while keeping them hydrated. Pieces of copper wire separate the crystals; x-ray shadows of the wires are useful for locating crystals once in the optically opaque cell. The cell is connected with a homemade adapter and standard high-pressure fittings to a hand-cranked liquid high-pressure press (High Pressure Equipment Company, Erie, PA) that is capable of reaching 200 MPa. The system is sealed and pressurized at least 30 min before data collection. Reversibility was ensured by examining the data collected on crystals at atmospheric pressure and on pressurized crystals after pressure release. In all cases, data at a given pressure refine to models more similar to each other than refined models from other pressures. Data were otherwise collected by using standard protocols at the F1 station of the Cornell High Energy Synchrotron Source and refined with the ccp4 suite (21) from Protein Data Bank structure 1L90. Resolution was limited to ≈2.1 Å by beryllium powder diffraction. Table 1 lists refinement statistics and unit-cell parameters at each pressure.
Table 1. X-ray refinement statistics.
| Pressure, MPa | 0.1 | 100 | 150 | 200 |
| Number of data sets | 3 | 3 | 1 | 3 |
| Resolution, Å | 2.3 | 2.1 | 2.1 | 2.1 |
| Unit-cell parameters | ||||
| a = b, Å | 60.96 | 60.76 | 60.68 | 60.61 |
| c, Å | 96.60 | 96.07 | 95.80 | 95.65 |
| Rwork | 0.15 | 0.17 | 0.16 | 0.16 |
| Rfree | 0.21 | 0.22 | 0.21 | 0.20 |
| Number of atoms | 1,407 | 1,473 | 1,475 | 1,497 |
| Protein | 1,289 | 1,289 | 1,289 | 1,289 |
| Ligand/ion | 10 | 10 | 10 | 10 |
| Water | 108 | 174 | 176 | 198 |
| B factors, Å2 | ||||
| Protein | 25.4 | 22.7 | 22.5 | 22.6 |
| Ligand/ion | 79.8 | 69.7 | 84.4 | 77.4 |
| Water | 45.4 | 44.0 | 45.4 | 45.5 |
| rms deviations | ||||
| Bond lengths, Å | 0.020 | 0.018 | 0.016 | 0.016 |
| Bond angles, ° | 1.58 | 1.53 | 1.44 | 1.36 |
Values are averaged over the data sets collected at each pressure.
Cavity Measurement and Construction of Difference-Density Maps. Observed difference electron-density maps are constructed as (Fo,hp – Fo,0.1 MPa)αcalc for each pair of data sets. Fo,hp and Fo,0.1 MPa are the experimentally measured structure factors at high pressure and 0.1 MPa. αcalc are phases calculated from the ambient pressure structure. Observed structure factors are scaled to calculated structure factors to put them on an absolute scale. Because the unit cell decreases in size by as much as 1 Å as pressure increases, the highest-resolution data yield only noise in the maps. We limited the resolution used in the maps to 4 Å for this reason. B factors of atoms surrounding the cavity are among the lowest in the model, excluding the possibility of partial cavity-wall collapse. Maps were masked by using cavity descriptions that were generated with the program voidoo (22) using a probe radius of 1.2 Å and standard optimized potentials for liquid simulations (OPLS) atomic radii. The masked maps were integrated by using the program mapman (23) and finally averaged over all data sets.
Molecular Dynamics Simulations. Molecular dynamics (MD) simulations of T4 lysozyme mutant L99A were performed with the amber 6.0 code (University of California, San Francisco) and parm94 force field (24). The initial structure (PDB ID code 1L90) was solvated by 4,964 three-point transferable intermolecular potential (TIP3P) water molecules (25) and 18 sodium and 27 chloride ions in an ≈52 × 54 × 63-Å3 rectangular box. After energy minimization, equilibrium MD simulations were performed at constant temperature (300 K) and pressure (0.1 and 200 MPa) with periodic boundary conditions, particle-mesh Ewald summation, and a 1-fs time step. After 54 ps of MD simulations at 0.1 MPa with an empty cavity, water molecules were transferred from the surrounding bulk into the cavity to create states with occupancy n = 1, 2, 3, 4, and 5. Those configurations were equilibrated for 50 to 300 ps, followed by production runs of 1- to 1.7-ns duration. Structures were saved for analysis every 0.5 ps. For of each of the 18 runs (three pressures, n = 0, 1,..., 5), the MD structures averaged over the final 0.25 ns deviated by <0.7 Å from the x-ray structure (rms deviation of all α carbons) and <0.55 Å for the N- and C-terminal domains, respectively, alone (residues 10–60 and 80–160).
Thermodynamics of Water Filling. The thermodynamics of cavity filling is determined effectively by a “grand-canonical partition function” for water molecules inside the cavity (17). The occupancy probabilities P(N) of having exactly N water molecules in the cavity are related through
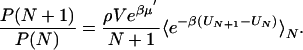 |
[1] |
P(0) is determined by normalization, 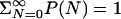 . V is a spherical volume with a radius of6Åcovering the cavity whose center is the instantaneous positional average of selected Cα atoms of residues lining the cavity. ρ and μ′ are the number density and excess chemical potential of bulk water at ambient conditions, respectively. The canonical average 〈... 〉N is over the Boltzmann factor of the potential-energy change ΔU = UN+1 – UN of randomly inserting a water molecule into V, already occupied by N water molecules. ΔU includes interactions with protein and solvent. We evaluate the canonical average by using Bennett's method of overlapping histograms for the water-insertion and -removal energies, pins(u) and prem(u), respectively (17). The ratio pins(u)/prem(u) is equal to exp(βΔU) times the average in Eq. 1. For the chemical potential of the reference bulk fluid at ambient conditions, we use the previously calculated μ′=–25.3 kJ/mol and ρ = 33.33 nm–3 (10). At higher pressures, we calculated the equation of state ρ(p, T = 298 K) of three-point transferable intermolecular potential (TIP3P) water from constant-pressure simulations. Integration then gives the change of the total bulk chemical potential,
. V is a spherical volume with a radius of6Åcovering the cavity whose center is the instantaneous positional average of selected Cα atoms of residues lining the cavity. ρ and μ′ are the number density and excess chemical potential of bulk water at ambient conditions, respectively. The canonical average 〈... 〉N is over the Boltzmann factor of the potential-energy change ΔU = UN+1 – UN of randomly inserting a water molecule into V, already occupied by N water molecules. ΔU includes interactions with protein and solvent. We evaluate the canonical average by using Bennett's method of overlapping histograms for the water-insertion and -removal energies, pins(u) and prem(u), respectively (17). The ratio pins(u)/prem(u) is equal to exp(βΔU) times the average in Eq. 1. For the chemical potential of the reference bulk fluid at ambient conditions, we use the previously calculated μ′=–25.3 kJ/mol and ρ = 33.33 nm–3 (10). At higher pressures, we calculated the equation of state ρ(p, T = 298 K) of three-point transferable intermolecular potential (TIP3P) water from constant-pressure simulations. Integration then gives the change of the total bulk chemical potential, 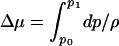 . At p1 = 100 and 200 MPa, we obtain Δμ = 1.82 and 3.64 kJ/mol, respectively, where exp(βΔμ) = [ρ2exp(βμ′2)]/[ρ1exp(βμ′1)]. The average occupancy is
. At p1 = 100 and 200 MPa, we obtain Δμ = 1.82 and 3.64 kJ/mol, respectively, where exp(βΔμ) = [ρ2exp(βμ′2)]/[ρ1exp(βμ′1)]. The average occupancy is 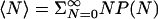 and can be calculated directly at the simulation pressures. At intermediate pressures we use perturbation theory at ≈200 MPa.
and can be calculated directly at the simulation pressures. At intermediate pressures we use perturbation theory at ≈200 MPa.
Results
The crystal structure of the cavity containing mutant L99A T4 lysozyme was determined at four different pressures by using 10 separate x-ray-diffraction data sets. Comparison of individual structures at any given pressure indicates that the uncertainty of backbone atom equilibrium positions is <0.1 Å. A number of small but statistically significant changes occur as the pressure increases from 0.1 MPa (atmospheric pressure) to 200 MPa. The largest of these changes includes displacement of the α/β N-terminal domain (residues 10–58) relative to the C-terminal domain (residues 80–162) by ≈0.25 Å and deformation of one end of helix C (at approximately residues 76–80) by ≈0.25 Å toward the main cavity. Despite these changes and other smaller deformations (≤0.15 Å) in the C-terminal domain, the cavity volume decreases by <3% up to 200 MPa. This essentially pressure-independent protein structure is an ideal system in which we can study interior hydration as a function of water activity, modulated here by pressure. As the pressure increases to 200 MPa, the principal change in the system is the increase in chemical potential of water, Δμwat = 1.4 kBT (1 kBT ≈ 2.5 kJ/mol at room temperature).
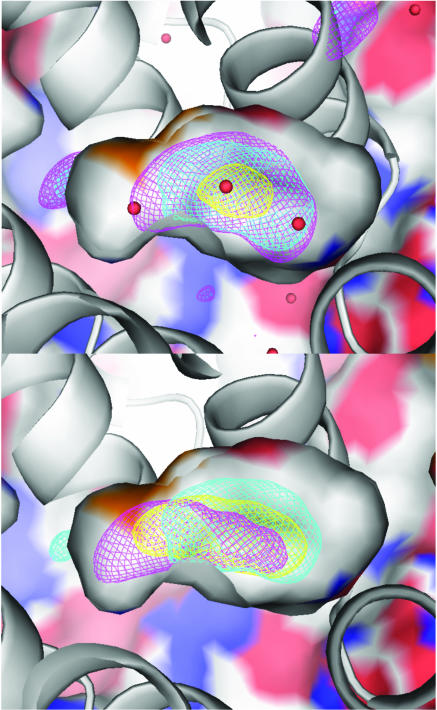
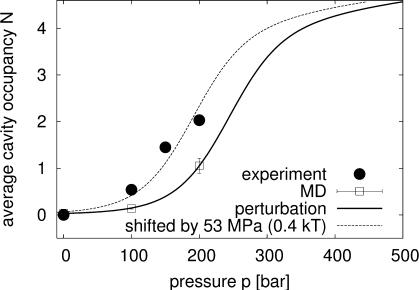
To locate possible water in the cavity, we constructed the obser ved electron-density difference maps (Fo,hp – Fo,0.1 MPa)αc,0.1 MPa (see Methods) at 100, 150, and 200 MPa. Maps averaged in real space over data at constant pressure are shown in Fig. 1. The maps were integrated over the cavity volume to obtain the average occupancies (Fig. 2). The principal feature in the maps is an increased electron density in the cavity, particularly at 150 and 200 MPa. At 100 MPa only a small peak is observed, corresponding to an average cavity occupancy of ≈0.5 water molecules (Fig. 2). This peak rapidly swells into a broad distribution at 150 MPa, increasing further to an average of approximately two water molecules in the cavity at 200 MPa. The average occupancy at 200 MPa together with the electron-density difference maps indicate a cooperative transition into a variety of configurations of at least two, and possibly as many as four, water molecules in the cavity.
Fig. 1.
Electron density in the main cavity of T4 lysozyme mutant L99A at high pressure. Helix E is shown behind a cut-away view of the ≈160-Å3 cavity. (A) Experimental density at 100 MPa (yellow), 150 MPa (cyan), and 200 MPa (magenta) is contoured at 0.1 electrons per Å3. (B) Experimental electron density at 150 MPa (cyan) compared with simulation density at 200 MPa (magenta), contoured at 0.1 electrons per Å3, viewed as described above. The distribution of atoms at 100 MPa (using the occupancies of N = 1, 2, 3, 4, 5 at 200 MPa) is shown in yellow for comparison. [The figures were made with pymol (http://pymol.sourceforge.net).]
Fig. 2.
Average number of water molecules inside the cavity as a function of pressure. Solid circles show the results from x-ray crystallography, dividing the integrated electron density by 10 electrons per water molecule. The open squares show the average occupancies calculated from the MD simulations. The solid line is the result of perturbation theory about the ≈200-MPa simulation reference state. Shifting the pressure by 53 MPa (or ≈0.4 kBT) produces the dashed line.
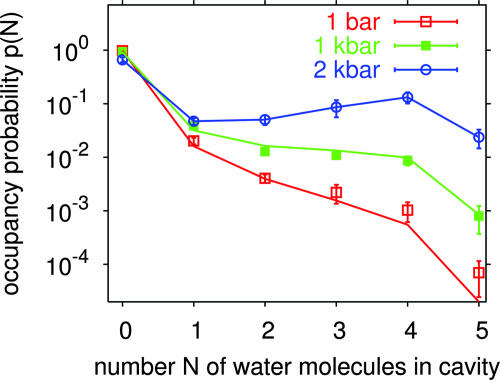
To explore the energetics and dynamics of interior water, we performed MD simulations of solvated T4 lysozyme at pressures of 0.1, 100, and 200 MPa, with cavity occupancies between zero and five water molecules. By constructing what is effectively a grand-canonical partition function of cavity water, we obtain the pressure-dependent equilibrium occupancy distributions. As shown in Figs. 2 and 3, the calculations indicate a sharp transition from a predominantly empty cavity at pressures below ≈100 MPa to a cavity cooperatively filled by approximately four water molecules at pressures above ≈200 MPa. The calculated electron densities (Fig. 1) and average occupancies (Fig. 2) are in good agreement with the experiments after shifting the chemical potential of the bulk water phase (or, equivalently, the average interaction energy of water with the protein cavity) by ≈0.4 kBT (1 kJ/mol).
Fig. 3.
Probability distribution (logarithmic scale) of the number N of water molecules in the cavity from computer simulations. Symbols show results from MD simulations at 0.1, 100, and 200 MPa. Lines are the results of perturbation theory using the 200-MPa simulations as a reference point. Error bars indicate statistical uncertainties corresponding to one estimated standard deviation.
The MD simulations indicate that water molecules confined to the cavity fluctuate between one-dimensional wires and closed hydrogen-bonded rings of four and five water molecules, as seen in experiments on gas-phase water clusters and simulations of confined water (26). Additional hydrogen bonds are formed with the backbone carbonyl oxygen of Ala-99.
During two simulations a water molecule escaped the cavity, one after ≈0.5 ns in the occupancy N = 1 simulation and one in the N = 5 simulation after 0.9 ps, both at atmospheric pressure (105 Pa). In each case, water escaped through a transient opening between the side chains of Phe-114, Ser-116, Asn-132, and Leu-133. The escaping water molecule transiently occupied the crystallographic water site Wat-196. Water escape is coupled to protein dynamics, in particular, motions of Phe-114. Indeed, the Phe-114 side-chain crystallographic B factors, a measure of atomic fluctuations, are almost twice as large as those of the four other phenylalanines in the L99A crystal structure. The water-escape route from our simulations corroborates earlier NMR data that suggested a pathway for binding of nonpolar molecules near the F and G helices (19).
We find that a small change of the chemical potential of water in the bulk phase (Δμwat ≈ 1.4 kBT at 293 K between 0.1 and 200 MPa) is sufficient to induce ≈50% filling of the cavity, on average. Such biphasic, environment-dependent behavior finds support in the coexistence of liquid and vapor water under ambient conditions (27). Consequently, filling under near ambient conditions could also be induced by lowering the average interaction energy of water with the surrounding protein through changes in the electrostatic environment of the cavity. The free energy of dissolving water into oil is remarkably high and largely an entropic penalty because of the formation of a water-sized cavity in oil. What contributes to the much more favorable free energy of transferring a water molecule into the protein?
Our MD simulations suggest that a significant part of the free energy comes from hydrogen bonds between multiple water molecules in the cavity, explaining the cooperativity of the transition. This cooperativity is reflected in the average potential energy of water in the cavity, which decreases from –23 kJ/mol (N = 1) to –60 kJ/mol (N = 4) per molecule, or approximately –10 kJ/mol per water–water hydrogen bond. Van der Waals interactions with the surrounding medium account for an additional approximately –10 kJ/mol per water molecule. Other electrostatic interactions with the protein should also contribute, as will entropy from the static-free volume of the preexisting cavity. The subtle thermodynamics of filling show that a simple description of the interior as hydrophobic fails to capture all of its relevant features.
Our results have direct implications for pressure unfolding of proteins. The observation that pressure unfolds most proteins is seemingly at odds with predictions from the hydrophobic effect (13), which suggest that the transfer of hydrocarbons into water should be unfavorable at typical unfolding pressures. The paradox can be resolved by noting that the pressure-unfolded state is relatively compact compared to its thermally denatured counterpart (14). It was predicted that the pressure-unfolded state corresponded to extensive hydration of the protein interior rather than transfer of buried hydrophobic residues into bulk water. Our experimental evidence of pressure-induced filling of an existing nonpolar cavity supports this hypothesis by demonstrating that the free-energy penalty of filling a cavity is small or even zero at low pressures. At higher pressures, cavity filling should become so favorable that new cavities will grow to accommodate water and the protein will partially unfold. Even at lower pressures, our work supports the idea that collapsed intermediate states in protein folding may be hydrated internally (4, 28, 29) and that dehydration may be a rate-limiting step in folding (4, 29–31).
Pressure-induced hydration may help explain why many proteins undergo large changes in activity under pressure (32). Interactions between water and protein hydrophobic surfaces is particularly important for molecular interfaces in ligand or substrate binding and complex formation (33) and in multidomain protein folding (30). Changes in the interior hydration also affect enzymatic function. Weakly screened electrostatic interactions in the protein interior provide a strong coupling between charge sites and internal water. Consequently, changes in protein conformation and charge states during enzyme turnover directly influence the free energy of water in the low-polarizability protein interior, with implications for protein function. Cytochrome P450 (11) and bacteriorhodopsin (12) are examples in which changes in redox states and amino acid protonation determine the presence or absence of functional water.
Acknowledgments
M.D.C. is indebted to Chris Heaton, Bill Miller, Marian Szebenyi, and David Schuller of MacCHESS for assistance with this work and Nozomi Ando and Gil Toombes for many helpful conversations and encouragement. G.H. thanks J. C. Rasaiah, S. Vaitheeswaran, and H. Yin for many helpful discussions. This work was supported by Department of Energy-Biological and Environmental Research Grant FG02-97ER62443 (to S.M.G.) and National Institutes of Health Grant GM21967 (to B.W.M.). The Cornell High Energy Synchrotron Source is supported by the National Science Foundation and National Institutes of Health through National Science Foundation Grant DMR-0225180. G.H. acknowledges support by the intramural research program of the National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases.
Author contributions: M.D.C., M.L.Q., G.H., and B.W.M. designed research; M.D.C., G.H., and M.L.Q. performed research; G.H. contributed new reagents/analytic tools; M.D.C., M.L.Q., B.W.M., G.H., and S.M.G. analyzed data; and M.D.C., G.H., and B.W.M. wrote the paper.
Conflict of interest statement: No conflicts declared.
Abbreviation: MD, molecular dynamics.
Data deposition: The atomic coordinates and structure factors have been deposited in the Protein Data Bank, www.pdb.org (PDB ID codes 2B6T, 2B6W, 2B6X, 2B6Y, 2B6Z, 2B70, 2B72, 2B73, 2B74, and 2B75).
References
- 1.Dill, K. A. (1990) Biochemistry 29, 7133–7155. [DOI] [PubMed] [Google Scholar]
- 2.Eriksson, A. E., Baase, W. A., Zhang, X. J., Blaber, M., Baldwin, E. P. & Matthews, B. W. (1992) Science 255, 178–183. [DOI] [PubMed] [Google Scholar]
- 3.Zhang, L. & Hermans, J. (1996) Proteins 24, 433–438. [DOI] [PubMed] [Google Scholar]
- 4.Buckle, A. M., Cramer, P. & Fersht, A. R. (1996) Biochemistry 35, 4298–4305. [DOI] [PubMed] [Google Scholar]
- 5.Denisov, V. P., Schlessman, J. L., Garcia-Moreno, E. B. & Halle, B. (2004) Biophys. J. 87, 3982–3994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yu, B., Blaber, M., Gronenborn, A. M., Clore, G. M. & Caspar, D. L. (1999) Proc. Natl. Acad. Sci. USA 96, 103–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ernst, J. A., Clubb, R. T., Zhou, H. X., Gronenborn, A. M. & Clore, G. M. (1995) Science 270, 1848–1849. [DOI] [PubMed] [Google Scholar]
- 8.Olano, L. R. & Rick, S. W. (2004) J. Am. Chem. Soc. 126, 7991–8000. [DOI] [PubMed] [Google Scholar]
- 9.Beckstein, O., Biggin, P. C. & Sansom, M. S. P. (2001) J. Phys. Chem. B 105, 12902–12905. [Google Scholar]
- 10.Hummer, G., Rasaiah, J. C. & Noworyta, J. P. (2001) Nature 414, 188–190. [DOI] [PubMed] [Google Scholar]
- 11.Schlichting, I., Berendzen, J., Chu, K., Stock, A. M., Maves, S. A., Benson, D. E., Sweet, R. M., Ringe, D., Petsko, G. A. & Sligar, S. G. (2000) Science 287, 1615–1622. [DOI] [PubMed] [Google Scholar]
- 12.Schobert, B., Brown, L. S. & Lanyi, J. K. (2003) J. Mol. Biol. 330, 553–570. [DOI] [PubMed] [Google Scholar]
- 13.Kauzmann, W. (1987) Nature 325, 763–764. [Google Scholar]
- 14.Hummer, G., Garde, S., Garcia, A. E., Paulaitis, M. E. & Pratt, L. R. (1998) Proc. Natl. Acad. Sci. USA 95, 1552–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Urayama, P., Phillips, G. N. & Gruner, S. M. (2002) Structure (London) 10, 51–60. [DOI] [PubMed] [Google Scholar]
- 16.Kundrot, C. E. & Richards, F. M. (1987) J. Mol. Biol. 193, 157–170. [DOI] [PubMed] [Google Scholar]
- 17.Eriksson, A. E., Baase, W. A. & Matthews, B. W. (1993) J. Mol. Biol. 229, 747–769. [DOI] [PubMed] [Google Scholar]
- 18.Morton, A., Baase, W. A. & Matthews, B. W. (1995) Biochemistry 34, 8564–8575. [DOI] [PubMed] [Google Scholar]
- 19.Mulder, F. A. A., Mittermaier, A., Hon, B., Dahlquist, F. W. & Kay, L. E. (2001) Nat. Struct. Biol. 8, 932–935. [DOI] [PubMed] [Google Scholar]
- 20.Quillin, M. L., Breyer, W. A., Griswold, I. J. & Matthews, B. W. (2000) J. Mol. Biol. 302, 955–977. [DOI] [PubMed] [Google Scholar]
- 21.Collaborative Computational Project, Number 4 (1994) Acta Crystallogr. D 50, 760–763.15299374 [Google Scholar]
- 22.Kleywegt, G. J. & Jones, T. A. (1994) Acta Crystallogr. D 50, 178–185. [DOI] [PubMed] [Google Scholar]
- 23.Kleywegt, G. J. & Jones, T. A. (1996) Acta Crystallogr. D 52, 826–828. [DOI] [PubMed] [Google Scholar]
- 24.Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz, K. M., Fergurson, D. M., Spellmeyer, D. C., Fox, T., Caldwell, J. W. & Kollman, P. A. (1995) J. Am. Chem. Soc. 117, 5179–5197. [Google Scholar]
- 25.Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W. & Klein, M. L. (1983) J. Chem. Phys. 79, 926–935. [Google Scholar]
- 26.Vaitheeswaran, S., Yin, H., Rasaiah, J. C. & Hummer, G. (2004) Proc. Natl. Acad. Sci. USA 101, 17002–17005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lum, K., Chandler, D. & Weeks, J. D. (1999) J. Phys. Chem. 103, 4570–4577. [Google Scholar]
- 28.Cheung, M. S., Garcia, A. E. & Onuchic, J. N. (2002) Proc. Natl. Acad. Sci. USA 99, 685–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Staniforth, R. A., Dean, J. L. E., Zhong, Q., Zerovnik, E. & Clarke, A. R. (2000) Proc. Natl. Acad. Sci. USA 97, 5790–5795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhou, R., Huang, X., Margulis, C. J. & Berne, B. J. (2004) Science 305, 1605–1609. [DOI] [PubMed] [Google Scholar]
- 31.Woenckhaus, J., Kohling, R., Thiyagarajan, P., Littrell, K. C., Seifert, S., Royer, C. A. & Winter, R. (2001) Biophys. J. 80, 1518–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mozhaev, V. V., Heremans, K., Frank, J., Masson, P. & Balny, C. (1996) Proteins Struct. Funct. Genet. 24, 81–91. [DOI] [PubMed] [Google Scholar]
- 33.Harries, D., Rau, D. C. & Parsegian, V. A. (2005) J. Am. Chem. Soc. 127, 2184–2190. [DOI] [PubMed] [Google Scholar]